Discovery of Regular Daily Ionospheric Scintillation
Abstract
1. Introduction
2. Data and Methods
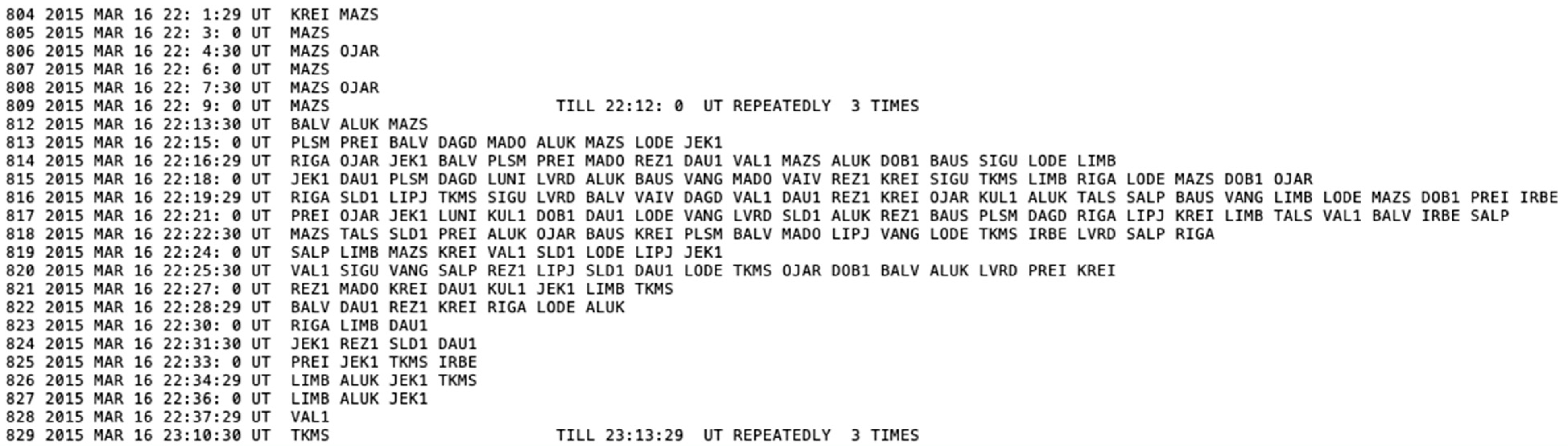
2.1. Ionospheric Scintillation Waves
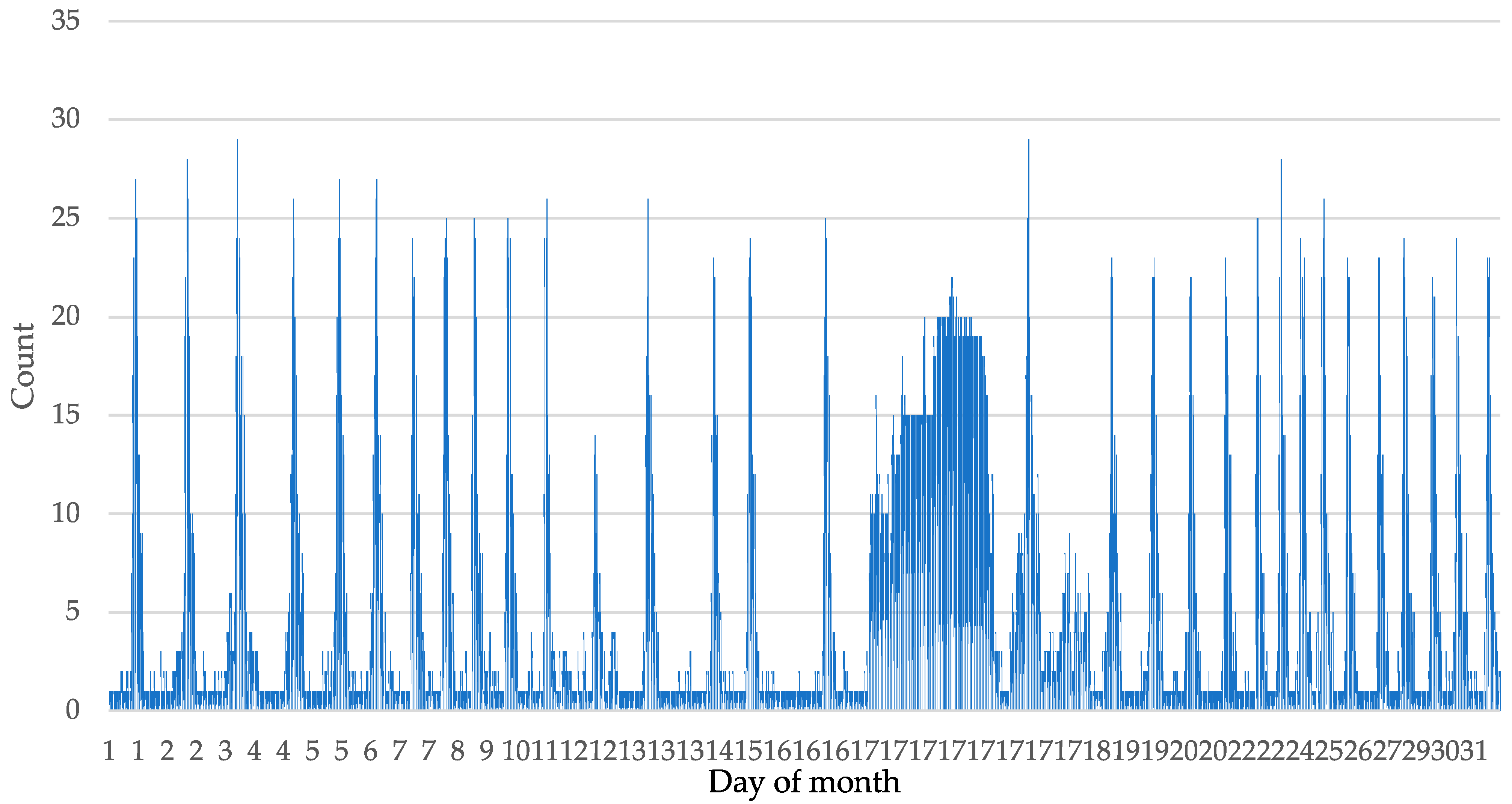
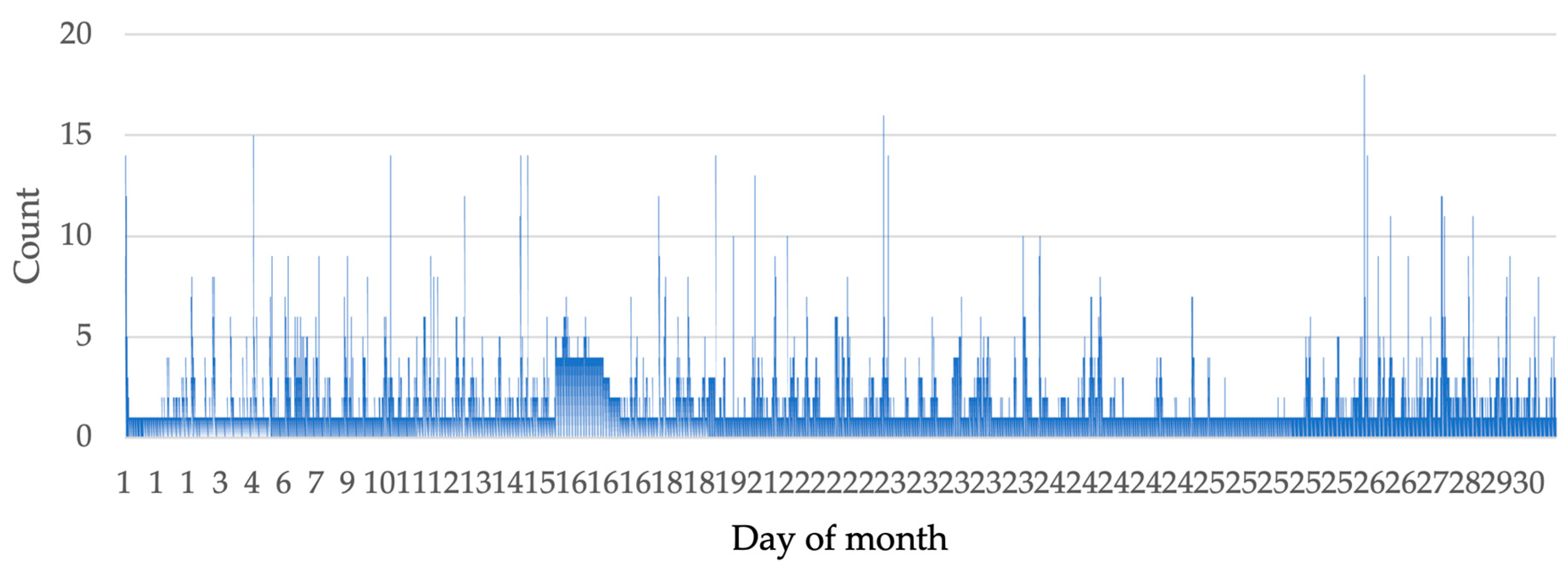
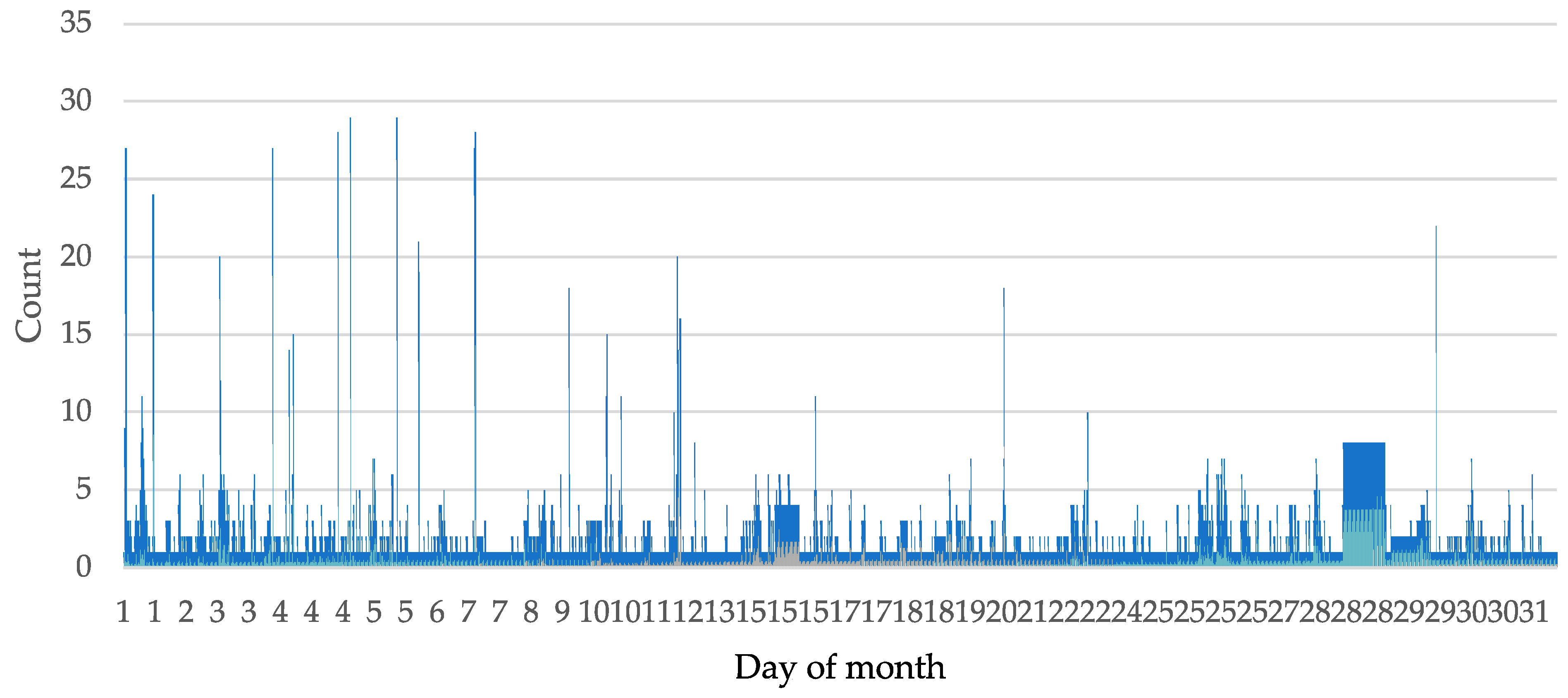
2.2. Graphical Representation of the Registered Ionospheric Wave Sets over the Month
2.3. The Classification of the Characteristic Elements of the Waves of Ionospheric Scintillation Clouds
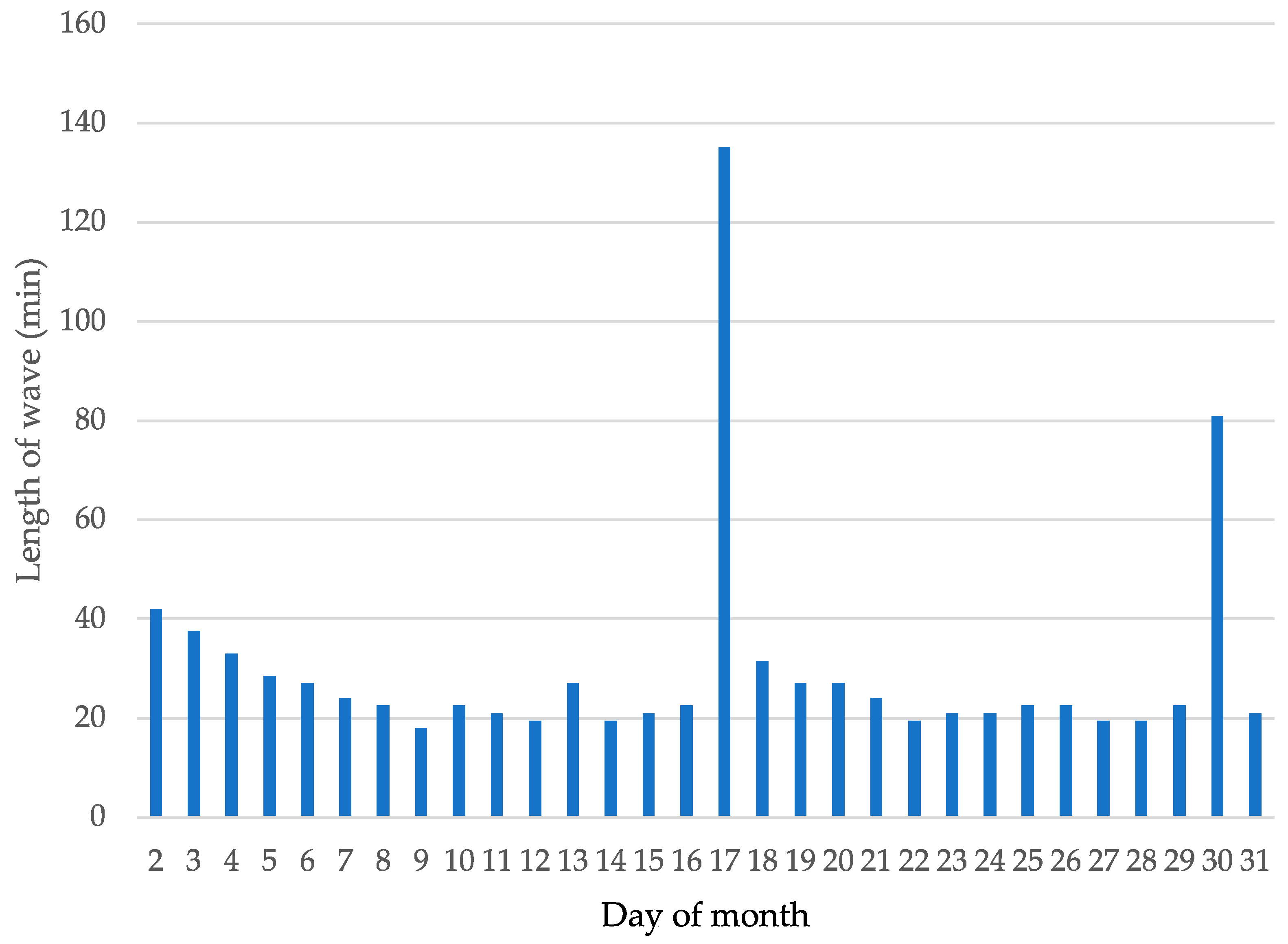
2.4. Characteristics of Regular Daily Wave Elements in March 2015
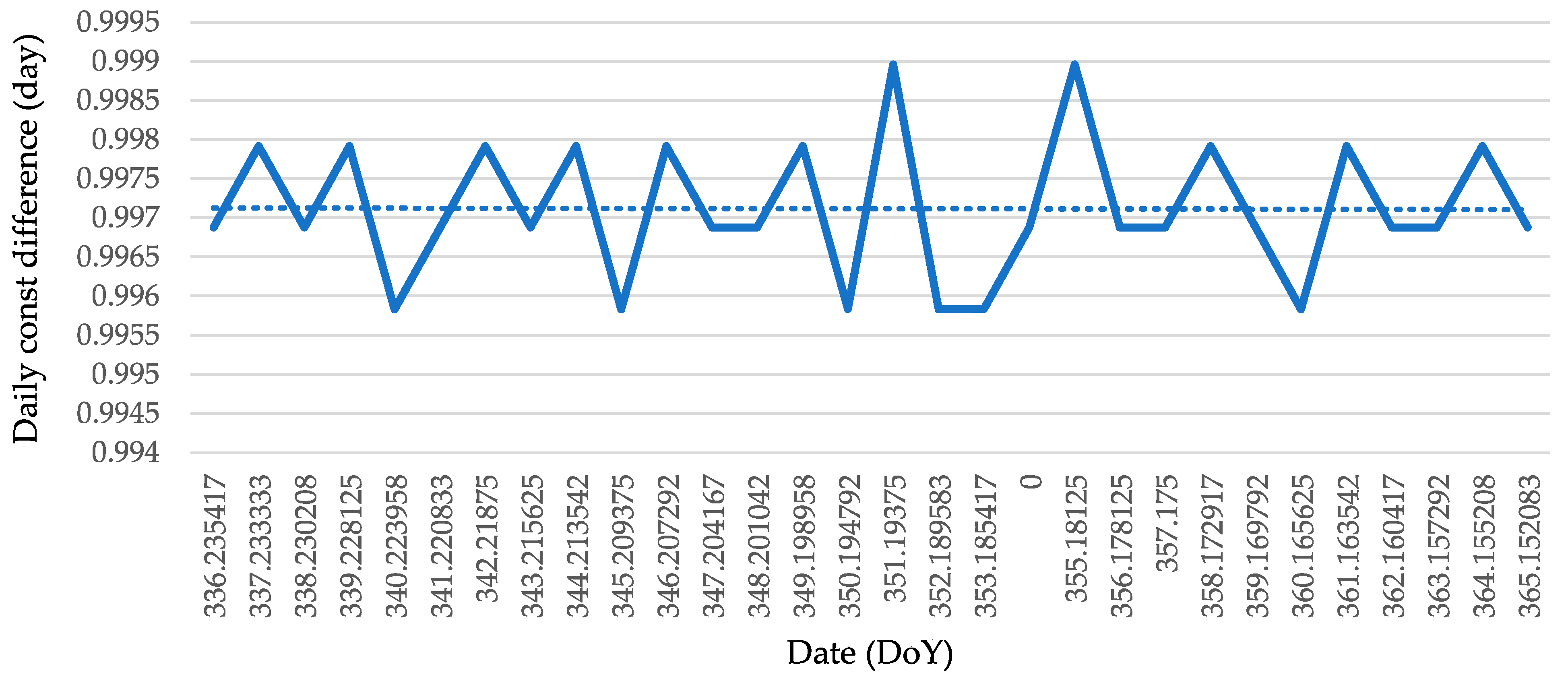
2.5. Search for Regular Daily Waves
2.6. ROTI@ground and Positioning Errors
3. Results
3.1. Linear Approximation
3.2. Solar Activity and Length of Regular Ionospheric Scintillation Waves
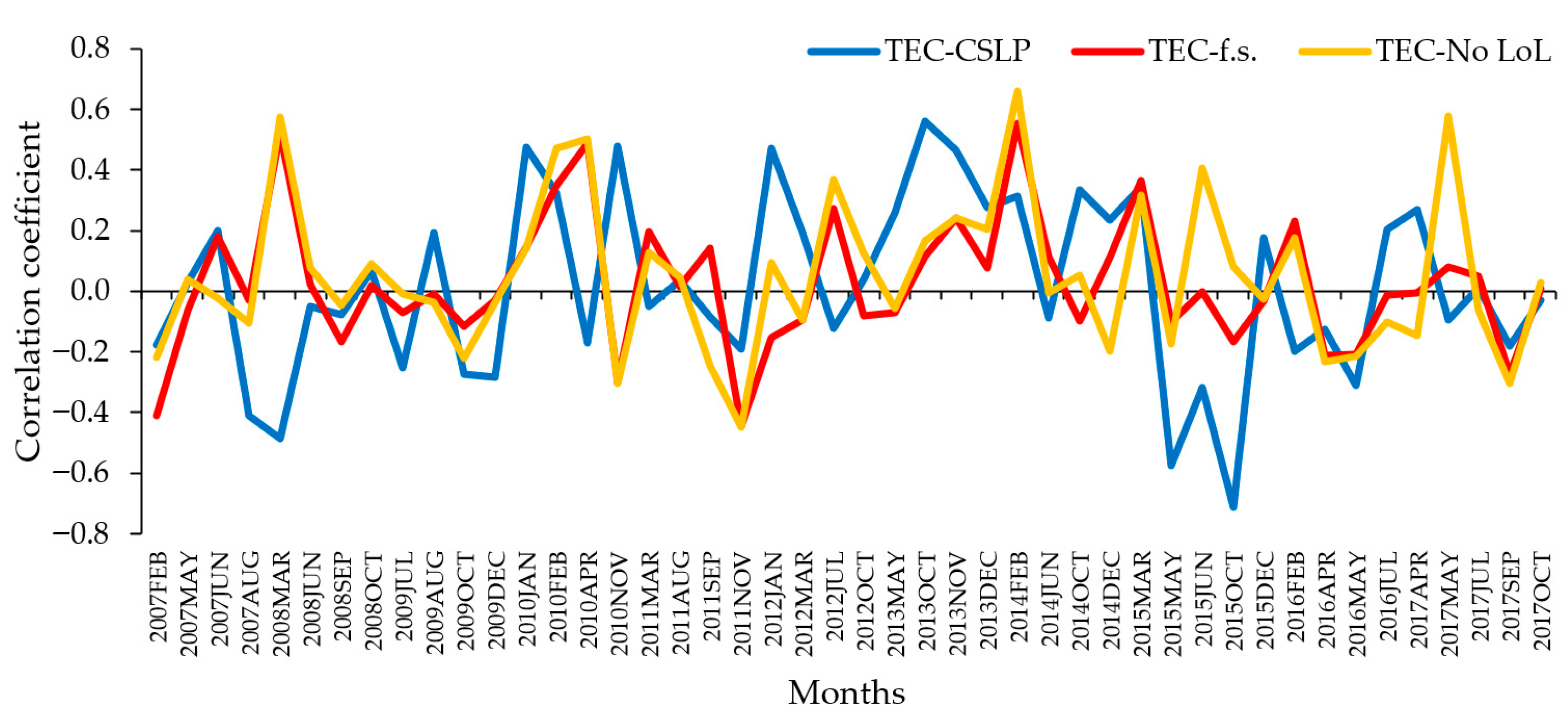
3.3. Pearson’s Correlation
- TEC-max over the territory of Latvia;
- The mean value of cycle slip counts found with Bernese GNSS software v5.2 for all volumes of reduced solutions, including faulty solutions (CSLP);
- The mean count of faulty solutions (F.sol.);
- The mean count of cycle slips discovered using the Bernese GNSS software v5.2 for faulty solutions.
3.4. The Impact of Daily Regular Ionospheric Waves on Positioning Accuracy
3.5. Time Lag of Daily Regular Ionospheric Scintillation Waves
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 135 | 56,809.751042 | 2014 JUN | 1 | 18:1:30 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 136 | 56,809.752083 | 2014 JUN | 1 | 18:3:0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 137 | 56,809.753125 | 2014 JUN | 1 | 18:4:30 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 138 | 56,809.754167 | 2014 JUN | 1 | 18:6:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 139 | 56,809.755208 | 2014 JUN | 1 | 18:7:29 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 140 | 56,809.756250 | 2014 JUN | 1 | 18:9:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 141 | 56,809.757292 | 2014 JUN | 1 | 18:10:30 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 142 | 56,809.758333 | 2014 JUN | 1 | 18:12:0 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 143 | 56,809.844792 | 2014 JUN | 1 | 20:16:30 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time lag | ||||||||||
| 135 | 56,809.751042 | 2014 JUN | 2 | 18:1:30 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |||||||
| 241 | 56,810.743750 | 2014 JUN | 2 | 17:51:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 242 | 56,810.744792 | 2014 JUN | 2 | 17:52:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 243 | 56,810.745833 | 2014 JUN | 2 | 17:54:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 244 | 56,810.746875 | 2014 JUN | 2 | 17:55:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 245 | 56,810.747917 | 2014 JUN | 2 | 17:57:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 246 | 56,810.748958 | 2014 JUN | 2 | 17:58:29 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 247 | 56,810.750000 | 2014 JUN | 2 | 18:0:0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 248 | 56,810.751042 | 2014 JUN | 2 | 18:1:30 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 249 | 56,810.752083 | 2014 JUN | 2 | 18:3:0 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 250 | 56,810.753125 | 2014 JUN | 2 | 18:4:30 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 251 | 56,810.754167 | 2014 JUN | 2 | 18:6:0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 252 | 56,810.755208 | 2014 JUN | 2 | 18:7:29 | 26 | 26 | 0 | 26 | 26 | 26 | 0 | −4.5 | 0.0 | −4.5 | 0.2 | −4.5 | 0.0 |
| 253 | 56,810.756250 | 2014 JUN | 2 | 18:9:0 | 26 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 254 | 56,810.757292 | 2014 JUN | 2 | 18:10:30 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 565 | 56,811.740625 | 2014 JUN | 3 | 17:46:29 | 2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||||
| 566 | 56,811.741667 | 2014 JUN | 3 | 17:48:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 567 | 56,811.743750 | 2014 JUN | 3 | 17:51:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 568 | 56,811.744792 | 2014 JUN | 3 | 17:52:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 569 | 56,811.745833 | 2014 JUN | 3 | 17:54:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 570 | 56,811.746875 | 2014 JUN | 3 | 17:55:29 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 571 | 56,811.747917 | 2014 JUN | 3 | 17:57:0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 572 | 56,811.748958 | 2014 JUN | 3 | 17:58:29 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 573 | 56,811.750000 | 2014 JUN | 3 | 18:0:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 574 | 56,811.751042 | 2014 JUN | 3 | 18:1:30 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 575 | 56,811.752083 | 2014 JUN | 3 | 18:3:0 | 11 | 11 | 0 | 11 | 0 | 11 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 576 | 56,811.753125 | 2014 JUN | 3 | 18:4:30 | 22 | 0 | 0 | 0 | 22 | 0 | 0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.0 |
| 577 | 56,811.754167 | 2014 JUN | 3 | 18:6:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 725 | 56,812.740625 | 2014 JUN | 4 | 17:46:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 726 | 56,812.741667 | 2014 JUN | 4 | 17:48:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 727 | 56,812.742708 | 2014 JUN | 4 | 17:49:29 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 728 | 56,812.743750 | 2014 JUN | 4 | 17:51:0 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 729 | 56,812.744792 | 2014 JUN | 4 | 17:52:30 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 730 | 56,812.745833 | 2014 JUN | 4 | 17:54:0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 731 | 56,812.746875 | 2014 JUN | 4 | 17:55:29 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 732 | 56,812.747917 | 2014 JUN | 4 | 17:57:0 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 733 | 56,812.748958 | 2014 JUN | 4 | 17:58:29 | 18 | 18 | 0 | 18 | 18 | 18 | 0 | −4.5 | 0.0 | −4.5 | −1.7 | −4.5 | 0.0 |
| 734 | 56,812.75000 | 2014 JUN | 4 | 18:0:0 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 735 | 56,812.751042 | 2014 JUN | 4 | 18:1:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 736 | 56,812.752083 | 2014 JUN | 4 | 18:3:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 737 | 56,812.753125 | 2014 JUN | 4 | 18:4:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 738 | 56,812.756250 | 2014 JUN | 4 | 18:9:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 739 | 56,812.757292 | 2014 JUN | 4 | 18:10:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 740 | 56,812.758333 | 2014 JUN | 4 | 18:12:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 741 | 56,812.773958 | 2014 JUN | 4 | 18:34:29 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 917 | 56,813.734375 | 2014 JUN | 5 | 17:37:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 918 | 56,813.735417 | 2014 JUN | 5 | 17:39:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 919 | 56,813.736458 | 2014 JUN | 5 | 17:40:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 920 | 56,813.737500 | 2014 JUN | 5 | 17:42:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 921 | 56,813.738542 | 2014 JUN | 5 | 17:43:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 922 | 56,813.739583 | 2014 JUN | 5 | 17:45:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 923 | 56,813.739583 | 2014 JUN | 5 | 17:46:29 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 924 | 56,813.741667 | 2014 JUN | 5 | 17:48:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 925 | 56,813.742708 | 2014 JUN | 5 | 17:49:29 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 926 | 56,813.743750 | 2014 JUN | 5 | 17:51:0 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 927 | 56,813.744792 | 2014 JUN | 5 | 17:52:30 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 928 | 56,813.745833 | 2014 JUN | 5 | 17:54:0 | 16 | 16 | 0 | 16 | 0 | 16 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 929 | 56,813.746875 | 2014 JUN | 5 | 17:55:29 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 930 | 56,813.747917 | 2014 JUN | 5 | 17:58:29 | 27 | 0 | 0 | 0 | 27 | 0 | 0 | 0.0 | 0.0 | 0.0 | 2.8 | 0.0 | 0.0 |
| 931 | 56,813.748958 | 2014 JUN | 5 | 17:58:29 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 932 | 56,813.750000 | 2014 JUN | 5 | 18:0:0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 933 | 56,813.751042 | 2014 JUN | 5 | 18:1:30 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 934 | 56,813.752083 | 2014 JUN | 5 | 18:3:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 935 | 56,813.753125 | 2014 JUN | 5 | 18:4:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 936 | 56,813.754167 | 2014 JUN | 5 | 18:6:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 937 | 56,813.755208 | 2014 JUN | 5 | 18:7:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 938 | 56,813.756250 | 2014 JUN | 5 | 18:9:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 1151 | 56,814.733333 | 2014 JUN | 6 | 17:36:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1152 | 56,814.734375 | 2014 JUN | 6 | 17:37:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1153 | 56,814.735417 | 2014 JUN | 6 | 17:39:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1154 | 56,814.736458 | 2014 JUN | 6 | 17:40:29 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1155 | 56,814.737500 | 2014 JUN | 6 | 17:42:0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1156 | 56,814.738542 | 2014 JUN | 6 | 17:43:30 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1157 | 56,814.739583 | 2014 JUN | 6 | 17:45:0 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1158 | 56,814.740625 | 2014 JUN | 6 | 17:46:29 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1159 | 56,814.741667 | 2014 JUN | 6 | 17:48:0 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1160 | 56,814.742708 | 2014 JUN | 6 | 17:49:29 | 16 | 16 | 0 | 16 | 0 | 16 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 1161 | 56,814.743750 | 2014 JUN | 6 | 17:51:0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1162 | 56,814.744792 | 2014 JUN | 6 | 17:52:30 | 24 | 0 | 0 | 0 | 24 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 1163 | 56,814.748958 | 2014 JUN | 6 | 17:58:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1164 | 56,814.750000 | 2014 JUN | 6 | 18:0:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 1203 | 56,815.734375 | 2014 JUN | 7 | 17:37:30 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1204 | 56,815.735417 | 2014 JUN | 7 | 17:39:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1205 | 56,815.736458 | 2014 JUN | 7 | 17:40:29 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1206 | 56,815.737500 | 2014 JUN | 7 | 17:42:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1207 | 56,815.738542 | 2014 JUN | 7 | 17:43:30 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1208 | 56,815.739583 | 2014 JUN | 7 | 17:45:0 | 12 | 12 | 0 | 12 | 0 | 12 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 1209 | 56,815.740625 | 2014 JUN | 7 | 17:46:29 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1210 | 56,815.741667 | 2014 JUN | 7 | 17:48:0 | 26 | 0 | 0 | 0 | 26 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 1211 | 56,815.742708 | 2014 JUN | 7 | 17:49:29 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 1297 | 56,816.729167 | 2014 JUN | 8 | 17:30:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1298 | 56,816.730208 | 2014 JUN | 8 | 17:31:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1299 | 56,816.731250 | 2014 JUN | 8 | 17:33:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1300 | 56,816.732292 | 2014 JUN | 8 | 17:34:30 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1301 | 56,816.733333 | 2014 JUN | 8 | 17:36:0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1302 | 56,816.734375 | 2014 JUN | 8 | 17:37:30 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1303 | 56,816.735417 | 2014 JUN | 8 | 17:39:0 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1304 | 56,816.736458 | 2014 JUN | 8 | 17:40:29 | 18 | 18 | 0 | 18 | 0 | 18 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 1305 | 56,816.737500 | 2014 JUN | 8 | 17:42:0 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1306 | 56,816.738542 | 2014 JUN | 8 | 17:43:30 | 20 | 0 | 0 | 0 | 20 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 1307 | 56,816.768750 | 2014 JUN | 8 | 18:27:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1308 | 56,816.769792 | 2014 JUN | 8 | 18:28:30 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 1382 | 56,817.700000 | 2014 JUN | 9 | 16:48:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1383 | 56,817.701042 | 2014 JUN | 9 | 16:49:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1384 | 56,817.702083 | 2014 JUN | 9 | 16:51:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1385 | 56,817.703125 | 2014 JUN | 9 | 16:52:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1386 | 56,817.704167 | 2014 JUN | 9 | 16:54:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1387 | 56,817.705208 | 2014 JUN | 9 | 16:55:29 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1388 | 56,817.706250 | 2014 JUN | 9 | 16:57:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1389 | 56,817.707292 | 2014 JUN | 9 | 16:58:30 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1390 | 56,817.708333 | 2014 JUN | 9 | 17:60: 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1391 | 56,817.709375 | 2014 JUN | 9 | 17:1:29 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1392 | 56,817.710417 | 2014 JUN | 9 | 17:3:0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1393 | 56,817.711458 | 2014 JUN | 9 | 17:4:29 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1394 | 56,817.712500 | 2014 JUN | 9 | 17:6:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1395 | 56,817.713542 | 2014 JUN | 9 | 17:7:30 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1396 | 56,817.714583 | 2014 JUN | 9 | 17:9:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1397 | 56,817.715625 | 2014 JUN | 9 | 17:10:29 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1398 | 56,817.716667 | 2014 JUN | 9 | 17:12:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1399 | 56,817.717708 | 2014 JUN | 9 | 17:13:29 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1400 | 56,817.718750 | 2014 JUN | 9 | 17:15:0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1401 | 56,817.719792 | 2014 JUN | 9 | 17:16:30 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1402 | 56,817.720833 | 2014 JUN | 9 | 17:18:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1403 | 56,817.721875 | 2014 JUN | 9 | 17:19:30 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1404 | 56,817.722917 | 2014 JUN | 9 | 17:21:0 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1405 | 56,817.723958 | 2014 JUN | 9 | 17:22:29 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1406 | 56,817.725000 | 2014 JUN | 9 | 17:24:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1407 | 56,817.726042 | 2014 JUN | 9 | 17:25:30 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1408 | 56,817.727083 | 2014 JUN | 9 | 17:27:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1409 | 56,817.728125 | 2014 JUN | 9 | 17:28:30 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1410 | 56,817.729167 | 2014 JUN | 9 | 17:30:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1411 | 56,817.730208 | 2014 JUN | 9 | 17:31:29 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1412 | 56,817.731250 | 2014 JUN | 9 | 17:33:0 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1413 | 56,817.732292 | 2014 JUN | 9 | 17:34:30 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1414 | 56,817.733333 | 2014 JUN | 9 | 17:36:0 | 23 | 23 | 0 | 23 | 0 | 23 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 1415 | 56,817.734375 | 2014 JUN | 9 | 17:37:30 | 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1416 | 56,817.735417 | 2014 JUN | 9 | 17:39:0 | 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1417 | 56,817.736458 | 2014 JUN | 9 | 17:40:29 | 29 | 0 | 0 | 0 | 29 | 0 | 0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.0 |
| 1418 | 56,817.743750 | 2014 JUN | 9 | 17:51:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 1520 | 56,818.723958 | 2014 JUN | 10 | 17:22:29 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1521 | 56,818.725000 | 2014 JUN | 10 | 17:24:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1522 | 56,818.726042 | 2014 JUN | 10 | 17:25:30 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1523 | 56,818.727083 | 2014 JUN | 10 | 17:27:0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1524 | 56,818.728125 | 2014 JUN | 10 | 17:28:30 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1525 | 56,818.729167 | 2014 JUN | 10 | 17:30:0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1526 | 56,818.730208 | 2014 JUN | 10 | 17:31:29 | 18 | 18 | 0 | 18 | 0 | 18 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 1527 | 56,818.731250 | 2014 JUN | 10 | 17:33:0 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1528 | 56,818.732292 | 2014 JUN | 10 | 17:34:30 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1529 | 56,818.733333 | 2014 JUN | 10 | 17:36:0 | 24 | 0 | 0 | 0 | 24 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 1530 | 56,818.734375 | 2014 JUN | 10 | 17:37:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1531 | 56,818.735417 | 2014 JUN | 10 | 17:39:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 1578 | 56,819.720833 | 2014 JUN | 11 | 17:18:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1579 | 56,819.721875 | 2014 JUN | 11 | 17:19:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1580 | 56,819.722917 | 2014 JUN | 11 | 17:21:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1581 | 56,819.723958 | 2014 JUN | 11 | 17:22:29 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1582 | 56,819.725000 | 2014 JUN | 11 | 17:24:0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1583 | 56,819.726042 | 2014 JUN | 11 | 17:25:30 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1584 | 56,819.727083 | 2014 JUN | 11 | 17:27:0 | 19 | 19 | 0 | 19 | 0 | 19 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 1585 | 56,819.728125 | 2014 JUN | 11 | 17:28:30 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1586 | 56,819.729167 | 2014 JUN | 11 | 17:30:0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1587 | 56,819.730208 | 2014 JUN | 11 | 17:31:29 | 22 | 0 | 0 | 0 | 22 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 1588 | 56,819.737500 | 2014 JUN | 11 | 17:42:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2049 | 56,820.718750 | 2014 JUN | 12 | 17:15:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2050 | 56,820.719792 | 2014 JUN | 12 | 17:16:30 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2051 | 56,820.720833 | 2014 JUN | 12 | 17:18:0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2052 | 56,820.721875 | 2014 JUN | 12 | 17:19:30 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2053 | 56,820.722917 | 2014 JUN | 12 | 17:21:0 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2054 | 56,820.723958 | 2014 JUN | 12 | 17:22:29 | 14 | 14 | 0 | 14 | 0 | 14 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2055 | 56,820.725000 | 2014 JUN | 12 | 17:24:0 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2056 | 56,820.726042 | 2014 JUN | 12 | 17:25:30 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2057 | 56,820.727083 | 2014 JUN | 12 | 17:27:0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2058 | 56,820.728125 | 2014 JUN | 12 | 17:28:30 | 26 | 0 | 0 | 0 | 26 | 0 | 0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.0 |
| 2059 | 56,820.729167 | 2014 JUN | 12 | 17:30:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2060 | 56,820.730208 | 2014 JUN | 12 | 17:31:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2061 | 56,820.732292 | 2014 JUN | 12 | 17:34:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2062 | 56,820.734375 | 2014 JUN | 12 | 17:37:30 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2196 | 56,821.707292 | 2014 JUN | 13 | 16:58:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2197 | 56,821.708333 | 2014 JUN | 13 | 17:60: 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2198 | 56,821.709375 | 2014 JUN | 13 | 17:1:29 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2199 | 56,821.710417 | 2014 JUN | 13 | 17:3:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2200 | 56,821.711458 | 2014 JUN | 13 | 17:4:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2201 | 56,821.712500 | 2014 JUN | 13 | 17:6:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2202 | 56,821.713542 | 2014 JUN | 13 | 17:7:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2203 | 56,821.714583 | 2014 JUN | 13 | 17:9:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2204 | 56,821.715625 | 2014 JUN | 13 | 17:10:29 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2205 | 56,821.716667 | 2014 JUN | 13 | 17:12:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2206 | 56,821.717708 | 2014 JUN | 13 | 17:13:29 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2207 | 56,821.718750 | 2014 JUN | 13 | 17:15:0 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2208 | 56,821.719792 | 2014 JUN | 13 | 17:16:30 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2209 | 56,821.720833 | 2014 JUN | 13 | 17:18:0 | 20 | 20 | 0 | 20 | 0 | 20 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2210 | 56,821.721875 | 2014 JUN | 13 | 17:19:30 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2211 | 56,821.722917 | 2014 JUN | 13 | 17:21:0 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2212 | 56,821.723958 | 2014 JUN | 13 | 17:22:29 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2213 | 56,821.725000 | 2014 JUN | 13 | 17:24:0 | 26 | 0 | 0 | 0 | 26 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 2214 | 56,821.727083 | 2014 JUN | 13 | 17:27:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2215 | 56,821.753125 | 2014 JUN | 13 | 18:4:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2216 | 56,821.754167 | 2014 JUN | 13 | 18:6:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2390 | 56,822.694792 | 2014 JUN | 14 | 16:40:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2391 | 56,822.695833 | 2014 JUN | 14 | 16:42:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2392 | 56,822.696875 | 2014 JUN | 14 | 16:43:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2393 | 56,822.697917 | 2014 JUN | 14 | 16:45:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2394 | 56,822.698958 | 2014 JUN | 14 | 16:46:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2395 | 56,822.700000 | 2014 JUN | 14 | 16:48:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2396 | 56,822.701042 | 2014 JUN | 14 | 16:49:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2397 | 56,822.702083 | 2014 JUN | 14 | 16:51:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2398 | 56,822.703125 | 2014 JUN | 14 | 16:52:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2399 | 56,822.704167 | 2014 JUN | 14 | 16:54:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2400 | 56,822.705208 | 2014 JUN | 14 | 16:55:29 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2401 | 56,822.706250 | 2014 JUN | 14 | 16:57:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2402 | 56,822.707292 | 2014 JUN | 14 | 16:58:30 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2403 | 56,822.708333 | 2014 JUN | 14 | 17:60: 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2404 | 56,822.709375 | 2014 JUN | 14 | 17:1:29 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2405 | 56,822.710417 | 2014 JUN | 14 | 17:3:0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2406 | 56,822.711458 | 2014 JUN | 14 | 17:4:29 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2407 | 56,822.712500 | 2014 JUN | 14 | 17:6:0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2408 | 56,822.713542 | 2014 JUN | 14 | 17:7:30 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2409 | 56,822.714583 | 2014 JUN | 14 | 17:9:0 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2410 | 56,822.715625 | 2014 JUN | 14 | 17:10:29 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2411 | 56,822.716667 | 2014 JUN | 14 | 17:12:0 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2412 | 56,822.717708 | 2014 JUN | 14 | 17:13:29 | 15 | 15 | 0 | 15 | 0 | 15 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2413 | 56,822.718750 | 2014 JUN | 14 | 17:15:0 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2414 | 56,822.719792 | 2014 JUN | 14 | 17:16:30 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2415 | 56,822.720833 | 2014 JUN | 14 | 17:18:0 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2416 | 56,822.721875 | 2014 JUN | 14 | 17:19:30 | 23 | 0 | 0 | 0 | 23 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 2417 | 56,822.722917 | 2014 JUN | 14 | 17:21:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2418 | 56,822.723958 | 2014 JUN | 14 | 17:22:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2419 | 56,822.725000 | 2014 JUN | 14 | 17:24:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2420 | 56,822.726042 | 2014 JUN | 14 | 17:25:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2421 | 56,822.727083 | 2014 JUN | 14 | 17:27:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2422 | 56,822.728125 | 2014 JUN | 14 | 17:28:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2423 | 56,822.747917 | 2014 JUN | 14 | 17:57:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2438 | 56,823.709375 | 2014 JUN | 15 | 17:1:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2439 | 56,823.710417 | 2014 JUN | 15 | 17:3:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2440 | 56,823.711458 | 2014 JUN | 15 | 17:4:29 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2441 | 56,823.712500 | 2014 JUN | 15 | 17:6:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2442 | 56,823.713542 | 2014 JUN | 15 | 17:7:30 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2443 | 56,823.714583 | 2014 JUN | 15 | 17:9:0 | 12 | 12 | 0 | 12 | 0 | 12 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2444 | 56,823.715625 | 2014 JUN | 15 | 17:10:29 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2445 | 56,823.716667 | 2014 JUN | 15 | 17:12:0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2446 | 56,823.717708 | 2014 JUN | 15 | 17:13:29 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2447 | 56,823.718750 | 2014 JUN | 15 | 17:15:0 | 15 | 0 | 0 | 0 | 15 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| 2448 | 56,823.746875 | 2014 JUN | 15 | 17:55:29 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2494 | 56,824.706250 | 2014 JUN | 16 | 16:57:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2495 | 56,824.707292 | 2014 JUN | 16 | 16:58:30 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2496 | 56,824.708333 | 2014 JUN | 16 | 17:60: 0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2497 | 56,824.709375 | 2014 JUN | 16 | 17:1:29 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2498 | 56,824.710417 | 2014 JUN | 16 | 17:3:0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2499 | 56,824.711458 | 2014 JUN | 16 | 17:4:29 | 17 | 17 | 0 | 17 | 0 | 17 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2500 | 56,824.712500 | 2014 JUN | 16 | 17:6:0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2501 | 56,824.713542 | 2014 JUN | 16 | 17:7:30 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2502 | 56,824.714583 | 2014 JUN | 16 | 17:9:0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2503 | 56,824.715625 | 2014 JUN | 16 | 17:10:29 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2504 | 56,824.716667 | 2014 JUN | 16 | 17:12:0 | 22 | 0 | 0 | 0 | 22 | 0 | 0 | 0.0 | 0.0 | 0.0 | 1.3 | 0.0 | 0.0 |
| 2505 | 56,824.717708 | 2014 JUN | 16 | 17:13:29 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2506 | 56,824.718750 | 2014 JUN | 16 | 17:15:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2507 | 56,824.719792 | 2014 JUN | 16 | 17:16:30 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2508 | 56,824.721875 | 2014 JUN | 16 | 17:19:30 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2556 | 56,825.703125 | 2014 JUN | 17 | 16:52:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2557 | 56,825.704167 | 2014 JUN | 17 | 16:54:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2558 | 56,825.705208 | 2014 JUN | 17 | 16:55:29 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2559 | 56,825.706250 | 2014 JUN | 17 | 16:57:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2560 | 56,825.707292 | 2014 JUN | 17 | 16:58:30 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2561 | 56,825.708333 | 2014 JUN | 17 | 17:60: 0 | 11 | 11 | 0 | 11 | 0 | 11 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2562 | 56,825.709375 | 2014 JUN | 17 | 17:1:29 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2563 | 56,825.710417 | 2014 JUN | 17 | 17:3:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2564 | 56,825.711458 | 2014 JUN | 17 | 17:4:29 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2565 | 56,825.712500 | 2014 JUN | 17 | 17:6:0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2566 | 56,825.713542 | 2014 JUN | 17 | 17:7:30 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2567 | 56,825.714583 | 2014 JUN | 17 | 17:9:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2568 | 56,825.715625 | 2014 JUN | 17 | 17:10:29 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2569 | 56,825.716667 | 2014 JUN | 17 | 17:12:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2570 | 56,825.717708 | 2014 JUN | 17 | 17:13:29 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2607 | 56,826.704167 | 2014 JUN | 18 | 16:54:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2608 | 56,826.705208 | 2014 JUN | 18 | 16:55:29 | 6 | 6 | 0 | 6 | 0 | 6 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2609 | 56,826.706250 | 2014 JUN | 18 | 16:57:0 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2610 | 56,826.707292 | 2014 JUN | 18 | 16:58:30 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2611 | 56,826.708333 | 2014 JUN | 18 | 17:60: 0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2612 | 56,826.709375 | 2014 JUN | 18 | 17:1:29 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2613 | 56,826.710417 | 2014 JUN | 18 | 17:3:0 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2614 | 56,826.712500 | 2014 JUN | 18 | 17:6:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2615 | 56,826.739583 | 2014 JUN | 18 | 17:45:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2616 | 56,826.740625 | 2014 JUN | 18 | 17:46:29 | 1 | 0 | 0 | 0 | 15 | 0 | 0 | 0.0 | 0.0 | 0.0 | −0.2 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2741 | 56,827.696875 | 2014 JUN | 19 | 16:43:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2742 | 56,827.697917 | 2014 JUN | 19 | 16:45:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2743 | 56,827.698958 | 2014 JUN | 19 | 16:46:29 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2744 | 56,827.700000 | 2014 JUN | 19 | 16:48:0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2745 | 56,827.701042 | 2014 JUN | 19 | 16:49:30 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2746 | 56,827.702083 | 2014 JUN | 19 | 16:51:0 | 9 | 9 | 0 | 9 | 0 | 9 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2747 | 56,827.703125 | 2014 JUN | 19 | 16:52:30 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2748 | 56,827.704167 | 2014 JUN | 19 | 16:54:0 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2749 | 56,827.705208 | 2014 JUN | 19 | 16:55:29 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2750 | 56,827.706250 | 2014 JUN | 19 | 16:57:0 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2751 | 56,827.707292 | 2014 JUN | 19 | 16:58:30 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2752 | 56,827.708333 | 2014 JUN | 19 | 17:60: 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2834 | 56,828.693750 | 2014 JUN | 20 | 16:39:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2835 | 56,828.694792 | 2014 JUN | 20 | 16:40:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2836 | 56,828.695833 | 2014 JUN | 20 | 16:42:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2837 | 56,828.696875 | 2014 JUN | 20 | 16:43:30 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2838 | 56,828.697917 | 2014 JUN | 20 | 16:45:0 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2839 | 56,828.698958 | 2014 JUN | 20 | 16:46:29 | 10 | 10 | 0 | 10 | 0 | 10 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2840 | 56,828.700000 | 2014 JUN | 20 | 16:48:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2841 | 56,828.701042 | 2014 JUN | 20 | 16:49:30 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2842 | 56,828.702083 | 2014 JUN | 20 | 16:51:0 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2843 | 56,828.703125 | 2014 JUN | 20 | 16:52:30 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2844 | 56,828.704167 | 2014 JUN | 20 | 16:54:0 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2845 | 56,828.705208 | 2014 JUN | 20 | 16:55:29 | 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2846 | 56,828.710417 | 2014 JUN | 20 | 17:3:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2895 | 56,829.693750 | 2014 JUN | 21 | 16:39:0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2896 | 56,829.694792 | 2014 JUN | 21 | 16:40:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2897 | 56,829.695833 | 2014 JUN | 21 | 16:42:0 | 5 | 5 | 0 | 5 | 0 | 5 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2898 | 56,829.696875 | 2014 JUN | 21 | 16:43:30 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2899 | 56,829.697917 | 2014 JUN | 21 | 16:45:0 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2900 | 56,829.698958 | 2014 JUN | 21 | 16:46:29 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2901 | 56,829.700000 | 2014 JUN | 21 | 16:48:0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2902 | 56,829.701042 | 2014 JUN | 21 | 16:49:30 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2903 | 56,829.702083 | 2014 JUN | 21 | 16:51:0 | 29 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2904 | 56,829.703125 | 2014 JUN | 21 | 16:52:30 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2905 | 56,829.704167 | 2014 JUN | 21 | 16:54:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2933 | 56,830.689583 | 2014 JUN | 22 | 16:33:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2934 | 56,830.690625 | 2014 JUN | 22 | 16:34:30 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2935 | 56,830.691667 | 2014 JUN | 22 | 16:36:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2936 | 56,830.692708 | 2014 JUN | 22 | 16:37:29 | 3 | 3 | 0 | 3 | 0 | 3 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 2937 | 56,830.693750 | 2014 JUN | 22 | 16:39:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2938 | 56,830.694792 | 2014 JUN | 22 | 16:40:30 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2939 | 56,830.695833 | 2014 JUN | 22 | 16:42:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2940 | 56,830.696875 | 2014 JUN | 22 | 16:43:30 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2941 | 56,830.697917 | 2014 JUN | 22 | 16:45:0 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2942 | 56,830.698958 | 2014 JUN | 22 | 16:46:29 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2943 | 56,830.721875 | 2014 JUN | 22 | 17:19:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2944 | 56,830.722917 | 2014 JUN | 22 | 17:21:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 2997 | 56,831.685417 | 2014 JUN | 23 | 16:27:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2998 | 56,831.686458 | 2014 JUN | 23 | 16:28:29 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2999 | 56,831.687500 | 2014 JUN | 23 | 16:30:0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3000 | 56,831.688542 | 2014 JUN | 23 | 16:31:30 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3001 | 56,831.689583 | 2014 JUN | 23 | 16:33:0 | 10 | 10 | 0 | 10 | 0 | 10 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 3002 | 56,831.690625 | 2014 JUN | 23 | 16:34:30 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3003 | 56,831.691667 | 2014 JUN | 23 | 16:36:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3004 | 56,831.692708 | 2014 JUN | 23 | 16:37:29 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3005 | 56,831.693750 | 2014 JUN | 23 | 16:39:0 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3006 | 56,831.694792 | 2014 JUN | 23 | 16:40:30 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3007 | 56,831.695833 | 2014 JUN | 23 | 16:42:0 | 26 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3008 | 56,831.696875 | 2014 JUN | 23 | 16:43:30 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3009 | 56,831.700000 | 2014 JUN | 23 | 16:48:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3010 | 56,831.712500 | 2014 JUN | 23 | 17:6:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 3061 | 56,832.678125 | 2014 JUN | 24 | 16:16:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3062 | 56,832.679167 | 2014 JUN | 24 | 16:18:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3063 | 56,832.680208 | 2014 JUN | 24 | 16:19:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3064 | 56,832.681250 | 2014 JUN | 24 | 16:21:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3065 | 56,832.682292 | 2014 JUN | 24 | 16:22:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3066 | 56,832.683333 | 2014 JUN | 24 | 16:24:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3067 | 56,832.684375 | 2014 JUN | 24 | 16:25:29 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3068 | 56,832.685417 | 2014 JUN | 24 | 16:27:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3069 | 56,832.686458 | 2014 JUN | 24 | 16:28:29 | 9 | 9 | 0 | 9 | 0 | 9 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 3070 | 56,832.687500 | 2014 JUN | 24 | 16:30:0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3071 | 56,832.688542 | 2014 JUN | 24 | 16:31:30 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3072 | 56,832.689583 | 2014 JUN | 24 | 16:33:0 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3073 | 56,832.690625 | 2014 JUN | 24 | 16:34:30 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3074 | 56,832.691667 | 2014 JUN | 24 | 16:36:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3075 | 56,832.692708 | 2014 JUN | 24 | 16:37:29 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3076 | 56,832.693750 | 2014 JUN | 24 | 16:39:0 | 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3077 | 56,832.694792 | 2014 JUN | 24 | 16:40:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3078 | 56,832.695833 | 2014 JUN | 24 | 16:42:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3079 | 56,832.696875 | 2014 JUN | 24 | 16:43:30 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3080 | 56,832.697917 | 2014 JUN | 24 | 16:45:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3081 | 56,832.698958 | 2014 JUN | 24 | 16:46:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3082 | 56,832.700000 | 2014 JUN | 24 | 16:48:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3083 | 56,832.712500 | 2014 JUN | 24 | 17:6:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3084 | 56,832.740625 | 2014 JUN | 24 | 17:46:29 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 3123 | 56,833.681250 | 2014 JUN | 25 | 16:21:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3124 | 56,833.682292 | 2014 JUN | 25 | 16:22:30 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3125 | 56,833.683333 | 2014 JUN | 25 | 16:24:0 | 4 | 4 | 0 | 4 | 0 | 4 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 3126 | 56,833.684375 | 2014 JUN | 25 | 16:25:29 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3127 | 56,833.685417 | 2014 JUN | 25 | 16:27:0 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3128 | 56,833.686458 | 2014 JUN | 25 | 16:28:29 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3129 | 56,833.687500 | 2014 JUN | 25 | 16:30:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3130 | 56,833.688542 | 2014 JUN | 25 | 16:31:30 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3131 | 56,833.689583 | 2014 JUN | 25 | 16:33:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3132 | 56,833.690625 | 2014 JUN | 25 | 16:34:30 | 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3133 | 56,833.691667 | 2014 JUN | 25 | 16:36:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3134 | 56,833.692708 | 2014 JUN | 25 | 16:37:29 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 3194 | 56,834.671875 | 2014 JUN | 26 | 16:7:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3195 | 56,834.672917 | 2014 JUN | 26 | 16:9:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3196 | 56,834.673958 | 2014 JUN | 26 | 16:10:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3198 | 56,834.676042 | 2014 JUN | 26 | 16:13:30 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3199 | 56,834.677083 | 2014 JUN | 26 | 16:15:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3200 | 56,834.678125 | 2014 JUN | 26 | 16:16:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3201 | 56,834.679167 | 2014 JUN | 26 | 16:18:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3202 | 56,834.680208 | 2014 JUN | 26 | 16:19:29 | 12 | 12 | 0 | 12 | 0 | 12 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 3203 | 56,834.681250 | 2014 JUN | 26 | 16:21:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3204 | 56,834.682292 | 2014 JUN | 26 | 16:22:30 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3205 | 56,834.683333 | 2014 JUN | 26 | 16:24:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3206 | 56,834.684375 | 2014 JUN | 26 | 16:25:29 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3207 | 56,834.685417 | 2014 JUN | 26 | 16:27:0 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3208 | 56,834.686458 | 2014 JUN | 26 | 16:28:29 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3209 | 56,834.687500 | 2014 JUN | 26 | 16:30:0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3210 | 56,834.688542 | 2014 JUN | 26 | 16:31:30 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 3236 | 56,835.668750 | 2014 JUN | 27 | 16:3:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3237 | 56,835.669792 | 2014 JUN | 27 | 16:4:30 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3238 | 56,835.670833 | 2014 JUN | 27 | 16:6:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3239 | 56,835.671875 | 2014 JUN | 27 | 16:7:30 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3240 | 56,835.672917 | 2014 JUN | 27 | 16:9:0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3241 | 56,835.673958 | 2014 JUN | 27 | 16:10:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3242 | 56,835.675000 | 2014 JUN | 27 | 16:12:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3243 | 56,835.676042 | 2014 JUN | 27 | 16:13:30 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3244 | 56,835.677083 | 2014 JUN | 27 | 16:15:0 | 6 | 6 | 0 | 6 | 0 | 6 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 3245 | 56,835.678125 | 2014 JUN | 27 | 16:16:29 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3246 | 56,835.679167 | 2014 JUN | 27 | 16:18:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3247 | 56,835.680208 | 2014 JUN | 27 | 16:19:29 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3248 | 56,835.681250 | 2014 JUN | 27 | 16:21:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3249 | 56,835.682292 | 2014 JUN | 27 | 16:22:30 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3250 | 56,835.683333 | 2014 JUN | 27 | 16:24:0 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3251 | 56,835.684375 | 2014 JUN | 27 | 16:25:29 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3252 | 56,835.685417 | 2014 JUN | 27 | 16:27:0 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3253 | 56,835.686458 | 2014 JUN | 27 | 16:28:29 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3254 | 56,835.687500 | 2014 JUN | 27 | 16:30:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 3278 | 56,836.671875 | 2014 JUN | 28 | 16:6:0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3279 | 56,836.672917 | 2014 JUN | 28 | 16:7:30 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3280 | 56,836.673958 | 2014 JUN | 28 | 16:10:29 | 4 | 4 | 0 | 4 | 0 | 4 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 3281 | 56,836.675000 | 2014 JUN | 28 | 16:12:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3282 | 56,836.676042 | 2014 JUN | 28 | 16:13:30 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3283 | 56,836.677083 | 2014 JUN | 28 | 16:15:0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3284 | 56,836.678125 | 2014 JUN | 28 | 16:16:29 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3285 | 56,836.679167 | 2014 JUN | 28 | 16:18:0 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3286 | 56,836.680208 | 2014 JUN | 28 | 16:19:29 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3287 | 56,836.681250 | 2014 JUN | 28 | 16:21:0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3288 | 56,836.682292 | 2014 JUN | 28 | 16:22:30 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3289 | 56,836.687500 | 2014 JUN | 28 | 16:30:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag | ||||||||||
| 3313 | 56,837.668750 | 2014 JUN | 29 | 16:3:0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3314 | 56,837.669792 | 2014 JUN | 29 | 16:4:30 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3315 | 56,837.670833 | 2014 JUN | 29 | 16:6:0 | 10 | 10 | 0 | 10 | 0 | 10 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 3316 | 56,837.671875 | 2014 JUN | 29 | 16:7:30 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3317 | 56,837.672917 | 2014 JUN | 29 | 16:9:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3318 | 56,837.673958 | 2014 JUN | 29 | 16:10:29 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3319 | 56,837.675000 | 2014 JUN | 29 | 16:12:0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3320 | 56,837.676042 | 2014 JUN | 29 | 16:13:30 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3321 | 56,837.677083 | 2014 JUN | 29 | 16:15:0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3322 | 56,837.678125 | 2014 JUN | 29 | 16:16:29 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3323 | 56,837.679167 | 2014 JUN | 29 | 16:18:0 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3324 | 56,837.680208 | 2014 JUN | 29 | 16:19:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3325 | 56,837.681250 | 2014 JUN | 29 | 16:21:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
References
- Coster, A.J. Space Weather and Its Effects on GNSS. Available online: http://cedar.openmadrigal.org/index.html/ (accessed on 7 March 2023).
- Vasylyev, D.; Beniguel, Y.; Volker, W.; Kriegel, M.; Berdermann, J. Modeling of ionospheric scintillation. J. Space Weather Space Clim. 2022, 12, 22. [Google Scholar] [CrossRef]
- Linty, N.; Minetto, A.; Dovis, F.; Spogli, L. Effects of Phase Scintillation on the GNSS Positioning Error During the September 2017 Storm at Svalbard. Space Weather 2018, 16, 1317–1329. [Google Scholar] [CrossRef]
- Marques, H.A.; Marques, H.A.S.; Aquino, M.; Veettil, S.V.; Monico, J.F.G. Accuracy assessment of Precise Point Positioning with multi-constellation GNSS data under ionospheric scintillation effects. J. Space Weather Space Clim. 2018, 8, A15. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Z.; Ji, S.; Chen, W. Assessing the Positioning Performance Under the Effects of Strong Ionospheric Anomalies with Multi-GNSS in Hong Kong. Radio Sci. 2020, 55, 1–18. [Google Scholar] [CrossRef]
- He, L.; Guo, C.; Yue, Q.; Zhang, S.; Qin, Z.; Zhang, J. A Novel Ionospheric Disturbance Index to Evaluate the Global Effect on BeiDou Navigation Satellite System Signal Caused by the Moderate Geomagnetic Storm on 12 May 2021. Sensors 2023, 23, 1183. [Google Scholar] [CrossRef] [PubMed]
- Paziewski, J.; Høeg, P.; Sieradzki, R.; Jin, Y.; Jarmolowski, W.; Hoque, M.M.; Berdermann, J.; Hernandez-Pajares, M.; Wielgosz, P.; Lyu, H.; et al. The implications of ionospheric disturbances for precise GNSS positioning in Greenland. J. Space Weather Space Clim. 2022, 12, 33. [Google Scholar] [CrossRef]
- Hayes, L.A.; O’Hara, O.S.D.; Murray, S.A.; Gallagher, P.T. Solar Flare Effects on the Earth’s Lower Ionosphere. Sol. Phys. 2021, 296, 1–17. [Google Scholar] [CrossRef]
- Hamza, A.M.; Song, K.; Meziane, K.; Jayachandran, P.T. Two-Component Phase Scintillation Spectra in the Auroral Region: Observations and Model. J. Geophys. Res. Phys. 2024, 129, e2023JA031998. [Google Scholar] [CrossRef]
- Grunwald, G.; Ciećko, A.; Kozakiewicz, T.; Krasuski, K. Analysis of GPS/EGNOS Positioning Quality Using Different Ionospheric Models in UAV Navigation. Sensors 2023, 23, 1112. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Zeng, J.; Zhou, Q.; Liu, Z.; Li, Q.; Li, Z.; Wang, G.; Ma, H.; Cui, J.; Chen, X. Initial Study of Adaptive Threshold Cycle Slip Detection on BDS/GPS Kinematic Precise Point Positioning during Geomagnetic Storms. Remote Sens. 2024, 16, 1726. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, C.; Mei, P.; Wang, L. A Spatiotemporical Sequence Prediction Framework Based on Mask Reconstruction: Application to Short-Duration Precipitation Radar Eshoes. J. Remote Sens. 2025, 17, 2326. [Google Scholar] [CrossRef]
- Jayachandran, P.T.; Langley, R.B.; MacDougall, J.W.; Mushini, S.C.; Pokhotelov, D.; Hamza, A.M.; Mann, I.R.; Milling, D.K.; Kale, Z.C.; Chadwick, R.; et al. Canadian High Arctic Ionospheric Network (CHAIN). Radio Sci. 2009, 44, 1–10. [Google Scholar] [CrossRef]
- Pan, Y.; Luo, X. Feasibility ana;ysisof the Doppler Index DI in ionospheric scintillation detection at High Arctic region of Canada. Surv. Rev. 2025, 1–15. [Google Scholar] [CrossRef]
- Kelley, M.C.; Makela, J.J.; Ledvina, B.M.; Kintner, P.M. Observations of equatorial spread-F from Haleakala, Hawaii. Geophys. Res. Lett. 2002, 29, 64-1–64-4. [Google Scholar] [CrossRef]
- Priyadarshi, S. A review of ionospheric scintillation models. Surv. Geophys. 2015, 36, 295–324. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Psiaki, M.L.; Hinks, J.C.; O’Hanlon, B.; Kintner, P.M. Simulating ionosphere-induced scintillation for testing GPS receiver phase tracking loops. IEEE J. Sel. Top. Signal Process. 2009, 3, 707–715. [Google Scholar] [CrossRef]
- Rino, C.; Breitsch, B.; Morton, Y.; Jiao, Y.; Xu, D.; Carrano, C. A compact multi-frequency GNSS scintillation model. Navigation 2018, 65, 563–569. [Google Scholar] [CrossRef]
- Snyder, R.; Koehler, A.; Ord, J. Forecasting for inventory control with exponential smoothing. Int. J. Forecast. 2002, 18, 5–18. [Google Scholar] [CrossRef]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2012, 106, 1513–1527. [Google Scholar] [CrossRef]
- Qi, M.; Zhang, G.P. Trend time-series modeling and forecasting with neural networks. IEEE Trans. Neural Netw. 2008, 19, 808–816. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef]
- Krypiak-Gregorczyk, A.; Wielgosz, P.; Borkowski, A. Ionosphere Model for European Region Based on Multi-GNSS Data and TPS Interpolation. Remote Sens. 2017, 9, 1221. [Google Scholar] [CrossRef]
- Sun, X.; Shu, Z.; Yao, J. Analyzing the Precise Precise Point Positioning Performance of Different Dual-Frequency Ionospheric-Free Combinations with BDS-3 and Galileo. Atmosphere 2025, 16, 316. [Google Scholar] [CrossRef]
- Berenyi, K.A.; Barta, V.; Szarnya, C.; Buzas, A.; Heilig, B. Subauroral and Auroral Conditions in the Mid- and Low-Midlatitude Ionosphere over Europe During the May 2024 Mother’s Day Superstorm. Remote Sens. 2025, 17, 2492. [Google Scholar] [CrossRef]
- Spogli, L.; Alberti, T.; Bagiacchi, P.; Cafarella, L.; Cesaroni, C.; Cianchini, G.; Coco, I.; Di Mauro, D.; Ghidoni, R.; Giannattasio, F.; et al. The Effects of the May 2024 Mother’s Day Superstorm over Mediterranean Sector: From Data to Public Communication. Ann. Geophys. 2024, 67, PA218. [Google Scholar] [CrossRef]
- Filjar, R.; Heđi, I.; Prpić-Oršić, J.; Iliev, T. An Ambient Adaptive Global Navigation Satellite System Total Electron Content Predictive Model for Short-Term Rapid Geomagnetic Storm Events. Remote Sens. 2024, 16, 3051. [Google Scholar] [CrossRef]
- Yang, Z.; Morton, Y.T.J.; Zakharenkova, I.; Cherniak, I.; Song, S.; Li, W. Global View of Ionospheric Disturbance Impacts on Kinematic GPS Positioning Solutions During the 2015 St. Patrick’s Day Storm. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027681. [Google Scholar] [CrossRef]
- Ma, M.; Jin, S.; Jin, X.T. Characteristics of Ionospheric Disturbances during the 2021 Typhoon Chanthu Based on, G.P.S.; GLONASS. Adv. Space Res. 2024, 74, 271–283. [Google Scholar] [CrossRef]
- Ayyagari, D.; Datta, S.; Das, S.; Datta, A. Ionospheric response during Tropical Cyclones-A Brief Review on Amphan and Nisarga. Adv. Space Res. 2023, 71, 2799–2817. [Google Scholar] [CrossRef]
- Ke, F.; Cui, W.; Ming, L.; Hu, X. Ionospheric response and the impact on GPS positioning accuracy during the Tonga volcano eruption on 15 January 2022. Adv. Space Res. 2024, 73, 1831–1842. [Google Scholar] [CrossRef]
- Pezzopane, M.; Pignalberi, A.; Coco, I.; Consolini, G.; De Michelis, P.; Giannattasio, F.; Marcucci, M.F.; Tozzi, R. Occurrence of GPS Loss of Lock Based on a Swarm Half-Solar Cycle Dataset and Its Relation to the Background Ionosphere. Remote Sens. 2021, 13, 2209. [Google Scholar] [CrossRef]
- Francia, P.; Regi, M.; De Lauretis, M.; Pezzopane, M.; Cesaroni, C.; Spogli, L.; Raita, T. A case study of correspondence between Pc1 activity and ionospheric irregularities at polar latitudes. Earth Planets Space 2020, 72, 59. [Google Scholar] [CrossRef]
- Mandea, M.; Isac, A. Geomagnetic Field, Measurement Techniques. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Encyclopedia of Earth Sciences Series; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- David, P.; Kriegel, M.; Berdermann, J.; Kauristie, K.; Jacobsen, K.S.; Fabbro, V.; Laurens, H.; Keil, R. Performance indicator development addressing mitigation of the space weather impacts on GNSS. J. Space Saf. Eng. 2023, 10, 324–330. [Google Scholar] [CrossRef]
- Lin, M.; Luo, Y.; Zhu, X.; Tu, G.; Lu, Z. Optimal GPS Acquisition Algorithm in Severe Ionospheric Scintillation Scene. Electronics 2023, 12, 1343. [Google Scholar] [CrossRef]
- Atabati, A.; Jazireeyan, I.; Alizadeh, M.; Langley, R.B. Prediction of Ionospheric Scintillation with ConvGRU Networks Using GNSS Ground-Based Data across South America. Remote Sens. 2024, 16, 2757. [Google Scholar] [CrossRef]
- Dobelis, D.; Zvirgzds, J.; Kaļinka, M. High Ionospheric Activity Effects on LatPos RTK Network Performance in Latvia. In Proceedings of the IOP Conference Series: Materials Science and Engineering, 3rd International Conference on Innovative Materials, Structures and Technologies (IMST 2017), Riga, Latvia, 27–29 September 2017; Institute of Physics Publishing: Bristol, UK, 2017; Volume 251. [Google Scholar]
- Balodis, J.; Normand, M.; Zarins, A. The Movement of GPS Positioning Discrepancy Clouds at a Mid-Latitude Region in March 2015. Remote Sens. 2023, 15, 2032. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, J.; Lv, T.; Yi, Y.; Lin, Z.; Dong, J.; Li, S. A Cloud Vertical Structure Optimization Algorithm Combining FY-4A and DSCOVR Satellite Data. Remote Sens. 2025, 17, 2484. [Google Scholar] [CrossRef]
- CDDIS Data Archive. Available online: https://cddis.nasa.gov/archive/gnss/products/ionex/ (accessed on 14 June 2021).
- Liu, J.; Wang, W.; Burns, A.; Yue, X.; Zhang, S.; Zhang, Y.; Huang, C. Profiles of Ionospheric Storm-enhanced Density during the 17 March 2015 Great Storm. J. Geophys. Res. Space Phys. 2016, 121, 727–744. [Google Scholar] [CrossRef]
- Kwak, J.; Hwang, J.; Park, J.; Kim, J.; Kim, H. Comparison of geomagnetic storm and non-storm periods midlatitude Pc1 pulsations characteristics. J. Space Weather Space Clim. 2024, 14, 26. [Google Scholar] [CrossRef]
- Pilipenko, V.A.; Fedorov, E.N.; Xu, Z.; Hartinger, M.D.; Engebretson, M.J.; Edwards, T.R. Incidence of Alfvenic SC pulse onto the conjugate ionospheres. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027397. [Google Scholar] [CrossRef]
- Lysak, R.L. Kinetic Alfvén waves and auroral particle acceleration: A review. Rev. Mod. Plasma Phys. 2023, 7, 6. [Google Scholar] [CrossRef] [PubMed]
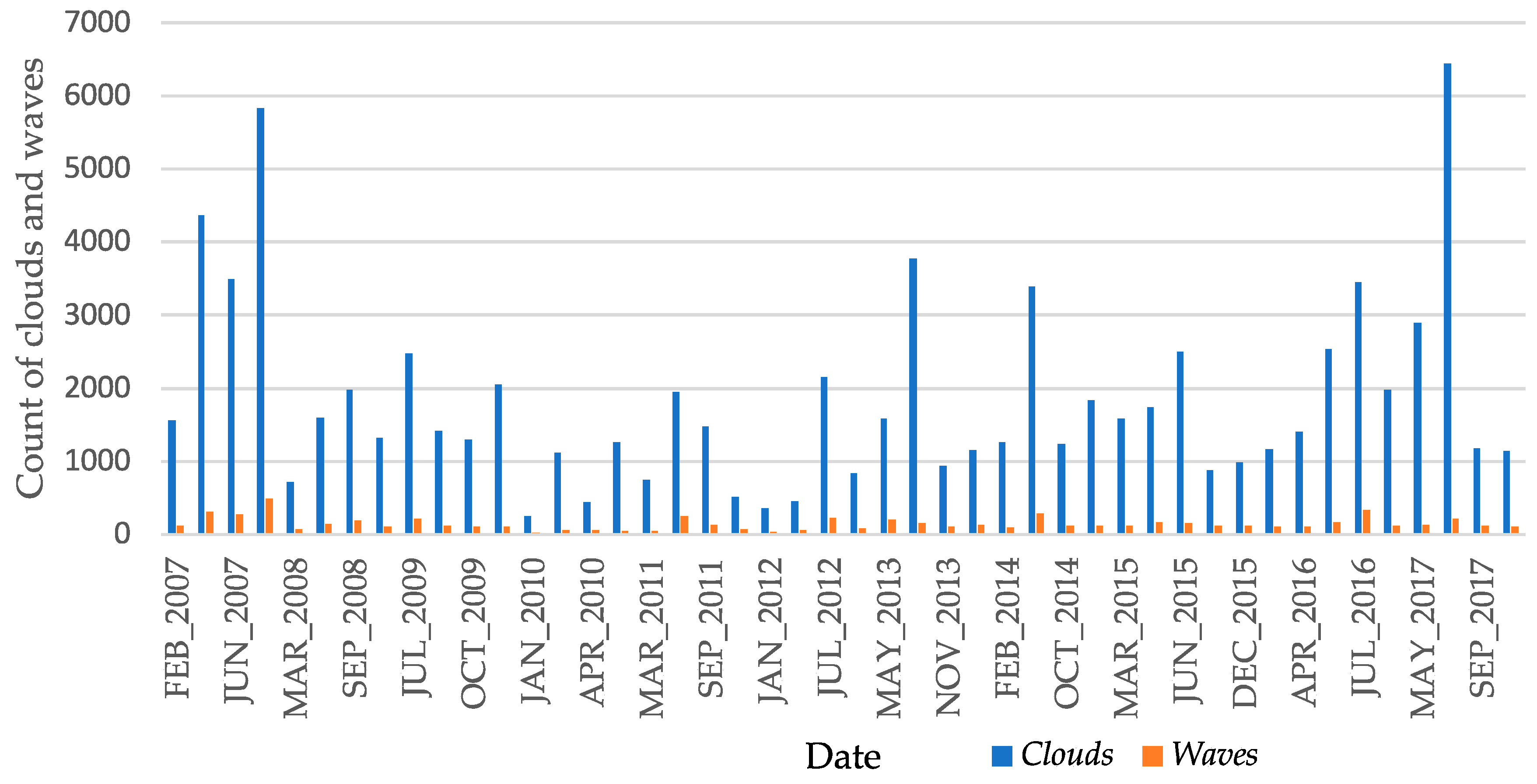

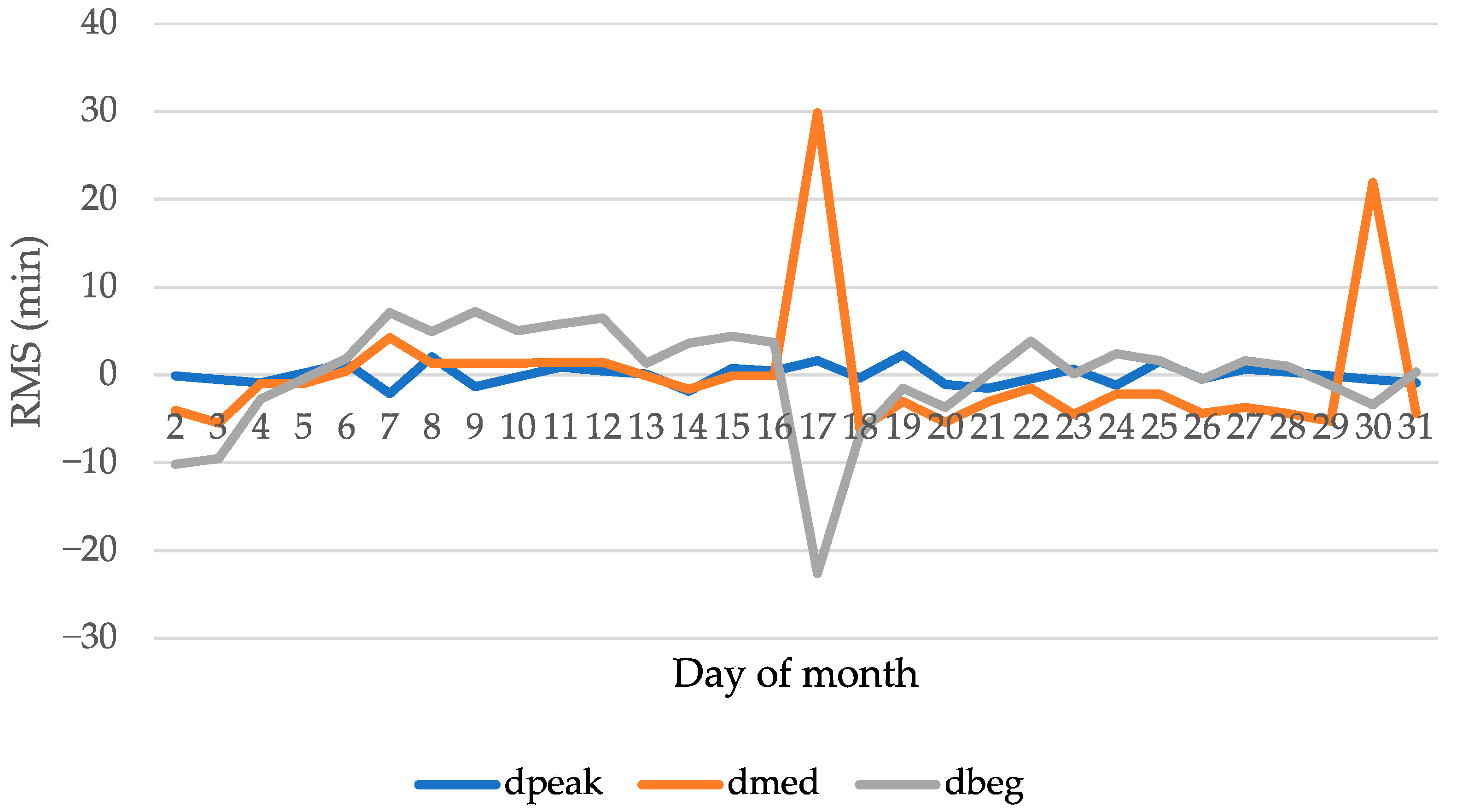





| # | Year | Month | Clouds | Waves | # | Year | Month | Clouds | Waves |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2007 | FEB | 1569 | 120 | 24 | 2012 | OCT | 837 | 88 |
| 2 | 2007 | MAY | 4359 | 308 | 25 | 2013 | MAY | 1587 | 201 |
| 3 | 2007 | JUN | 3501 | 272 | 26 | 2013 | OCT | 3772 | 152 |
| 4 | 2007 | AUG | 5830 | 491 | 27 | 2013 | NOV | 935 | 114 |
| 5 | 2008 | MAR | 726 | 69 | 28 | 2013 | DEC | 1155 | 136 |
| 6 | 2008 | JUN | 1600 | 140 | 29 | 2014 | FEB | 1268 | 99 |
| 7 | 2008 | SEP | 1986 | 193 | 30 | 2014 | JUN | 3393 | 295 |
| 8 | 2008 | OCT | 1328 | 107 | 31 | 2014 | OCT | 1241 | 117 |
| 9 | 2009 | JUL | 2473 | 216 | 32 | 2014 | DEC | 1837 | 126 |
| 10 | 2009 | AUG | 1413 | 126 | 33 | 2015 | MAR | 1584 | 119 |
| 11 | 2009 | OCT | 1304 | 107 | 34 | 2015 | MAY | 1749 | 170 |
| 12 | 2009 | DEC | 2056 | 115 | 35 | 2015 | JUN | 2499 | 154 |
| 13 | 2010 | JAN | 255 | 20 | 36 | 2015 | OCT | 880 | 118 |
| 14 | 2010 | FEB | 1123 | 66 | 37 | 2015 | DEC | 988 | 119 |
| 15 | 2010 | APR | 449 | 59 | 38 | 2016 | FEB | 1166 | 104 |
| 16 | 2010 | NOV | 1263 | 45 | 39 | 2016 | APR | 1401 | 105 |
| 17 | 2011 | MAR | 747 | 48 | 40 | 2016 | MAY | 2541 | 175 |
| 18 | 2011 | AUG | 1943 | 248 | 41 | 2016 | JUL | 3445 | 339 |
| 19 | 2011 | SEP | 1477 | 134 | 42 | 2017 | APR | 1980 | 120 |
| 20 | 2011 | NOV | 523 | 77 | 43 | 2017 | MAY | 2894 | 136 |
| 21 | 2012 | JAN | 366 | 35 | 44 | 2017 | JUL | 6442 | 214 |
| 22 | 2012 | MAR | 461 | 56 | 45 | 2017 | SEP | 1181 | 126 |
| 23 | 2012 | JUL | 2155 | 227 | 46 | 2017 | OCT | 1145 | 112 |
| b | e | p | l | n | P | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 WAVE | 516 | 57,092.991667 | 57,092.998958 | PK 57,092.992708 | MED 57,092.995313 | DIFF 0.007291 | 0.002084 | 0.009375 | 0.003125 | 0.005730 | PK 8 | 3 |
| 51 WAVE | 525 | 57,093.534375 | 57,093.581250 | PK 57,093.534375 | MED 57,093.557813 | DIFF 0.046875 | 0.542708 | 0.582292 | 0.541667 | 0.562500 | PK 3 | 2 |
| 52 WAVE | 534 | 57,093.817708 | 57,093.894792 | PK 57,093.817708 | MED 57,093.856250 | DIFF 0.077084 | 0.283333 | 0.313542 | 0.283333 | 0.298437 | PK 2 | 3 |
| 53 WAVE | 540 | 57,093.902083 | 57,093.906250 | PK 57,093.903125 | MED 57,093.904166 | DIFF 0.004167 | 0.084375 | 0.011458 | 0.085417 | 0.047916 | PK 4 | 4 |
| 54 WAVE | 551 | 57,093.938542 | 57,093.952083 | PK 57,093.941667 | MED 57,093.945312 | DIFF 0.013541 | 0.036459 | 0.045833 | 0.038542 | 0.041146 | PK 14 | 15 |
| 55 WAVE | 569 | 57,093.986458 | 57,093.997917 | PK 57,093.990625 | MED 57,093.992188 | DIFF 0.011459 | 0.047916 | 0.045834 | 0.048958 | 0.046875 | PK 12 | 4 |
| 56 WAVE | 608 | 57,094.932292 | 57,094.951042 | PK 57,094.938542 | MED 57,094.941667 | DIFF 0.018750 | 0.945834 | 0.953125 | 0.947917 | 0.949479 | PK 19 | 27 |
| 57 WAVE | 649 | 57,094.975000 | 57,094.976042 | PK 57,094.975000 | MED 57,094.975521 | DIFF 0.001042 | 0.042708 | 0.025000 | 0.036458 | 0.033854 | PK 2 | 2 |
| Date | MJD | Shift | Peak | Med | Beg | Length | p − b | m − p | p − e |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 57,083.969792 | −0.1 | −4 | −10.2 | 42 | 24 | −3 | 18 | |
| 3 | 57,084.966667 | −4.5 | −0.5 | −5.5 | −9.5 | 37.5 | 22.5 | −3.7 | 15 |
| 4 | 57,085.963542 | −4.5 | −0.9 | −1 | −2.7 | 33 | 15 | 1.5 | 18 |
| 5 | 57,086.961458 | −3.0 | 0.2 | −1 | −0.4 | 28.5 | 13.5 | 0.8 | 15 |
| 6 | 57,087.959375 | −3.0 | 1.3 | 0.5 | 1.9 | 27 | 12 | 1.5 | 15 |
| 7 | 57,088.954167 | −7.5 | −2.1 | 4.3 | 7.1 | 24 | 3 | 9 | 21 |
| 8 | 57,089.954167 | 0.0 | 2.1 | 1.3 | 4.9 | 22.5 | 9 | 2.2 | 13.5 |
| 9 | 57,090.948958 | −7.5 | −1.3 | 1.3 | 7.2 | 18 | 3 | 6 | 15 |
| 10 | 57,091.946875 | −3.0 | −0.2 | 1.3 | 5 | 22.5 | 6 | 5.3 | 16.5 |
| 11 | 57,092.944792 | −3.0 | 0.9 | 1.4 | 5.8 | 21 | 6 | 4.5 | 15 |
| 12 | 57,093.941667 | −4.5 | 0.5 | 1.4 | 6.5 | 19.5 | 4.5 | 5.2 | 15 |
| 13 | 57,094.938542 | −4.5 | 0.1 | −0.1 | 1.3 | 27 | 9 | 4.5 | 18 |
| 14 | 57,095.934375 | −6.0 | −1.8 | −1.6 | 3.6 | 19.5 | 4.5 | 5.3 | 15 |
| 15 | 57,096.933333 | −1.5 | 0.8 | −0.1 | 4.4 | 21 | 6 | 4.5 | 15 |
| 16 | 57,097.930208 | −4.5 | 0.4 | −0.1 | 3.7 | 22.5 | 6 | 5.3 | 16.5 |
| 17 | 57,098.928125 | −3.0 | 1.6 | 29.9 | −22.6 | 135 | 33 | 34.5 | 102 |
| 18 | 57,099.923958 | −6.0 | −0.3 | −6.1 | −6.8 | 31.5 | 15 | 0.8 | 16.5 |
| 19 | 57,100.922917 | −1.5 | 2.3 | −3 | −1.5 | 27 | 12 | 1.5 | 15 |
| 20 | 57,101.917708 | −7.5 | −1.1 | −5.3 | −3.7 | 27 | 10.5 | 3 | 16.5 |
| 21 | 57,102.914583 | −4.5 | −1.5 | −3 | 0.1 | 24 | 6 | 6 | 18 |
| 22 | 57,103.912500 | −3.0 | −0.4 | −1.5 | 3.8 | 19.5 | 3 | 6.8 | 16.5 |
| 23 | 57,104.910417 | −3.0 | 0.7 | −4.5 | 0.1 | 21 | 7.5 | 3 | 13.5 |
| 24 | 57,105.906250 | −6.0 | −1.2 | −2.2 | 2.4 | 21 | 3 | 7.5 | 18 |
| 25 | 57,106.905208 | −1.5 | 1.5 | −2.2 | 1.7 | 22.5 | 6 | 5.3 | 16.5 |
| 26 | 57,107.901042 | −6.0 | −0.4 | −4.4 | −0.5 | 22.5 | 6 | 5.2 | 16.5 |
| 27 | 57,108.898958 | −3.0 | 0.7 | −3.7 | 1.7 | 19.5 | 4.5 | 5.3 | 15 |
| 28 | 57,109.895833 | −4.5 | 0.3 | −4.4 | 1 | 19.5 | 4.5 | 5.3 | 15 |
| 29 | 57,110.892708 | −4.5 | −0.1 | −5.2 | −1.2 | 22.5 | 6 | 5.3 | 16.5 |
| 30 | 57,111.889583 | −4.5 | −0.5 | 21.9 | −3.4 | 81 | 7.5 | 33 | 73.5 |
| 31 | 57,112.886458 | −4.5 | −0.9 | −4.4 | 0.3 | 21 | 3 | 7.5 | 18 |
| # | Date | Time UT | DOME | # | dN | dE | dh | 3D | Az | ROTI |
|---|---|---|---|---|---|---|---|---|---|---|
| 258 | 2015 MAR 5 | 22:58:30 UT | IRBE | 1211 | 0.017 | 0.004 | 0.105 | 0.106 | 13.2 | 0.0394 |
| OJAR | 1214 | −0.005 | −0.007 | −0.110 | 0.110 | −125.5 | 0.0403 | |||
| DAU1 | 1210 | 0.024 | 0.003 | 0.115 | 0.118 | 7.1 | 0.0384 | |||
| KREI | 1212 | −0.029 | −0.002 | −0.150 | 0.153 | −176.1 | 0.0403 | |||
| VANG | 1215 | 0.043 | 0.006 | 0.154 | 0.160 | 7.9 | 0.0403 | |||
| MAZS | 1213 | 0.059 | −0.001 | 0.219 | 0.227 | −1.0 | 0.0407 | |||
| ALUK | 1209 | −0.076 | 0.009 | −0.236 | 0.248 | 173.2 | 0.0403 |
| # | MJD | Date | Day | Time UT | Stations | Stations/Cloud | Adj. Days’ Time Lag (min) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 31 | 55,867.073958 | 2011 NOV | 2 | 1:46:29 | 4 | 4 | 0 | 4 | 0 | 4 | 0 | −4.5 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 32 | 55,867.075000 | 2011 NOV | 2 | 1:48:0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0.0 | −3.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 33 | 55,867.076042 | 2011 NOV | 2 | 1:49:30 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 50 | 55,868.070833 | 2011 NOV | 3 | 1:42:0 | 3 | 0 | 0 | 3 | 0 | 3 | 0 | 0.0 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 51 | 55,868.071875 | 2011 NOV | 3 | 1:43:29 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 52 | 55,868.072917 | 2011 NOV | 3 | 1:45:0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 53 | 55,868.073958 | 2011 NOV | 3 | 1:46:29 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0.0 | −1.5 | 0.0 | 0.0 | 0.0 | 0.0 |
| 54 | 55,868.077083 | 2011 NOV | 3 | 1:51:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 114 | 55,871.063542 | 2011 NOV | 6 | 1:31:30 | 2 | 0 | 0 | 2 | 0 | 2 | 0 | 0.0 | 0.0 | −3.0 | 0.0 | −3.0 | 0.0 |
| 115 | 55,871.064583 | 2011 NOV | 6 | 1:33:0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0.0 | −4.5 | 0.0 | 0.0 | 0.0 | 0.0 |
| 127 | 55,872.059375 | 2011 NOV | 7 | 1:25:29 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 128 | 55,872.060417 | 2011 NOV | 7 | 1:27:0 | 5 | 0 | 0 | 5 | 0 | 5 | 0 | 0.0 | 0.0 | −4.5 | 0.0 | −4.5 | 0.0 |
| 129 | 55,872.061458 | 2011 NOV | 7 | 1:28:29 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0.0 | −4.5 | 0.0 | 0.0 | 0.0 | 0.0 |
| 130 | 55,872.062500 | 2011 NOV | 7 | 1:30:0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
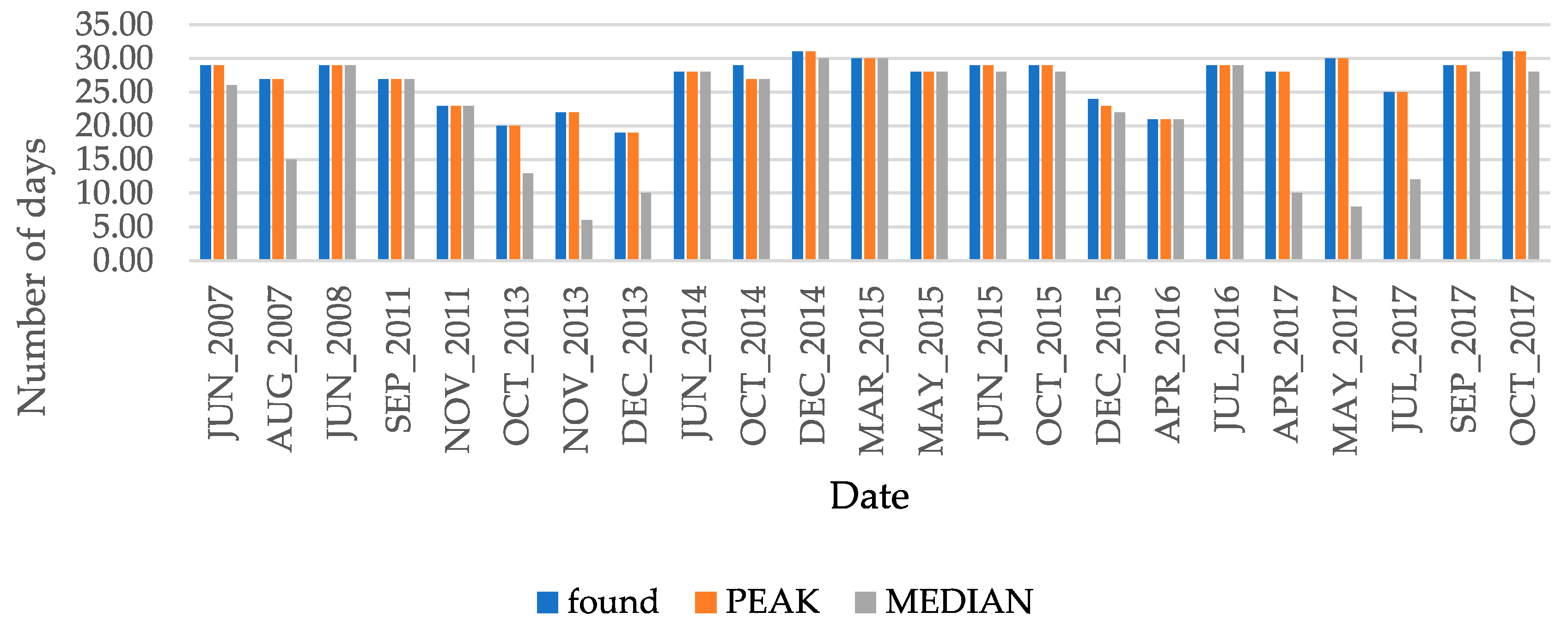
| # | Year | Month | Pred | Not | Found | Wlen | For-mean | Mean | Outliers | Thr |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2007 | JUN | 30 | 1 | 30 | 39.2 | 27 | 11.7 | 3 | 60.0 |
| 2 | 2007 | AUG | 31 | 4 | 31 | 11.6 | 31 | 11.6 | 0 | 60.0 |
| 3 | 2008 | JUN | 30 | 1 | 30 | 14.2 | 29 | 13.3 | 1 | 60.0 |
| 4 | 2011 | SEP | 30 | 3 | 28 | 36.1 | 27 | 10.4 | 3 | 60.0 |
| 5 | 2011 | NOV | 30 | 8 | 5 | 28.5 | 4 | 2.3 | 26 | 60.0 |
| 6 | 2013 | OCT | 24 | 5 | 8 | 11.4 | 8 | 11.4 | 16 | 60.0 |
| 7 | 2013 | NOV | 30 | 8 | 26 | 31.6 | 24 | 3.4 | 6 | 60.0 |
| 8 | 2013 | DEC | 31 | 2 | 23 | 41.2 | 20 | 2.4 | 11 | 60.0 |
| 9 | 2014 | JUN | 30 | 2 | 30 | 26.8 | 29 | 25.4 | 1 | 60.0 |
| 10 | 2014 | OCT | 31 | 2 | 31 | 82.2 | 28 | 14.6 | 3 | 60.0 |
| 11 | 2014 | DEC | 31 | 0 | 31 | 57.6 | 24 | 25.3 | 7 | 60.0 |
| 12 | 2015 | MAR | 31 | 1 | 31 | 29.1 | 29 | 23.6 | 2 | 60.0 |
| 13 | 2015 | MAY | 31 | 3 | 31 | 22.6 | 29 | 10.2 | 2 | 60.0 |
| 14 | 2015 | JUN | 30 | 1 | 30 | 45.0 | 28 | 13.9 | 2 | 60.0 |
| 15 | 2015 | OCT | 31 | 2 | 30 | 57.6 | 26 | 6.1 | 5 | 60.0 |
| 16 | 2015 | DEC | 31 | 7 | 9 | 34.7 | 8 | 3.0 | 23 | 60.0 |
| 17 | 2016 | APR | 30 | 9 | 6 | 6.9 | 6 | 9.2 | 24 | 60.0 |
| 18 | 2016 | JUL | 31 | 2 | 28 | 28.3 | 25 | 8.9 | 6 | 60.0 |
| 19 | 2017 | APR | 30 | 2 | 28 | 57.6 | 25 | 11.0 | 5 | 60.0 |
| 20 | 2017 | MAY | 31 | 1 | 31 | 129.0 | 24 | 14.9 | 7 | 60.0 |
| 21 | 2017 | JUL | 31 | 6 | 31 | 143.2 | 26 | 16.8 | 5 | 60.0 |
| 22 | 2017 | SEP | 30 | 1 | 30 | 23.3 | 27 | 9.0 | 3 | 60.0 |
| 23 | 2017 | OCT | 31 | 0 | 28 | 33.8 | 24 | 5.6 | 7 | 60.0 |
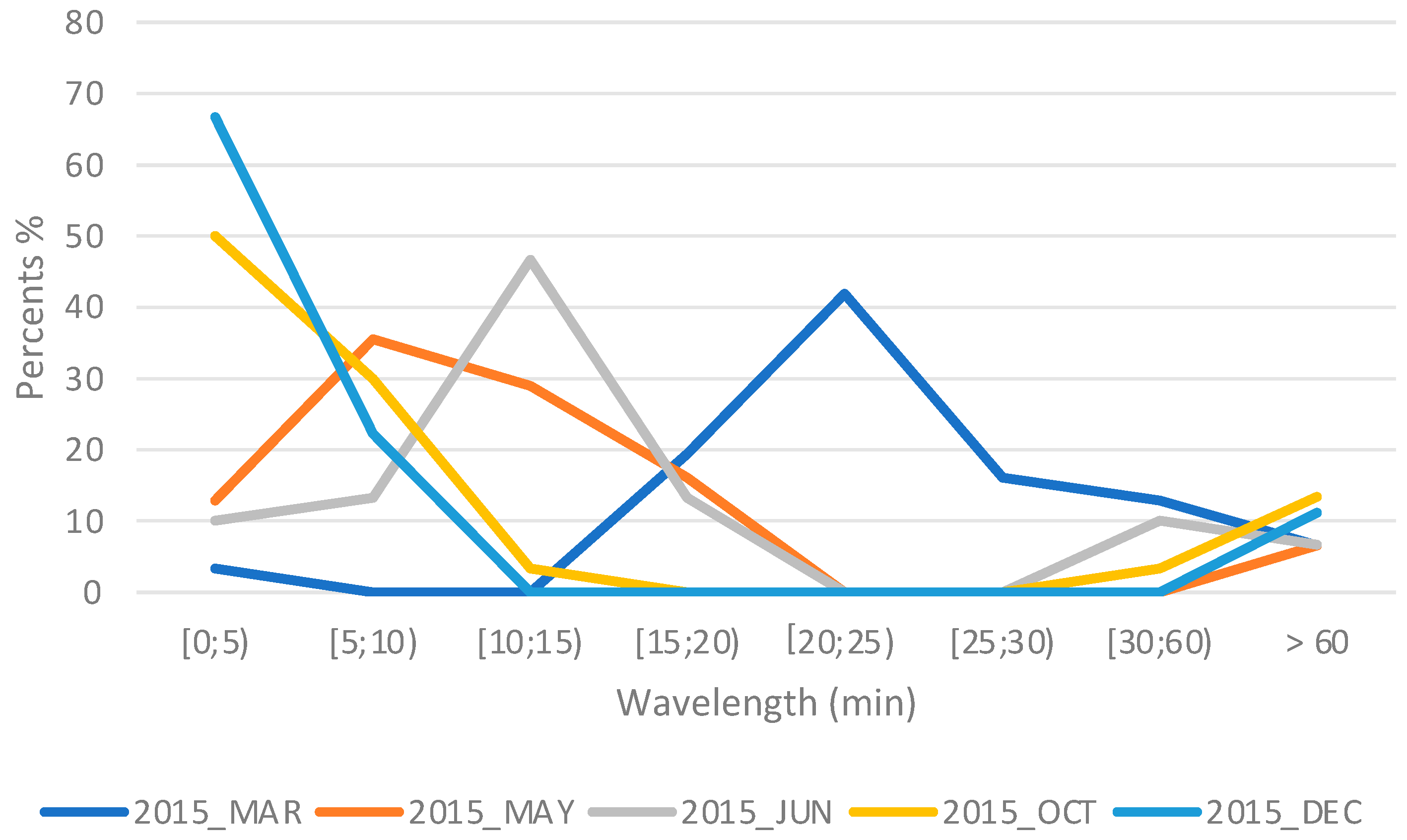
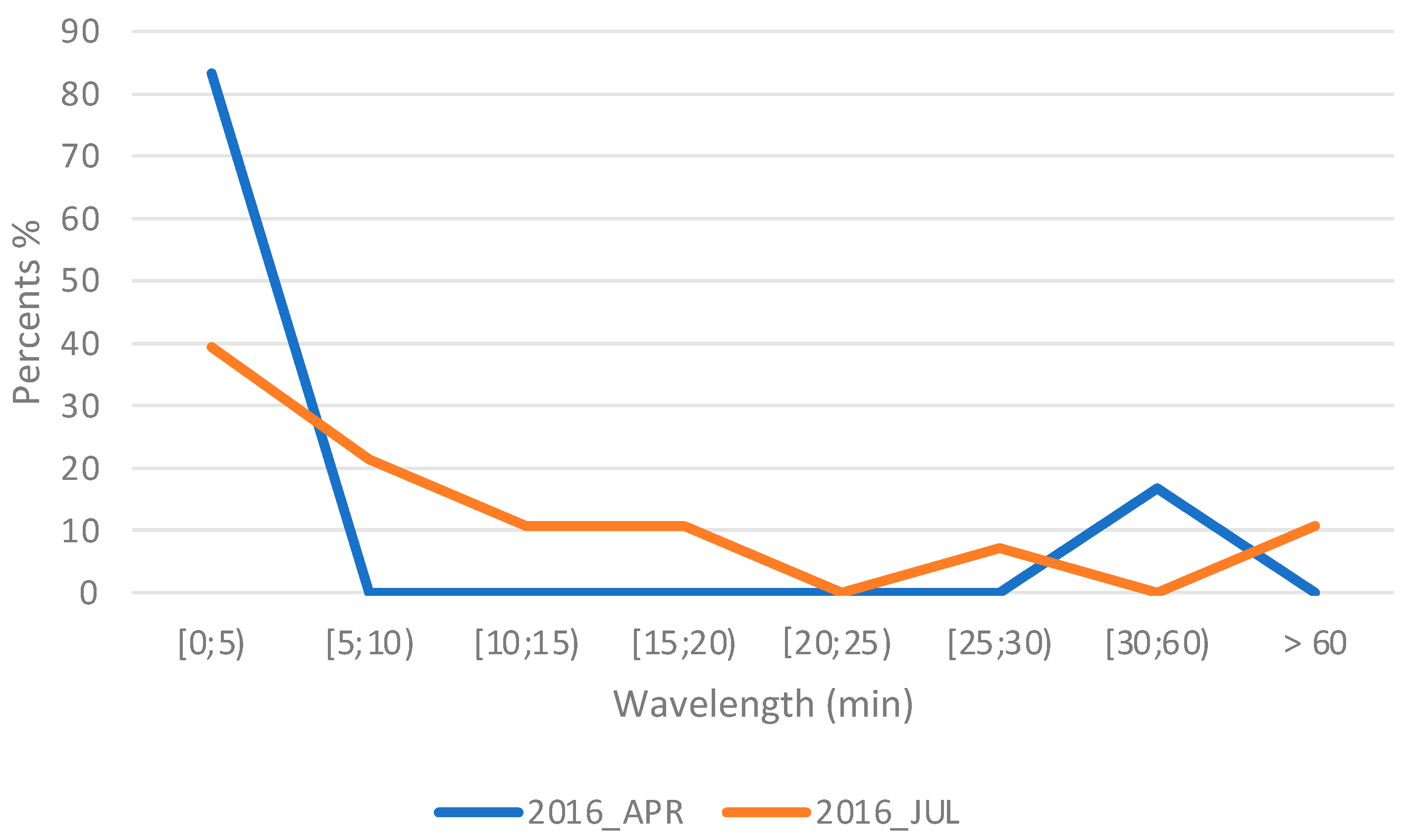
| Year | Month | [0; 5) | [5; 10) | [10; 15) | [15; 20) | [20; 25) | [25;30) | [30; 60) | >60 |
|---|---|---|---|---|---|---|---|---|---|
| 2007 | JUN | 10.0 | 20.0 | 33.3 | 26.7 | 0.0 | 0.0 | 0.0 | 10.0 |
| 2007 | AUG | 6.5 | 35.4 | 32.3 | 19.4 | 3.2 | 3.2 | 0.0 | 0.0 |
| 2008 | JUN | 0.0 | 20.0 | 60.1 | 6.7 | 3.3 | 3.3 | 3.3 | 3.3 |
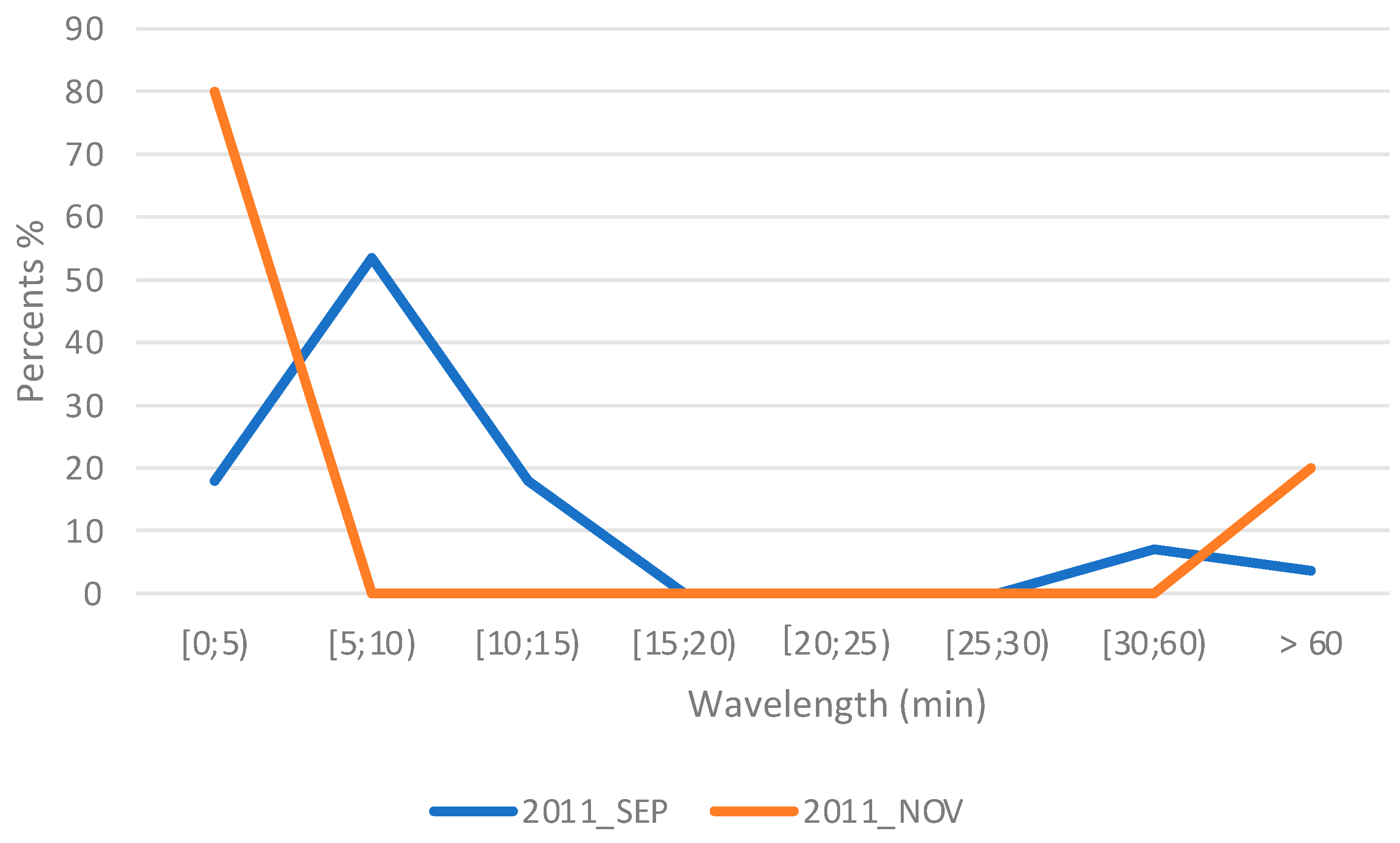
| 2011 | SEP | 17.9 | 53.5 | 17.9 | 0.0 | 0.0 | 0.0 | 7.1 | 3.6 |
| 2011 | NOV | 80.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 20.0 |
| 2013 | OCT | 62.5 | 12.5 | 0.0 | 0.0 | 12.5 | 0.0 | 12.5 | 0.0 |
| 2013 | NOV | 69.3 | 19.2 | 3.8 | 0.0 | 0.0 | 0.0 | 0.0 | 7.7 |
| 2013 | DEC | 82.7 | 0.0 | 4.3 | 0.0 | 0.0 | 0.0 | 0.0 | 13.0 |
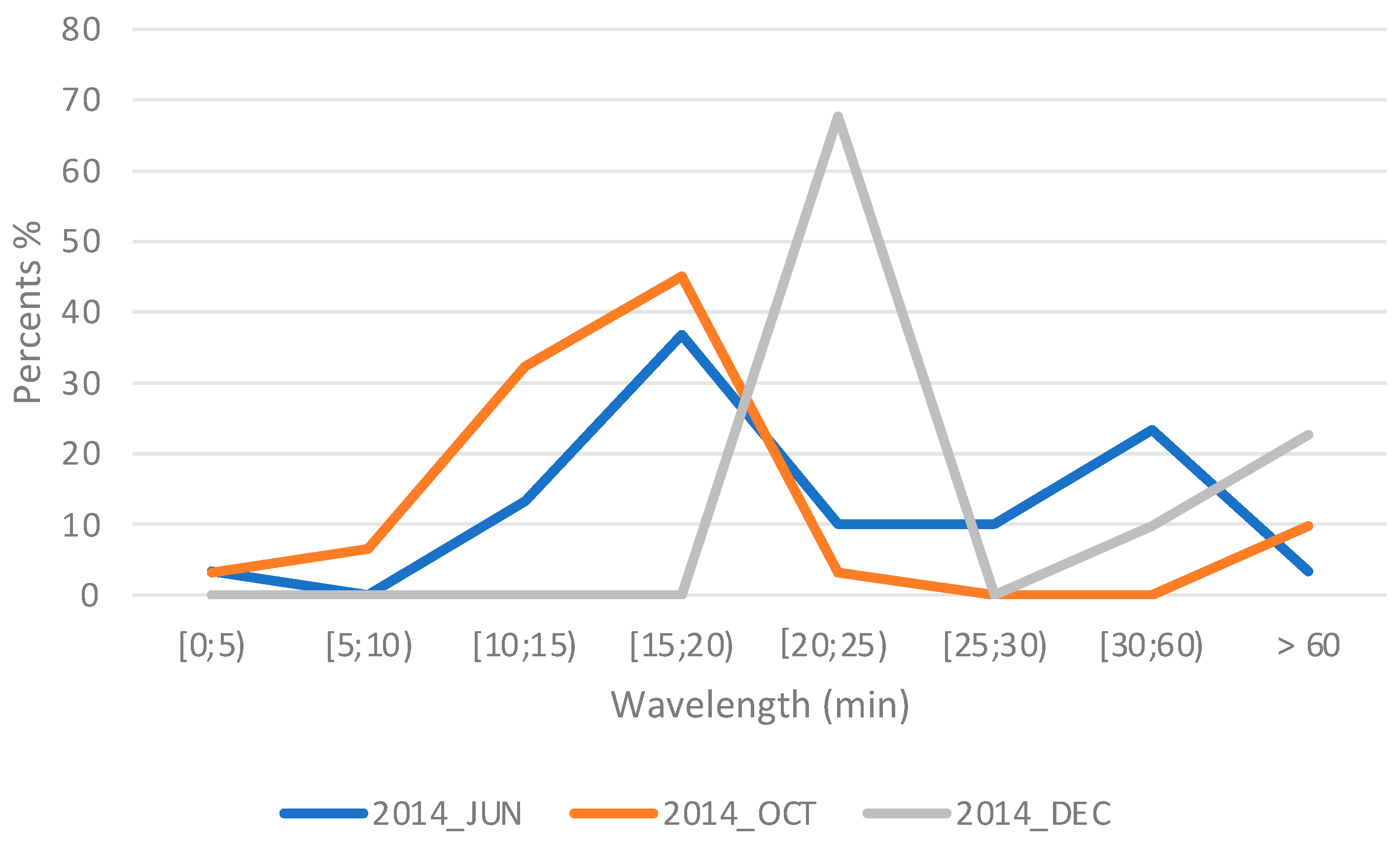
| 2014 | JUN | 3.3 | 0.0 | 13.3 | 36.8 | 10.0 | 10.0 | 23.3 | 3.3 |
| 2014 | OCT | 3.2 | 6.5 | 32.3 | 45.1 | 3.2 | 0.0 | 0.0 | 9.7 |
| 2014 | DEC | 0.0 | 0.0 | 0.0 | 0.0 | 67.7 | 0.0 | 9.7 | 22.6 |
| 2015 | MAR | 3.3 | 0.0 | 0.0 | 19.4 | 41.9 | 16.1 | 12.9 | 6.5 |
| 2015 | MAY | 12.9 | 35.5 | 29.0 | 16.1 | 0.0 | 0.0 | 0.0 | 6.5 |
| 2015 | JUN | 10.0 | 13.3 | 46.7 | 13.3 | 0.0 | 0.0 | 10.0 | 6.7 |
| 2015 | OCT | 50.0 | 30.0 | 3.3 | 0.0 | 0.0 | 0.0 | 3.3 | 13.4 |
| 2015 | DEC | 66.7 | 22.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 11.1 |
| 2016 | APR | 83.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 16.7 | 0.0 |
| 2016 | JUL | 39.4 | 21.4 | 10.7 | 10.7 | 0.0 | 7.1 | 0.0 | 10.7 |
| 2017 | APR | 0.0 | 25.0 | 57.2 | 7.1 | 0.0 | 0.0 | 0.0 | 10.7 |
| 2017 | MAY | 0.0 | 0.0 | 61.3 | 9.7 | 3.2 | 0.0 | 3.2 | 22.6 |
| 2017 | JUL | 3.2 | 0.0 | 42.0 | 25.8 | 3.2 | 3.2 | 6.5 | 16.1 |
| 2017 | SEP | 10.0 | 50.0 | 23.4 | 3.3 | 3.3 | 0.0 | 0.0 | 10.0 |
| 2017 | OCT | 42.8 | 35.7 | 3.6 | 3.6 | 0.0 | 0.0 | 0.0 | 14.3 |
| AVERAGE | 28.6 | 17.4 | 20.6 | 10.6 | 6.6 | 1.9 | 4.7 | 9.6 | |
| TEC and Cycle Slips | TEC and Faulty Solutions | TEC and Cycle Slips from Faulty Solutions | Cycle Slips and Faulty Solutions | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] | [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] | [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] | [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] |
| 18 | 5 | 0 | 23 | 18 | 4 | 0 | 24 | 25 | 4 | 0 | 17 | 25 | 1 | 2 | 18 |
| 19 | 5 | 0 | 22 | 16 | 6 | 0 | 24 | 26 | 3 | 0 | 17 | 21 | 0 | 2 | 23 |
| ROTI and Cycle Slips | ROTI and Faulty Solutions | ROTI and Cycle Slips from Faulty Solutions | ROTI and TEC | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] | [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] | [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] | [0; 0.4) | [0.4; 0.7) | [0.7; 1] | (0; −1] |
| 18 | 5 | 3 | 8 | 13 | 6 | 1 | 14 | 15 | 4 | 1 | 14 | 18 | 7 | 0 | 9 |
| # | Date | Time UT | Stations | ROTI@ground | Mean Discr (m) |
|---|---|---|---|---|---|
| 1328 | 23 MAR 2015 | 21:43:29 | 2 | 0.0190 | 0.061 |
| 1329 | 23 MAR 2015 | 21:45:0 | 3 | 0.0325 | 0.246 |
| 1330 | 23 MAR 2015 | 21:46:30 | 7 | 0.0379 | 0.341 |
| 1331 | 23 MAR 2015 | 21:48:0 | 13 | 0.0386 | 1.783 |
| 1332 | 23 MAR 2015 | 21:49:29 | 23 | 0.0386 | 0.963 |
| 1333 | 23 MAR 2015 | 21:51:0 | 29 | 0.0389 | 0.408 |
| 1334 | 23 MAR 2015 | 21:52:29 | 18 | 0.0390 | 0.326 |
| 1335 | 23 MAR 2015 | 21:54:0 | 16 | 0.0394 | 0.213 |
| 1336 | 23 MAR 2015 | 21:55:30 | 14 | 0.0392 | 0.197 |
| 1337 | 23 MAR 2015 | 21:57:0 | 9 | 0.0391 | 0.169 |
| 1338 | 23 MAR 2015 | 21:58:30 | 14 | 0.0394 | 0.165 |
| 1339 | 23 MAR 2015 | 22:0:0 | 6 | 0.0391 | 0.182 |
| 1340 | 23 MAR 2015 | 22:1:29 | 7 | 0.0398 | 0.140 |
| 1341 | 23 MAR 2015 | 22:3:0 | 2 | 0.0395 | 0.167 |
| 1342 | 23 MAR 2015 | 22:4:30 | 3 | 0.0390 | 0.150 |
| 22 WAVE No. 1328 | AVERAGE | 0.0373 | 0.368 |
| # | Date | Time UT | Stations | ROTI@ground | Mean Discr (m) |
|---|---|---|---|---|---|
| 63 | 4 NOV 2011 | 1:39:0 | 6 | 0.0334 | 0.179 |
| 64 | 4 NOV 2011 | 1:40:30 | 3 | 0.0391 | 0.160 |
| 3 WAVE No 63 | AVERAGE | 0.0363 | 0.169 | ||
| 114 | 6 NOV 2011 | 1:31:30 | 2 | 0.0173 | 0.097 |
| 115 | 6 NOV 2011 | 1:33:0 | 2 | 0.0255 | 0.141 |
| 4 WAVE No 114 | AVERAGE | 0.0214 | 0.119 | ||
| 127 | 7 NOV 2011 | 1:25:29 | 2 | 0.0187 | 0.066 |
| 128 | 7 NOV 2011 | 1:27:0 | 5 | 0.0343 | 0.159 |
| 129 | 7 NOV 2011 | 1:28:29 | 2 | 0.0353 | 0.147 |
| 5 WAVE No. 127 | AVERAGE | 0.0294 | 0.124 |
| Date | ROTI@ground | Discr | TEC | CSLP | Date | ROTI@ground | Discr | TEC | CSLP |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.0386 | 0.271 | 31 | 2 | 17 | 0.0532 | 3.993 | 40 | 29 |
| 3 | 0.0383 | 0.378 | 29.4 | 3 | 18 | 0.0387 | 1.423 | 18.4 | 2 |
| 4 | 0.0385 | 1.202 | 31.9 | 3 | 19 | 0.0379 | 0.329 | 25.2 | 5 |
| 5 | 0.0396 | 0.422 | 33.8 | 1 | 20 | 0.0366 | 0.301 | 19.9 | 2 |
| 6 | 0.0409 | 0.334 | 35.1 | 3 | 21 | 0.0386 | 0.371 | 25 | 2 |
| 7 | 0.0382 | 0.354 | 31.2 | 3 | 22 | 0.0373 | 0.64 | 33.5 | 1 |
| 8 | 0.0413 | 0.363 | 34.7 | 0 | 23 | 0.0419 | 0.368 | 31.7 | 1 |
| 9 | 0.0398 | 0.424 | 28 | 2 | 24 | 0.0404 | 0.343 | 32.3 | 2 |
| 10 | 0.0391 | 0.672 | 30.2 | 2 | 25 | 0.0396 | 1.495 | 32.9 | 2 |
| 11 | 0.0428 | 0.822 | 31.3 | 2 | 26 | 0.0413 | 0.407 | 33.3 | 0 |
| 12 | 0.0413 | 0.686 | 30 | 2 | 27 | 0.0388 | 0.38 | 30.9 | 2 |
| 13 | 0.0414 | 0.306 | 33.4 | 0 | 28 | 0.0368 | 0.466 | 36.4 | 3 |
| 14 | 0.039 | 0.597 | 30.3 | 1 | 29 | 0.0372 | 0.641 | 35.6 | 1 |
| 15 | 0.5576 | 0.414 | 30 | 0 | 30 | 0.0374 | 0.4 | 29 | 1 |
| 16 | 0.1046 | 0.318 | 29.3 | 2 | 31 | 0.0372 | 0.932 | 36.3 | 0 |
| # | Time Span | Daily Shift (day) | Daily Shift (min) |
|---|---|---|---|
| 1 | JUN 2007–30 AUG 2007 | 0.997210 | –4.0 |
| 2 | SEP 2011–28 NOV 2011 | 0.997195 | –4.0 |
| 3 | OCT 2013–23 DEC 2013 | 0.997055 | –4.2 |
| 4 | JUN 2014–30 DEC 2014 | 0.997155 | –4.1 |
| 5 | MAR 2015–31 DEC 2015 | 0.997177 | –4.1 |
| 6 | APR 2016–30 JUL 2016 | 0.997153 | –4.1 |
| 7 | APR 2017–30 OCT 2017 | 0.997145 | –4.1 |
| Average | 0.997156 | ||
| STDV | 0.000046 | 0.1 min |
| # | Date of Pc1 Waves | Pc1 Waves | Dur. (min) | CPS d. Waves | Dur. (min) |
|---|---|---|---|---|---|
| 1 | 4 November 2011 | 1 | 10 | 1 | 1.5 |
| 2 | 29 November 2011 | 1 | 30 | 1 | 7.5 |
| 3 | 18 March 2015 | 2 | 12 | 1 | 31.5 |
| 4 | 19 March 2015 | 4 | 10 | 3 | 3; 27; 4.1 |
| 5 | 23 March 2015 | 4 | 46 | 1 | 21 |
| 6 | 29 March 2015 | 3 | 19 | 1 | 22.5 |
| 7 | 25 June 2015 | 1 | 2 | 3 | 12; 4.5; 6 |
| 8 | 28 June 2015 | 1 | 4 | 4 | 1.5; 3; 4.5; 607.5 |
| 9 | 3 April 2017 | 1 | 8 | 2 | 1.5; 7.5 |
| 10 | 9 April 2017 | 1 | 88 | 2 | 16.6; 16.5 |
| 11 | 26 April 2017 | 1 | 10 | 3 | 255; 1.5; 10.5 |
| 12 | 27 April 2017 | 1 | 10 | 1 | 12 |
| 13 | 19 May 2017 | 1 | 36 | 6 | 82.5; 3; 1.5; 16.5; 126; 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balodis, J.; Normand, M.; Mitrofanovs, I. Discovery of Regular Daily Ionospheric Scintillation. Atmosphere 2025, 16, 1330. https://doi.org/10.3390/atmos16121330
Balodis J, Normand M, Mitrofanovs I. Discovery of Regular Daily Ionospheric Scintillation. Atmosphere. 2025; 16(12):1330. https://doi.org/10.3390/atmos16121330
Chicago/Turabian StyleBalodis, Janis, Madara Normand, and Ingus Mitrofanovs. 2025. "Discovery of Regular Daily Ionospheric Scintillation" Atmosphere 16, no. 12: 1330. https://doi.org/10.3390/atmos16121330
APA StyleBalodis, J., Normand, M., & Mitrofanovs, I. (2025). Discovery of Regular Daily Ionospheric Scintillation. Atmosphere, 16(12), 1330. https://doi.org/10.3390/atmos16121330







