Modulation of the Semi-Annual Oscillation by Stratospheric Sudden Warmings as Seen in the High-Altitude JAWARA Re-analyses
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
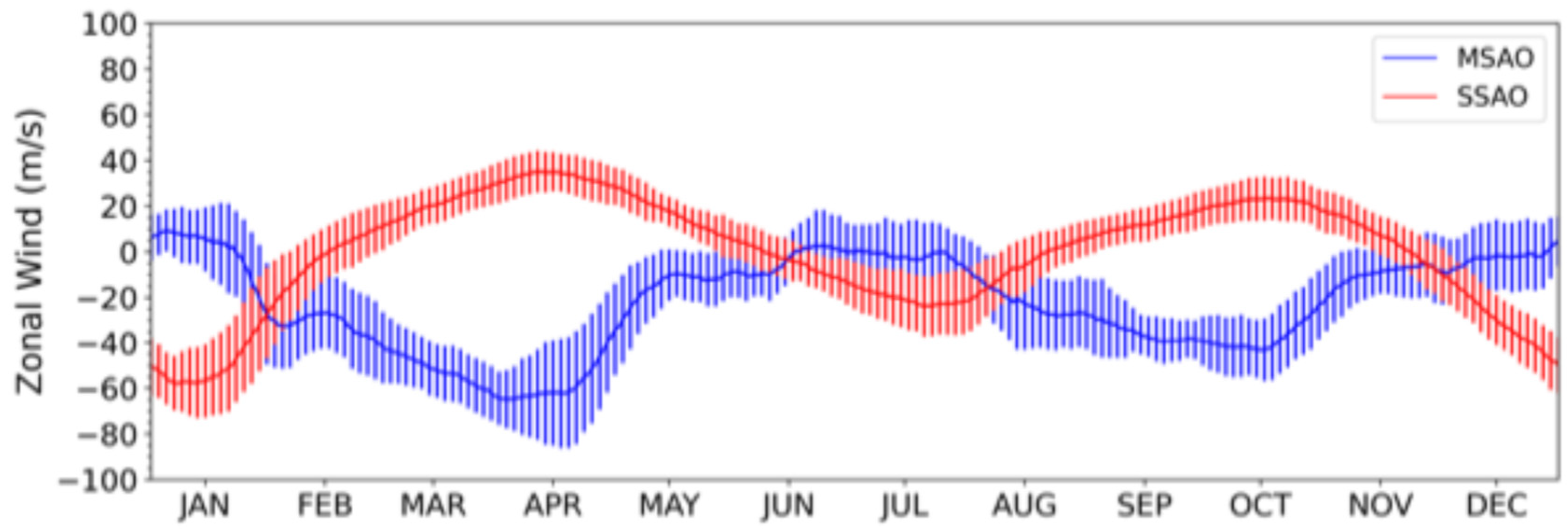
- The basic features of the SAO are well captured by JAWARA. Throughout the entire period from 2004 to 2024, SSAO and MSAO are evident at about 50 km and 85 km, respectively. As expected, the first cycle for both components is stronger than the second cycle.
- A strong response in SAO is identified during the NH winter of 2023/24. At 50 km, the equatorial zonal-mean zonal winds are anomalously strong, i.e., more westward than climatology, at the onset of the mid-January SSW and anomalously weak (eastward) at the onset of the March SSW. At 85 km, the eastward zonal winds are anomalously stronger than climatology in December and January, in agreement with the composite, except for a brief reversal “hiccup” period (Figures S2 and S3). Following the early March SSW, zonal winds are westward and slightly weaker than climatology, in agreement with the composite.
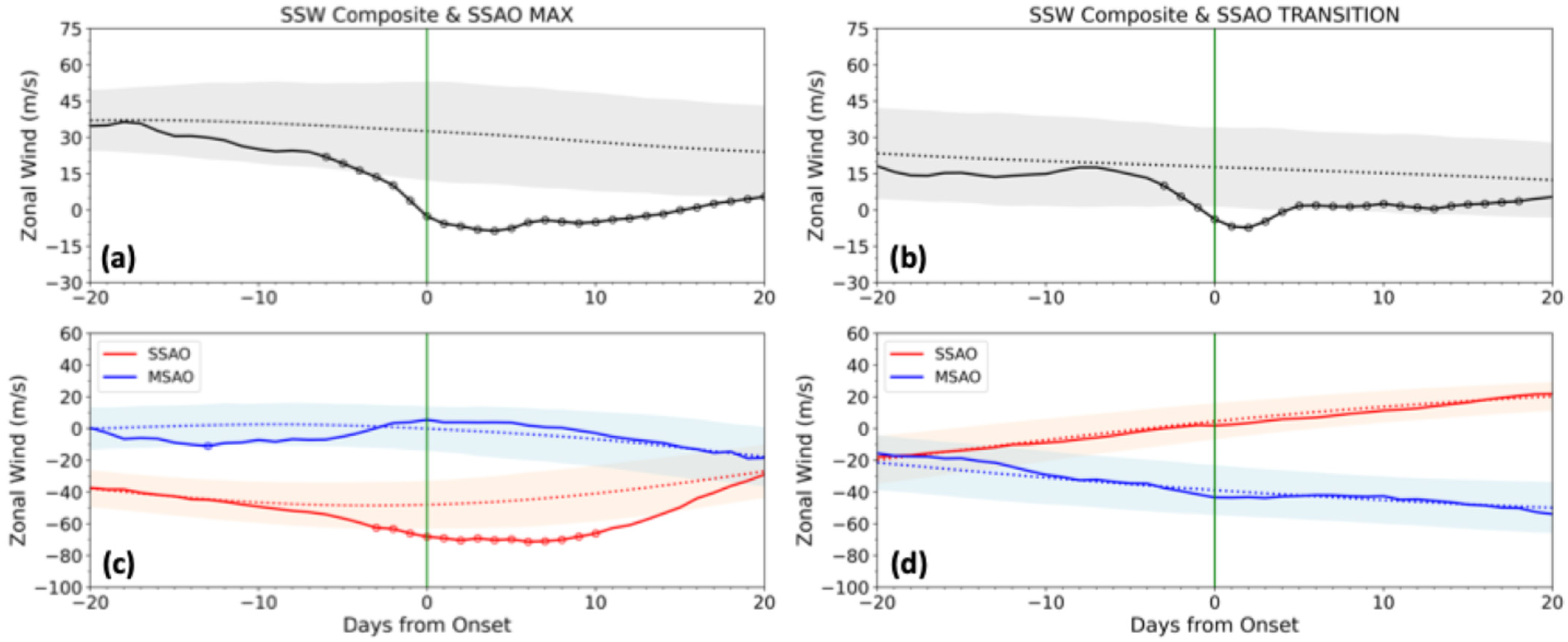
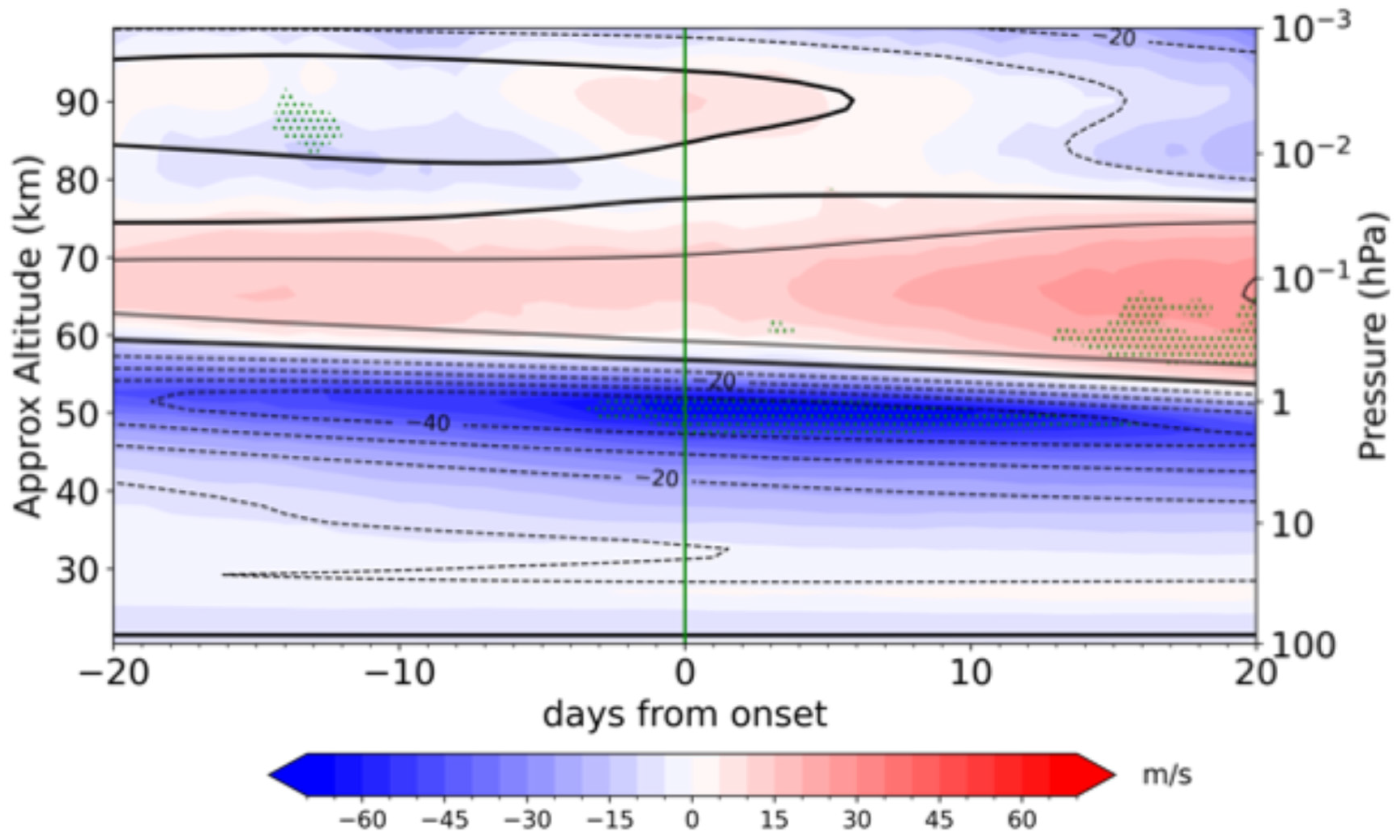
- The SSW composite shows that early winter SSWs tend to significantly intensify the westward SSAO, while late winter SSWs tend to weaken the eastward SSAO. On the other hand, the eastward MSAO is amplified during early winter SSWs, while the westward MSAO is slightly weakened during late winter SSWs. The weak MSAO response is probably due to its smaller climatological magnitude.
- The residual mean meridional circulation changes associated with SSWs explain how early winter SSWs modulate the SAO. Resolved and GW forcings drive a pair of residual circulation cells, with a lower stratospheric cell characterized by poleward and upward motions and an opposite cell aloft. The anomalous upward (downward) motion in the stratosphere (mesosphere) induces cooling below 50 km (warming above 50 km) at the equator. The meridional temperature curvature induces westward (eastward) acceleration in the SSAO (MSAO) through thermal wind balance, thereby amplifying the SSAO and MSAO.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reed, R.J. Zonal wind behavior in the equatorial stratosphere and lower mesosphere. J. Geophys. Res. 1966, 71, 4223–4233. [Google Scholar] [CrossRef]
- Venkateswara Rao, N.; Tsuda, T.; Riggin, D.M.; Gurubaran, S.; Reid, I.M.; Vincent, R.A. Long-term variability of mean winds in the mesosphere and lower thermosphere at low latitudes. J. Geophys. Res. Space Phys. 2012, 117, A10312. [Google Scholar] [CrossRef]
- Ray, E.A.; Alexander, M.J.; Holton, J.R. An analysis of the structure and forcing of the equatorial semiannual oscillation in zonal wind. J. Geophys. Res. Atmos. 1998, 103, 1759–1774. [Google Scholar] [CrossRef]
- Hirota, I. Equatorial waves in the upper stratosphere and mesosphere in relation to the semiannual oscillation of the zonal wind. J. Atmos. Sci. 1978, 35, 714–722. [Google Scholar] [CrossRef]
- Hirota, I. Observational evidence of the semiannual oscillation in the tropical middle atmosphere—A review. Pure Appl. Geophys. 1980, 118, 217–238. [Google Scholar] [CrossRef]
- Garcia, R.R.; Dunkerton, T.J.; Lieberman, R.S.; Vincent, R.A. Climatology of the semiannual oscillation of the tropical middle atmosphere. J. Geophys. Res. Atmos. 1997, 102, 26019–26032. [Google Scholar] [CrossRef]
- Smith, A.K.; Garcia, R.R.; Moss, A.C.; Mitchell, N.J. The semiannual oscillation of the tropical zonal wind in the middle atmosphere derived from satellite geopotential height retrievals. J. Atmos. Sci. 2017, 74, 2413–2425. [Google Scholar] [CrossRef]
- Smith, A.K.; Gray, L.J.; Garcia, R.R. Evidence for the influence of the quasi-biennial oscillation on the semiannual oscillation in the tropical middle atmosphere. J. Atmos. Sci. 2023, 80, 1755–1769. [Google Scholar] [CrossRef]
- Vorobeva, E.; Orsolini, Y. The impact of tropospheric blocking on the duration of the sudden stratospheric warmings in boreal winter 2023/24. Weather Clim. Dyn. 2025, 6, 1015–1026. [Google Scholar] [CrossRef]
- Qian, L.; Rao, J.; Ren, R.; Shi, C.; Liu, S. Enhanced stratosphere-troposphere and tropics-Arctic couplings in the 2023/24 winter. Commun. Earth Environ. 2024, 5, 631. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Y.; Pautet, P.D.; Scherliess, L.; Taylor, M.J.; Liu, H. Gravity wave activity during the 2024 sudden stratospheric warmings observed by atmospheric waves experiment (AWE). Geophys. Res. Lett. 2025, 52, e2024GL114187. [Google Scholar] [CrossRef]
- Zorkaltseva, O.S.; Antokhina, O.Y.; Gochakov, A.V.; Artamonov, M.F. Evolution of the stratospheric polar vortex as evidenced by the winters 2022–2024. Sol.-Terr. Phys. 2025, 11, 78–87. [Google Scholar]
- Charlton, A.J.; Polvani, L.M. A new look at stratospheric sudden warmings. Part I: Climatology and modeling benchmarks. J. Clim. 2007, 20, 449–469. [Google Scholar] [CrossRef]
- Koshin, D.; Sato, K.; Watanabe, S.; Miyazaki, K. The JAGUAR-DAS whole neutral atmosphere reanalysis: JAWARA. Prog. Earth Planet. Sci. 2025, 12, 1. [Google Scholar] [CrossRef]
- Dunkerton, T. On the role of the Kelvin wave in the westerly phase of the semiannual zonal wind oscillation. J. Atmos. Sci. 1979, 36, 32–41. [Google Scholar] [CrossRef]
- Holton, J.R.; Wehrbein, W.M. A numerical model of the zonal mean circulation of the middle atmosphere. Pure Appl. Geophys. 1980, 118, 284–306. [Google Scholar] [CrossRef]
- Hamilton, K.; Mahlman, J.D. General circulation model simulation of the semiannual oscillation of the tropical middle atmosphere. J. Atmos. Sci. 1988, 45, 3212–3235. [Google Scholar] [CrossRef]
- Hitchman, M.H.; Leovy, C.B. Estimation of the Kelvin wave contribution to the semiannual oscillation. J. Atmos. Sci. 1988, 45, 1462–1475. [Google Scholar] [CrossRef]
- Garcia, R.R. The role of equatorial waves in the semiannual oscillation of the middle atmosphere. Geophys. Monogr. Ser. 2000, 123, 161–176. [Google Scholar]
- Ern, M.; Diallo, M.; Preusse, P.; Mlynczak, M.G.; Schwartz, M.J.; Wu, Q.; Riese, M. The semiannual oscillation (SAO) in the tropical middle atmosphere and its gravity wave driving in reanalyses and satellite observations. Atmos. Chem. Phys. Discuss. 2021, 2021, 13763–13795. [Google Scholar] [CrossRef]
- Sato, K.; Koshin, D.; Suclupe, J.; Chau, J.L.; Lima, L.M.; Li, G.; Rao, S.V.B.; Ratnam, M.V.; Rodriguez, R.; Scipion, D. Causes of the abnormally strong easterly phase of the mesopause semiannual oscillation during the March equinox of 2023 revealed by a new reanalysis data covering the entire middle atmosphere. Geophys. Res. Lett. 2025, 52, e2025GL114658. [Google Scholar] [CrossRef]
- Limpasuvan, V.; Thompson, D.W.; Hartmann, D.L. The life cycle of the Northern Hemisphere sudden stratospheric warmings. J. Clim. 2004, 17, 2584–2596. [Google Scholar] [CrossRef]
- Sato, K.; Tomikawa, Y.; Kohma, M.; Yasui, R.; Koshin, D.; Okui, H.; Watanabe, S.; Miyazaki, K.; Tsutsumi, M.; Murphy, D.; et al. Interhemispheric Coupling Study by Observations and Modelling (ICSOM): Concept, campaigns, and initial results. J. Geophys. Res. Atmos. 2023, 128, e2022JD038249. [Google Scholar] [CrossRef]
- Kawatani, Y.; Hamilton, K.; Miyazaki, K.; Fujiwara, M.; Anstey, J.A. Representation of the tropical stratospheric zonal wind in global atmospheric reanalyses. Atmos. Chem. Phys. 2016, 16, 6681–6699. [Google Scholar] [CrossRef]
- Andrews, D.G.; Leovy, C.B.; Holton, J.R. Middle Atmosphere Dynamics; Academic Press: Cambridge, MA, USA, 1987; Volume 40. [Google Scholar]
- Newman, P.A.; Coy, L.; Pawson, S.; Lait, L.R. The anomalous change in the QBO in 2015–2016. Geophys. Res. Lett. 2016, 43, 8791–8797. [Google Scholar] [CrossRef]
- North, G.R.; Pyle, J.A.; Zhang, F. (Eds.) Encyclopedia of Atmospheric Sciences; Elsevier: Amsterdam, The Netherlands, 2014; Volume 1. [Google Scholar]
- Gray, L.J.; Brown, M.J.; Knight, J.; Andrews, M.; Lu, H.; O’Reilly, C.; Anstey, J. Forecasting extreme stratospheric polar vortex events. Nat. Commun. 2020, 11, 4630. [Google Scholar] [CrossRef] [PubMed]
- Gray, L.J.; Lu, H.; Brown, M.J.; Knight, J.R.; Andrews, M.B. Mechanisms of influence of the Semi-Annual Oscillation on stratospheric sudden warmings. Q. J. R. Meteorol. Soc. 2022, 148, 1223–1241. [Google Scholar] [CrossRef]
- Rhodes, C.T.; Limpasuvan, V.; Orsolini, Y. The composite response of traveling planetary waves in the middle atmosphere surrounding sudden stratospheric warmings through an overreflection perspective. J. Atmos. Sci. 2023, 80, 2635–2652. [Google Scholar] [CrossRef]
- Jaison, A.M.; Gray, L.J.; Osprey, S.; Smith, A.K.; Garcia, R.R. A momentum budget study of the semi-annual oscillation in the Whole Atmosphere Community Climate Model. Q. J. R. Meteorol. Soc. 2024, 150, 3544–3565. [Google Scholar] [CrossRef]
- Koushik, N.; Kumar, K.K.; Pramitha, M. A tropical stratopause precursor for sudden stratospheric warmings. Sci. Rep. 2022, 12, 2937. [Google Scholar] [CrossRef]
- Suclupe, J.; Chau, J.L.; Conte, J.F.; Pedatella, N.M.; Garcia, R.; Sato, K.; Zülicke, C.; Lima, L.M.; Li, G.; Rao, S.V.B.; et al. On the abnormally strong westward phase of the mesospheric semiannual oscillation at low latitudes during March equinox 2023. Geophys. Res. Lett. 2024, 51, e2024GL110331. [Google Scholar] [CrossRef]



| Year | January | February | March |
|---|---|---|---|
| 2004–2005 | |||
| 2005–2006 | 21 January 2006 | ||
| 2006–2007 | 24 February 2007 | ||
| 2007–2008 | 22 February 2008 | 28 March 2008 | |
| 2008–2009 | 24 January 2009 | ||
| 2009–2010 | 9 February 2010 | 24 March 2010 | |
| 2010–2011 | |||
| 2011–2012 | |||
| 2012–2013 | 6 January 2013 | ||
| 2013–2014 | |||
| 2014–2015 | |||
| 2015–2016 | |||
| 2016–2017 | |||
| 2017–2018 | 12 February 2018 | 20 March 2018 | |
| 2018–2019 | 1 January 2019 | ||
| 2019–2020 | |||
| 2020–2021 | 5 January 2021 | 1 February 2021 | |
| 2021–2022 | |||
| 2022–2023 | 16 February 2023 | ||
| 2023–2024 | 16 January 2024 | 4 March 2024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Orsolini, Y.; Sato, K. Modulation of the Semi-Annual Oscillation by Stratospheric Sudden Warmings as Seen in the High-Altitude JAWARA Re-analyses. Atmosphere 2025, 16, 1320. https://doi.org/10.3390/atmos16121320
Zhang J, Orsolini Y, Sato K. Modulation of the Semi-Annual Oscillation by Stratospheric Sudden Warmings as Seen in the High-Altitude JAWARA Re-analyses. Atmosphere. 2025; 16(12):1320. https://doi.org/10.3390/atmos16121320
Chicago/Turabian StyleZhang, Jiarong, Yvan Orsolini, and Kaoru Sato. 2025. "Modulation of the Semi-Annual Oscillation by Stratospheric Sudden Warmings as Seen in the High-Altitude JAWARA Re-analyses" Atmosphere 16, no. 12: 1320. https://doi.org/10.3390/atmos16121320
APA StyleZhang, J., Orsolini, Y., & Sato, K. (2025). Modulation of the Semi-Annual Oscillation by Stratospheric Sudden Warmings as Seen in the High-Altitude JAWARA Re-analyses. Atmosphere, 16(12), 1320. https://doi.org/10.3390/atmos16121320






