Abstract
We investigate the excitation and variability of migrating and non-migrating diurnal and semi-diurnal tides in the mesosphere and lower thermosphere (MLT) during the 2021 Northern Hemisphere sudden stratospheric warming (SSW). Zonal wind data from MERRA-2 reanalysis are decomposed into tidal components using a two-dimensional least-squares harmonic fitting technique. The migrating diurnal tide (DW1) strengthens at low latitudes following the SSW onset, whereas the migrating semi-diurnal tide (SW2) intensifies at high latitudes. Non-migrating diurnal tides (D0, DW2, DW3) arise from nonlinear interactions between DW1 and stationary planetary waves (SPWs), while non-migrating semi-diurnal tides (SW1, SW3) are modulated by stratospheric ozone variability linked to planetary-wave activity. The zonally symmetric semi-diurnal tide (S0) responds primarily to dynamical perturbations associated with the SSW. Eastward non-migrating diurnal tides (DE2, DE3) correlate strongly with total precipitable water vapor (TPWV), indicating tropospheric latent-heat forcing, whereas DE1 exhibits weak coupling. These results reveal distinct, latitude-dependent excitation pathways connecting stratospheric and tropospheric dynamics to tidal variability in the MLT during major SSW events.
1. Introduction
Atmospheric tides are global-scale oscillations with periods that are harmonics of a solar day, commonly expressed as diurnal (24 h), semi-diurnal (12 h), terdiurnal (8 h), and quarter-diurnal (6 h) components. These tides play a crucial role in shaping the dynamics of the mesosphere and lower thermosphere (MLT) through their influence on wind, temperature, and composition. Tides are generally classified into migrating and non-migrating types based on their propagation characteristics. Migrating tides are Sun-synchronous and propagate westward. They are primarily excited by periodic solar radiative heating, particularly through tropospheric water vapor absorption and ultraviolet (UV) and extreme ultraviolet (EUV) absorption by ozone and molecular oxygen in the middle and upper atmosphere [1]. In contrast, non-migrating tides are not Sun-synchronous and can propagate eastward, westward, or remain stationary. These are generated by a variety of mechanisms, including latent heat release from deep tropical convection or through nonlinear interactions with Planetary waves (PWs) or other tidal components [2,3,4,5,6].
One of the most prominent disturbances in the stratosphere that impacts tidal behavior is the sudden stratospheric warming (SSW). SSWs are large-scale wintertime phenomena characterized by a rapid rise in polar stratospheric temperatures and, in the case of major events, a reversal of the climatological westerly zonal winds into easterly. These events are driven by the upward propagation of planetary waves and their interaction with the mean flow, as first described by Matsuno [7] and further expanded by Matsuno and Nakamura [8]. The wave–mean flow interaction decelerates the polar jet, disrupts the geostrophic balance, and induces a meridional circulation that leads to adiabatic warming in the lower stratosphere and cooling in the mesosphere. Although they originate in the stratosphere, the effects of SSWs extend into the MLT region, modifying temperature structures, wind fields, and the propagation environment for tides and gravity waves [9,10].
During SSW events, dramatic changes in the zonal-mean wind and temperature profiles can significantly alter tidal propagation conditions, often resulting in notable modulations of both the amplitude and phase of migrating and non-migrating tides. These changes are well documented in observational and modeling studies. For example, Pancheva and Mukhtarov [11], and Yamazaki and Richmond [12] reported enhanced tidal activity and variability in the MLT during and after SSWs. Chandran and Collins [13] further illustrated how upward-propagating planetary waves can interact not only with mean flow but also with tides to amplify or suppress specific tidal components. More recently, Liu et al. [14] observed amplified diurnal and semi-diurnal wind tides during the 2019 Southern Hemisphere SSW, whereas Siddiqui et al. [15] reported significant reductions in DW1 amplitudes in low-latitude regions during both Northern and Southern Hemisphere SSW events, attributed to altered latitudinal shear in zonal winds. Hibbins et al. [16] showed that the migrating semidiurnal tide weakens after SSW onset and then intensifies 10–17 days later due to changes in background wind. Pancheva et al. [17] also showed that SSWs can enhance stationary and non-migrating tidal components such as D0 (zonal symmetric component of the diurnal tide) and DW2 (westward non-migrating diurnal tide with zonal wavenumber 2), likely through nonlinear interactions with stationary planetary waves (SPWs) [18].
Apart from PWs-driven modulations, recent studies emphasize the important roles of ozone and water vapor variability in modulating tidal structures during SSWs, while radiative heating is the primary excitation mechanism for migrating tides. Ozone contributes significantly to solar UV absorption in the stratosphere and mesosphere, which influences both the direct forcing and background thermal structure that supports tidal propagation. Zhang et al. [19] indicated that SW2 enhancement after an SSW is driven by increased ozone-induced tidal forcing and reduced asymmetry of the background zonal wind. Mitra et al. [20] demonstrated that the enhancement of DW1, DE3, and SW2 components during the 2019 SSW is closely linked to increased convective activity and stratospheric ozone variability. Extending this, Mitra et al. [21] proposed that solar UV heating modulated by ozone abundance could even drive stationary tides such as S0. Meanwhile, tropospheric water vapor, through latent heat release in convective regions, plays a dominant role in exciting diurnal tides like DW1, particularly in the tropics. These forcing mechanisms, which can vary seasonally and longitudinally, are particularly sensitive to large-scale meteorological changes such as those induced by SSWs.
Despite considerable advances, uncertainties remain regarding the relative importance and interactions of these various tidal forcing mechanisms, especially in the context of longitudinal asymmetries and the excitation of non-migrating tides. Many aspects of tide–SSW coupling, such as the interplay between planetary wave–tide interactions, ozone-induced effects, and convective heating, are not yet fully resolved. This study seeks to investigate the extent of influence of SSW in the modulation of tides through these drivers by examining the longitudinal and temporal variations in atmospheric tidal responses to the 2021 SSW events. Particular emphasis is placed on disentangling the roles of nonlinear interactions, stratospheric ozone variability, and latent heat forcing in modulating migrating and non-migrating tides. The findings provide insights into the broader dynamics of vertical coupling in the atmosphere and contribute to a more comprehensive understanding of tidal variability during extreme meteorological events. The remainder of this paper is organized as follows: Section 2 describes the data and methodology, Section 3 presents the results, Section 4 discusses the findings, and Section 5 concludes with a summary of key insights.
2. Materials and Methods
The zonal wind (U) component from the Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2) from 10 to 0.01 hPa is used in this study to extract wave components in the stratosphere and MLT. The dataset, sampled at 3 h intervals, has a resolution of horizontal grid size and covers the period from 1980 to the present. It includes 72 model levels ranging from 985 to 0.01 hPa (approximately 80 km) and is available for download from https://disc.gsfc.nasa.gov/datasets. The analyses focus on the Northern Hemisphere (0∘–90 ∘N) to capture the stratospheric and mesospheric variability associated with the January 2021 SSW event. To determine the wave perturbations due to the SSW event, we decompose zonal wind perturbations into migrating and non-migrating tides, stationary planetary waves, zonally symmetric oscillations, and transient planetary waves (PWs) using a two-dimensional least-square fitting method [17,22]. A 62-day sliding window, to capture all wave components with a period ranging from 6 h to 31 days, is applied on the data within a latitude band in the least-squares fitting:
The first term in the equation, , represents the zonal daily mean wind. The second term corresponds to the tidal components, where t is the universal time, n denotes the subharmonics of a solar day (i.e., periods of 24 h, 12 h, 8 h, and 6 h), s are integers specifying the zonal wavenumbers of the tides, is the longitude (in radians) and is the frequency of the 24 h tide. The third term represents the SPWs. and denote the amplitudes and phases, respectively, and k is the zonal wavenumber. The final term describes the PWs, where are the amplitudes, the frequencies, the zonal wavenumbers, and the phases of the PWs.
To effectively examine the impact of the SSW event, which peaks on approximately 5 January 2021, hereafter referred to as “day 0” throughout the analysis (see Figure 1), the study focuses on the period from 16 December 2020, to 13 February 2021. To accommodate the 62-day sliding window, the wind dataset is extended by including 30 days before and after this period. This timeframe captures the preconditioning, peak, and recovery phases of the event, ensuring a comprehensive assessment of PWs and tidal variations during the SSW. The calculations incorporate eastward-propagating planetary waves, westward-propagating planetary waves, and SPWs with zonal wavenumbers ranging from to 8. Additionally, diurnal (), semi-diurnal (), tridiurnal (), and quatradiurnal () tides with zonal wavenumbers from to 3 are included. The present study considers only tidal analysis, focusing on the diurnal and semi-diurnal tidal components during the 2021 NH SSW event.
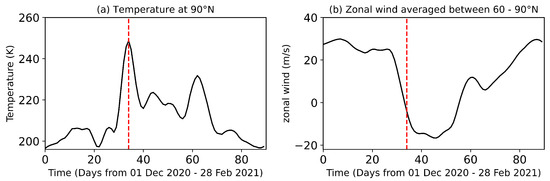
Figure 1.
Stratospheric conditions at 10 hPa during the 2020/2021 boreal winter: (a) Temperature anomalies (K) at 90 ∘N and (b) Zonal wind anomalies (m/s) averaged between 60 and 90 ∘N. The vertical red dashed lines mark the SSW peak.
3. Results
3.1. Diurnal and Semi-Diurnal Westward Migrating and Non-Migrating Tides
Figure 2 shows the latitudinal vertical structure of the diurnal component in the NH winter period. The analysis reveals predominant diurnal tides within the low-latitude region, particularly between 10∘ and 40 ∘N. All tidal components (DO, DW1, DW2, and DW3) show upward vertical propagation, with peak amplitudes consistently observed near 70–75 km. Among the tidal modes, DW1 is the most dominant, exhibiting peak amplitudes of approximately 11 m/s. This mode is characterized by an extended amplitude tail that propagates into the mid-latitudes and polar regions, indicating efficient vertical and meridional energy transport. Other diurnal tidal components, including DW2, DW3 (westward non-migrating diurnal tide with zonal wavenumber 3), and D0, exhibit comparatively lower maximum amplitudes of approximately 6 m/s, 2.5 m/s, and 1.6 m/s, respectively. The semi-diurnal tides, shown in Figure 3, exhibit a similar vertical structure and peak altitude but are largely confined to mid- to high-latitude regions. Specifically, the S0 and SW1 (westward non-migrating semi-diurnal tide with zonal wavenumber 1) modes show enhanced amplitudes around 70∘–80 ∘N, while the SW2 and SW3 (westward non-migrating semi-diurnal tide with zonal wavenumber 3) modes are concentrated near 50∘–65 ∘N.
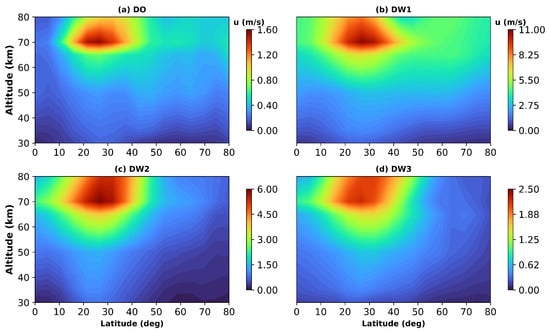
Figure 2.
Latitude–altitude structure of diurnal tidal wind amplitudes (m/s) for D0, DW1, DW2, and DW3 during the 2020/2021 winter. Amplitudes are averaged over the period 16 December 2020 to 13 February 2021.
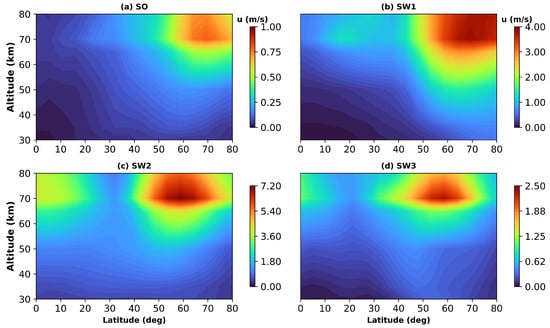
Figure 3.
Latitude–altitude structure of semi-diurnal tidal wind amplitudes (m/s) for S0, SW1, SW2, and SW3 during the 2020/2021 winter. Amplitudes are averaged over the period 16 December 2020 to 13 February 2021.
To investigate the temporal behavior and potential modulation of tidal activity by the SSW event, Figure 4 shows the latitudinal–time structure of diurnal tides at approximately 70 km altitude. The vertical black dashed line denotes the onset of the SSW. A distinct enhancement in the DW1 amplitude is observed from day 0 to day 40, suggesting that the SSW significantly modulates the energy conditions of DW1 tidal activity. According to Siddiqui et al. [15], the SSW-induced changes in the latitudinal shear of low-latitude zonal winds strongly affect DW1 propagation in the MLT. The DW2 exhibits similar characteristics to DW1, albeit with reduced amplitudes of approximately 9 m/s. In contrast, the DW3 tide shows a double-peak structure: a pre-SSW maximum (2 m/s), followed by a suppression (0.2 m/s from day 0 to day 13), and a secondary peak (4 m/s) around 20 days post-SSW. A similar feature is also evident in the D0 tide, although the peak amplitude (2.8 m/s) occurs prior to the SSW onset.
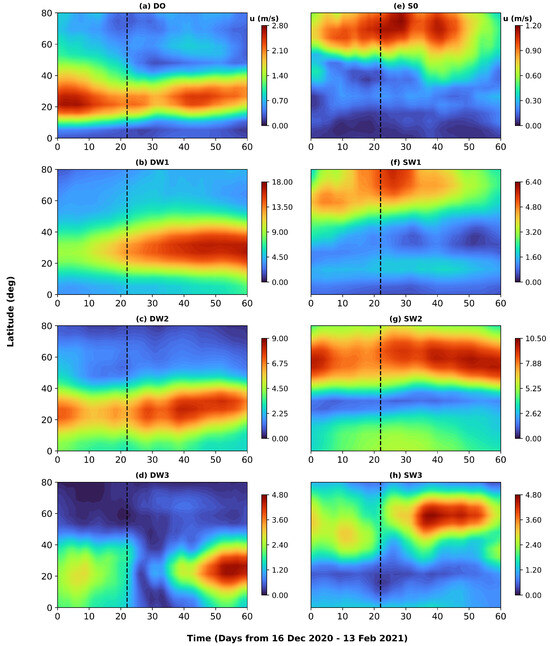
Figure 4.
Latitude–time evolution of diurnal (D0, DW1, DW2, DW3) and semi-diurnal (S0, SW1, SW2, SW3) tidal wind amplitudes (m/s) at 70 km altitude during the 2020/2021 winter. The vertical black dashed lines denote the onset of the SSW event.
The semi-diurnal tides, on the other hand, show a rather striking response to the SSW event. Notably, the migrating tide (SW2) shows the largest amplitude (10 m/s) throughout the SSW period, peaking at 60 ∘N. The SW1 tide also shows a pronounced maximum (6 m/s) associated with the SSW onset. The pattern of the S0 evolves gradually but stays similar to that in SW1, especially the position of the peak amplitude. This similarity suggests that changes in mesospheric winds, influenced by SSW-related modulation, favor these tidal activities at higher latitudes. Interestingly, the peak amplitude of the SW3 tide occurs approximately 10 days after the SSW onset, indicating a lagged response. This suggests that SW3 tidal enhancement is not an instantaneous consequence of the SSW-induced zonal wind perturbations but rather involves secondary processes. These processes may involve delayed chemical feedbacks associated with small yet dynamically significant ozone variation [23]. Furthermore, temperature gradient changes and nonlinear wave–wave interactions in the MLT may also play a role. Previous studies have highlighted that post-SSW semi-diurnal tide enhancements are associated with elevated mesospheric ozone and nonlinear interactions between PWs and tides [9,21]. The observed delay in enhancement during the event under investigation in this study arises from a more complex interaction of mechanisms, potentially involving coupled dynamics between the SSW event and a sudden increase in ozone transport. We investigated this aspect further in Section 3.2.
3.2. Excitation Mechanism of Diurnal Non-Migrating Tides
The generation of tidal components in the MLT is largely influenced by the absorption of solar radiation, primarily through water vapor, which drives the formation of migrating diurnal and semi-diurnal tides [1]. However, the formation of non-migrating tides is more complex and involves mechanisms such as zonally asymmetric thermal forcing and nonlinear interactions [24]. Nonlinear wave interactions, in particular, can significantly influence the amplitude and structure of these tides, especially during phenomena like SSWs, where complex wave interactions take place.
We specifically investigate the potential for nonlinear interactions in two scenarios. First, the temporal and latitudinal variations of SPWs suggest the possibility of nonlinear modulation of tidal amplitudes. In particular, the SPW amplitudes decrease from 10 days before to 15 days after the SSW onset (Figure A1), in contrast to the enhanced DW1 observed during and after this period (Figure 4c). This pattern could indicate the modulation of tidal amplitudes through nonlinear interactions, specifically the formation of non-migrating tides such as D0 and DW2, which may result from wave–wave interactions between SPW1 and DW1. Second, although the zonal wavenumbers of DW3 align with the expected child waves generated by the interaction between DW1 and SPW2, DW3 peaks much later, approximately 15 days after the SSW onset (Figure 4d). According to wave–wave interaction theory, two parent waves with frequency–wavenumber pairs and interact to produce a child wave with frequency–wavenumber pairs [25], which supports the hypothesis of nonlinear generation of DW3. However, the delayed enhancement (after day 13) of DW3 suggests that this component may not solely result from immediate nonlinear interactions. Instead, it could be influenced by additional mechanisms. For instance, coupling between different wave types, such as gravity waves (GWs) and larger-scale tidal and PWs, might redistribute energy that contributes to the enhancement of DW3. Additionally, the change in the atmospheric background state following the SSW could affect the propagation conditions for waves, resulting in a delayed amplification of certain tidal components. Remarkably, Figure A2 shows a significant increase in the westerly flow between day 0 to 13 (10 m/s) at 70 km at low latitude, coinciding with the period of DW3 suppression. It appears that strong eastward wind following the SSW onset is an unfavorable condition for DW3 tide.
Figure 5a–c show a simple correlation analysis between non-migrating tides and SPWs at 32.5 ∘N. Strong positive correlations are observed between SPW1 and D0 (), moderate correlations between SPW1 and DW2 (), and between SPW2 and DW3 (), indicating a potential interaction between SPWs and non-migrating tides. Xu et al. [26] established similar correlations between PWs and tides using their potential energy, which is directly proportional to the square of the amplitude of the waves, in contrast to our approach, which employs correlation between amplitudes. To further investigate this hypothesis, we apply bispectral analysis following the method implemented by Xu et al. [26]. In a similar approach, time series comprising the daily amplitudes and phases of waves and tides are employed. Following this methodology, a selected child wave representing a non-migrating tide is analyzed, and the bispectral results are compared across SPW–tide and tide–tide triads that satisfy the theoretical criteria for its generation. A higher bispectral amplitude for a given triad reflects stronger amplitudes and coherent variability among the contributing waves, indicating a greater likelihood that they mediate the generation of the specific non-migrating tide.
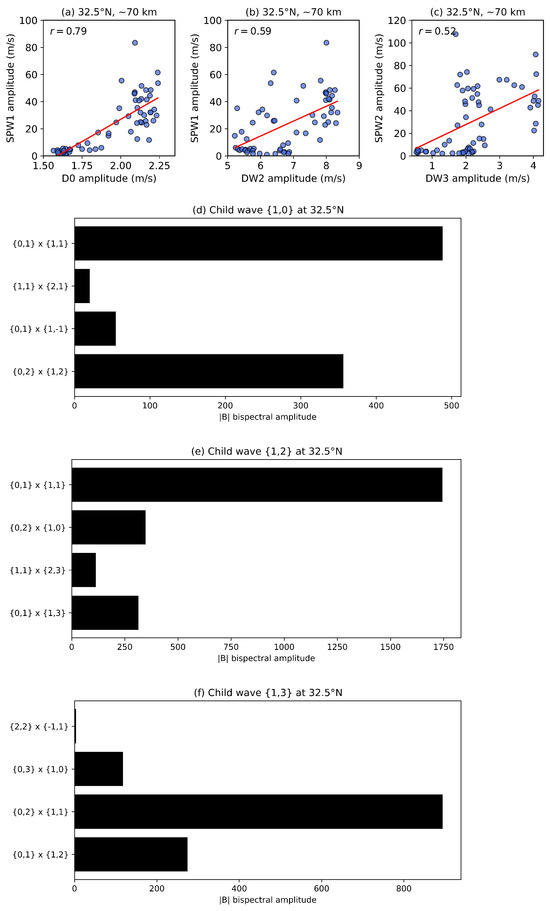
Figure 5.
Correlations between stationary planetary waves (SPWs) and non-migrating (a–c) diurnal (D0, DW2, DW3) at 70 km altitude during the 2020/2021 winter. The figure shows results at 32.5 ∘N. Positive R values indicate in-phase relationships, demonstrating latitude-dependent coupling mechanisms between SPWs and tidal components during the SSW event. Panels (d–f) show the corresponding bispectra analysis, illustrating nonlinear wave–tide/tide–tide interactions.
Figure 5d–f show the bispectral amplitudes of potential wave–tide and tide–tide interaction pairs exhibiting the strongest signals at 32.5 ∘N. As shown in Figure 5d, the largest amplitude (approximately 480) contributing to the formation of the child wave D0, i.e., {1,0}, is associated with the interaction {0,1} × {1,1}, corresponding to SPW1 and DW1. Strongly coupled pairs, including {0,2} × {1,2}, also contribute notably to the formation of D0. Other, weaker contributors to D0 (amplitudes < 100) arise from interactions such as {1,1} × {2,1} and {0,1} × {1,−1}. Similarly, the dominant coupling pair (approximately 1700) contributing to the formation of child wave DW2, represented by {1,2}, is associated with the {0,1} × {1,1} interaction, in more common terms, a nonlinear interaction between SPW1 and DW1 (Figure 5e). Other coupling pairs, such as {0,2} × {1,0}, {1,1} × {2,3}, and {0,1} × {1,3}, exhibit amplitudes below 400, suggesting that they play a lesser role in generating DW2. The child wave DW3, denoted as {1,3}, also exhibits a pronounced bispectral signature from the interaction between {0,2} × {1,1}, indicating a strong nonlinear interaction between SPW2 and DW1 (Figure 5f). These findings align with previous studies that emphasize the role of nonlinear interactions between migrating and non-migrating tides in the MLT. For instance, Goncharenko et al. [9] and Mitra et al. [21] demonstrated that nonlinear wave–wave interactions lead to enhanced tidal amplitudes, particularly in regions where phenomena like SSWs influence wave dynamics. Our study supports these findings, suggesting that nonlinear interactions between DW1 and SPWs are key drivers of the observed tidal response during and after the SSW event.
3.3. Excitation Mechanism of Semi-Diurnal Non-Migrating Tides
To further elucidate the excitation mechanisms of non-migrating semidiurnal tides, particularly at high latitudes, we investigate the relationship between total column ozone (TCO) and the amplitudes of the S0, SW1, and SW3 tidal components, using TCO as a proxy for the influence of stratospheric PWs on tidal variability. This complements the previous analysis in Section 3.2, which suggested that nonlinear interactions primarily influence tidal responses at lower latitudes, whereas different mechanisms might dominate at higher latitudes. Ozone plays a crucial role in the forcing of tides in the MLT through solar UV absorption, especially during periods of elevated ozone concentration. Previous studies, such as Sridharan et al. [18], attributed non-migrating semi-diurnal tide enhancement to elevated ozone concentration during the 2009 SH minor SSW. Similarly, earlier studies have shown that solar radiation absorption by ozone is a dominant driver for semi-diurnal tidal excitation at high latitudes [20,27]. This mechanism becomes particularly relevant during SSWs when ozone-rich air is transported to higher altitudes due to vertical mixing and PWs-induced disturbances in the polar vortex [13].
Figure 6a–c show the time series of total column ozone (TCO) and the amplitudes of the S0, SW1, and SW3 at 62.5 ∘N and 72.5 ∘N. At 72.5 ∘N, the amplitudes of the S0 (Figure 6a) and SW1 (Figure 6b) tides initially track the TCO variations prior to the SSW, suggesting possible coupling. However, approximately 22 days after the SSW onset, the tidal amplitudes vary differently from the TCO, suggesting a decoupling in their relationship. This decoupling may reflect the onset of alternate forcing mechanisms such as SSW-induced changes in wind filtering or background wind–tide interactions that become more dominant post-SSW [28]. In contrast, at 62.5 ∘N, a more consistent relationship throughout the observation period is evident between TCO and the SW3 amplitude (Figure 6c). Specifically, both TCO and SW3 amplitude decrease leading up to the SSW onset, followed by a synchronized increase shortly thereafter.
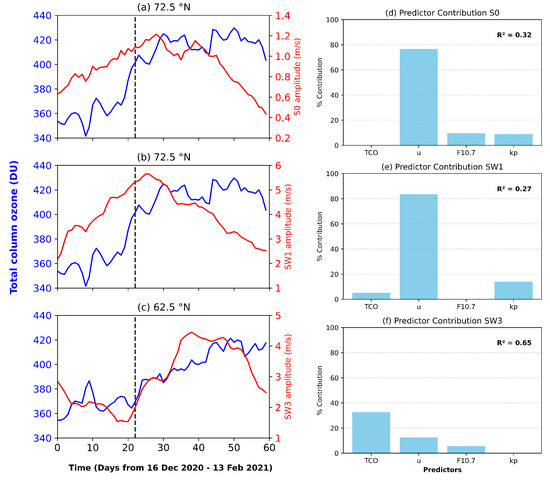
Figure 6.
Coupling between stratospheric ozone and non-migrating semi-diurnal tides at high-latitude during the 2020/2021 SSW event. (a–c) Temporal evolution of total column ozone (TCO; blue) and tidal amplitudes (S0, SW1, SW3; red) at 70 km altitude. (d–f) Predictor contribution (%) to the non-migrating semi-diurnal tide for (d) S0, (e) SW1, and (f) SW3 components using TCO, zonal wind shear between 10 to 0.01 hPa (u), solar flux (F10.7), and geomagnetic activity (Kp) as predictors.
To quantify the influence of ozone on semi-diurnal tidal variability, a multiple linear regression (MLR) analysis is performed using TCO, zonal wind shear between 10 to 0.01 hPa (u), geomagnetic activity (), and solar activity () as predictors of semi-diurnal tidal amplitudes. The fractional contributions of each parameter are shown in Figure 6d–f. Although the models indicate relatively weak to moderate coefficients of determination (–), they provide meaningful insight into the relative importance of the individual predictors to the enhancement of non-migrating semi-diurnal tides in the MLT. For the S0 tide, the model exhibits a moderate coefficient of determination (). The zonal mean wind shear contributes the largest fraction of the total variance (∼78%), followed by and (∼15%). In contrast, TCO exhibits negligible effect on the model. This suggests that dynamical processes play a key role in the excitation of the S0 semi-diurnal component and not ozone variability. For the SW1 tide, the MLR model shows a coefficient of determination (). Similarly, the zonal mean wind shear overwhelmingly dominates the explained variance (>80%). The pronounced sensitivity of SW1 to background wind variability indicates that this non-migrating component is also governed by dynamical processes, likely originating from the SSW event, with ozone variability exerting only a secondary influence. In contrast, the SW3 model shows comparatively higher predictability (), with TCO explaining the highest percentage of the total variance of the model (∼38%). The zonal mean wind shear and exhibit contributions of less than 12% of the total variance of the model. This clearly indicates that the SW3 tide is strongly modulated by ozone variability, with less impact originating from dynamical processes.
The key question that arises is how dynamical and chemical ozone processes occurring primarily in the upper troposphere and stratosphere (20–50 km) can modulate tidal activity in the MLT. To explore this coupling, we employ cross-wavelet analysis on semi-diurnal tide amplitude and TCO. Since the MLR indicates negligible contribution of TCO to the S0 tide, the analysis focuses on the SW1 and SW3 tides. Figure 7a,b presents the cross-wavelet spectra between TCO and the amplitudes of the SW1 and SW3 tides. The 95% confidence level in each cross-wavelet spectrum is indicated by black contour lines. The combined spectra reveal the following features: in the SW1–TCO spectrum, the main oscillation is quasi-20 days and is stronger prior to and during the SSW event. In the SW3–TCO spectrum, quasi-10 and 13 days oscillations dominate the spectrum prior to the SSW. However, quasi-10 and 12 days oscillations are stronger following the SSW onset. These periodicities are consistent with those reported by [29], who linked variations in the semi-diurnal tide amplitude to nonlinear interaction between the semi-diurnal tide and PWs in the stratospheric circulation. According to [29], at altitudes of 10–20 km in the mid- and high-latitudes, ozone has a long photochemical lifetime relative to advection. Therefore, variations in TCO are controlled by the circulation of the lower stratosphere, which redistributes ozone molecules. This indicates that the dynamical state of the lower stratosphere strongly influences the variability of semi-diurnal tides in winter. Hence, it is possible that the SW1 and SW3 consist of a wave that propagates upward directly from its source of excitation.
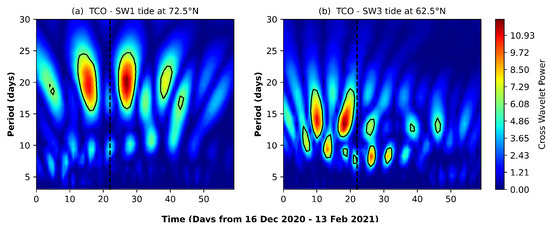
Figure 7.
Cross-wavelet power spectra between total column ozone (TCO) and (a) the SW1 tide at 72.5 ∘N and (b) the SW3 tide at 62.5 ∘N during 16 December 2020–13 February 2021, band-pass filtered for variability within 3–30 day periods. The color shading indicates the cross-wavelet power, and the black contours denote the 95% confidence level. The vertical dashed line marks the onset of the SSW event.
In general, these findings align with the idea that different tidal components can be governed by different excitation mechanisms depending on their zonal wavenumber and latitude. This nuanced understanding underscores the importance of examining multiple pathways, dynamical and nonlinear, in the excitation of tides during SSW events [30,31].
3.4. Diurnal Eastward Non-Migrating Tides
Extending the investigation of tidal responses, we next examine the variability of eastward non-migrating diurnal tides. Figure 8a–c illustrate the latitudinal-altitude distribution of eastward non-migrating diurnal tides (DE1, DE2, DE3) during the NH winter period. Consistent with previous observational and modeling studies [5,32], DE tides are confined to low latitudes. In particular, the DE3 tide (eastward non-migrating diurnal tide with zonal wavenumber 3) amplitude is strongest near the equator at 70 km, reflecting its strong equatorial trapping. Previous studies further suggest that DE3 exhibits a symmetric structure in the lower thermosphere and an anti-symmetric structure in the upper mesosphere [33], indicating that its vertical structure undergoes a distinct transformation with altitude. A comparable vertical orientation is also evident in the DE2 tide (eastward non-migrating diurnal tide with zonal wavenumber 2). In contrast, the DE1 (eastward non-migrating diurnal tide with zonal wavenumber 1) tide appears to migrate toward the mid-latitudes with height, showing a distinct poleward tilt.
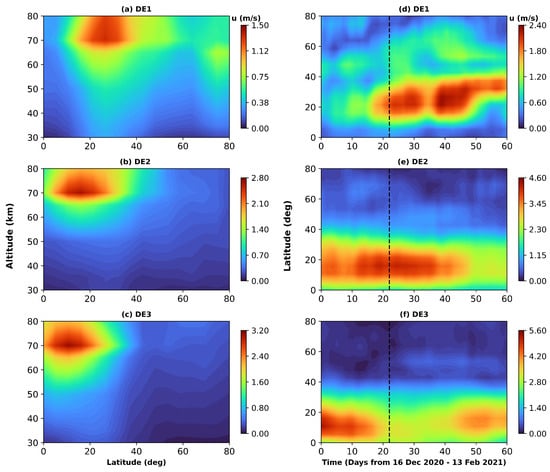
Figure 8.
Latitude–altitude structure of diurnal tidal wind amplitudes (m/s) for DE1, DE2, and DE3 during the 2020/2021 winter (a–c). Amplitudes are averaged over the period 16 December 2020 to 13 February 2021. Panels (d–f) present the latitude–time evolution of tidal amplitudes at 70 km altitude. The vertical black dashed lines denote the onset of the SSW event.
The temporal structure and potential modulation of tidal activity by the SSW event are shown in Figure 8d–f. Among the diurnal eastward non-migrating tidal components, DE3 stands out as the dominant mode in the MLT region, consistent with its well-documented strength in the low latitudes [5]. Notably, peak amplitudes (approximately 3.2 m/s) occur before and after the SSW. However, a reduction of approximately 2 m/s in amplitude is evident during the onset phase (day 2 to day 20), indicating that SSW-induced conditions are not favorable for tidal amplification. This attenuation of DE3 is likely driven by SSW-related modifications in the background zonal wind, which may enhance tidal absorption. In contrast, the DE2 tidal component exhibits a weaker amplitude (approximately 2.8 m/s) and a delayed response, with peak activity occurring during the period of maximum SSW intensity. This lagged amplification implies a potential sensitivity of DE2 to secondary generation processes. Meanwhile, the DE1 tide is more localized off the equator (between 20 ∘N and 30 ∘N), and its amplitude gradually increases following the SSW onset, culminating in a well-defined peak of 2.4 m/s emerging 20 days post-SSW onset.
3.5. Excitation Mechanism of Diurnal Eastward Non-Migrating Tides
To further elucidate the role of tropospheric latent heating in modulating eastward non-migrating diurnal tides, we compared the daily variation in total precipitable water vapor (TPWV) from MERRA-2 with the amplitudes of DE1, DE2, and DE3. While Jones et al. [34] suggest in situ forcing as a driver for DE1, several studies have linked latent heat from tropical cumulus convection to DE1, DE2, and DE3 [5,35]. More recently, Sridharan [27] associated enhancements of DE3 and DE4 amplitudes with TPWV, a proxy for latent heat release. Figure 9 shows the time series of TPWV (blue) and non-migrating eastward diurnal tide amplitudes (red) at 7.5 ∘N, 17.5 ∘N, and 22.5 ∘N. At 22.5 ∘N, DE1 exhibits a quasi-parabolic amplitude with time, while TPWV declines overall; however, coincident short-term peaks (TPWV > 22 kg/m2 and DE1 > 1.5 m/s) near the SSW onset suggest possible episodic coupling. At 17.5 ∘N, DE2 and TPWV show a coherent pattern, with larger amplitudes during the pre-SSW and onset periods. A similar relationship holds for DE3, although slight deviations appear during the peak SSW intensity (−3 to +8 days), likely reflecting altered propagation conditions due to background wind changes [30].
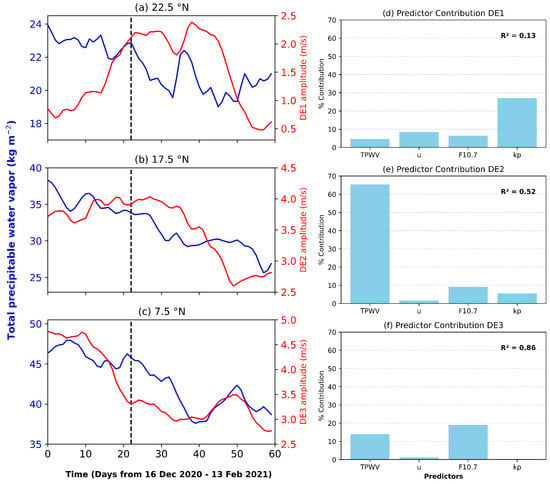
Figure 9.
Coupling between total precipitable water vapor (TPWV) and non-migrating diurnal tides at low latitude during the 2020/2021 SSW event. (a–c) Temporal evolution of TPWV (TPWV; blue) and tidal amplitudes (DE1, DE2, DE3; red) at 70 km altitude. (d–f) Predictor contribution (%) to the non-migrating diurnal tide for (d) DE1, (e) DE2, and (f) DE3 components using TPWV, zonal wind shear between 10 to 0.01 hPa (u), solar flux (F10.7), and geomagnetic activity (Kp) as predictors.
Similarly, the contribution of TPWV to non-migrating diurnal tides in the MLT is assessed through MRL, with zonal wind shear between 10 and 0.01 hPa, geomagnetic activity (Kp), and solar activity (F10.7) included as predictors. The fractional contributions of each parameter are shown in Figure 9d–f. For DE1, the model shows an of 0.13. In addition, predictors such as TPWV, zonal wind shear, and F10.7 exhibit weaker coupling with the DE1 tide (<10%), except Kp, which accounts for 28% of the variance. This suggests that additional processes, such as in situ thermal forcing, nonlinear interactions between PWs and tides, or tide–tide interactions, may contribute significantly to the excitation of the DE1 tide. For the DE2 tide, the model shows a coefficient of determination, . Remarkably, TPWV overwhelmingly dominates the explained variance (>60%), whereas the rest of the predictors contribute less than 10% of the variance, indicating that DE2 is strongly excited by tropospheric latent heating. Interestingly, the model depicts a coefficient of determination, , for the DE3 prediction. The largest contributions come from F10.7 (∼20%) and TPWV (∼15%), while zonal wind shear and Kp have minimal effects (∼2% and ∼1%, respectively). This suggests that the combination of solar activity and tropospheric TPWV variability are the primary drivers of the DE3 tide in the MLT. Although most of the TPWV is concentrated in the troposphere and lower stratosphere, its variations are closely linked to latent heat release through condensation processes associated with deep convection, cloud formation, and precipitation in the troposphere. Therefore, the excitation of the DE2 and DE3 tides is likely modulated by the distribution and intensity of latent heating arising from water vapor condensation in the troposphere and lower stratosphere [29].
4. Discussion
This study provides a comprehensive analysis of migrating and non-migrating diurnal and semi-diurnal tides in the MLT during the 2021 NH SSW event. Our findings highlight the influence of nonlinear interactions and external factors, particularly TCO and TPWV, on atmospheric tidal variability. A prominent feature of our results is the enhancement of migrating tides during the SSW, with DW1 amplitudes increasing at low latitudes and SW2 amplitudes increasing at high latitudes. The amplification of DW1 is consistent with previous studies (e.g., [15]), which attributed such variations to SSW-induced modifications of the zonal mean wind and associated latitudinal shear in the lower mesosphere. Similarly, the observed enhancement of SW2 at high latitude agrees with prior work (e.g., [31,36]), indicating that SSW-driven mesospheric wind perturbations modulate tidal activity.
The behaviour of non-migrating diurnal tides during the SSW further highlights the role of nonlinear interactions. Our findings show that the D0, DW2, and DW3 tides exhibit a comparative phase relationship with SPWs (Figure 5a–c) in the low latitudes. Bispectral analysis further suggests that wave–wave interactions are a primary mechanism for the generation of these non-migrating diurnal tides in the lower latitude. These child waves appear to result from the superposition of frequency and wavenumber pairs between DW1 and SPWs. These observations are consistent with Niu et al. [37], who reported that SPW1–DW1 coupling can generate secondary waves such as DW2 and D0, with their interannual variability largely controlled by changes in SPW1 structure and background propagation conditions. Moreover, our results extend the observations of Teng et al. [38], who reported enhanced DW2 and D0 during the 2018/2019 SSW events due to nonlinear interactions between the dominant SPW1 and DW1 in the low latitudes. In contrast, non-migrating semi-diurnal tides exhibit different forcing mechanisms at mid- and high latitudes. Components such as S0 and SW1 show a direct influence from zonal wind shear, suggesting modulation by SSW-induced zonal wind changes. In addition, the study highlights the contributions of both dynamical and ozone-induced modulation to the excitation of SW1 and SW3, with ozone-driven forcing exerting a more dominant influence on the delayed response of SW3. Prior studies (e.g., [28,29]) have demonstrated that SSW-related ozone enhancements, driven by Brewer–Dobson circulation, can induce tidal variability. Pancheva et al. [29] showed that semi-diurnal tidal amplitude modulations, particularly at periods of 10, 16, and 25–28 days, strengthen significantly during stratospheric warmings due to nonlinear interactions between the semi-diurnal tide and PWs in the stratosphere. This modulation arises because the long photochemical lifetime of ozone dominates the lower atmosphere at mid- and high latitudes, meaning that total ozone variations primarily reflect lower-stratospheric circulation. Consequently, the observed relationship between TCO and the semi-diurnal tide indicates that the dynamical state of the lower stratosphere strongly influences tidal variability. Since the upward-propagating semi-diurnal tide consists of a wave that originates directly from its source of excitation, it is possible that variations in the lower-stratospheric conditions can directly modulate the amplitude and structure of the tide as it propagates into higher altitudes.
The response of eastward-propagating non-migrating diurnal tides (DE1, DE2, DE3) to the SSW event exhibits distinct dynamical behavior. While DE1 and DE2 amplitudes increase in response to SSW-induced perturbations in the MLT, DE3 is notably suppressed during SSW onset. As shown in Figure 8f, DE3 amplitudes over low latitudes (0–10 ∘N) reach 5.6 m/s during the pre-SSW phase, closely following changes in the zonal wind (Figure A2b). Approximately 16 days before the SSW onset, the zonal wind declines steadily from over 12 m/s to a minimum of ∼6.5 m/s, coinciding with the DE3 maximum amplitude. Thereafter, the zonal wind intensifies sharply, peaking above 14 m/s around 14 days after the SSW peak, corresponding to the suppression of DE3 to its minimum value. During the post-SSW phase, DE3 shows only partial recovery, with amplitudes remaining below pre-SSW levels, suggesting a delayed restoration of conditions favorable for its full development, as evident between days 45 and 55. These observations indicate that DE3 is highly sensitive to changes in eastward zonal flow associated with the SSW impact in the low-latitude region. Forbes et al. [39] reported that wave stress can influence the propagation of tidal amplitudes in the MLT. When gravity waves break in this region, they deposit momentum into the zonal mean flow, generating gravity-wave-induced stress. This momentum deposition acts as a drag on tidal winds, thereby damping or suppressing tidal amplitudes. In addition, nonlinear interactions with other tides can transfer energy away from DE3, further contributing to its suppression. Hagan et al. [40] showed that SPW4 in the low-latitude MLT is excited through nonlinear interactions between DE3 and the DW1.
Beyond the direct influence of the SSW on individual tidal components, we find a clear linkage between DE2, DE3, and TPWV, highlighting the role of tropical latent heat release in their excitation ([4,5]) consistent with [41]. In contrast to [42], who suggested that eastward-propagating tides may be generated from nonlinear interactions between the migrating DW1 and SPWs. In this study, our results do not reveal a significant relationship between DE2, DE3, and SPWs). This indicates that the observed variability is more strongly affected by changes in background winds and and variation in TPWV rather than with direct wave–tide coupling to SPWs. This distinction underscores the role of tropospheric latent heating and dynamical process in controlling the non-migrating eastward diurnal tides during the SSW.
5. Conclusions
The 2021 NH SSW event served as an ideal case study to investigate planetary-scale waves and atmospheric tides in the MLT. Using a linear two-dimensional (time–longitude) least-squares fitting method, we derived amplitudes and phases of migrating and non-migrating diurnal and semi-diurnal tidal responses across latitudes. We summarize our key findings as follows:
- The diurnal tides dominate at low latitudes, with the migrating diurnal tide (DW1) peaking between 10 ∘N and 40 ∘N following the SSW onset. In contrast, the semi-diurnal tides are most pronounced in mid-to-high latitudes, with the migrating semi-diurnal tide (SW2) exhibiting the largest amplitude enhancement near 60 ∘N.
- The non-migrating diurnal tides (D0, DW2, DW3) show amplitude variations consistent with nonlinear interactions between the migrating DW1 tide and SPWs at low latitudes.
- The S0 tide at high latitudes exhibits a strong interaction with zonal wind shear, indicating that the SSW-induced dynamical response drives the excitation of this tide.
- SW1 and SW3 tides at high latitudes are closely associated with TCO, suggesting that ozone-related variability contributes to the tidal amplification.
- The eastward-propagating non-migrating tides (DE2 and DE3) exhibit a strong phase relationship with TPWV at low latitudes, suggesting a role of latent heat release from tropical convection in their modulation. In contrast, DE1 shows a weak relationship with TPWV.
In brief, the findings from this study contribute to our understanding of atmospheric tidal response to SSW events, emphasizing the complex relationship between tides and other external factors, such as total TCO and TPWV. Notwithstanding this, further modeling studies are needed to quantify the relative contributions of ozone-driven and convective latent heat release to tidal variability during SSWs based on multiple SSW events over a longer period of time.
Author Contributions
R.A.A.: Formal analysis; investigation; writing—original draft; writing—review and editing. G.M.T.: Supervision; conceptualization; analysis and investigation; writing—review and editing. G.F.G.: Supervision; writing—review and editing. L.K.A.: Supervision; writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The first author acknowledges funding from the Pan African Planetary and Space Science Network (PAPSSN). PAPSSN is supported by the Intra-Africa Academic Mobility Scheme of the European Union under grant agreement number 624224.
Data Availability Statement
Monthly reanalyses datasets are obtained from the Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2), available at https://disc.gsfc.nasa.gov/datasets, accessed on 11 September 2024. Code used in this study is available from the authors upon request.
Acknowledgments
The second author gratefully acknowledges that this work is conducted with support from the O.R. Tambo Africa Research Chairs Initiative, as facilitated by the Botswana International University of Science and Technology, the Ministry of Tertiary Education, Science and Technology; the National Research Foundation of South Africa (NRF); the Department of Science and Innovation of South Africa (DSI); the International Development Research Centre of Canada (IDRC); and the Oliver & Adelaide Tambo Foundation (OATF).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
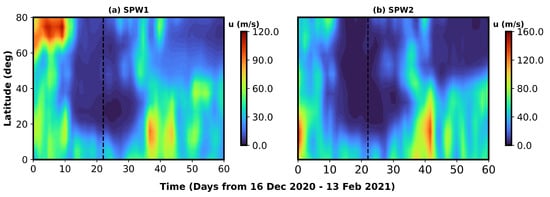
Figure A1.
Latitude–time cross-sections of (a) SPW1 and (b) SPW2 zonal wind amplitudes (m s−1) at ∼70 km altitude during the 2020/2021 winter. The vertical black dashed lines indicate the onset of the SSW event.
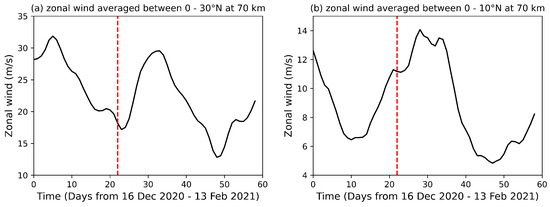
Figure A2.
Zonal wind at 70 km during the 2020/2021 SSW event. Panel (a) shows the wind averaged over 0–30 ∘N, and panel (b) shows the wind averaged over 0–10 ∘N. The vertical red dashed lines indicate the onset of the SSW event.
References
- Forbes, J.M.; Zhang, X.; Hagan, M.E. Simulations of diurnal tides due to tropospheric heating from the NCEP/NCAR Reanalysis Project. Geophys. Res. Lett. 2001, 28, 3851–3854. [Google Scholar] [CrossRef]
- Teitelbaum, H.; Vial, F.; Manson, A.H.; Giraldez, R.; Massebeuf, M. Non-linear interaction between the diurnal and semidiurnal tides: Terdiurnal and diurnal secondary waves. J. Atmos. Terr. Phys. 1989, 51, 627–634. [Google Scholar] [CrossRef]
- Pancheva, D.; Mitchell, N.J.; Hagan, M.E.; Manson, A.H.; Meek, C.E.; Luo, Y.; Riggin, D.M. Global-scale tidal structure in the mesosphere and lower thermosphere during the PSMOS campaign of June–August 1999 and comparisons with the global-scale wave model. J. Atmos. Sol.-Terr. Phys. 2002, 64, 1011–1035. [Google Scholar] [CrossRef]
- Oberheide, J.; Hagan, M.E.; Roble, R.G.; Offermann, D. Sources of nonmigrating tides in the tropical middle atmosphere. J. Geophys. Res. Atmospheres 2002, 107, ACL 6-1–ACL 6-14. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Pancheva, D.; Mukhtarov, P.; Jin, H.; Fujiwara, H.; Shinagawa, H. Excitation mechanism of non-migrating tides. J. Atmos. Sol.-Terr. Phys. 2017, 156, 24–36. [Google Scholar] [CrossRef]
- Lilienthal, F.; Jacobi, C. Nonlinear forcing mechanisms of the migrating terdiurnal solar tide and their impact on the zonal mean circulation. Ann. Geophys. 2019, 37, 943–953. [Google Scholar] [CrossRef]
- Matsuno, T. A dynamical model of the stratospheric sudden warming. J. Atmos. Sci. 1971, 28, 1479–1494. [Google Scholar] [CrossRef]
- Matsuno, T.; Nakamura, K. The Eulerian- and Lagrangian-mean meridional circulations in the stratosphere at the time of a sudden warming. J. Atmos. Sci. 1979, 36, 640–654. [Google Scholar] [CrossRef]
- Goncharenko, L.P.; Coster, A.J.; Plumb, R.A.; Domeisen, D.I. The potential role of stratospheric ozone in the stratosphere–ionosphere coupling during stratospheric warmings. Geophys. Res. Lett. 2012, 39, L08106. [Google Scholar] [CrossRef]
- Zorkaltseva, O.; Saunkin, A.; Vasilyev, R.; Gavrilyeva, G.; Artamonov, M.; Antokhina, O. Effects of sudden stratospheric warmings on airglow emissions layers over Siberia. Adv. Space Res. 2025, 75, 5603–5614. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P. Atmospheric tides and planetary waves: Recent progress based on SABER/TIMED temperature measurements (2002–2007). In Aeronomy of the Earth’s Atmosphere and Ionosphere; Abdu, M.A., Pancheva, D., Bhattacharyya, A., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 19–56. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Richmond, A.D. A theory of ionospheric response to upward-propagating tides: Electrodynamic effects and tidal mixing effects. J. Geophys. Res. Space Phys. 2013, 118, 5891–5905. [Google Scholar] [CrossRef]
- Chandran, A.; Collins, R.L. Stratospheric sudden warming effects on winds and temperature in the middle atmosphere at middle and low latitudes: A study using WACCM. Ann. Geophys. 2014, 32, 859–874. [Google Scholar] [CrossRef]
- Liu, G.; Janches, D.; Ma, J.; Lieberman, R.S.; Stober, G.; Moffat-Griffin, T.; Murphy, D.J. Mesosphere and lower thermosphere winds and tidal variations during the 2019 Antarctic sudden stratospheric warming. J. Geophys. Res. Space Phys. 2022, 127, e2021JA030177. [Google Scholar] [CrossRef]
- Siddiqui, T.A.; Chau, J.L.; Stolle, C.; Yamazaki, Y. Migrating solar diurnal tidal variability during northern and southern hemisphere sudden stratospheric warmings. Earth Planets Space 2022, 74, 101. [Google Scholar] [CrossRef]
- Hibbins, R.E.; Espy, P.J.; Orsolini, Y.J.; Limpasuvan, V.; Barnes, R.J. SuperDARN observations of semidiurnal tidal variability in the MLT and the response to sudden stratospheric warming events. J. Geophys. Res. Atmos. 2019, 124, 4862–4872. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Andonov, B. Nonmigrating tidal activity related to the sudden stratospheric warming in the Arctic winter of 2003/2004. Ann. Geophys. 2009, 27, 975–987. [Google Scholar] [CrossRef]
- Sridharan, S. Seasonal variations of low-latitude migrating and nonmigrating diurnal and semidiurnal tides in TIMED-SABER temperature and their relationship with source variations. J. Geophys. Res. Space Phys. 2019, 124, 3558–3572. [Google Scholar] [CrossRef]
- Zhang, J.; Limpasuvan, V.; Orsolini, Y.J.; Espy, P.J.; Hibbins, R.E. Climatological westward-propagating semidiurnal tides and their composite response to sudden stratospheric warmings in SuperDARN and SD-WACCM-X. J. Geophys. Res. Atmos. 2021, 126, e2020JD032895. [Google Scholar] [CrossRef]
- Mitra, G.; Guharay, A.; Batista, P.P.; Buriti, R.A.; Moffat-Griffin, T. Investigation on the MLT tidal variability during September 2019 minor sudden stratospheric warming. Adv. Space Res. 2023, 71, 869–882. [Google Scholar] [CrossRef]
- Mitra, G.; Guharay, A.; Paulino, I. Signature of a zonally symmetric semidiurnal tide during major sudden stratospheric warmings and plausible mechanisms: A case study. Sci. Rep. 2024, 14, 23806. [Google Scholar] [CrossRef]
- Tsidu, G.M.; Abraha, G. Moderate geomagnetic storms of January 22–25, 2012 and their influences on the wave components in ionosphere and upper stratosphere-mesosphere regions. Adv. Space Res. 2014, 54, 1793–1812. [Google Scholar] [CrossRef]
- Mlynczak, M.; Martin-Torres, F.J.; Russell, J.; Beaumont, K.; Jacobson, S.; Kozyra, J.; Paxton, L. The natural thermostat of nitric oxide emission at 5.3 μm in the thermosphere observed during the solar storms of April 2002. Geophys. Res. Lett. 2003, 30, 2100. [Google Scholar] [CrossRef]
- Forbes, J.M.; Wu, D. Solar tides as revealed by measurements of mesosphere temperature by the MLS experiment on UARS. J. Atmos. Sci. 2006, 63, 1776–1797. [Google Scholar] [CrossRef]
- Teitelbaum, H.; Vial, F. On tidal variability induced by nonlinear interaction with planetary waves. J. Geophys. Res. Space Phys. 1991, 96, 14169–14178. [Google Scholar] [CrossRef]
- Xu, J.; Smith, A.K.; Liu, M.; Liu, X.; Gao, H.; Jiang, G.; Yuan, W. Evidence for nonmigrating tides produced by the interaction between tides and stationary planetary waves in the stratosphere and lower mesosphere. J. Geophys. Res. Atmos. 2014, 119, 471–489. [Google Scholar] [CrossRef]
- Sridharan, S.; Sathishkumar, S.; Gurubaran, S. An unusual reduction in the mesospheric semi-diurnal tidal amplitude over Tirunelveli (8.7∘ N, 77.8∘ E) prior to the 2011 minor warming and its relationship with stratospheric ozone. J. Atmos. Sol.-Terr. Phys. 2012, 89, 27–32. [Google Scholar] [CrossRef]
- McCormack, J.P.; Eckermann, S.D.; Coy, L.; Allen, D.R.; Kim, Y.J.; Hogan, T.; Trepte, C.R. NOGAPS-ALPHA model simulations of stratospheric ozone during the SOLVE2 campaign. Atmos. Chem. Phys. 2004, 4, 2401–2423. [Google Scholar] [CrossRef]
- Pancheva, D.; Mitchell, N.; Middleton, H.; Muller, H. Variability of the semidiurnal tide due to fluctuations in solar activity and total ozone. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1–19. [Google Scholar] [CrossRef]
- Limpasuvan, V.; Thompson, D.W.; Hartmann, D.L. The life cycle of the Northern Hemisphere sudden stratospheric warmings. J. Clim. 2004, 17, 2584–2596. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Forbes, J.M. Evidence for stratosphere sudden warming–ionosphere coupling due to vertically propagating tides. Geophys. Res. Lett. 2010, 37, L11101. [Google Scholar] [CrossRef]
- Forbes, J.M.; Russell, J.; Miyahara, S.; Zhang, X.; Palo, S.; Mlynczak, M.; Hagan, M.E. Troposphere–thermosphere tidal coupling as measured by the SABER instrument on TIMED during July–September 2002. J. Geophys. Res. Space Phys. 2006, 111, A10308. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Palo, S.; Russell, J.; Mertens, C.J.; Mlynczak, M. Tidal variability in the ionospheric dynamo region. J. Geophys. Res. Space Phys. 2008, 113, A02303. [Google Scholar] [CrossRef]
- Jones, M.; Forbes, J.M.; Hagan, M.E.; Maute, A. Non-migrating tides in the ionosphere-thermosphere: In situ versus tropospheric sources. J. Geophys. Res. Space Phys. 2013, 118, 2438–2451. [Google Scholar] [CrossRef]
- Häusler, K.; Lühr, H.; Hagan, M.E.; Maute, A.; Roble, R.G. Comparison of CHAMP and TIME-GCM nonmigrating tidal signals in the thermospheric zonal wind. J. Geophys. Res. Atmos. 2010, 115, D1. [Google Scholar] [CrossRef]
- Chau, J.L.; Hoffmann, P.; Pedatella, N.M.; Matthias, V.; Stober, G. Upper mesospheric lunar tides over middle and high latitudes during sudden stratospheric warming events. J. Geophys. Res. Space Phys. 2015, 120, 3084–3096. [Google Scholar] [CrossRef]
- Niu, X.; Du, J.; Zhu, X. Statistics on nonmigrating diurnal tides generated by tide-planetary wave interaction and their relationship to Sudden Stratospheric Warming. Atmosphere 2018, 9, 416. [Google Scholar] [CrossRef]
- Teng, C.K.M.; Fan, Z.; Cheng, W.; Qin, Y.; Yang, Z.; Sun, J. SD-WACCM-X Study of Nonmigrating Tidal Responses to the 2019 Antarctic Minor SSW. Atmosphere 2025, 16, 848. [Google Scholar] [CrossRef]
- Forbes, J.M.; Jun, G.; Saburo, M. On the interactions between gravity waves and the diurnal propagating tide. Planet. Space Sci. 1991, 39, 1249–1257. [Google Scholar] [CrossRef]
- Hagan, M.E.; Maute, A.; Roble, R.G. Tropospheric tidal effects on the middle and upper atmosphere. J. Geophys. Res. Space Phys. 2009, 114, A1. [Google Scholar] [CrossRef]
- Zhang, X.; Forbes, J.M.; Hagan, M.E. Seasonal-latitudinal variation of the eastward-propagating diurnal tide with zonal wavenumber 3 in the MLT: Influences of heating and background wind distribution. J. Atmos. Sol.-Terr. Phys. 2012, 78, 37–43. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Forget, F.; Millour, E.; Kleinböhl, A. Solar tides in the middle and upper atmosphere of Mars. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).