Indications of the Impact of the Influence of Large-Scale Atmospheric Disturbances on Quasiperiodic ELF/VLF Emissions Inside the Plasmasphere
Abstract
1. Introduction
2. Conditions of Excitation of Quasiperiodic VLF Radiations Inside the Plasmasphere
2.1. Cyclotron Instability of Electron Radiation Belts
2.2. Basic Equations of Plasma Magnetospheric Maser
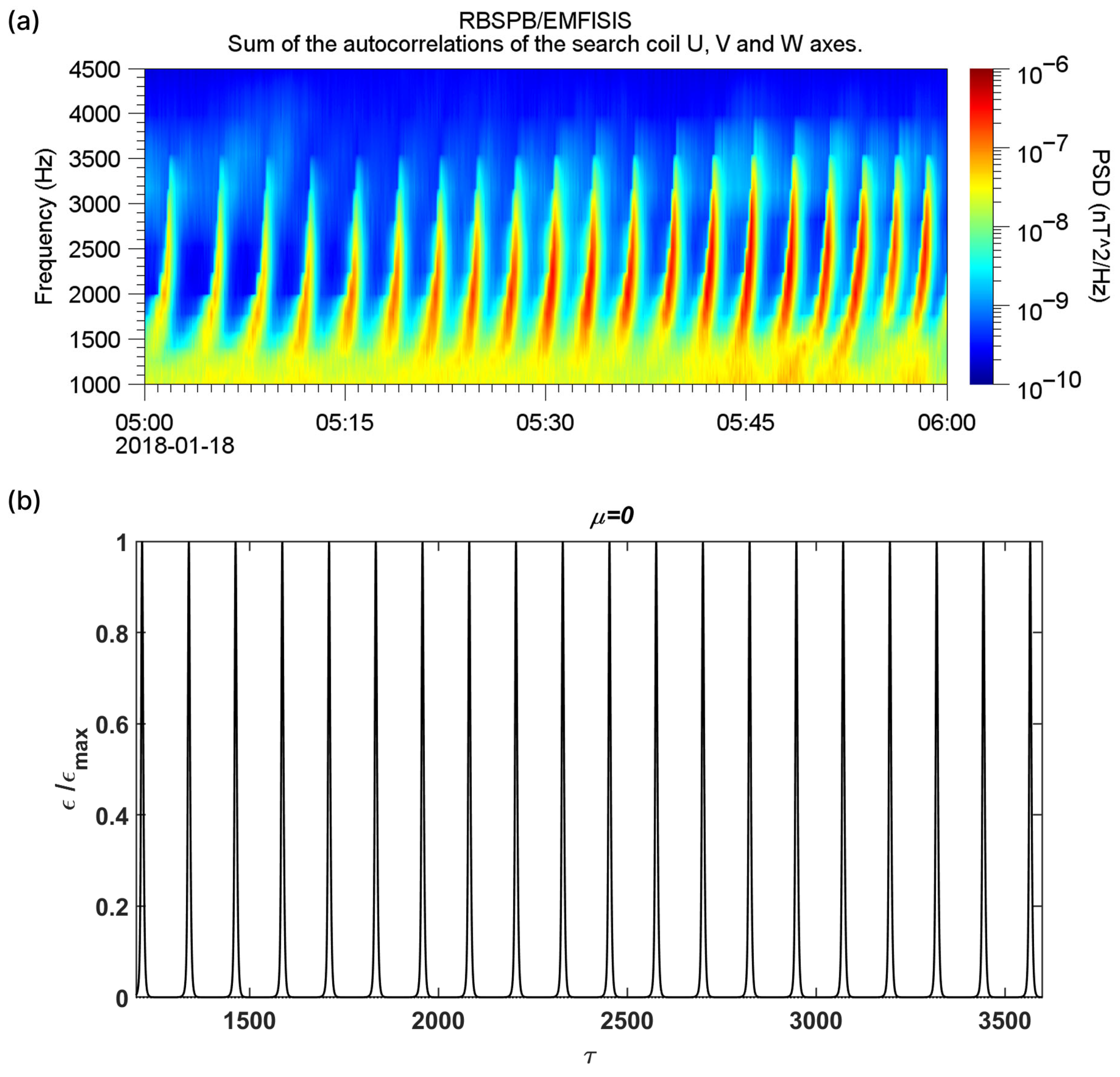
2.3. Eigen-Frequency of PMM and QP 1 Emissions Excitation
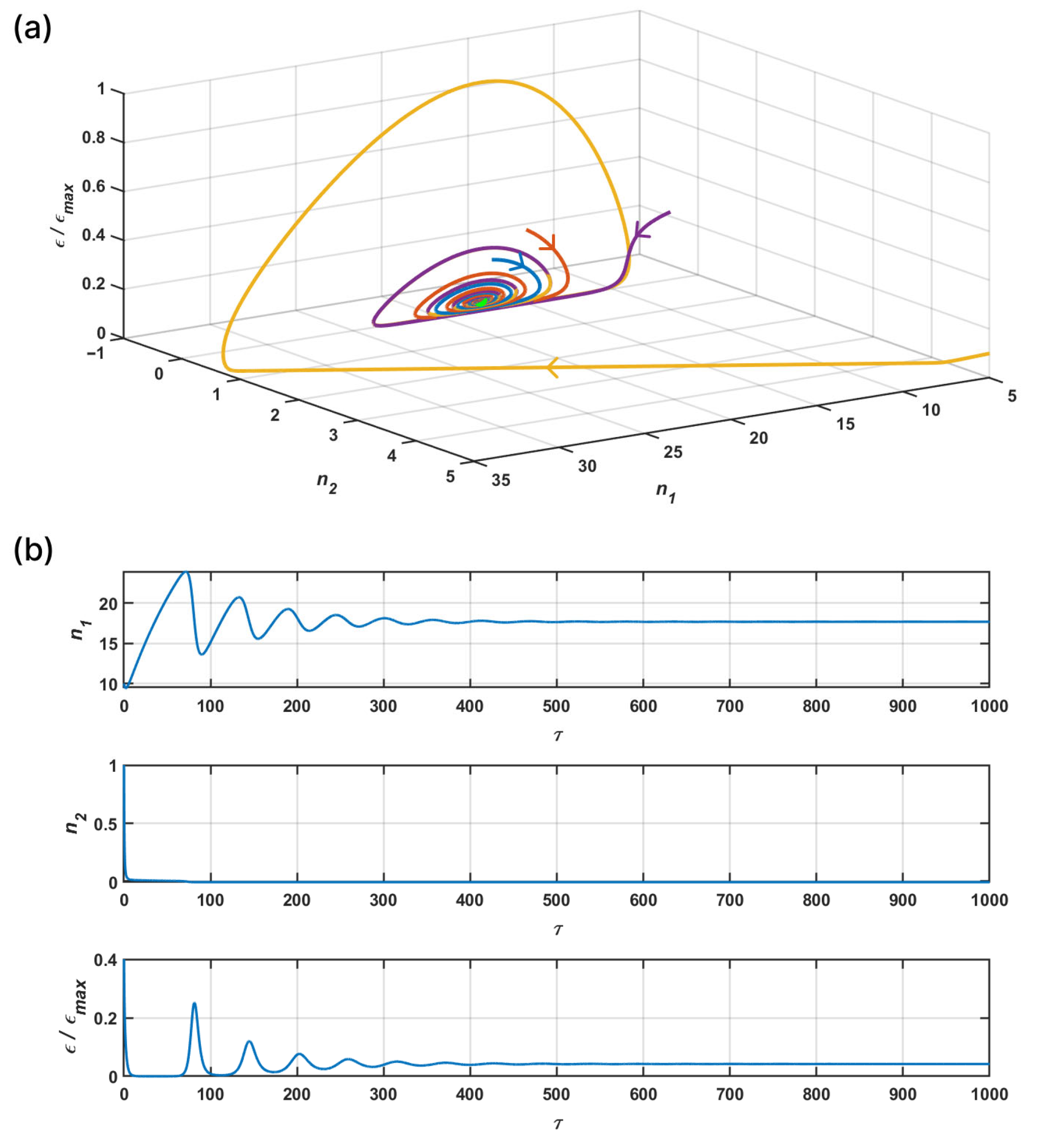
2.4. Self-Oscillations in the PMM and Excitation of QP 2 Emission
2.5. Quantitative Characteristics of Quasiperiodic VLF Emissions
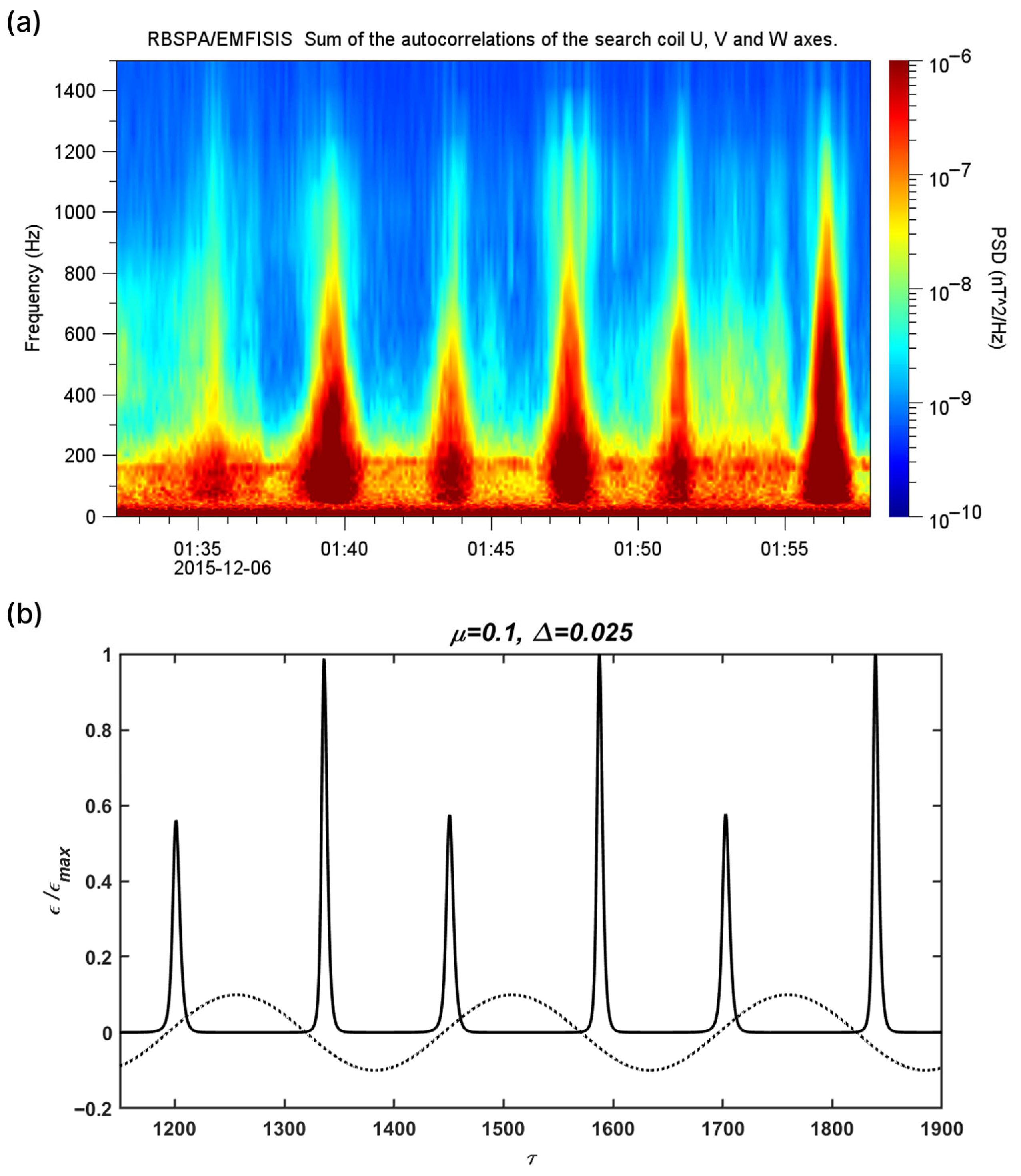
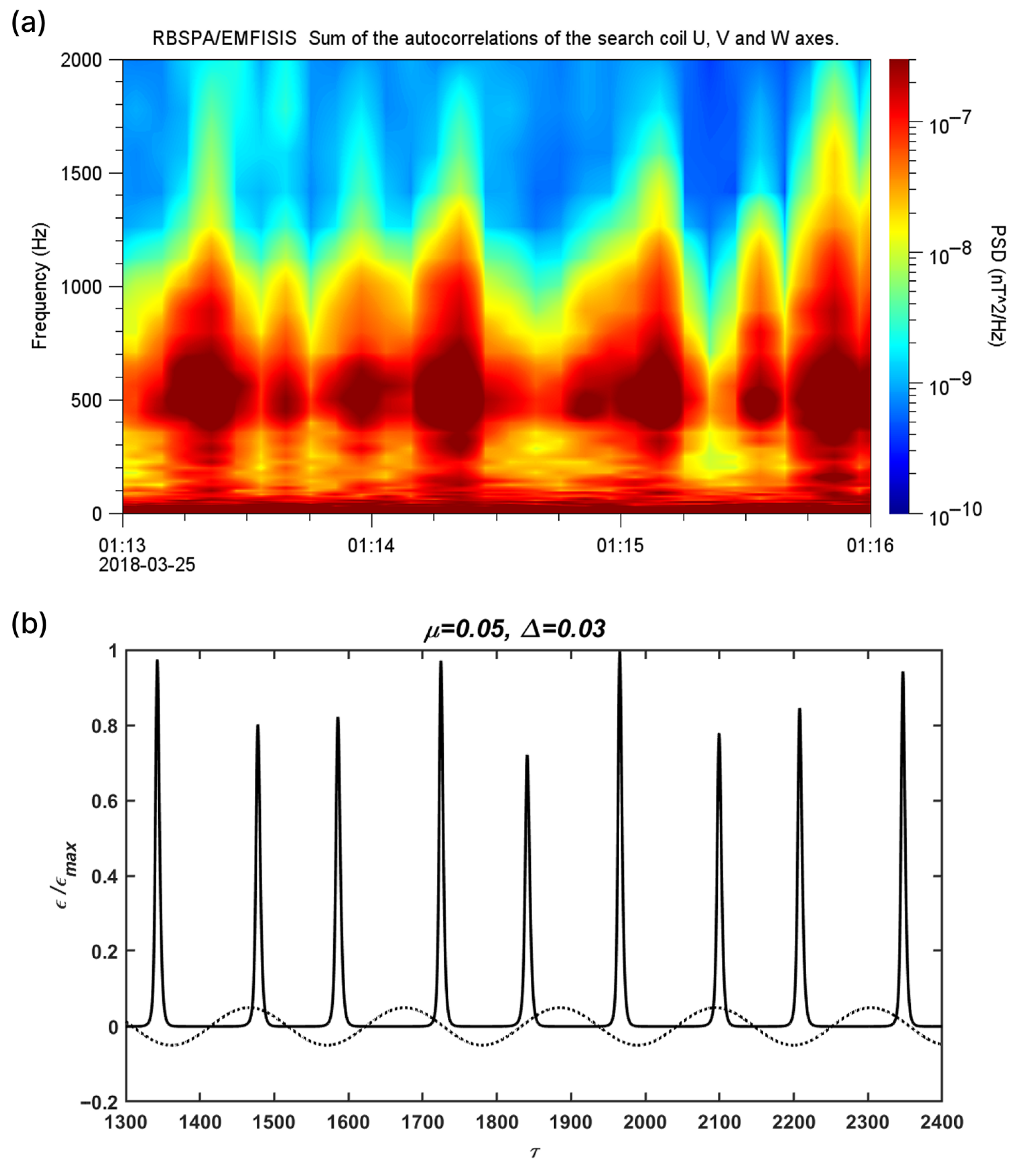
2.6. Atypical QP 2 Emissions
2.7. Broadband QP 2 Emissions
3. Some Channels of Influence of Natural Atmospheric Processes on the Operating Modes of PMM and Quasiperiodic VLF Radiations
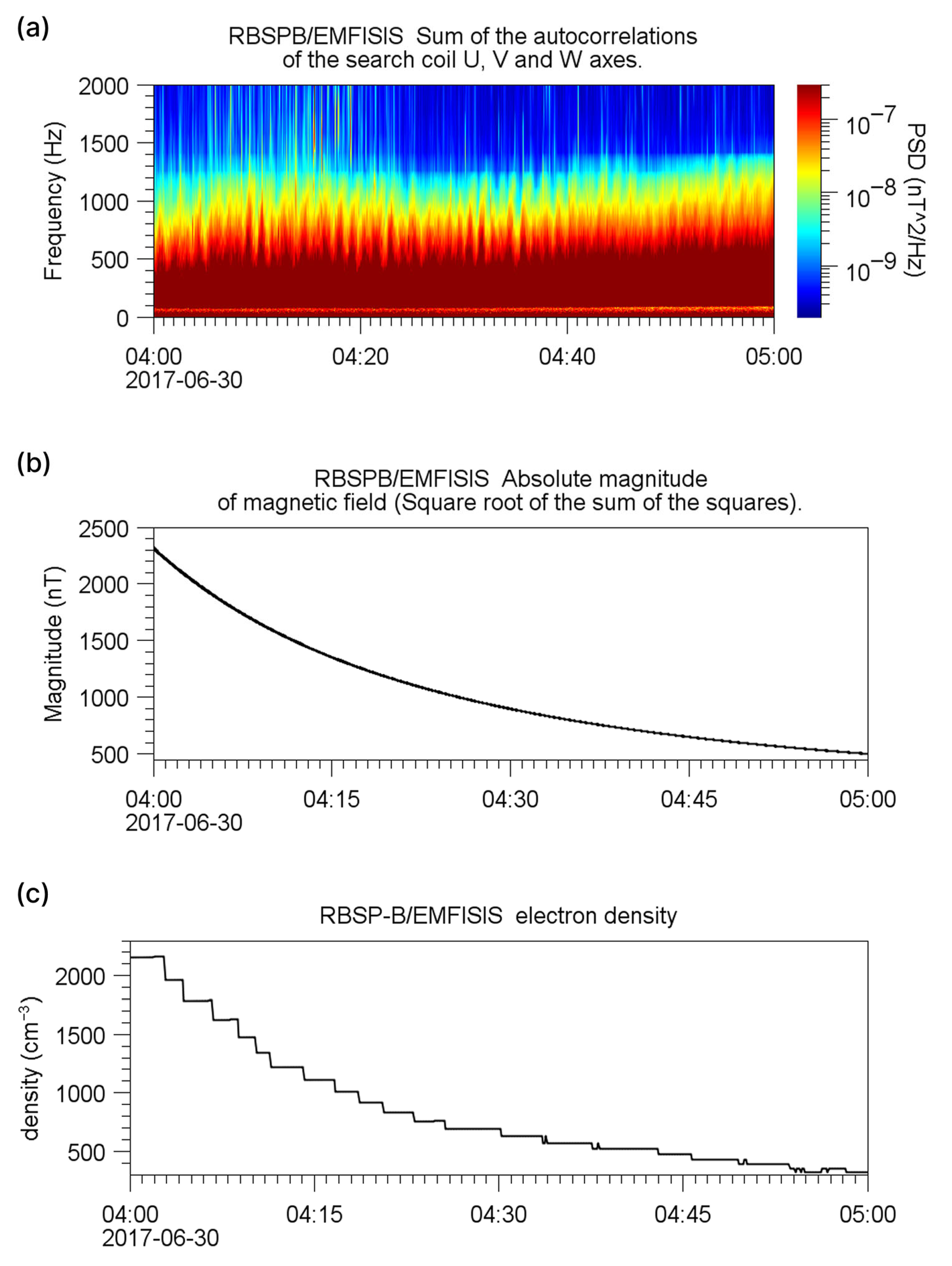
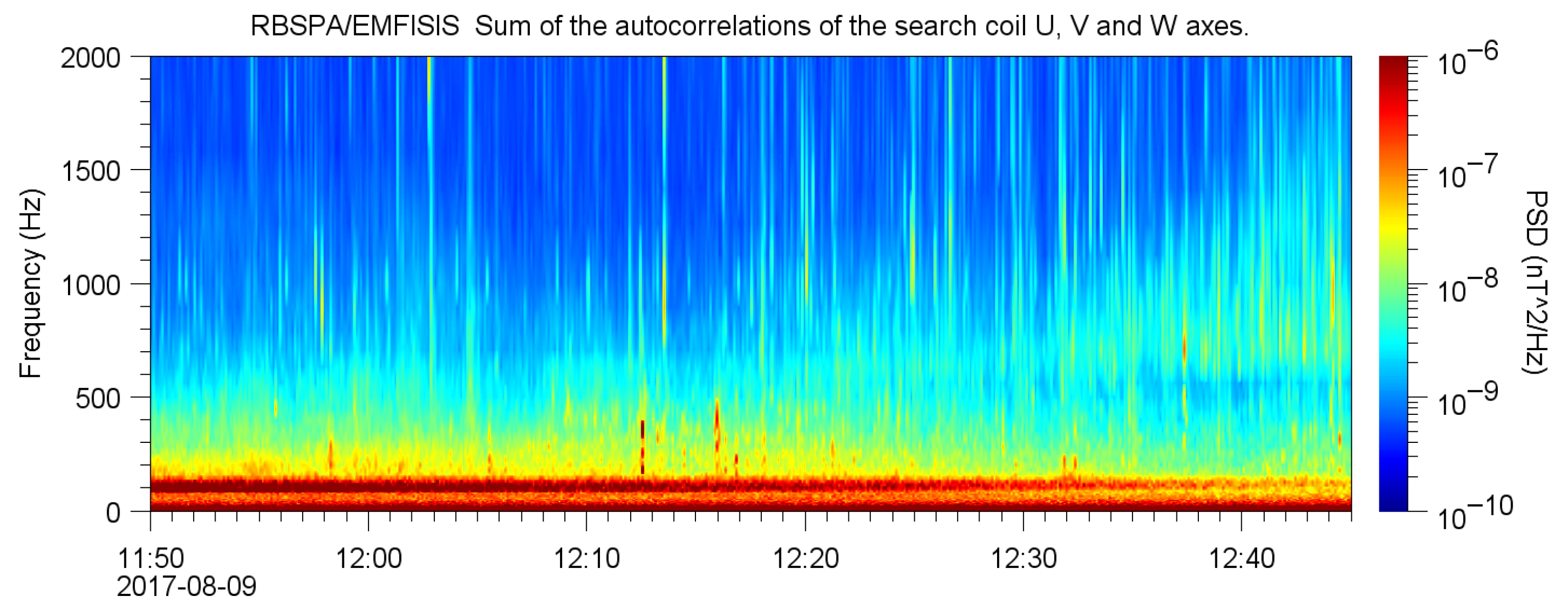
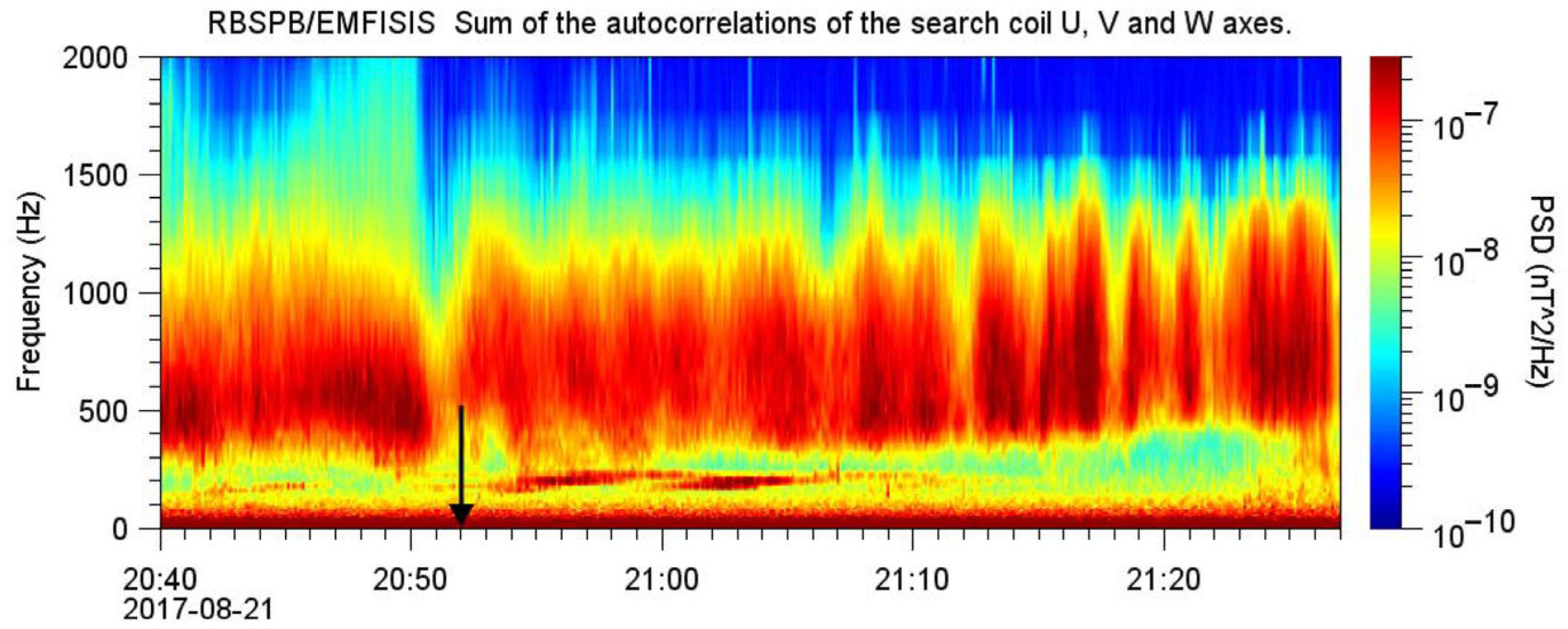
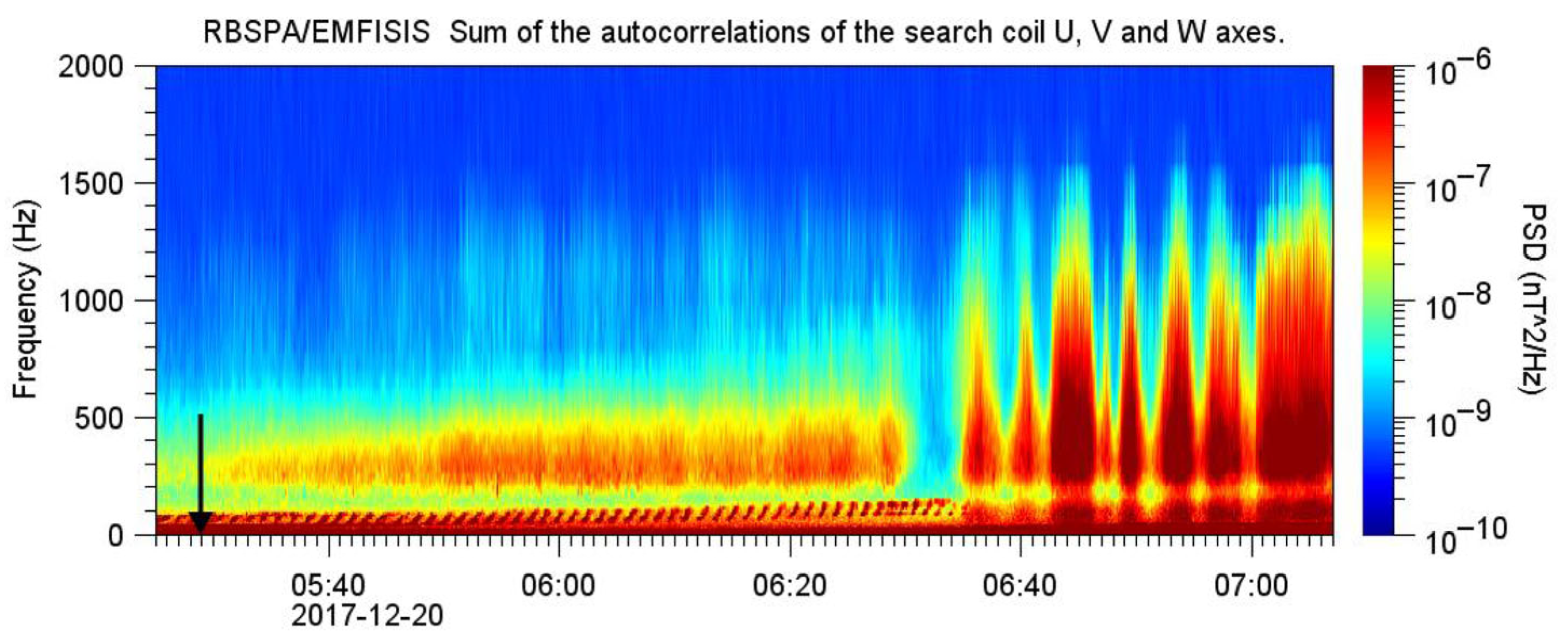
4. Signs of Connection Between Large-Scale Atmospheric Events and Atypical QP 2 Emissions from the Van Allen Probes Spacecraft
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Helliwell, R.A. Whistlers and Related Ionospheric Phenomena, Chapter 3; Stanford University Press: Stanfort, CA, USA, 1965. [Google Scholar]
- Sazhin, S.S.; Hayakawa, M. Periodic and quasiperiodic VLF emissions. J. Atmos. Terr. Phys. 1994, 56, 735. [Google Scholar] [CrossRef]
- Hayakawa, M.; Sazhin, S.S. Mid-latitude and plasmaspheric hiss: A review. Planet. Space Sci. 1992, 40, 1325. [Google Scholar] [CrossRef]
- Trakhtengerts, V.Y.; Rycroft, M.J. Whistler and Alfvén Mode Cyclotron Masers in Space; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Bespalov, P.A.; Trakhtengerts, V.Y. Cyclotron Instability of the Earth Radiation Belts; Reviews of Plasma Physics; Consultants Bureau: New York, NY, USA, 1986; Volume 10, pp. 155–292. [Google Scholar]
- Sato, N.; Kokubun, S. Interaction between ELF-VLF emissions and geomagnetic pulsations: Quasi-periodic ELF-VLF emissions associated with Pc 3-4 magnetic pulsations and their geomagnetic conjugacy. J. Geophys. Res. 1980, 85, 101–113. [Google Scholar] [CrossRef]
- Smith, A.J.; Engebretson, M.J.; Klatt, E.M.; Inan, U.S.; Arnoldy, R.L.; Fukunishi, H. Periodic and quasiperiodic ELF/VLF emissions observed by an array of Antarctic stations. J. Geophys. Res. 1998, 103, 23611. [Google Scholar] [CrossRef]
- Engebretson, M.J.; Posch, J.L.; Halford, A.J.; Shelburne, G.A.; Smith, A.J.; Spasojevic, M.; Inan, U.S.; Arnoldy, R.L. Latitudinal and seasonal variations of quasiperiodic and periodic VLF emission in the outer magnetosphere. J. Geophys. Res. 2004, 105, A05216. [Google Scholar] [CrossRef]
- Nemec, F.; Hospodarsky, G.; Pickett, J.S.; Santolik, O.; Kurth, W.S.; Kletzing, C. Conjugate observations of quasiperiodic emissions by the Cluster, Van Allen Probes, and THEMIS spacecraft. J. Geophys. Res. Space Phys. 2016, 121, 7647. [Google Scholar] [CrossRef]
- Nemec, F.; Bezdekova, B.; Manninen, J.; Parrot, M.; Santolik, O.; Hayosh, M.; Turunen, T. Conjugate observations of a remarkable quasiperiodic event by the low-altitude DEMETER spacecraft and ground-based instruments. J. Geophys. Res. Space Phys. 2016, 121, 8790. [Google Scholar] [CrossRef]
- Hayosh, M.F.; Nemec, F.; Santolik, O.; Parrot, M. Statistical investigation of VLF quasiperiodic emissions measured by the DEMETER spacecraft. J. Geophys. Res. Space Phys. 2014, 119, 8063. [Google Scholar] [CrossRef]
- Titova, E.E.; Kozelov, B.V.; Demekhov, A.G.; Manninen, J.; Santolik, O.; Kletzing, C.A.; Reeves, G. Identification of the source of quasiperiodic VLF emissions using ground-based and Van Allen Probes observations. Geophys. Res. Lett. 2015, 42, 6137. [Google Scholar] [CrossRef]
- Smith, A.J.; Carpenter, Y.; Corcuff, Y.; Rash, J.P.S.; Bering, E.A. The longitudinal dependence of whistler and chorus characteristics observed on the ground near L = 4. J. Geophys. Res. Space Phys. 1991, 96, 275. [Google Scholar] [CrossRef]
- Manninen, J.; Kleimenova, N.G.; Kozyreva, O.V.; Bespalov, P.A.; Kozlovsky, A.E. Non-typical ground-based quasi-periodic VLF emissions observed at L~5.3 under quiet geomagnetic condition at night. J. Atmos. Solar-Terr. Phys. 2013, 99, 123. [Google Scholar] [CrossRef]
- Bezdeková, B.; Nemec, F.; Manninen, J.; Hospodarsky, G.B.; Santolik, O.; Kurth, W.S.; Hartley, D.P. Conjugate observations of quasiperiodic emissions by the Van Allen probes spacecraft and ground-based station Kannuslehto. J. Geophys. Res. Space Phys. 2020, 125, e27793. [Google Scholar] [CrossRef]
- Raspopov, O.M.; Kleimenova, N.G. Vozmushcheniya Elektromagnitnogo Polya Zemli. Ch. 3. In ONCh Izlucheniya (Disturbances of the Earth’s Magnetic Field. Part 3. VLF Emissions); LGU: Leningrad, Russia, 1977. [Google Scholar]
- Sato, N.; Hayasfi, K.; Kokubun, S.; Oguti, T.; Fukunishi, H. Relationships between quasi-periodic VLF-emission and geomagnetic pulsation. J. Atm. Terr. Phys. 1974, 36, 1515. [Google Scholar] [CrossRef]
- Sato, N.; Fukunishi, H. Interaction between ELF-VLF-emissions: Classification of quasi-periodic ELF-VLF-emissions based on frequency-time spectra. J. Geophys. Res. 1981, 86, 19. [Google Scholar] [CrossRef]
- Bespalov, P.A. Self-modulation of radiation of a plasma cyclotron “maser”. JETP Lett. 1981, 33, 182. [Google Scholar]
- Bespalov, P.A. Self-Excitation of Periodic Cyclotron Instability Regimes in a Plasma Magnetic Trap. Phys. Scr. 1982, 1982, 576. [Google Scholar] [CrossRef]
- Ginzburg, V.L. The Propagation of Electromagnetic Waves in Plasmas; Pergamon Press: Oxford, NY, USA, 1970. [Google Scholar]
- Kennel, C.F.; Petschek, H.E. Limit on stably trapped particle fluxes. J. Geophys. Res. 1966, 71, 1–28. [Google Scholar] [CrossRef]
- Li, J.; Bortnik, J.; Ma, Q.; Li, W.; Shen, X.; Nishimura, Y.; An, X.; Thaller, S.; Breneman, A.; Wygant, J.; et al. Multipoint observations of quasiperiodic emission intensification and effects on energetic electron precipitation. J. Geophys. Res. Space Phys. 2021, 126, e28484. [Google Scholar] [CrossRef]
- Bespalov, P.A.; Kleimenova, N.G. Effect of geomagnetic pulsations on whistlers near the plasmapause (Review). Geomagn. Aeronom. 1989, 29, 177–191. [Google Scholar]
- Bespalov, P.A. Effective saturation of absorption in a plasma magnetospheric maser. In Nonlinear Space Plasma Physics; Sagdeev, R.Z., Ed.; American Institute of Physics: College Park, MD, USA, 1993; pp. 339–346. [Google Scholar]
- Bespalov, P.A.; Savina, O.N. Possibility of magnetospheric VLF response to atmospheric infrasonic waves. Earth Planets Space 2012, 64, 451–458. [Google Scholar] [CrossRef]
- Mizonova, V.G.; Bespalov, P.A. Response of propagation of ELF electromagnetic waves through the morning ionosphere to small density variations caused by infrasonic wave. Adv. Space Res. 2024, 73, 3743. [Google Scholar] [CrossRef]
- Bespalov, P.A.; Savina, O.N.; Neshchetkin, G.M.; Zharavina, P.D. Quasi-periodic ELF/VLF emissions with atypical time structure inside the plasmasphere. Results Phys. 2023, 46, 106291. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Method for Physics, Chemistry, and the Natural Sciences; Springer: Berlin, Germany, 1994. [Google Scholar]
- Shalimov, S.L. On the amplitude of low-frequency signals in the nighttime ionosphere over thunderstorm discharges. Cosmic Res. 2012, 50, 211. [Google Scholar] [CrossRef]
- Cummer, S.A.; Inan, U.S.; Bell, T.F.; Barrington-Leigh, C.P. ELF Radiation Produced by Electrical Currents in Sprites. Geophys. Res. Lett. 1998, 25, 1281. [Google Scholar] [CrossRef]
- Honda, R.H.; Kherani, E.A.; Figueiredo, C.A.O.B.; Astafyeva, E.; Wrasse, C.M.; Naccarato, K.P. Resonant infrasonic disturbances in total-electron-content during a severe thunderstorm on 23 October 2021. J. Geophys. Res. Space Phys. 2025, 130, e2024JA033679. [Google Scholar] [CrossRef]
- Zettergren, M.D.; Snively, J.B. Ionospheric response to infrasonic-acoustic waves generated by natural hazard events. J. Geophys. Res. Space Phys. 2015, 120, 8002. [Google Scholar] [CrossRef]
- Nozuka, Y.; Inchin, P.A.; Kaneko, Y.; Sabatini, R.; Snively, J.B. Earthquake source impacts on the generation and propagation of seismic infrasound to the upper atmosphere. Geophys. J. Int. 2024, 238, 537. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Perevalova, N.P.; Plotnikov, A.V.; Uralov, A.M. The shock-acoustic waves generated by earthquakes. Ann. Geophys. 2001, 19, 395. [Google Scholar] [CrossRef]
- Dautermann, T.; Eric Calais, E.; Lognonné, P.; Mattioli, G.S. Lithosphere—Atmosphere—Ionosphere coupling after the 2003 explosive eruption of the Soufriere Hills Volcano, Montserrat. Geophys. J. Int. 2009, 179, 1537. [Google Scholar] [CrossRef]
- Artru, J.; Farges, T.; Lognonné, P.H. Acoustic waves generated from seismic surface waves: Propagation properties determined from Doppler sounding observations and normal-mode modeling. Geophys. J. Int. 2004, 158, 1067. [Google Scholar] [CrossRef]
- Chum, J.; Cabrera, M.A.; Mošna, Z.; Fagre, M.; Baše, J.; Fišer, J. Nonlinear acoustic waves in the viscous thermosphere and ionosphere above earthquake. J. Geophys. Res. Space Phys. 2016, 121, 121–126. [Google Scholar] [CrossRef]
- Gossard, E.E.; Hooke, W.H. Waves in the Atmosphere: Atmospheric Infrasound and Gravity Waves—Their Generation and Propagation; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Bespalov, P.A.; Savina, O.N.; Misonova, V.G. Reflection from and transmission through the ionosphere of VLF electromagnetic waves incident from the mid-latitude magnetosphere. J. Atm. Sol. Terr. Phys. 2018, 175, 40. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bespalov, P.; Savina, O.; Shkareva, P. Indications of the Impact of the Influence of Large-Scale Atmospheric Disturbances on Quasiperiodic ELF/VLF Emissions Inside the Plasmasphere. Atmosphere 2025, 16, 1310. https://doi.org/10.3390/atmos16111310
Bespalov P, Savina O, Shkareva P. Indications of the Impact of the Influence of Large-Scale Atmospheric Disturbances on Quasiperiodic ELF/VLF Emissions Inside the Plasmasphere. Atmosphere. 2025; 16(11):1310. https://doi.org/10.3390/atmos16111310
Chicago/Turabian StyleBespalov, Peter, Olga Savina, and Polina Shkareva. 2025. "Indications of the Impact of the Influence of Large-Scale Atmospheric Disturbances on Quasiperiodic ELF/VLF Emissions Inside the Plasmasphere" Atmosphere 16, no. 11: 1310. https://doi.org/10.3390/atmos16111310
APA StyleBespalov, P., Savina, O., & Shkareva, P. (2025). Indications of the Impact of the Influence of Large-Scale Atmospheric Disturbances on Quasiperiodic ELF/VLF Emissions Inside the Plasmasphere. Atmosphere, 16(11), 1310. https://doi.org/10.3390/atmos16111310







