Review of Subionospheric VLF/LF Radio Signals for the Study of Seismogenic Lower-Ionospheric Perturbations
Abstract
1. Introduction to Seismo-Electromagnetics
2. Early Studies on VLF/LF Radio Sounding of Ionospheric Perturbations Associated with EQs
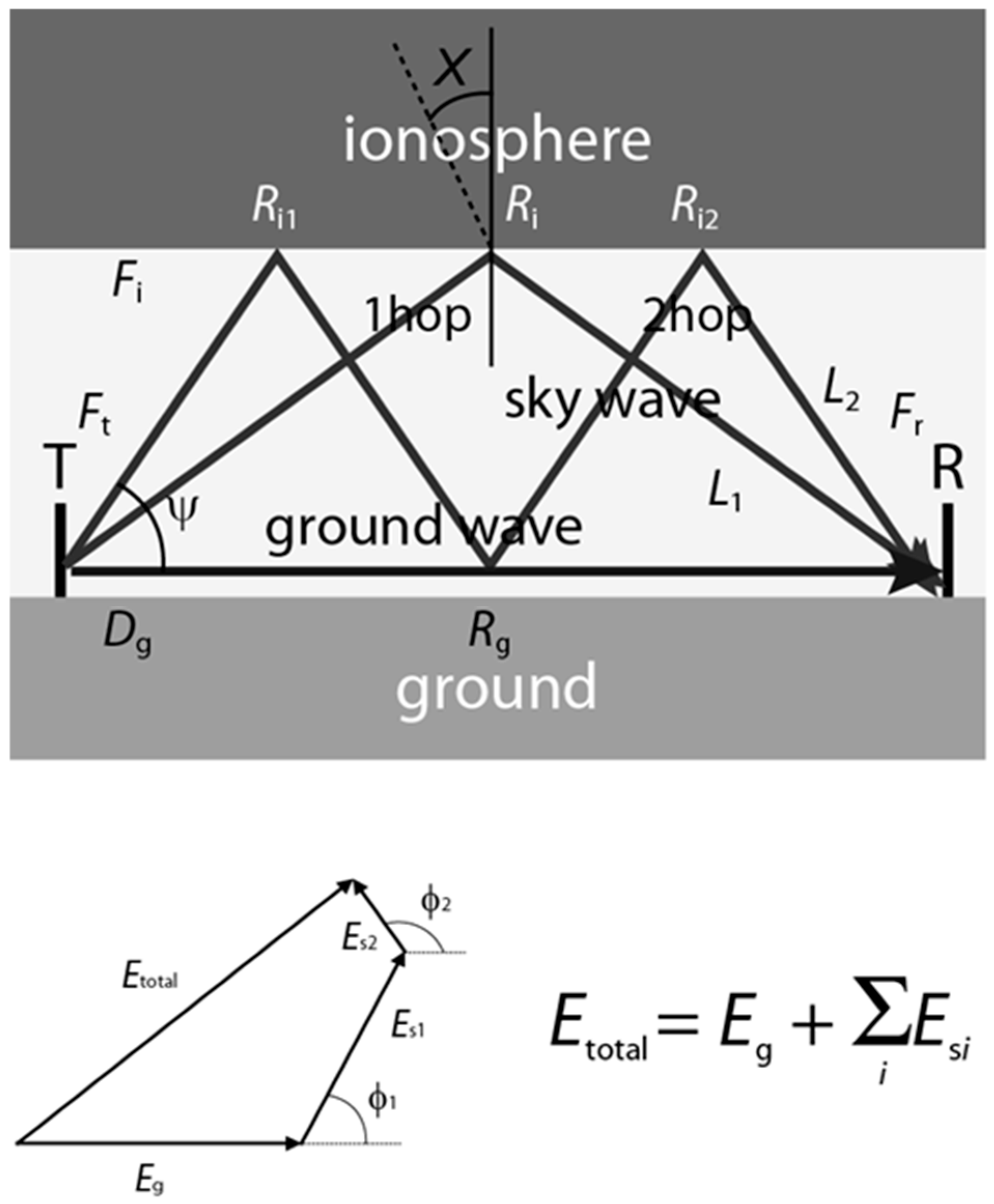
2.1. The Use of VLF/LF Subionospheric Propagation as a New Methodology
2.2. Brief History of VLF/LF Probing of Seismo-Ionospheric Perturbations
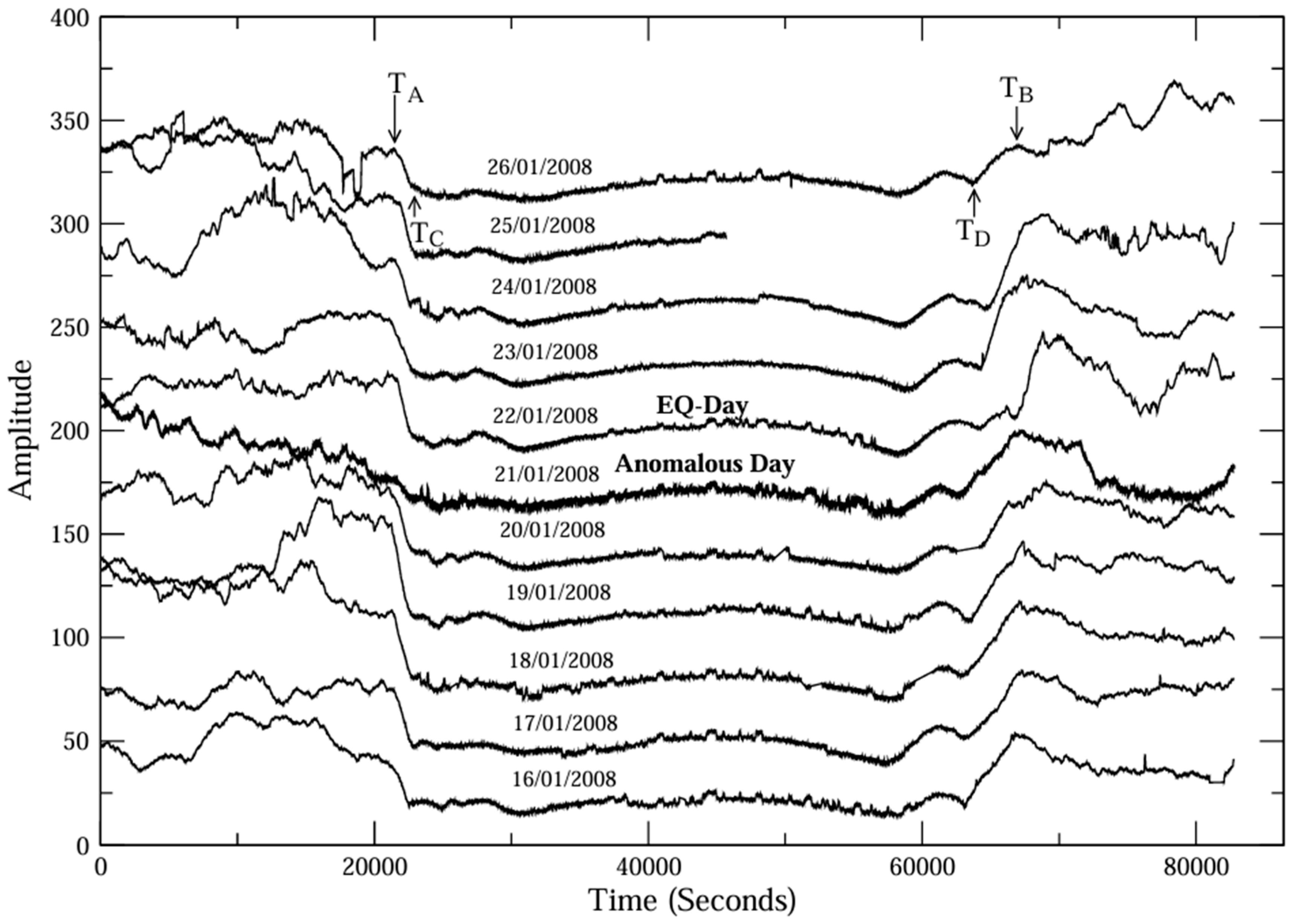
3. VLF Propagation Anomaly for the 1995 Kobe EQ
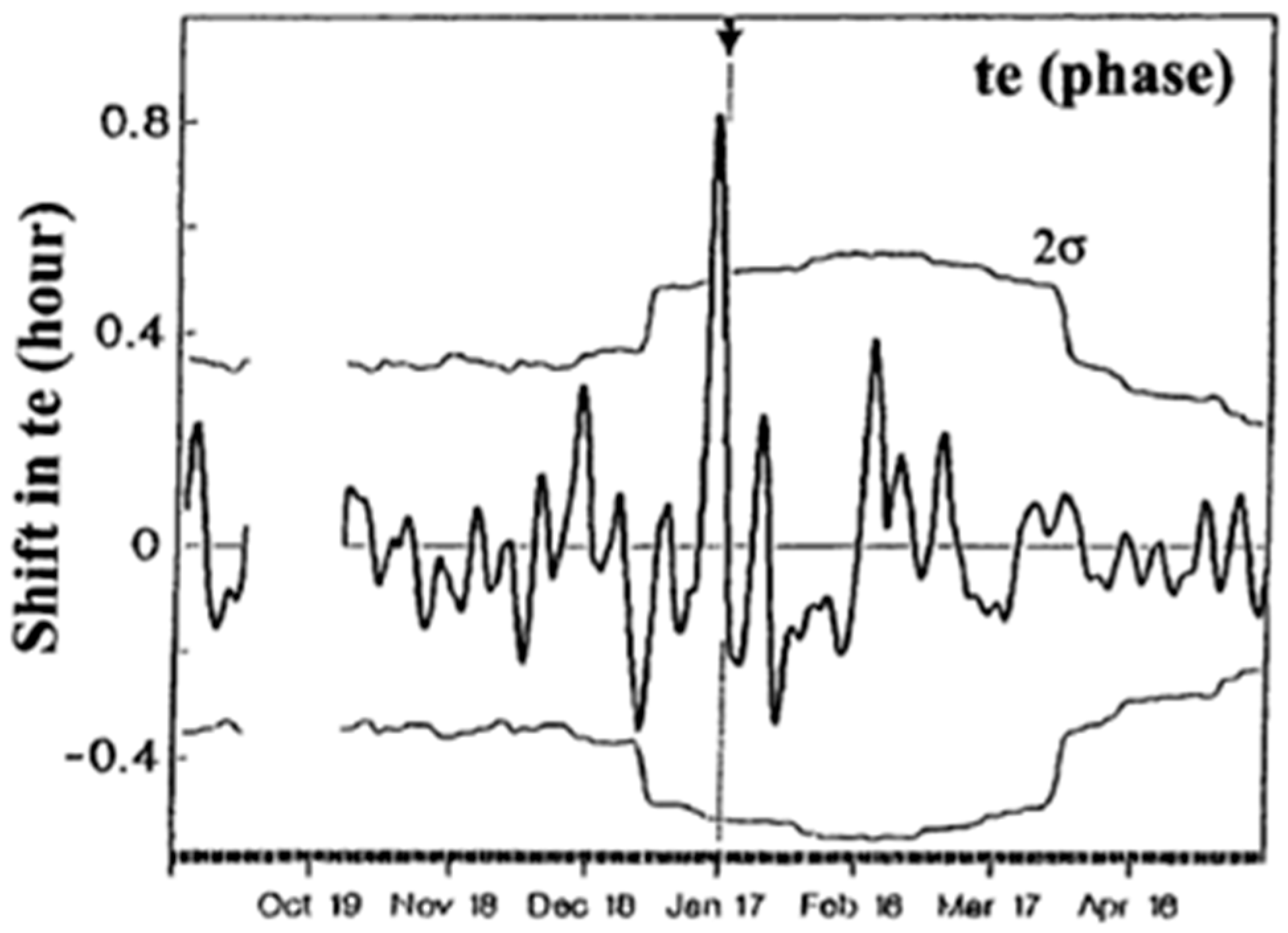
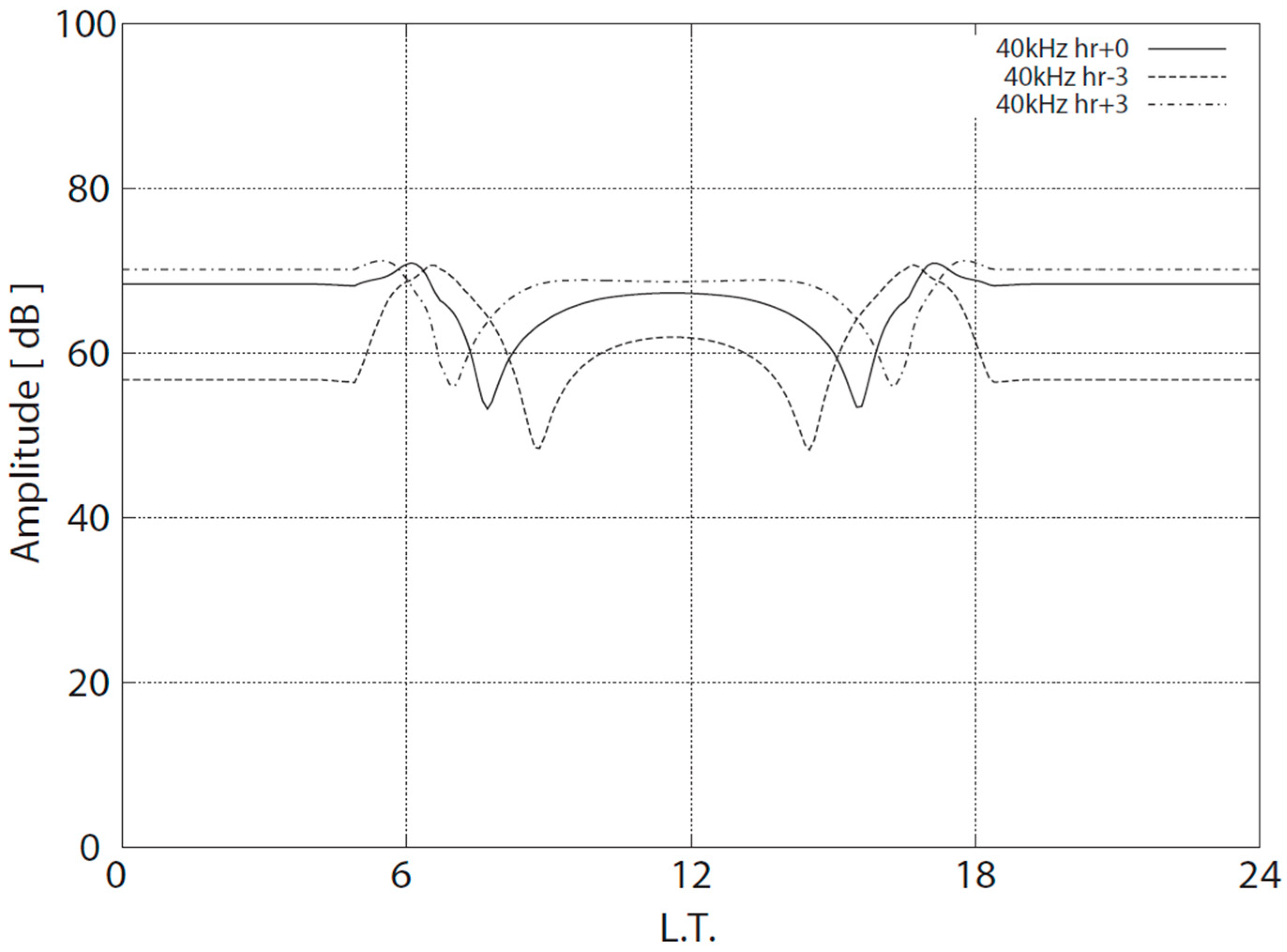
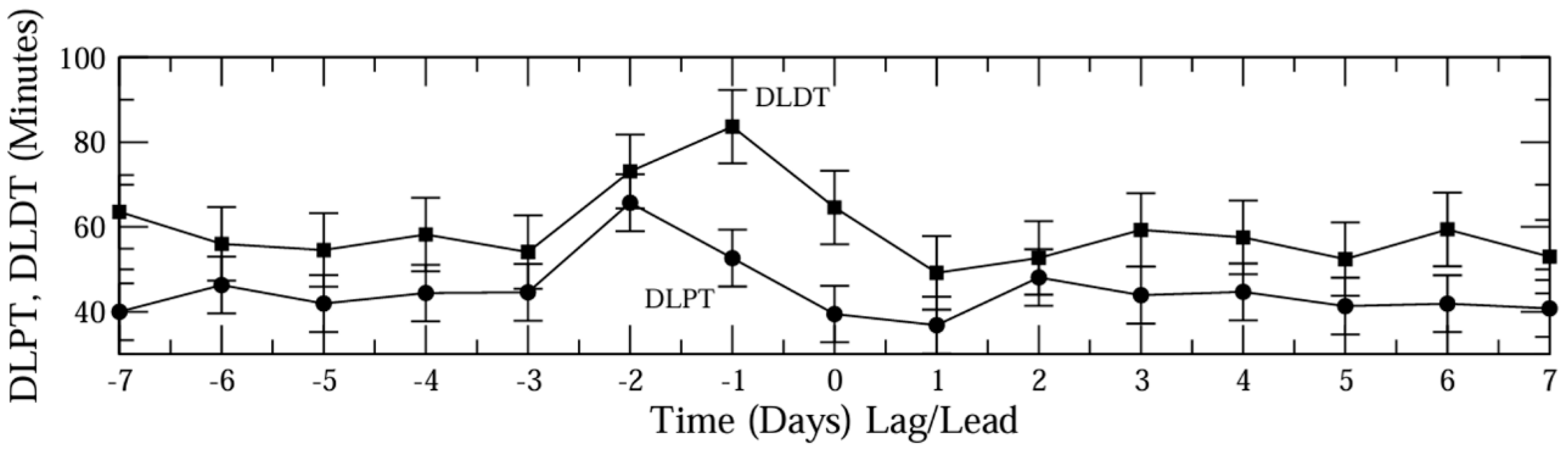
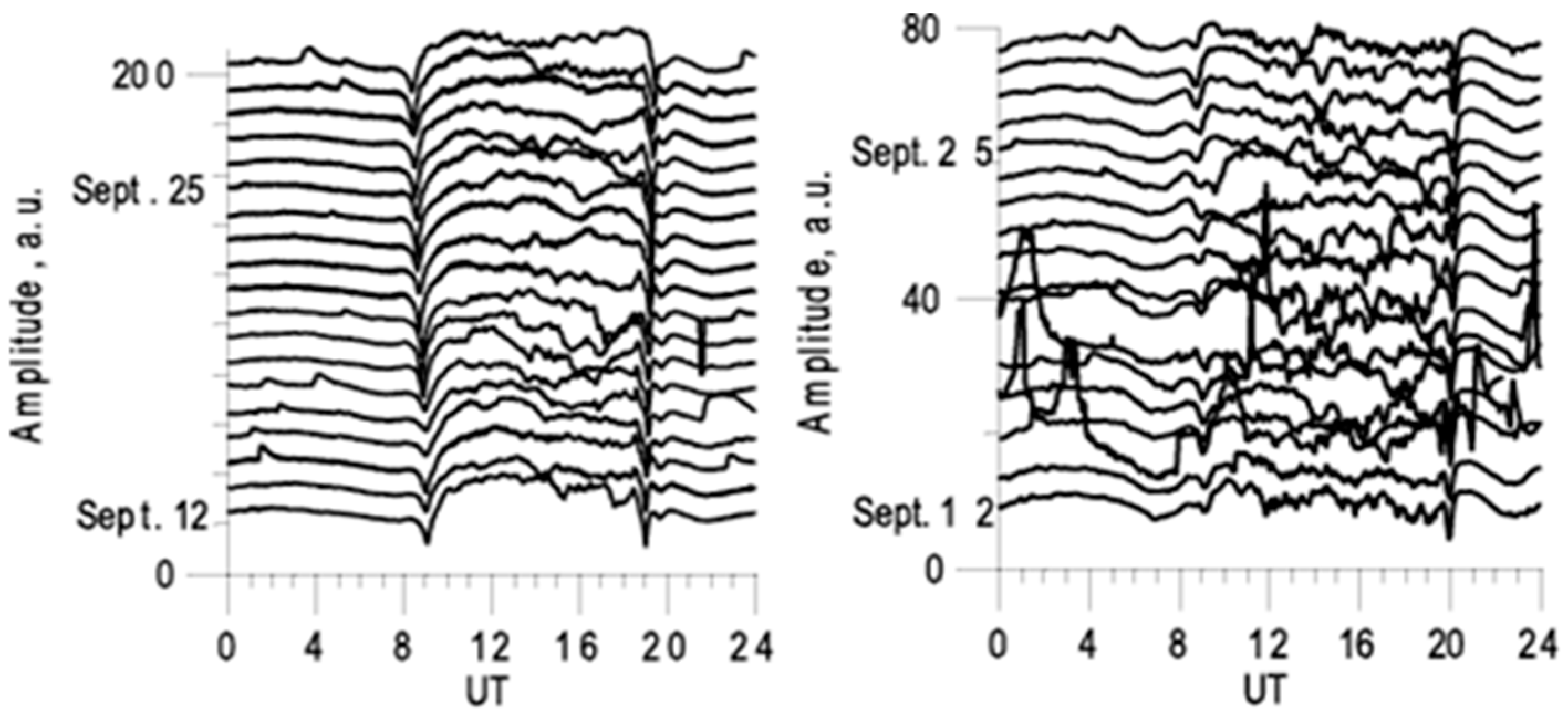
3.1. Terminator Time Method for the Study of Seismo-Ionospheric Perturbations
- (1)
- As for shallow (depth smaller than 30 km) EQs, four EQs from five exhibited the same terminator time anomaly as the Kobe EQ (as in Figure 1b) (with the same 2σ criterion).
- (2)
- When the depth of the EQs was in a medium range of 30–100 km, there were two events observed—one event exhibited the same terminator time anomaly, while another indicated a different type of anomaly.
- (3)
- Deep (depth larger than 100 km) EQs (four events) did not show any anomalies. Two of them had an extremely large magnitude (greater than 7.0) but had no propagation anomaly.
3.2. The Shift in Terminator Time for the Study of Ionospheric Changes Associated with EQs
4. Japanese VLF/LF Network During the Former NASDA’s EQ Remote-Sensing Frontier Project
4.1. NASDA’s EQ Remote-Sensing Frontier Project
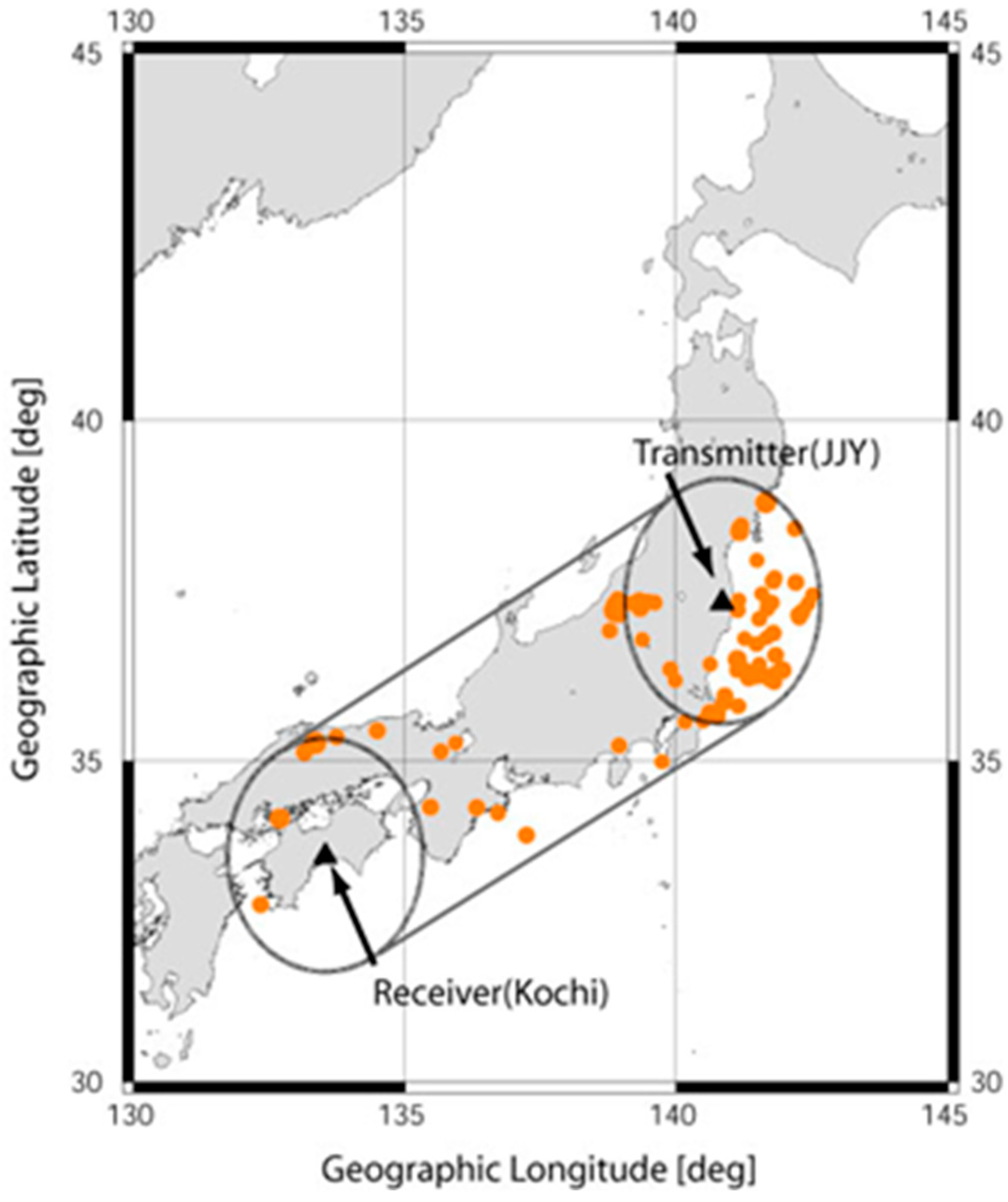
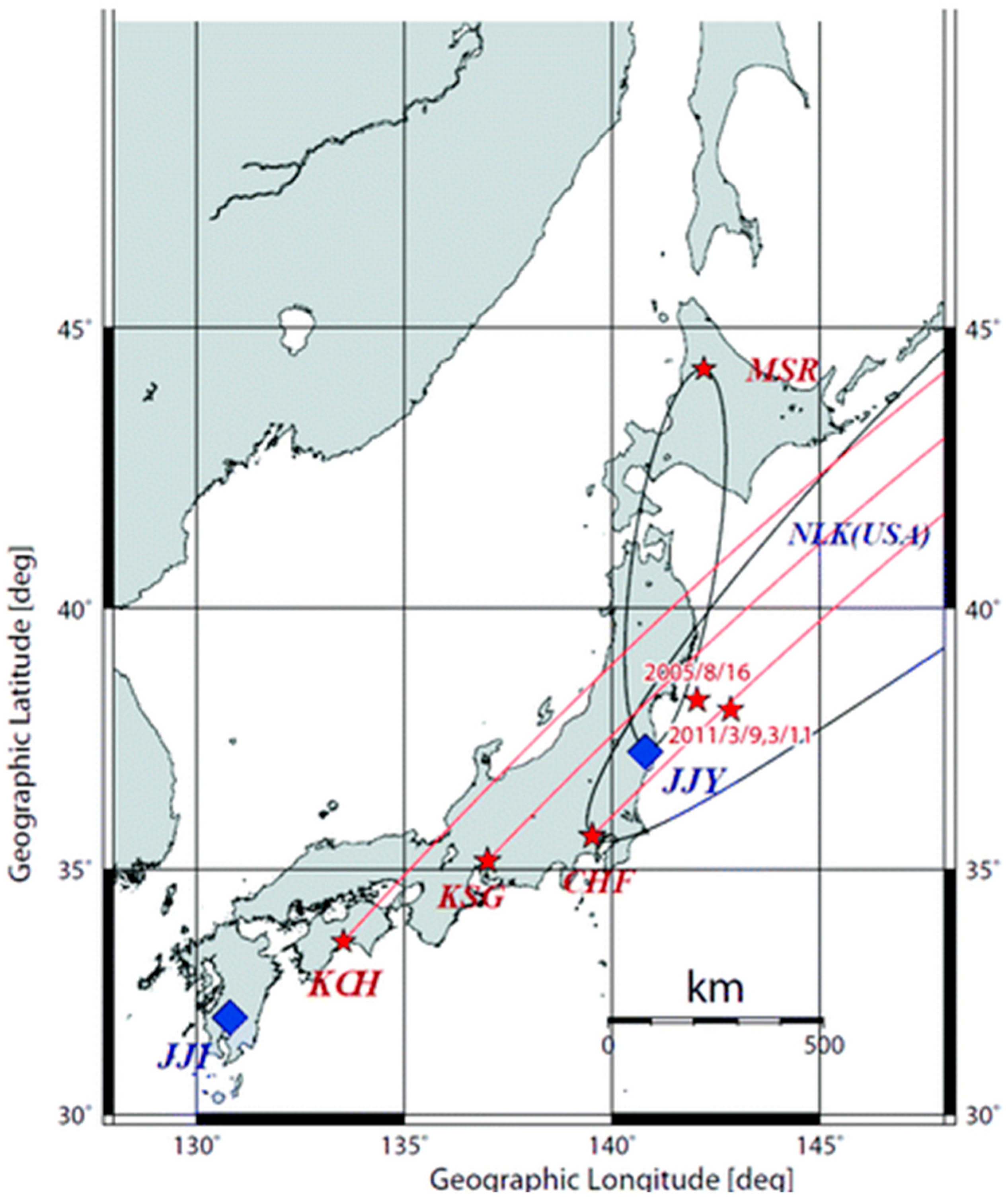
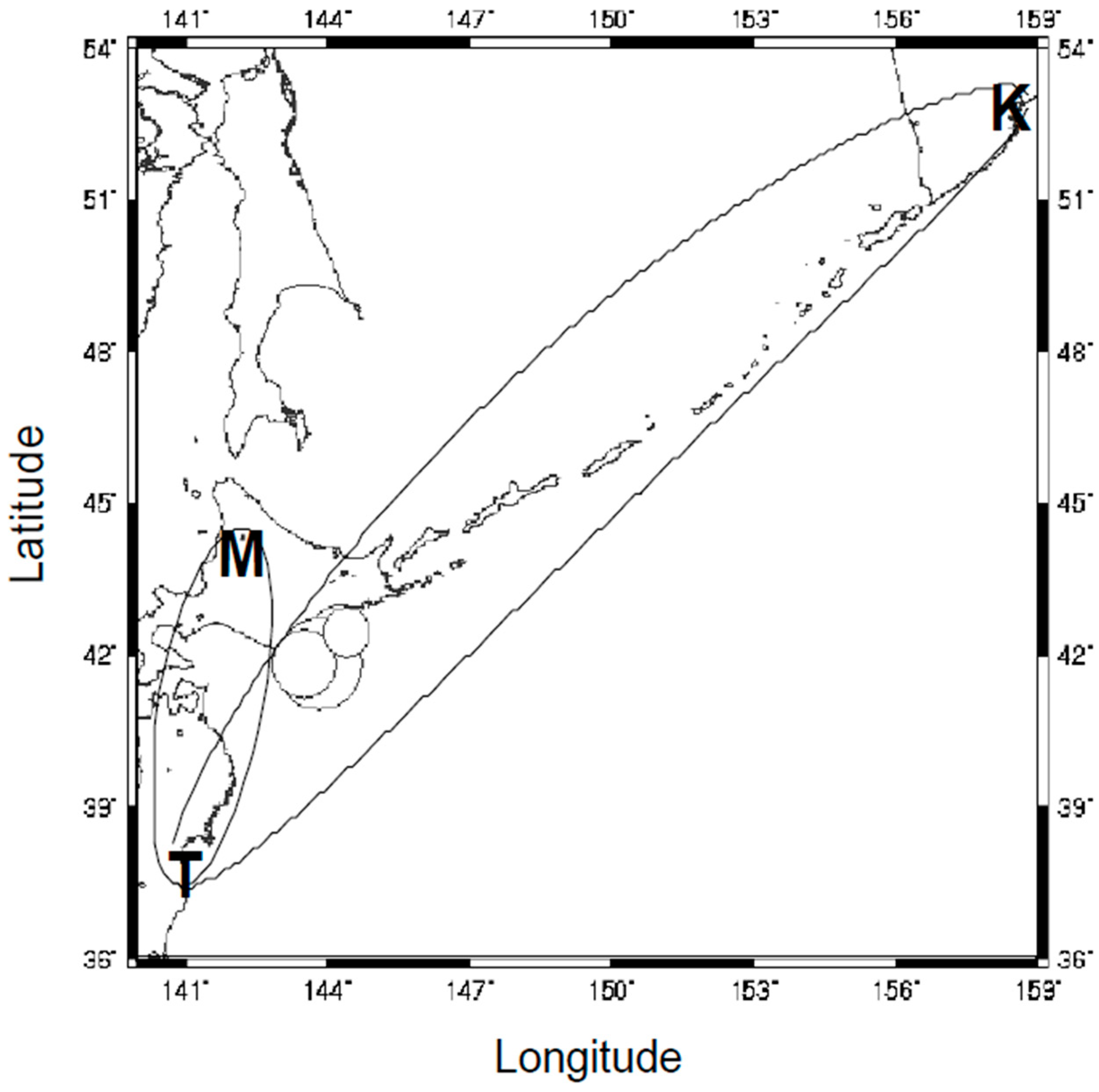
4.2. Japanese Subionospheric VLF/LF Network
4.3. Other VLF/LF Networks
- (a)
- Asia–Pacific network
- (b)
- European INFREP network
- (c)
- Chinese network
5. Further Evidence on Seismo-Ionospheric Perturbations
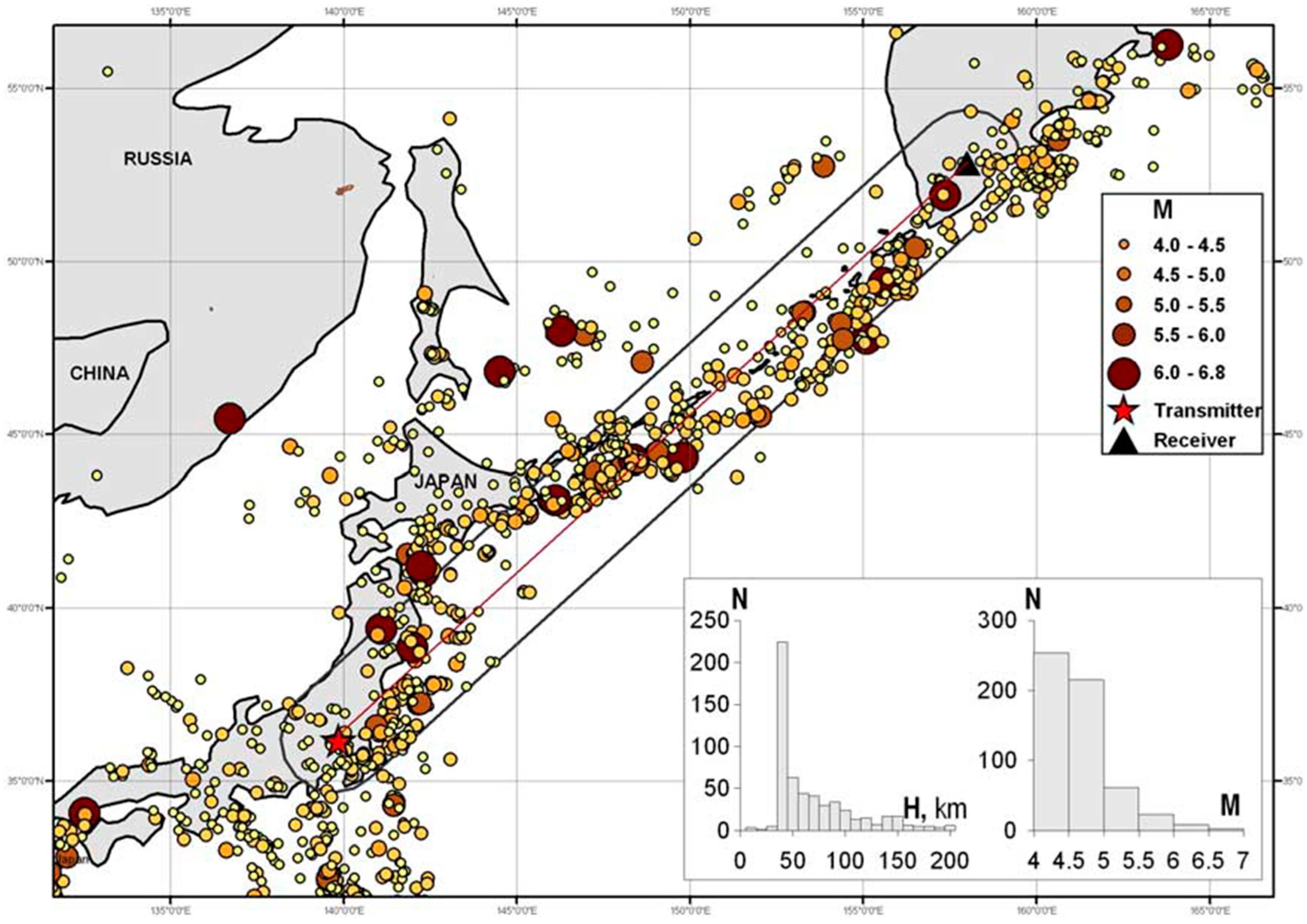
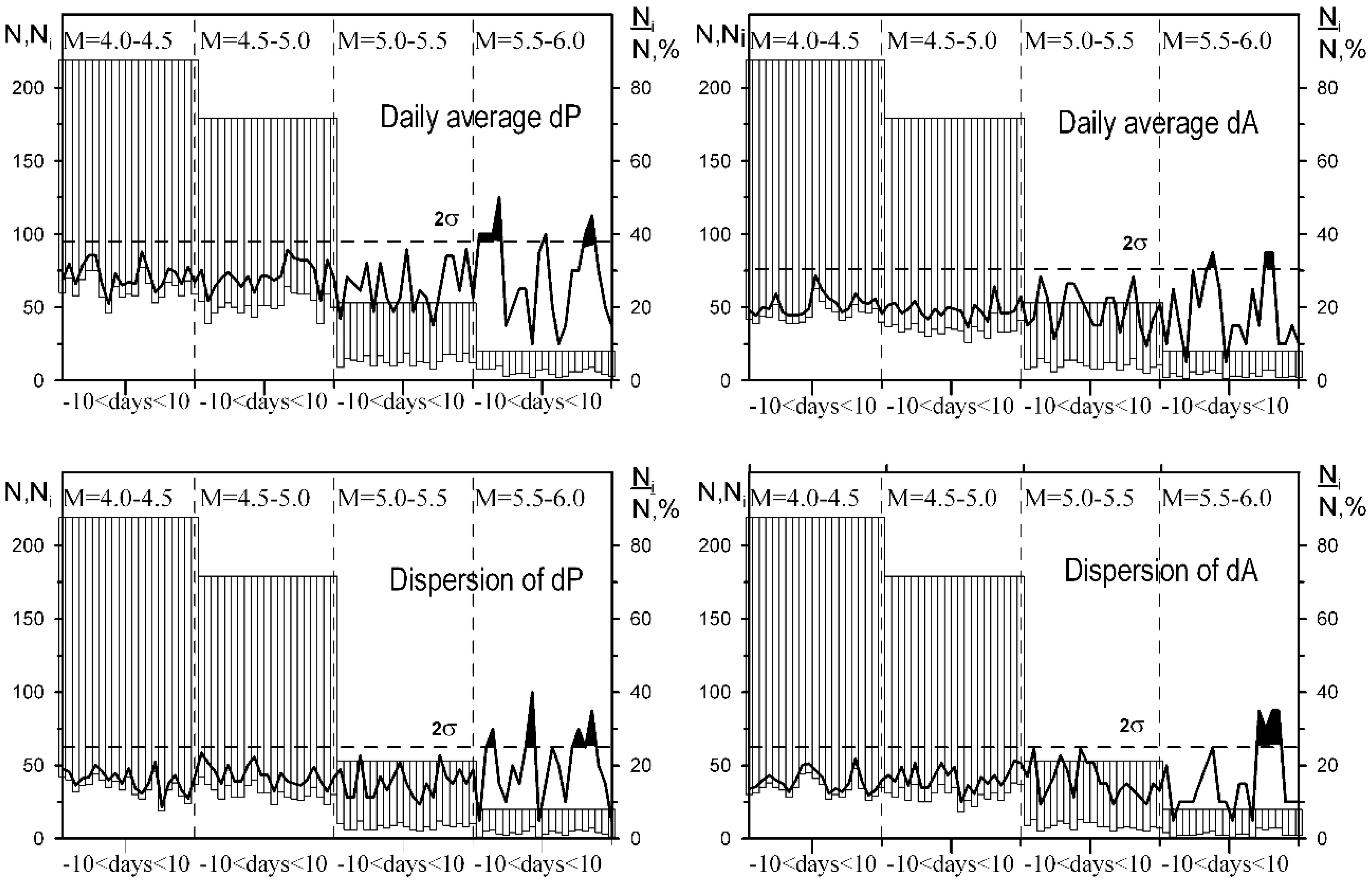
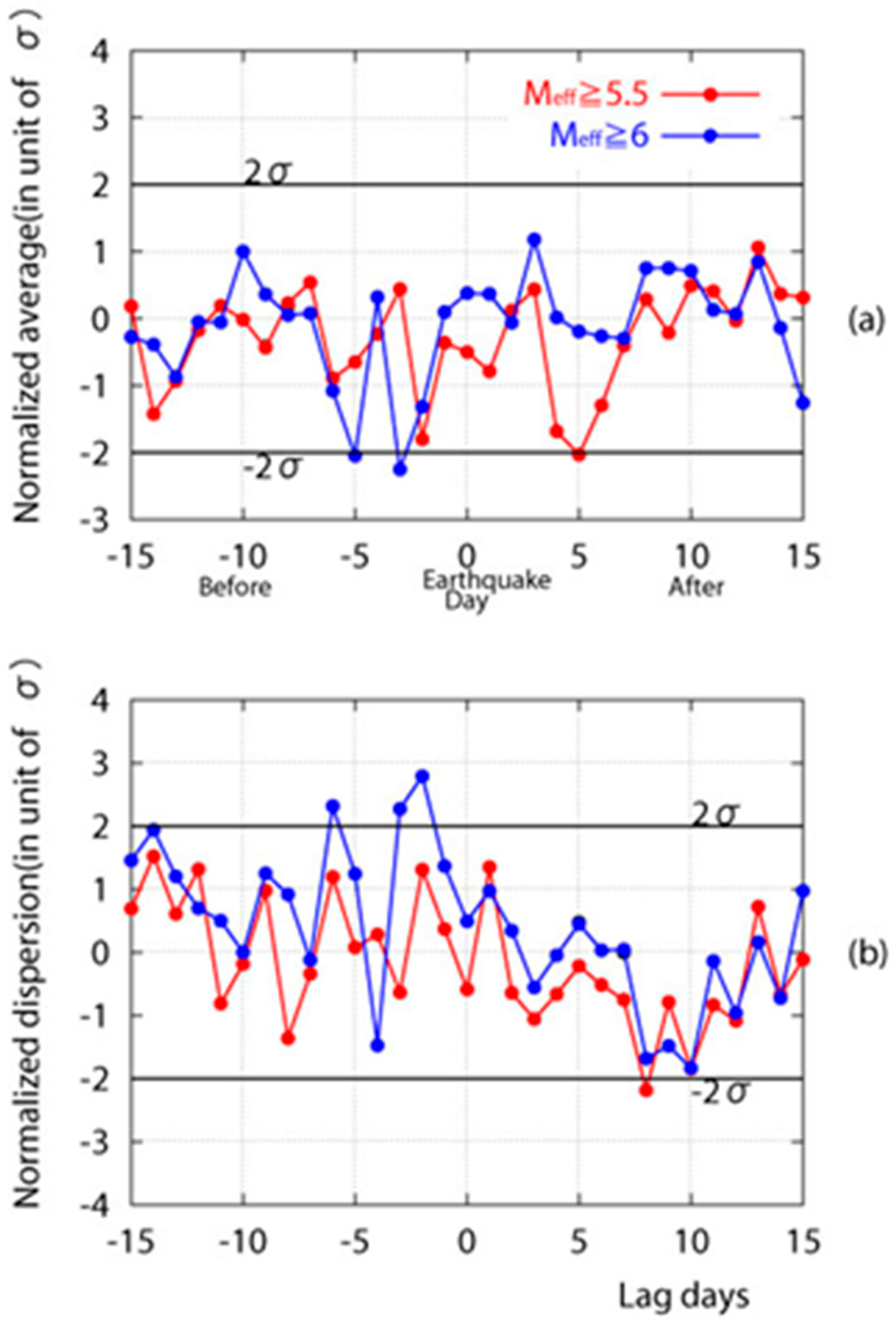
5.1. Statistical Studies
- (a)
- Statistical study of the path, Japan–Kamchatka
- (b)
- Statistical study of the Japanese EQs
5.2. Case Studies
- (a)
- The disastrous 2011 Tohoku EQ
6. Scientific Topics and Underlying Physics as Studied with VLF/LF Information
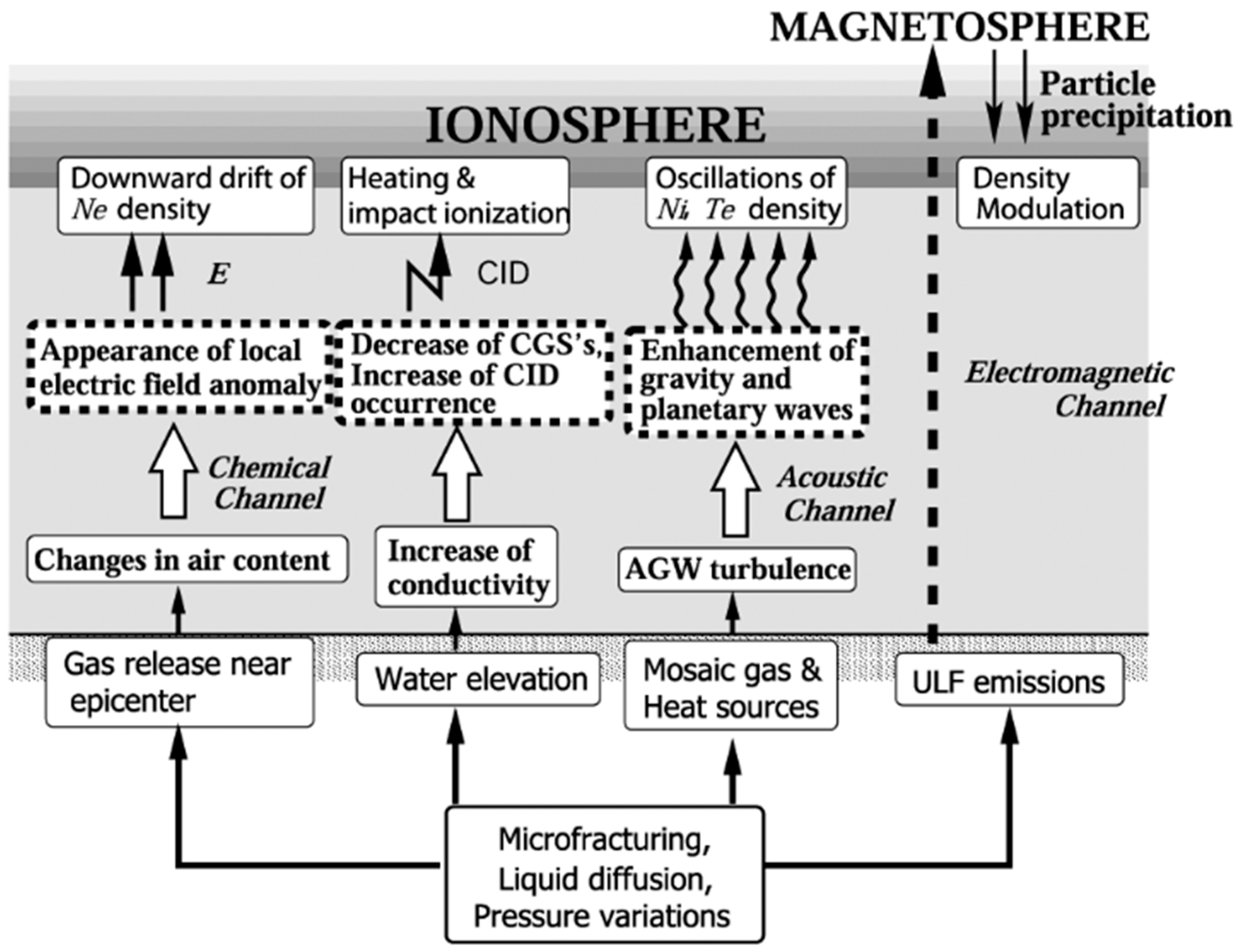
6.1. LAIC Channels
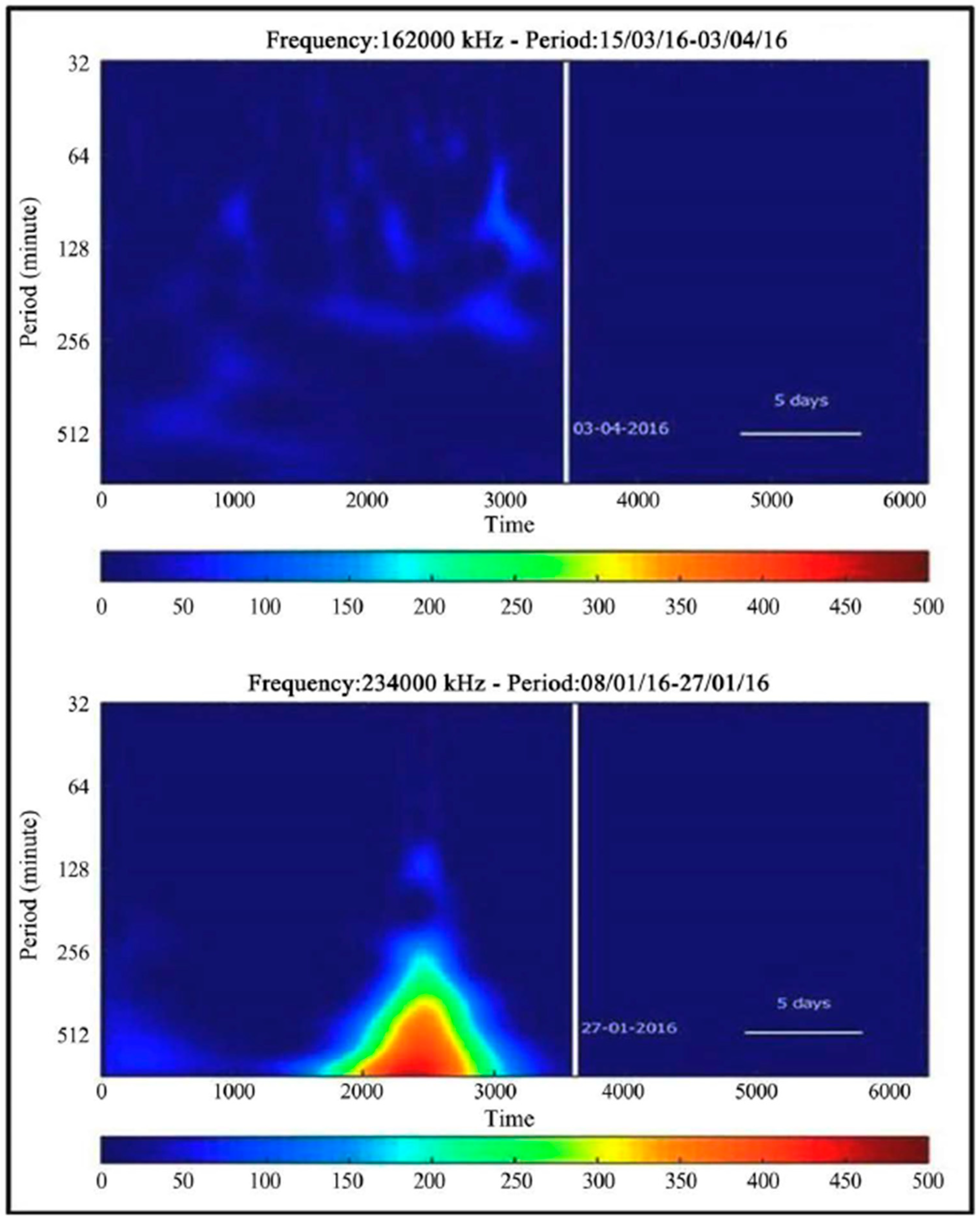
6.2. Slow Fluctuations in VLF/LF Amplitude and Phase: AGWs
6.3. Doppler-Shift Observation
6.4. Imminent VLF/LF Precursor
6.5. Fast Fluctuations in VLF/LF Amplitude
6.6. A New VLF Network and Design of New VLF Receivers
6.7. Satellite Observation of VLF/LF Transmitter Signals from On-Board Satellites
6.8. Correlation of Satellite Observations of Attenuation Band of ELF Signals with VLF/LF Subionospheric Anomalies
6.9. Numerical Modeling of Perturbed Lower Ionosphere
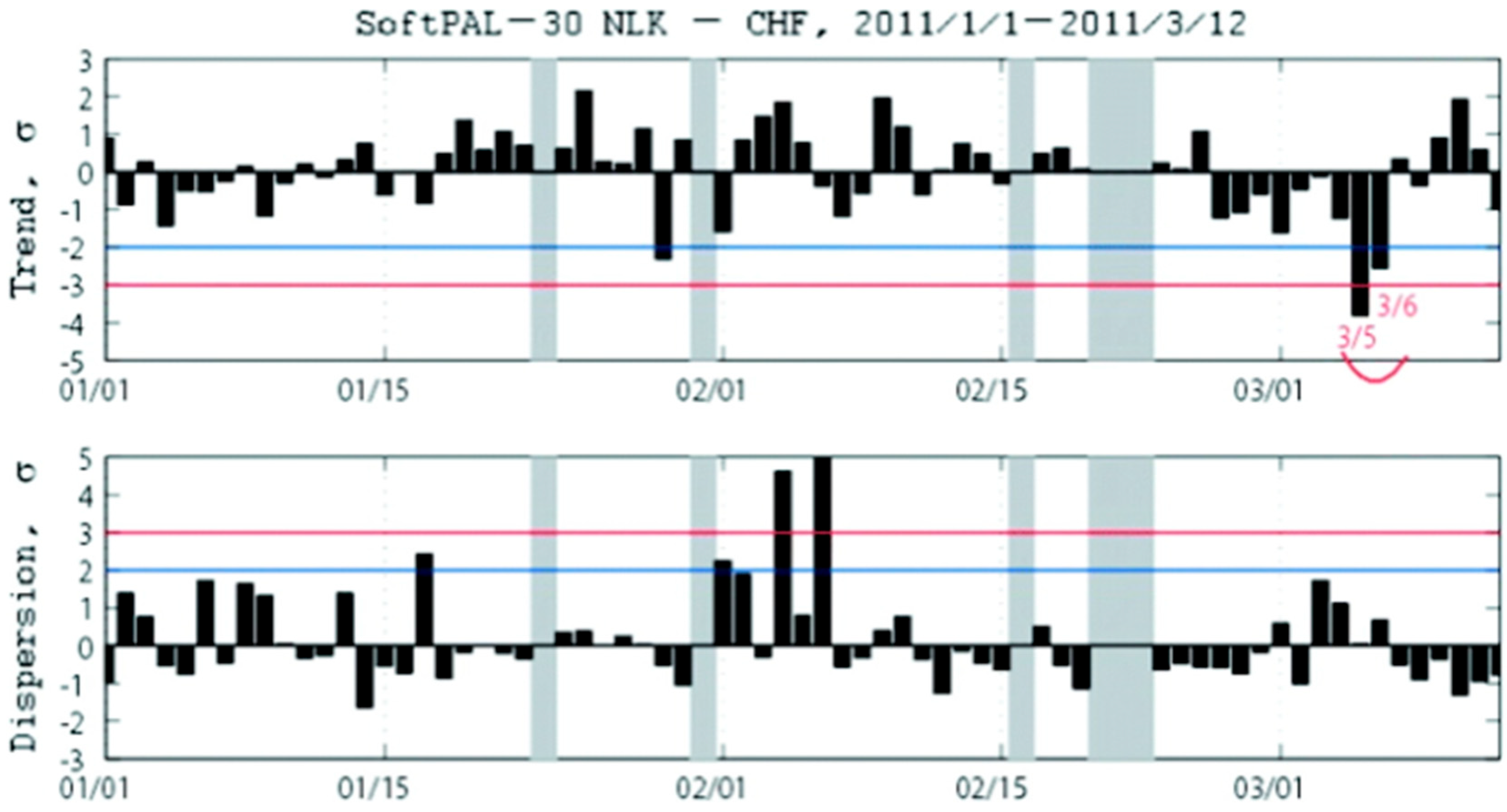
6.10. Application of Artificial Intelligence (Machine/Deep Learning) and Critical Analysis to VLF Anomalies
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hayakawa, M. Earthquake Precursors Studies in Japan. In Pre-Earthquake Process: A Multidisciplinary Approach to Earthquake Prediction Studies; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; American Geophysical Union: Washington, DC, USA; Wiley: Hoboken, NJ, USA, 2018; Chapter 2; pp. 7–18. [Google Scholar]
- Hayakawa, M. (Ed.) Electromagnetic Phenomena Associated with Earthquakes; Transworld Research Network: Trivandrum, India, 1999; 279p. [Google Scholar]
- Hayakawa, M.; Molchanov, O.A. (Eds.) Seismo-Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling; TERRAPUB: Tokyo, Japan, 2002; 477p. [Google Scholar]
- Molchanov, O.A.; Hayakawa, M. Seismo-Electromagnetics and Related Phenomena: History and Latest Results; TERRAPUB: Tokyo, Japan, 2008; 189p. [Google Scholar]
- Hayakawa, M. Earthquake Prediction with Radio Techniques; John Wiley & Sons: Singapore, 2015; 274p. [Google Scholar]
- Ouzounov, D.; Pulinets, S.; Hattori, K.; Taylor, P. (Eds.) Pre-Earthquake Process: A Multidisciplinary Approach to Earthquake Prediction Studies; American Geophysical Union: Washington, DC, USA; Wiley: Hoboken, NJ, USA, 2018; 365p. [Google Scholar]
- Pulinets, S.; Ouzounov, D.; Karelin, A.; Boyarchuk, K. Earthquake Precursors in the Atmosphere and Ionosphere: New Concepts; Springer: Berlin/Heidelberg, Germany, 2022; 294p. [Google Scholar]
- Surkov, V.V. An overview of theoretical studies of non-seismic phenomena accompanying earthquakes. Surv. Geophys. 2024, 46, 7–70. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y. Current status of seismo-electromagnetics for short-term earthquake prediction. Geomat. Nat. Hazards Risk 2010, 1, 115–155. [Google Scholar] [CrossRef]
- Watt, A.D. VLF Radio Engineering; Pergamon: Oxford, UK; New York, NY, USA, 1967; 703p. [Google Scholar]
- Wait, J.R. Electromagnetic Waves in Stratified Media; Pergamon Press: Oxford, UK; New York, NY, USA, 1962; 372p. [Google Scholar]
- Rodgers, C.; McCormic, R.J. Remote Sensing of the Upper Atmosphere by VLF. In Sprites, Elves and Intense Lighting Discharges; Füllekrug, M., Mareev, E.A., Rycrof, M.J., Eds.; NATO Science Series II; Springer: Berlin/Heidelberg, Germany, 2006; pp. 167–190. [Google Scholar]
- Dowden, R.L.; Adams, C.D.D. Location of lightning-induced electron precipitation from measurements of VLF phase and amplitude perturbations on spaced antennas and on two frequencies. J. Geophys. Res. 1990, 95, 4135–4145. [Google Scholar] [CrossRef]
- Inan, U.S.; Cummer, S.A.; Marshall, R.A. A survey of ELF and VLF research on lightning-ionosphere interactions and causative discharges. J. Geophys. Res. 2010, 115, A00E36. [Google Scholar] [CrossRef]
- Gokhberg, M.B.; Gufeld, I.L.; Rozhnoi, A.A.; Marenko, V.F.; Yampolshy, V.S.; Ponomarev, E.A. Study of seismic influence on the ionosphere by super long wave proding of the Earth–ionosphere waveguide. Phys. Earth Planet. Inter. 1989, 57, 64–67. [Google Scholar] [CrossRef]
- Gufeld, I.L.; Rozhnoi, A.A.; Tyumensev, S.N.; Sherstuk, S.V.; Yampolsky, V.S. Radiowave disturbances in period to Rudber and Rachinsk earthquakes. Phys. Solid Earth 1992, 28, 267–270. [Google Scholar]
- Gufeld, I.L.; Marenko, V.F. The short-time prediction for the time of strong earthquakes with the help of radiowave technique. Dokl. RAN 1992, 323, 1064–1070. [Google Scholar]
- Gufeld, I.L.; Gusev, G.; Pokhotelov, O. Is the Prediction of Earthquake Date Possible by VLF Radio Wave Monitoring Method? In Electromagnetic Phenomena Related to Earthquake Prediction; Hayakawa, M., Fujinawa, Y., Eds.; TERRAPUB: Tokyo, Japan, 1994; pp. 381–390. ISBN 4-88704-113-6. [Google Scholar]
- Hayakawa, M.; Molchanov, O.A.; Ondoh, T.; Kawai, E. On the precursory signature of Kobe earthquake in subionospheric VLF propagation. J. Comm. Res. Lab. 1996, 43, 169–180. [Google Scholar]
- Molchanov, O.A.; Hayakawa, M. Subionospheic VLF signal perturbations possibly related to earthquakes. J. Geophys. Res. 1998, 103, 17489–17504. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M.; Miyaki, K. VLF/LF sounding of the lower ionosphere to study the role of atmospheric oscillations in the lithosphere-ionosphere coupling. Adv. Polar Upper Atmos. Res. 2001, 15, 146–158. [Google Scholar] [CrossRef]
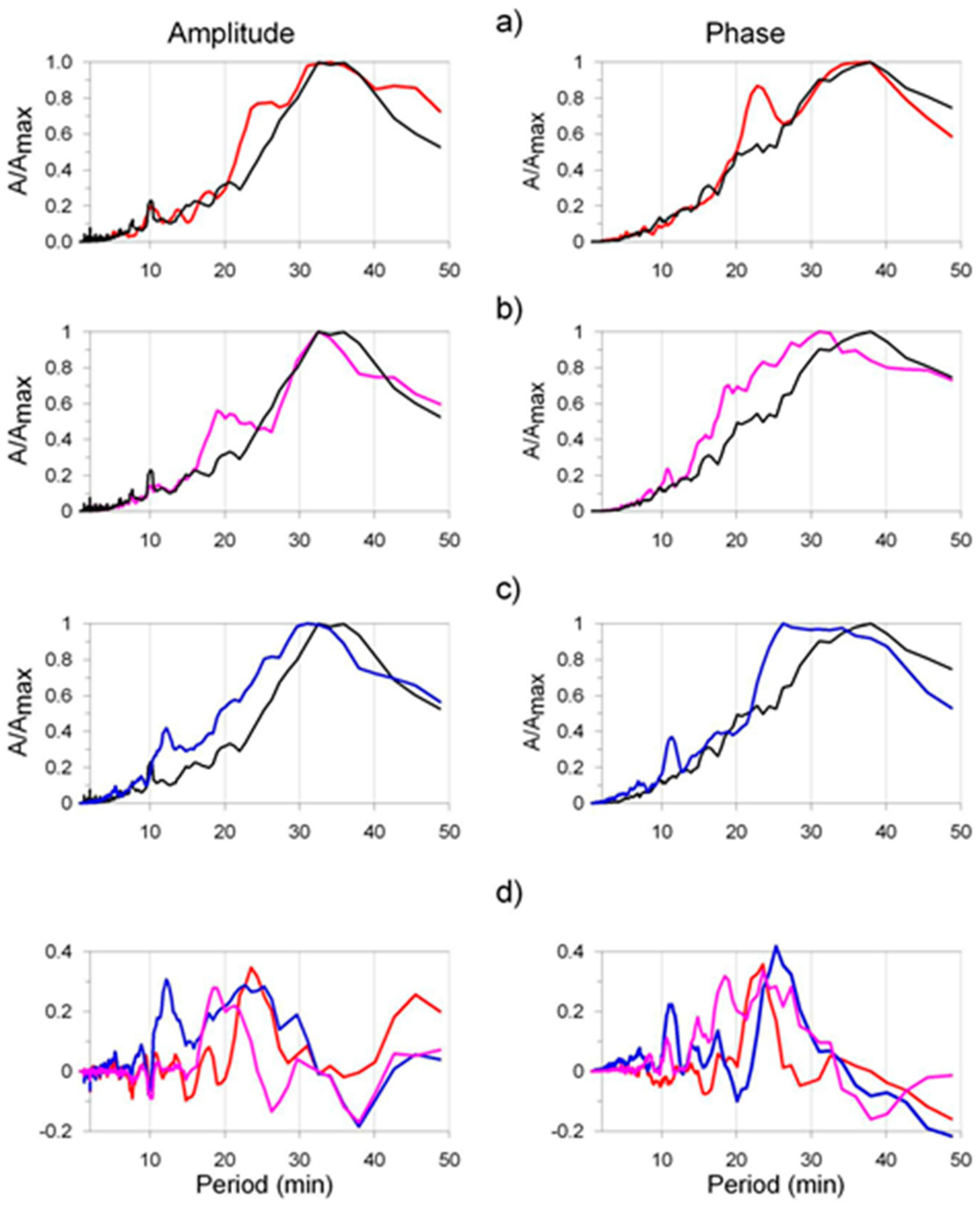
- Yoshida, M.; Yamauchi, T.; Horie, T.; Hayakawa, M. On the generation mechanism of terminator times in subionospheric VLF/LF propagation and its possible application to seismogenic effects. Nat. Hazards Earth Syst. Sci. 2008, 8, 129–134. [Google Scholar] [CrossRef]
- Maurya, A.K.; Venkatesham, K.; Tiwari, P.; Vijaykumar, K.; Singh, R.; Singh, A.K.; Ramesh, D.S. The 25 April 2015 Nepal earthquake: Investigation of precursor in VLF subionospheric signal. J. Geophys. Res. Space Phys. 2016, 121, 416. [Google Scholar] [CrossRef]
- Phanikumar, D.V.; Maurya, A.K.; Kumar, K.N.; Venkateshan, K.; Singh, R.; Sharma, S.; Naja, M. Anomalous variations of VLF sub-ionospheric signal and mesospheric ozone prior to the 2015 Nepal earthquake. Sci. Rep. 2018, 8, 9381. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, S.; Chakrabarti, S.K.; Ray, S. Unusual Very Low Frequency signal during the earthquake at Honshu, Japan on 11 March, 2011. Indian J. Phys. 2014, 88, 1013–1019. [Google Scholar] [CrossRef]
- Ghosh, S.; Chakraborty, S.; Samal, S.; Basak, T.; Chakrabarti, S.K.; Samanta, A. Comparative study of the possible anomalies in D-region electron density as computed from unusual terminator shifts in sub-ionospheric Very Low Frequency (VLF) signal during Honshu, 2011 and Nepal, 2015 earthquakes. In Proceedings of the 42nd COSPAR Scientific Assembly, Pasadena, CA, USA, 14–22 July 2018; Volume 42. [Google Scholar]
- Boudajada, M.Y.; Biagi, P.F.; Eichelberger, H.U.; Nico, G.; Galopeau, P.H.M.; Ermini, A.; Solovieva, M.; Hayakawa, M.; Lammer, H.; Volker, W.; et al. Analysis of pre-seismic ionospheric disturbances prior to 2020 Croatian earthquakes. Remote Sens. 2024, 16, 529. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Sasmal, S.; Chakrabarti, S. Ionospheric anomaly due to seismic activities—Part 2: Evidence from D-layer preparation and disappearance times. Nat. Hazards Earth Syst. Sci. 2010, 10, 1751–1757. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Sasmal, S.; Pal, S. ICSP Detections of Anomalous VLF Radio Wave Signals Prior to Major Earthquakes. In Earthquake Prediction Studies: Seismo Electromagnetics; Hayakawa, M., Ed.; TERRAPUB: Tokyo, Japan, 2013; pp. 49–55. [Google Scholar]
- Choudhury, A.; De, B.K.; Guha, A.; Roy, R. Long-duration geomagnetic storm effects on the D region of the ionosphere: Some case studies using VLF signal. J. Geophys. Res. Space Phys. 2015, 120, 778–787. [Google Scholar] [CrossRef]
- Hayakawa, M.; Molchanov, O.A. NASDA/UEC team Achievements of NASDA’s Earthquake Remote Sensing Frontier Project. Terr. Atmos. Ocean. Sci. 2004, 15, 311–328. [Google Scholar] [CrossRef]
- Kopytenko, Y.A.; Matiashvily, T.G.; Voronov, P.M.; Kopytenko, E.A.; Molchanov, O.A. Detection of ULF Emission Connected with the Spitak Earthquake and Its Aftershock Activity Based on Geomagnetic Pulsations Data at Dusheti and Vardziya Observatories. Phys. Earth Planet. Inter. 1990, 77, 85–95. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; Bernardi, A.; McGill, P.R.; Ladd, M.E.; Helliwell, R.A.; Villard, O.G., Jr. Low-frequency magnetic field measurements near the epicenter of the Ms 7.1 Loma Prieta earthquake. Geophys. Res. Lett. 1990, 17, 1465–1468. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Kopytenko, Y.A.; Voronov, P.M.; Kopytenko, E.A.; Matiashvily, T.G.; Fraser-Smith, A.C.; Bernardi, A. Results of ULF magnetic field measurements near the epicenters of the Spitac (Ms = 6.9) and Loma Prieta (Ms = 7.1) earthquakes: Comparative Analysis. Geophys. Res. Lett. 1992, 19, 1495–1498. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kawate, R.; Molchanov, O.A.; Yumoto, K. Results of ultra-low-frequency magnetic field measurements during the Guam earthquake of 8 August 1993. Geophys. Res. Lett. 1996, 23, 241–244. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hattori, K.; Ohta, K. Monitoring of ULF (ultra low frequency) geomagnetic variations associated with earthquakes. Sensors 2007, 7, 1108–1122. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Izutsu, J.; Nickolaenko, A.P. Seismogenic effects in ULF/ELF/VLF electromagnetic waves. Int. J. Electron. Appl. Res. 2019, 6, 1–86. [Google Scholar] [CrossRef]
- Gorny, V.I.; Salman, A.G.; Troni, A.A.; Shilin, B.B. The Earth’s outgoing IR radiation as an indicator of seismic activity. Proc. USSR Acad. Sci. 1988, 30, 67–69. [Google Scholar]
- Qiang, Z.J.; Xu, X.D.; Dian, C.G. Thermal infrared anomaly precursor of impending earthquakes. Chin. Sci. Bull. 1991, 36, 319–323. [Google Scholar] [CrossRef]
- Tronin, A. Satellite thermal survey-a new tool for the study of seismoactive regions. Int. J. Remote Sens. 1996, 17, 1439–1455. [Google Scholar] [CrossRef]
- Tronin, A.A.; Hayakawa, M.; Molchanov, O.A. Thermal IR satellite data application for earthquake research in Japan and China. J. Geodyn. 2002, 33, 319–534. [Google Scholar] [CrossRef]
- Dey, S.; Singh, R.P. Surface latent heat flux as an earthquake precursor. Nat. Hazards Earth Syst. Sci. 2003, 3, 749–755. [Google Scholar] [CrossRef]
- Ouzounov, D.; Freund, F. Mid-infrared emission prior to strong earthquakes analyzed by remote sensing data. Adv. Space Res. 2004, 33, 268–273. [Google Scholar] [CrossRef]
- Tramutoli, V.; Cuomo, V.; Filizzola, C.; Pergola, N.; Pietrapertosa, C. Assessing the potential of thermal infrared satellite surveys for monitoring seismically active areas: The case of Kocaeli (Izmit) earthquake, August 17, 1999. Remote Sens. Environ. 2005, 96, 409–426. [Google Scholar] [CrossRef]
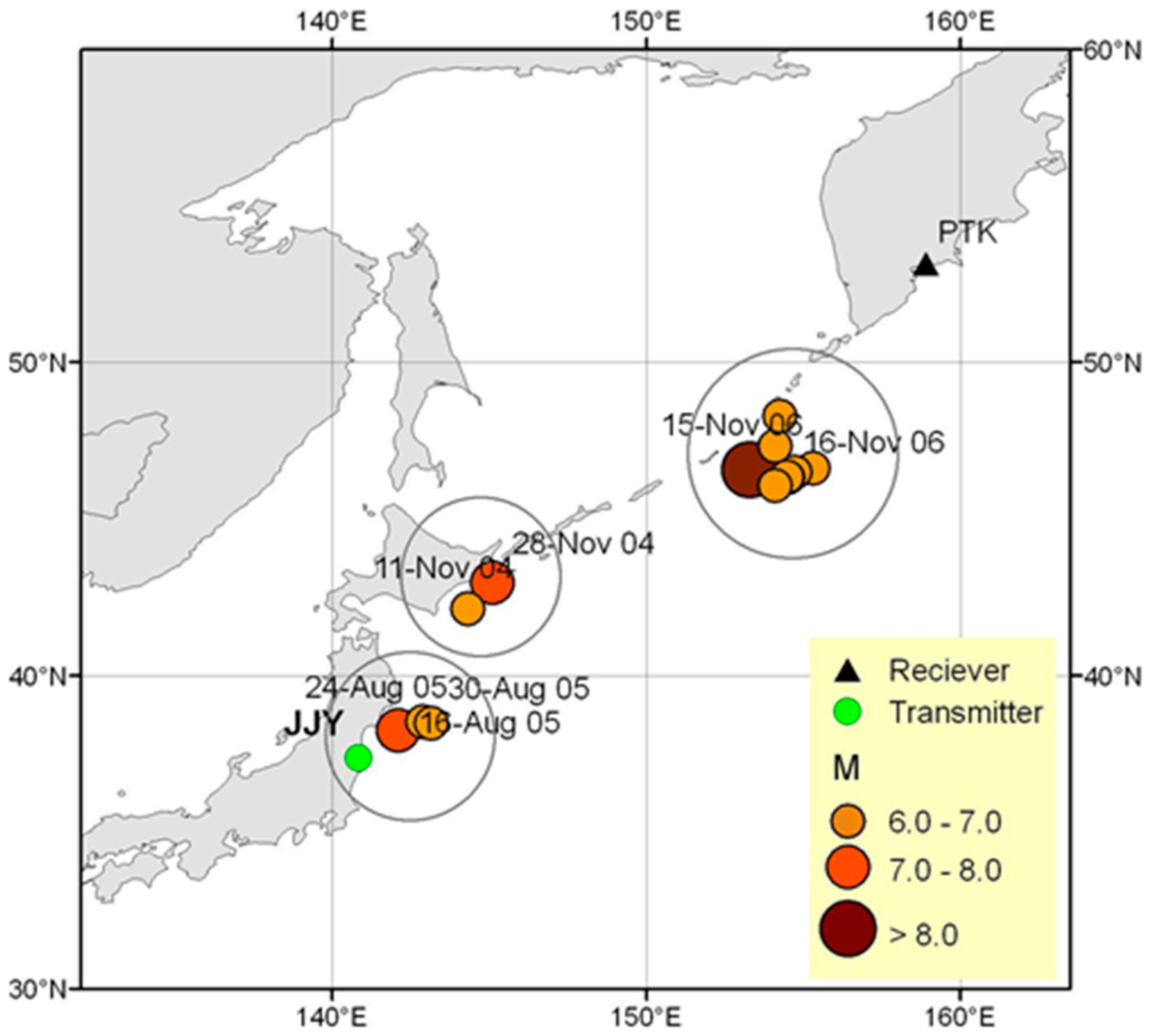
- Cervone, G.; Maekawa, S.; Singh, R.P.; Hayakawa, M.; Kafatos, M.; Shvets, A. Surface latent heat flux and nighttime LF anomalies prior to the Mw = 8.3 Tokachi-Oki earthquake. Nat. Hazards Earth Syst. Sci. 2006, 6, 109–114. [Google Scholar] [CrossRef]
- Blackett, M.; Wooster, M.J.; Malamud, B.D. Exploring land surface temperature earthquake precursors: A focus on the Gujarat (India) earthquake of 2001. Geophys. Res. Lett. 2011, 38, L15303. [Google Scholar] [CrossRef]
- Shah, M.; Khan, M.; Ullah, H.; Ali, S. Thermal anomalies prior to the 2015 Gorkha (India) earthquake from MODIS land surface temperature and outgoing longwave radiation. Geodyn. Tectonophys. 2018, 9, 123–138. [Google Scholar] [CrossRef]
- Piscini, A.; De Santis, A.; Marchetti, D.; Cianchini, G. A multiparametric climatological approach to study the 2016 Amatrice Norcia (Central Italy) earthquake preparatory phase. Pure Appl. Geophys. 2017, 174, 3673–3688. [Google Scholar] [CrossRef]
- Draz, M.U.; Shah, M.; Jamjareegulgarn, P.; Shahzed, R.; Hasan, A.M.; Ghamry, N.A. Deep machine learning based possible atmospheric and ionospheric precursors of the 2021 Mw7.1 Japan earthquake. Remote Sens. 2023, 15, 1904. [Google Scholar] [CrossRef]
- Ghosh, S.; Sasmal, S.; Potirakis, S.; Hayakawa, M. Thermal anomaly observed during the Crete earthquake on 27 September, 2021. Geosciences 2023, 14, 73. [Google Scholar] [CrossRef]
- Ghosh, S.; Chowdhury, S.K.; Kundu, S.; Sasmal, S.; Politis, D.Z.; Potirakis, S.M.; Hayakawa, M.; Chakraborty, S.; Chakrabarti, S.K. Unusual surface latent heat flux variations and their critical dynamics revealed before strong earthquakes. Entropy 2022, 24, 23. [Google Scholar] [CrossRef]
- Ouzounov, D.; Liu, D.; Chunli, K.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing long wave radiation variability from satellite data prior to major earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Venkatanathan, N.; Natyaganov, V. Outgoing longwave radiations as pre-earthquake signals: Preliminary results of 24 September 2013 M7.7 earthquake. Curr. Sci. 2014, 106, 1291–1297. [Google Scholar]
- Xiong, P.; Shen, X.H.; Bi, X.X.; Kang, C.L.; Chen, J.Z.; Jing, F.; Chen, Y. Study of outgoing longwave radiation anomalies associated with Haiti earthquake. Nat. Hazards Earth Syst. Sci. 2010, 10, 2169–2178. [Google Scholar] [CrossRef]
- Shah, M.; Ehsan, M.; Abbas, A.; Ahmed, A.; Jamjareegulgarn, P. Possible thermal anomalies associated with global terrible earthquakes during 2000-2019 based on MODIS-LST. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1002705. [Google Scholar] [CrossRef]
- Zarchi, A.K.; Maharan, M.R.S. Fault distance-based approach in thermal anomaly detection before strong earthquakes. Nat. Hazards Earth Syst. Sci. Prepr. 2020, 391. [Google Scholar] [CrossRef]
- Genzano, N.; Filizzaola, C.; Hattori, K.; Pergola, N.; Tramutoli, V. Statistical correlation analysis between thermal infrared anomalies observed from MTSATs and large earthquakes occurred in Japan (2005–2015). J. Geophys. Res. Solid Earth 2021, 126, e2020JB020108. [Google Scholar] [CrossRef]
- Sharma, P.; Bardhan, A.; Kumari, R.; Sharma, D.K.; Sharma, A.K. Variation of surface latent heat flux (SLHF) observed during high-magnitude earthquakes. J. Ind. Geophys. Union 2024, 28, 131–142. [Google Scholar]
- Hayakawa, M.; Hironaka, S.; Michimoto, K.; Potirakis, S.M.; Hobara, Y. Meteorological anomalies during earthquake preparation: A case study for the 1995 Kobe earthquake based on statistical and machine learning-based analyses. Atmosphere 2025, 16, 88. [Google Scholar] [CrossRef]
- Hinata, H.; Michimoto, K.; Ozawa, Y.; Hayakawa, M. A study of lithosphere-atmosphere-ionosphere coupling channel for the 1995 Kobe earthquake, by including ground-based meteorological anomalies. Open J. Earthq. Res. 2025, 14, 85–105. [Google Scholar] [CrossRef]
- Fukumoto, Y.; Hayakawa, M.; Yasuda, H. Investigation of over-horizon VHF radio signals associated with earthquakes. Nat. Hazards Earth Syst. Sci. 2001, 1, 107–112. [Google Scholar] [CrossRef]
- Fujiwara, H.; Kamogawa, M.; Ikeda, M.; Liu, J.Y.; Sakata, H.; Chen, Y.I.; Ofuruton, H.; Uramatsu, S.; Chuo, J.Y.; Ohtsuki, Y.H. Atmospheric anomalies observed during earthquake occurrences. Geophys. Res. Lett. 2004, 31, L17110. [Google Scholar] [CrossRef]
- Hayakawa, M.; Surkov, V.V.; Fukumoto, Y.; Yonaiguchi, N. Characteristics of VHF over-horizon signals possibly related to impending earthquakes and a mechanism of seismo-atmospheric perturbations. J. Atmos. Sol. Terr. Phys. 2007, 69, 1057–1062. [Google Scholar] [CrossRef]
- Ouzounov, D.; Velichkova-Yotsova, S.; Pulinets, S. Sudden modulation in the UHF wireless signals probably caused by the activation of pre-earthquake processes. Case studies for the Balkans (SE Europe). Ann. Geophys. 2024, 66, SE647. [Google Scholar] [CrossRef]
- Yang, S.-S.; Asano, T.; Hayakawa, M. Abnormal gravity wave activity in the stratosphere prior to the 2016 Kumamoto earthquakes. J. Geophys. Res. Space Phys. 2019, 124, 1410–1425. [Google Scholar] [CrossRef]
- Yang, S.S.; Hayakawa, M. Gravity wave activity in the stratosphere before the 2011 Tohoku earthquake as the mechanism of lithosphere-atmosphere-ionosphere coupling. Entropy 2020, 22, 110. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Chuo, Y.J.; Chen, C.S. A statistical investigation of pre-earthquake ionospheric anomaly. J. Geophys. Res. 2006, 111, A05304. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, C.H.; Chen, Y.I.; Yang, W.H.; Oyama, K.I.; Juo, K.W. A statistical study of ionospheric earthquake precursors monitored by using equatorial ionization anomaly of GPS TEC in Tawan during 2001–2007. J. Asian Earth Sci. 2010, 39, 76–80. [Google Scholar] [CrossRef]
- Afonin, V.V.; Molchanov, O.A.; Kodama, T.; Hayakawa, M.; Akentieva, O.A. Statistical Study of Ionospheric Plasma Response to Seismic Activity: Search for Reliable Result from Satellite Observations. In Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes; Hayakawa, M., Ed.; TERRAPUB: Tokyo, Japan, 1999; pp. 597–618. [Google Scholar]
- Parrot, M. Special Issue Planetary and Space Science “DEMETER”. Planet. Space Sci. 2006, 54, 411–412. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Huang, Q.; Shao, Z.; Liu, J.; Zhang, X.; Ma, W.; Parrot, M. Statistical correlation between DEMETER satellite electronic perturbations and global earthquakes with M >4.8. Trans. Geosci. Remote Sens. 2023, 61, 2001118. [Google Scholar] [CrossRef]
- Yan, R.; Huang, J.; Lin, J.; Wang, Q.; Zhang, Z.; Yang, Y.; Chu, W.; Liu, D.; Xu, S.; Lu, H.; et al. Retrospective study on seismo ionospheric anomalies based on five-year observations from CSES. Remote Sens. 2024, 16, 4426. [Google Scholar] [CrossRef]
- Molchanov, O.; Fedorov, E.; Schekotov, A.; Gordeev, E.; Chebrov, V.; Surkov, V.; Rozhnoi, A.; Andreavsky, A.; Iudin, D.; Yunga, S.; et al. Lithosphere-atmosphere-ionosphere coupling as governing mechanism for preseismic short-term events in atmosphere and ionosphere. Nat. Hazards Earth Syst. Sci. 2004, 4, 757–767. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere-atmosphere-ionosphere coupling (LAIC)—A unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Hayakawa, M.; Horie, T.; Muto, F.; Kasahara, Y.; Ohta, K.; Liu, J.Y.; Hobara, Y. Subionospheric VLF/LF probing of ionospheric perturbations associated with earthquakes: A possibility of earthquake prediction. SICE J. Control Meas. Syst. Integr. 2010, 3, 10–14. [Google Scholar] [CrossRef]
- Dowden, R.L.; Brundel, J.B.; Hayakawa, M. Remote sensing by VLF using “Absolute OmniPAL”. 1. Investigation of short path propagation for possible earthquake precursor detection. In Proceedings of the 1998 International Conference on Mathematical Model in Electromagnetic Theory, Kharkov, Ukraine, 2–5 June 1998; pp. 29–34. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.S.; Molchanov, O.A.; Hayakawa, M. Middle latitude LF (40 kHz) phase variations associated with earthquakes for quiet and disturbed geomagnetic conditions. Phys. Chem. Earth 2004, 29, 589–598. [Google Scholar] [CrossRef]
- Biagi, P.F.; Castellana, L.; Maggipinto, T.; Piccolo, R.; Minafra, A.; Ermini, A.; Martellucci, S.; Bellecci, C.; Perna, G.; Capozzi, V.; et al. A possible preseismic anomaly in the ground wave of a radio broadcasting (216 kHz) during July-August 1998 (Italy). Nat. Hazards Earth Syst. Sci. 2005, 5, 727–732. [Google Scholar] [CrossRef]
- Biagi, P.F.; Castellana, L.; Maggipinto, T.; Piccolo, R.; Minafra, A.; Ermini, A.; Martellucci, S.; Bellecci, C.; Perna, G.; Capozzi, V.; et al. LF radio anomalies revealed in Italy by the wavelet analysis: Possible preseismic effects during 1997–1998. Phys. Chem. Earth 2006, 31, 403–408. [Google Scholar] [CrossRef]
- Biagi, P.F.; Castellana, L.; Maggipinto, T.; Ermini, A. An overview on preseimic anomalies in LF radio signals revealed in Italy by wavelet analysis. Ann. Geophys. 2008, 51, 237–246. [Google Scholar] [CrossRef]
- Doleaa, P.; Cristeaa, C.; Dascala, P.V.; Moldovanb, I.-A.; Biagi, P.F. Aspects regarding the use of the INFREP network for identifying possible seismic precursors. Phys. Chem. Earth 2015, 85, 34–43. [Google Scholar] [CrossRef]
- Biagi, P.F.; Colella1, R.; Schiavulli1, L.; Ermini, A.; Boudjada, M.; Eichelberger, H.; Schwingenschuh, K.; Katzis, K.; Contadakis, M.E.; Skeberis, C.; et al. The INFREP network: Present situation and recent results. Open J. Earthq. Res. 2019, 8, 101–115. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform of time-frequency localization and signal analysis. IEEE Trans. Inform. Theory 1990, 36, 961–1004. [Google Scholar] [CrossRef]
- Zhao, S.; Shen, X.; Liao, L.; Zhima, Z.; Zhou, C.; Wang, Z.; Cui, J.; Lu, H. Investigation of precursors in VLF subionospheric signals related to strong earthquakes (M > 7) in western China and possible explanations. Remote Sens. 2020, 12, 3563. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Muto, F.; Horie, T.; Maekawa, S.; Hobara, Y.; Rozhnoi, A.A.; Solovieva, M.; Molchanov, O.A. A statistical study on the correlation between lower ionospheric perturbations as seen by subionospheric VLF/LF propagation and earthquakes. J. Geophys. Res. 2010, 115, A09305. [Google Scholar] [CrossRef]
- Maekawa, S.; Horie, T.; Yamauchi, T.; Sawaya, T.; Ishikawa, M.; Hayakawa, M.; Sasaki, H. A statistical study on the effect of earthquakes on the ionosphere, based on the subionospheric LF propagation data in Japan. Ann. Geophys. 2006, 24, 2219–2225. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B.; Pundhir, D. Ionospheric perturbations due to earthquakes as determined from VLF and GPS-TEC data analysis at Agra, India. Adv. Space Res. 2018, 61, 1952–1965. [Google Scholar] [CrossRef]
- Maurya, A.K.; Singh, R.; Veenadhari, B.; Kumar, S. Sub-ionospheric very low frequency perturbations associated with the 12 May 2008 M=7.9 Wenchuan earthquake. Nat. Hazards Earth Syst. Sci. 2013, 13, 2331–2336. [Google Scholar] [CrossRef]
- Tojiev, S.R.; Ahmedov, B.J.; Eshkuvatov, H.E. Ionospheric precursors of earthquakes recorded by VLF receiver at Tashkent IHY station. Adv. Space Res. 2014, 54, 628–643. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, S.; Kumar, A. Earthquakes associated subionospheric VLF anomalies recorded at two low latitude stations in the South Pacific region. J. Atmos. Sol. Terr. Phys. 2022, 229, 105834. [Google Scholar] [CrossRef]
- Politis, D.Z.; Sasmal, S.; Hayakawa, M.; Haralambous, H.; Datta, A.; Potirakis, S.M. A Six-Year (2014–2020) Statistical Correlation Study of VLF Terminator Time Shift with Earthquakes in Japan. Remote Sens. 2024, 16, 4162. [Google Scholar] [CrossRef]
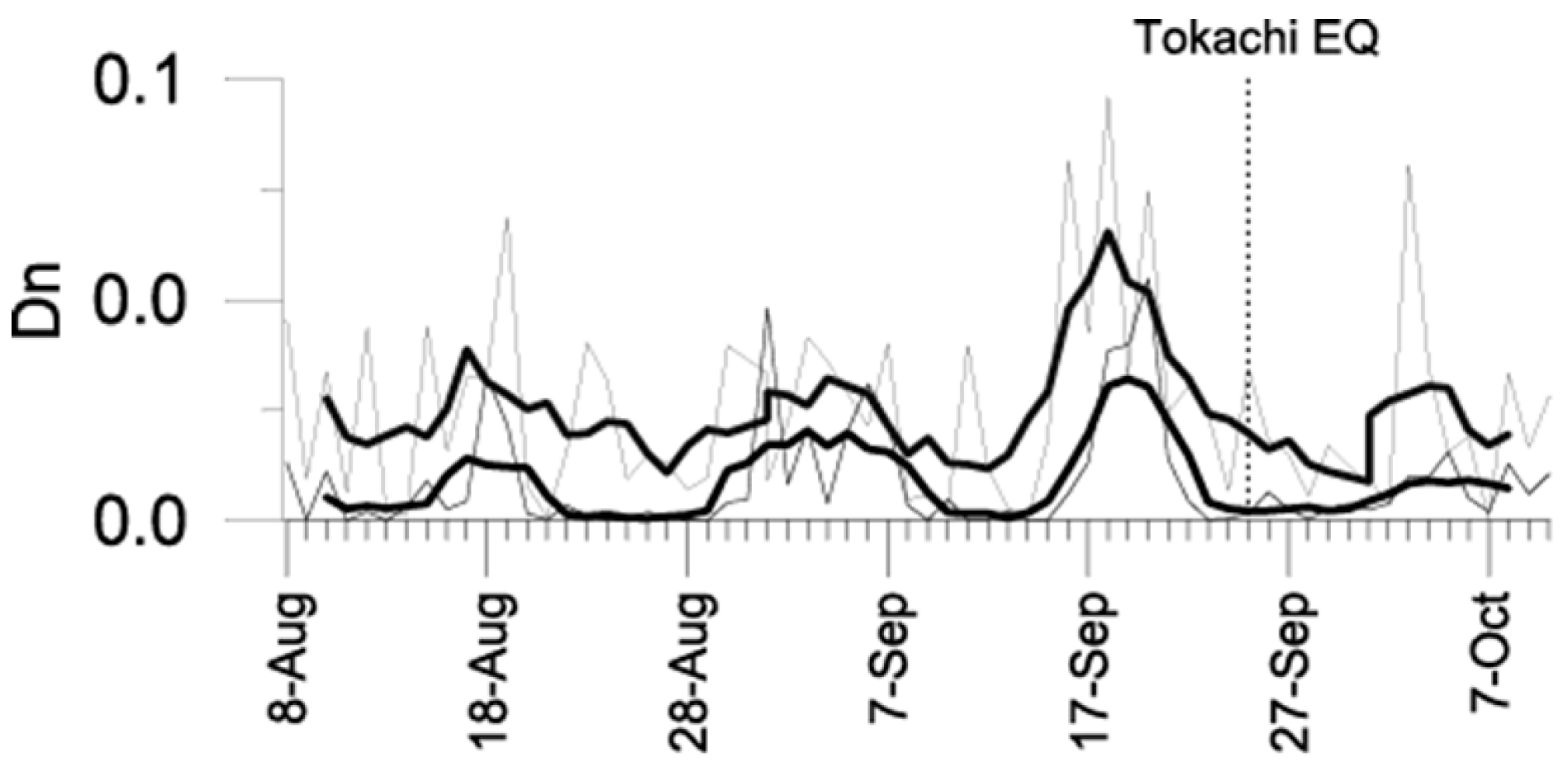
- Shvets, A.V.; Hayakawa, M.; Maekawa, S. Results of subionospheric radio LF monitoring prior to the Tokachi (M=8, Hokkaido, 25 September 2003) earthquake. Nat. Hazards Earth Syst. Sci. 2004, 4, 647–653. [Google Scholar] [CrossRef]
- Ohta, K.; Makita, K.; Hayakawa, M. On the association of anomalies in subionospheric VLF propagation at Kasugai with earthquakes in the Tokai area. J. Atmos. Electr. 2000, 20, 85–95. [Google Scholar] [CrossRef]
- Hayakawa, M.; Ohta, K.; Maekawa, S.; Yamauchi, T.; Ida, Y.; Gotoh, T.; Yonaiguchi, N.; Sasaki, H.; Nakamura, T. Electromagnetic precursors to the 2004 Mid Niigata Prefecture earthquake. Phys. Chem. Earth 2006, 31, 356–364. [Google Scholar] [CrossRef]
- Yamauchi, T.; Maekawa, S.; Horie, T.; Hayakawa, M.; Soloviev, O. Subionospheric VLF/LF monitoring of ionospheric perturbations for the 2004 Mid-Niigata earthquake and their structure and dynamics. J. Atmos. Sol. Terr. Phys. 2007, 69, 793–802. [Google Scholar] [CrossRef]
- Ohta, K.; Umeda, K.; Watanabe, N.; Hayakawa, M. ULF/ELF emissions observed in Japan, possibly associated with the Chi-Chi earthquake in Taiwan. Nat. Hazards Earth Syst. Sci. 2001, 1, 37–42. [Google Scholar] [CrossRef]
- Horie, T.; Maekawa, S.; Yamauchi, T.; Hayakawa, M. A possible effect of ionospheric perturbations associated with the Sumatra earthquake, as revealed from subionospheric very-low-frequency (VLF) propagation (NWC-Japan). Int. J. Remote Sens. 2007, 28, 3133–3139. [Google Scholar] [CrossRef]
- Horie, T.; Yamauchi, T.; Yoshida, M.; Hayakawa, M. The wavelike structures of ionospheric perturbation associated with Sumatra earthquake of 26 December 2004, as revealed from VLF observation in Japan of NWC signals. J. Atmos. Sol. Terr. Phys. 2007, 69, 1021–1028. [Google Scholar] [CrossRef]
- Hayakawa, M.; Raulin, J.P.; Kasahara, Y.; Bertoni, F.C.P.; Hobara, Y.; Guevara-Day, W. Ionospheric perturbations in possible association with the 2010 Haiti earthquake, as based on medium-distance subionospheric VLF propagation data. Nat. Hazards Earth Syst. Sci. 2011, 11, 513–518. [Google Scholar] [CrossRef]
- Hayakawa, M.; Rozhnoi, A.; Solovieva, M.; Hobara, Y.; Ohta, K.; Schekotov, A.; Fedorov, E. The lower ionospheric perturbation as a precursor to the 11 March 2011 Japan earthquake. Geomat. Nat. Hazards Risk 2013, 4, 275–287. [Google Scholar] [CrossRef]
- Asano, T.; Hayakawa, M. On the tempo-spatial evolution of the lower ionospheric perturbation for the 2016 Kumamoto earthquakes from comparisons of VLF Propagation data observed at multiple stations with wave-hop theoretical computations. Open J. Earthq. Res. 2018, 7, 161–185. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Schekotov, A.; Koulouras, G.E.; Contoyiannis, Y.; Balasis, G.; Melis, N.S.; Boutsi, A.Z.; Hayakawa, M.; Eftaxias, K.; Nomicos, C. On possible electromagnetic precursors to a significant earthquake (Mw = 6.3) occurred in Lesvos (Greece) on 12 June 2017. Entropy 2019, 21, 241. [Google Scholar] [CrossRef]
- Politis, D.Z.; Potirakis, S.M.; Contoyiannis, Y.F.; Biswas, S.; Sasmal, S.; Hayakawa, M. Statistical and criticality analysis of the lower ionosphere prior to the 30 October 2020 Samos (Greece) earthquake (M6.9), based on VLF electromagnetic propagation data as recorded by a new VLF/LF receiver installed in Athens (Greece). Entropy 2021, 23, 676. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer: Berlin/Heidelberg, Germany, 2004; 315p. [Google Scholar]
- Sorokin, V.M.; Yaschenko, A.K.; Chmyrev, V.M.; Hayakawa, M. DC electric field amplification in the mid-latitude ionosphere over seismically active faults. Phys. Chem. Earth 2006, 31, 447–453. [Google Scholar] [CrossRef]
- Miyaki, K.; Hayakawa, M.; Molchanov, O.A. The Role of Gravity Waves in the Lithosphere-Ionosphere Coupling, as Revealed from the Subionospheric LF Propagation Data. In Seismo Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling; Hayakawa, M., Molchanov, O.A., Eds.; TERRAPUB: Tokyo, Japan, 2002; pp. 229–232. [Google Scholar]
- Hooke, W.H. Ionospheric irregularities produced by internal atmospheric gravity waves. J Atmos. Terr. Phys. 1968, 30, 795–823. [Google Scholar] [CrossRef]
- Hooke, W.H. Rossby-Planetary Waves, Tides, Gravity Waves in the Upper Atmosphere. In The Upper Atmosphere and Magnetosphere; National Academy Science: Washington, DC, USA, 1970; pp. 130–140. [Google Scholar]
- Grossard, E.E.; Hooke, W.H. Waves in the Atmosphere (Atmospheric Infrasound and Gravity Wave—Their Generation and Propagation); Elsevier: Amsterdam, The Netherlands, 1975; 440p. [Google Scholar]
- Molchanov, O.A.; Mazhaeva, O.A.; Goliavin, A.N.; Hayakawa, M. Observations by the Intercosmos-24 satellite of ELF-VLF electromagnetic emissions associated with earthquakes. Ann. Geophysicae 1993, 11, 431–440. [Google Scholar]
- Freund, F. Stress-Activated Positive Hole Charge Carriers in Rocks and the Generation of Pre-Earthquake Signals. In Electromagnetic Phenomena Associated with Earthquakes; Hayakawa, M., Ed.; Transworld Research Network: Trivandrum, India, 2009; pp. 41–96. [Google Scholar]
- Freund, F. Earthquake forewarning—A multidisciplinary challenge from the ground up to space. Acta Geophys. 2013, 61, 775–807. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Chmyrev, V.M.; Hayakawa, M. A Review on Electrodynamic Influence of Atmospheric Processes to the Ionosphere. Open J. Earthq. Res. 2020, 9, 113–141. [Google Scholar] [CrossRef]
- De Santis, A.; Balasis, G.; Pavón-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential earthquake precursory pattern from space: The 2015 Nepal event as seen by magnetic Swarm satellites. Earth Planet. Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef]
- De Santis, A.; Cianchini, G.; Marchetti, D.; Piscini, A.; Sabbagh, D.; Perrone, L.; Campuzano, S.A.; Inan, S. A multiparametric approach to study the preparation phase of the 2019 M7.1 Ridgecrest (California, USA) earthquake. Front. Earth Sci. 2020, 8, 540398. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Piscini, A.; Jin, S. Anomalous seismo-LAI variations potentially associated with the 2017 Mw = 7.3 Sarpol-e Zahab (Iran) earthquake from Swarm satellites, GPS-TEC and meteorological data. Adv. Space Res. 2019, 64, 143–158. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Davidenko, D.; Rozhnoi, A.; Solovieva, M.; Fedun, V.; Dwivedi, B.N.; Rybin, A.; Kafatos, M.; Taylor, P. Transient effects in atmosphere and ionosphere preceding the 2015 M7.8 and M7.3 Gorkha–Nepal earthquakes. Front. Earth Sci. 2021, 9, 757358. [Google Scholar] [CrossRef]
- Parrot, M.; Tramutoli, V.; Liu, J.Y.; Pulinets, S.; Ouzounov, D.; Genzaro, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and ionospheric coupling phenomena associated with large earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 197–225. [Google Scholar] [CrossRef]
- Sasmal, S.; Chowdhury, S.; Kundu, S.; Politis, D.Z.; Potirakis, S.M.; Balasis, G.; Hayakawa, M.; Chakrabarti, S.K. Pre-seismic irregularities during the 2020 Samos (Greece) earthquake (M = 6.9) as investigated from multi-parameter approach by ground and space-based techniques. Atmosphere 2021, 12, 1059. [Google Scholar] [CrossRef]
- Hayakawa, M.; Izutsu, J.; Schekotov, A.; Yang, S.S.; Solovieva, M.; Budilova, E. Lithosphere-atmosphere-ionosphere coupling effects based on multiparameter precursor observations for February–March 2021 earthquakes (M~7) in the offshore of Tohoku area of Japan. Geosciences 2021, 11, 481. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Izutsu, J.; Yang, S.S.; Solovieva, M.; Hobara, Y. Multi-parameter observations of seismogenic phenomena related to the Tokyo earthquake (M = 5.9) on 7 October 2021. Geosciences 2022, 12, 265. [Google Scholar] [CrossRef]
- D’Arcangelo, S.; Regi, M.; De Santis, A.; Perrone, L.; Cianchini, G.; Soldani, M.; Piscini, A.; Fidani, C.; Sabbagh, D.; Lepidi, S.; et al. A multiparametric-multilayer comparison of two geophysical events in the Tonga-Kermadec subduction zone: The 2019 M7.2 earthquake and 2022 Hunga Ha’apai eruption. Front. Earth Sci. 2023, 11, 12677411. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; De Santis, A.; Perrone, L.; Xiong, P.; Zhang, X.; Du, X. Lithoshere-atmosphere-ionosphere coupling associated with four Yutian earthquakes in China from GPS TEC and electromagnetic observations onboard satellites. J. Geodyn. 2023, 155, 101943. [Google Scholar] [CrossRef]
- Marchetti, D.; Zhu, Z.; Picsini, A.; Ghamry, E.; Shen, X.; Yan, R.; He, X.; Wang, T.; Chen, W.; Wen, J.; et al. Changes in the lithosphere, atmosphere and ionosphere before and after the Mw = 7.7 Jamaica 2020 earthquake. Remote Sens. Environ. 2024, 307, 114146. [Google Scholar] [CrossRef]
- Sasmal, S.; Chowdhury, S.; Kundu, S.; Ghosh, S.; Politis, A.Z.; Potirakis, S.M.; Hayakawa, M. Multi-parametric study of seismogenic anomalies during the 2021 Crete earthquake (M = 6.0). Ann. Geophys. 2024, 66, SE646. [Google Scholar] [CrossRef]
- Cianchini, G.; Calcara, M.; De Santis, A.; Piscini, A.; D’Arcangelo, S.; Fidani, C.; Sabbagh, D.; Orlando, M.; Perrone, L.; Campuzano, S.A.; et al. The preparation phase of the 2023 Kahramanmaras (Turkey) major earthquakes from a multidisciplinary and comparative perspective. Remote Sens. 2024, 16, 2766. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, C.-H. Lithosphere–atmosphere ionosphere coupling processes for pre-, co-, and post-earthquakes. Atmosphere 2023, 14, 4. [Google Scholar] [CrossRef]
- Pilipenko, V.A.; Surkov, V. Seismoelectromagnetic and seismoionospheric phenomena: From the pioneering works to G. A. Sobolev to present. Phys. Solid Earth 2025, 61, 609–625. [Google Scholar] [CrossRef]
- Tachema, A. Identifying pre-seismic ionospheric disturbances using space geodesy: A case study of the 2011 Lorca earthquake (Mw5.1), Spain. Earth Sci. Inform. 2024, 17, 2055–2071. [Google Scholar] [CrossRef]
- Adhikari, B.; Klausner, V.; Cândido, C.M.N.; Poudel, P.; Gimenes, H.M.; Silwal, A.; Gautam, S.P.; Calabia, A.; Shah, M. Lithosphere-atmosphere-ionosphere coupling during the September 2015 Coquimbo earthquake. J. Earth System. Sci. 2024, 133, 35. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y. Integrated analysis of multi-parameter precursors to the Fukushima offshore earthquake (Mj = 7.3) on 13 February 2021 and lithosphere-atmosphere-ionosphere coupling channels. Atmosphere 2024, 15, 1015. [Google Scholar] [CrossRef]
- Chen, C.H.; Sun, Y.Y.; Zhang, X.; Gao, Y.; Yisimayili, A.; Qing, H.; Yeh, T.K.; Lin, K.; Wang, F.; Yen, H.Y.; et al. Double resonance in seismo-lithosphere-atmosphere-ionosphere coupling. Ann. Geophysics 2024, 66, SE641. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.; Molchanov, O.; Biagi, P.F.; Hayakawa, M. Observation evidences of atmospheric gravity waves induced by seismic activity from analysis of subionospheric LF signal spectra. Nat. Hazards Earth Syst. Sci. 2007, 7, 625–628. [Google Scholar] [CrossRef]
- Rapoport, Y.; Reshetnyk, V.; Grytsai, A.; Grimalsky, V.; Liashchuk, O.; Fedorenko, A.; Hayakawa, M.; Krankowski, A.; Błaszkiewicz, L.; Flisek, P. Spectral analysis and information entropy approaches to data of VLF disturbances in the waveguide Earth-ionosphere. Sensors 2022, 22, 8191. [Google Scholar] [CrossRef]
- Zhao, F.; Feng, P.; Qi, Z.; Cheng, L.; Wang, X.; Huang, L.; Liu, Q.; Chen, Y.; Ren, X.; Hua, Y. Investigation on the impact of the 2022 Luding M6.8 earthquake on regional low-frequency time code signals in northern China. Atmosphere 2024, 15, 1419. [Google Scholar] [CrossRef]
- Asai, S.; Yamamoto, S.; Kasahara, Y.; Hobara, Y.; Inaba, T.; Hayakawa, M. Measurement of Doppler shifts of short-distance subionospheric LF transmitter signals and seismic effects. J. Geophys. Res. 2011, 116, A02311. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kasahara, Y.; Endoh, T.; Hobara, Y.; Asai, S. The observation of Doppler shifts of subionospheric LF signal in possible association with earthquakes. J. Geophys. Res. 2012, 117, A09304. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Izutsu, J.; Nickolaenko, A.P.; Hobara, Y. Seismogenic ULF/ELF wave phenomena: Recent advances and future perspectives. Open J. Earthq. Res. 2023, 12, 45–113. [Google Scholar] [CrossRef]
- Heki, K. Ionospheric electron enhancement preceding the 2011 Tohoku-Oki earthquake. Geophys. Res. Lett. 2011, 38, L17312. [Google Scholar] [CrossRef]
- Heki, K.; Enomoto, Y. Preseismic ionospheric electron enhancements revisited. J. Geophys. Res. Space Phys. 2013, 118, 6618–6626. [Google Scholar] [CrossRef]
- Iwata, T.; Umeno, K. Preseismic ionospheric anomalies detected before the 2016 Kumamoto earthquake. J. Geophys. Res. Space Phys. 2017, 122, 3602–3616. [Google Scholar] [CrossRef]
- Eisenbeis, J.; Occhipinti, G. The TEC enhancement before seismic events is an artifact. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028733. [Google Scholar] [CrossRef]
- Nina, A.; Biagi, P.F.; Pulinets, S.; Nico, G.; Mitrović, S.T.; Čadež, V.M.; Radovanović, M.; Urošev, M.; Popović, L.Č. Variation in the VLF signal noise amplitude during the period of intense seismic activity in Central Italy from 25 October to 3 November 2016. Front. Environ. Sci. 2022, 10, 1005575. [Google Scholar] [CrossRef]
- Nina, A.; Biagi, F.P.; Mitrovic, S.T.; Pulinets, S.; Nico, G.; Radovanovic, M.; Popovic, L.C. Reduction of the VLF signal phase noise before earthquakes. Atmosphere 2021, 12, 444. [Google Scholar] [CrossRef]
- Nina, A. VLF signal noise reduction during intense seismic activity: First study of wave excitations and attenuations in the VLF signal amplitude. Remote Sens. 2024, 16, 1330. [Google Scholar] [CrossRef]
- Silber, I.; Price, C. On the use of narrowband measurements to study the lower ionosphere and the mesosphere-lower thermosphere. Surv. Geophys. 2017, 38, 407–441. [Google Scholar] [CrossRef]
- Galopeau, P.H.M.; Maxworth, A.S.; Boudjada, M.Y.; Eichelberger, H.U.; Meftah, M.; Biagi, P.F.; Schwingenschuh, K. A VLF/LF facility network for preseismic electromagnetic investigations. Geosci. Instrum. Method Data Syst. 2023, 12, 231–237. [Google Scholar] [CrossRef]
- Malkotsis, F.; Politis, D.Z.; Dimakos, D.; Potirakis, S.M. An amateur-radio-based open-source (HW/SW) VLF/LF receiver for lower ionosphere monitoring, Examples of identified perturbations. Foundations 2022, 2, 639–663. [Google Scholar] [CrossRef]
- Molchanov, O.; Rozhnoi, A.; Solovieva, M.; Akentieva, O.; Berthelier, J.J.; Parrot, M.; Lefeuvre, F.; Biagi, P.F.; Castellana, L.; Hayakawa, M. Global diagnostics of the ionospheric perturbations related to the seismic activity using the VLF radio signals collected on the DEMETER satellite. Nat. Hazards Earth Syst. Sci. 2006, 6, 745–753. [Google Scholar] [CrossRef]
- Hayakawa, M. Whistlers. In Handbook of Atmospheric Electrodynamics; Volland, H., Ed.; CRC Press: Boca Raton, FL, USA, 1995; Volume II, pp. 155–193. [Google Scholar]
- Hayakawa, M.; Hobara, Y. The Effects of Lightning on the Ionosphere/Magnetosphere: Whistlers and Ionospheric Alfven Resonator. In Lightning Electromagnetics; Cooray, V., Rachidi, F., Rubinstein, M., Eds.; IET: London, UK, 2022; pp. 475–525. [Google Scholar]
- Muto, M.; Yoshida, T.; Horie, M.; Hayakawa, M.; Parrot, M.; Molchanov, O.A. Detection of ionospheric perturbations associated with Japanese earthquakes on the basis of reception of LF transmitter signals on the satellite DEMETER. Nat. Hazards Earth Syst. Sci. 2008, 8, 135–141. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.; Molchanov, O.; Biagi, P.F.; Hayakawa, M.; Schwingenschuh, K.; Boudjada, M.; Parrot, M. Variations of VLF/LF signals observed on the ground and satellite during a seismic activity in Japan region in May–June 2008. Nat. Hazards Earth Syst. Sci. 2010, 10, 529–534. [Google Scholar] [CrossRef]
- Boudjada, M.Y.; Schwingenschuh, K.; Doller, R.; Rozhnoi, A.; Parrot, M.; Biagi, P.F.; Galopeau, P.H.M.; Solovieva, M.; Molchanov, O.; Biernat, K.; et al. Decrease of VLF transmitter signal and chorus-whistler waves before l’Aquila earthquake occurrence. Nat. Hazards Earth Syst. Sci. 2010, 10, 1487–1494. [Google Scholar] [CrossRef]
- Slominska, E.; Blecki, J.; Parrot, M.; Slominski, J. Satellite study of VLF ground-based transmitter signals during seismic activity in Honshu island. Phys. Chem. Earth 2009, 34, 464–473. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.; Parrot, M.; Hayakawa, M.; Biagi, P.F.; Schwingenschuh, K.; Fedun, V. VLF/LF signal studies of the ionospheric response to strong seismic activity in the Far Eastern region combing the DEMETER and ground-based observations. Phys. Chem. Earth 2015, 141, 85–86. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Huang, J.; Li, X.; Han, Y.; Yang, X.; Li, Z. Study on VLF electric field anomalies caused by seismic activity on the Western coast of the Pacific Rim. Atmosphere 2023, 14, 1676. [Google Scholar] [CrossRef]
- Nemec, F.; Santolík, O.; Parrot, M.; Berthelier, J.J. Spacecraft observations of electromagnetic perturbations connected with seismic activity. Geophys. Res. Lett. 2008, 35, L05109. [Google Scholar] [CrossRef]
- Nemec, F.; Santolík, O.; Parrot, M. Decrease of intensity of ELF/VLF waves observed in the upper ionosphere close to earthquakes. J. Geophys. Res. 2009, 114, A04303. [Google Scholar] [CrossRef]
- Pisa, D.; Nemec, F.; Santolik, O.; Parrot, M.; Rycroft, M. Additional attenuation of natural VLF electromagnetic waves observed by the DEMETER spacecraft resulting from preseismic activity. J. Geophys. Res. Space Phys. 2013, 118, 5286–5295. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Hayakawa, M. Resonances in the Earth–Ionosphere Cavity; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; 381p. [Google Scholar]
- Harrison, R.G.; Alpin, K.; Rycroft, M. Atmospheric electricity coupling between earthquake regions and the ionosphere. J. Atmos. Sol. Terr. Phys. 2010, 72, 376–381. [Google Scholar] [CrossRef]
- Ghosh, S.; Chakraborty, S.; Sasmal, S.; Basak, T.; Chakrabarti, S.K.; Samanta, A. Comparative study of the possible lower ionospheric anomalies in very low frequency (VLF) signal during Honshu, 2011 and Nepal, 2015 earthquakes. Geomat. Nat. Hazards Risk 2019, 10, 1596–1612. [Google Scholar] [CrossRef]
- Biswas, S.; Chowdhury, S.; Sasmal, S.; Politis, D.Z.; Potirakis, S.M.; Hayakawa, M. Numerical modelling of sub-ionospheric Very Low Frequency radio signal anomalies during the Samos (Greece) earthquake (M = 6.9) on October 30, 2020. Adv. Space Res. 2022, 70, 1453–1471. [Google Scholar] [CrossRef]
- Politis, D.Z.; Potirakis, S.M.; Sasmal, S.; Malkotsis, F.; Dimakos, D.; Hayakawa, M. Possible pre-seismic indications prior to strong earthquakes that occurred in Southeastern Mediterranean as observed simultaneously by three VLF/LF stations installed in Athens (Greece). Atmosphere 2013, 14, 673. [Google Scholar] [CrossRef]
- Hayakawa, M.; Solovieva, M.; Kopylova, G.; Hirooka, S.; Sasmal, S.; Nanda, K.; Yang, S.S.; Michimoto, K.; Hinata, H. Multi Parameter and Multi Layer Observations of Electromagnetic Precursors to a Large Hokkaido Earthquake (M = 6.7) on 5 September 2018, and Lithosphere–Atmosphere–Ionosphere Coupling Channel. Atmosphere 2025. submitted. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New Concept of Time; Springer: Berlin/Heidelberg, Germany, 2011; 449p. [Google Scholar]
- Uyeda, S.; Nagao, T.; Hattori, K.; Hayakawa, M.; Miyaki, K.; Molchanov, O.; Gladychev, V.; Baransky, L.; Chtchekotov, A.; Fedorov, E.; et al. Geophysical Observatory in Kamchatka region for monitoring of phenomena connected with seismic activity Geophysical Observatory in Kamchatka region for monitoring of phenomena connected with seismic activity. Nat. Hazards Earth Syst. Sci. 2001, 1, 3–7. [Google Scholar] [CrossRef]
- Chen, C.H.; Sun, Y.Y.; Lin, K.; Zhou, C.; Xu, R.; Qing, H.; Gao, Y.; Chen, T.; Wang, F.; Yu, H.; et al. A new instrumental array in Sichuan, China, to monitor vibrations and perturbations of the lithosphere, atmosphere, and ionosphere. Surv. Geophys. 2021, 42, 1425–1442. [Google Scholar] [CrossRef]
- Anagnostopoulos, G. On the origin of ULF magnetic waves before the Taiwan Chi-Chi 1999 earthquake. Front. Earth Sci. 2021, 9, 730162. [Google Scholar] [CrossRef]
- Raulin, J.P.; Bertoni, F.C.; Kaufmann, P.; Gavilan, H.R.; Correia, E.; Hadano, R.; Schuch, N.J. Solar-terrestrial, ionospheric and natural phenomena studies using the South America VLF network (SAVNET). J. Atmos. Sol. Terr. Phys. 2010, 73, 1581–1586. [Google Scholar] [CrossRef]



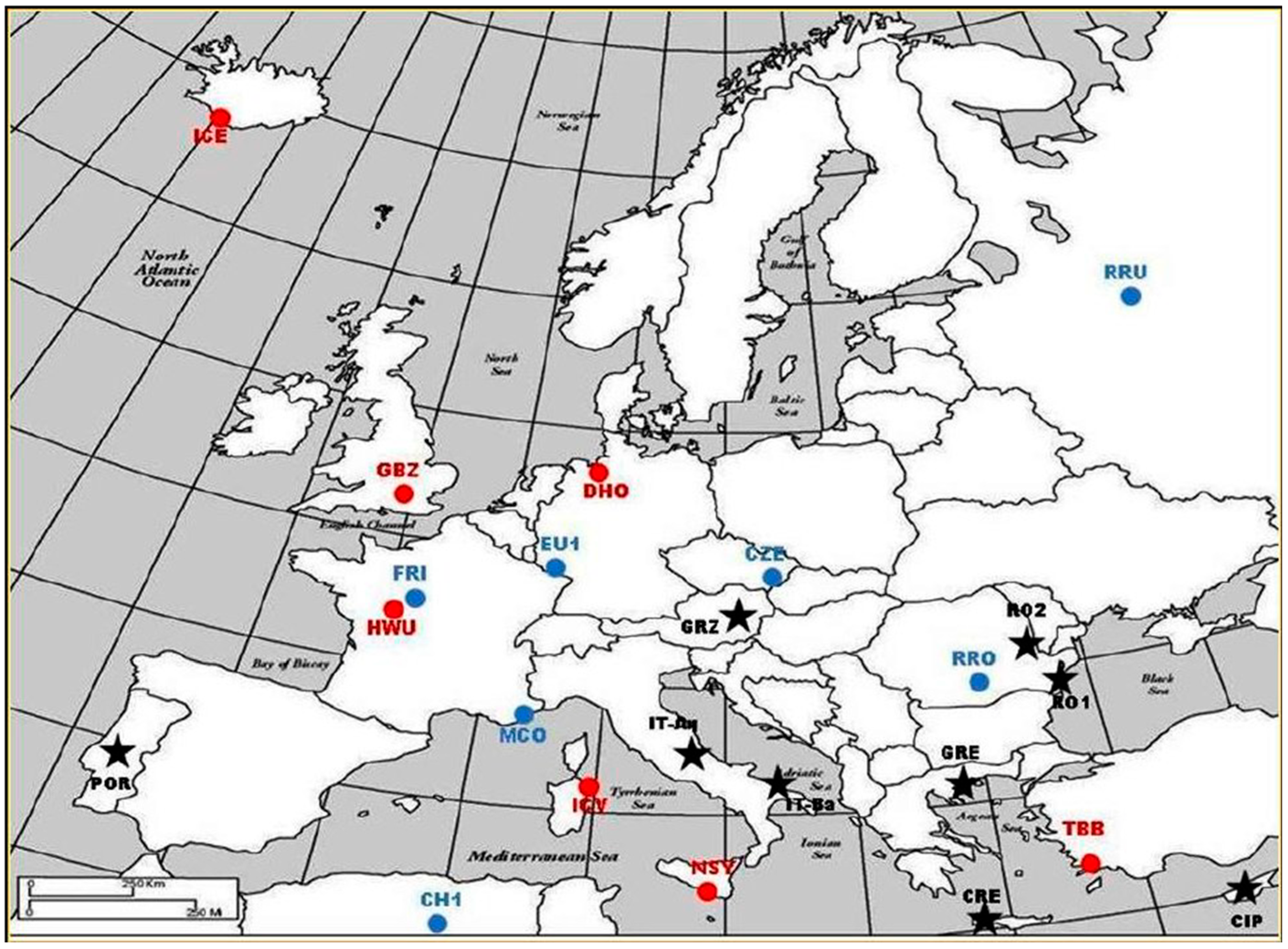
| VLF | Frequency (kHz) | LF | Frequency (kHz) |
|---|---|---|---|
| GBZ | 19.58 | RRO | 153 |
| ICV | 20.27 | FRI | 162 |
| HWU | 21.75 | EU1 | 183 |
| DHO | 23.4 | CH1 | 198 |
| TBB | 26.7 | MCO | 216 |
| ICE | 37.5 | RRU | 261 |
| NSY | 45.9 | CZE | 270 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayakawa, M. Review of Subionospheric VLF/LF Radio Signals for the Study of Seismogenic Lower-Ionospheric Perturbations. Atmosphere 2025, 16, 1312. https://doi.org/10.3390/atmos16111312
Hayakawa M. Review of Subionospheric VLF/LF Radio Signals for the Study of Seismogenic Lower-Ionospheric Perturbations. Atmosphere. 2025; 16(11):1312. https://doi.org/10.3390/atmos16111312
Chicago/Turabian StyleHayakawa, Masashi. 2025. "Review of Subionospheric VLF/LF Radio Signals for the Study of Seismogenic Lower-Ionospheric Perturbations" Atmosphere 16, no. 11: 1312. https://doi.org/10.3390/atmos16111312
APA StyleHayakawa, M. (2025). Review of Subionospheric VLF/LF Radio Signals for the Study of Seismogenic Lower-Ionospheric Perturbations. Atmosphere, 16(11), 1312. https://doi.org/10.3390/atmos16111312





