Abstract
With the rapid acceleration of industrialization and urbanization in China, PM2.5 pollution has emerged as a major challenge to public health and sustainable development of the society and economy. At the interprovincial level, PM2.5 exhibits a complex spatial correlation network structure. Using data from 31 provinces in China from 2000 to 2023, this study constructed a spatial correlation network of PM2.5 and analyzed its structural characteristics and formation mechanisms. The results reveal that China’s PM2.5 spatial correlation network is both complex and stable, underscoring the severity of the pollution problem. The network demonstrates a distinct ‘core–periphery’ distribution, with provinces such as Jiangsu, Shandong, and Henan occupying central positions and functioning as critical bridges. Block model analysis showed a clear role of differentiation among provinces in the diffusion of pollution. Temporal exponential random graph model suggests that geographical proximity, industrial structure, vehicle ownership, and government intervention are key factors shaping the network. Geographically adjacent provinces are more likely to form close connections, whereas environmental regulation and vehicle ownership tend to constrain the spread of pollution. This study provides a novel theoretical framework for understanding the spatial diffusion pathways of PM2.5 pollution and offers important policy implications for optimizing and implementing cross-regional air quality governance strategies in China.
1. Introduction
With the large-scale migration of the population to urban areas, air pollution in cities has become increasingly severe [1]. Among the various pollutants, PM2.5 has emerged as a particularly critical concern [2], ranking as one of the leading contributors to rising global mortality rates [3]. In China, deaths attributable to PM2.5 account for nearly one-third of the global total [4]. Rapid industrialization and urbanization in industrial hubs across the country have profoundly shaped temporal and spatial patterns of PM2.5 concentrations [5]. High levels of PM2.5 not only undermine public health and well-being but also pose a substantial obstacle to the sustainable development of the society and economy [6]. Although numerous studies have explored the spatial distribution characteristics and formation mechanisms of PM2.5 from multiple perspectives [7,8,9], limited attention has been given to the structural properties of its spatial networks and their driving factors [10].
The control of PM2.5 has long been a focal point of both academic research and policy practice, with a wide variety of emerging research perspectives. Several studies have examined the primary emission sources and chemical compositions of PM2.5 [11,12,13,14], providing valuable evidence for pollution management. Another body of research identified the drivers of ambient PM2.5 concentrations, broadly categorized into socioeconomic and natural factors [15]. Socioeconomic factors include urban size, industrial production, road traffic, construction activity, and residential activities [16,17,18], which are widely recognized as the most direct determinants of PM2.5 levels. Natural factors such as temperature, humidity, wind speed, and topography are viewed as indirect influences on PM2.5 concentrations [15,19,20]. Researchers have also highlighted the spatial correlation of PM2.5. Building on this recognition, some studies have applied spatial statistics and econometric methods to analyze the spatial heterogeneity and spillover effects of PM2.5. These studies suggest that PM2.5 pollution is no longer a localized environmental problem but exhibits cross-regional spillover effects and dynamic diffusion patterns [21,22,23,24,25]. This phenomenon calls for shifting research attention beyond single-region emission sources to broader diffusion mechanisms of pollutants and their complex spatial interactions [26]. More recently, a growing number of studies have focused on spatial correlation networks of PM2.5, exploring their structural features and formation mechanisms [10,27,28]. However, this research remains concentrated on specific regions or urban agglomerations, with limited investigation of the spatial correlation networks of PM2.5 across all 31 provincial-level regions in China. Moreover, most existing studies have relied on static network models that fail to fully capture the dynamic structures and driving forces of the spatial networks of PM2.5.
Against these gaps, this study constructs annual interprovincial PM2.5 spatial-correlation networks for all 31 provincial-level regions in China and integrates social network analysis with the temporal exponential random graph model (TERGM). This design allows us to examine how endogenous network processes (e.g., closure and bridging) and exogenous socioeconomic/natural drivers jointly shape the evolution of interregional linkages over time. Our contributions are threefold: (1) we provide a nationwide, time-varying depiction of China’s PM2.5 spatial-correlation network; (2) we advance methodology by applying TERGM to environmental diffusion to jointly identify network-endogenous mechanisms and covariate effects; and (3) we develop a network-based perspective that can later inform differentiated cross-regional coordination strategies. The remainder of the article proceeds as follows: Section 2 details Materials and Methods; Section 3 presents the Results; Section 4 discusses the findings; and Section 5 concludes.
2. Materials and Methods
2.1. Construction of the PM2.5 Spatial Correlation Network
This study selected 31 provinces (including municipalities and autonomous regions) of China as the research areas. Each province is treated as a node in the network. Based on these 31 nodes, we construct a gravity model [Equation (1)] to capture the spatial correlation effects of PM2.5.
where represents the spatial correlation intensity of PM2.5 from region to region , captures the contribution of region to the correlation intensity between regions and , and denotes the ‘economic–geographic distance’ between regions and . The variables denote the population size, PM2.5 concentration, GDP, and per capita GDP, respectively, and indicates the geographical distance between regions and .
Based on Equation (1), we computed the gravity matrix of the spatial correlations of PM2.5. We then considered the row mean of this matrix as the threshold. Values greater than or equal to the threshold were coded as 1, indicating the presence of a spatial correlation of PM2.5 concentrations between the corresponding regions; otherwise, they were coded as 0, indicating the absence of correlation. This procedure yields a directed, unweighted, asymmetric binary adjacency matrix that characterizes the spatial correlation network of PM2.5 across China.
Gravity models are widely used to approximate how interregional interactions decay with “mass” (e.g., population, economic scale, emissions) and distance. However, in the province–year setting of a PM2.5 spatial association network they face several limitations:
(1) Restrictive functional form, which is ill-suited to capture the directional and anisotropic nature of atmospheric transport;
(2) Omission of endogenous network dependencies and higher-order structures (e.g., reciprocity, triadic closure, brokerage), conflicting with the implicit assumption of dyadic independence;
(3) Aggregation to provinces and annual means, which can induce modifiable areal unit problems (MAUP) and aggregation bias.
Accordingly, we use the gravity formulation only to construct the binary interprovincial network Y, and then estimate a TERGM that incorporates endogenous network processes and exogenous dyadic covariates (e.g., distance bins) to more reliably identify structural features and their evolution.
2.2. Characterization of Structural Features of the Spatial Correlation Network of PM2.5
Using PM2.5 spatial connectivity as the main analytical thread, this study employed block modeling and motif structure analysis to examine PM2.5 spatial connectivity patterns and their temporal variations at both the macro and micro levels. We further confirmed the roles played by different regions within the network. Table 1 summarizes the primary indicators employed to characterize the spatial correlation network of PM2.5.

Table 1.
Indicators of PM2.5 Spatial Correlation Network Structure.
The centrality of nodes reflects the importance of different regions within the PM2.5 spatial correlation network. The out-degree is defined as the number of spatial linkages of PM2.5 emitted from region to the other regions, as expressed in Equation (2).
where denotes the total number of outgoing linkages from region , N is the total number of regions (31 in this study), and represents the number of PM2.5 connections from region to region . The average centrality (AC) is defined as the ratio of the total number of outgoing linkages to the total number of regions, as expressed in Equation (3).
At the macro level, block modeling is employed to cluster regions based on PM2.5 correlations and identify their structural positions and roles within the network [29]. At the micro level, motif structure analysis is applied to investigate the preferred micro-correlation patterns among regions [30].
Motifs are recurrent subgraph structures in complex networks that typically consist of three or four nodes. They serve as essential tools for revealing micro-level connectivity patterns. By comparing the frequency of substructures in real networks with those in random networks, motifs that appear significantly more frequently in real networks can be identified, highlighting cooperative and feedback relations within the network.
Motif analysis involves three steps: the generation of random networks, enumeration of subgraphs, and conducting significance tests. First, many random networks are generated with the same number of nodes and edges as those in the observed network. Second, the occurrence frequencies of all types of triad subgraphs are calculated for both the real and random networks. Finally, statistical measures, such as frequency, p-value, and z-scores, are computed. The frequency indicates the number of times a motif appears in the network, the p-value reflects the probability that a motif appears more frequently in random networks than in the real network (a smaller p-value suggests greater significance), and the z-score measures the standardized difference in motif occurrence between the real network and random networks. A positive and larger z-score indicates greater importance of the motif, while a z-score ≤ 0 suggests insignificance. Based on these tests, we identified significant motifs in the spatial correlation network of PM2.5, providing a foundation for subsequent micro-level analyses.
2.3. Identification of Formation Mechanisms of the Spatial Correlation Network of PM2.5: Temporal Exponential Random Graph Model (TERGM)
To identify the driving factors underlying the formation of the regional spatial correlation network of PM2.5, this study employed the TERGM. The exponential random graph model (ERGM) is regarded as one of the most effective tools in social network analysis, as it facilitates the comprehensive evaluation of various factors influencing network formation [31,32,33]. ERGMs typically rely on interdependencies among variables and employ exponential functions to assess whether the aggregation of local network structures can explain global structural properties [34,35,36].
The TERGM extends the traditional cross-sectional ERGM to capture the temporal evolution of networks. Unlike ERGMs, which model static networks, TERGMs account for dependencies between sequentially observed network structures, making them well-suited for analyzing network dynamics. The general form of the TERGM used in this study is as follows:
The btergm (version 1.11.1) package in R (version 4.5.1) [37] was used to estimate TERGM. Model fit and parsimony were evaluated using the Akaike information criterion (AIC) and Bayesian information criterion (BIC) [38]. We estimate the TERGM primarily using the MCMC-MLE procedure in the btergm package. For robustness, we additionally report results from the MPLE approach with 95% bootstrap confidence intervals (Supplementary Materials, Tables S1 and S2).Additionally, a goodness-of-fit (GOF) test was conducted to assess whether the structural features of the simulated networks were consistent with those of the observed network, thereby ensuring the robustness of the model estimates [39].
2.4. Data
This study compiles a province-year panel for 31 Chinese provinces (2000~2024). Socio-economic covariates are taken from the China Statistical Yearbook and the China Environmental Statistical Yearbook; monetary variables (e.g., per-capita GDP and GDP) are deflated to constant 2000 prices to ensure comparability.
For the key variable—PM2.5—we use China High PM2.5 (https://zenodo.org/records/6398971#.ZI51Qu1BxPY (accessed on 6 October 2025)), a component of the China High Air Pollutants (CHAP) suite that provides long-term, seamless, high-resolution, high-quality air-pollutant datasets for China [40,41,42]. CHAP have been widely used in studies of atmospheric composition and air quality monitoring [43,44,45]. CHAP fuses ground measurements, satellite remote sensing, atmospheric reanalysis, and model simulations with artificial-intelligence methods that explicitly account for the spatio temporal heterogeneity of air pollution. The product offers daily, monthly, and yearly 1 km grids (D1K/M1K/Y1K) from 2000 to the 2024, with high daily-scale accuracy (cross-validation , , ). In our analysis we use the annual Y1K product for 2000~2024. Gridded fields are clipped to official provincial boundaries and aggregated to the provincial level using an area-weighted (geographical) mean in an equal-area projection:
where is the 1 km grid value in province and year , and is the corresponding cell area.
Building on the high grid-level accuracy documented at the daily scale, we further reduce random measurement errors through temporal averaging (aggregating daily grids to annual values) and spatial averaging (province-level area weighting) over a long time span and large spatial units. Under standard independence assumptions, the attenuation follows the rate, i.e., ; even with weak temporal or spatial dependence, the effective sample size at our analysis scale remains large. Consequently, the residual measurement uncertainty is unlikely to materially affect our province–year estimates and conclusions.
3. Results
3.1. Evolutionary Dynamics of the PM2.5 Spatial Correlation Network Structure
3.1.1. Structural Characteristics of the PM2.5 Spatial Correlation Network
We employed heatmaps to visualize the temporal correlation coefficients of China’s regional PM2.5 spatial correlation networks from 2000 to 2023, calculated using QAP correlation analysis (Figure 1). As shown in Figure 1, the topological structure of the spatial correlation network of PM2.5 exhibited a high degree of similarity and self-stability throughout the period, indicating that the network structure did not undergo substantial variation in the short term. However, the correlation coefficients gradually decreased, suggesting that the network structure underwent an incremental evolutionary process. In recent years, interregional cooperation has intensified in response to increasing pressure for air pollution control, thereby promoting gradual adjustments and optimization of the spatial correlation network of PM2.5. Notably, the correlation coefficients between the overall network structure (averaged across 2000–2023) and those of the other individual years remained above 0.6. This finding justifies the use of the full-sample average network for 2000–2023 as a representative framework for analyzing the overall spatial structure of PM2.5 in China.
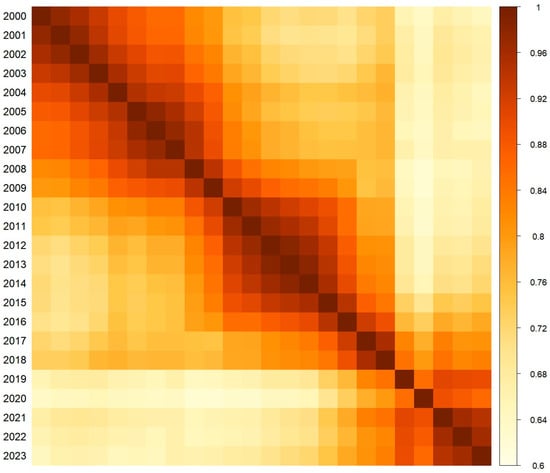
Figure 1.
Temporal Correlation Coefficients of Regional PM2.5 Spatial Correlation Networks in China for the Period 2000–2023.
3.1.2. Community Structure and Block Characteristics of the Spatial Correlation Network: Roles and Relational Patterns
To identify the roles and relational patterns of different regions in the spatial correlation network of PM2.5, we conducted CONCOR block partitioning for the period 2000–2022. Using iterative CONCOR analysis based on the spatial correlation matrix of PM2.5, with a maximum partition depth of 2 and a convergence criterion of 0.2, the spatial network was divided into four blocks. The partitioning results are listed in Table 2 and Table 3. Table 2 reports the inflow and outflow relationships among the blocks in China’s PM2.5 spatial network, and Table 3 displays the density matrix and image matrix.

Table 2.
Block Structure of the Provincial PM2.5 Spatial Correlation Network in China.

Table 3.
Density Matrix and Image Matrix of the Four Major Blocks in China’s Interprovincial PM2.5 Spatial Correlation Network.
According to CONCOR partitioning, four blocks with distinct characteristics were identified: Blocks I, II, III, and IV. Their members and structural features are as follows:
Block I (Beijing, Tianjin, Inner Mongolia, and Shandong; four provinces/municipalities) primarily represents the Bohai Rim Economic Circle, an area of rapid economic growth in China. As shown in Table 2, the actual intra-block inflow ratio (34.78%) exceeded the expected inflow ratio (10.00%), indicating that the PM2.5 in Block I is mainly influenced by other provinces within the same block, with relatively weak external spillover effects. The actual intra-block outflow ratio (13.56%) was close to the expected value, suggesting balanced spillover dynamics between internal and external flows. Therefore, Block I is classified as a ‘two-way spillover block’, playing a pivotal role in mediating PM2.5 transmission both within and beyond the region.
Block II (Jiangsu, Zhejiang, Shanghai, Guangdong, and Fujian; five provinces/municipalities) is located in the southeastern coastal region and is the most economically concentrated area in China. Table 2 shows that the actual intra-block inflow ratio (22.50%) exceeds the expected value (13.33%), implying that the PM2.5 in this block is predominantly influenced by other provinces within the block, with relatively limited external influence. Meanwhile, the actual intra-block outflow ratio (9.28%) is substantially lower than the expected ratio (13.33%), suggesting a strong external spillover effect. Consequently, Block II is identified as a ‘net spillover block’, exerting significant influence on air quality in other regions through PM2.5 diffusion.
Block III (Liaoning, Jilin, Heilongjiang, Hebei, Shanxi, Shaanxi, Gansu, Qinghai, Ningxia, Xinjiang, Tibet, and Chongqing; 12 provinces/municipalities) mainly comprises the resource-rich yet economically underdeveloped regions of Northeast and Northwest China. As indicated in Table 2, the actual intra-block inflow ratio (11.11%) is far below the expected value, suggesting that the PM2.5 levels in Block III are largely shaped by external influences rather than internal dynamics. In contrast, the actual intra-block outflow ratio (45.45%) exceeds the expected ratio (36.67%), indicating that the block exerts stronger internal than external impacts. Therefore, Block III is classified as a ‘net beneficiary block’, reflecting its weaker influence on external regions and its greater susceptibility to external spillovers.
Block IV (Anhui, Jiangxi, Hubei, Hunan, Henan, Yunnan, Guangxi, Hainan, Sichuan, and Guizhou; 10 provinces/municipalities) is concentrated in Central and Southwestern China. Table 2 reveals that both the actual intra-block inflow (11.43%) and outflow (17.78%) ratios are considerably lower than the expected values (30.00%). This suggests that PM2.5 in Block IV is simultaneously affected by external regions, while also transmitting pollution outward. As such, Block IV is categorized as a ‘broker block’, serving as a bridge in PM2.5 transmission and diffusion by linking pollution source regions with other areas.
To examine inter-block interactions in PM2.5, we computed the corresponding network density matrix based on the distribution of linkages reported in Table 2 and, on this basis, derived the image matrix; the results are presented in Table 3.
Based on the density and image matrices reported in Table 3, the interactions among the four major blocks of China’s interprovincial PM2.5 spatial correlation network exhibit significant heterogeneity. As shown in Table 3, Blocks I and II not only display strong internal spillovers but also exert substantial spillover effects on Blocks III and IV. This indicates that economically developed regions exert pronounced spillover influences on less-developed areas within the PM2.5 correlation network. Specifically, the spillover density from Blocks I to III was 0.729, whereas that from Blocks II to IV reached 0.900. Blocks I and II demonstrate strong spillover effects on Blocks III and IV, with geographical proximity amplifying the magnitude of these effects. In contrast, Blocks III and IV exhibit weak internal spillovers and limited intra-block interactions. Their external spillovers are generally modest except for Block IV, which exerts a significant spillover effect on Block II (density = 0.580). This suggests that the provinces in Central and Southwestern China also have notable spillover effects on the southeastern coastal region.
Furthermore, the average spatial distribution of provincial PM2.5 and their interconnections for 2000–2023 are illustrated in Figure 2. The number and direction of linkages reflect both the intensity and directionality of interprovincial PM2.5 associations. Strong correlations were observed among northern and central-eastern provinces, such as Beijing, Tianjin, Hebei, Jiangsu, and Zhejiang, highlighting their high levels of interaction in pollution transmission, which are likely associated with rapid industrialization and high population density. In contrast, provinces in the western and southern regions, including Xinjiang, Gansu, Guangdong, and Guangxi, showed relatively weak correlations with other provinces, suggesting a more localized and independent pattern of pollution. In addition, the directional nature of the linkages further reveals the diffusion pathways of pollution, underscoring the substantial impacts of certain industrially concentrated regions on the PM2.5 levels in neighboring provinces.
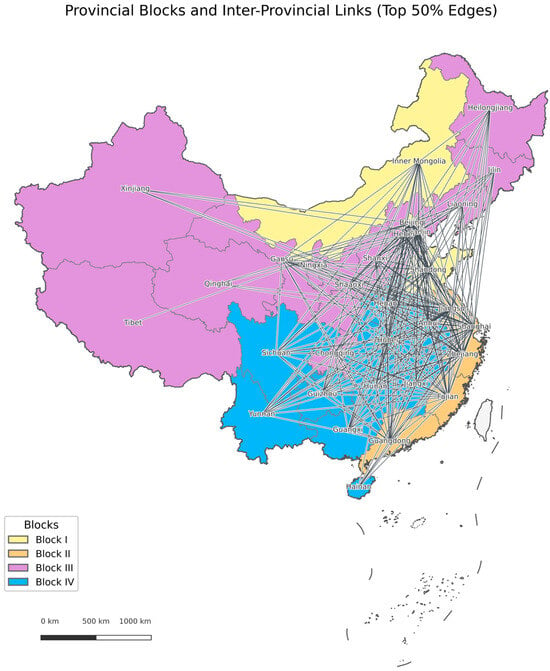
Figure 2.
Spatial Distribution of Blocks and Interconnections in the Average Regional PM2.5 Spatial Correlation Network for the Period 2000–2023.
3.1.3. Micro-Level Association Patterns of Regional PM2.5 Spatial Correlation Networks
Analysis of the 13 types of motifs in China’s regional PM2.5 spatial correlation network during 2000–2023 revealed the underlying micro-level association patterns (see Table 4). Based on their structural characteristics, these motifs can be grouped into four categories, each corresponding to a distinct relational form:

Table 4.
Fundamental Motif Structures of the Regional PM2.5 Spatial Correlation Network.
(1) Unidirectional dependency structures
Motifs such as F8R, F7F, and GCR contain only unidirectional inputs or outputs, without feedback loops. These unidirectional dependencies lead to unstable linkages, limited information sharing, and weak policy coordination. Although this category of motifs occurred at a relatively high frequency, their p-values exceeded 0.05 and their z-scores were less than or equal to zero, indicating statistical insignificance. This suggests that unidirectional dependencies are ineffective in the spatial correlation network of PM2.5, as most inter-regional linkages are characterized by two-way interactions and governance cooperation.
(2) Star-shaped motifs: Core–periphery structures
Motifs such as GCX, F8X, IMF, and GOX exhibited small p-values and positive z-scores, indicating strong significance. Structurally, these motifs resemble star-shaped configurations with a central node transmitting or receiving PM2.5, influenced by two peripheral nodes, reflecting a hierarchical pattern. Certain core cities serve as radiating hubs for pollution governance cooperation, whereas the peripheral regions maintain predominantly unidirectional ties with the core. This manifested as a clear core–periphery structure within the network.
(3) Partially reciprocal motifs: Localized clustering structures
Motifs such as GQX, JQF, FMF, and GDF include two reciprocal ties and one unidirectional tie, reflecting both bilateral cooperation and incomplete link closure. These motifs exhibited significantly positive z-scores and moderate frequencies, suggesting that some regions have begun to establish cooperative mechanisms and information feedback loops although they lack fully closed triadic structures. Consequently, the pollution governance network demonstrates the characteristics of localized clustering.
(4) Fully reciprocal motifs: Closely knit structures
The K4F motif, characterized by three reciprocal ties forming a fully closed triangle, represents a complete triadic closure. Although it occurred the least frequently, it recorded the highest z-score, underscoring its critical importance in the network. This motif signifies a stable, tightly integrated trilateral cooperation, serving as a model for joint PM2.5 governance. However, its rarity indicates the persistence of fragmented governance, with regionalized “warlord economies” whereby close cooperative structures emerge only among a limited subset of provinces.
In summary, the micro-level patterns of China’s PM2.5 spatial correlation network are highly diverse: hierarchical core–periphery configurations coexist with emerging localized reciprocal clusters and a small number of highly integrated reciprocal groups. These differences highlight the existing deficiencies in interregional cooperation and feedback mechanisms for PM2.5 governance. Moving forward, enhancing reciprocal ties and promoting multilateral cooperation are essential for strengthening collaborative governance capacity.
3.2. Driving Factors Behind the Formation of the PM2.5 Spatial Correlation Network
After analyzing the inter-block and interregional association patterns of PM2.5, this section further employs the TERGM to examine the evolutionary mechanisms underlying the formation of the regional PM2.5 spatial correlation network with the aim of identifying the key driving factors shaping its development.
3.2.1. Variable Selection
Endogenous Network Variables
The internal organizational processes of a network are often the fundamental drivers of network formation. The preceding analysis provides supporting evidence, as the regional PM2.5 spatial correlation network in China exhibits micro-level patterns characterized by reciprocity, connectivity, cyclicality, and clustering. Following related studies [46,47], we calculated four fundamental endogenous structural variables—edges, mutual, geometrically weighted edgewise shared partners, capturing clustering effects (gwesp), and geometrically weighted dyadwise shared partners (gwdsp), capturing closure effects and incorporating them into TERGM to examine the influence of self-organizing dynamics on the formation of the PM2.5 spatial correlation network.
Temporal-Dependence Terms
The temporal-dependence terms in the model include autoregression, loss, innovation, and stability. These variables account for temporal dependence within the network. Autoregression reflects the persistence of ties over time, loss represents the dissolution of existing ties, innovation captures the formation of new ties, and stability denotes the overall structural stability of network connections.
Actor Attribute Variables
These variables capture the effects of actor-specific characteristics on the formation of a PM2.5 spatial correlation network. Certain attributes of regional nodes may increase their likelihood of sending or receiving PM2.5, thereby influencing the directionality of the associations. This corresponds to the “sending effect,” “receiving effect,” and “assortativity effect” described earlier. Based on data availability and prior studies [47,48], we select the following node attributes: per capita GDP (PGDP, 10,000 yuan per person), share of secondary industry output (IS), urbanization rate (UR, proportion of urban population), and number of civilian vehicles (CO, 10,000 units).
Exogenous Network Variables
As an economic activity reflecting spatial linkage effects, the regional PM2.5 spatial correlation network does not operate in isolation within its internal structure but is inevitably shaped by external environmental factors. To capture these effects, we constructed distance-based network variables with intervals of [0–500], [500–1000], [1000–1500], and [1500–2000] kilometers in order to assess the influence of geographical distance on the formation of the PM2.5 spatial correlation network.
The original statistical data for the above variables were derived from the China Statistical Yearbook, China Environmental Statistical Yearbook, China Urban Statistical Yearbook, and the statistical yearbooks of individual provinces. Table 5 presents a description of the variables.

Table 5.
Model variable settings and descriptions.
3.2.2. TERGM Regression Results and Goodness-of-Fit Tests
This section applies the TERGM to analyze the evolutionary mechanisms driving the formation of the regional PM2.5 spatial correlation network, with a particular focus on identifying the key factors influencing its development. The regression results are presented in Table 6 and Table 7. In Table 6, Model 1 incorporates endogenous and exogenous distance-based network variables and Models 2–5 sequentially add four temporal-dependence terms. In Table 7, Models 6–9 incorporate the four actor attribute variables sequentially.

Table 6.
TERGM Regression Results.

Table 7.
TERGM Regression Results with the Inclusion of Actor Attribute Variables.
Analysis of Endogenous Network Structure Variables
As shown in Table 6, the regression results indicate that endogenous network structure variables, including edges, mutuality, gwesp, and gwdsp, exert significant effects on the formation of the spatial correlation network of PM2.5. The coefficient of edges is consistently negative and statistically significant in most models, suggesting that direct connections between nodes tend to reduce the overall intensity of PM2.5 spatial associations. In contrast, mutuality was positive and highly significant across all models, demonstrating the pivotal role of reciprocity in reinforcing network stability and cooperation. Gwesp generally exhibited a positive influence, whereas gwdsp showed a consistently negative effect, implying that the spatial correlation network of PM2.5 is more inclined to form clustered triangular structures rather than closed dyadic paths. Overall, the network displayed a tendency toward clustering-based connectivity.
Analysis of Temporal-Dependence Terms
Temporal-dependence terms play a critical role in understanding the formation and evolution of the PM2.5 spatial correlation network. These terms capture the dynamic nature of a network over time, and include autoregression, loss, innovation, and stability.
(1) Autoregression: This variable measures the persistence of network connections over time, indicating whether ties are likely to persist over time. The regression coefficient is positive and significant, suggesting that PM2.5 spatial linkages tend to endure over time. In other words, historical inter-regional PM2.5 associations are likely to persist into the future, reflecting the strong temporal stability in pollution interactions.
(2) Loss: This variable captures the dissolution of existing ties. The regression coefficient is negative and significant, indicating that the existing connections in China’s PM2.5 spatial correlation network are unlikely to dissolve over time. This implies that once established, inter-regional PM2.5 linkages remain stable and are difficult to weaken, highlighting the challenges in curbing pollution spillovers.
(3) Innovation: This variable measures the formation of new ties, reflecting the expansion of the network and the emergence of new inter-regional interactions, often driven by external forces such as policies or economic change. The regression coefficient is negative and significant, suggesting that the newly formed PM2.5 linkages are relatively short-lived or limited in scope. It may take considerable time for these new ties to produce substantial spatial spillover effects.
(4) Stability: This variable assesses the overall stability of network ties over time. A positive and significant coefficient across all models indicates that the spatial correlation network of PM2.5 is characterized by strong structural stability. Despite occasional fluctuations, interregional pollution linkages generally persisted, and the overall network structure exhibited resilience to external disturbances.
Analysis of Exogenous Network Variables
Exogenous network variables capture the dynamic changes in the spatial correlation network of PM2.5 under the influence of external factors. Geographical distance plays a particularly important role in the formation and evolution of the spatial correlation network of PM2.5, as it largely determines the intensity of interregional interactions and the magnitude of pollution spillover effects. In this study, the distance variables were divided into four intervals: [0–500], [500–1000], [1000–1500], and [1500–2000] km. By analyzing the regression coefficients of these exogenous variables, we assessed how geographical distance affected the formation of the spatial correlation network of PM2.5. Across all models, the [0–500] km distance bin is positive and statistically significant, indicating that—at the province–year level—shorter interregional separations are associated with stronger and more persistent spatial associations in PM2.5. By contrast, the coefficients for longer distance bins are not statistically significant in this setting, which reflects the attenuation of episodic long-range transport after aggregation to annual means and provincial units rather than the absence of such events.
Analysis of Actor Attribute Variables
Table 7 reports the TERGM regression results incorporating actor attribute effects. Actor attributes such as per capita GDP (PGDP), the share of secondary industry output (IS), the urbanization rate (UR), and the number of civilian vehicles (CO) exert significant influences on the PM2.5 spatial correlation network.
First, PGDP shows significant effects on both the receiver and sender dimensions. The coefficient of the receiver effect is positive, whereas that of the sender effect is negative. This suggests that economically developed regions tend to receive more PM2.5 spillovers from other regions, while their own pollution outflows are relatively smaller. Furthermore, larger inter-regional disparities in per capita GDP are more likely to generate spillover linkages.
Second, IS has a significantly positive coefficient for receiver and sender effects. This implies that regions with a stronger secondary industry base, particularly those with higher levels of industrialization, are more actively involved in the formation of the PM2.5 spatial correlation network and serve as major sources of PM2.5 emissions.
In contrast, the impacts of UR and CO on the PM2.5 spatial correlation network are relatively limited. Both variables showed only minor significant effects in the receiver dimension.
Finally, to verify the robustness and validity of Model 9, we conducted GOF tests using typical statistical indicators, including edgewise shared partners, dyadwise shared partners, degree distribution, indegree, geodesic distance, and receiver operating characteristic (ROC) curves; the results are shown in Figure 3. When the solid black line falls within the dashed box representing the 95% confidence interval of the simulated network, the observed and simulated results are consistent, indicating a good model fit. Moreover, the closer the ROC curve approaches the upper left corner and the precision-recall (PR) curve approaches the upper right corner, the better is the model fit. As illustrated in Figure 3, the TERGM exhibits a satisfactory GOF, and the exogenous network variables pass the model validation tests.
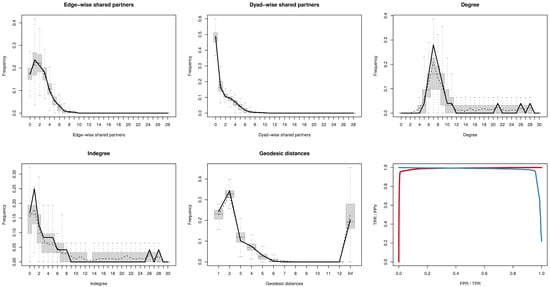
Figure 3.
Goodness-of-Fit Test Results of the TERGM.
4. Discussion
Based on data from 2000 to 2023, this study revealed the structural characteristics and evolutionary mechanisms of the spatial correlation network of PM2.5 across 31 Chinese provinces (including municipalities and autonomous regions). The findings showed that the network exhibited strong overall temporal stability while undergoing continuous adjustment and optimization. The four blocks identified through the CONCOR method highlight regional heterogeneity in pollution diffusion, while the TERGM further confirms that endogenous structural factors, temporal dependence, and exogenous variables, such as per capita GDP, industrialization, urbanization, vehicle ownership, and geographical distance, are key drivers of network formation.
These results are broadly consistent with those reported previously. First, PM2.5 pollution demonstrated significant spatial correlation and exhibited typical spatial clustering characteristics [49]. In addition, China’s interprovincial PM2.5 network, with increasing stability, complexity, and density, resembles the carbon emission network [50]. The study also finds that economically developed eastern coastal provinces (such as Shanghai, Jiangsu, Zhejiang, Fujian, and Guangdong) form ‘net spillover blocks’, exerting substantial pollution spillover effects on the surrounding regions, which is consistent with the conclusions of Mao et al. [51]. Moreover, higher levels of urbanization and industrialization as well as closer geographical proximity led to stronger spatial associations of PM2.5 among regions, which aligns with the results of previous studies [10,30]. However, this study concluded that economic development levels exert a significant influence on the structure of the spatial correlation network of PM2.5, which diverges from earlier findings [10]. This discrepancy is primarily due to methodological differences. Prior research largely employed static ERGM, which are unable to capture the dynamic evolution of network structures and may result in biased estimates [52]. In contrast, this study applied the TERGM, which effectively overcomes the limitations of static models by addressing temporal dependence in longitudinal network data and enhancing the analysis of dynamic structural changes [53]. The reliability and applicability of the TERGM have been demonstrated in diverse fields, including national agricultural trade networks [54], labor mobility networks [55], urban networks [56], and green technology transfer networks [57].
Despite providing a comprehensive analysis of China’s inter-provincial PM2.5 network, this study has some limitations. First, the dataset covers only the period 2000–2023, and future research should employ longer timespans to capture long-term evolutionary patterns. Second, the analysis did not incorporate potential socioeconomic variables, such as differences in local environmental policies, which may influence pollution diffusion mechanisms. Third, this study assumes homogeneity in inter-provincial spillover effects, overlooking intra-urban pollution disparities that may shape the network structures. Therefore, future studies should conduct similar analyses at finer spatial scales (e.g., city or county levels) and incorporate policy heterogeneity and other socioeconomic variables to uncover more detailed pathways for pollution transmission and governance mechanisms.
5. Conclusions
Using an improved gravity model, SNA, and TERGM, this study constructs a PM2.5 association network for 31 provinces (2000–2023) and finds a highly connected, stable structure with significant cross-provincial spillovers and stronger short-range links. The network exhibits a core–periphery pattern, with Jiangsu, Shandong, and Henan serving as bridges; blocks show marked role differentiation. TERGM results indicate that geographical proximity, industrial structure, and government intervention promote interprovincial ties, whereas vehicle ownership and environmental regulation differences inhibit them.
Our findings have several important implications for future studies. First, significant spillover effects necessitate stronger cross-regional cooperation, with the developed eastern provinces playing a leading role. Second, differentiated strategies should be adopted: net spillover provinces should tighten emissions control, net beneficiary provinces should strengthen monitoring and adaptive measures, and broker provinces should serve as coordinators of interregional governance. Third, policies should promote green industrial upgrades, cleaner transportation, and improved energy efficiency to mitigate emissions. Fourth, given the persistence of non-reciprocal structures, policymakers must overcome the “prisoner’s dilemma” by encouraging reciprocal cooperation. Finally, the strong influence of geographical proximity suggests that neighboring provinces should establish joint mechanisms, such as shared monitoring and coordinated emergency responses. Overall, this study provides actionable guidance for optimizing regional air quality governance and advancing more effective PM2.5 mitigation strategies for China.
However, this study is constrained by its temporal coverage (2000–2022), omits certain key socioeconomic/policy heterogeneities, and—within the provincial framework—implicitly assumes homogeneous interprovincial spillovers without explicitly modeling intra-urban disparities; future work should incorporate policy and socioeconomic heterogeneity at finer spatial scales to test and refine the conclusions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos16101211/s1, Table S1 TERGM Regression Results with bootstrap confidence intervals, Table S2 TERGM Regression Results Including Actor Attribute Variables with Bootstrap Confidence Intervals.
Author Contributions
Conceptualization, X.W. and L.Z.; methodology, L.Z.; software, L.Z.; validation, X.W.; formal analysis, X.W.; investigation, X.W.; resources, X.W.; data curation, L.Z.; writing—original draft preparation, X.W. and L.Z.; writing—review and editing, X.W. and L.Z.; visualization, L.Z.; supervision, X.W.; project administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TERGM | Temporal exponential random graph model |
| SNA | Social network analysis |
| QAP | Quadratic Assignment Procedure |
References
- Chan, F.K.S.; Chan, H.K. Recent research and challenges in sustainable urbanisation. Resour. Conserv. Recycl. 2022, 184, 106346. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, T.; Wang, D. Effects of urbanisation on PM2.5 concentrations: A systematic review and meta-analysis. Sci. Total Environ. 2023, 900, 166493. [Google Scholar] [CrossRef] [PubMed]
- Polk, H.S. State of Global Air 2019: A Special Report on Global Exposure to Air Pollution and Its Disease Burden; Health Effects Institute: Boston, MA, USA, 2019. [Google Scholar]
- World Health Organization. WHO Global Air Quality Guidelines: Particulate Matter (PM2.5 and PM10), Ozone, Nitrogen Dioxide, Sulfur Dioxide and Carbon Monoxide; World Health Organization: Geneva, Switzerland, 2021. [Google Scholar]
- Feng, T.; Du, H.; Lin, Z.; Zuo, J. Spatial spillover effects of environmental regulations on air pollution: Evidence from urban agglomerations in China. J. Environ. Manag. 2020, 272, 110998. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, L.; Tang, Z.; Zhang, K.; Wang, T. Spatial effects of urban expansion on air pollution and eco-efficiency: Evidence from multisource remote sensing and statistical data in China. J. Clean. Prod. 2022, 367, 132973. [Google Scholar] [CrossRef]
- Huang, Y.; Yan, Q.; Zhang, C. Spatial–temporal distribution characteristics of PM2.5 in China in 2016. J. Geovisualization Spat. Anal. 2018, 2, 12. [Google Scholar] [CrossRef]
- Fang, C.; Wang, Z.; Xu, G. Spatial-temporal characteristics of PM2.5 in China: A city-level perspective analysis. J. Geogr. Sci. 2016, 26, 1519–1532. [Google Scholar] [CrossRef]
- Lee, U.J.; Kim, M.J.; Kim, E.J.; Lee, D.W.; Lee, S.D. Spatial distribution characteristics and analysis of PM2.5 in South Korea: A geographically weighted regression analysis. Atmosphere 2024, 15, 69. [Google Scholar] [CrossRef]
- Wang, H.; Ge, Q. Spatial association network of PM2.5 and its influencing factors in the Beijing–Tianjin–Hebei urban agglomeration. Environ. Sci. Pollut. Res. 2023, 30, 70541–70557. [Google Scholar] [CrossRef]
- Qin, Y.; Kim, E.; Hopke, P.K. The concentrations and sources of PM2.5 in metropolitan New York City. Atmos. Environ. 2006, 40, 312–332. [Google Scholar] [CrossRef]
- Wang, Y.; Zhuang, G.; Tang, A.; Yuan, H.; Sun, Y.; Chen, S.; Zheng, A. The ion chemistry and the source of PM2.5 aerosol in Beijing. Atmos. Environ. 2005, 39, 3771–3784. [Google Scholar] [CrossRef]
- Kumar, N.; Park, R.J.; Jeong, J.I.; Woo, J.H.; Kim, Y.; Johnson, J.; Yarwood, G.; Kang, S.; Chun, S.; Knipping, E. Contributions of international sources to PM2.5 in South Korea. Atmos. Environ. 2021, 261, 118542. [Google Scholar] [CrossRef]
- Makkonen, U.; Vestenius, M.; Huy, L.N.; Anh, N.T.N.; Linh, P.T.V.; Thuy, P.T.; Phuong, H.T.M.; Nguyen, H.; Thuy, L.T.; Aurela, M.; et al. Chemical composition and potential sources of PM2.5 in Hanoi. Atmos. Environ. 2023, 299, 119650. [Google Scholar] [CrossRef]
- Xu, G.; Ren, X.; Xiong, K.; Li, L.; Bi, X.; Wu, Q. Analysis of the driving factors of PM2.5 concentration in the air: A case study of the Yangtze River Delta, China. Ecol. Indic. 2020, 110, 105889. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, X.; Zhu, W.; Shi, Q. Socioeconomic driving factors of PM2.5 emission in Jing-Jin-Ji region, China: A generalized Divisia index approach. Environ. Sci. Pollut. Res. 2021, 28, 15995–16013. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, B.; Fang, D.; Zhang, B.; Bai, J.; Liu, G.; Zhang, Y. Drivers of energy-related PM2.5 emissions in the Jing-Jin-Ji region between 2002 and 2015. Appl. Energy 2021, 288, 116668. [Google Scholar] [CrossRef]
- Chen, X.; Shuai, C.; Gao, J.; Wu, Y. Analyzing the socioeconomic determinants of PM2.5 air pollution at the global level. Environ. Sci. Pollut. Res. 2023, 30, 27257–27269. [Google Scholar] [CrossRef]
- Megaritis, A.G.; Fountoukis, C.; Charalampidis, P.E.; Denier Van Der Gon, H.A.C.; Pilinis, C.; Pandis, S.N. Linking climate and air quality over Europe: Effects of meteorology on PM 2.5 concentrations. Atmos. Chem. Phys. 2014, 14, 10283–10298. [Google Scholar] [CrossRef]
- Zhang, C.; Ni, Z.; Ni, L. Multifractal detrended cross-correlation analysis between PM2.5 and meteorological factors. Phys. A Stat. Mech. Its Appl. 2015, 438, 114–123. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, Y.M. The influential factors of urban PM2.5 concentrations in China: A spatial econometric analysis. J. Clean. Prod. 2016, 112, 1443–1453. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, M.; Zhang, B. The effects of urbanization on PM2.5 concentrations in China’s Yangtze River Economic Belt: New evidence from spatial econometric analysis. J. Clean. Prod. 2019, 239, 118065. [Google Scholar] [CrossRef]
- Fu, Z.; Li, R. The contributions of socioeconomic indicators to global PM2.5 based on the hybrid method of spatial econometric model and geographical and temporal weighted regression. Sci. Total Environ. 2020, 703, 135481. [Google Scholar] [CrossRef]
- Yang, Y.; Lan, H.; Li, J. Spatial econometric analysis of the impact of socioeconomic factors on PM2.5 concentration in China’s inland cities: A case study from Chengdu Plain Economic Zone. Int. J. Environ. Res. Public Health 2020, 17, 74. [Google Scholar] [CrossRef]
- Du, Y.; Sun, T.; Peng, J.; Fang, K.; Liu, Y.; Yang, Y.; Wang, Y. Direct and spillover effects of urbanization on PM2.5 concentrations in China’s top three urban agglomerations. J. Clean. Prod. 2018, 190, 72–83. [Google Scholar] [CrossRef]
- Yang, S.; Duan, F.; Ma, Y.; Li, H.; Ma, T.; Zhu, L.; Huang, T.; Kimoto, T.; He, K. Mixed and intensive haze pollution during the transition period between autumn and winter in Beijing, China. Sci. Total Environ. 2020, 711, 134745. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wu, B.; Wu, W. Analysis of PM2.5 spatial association evolution in the Sichuan Basin and its driving factors. Front. Environ. Sci. 2023, 11, 1101736. [Google Scholar]
- Zhang, S.; Tao, F.; Wu, Q.; Han, Q.; Wang, Y.; Zhou, T. Structural Differences of PM2.5 Spatial Correlation Networks in Ten Metropolitan Areas of China. ISPRS Int. J. Geo-Inf. 2022, 11, 267. [Google Scholar] [CrossRef]
- White, H.C.; Boorman, S.A.; Breiger, R.L. Social structure from multiple networks. I. Blockmodels of roles and positions. Am. J. Sociol. 1976, 81, 730–780. [Google Scholar] [CrossRef]
- Artzy-Randrup, Y.; Fleishman, S.J.; Ben-Tal, N.; Stone, L. Comment on “Network motifs: Simple building blocks of complex networks” and “Superfamilies of evolved and designed networks”. Science 2004, 305, 1107. [Google Scholar] [CrossRef]
- Contractor, N.S.; Wasserman, S.; Faust, K. Testing multitheoretical, multilevel hypotheses about organizational networks: An analytic framework and empirical example. Acad. Manag. Rev. 2006, 31, 681–703. [Google Scholar] [CrossRef]
- Hunter, D.R.; Handcock, M.S.; Butts, C.T.; Goodreau, S.M.; Morris, M. ergm: A package to fit, simulate and diagnose exponential-family models for networks. J. Stat. Softw. 2008, 24, 1–29. [Google Scholar] [CrossRef]
- Xiong, J.; Feng, X.; Tang, Z. Understanding user-to-User interaction on government microblogs: An exponential random graph model with the homophily and emotional effect. Inf. Process. Manag. 2020, 57, 102229. [Google Scholar] [CrossRef]
- Frank, O.; Strauss, D. Markov graphs. J. Am. Stat. Assoc. 1986, 81, 832–842. [Google Scholar] [CrossRef]
- Holland, P.W.; Leinhardt, S. An exponential family of probability distributions for directed graphs. J. Am. Stat. Assoc. 1981, 76, 33–50. [Google Scholar] [CrossRef]
- Monge, P.R.; Contractor, N.S. Theories of Communication Networks; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Leifeld, P.; Cranmer, S.J.; Desmarais, B.A. Temporal exponential random graph models with btergm: Estimation and bootstrap confidence intervals. J. Stat. Softw. 2018, 83, 1–36. [Google Scholar] [CrossRef]
- Hunter, D.R.; Goodreau, S.M.; Handcock, M.S. Goodness of fit of social network models. J. Am. Stat. Assoc. 2008, 103, 248–258. [Google Scholar] [CrossRef]
- Cowles, M.K.; Carlin, B.P. Markov chain Monte Carlo convergence diagnostics: A comparative review. J. Am. Stat. Assoc. 1996, 91, 883–904. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Cribb, M. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Cribb, M.; Huang, W.; Xue, W.; Sun, L.; Guo, J.; Peng, Y.; Li, J.; Lyapustin, A.; et al. Improved 1 km resolution PM2.5 estimates across China using enhanced space-time extremely randomized trees. Atmos. Chem. Phys. 2020, 20, 3273–3289. [Google Scholar] [CrossRef]
- Xun, N.; Zhang, X.; Zhang, H.; Su, C.; Liu, Y.; Guo, H.; Hou, X. Multiscale applicability assessment of PM2.5 datasets in Chinese urban agglomerations: Accuracy, spatiotemporal variability, and uncertainty. Environ. Pollut. 2025, 383, 126810. [Google Scholar] [CrossRef]
- Chen, M.; Liu, J.; Chu, B.; Zhao, D.; Li, R.; Chen, T.; Ma, Q.; Wang, Y.; Zhang, P.; Li, H.; et al. Research on the influencing factors of PM2.5 in China at different spatial scales based on machine learning algorithm. Environ. Int. 2025, 200, 109536. [Google Scholar] [CrossRef]
- Li, Y.; Ma, C.; Yang, T.; Wu, Z.; Yao, R.; Zhao, G.; Ning, X.; Kang, P. Monitoring and determinants analysis of canopy layer urban heat island in China based on both air temperature and apparent temperature. Urban Clim. 2025, 64, 102631. [Google Scholar] [CrossRef]
- Yan, L.; He, C.; Ni, J.; Hu, Q.; Lei, J.; Niu, X.; Tang, Y. Spatial-temporal correlation effects and persistent syner-gistic control benefits of fine particulate matter and carbon emissions in China. J. Environ. Manag. 2025, 374, 124135. [Google Scholar] [CrossRef]
- Snijders, T.A.; Pattison, P.E.; Robins, G.L.; Handcock, M.S. New specifications for exponential random graph models. Sociol. Methodol. 2006, 36, 99–153. [Google Scholar] [CrossRef]
- Lusher, D.; Koskinen, J.; Robins, G. Exponential Random Graph Models for Social Networks: Theory, Methods, and Applications; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Copeland, B.R.; Taylor, M.S. North-South trade and the environment. In International Trade and the Environment; Routledge: London, UK, 2017; pp. 205–238. [Google Scholar]
- Cheng, Z.; Li, L.; Liu, J. Identifying the spatial effects and driving factors of urban PM2.5 pollution in China. Ecol. Indic. 2017, 82, 61–75. [Google Scholar] [CrossRef]
- Gong, Y.; Sun, H.; Wang, Z.; Ding, C. Spatial correlation network pattern and evolution mechanism of natural gas consumption in China—Complex network-based ERGM model. Energy 2023, 285, 129400. [Google Scholar] [CrossRef]
- Mao, Y.; Li, X.; Jiao, D.; Zhao, X. Characterizing the spatial correlation network structure and impact mechanism of carbon emission efficiency: Evidence from China’s transportation sector. Energy 2024, 313, 133886. [Google Scholar] [CrossRef]
- Liu, H.; Chen, W.; Yuan, P.; Dong, X. Dynamic evolution and driving mechanisms of tourism carbon reduction networks: A TERGM-based study. Curr. Issues Tour. 2025, 1–25. [Google Scholar] [CrossRef]
- Song, J.; Xiao, H.; Liu, Z. Analysis of the driving mechanism of urban carbon emission correlation network in Shandong Province based on TERGM. Sustainability 2024, 16, 4233. [Google Scholar] [CrossRef]
- Ding, S.; Wang, L.; Zhou, Q. Study on Evolution Mechanism of Agricultural Trade Network of RCEP Countries—Complex System Analysis Based on the TERGM Model. Systems 2025, 13, 593. [Google Scholar] [CrossRef]
- Jiang, Z.; Shao, Z.; Wang, Q. Research on the employment mobility patterns and driving factors of graduates from double first-class universities in the central China. Sci. Rep. 2025, 15, 17373. [Google Scholar] [CrossRef]
- Hu, S.; Chen, G.; Miao, C. Understanding the structural evolution and driving mechanisms of urban network using firm-level big data and TERGM modeling. Cities 2025, 161, 105869. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, K. Technology transfers to whom and why? TERGM analysis across regional green technology transfer network in China. Int. J. Technol. Manag. 2024, 96, 64–93. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).