1. Introduction
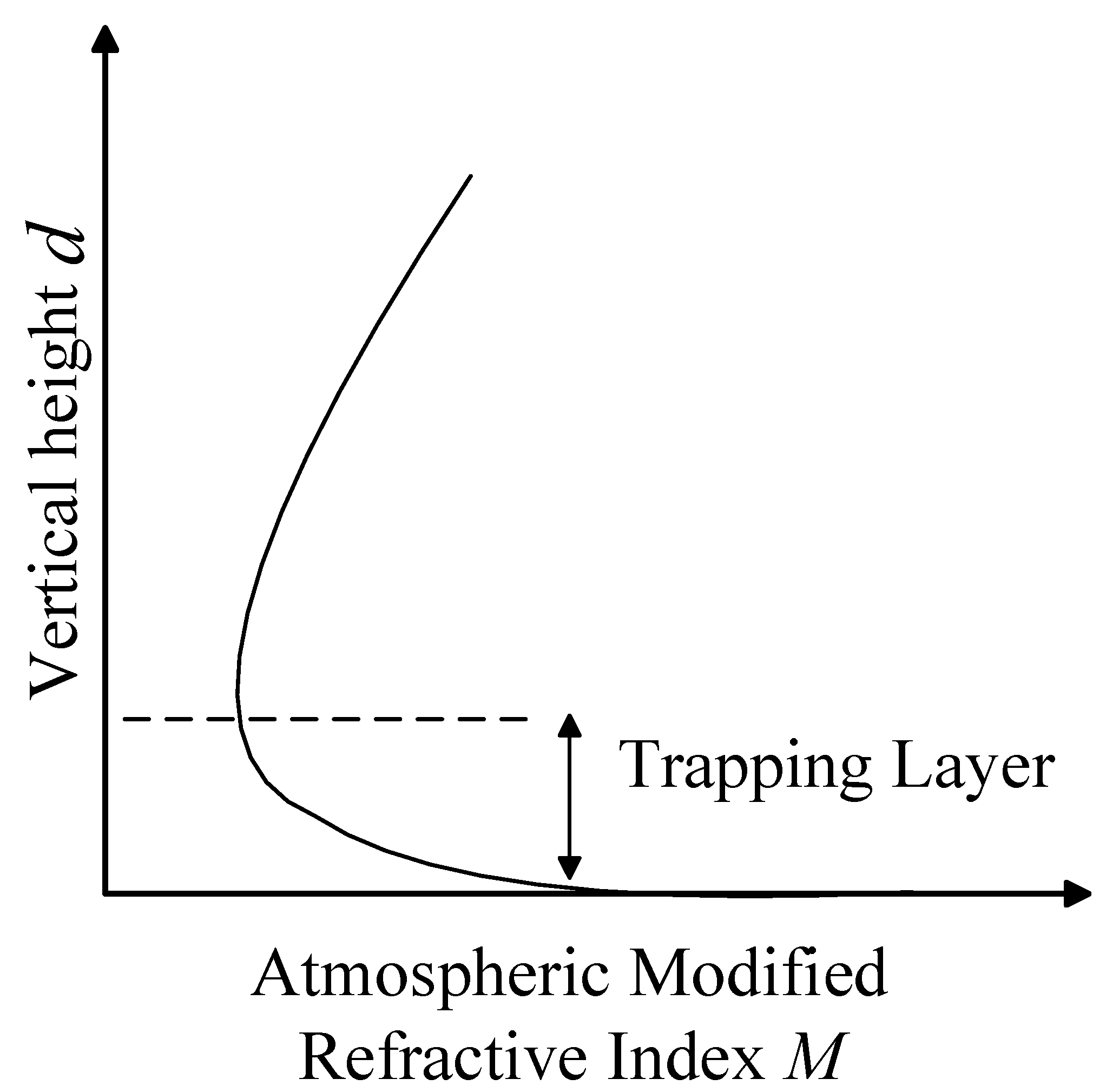
The propertiesof the atmospheric medium significantly alter electromagnetic wave propagation behavior. When abnormal gradients occur in the vertical distribution of atmospheric refractivity, such as temperature inversions or sharp humidity drops, atmospheric ducts can form, trapping electromagnetic waves for propagation within them [
1,
2,
3,
4]. The presence of atmospheric ducts allows electromagnetic waves to achieve beyond-line-of-sight propagation with low energy attenuation, which is highly significant for communications, radar detection, and radar blind spot correction [
5,
6,
7]. Evaporation ducts primarily form due to the evaporation of sea surface moisture. An imbalance in the thermal structure of the marine atmospheric boundary layer [
8] causes significant water vapor to accumulate near the sea surface through air–sea interactions. Wind transport then diffuses this moisture over a certain region. Above this region lies dry air with low moisture content, while below lies moist air carrying ample water vapor. Since sea surface moisture content is saturated, the moisture content decreases sharply with increasing height above the sea surface [
8], creating a gradient in water vapor flux and thus forming an evaporation duct. The EDH can be derived from the modified refractivity profile—the height corresponding to the minimum value of the modified atmospheric refractivity, as shown in
Figure 1.
As a major form of marine atmospheric duct, evaporation ducts have an occurrence rate as high as 85% in the South China Sea [
9,
10,
11]. Evaporation ducts alter the propagation path and energy distribution of electromagnetic waves, impacting microwave systems like radar and communications [
12]. Therefore, obtaining accurate short-term EDH forecasts is a critical task.
Numerous scholars have proposed evaporation duct models based on similarity theory to calculate modified refractivity profiles within tens of meters above the sea surface. These models commonly utilize hydro-meteorological elements such as atmospheric temperature, humidity, pressure, wind speed, and sea surface temperature at a certain height near the sea surface to compute evaporation duct parameters [
13,
14]. The Jeske model (1973) [
15] used potential refractivity, potential temperature, and potential water vapor pressure instead of atmospheric refractivity, temperature, and water vapor pressure, employing the bulk Richardson number to determine atmospheric stability and the Monin–Obukhov (M–O) similarity length, subsequently solving for EDH. In 1985, Paulus [
16] modified the Jeske model using new similarity variable relationships obtained from field experiments, resulting in the Paulus–Jeske (P–J) model. This model requires input variables (atmospheric temperature, relative humidity, wind speed, and sea surface temperature) measured at heights no lower than 6 m. In 1992, Musson-Genon et al. [
17] proposed the MGB model, based on M–O similarity theory, using an analytical solution widely applied in numerical weather prediction to compute EDH, simplifying the process for operational use. In 1996, Babin et al. [
18] introduced the BYC evaporation duct prediction model, which incorporated air pressure parameters compared to the P–J model, resulting in higher prediction accuracy. In 2000, Frederickson et al. [
19] proposed the NPS evaporation duct diagnostic model. This model calculates atmospheric temperature and humidity profiles using M–O similarity theory and derives the vertical pressure distribution using the ideal gas law and hydrostatic equations, offering better stability than other models. In 2016, Yang Shaobo et al. [
20] conducted an applicability analysis of the NPS evaporation duct diagnostic model in the South China Sea region. The results showed that the directly measured daily average evaporation duct height was 10.68 m with a duct occurrence probability of 92.5%, while the NPS model’s predicted values yielded a daily average height of 10.25 m and an occurrence probability of 89.4%. The 0.43 m difference in daily average height demonstrates that the NPS model predictions remain largely consistent with actual measurements under stable atmospheric conditions. These duct models differ in criteria for determining EDH and other characteristic quantities. This study uses the Climate Forecast System Reanalysis version 2 (CFSv2) dataset from the National Centers for Environmental Prediction (NCEP), including 2 m air temperature, sea surface temperature, 2 m specific humidity, 10 m U and V wind components, and sea-level pressure data. These data are input into the NPS model to calculate the EDH for the Yongshu Reef area in the South China Sea.
With the booming development of artificial intelligence in the 21st century, machine learning methods have been applied across various fields. Some researchers have utilized machine learning for EDH prediction. Given that the evaporation duct height (EDH) in evaporation duct models can be regarded as a function of atmospheric temperature, sea surface temperature, sea surface pressure, relative humidity, and wind speed, Zhu et al. (2018) [
21] collected a large set of point-based meteorological observations and used them as inputs to a multilayer perceptron (MLP) deep learning model, with EDH as the output. Their results showed that the deep neural network approach improved prediction accuracy by at least 80%. Later, Zhao et al. (2020) [
22] employed single-station data to drive a backpropagation neural network (BP-NN) for EDH prediction and found that, compared with baseline methods such as the P–J model and support vector regression (SVR), the BP-NN model demonstrated significantly better overall performance as well as strong generalization capability. In 2021, Hong et al. [
23] proposed a Seasonal Autoregressive Integrated Moving Average (ARIMA) model, using it to forecast EDH variations in the South China Sea in 2018 with a 95% confidence interval, achieving high prediction accuracy. Zhao et al. [
24] constructed an EDH prediction model based on Long Short-Term Memory (LSTM) neural networks. Compared to the BYC, NPS, and XGB models, the LSTM–EDH model showed significantly reduced root mean square error (RMSE) and better fit to measured EDH. Han et al. [
12] used EDH data measured in the Yellow Sea, China, between July 2017 and March 2019, comparing LSTM with Support Vector Machine (SVM) and Artificial Neural Network (ANN). The results indicated LSTM errors that were significantly smaller than in other models, highlighting LSTM’s advantage in time series prediction. In 2020, Mai Yanbo [
25] employed the Darwinian Evolutionary Algorithm (DEA), Support Vector Machine (SVM), and BP neural network to diagnose the evaporation duct height (EDH). Compared with Support Vector Regression (SVR) and BP neural network, the DEA algorithm not only improved diagnostic accuracy but also provided a nonlinear expression of EDH, facilitating early prediction and mitigation of the impact of evaporation ducts on electromagnetic wave propagation. In the same year, Zhao Wenpeng [
26] addressed the limitations of existing EDH diagnostic models by introducing the XGBoost algorithm for the first time in this field, proposing the XGB model. Comparative experiments with the P–J model and multilayer perceptron (MLP) demonstrated that the XGB model exhibited superior accuracy and generalization capability. In 2023, Zhang et al. [
27] proposed and validated a Multi-Model Fusion (MMF)-based EDH diagnostic method, utilizing the LIBSVM library for model fusion. The experimental results showed that, compared to the BYC, NPS, NWA, NRL, and LKB models, the MMF model achieved higher diagnostic accuracy and stability under varying meteorological conditions. These studies indicate that point-based modeling can achieve satisfactory accuracy while maintaining computational efficiency, making it particularly suitable for localized applications. In practice, EDH data are spatially sparse, making regional-scale prediction infeasible; therefore, investigating single-point time series prediction is a necessary first step.
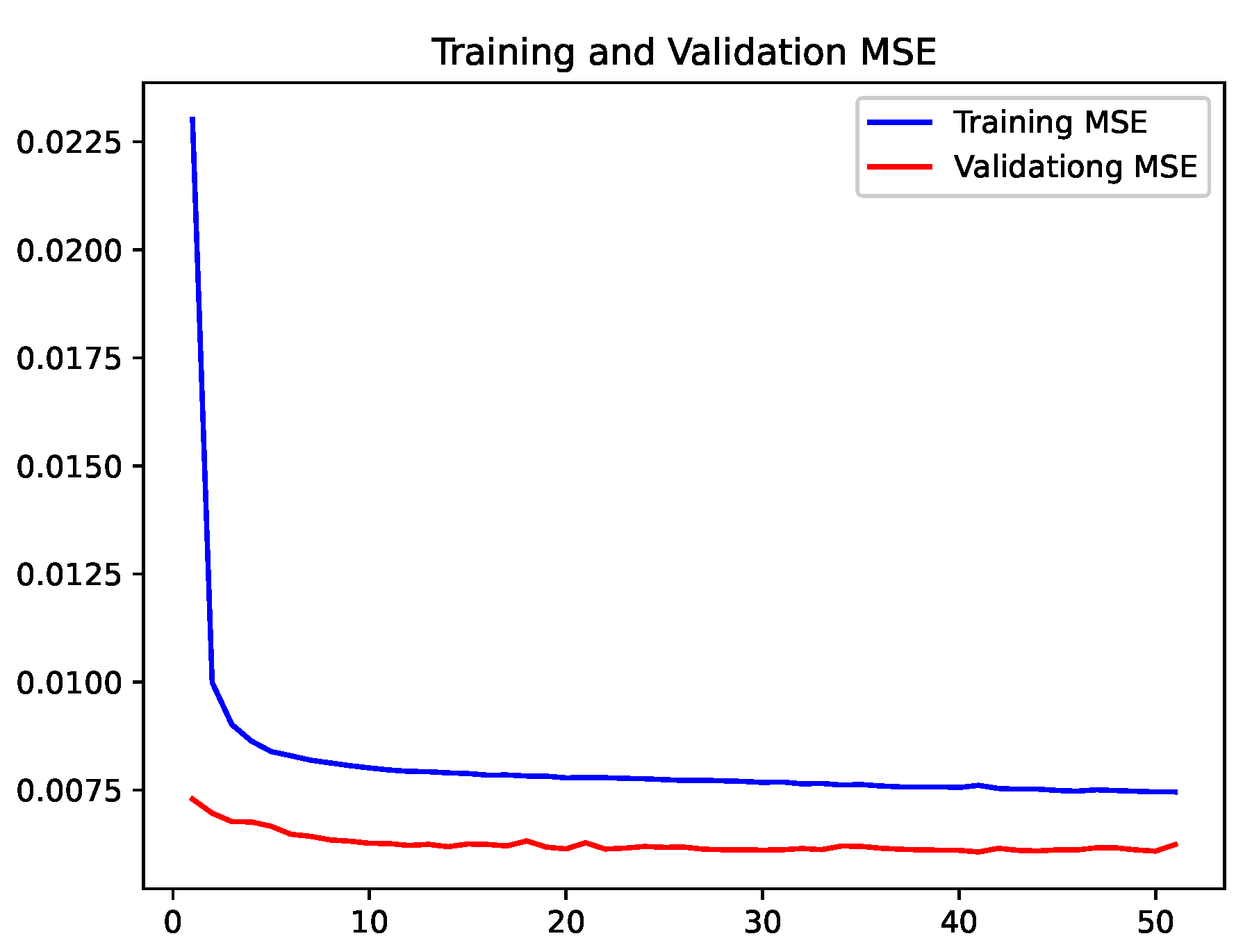
Despite the effectiveness of AI methods for time series problems, model hyperparameter settings often rely on empirical trial-and-error from prior studies or practice, greatly reducing model generalization [
28]. Bayesian optimization (BO) is a common black-box function optimization method [
29] that effectively addresses poor hyperparameter adaptability. Liu Heng et al. (2019) [
30] improved a conventional BP neural network using a Bayesian regularization algorithm, overcoming the issue of random initial weights leading to local optima. The analysis showed that the improved BP method’s prediction accuracy was 42.81% higher than the traditional BP method. In 2022, Cui et al. [
31] used GPS signal inversion and BO-based deep learning to improve EDH prediction accuracy, achieving a smaller RMSE than traditional methods and demonstrating efficient and accurate duct parameter inversion in noisy environments.
To address the challenges of neural network overfitting during training and low efficiency in manual parameter tuning for traditional evaporation duct height (EDH) prediction, this study proposes the application of Bayesian optimization (BO)-based deep learning technology to EDH forecasting. We construct a novel BO–LSTM hybrid model to enhance prediction accuracy, where the BO algorithm automatically optimizes the hyperparameters of the LSTM network for 24 h EDH prediction. The paper is organized as follows:
Section 2.1 describes the EDH calculation.
Section 2.2 explains Bayesian optimization theory.
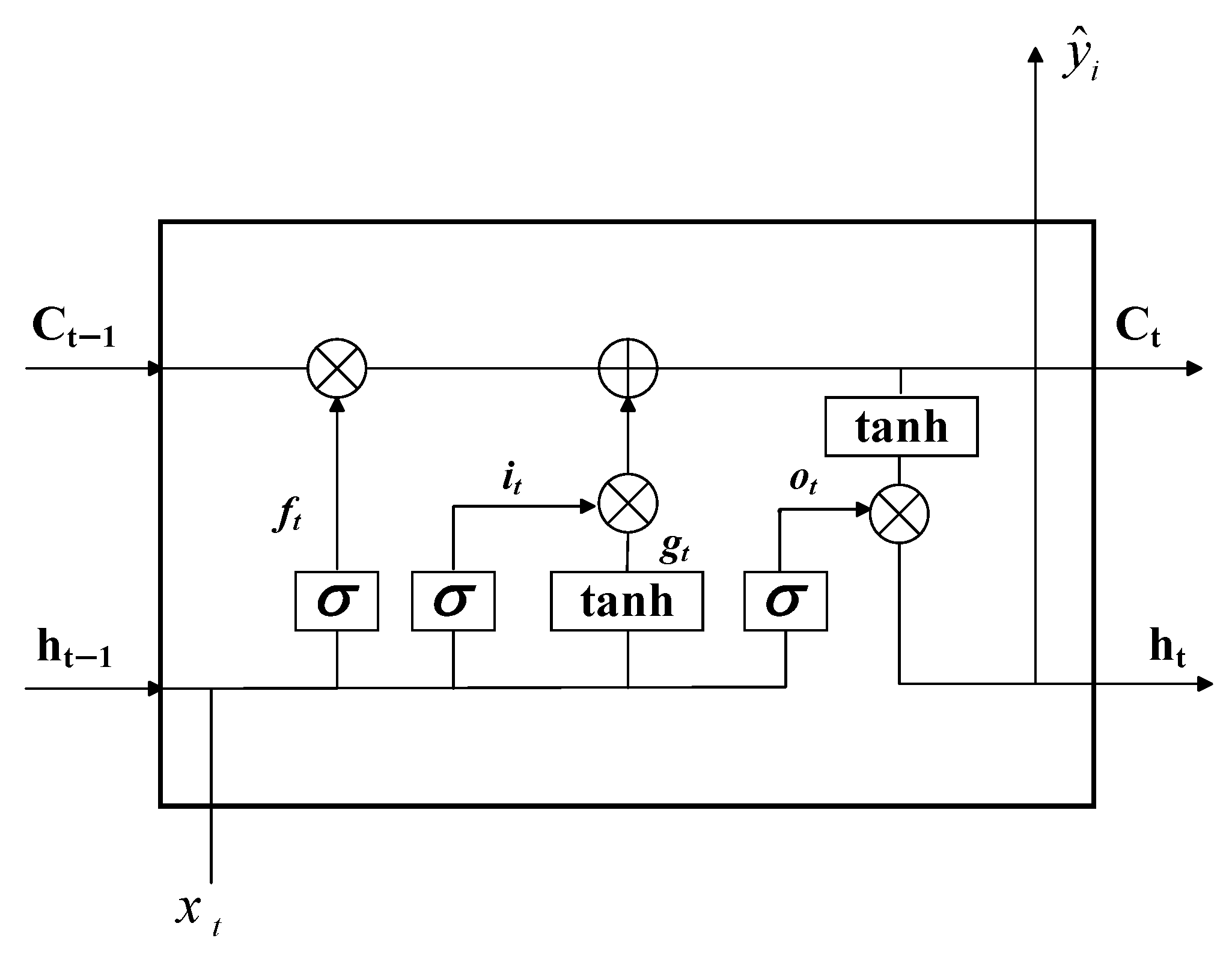
Section 2.3 details the LSTM prediction model theory.
Section 3 presents the experimental results, including the proposed model’s effectiveness in 24 h EDH prediction and its superiority over the baseline LSTM model. The conclusions are presented in
Section 4.
4. Conclusions
This study utilized CFSv2 reanalysis data and the NPS evaporation duct diagnostic model to conduct 1–24 h forecasting of evaporation duct height (EDH) in the Yongshu Reef area of the South China Sea. The main findings are as follows:
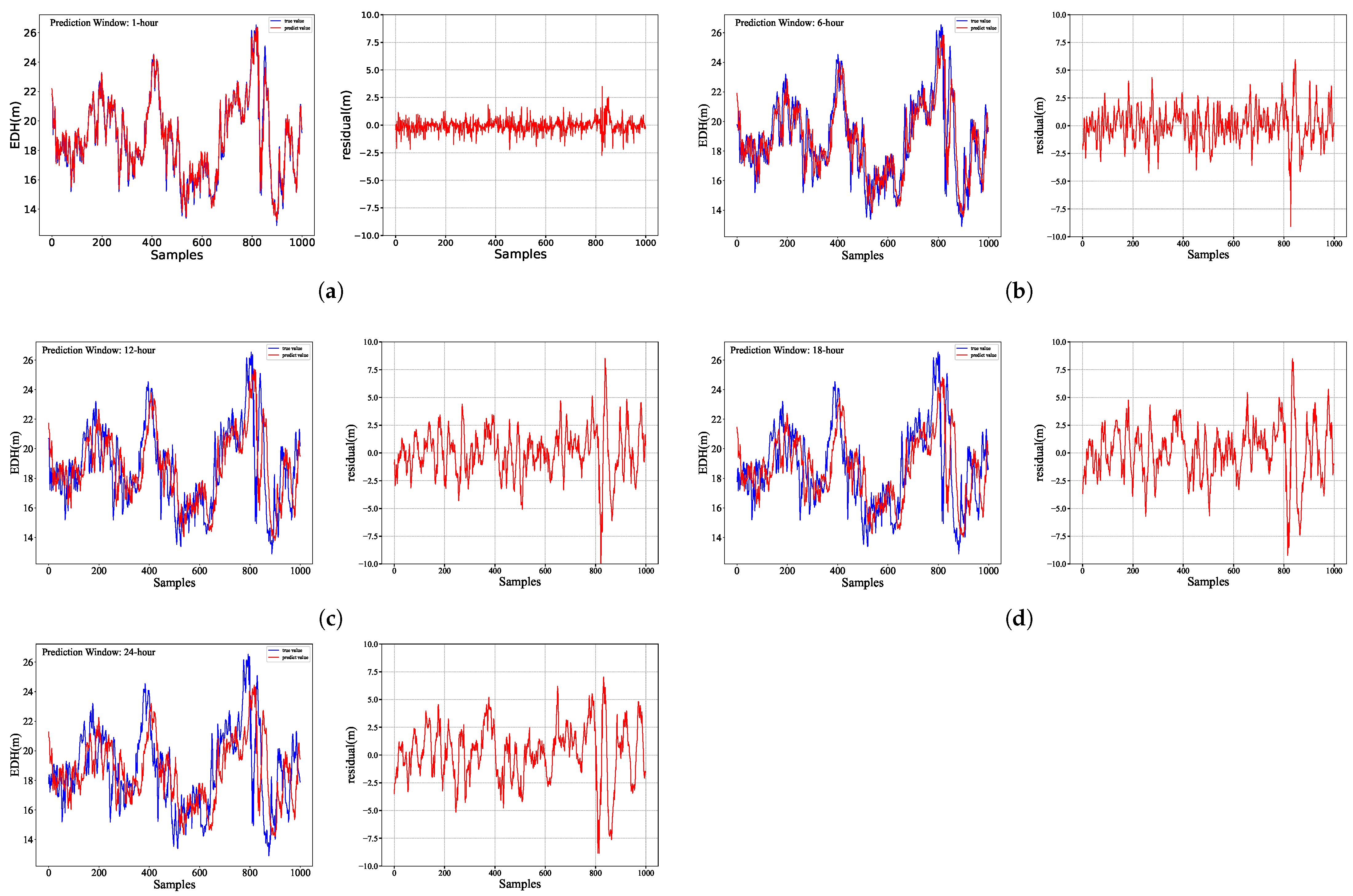
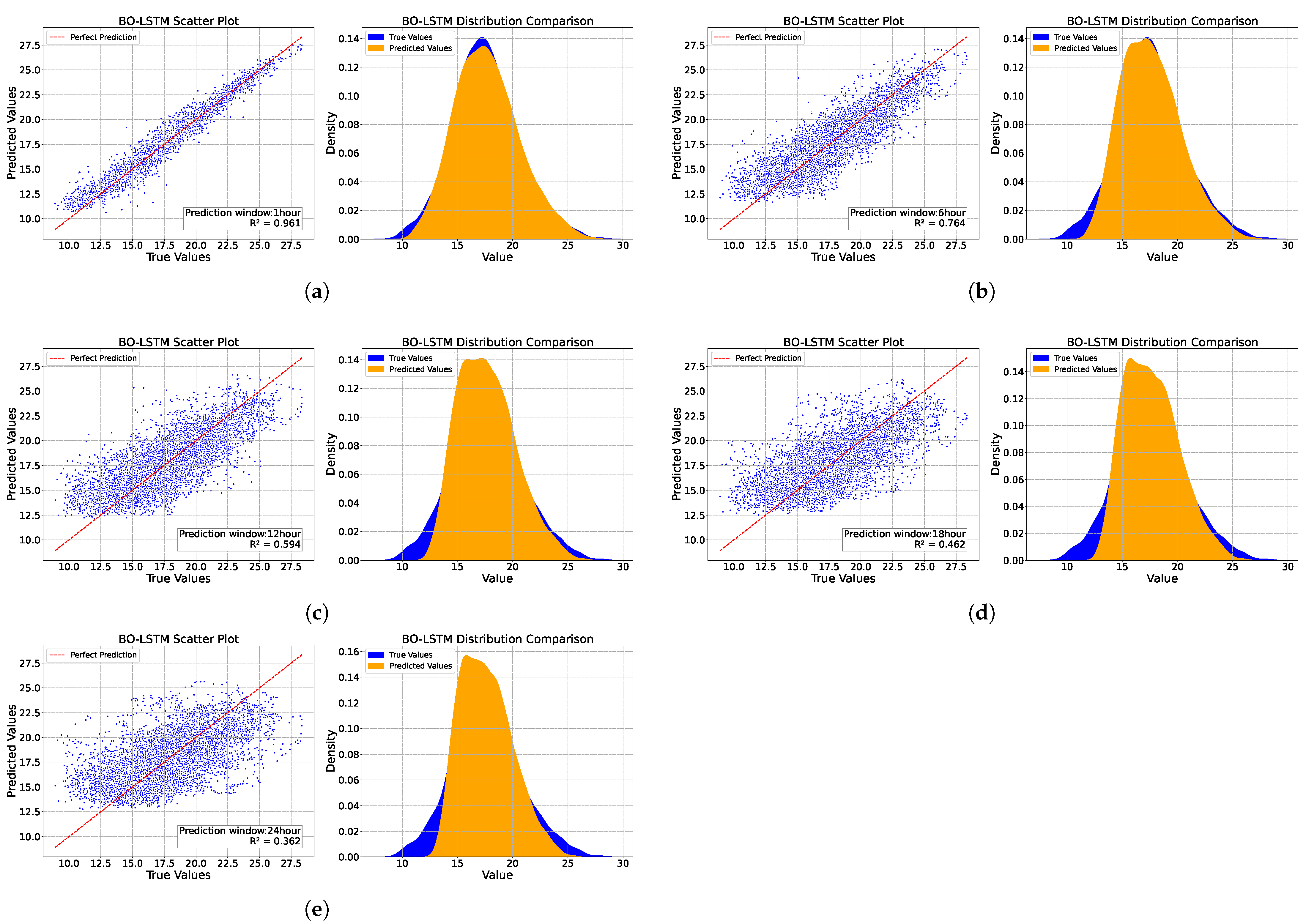
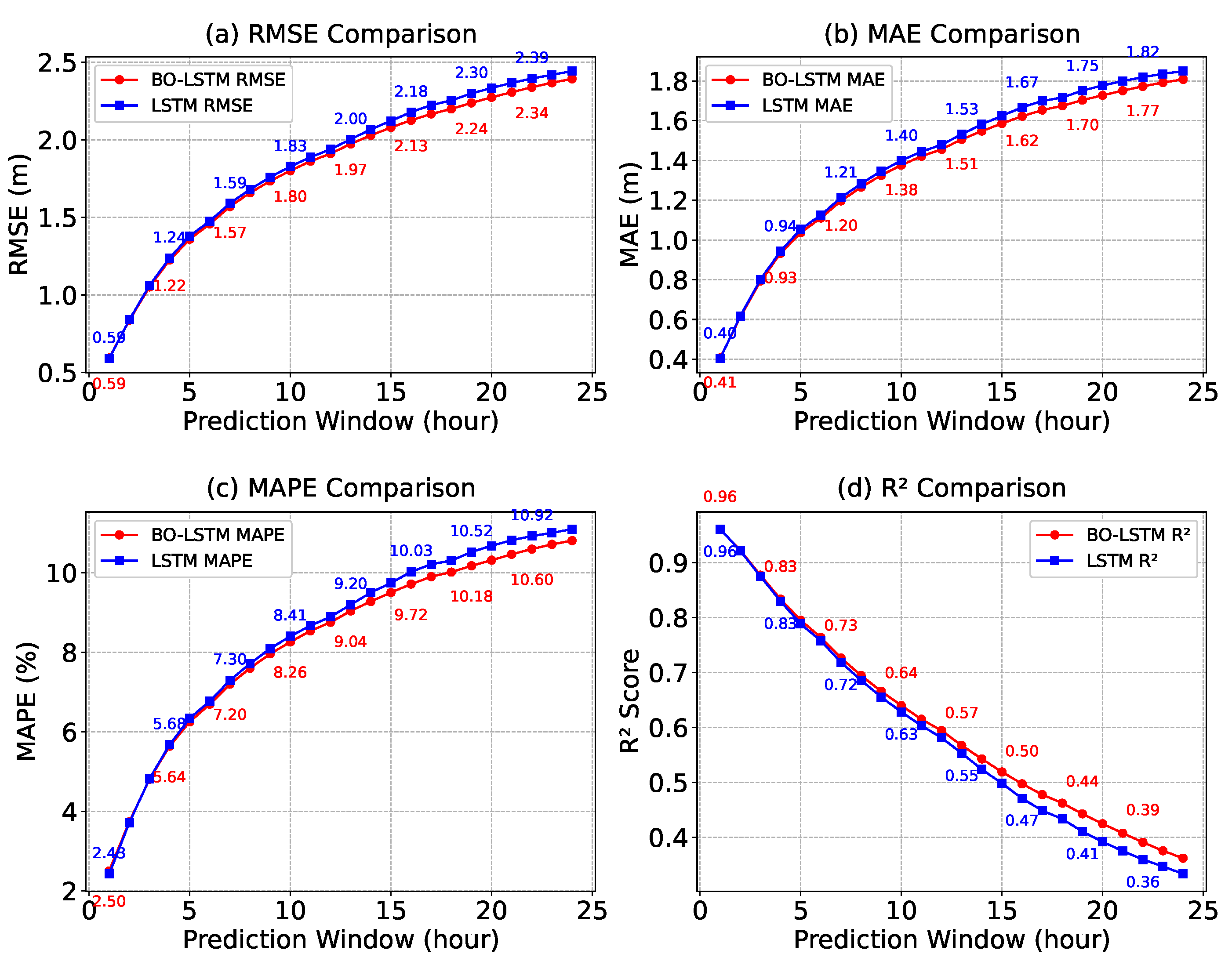
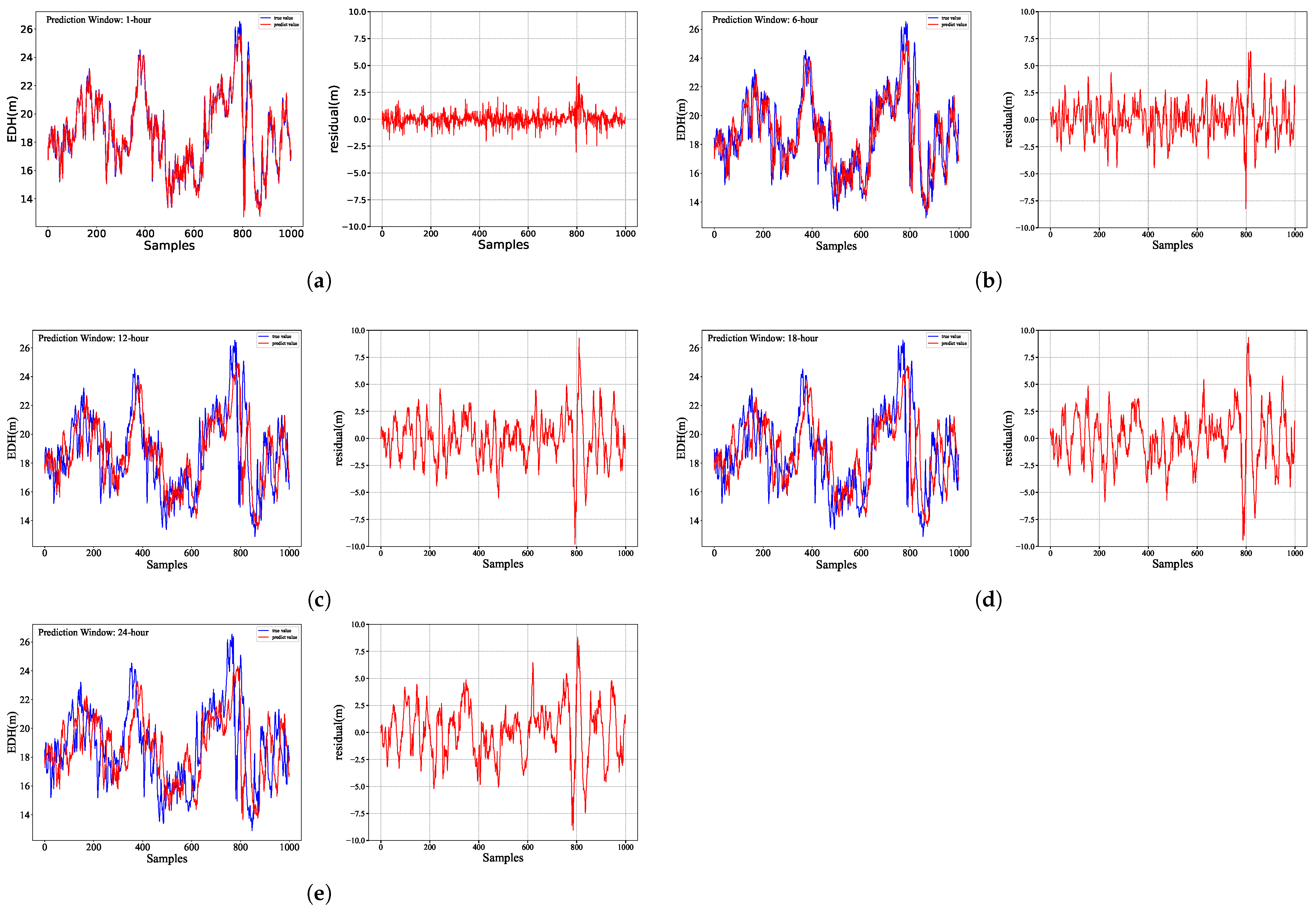
(1) The BO–LSTM model developed in this study demonstrates the capability to effectively predict EDH values up to 24 h in advance, although its predictive accuracy decreases with increasing forecast horizon. For the 1 h forecast, the model achieves a root mean square error (RMSE) of 0.592 m, a mean absolute error (MAE) of 0.407 m, and a coefficient of determination (R2) of 0.961, indicating strong agreement with the observations. In contrast, for the 24 h forecast, the RMSE and MAE increase to 2.393 m and 1.808 m, respectively, while the R2 drops substantially to 0.362, reflecting a notable decline in predictive skill over longer time scales.
(2) To validate the effectiveness of Bayesian optimization (BO), we compared the BO–LSTM model with the baseline LSTM model. The results demonstrate comparable prediction accuracy between BO–LSTM and LSTM for 1–15 h forecasts, with BO–LSTM showing marginally better performance. As the prediction horizon increases, the prediction accuracy of the BO–LSTM model gradually surpasses that of the LSTM model, indicating that the Bayesian-based automatic hyperparameter optimization approach can enhance the model’s predictive performance.
The BO–LSTM model proposed in this study integrates Bayesian optimization with deep learning techniques, improving the accuracy of short-term EDH prediction. Consequently, it can help to mitigate maritime communication interference and enhance the efficiency of over-the-horizon (OTH) communication and radar detection at sea. Given its advantages, this optimization approach is not only applicable to EDH prediction but can also be extended to other fields requiring high-precision time series forecasting, such as atmospheric science and space weather research.
However, our study focused solely on evaporation duct height (EDH) prediction at a single-point location (Yongshu Reef in the South China Sea) and thus could not capture the spatial heterogeneity of EDH. Future research should extend this work to regional-scale EDH prediction to obtain a more comprehensive perspective. Additionally, when validating model accuracy, we used the output of the NPS model as ground truth without incorporating actual measurement data. Consequently, the reported 24 h EDH prediction errors are relative to the NPS model’s output rather than observational benchmarks. Furthermore, our study exclusively utilized CFSv2 reanalysis data as input to the NPS model for deriving EDH values at Yongshu Reef, representing a relatively limited data source. We did not account for the inherent uncertainties in either the CFSv2 reanalysis or the NPS model itself. Therefore, future studies should incorporate comparative analyses of multiple observational datasets and reanalysis products to enhance the accuracy and reliability of the research findings.