Excitation of ULF, ELF, and VLF Resonator and Waveguide Oscillations in the Earth–Atmosphere–Ionosphere System by Lightning Current Sources Connected with Hunga Tonga Volcano Eruption
Abstract
1. Introduction
2. Goals of the Work and the Corresponding Methodological Approaches
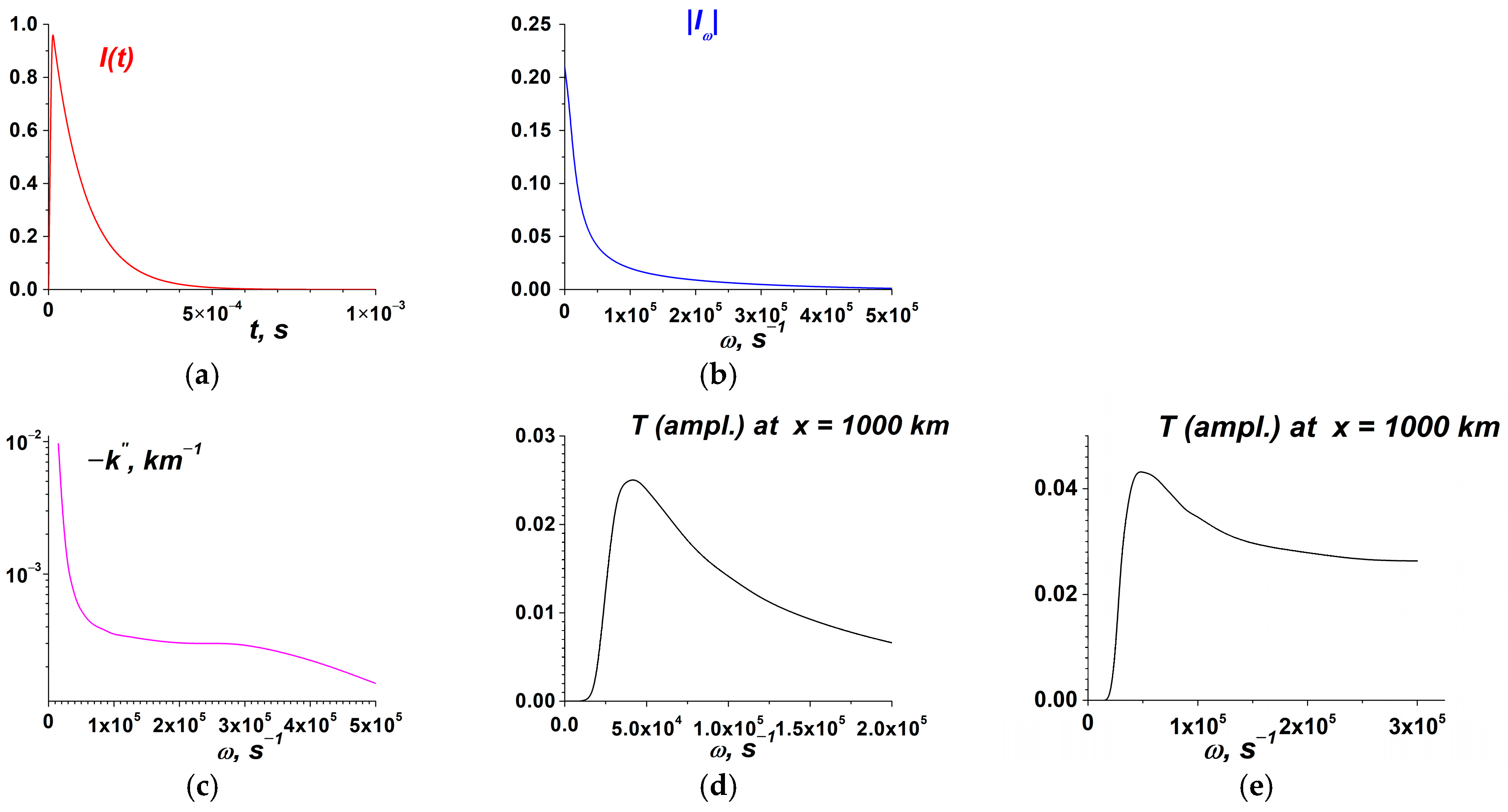
3. Current Sources Due to Lightning Connected to Hunga Tonga Eruption in ULF, ELF, and VLF Ranges. Values and Spectral Characteristics

4. Excitation of LEAIM by ULF, ELF, and VLF Current Sources
4.1. Penetration of ULF Electric Fields into the Ionosphere
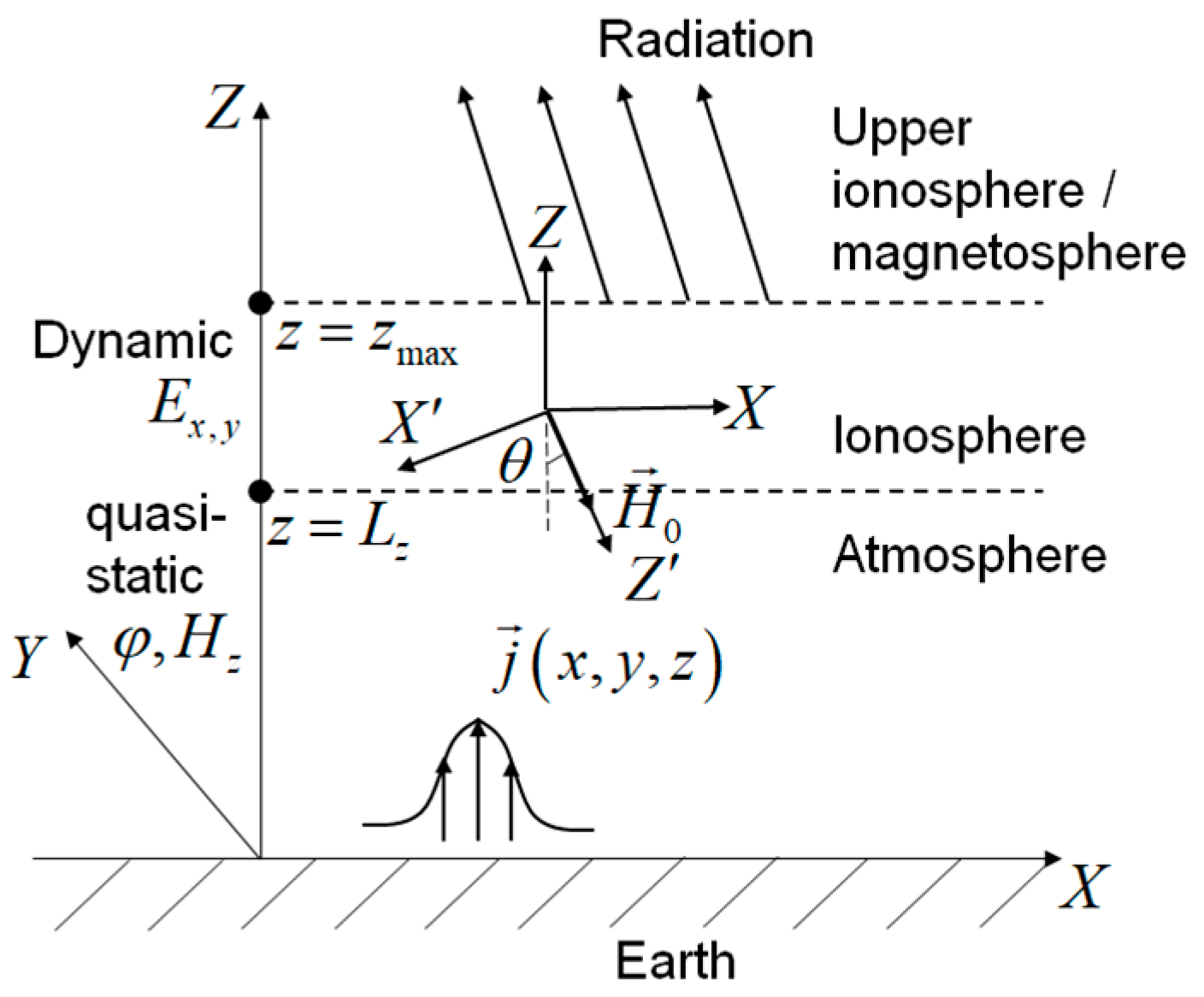
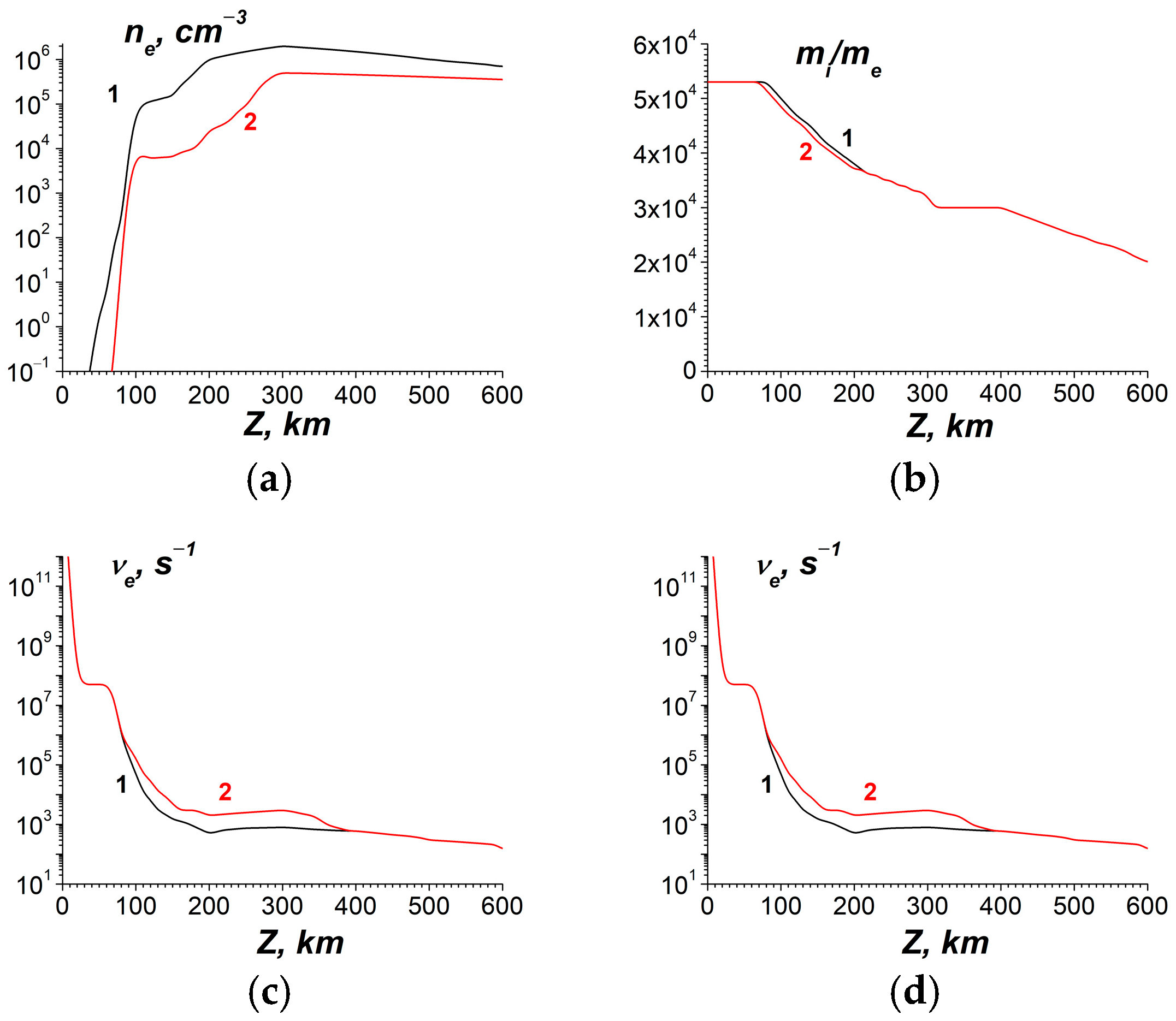
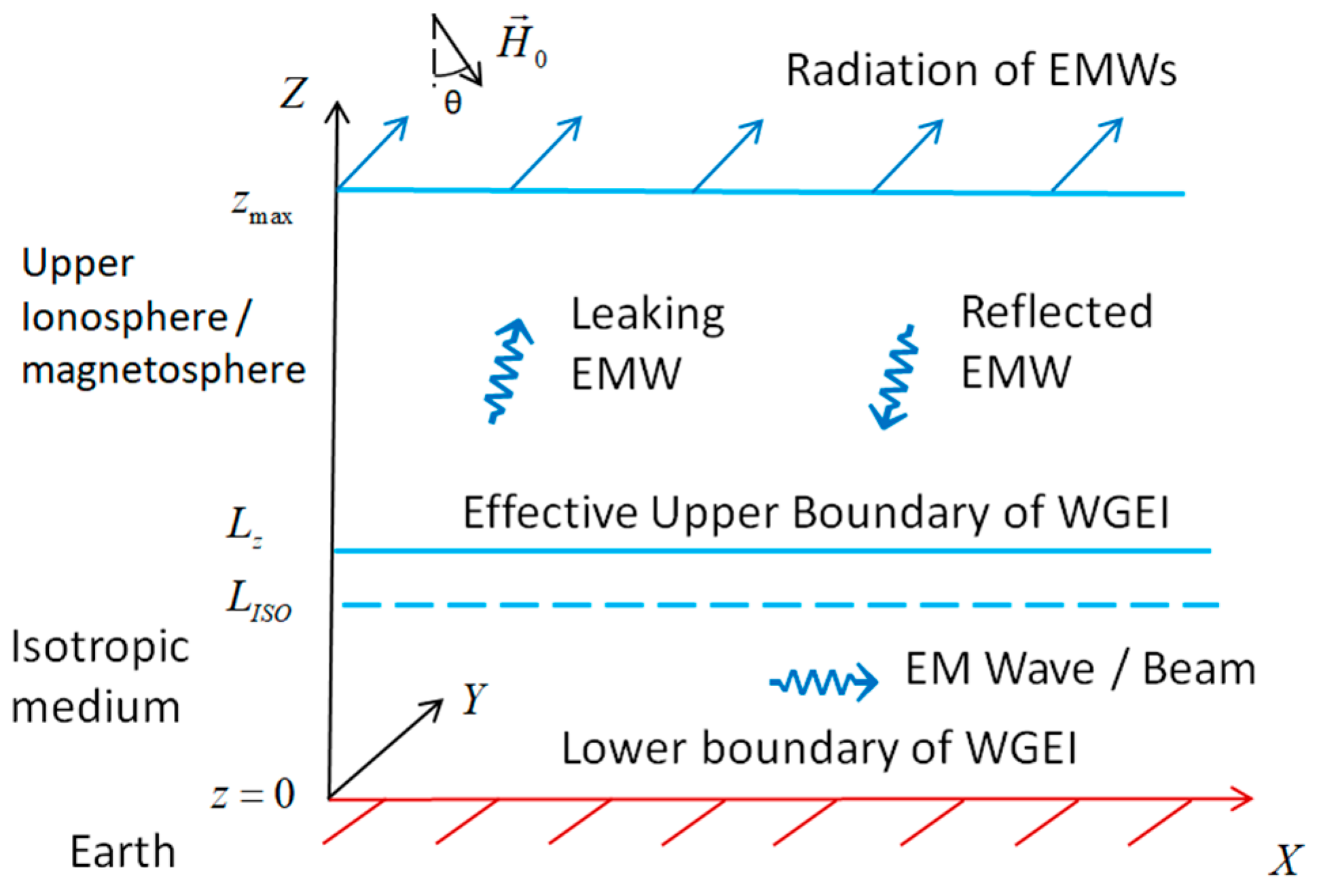
4.1.1. Formulation and Geometry of the Problem—The Model and Basic Equations
- (i)
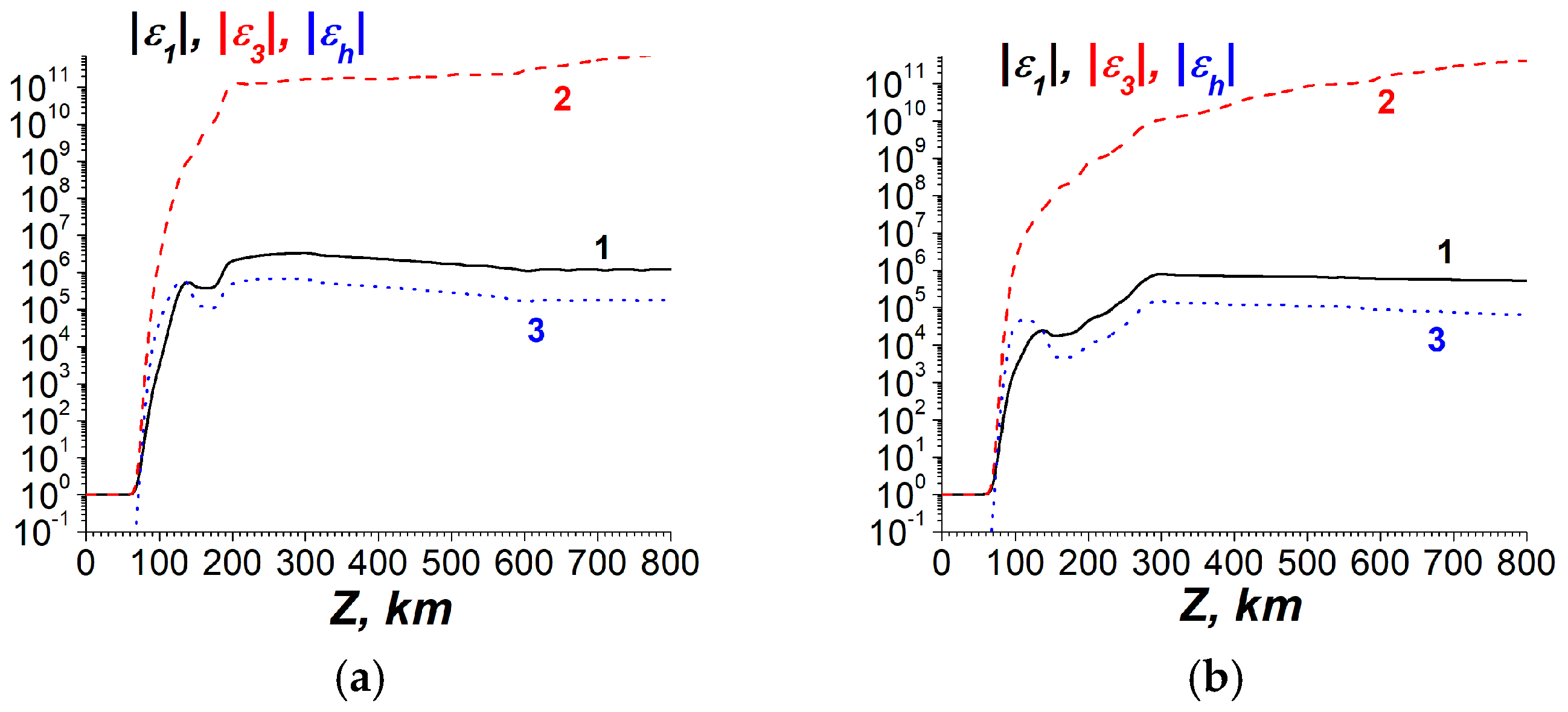
- The dynamic model, as explained above, should be used in the ionosphere. Mathematically, this model can be described by a system of two second-order differential equations with respect to the horizontal components of the electric field (the corresponding matrix Equation (22) is given in Section 4.1.3). This means that in the lower part of LEAIM, i.e., in the atmosphere, including the region near Earth’s surface, at the lowest frequencies of the ULF range, both potential electric and magnetic quasi-stationary fields must be taken into account. Thus, an advantage of our approach is the “restoration” of the magnetic component of the quasi-stationary EM field. That component was lost in most works on atmospheric electricity and the theory of the global electrical network (see, for example, [70]).
- (ii)
- There is a decrease by many orders of magnitude in the ratio of magnetic and electric fields at the lowest frequencies of the ULF range in the lower atmosphere near Earth’s surface. Consequently, when attempting to apply a dynamic model not only in the ionosphere but also in the atmosphere, a significant decrease in accuracy may occur when calculating field components corresponding to a “weak” magnetic mode against the background of a “strong” quasi-stationary electrical mode. At the same time, all the above-mentioned fields, both in the ionosphere and in the atmosphere, ultimately should be coupled into a single system of equations with coefficients varying in height.
4.1.2. Quasi-Stationary Region
4.1.3. The Dynamic Region—Ionosphere and Magnetosphere Waveguide Propagation and the Upper Boundary Conditions
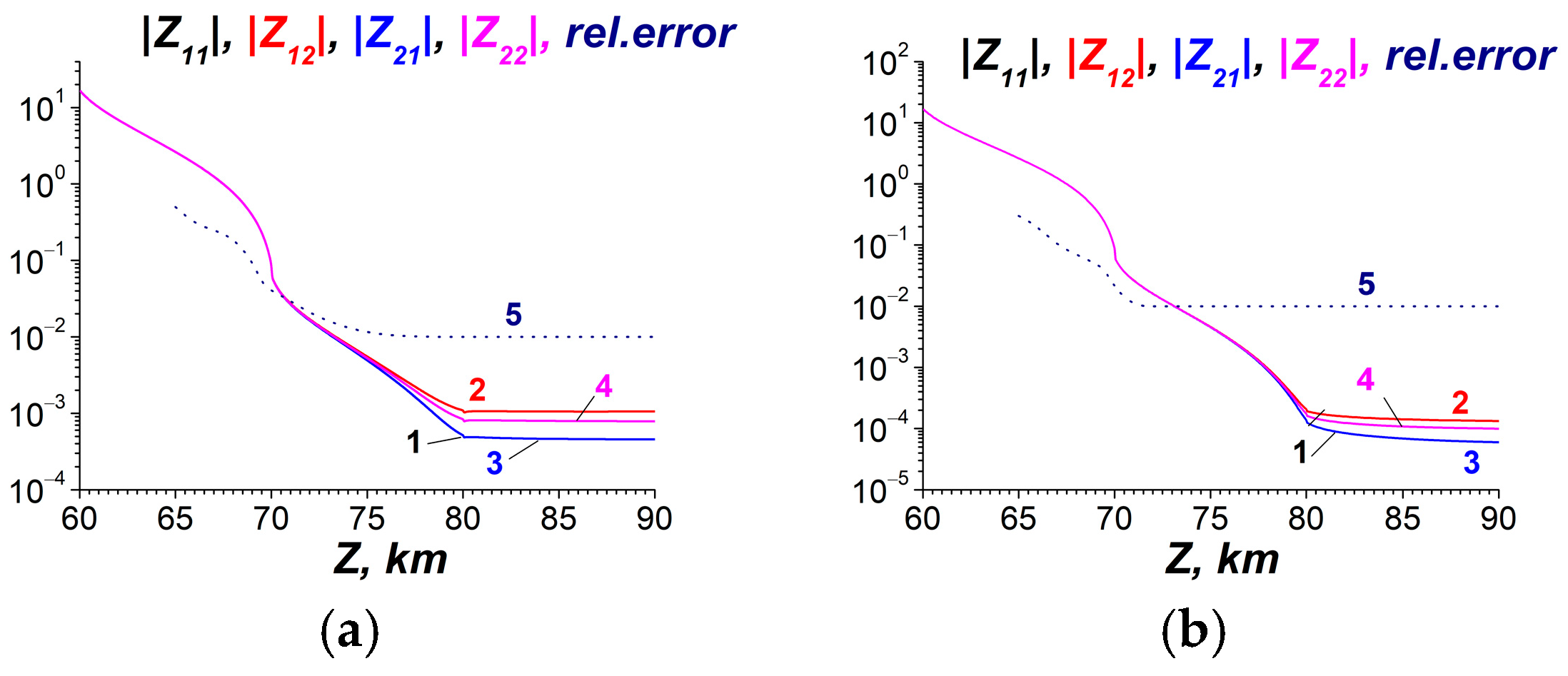
4.1.4. Tensor Impedance and Quasi-Stationary Boundary Conditions
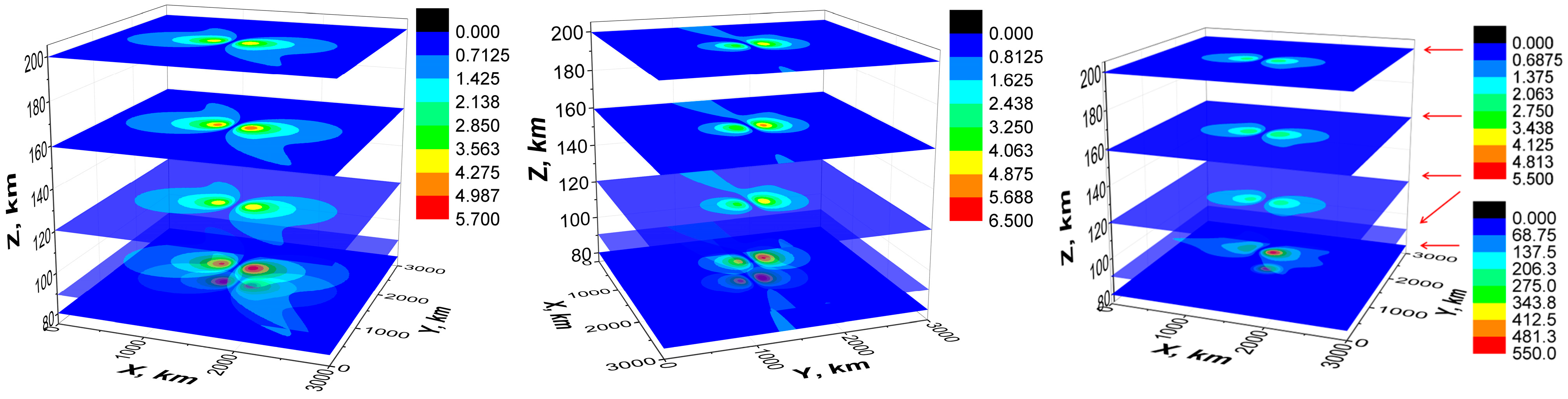
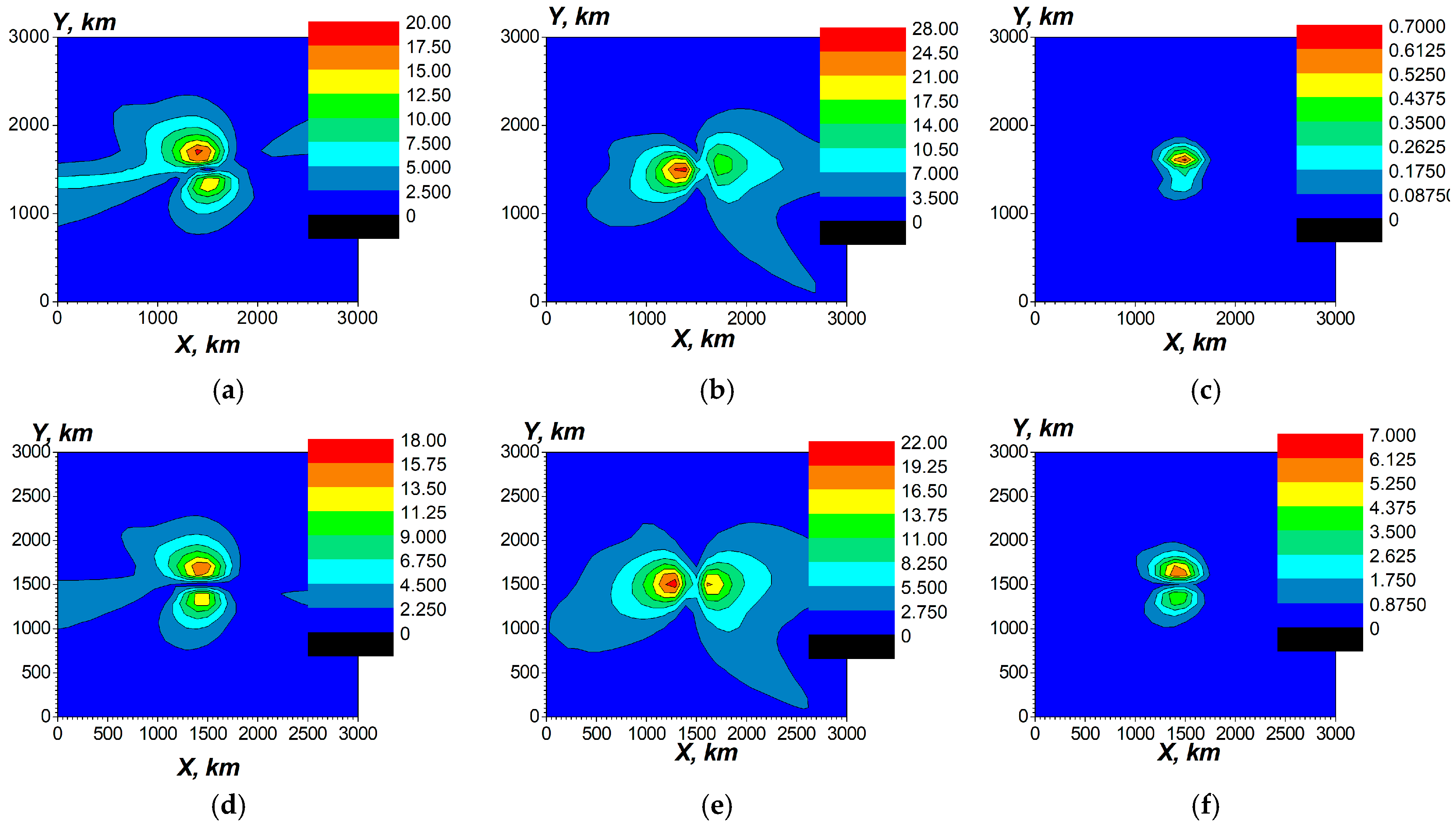
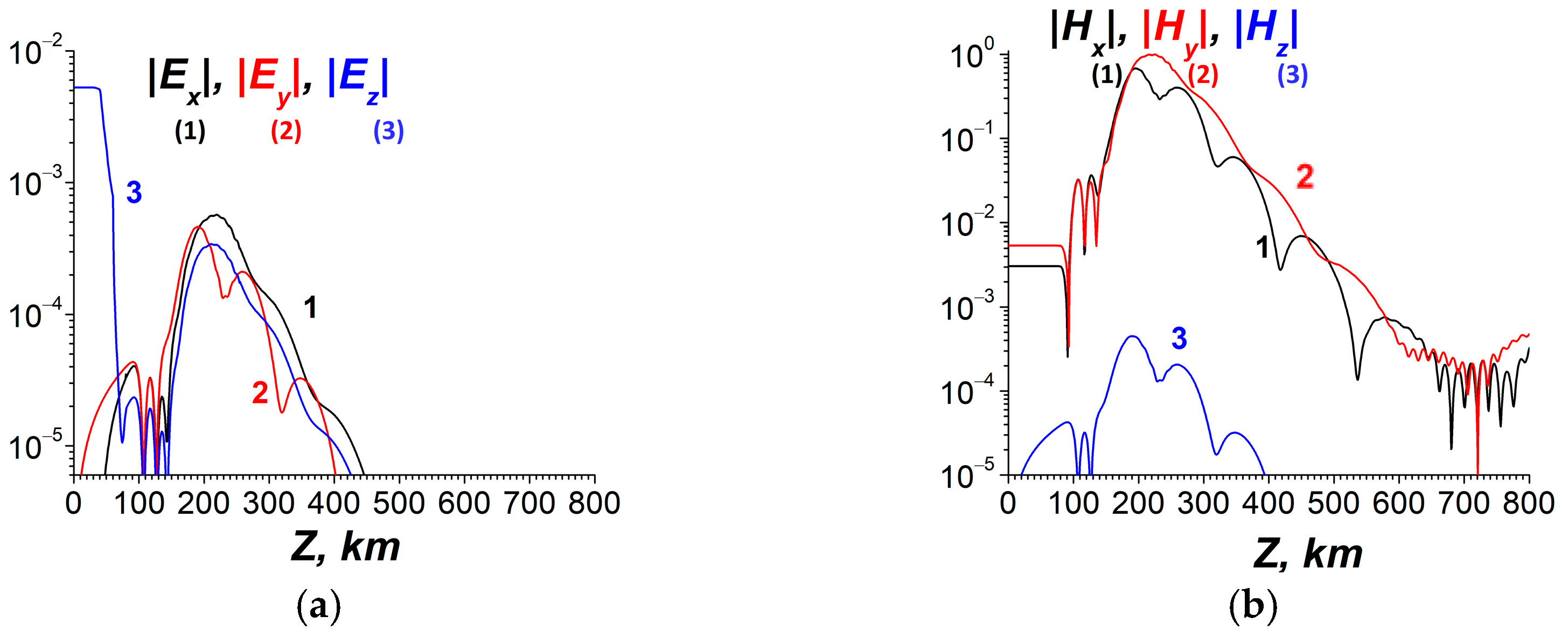
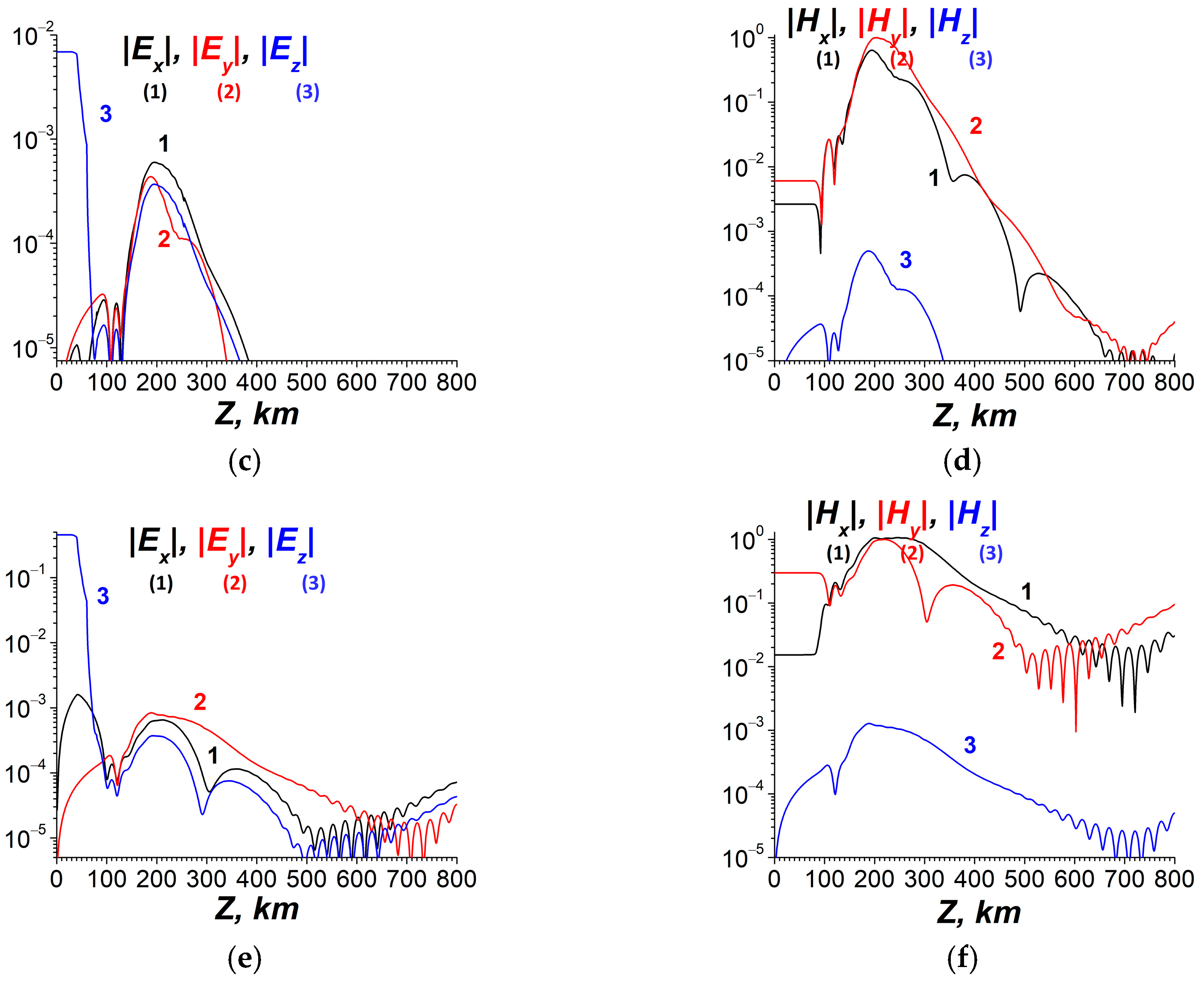
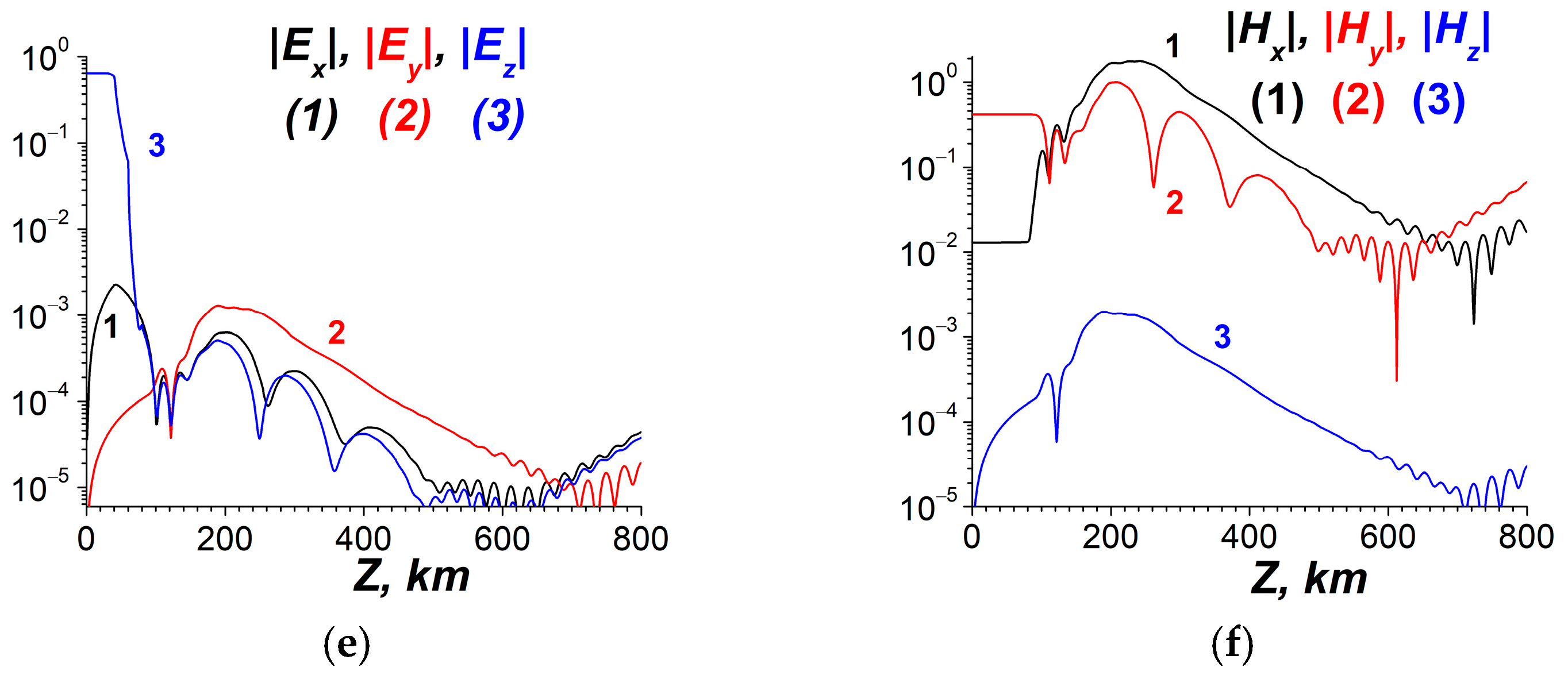
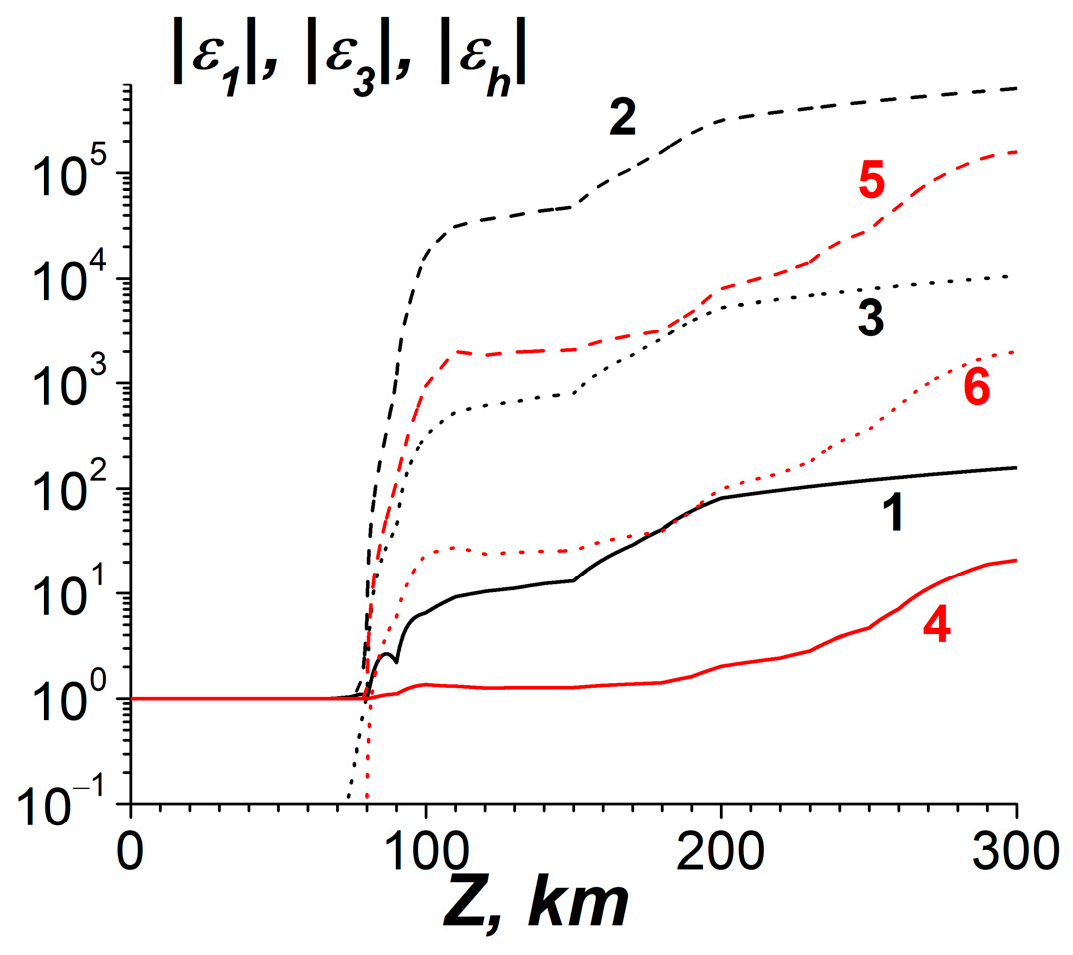
4.1.5. Numerical Simulations on Penetration of ULF Electric Fields into the Ionosphere— Possible Action in the Ionosphere and Comparison with Observations and Other Investigations
4.2. Generation of the Resonant Oscillations/Eigenmodes: Schumann Resonators—Ionospheric Alfvén Resonator for ELF Oscillations
4.2.1. Simplified Model of Excitation of the Schumann Resonator by Current Sources of the Volcanic Origin
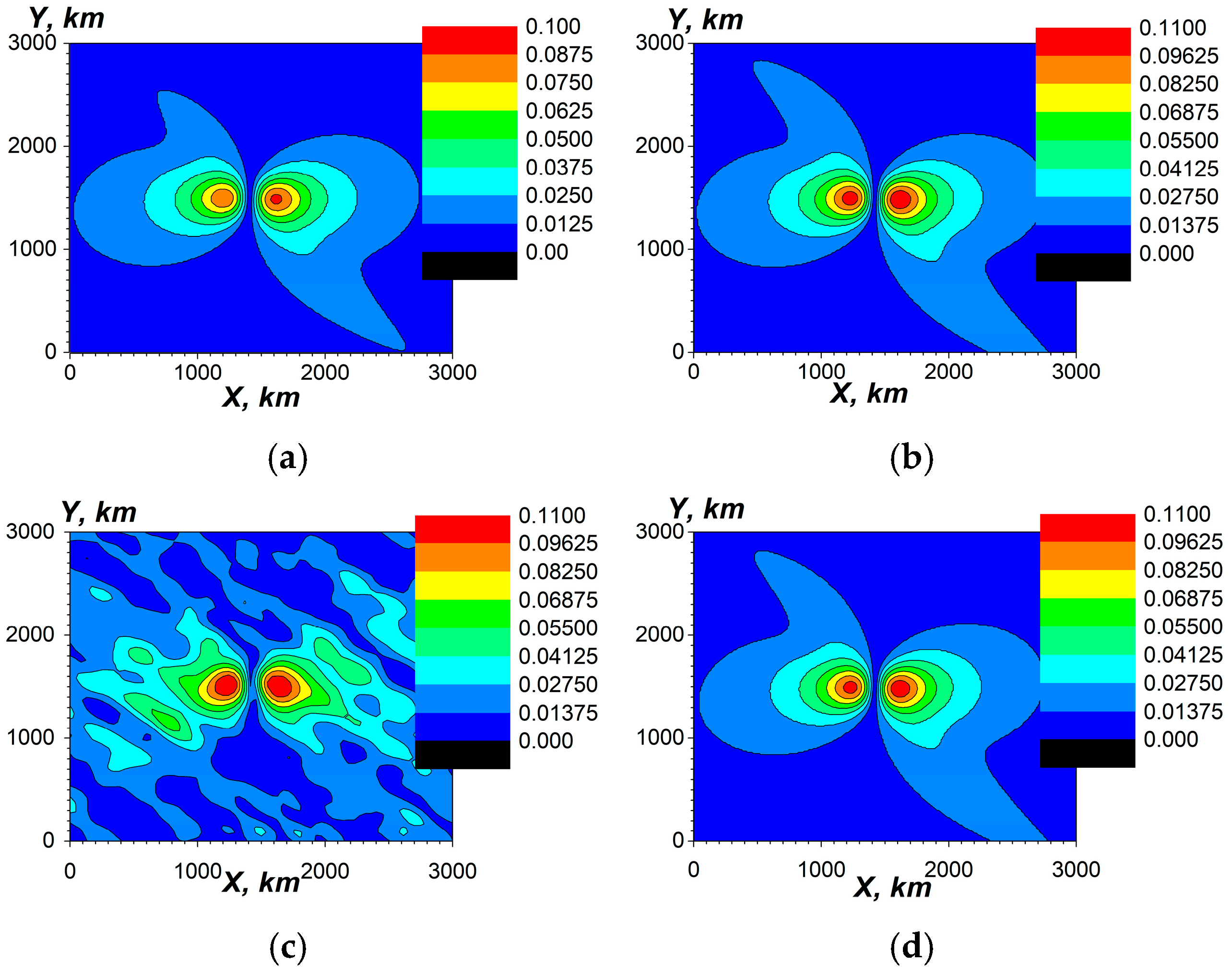
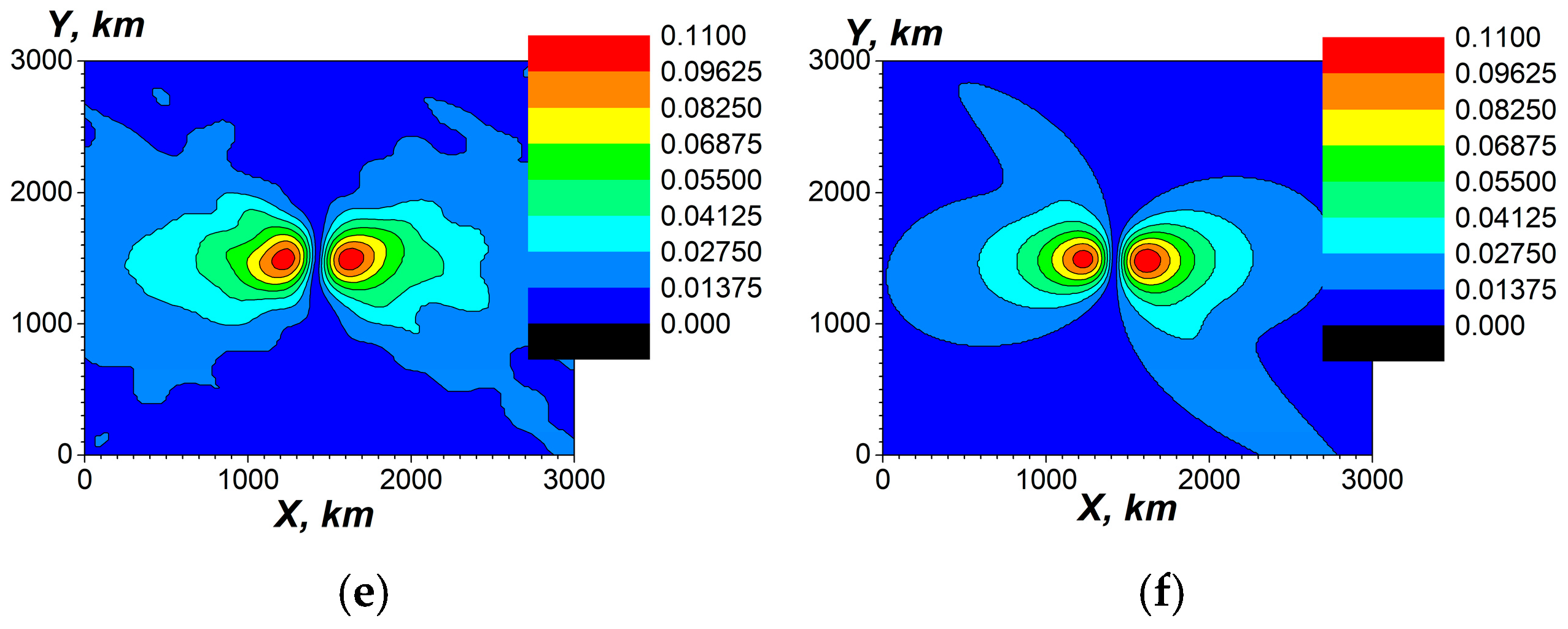
- It is possible to get the correct, within an accuracy of 3%, resonant frequencies of the 1st and 2nd Schumann modes using the simplified local plane model where the periodic boundary conditions of the period equal to Earth’s equator are applied in the horizontal plane. In the spherical geometry with the ideal boundary conditions, the error is 1 order bigger and is ≥20% [47]. For both daytime and nighttime conditions, as well as for the angles between the vertical direction and geomagnetic field lying in the range from 0 to 50°, the values of the resonant frequencies of the 1st mode of SR possess a small difference of about 5%.
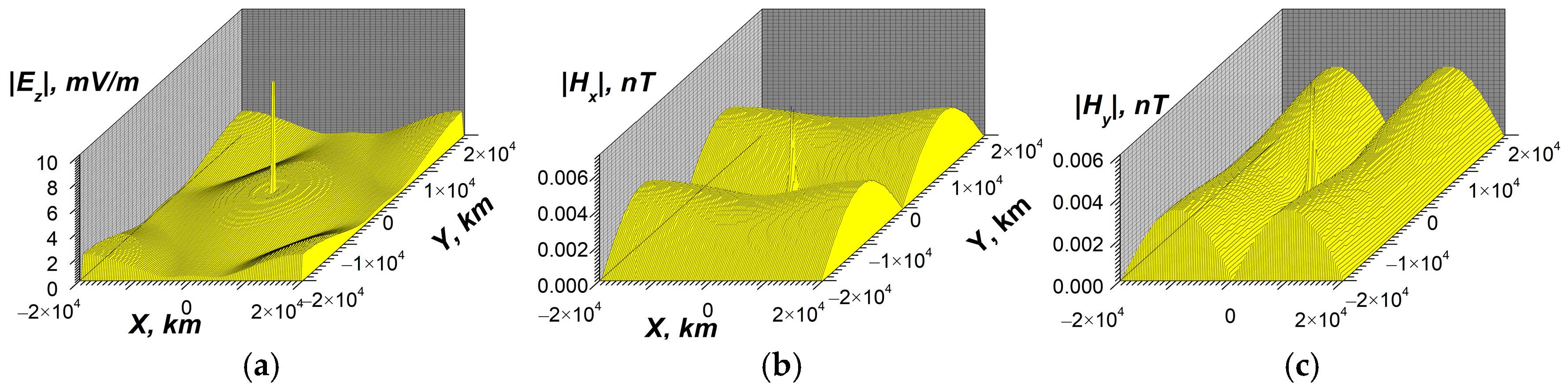
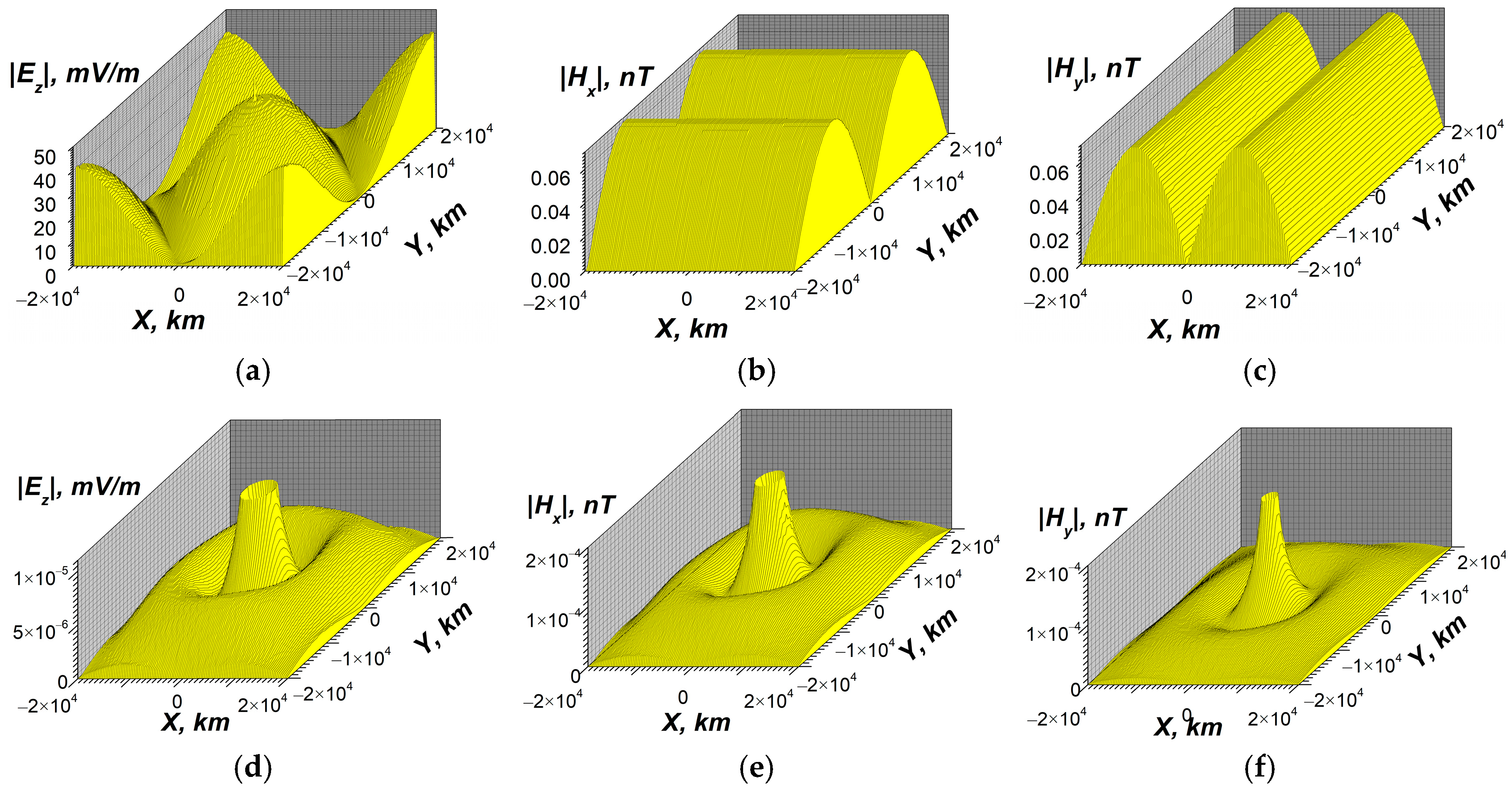
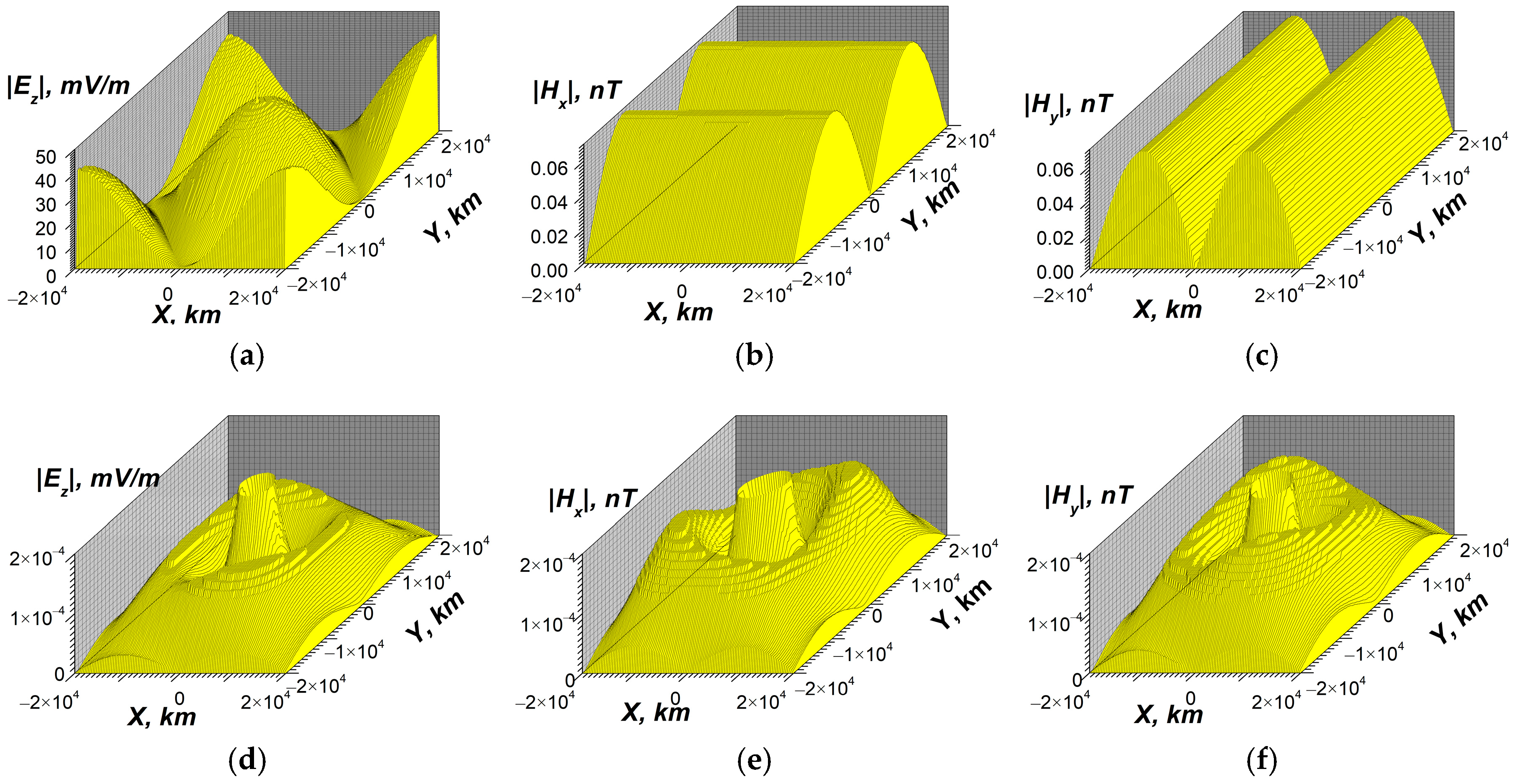
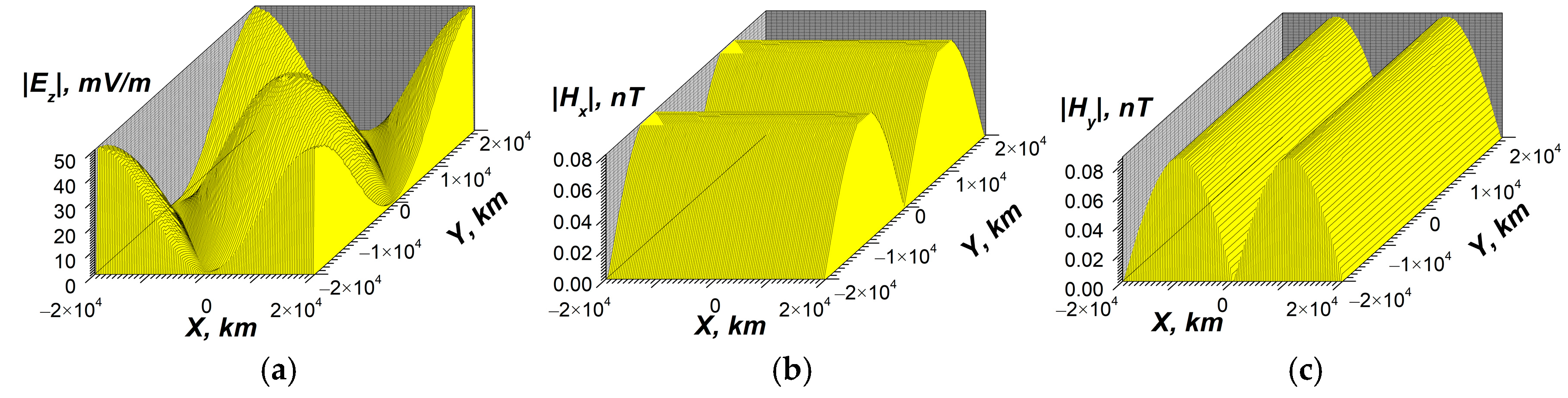
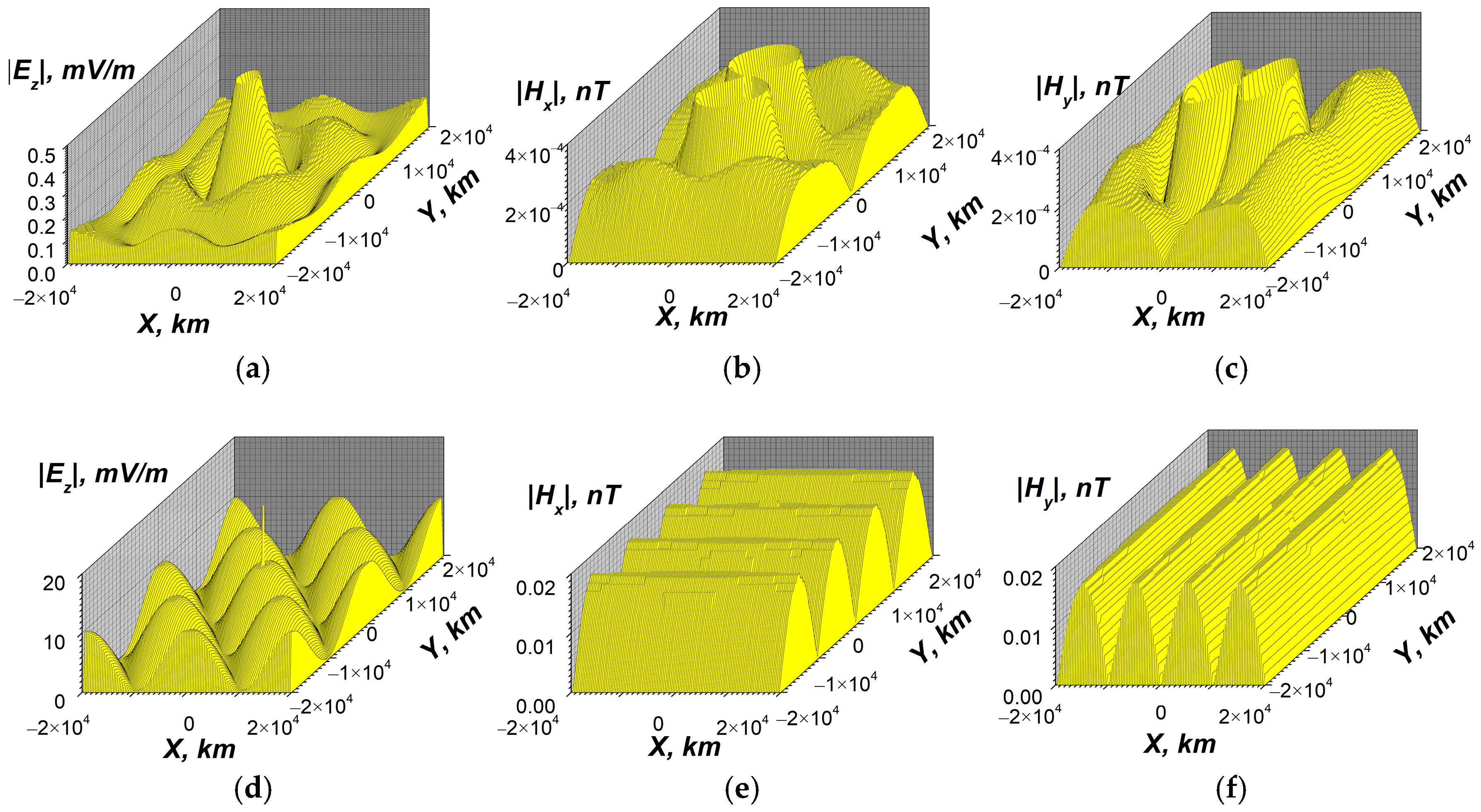
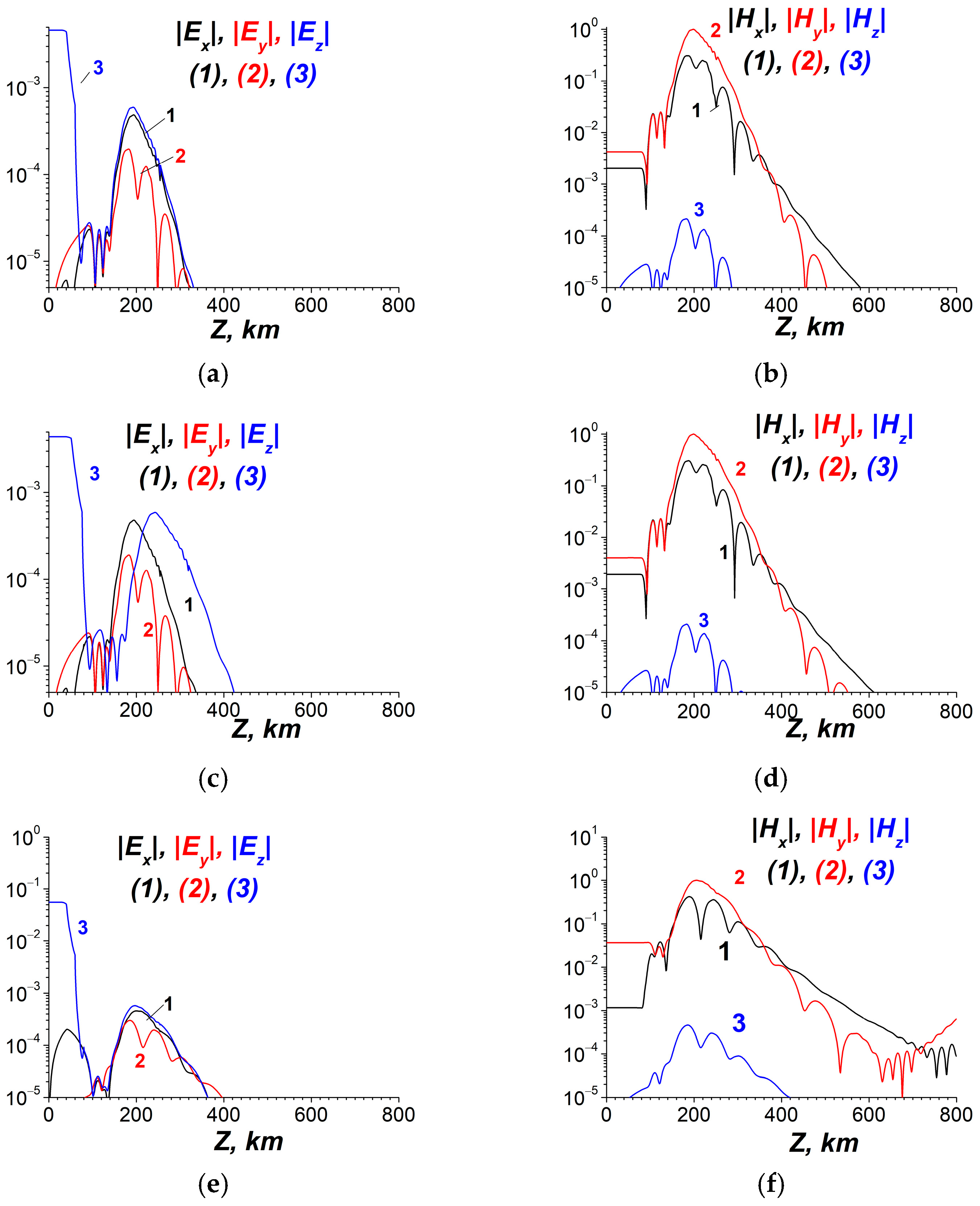
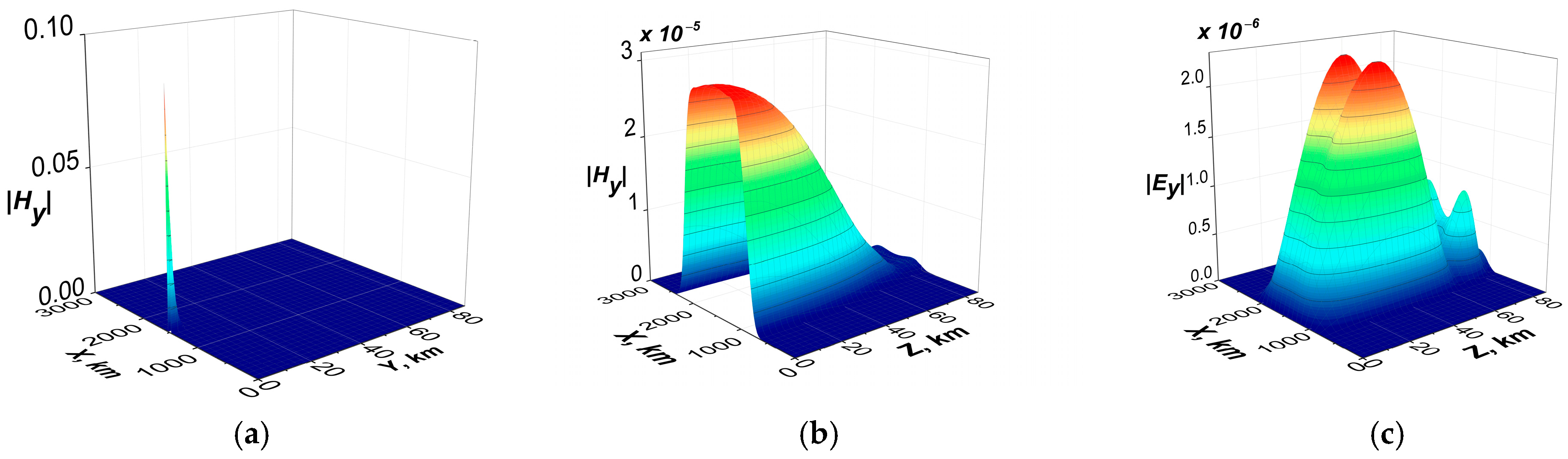
- In the local plane model, it is also possible to estimate the maximum values and the spatial distributions of ELF EM fields of the Schumann resonances caused by the electric current excitation at the resonant frequencies. The resonant horizontal components of the ELF magnetic field at z = 0 reach a value of about 60 pT (Figure 15b,c, Figure 16b,c, and Figure 18b,c). There is an effective excitation of oscillations, particularly the 1st mode of SR, both in daytime and nighttime conditions, as well as highly efficient excitation of SR as a whole close to resonant frequency (see Figure 15, Figure 16 and Figure 18). This indicates qualitatively the possibility of propagation of ELF excitations along Earth’s surface over long distances.
- At the same time, taking into account calculations for for several frequencies, as illustrated in Figure 14a, Figure 15a, Figure 16a, and Figure 18a, the estimations for the quality factor Q of the Schumann resonance at the 1st mode yield a value of it Q ≥ 50, which is one order higher than the measured value. The quality factor has been estimated as the ratio of the maximum amplitudes of Ez component of the electric field at the resonant frequency ω = 47.1 s−1 (f = 7.50 Hz) and at the frequency between the 1st and the 2nd Schumann modes ω = 70.5 s−1 (f = 11.22 Hz). The estimations have also been conducted by means of the spectral width of the excitation of Ez near the resonance. To obtain correct values of the quality factors, it is necessary to account for the dependencies of the ionospheric plasma parameters in the vertical direction on the spherical angles Θ, φ, or on the local horizontal coordinates x, y.
4.2.2. Possible Coupled Oscillations in the Schumann Resonator and Ionospheric Alfvėn Resonator
4.3. Propagation of Electromagnetic Waves in the Waveguide Earth—Ionosphere in VLF Range; Mode and Beam Presentations
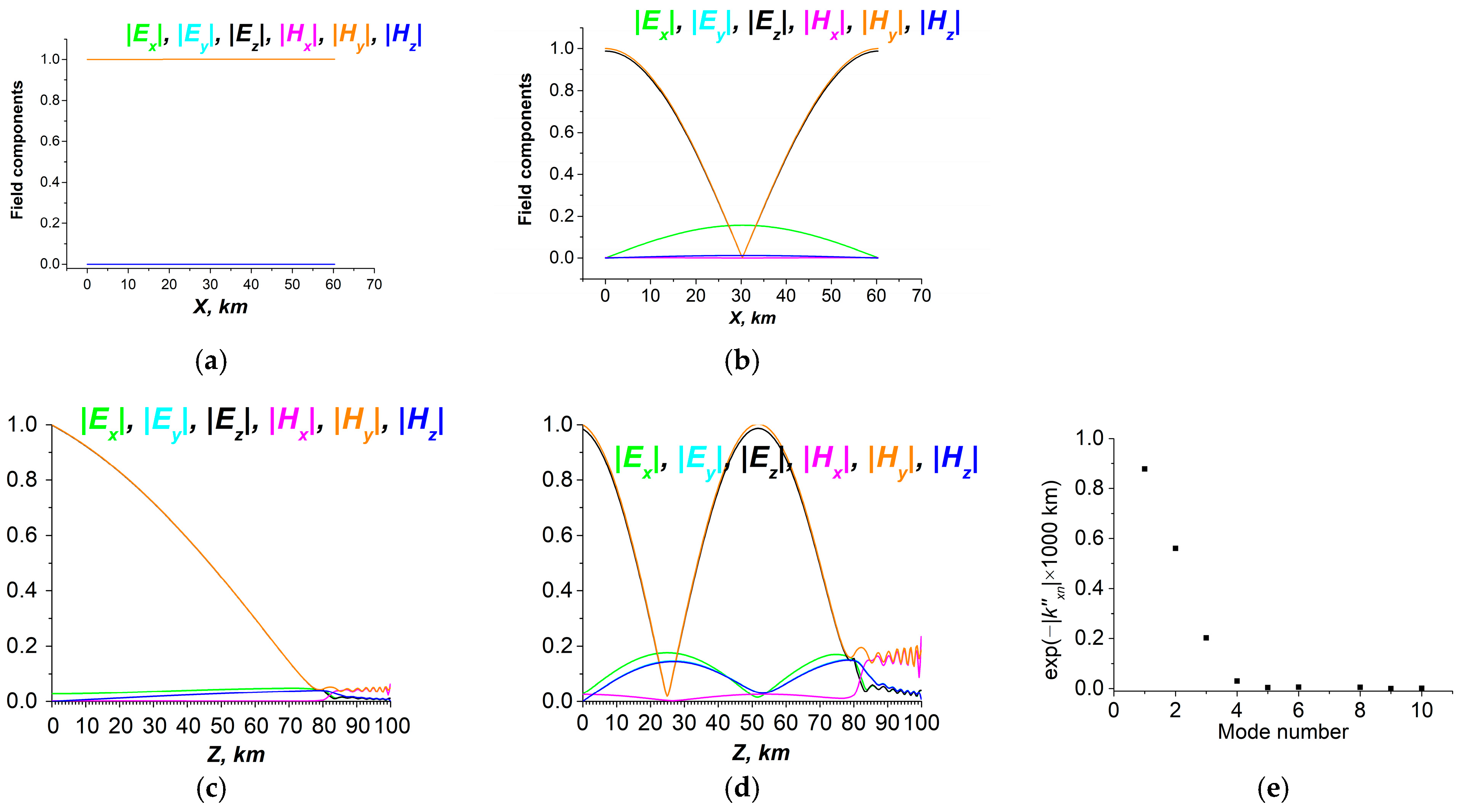
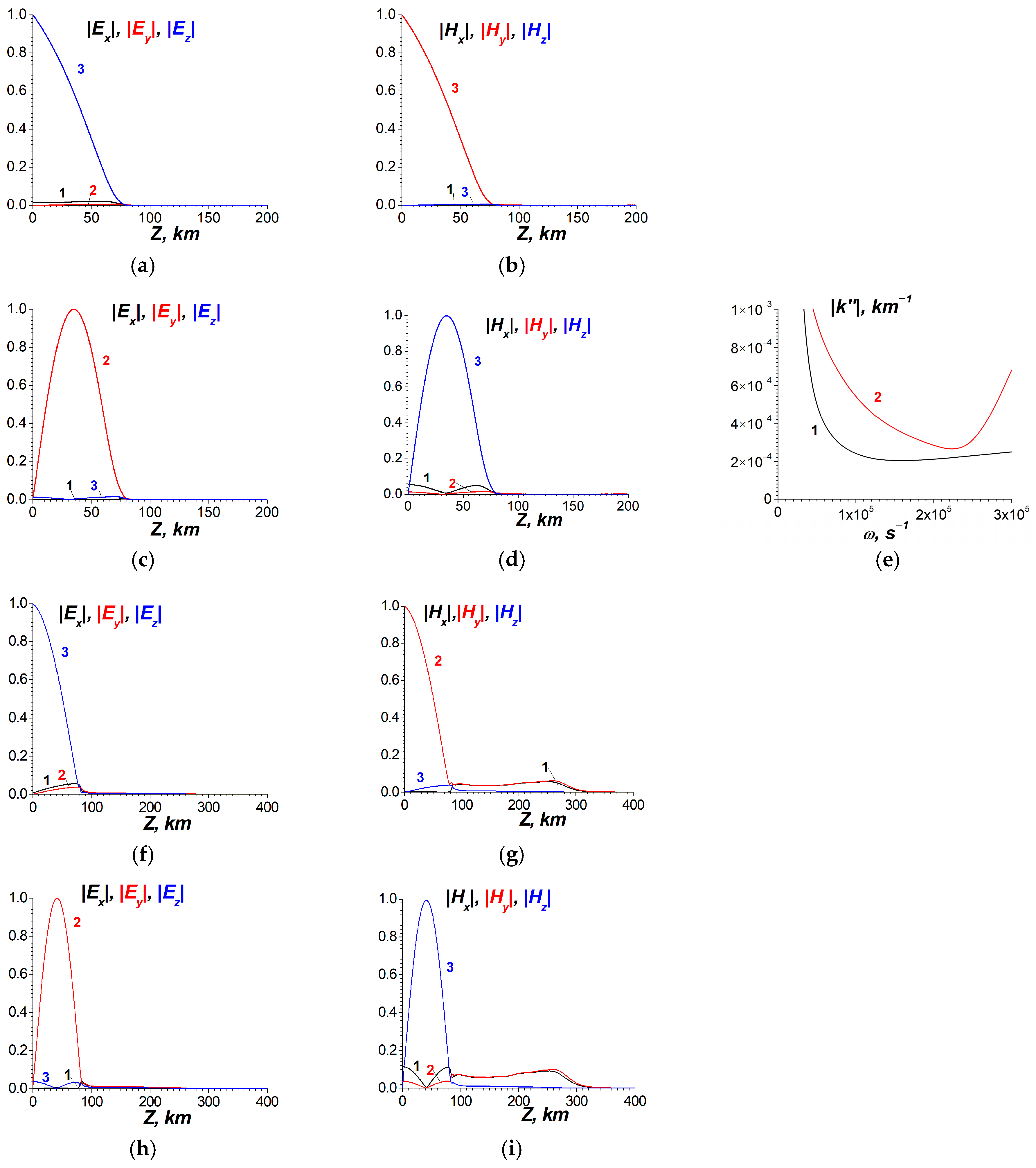
4.3.1. The Mode Excitation in the Waveguide Earth–Ionosphere
4.3.2. Qualitative Picture of the Transformation of VLF Beams Due to the Anisotropy and Gyrotropy in the Waveguide Earth–Ionosphere with Anisotropic Boundary Condition
5. Discussion—Comparison Between Theoretical and Experimental Results
- (1)
- It is reasonable to assume that the lowest frequency part of the ULF range is limited from below by a frequency of about 10−4 Hz. This is due to both the non-stationarity of any real current source, including the ULF part of LCSHTE, as well as the diurnal changes in the parameters of the ionospheric plasma [21].
- (2)
- As shown in [21,38], both quasi-stationary and dynamic approaches to simulating ULF electric fields are adequate in the case of closed geomagnetic field lines. However, for open geomagnetic field lines, the dynamic approach is only applicable in the ionosphere with the radiation condition into the magnetosphere.
- (3)
- It is impossible to ignore the quasi-stationary magnetic field in the lower atmosphere. This clearly follows from the fundamental impossibility of matching electric fields by using two independent components, for example, horizontal components of the electric field in the ionosphere and a single component of the quasi-stationary potential electric field in the atmosphere. This problem has been solved completely, including the necessary numerical calculations of EM fields using the proposed analytical/numerical method. This method restores the quasi-stationary magnetic component, lost in most works on atmospheric electricity and the global electric circuit.
- (1)
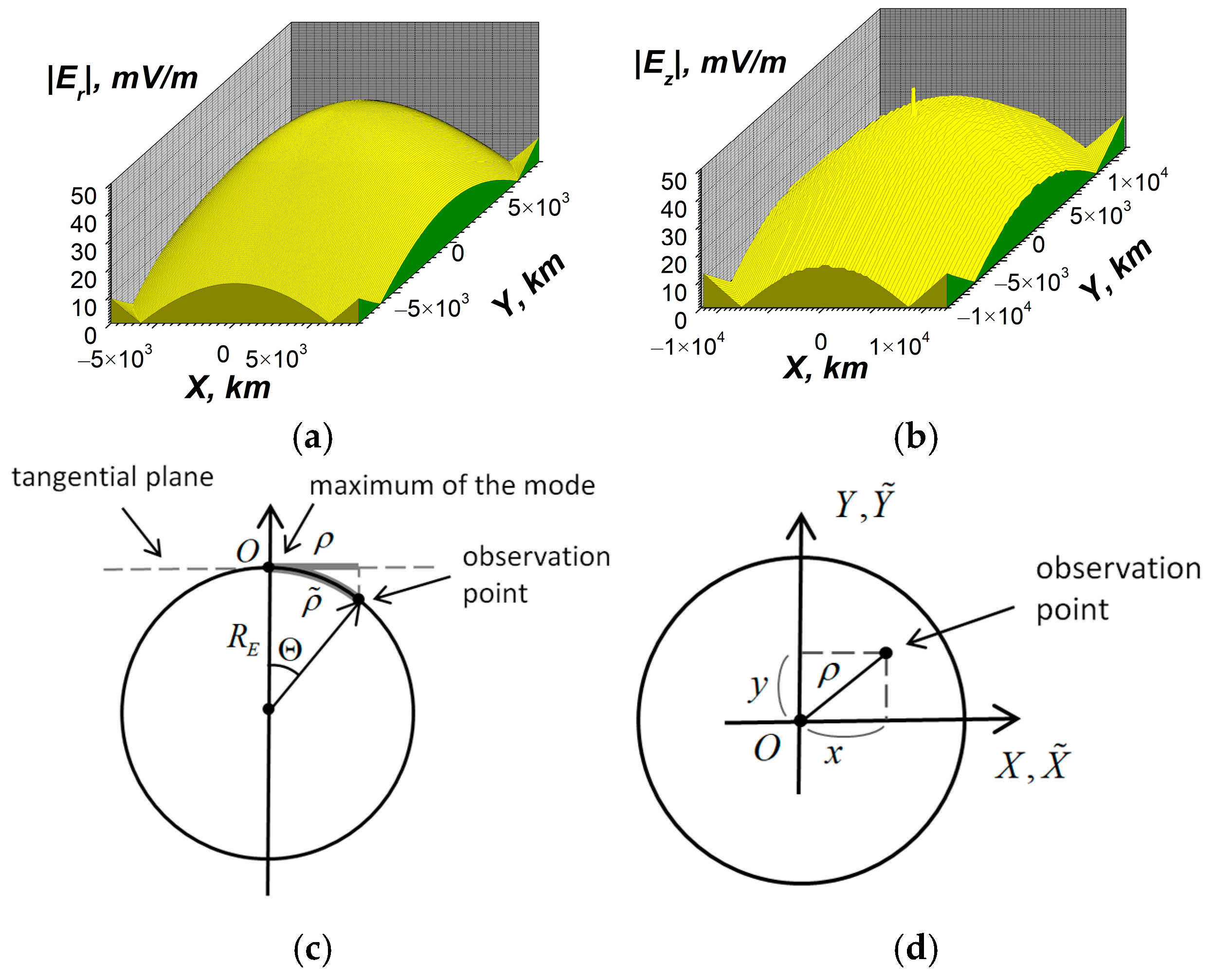
- The model we used does not take into account the curvature of Earth, and the plane Earth model is used jointly with periodic conditions in the horizontal direction, with a period L = 2πRE (Figure 12).
- (2)
- For each specific calculation, the planar resonator approximation has been used, which is homogeneous in the horizontal directions with a constant value of the angle between the geomagnetic field and the vertical axis and other parameters in these directions. Ignoring the inhomogeneities, simultaneous daytime and nighttime conditions in different parts of the real SR may lead to the overestimation of the quality factor. The simulated values of magnetic fields at Earth’s surface during the resonance are twice bigger than the corresponding experimental values. The quality factors obtained on the base of the developed model exceed the corresponding experimental values by one order of magnitude. Finally the qualitative estimations given above (see Section 4.2.1) show that the horizontal inhomogeneity is the most important reason that can reduce the quality factor of SR.
6. Conclusions
- (1)
- The simulations presented in this paper are based on the observational data of lightning electric currents associated with the eruption of the Hunga Tonga volcano in January 2022. Based on a data-driven approach, the characteristics of effective current sources have been obtained in ULF (mHz), ELF (Hz), and VLF (kHz) ranges. The obtained sources have been used to calculate the corresponding EM excitations captured in resonators or having waveguiding characteristics in the atmosphere–ionosphere. The spectra of current sources decrease monotonously in the VLF range but have many significant details, including local oscillations in the ELF range and a local maximum in the ULF range. The current sources in ELF and ULF, and even in VLF ranges, possess practically isotropic directional diagrams in the horizontal plane.
- (2)
- In the ULF range, the dynamic method should be used in the general case to investigate the penetration of EM fields into the ionosphere due to the principle of causality, the non-stationary nature of any geophysical source, and diurnal changes in the environment. The dynamic method is equivalent to the Maxwell equations in the spectral domain. The use of the dynamic method in the atmosphere and the lower ionosphere causes mathematical problems connected with the stiffness of the system of the dynamic differential equations. The combined dynamic–quasi-stationary method has been developed to simulate ULF field penetration through the LEAIM system. This method is suitable for frequencies down to 10−4 Hz (~10−3 s−1), which is a reasonable minimum value of the ULF frequency. The EM field is determined from a dynamic approach in the ionosphere and from a quasi-stationary one in the atmosphere. In the atmosphere, not only the electric field components but also the magnetic ones are taken into account. The combined method includes a proper choice of the altitude where EM fields in the atmosphere and ionosphere are matched, 70–120 km. As a result of the application of the combined method, the pointed above mathematically stiff problem has been solved successfully.
- (3)
- There is a methodological unity of approaches to ULF, ELF, and VLF disturbances generated by lightning currents associated with the eruption of the Hunga Tonga volcano. The investigated fundamental modes are either captured in the corresponding resonators, ELF oscillations or propagate in the WGEI, like VLF waves. The excited ULF fields in LEAIM propagate in the upper ionosphere–magnetosphere and are directed along the geomagnetic field lines. This property determines the upper boundary condition for ULF waves, which satisfies the principle of causality. The proposed method for derivation of the tensor impedance boundary conditions is applicable to ULF, ELF, and VLF ranges. These boundary conditions have differences in their physical meaning for excitation in each of these frequency ranges. Nevertheless, the method for the derivation of the tensor impedance is unified. To solve the differential equations for the EM field in different frequency ranges in the plasma-like system LEAIM, the combined spectral–partial difference method is applied based on the matrix elimination method.The excitation of SR in the ELF range has been realized within the model of the local planar resonator. The applicability of this model has been checked. In the local planar resonator model, 2D periodicity with the spatial period equal to Earth’s equator is assumed. The simulated 1st and 2nd resonant frequencies coincide with the corresponding observed values. The simulated structure of EM fields is close to that obtained using the spherical resonator model in the vicinity of the maximum of the 1st mode of SR. For future work, EM fields near the source may be investigated within the local plane approximation, and the simulations of the global field of the total resonator should take into account Earth’s curvature and, most importantly, the inhomogeneity of the ionospheric characteristics both in the vertical direction and along Earth’s surface.An analytical/numerical method has been developed to find the resonant frequencies of the SR and CSIAR in the ELF range and the longitudinal wave numbers of WGEI in the VLF range. The mode method for VLF waves agrees with the beam method, including the conversion of transverse-magnetic to transverse-electric polarizations at distances of about 500–1000 km. The given parameter is either the real frequency or the longitudinal real wave number in the horizontal direction. The unknown quantity is either the complex longitudinal wave number or the complex frequency, respectively. This method involves the derivation of a complex dispersion equation for low-frequency EM excitations. The dispersion equation is determined based on an analytical/numerical procedure, which utilizes the elimination method with tridiagonal matrices and field matching inside the corresponding Earth–ionosphere waveguide/resonator.
- (4)
- The work presents an integrated approach to the low-frequency part of global excitations in LEAIM generated by LCSHTE. Low-frequency excitations include the ULF, ELF, and VLF frequency ranges. The integrated approach is supported by the following factors: the common current source, the unity of approaches to their description, including analytical and numerical methods, and all the above excitations occur in LEAIM simultaneously and have large values.The amplitudes of the excited ULF fields turn out to be sufficient at least to consider these fields among other possible drivers of highly nonlinear phenomena observed in the ionospheric F region. In the case of ELF and VLF disturbances in the SR, CSIAR, and the WGEI, the lightning source associated with the eruption causes intense disturbances, even at significant distances from the volcano area, of 10,000 km. The intensities of such disturbances exceed from several times to one order of magnitude the intensities corresponding to ordinary lightning activity.The system of simultaneous strong effects in the three low frequency ranges due to the same unprecedented lightning source results in the possibility of combining ULF, ELF, and VLF responses in monitoring ionospheric space weather connected with powerful sources like tropical cyclones/hurricanes, earthquakes, and volcanoes. Practically, corresponding improvement in the quality of monitoring of ionospheric space weather is important, in particular, for communication systems, the reliability of power lines and human health. The simultaneous presence of the corresponding, rather strong, ionospheric response in the abovementioned frequency ranges will be investigated as a nonlinear interaction between the corresponding disturbances in LEAIM. This may indicate the presence of sufficiently powerful sources and should be involved in the analysis using multi-parameter monitoring systems. A possible nonlinear synergetic interaction between the excitations in the three considered frequency ranges may be a subject of future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| AGW | acoustic-gravity waves |
| CSIAR | coupled global Schumann and local ionospheric Alfvén resonators |
| EM | electromagnetic |
| IAR | ionospheric Alfvén resonator |
| ELF | extremely low frequency |
| FFT | fast Fourier transform |
| LCSHTE | lightning current source associated with the Hunga Tonga eruption |
| LOFAR | Low-Frequency Array (radio telescope) |
| MHD | magnetohydrodynamic |
| LEAIM | Lithosphere (Earth)–Atmosphere–Ionosphere–Magnetosphere |
| SR | Schumann resonator |
| TIDs | traveling ionospheric disturbances |
| ULF | ultra-low frequency |
| VLF | very low frequency |
| WGEI | waveguide Earth–ionosphere |
Appendix A. The Matrix Elimination Method for the Dynamic Problem in the Ionosphere
Appendix B. The Analytical/Numerical Method for the Derivation of Dispersion Equation for the Eigenvalues of Waves in Inhomogeneous Lossy Anisotropic and Gyrotropic Media: Application for Simulating ELF and VLF Modes. Method for Derivation of the Complex Tensor Impedance for ELF and VLF Ranges
Appendix C. Numerical Solution of Dispersion Equation: Application for the ELF and VLF Perturbations
References
- Kamide, Y.; Chian, A. (Eds.) Handbook of the Solar-Terrestrial Environment; Springer: Berlin/Heidelberg, Germany, 2007; 539p. [Google Scholar] [CrossRef]
- Hapgood, M. Space Weather; IOP Publishing Ltd.: Bristol, UK, 2017; 33p. [Google Scholar] [CrossRef]
- Chernogor, L.F. A Tropical Cyclone or Typhoon as an Element of the Earth–Atmosphere–Ionosphere–Magnetosphere System: Theory, Simulations, and Observations. Remote Sens. 2023, 15, 4919. [Google Scholar] [CrossRef]
- Chernogor, L.F.; Rozumenko, V.T. Earth—Atmosphere—Geospace as an Open Nonlinear Dynamical System. Radio Phys. Radio Astron. 2008, 13, 120–137. [Google Scholar]
- Harding, B.J.; Wu, Y.J.; Alken, P.; Yamazaki, Y.; Triplett, C.C.; Immel, T.J.; Gasque, L.C.; Mende, S.B.; Xiong, C. Impacts of the January 2022 Tonga volcanic eruption on the ionospheric dynamo: ICON-MIGHTI and Swarm observations of extreme neutral winds and currents. Geophys. Res. Lett. 2022, 49, e2022GL098577. [Google Scholar] [CrossRef]
- Bór, J.; Bozóki, T.; Sátori, G.; Williams, E.; Behnke, S.A.; Rycroft, M.J.; Buzás, A.; Silva, H.G.; Kubicki, M.; Said, R.; et al. Responses of the AC/DC global electric circuit to volcanic electrical activity in the Hunga Tonga-Hunga Ha’apai eruption on 15 January 2022. J. Geophys. Res. Atmos. 2023, 128, e2022JD038238. [Google Scholar] [CrossRef]
- Van Eaton, A.R.; Lapierre, J.; Behnke, S.A.; Vagasky, C.; Schultz, C.J.; Pavolonis, M.; Bedka, K.; Khlopenkov, K. Lightning rings and gravity waves: Insights into the giant eruption plume from Tonga’s Hunga Volcano on 15 January 2022. Geophys. Res. Lett. 2023, 50, e2022GL102341. [Google Scholar] [CrossRef]
- Shinbori, A.; Otsuka, Y.; Sori, T.; Nishioka, M.; Septi, P.; Tsuda, T.; Nishitani, N.; Kumamoto, A.; Tsuchiya, F.; Matsuda, S.; et al. New aspects of the upper atmospheric disturbances caused by the explosive eruption of the 2022 Hunga Tonga–Hunga Ha’apai volcano. Earth Planets Space 2023, 75, 175. [Google Scholar] [CrossRef]
- Chum, J.; Sindelarova, T.; Koucka, P.K.; Podolska, K.; Rusz, J.; Base, J.; Nakata, H.; Hosokawa, K.; Danielides, M.; Schmidt, C.; et al. Atmospheric and ionospheric waves induced by the Hunga eruption on 15 January 2022: Doppler sounding and infrasound. Geophys. J. Int. 2023, 233, 1429–1443. [Google Scholar] [CrossRef]
- Rakov, V.A.; Uman, M.A. Lightning: Physics and Effects; Cambridge University Press: Cambridge, UK, 2003; ISBN 978-0521035415. [Google Scholar]
- Chandrasekhar, N.P.; Archana, R.; Arora, K. Lightning and gravity wave signatures produced by the Hunga-Tonga volcanic eruption on global geomagnetic data. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031767. [Google Scholar] [CrossRef]
- Koloskov, O.; Jayachandran, P.T.; Yampolski, Y. On the performance of CARISMA—Akademik Vernadsky station Schumann resonance monitoring. Ukr. Antarct. J. 2023, 21, 37–54. [Google Scholar] [CrossRef]
- Mezentsev, A.; Nickolaenko, A.P.; Shvets, A.V.; Galuk, Y.P.; Schekotov, A.Y.; Hayakawa, M.; Romero, R.; Izutsu, J.; Kudintseva, I.G. Observational and model impact of Tonga volcano eruption on Schumann resonance. J. Geophys. Res. Atmos. 2023, 128, e2022JD037841. [Google Scholar] [CrossRef]
- Gavrilov, B.G.; Poklad, Y.V.; Ryakhovsky, I.A.; Ermak, V.M.; Achkasov, N.S.; Kozakova, E.N. Global electromagnetic disturbances caused by the eruption of the Tonga volcano on 15 January 2022. J. Geophys. Res. Atmos. 2022, 127, e2022JD037411. [Google Scholar] [CrossRef]
- Shvets, A.V.; Hobara, Y.; Hayakawa, M.; Shvets, A.A.; Koloskov, O.V.; Yampolsky, Y.M. Estimation of Lightning Strokes Count from Measurements of VLF Atmospherics During the Eruption of Hunga Tonga-Hunga Ha’apai Volcano on 15 January 2022. In Proceedings of the URSI GASS 2023, Sapporo, Japan, 19–26 August 2023. [Google Scholar] [CrossRef]
- Holzworth, R.H. Quasistatic Electromagnetic Phenomena in the Atmosphere and Ionosphere. In Handbook of Atmospheric Electrodynamics; Volland, H, Ed.; CRC Press: Boca Raton, FL, USA, 1995; pp. 235–266. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Chmyrev, V.M.; Hayakawa, M. A Review on Electrodynamic Influence of Atmospheric Processes to the Ionosphere. Open J. Earthq. Res. 2020, 9, 113–141. [Google Scholar] [CrossRef]
- Denisenko, V.V.; Nesterov, S.A.; Boudjada, M.Y.; Lammer, H. A mathematical model of quasistationary electric field penetration from ground to the ionosphere with inclined magnetic field. J. Atmos. Sol. Terr. Phys. 2018, 179, 527–537. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Izutsu, J.; Nickolaenko, A.P.; Hobara, Y. Seismogenic ULF/ELF Wave Phenomena: Recent Advances and Future Perspectives. Open J. Earthq. Res. 2023, 12, 45–113. [Google Scholar] [CrossRef]
- Kalinin, A.V.; Slyunyaev, N.N.; Mareev, E.A.; Zhidkov, A.A. Stationary and Nonstationary Models of the Global Electric Circuit: Well-Posedness, Analytical Relations, and Numerical Implementation. Izv. Atmos. Ocean. Phys. 2014, 50, 314–322. [Google Scholar] [CrossRef]
- Yutsis, V.; Rapoport, Y.; Grimalsky, V.; Grytsai, A.; Ivchenko, V.; Petrishchevskii, S.; Fedorenko, A.; Krivodubskij, V. ULF Activity in the Earth Environment: Penetration of Electric Field from the Near-Ground Source to the Ionosphere under Different Configurations of the Geomagnetic Field. Atmosphere 2021, 12, 801. [Google Scholar] [CrossRef]
- Rapoport, Y.; Reshetnyk, V.; Grytsai, A.; Grimalsky, V.; Liashchuk, O.; Fedorenko, A.; Hayakawa, M.; Krankowski, A.; Błaszkiewicz, L.; Flisek, P. Spectral Analysis and Information Entropy Approaches to Data of VLF Disturbances in the Waveguide Earth-Ionosphere. Sensors 2022, 22, 8191. [Google Scholar] [CrossRef]
- Khazanov, G.V. (Ed.) Space Weather Fundamentals; CFS Press: Keswick, UK, 2016; ISBN 978-1498749077. [Google Scholar]
- Cander, L.R. Ionospheric Space Weather; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Shi, X.; Hartinger, M.D.; Baker, J.B.H.; Murphy, B.S.; Bedrosian, P.A.; Kelbert, A.; Rigler, E.J. Characteristics and sources of intense geoelectric fields in the United States: Comparative analysis of multiple geomagnetic storms. Space Weather 2022, 20, e2021SW002967. [Google Scholar] [CrossRef]
- Zheng, Y.; Chernogor, L.F.; Garmash, K.P.; Guo, Q.; Rozumenko, V.T.; Luo, Y. Disturbances in the ionosphere and distortion of radio wave characteristics that accompanied the super typhoon Lekima event of 4–12 August 2019. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030553. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Hattori, K.; Taylor, P. Pre-Earthquake Processes. A Multidisciplinary Approach to Earthquake Prediction Studies; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.Y.; Lin, K.; Zhou, C.; Xu, R.; Qing, H.; Gao, Y.; Chen, T.; Wang, F.; Yu, H.; et al. New Instrumental Array in Sichuan, China, to Monitor Vibrations and Perturbations of the Lithosphere, Atmosphere, and Ionosphere. Surv. Geophys. 2021, 42, 1425–1442. [Google Scholar] [CrossRef]
- Kolmašová, I.; Santolík, O.; Kašpar, P.; Popek, M.; Pizzuti, A.; Spurný, P.; Borovička, J.; Mlynarczyk, J.; Manninen, J.; Macotela, E.L.; et al. First observations of elves and their causative very strong lightning discharges in an unusual small-scale continental spring-time thunderstorm. J. Geophys. Res. Atmos. 2021, 126, e2020JD032825. [Google Scholar] [CrossRef]
- Chernogor, L.F.; Garmash, K.P.; Guo, Q.; Rozumenko, V.T.; Zheng, Y. Effects of the super-powerful tropospheric western Pacific phenomenon of September–October 2018 on the ionosphere over China: Results from oblique sounding. Ann. Geophys. 2023, 41, 173–195. [Google Scholar] [CrossRef]
- Rycroft, M.J.; Harrison, R.G.; Nicoll, K.A.; Mareev, E.A. An Overview of Earth’s Global Electric Circuit and Atmospheric Conductivity. Space Sci. Rev. 2008, 137, 83–105. [Google Scholar] [CrossRef]
- Williams, E.; Mareev, E. Recent Progress on the Global Electrical Circuit. Atmos. Res. 2014, 135, 208–227. [Google Scholar] [CrossRef]
- Jánsky, J.; Pasko, V.P. Charge balance and ionospheric potential dynamics in time-dependent global electric circuit model. J. Geophys. Res. Space Phys. 2014, 119, 203. [Google Scholar] [CrossRef]
- Debnath, M. Electromagnetic terrestrial environment and the contribution of the main emission sources. Brainwave Multidiscip. J. 2022, 3, 238–252. [Google Scholar]
- Dementyeva, S.O.; Mareev, E.A. On the Contribution of Turbulence to the Electrification of Thundercloud. Izv. Atmos. Ocean. Phys. 2018, 54, 25–31. [Google Scholar] [CrossRef]
- Morozov, V.N. The influence of convective current generator on the global current. Nonlinear Process. Geophys. 2006, 13, 243–246. Available online: https://npg.copernicus.org/articles/13/243/2006/ (accessed on 1 January 2025). [CrossRef]
- Alexandrov, A.F.; Bogdankevich, L.S.; Rukhadze, A.A. Fundamentals of Plasma Electrodynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Rapoport, Y.; Grimalsky, V.; Krankowski, A.; Pulinets, S.; Fedorenko, A.; Petrishchevskii, S. Algorithm for modeling electromagnetic channel of seismo-ionospheric coupling (SIC) and the variations in the electron concentration. Acta Geophys. 2020, 68, 253–278. [Google Scholar] [CrossRef]
- Knudsen, D.J. Alfvén Waves and Static Fields in Magnetosphere/Ionosphere Coupling: In-situ Measurements and a Numerical Model. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1990; 195p. Available online: https://apps.dtic.mil/sti/tr/pdf/ADA356871.pdf (accessed on 1 January 2025).
- Molchanov, O.A.; Hayakawa, M.; Rafalsky, V.A. Penetration characteristics of electromagnetic emissions from an underground seismic source into the atmosphere, ionosphere and magnetosphere. J. Geophys. Res. 1995, 100, 1691–1712. [Google Scholar] [CrossRef]
- Grimalsky, V.V.; Kremenetsky, I.A.; Rapoport, Y.G. Excitation of electromagnetic waves in the Lithosphere and their penetration into ionosphere and magnetosphere. J. Atmos. Electr. 1999, 19, 101–117. [Google Scholar]
- Anagnostopoulos, G. On the Origin of ULF Magnetic Waves Before the Taiwan Chi-Chi 1999 Earthquake. Front. Earth Sci. 2021, 9, 730162. [Google Scholar] [CrossRef]
- Rapoport, Y.; Grimalsky, V.; Hayakawa, M.; Ivchenko, V.; Juarez-R, D. Change of ionospheric plasma parameters under the influence of electric field which has lithospheric origin and due to radon emanation. Phys. Chem. Earth Parts A/B/C 2004, 29, 579–587. [Google Scholar] [CrossRef]
- Rapoport, Y.G.; Gotynyan, O.E.; Ivchenko, V.N.; Hayakawa, M.; Grimalsky, V.V.; Koshevaya, S.V.; Juarez-R, D. Modeling electrostatic-photochemistry seismoionospheric coupling in the presence of external currents. Phys. Chem. Earth Parts A/B/C 2006, 31, 437–446. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Shinbori, A.; Otsuka, Y.; Sori, T.; Nishioka, M.; Perwitasari, S.; Tsuda, T.; Nishitani, N. Electromagnetic conjugacy of ionospheric disturbances after the 2022 Hunga Tonga-Hunga Ha’apai volcanic eruption as seen in GNSS-TEC and SuperDARN Hokkaido pair of radars observations. Earth Planets Space 2022, 74, 106. [Google Scholar] [CrossRef]
- Bliokh, P.V.; Nikolaenko, A.P.; Filippov, Y.F. Schumann Resonances in the Earth-Ionosphere Cavity; IEEE Publishing: London, UK, 1980; p. 164. [Google Scholar]
- Marchenko, V.; Kulak, A.; Mlynarczyk, J. Finite-difference time-domain analysis of ELF radio wave propagation in the spherical Earth–ionosphere waveguide and its validation based on analytical solutions. Ann. Geophys. 2022, 40, 395–406. [Google Scholar] [CrossRef]
- Hayakawa, M.; Izutsu, J.; Schekotov, A.Y.; Nickolaenko, A.P.; Galuko, Y.P.; Kudintseva, I.G. Anomalies of Schumann resonances as observed near Nagoya associated with two huge (M~7) Tohoku offshore earthquakes in 2021. J. Atmos. Sol.–Terr. Phys. 2021, 225, 105761. [Google Scholar] [CrossRef]
- Constable, C.; Constable, S. A grand spectrum of the geomagnetic field. Phys. Earth Planet. Inter. 2023, 344, 107090. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Li, Z.; Zhao, Z.; Zeren, Z.; Shen, X.; Wang, Q. Recent Advances and Challenges in Schumann Resonance Observations and Research. Remote Sens. 2023, 15, 3557. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Pokhotelov, O.A. Geoelectromagnetic Waves; Taylor & Francis: Abingdon, UK, 1996; ISBN 978-0750300520. [Google Scholar]
- Grimalsky, V.; Koshevaya, S.; Kotsarenko, A.; Chavez, M.A.C. Simulation of Modes of Ionosphere Alfvén Resonator with High Quality Factors in the Case of Oblique Geomagnetic Field. J. Electromagn. Anal. Appl. 2012, 4, 192–198. [Google Scholar] [CrossRef][Green Version]
- Dudkin, D.; Pilipenko, V.; Korepanov, V.; Klimov, S.; Holzworth, R. Electric field signatures of the IAR and Schumann resonance in the upper ionosphere detected by Chibis-M microsatellite. J. Atmos. Sol. Terr. Phys. 2014, 117, 81–87. [Google Scholar] [CrossRef]
- Ermakova, E.N.; Ryabov, A.V. Influence of ionospheric resonators on daily dynamics of the first Schumann resonance spectral parameters according to data from a meridional chain of ULF magnetometers. Sol.-Terr. Phys. 2024, 10, 62–73. [Google Scholar] [CrossRef]
- Rapoport, Y.; Grimalsky, V.; Fedun, V.; Agapitov, O.; Bonnell, J.; Grytsai, A.; Milinevsky, G.; Liashchuk, A.; Rozhnoi, A.; Solovieva, M.; et al. Model of the propagation of very low-frequency beams in the Earth–ionosphere waveguide: Principles of the tensor impedance method in multi-layered gyrotropic waveguides. Ann. Geophys. 2020, 38, 207–230. [Google Scholar] [CrossRef]
- Shvets, A.; Hobara, Y.; Hayakawa, M.; Shvets, A.; Koloskov, O.; Yampolsky, Y. Investigation of anomalous lightning activity during the January 15, 2022 Tonga volcano eruption based on measurements of the VLF and ELF electromagnetic fields. J. Atmos. Sol. Terr. Phys. 2024, 264, 106344. [Google Scholar] [CrossRef]
- Kuzichev, I.V.; Vasko, I.Y.; Malykhin, A.Y.; Soto-Chavez, A.R. On the ionospheric propagation of VLF waves generated by currents in the lower ionosphere. J. Atmos. Sol.-Terr. Phys. 2018, 179, 138–148. [Google Scholar] [CrossRef]
- Maurya, A.K.; Tripathi, G.; Singh, S.B.; Singh, R.; Singh, A.K. Chapter 16—Low-latitude upper atmosphere remote sensing using very low frequency (VLF) waves. In Earth Observation, Atmospheric Remote Sensing; Singh, A.K., Tiwari, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 283–306. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Zank, G.P.; Sterken, V.J.; Shibata, K.; Nagai, T.; Mannucci, A.J.; Malaspina, D.M.; Lakhina, G.S.; Kanekal, S.G.; Hosokawa, K.; et al. Space Plasma Physics: A Review. IEEE Trans. Plasma Sci. 2023, 51, 1595–1655. [Google Scholar] [CrossRef]
- Muafiry, I.N.; Meilano, I.; Heki, K.; Wijaya, D.D.; Nugraha, K.A. Ionospheric Disturbances after the 2022 Hunga Tonga-Hunga Ha’apai Eruption above Indonesia from GNSS-TEC Observations. Atmosphere 2022, 13, 1615. [Google Scholar] [CrossRef]
- Chernogor, L.F. Physical effects from the powerful Tonga volcanic eruption of January 15, 2022, in the earth–atmosphere–ionosphere–magnetosphere system. J. Atmos. Sol. -Terr. Phys. 2023, 253, 106157. [Google Scholar] [CrossRef]
- Somu, V.B.; Rakov, V.A.; Haddad, M.A.; Cumm, S.A. A study of changes in apparent ionospheric reflection height within individual lightning flashes. J. Atmosph. Sol. Terr. Phys. 2015, 136, 66–79. [Google Scholar] [CrossRef]
- Dorrian, G.; Fallows, R.; Wood, A.; Themens, D.R.; Boyde, B.; Krankowski, A.; Bisi, M.; Dąbrowski, B.; Vocks, C. LOFAR observations of substructure within a traveling ionospheric disturbance at mid-latitude. Space Weather 2023, 21, e2022SW003198. [Google Scholar] [CrossRef]
- Boyde, B.; Wood, A.; Dorrian, G.; Fallows, R.A.; Themens, D.; Mielich, J.; Elvidge, S.; Mevius, M.; Zucca, P.; Dabrowski, B.J. Lensing from small-scale travelling ionospheric disturbances observed using LOFAR. J. Space Weather Space Clim. 2022, 12, 34. [Google Scholar] [CrossRef]
- Pradipta, R.; Lai, P.-C. Observations of Ionospheric Disturbances Associated with the 4 August 2020 Port Beirut Explosion by DMSP and Ionosondes. ANGEO 2024, 42, 301–312. [Google Scholar] [CrossRef]
- Haken, H. Information and Self-Organization: A Macroscopic Approach to Complex Systems, 3rd ed.; Springer Nature: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Pulinets, S. The synergy of earthquake precursors. Earthq. Sci. 2011, 24, 535–548. [Google Scholar] [CrossRef]
- Wu, L.; Qi, Y.; Mao, W.; Lu, J.; Ding, Y.; Peng, B.; Xie, B. Scrutinizing and rooting the multiple anomalies of Nepal earthquake sequence in 2015 with the deviation–time–space criterion and homologous lithosphere–coversphere–atmosphere–ionosphere coupling physics. Nat. Hazards Earth Syst. Sci. 2023, 23, 231–249. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Eftaxias, K.; Schekotov, A.; Yamaguchi, H.; Hayakawa, M. Criticality features in ultra-low frequency magnetic fields prior to the 2013 M6.3 Kobe earthquake. Ann. Geophys. 2016, 59, S0317. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Davidenko, D.; Rozhnoi, A.; Solovieva, M.; Fedun, V.; Dwivedi, B.N.; Rybin, A.; Kafatos, M.; Taylor, P. Transient Effects in Atmosphere and Ionosphere Preceding the 2015 M7.8 and M7.3 Gorkha–Nepal Earthquakes. Front. Earth Sci. 2021, 9, 757358. [Google Scholar] [CrossRef]
- De Santis, A.; Perrone, L.; Calcara, M.; Campuzano, S.A.; Cianchini, G.; D’Arcangelo, S.; Di Mauro, D.; Marchetti, D.; Nardi, A.; Orlando, M.; et al. A comprehensive multiparametric and multilayer approach to study the preparation phase of large earthquakes from ground to space: The case study of the June 15 2019, M7.2 Kermadec Islands (New Zealand) earthquake. Remote Sens. Environ. 2022, 283, 113325. [Google Scholar] [CrossRef]
- Marchuk, G.I. Splitting and Alternating Direction Methods. In Handbook of Numerical Analysis, Vol. I. Finite Difference Methods (Part I)-Solution of Equations in R” (Part 1); Ciarlet, P.G., Lions, J.L., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 203–462. [Google Scholar]
- Samarskii, A.A. The Theory of Difference Schemes; Marcel Dekker, Inc: New York, NY, USA, 2001; 761p, ISBN 0-8247-0468-1. [Google Scholar]
- MacGorman, D.R.; Rust, W.D.; Williams, E.R. The Electrical Nature of Storms; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Harrison, R.G.; Carslaw, K.S. Ion-aerosol-cloud processes in the lower atmosphere. Rev. Geophys. 2003, 41, 5536. [Google Scholar] [CrossRef]
- Van Eaton, A.; Behnke, S.; Lapierre, J.; Vagasky, C.; Schultz, C.; Pavolonis, M.; Bedka, K.; Khlopenkov, K. Lightning and volcanic plume data from the climactic eruption of Hunga Volcano, Tonga, in January 2022. Zenodo 2023, 50, e2022GL102341. [Google Scholar] [CrossRef]
- Al’pert, Y.L. Propagation of Electromagnetic Waves and the Ionosphere; Nauka: Moscow, Russia, 1972. (In Russian) [Google Scholar]
- Alperovich, L.S.; Fedorov, E.N. Hydromagnetic Waves in the Magnetosphere and the Ionosphere; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Jursa, A.S. (Ed.) Handbook of Geophysics and the Space Environment; Air Force Geophysics Lab.: Hanscom AFB, MA, USA, 1985. [Google Scholar]
- Kelley, M.C. The Earth’s Ionosphere Plasma Physics and Electrodynamics; Academic Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Shokri, B.; Rukhadze, A.A. Electrodynamics of Conducting Dispersive Media; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Collin, R.E. Field Theory of Guided Waves; Wiley-IEEE Press: Hoboken, NJ, USA, 1991; ISBN 978-0879422370. [Google Scholar]
- Vainstein, L.A. Electromagnetic Waves; Moscow Izdatel Radio i Sviaz: Moscow, Russia, 1988. (In Russian) [Google Scholar]
- Chernogor, L.F. The Earth–Atmosphere–Geospace System: Main Properties and Processes. Int. J. Remote Sens. 2011, 32, 3199–3218. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chang, F.Y.; Chen, Y.I.; Chang, L.C.; Wen, Y.C.; Wu, T.Y.; Chao, C.K. Pre-earthquake Ionospheric Anomalies and Ionospheric Storms Observed by FORMOSAT-5/AIP and GIM TEC. Surv. Geophys. 2023, 45, 577–602. [Google Scholar] [CrossRef]
- Gorbunova, E.M.; Ryakhovskiy, I.A.; Gavrilov, B.G.; Poklad, Y.V.; Petukhova, S.M.; Besedina, A.N. Variations in Geophysical Fields during the Tonga Volcanic Eruption According to the Data of the Mikhnevo Large-Scale Research Facility. Izv. Atmos. Ocean. Phys. 2022, 58, 1350–1366. [Google Scholar] [CrossRef]
- Surkov, V.; Hayakawa, M. Ultra and Extremely Low Frequency Electromagnetic Fields; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Senior, T.B.A.; Volakis, J.L. Approximate Boundary Conditions in Electromagnetics; IEEE Publishing: London, UK, 1995; ISBN 978-0852968499. [Google Scholar]
- Wait, J.R. Electromagnetic Waves in Stratified Media; McMillan: New York, NY, USA, 1979. [Google Scholar]
- Hayakawa, M. Earthquake Prediction with Radio Techniques. Wiley: Singapore, 2015; 294p. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1998; ISBN 978-0471309321. [Google Scholar]
- Kong, J.A. Electromagnetic Wave Theory; John Wiley & Sons: New York, NY, USA, 1990; ISBN 978-0471522140. [Google Scholar]
- Dumaeva, L.V.; Ezaova, A.G. Numerical model return stroke of lightning. Fundam. Res. 2015, 9, 440–443. (In Russian) [Google Scholar]
- D’Arcangelo, S.; Regi, M.; De Santis, A.; Perrone, L.; Cianchini, G.; Soldani, M.; Piscini, A.; Fidani, C.; Sabbagh, D.; Lepidi, S.; et al. A multiparametric-multilayer comparison of the preparation phase of two geophysical events in the Tonga-Kermadec subduction zone: The 2019 M7.2 Kermadec earthquake and 2022 Hunga Ha’apai eruption. Front. Earth Sci. 2023, 11, 1267411. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Chao, C.-K. An observing system simulation experiment for FORMOSAT-5/AIP detecting seismo-ionospheric precursors. Terr. Atmos. Ocean. Sci. 2017, 28, 117–127. [Google Scholar] [CrossRef]
- Namgaladze, A.A.; Zolotov, O.V.; Zakharenkova, I.E.; Shagimuratov, I.I.; Martynenko, O.V. Ionospheric total electron content variations observed before earthquakes: Possible physical mechanism and modeling. Proc. MSTU 2009, 12, 308–315. [Google Scholar]
- Kuo, C.L.; Huba, J.D.; Joyce, G.; Lee, L.C. Ionosphere plasma bubbles and density variations induced by pre-earthquake rock currents and associated surface charges. J. Geophys. Res. Space Phys. 2011, 116, A10317. [Google Scholar] [CrossRef]
- Madonia, P.; Bonaccorso, A.; Bonforte, A.; Buonocunto, C.; Cannata, A.; Carleo, L.; Cesaroni, C.; Currenti, G.; De Gregorio, S.; Di Lieto, B.; et al. Propagation of Perturbations in the Lower and Upper Atmosphere over the Central Mediterranean, Driven by the 15 January 2022 Hunga Tonga-Hunga Ha’apai Volcano Explosion. Atmosphere 2023, 14, 65. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Koloskov, A.V.; Yampolsky, Y.M.; Budanov, O.V.; Shvets, A.A. Low-frequency (ELF–VLF) radio atmospherics study at the Ukrainian Antarctic Akademik Vernadsky station. Ukr. Antarct. J. 2019, 1, 116–127. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Schekotov, A.Y.; Hayakawa, M.; Romero, R.; Izutsu, J. Electromagnetic manifestations of Tonga eruption in Schumann resonance band. J. Atmos. Sol.-Terr. Phys. 2022, 237, 105897. [Google Scholar] [CrossRef]
- Kubisz, J.; Gołkowski, M.; Ostrowski, M.; Młynarczyk, J.; Michalec, A. New Method for Determining Azimuths of ELF Signals Associated with the Global Thunderstorm Activity and the Hunga Tonga Volcano Eruption. J. Geophys. Res. Atmos. 2024, 129, e2023JD040318. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.; Parrot, M.; Hayakawa, M.; Biagi, P.-F.; Schwingenschuh, K.; Fedun, V. VLF/LF signal studies of the ionospheric response to strong seismic activity in the Far Eastern region combining the DEMETER and ground-based observations. Phys. Chem. Earth 2015, 85–86, 141–149. [Google Scholar] [CrossRef]
- Forte, B.; Fallows, R.A.; Bisi, M.M.; Zhang, J.; Krankowski, A.; Dabrowski, B.; Rothkaehl, H.; Vocks, C. Interpretation of radio wave scintillation observed through LOFAR radio telescopes. Astrophys. J. Suppl. Ser. 2022, 263, 36. [Google Scholar] [CrossRef]
- Rapoport, Y.; Grimalsky, V.; Petrishchevskii, S.; Grytsai, A.; Liashchuk, O.; Krankowski, A. Modelling Wave Structures in the Earth-Atmosphere-Ionosphere and Radiodiagnostics of Ionospheric Space Weather (ISW). In Proceedings of the International Conference on Recent Trends in Geoscience Research and Applications 2023, Belgrade, Serbia, 23–27 October 2023; pp. 11–12. [Google Scholar]
- Gurevich, A.V. Nonlinear Phenomena in the Ionosphere; Springer: New York, NY, USA, 1978; 372p. [Google Scholar]
- Kadomtsev, B.B. Collective Phenomena in Plasma; Nauka: Moscow, Russia, 1988; 304p. (In Russian) [Google Scholar]
- Zhima, Z.; Huang, J.; Shen, X.; Xia, Z.; Chen, L.; Piersanti, M.; Yang, Y.; Wang, Q.; Zeng, L.; Lei, J.; et al. Simultaneous Observations of ELF/VLF Rising-Tone Quasiperiodic Waves and Energetic Electron Precipitations in the High-Latitude Upper Ionosphere. J. Geophys. Res. Space Phys. 2020, 125, 5. [Google Scholar] [CrossRef]
- Zhao, S.; Zhou, C.; Shen, X.; Zhima, Z. Investigation of VLF Transmitter Signals in the Ionosphere by ZH-1 Observations and Full-Wave Simulation. J. Geophys. Res. Space Phys. 2019, 124, 4697–4709. [Google Scholar] [CrossRef]
- Lv, F.; Hu, Y.; Zhima, Z.; Sun, X.; Lu, C.; Yang, D. The upward propagating ionospheric hiss waves during the seismic time observed by the China seismoelectromagnetic satellite. Front. Astron. Space Sci. 2023, 10, 1127738. [Google Scholar] [CrossRef]
- Zhima, Z.; Yan, R.; Lin, J.; Wang, Q.; Yang, Y.; Lv, F.; Huang, J.; Cui, J.; Liu, Q.; Zhao, S.; et al. The Possible Seismo-Ionospheric Perturbations Recorded by the China-Seismo-Electromagnetic Satellite. Remote Sens. 2022, 14, 905. [Google Scholar] [CrossRef]
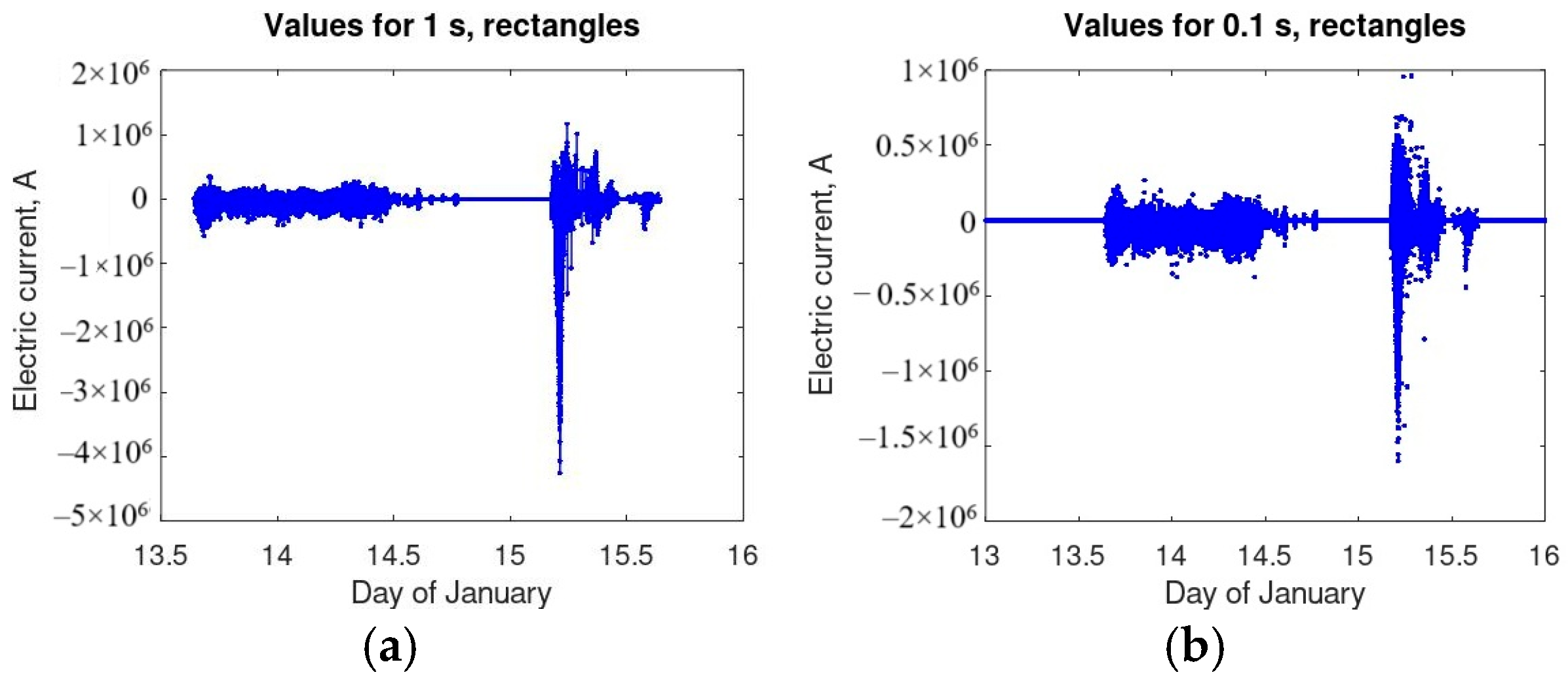
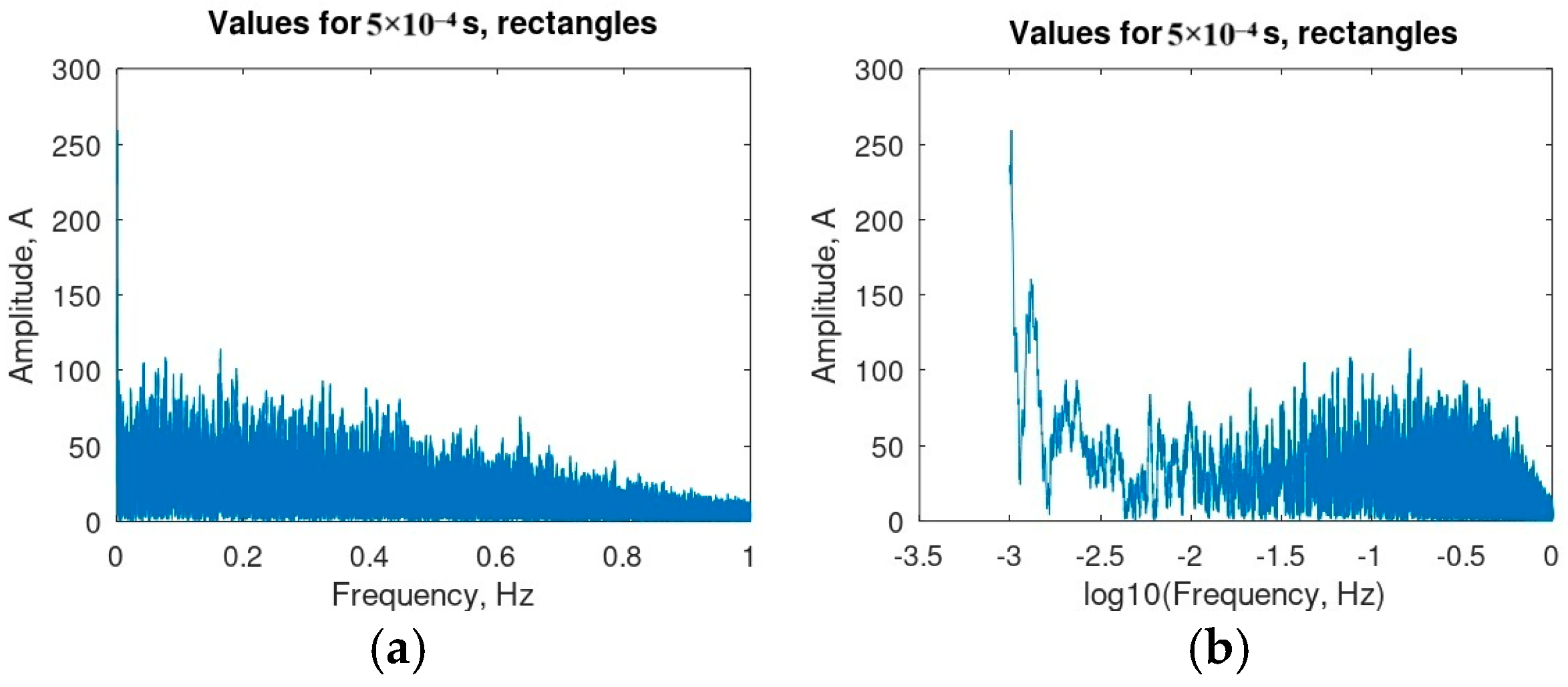
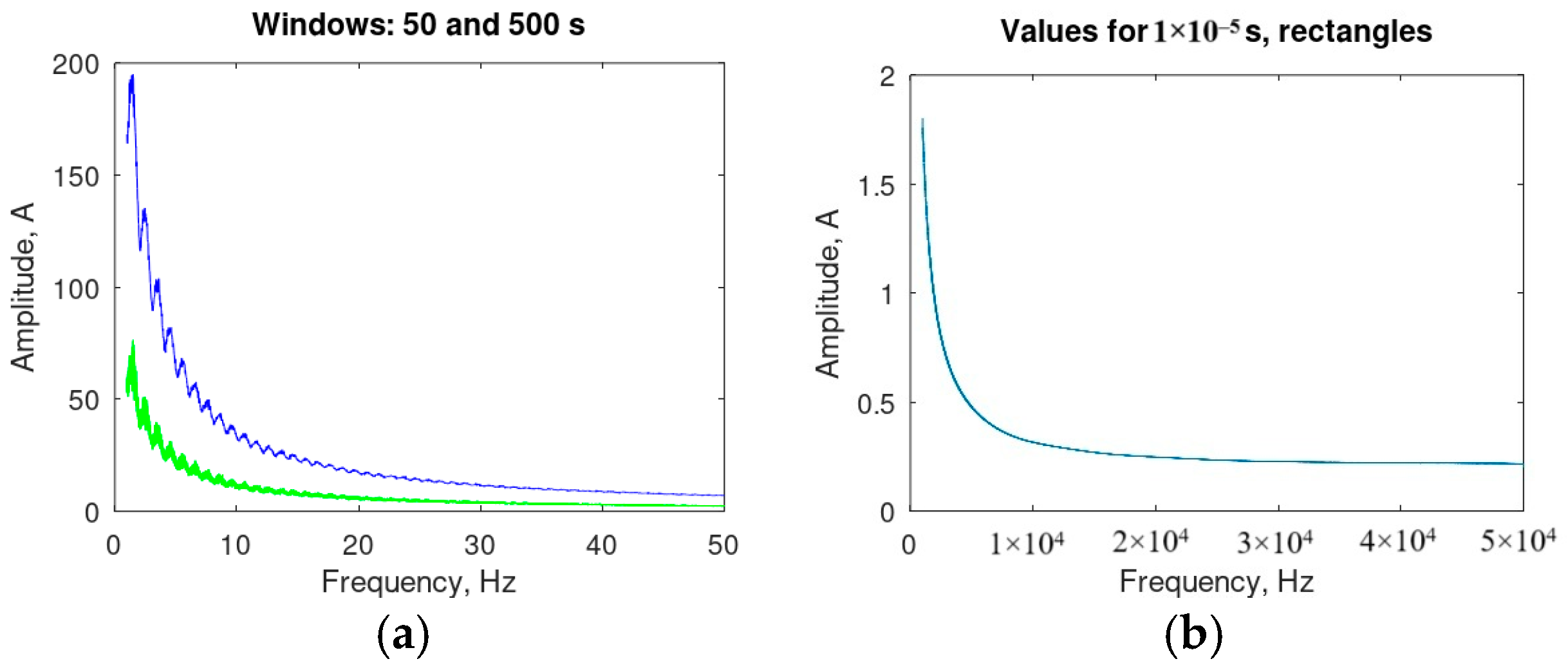



| Mode 1, Hz | Mode 2, Hz | Q-Factor, Mode 1 | Q-Factor, Mode 2 | |
|---|---|---|---|---|
| 1. Koloskov et al., 2023 [12] | 7.5 | 14 | 5 | 9 |
| 2. Bór et al., 2023 [6] | 7.5 | 14 | 5 | 7 |
| 3. Mezentsev et al., 2023 [13] | 7.5 | 14 | 6 | 10 |
| 4. Chandrasekhar et al., 2023 [11] | 7.5 | 13.5 | 10 | 10 |
| 5. Gavrilov at al., 2022 [14] | 7.5 | 14 | 6 | 14 |
| 6. Nickolaenko et al., 2022 [101] | 7.8 | 14.1 | 9 | 13 |
| 7. D’Arcangelo et al., 2022 [95] | 8 | 14 | 6 | 7 |
| 8. Shvets et al., 2024 [57] | 7.8 | 13.8 | 5 | 8 |
| 9. Kubish et al., 2023 [102] | 8 | 14 | 5 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rapoport, Y.G.; Grimalsky, V.V.; Krankowski, A.; Grytsai, A.; Petrishchevskii, S.S.; Błaszkiewicz, L.; Chen, C.-H. Excitation of ULF, ELF, and VLF Resonator and Waveguide Oscillations in the Earth–Atmosphere–Ionosphere System by Lightning Current Sources Connected with Hunga Tonga Volcano Eruption. Atmosphere 2025, 16, 97. https://doi.org/10.3390/atmos16010097
Rapoport YG, Grimalsky VV, Krankowski A, Grytsai A, Petrishchevskii SS, Błaszkiewicz L, Chen C-H. Excitation of ULF, ELF, and VLF Resonator and Waveguide Oscillations in the Earth–Atmosphere–Ionosphere System by Lightning Current Sources Connected with Hunga Tonga Volcano Eruption. Atmosphere. 2025; 16(1):97. https://doi.org/10.3390/atmos16010097
Chicago/Turabian StyleRapoport, Yuriy G., Volodymyr V. Grimalsky, Andrzej Krankowski, Asen Grytsai, Sergei S. Petrishchevskii, Leszek Błaszkiewicz, and Chieh-Hung Chen. 2025. "Excitation of ULF, ELF, and VLF Resonator and Waveguide Oscillations in the Earth–Atmosphere–Ionosphere System by Lightning Current Sources Connected with Hunga Tonga Volcano Eruption" Atmosphere 16, no. 1: 97. https://doi.org/10.3390/atmos16010097
APA StyleRapoport, Y. G., Grimalsky, V. V., Krankowski, A., Grytsai, A., Petrishchevskii, S. S., Błaszkiewicz, L., & Chen, C.-H. (2025). Excitation of ULF, ELF, and VLF Resonator and Waveguide Oscillations in the Earth–Atmosphere–Ionosphere System by Lightning Current Sources Connected with Hunga Tonga Volcano Eruption. Atmosphere, 16(1), 97. https://doi.org/10.3390/atmos16010097








