CNN vs. LSTM: A Comparative Study of Hourly Precipitation Intensity Prediction as a Key Factor in Flood Forecasting Frameworks

Abstract

Accurate precipitation intensity forecasting is crucial for effective flood management and early warning systems. This study evaluates the performances of convolutional neural network (CNN) and long short-term memory (LSTM) models in predicting hourly precipitation intensity using data from Sainte Catherine de la Jacques Cartier station near Québec City. The models predict precipitation levels from one to six hours ahead, which are categorized into slight, moderate, heavy, and very heavy precipitation intensities. Our methodology involved gathering hourly precipitation data, defining input combinations for multistep ahead forecasting, and employing CNN and LSTM models. The performances of these models were assessed through qualitative and quantitative evaluations. The key findings reveal that the LSTM model excelled in the short-term (1HA to 2HA) and long-term (3HA to 6HA) forecasting, with higher R² (up to 0.999) and NSE values (up to 0.999), while the CNN model was more computationally efficient, with lower AICc values (e.g., −16,041.1 for 1HA). The error analysis shows that the CNN demonstrated higher precision in the heavy and very heavy categories, with a lower relative error, whereas the LSTM performed better for the slight and moderate categories. The LSTM outperformed the CNN in minor- and high-intensity events, but the CNN exhibited a better performance for significant precipitation events with shorter lead times. Overall, both models were adequate, with the LSTM providing better accuracy for extended forecasts and the CNN offering efficiency for immediate predictions, highlighting their complementary roles in enhancing early warning systems and flood management strategies.

1. Introduction

Precipitation is a critical component of the hydrological cycle [1], significantly influencing water availability [2], agricultural productivity [3,4,5], and natural ecosystems [4,6]. Accurate precipitation forecasting is vital for water resources management, agricultural planning, and disaster preparedness. In particular, runoff generated by precipitation events can profoundly affect watersheds, leading to erosion, sediment transport, and nutrient loading in water bodies [7]. Predicting precipitation intensity accurately is essential for early flood prediction, enabling timely and effective mitigation measures to protect lives and property.

The frequency and intensity of rainfall events in North America have increased because of climate change [8,9], leading to more extreme and frequent storms and posing new challenges for flood forecasting. The U.S. National Weather Service defines flash floods as rapid flooding events caused by intense rainfall within a short period, occurring within six hours subsequent to the initial event, often resulting in significant damage [10]. Predicting these events is challenging due to their sudden onset and localized nature. Research indicates that accurate hourly precipitation forecasts are crucial for predicting flash floods, as they provide detailed information on the timing and intensity of rainfall, which is essential for timely flood warnings and responses [11]. Developing reliable forecasting models is crucial to improve the accuracy and timeliness of precipitation predictions, thus enhancing flood preparedness and response strategies. Forecasting precipitation and flood events requires consideration of various temporal and spatial scales. Flash floods, for example, necessitate precise and timely forecasts due to their rapid development. Climate change exacerbates the challenge, with factors such as heavy rainfall and rain-on-snow events in spring being major contributors to flooding in Canada [12]. Accurate and detailed forecasts are essential to address the increasing risks associated with climatic changes.

Short-term forecasting is particularly important for flood management but presents several challenges due to rainfall prediction uncertainties [13]. Numerical models, traditionally used for short-term forecasts [14], often struggle with accuracy and computational demands [15]. This limitation has led to the adoption of machine learning (ML) techniques, which offer improved performance and efficiency for short-term predictions [16,17]. Advancements in science and technology have significantly enhanced hydrological prognostication, with ML methods playing a crucial role [18]. ML techniques, categorized into traditional machine learning and deep learning (DL), offer distinct advantages. DL, in particular, excels with larger datasets, providing better performance and generalization capabilities compared to traditional ML methods [19]. These advancements have opened new possibilities for accurate and efficient precipitation forecasting.

Recent studies have explored using convolutional neural networks (CNNs) and long short-term memory (LSTM) to improve precipitation forecasting. Wang et al. [20] successfully utilized LSTM models to estimate precipitation using raindrop spectrum data in Guizhou, demonstrating the effectiveness of deep learning approaches in enhancing the accuracy of precipitation forecasting in meteorologically complex regions. Their study highlights the potential of LSTMs in capturing temporal dependencies in precipitation patterns, offering valuable insights for improving hydrological predictions. Kong et al. [21] explored the use of deep learning models, specifically ConvLSTM and PredRNN, for precipitation nowcasting in Guizhou, China, demonstrating that these models can outperform traditional methods like the LK Optical Flow in capturing complex nonlinear precipitation patterns. Their study highlights the superior performance of a PredRNN, especially when trained with high-quality, long-term datasets, making it a valuable approach for short-term, high-resolution precipitation forecasting. Fouotsa Manfouo et al. [22] conducted a comparative study between statistical downscaling models (SDSMs) and long short-term memory (LSTM) networks for long-term temperature and precipitation forecasting in the Lake Chad Basin, finding that LSTMs consistently outperformed SDSMs in terms of accuracy. Jiang et al. [23] developed a hybrid MLP-CNN model that effectively combines multilayer perceptron and convolutional neural network architectures to predict extreme precipitation events in central-eastern China. Their model demonstrates superior performance compared to traditional machine learning approaches, particularly in scenarios with imbalanced data, making it a promising tool for improving the accuracy of short-term extreme weather forecasts.

The primary aim of this research is to compare DL-based models, specifically a CNN and LSTM, designed for hourly precipitation forecasting in Québec City. The models’ performances were evaluated across multiple forecast steps, from one to six hours ahead, for various precipitation intensities, including light, moderate, heavy, and very heavy precipitation. The performances of these models were compared both generally and within different categories using quantitative and qualitative indices, focusing on accuracy and simplicity. By utilizing the strengths of DL, this study seeks to enhance the accuracy and reliability of precipitation forecasts, thereby contributing to more effective flood management strategies.

While CNNs and LSTMs are widely recognized for their capabilities in forecasting and prediction tasks, the novelty of this research lies in its unique comparative analysis of these models, specifically applied to hourly precipitation intensity prediction across multiple lead times (1 to 6 h). Unlike previous studies that often focus on a single model or do not fully explore the performance variations across different precipitation intensity categories, this study rigorously evaluated both the CNN and LSTM models across the following four distinct precipitation categories: slight, moderate, heavy, and very heavy. Additionally, the research extends the application of these models to a high-resolution, real-world dataset from the Sainte Catherine de la Jacques Cartier station, providing insights into their practical effectiveness in operational flood forecasting scenarios. By assessing these models’ predictive accuracy, computational efficiency, and complexity, this study offers a comprehensive evaluation highlighting the specific conditions under which each model excels, thereby providing practical guidance for their application in real-time flood management systems.

2. Materials and Methods

2.1. Data Collection and Study Area

The present study focuses on the Sainte Catherine de la Jacques Cartier station, located at a latitude of 46.8378 and a longitude of −71.6217 in Québec City, Canada (Figure 1). This region has a humid continental climate [24], characterized by the following two distinct seasons: cold, snowy winters and warm, humid summers. The city experiences significant seasonal variations in temperature and precipitation, with winter temperatures often dropping well below freezing and substantial snowfall, while summers can be warm, with temperatures occasionally exceeding 25 °C (77 °F). Precipitation is relatively evenly distributed throughout the year, though slightly higher in summer due to increased convective activity. Based on the National Centers for Environmental Information (https://www.ncei.noaa.gov/ (accessed on 1 January 2023)), the average high temperature reaches approximately 25 °C in July, whereas the average low temperature plummets to −15 °C in January. Hourly precipitation data were collected from 14 December 1994, to 31 October 2022 by the “Ministère de l’Environnement et de la Lutte contre les changements climatiques, de la Faune et des Parcs” [25] of Québec, QC, Canada. The dataset was divided into training, validation, and testing sets, comprising 50%, 20%, and 30% of the data, respectively. After addressing significant gaps and eliminating samples with zero values in all rows (i.e., no rain for several consecutive hours), the final count of samples was 5683 for training, 2274 for validation, and 3410 for testing.

Figure 1 shows the distribution and statistical analysis of hourly precipitation. The bar chart illustrates the percentage distribution of precipitation intensities. The slight (0–0.5 mm/h) category represents light precipitation events, typically including drizzles or light rain. The bar chart shows that approximately 29.8% of the precipitation events fall into this category, indicating a significant frequency of light rainfall within the dataset. The moderate (0.5–4 mm/h) category encompasses moderate precipitation events, which are more intense than slight precipitation but not as heavy as the following categories. The bar chart reveals that this category has the highest frequency, with about 64.36% of the precipitation events being moderate. This suggests that moderate rainfall is the most common intensity in the dataset. The heavy (4–8 mm/h) category includes heavy precipitation events, which are less frequent but indicate significant rainfall intensity. The chart demonstrates that around 4.44% of the events fall into this category, showing a noticeable but less common occurrence of heavy rain. Finally, the very heavy (>8 mm/h) category represents the most intense precipitation events, often associated with severe weather conditions like thunderstorms or torrential downpours. The chart shows that this category is the least frequent, with only about 1.4% of the events classified as very heavy precipitation. Thus, moderate precipitation events dominate, followed by slight precipitation. In contrast, heavy and very heavy precipitation events are relatively rare, reflecting their typically extreme nature and lower frequency of occurrence.

The box plots display the distribution of the precipitation values, with a detailed view focusing on the lower range up to 5 mm/h, highlighting the prevalence and range of typical precipitation events. This plot displays several key statistics, as follows: the minimum value in the dataset is 0.2 mm/h, representing the smallest precipitation measurement. The first quartile (Q1) is 0.4 mm/h, indicating that 25% of the precipitation values are below this threshold. The median, which is the 50th percentile, is 0.8 mm/h, meaning half of the precipitation values fall below this rate. The third quartile (Q3) is 1.6 mm/h, showing that 75% of the precipitation values are below this level. The maximum value recorded is 18.4 mm/h, the highest precipitation rate in the dataset. The interquartile range (IQR) is also 1.2 mm/h, calculated as the difference between Q3 and Q1 (1.6 mm/h–4 mm/h), which measures the statistical dispersion. The mean precipitation value is 1.41 mm/h, while the standard deviation is 1.93 mm/h, reflecting the variation in precipitation values around the mean.

The main part of the box plot spans from Q1 (0.4 mm/h) to Q3 (1.6 mm/h), representing the interquartile range (IQR) and containing the middle 50% of the data. The whiskers extend from the box to show the range of the data outside the middle 50%, with the lower whisker extending from Q1 to the minimum value (0.2 mm/h) and the upper whisker extending from Q3 to the maximum value (18.4 mm/h). Inside the box, the line indicates the median value (0.8 mm/h). Outliers, which are data points significantly higher than the rest, are displayed as individual points beyond the whiskers. In this case, values significantly higher than 1.6 mm/h, up to the maximum of 18.4 mm/h, are considered outliers.

The interpretation of this box plot reveals that the majority of precipitation events (middle 50%) fall between 0.4 mm/h and 1.6 mm/h, indicating that most hourly precipitation rates are within this range. The median value of 0.8 mm/h suggests that half of the precipitation events are below this rate, highlighting a skew toward lower precipitation values. Outliers, particularly on the higher end, indicate occasional heavy precipitation events that significantly exceed the typical values.

2.2. Convolutional Neural Network (CNN)

A convolutional neural network (CNN) is a type of deep learning algorithm specifically designed for processing structured grid data, such as images. The visual cortex inspired it in animals [26,27] and is particularly effective at recognizing patterns and objects in visual data [28]. CNNs are composed of multiple layers that automatically and adaptively learn spatial hierarchies of features from input images [29].

CNNs perform better than traditional neural networks [30], especially for image and video recognition tasks, because they leverage spatial correlations in the input data. Unlike traditional neural networks that fully connect each neuron to every other neuron in adjacent layers [31,32], CNNs use a specialized kind of layer called a convolutional layer, which only connects each neuron to a small, localized region of the input (Pinaya et al., 2020). This connectivity pattern reduces the number of parameters in the network, making it more efficient and scalable for large images [33].

One of the main advantages of CNNs is their ability to automatically identify significant features without any human intervention [34]. This is achieved through convolutional, pooling, and fully connected layers. Convolutional layers apply a set of filters to the input, detecting features such as edges, textures, and patterns. Pooling layers reduce the spatial dimensions of the feature maps, thus reducing computational complexity and the risk of overfitting. Fully connected layers integrate the features learned by the convolutional and pooling layers to make the final prediction.

The training process of a CNN involves several steps. Initially, the network’s weights are set to small random values. The network processes a batch of training images during training and computes the output predictions. These predictions are compared to the actual labels using a loss function, which measures the discrepancy between the predicted and true labels. The network then adjusts the weights using backpropagation, which calculates the gradient of the loss function concerning each weight and updates the weights in the direction that minimizes the loss. This process is repeated for many iterations, gradually improving the network’s accuracy.

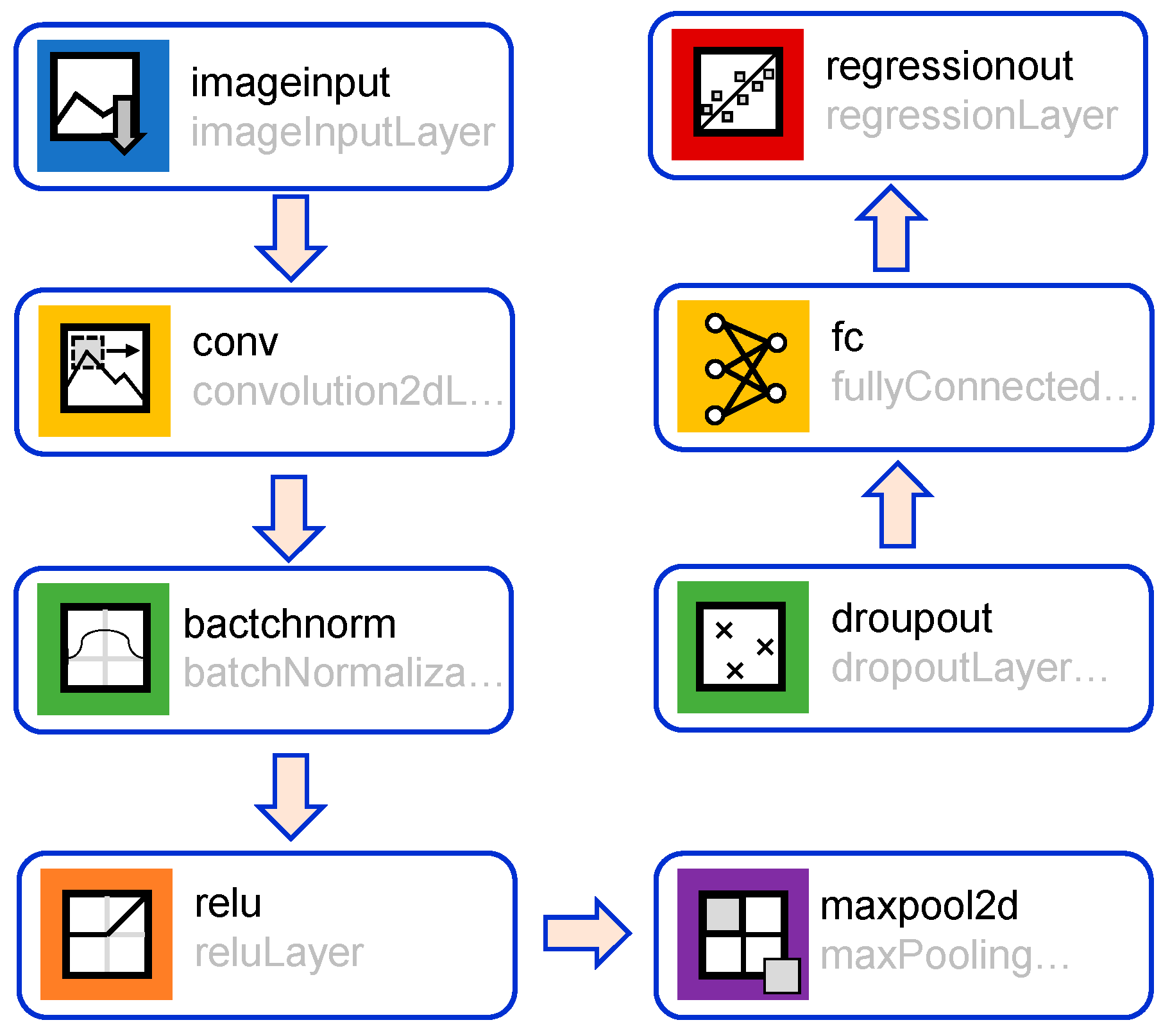
Figure 2 shows the structure of the applied CNN in the current study. It includes various layers designed to extract and learn features from the input image data. The first layer is the imageInputLayer, which serves as the entry point for the image data into the network. This layer specifies the dimensions of the input images, including their heights, widths, and numbers of channels, allowing the network to properly process the incoming data. By defining these parameters, the network can properly process the incoming images. Following the input layer is the convolution layer, which applies a set of learnable filters [35] to the input image. Each filter scans across the image to detect specific features, such as edges, textures, or patterns [36]. The result is a set of feature maps that highlight the presence of these features in different regions of the image. This layer is crucial for the network’s ability to recognize complex patterns in the data [37]. Next, the batch normalization layer is used to normalize the activations of the previous layer [38]. This helps to stabilize [39] and accelerate the training process [40] by reducing the internal covariate shift [41].

By normalizing the output of the convolutional layer, the network can achieve faster convergence and improved performance [42]. The ReLu layer, or rectified linear unit layer, follows the batch normalization layer, which replaces all negative values with zero, allowing the network to learn complex patterns and interactions among the features. This function can prevent gradient vanishing and ensure the model attains optimal performance efficiency [43,44]. The max pooling layer is employed to reduce the spatial dimensions of the feature maps and make the network more computationally efficient. 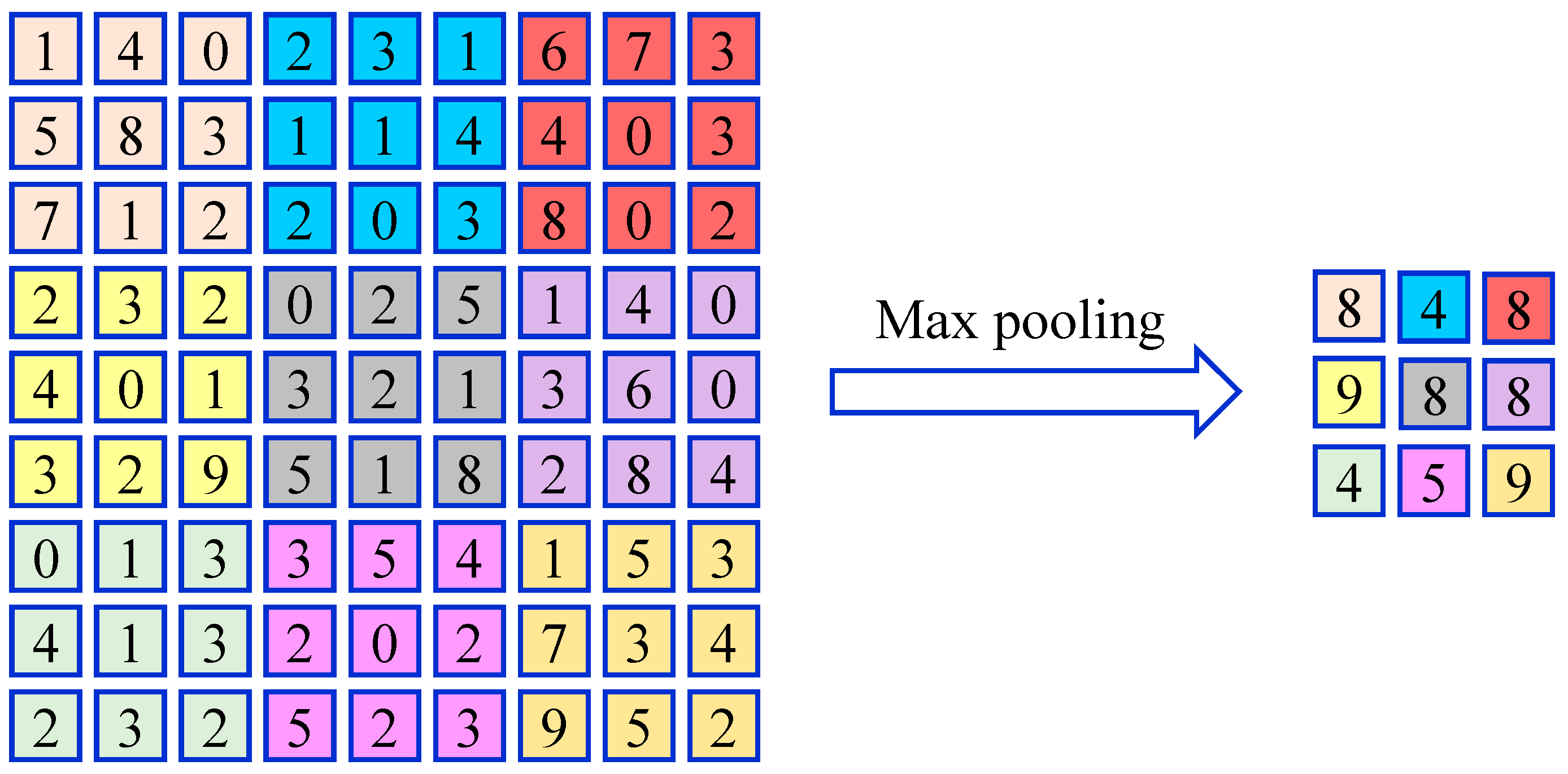This layer performs downsampling by selecting the maximum value from each region of the feature maps [45]. A schematic example of the max pooling is provided in Figure 3. Doing so reduces the number of parameters and mitigates the risk of overfitting [46].

The dropout layer is included to prevent overfitting [47] by randomly setting a fraction of the input units to zero during training. This forces the network to learn more robust features and prevents it from becoming too reliant on any single neuron. The dropout rate specifies the proportion of neurons to be dropped out, which helps to improve the network’s generalization capabilities [48]. Toward the end of the network, the fullyConnectedLayer integrates the features learned by the previous layers to make the final prediction. Each neuron in this layer is connected to all the neurons in the previous layer, allowing it to combine the extracted features and produce the final output. Finally, the regressionLayer is used for regression tasks, where the goal is to predict continuous values. This layer computes the loss between the predicted values and the actual target values, guiding the network’s learning process. The network learns to make accurate predictions based on the input images by minimizing this loss during training.

2.3. Long Short-Term Memory (LSTM)

Long short-term memory (LSTM) is a type of recurrent neural network (RNN) architecture designed to address the limitations of traditional RNNs, especially when it comes to learning long-term dependencies. Traditional RNNs struggle with the vanishing gradient problem [49,50], making learning and remembering information from long sequences difficult. LSTMs, introduced by Hochreiter and Schmidhuber [51], overcome this issue through a more complex unit structure that allows for better information retention over extended periods [52,53].

An LSTM network consists of a series of cells, each containing a set of gates that control the flow of information. These gates include the input, forget, and output gates [54]. The input gate regulates the extent to which new information flows into the cell state, the forget gate determines how much of the past information to retain, and the output gate controls the output based on the cell state [54]. This architecture allows LSTMs to maintain and update the cell state in a way that preserves long-term dependencies more effectively than traditional RNNs [53].

Figure 4 represents the architecture of an LSTM network, specifically illustrating the components and data flow within an LSTM block. This figure includes the following four main components: the input layer, hidden layer, LSTM block, and gates. The input layer (x(t)) is where the input data at time step t enter the LSTM network. This layer passes the data to the hidden layer for processing. The hidden layer (h(t)) contains the LSTM blocks, which process the input data and the previous hidden state to produce the current hidden state and cell state. The hidden layer is the core of the LSTM, where all computations take place.

The LSTM block is the fundamental unit of the LSTM network and consists of several key components. The input gate (I) controls how much of the new input x(t) is passed to the cell state. The forget gate (F) determines how much of the previous cell state C(t − 1) should be forgotten. The output gate (O) decides how much of the cell state should be output as the hidden state h(t). The cell state (CEC—constant error carousel) is the memory of the LSTM block that carries information across different time steps. The cell state is modified by the input (I), forget (F), and output (O) gates.

The input x(t) is fed into the LSTM block. The previously hidden state h(t − 1) and the input x(t) are used to compute the activations for the input, forget, and output gates (I, F, and O). The input gate (I) determines how much of the new input should be added to the cell state. The forget gate (F) decides how much of the previous cell state C(t − 1) should be retained. The cell state (CEC) is updated by combining the retained cell state and the new input, scaled by their respective gates. The output gate (O) determines how much of the updated cell state should be passed to the next hidden state, h(t). The hidden state h(t) is then passed to the next time step and to the output layer.

LSTMs outperform traditional neural networks and basic RNNs in tasks involving sequential data, such as time series prediction. Traditional neural networks, like feedforward networks, do not have the capability to remember past inputs, making them unsuitable for tasks where context and order are essential. LSTMs, on the other hand, can capture the temporal dynamics of data [55], making them particularly useful for tasks requiring an understanding of temporal sequences. Another advantage of LSTMs is their ability to mitigate the vanishing gradient problem, enabling them to learn from longer sequences without losing relevant information. They can also selectively remember and forget information, allowing them to focus on the most pertinent parts of the sequence. This selective memory feature makes LSTMs highly effective in tasks where context and long-term dependencies are crucial.

Figure 5 shows the structure of the applied LSTM network in the current study. It includes various layers designed to handle and learn from sequential data. The main differences between the LSTM network and the previously discussed CNN are the use of the sequence input layer instead of the image input layer, as well as the LSTM layer instead of the convolution layer, and the absence of the max pooling layer. Indeed, it is unsuitable for LSTM networks because it is designed for spatial data reduction, which does not align with the sequential and temporal nature of the data LSTMs are intended to process. LSTMs rely on maintaining and learning from the order of sequences, and pooling operations would disrupt this crucial aspect.

The first layer in the LSTM network is the sequence input layer, which is tailored for sequential data inputs. This layer specifies the number of input variables, preparing the data for the subsequent layers. Unlike the image input layer in the CNN that handles image data, this layer is designed to process time series or other sequence data, where the order of the data points is crucial. Next is the LSTM layer, which effectively addresses the vanishing gradient problem that can occur in traditional RNNs, making them well-suited for tasks involving time-series forecasting and natural language processing. Following the LSTM layer, there is the batch normalization layer. As in the CNN structure, this layer normalizes the activations of the previous layer, stabilizing and accelerating the training process by reducing internal covariate shifts. The ReLU layer introduces nonlinearity into the network by applying the ReLU activation function to the input. The network employs a dropout layer to prevent overfitting, forcing the network to learn more robust features and preventing reliance on any single neuron. This mechanism enhances the network’s generalization capabilities. Toward the end of the network, the fully connected layer integrates the features learned by the previous layers to make the final prediction. Each neuron in this layer is connected to all neurons in the preceding layer, allowing it to combine the extracted features and produce the final output. Finally, the regression layer is used to compute the loss between the predicted and target values, guiding the network’s learning process.

2.4. Hourly Precipitation Intensity Prediction Framework

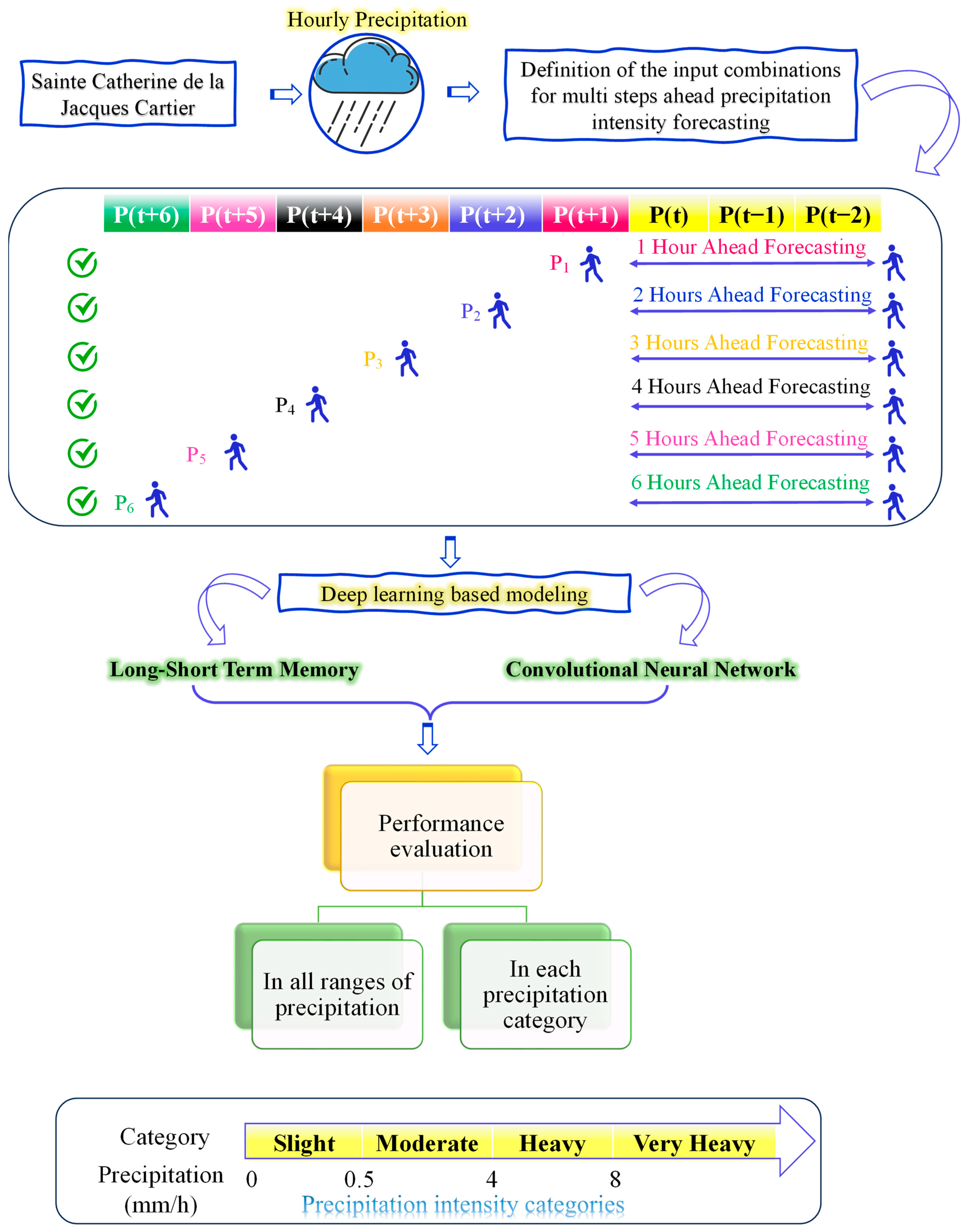
Figure 6 reveals the hourly precipitation intensity forecasting. This figure illustrates the step-by-step process of predicting hourly precipitation intensity using deep learning models. The initial phase in the precipitation intensity forecasting workflow involves gathering hourly precipitation data from Sainte Catherine de la Jacques Cartier station, located near Québec City. These data are meticulously recorded by MELCCFP [25]. Next, the workflow focuses on defining the input combinations necessary for multistep ahead precipitation intensity forecasting. This process involves using the current and past precipitation values as inputs to predict future precipitation levels. The forecasting process is conducted in several steps. The process of multihour ahead precipitation intensity forecasting relies on using past precipitation data to predict future precipitation levels. This method involves several steps, each tailored to forecast the intensity of the precipitation at different future time intervals, ranging from one hour ahead to six hours ahead.

The model predicts future precipitation using data from the previous three hours. For a one-hour-ahead forecast (1HA), it utilizes P(t), P(t − 1), and P(t − 2) to predict P(t + 1). The same input data are used for forecasting two hours ahead (2HA) with P(t + 2) as the target, and this pattern continues for three, four, five, and six hours ahead (3HA to 6HA), where the output shifts respectively to P(t + 3) through P(t + 6). The model successfully tracks recent precipitation trends by maintaining the same input data across all forecasting timeframes while shifting the target output to extend the prediction range from one to six hours ahead. It should be noted that the lead times were defined before any data were removed from the dataset. After establishing all lead times with three inputs and one output, any rows containing all zero values were subsequently removed.

In each of these forecasting steps, the model dynamically adjusts the input data window to suit the desired prediction interval. This strategic use of past precipitation values enables the model to effectively predict future precipitation intensities across multiple time horizons, ensuring that both short-term and long-term weather patterns are effectively captured and analyzed and providing valuable insights for weather forecasting and flood management. Advanced deep learning models are integral to this workflow. Specifically, long short-term memory (LSTM) networks, known for their ability to retain long-term dependencies, and convolutional neural networks (CNNs), which are adept at identifying patterns and features within the data, are utilized for forecasting tasks.

The forecasted precipitation intensities are systematically categorized into four distinct classes to understand and manage different rainfall scenarios better. According to the United States Geological Survey (USGS https://water.usgs.gov/edu/activity-howmuchrain-metric.html (accessed on 1 January 2023)), these classes are defined based on the intensity of the rainfall. The first category, “slight”, includes precipitation levels ranging from 0 to 0.5 mm/h. The “moderate” category covers precipitation intensities from 0.5 to 4 mm/h, providing a broad range that captures the most common rainfall events. The higher intensity classes include “heavy” rainfall, which spans from 4 to 8 mm/h, and “very heavy” rainfall, defined as any precipitation exceeding 8 mm/h. These classifications help assess the severity of rainfall events and are crucial for flood management and early warning systems, ensuring appropriate responses to varying precipitation levels.

The final step in this workflow is to assess the effectiveness of the forecasting models using the following two primary approaches: qualitative and quantitative performance evaluations. Qualitative assessments (such as scatter plots and Taylor diagrams) and quantitative assessments (such as statistical indices and relative error distribution) involve evaluating the model’s accuracy across all precipitation ranges and within each specific precipitation category. These approaches ensure that the model not only performs well overall but also accurately predicts precipitation intensity in each defined category. Together, these assessment methods provide a comprehensive evaluation of the model’s effectiveness in forecasting precipitation intensity.

Two major causes of flooding in Canada are heavy rainfall and rain on snow [56,57]. Consequently, dependable forecasting of precipitation intensity, particularly for high-intensity events, is essential for early flood detection systems. By integrating historical precipitation data with advanced deep learning models, this workflow provides a robust method for predicting future precipitation intensities at various time intervals, thereby supporting adequate early warning and flood management strategies.

2.5. Alignment Quality Metrics

Table 1. Performance criteria for evaluating model accuracy using different statistical measures.

References	Equation	Descriptive Performance	Value Ranges
[38,58]	$R^2={\left({\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N\left(P_O^i-\overline{P_O}\right)} {\displaystyle {\sum }_{i=1}^N\left(P_M^i-\overline{P_M}\right)}}{\sqrt{{\displaystyle {\sum }_{i=1}^N{\left(P_O^i-\overline{P_O}\right)}^2 }{\displaystyle {\sum }_{i=1}^N{\left(P_M^i-\overline{P_M}\right)}^2}}}}\right)}^2$	Unsatisfactory	R2 < 0.5
		Satisfactory	0.5 < R2 < 0.6
		Good	0.6 < R2 < 0.7
		Very Good	0.7 < R2 < 1
[38,58,59]	$NSE=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N{\left(P_M^i-P_O^i\right)}^2}}{{\displaystyle {\sum }_{i=1}^N{\left(P_M^i-\overline{P_O}\right)}^2}}}$	Unsatisfactory	NSE < 0.4
		Acceptable	0.4 < NSE < 0.5
		Satisfactory	0.5 < NSE < 0.65
		Good	0.65 < NSE < 0.75
		Very Good	0.75 < NSE < 1
[38,60]	$PBIAS={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N\left(P_M^i-P_O^i\right)}}{{\displaystyle {\sum }_{i=1}^N{P}_O^i}}}\times 100$	Unsatisfactory	PBIAS ≥ ±25%
		Satisfactory	±15% ≥ PBIAS > ±25%
		Good	±10% ≥ PBIAS > ±5%
		Very Good	±5% ≥ PBIAS
[38,61]	$NRMSE={\displaystyle \frac{\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{\left(P_O^i-P_M^i\right)}^2}}}{{\displaystyle {\sum }_{i=1}^N\left(P_O^i\right)}}}$	Unsatisfactory	30% < NRMSE
		Satisfactory	20% < NRMSE< 30%
		Good	10% < NRMSE < 20%
		Very Good	NRMSE < 10%
[38,58,62]	$RSR={\displaystyle \frac{RMSE}{S{D}_O}}={\displaystyle \frac{\sqrt{{\displaystyle {\sum }_{i=1}^N{\left(P_O^i-P_M^i\right)}^2}}}{\sqrt{{\displaystyle {\sum }_{i=1}^N{\left(P_O^i-\overline{P_O}\right)}^2}}}}$	Unsatisfactory	0.7 < RSR
		Satisfactory	0.6 < RSR < 0.7
		Good	0.5 < RSR < 0.6
		Very good	0 < RSR < 0.5

P_O: observed precipitation; P_M: modeled precipitation; $\overline{P_O}$: average of the observed precipitation.

summarizes performance criteria for evaluating model accuracy using various statistical measures. These measures include the coefficient of determination (R²), Nash–Sutcliffe efficiency (NSE), the percent bias (PBIAS), the normalized root mean square error (NRMSE), and the RMSE–observations standard deviation ratio (RSR). The mathematical formulations for all these indices are presented in this table. The R² assesses how well the observed outcomes are replicated by the model, indicating the proportion of the variance in the dependent variable that is predictable from the independent variables. Its sensitivity to the variance in the data makes it helpful in assessing how well the model captures the overall trend. The range of R² is from 0 to 1, where 0 indicates no explanatory power, and 1 indicates perfect explanatory power. R² is essential for understanding the model’s goodness of fit but does not consider model complexity or overfitting. The NSE evaluates the predictive power of the model, comparing the observed data variance to the variance of the residuals (differences between observed and predicted values). Its sensitivity to how well the model predicts outcomes makes it a good measure of model accuracy. The NSE indicates how well the model predictions match the observed data, with higher values representing better predictive performance. The range of NSE is from −1 to 1, with values closer to 1 indicating better predictive performance.

PBIAS measures the average tendency of the simulated values to be larger or smaller than their observed counterparts. It provides insight into whether the model systematically overestimates or underestimates the observations. The range of PBIAS can be from −∞ to +∞, with values closer to 0 indicating unbiased predictions. PBIAS is valuable for identifying systematic errors but does not provide a measure of overall fit or predictive accuracy. The NRMSE standardizes the RMSE by the range of observed values, making it a dimensionless measure. Its sensitivity to the differences between the observed and predicted values allows for a normalized measure of prediction error. The range of NRMSE is from 0 to ∞, with lower values indicating better model performance. It quantifies the deviation between observed and predicted values, allowing for comparison across different datasets and scales, but does not account for bias. The RSR combines the benefits of error index statistics and standard deviation statistics. Standardizing the RMSE using the standard deviation of the observed data provides a normalized measure of the model’s error, facilitating comparisons across different models and datasets. Its sensitivity to both error and variability makes it a comprehensive measure. The range of RSR is from 0 to ∞, with lower values indicating better performance. RSR is advantageous for a balanced assessment but may be influenced by extreme values.

Combining these indices allows for a more comprehensive evaluation of model performance. Each index captures different aspects of model accuracy, bias, and predictive power. By considering multiple indices, one can ensure a balanced assessment that accounts for both fit and complexity, avoiding over-reliance on a single measure that might overlook specific model weaknesses. This holistic approach provides a more robust and reliable model comparison [63,64].

While the previous indices provided in Table 1 focus solely on model accuracy, a more comprehensive evaluation requires an index that balances both accuracy and simplicity for a fair comparison of different types of models (CNN and LSTM). Then, the corrected Akaike information criterion (AICc) is used in the current study.

The AICc is a widely used metric for model selection in statistical and machine learning contexts. It evaluates a model based on both its accuracy and complexity, helping to identify the best model among a set of candidates. The AICc is particularly useful when comparing models with different structures and complexities [10,65]. The mathematic formulation of this index is as follows:

$$AICc=N\times Ln\left({\displaystyle \frac{1}{N}}{\displaystyle {\sum }_{i=1}^N{\left(P_O^i-P_M^i\right)}^2}\right)+2K+{\displaystyle \frac{2KN}{N-K-1}}$$

(1)

where N is the number of samples, P_O represents the observed precipitation, P_M denotes the modeled precipitation, and K is the number of parameters tuned during the training phase. In this equation, the first term is the accuracy term, while the second is the complexity term.

The accuracy term measures the goodness of fit of the model. It is based on the variance in the residuals (the differences between observed and estimated values). The Ln of the variance ensures that the term scales appropriately with the size of the residuals. Lower values of this term indicate a better fit, meaning the model’s predictions are closer to the actual observed values.

The complexity term penalizes the model for its complexity. The first part of this term is a basic penalty for the number of parameters. The second part provides an additional penalty, especially when the number of parameters is close to the number of observations, adjusting for small sample sizes. This penalty term ensures that overly complex models, which might fit the training data very well but generalize poorly to new data (i.e., overfitting), are discouraged.

The overall AIC value balances the following two aspects: accuracy and simplicity. A lower AIC value indicates a model with an excellent fit to the data (i.e., low residual variance) while maintaining simplicity (i.e., fewer parameters). It is important to note that the AIC value does not need to be positive or negative; it focuses on the relative comparison among models. The model with the lowest AIC value is generally considered the best.

Using AIC allows for an objective and quantitative comparison of models, making it a valuable tool in model selection. By considering both the fit and the complexity, AIC helps avoid the pitfalls of overfitting while still striving for accurate predictions. This dual consideration makes it a preferred choice for comparing models with different structures and parameter counts, ensuring that the selected model achieves a balance between accuracy and simplicity.

3. Result

The optimal values for the LSTM and CNN hyperparameters were determined through a grid search across a wide range of parameters. The most optimal values for each are presented in

Table 2. Optimal hyperparameter values for the LSTM and CNN models identified through a grid search.

Hyperparameter	CNN	LSTM
Input Size	[3, 1, 1]	3
Filter Size (Kernel Size)	5 × 5	-
Number of Filters	4	-
Padding	“same”	-
Stride	1 × 1 (default)	-
Activation Function	ReLU	ReLU
Pool Size	2 × 2
Dropout Rate	0.2	0.2
Number of Units (Neurons)	1	1
Optimizer	“sgdm”	“rmsprop”
Max Epochs	1000	1000
Number of LSTM Units	-	3

.

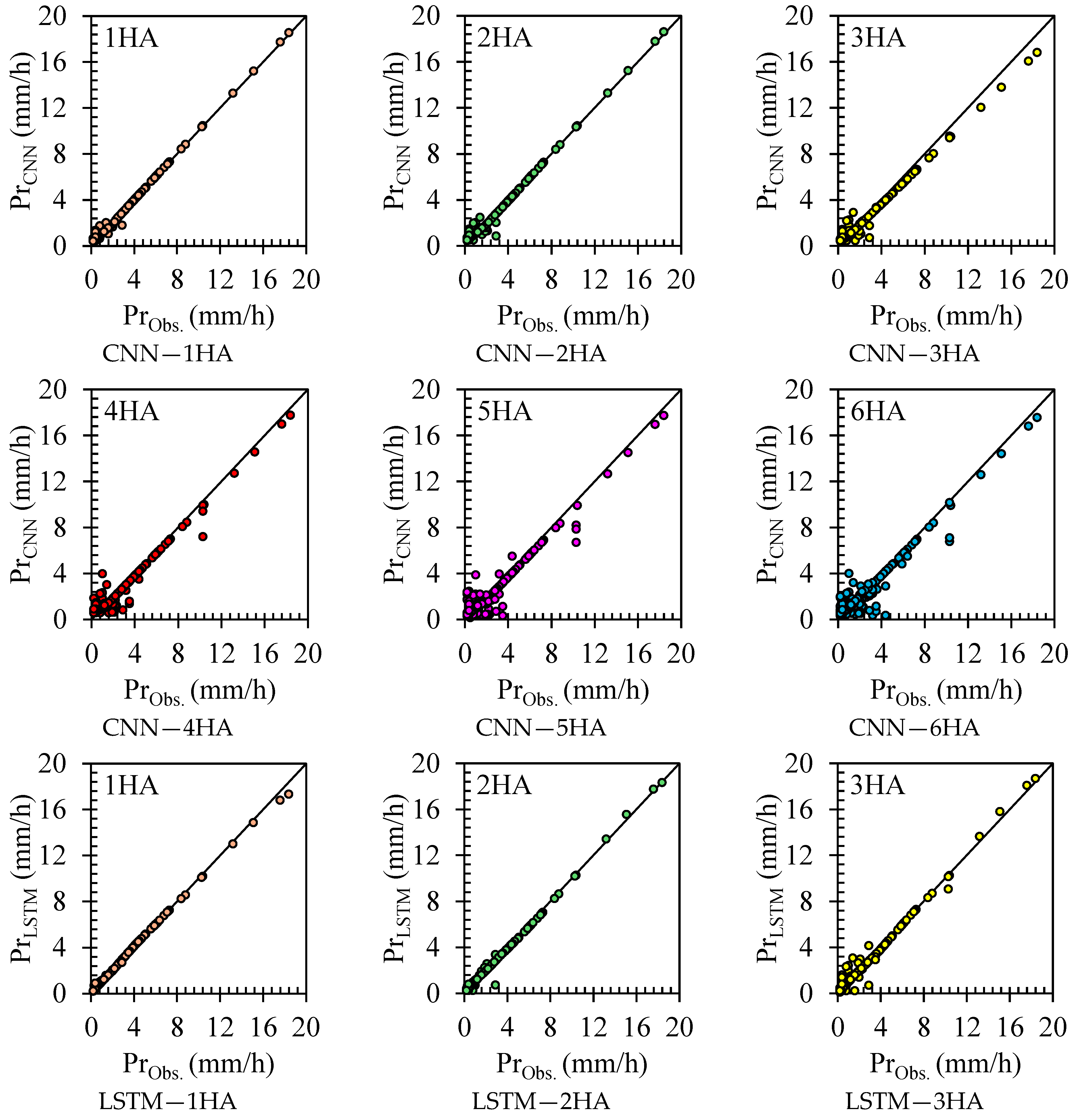
Figure 7 represents scatter plots comparing the observed precipitation values with predicted values for the CNN and LSTM models for 1 h ahead (1HA) to 6 h ahead (6HA) forecasts. For 1 h ahead (1HA) forecasting, both the CNN and LSTM models show a relatively high correlation between the observed and predicted values, indicating good short-term prediction accuracy. The scatter points for the LSTM are more tightly clustered around the line of equality (y = x) compared to the CNN, suggesting slightly better performance by LSTM for immediate forecasts. Both models maintain strong correlations for 2 h ahead (2HA) forecasting, but the spread of scatter points increases slightly compared to 1HA. The LSTM continues to show a tighter cluster around the line of equality than the CNN, similar to 1HA. The performances of both models remain high, but the LSTM maintains its slight edge. For 3 h ahead (3HA) forecasting, the correlation between the observed and predicted values starts to decrease for both models compared to 2HA, with a noticeable increase in the spread of the scatter points. The LSTM’s predictions remain closer to the observed values than those of CNN, as seen in the 1HA and 2HA forecasts. The decrease in correlation indicates a reduction in predictive accuracy as the forecast horizon extends.

For 4 h ahead (4HA) forecasting, the prediction accuracy further decreases as the forecast horizon extends, with both models showing increased scatter. LSTM still performs marginally better than the CNN, with less scatter. The trend of decreasing correlation continues from the 3HA forecast, marking a significant change from the short-term forecasts. Both models show significant scatter for 5 h ahead (5HA) forecasting, indicating lower prediction accuracy for longer forecast horizons. The difference between the CNN and LSTM performance becomes less pronounced, but LSTM still shows a slight edge. Compared to the 4HA forecast, the accuracy decreases further, reinforcing the challenge of predicting longer-term precipitation. For 6 h ahead (6HA) forecasting, the predictions for both models exhibit considerable scatter and lower correlation with observed values. LSTM and CNN show close performance, with the LSTM maintaining a slight advantage. This aligns with the trend observed in the 5HA forecast, with both models struggling with extended forecasts. The high scatter in 6HA forecasts indicates that predictive accuracy is significantly lower than in the earlier horizons.

Some points in the scatter plots exhibit higher differences from the observed values than others. These outliers can significantly impact the model’s predictive accuracy, especially in high precipitation conditions. Notably, the CNN model shows more such outliers than the LSTM model, particularly in the 4HA to 6HA forecasts. These higher differences indicate that while both models struggle with longer-term predictions, LSTM generally handles these scenarios better than the CNN.

Flood forecasting, particularly in regions like Canada, is heavily dependent on precise precipitation predictions due to frequent heavy rainfall and rain-on-snow events. This forecasting is critical for mitigating the impacts of floods, which can cause significant damage to infrastructure and pose risks to public safety. Models like convolutional neural networks (CNNs) and long short-term memory (LSTM) networks are commonly employed to achieve accurate forecasts.

Both the CNN and LSTM models are well-suited for short-term forecasts, specifically predicting precipitation one to two hours ahead (1HA to 2HA). These short-term predictions are essential for immediate flood warnings, allowing for timely interventions. However, as the forecast horizon extends to three to six hours ahead (3HA to 6HA), the accuracy of these models diminishes. This reduction in accuracy presents a challenge for medium- to long-term flood forecasting, where predictions become less reliable.

As illustrated in

Table 3. Performance evaluations of the LSTM and CNN models for multihour ahead precipitation intensity forecasting across different categories.

Category	Method	Model	R2	NSE	NRMSE	PBIAS (%)	RSR	AICc
All	CNN	1HA	0.998	0.996	0.08	−4.64	0.06	−16,041.1
		2HA	0.994	0.990	0.12	−5.95	0.10	−12,228.8
		3HA	0.996	0.979	0.18	3.88	0.14	−9425.3
		4HA	0.990	0.981	0.17	−4.30	0.14	−9548.2
		5HA	0.985	0.976	0.21	4.51	0.16	−8615.8
		6HA	0.983	0.975	0.20	−1.62	0.16	−8360.6
	LSTM	1HA	0.999	0.999	0.05	−0.02	0.04	35,785.3
		2HA	0.999	0.998	0.06	0.72	0.04	36,298.2
		3HA	0.997	0.997	0.08	1.48	0.05	38,346.1
		4HA	0.995	0.992	0.12	3.09	0.09	41,060.2
		5HA	0.985	0.984	0.19	1.31	0.13	44,456.4
		6HA	0.987	0.987	0.16	1.11	0.11	43,329.7
Slight	CNN	1HA	0.688	−3.560	0.32	−30.25	2.13	−5705.0
		2HA	0.709	−10.440	0.42	−41.39	3.38	−5771.0
		3HA	0.560	−5.788	0.34	−31.70	2.60	−5355.1
		4HA	0.333	−14.304	0.46	−44.44	3.91	−4851.9
		5HA	0.125	−0.998	0.40	−28.99	1.41	−3688.4
		6HA	0.095	−1.456	0.49	−38.28	1.57	−3238.9
	LSTM	1HA	0.946	0.919	0.07	−4.05	0.28	38,309.1
		2HA	0.910	0.840	0.09	−3.26	0.40	38,914.8
		3HA	0.603	0.587	0.19	1.41	0.64	40,581.7
		4HA	0.547	0.541	0.25	2.82	0.68	41,071.0
		5HA	0.270	−0.451	0.26	−14.67	1.20	41,180.0
		6HA	0.105	−0.137	0.39	−15.03	1.07	42,256.6
Moderate	CNN	1HA	0.994	0.987	0.06	−2.32	0.12	−10,791.5
		2HA	0.985	0.958	0.10	−1.75	0.20	−8364.5
		3HA	0.984	0.938	0.14	7.90	0.25	−8310.3
		4HA	0.957	0.922	0.14	0.37	0.28	−6969.4
		5HA	0.933	0.856	0.21	9.68	0.38	−6216.6
		6HA	0.926	0.900	0.17	2.17	0.32	−6284.7
	LSTM	1HA	0.999	0.999	0.02	−0.11	0.03	33,313.9
		2HA	0.995	0.992	0.05	0.49	0.09	37,413.0
		3HA	0.985	0.981	0.08	2.08	0.14	39,265.6
		4HA	0.968	0.961	0.11	2.35	0.20	40,871.0
		5HA	0.949	0.922	0.16	5.54	0.28	41,996.5
		6HA	0.943	0.938	0.15	2.80	0.25	42,041.1
Heavy	CNN	1HA	0.999	0.999	0.00	−0.04	0.01	−236.9
		2HA	0.999	0.994	0.02	1.48	0.08	−25.5
		3HA	0.999	0.710	0.10	10.12	0.54	392.9
		4HA	0.997	0.929	0.05	5.05	0.27	281.3
		5HA	0.987	0.855	0.08	7.15	0.38	488.0
		6HA	0.883	0.779	0.10	6.63	0.47	824.8
	LSTM	1HA	0.999	0.996	0.01	−0.47	0.06	43,219.7
		2HA	0.999	0.946	0.04	4.30	0.23	43,178.1
		3HA	0.999	0.991	0.02	1.65	0.10	43,241.6
		4HA	0.999	0.919	0.06	5.66	0.28	43,051.3
		5HA	0.999	0.968	0.04	3.11	0.18	43,475.7
		6HA	0.910	0.869	0.07	4.16	0.36	43,771.2
Very Heavy	CNN	1HA	0.999	0.999	0.01	−0.65	0.02	329.4
		2HA	0.999	0.999	0.01	−0.68	0.03	396.1
		3HA	0.999	0.878	0.10	9.61	0.35	529.3
		4HA	0.989	0.968	0.05	4.34	0.18	546.3
		5HA	0.973	0.929	0.08	6.60	0.26	597.4
		6HA	0.976	0.940	0.07	5.52	0.24	586.5
	LSTM	1HA	0.998	0.975	0.04	3.48	0.16	43,795.4
		2HA	0.998	0.997	0.02	−0.29	0.05	43,749.4
		3HA	0.996	0.990	0.03	−1.38	0.10	43,806.5
		4HA	0.989	0.975	0.05	3.44	0.16	43,825.7
		5HA	0.975	0.886	0.11	−7.96	0.33	43,907.1
		6HA	0.973	0.967	0.06	0.57	0.18	43,875.2

, the performance of the CNN and LSTM models is assessed through several metrics, including R², Nash–Sutcliffe efficiency (NSE), normalized root mean square error (NRMSE), percent bias (PBIAS), and root mean square error to standard deviation ratio (RSR). Across these metrics, the LSTM model consistently outperforms the CNN model, particularly as the forecast lead time increases. The LSTM maintains higher R² values, indicating a better fit between predicted and observed data, and higher NSE values, reflecting more accurate predictions.

The CNN model’s performance declines significantly for slight precipitation events as the lead time increases. The R² values for the CNN decrease from satisfactory levels to unsatisfactory as the prediction horizon extends, and NSE values become negative, indicating poor predictive capability. NRMSE and RSR values also worsen, indicating higher error rates and reduced reliability. In contrast, the LSTM model, while also experiencing a decrease in performance, remains relatively more accurate, with better R² and NSE values across all lead times.

Both the CNN and LSTM models perform well in moderate precipitation scenarios, but the LSTM continues to show superior accuracy. The LSTM maintains higher R² and NSE values, reflecting better predictive performance. The NRMSE values for the LSTM remain lower than those for the CNN, indicating more precise error metrics. The PBIAS values for the LSTM are also closer to zero, suggesting less bias in the predictions, making the LSTM the more reliable model for forecasting moderate rainfall and assessing flood risks.

When forecasting heavy precipitation, both models perform strongly, but the LSTM again shows slightly better results. The LSTM maintains high R² and NSE values, with lower NRMSE and RSR values, indicating more accurate and reliable predictions. The performance of both models in this category is crucial for anticipating and mitigating severe flood events, which can significantly impact communities and infrastructure.

Both the CNN and LSTM models perform well for very heavy precipitation, but the LSTM holds a slight edge in most performance indices. The LSTM achieves higher R² and NSE values and maintains lower NRMSE and RSR values, indicating less bias and better accuracy. This makes the LSTM particularly effective for predicting extreme weather events that can lead to catastrophic flooding.

Despite the LSTM’s superior accuracy, CNN models generally have lower corrected Akaike information criterion (AICc) values, which take into account both model accuracy and complexity. The lower AICc values suggest that CNN models are less complex and more computationally efficient, making them suitable for scenarios in which simplicity and speed are prioritized. This trade-off between accuracy and complexity means that, while an LSTM is the preferred model for accuracy, a CNN may be more practical in operational settings where limited resources or simpler models suffice.

The observed trends indicate that both models experience a decline in performance as lead time increases, but the LSTM maintains better performance compared to the CNN across different precipitation categories. This suggests that the LSTM models are more reliable for extended lead-time forecasts, which is critical for effective precipitation intensity forecasting as a key factor for flood forecasting frameworks. Accurate long-term predictions allow for timely flood warnings and better preparedness, reducing potential damage and improving safety. However, with its simpler structure, the CNN model might still be helpful for short-term predictions where computational efficiency is essential. The decline in the CNN’s performance over longer lead times highlights the need for hybrid approaches that leverage the LSTM’s accuracy in critical flood forecasting while utilizing a CNN for rapid, short-term assessments.

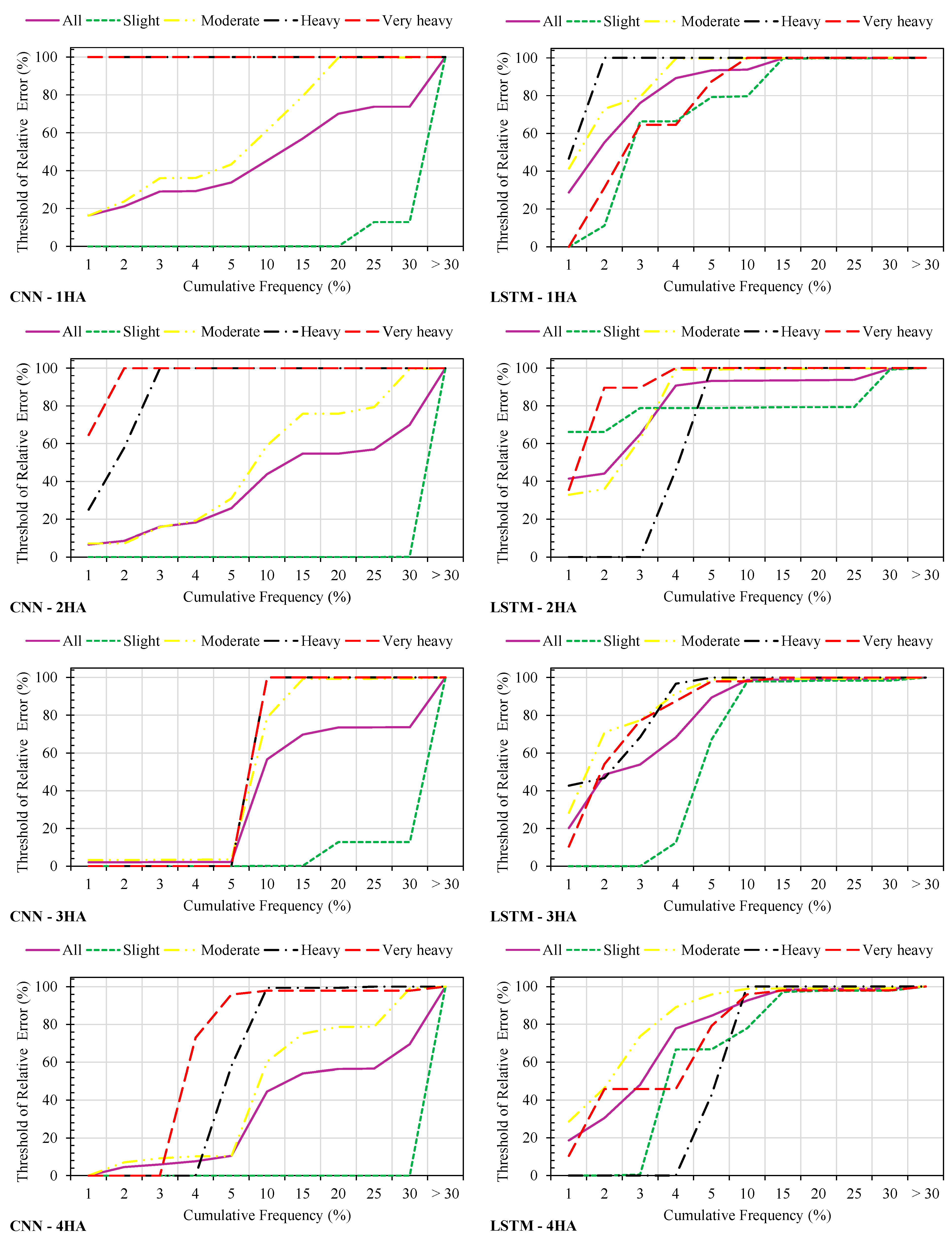
Figure 8 indicates the relative error distribution of the CNN and LSTM techniques for multihours ahead precipitation intensity forecasting across different categories. For the 1 h ahead forecast, the CNN demonstrates a significant advantage in the heavy and very heavy categories, estimating all samples with a relative error of less than 1%. This indicates CNN’s higher precision in forecasting significant precipitation events crucial for immediate flood warnings. In contrast, the LSTM performs exceptionally well in the moderate category, with more than 99% of samples estimated within a 5% error margin, showing its reliability for less intense precipitation. However, while the CNN achieves perfect accuracy within 1% error for the very heavy category, the LSTM still provides valuable forecasts, with 87.5% of samples within 5% error and all within 10%, underscoring its utility despite slightly lower precision.

At 2 h ahead, the CNN continues to excel in the heavy and very heavy categories, estimating 57.89% of heavy samples and all very heavy samples within 2% error. This high accuracy is crucial for medium-term flood forecasting and immediate response planning. LSTM, while not as precise in these categories, still offers competitive performance with 46.05% of heavy samples within 4% error and, all within 5% error, and all very heavy samples within 4% error. For the moderate category, the LSTM outperforms the CNN, with 99.22% of samples within 5% error compared to the CNN’s 30.99%, indicating its robustness in forecasting less severe precipitation over medium-term periods.

For the 3 h ahead forecast, the LSTM shows a substantial advantage in the moderate and heavy categories, estimating 67.13% of slight samples and all heavy samples within 5% error and 96.71% of heavy samples within 4% error, demonstrating its robustness for mid-term flood forecasting. While less precise in these categories, the CNN still provides reliable forecasts, especially in the very heavy category, where both models almost achieve 100% accuracy within 10% error. This indicates that both the CNN and LSTM can be relied upon for extreme precipitation forecasts at this lead time. However, the LSTM’s superior performances in the moderate and heavy categories highlights its overall better suitability for longer-term flood risk management.

At 4 h ahead, the CNN maintains a lead in the very heavy category, with 72.92% of samples estimated within 4% error, highlighting its precision for significant precipitation forecasting essential for flood response strategies. The LSTM, however, excels in the slight and moderate categories, providing more accurate forecasts with 89% of moderate samples within 4% error and all heavy samples within 10% error. Both models perform equally well for the very heavy category, maintaining almost 98% accuracy within 15% error, ensuring reliable predictions for extreme weather events necessary for effective flood preparedness.

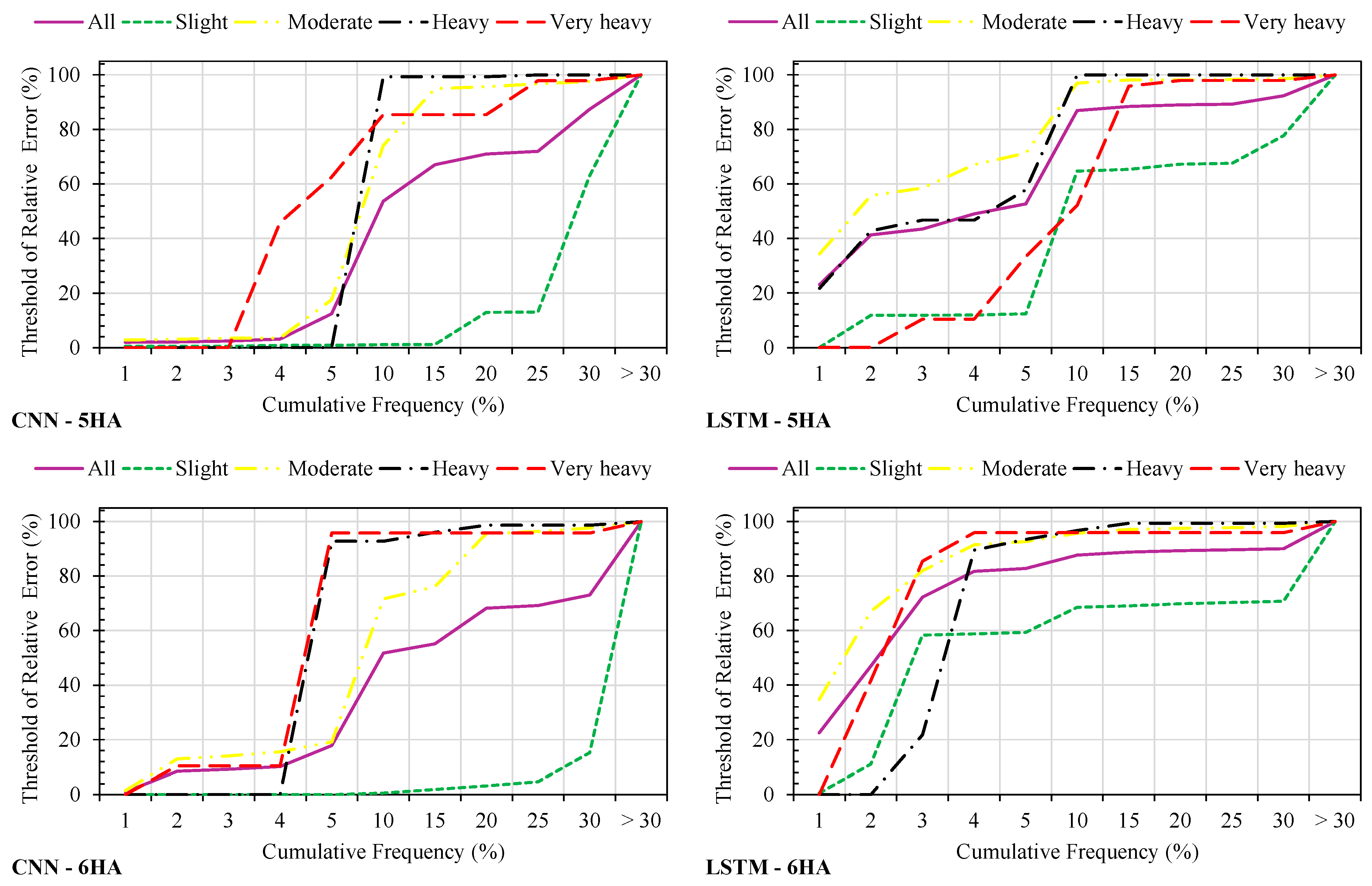
For 5 h ahead, the CNN continues to demonstrate superior accuracy in the very heavy category, estimating 85.42% of samples within 10% error, making it highly reliable for extended flood forecasting. The LSTM shows higher accuracy in the slight and moderate categories, with 64.67% of slight samples and 96.99% of moderate samples within 10% error, indicating its strength in forecasting less severe precipitation over longer periods. Both models maintain high accuracy for the heavy category, with almost all samples estimated within 10% error, underscoring their reliability in predicting extreme precipitation events critical for flood risk mitigation.

At 6 h ahead, the LSTM demonstrates superior performance in the moderate and heavy categories, with 95.67% of moderate samples and 96.71% of heavy samples estimated within 10% error, highlighting its robustness for long-term flood forecasting. The CNN, while slightly less accurate, still provides reliable forecasts, with 71.6% of moderate samples and 92.76% of heavy samples within 10% error. Both models perform equally well in the very heavy category, maintaining 100% accuracy within 30% error, ensuring dependable predictions for extreme weather events necessary for long-term flood preparedness and response planning.

In conclusion, while the CNN generally exhibited a better performance in forecasting significant precipitation (heavy and very heavy categories) at shorter lead times, making it crucial for immediate flood forecasting, the LSTM demonstrated superior accuracy in the moderate category and for longer lead times. This makes the LSTM valuable for extended forecasting and preparedness. Both models maintain high reliability for very heavy precipitation, ensuring effective flood risk management and mitigation strategies. Selecting the appropriate model based on specific forecasting needs and lead times can significantly enhance flood forecasting accuracy and preparedness efforts.

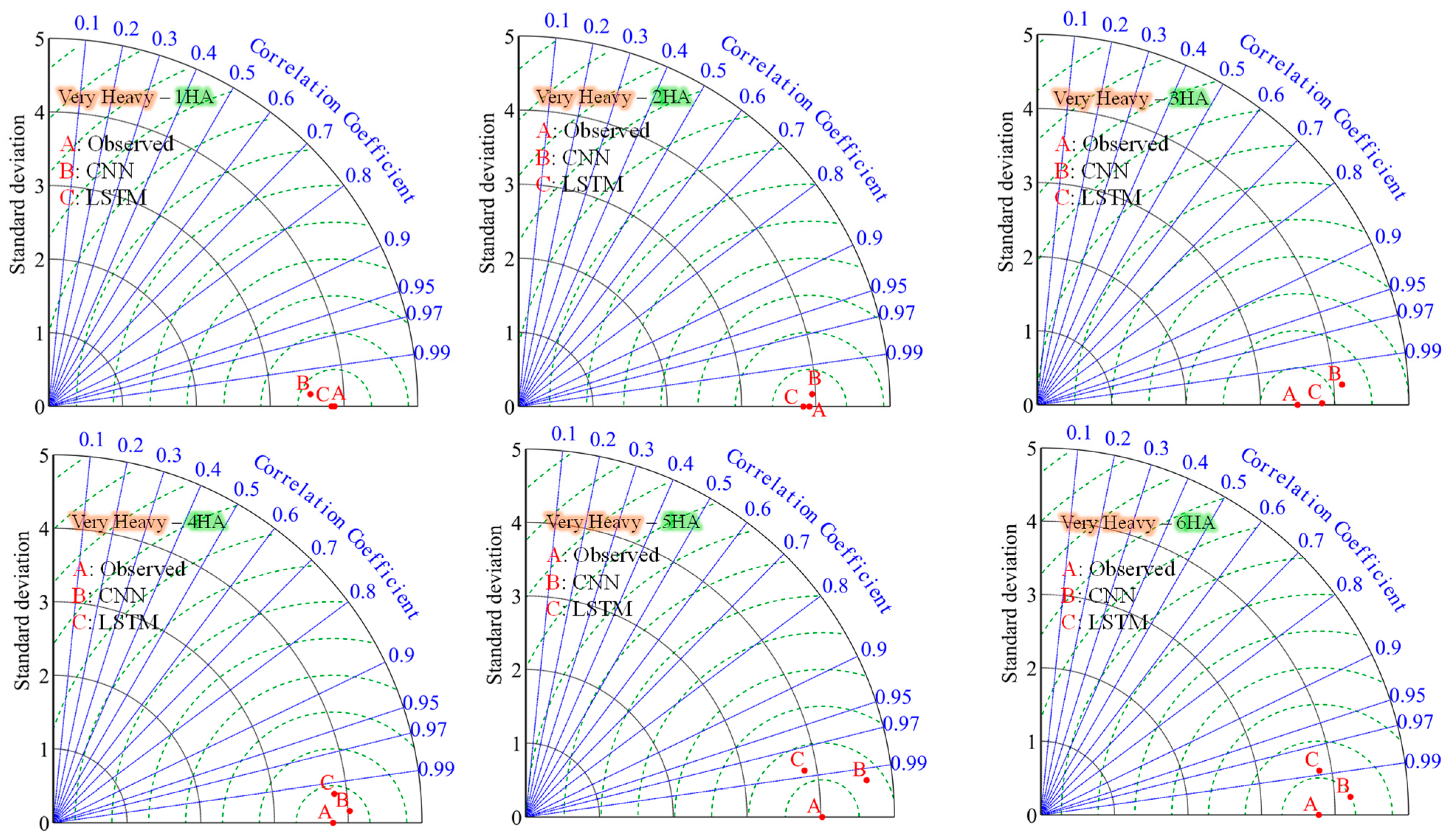
Figure 9 presents Taylor diagrams comparing the CNN and LSTM techniques for multihour ahead precipitation intensity forecasting across various categories. For the “All” category, the comparison between LSTM and CNN shows mixed results across different lead times. LSTM outperforms CNN at 1HA, 3HA, and 5HA, though the differences are generally insignificant or almost zero, indicating that both models perform comparably well. CNN is better at 2HA, 4HA, and 6HA, but again, the differences are insignificant, highlighting that both models are capable but may have slight advantages depending on the specific lead time.

In the “slight” category, the CNN significantly outperformed the LSTM in most lead times, particularly at 2HA, 3HA, 4HA, and 6HA, where the differences are marked as significant. This suggests that, based on the criteria defined in the Taylor diagram, a CNN is more effective in predicting slight precipitation events. The differences at 1HA and 5HA are almost zero or insignificant, indicating that both models perform similarly for very short-term and specific lead-time forecasts.

For the “moderate” category, the CNN consistently outperformed the LSTM across all lead times. The differences at 4HA, 5HA, and 6HA are significant, indicating a clear advantage for the CNN in predicting moderate precipitation events. The differences are insignificant for shorter lead times (1HA to 3HA), suggesting that both models perform similarly for short-term forecasts.

In the “heavy” category, the LSTM generally outperformed the CNN, particularly at shorter lead times (1HA, 2HA, and 3HA), though the differences are insignificant. This suggests that the LSTM is slightly better for short-term forecasts of heavy precipitation. With significant differences, the CNN outperformed the LSTM at 6HA, indicating that the CNN may be more effective for longer-term forecasts of heavy precipitation.

For the “very heavy” category, the performance is mixed. LSTM outperforms CNN at 1HA, 2HA, 3HA, and 5HA, with significant differences at 1HA and 3HA, indicating better accuracy in predicting very heavy precipitation in the short term. With significant differences, the CNN was better at 4HA and 6HA, suggesting that a CNN may be more effective for longer-term forecasts of very heavy precipitation.

Overall, the CNN outperformed the LSTM in certain categories and lead times, particularly for slight and moderate precipitation events, where the differences are often significant. Conversely, LSTM generally performs better for heavy and very heavy precipitation events, especially at shorter lead times, though the differences are sometimes insignificant or almost zero. Based on the provided data, CNN is better in 16 out of 30 cases, making up approximately 53.3%, while LSTM is better in 14 out of 30 cases, accounting for around 46.7%. These results indicate that both models perform comparably, with a CNN being slightly more effective for slight and moderate precipitation forecasts and LSTM often excelling in predicting heavy and very heavy precipitation, particularly in the short term.

4. Discussion

In this study, the comparison between the CNN and LSTM networks reveals important insights into their respective strengths and weaknesses for predicting hourly precipitation intensity, a critical factor in flood forecasting. Unlike typical applications where CNNs are used to recognize patterns in spatial data, this study exclusively deals with temporal data, precisely historical hourly precipitation values. Although not traditionally designed for purely temporal data, the CNN model was adapted to capture localized patterns in the time series. However, CNNs tend to be more effective for short-term predictions (1 to 2 h ahead), where recent precipitation trends are most influential. Their efficiency in capturing these immediate patterns makes CNNs computationally less demanding. However, their performance diminishes for longer-term forecasts as they struggle to capture the temporal dependencies necessary for accurate predictions over extended periods.

LSTM networks, by contrast, are inherently better suited to this task due to their architecture, which is designed to retain and process information across longer time sequences. This characteristic makes LSTMs particularly effective for longer-term forecasts (3 to 6 h ahead), where understanding the temporal progression of precipitation is crucial. The study’s results show that the LSTM model consistently outperformed the CNN across various precipitation categories, including slight, moderate, heavy, and very heavy, especially as the forecast horizon extends.

When analyzing the errors produced by each model, it is evident that the CNN demonstrated higher precision for the heavy and very heavy precipitation categories at shorter lead times, with lower relative errors. However, as the forecast horizon increases, the error rates, including the RMSE, NSE, and RSR, rise significantly for the CNN, indicating their limited capability to capture long-term dependencies. On the other hand, the LSTM model maintained lower errors across all indices, such as the RMSE, NSE, and PBIAS, reflecting their superior performance in modeling the temporal dynamics of precipitation data over more extended periods.

Overfitting and underfitting are common challenges in machine learning, and both models have strategies to address them. CNNs, with their simpler structure, are less prone to overfitting but may underfit when dealing with complex, longer-term predictions due because of their limited capacity to model temporal dependencies. LSTM models, while more complicated and prone to overfitting, manage this risk through techniques such as dropout and careful tuning of hyperparameters. The high performance of the LSTM across various indices in this study suggests that these measures have effectively balanced the model’s complexity and its ability to generalize well from the training data.

Although the impact of training data size was not directly evaluated in this study, it is a critical factor that warrants further investigation. Larger datasets could potentially improve the performance of LSTM models even further, as they rely on extensive temporal data to capture long-term dependencies accurately. Future studies should consider examining how varying the size and diversity of training data affects model performance, particularly for LSTM networks.

Regarding practical implications, while LSTM models offer higher accuracy and are better suited for long-term forecasts and predicting complex precipitation patterns, CNN models are less complex and more computationally efficient. This makes CNNs advantageous in scenarios where quick, short-term predictions are necessary, such as immediate flood warnings based on heavy and very heavy precipitation. However, for critical applications that require accurate extended forecasts, such as flood management strategies, LSTM models should be preferred despite their higher computational demands.

Lastly, both CNN and LSTM models have their unique strengths and weaknesses, making them suitable for different forecasting needs. LSTM models are more accurate and reliable for long-term forecasts and high-intensity precipitation events, which are crucial for effective flood forecasting. Conversely, CNN models offer better computational efficiency and are more appropriate for short-term predictions and operational settings where resources may be limited. Future research should focus on integrating these models into a hybrid framework to employ both strengths and explore the impact of larger datasets on model performance to enhance the accuracy and reliability of precipitation intensity forecasts. This study highlights the importance of using advanced deep learning models in conjunction with historical precipitation data to improve early warning systems and support effective flood preparedness and response efforts.

5. Conclusions

This study comprehensively evaluates precipitation intensity forecasting using CNN and LSTM models, focusing on their performances across various lead times and precipitation categories. Our methodology involved gathering hourly precipitation data from Sainte Catherine de la Jacques Cartier station, defining input combinations for multistep ahead forecasting, and utilizing advanced deep learning models to predict precipitation intensities. The models were then assessed through qualitative and quantitative performance evaluations. Key findings from the study are summarized as follows:

○

Short-Term Forecasting: Both CNN and LSTM models exhibited high accuracy for short-term forecasts (1HA to 2HA). However, the LSTM model generally demonstrated a tighter clustering around the line of equality, suggesting slightly better performance for immediate forecasts;

○

Medium to Long-Term Forecasting: As the forecast horizon was extended (3HA to 6HA), the predictive accuracy of both models declined. The LSTM maintained a consistent edge over the CNN, performing better and handling longer-term forecasts more effectively;

○

Performance Across Precipitation Categories:

➢

Slight Precipitation: The LSTM significantly outperformed the CNN, indicating better predictive accuracy for minor precipitation events;

➢

Moderate Precipitation: The LSTM maintained higher performance indices, making it more reliable for less severe precipitation forecasting;

➢

Heavy and Very Heavy Precipitation: Both models performed well, with the LSTM showing a slight advantage in handling high-intensity events. The CNN, however, demonstrated higher precision for significant precipitation events at shorter lead times.

○

Relative Error Analysis: The relative error distribution indicates that the CNN excels in forecasting significant precipitation events, while the LSTM shows greater reliability for less intense precipitation. This highlights the strengths of each model in different scenarios;

○

Model Complexity, Efficiency, and AICc Evaluation: While LSTM models offer better accuracy, CNN models are less complex, more computationally efficient, and generally have lower AICc values, indicating a better balance between model accuracy and complexity. This trade-off suggests that a CNN may be preferred for short-term predictions, general forecasting, and operational settings with limited computational resources;

○

Taylor Diagram Comparison: The comparison between the CNN and LSTM using Taylor diagrams reveals mixed results. The CNN outperforms the LSTM in slight and moderate precipitation forecasts, while the LSTM excels in heavy and very heavy precipitation predictions, particularly for shorter lead times.

In conclusion, both the CNN and LSTM models have their unique strengths and weaknesses, making them suitable for different forecasting needs. LSTM models are more accurate and reliable for long-term forecasts and high-intensity precipitation events, making them valuable for critical applications like flood forecasting. Conversely, CNN models offer better computational efficiency and are more suitable for short-term predictions and operational settings. Selecting the appropriate model based on specific forecasting requirements and lead times can significantly enhance precipitation intensity forecasting and flood management strategies. This study underscores the importance of integrating advanced deep learning models with historical precipitation data to improve early warning systems and support effective flood preparedness and response efforts.