Relative Homogenization of Climatic Time Series
Abstract
1. Introduction
2. Advance in Relative Homogenization: Concepts and Milestones of Development
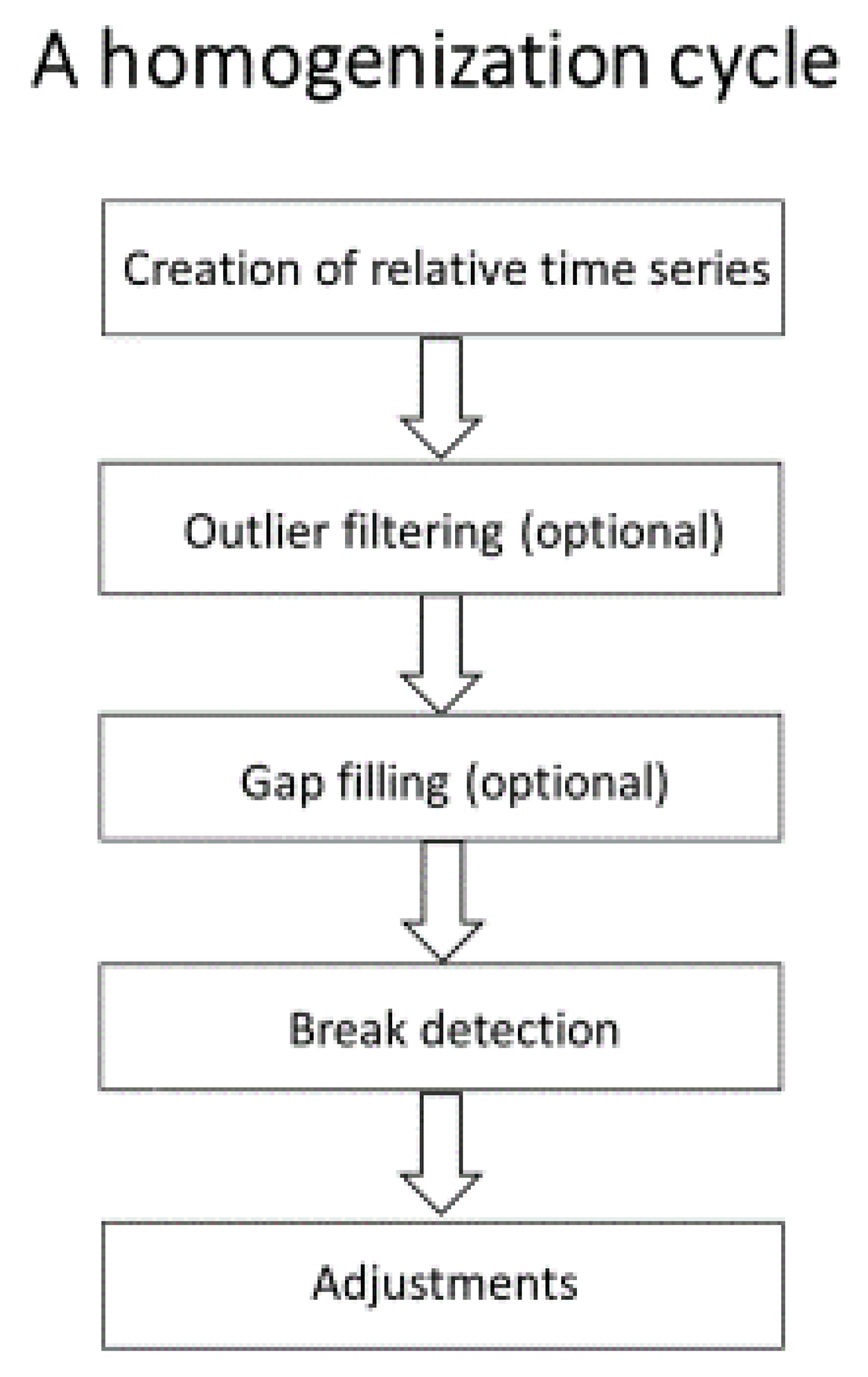
2.1. Basic Concepts
2.2. Traditional Scheme versus Modern Scheme of Relative Homogenization
2.3. Single-Break Detection Methods
2.4. Detection of Gradually Growing Inhomogeneity Biases
2.5. Ensemble Homogenization and MASH
2.6. Combination of Break Detection Methods or Homogenization Methods
2.7. RHtests
2.8. Automatic Evaluation of Pairwise Comparisons
2.9. Members of the PRODIGE Method Family
- (i)
- HOMER includes a break detection method in which the optimization of break positions is jointly performed for a network of time series, and this method is called joint segmentation [68]. Joint segmentation is likely an even more effective method than independently performed step function fittings to individual time series, but the efficiency of joint segmentation has not been tested yet. Note that joint segmentation may be included in homogenization procedures [69,70] others than HOMER.
- (ii)
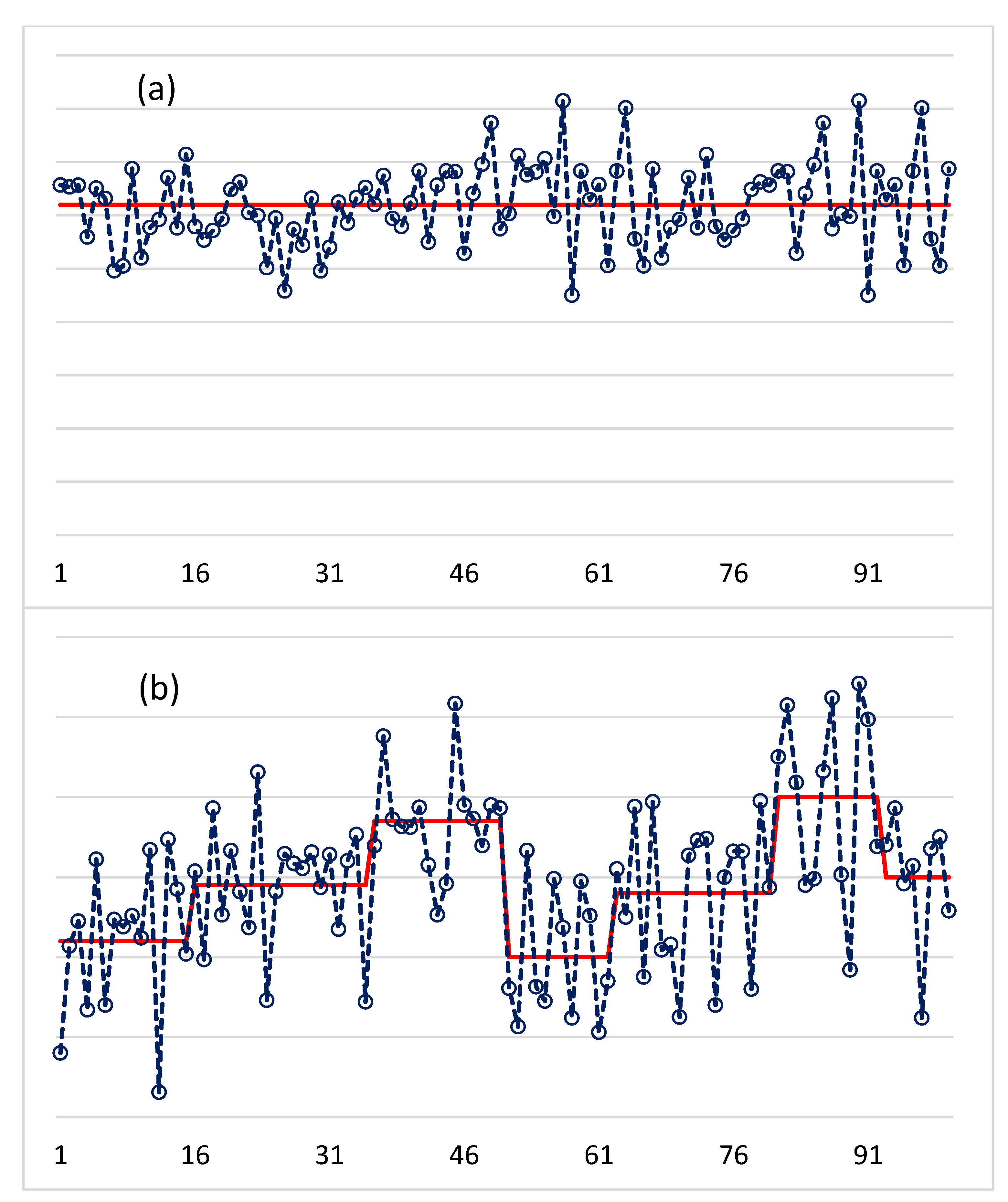
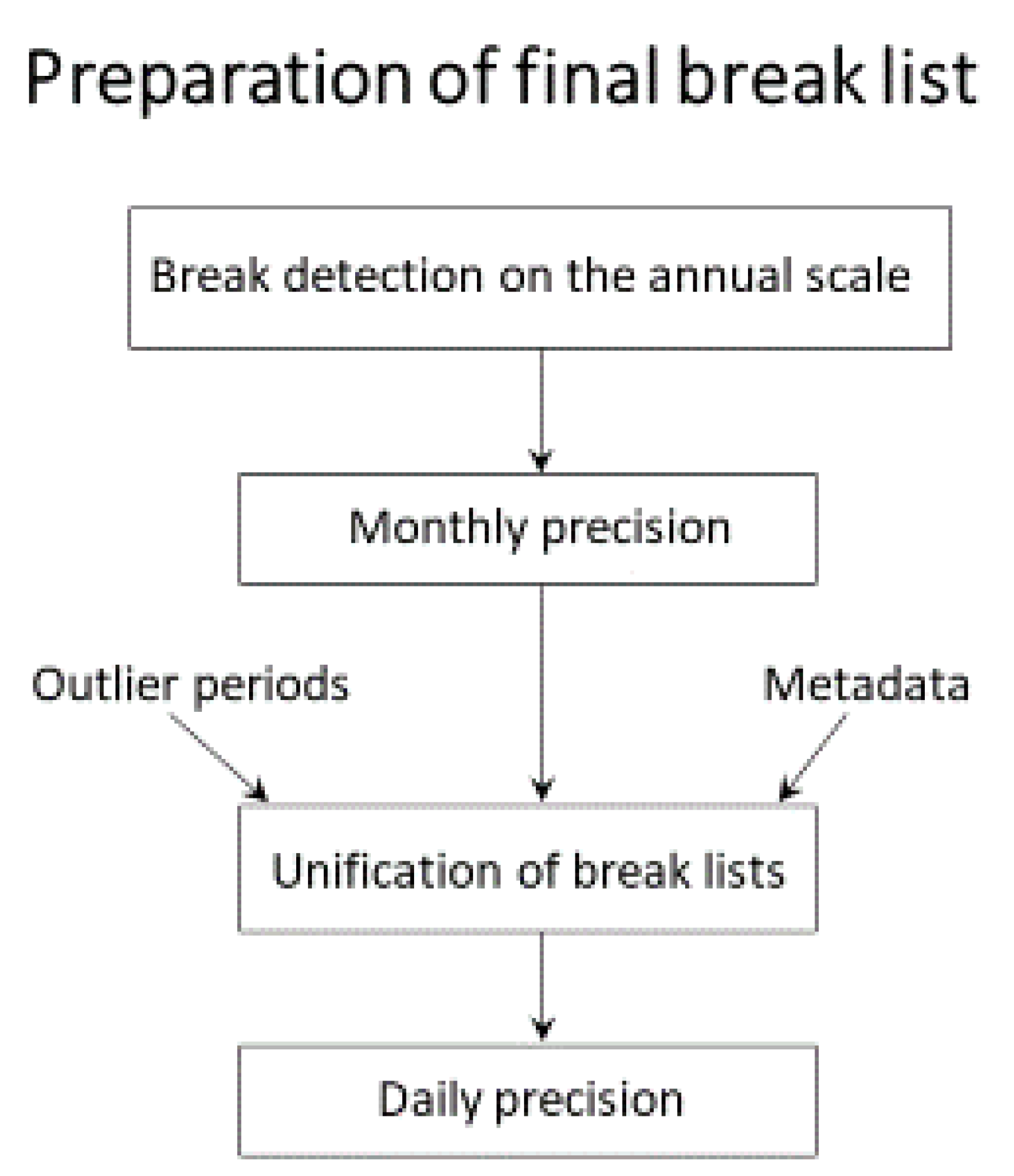
- The harmonization between the use of different time scales is renewed by the introduction of monthly precision steps both to HOMER and ACMANT. Break detections are performed on the annual time scale, then the first obtained detection results are refined on the monthly scale. Daily data can also be homogenized with ACMANT. In ACMANT, possible large magnitude short-term biases are treated in a distinct way from long-lasting biases.
- (iii)
- Where the annual cycle of solar radiation is approximately sinusoid, bivariate break detection is applied for climate variables whose inhomogeneity biases often depend on radiation effects. The two variables are the annual mean and the amplitude of the annual cycle. This method is applied both in HOMER and ACMANT. The advantage of bivariate detection is that while the noise is independent for the two variables, the sign is stronger due to the fact that the breakpoints are common for them. This bivariate detection is useful when more than ~50% of the breaks are related directly or indirectly to radiation changes (e.g., station relocation, type or installation change in the instrument, or change in the microenvironment of the instrument). It can be applied to climate data observed on mid or high latitudes. Small deviations from the astronomic annual cycle due to cloudiness variations do not detract from the usefulness of the method, but it cannot be applied to data from subtropical monsoon regions. In HOMER, the joint treatment of the two mentioned variables is restricted to the break detection part, while in ACMANT it is extended to some other operations of the homogenization procedure. Note that in spite of HOMER and ACMANT having a common root, they differ in many details [34], e.g., ACMANT includes an automatic network edition for input time series and also ensemble homogenization [65].
2.10. Homogenization of Probability Distribution with Quantile Matching
2.11. Climatol Homogenization Method
2.12. Summary Table of Homogenization Method
3. Accuracy of Homogenization Methods
4. Influencing Factors of Homogenization Accuracy
4.1. Time Resolution of Examinations in a Homogenization Procedure
4.2. Comparison of Time Series
- (i)
- We usually accept time series to be neighbor series if they are composed of the same climatic element and originate from the same climatic area as the kind and origin of the candidate series. A problem is that there are no fixed rules for the delimitation of climatic areas. A neighbor series is suitable when its long-term climate signal is approximately the same as that of the candidate series, but before homogenization, we do not know the climate signal. In practical homogenization, usually the geographical distance and/or the spatial correlations between the time series indicate if two series can be compared in a relative homogenization procedure or not. A frequently applied indicator is the spatial correlation calculated from the increment series of the de-seasonalized monthly values [110]. The advantage of using spatial correlations over geographical distances is that the former is more suitable over heterogeneous landscapes, while the use of increment series aims to reduce the effects of possible inhomogeneities on the calculated empirical correlations. In dense observing networks, the optimal number of neighbor series [111] is about 20 to 30, which can be augmented when the period of observation varies between time series. When the station density is low, or when clustered breaks affect the homogeneity of the time series, the search for neighbor series might extend over the usual limits, and, e.g., re-analysis data can also be used as neighbor series [93,112,113].
- (ii)
- The two principal form of time series comparisons are the use of composite reference series or the application of pairwise comparisons (Section 2.1), although sometimes some combinations of the two principal methods are applied [35,74,114]. The SNR is generally higher when composite reference series are used, but pairwise comparisons also have some favorable features: they cope with clustered break problems more effectively than break detection with composite reference series, and they are more applicable to case studies with graphical analyses of inhomogeneity problems [67,105,115].
- (iii)
- The different suitabilities of neighbor series can be considered by their weighting (Equation (3)). The theoretically optimal weights can be obtained by an appropriately designed kriging method, and when no specific geographical features are considered, which is the usual case in the weighting of neighbor series, the weights are provided by the ordinary kriging [36,90]. When using ordinary kriging, also referred to as the optimal interpolation method, a large number of parameters, i.e., all components of the covariance matrix of the considered time series are estimated from the observed data. In spite of possible parameter estimation errors, test results indicate the general superiority of the ordinary kriging method both in practical homogenization and gap filling [102], although with some exceptions: (a) the weighting with the optimal interpolation method does not show any advantage in the homogenization of small networks (N < 7); (b) weighting the neighbor series with the optimal interpolation method is not recommended before the first inhomogeneity bias removal has been applied for the neighbor series. In other words, the use of the optimal interpolation method is recommended only from the second homogenization cycle of a homogenization procedure. Note that the weighting of a neighbor series has relatively little effect on the homogenization accuracy, and thus the use of a simpler method than the optimal weighting may be a reasonable choice for reducing computational time consumption.
4.3. Break Detection Strategies
4.4. Inhomogeneity Bias Removal
4.5. Homogenization of Probability Distribution
- (i)
- The SNR is lower for the homogenization of the standard deviation and percentile values than for that of the section mean values. In the case of high station density, the SNR can be sufficient for the homogenization of the probability distribution, but there is little knowledge about the effective strategies of time series comparisons. Some studies suggest using only the most suitable neighbor series as reference series [80,115], while in the majority of studies, a set of neighbor series is selected for each candidate series, and this is better. However, the limit distance or limit spatial correlation vary widely, e.g., the suggested spatial correlation thresholds are 0.6 and 0.9 in [58] and [119], respectively.
- (ii)
- In automatic and semiautomatic homogenization procedures, usually the last homogeneous section is selected to be the benchmark section. Even when this choice results in an incorrect representation of the local climate regarding the long-term climatic means, it has no effect on the time variation in the studied climatic element. However, this is true only in the homogenization of section means. Using a section with erroneous data as the benchmark section in the homogenization of higher moments could delete some extreme ranges of the correct probability distribution for the entire time series.
- (iii)
- Quantile matching methods need the use of neighbor series which have a sufficiently long homogeneous section around the breakpoint of the candidate series. One problem is that break detection results are imperfect, and even when a section is approximately homogeneous considering the means of its subperiods, its variance might include significant inhomogeneities. Some methodological developments aim to homogenize the means and standard deviations in joint homogenization procedures [37,120]. While these methods include some progressive elements, their practical usability needs further examination.
5. Concluding Remarks
- The efficiency of relative homogenization depends on the characteristics of the given homogenization task, the homogenization method, the availability and use of metadata and on random factors. Homogenization mostly improves but sometimes worsens data accuracy; therefore, its effective use needs carefulness.
- The homogenization of the means generally gives more reliable results than the homogenization of other statistical properties. A statistical homogenization without metadata generally benefits the data accuracy of the individual time series more than the accuracy of regional mean series.
- Due to the large variety of homogenization tasks and the complexity of homogenization methods, the use of exhaustively tested methods should be preferred. The currently available method comparison test results should be considered in method selections, particularly in the homogenization of large, continental or global scale datasets; meanwhile, developments for using more high-quality test datasets are also required.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Climate Change 2021: The Physical Science Basis; Working Group I contribution to the IPCC Sixth Assessment Report; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [CrossRef]
- Venema, V.; Trewin, B.; Wang, X.L.; Szentimrey, T.; Lakatos, M.; Aguilar, E.; Auer, I.; Guijarro, J.; Menne, M.; Oria, C.; et al. Guidelines on Homogenization; WMO-No. 1245; World Meteorological Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Auer, I.; Böhm, R.; Jurkovic, A.; Orlik, A.; Potzmann, R.; Schöner, W.; Ungersböck, M.; Brunetti, M.; Nanni, T.; Maugeri, M.; et al. A new instrumental precipitation dataset for the Greater Alpine Region for the period 1800–2002. Int. J. Climatol. 2005, 25, 139–166. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N.; Vose, R.S. The U.S. Historical Climatology Network Monthly Temperature Data, Version 2. Bull. Am. Meteor. Soc. 2009, 90, 993–1008. [Google Scholar] [CrossRef]
- Venema, V.; Mestre, O.; Aguilar, E.; Auer, I.; Guijarro, J.A.; Domonkos, P.; Vertacnik, G.; Szentimrey, T.; Štěpánek, P.; Zahradníček, P.; et al. Benchmarking monthly homogenization algorithms. Clim. Past 2012, 8, 89–115. [Google Scholar] [CrossRef]
- Moberg, A.; Alexandersson, H. Homogenization of Swedish temperature data. Part II: Homogenized gridded air temperature compared with a subset of global gridded air temperature since 1861. Int. J. Climatol. 1997, 17, 35–54. [Google Scholar] [CrossRef]
- Begert, M.; Schlegel, T.; Kirchhofer, W. Homogeneous temperature and precipitation series of Switzerland from 1864 to 2000. Int. J. Climatol. 2005, 25, 65–80. [Google Scholar] [CrossRef]
- Gubler, S.; Hunziker, S.; Begert, M.; Croci-Maspoli, M.; Konzelmann, T.; Brönnimann, S.; Schwierz, C.; Oria, C.; Rosas, G. The influence of station density on climate data homogenization. Int. J. Climatol. 2017, 37, 4670–4683. [Google Scholar] [CrossRef]
- Yosef, Y.; Aguilar, E.; Alpert, P. Changes in extreme temperature and precipitation indices: Using an innovative daily homogenized database in Israel. Int. J. Climatol. 2019, 39, 5022–5045. [Google Scholar] [CrossRef]
- Domonkos, P. Automatic homogenization of time series: How to use metadata? Atmosphere 2022, 13, 1379. [Google Scholar] [CrossRef]
- Domonkos, P.; Tóth, R.; Nyitrai, L. Climate Observations: Data Quality Control and Time Series Homogenization; Elsevier: Amsterdam, The Netherlands, 2022; 302p. [Google Scholar]
- Lindau, R.; Venema, V.K.C. The uncertainty of break positions detected by homogenization algorithms in climate records. Int. J. Climatol. 2016, 36, 576–589. [Google Scholar] [CrossRef]
- Bodine, D.; Klein, P.M.; Arms, S.C.; Shapiro, A. Variability of surface air temperature over gently sloped terrain. J. Appl. Meteor. Climatol. 2009, 48, 1117–1141. [Google Scholar] [CrossRef]
- Brunet, M.; Asin, J.; Sigró, J.; Bañon, M.; García, F.; Aguilar, E.; Palenzuela, J.E.; Peterson, T.C.; Jones, P. The minimization of the screen bias from ancient Western Mediterranean air temperature records: An exploratory statistical analysis. Int. J. Climatol. 2011, 31, 1879–1895. [Google Scholar] [CrossRef]
- Allard, J.; Vincent, P.C.; McElwaney, J.R.; Hoogenboom, G. A comparison of temperature data from automated and manual observing networks in Georgia and impacts of siting characteristics. J. Atmos. Oceanic Technol. 2016, 33, 1473–1494. [Google Scholar] [CrossRef]
- Caussinus, H.; Mestre, O. Detection and correction of artificial shifts in climate series. J. R. Stat. Soc. Ser. C Appl. Stat. 2004, 53, 405–425. [Google Scholar] [CrossRef]
- Easterling, D.R.; Peterson, T.C. A new method for detecting undocumented discontinuities in climatological time series. Int. J. Climatol. 1995, 15, 369–377. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N., Jr. Detection of undocumented changepoints using multiple test statistics and composite reference series. J. Clim. 2005, 18, 4271–4286. [Google Scholar] [CrossRef]
- Domonkos, P. Efficiency evaluation for detecting inhomogeneities by objective homogenisation methods. Theor. Appl. Climatol. 2011, 105, 455–467. [Google Scholar] [CrossRef]
- Van Malderen, R.; Pottiaux, E.; Klos, A.; Domonkos, P.; Elias, M.; Ning, T.; Bock, O.; Guijarro, J.; Alshawaf, F.; Hoseini, M.; et al. 2020: Homogenizing GPS integrated vapor time series: Benchmarking break detection methods on synthetic datasets. Earth Space Sci. 2020, 7, e2020EA001121. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Maronna, R.; Yohai, V.J. A bivariate test for the detection of a systematic change in mean. J. Am. Stat. Assoc. 1978, 73, 640–645. [Google Scholar] [CrossRef]
- Perreault, L.; Haché, M.; Slivitzky, M.; Bobée, B. Detection of changes in precipitation and runoff over eastern Canada and U.S. using a Bayesian approach. Stoch. Environ. Res. Risk Assess. 1999, 13, 201–216. [Google Scholar] [CrossRef]
- Wang, X.L.; Wen, Q.H.; Wu, Y. Penalized maximal t test for detecting undocumented mean change in climate data series. J. Appl. Meteor. Climatol. 2007, 46, 916–931. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitationdata. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J. On the critical values of the standard normal homogeneity test (SNHT). Int. J. Climatol. 2007, 27, 681–687. [Google Scholar] [CrossRef]
- Pandžić, K.; Kobold, M.; Oskoruš, D.; Biondić, B.; Biondić, R.; Bonacci, O.; Likso, T.; Curić, O. Standard normal homogeneity test as a tool to detect change points in climate-related river discharge variation: Case study of the Kupa River Basin. Hydrol. Sci. J. 2020, 65, 227–241. [Google Scholar] [CrossRef]
- Tadić, L.; Tamás, E.A.; Mihaljević, M.; Janjić, J. Potential climate impacts of hydrological alterations and discharge variabilities of the Mura, Drava, and Danube rivers on the natural resources of the MDD UNESCO biosphere reserve. Climate 2022, 10, 139. [Google Scholar] [CrossRef]
- Vrsalović, A.; Andrić, I.; Bonacci, O.; Kovčić, O. Climate variability and trends in Imotski, Croatia: An analysis of temperature and precipitation. Atmosphere 2023, 14, 861. [Google Scholar] [CrossRef]
- Alexandersson, H.; Moberg, A. Homogenization of Swedish temperature data. Part I: Homogeneity test for linear trends. Int. J. Climatol. 1997, 17, 25–34. [Google Scholar] [CrossRef]
- Vincent, L.A. A technique for the identification of inhomogeneities in Canadian temperature series. J. Clim. 1998, 11, 1094–1104. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams Jr, C.N. Homogenization of temperature series via pairwise comparisons. J. Clim. 2009, 22, 1700–1717. [Google Scholar] [CrossRef]
- Domonkos, P.; Coll, J. Time series homogenisation of large observational datasets: The impact of the number of partner series on the efficiency. Clim. Res. 2017, 74, 31–42. [Google Scholar] [CrossRef]
- Szentimrey, T. Multiple Analysis of Series for Homogenization (MASH). In Second Seminar for Homogenization of Surface Climatological Data; Szalai, S., Szentimrey, T., Szinell, C., Eds.; WCDMP-41; WMO: Geneva, Switzerland, 1999; pp. 27–46. [Google Scholar]
- Izsák, B.; Szentimrey, T. To what extent does the detection of climate change in Hungary depend on the choice of statistical methods? Int. J. Geomath. 2020, 11, 17. [Google Scholar] [CrossRef]
- Szentimrey, T. Overview of mathematical background of homogenization, summary of method MASH and comments on benchmark validation. Int. J. Climatol. 2023, 43, 6314–6329. [Google Scholar] [CrossRef]
- Spinoni, J.; Szalai, S.; Szentimrey, T.; Lakatos, M.; Bihari, Z.; Nagy, A.; Németh, Á.; Kovács, T.; Mihic, D.; Dacic, M.; et al. Climate of the Carpathian Region in the period 1961–2010: Climatologies and trends of 10 variables. Int. J. Climatol. 2015, 35, 1322–1341. [Google Scholar] [CrossRef]
- Ilona, J.; Bartók, B.; Dumitrescu, A.; Cheval, S.; Gandhi, A.; Tordai, Á.V.; Weidinger, T. Using long-term historical meteorological data for climate change analysis in the Carpathian region. Atmosphere 2022, 13, 1751. [Google Scholar] [CrossRef]
- Li, Z.; Shi, Y.; Argiriou, A.A.; Ioannidis, P.; Mamara, A.; Yan, Z. A comparative analysis of changes in temperature and precipitation extremes since 1960 between China and Greece. Atmosphere 2022, 13, 1824. [Google Scholar] [CrossRef]
- Szentes, O.; Lakatos, M.; Pongrácz, R. New homogenized precipitation database for Hungary from 1901. Int. J. Climatol. 2023, 43, 4457–4471. [Google Scholar] [CrossRef]
- Trewin, B.; Braganza, K.; Fawcett, R.; Grainger, S.; Jovanovic, B.; Jones, D.; Martin, D.; Smalley, R.; Webb, V. An updated long-term homogenized daily temperature data set for Australia. Geosci. Data J. 2020, 7, 149–169. [Google Scholar] [CrossRef]
- Mohammed, R.; Scholz, M. Quality control and homogeneity analysis of precipitation time series in the climatic region of Iraq. Atmosphere 2023, 14, 197. [Google Scholar] [CrossRef]
- Stefanini, C.; Becherini, F.; della Valle, A.; Rech, F.; Zecchini, F.; Camuffo, D. Homogeneity assessment and correction methodology for the 1980–2022 daily temperature series in Padua, Italy. Climate 2023, 11, 244. [Google Scholar] [CrossRef]
- Tejada, A.T., Jr.; Sanchez, P.A.J.; Faderogao, F.J.F.; Gigantone, C.B.; Luyun, R.A., Jr. Spatiotemporal analysis of extreme rainfall and meteorological drought events over the Angat watershed, Philippines. Atmosphere 2023, 14, 1790. [Google Scholar] [CrossRef]
- Brugnara, Y.; McCarthy, M.P.; Willett, K.M.; Rayner, N.A. Homogenization of daily temperature and humidity series in the UK. Int. J. Climatol. 2023, 43, 1693–1709. [Google Scholar] [CrossRef]
- Fioravanti, G.; Piervitali, E.; Desiato, F. A new homogenized daily data set for temperature variability assessment in Italy. Int. J. Climatol. 2019, 39, 5635–5654. [Google Scholar] [CrossRef]
- Randriamarolaza, L.Y.A.; Aguilar, E.; Skrynyk, O.; Vicente-Serrano, S.M.; Domínguez-Castro, F. Indices for daily temperature and precipitation in Madagascar, based on quality-controlled and homogenized data, 1950–2018. Int. J. Climatol. 2022, 42, 265–288. [Google Scholar] [CrossRef]
- Skrynyk, O.; Sidenko, V.; Aguilar, E.; Guijarro, J.; Skrynyk, O.; Palamarchuk, L.; Oshurok, D.; Osypov, V.; Osadchyi, V. Data quality control and homogenization of daily precipitation and air temperature (mean, max and min) time series of Ukraine. Int. J. Climatol. 2023, 43, 4166–4182. [Google Scholar] [CrossRef]
- Chimani, B.; Bochníček, O.; Brunetti, M.; Ganekind, M.; Holec, J.; Izsák, B.; Lakatos, M.; Tadić, M.P.; Manara, V.; Maugeri, M.; et al. Revisiting HISTALP precipitation dataset. Int. J. Climatol. 2023, 43, 7381–7411. [Google Scholar] [CrossRef]
- Wang, X.L.; Feng, Y. RHtestsV4 User Manual; Climate Research Division, Atmospheric Science and Technology Directorate, Science and Technology Branch, Environment Canada: Toronto, ON, Canada, 2013; 28p, Available online: https://github.com/ECCC-CDAS (accessed on 6 April 2024).
- Wang, X.L.; Feng, Y.; Cheng, V.Y.S.; Xu, H. Observed precipitation trends inferred from Canada’s homogenized monthly precipitation dataset. J. Clim. 2023, 36, 7957–7971. [Google Scholar] [CrossRef]
- Lund, R.; Wang, X.L.; Lu, Q.Q.; Reeves, J.; Gallagher, C.; Feng, Y. Changepoint detection in periodic and autocorrelated time series. J. Clim. 2007, 20, 5178–5190. [Google Scholar] [CrossRef]
- Xu, W.; Sun, C.; Zuo, J.; Ma, Z.; Li, W.; Yang, S. Homogenization of monthly ground surface temperature in China during 1961–2016 and performances of GLDAS reanalysis products. J. Clim. 2019, 32, 1121–1135. [Google Scholar] [CrossRef]
- Cao, J.; Li, M.; Wang, M.; Li, B. Impacts of temperature and humidity changes on air-conditioning design load under the climate change conditions in different climate zones of China. Meteorol. Appl. 2021, 28, e2026. [Google Scholar] [CrossRef]
- Hague, B.S.; Jones, D.A.; Trewin, B.; Jakob, D.; Murphy, B.F.; Martin, D.J.; Braganza, K. ANCHORS: A multi-decadal tide gauge dataset to monitor Australian relative sea level changes. Geosci. Data J. 2022, 9, 256–272. [Google Scholar] [CrossRef]
- Ryan, C.; Curley, M.; Walsh, S.; Murphy, C. Long-term trends in extreme precipitation indices in Ireland. Int. J. Climatol. 2022, 42, 4040–4061. [Google Scholar] [CrossRef]
- Trewin, B. A daily homogenized temperature data set for Australia. Int. J. Climatol. 2013, 33, 1510–1529. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N.; Gleason, B.E.; Rennie, J.J.; Lawrimore, J.H. The Global Historical Climatology Network monthly temperature dataset, version 4. J. Clim. 2018, 31, 9835–9854. [Google Scholar] [CrossRef]
- Williams, C.N.; Menne, M.J.; Thorne, P. Benchmarking the performance of pairwise homogenization of surface temperatures in the United States. J. Geophys. Res. 2012, 117, D05116. [Google Scholar] [CrossRef]
- Hausfather, Z.; Cowtan, K.; Menne, M.J.; Williams, C.N., Jr. Evaluating the impact of U.S. Historical Climatology Network homogenization using the U.S. Climate Reference Network. Geophys. Res. Lett. 2016, 43, 1695–1701. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Willett, K.M.; Morice, C.P.; Parker, D.E. Pairwise homogeneity assessment of HadISD. Clim. Past 2014, 10, 1501–1522. [Google Scholar] [CrossRef]
- O’Neill, P.; Connolly, R.; Connolly, M.; Soon, W.; Chimani, B.; Crok, M.; de Vos, R.; Harde, H.; Kajaba, P.; Nojarov, P.; et al. Evaluation of the homogenization adjustments applied to European temperature records in the Global Historical Climatology Network Dataset. Atmosphere 2022, 13, 285. [Google Scholar] [CrossRef]
- Chan, D.; Gebbie, G.; Huybers, P. An improved ensemble of land surface air temperatures since 1880 using revised pair-wise homogenization algorithms accounting for autocorrelation. J. Clim. 2024, 37, 2325–2345. [Google Scholar] [CrossRef]
- Domonkos, P. ACMANTv4: Scientific Content and Operation of the Software. 71p. 2020. Available online: https://github.com/dpeterfree/ACMANT/blob/ACMANTv4.4/ACMANTv4_description.pdf (accessed on 6 April 2024).
- Prohom, M.; Domonkos, P.; Cunillera, J.; Barrera-Escoda, A.; Busto, M.; Herrero-Anaya, M.; Aparicio, A.; Reynés, J. CADTEP: A new daily quality-controlled and homogenized climate database for Catalonia (1950–2021). Int. J. Climatol. 2023, 43, 4771–4789. [Google Scholar] [CrossRef]
- Mestre, O.; Domonkos, P.; Picard, F.; Auer, I.; Robin, S.; Lebarbier, E.; Böhm, R.; Aguilar, E.; Guijarro, J.; Vertacnik, G.; et al. HOMER: Homogenization software in R—Methods and applications. Időjárás 2013, 117, 47–67. [Google Scholar]
- Picard, F.; Lebarbier, E.; Hoebeke, M.; Rigaill, G.; Thiam, B.; Robin, S. Joint segmentation, calling, and normalization of multiple CGH profiles. Biostatistics 2011, 12, 413–428. [Google Scholar] [CrossRef] [PubMed]
- Hannak, L.; Friedrich, K.; Imbery, F.; Kaspar, F. Analyzing the impact of automatization using parallel daily mean temperature series including breakpoint detection and homogenization. Int. J. Climatol. 2020, 40, 6544–6559. [Google Scholar] [CrossRef]
- Kunert, L.; Friedrich, K.; Imbery, F.; Kaspar, F. Homogenization of German daily and monthly mean temperature time series. Int. J. Climatol. 2024, 44, 775–791. [Google Scholar] [CrossRef]
- Coll, J.; Domonkos, P.; Guijarro, J.; Curley, M.; Rustemeier, E.; Aguilar, E.; Walsh, S.; Sweeney, J. Application of homogenization methods for Ireland’s monthly precipitation records: Comparison of break detection results. Int. J. Climatol. 2020, 40, 6169–6188. [Google Scholar] [CrossRef] [PubMed]
- Joelsson, L.M.T.; Sturm, C.; Södling, J.; Engström, E.; Kjellström, E. Automation and evaluation of the interactive homogenization tool HOMER. Int. J. Climatol. 2022, 42, 2861–2880. [Google Scholar] [CrossRef]
- Joelsson, L.M.T.; Engström, E.; Kjellström, E. Homogenization of Swedish mean monthly temperature series 1860–2021. Int. J. Climatol. 2023, 43, 1079–1093. [Google Scholar] [CrossRef]
- Domonkos, P. Combination of using pairwise comparisons and composite reference series: A new approach in the homogenization of climatic time series with ACMANT. Atmosphere 2021, 12, 1134. [Google Scholar] [CrossRef]
- Bertrand, C.; Ingels, R.; Journée, M. Homogenization and trends analysis of the Belgian historical precipitation time series. Int. J. Climatol. 2021, 41, 5277–5294. [Google Scholar] [CrossRef]
- Sajjad, S.H.; Blond, N.; Mohsin, T.; Shakrullah, K.; Clappier, A. Temperature variability over urban, town, and rural areas: The case of Pakistan. Int. J. Climatol. 2022, 42, 2881–2900. [Google Scholar] [CrossRef]
- Cornes, R.C.; Jones, P.D.; Brandsma, T.; Cendrier, D.; Jourdain, S. The London, Paris and De Bilt sub-daily pressure series. Geosci. Data J. 2024, 11, 330–341. [Google Scholar] [CrossRef]
- Adeyeri, O.E.; Laux, P.; Ishola, K.A.; Zhou, W.; Balogun, I.A.; Adeyewa, Z.D.; Kunstmann, H. Homogenising meteorological variables: Impact on trends and associated climate indices. J. Hydrol. 2022, 607, 127585. [Google Scholar] [CrossRef]
- Molina-Carpio, J.; Rivera, I.A.; Espinoza-Romero, D.; Cerón, W.L.; Espinoza, J.-C.; Ronchail, J. Regionalization of rainfall in the upper Madeira basin based on interannual and decadal variability: A multi-seasonal approach. Int. J. Climatol. 2023, 43, 6402–6419. [Google Scholar] [CrossRef]
- Della-Marta, P.M.; Wanner, H. A method of homogenizing the extremes and mean of daily temperature measurements. J. Clim. 2006, 19, 4179–4197. [Google Scholar] [CrossRef]
- Štěpánek, P.; Zahradnicek, P.; Farda, A. Experiences with data quality control and homogenisation of daily records of various meteorological elements in the Czech Republic in the period 1961–2010. Időjárás 2013, 117, 123–141. [Google Scholar]
- Squintu, A.A.; van der Schrier, G.; Brugnara, Y.; Klein Tank, A. Homogenization of daily temperature series in the European Climate Assessment & Dataset. Int. J. Climatol. 2019, 39, 1243–1261. [Google Scholar] [CrossRef]
- Resch, G.; Koch, R.; Marty, C.; Chimani, B.; Begert, M.; Buchmann, M.; Aschauer, J.; Schöner, W. A quantile-based approach to improve homogenization of snow depth time series. Int. J. Climatol. 2023, 43, 157–173. [Google Scholar] [CrossRef]
- Guijarro, J.A. Homogenization of Climatic Series with Climatol. 2018. Available online: https://www.climatol.eu (accessed on 6 April 2024).
- Azorin-Molina, C.; Guijarro, J.A.; McVicar, T.R.; Trewin, B.C.; Frost, A.J.; Chen, D. An approach to homogenize daily peak wind gusts: An application to the Australian series. Int. J. Climatol. 2019, 39, 2260–2277. [Google Scholar] [CrossRef]
- Montero-Martínez, M.J.; Andrade-Velázquez, M. Effects of urbanization on extreme climate indices in the valley of Mexico Basin. Atmosphere 2022, 13, 785. [Google Scholar] [CrossRef]
- Kessabi, R.; Hanchane, M.; Guijarro, J.A.; Krakauer, N.Y.; Addou, R.; Sadiki, A.; Belmahi, M. Homogenization and trends analysis of monthly precipitation series in the Fez-Meknes region, Morocco. Climate 2022, 10, 64. [Google Scholar] [CrossRef]
- Pauca-Tanco, G.A.; Arias-Enríquez, J.F.; Quispe-Turpo, J.d.P. High-resolution bioclimatic surfaces for Southern Peru: An approach to climate reality for biological conservation. Climate 2023, 11, 96. [Google Scholar] [CrossRef]
- Jupin, J.L.J.; Garcia-López, A.A.; Briceño-Zuluaga, F.J.; Sifeddine, A.; Ruiz-Fernández, A.C.; Sanchez-Cabeza, J.-A.; Cardoso-Mohedano, J.G. Precipitation homogenization and trends in the Usumacinta River Basin (Mexico-Guatemala) over the period 1959–2018. Int. J. Climatol. 2024, 44, 108–125. [Google Scholar] [CrossRef]
- Szentimrey, T. Methodological questions of series comparison. In Sixth Seminar for Homogenization and Quality Control in Climatological Databases; Lakatos, M., Szentimrey, T., Bihari, Z., Szalai, S., Eds.; WCDMP-76; WMO: Geneva, Switzerland, 2010; pp. 1–7. [Google Scholar]
- Bock, O.; Collilieux, X.; Guillamon, F.; Lebarbier, E.; Pascal, C. A breakpoint detection in the mean model with heterogeneous variance on fixed time-intervals. Stat. Comput. 2020, 30, 195–207. [Google Scholar] [CrossRef]
- Lindau, R.; Venema, V.K.C. On the reduction of trend errors by the ANOVA joint correction scheme used in homogenization of climate station records. Int. J. Climatol. 2018, 38, 5255–5271. [Google Scholar] [CrossRef]
- Gillespie, I.M.; Haimberger, L.; Compo, G.P.; Thorne, P.W. Assessing potential of sparse-input reanalyses for centennial-scale land surface air temperature homogenization. Int. J. Climatol. 2021, 41, E3000–E3020. [Google Scholar] [CrossRef]
- Katata, G.; Connolly, R.; O’Neill, P. Evidence of urban blending in homogenized temperature records in Japan and in the United States: Implications for the reliability of global land surface air temperature data. J. Appl. Meteor. Climatol. 2023, 62, 1095–1114. [Google Scholar] [CrossRef]
- Thorne, P.W.; Menne, M.J.; Williams, C.N.; Rennie, J.J.; Lawrimore, J.H.; Vose, R.S.; Peterson, T.C.; Durre, I.; Davy, R.; Esau, I.; et al. Reassessing changes in diurnal temperature range: A new data set and characterization of data biases. J. Geophys. Res. Atmos. 2016, 121, 5115–5137. [Google Scholar] [CrossRef]
- Lindau, R.; Venema, V.K.C. The joint influence of break and noise variance on the break detection capability in time series homogenization. Adv. Stat. Clim. Meteorol. Oceanogr. 2018, 4, 1–18. [Google Scholar] [CrossRef]
- Lindau, R.; Venema, V.K.C. A new method to study inhomogeneities in climate records: Brownian motion or random deviations? Int. J. Climatol. 2019, 39, 4769–4783. [Google Scholar] [CrossRef]
- Lindau, R.; Venema, V.K.C. Random trend errors in climate station data due to inhomogeneities. Int. J. Climatol. 2020, 40, 2393–2402. [Google Scholar] [CrossRef]
- Guijarro, J.A.; López, J.A.; Aguilar, E.; Domonkos, P.; Venema, V.K.C.; Sigró, J.; Brunet, M. Homogenization of monthly series of temperature and precipitation: Benchmarking results of the MULTITEST project. Int. J. Climatol. 2023, 43, 3994–4012. [Google Scholar] [CrossRef]
- Guijarro, J.A. Influence of network density on homogenization performance. In Seventh Seminar for Homogenization and Quality Control in Climatological Databases; Lakatos, M., Szentimrey, T., Vincze, E., Eds.; WCDMP-78; WMO: Geneva, Switzerland, 2011; pp. 11–18. [Google Scholar]
- Domonkos, P.; Guijarro, J.A.; Brunet, M.; Venema, V.; Sigró, J. Benchmark Dataset of MULTITEST—TEMP12. Webpage, 2020. Available online: https://zenodo.org/records/3934835#.XwTjF-dS_IU (accessed on 7 May 2024).
- Domonkos, P.; Guijarro, J.A.; Venema, V.; Brunet, M.; Sigró, J. Efficiency of time series homogenization: Method comparison with 12 monthly temperature test datasets. J. Clim. 2021, 34, 2877–2891. [Google Scholar] [CrossRef]
- Killick, R.E. Benchmarking the Performance of Homogenisation Algorithms on Daily Temperature Data. Ph.D. Thesis, University of Exeter, Exeter, UK, 2016. Available online: https://ore.exeter.ac.uk/repository/handle/10871/23095 (accessed on 6 April 2024).
- Guijarro, J.A. Recommended Homogenization Techniques Based on Benchmarking Results. WP-3 Report of INDECIS Project. 2019. Available online: http://www.indecis.eu/docs/Deliverables/Deliverable_3.2.b.pdf (accessed on 6 April 2024).
- Kuglitsch, F.G.; Toreti, A.; Xoplaki, E.; Della-Marta, P.M.; Luterbacher, J.; Wanner, H. Homogenization of daily maximum temperature series in the Mediterranean. J. Geophys. Res. 2009, 114, D15108. [Google Scholar] [CrossRef]
- Wang, X.L.; Chen, H.; Wu, Y.; Feng, Y.; Pu, Q. New techniques for the detection and adjustment of shifts in daily precipitation data series. J. Appl. Meteor. Climatol. 2010, 49, 2416–2436. [Google Scholar] [CrossRef]
- Hewaarachchi, A.P.; Li, Y.; Lund, R.; Rennie, J. Homogenization of daily temperature data. J. Clim. 2017, 30, 985–999. [Google Scholar] [CrossRef]
- Woody, J.; Xu, Y.; Dyer, J.; Lund, R.; Hewaarachchi, A.P. A statistical analysis of daily snow depth trends in North America. Atmosphere 2021, 12, 820. [Google Scholar] [CrossRef]
- Lund, R.B.; Beaulieu, C.; Killick, R.; Lu, Q.; Shi, X. Good practices and common pitfalls in climate time series changepoint techniques: A review. J. Clim. 2023, 36, 8041–8057. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R. Creation of homogeneous composite climatological reference series. Int. J. Climatol. 1994, 14, 671–679. [Google Scholar] [CrossRef]
- Domonkos, P. Time series homogenization with ACMANT: Comparative testing of two recent versions in large-size synthetic temperature datasets. Climate 2023, 11, 224. [Google Scholar] [CrossRef]
- Haimberger, L.; Tavolato, C.; Sperka, S. Homogenization of the global radiosonde temperature dataset through combined comparison with reanalysis background series and neighboring stations. J. Clim. 2012, 25, 8108–8131. [Google Scholar] [CrossRef]
- Nguyen, K.N.; Quarello, A.; Bock, O.; Lebarbier, E. Sensitivity of change-point detection and trend estimates to GNSS IWV time series properties. Atmosphere 2021, 12, 1102. [Google Scholar] [CrossRef]
- Rustemeier, E.; Kapala, A.; Meyer-Christoffer, A.; Finger, P.; Schneider, U.; Venema, V.; Ziese, M.; Simmer, C.; Becker, A. AHOPS Europe—A gridded precipitation data set from European homogenized time series. In Proceedings of the Ninth Seminar for Homogenization and Quality Control in Climatological Databases, Budapest, Hungary, 3–7 April 2017; Szentimrey, T., Lakatos, M., Hoffmann, L., Eds.; WCDMP-85. WMO: Geneva, Switzerland, 2017; pp. 88–101. [Google Scholar]
- Nemec, J.; Gruber, C.; Chimani, B.; Auer, I. Trends in extreme temperature indices in Austria based on a new homogenised dataset. Int. J. Climatol. 2013, 33, 1538–1550. [Google Scholar] [CrossRef]
- Štěpánek, P. Homogenization of air temperature series in the Czech Republic during a period of instrumental measurements. In Proceedings of the Fourth Seminar for Homogenization and Quality Control in Climatological Databases, Budapest, Hungary, 6–10 October 2003; Szalai, S., Ed.; WCDMP 56. WMO: Geneva, Switzerland, 2004; pp. 117–133. [Google Scholar]
- Shi, X.; Gallagher, C.; Lund, R.; Killick, R. A comparison of single and multiple changepoint techniques for time series data. Comput. Stat. Data Anal. 2022, 170, 107433. [Google Scholar] [CrossRef]
- Domonkos, P.; Joelsson, L.M.T. ANOVA (Benova) correction in relative homogenization: Why it is indispensable. Int. J. Climatol. 2024; in production. [Google Scholar]
- Mestre, O.; Gruber, C.; Prieur, C.; Caussinus, H.; Jourdain, S. SPLIDHOM: A method for homogenization of daily temperature observations. J. Appl. Meteorol. Climatol. 2011, 50, 2343–2358. [Google Scholar] [CrossRef]
- Toreti, A.; Kuglitsch, F.G.; Xoplaki, E.; Luterbacher, J. A novel approach for the detection of inhomogeneities affecting climate time series. J. Appl. Meteorol. Climatol. 2012, 51, 317–326. [Google Scholar] [CrossRef]


| Homogenization Method | Comparison of Time Series | Break Detection Method | Adjustments | Number of Cycles |
|---|---|---|---|---|
| ACMANT [65,66] | Mainly composite reference series | Step function fitting | Benova | 3 |
| Bart [72,73] | Mainly pairwise comparisons | Step function fitting | Benova | 2 |
| Climatol [84] | Composite reference series | SHNT | Spatial interpolation | Many |
| DAP [81] | Composite reference series | Combination of 3 methods | Quantile matching | 1 |
| HOMER [67] | Mainly pairwise comparisons | Step function fitting | Benova | 2 or 3 |
| MASH [35,36,37] | Multiple reference series | Multiple t-test | Fitting to reference series | Many |
| PHA [33] | Pairwise comparisons | SNHT | Fitting to homogeneous sections | 1 |
| PRODIGE [16] | Pairwise comparisons | Step function fitting | Benova | 2 or 3 |
| RHtests [25,51] | Composite reference series | Penalized maximal t-test | Fitting to reference series and quantile matching | Many |
| SNHT [6,26] | Composite reference series | SNHT | Fitting to reference series | Many |
| E (Trb-Individual) | ||
|---|---|---|
| Mean | P95 | |
| ACMANT | 67.9 | 69.2 |
| Climatol | 58.8 | 61.5 |
| RHtests | 52.4 | 57.4 |
| MASH | 52.2 | 55.9 |
| PHA | 48.6 | 47.8 |
| E (Trb-Net) All Datasets | E (Trb-Net) Best Dataset | |||
|---|---|---|---|---|
| Mean | P95 | Mean | P95 | |
| ACMANT | 36.0 | 31.0 | 79.6 | 77.0 |
| PHA | 27.7 | 20.4 | 62.7 | 58.3 |
| MASH | 21.0 | 11.0 | 46.9 | 51.0 |
| Climatol | 11.1 | −2.1 | 55.8 | 56.2 |
| RHtests | −12.8 | −25.1 | 5.0 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domonkos, P. Relative Homogenization of Climatic Time Series. Atmosphere 2024, 15, 957. https://doi.org/10.3390/atmos15080957
Domonkos P. Relative Homogenization of Climatic Time Series. Atmosphere. 2024; 15(8):957. https://doi.org/10.3390/atmos15080957
Chicago/Turabian StyleDomonkos, Peter. 2024. "Relative Homogenization of Climatic Time Series" Atmosphere 15, no. 8: 957. https://doi.org/10.3390/atmos15080957
APA StyleDomonkos, P. (2024). Relative Homogenization of Climatic Time Series. Atmosphere, 15(8), 957. https://doi.org/10.3390/atmos15080957






