Abstract
El Niño–Southern Oscillation (ENSO) usually peaks in the boreal winter—November to January of the following year. This particular feature of ENSO is known as the seasonal phase locking of ENSO. In this study, based on 34 climate models from the Coupled Model Intercomparison Project Phase 6 (CMIP6), the seasonal phase-locking characteristics of the model-simulated El Niño and La Niña events are evaluated in terms of the evolution of the SST anomalies associated with ENSO and the probability distribution of the peak month—the time at which ENSO peaks. It is found that CMIP6 models underestimate the phase-locking strength of ENSO for both El Niño and La Niña events. The ensemble mean peak month matches the observations, but the inter-model spread is large. The models simulate the phase locking of El Nino events better than that of La Niña events, and the large simulation bias of CMIP6 for La Niña phase-locking in the models may have an impact on the simulation of seasonal phase-locking in the ENSO.
1. Introduction
El Niño–Southern Oscillation (ENSO) is the largest contributor to interannual global climate variability, with important implications for global weather, ecology, and societies [1,2,3,4,5,6,7,8,9]. One of the many interesting things about ENSO events is that the associated SST anomaly in the central-eastern equatorial Pacific Ocean tends to peak in the boreal winter, November to January, a phenomenon often referred to as the seasonal phase locking of ENSO [8,10,11,12,13]. Through atmospheric teleconnection [14,15,16,17], the ENSO seasonality is an important factor in determining the impacts of ENSO on global weather and climate and, by extension, agricultural and other human activities. Studies have also underscored the particularly important roles of this seasonal character of ENSO in understanding and predicting weather and climate over China and India, where more than 1/3 of the world population lives [18,19,20].
Through the utilization of observational data and simulations by the regional and global climate models with different levels of complexity, significant progress has been made in understanding the seasonal phase-locking of ENSO. A series of comprehensive studies on the development, evolution, spatial and temporal distribution characteristics, seasonal characteristics, and global climate impacts of ENSO have been carried out, and a lot of significant progresses have been made [4,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. The approach to ENSO research has evolved from analyzing observed data and historical ENSO events to climate model simulations, which have proposed various conjectures and mechanisms to explain the seasonal phase-locking of ENSO, but the phenomenon of ENSO peaking in the boreal winter has not yet been fully explained or simulated. Whether the models are linear ones of different levels of complexity, nonlinear ones, or the most complex coupled climate models, they have different levels of problems in correctly explaining or simulating the ENSO seasonal phase-locking characteristics as seen in observations [26,27,30,33,34,35,36].
Coupled General Circulation Models (CGCMs), being the most complex ocean-atmosphere models, have become the key tools to understand and simulate the development and evolution of ENSO and to predict the future changes in the ENSO in the context of global climate change. The development and improvement of coupled climate models have indeed played an important role in ENSO research. Considerable and encouraging progress has been made in the past decades in coupled climate model simulations of basic aspects of ENSO, such as the amplitude, the distribution and evolution of SST anomalies in the equatorial Pacific associated with ENSO, the frequency, and the diversity of ENSO [4,24,25,41,42,43,44,45]. However, the results of the current study—a study focusing on evaluating the simulation of the seasonal phase-locking of ENSO by coupled climate models—indicate that the simulation of the ENSO winter peak phenomenon by climate models is still biased in a significant way in many models, and that correctly simulating the seasonal phase-locking phenomenon of ENSO is still a great challenge for CGCMs.
Difficulties for early coupled climate models to simulate the observed ENSO winter phase-locking have been reported. Some of the models even show the opposite ENSO phase-locking season to observations: that of summer. In the evaluation of the Coupled Climate Model Intercomparison Program (CMIP), the results show that both CMIP3 and CMIP5 models have been found to be unable to properly simulate the seasonal phase-locking characteristics of ENSO [24,29]. CMIP5 models have significant improvements in the simulations of the basic state of the SST and the basic characteristics of ENSO, such as the amplitude in the equatorial Pacific, when compared with CMIP3, but have limited improvements in the simulations of the seasonal phase-locking of ENSO. Ham et al. [29] evaluated the simulations of ENSO phase-locking in CMIP3 and CMIP5 models using the ENSO phase-locking performance index (PP Index), which is defined as the correlation between the standard deviations of Nino3 SST anomaly (SSTA) for each model and observation in each calendar month. They found that only 33% of the selected models show a PP Index higher than 0.6, which implies weaker phase locking in the models. For the constructive part of the study, they further attributed the poor simulations of ENSO’s phase-locking in the models to the colder seasonal-mean sea-surface temperature (SST) during the boreal summer, as well as the associated shallower thermocline depth over the eastern Pacific. The accurate modeling of the climatological state and seasonal cycle of the tropical Pacific background field is essential to simulate ENSO’s winter phase locking. This study has also shown that from CMIP3 to CMIP5, there are no significant improvements in the simulation of the seasonal phase-locking of the ENSO. In both the CMIP3 and CMIP5 models, there is a large inter-model variability in the peak time of ENSO, with many models having ENSO events peaking in the summer [24,29,34,35]. Cross-validation studies, with intermediate and coupled models, have pointed out that seasonal variations in coupling strength and accurate simulation of the annual cycle of the background field in the equatorial Pacific, as well as advection feedback, are essential for climate models to simulate the correct ENSO phase-locking. On the other hand, it has also been shown that seasonal variations in wind stress anomalies in the equatorial Pacific may also play an important role in ENSO phase locking in winter. Overall, the coupled climate models provide a powerful tool for an insight on what determines or influences the seasonal preference of ENSO events.
The publication of the climate simulations by the latest generation of climate models, the CMIP6 models, has provided an opportunity to further assess and analyze the simulations of the phase-locking simulation capabilities of ENSO by our most sophisticated climate models. However, it has been shown that the seasonal phase locking of ENSO in the CMIP6 ensemble remains weaker than the observed phase locking, with little improvement from CMIP5 to CMIP6 [26,27,33,34]. Weaker phase-locking strength and large inter-model variabilities demonstrate that there are also no significant improvements in the ENSO phase-locking simulations from CMIP5 to CMIP6 [25,27,33,34]. Liao et al. (2021) [34] used the proportion of model-simulated winter-peaking ENSO events (PPL index) as an indicator to validate the simulation of ENSO seasonal phase locking in CMIP6 models. Chen and Jin (2022) [26] have investigated different oceanic feedback processes using the RO model and found that the seasonal modulation of the SST growth rate is determined by the seasonal modulation of the SST growth rate. Seasonal modulation of the growth rate determines the winter peak characteristics of ENSO in the model, further suggesting that the phase-locking bias in the climate model is related to the specific latitudinal advection feedback and shortwave feedback simulations. The phase-locked simulation of the CMIP6 model is also evaluated using histograms of peak month probability distributions and preference strengths, noting that CMIP6 is poorly simulated for seasonal phase locking, and inverted using the sLIM method. However, although the basic feature of ENSO’s phase locking has been widely studied and discussed, there is no unified and perfect mechanism and explanation for the physical mechanism and theoretical research behind it, especially in CGCMs.
However, these studies have only explored the overall ENSO amplitude or the phase locking of El Niño and have not been specifically concerned with the phase-locking simulation of La Niña events, the cold phase of ENSO. In Zhao and Sun 2022 [45], it was pointed out that the overestimation of La Niña event amplitude in the CMIP6 model led to the overestimation of the overall ENSO amplitude in the model. A comprehensive assessment of the seasonal phase-locking characteristics of ENSO events simulated by coupled climate models also needs to be explored, which includes both the El Niño and La Niña events. In this study, we use the latest CMIP6 to evaluate and analyze the model simulations of the seasonal phase-locking characteristics of El Niño and La Niña events. We will report that while the CMIP6 Models generally underestimate the strength of the seasonal phase locking of ENSO, the simulations of the phase locking of El Niño by the models are superior to the simulations of the seasonal phase locking of La Niña events. The poorer simulations of the La Niña seasonal phase locking in models affect the model’s simulation of the overall seasonal phase locking of ENSO.
2. Materials and Methods
The sea surface temperature (SST) data for observations used in this study are from the Hadley Centre Sea Ice and Sea Surface Temperature dataset (HadISST1) [46] over the period 1950–2014. In order to investigate the performance of the CMIP6 models in the simulation of ENSO seasonal phase-locking, the historical simulation experiments (r1i1p1f1) outputs from 34 CMIP6 climate models used in this study are listed in Table 1 [47].

Table 1.
List of the 34 selected CMIP6 models for investigating the phase-locking of ENSO in historical simulation runs. The first column represents the model number, the second column denotes the model name, and the third column provides information on the model center and country.
These models were selected to cover as many different regions and resolutions of climate models as possible, and the time period for the study was from 1950 to 2014. Each historical simulation was initialized from a preindustrial control simulation spin-up experiment and subsequently driven by data on solar radiation, volcanic activity, aerosols, and greenhouse gasses. At the same time, in order to provide an easy comparison and analysis with the observation results, all the selected model data are uniformly preprocessed, and the model ensemble mean results are used for a quantitative comparison and analysis with the observations. The model’s monthly mean data are uniformly interpolated to the same grid point resolution of 1° × 1°.
In this study, the El Niño events (La Niña events) are defined as periods when the SST anomalies in Niño3 region (5° S–5° N, 150° W–90° W) exceeds 0.5 °C (−0.5 °C) for five consecutive months. Composites of SST anomalies were used for both El Niño and La Niña events. We calculated the composite evolution of consecutive Niño3 SST anomalies during El Niño and La Niña events, which can more intuitively characterize the winter peak of Niño3 SST anomalies in December during the development of ENSO events. The seasonal phase-locking simulation of the models is portrayed and represented in a more general way, using the peak month probability distributions and specific peak months of the composite distribution of SST anomalies for the two warm and cold phases of ENSO-El Niño and La Niña events.
In this paper, with reference to Liao et al. 2021 [34], we define winter-peaking El Niño events and winter-peaking La Niña events to evaluate phase-locking simulations in the CMIP6 models. ENSO events tend to peak during the boreal winter months of November to January (NDJ) in next year, and this synchronization of ENSO peaks with the winter season is called ENSO seasonal phase-locking. To keep the comparison as straightforward as possible, we define the winter-peaking El Niño (La Niña) events as El Niño (La Niña) events that reached their maximum during the November to January (NDJ). In addition to using the synthetic evolution of SST anomalies in the Nino3 region of El Niño and La Niña events to explore the model simulation of seasonal phase-locking of the two ENSO phases in a whole, this study evaluates the simulation of the seasonal phase-locking of ENSO in the CMIP6 model by using the proportion of winter peak El Niño events and La Niña events among all El Niño and La Niña events.
3. Results
3.1. Phase-Locking Performance of El Niño and La Niña Events in CMIP6 Models
ENSO events in the observations were found to reach their maximum in the boreal winter. For both El Niño and La Niña events, the most common month for the events to peak is December. Figure 1 shows the evolution of Niño3 SST anomalies in the development and progression of El Niño and La Niña events, and it clearly shows this intriguing winter peak phenomenon of the Niño3 SST anomalies reaching their maximum in December. Peak months for the curves are marked by crosses. As shown in Figure 1, the CMIP6 model ensemble mean is able to capture the winter phase-locking characteristics of El Niño and La Niña events, especially for El Niño. The model ensemble mean and the observations both peak in December.
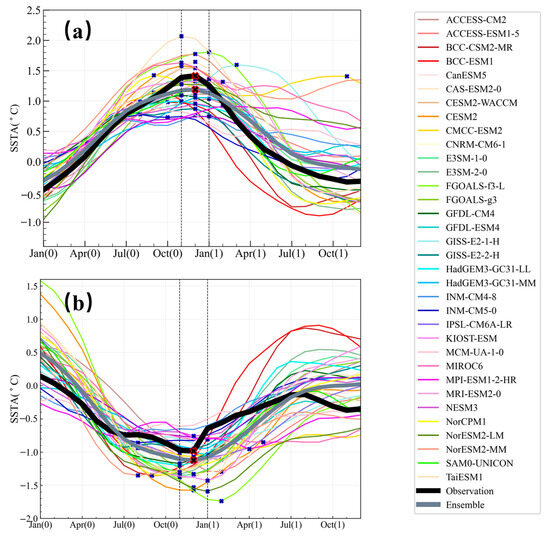
Figure 1.
Evolution of the composite distribution of SSTA in the Niño3 region during El Niño (a) and La Niña (b) events in Observations (black line) and 34 CMIP6 models (other colored lines). The gray line is for the model ensemble mean. The crosses in (a,b) represent the peak points of the different curves, which are defined as the peak month of El Niño (a) and La Niña (b) events.
Although El Niño events in most of the models peak in the winter months, November, December, and January (NDJ), there are still some models with large phase-locking bias, and there are also models with double-peak problems, such as the CMCC-ESM2 model. Overall, El Niño events in the models fit those from observations well. Both the model ensemble mean results and the observations reach the maximum point in December. The model ensemble mean results for the La Niña events show a larger bias from the observations than those for El Niño events. Figure 1b shows the evolution of SST anomalies in the Niño3 region simulated by the CMIP6 models and that in the observations during the La Niña events. It can be seen that the SST anomalies simulated by the model ensemble mean results are consistent with the observations—La Niña events in both models and the observations peak in December. There is an overestimation of the peak strength of the La Niña, and this bias continues from July of the first year to June of the following summer. This is consistent with the overestimation of La Niña intensity in the model found in Zhao and Sun 2022.
To provide another measure for a more detailed assessment of the seasonal phase-locking of model-simulated El Niño and La Niña events, we have also investigated the peak month and probability distribution of the peak month of the model-simulated composite distribution of Niño3 SST anomalies for El Niño and La Niña events (Figure 2). Of the selected models, up to 74 percent of them can simulate a winter-peaking of El Niño events (Figure 2b), and 63 percent of them simulate a winter-peaking of La Niña events (Figure 2d). The CMIP6 models perform better in modeling El Niño phase locking than in modeling the phase locking of La Niña events. The overall model simulations of La Niña’s peak month are slightly worse than those of El Niño, and some of the model simulations of La Niña events reach their maximum in the summer from June–August (JJA), showing a seasonal phase-locking that has a phase opposite to that from the observations. There are two major problems with the model simulations of La Niña. One is the large inter-model differences in their respective peak months. The other is that the distribution of the peak months of La Niña events in the models is more dispersed compared with that of El Niño events. Although most of the models capture the fact that the peak month of La Niña tends to be in the boreal winter, some models such as MIRCO6, MPI-ESM1-2-HR, GISS-E2-1-H and NorESM2-MM have very poor simulations of the phase-locking of ENSO, and have their ENSO peaking in the spring and summer. The models significantly overestimate the SST anomalies of La Niña events: the negative SST anomalies are significantly larger in the models, compared to the observations. The accuracy in the simulations of the SST background field in the tropical Pacific may play an important role in the bias in the simulations of ENSO seasonal phase-locking. Liao et al. (2021) have found that the seasonal cycle of the zonal SST gradient along the equator can explain approximately 24% and 27% of the variance in the ENSO phase-locking for CMIP5 and CMIP6. This variability in the simulations of the phase-locking properties of the warm and cold events in the models may be linked to the inadequate representations of the nonlinear dynamical processes of the ENSO events in the models and the weak ENSO asymmetry in the model simulations. To be sure, the mechanisms behind it are far from being clear and need further discussion and research. Another noteworthy aspect is that the model ensemble mean results largely filter out the much larger biases in the individual models, providing an example for how different models may complement each other in a way to reduce the biases in the ensemble mean simulations of the concerned phenomenon.
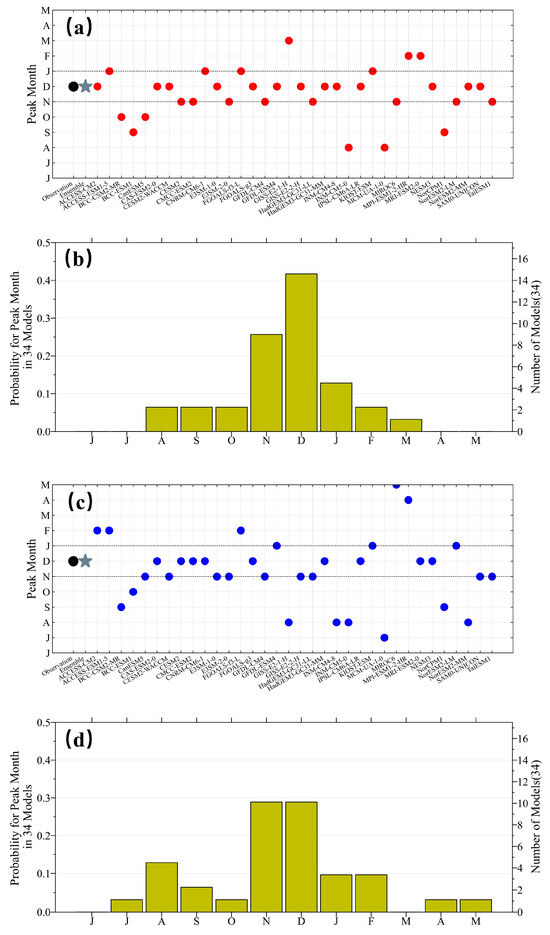
Figure 2.
The peak month and probability distribution of the peak month for El Niño (a,b) and La Niña (c,d) events in the observations and CMIP6 models. The peak month is defined as the calendar month at which the Niño3 SSTA has its maximum value during the El Niño (a) and La Niña (c). The black dots in (a,c) represent the peak month in observations, and the gray stars represent the model ensemble mean. The red dots in (a) indicate the peak month of El Niño events for individual model members in CMIP6. The blue dots in (c) indicate the peak month of La Niña events for individual model members in CMIP6.
3.2. Comparision of the Phase-Locking Simulations between El Niño and La Niña Events
The peak month cannot represent the strength of the simulated phase-locking behavior. In addition to making an assessment using the peak month plots of the composite distribution of SST anomalies, we have also estimated the probability distribution of the peak months of El Niño and La Niña events simulated by the models and those that have been seen in the real world. The diagrams for the phase locking probability distributions for different months of El Niño and La Niña events (histograms) are provided in Figure 3 and Figure 4, respectively. We define the El Niño events (La Niña events) as periods when the SST anomalies in the Niño3 region (5° S–5° N, 150° W–90° W) exceeds 0.5 °C (−0.5 °C) for five consecutive months. All El Niño and La Niña events in the study time period are singled out, and the probability distribution of the peak months of these events are examined for a more detailed examination of the seasonal phase-locking characteristics of the peak months.
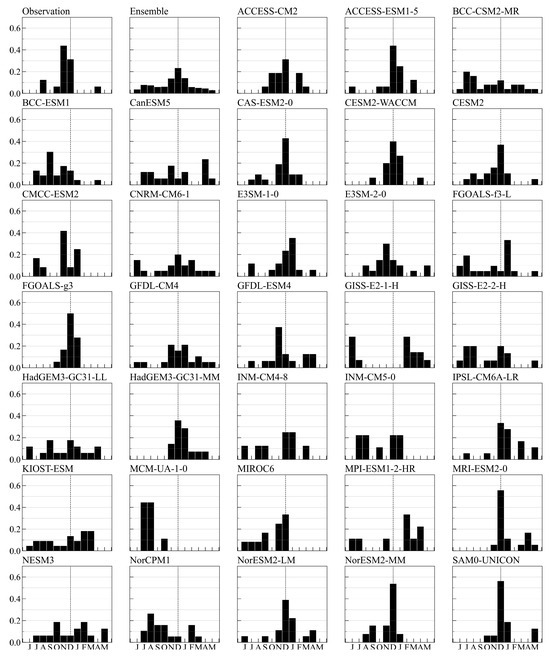
Figure 3.
Probability distribution (histogram) of peak month of El Niño events.
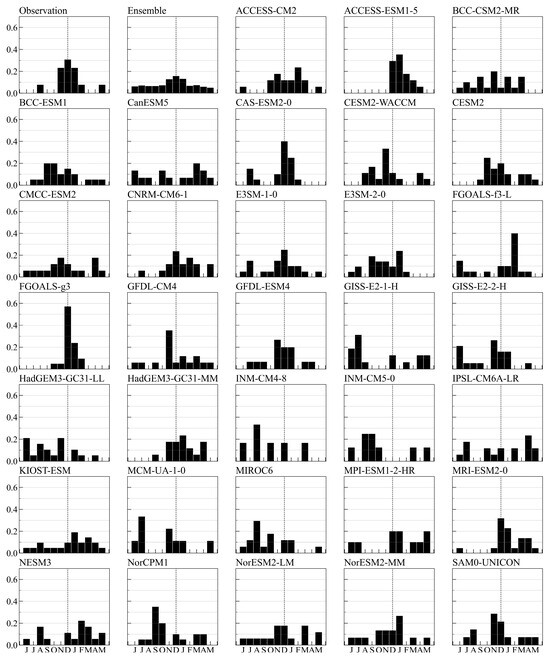
Figure 4.
Probability distribution of peak month of La Niña events.
Figure 3 shows the probability distribution of the peak months of all El Niño events in the observations and the simulations by the models. The El Niño events in the observations show a pronounced single-peak distribution, and the peak months for El Niño events in the observations are concentrated in November–December. In the CMIP6 models, on the other hand, the probability distribution of the peak months of El Niño can be generally classified into two types. One is a single-peak structure of the winter peak similar to the observations, such as ACCESS-ESM1-5, CAS-ESM2-0, CESM2-WACCM, CESM2, CMCC-ESM2, E3SM-1-0, E3SM-2-0, FGOALS-g3, GFDL-ESM4, HadGEM3-GC31-MM, IPSL-CM6A-LR, MIROC6, MRI-ESM2-0, NorESM2-LM, NorESM2-MM, SAM0-UNICON, and TaiESM1. The other group consists of models with large differences from the observed probability distribution. Models that have large differences from observations, such as CNRM-CM6-1, HadGEM3-GC31-L, KIOST-ESM, and NESM3, have more uniform probability distributions throughout the year. On the other hand, some models such as GISS-E2-1-H have single-peak distributions, but with the peak month realized in the summer.
Similar to the peak month distribution of El Niño events, the observed peak months of La Niña events show a single-peak distribution structure, with the peak month located in winter (November–January) (Figure 4). However, there is greater inter-model variability in the probability distribution of the peak month of La Niña events in the model, with an even smaller number of models having a single peak located in the winter season. Models with a single peak located in the winter season in the peak month distribution of La Niña are ACCESS-ESM1-5, CAS-ESSM2-0, CESM2-WACCM, CESM2, CNRM-CM6-1, ESM-1-0, ESM-2-0, FGOALS-g3, GFDL-CM4, GFDL-ESM4, HadGEM3-GC31-MM, MRI-ESM2-0, NorESM2-MM, SAM0-UNICON, and TaiESM1.
Some models that have more flattened probability distributions of peak month, such as BCC-CSM2-MR, BCC-ESM1, CanESM5, GISS-E2-1-H, HadGEM3-GC31-LL, INM-CM4-8, INM-CM5-0, MIROC6, and NorCPM1, do not have a significant winter-locking of La Niña events. There are even some models with larger differences between the probability distributions of phase-locking months and observations, such as MCM-UA1-0, where the simulated El Niño events are more inclined to peak in summer. This suggests that, although the CMIP6 models can capture the winter phase-locking phenomena similar to observations in terms of the composite distribution of Niño3 SST anomalies for El Niño and La Niña events, there are still many shortcomings in such simulations. The large inter-model spread of peak months shown in Figure 3 and Figure 4 indicates that the CMIP6 models still need to be improved. This result is consistent with the results in the previous studies on the generalized bias of the weaker seasonal phase-locking properties that exist in the coupled climate models. The enhancement of the model from CMIP3 to CMIP5 to the latest generation of CMIP6 models is not significant, and the intra-model variability is somewhat reduced but not to a large extent. Accurately simulating this seasonal phase-locking feature of ENSO remains a challenge and requires more attention.
In addition to the previously mentioned biases in the El Niño and La Niña peak month simulations, there are still large biases in the probability distributions of the peak months of independent El Niño events in the models (Figure 3 and Figure 4). The probability distributions describe this model’s inadequate simulation of ENSO seasonal phase-locking, and it is important to fully explore this inter-model difference in the simulation of the peak month of independent El Niño events. They may provide useful information for the causes of the inadequacies of ENSO phase-locked characteristics in our best climate models. Here, we further quantify the inter-model differences by comparing the number of winter-peaking El Niño events and winter-peaking La Niña events, relative to their respective total number of events in the models. ENSO events tend to peak during the boreal winter months of November to January (NDJ) of the next year in observations. We define the winter-peaking El Niño (La Niña) events as El Niño (La Niña) events that reached their maximum during the November to January (NDJ). Figure 5a shows the proportion of winter-peaking El Niño events to all El Niño events in the observations and CMIP6 model, and Figure 5b also shows the proportion of winter-peaking La Niña events to all La Niña events, which is an important measure of the seasonal phase-locking strength of El Niño and La Niña events simulated by the models.
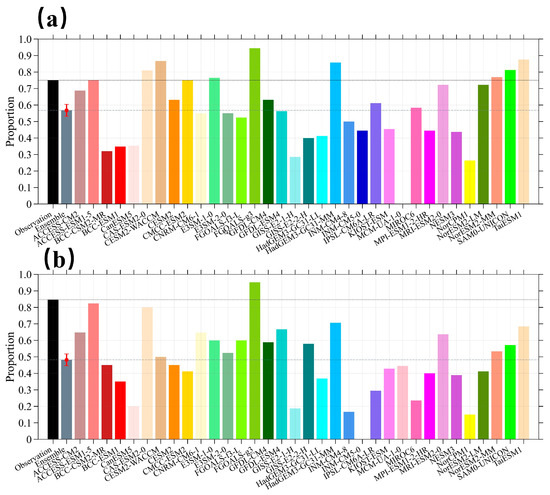
Figure 5.
Proportion of winter-peaking El Niño (a) and La Niña (b) events in observations (in black) and CMIP6 models (in colors). The gray bar represents the model ensemble mean.
The proportion of winter-peaking El Niño events in the observations is as high as 75% of the total events, while, on average, the CMIP6 models have approximately 58% of the events peaking in winter, which is more than 20% lower than the observations. This suggests that there is a significant underestimation of the proportion of winter-peaking El Niño events in the CMIP6 models. Thus, the models underestimate the seasonal phase-locking of El Niño events. The proportion of the winter-peaking El Niño events in the model is lower than that of observations, except for CAS-ESM2-0, CESM2-WACCM, CMCC-ESM2, E3SM-2-0, FGOALS-g3, HadGEM3-GC31-MM, NorESM2-MM, SAM0-UNICON, and TaiESM1, totaling nine models. BCC-CSM2-MR, BCC-ESM1, CanESM5, GISS-E2-1-H, MCM-UA-1-0, and NorCPM1 have only about 30% of the winter-peaking El Niño events, and none of the El Niño events simulated by the MCM-UA-1-0 model peaks in winter.
This underestimation of seasonal phase locking is also found in the simulation of La Niña events, and the CMIP6 models underestimate the winter-peaking La Niña events more significantly than the El Niño events. While the observed winter-peaking La Niña events account for 84% of the total, the CMIP6 model ensemble mean results account for less than 50% of the winter-peaking La Niña events, which is lower than that of the observations by more than 40%, showing a significant underestimation bias (Figure 5b). With the exception of FGOALS-g3, all models simulate a significantly lower proportion of winter-peaking La Niña events than the observations. Some models, such as CanESM5, GISS-E2-1-H, INM-CM-4-8, INM-CM-5-0, and NorCPM1, have a 20% lower proportion of winter-peaking La Niña events. Whether the inadequacy in the simulations of the seasonal phase-locking of La Niña events affects the model’s simulations of other weather and climate systems associated with them as a whole warrants further investigation.
We have also found that models that perform poorly in modeling the proportion of winter-peaking El Niño events tend to perform poorly in modeling the proportion of winter-peaking La Niña events. Figure 6 presents a scatter plot of the correlation between the proportion of winter-peaking El Niño events and the proportion of winter-peaking La Niña events among the observations and models. The results show that there is a moderate positive correlation between the proportion of winter-peaking El Niño events and the proportion of winter-peaking La Niña events. The correlation coefficient (0.62) passes the significance test of 99.9%.
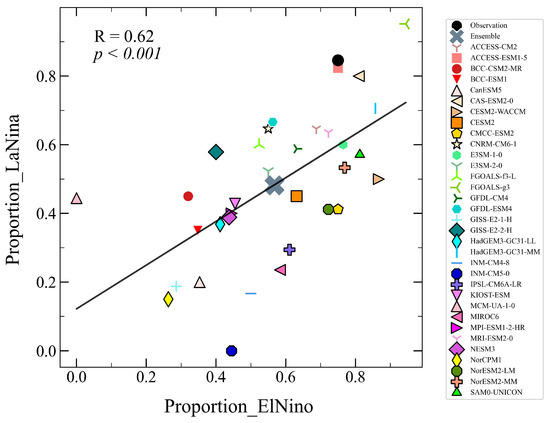
Figure 6.
Scatter plots of the simulated proportion of winter-peaking El Niño events and the simulated proportion of winter-peaking La Niña events (the black dot) and CMIP6 Models (the other colored symbols). The horizontal axis is for the model-simulated proportion of winter-peaking El Niño events. The vertical axis is for the simulated proportion of winter-peaking La Niña events. The gray crossed symbol represents the model ensemble mean.
From the above results, it is evident that the CMIP6 models still have considerable weaknesses in simulating the seasonal phase-locking of El Niño and La Niña events. The models underestimate the proportion of winter-peaking El Niño and La Niña events, leading to a weaker overall seasonal phase locking strength. Interestingly, the model performs better in simulating the seasonal phase locking of El Niño events than that of La Niña events. To further improve the performance of today’s coupled climate models in their simulations of the seasonal phase-locking of ENSO events, more attention may need be given to the improvement in the underestimation of the seasonal phase-locking of La Niña events.
4. Discussion
Based on the historical simulations from the latest generation of coupled climate models, we have evaluated and analyzed the seasonal phase-locking of the warm and cold phases of ENSO in 34 CMIP6 models. In particular, we have examined the anomalous SST evolution of the El Niño and La Niña events and the probability distribution of the peak month for El Niño and La Niña events. We have found that the CMIP6 model can largely capture the seasonal phase-locking characteristics of El Niño and La Niña, but there is a general underestimation of the winter phase-locking strength of the two ENSO phases in the models. On average, the peak month—the month an ENSO event peaks—in the models also matches that in the observations; although, there is a considerable spread in this regard among the models. Causes of these biases need to be further studied, especially in consideration of the fact that the biases in the simulations of the seasonal phase-locking of ENSO by the coupled climate models likely affect the seasonal aspects of ENSO predictions, such as the Spring Predictability Barrier. Combined with previous studies on ENSO seasonal phase-locking in coupled climate models, the weaker phase-locking strength and large inter-model variability remain to be resolved from CMIP3 to CMIP5, and then to the latest generation of CMIP6 models. Both reliable ENSO projections and global warming prognostics will require particularly careful consideration of this demonstrated seasonal phase-locking simulation bias in the model associated with the simulation of the seasonal cycle in the Pacific.
It is of interest to note that the CMIP6 models simulate the seasonal phase-locking of El Nino events better than the seasonal phase locking of La Niña events, and that the model’s poorer simulation of the winter peak La Niña events is the bigger contributor to the model’s poor simulations of the overall seasonal phase-locking of ENSO. Why it is more difficult to simulate the seasonal phase-locking of La Nina warrants further studies. The significant underestimation of the proportion of winter-peaking El Niño and La Niña events to all events in the models further supports the underestimation of the model’s simulation of ENSO seasonal phase-locking. Exploring the seasonal phase-locking simulation bias of El Niño and La Niña events can help to understand the mechanisms associated with ENSO seasonal phase-locking and improve the ENSO Spring Prediction Barrier in climate models.
The finding that the state-of-the-art climate models are unable to simulate the seasonal phase-locking to the same intensity as seen in observations underscores that it remains a challenge for the climate models to accurately and comprehensively simulate the ENSO phenomenon. Note that the phenomenon is not only important in its own right but may also play an important role in global climate change [48,49].
The persistent existence of the model biases in the simulation of ENSO seasonal phase-locking—a weaker phase-locking strength and large inter-model variability in the models—from CMIP3 to CMIP5, and then to the latest generation of CMIP6 models should help to call more attention to the problem. Both reliable ENSO projections and global warming prognostics will require improved simulations by the models of seasonal phase-locking of the ENSO phenomenon. This provides a promising perspective for understanding and studying ENSO seasonal phase-locking simulations in coupled climate models and exploring theoretical mechanisms. Through the multi-model ensemble mean method of analysis, the bias in seasonal phase-locking simulations of individual models can be reduced, but it is worth noticing the large inter-model differences in the simulation of seasonal phase-locking within the models. Improvements in ENSO seasonal phase locking simulations by subsequent models should continue to take into account this difference in the strengths and weaknesses of seasonal phase-locking simulations of El Niño and La Niña events on the one hand, and the seasonal cycle of ocean-atmosphere interactions on the other hand, which may also play an important role. The further mechanisms and implications of this generalized bias should be further explored in our subsequent studies. In a follow-up study, we can categorize the models that simulate ENSO seasonal phase-locking better and explore which specific meteorological element cycles, feedback processes, or background field state evolutions play an important role in improving model seasonal phase-locking simulations in CGCMs.
Author Contributions
Conceptualization, D.-Z.S.; methodology, Y.Y.; validation, Y.Y.; formal analysis, Y.Y.; investigation, Y.Y.; data curation, Y.Y.; writing—original draft preparation, Y.Y.; writing—review and editing, D.-Z.S.; visualization.; supervision, D.-Z.S.; funding acquisition, D.-Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 42250710154.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data from CMIP6 coupled models can be downloaded online: https://aims2.llnl.gov/search/cmip6/ (accessed on 21 January 2024). The observations dataset used in this research can be accessed via the following websites: The HadISST data are available at https://www.metoffice.gov.uk/hadobs/hadisst/data/download.html (accessed on 21 January 2024).
Acknowledgments
We thank the climate modeling groups for producing and making available their model output, the Earth System Grid Federation (ESGF) for archiving and providing access to data, and the multiple funding agencies who support CMIP and ESGF. And we sincerely thank WCRP for providing the simulations by CMIP6 models, the Hadley Centre for the SST.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Allan, R.J.; Reason, C.J.C.; Lindesay, J.A.; Ansell, T.J. Protracted’ ENSO episodes and their impacts in the Indian Ocean region. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2003, 50, 2331–2347. [Google Scholar] [CrossRef]
- Atems, B.; Maresca, M.; Ma, B.; McGraw, E. The impact of El Nio-Southern Oscillation on U.S. food and agricultural stock returns. Water Resour. Econ. 2020, 32, 100157. [Google Scholar] [CrossRef]
- Cai, W.; McPhaden, M.J.; Grimm, A.M.; Rodrigues, R.R.; Taschetto, A.S.; Garreaud, R.D.; Dewitte, B.; Poveda, G.; Ham, Y.G.; Santoso, A.; et al. Climate impacts of the El Niño–Southern Oscillation on South America. Nat. Rev. Earth Environ. 2020, 1, 215–231. [Google Scholar] [CrossRef]
- Chen, C.; Cane, M.A.; Wittenberg, A.T.; Chen, D. ENSO in the CMIP5 simulations: Life cycles, diversity, and responses to climate change. J. Clim. 2017, 30, 775–801. [Google Scholar] [CrossRef]
- Hansen, J.W.; Hodges, A.W.; Jones, J.W. ENSO Influences on Agriculture in the Southeastern United States. J. Clim. 1998, 11, 404–411. [Google Scholar] [CrossRef]
- Kim, H.J.; Hyeong, K.; Park, J.Y.; Jeong, J.H.; Jeon, D.; Kim, E.; Kim, D. Influence of Asian monsoon and ENSO events on particle fluxes in the western subtropical Pacific. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2014, 90, 139–151. [Google Scholar]
- Mcphaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an integrating concept in Earth science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef] [PubMed]
- Philander, S.G.H. El Niño Southern Oscillation phenomena. Nature 1983, 302, 295–301. [Google Scholar] [CrossRef]
- Wang, C.; Picaut, J. Understanding Enso Physics—A Review. Earth’s Clim. 2004, 147, 21–48. [Google Scholar]
- Harrison, D.E.; Vecchi, G.A. On the termination of El Niño. Geophys. Res. Lett. 1999, 26, 1593–1596. [Google Scholar] [CrossRef]
- Rasmusson, E.M.; Carpenter, T.H. Variations in Tropical Sea Surface Temperature and Surface Wind Fields Associated with the Southern Oscillation/El Niño. Mon. Weather Rev. 1982, 110, 354–384. [Google Scholar] [CrossRef]
- Tziperman, E.; Cane, M.A.; Zebiak, S.E.; Xue, Y. Blumenthal, B Locking of El Niño’s Peak Time to the End of the Calendar Year in the Delayed Oscillator Picture of ENSO. J. Clim. 1998, 11, 2191–2199. [Google Scholar] [CrossRef]
- Tziperman, E.; Zebiak, S.E.; Cane, M.A. Mechanisms of Seasonal—ENSO Interaction. J. Atmos. Sci. 1997, 54, 61–71. [Google Scholar] [CrossRef]
- An, S.; Jin, F. Linear solutions for the frequency and amplitude modulation of ENSO by the annual cycle. Tellus 2011, 63, 238–243. [Google Scholar] [CrossRef]
- Brönnimann, S.; Luterbacher, J.; Staehelin, J.; Svendby, T.M.; Hansen, G.; Svenøe, T. Extreme climate of the global troposphere and stratosphere in 1940–1942 related to El Niño. Nature 2004, 431, 971–974. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Wu, L.; Lengaigne, M.; Li, T.; McGregor, S.; Kug, J.S.; Yu, J.Y.; Stuecker, M.F.; Santoso, A.; Li, X.; et al. Pantropical climate interactions. Science 2019, 363, eaav4236. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Qiangen, Z.; Tiehan, Z. Monsoon circulation related to enso phase-locking. Adv. Atmos. Sci. 1998, 15, 267–276. [Google Scholar]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean. 2007, 112, C11. [Google Scholar] [CrossRef]
- Wang, B.; Wu, R.; Li, T. Atmosphere–Warm Ocean Interaction and Its Impacts on Asian–Australian Monsoon Variation. J. Clim. 2003, 16, 1195–1211. [Google Scholar] [CrossRef]
- Xie, S.P.; Hu, K.; Hafner, J.; Tokinaga, H.; Du, Y.; Huang, G.; Sampe, T. Indian Ocean Capacitor Effect on Indo–Western Pacific Climate during the Summer following El Niño. J. Clim. 2009, 22, 730–747. [Google Scholar] [CrossRef]
- Andrews, M.B. Historical simulations with HadGEM3-GC3.1 for CMIP6. J. Adv. Model Earth Syst. 2020, 12, e2019MS001995. [Google Scholar] [CrossRef]
- Bayr, T.; Dommenget, D.; Latif, M. Walker circulation controls ENSO atmospheric feedbacks in uncoupled and coupled climate model simulations. Clim. Dyn. 2020, 54, 2831–2846. [Google Scholar] [CrossRef]
- Bayr, T.; Wengel, C.; Latif, M.; Dommenget, D.; Lübbecke, J.; Park, W. Error compensation of ENSO atmospheric feedbacks in climate models and its influence on simulated ENSO dynamics. Clim. Dyn. 2019, 53, 155–172. [Google Scholar] [CrossRef]
- Bellenger, H.; Guilyardi, E.; Leloup, J.; Lengaigne, M.; Vialard, J. ENSO representation in climate models: From CMIP3 to CMIP5. Clim. Dyn. 2014, 42, 1999–2018. [Google Scholar] [CrossRef]
- Brown, J.R. Comparison of past and future simulations of ENSO in CMIP5/PMIP3 and CMIP6/PMIP4 models. Clim. Past 2020, 16, 1777–1805. [Google Scholar] [CrossRef]
- Chen, H.-C.; Jin, F.-F. Dynamics of ENSO Phase–Locking and Its Biases in Climate Models. Geophys. Res. Lett. 2022, 49, e2021GL097603. [Google Scholar] [CrossRef]
- Chen, H.-C.; Jin, F.-F. Fundamental Behavior of ENSO Phase Locking. J. Clim. 2020, 33, 1953–1968. [Google Scholar] [CrossRef]
- Chen, H.C.; Jin, F.F.; Zhao, S.; Wittenberg, A.T.; Xie, S. ENSO dynamics in the E3SM-1-0, CESM2, and GFDL-CM4 climate models. J. Clim. 2022, 34, 9365–9384. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kug, J.-S. ENSO phase-locking to the boreal winter in CMIP3 and CMIP5 models. Clim. Dyn. 2014, 43, 305–318. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kug, J.S.; Kim, D.; Kim, Y.H.; Kim, D.H. What controls phase-locking of ENSO to boreal winter in coupled GCMs? Clim. Dyn. 2013, 40, 1551–1568. [Google Scholar] [CrossRef]
- Hirst, A. Unstable and damped equatorial modes in simple coupled ocean–atmosphere models. J. Atmos. Sci. 1986, 43, 606–632. [Google Scholar] [CrossRef]
- Kallummal, R.; Kirtman, B. Validity of a linear stochastic view of ENSO in an ACGCM. J. Atmos. Sci. 2008, 65, 3860–3879. [Google Scholar] [CrossRef]
- Liao, H.; Cai, Z.; Guo, J.; Song, Z. Effects of ITCZ Poleward Location Bias on ENSO Seasonal Phase-Locking Simulation in Climate Models. J. Clim. 2023, 36, 5233–5249. [Google Scholar] [CrossRef]
- Liao, H.; Wang, C.; Song, Z. ENSO phase-locking biases from the CMIP5 to CMIP6 models and a possible explanation. Deep-Sea Res. II 2021, 189, 104943. [Google Scholar] [CrossRef]
- Liu, M.; Ren, H.L.; Zhang, R.; Ineson, S.; Wang, R. ENSO phase-locking behavior in climate models: From CMIP5 to CMIP6. Environ. Res. Commun. 2021, 3, 031004. [Google Scholar] [CrossRef]
- Stein, K.; Schneider, N.; Timmermann, A.; Jin, F.F. Seasonal Synchronization of ENSO Events in a Linear Stochastic Model. J. Clim. 2010, 23, 5629–5643. [Google Scholar] [CrossRef]
- Stein, K.; Timmermann, A.; Schneider, N.; Jin, F.F.; Stuecker, M.F. ENSO Seasonal Synchronization Theory. J. Clim. 2014, 27, 5285–5310. [Google Scholar] [CrossRef]
- Stuecker, M.F.; Timmermann, A.; Jin, F.F.; McGregor, S.; Ren, H.L. A combination mode of the annual cycle and the El Niño/Southern Oscillation. Nat. Geosci. 2013, 6, 540–544. [Google Scholar] [CrossRef]
- Wengel, C.; Latif, M.; Park, W.; Harlaß, J.; Bayr, T. Seasonal ENSO phase locking in the Kiel Climate Model: The importance of the equatorial cold sea surface temperature bias. Clim. Dyn. 2018, 50, 901–919. [Google Scholar] [CrossRef]
- Wittenberg, A.T.; Rosati, A.; Lau, N.C.; Ploshay, J.J. GFDL’s CM2 Global Coupled Climate Models. Part III: Tropical Pacific Climate and ENSO. J. Clim. 2006, 19, 698–722. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, D.Z.; Wu, L.; Wang, F. Western Pacific warm pool and ENSO asymmetry in CMIP3 models. Adv. Atmos. Sci. 2013, 30, 940–953. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, F.; Sun, D.Z. Weak ENSO asymmetry due to weak nonlinear air–sea interaction in CMIP5 climate models. Adv. Atmos. Sci. 2016, 33, 352–364. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteor. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Timmermann, A. El Niño–Southern Oscillation complexity. Nature 2018, 559, 535–545. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Sun, D.-Z. ENSO Asymmetry in CMIP6 Models. J. Clim. 2022, 35, 5555–5572. [Google Scholar] [CrossRef]
- Rayner, N.A.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108, 4407. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Liang, J.; Yang, X.Q.; Sun, D.Z. The effect of ENSO events on the Tropical Pacific Mean Climate: Insights from an Analytical Model. J. Clim. 2012, 25, 7590–7606. [Google Scholar] [CrossRef]
- Liang, J.; Yang, X.Q.; Sun, D.Z. Rectification of El Nino-Southern Oscillation into Climate Anomalies of Decadal and Longer Time-scales: Results from Forced Ocean GCM Experiments. J. Clim. 2014, 27, 2545–2561. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).