Sea Surface Temperature and Marine Heat Wave Predictions in the South China Sea: A 3D U-Net Deep Learning Model Integrating Multi-Source Data
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
3. Results
3.1. Comparison of the 3D U-Net Model with the ConvLSTM Model
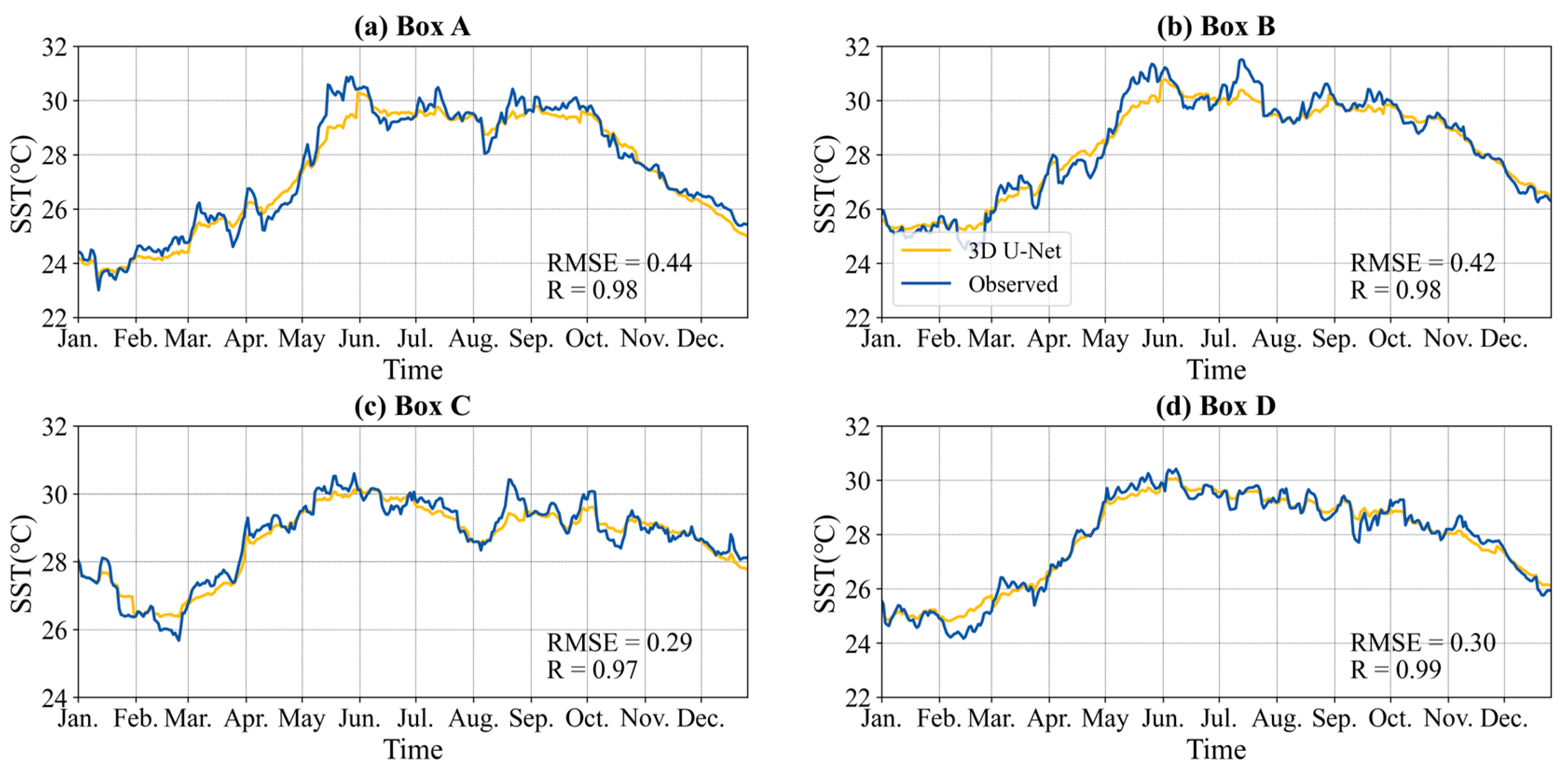
3.2. Evaluation of the 3D U-Net Model
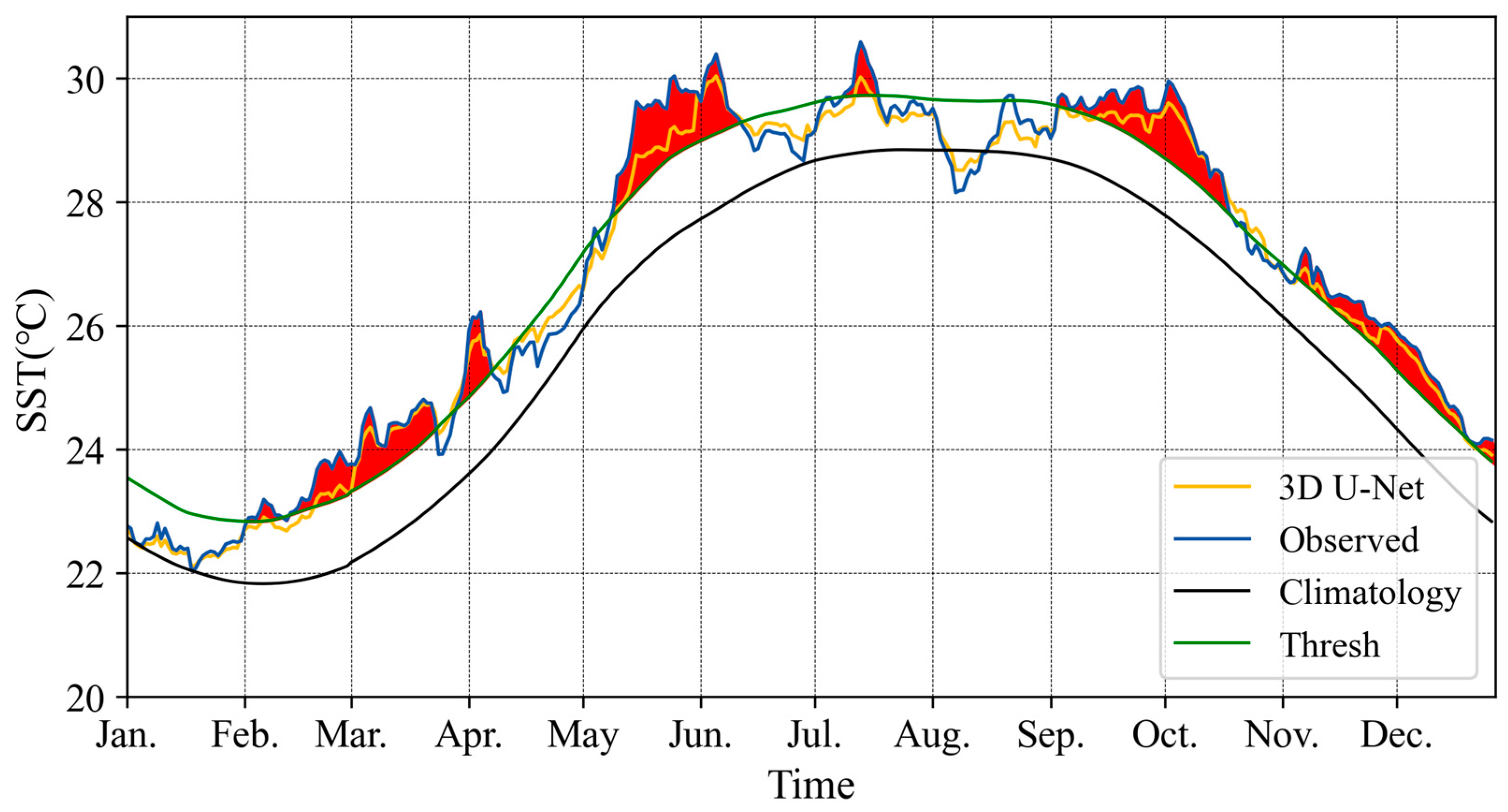
3.3. Comparison of Marine Heat Wave (MHW) Events
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McPhaden, M.J.; Busalacchi, A.J.; Cheney, R.; Donguy, J.R.; Gage, K.S.; Halpern, D.; Ji, M.; Julian, P.; Meyers, G.; Mitchum, G.T. The Tropical Ocean-Global Atmosphere observing system: A decade of progress. J. Geophys. Res. Ocean. 1998, 103, 14169–14240. [Google Scholar] [CrossRef]
- Namias, J.; Cayan, D.R. Large-scale air-sea interactions and short-period climatic fluctuations. Science 1981, 214, 869–876. [Google Scholar] [CrossRef]
- Neelin, J.; Latif, M.; Allaart, M.; Cane, M.; Cubasch, U.; Gates, W.; Gent, P.; Ghil, M.; Gordon, C.; Lau, N. Tropical air-sea interaction in general circulation models. Clim. Dyn. 1992, 7, 73–104. [Google Scholar] [CrossRef]
- Alexander, L.V.; Uotila, P.; Nicholls, N. Influence of sea surface temperature variability on global temperature and precipitation extremes. J. Geophys. Res. Atmos. 2009, 114, D18. [Google Scholar] [CrossRef]
- McGowan, J.A.; Cayan, D.R.; Dorman, L.M. Climate-ocean variability and ecosystem response in the Northeast Pacific. Science 1998, 281, 210–217. [Google Scholar] [CrossRef]
- Wang, C.; Fiedler, P.C. ENSO variability and the eastern tropical Pacific: A review. Prog. Oceanogr. 2006, 69, 239–266. [Google Scholar] [CrossRef]
- Behera, S.K.; Yamagata, T. Subtropical SST dipole events in the southern Indian Ocean. Geophys. Res. Lett. 2001, 28, 327–330. [Google Scholar] [CrossRef]
- Feng, M.; Meyers, G. Interannual variability in the tropical Indian Ocean: A two-year time-scale of Indian Ocean Dipole. Deep Sea Res. Part II Top. Stud. Oceanogr. 2003, 50, 2263–2284. [Google Scholar] [CrossRef]
- Yu, K. Coral reefs in the South China Sea: Their response to and records on past environmental changes. Sci. China Earth Sci. 2012, 55, 1217–1229. [Google Scholar] [CrossRef]
- Chang, S.W.; Madala, R.V. Numerical simulation of the influence of sea surface temperature on translating tropical cyclones. J. Atmos. Sci. 1980, 37, 2617–2630. [Google Scholar] [CrossRef][Green Version]
- Vecchi, G.A.; Soden, B.J. Effect of remote sea surface temperature change on tropical cyclone potential intensity. Nature 2007, 450, 1066–1070. [Google Scholar] [CrossRef]
- Yu, J.; Li, T.; Tan, Z.; Zhu, Z. Effects of tropical North Atlantic SST on tropical cyclone genesis in the western North Pacific. Clim. Dyn. 2016, 46, 865–877. [Google Scholar] [CrossRef]
- Qiao, F.; Yuan, Y.; Yang, Y.; Zheng, Q.; Xia, C.; Ma, J. Wave-induced mixing in the upper ocean: Distribution and application to a global ocean circulation model. Geophys. Res. Lett. 2004, 31, 11. [Google Scholar] [CrossRef]
- Yang, Q.; Zhao, W.; Liang, X.; Tian, J. Three-dimensional distribution of turbulent mixing in the South China Sea. J. Phys. Oceanogr. 2016, 46, 769–788. [Google Scholar] [CrossRef]
- Roxy, M.; Tanimoto, Y. Influence of sea surface temperature on the intraseasonal variability of the South China Sea summer monsoon. Clim. Dyn. 2012, 39, 1209–1218. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, X.; Xie, S.P.; Liu, W.T. A gap in the Indo-Pacific warm pool over the South China Sea in boreal winter: Seasonal development and interannual variability. J. Geophys. Res. Ocean. 2004, 109, C7. [Google Scholar] [CrossRef]
- Su, J. Overview of the South China Sea circulation and its influence on the coastal physical oceanography outside the Pearl River Estuary. Cont. Shelf Res. 2004, 24, 1745–1760. [Google Scholar] [CrossRef]
- Liu, Q.; Kaneko, A.; Su, J. Recent progress in studies of the South China Sea circulation. J. Oceanogr. 2008, 64, 753–762. [Google Scholar] [CrossRef]
- Vaid, B.; Preethi, B.; Kripalani, R. The Asymmetric Influence of the South China Sea Biweekly SST on the abnormal Indian monsoon rainfall of 2002. Pure Appl. Geophys. 2018, 175, 4625–4642. [Google Scholar] [CrossRef]
- Krishnamurti, T.; Chakraborty, A.; Krishnamurti, R.; Dewar, W.K.; Clayson, C.A. Seasonal prediction of sea surface temperature anomalies using a suite of 13 coupled atmosphere–ocean models. J. Clim. 2006, 19, 6069–6088. [Google Scholar] [CrossRef]
- Li, W.; Xie, Y.; He, Z.; Han, G.; Liu, K.; Ma, J.; Li, D. Application of the multigrid data assimilation scheme to the China Seas’ temperature forecast. J. Atmos. Ocean. Technol. 2008, 25, 2106–2116. [Google Scholar] [CrossRef]
- Stockdale, T.N.; Balmaseda, M.A.; Vidard, A. Tropical Atlantic SST prediction with coupled ocean–atmosphere GCMs. J. Clim. 2006, 19, 6047–6061. [Google Scholar] [CrossRef]
- Johnson, S.D.; Battisti, D.S.; Sarachik, E. Empirically derived Markov models and prediction of tropical Pacific sea surface temperature anomalies. J. Clim. 2000, 13, 3–17. [Google Scholar] [CrossRef]
- Xue, Y.; Leetmaa, A. Forecasts of tropical Pacific SST and sea level using a Markov model. Geophys. Res. Lett. 2000, 27, 2701–2704. [Google Scholar] [CrossRef]
- Landman, W.A.; Mason, S.J. Forecasts of near-global sea surface temperatures using canonical correlation analysis. J. Clim. 2001, 14, 3819–3833. [Google Scholar] [CrossRef]
- Kug, J.S.; Kang, I.S.; Lee, J.Y.; Jhun, J.G. A statistical approach to Indian Ocean sea surface temperature prediction using a dynamical ENSO prediction. Geophys. Res. Lett. 2004, 31, 9. [Google Scholar] [CrossRef]
- Lins, I.D.; Araujo, M.; das Chagas Moura, M.; Silva, M.A.; Droguett, E.L. Prediction of sea surface temperature in the tropical Atlantic by support vector machines. Comput. Stat. Data Anal. 2013, 61, 187–198. [Google Scholar] [CrossRef]
- Aparna, S.; D’souza, S.; Arjun, N. Prediction of daily sea surface temperature using artificial neural networks. Int. J. Remote Sens. 2018, 39, 4214–4231. [Google Scholar] [CrossRef]
- Patil, K.; Deo, M.C. Prediction of daily sea surface temperature using efficient neural networks. Ocean Dyn. 2017, 67, 357–368. [Google Scholar] [CrossRef]
- Liu, J.; Tang, Y.; Wu, Y.; Li, T.; Wang, Q.; Chen, D. Forecasting the Indian Ocean Dipole with deep learning techniques. Geophys. Res. Lett. 2021, 48, e2021GL094407. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of sea surface temperature using long short-term memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef]
- Choi, H.-M.; Kim, M.-K.; Yang, H. Deep-learning model for sea surface temperature prediction near the Korean Peninsula. Deep Sea Res. Part II Top. Stud. Oceanogr. 2023, 208, 105262. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Gong, J.; Chen, Z. Short and mid-term sea surface temperature prediction using time-series satellite data and LSTM-AdaBoost combination approach. Remote Sens. Environ. 2019, 233, 111358. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM model for sea surface temperature prediction. IEEE Geosci. Remote Sens. Lett. 2017, 15, 207–211. [Google Scholar] [CrossRef]
- Taylor, J.; Feng, M. A deep learning model for forecasting global monthly mean sea surface temperature anomalies. Front. Clim. 2022, 4, 178. [Google Scholar] [CrossRef]
- Song, T.; Jiang, J.; Li, W.; Xu, D. A deep learning method with merged LSTM neural networks for SSHA prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2853–2860. [Google Scholar] [CrossRef]
- Hao, P.; Li, S.; Song, J.; Gao, Y. Prediction of Sea Surface Temperature in the South China Sea Based on Deep Learning. Remote Sens. 2023, 15, 1656. [Google Scholar] [CrossRef]
- Shao, Q.; Li, W.; Han, G.; Hou, G.; Liu, S.; Gong, Y.; Qu, P. A deep learning model for forecasting sea surface height anomalies and temperatures in the South China Sea. J. Geophys. Res. Ocean. 2021, 126, e2021JC017515. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, C.; Zhang, X.; Zhang, L. A Multivariable Convolutional Neural Network for Forecasting Synoptic-Scale Sea Surface Temperature Anomalies in the South China Sea. Weather Forecast. 2023, 38, 849–863. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.-M. Improvements of the daily optimum interpolation sea surface temperature (DOISST) version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Fernández, J.G.; Abdellaoui, I.A.; Mehrkanoon, S. Deep coastal sea elements forecasting using UNet-based models. Knowl.-Based Syst. 2022, 252, 109445. [Google Scholar] [CrossRef]
- Ren, Y.; Li, X. Predicting the Daily Sea Ice Concentration on a Sub-Seasonal Scale of the Pan-Arctic During the Melting Season by a Deep Learning Model. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4301315. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, X.; Ren, Y.; Bushuk, M.; Shu, Q.; Li, C.; Li, X. Subseasonal prediction of regional Antarctic sea ice by a deep learning model. Geophys. Res. Lett. 2023, 50, e2023GL104347. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 424–432. [Google Scholar] [CrossRef]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 221–231. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 1. [Google Scholar]
- Terrell, G.R.; Scott, D.W. Variable kernel density estimation. Ann. Stat. 1992, 20, 1236–1265. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018. [Google Scholar] [CrossRef]
- Hobday, A.J.; Alexander, L.V.; Perkins, S.E.; Smale, D.A.; Straub, S.C.; Oliver, E.C.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Feng, M. A hierarchical approach to defining marine heatwaves. Prog. Oceanogr. 2016, 141, 227–238. [Google Scholar] [CrossRef]
- Wang, P.; Tang, J.; Sun, X.; Wang, S.; Wu, J.; Dong, X.; Fang, J. Heat waves in China: Definitions, leading patterns, and connections to large-scale atmospheric circulation and SSTs. J. Geophys. Res. Atmos. 2017, 122, 10679–10699. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, C. Variations in summer marine heatwaves in the South China Sea. J. Geophys. Res. Ocean. 2021, 126, e2021JC017792. [Google Scholar] [CrossRef]
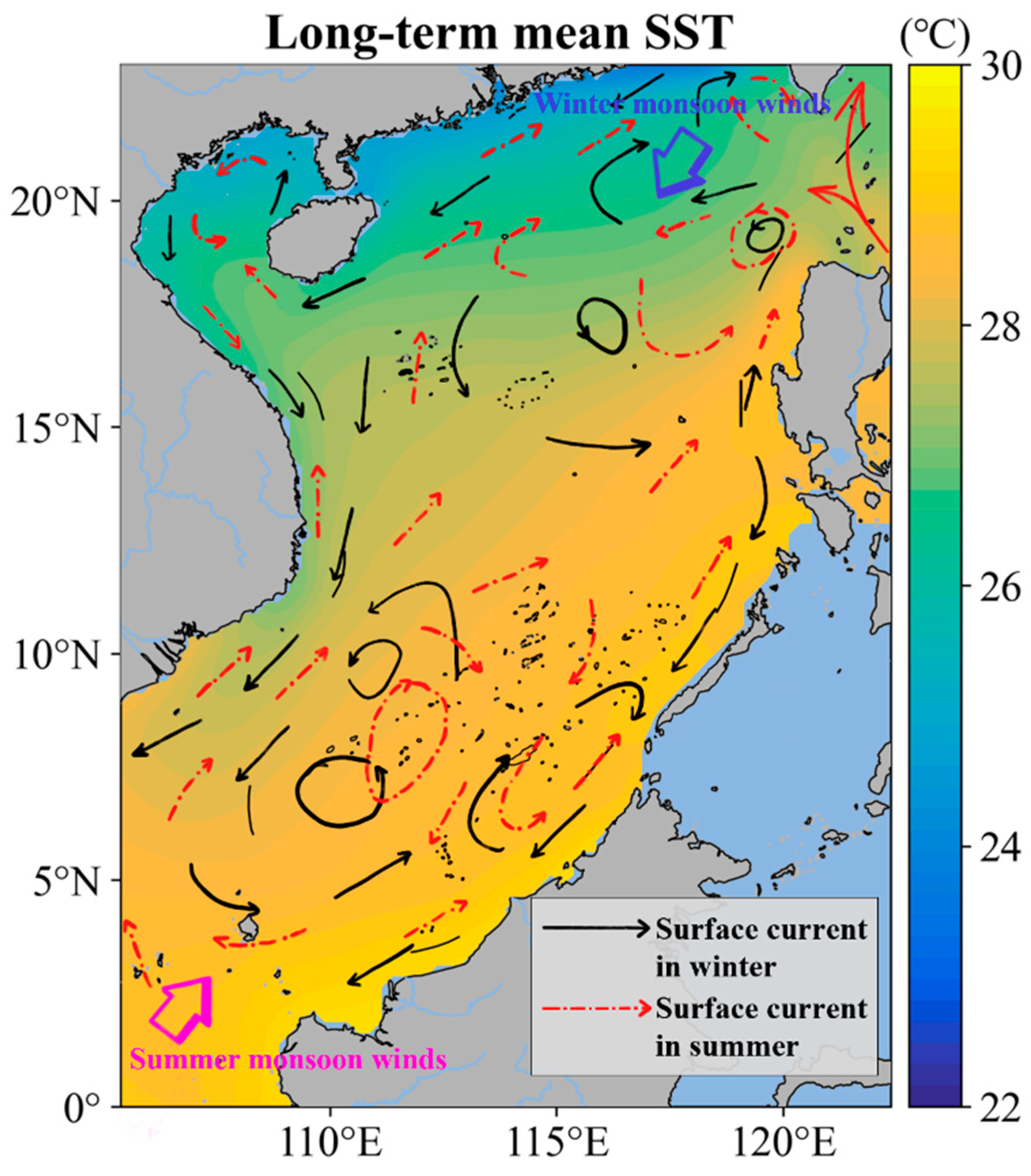



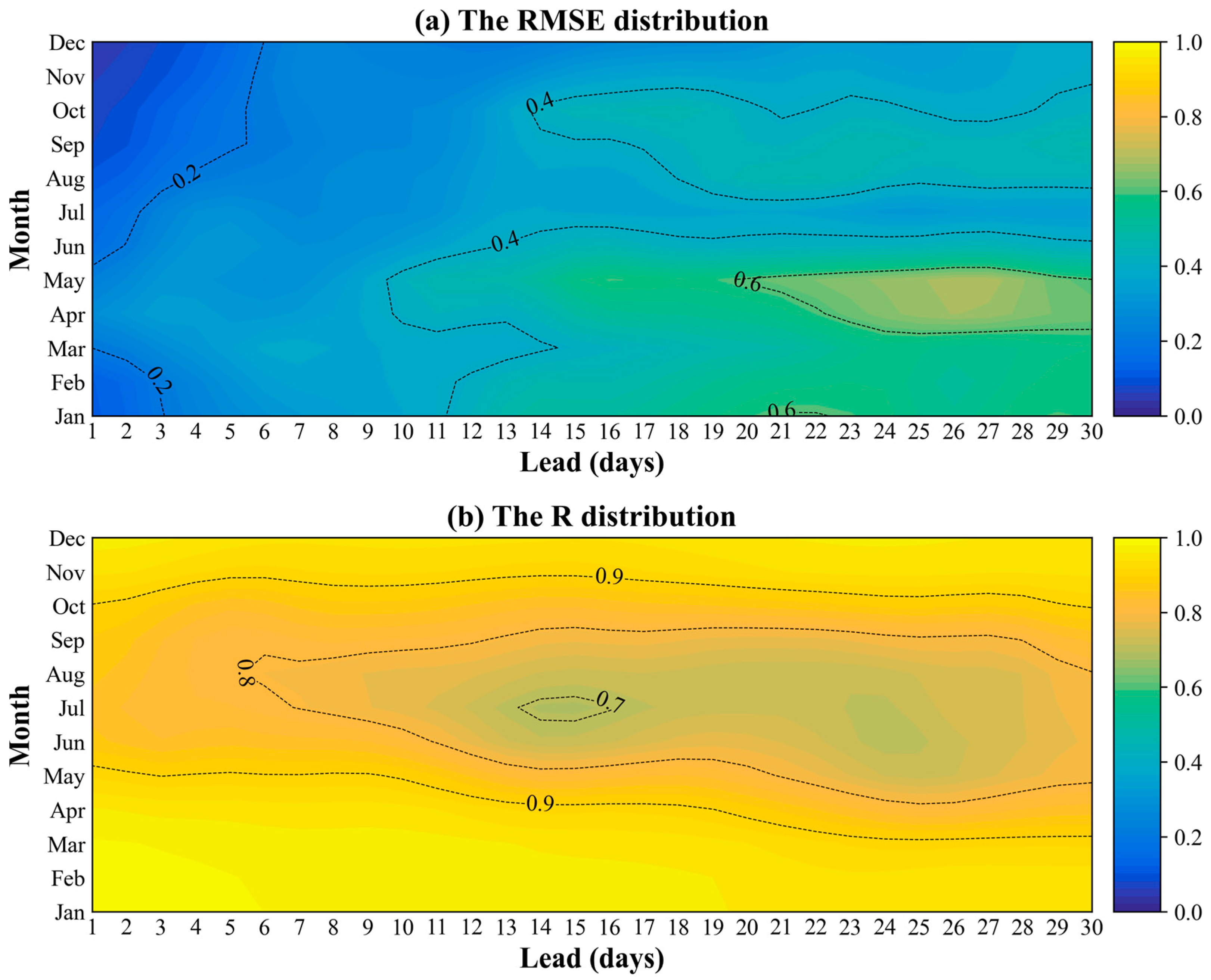
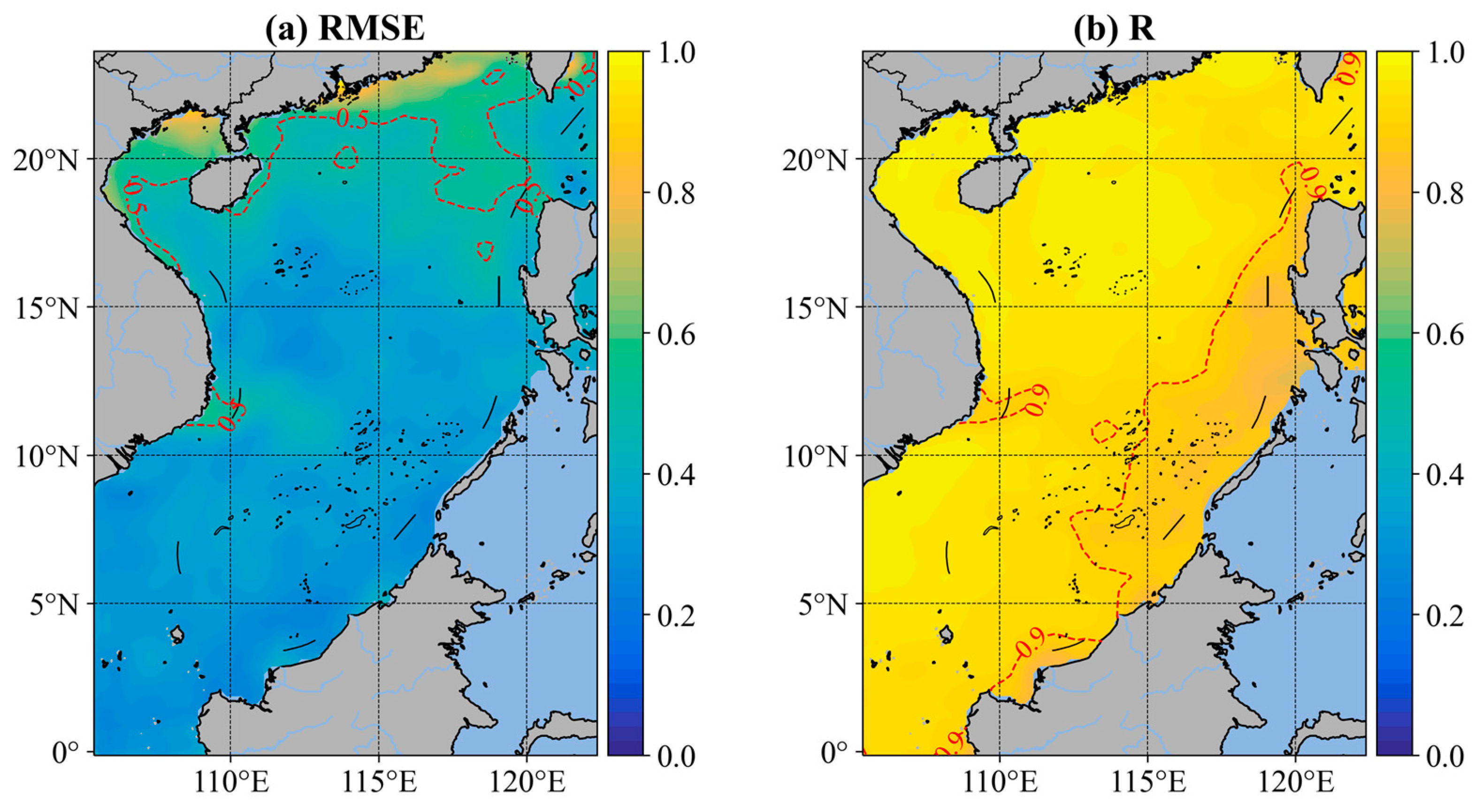
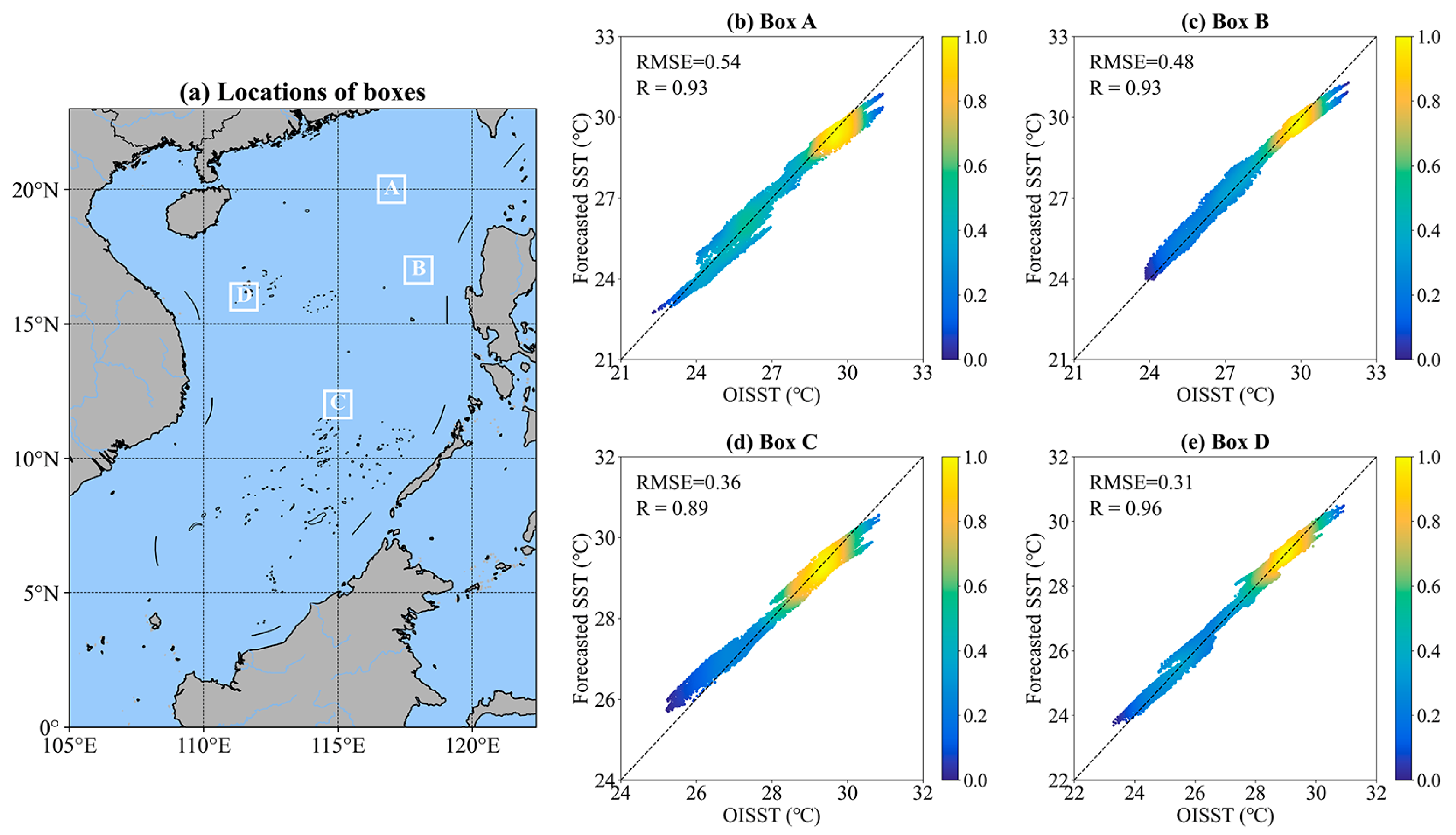


| Index | Details | |||
|---|---|---|---|---|
| Study Area | 105° E–122.5° E, 0°–23° N | South China Sea | ||
| Data | SST | 1993–2021 | NOAA | 0.25° × 0.25° Daily |
| SSHA | 1993–2021 | CMEMS | ||
| SSW (ESSW, NSSW) | 1993–2021 | CCMP | ||
| Training set | 1993–2020 | |||
| Testing set | 2021 | |||
| Models | Parameters | |
|---|---|---|
| ConvLSTM | num_layers = 3, hidden_dim = [64, 64, 30], kernel_size = (3, 3), bias = True, return_all_layers = False, padding = 1 | batch size: 12, activation function: elu, validation frequency: per epoch; loss function: mse, optimizer: radam, learning rate: 0.01, epoch: 1000, earlystopping; |
| 3D U-Net | num_layers = 3, size = [64, 128, 256], groupnorm = 4, conv_kernel_size = 3, pool_kernel_size = 2, conv_padding = 1 | |
| Models | Metrics | Prediction Lead (Day) | |||
|---|---|---|---|---|---|
| 1 | 7 | 14 | 30 | ||
| ConvLSTM | MAE | 0.27 | 0.43 | 0.51 | 0.57 |
| RMSE | 0.38 | 0.60 | 0.69 | 0.77 | |
| MAPE | 0.95% | 1.54% | 1.81% | 2.01% | |
| R | 0.98 | 0.96 | 0.94 | 0.92 | |
| 3D U-Net | MAE | 0.23 | 0.39 | 0.46 | 0.51 |
| RMSE | 0.31 | 0.52 | 0.61 | 0.69 | |
| MAPE | 0.83% | 1.39% | 1.64% | 1.83% | |
| R | 0.99 | 0.97 | 0.95 | 0.93 | |
| Area | Metrics | Prediction Lead (Day) | |||
|---|---|---|---|---|---|
| 1 | 7 | 14 | 30 | ||
| Box A | MAE | 0.25 | 0.51 | 0.61 | 0.72 |
| RMSE | 0.33 | 0.65 | 0.78 | 0.91 | |
| MAPE | 0.91% | 1.82% | 2.20% | 2.59% | |
| R | 0.99 | 0.96 | 0.94 | 0.91 | |
| Box B | MAE | 0.28 | 0.50 | 0.60 | 0.59 |
| RMSE | 0.36 | 0.63 | 0.75 | 0.74 | |
| MAPE | 0.98% | 1.75% | 2.08% | 2.06% | |
| R | 0.99 | 0.95 | 0.93 | 0.93 | |
| Box C | MAE | 0.19 | 0.36 | 0.44 | 0.47 |
| RMSE | 0.25 | 0.46 | 0.54 | 0.60 | |
| MAPE | 0.67% | 1.25% | 1.55% | 1.66% | |
| R | 0.19 | 0.36 | 0.44 | 0.47 | |
| Box D | MAE | 0.21 | 0.35 | 0.42 | 0.47 |
| RMSE | 0.27 | 0.45 | 0.53 | 0.58 | |
| MAPE | 0.75% | 1.26% | 1.51% | 1.69% | |
| R | 0.99 | 0.97 | 0.95 | 0.94 | |
| Index | Definition | Formulas | Unit |
|---|---|---|---|
| HWN | The number of MHW events | Times | |
| HWT | The total duration of MHW events | Days | |
| HWDU | The average duration of MHW events | Days/time | |
| HWI | The average cumulative intensity of MHW events | Degree-days/time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, B.; Qi, J.; Yang, S.; Sun, G.; Feng, Z.; Yin, B.; Wang, W. Sea Surface Temperature and Marine Heat Wave Predictions in the South China Sea: A 3D U-Net Deep Learning Model Integrating Multi-Source Data. Atmosphere 2024, 15, 86. https://doi.org/10.3390/atmos15010086
Xie B, Qi J, Yang S, Sun G, Feng Z, Yin B, Wang W. Sea Surface Temperature and Marine Heat Wave Predictions in the South China Sea: A 3D U-Net Deep Learning Model Integrating Multi-Source Data. Atmosphere. 2024; 15(1):86. https://doi.org/10.3390/atmos15010086
Chicago/Turabian StyleXie, Bowen, Jifeng Qi, Shuguo Yang, Guimin Sun, Zhongkun Feng, Baoshu Yin, and Wenwu Wang. 2024. "Sea Surface Temperature and Marine Heat Wave Predictions in the South China Sea: A 3D U-Net Deep Learning Model Integrating Multi-Source Data" Atmosphere 15, no. 1: 86. https://doi.org/10.3390/atmos15010086
APA StyleXie, B., Qi, J., Yang, S., Sun, G., Feng, Z., Yin, B., & Wang, W. (2024). Sea Surface Temperature and Marine Heat Wave Predictions in the South China Sea: A 3D U-Net Deep Learning Model Integrating Multi-Source Data. Atmosphere, 15(1), 86. https://doi.org/10.3390/atmos15010086







