A Graph Attention Recurrent Neural Network Model for PM_2.5 Prediction: A Case Study in China from 2015 to 2022

Abstract

Accurately predicting PM_2.5 is a crucial task for protecting public health and making policy decisions. In the meanwhile, it is also a challenging task, given the complex spatio-temporal patterns of PM_2.5 concentrations. Recently, the utilization of graph neural network (GNN) models has emerged as a promising approach, demonstrating significant advantages in capturing the spatial and temporal dependencies associated with PM_2.5 concentrations. In this work, we collected a comprehensive dataset spanning 308 cities in China, encompassing data on seven pollutants as well as meteorological variables from January 2015 to September 2022. To effectively predict the PM_2.5 concentrations, we propose a graph attention recurrent neural network (GARNN) model by taking into account both meteorological and geographical information. Extensive experiments validated the efficiency of the proposed GARNN model, revealing its superior performance compared to other existing methods in terms of predictive capabilities. This study contributes to advancing the understanding and prediction of PM_2.5 concentrations, providing a valuable tool for addressing environmental challenges.

1. Introduction

PM_2.5 can be emitted directly from various sources, including moving vehicles, industrial activities, and chemical reactions. The long-time exposure to PM_2.5 can cause serious health problems, including respiratory system diseases [1], chronic kidney diseases [2], and cardiovascular diseases [3]. In addition to harmful effects on public health, various studies have shown that PM_2.5 also leads to economic losses. According to [4], the total economic loss due to PM_2.5 exposure was about 0.91% of the total Chinese GDP in 2016. In a seminal work [5], evidence showed that from 2014 to 2016, China experienced a downward trend in total economic losses, while some regions such as Beijing–Tianjin–Hebei experienced great annual economic losses. To mitigate its adverse impacts, many countries have implemented policies and regulations aimed at reducing exposure to PM_2.5. For instance, the State Council of China released the Action Plan for the Control of Air Pollution as early as 2013, which is a guideline document to control air pollution. Controlling PM_2.5 concentration is crucial for protecting public health and making informed policy decisions related to air pollution [6].

However, accurately predicting PM_2.5 is a challenging task due to the following two reasons. First, PM_2.5 is a complex pollutant that can be influenced by many factors such as meteorological effects, emission behaviors, and land use and land cover (LULC) [7]. In a recent work [8], it was also found that wind speed and terrain elevation are main factors influencing PM_2.5 concentration. Thus, accurately capturing the spatio-temporal patterns of PM_2.5 concentrations requires considering multiple variables [9]. Second, the concentration of PM_2.5 can vary drastically across different locations and over time. Figure 1 shows the time series of PM_2.5 concentrations in Beijing and Shanghai from 1 January 2021 to 31 March 2021. As can be seen, the concentration of PM_2.5 in Beijing exhibited significant fluctuations, ranging from 3 to 488 μg/m³, while the concentration in Shanghai varied from 7 to 149 μg/m³ during the same period. Such spatial and temporal variations pose major challenges for accurately predicting PM_2.5 concentrations.

Despite all these challenges, advanced deep learning models like recurrent neural networks (RNNs) and long short-term memory (LSTM) have shown promising results in predicting PM_2.5 concentrations, resulting in superior forecasting accuracy [10,11]. Moreover, a linear machine learning model was designed to deliver superior performance in capturing rare peaks of air pollution concentrations [12]. However, RNNs or LSTM models do not fully consider spatial dependencies. To tackle this problem, image-based and graph-based methods have been developed based on the input data structure [13]. In image-based methods, the input data are typically a two-dimensional map of the geographical area, with each pixel representing the PM_2.5 concentrations at a specific location. Accordingly, convolutional neural network (CNN) models can be utilized to handle the spatial dependencies. To simultaneously consider the temporal dependencies, models such as LSTM and the gated recurrent unit (GRU) are integrated with CNNs for the spatio-temporal modeling of PM_2.5 [14,15].

In contrast to image-based approaches, the graph-based methods represent air quality monitoring stations or air sensors as nodes, and their spatial dependencies can be expressed as edges through a graph structure. Graph neural network (GNN) models are extensively used along this line, showcasing huge advantages over CNN-based models due to their ability to capture the complex spatial relationships and dependencies between different geographical regions. For instance, Ref. [16] introduced a novel geo-context-based diffusion convolutional recurrent neural network (GC-DCRNN) model for short-term PM_2.5 concentration forecasting. This model can effectively capture spatial and temporal dependencies in location-dependent time series data. In a similar vein, Ref. [17] proposed a hybrid model that integrated graph convolutional networks (GCNs) and LSTM networks (GC-LSTM) to model and predict the spatio-temporal variation of PM_2.5 concentrations. More recently, Ref. [13] developed a PM_2.5 forecasting model that combines a knowledge-enhanced GNN with a spatio-temporal RNN, which can capture long-term dependencies.

In this work, we propose a GNN framework for PM_2.5 concentration prediction by incorporating the GRU module, which is referred to as a graph attention recurrent neural network (GARNN) model. The GARNN model predicts future PM_2.5 concentrations by utilizing both meteorological and geographical information. To this end, an attention-based graph neural network is first designed to capture the spatial patterns and calculate the interactions between neighboring cities based on the graph convolution operations and residual attention mechanism. Then, a gated recurrent unit is employed to further establish the spatio-temporal modeling of PM_2.5. Extensive experiments demonstrate the superior performance of GARNN compared to other existing models in terms of predictive capabilities. The main contributions of this paper are threefold. (1) We build a comprehensive dataset spanning 308 cities in China, encompassing data on seven pollutants and the meteorological variables from January 2015 to September 2022. (2) We establish a novel GNN-based deep learning framework to effectively predict PM_2.5 concentrations. (3) We conduct a comparative study and an ablation study to highlight the superior performance of the proposed method over other existing methods.

The remainder of this paper is organized as follows. In Section 2, we introduce the data sources, including pollutant data, meteorological data, and geographical data. The methodology is illustrated in Section 3, showing the detailed structure of the proposed GARNN model. In Section 4, various experiments are conducted to demonstrate the practical usefulness of GARNN in comparison with other existing methods; this is followed by concluding remarks in Section 5.

2. Data Sources

Our work utilized three sets of data to forecast PM_2.5, i.e., pollutant concentrations, meteorological variables, and geographic distributions. Specifically, the original data were collected at a one-hour frequency. To balance the computational burden and prediction accuracy, we selected data from January 2015 to September 2022 at a three-hour frequency.

2.1. Pollutant Data

The pollutant data were obtained from the Ministry of Environmental Protection of China and the China National Environmental Monitoring Center, in terms of automatic measurement type. We acquired data from 308 cities in China, each with 22,640 observations of 7 pollutant variables, including PM_2.5, PM₁₀, SO₂, NO₂, CO, O₃, and the Air Quality Index (AQI). Internal correlations among pollutants are useful for predicting PM_2.5 concentrations. PM_2.5 concentration exhibited a strong positive correlation with AQI, CO, PM₁₀, NO₂, and SO₂, with time series correlation coefficients of 0.82, 0.62, 0.60, 0.54, and 0.36, respectively. In contrast, there was a weak negative correlation between O₃ and PM_2.5 concentrations, with a Pearson correlation coefficient of −0.21.

2.2. Meteorological Data

Meteorological data were collected from the European Centre for Medium-Range Weather Forecasts (ECMWF), which provides hourly forecast data across the whole world. In line with previous research [13], we selected the following meteorological variables: 2m temperature, total precipitation, boundary layer height, K index, relative humidity, surface pressure, wind speed, and wind direction. A detailed description of the meteorological variables is provided in

Table 1. Descriptions of meteorological variables.

Variables	Unit Description
2m Temperature	K	The temperature of the air at 2m above the surface of land, sea, or inland waters.
Total Precipitation	m	The accumulated liquid and frozen water, comprising rain and snow, that falls on the earth’s surface.
Boundary Layer Height	m	The depth of air next to the earth’s surface, which is most affected by the resistance to the transfer of momentum, heat, or moisture across the surface.
K Index	K	A measure of the potential for a thunderstorm to develop, which is calculated from the temperature and dew point temperature in the lower part of the atmosphere.
Relative Humidity	%	The water vapor pressure as a percentage of the value at which the air becomes saturated.
Surface Pressure	Pa	The pressure (force per unit area) of the atmosphere at the surface of land, sea, and inland water.
Wind Speed	m/s	The speed of air at a height of 950 m above the surface of the earth.
Wind Direction	°	The degree of angle between wind direction and north direction.

, which is in line with ECMWF. These variables are extensively studied and known to affect the transfer and dissipation of pollutants.

2.3. Geographical Data

We selected 308 cities in China as the study area in this work, encompassing a comprehensive representation of the country’s diverse regions. By integrating both the temporal and the spatial aspects, our dataset comprised a total of 6,973,120 observations.

3. Methodology

In this work, we constructed the GARNN structure upon domain knowledge, characterizing the pattern of PM_2.5 concentration via the combination of RNN and GNN. From a local perspective, factors such as boundary layer height, rainfall, and humidity can affect the accumulation and dissipation of pollutants locally, while the concentration levels of other pollutants like PM₁₀ maintain a long-term correlation with the PM_2.5 concentrations. From an external perspective, wind is the primary driving force for transport, and factors such as distance, wind direction, and wind speed can influence the strength of transmission from surrounding cities to the target city. Based on the spatial geographic location of each city, we abstracted them into a graph, with geographic variables such as boundary layer height, temperature, and humidity, as well as pollutant variables such as PM_2.5 and PM₁₀ concentrations, serving as node attributes in the graph. Variables such as distance between two locations, wind speed, wind direction, and the angle between the connection lines were used as edge attributes in the graph. At each time point, information from the current location was first transmitted with information from the surrounding locations, and the integrated hidden layer vector was then fed into the RNN to output future PM_2.5 predictions over time. 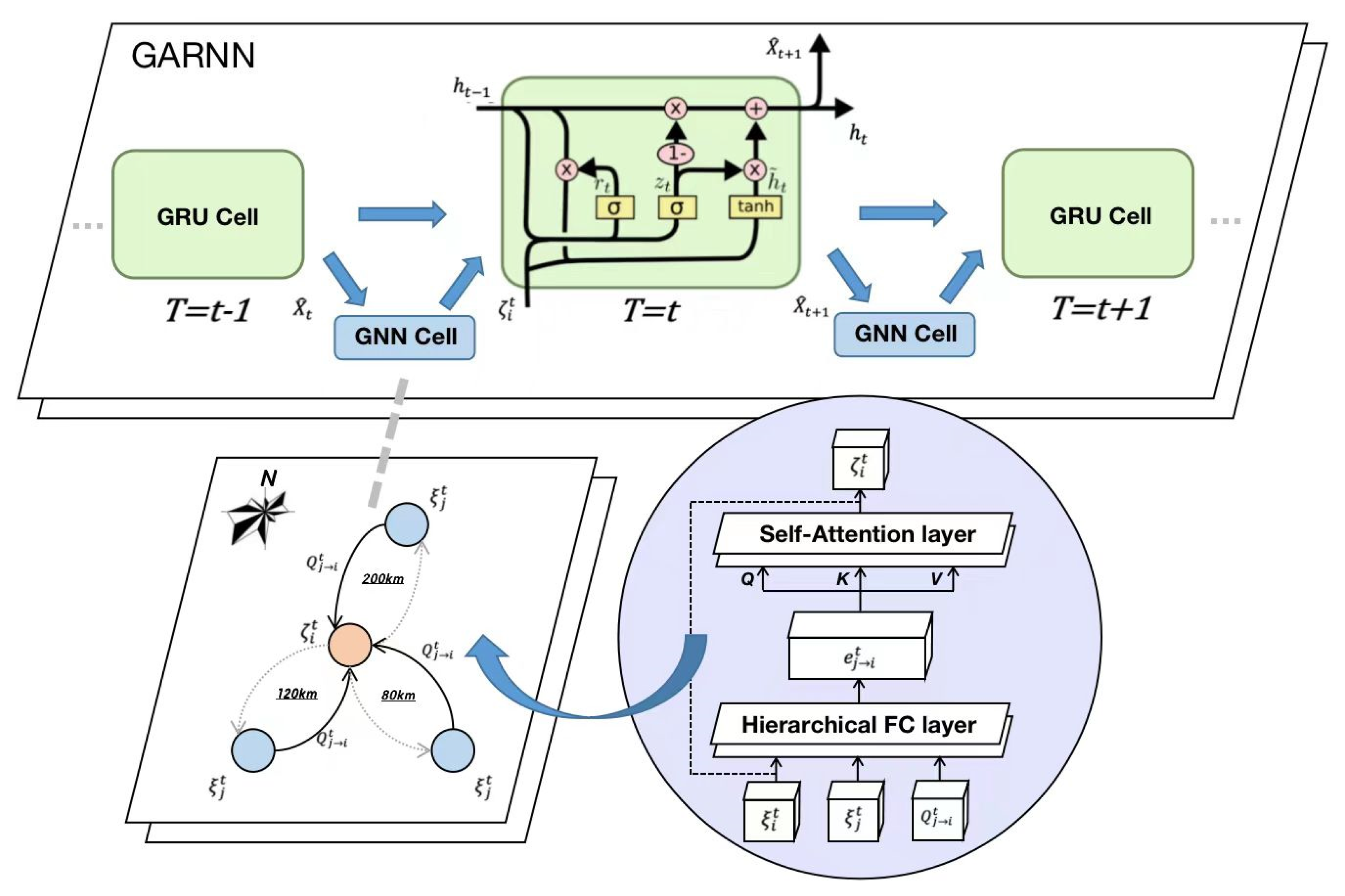Figure 2 shows the workflow of the proposed GARNN, which mainly consists of two modules, i.e., an attention-based graph neural network and a GRU model.

3.1. Graph Construction

A directed graph $G=\left(V,E\right)$ is defined as a collection of cities (i.e., nodes) and their interactions (i.e., edges). The set $V$ corresponds to the nodes, while $E$ refers to the set of edges. We denoted the number of nodes as $N=\left|V\right|$ and the number of directed edges as $M=\left|E\right|$. Furthermore, we predefined a distance threshold of 400 km and a height threshold of 1200 m. If the distance between two cities was less than the distance threshold and the path connecting them did not exceed the mountain range height threshold, then we considered that there existed a connection relationship between the two cities. In other words, these two nodes could be represented as having a two-way connection in the graph structure [13].

3.2. Problem Definition

Let $X^t\in R^{N\times d}$ be the collection of d pollutants, i.e., PM_2.5, PM₁₀, SO₂, NO₂, CO, O₃, and AQI, in $N$ locations at time $t$. Let $P^t\in R^{N\times p}$ be the collection of $p$ meteorological variables in $N$ locations at time $t$. In addition, $Q^t\in R^{M\times q}$ denotes the geographical variables on $M$ edges, i.e., the distance between two locations and its angle direction. Consequently, $P^t$ and $Q^t$ represent nodal and edge attributes, respectively. In general, geographical attributes do not change over time. However, for the sake of notation consistency, we still denoted them as $Q^t$. Moreover, the meteorological attributes for the next 72 h could be obtained through the ECMWF. Furthermore, only historical pollutant concentrations (e.g., PM_2.5) were available. As a result, our primary objective was to predict the pollutant concentrations, particularly those of PM_2.5, in a dynamic way. Specifically, we aimed to solve the following prediction problem:

$$\begin{array}{c}\left[X^{t-T_0},\dots , X^t;P^{t-T_0},\dots , P^{t+T_1};Q^{t-T_0},\dots ,Q^{t+T_1};G\right]\\ \stackrel{f\left(x\right)}{\to }\left[{\widehat{X}}^{t+1},\dots , {\widehat{X}}^{t+T_1}\right]\end{array}$$

(1)

where $T_0$ is the length of historical information, and $T_1$ is the number of steps that we intend to predict. Based on prior knowledge, we set $T_1=24$ so that the PM_2.5 concentrations in the next 72 h could be predicted since our data were collected at a three-hour frequency.

3.3. The Attention-Based Graph Neural Network

A GNN is a type of neural network designed to process data in the form of graph structures. It operates by aggregating information from neighboring nodes in the graph through the use of differentiable functions, thereby simulating complex processes such as pollutant transport and movement with the atmosphere. At each node, pollutant concentration and meteorological variables are encoded into a hidden layer representation through a fully connected layer and nonlinear operations. This hidden layer represents the current pollution and meteorological conditions of the node. Next, the transfer of information between nodes is calculated based on hidden layer status, distance, and angle direction for each directed edge in the graph. Therefore, two hidden layers and edge attributes can be input into the graph neural network operation layer to calculate the information received by each city from surrounding cities. To reduce the noise of unimportant city information, the residual attention mechanism from the graph attention network (GAT) is applied to the final layer, which allows each city to selectively receive information from surrounding important cities. This attention mechanism is implemented by defining the three projection matrices of “query, key, and value”.

The GNN structure is defined as follows. First, at time step $t$, the pollutant concentration $X^t$ or the predicted concentration ${\widehat{X}}^t$ is concatenated with the meteorological variables $P^t$ and passed through the first fully connected layer $\mathsf{\Phi }\left(·\right)$ to obtain the initial hidden layer ${\xi }_i^t$ for each node. The GNN operation is then performed, where information is transfer from node $j$ to node $i$, denoted as $e_{j\to i}^t$. It is calculated based on the hidden layer states ${\xi }_i^t$ and ${\xi }_j^t$, as well as on the directed edge attribute $Q_{j\to i}^t$. Note that $\psi \left(·\right)$ in Equation (2) represents a fully connected layer.

$$\begin{array}{c}{\xi }_i^t=\mathsf{\Phi }\left(\left[X_i^t,P_i^t\right]\right) or \mathsf{\Phi }\left(\left[{\widehat{X}}_i^t,{\widehat{P}}_i^t\right]\right)\\ e_{j\to i}^t=\psi \left(\left[{\xi }_j^t,{\xi }_i^t,Q_{j\to i}^t\right];G\right)\end{array}$$

(2)

After obtaining the information transmission amount of each directed edge $e_{j\to i}^t$, the information from each edge is weighted and aggregated using the residual attention mechanism. More specifically, the query hidden layer $q_i^t$, the key hidden layer $k_{j\to i}^t$, and the value hidden layer $v_{j\to i}^t$ of the neighboring node $j$ to the central node $i$ are, respectively, calculated in Equation (3) for information transmission, where $W_q$, $W_k$, and $W_v$ are the three learnable projection matrices of the attention layer,

$$\begin{array}{c}{q}_i^t=W_q{\xi }_i^t+b_q\hfill \\ k_{j\to i}^t=W_k{e}_{j\to i}^t+b_k\hfill \\ v_{j\to i}^t=W_v{e}_{j\to i}^t+b_v\hfill \end{array}$$

(3)

and $b_q$, $b_k$, and $b_v$ are the bias terms.

Finally, the query result weights are normalized as $a_{j\to i}^t$. All the information from the neighboring nodes is aggregated, and the original information and the updated information are aggregated by residual connection as follows:

$$\begin{array}{c}\hfill a_{j\to i}^t=\frac{\exp \left(q_i^t{k}_{j\to i}^t\right)}{\exp \left({{\displaystyle \sum }}_{j\in N\left(i\right)}{q}_i^t{k}_{j\to i}^t\right)}\\ \hfill {\zeta }_{j\to i}^t={{\displaystyle \sum }}_{j\in N\left(i\right)} a_{j\to i}^t{v}_{j\to i}^t+{\xi }_i^t\end{array}$$

(4)

where $N\left(i\right)$ refers to the collection of connected neighbors of node $i$.

3.4. The GRU Model

The GNN structure models the cross-sectional pattern of pollutant concentration in each time slice. To learn the temporal pattern, it is also necessary to build an RNN structure. Since the historical time length considered in this work was relatively long, i.e., $T_0$, a common RNN is prone to gradient disappearance, which affects the overall model convergence efficiency. Therefore, we employed the GRU network for the RNN part of the model, which includes two gates, i.e., a reset gate and an update gate. The RNN structure is shown in Equation (5). More specifically, at each time step t, the hidden layer ${\zeta }_i^t$ derived from the GNN is used as the input of the GRU network. After the calculation of the reset gate and the update gate, the hidden layer update value $h_i^t$ is computed, and the predicted value ${\widehat{X}}_i^{t+1}$ of pollutant concentration at the next time step is the output

$$\begin{array}{c}{z}_i^t=\sigma \left(W_z\left[h_i^{t-1},{\zeta }_i^t\right]\right)\\ r_i^t=\sigma \left(W_r\left[h_i^{t-1},{\zeta }_i^t\right]\right)\\ \begin{array}{c}{\tilde{h}}_i^t=\tan \mathrm{h}\left(W\left[r_i^t\odot h_i^{t-1},{\zeta }_i^t\right]\right)\\ h_i^t=\left(1-z_i^t\right)\odot h_i^{t-1}+z_i^t\odot {\tilde{h}}_i^t\\ {\widehat{X}}_i^{t+1}=\mathsf{\Omega }\left(h_i^t\right)\end{array}\end{array}$$

(5)

where $W$, $W_z$, and $W_r$ are learnable matrix parameters, $\sigma \left(·\right)$ denotes the sigmoid active function, $tanh\left(·\right)$ denotes the tanh active function, and $\mathsf{\Omega }\left(·\right)$ represents the fully connected layer function. Furthermore, $\odot$ denotes the element-wise product operation.

4. Experiments

4.1. Comparative Study

To demonstrate the effectiveness of the proposed GARNN model, we compared it with other existing methods, including MLP, LSTM, GRU, GC-LSTM, nodesFC-GRU, and PM_2.5-GNN. Specifically, these models were carefully selected for the following two main reasons. On one hand, these models are extensively utilized for PM_2.5 prediction, exhibiting a strong ability in accurate prediction. On the other hand, these models represent three different aspects of modeling. The LSTM model only considers time information, the second model takes both temporal and spatial information into consideration, with spatial information being incorporated via GCN, and the PM_2.5-GNN model employs a GNN to deal with spatio-temporal dependencies.

The Multilayer Perceptron (MLP) is a neural network architecture that does not explicitly model the temporal or spatial dependencies of the input data. Instead, it takes as input the pollutant concentration $X^t$ and the meteorological variables $P^t$ in each city and processes them using a 5-layer fully connected neural network with a hidden layer size of 16.

The Long Short-Term Memory (LSTM) [18] architecture is an RNN that is well-suited for modeling temporal dependencies. To capture the temporal relationships between pollutant concentrations $X^t$ and meteorological variables $P^t$, we employed a 2-layer LSTM model with a hidden layer size of 16.

The Gated Recurrent Unit (GRU) [19] is a type of RNN that is computationally more efficient than the LSTM architecture and it uses fewer parameters. To leverage the temporal dependencies in the pollutant concentration $X^t$ and meteorological variables $P^t$ for each city, we employed a 2-layer GRU model with a hidden layer size of 16.

The GC-LSTM [17] is a hybrid model that combines GCN and LSTM to model both the spatial and the temporal patterns of pollutant concentrations. The GCN component is constructed using an undirected graph that does not consider edge attributes but captures the transmission of spatial information among the nodes. However, this model does not incorporate critical factors such as air flow, wind speed, wind direction, or other pollutant information.

The nodesFC-GRU [13] architecture was developed to model the spatio-temporal dependencies in pollutant concentration data. This model combines fully connected layers and GRU units to capture both spatial and temporal patterns in the given data. The fully connected layers enable the direct summarization of information from all adjacent nodes, while the GRU network learns the temporal dependencies between pollutant concentrations over time. However, this model lacks the characterization of factors such as air flow, wind speed, and wind direction.

The PM_2.5-GNN model [13] employs a GNN to model the spatial patterns of PM_2.5 concentrations. A directed graph with bidirectional edges is constructed, and the domain knowledge is used. However, this model does not incorporate historical information or other pollutant information, which may limit its accuracy and applicability in certain scenarios.

4.2. Experimental Setting and Performance Assessment

To evaluate and compare the predictive capabilities of different models, we employed the evaluation metrics root-mean-square error (RMSE) and mean absolute error (MAE) to carry out performance assessment. We further followed the China Ambient Air Quality Standard (https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/dqhjbh/dqhjzlbz/201203/t20120302_224165.shtml, accessed on 30 June 2024) and set the threshold to build the confusion matrix at 75 μg/m³. This standard is the daily average concentration, which is in line with the WHO standard. As a result, commonly utilized meteorological metrics can be applied, including critical success index (CSI), probability of detection (POD), and false alarm rate (FAR). Among these metrics, higher values for CSI and POD indicate superior performance.

4.3. Experimental Results

Selecting the PM_2.5 concentrations for the next three days ($T_1=24$) as the prediction target, we used all data from 2015 to 2022 from all monitoring stations as the dataset. Training was performed in a rolling manner, where the training set included data from 1 January 2015 to 31 December 2019, the validation set consisted of data from 1 January 2020 to 31 December 2020, and the testing set comprised data from 1 January 2021 to 31 December 2022.

Table 2. Experimental results for evaluation metrics with different methods. The GARNN model is the proposed method in this work. Standard deviation is also reported, which was calculated by replicating the experiments 5 times. The upward arrow indicates that the higher the value, the better the model performance; The downward arrow indicates that the lower the value, the better the model performance.

$({\mathit{T}}_0=1$$, {\mathit{T}}_1=24)$	RMSE ↓	MAE ↓	CSI (%) ↑	POD (%) ↑	FAR (%) ↓
MLP	16.81 ± 0.11	13.64 ± 0.13	29.63 ± 2.99	36.63 ± 5.81	37.84 ± 3.22
LSTM	15.17 ± 0.09	12.16 ± 0.11	35.33 ± 1.15	42.82 ± 2.29	32.90 ± 1.55
GRU	15.37 ± 0.11	12.39 ± 0.13	36.46 ± 0.62	45.66 ± 1.57	35.50 ± 1.45
GC-LSTM	15.18 ± 0.05	12.15 ± 0.06	37.01 ± 0.55	45.87 ± 1.18	34.24 ± 0.71
nodesFC-GRU	14.79 ± 0.15	11.77 ± 0.16	38.94 ± 1.01	49.41 ± 2.71	34.96 ± 2.13
PM2.5-GNN	14.47 ± 0.10	11.54 ± 0.11	38.90 ± 0.98	47.43 ± 2.14	31.45 ± 1.56
GARNN	14.12 ± 0.06	11.19 ± 0.08	40.15 ± 0.52	48.48 ± 1.05	29.95 ± 0.87
(${\mathit{T}}_{\mathbf{0}}\mathbf{=}\mathbf{24}$,  ${\mathit{T}}_{\mathbf{1}}\mathbf{=}\mathbf{24}\mathbf{)}$
LSTM	14.40 ± 0.19	11.47 ± 0.23	39.20 ± 0.75	48.65 ± 1.86	33.00 ± 1.39
GRU	14.43 ± 0.06	11.50 ± 0.07	38.91 ± 0.10	48.70 ± 2.52	33.84 ± 1.97
GC-LSTM	14.40 ± 0.09	11.45 ± 0.10	39.81 ± 0.41	49.36 ± 1.21	32.65 ± 1.11
nodesFC-GRU	14.27 ± 0.17	11.34 ± 0.17	41.18 ± 0.11	52.91 ± 2.28	34.88 ± 1.38
PM2.5-GNN	13.82 ± 0.11	10.98 ± 0.14	42.78 ± 0.36	53.61 ± 0.85	32.05 ± 0.53
GARNN	13.51 ± 0.05	10.68 ± 0.07	43.44 ± 0.75	54.52 ± 2.08	31.76 ± 1.51

shows the experimental results. The top panel shows the results obtained without utilizing historical information ($T_0=1$). The GNN methods that consider information exchange between nodes (i.e., GC-LSTM, nodesFC-GRU, PM_2.5-GNN, GARNN) exhibited stronger predictive capabilities compared to methods that independently predicted the values at each station (i.e., MLP, LSTM, GRU). To be specific, the MLP model exhibited the highest average RMSE, amounting to 16.81. Other models, such as LSTM and GRU, which only incorporate temporal information, yielded an average RMSE value exceeding 15. In contrast, approaches that integrate both temporal and spatial information demonstrated superior performance, with an average RMSE below 15. It is noteworthy that our GARNN model achieved the lowest average RMSE, i.e., 14.12. The bottom panel shows the results obtained by utilizing historical information from the past 24 steps ($T_0=24$). It can be seen that the GNN method incorporating temporal dependencies (i.e., GC-LSTM) showed a certain improvement in prediction accuracy compared to the LSTM or GRU models, although the improvement was relatively small (i.e., from 15.18 to 14.40). Furthermore, the average RMSE of our proposed GARNN decreased from 14.12 to 13.51. Overall, the GNN methods that incorporate information exchange between nodes achieved better results in predicting pollutant concentrations. Moreover, in scenarios with less historical information, the interaction between nodes becomes more important, highlighting the advantages of GNN methods.

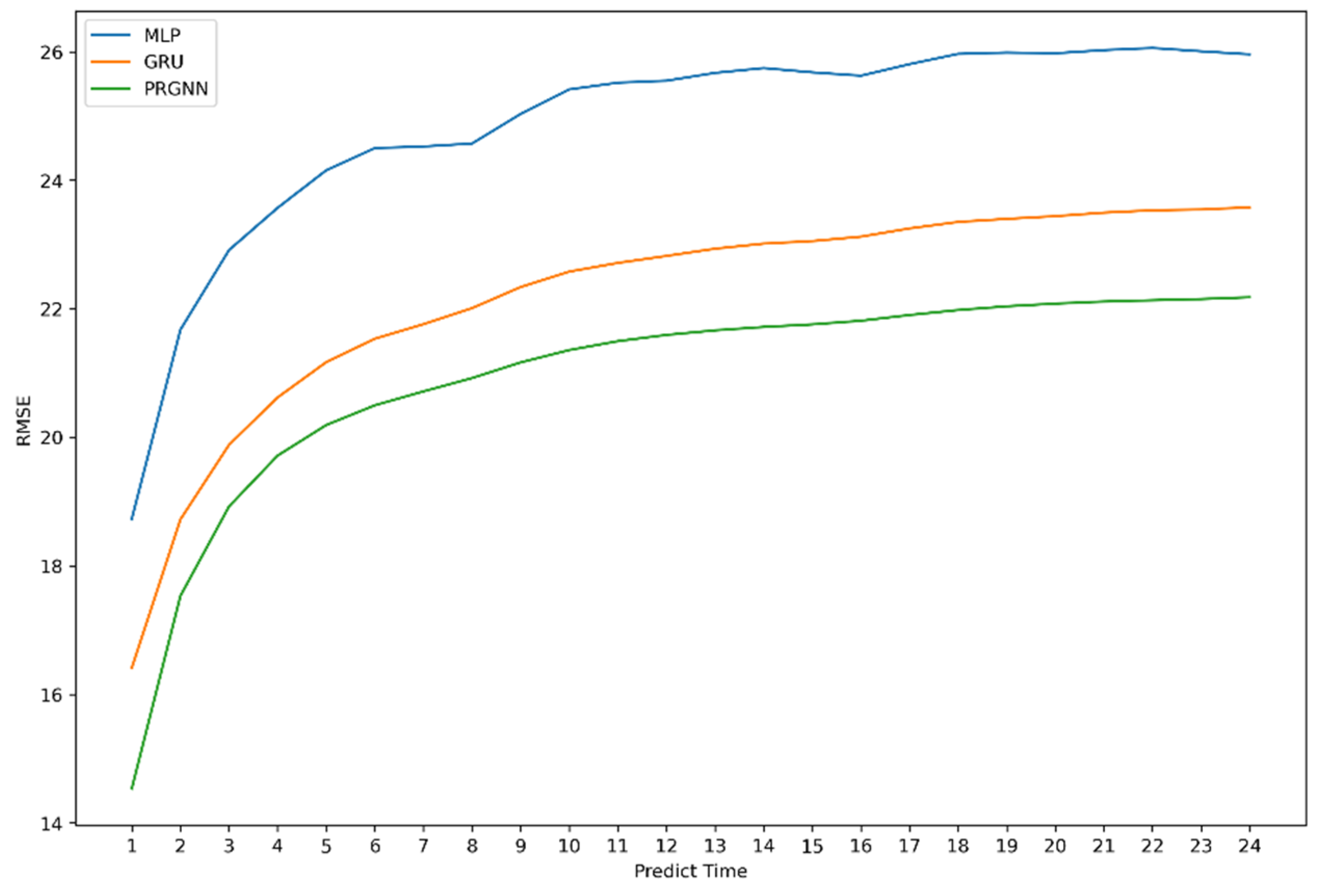
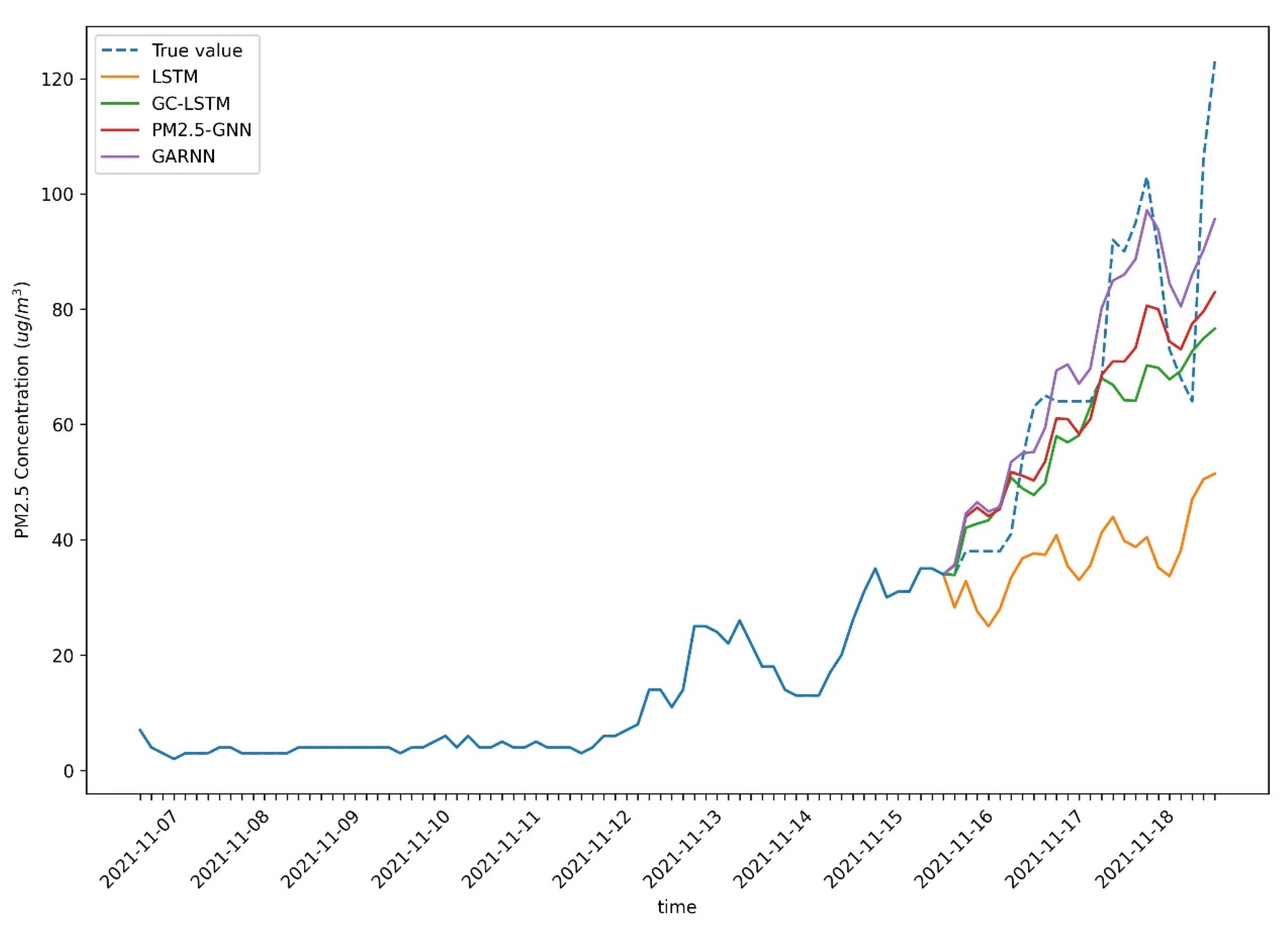
Furthermore, the GARNN model could predict the future PM_2.5 concentrations in each city for a period of time based on historical data. We also compared the results of three representative neural networks, i.e., MLP, GRU, and GARNN, in different prediction periods. The RMSE of the predictions was calculated for future periods from $T_0=1$ to 24. Figure 3 illustrates that the RMSE values of the three models increased as the prediction period grew, indicating that the uncertainty of the predictions also increased with the prediction period. Additionally, the difference in accuracy among these three models was relatively small for the future one-period predictions. However, as the prediction period increased, the advantage of neural network models with temporal information (e.g., GRU and GARNN) became more apparent. Additionally, a detailed illustration of the testing data is provided in Figure 4, with predicted values. The data were selected from Beijing, spanning from 17 November 2021 to 29 November 2021. It can be seen that the model that only considered temporal information heavily underestimated the PM_2.5 concentration (yellow line indicating the LSTM model). Compared with other GCN (i.e., GC-LSTM) and GNN (i.e., PM_2.5-GNN) methods, our newly proposed GARNN model captured the pattern of PM_2.5 concentration very well.

4.4. Variable Importance

In this subsection, we conducted a variable importance analysis on the meteorological variables and other pollutants used in this paper. The permutation test, also known as bootstrap test, was initially introduced in the 1930s by Fisher and others as a method of statistical inference [20,21]. It falls under the category of non-parametric tests, requiring no assumptions about the sample population distribution. With the advancement of deep machine learning models, the concept of permutation test has also been applied to evaluate variable importance in “black-box” algorithms [22]. This process can involve individually shuffling the order of each feature in the test set and subsequently employing a pre-trained model for inference and prediction. The more pronounced the decline in model performance after shuffling a particular variable, the more important that variable within the original model.

To be more specific, the GARNN model trained in Section 4 was utilized. For each variable, a permutation test was performed on the test set. During the permutation, the values of that variable across all cities and time steps were simultaneously extracted. These values were then randomly shuffled and reassigned to each observation. Subsequently, the pre-trained GARNN model was employed for prediction. The changes in the model’s predictive performance after permuting each variable were compared. The results are presented in

Table 3. The predictive performance of variables after the permutation test in the GARNN model. The upward arrow indicates that the higher the value, the better the model performance; The downward arrow indicates that the lower the value, the better the model performance. Bold values are best/highest values in their columns.

$\mathbf{(}{\mathit{T}}_{\mathbf{0}}\mathbf{=}\mathbf{1}$$, {\mathit{T}}_{\mathbf{1}}\mathbf{=}\mathbf{24}\mathbf{)}$	RMSE ↓	MAE ↓	CSI (%) ↑	POD (%) ↑	FAR (%) ↓
GARNN	13.43	10.60	42.53	51.81	29.64
- 2m Temperature	+3.28	+2.95	−5.27	−4.53	+3.52
- Boundary Layer Height	+2.22	+1.88	−6.99	−5.66	+2.85
- K Index	+0.5	+0.44	−0.90	−0.99	+0.60
- Surface Pressure	+1.71	+0.86	−3.98	−2.84	+1.85
- Total Precipitation	+0.45	+0.36	−1.55	−1.90	+0.46
- Relative Humidity	+1.29	+1.21	−3.68	−1.62	+2.73
- Wind Speed	+0.33	+0.28	−1.00	−0.76	+0.36
- Wind Direction	+0.85	+0.76	−2.08	−0.14	+0.79
- AQI	+0.91	+0.82	−1.35	−1.12	+1.30
- PM 10	+0.64	+0.53	−0.89	−0.54	+0.42
- SO2	+0.48	+0.38	−0.81	−0.68	+0.36
- NO2	+0.33	+0.28	−0.60	−0.73	+0.22
- CO	+0.49	+0.38	−1.00	−0.76	+0.36
- O3	+0.62	+0.50	−0.82	−0.67	+0.34

. As can be seen, among all meteorological variables, the 2m temperature and boundary layer height variables stood out as, relatively, the most significant. After shuffling the 2m temperature, the model’s average RMSE increased by 3.28, MAE increased by 2.95, and FAR increased by 3.52%. After shuffling the boundary layer height, the model’s average CSI decreased by 6.99% and POD decreased by 5.66%. These findings are consistent with the existing literature [23] on exploring meteorological influences on PM_2.5 concentrations.

4.5. Dissociation Experiment

An important component of the GARNN model established in this work is the GNN. To analyze the functionality of the components of the GNN, we attempted to replace the computational mechanism of the GNN in this subsection. Specifically, we experimented with scenarios where graph information propagation was not performed (i.e., GARNN-no-graph) and where modeling was conducted using the average propagation among neighboring cities (i.e., GARNN-wavg).

As shown in

Table 4. A summary of predictive evaluation metrics for the GARNN model under different graph message passing mechanisms. The upward arrow indicates that the higher the value, the better the model performance; The downward arrow indicates that the lower the value, the better the model performance.

$\mathbf{(}{\mathit{T}}_{\mathbf{0}}\mathbf{=}\mathbf{1}$$, {\mathit{T}}_{\mathbf{1}}\mathbf{=}\mathbf{24}\mathbf{)}$	RMSE ↓	MAE ↓	CSI (%) ↑	POD (%) ↑	FAR (%) ↓
GARNN-no-graph	15.37 ± 0.11	12.39 ± 0.13	36.46 ± 0.62	45.66 ± 1.57	35.50 ± 1.45
GARNN-wavg	14.35 ± 0.06	11.42 ± 0.08	40.20 ± 0.33	50.65 ± 1.72	32.54 ± 1.28
GARNN	13.51 ± 0.05	10.68 ± 0.07	43.44 ± 0.75	54.52 ± 2.08	31.76 ± 1.51

, when no graph information propagation was performed, the GARNN-no-graph model could only build its predictions based on the historical pollutant concentrations and meteorological variables of the current site. Therefore, its predictive capability for the next three days was significantly weaker compared to that of the other two models that considered information from surrounding cities. When using the average of neighboring city hidden layers for information propagation (GARNN-wavg), the model did not take into consideration factors like inter-city distances, angular directions, wind speed, and wind direction. As a result, it could only provide a vague representation of pollutant environments and climatic conditions around it. The GARNN model first incorporated the feature hidden layers of pairwise cities along with edge attributes into a hierarchical fully connected layer for information exchange. Then, an attention mechanism was applied to re-weight the information from all neighboring cities. This allowed different neighboring cities to contribute differentially to the central city, enhancing the predictive capabilities compared to those achieved when modeling through average information propagation from surrounding cities (GARNN-wavg).

In addition to the graph information propagation module affecting the effectiveness of the GNN, the construction of the graph also has a certain impact on the model performance. By experimenting with variations in the distance threshold used in constructing the urban network graph, as shown in

Table 5. A summary of predictive evaluation metrics for the GARNN model using different distance thresholds. The upward arrow indicates that the higher the value, the better the model performance; The downward arrow indicates that the lower the value, the better the model performance.

$\mathbf{(}{\mathit{T}}_{\mathbf{0}}\mathbf{=}\mathbf{1}$$, {\mathit{T}}_{\mathbf{1}}\mathbf{=}\mathbf{24}\mathbf{)}$	RMSE ↓	MAE ↓	CSI (%) ↑	POD (%) ↑	FAR (%) ↓
GARNN-dis-300	13.71 ± 0.07	10.80 ± 0.11	43.22 ± 0.79	53.69 ± 2.32	31.50 ± 1.32
GARNN-dis-400	13.51 ± 0.05	10.68 ± 0.07	43.44 ± 0.75	54.52 ± 2.08	31.76 ± 1.51
GARNN-dis-500	13.57 ± 0.06	10.72 ± 0.09	43.39 ± 0.39	54.55 ± 1.77	31.44 ± 1.82

, it became evident that as the distance threshold increased, the predictive performance of the GARNN model initially improved and then began to decline. More particularly, when the distance threshold was set at 300 km, the model’s performance across all metrics was at its lowest. Notably, the most substantial enhancement in performance was observed as the distance threshold increased from 300 km to 400 km. Beyond the 400 km threshold, the model’s efficacy experienced only marginal gains, with just two evaluation metrics displaying improvement.

However, when we took into account the number of edges, we found that at a distance threshold of 300 km, the graph contained a total of 3796 edges, while at 400 km, there were 5852 edges, and at 500 km, 8092 edges. As the distance threshold increased, the temporal and spatial complexity of each GNN computation grew. Therefore, when balancing predictive performance and computational complexity, a distance threshold of 400 km is more appropriate for the GARNN model.

5. Conclusions

This study proposes a novel graph neural network named GARNN for PM_2.5 predictions. GARNN integrates three crucial components, i.e., historical information, meteorological variables, and geographical information, ensuring accurate forecasting of PM_2.5. Notably, the attention-based GNN was designed to capture spatial patterns, while the GRU module was employed for an effective temporal modeling of PM_2.5. To empirically demonstrate the effectiveness of the GARNN model, we gathered pollutant and meteorological data from 308 cities in China, obtaining a dataset of 6,973,120 observations. Rigorous experiments suggested that the GARNN model outperforms alternative methods in terms of predictive accuracy. Additionally, a variable importance analysis highlighted that 2m temperature and boundary layer height played pivotal roles in determining the accuracy of PM_2.5 predictions. Various graph message passing mechanisms were also explored, accompanied by the evaluation of different distance thresholds. This exploration served to illustrate the operational effectiveness of the components within the GARNN framework. To summarize, this paper provides a potential solution for PM_2.5 predictions in large-scale scenarios, contributing to the effective prevention and control of air pollution.

For future studies, we propose three possible directions. Firstly, our model could be applied in the field of social network analysis. This is because the network structure can be seen as a graph so that the GARNN framework can be utilized. Under such circumstances, some model objects, rather than measurement objects, can be studied such as the number of posts of a user on social network platforms. Secondly, utilizing multimodal data including satellite imagery and GIS geospatial data could effectively improve the model performance. In future work, these data can be combined for more accurate PM_2.5 prediction, if available. Thirdly, we investigated the model complexity and efficiency of our GARNN model and the competitors. The number of parameters in our model is more than twenty thousand with a training cost of 2.8 min per epoch on average. We admit that the efficiency of our model is not the best. This is mainly because the GARNN model has a very complex structure, which allowed it to achieve the best prediction accuracy in this study. In the future, a possible research direction is to balance the model complexity and prediction ability. Fourthly, regarding data availability, if the current values of air pollution and meteorological variables cannot be obtained, our methodology can still be applied.