1. Introduction
A flare is a combustion device used to burn off excess or unwanted gases in a safe and controlled way. Flares are found across the oil and gas industry, including upstream (oil and gas production), midstream (transportation and storage, LNG facilities), and downstream (refining and distribution), and may also be found in other settings such as biogas facilities. As such, the size and design of flares varies significantly from simple pipe flares, where the gas pressure alone maintains combustion, to highly sophisticated flares that incorporate assist gases (air, steam) and advanced flare-tip geometries intended to optimize combustion whilst suppressing unwanted visible impacts of flaring such as soot formation [
1]. Also, for unassisted flares such as those commonly encountered in upstream oil and gas production, information remains scarce due to the complexity of conducting full-scale tests. The composition of flare gas depends on its source and may include natural gas, inflammable gases such as carbon dioxide and nitrogen, and toxic gases such as hydrogen sulfide. Methane is the primary component of natural gas and is often present in flare gas from upstream production.
Since the industrial revolution, atmospheric methane concentrations have more than doubled, accounting for 25% of anthropogenic global warming [
2]. Methane from oil and gas production and usage accounts for approximately a third of those emissions and is widely seen as the most accessible opportunity for achieving emissions reductions. The World Bank estimates that over 138,000 million m
3 of gas is flared annually, of which the majority (around 80%) is methane [
3]. However, unlike some other key sources of fossil fuel emissions, such as fugitives or the use of pneumatic devices, the flare is an integral part of the design and safe operation of many existing oil and gas facilities with limited alternatives for replacement or removal. Therefore, whilst initiatives such as the World Bank zero routine flaring by 2030 initiative has led to pledges and reductions in gas flared routinely during production, the use of flares to maintain safe operations (safety flaring, which includes low level flaring to maintain a lit flare in case of emergency) and during plant upset and maintenance (non-routine flaring) is likely to persist well into the energy transition.
Quantifying flare combustion uses two closely related values: combustion efficiency (CE) and destruction and removal efficiency (DRE). CE is a measure of the conversion of hydrocarbons to CO
2, whereas (DRE) also accounts for the incomplete combustion products of CO and soot. There is a convention that assumes 2% of all flared natural gas in upstream oil and gas production operations escapes to the atmosphere as unburnt hydrocarbons (often referred to as 98% DRE). However, this generalization is coming under increased scrutiny with a focus on climate change and the risk that flaring poses to meeting methane emission targets. For example, recent studies including those by Plant et al. (2022) have shown that flares operating in an onshore oil production setting can vary from <70 to >99% efficiency, including those which are unlit [
4]. By contrast, measurements taken in the offshore setting of the Norwegian North Sea by Shaw et al. yielded a much narrower range in efficiency, with an average of 98.4% [
5]. Fabrizio et al. conducted methane emissions measurement for the onshore LNG industry using fully traceable differential absorption LiDAR (DIAL). The measurement approach was to quantify emissions, determine emissions factors to enable accurate inventory reporting, and targeted maintenance and repair [
6]. If emissions from flares are to be better understood and measurements made available to mitigate them, then these differences need to be better measured and tracked.
Previous research has demonstrated that flaring is a complex process which involves numerous factors that contribute to the CE/DRE. These parameters include compositional factors such as the lower flammability limit (LFL) and net heating value of the combustion zone gas (NHVcz) as well as the way that the flared gas mixes in the air, including the stoichiometric air ratio (SR), momentum flux ratio (MFR), and flare tip velocity [
7].
Among the different environmental factors that can affect a flare, the most significant is crosswinds. Exploration of the modifying effects of crosswinds have relied primarily upon the use of scaled experiments [
8] demonstrating that flare performance can be reduced under high winds that can strip unburnt hydrocarbons from the combustion zone. However, such tests are complex to perform and may encounter scaling problems when applied to some of the more advanced designs of flare. Seebold et al. (2004) stated that CE may be adversely impacted in the wake-dominated mixing regime due to fuel stripping, where unburned hydrocarbons detected downwind in a wake-dominated flare burn with a crosswind velocity of 8 m per second (m/s), or approximately 18 mph [
9].
Full-scale tests have focused on the performance of air- and steam-assisted flares, and until recently, the impact of localized environmental effects such as visible soot formation have been the primary concern. Such flares are most often encountered in the downstream (refinery) sector [
10,
11]. The heightened focus on methane emissions has increased the interest in the performance of unassisted flares, which are commonplace in production settings and account for the bulk of global flaring. The amount of publicly available data on the performance of these flares is limited. To help redress that problem, Evans et al. [
12] conducted further experiments on the unassisted flares of different designs that were used by Chong et al. [
13] to verify a parametric model capable of near real-time tracking of flare combustion. Such experiments are, however, limited by their capacity to measure the modifying influence of crosswinds on flare combustion. Besides the challenge of needing consistent and predictable wind speeds, it would be unsafe to use extractive systems during high wind speed events as well as extremely challenging to position the extractive system over the combustion plume in a reproducible way. This is a significant shortfall, as many flares operate in extremely harsh environments, including offshore, where high wind speeds are frequently encountered.
Recent advances in the availability of advanced computing facilities and software have improved the viability of using computational fluid dynamics (CFD) to augment understanding of flare combustion. CFD simulation is an important tool for understanding and optimizing the combustion process, as it allows us to analyze the complex interactions between different factors, such as fuel properties, mixing, ignition, flame propagation, and heat transfer. The main challenge in simulating an industrial flare is the accurate representation of the flow dynamics and gas combustion.
Pitsch et al. [
14] applied large eddy simulation (LES) to simulate a premixed methane/air diffusion flame (Sandia flame D). Flame D is one of a suite of highly studied reference flame data sets and fulfils the role of a de facto reference standard for simulation studies. Jaravel et al. [
15] performed LES with direct integration of reduced chemical kinetics including nitrogen monoxide chemistry on flame D. Jones [
16] simulated the Sandia Flame Series (D–F) with augmented reduced mechanism (ARM) and demonstrated the ability of the method in capturing extinction and re-ignition in turbulent flames. Castiñeira et al. [
17] conducted CFD simulation studies of steam-assisted and air-assisted flares to study the thermochemistry effects of steam and air on CE. Kanwar Devesh. Singh et al. [
18] modeled industrial steam- and air-assisted flaring and compared it to full-scale empirical tests conducted by Allen et al. [
19]. Wang et al. developed a reduced C1-C4 combustion mechanism called Vsoot and performed CFD models with Vsoot to simulate flaring events [
20].
CFD studies of crosswinds have concentrated on laboratory-scale flame simulations. Castiñeira et al. conducted a CFD simulation of wind tunnel experiments. Inefficient combustion was observed at high crosswinds. The CE of low-momentum flares were higher than expected due to recirculating zone results from crosswind [
21]. David et al. applied the eddy dissipation concept (EDC) to study the effects of crosswind on Flame D and found that high-momentum flames are more sensitive to crosswind problems as the jet velocity increases [
22]. Priere. et al. applied LES to investigate the performance of mixing devices in jets subjected to crossflow conditions and successfully validated their predictions against experimental data [
23]. CFD simulation was used by Kermani et al. to explore wind effects on temperature distribution, air–fuel mixing, and combustion efficiency for gas refinery flares [
24].
Despite these advances, there have been limited examples in which a CFD model is verified against reference data before being compared to full-sale empirical data and used to investigate the impacts of crosswinds. Such a full value chain assessment is necessary if CFD is to be accepted as an alternative to the empirical testing of flares and accelerate the development of new flare designs and measurement systems used to track flare combustion in a trusted way. This work was designed to fulfil that need when applied to unassisted flares and, in doing so, reduce the risks associated with quantifying the emissions of methane from flaring.
2. Methods
All of the CFD simulations in this work were conducted using ANSYS Fluent 21R2 software at the BP High Performance Computing facility (HPC) in Houston, TX. The HPC enables partitioning of the computational mesh and distribution of the solver workload across multiple processors, thereby compressing the overall wall clock time for the simulations. Each simulation case was run using 5 nodes of 96 cores each (i.e., a total of 480 CPUs) on an Intel Cascade Lake cluster. Inter-node communication was facilitated by InfiniBand Interconnect and Intel MPI (message passing interface). Typical run time per simulation case was 8 h.
A two-step process was employed for assembling, validating, and applying the model as follows: (1) The model was compared to full-scale empirical data published by Evans et al. [
12] to ensure that the model accuracy was scale independent; (2) the model was applied to explore the effect of crosswinds.
2.1. Simulation Methodology
The main challenge in simulating industrial flares is the accurate representation of the flow dynamics and gas combustion. Industrial flares are turbulent in nature and encompass a wide range of time and length scales. The governing transport equations for flares typically include the conservation equations for mass, momentum, and energy, as well as species and radiation transport equations. These are the typical equations used in the ANSYS Fluent Software package. A discrete ordinates (DO) radiation model is applied in combustion simulation, and the weighted sum of gray gases model (WSGGM) is used for the absorption coefficient. Angular discretization was set up with theta divisions (N
θ) of 3, phi divisions (N
Φ) of 3, theta pixels of 2, and phi pixels of 2. Turbulence was modelled using the k-omega SST model. The SST-k-omega model is designed for a wide range of Reynolds numbers—covering transition to highly turbulent flows—and different scenarios: shear, buoyancy, or rotational turbulence [
25].
Combustion chemistry and its interaction with turbulent structures was modelled using a reduced-order technique called flamelet-generated manifold (FGM) [
25]. FGM is a partially premixed combustion model that is based on a non-premixed combustion model and a premixed combustion model. In fast chemistry scenarios (such as hydrocarbon flames), the FGM approach is valid and enables the problem to be solved efficiently. In this approach, a representative 1-D flame is simulated a priori, and the generated chemical information is tabulated against a reduced number of control variables, thereby creating a low-dimensional manifold. Density weighted mean scalars (such as species fractions and temperature), denoted by Φ, are calculated from the probability density function (PDF) of f and c as in Equation (1):
where:
c = reaction progress variable defined as reduced product mass fraction.
f = Mixture fraction, which tracks the variation of air-to-fuel ratio; air and fuel are not fully mixed.
The FGM model assumes that the thermochemical states in a turbulent flame are like the states in a laminar flame and parameterize these by mixture fraction and reaction progress. Within the laminar flame, reaction progress increases from c = 0 in the unburnt reactants to c = 1 in the burnt products, over a nonzero flame thickness. A point within the turbulent flame brush with 0 < c < 1 has contributions from both fluctuating flame fronts, also intermediate reaction progress [
25]. Since equilibrium assumption is not made, it is expected that species like CO and OH can be predicted more accurately. Assumed probability density functions account for the turbulence–chemistry interaction. Thus, this model assumes that the fundamental nature of the flame structure is unaltered by the turbulent eddies, but the turbulent flame brush is made up of an ensemble of laminar flamelets. The widely used combustion mechanism developed by the Gas Research Institute (University of California, Berkeley), GRI-Mech 3.0, is employed to simulate the representative 1-D flame. The mechanism consists of 53 species and 325 elementary reactions and is optimized for methane combustion but also includes ethane and propane combustion chemistry [
26]. Previous studies using a similar methodology simulated Sandia Flame D and validated the approach by comparing the predicted species and temperature profiles against the measurements.
A steady-state RANS (Reynolds averaged Navier–Stokes) solver is selected for this study to predict the mean flame behavior. While a transient solver may capture the flame dynamics better, it would require a prohibitively high computational cost for simulating the selected range of operating scenarios.
CE was calculated by averaging the species mass fluxes at the outlet using the following Equation (2).
DRE is calculated as the mass percentage of hydrocarbon destroyed relative to the quantity entering the flare using Equation (3).
The equation requires the mass flow rates of various species entering and exiting the domain. A surface integral of the speciated flow rate was constructed over the gas inlet/outlet surfaces to determine the net fuel flow rate. A similar surface integral is implemented over all the pressure outlet surfaces to calculate the net fluxes of the combustion products. The mass flow of each species was calculated as shown below in Equation (4).
where
is the mass flow rate of species
i through a boundary,
is density,
is mass fraction,
is velocity vector, and
is area projections over the faces of zone.
Carbon mass balance is used as an additional measure to verify proper convergence of the species fields to a steady-state solution. Net carbon flux is calculated by multiplying the mass flux of each species across all the boundaries with its carbon mass fraction and summing it over all the modelled species. Net carbon flux is maintained within a tight error tolerance to ensure solution accuracy.
2.2. Simulation Flare Design
Simulation models were built to replicate the design of two test flares used by Evans et al. [
12]. The first design, hereafter referred to as the utility flare, is of a straight pipe design with an outer diameter of 14” and a wall thickness of 0.322”. The effective diameter is 11 inches (95.03 in
2). It represents some of the simplest flare designs found routinely in oil and gas facilities. The second design, hereafter referred to as sonic flare, is a single arm, pressure-assisted flare tip with an 8” outer diameter and 0.322” wall thickness. Pressure at the tip is raised by forcing the flow through the fixed inside gas discharge slot, which is a metal cone creating an effective cross-sectional area of 21.7 in
2. Flares of this design increase the exit velocity of the gas to facilitate turbulent mixing with the air. There are many further designs of flare tip adopting an array of multi-arm designs that split the flared gas over multiple paths. However, when measuring CE/DRE using field laboratory methods, Evans et al. concluded that at the current levels of measurement uncertainty, the impact of these modifications was not possible to discern.
For utility flares, there is a slight restriction at the exit due to the flame stabilizer tab. Additionally, small holes in each flame tab around the pipe exit and the void between each flame tab were not considered.
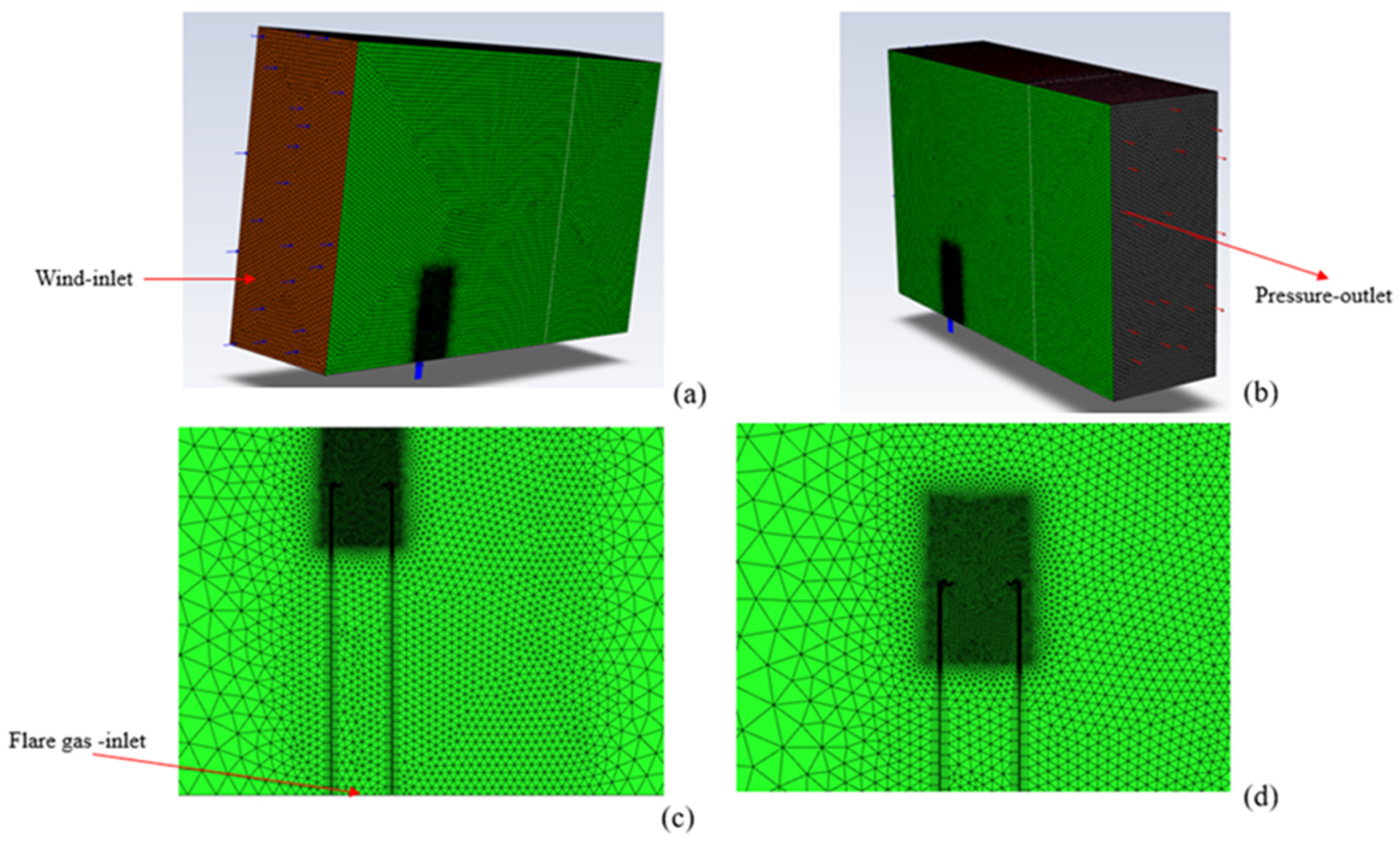
Figure 1 and
Figure 2 show the developed 3-dimensional models and the corresponding base (initial) computational mesh. A finer mesh was employed around the exit of the flare tip where the combustion reactions are expected to improve the accuracy. Base mesh size is approximately 850K cells. Solution-based dynamic adaptive meshing is used to further improve the accuracy. As a result, final mesh size increased to about 8 million cells during the simulation.
In empirical tests, a 2-inch flare pilot burning Tulsa natural gas (TNG) was used to ignite the flare and keep it lit for low NHV gas. Pilots operate at effectively 100% CE/DRE, and their design and operation are not a main part of this study. To replicate this, in the model, the ignition source for the flare gas exiting the flare tip is provided numerically. This is achieved by setting the combustion progress variable to 1 in a small region directly above the flare tip. This simplified approach eliminates the need for explicit modelling of the pilot lines in the simulation.
The addition of a fully simulated pilot within the experiment would substantially increase computation time. To further investigate pilot effects, extra studies were performed using the sonic flare tip with a pilot model under a range of conditions. Pilot effects were proven to be more sensitive to high wind condition with the same NHV cases. This pilot effects study will be included in our future publications.
Boundary conditions were defined as follows. The left side of the domain was designated as the wind inlet with a specified velocity condition, while the right side served as the outlet subjected to the atmospheric pressure conditions. The flare gas inlet was situated at the bottom of the flare tip. The flare pipe surfaces were assumed to be adiabatic, no-slip walls, while the atmospheric domain boundaries (except for the wind inlet and outlet) were assumed to be adiabatic, shear-free walls. A sufficiently large atmospheric domain was modelled so that the flame was unconfined for all practical purposes. The temperature measurements used in the simulation replicated those recorded during empirical testing.
2.3. Validation Experimental Design
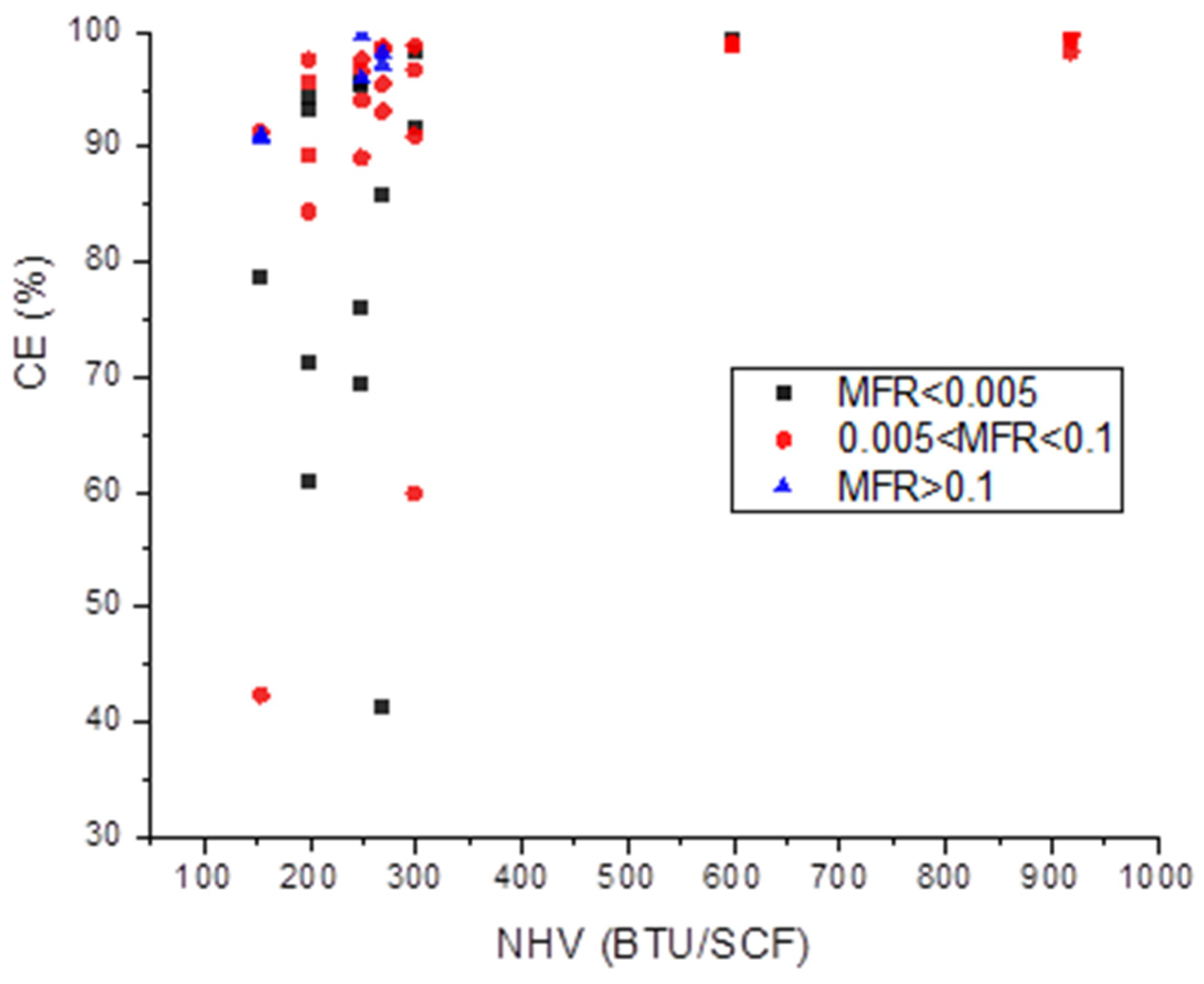
The net heating value of vent gas (NHV) is critical to flare ignition and sustained burning. This is normally expressed for unassisted flares in BTU/SCF, with alternate equations available for air- and steam-assisted flares to account for the role of these additional gases. Turbulent mixing of the vented gas and ambient air dictates whether the mixture attains flammable conditions to maintain a high CE/DRE. Mixing characteristics are, in turn, a function of the gas flow rate, the speed at which it exits the flare tip, and ambient air conditions and crosswinds. MFR (momentum flux ratio) is a parameter used in flare combustion studies to quantify the momentum transfer from the gas to the surrounding atmosphere that includes consideration of crosswinds. A high MFR indicates a strong momentum transfer and better mixing of the combustion products with the surrounding air, which can improve combustion efficiency and reduce emissions. As the MFR increases, the behavior of the flare flame can be classified into three distinct regimes: wake-dominated, buoyancy-dominated, and inertia-dominated [
27]. MFR is defined as:
where
MFR is the calculated momentum flux ratio, unitless;
is the density of flare waste gas, lb/scf;
is the flare vent gas velocity, ft/s;
is the density of air, lb/scf; and
is the wind velocity, ft/s.
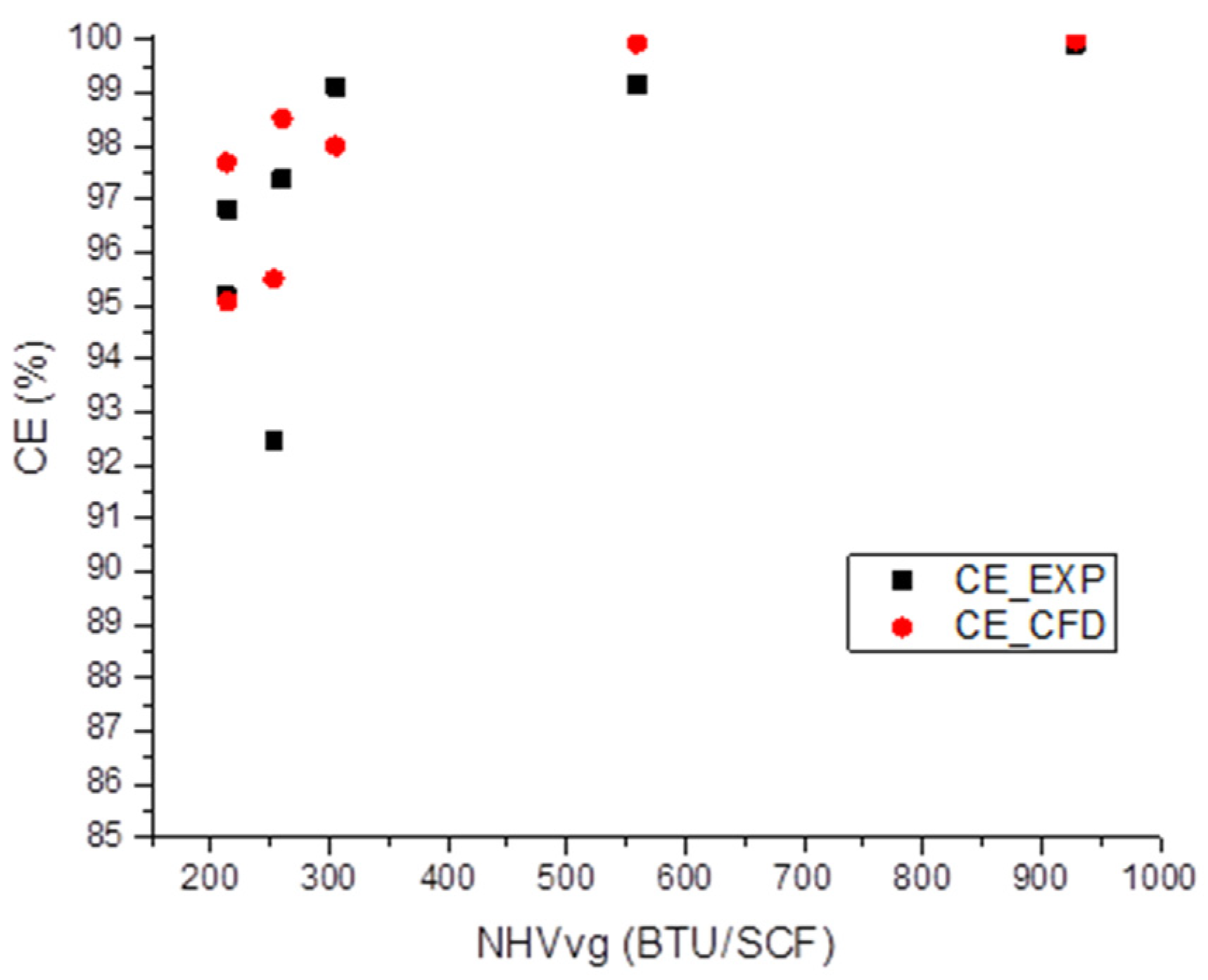
Validation relative to empirical data was conducted by simulating conditions tested by Evans et al. Seven single-pipe utility flare tip cases with NHV values ranging from 200 BTU/SCF to 930 BTU/SCF and jet velocities ranging from 0.2 m/s to 5 m/s were investigated as shown in
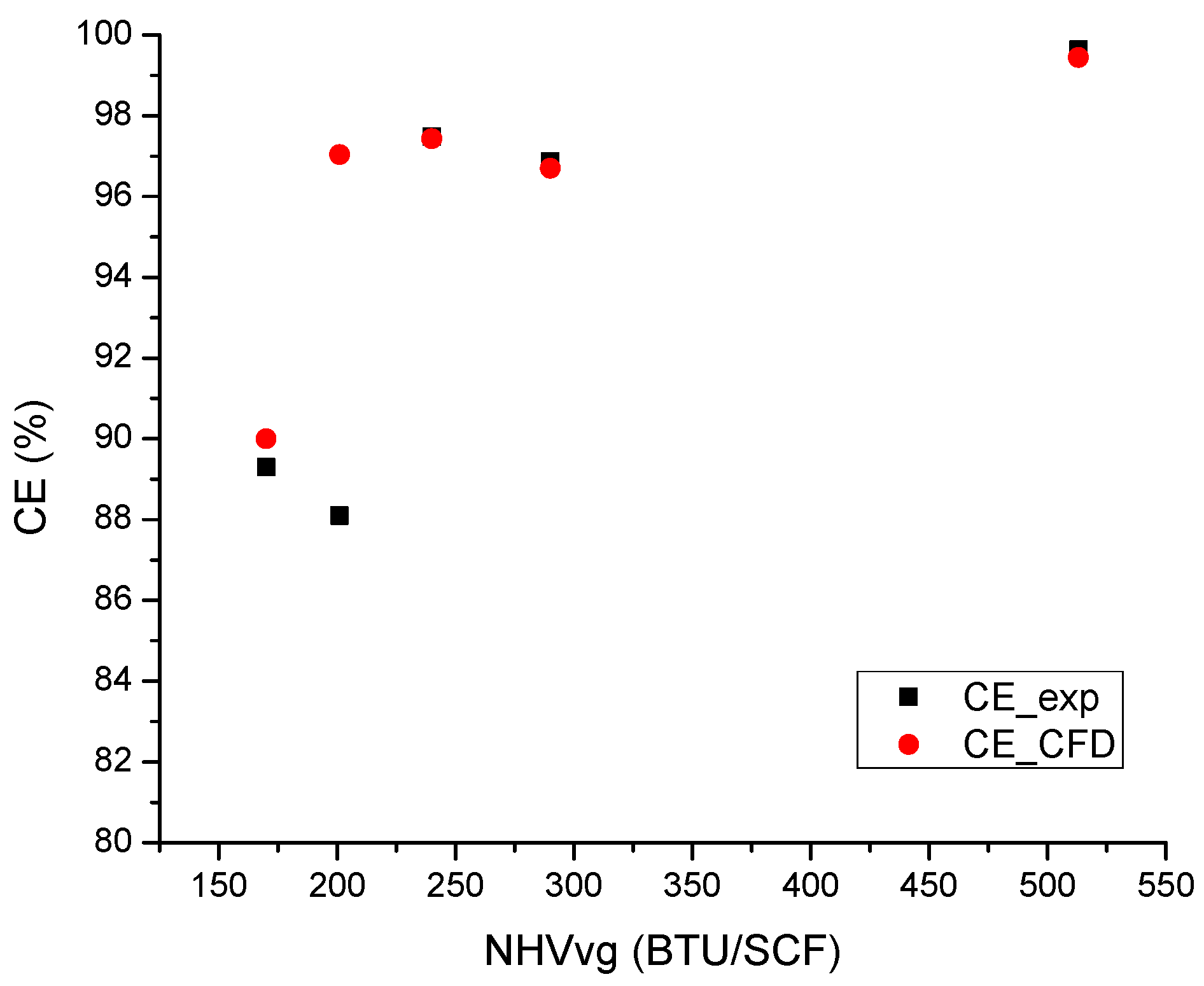
Table 1. Five sonic flare tip cases with NHV values ranging from 170 BTU/SCF to 600 BTU/SCF and jet velocities ranging from 0.5 m/s to 2 m/s were investigated as shown in
Table 2. Gas composition replicated the same gases used by Evans et al., in which a range of NHV values were formulated by mixing TNG with nitrogen. These tables show, for each case, the gas composition, net heating value of vent gas (NHV), jet velocity (V
jet), crosswind velocity (U), and momentum flux ratio (MFR).
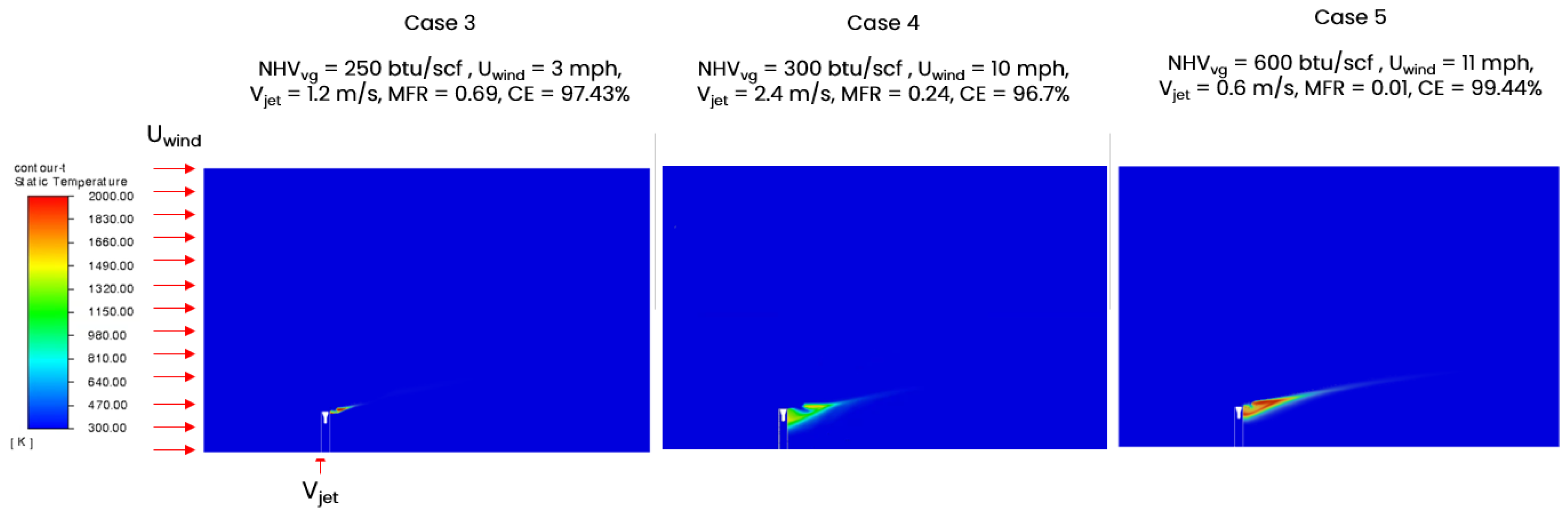
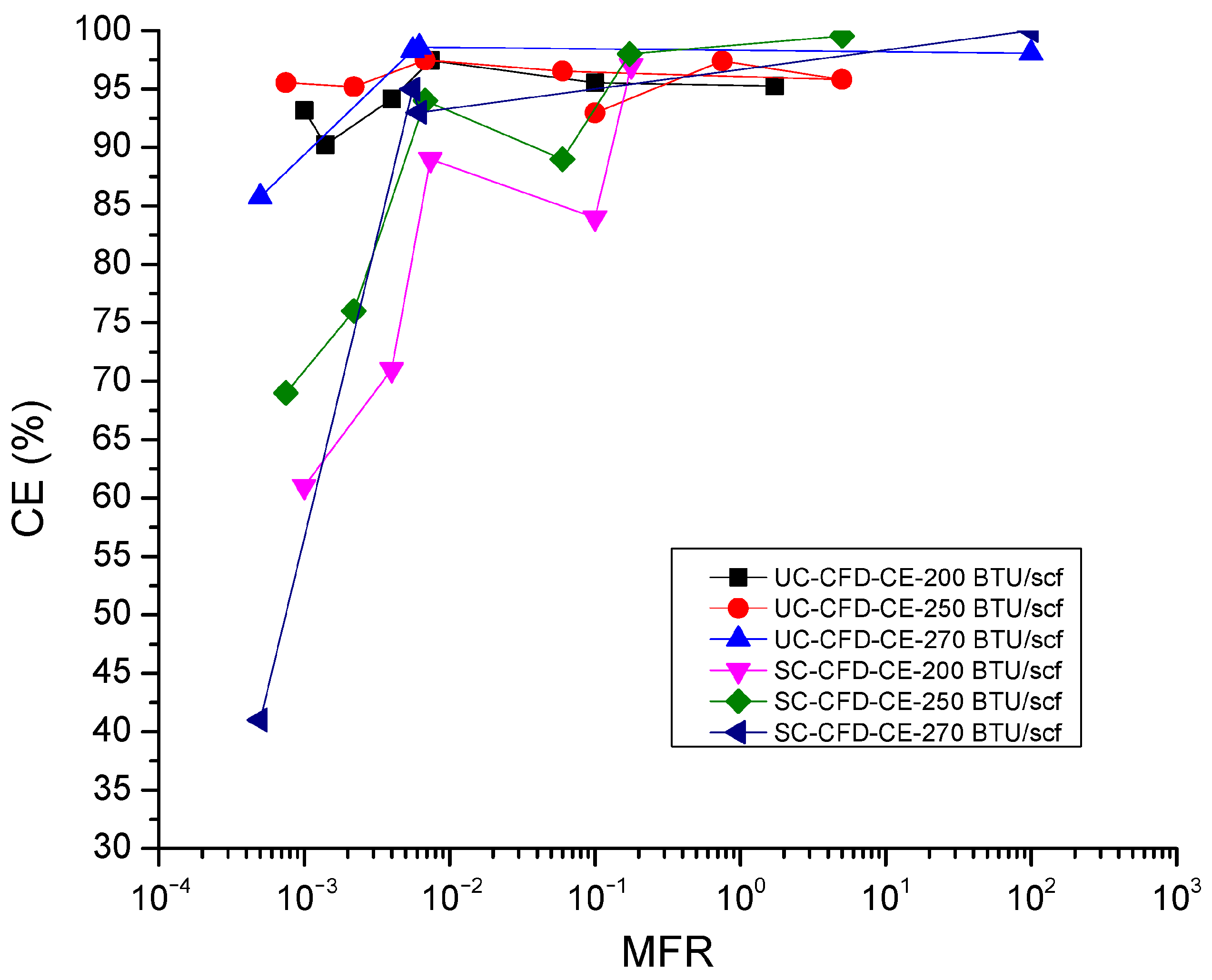
2.4. Investigation of Crosswind
In order to assess the effect of high crosswind speed on CE and DRE, the MFR range considered was varied from 10
−4 to 10
3, covering the different combustion regimes as defined by Seebold et al. [
27]. Four flare tip velocities (0.6 m/s, 1.2 m/s, 2.4 m/s, and 5 m/s) were designed to cover the range of operating flow rates of gas in keeping with previous empirical studies. The NHV varied from 100 to 920 BTU/SCF. The input conditions for 24 utility flare corner (UC) cases and 24 sonic flare corner (SC) cases are listed in
Table A1 and
Table A2 in the
Appendix A.
5. Conclusions
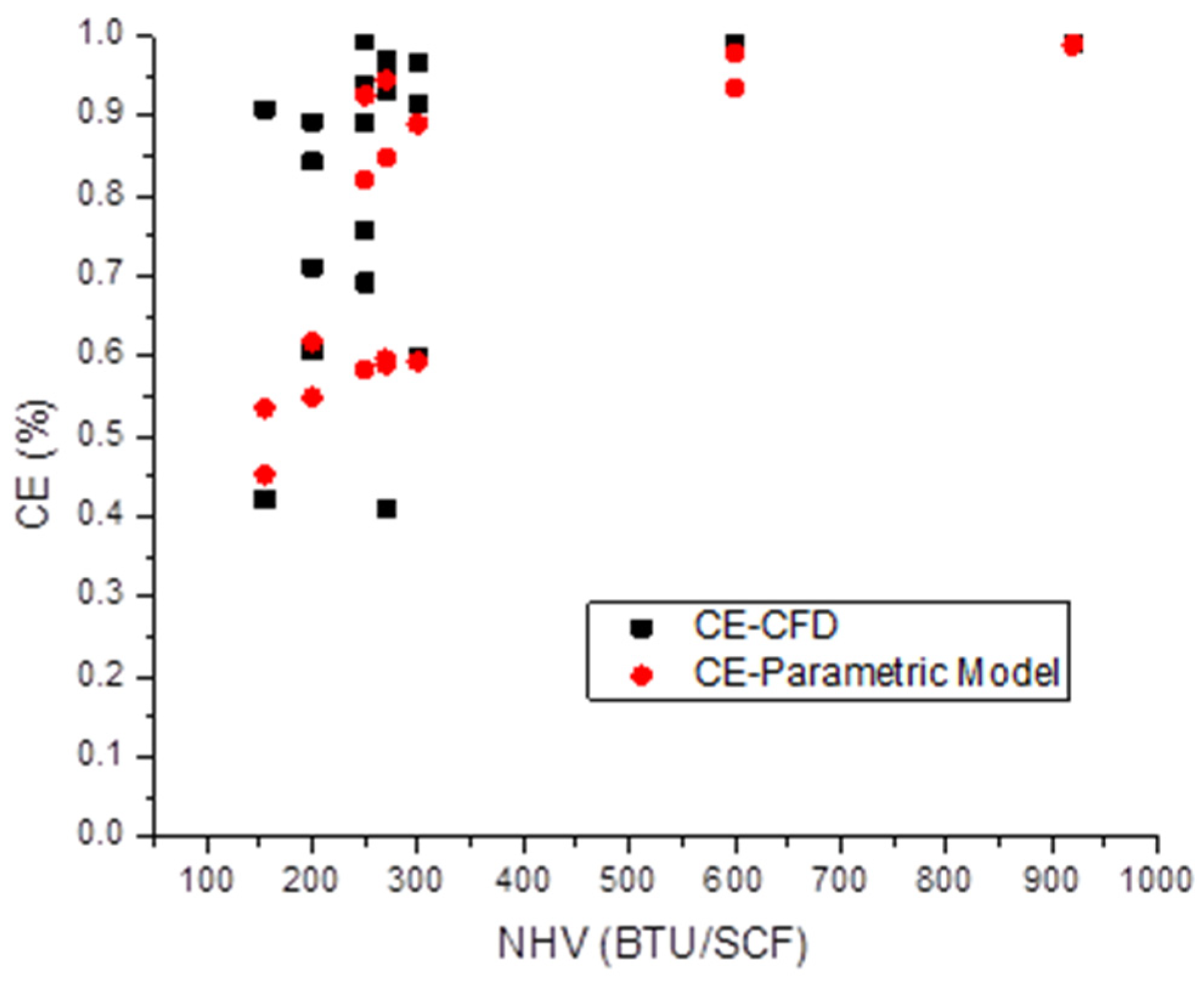
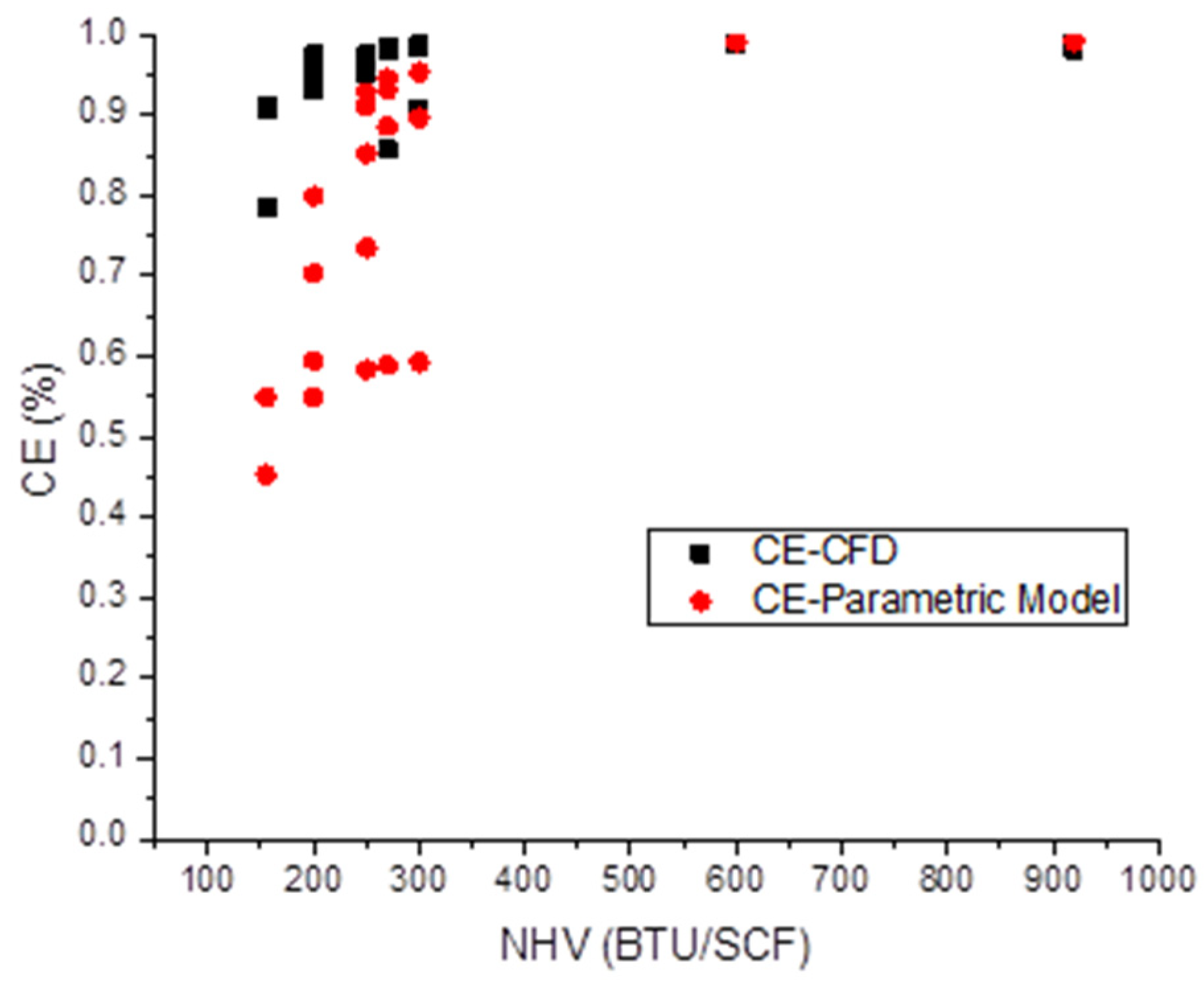
Computational fluid dynamics methodology was used to simulate a 14” utility flare and an 8” pressure-assisted sonic flare. First, the model was benchmarked against the physical tests by replicating a range of test conditions. The CFD model-predicted CE matched reasonably well with the test-measured CE. When the gas NHV was greater than the critical threshold of 300 BTU/SCF, the simulation-predicted CE was within 1%. At lower NHV levels, there was greater departure between the CFD model-predicted and the measured values. However, it is important to note that higher uncertainties were also reported in the measured values for gas NHV levels < 300 BTU/SCF.
A DoE (design of experiments) with a total of 48 cases was created covering a wide range of gas heating values (100–920 BTU/SCF), gas exit velocities (0.2–5 m/s), and wind speeds (0–50 m/s). CE dependence on the flare gas NHV and the momentum flux ratio (MFR) was explored. The results confirmed that the CE remained high (>95%) above and fell steeply below a critical flare gas NHV near 300 BTU/SCF. The results also confirmed that the critical NHV where the transition occurred was a function of MFR. Generally, a low MFR moved the critical NHV to higher values. Further investigation using simulations and field tests will help in better understanding the multivariate dependencies of CE (for instance, on NHV, MFR, and flare tip design).
While the CFD models are derived from fundamental physical principles and, thus, are considered to be of higher rigor, the simulations are time intensive and cannot be used in real time as digital twins. Numerical parametric models, on the other hand, are lightweight and can be used for real-time flare monitoring. However, they must be tested against reliable flare data for proper benchmarking. Simulations performed in this work enabled us to further verify the numerical parametric model published earlier in more operating scenarios, including some extreme scenarios (high crosswinds, low NHV). The comparison demonstrated that the simulations predicted similar CE to the parametric model at NHV > 300 BTU/SCF, while simulations showed generally higher CE at NHV < 300 BTU/SCF. This work demonstrates the feasibility of detailed physics-based models not only in supporting the design and operation of flares but also to complement physical testing programs by simulating flare conditions that are hard to manage in controlled test environments.
A flare pilot was used to ignite the flare and keep it lit at low NHV gas levels. Its effect on the measured CE/DRE was accounted for in this upstream industry flare experiment study. However, in CFD simulations, pilot effects are not taken into consideration. More CFD studies are needed to quantify pilot effects on CE under different operating conditions. Moreover, more precise CFD studies, incorporating unsteady states with an LES turbulence model and the eddy dissipation concept with a detailed combustion mechanism, are essential to gain a deeper understanding of how the pilot system, wind speed, NHV, vent gas velocity, and their combination influence flare emissions.