Dew and Rain Evolution from Climate Change in Semi-Arid South-Western Madagascar between 1991 and 2033 (Extrapolated)
Abstract
1. Introduction
2. Materials and Methods
2.1. Studied Sites
2.2. Meteorological Data
2.3. Dew Evolution
2.3.1. Energy Model
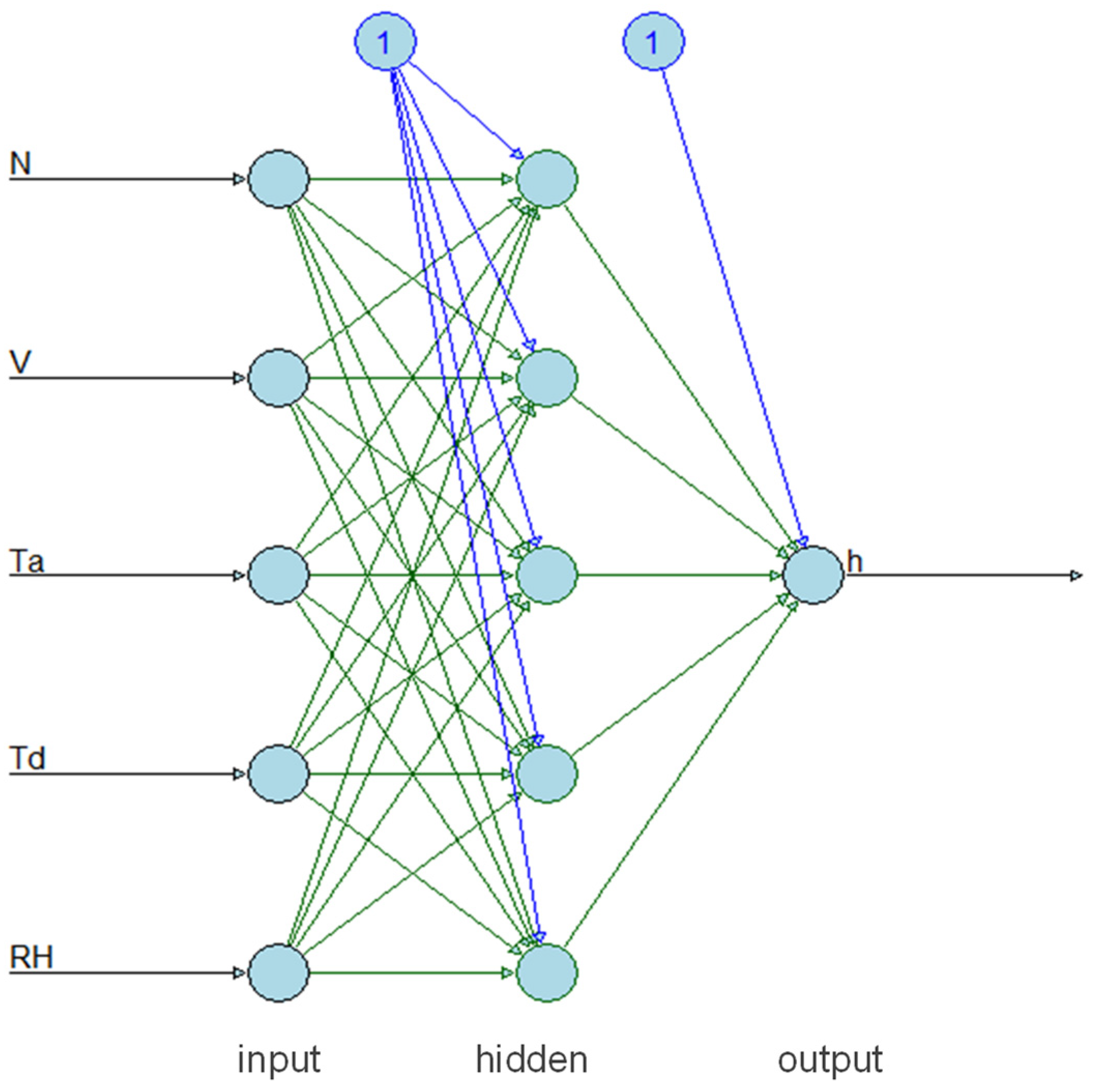
2.3.2. Perceptron Analysis for Extrapolation
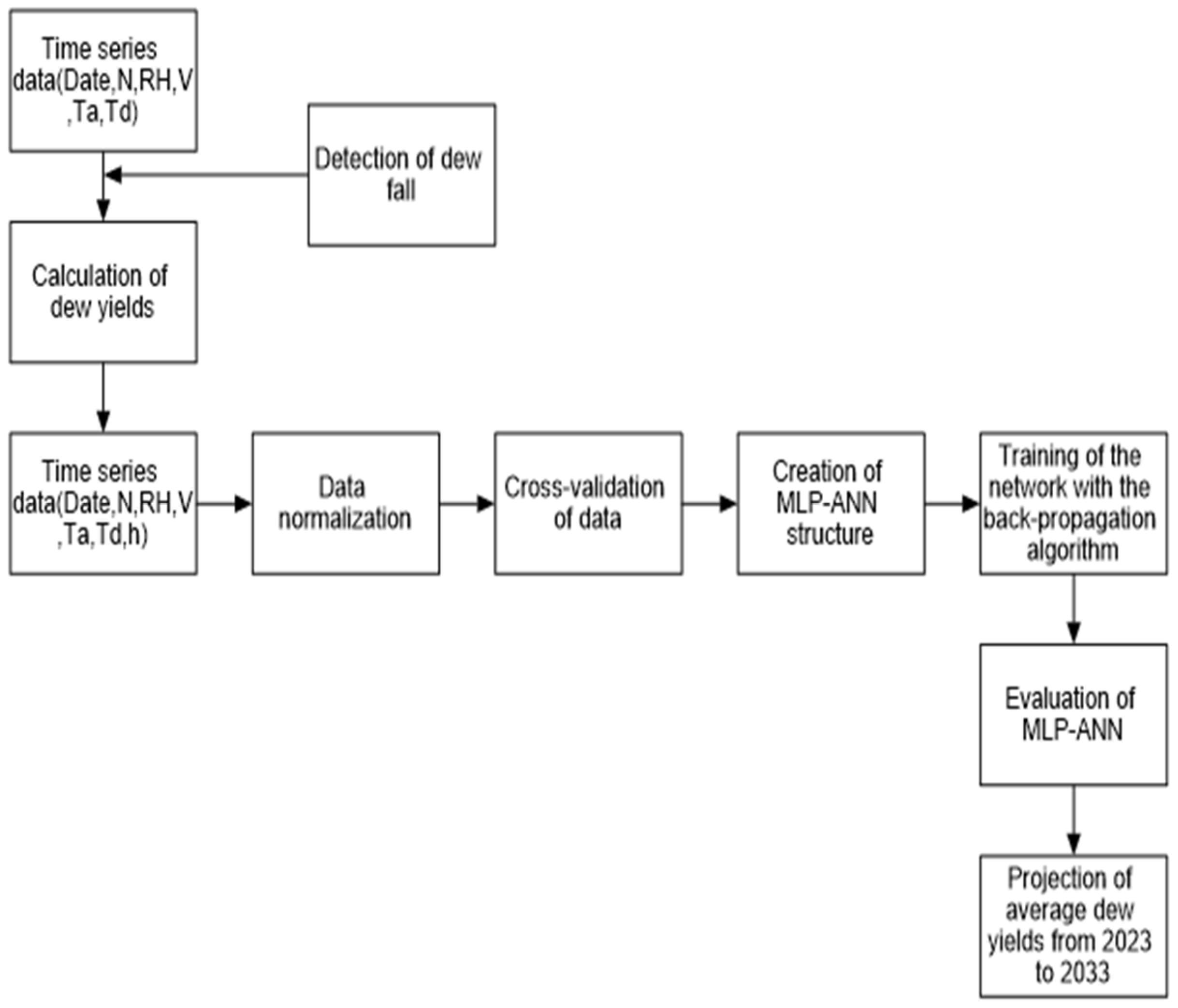
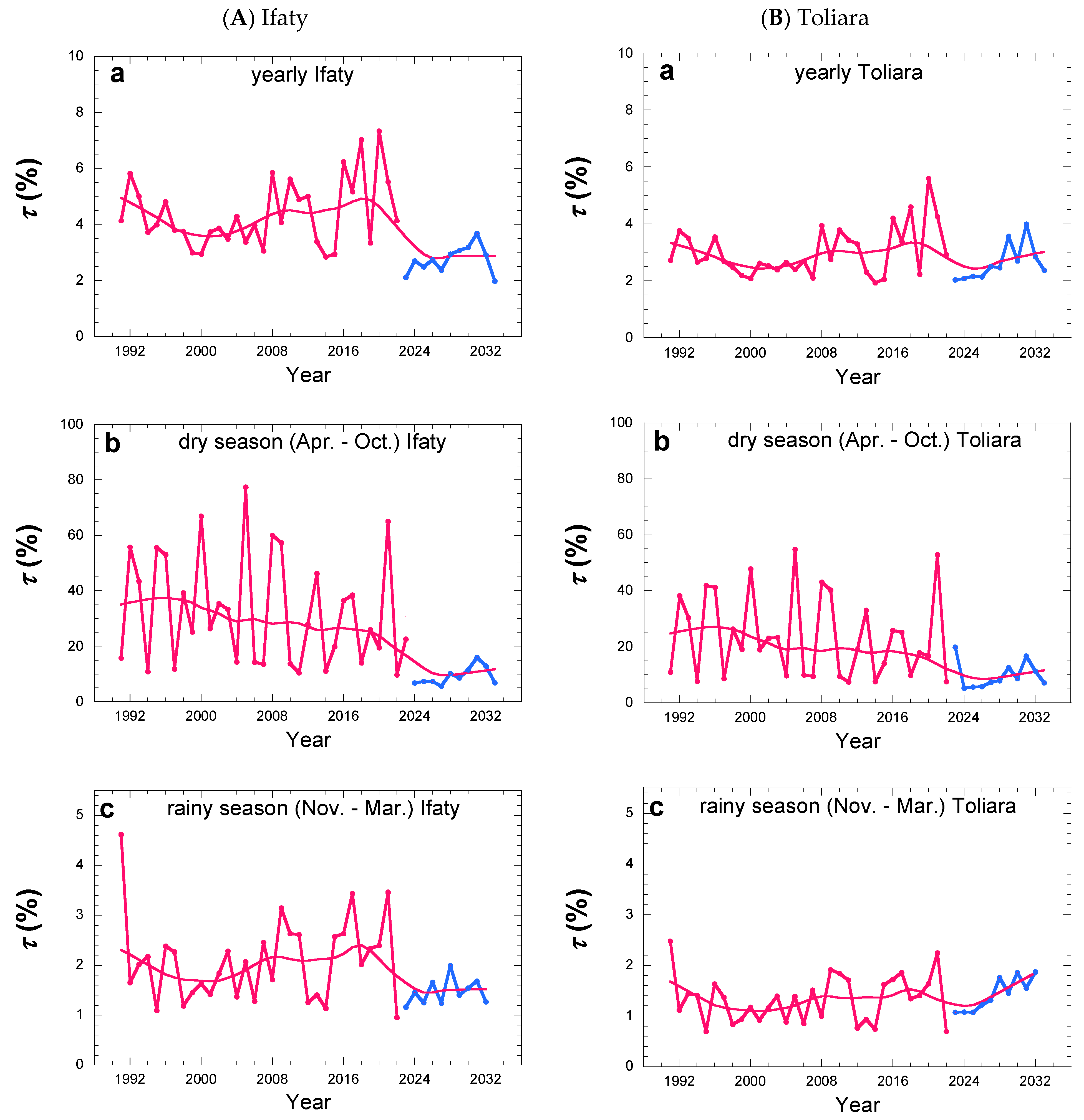
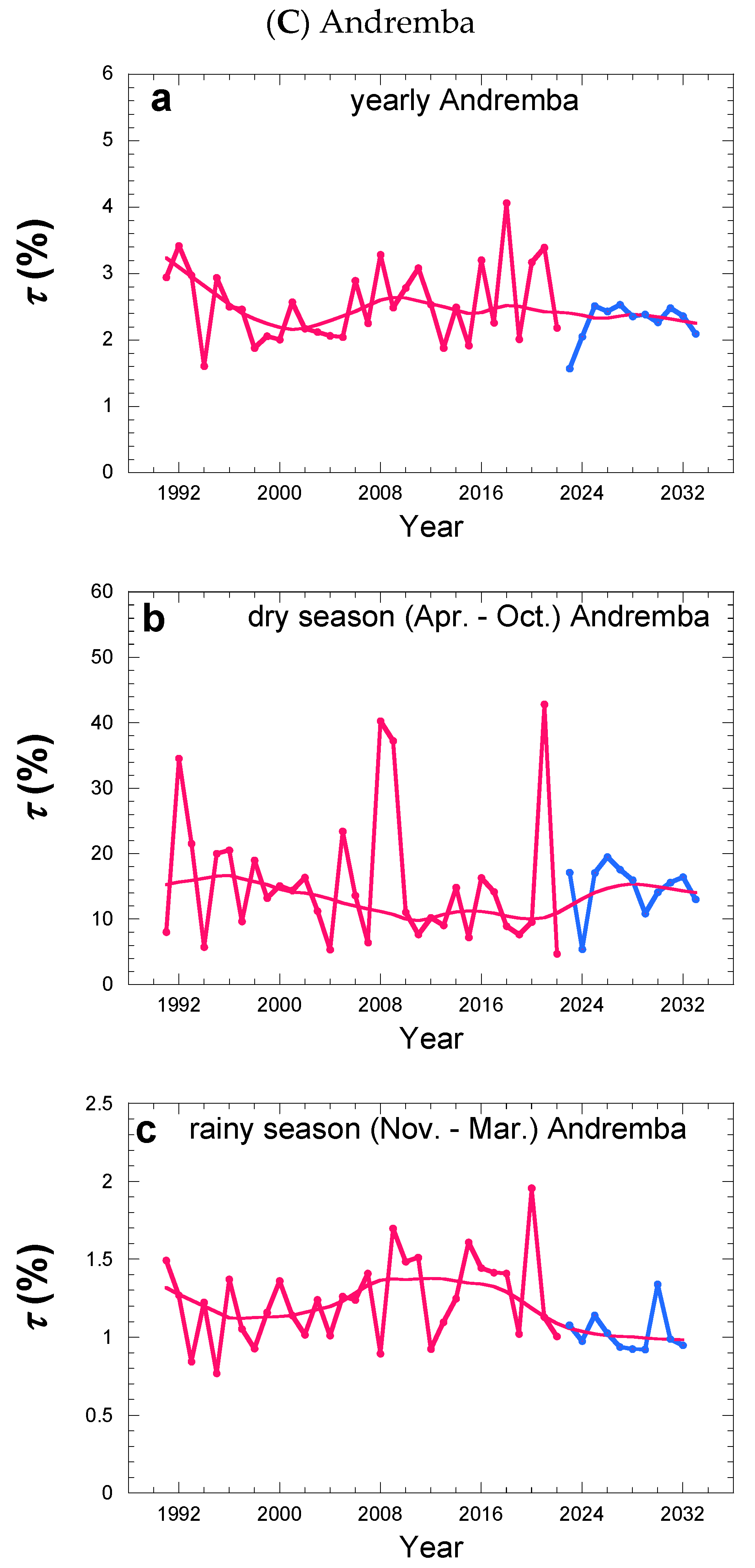
3. Results
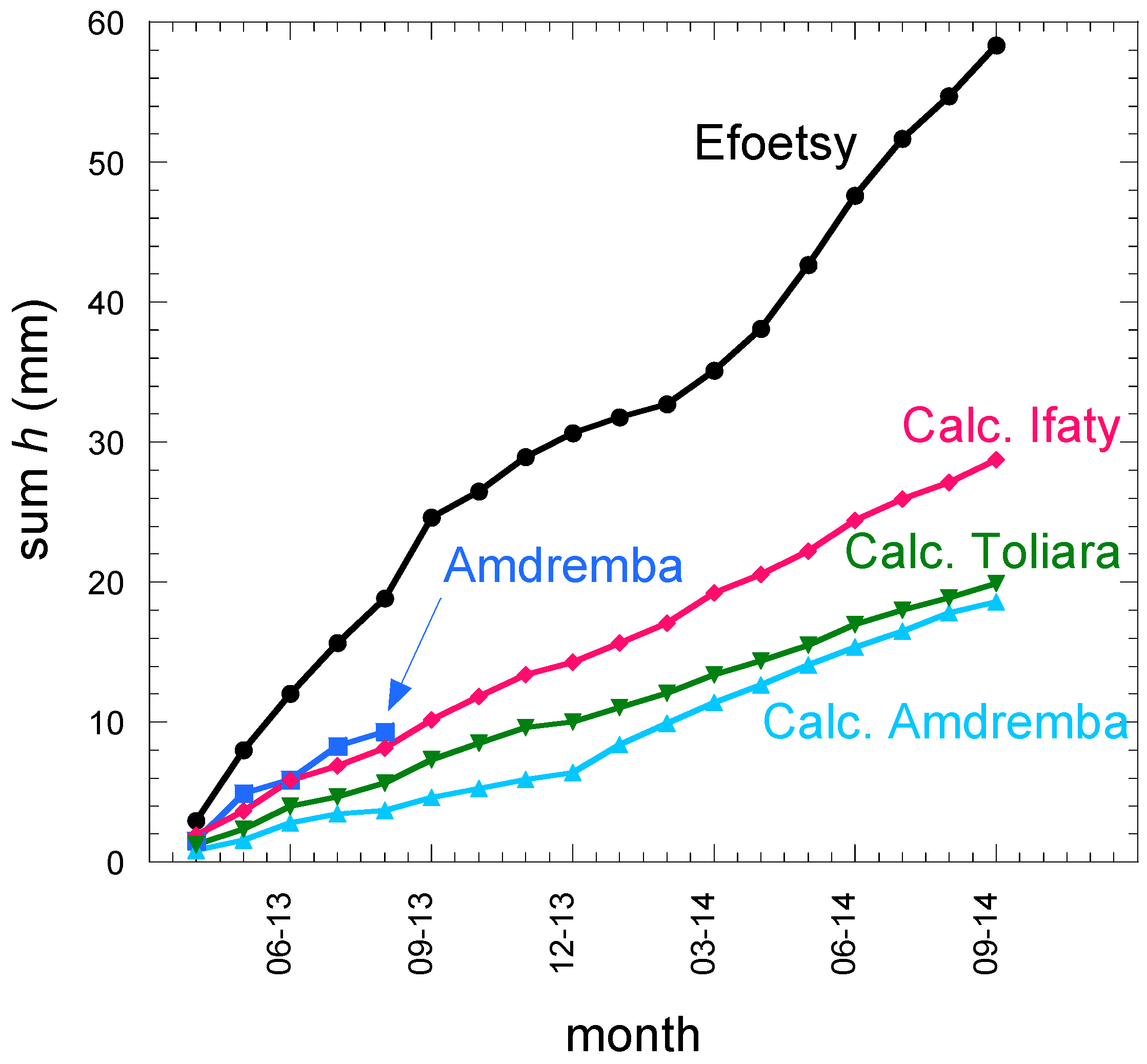
3.1. Comparison with Direct Measurements
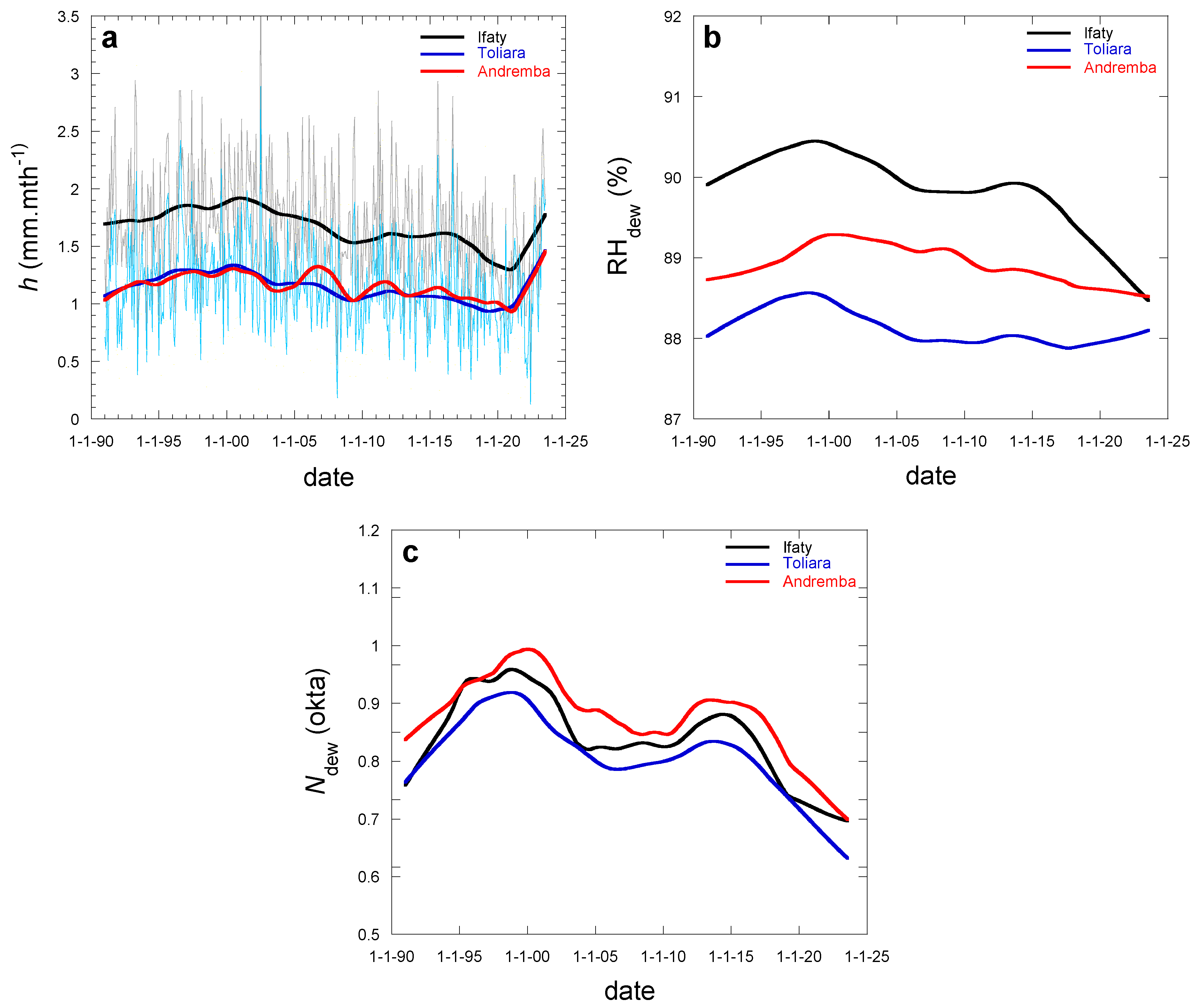
3.2. Dew Evolution
3.2.1. Years 1/1991–7/2023
3.2.2. Extrapolation for Years 8/2023–7/2033
3.3. Rain Evolution
3.3.1. Years 1/1991–7/2023
3.3.2. Extrapolation 8/2023–7/2033
3.3.3. Dew–Rain Ratios
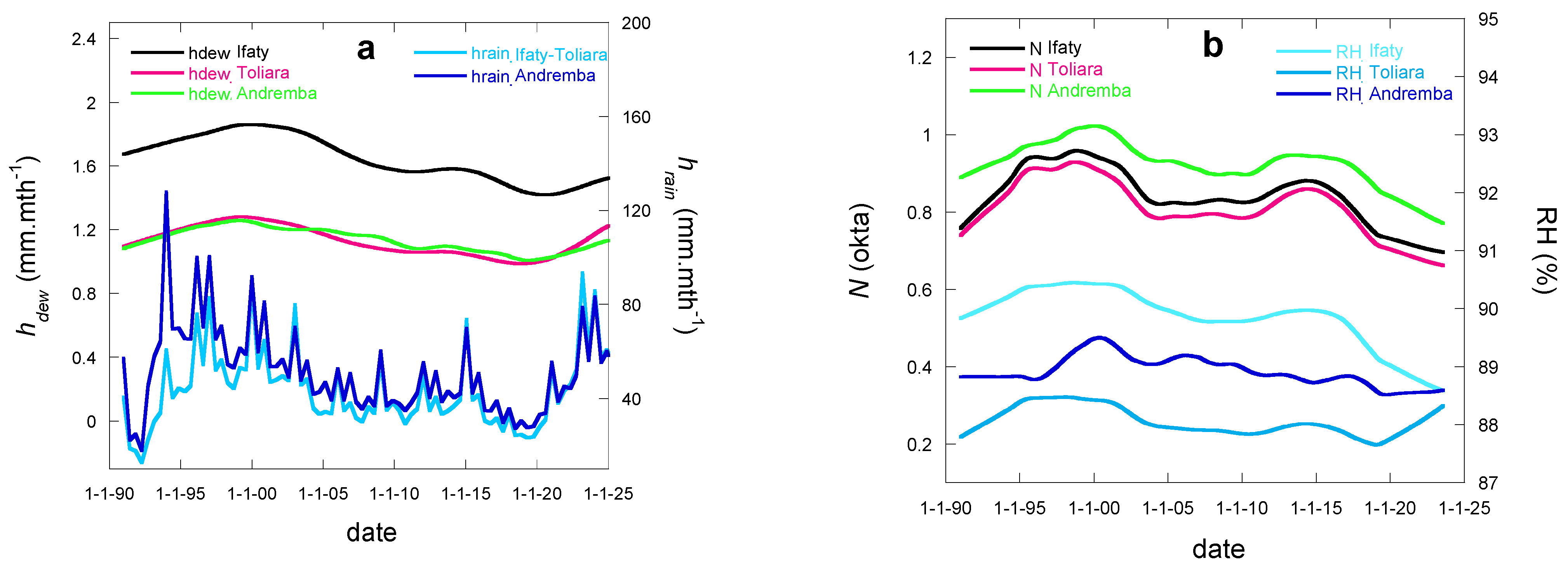
4. General Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Monteith, J.L. Dew. Q. J. R. Meteorol. Soc. 1957, 83, 322–341. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics: Plants, Animals, and the Atmosphere, 4th ed.; Academic Press: Oxford, UK, 1990. [Google Scholar]
- Beysens, D. Dew nucleation and growth. C. R. Phys. 2006, 7, 1082. [Google Scholar] [CrossRef]
- Beysens, D. Dew Water; River Publishers: Gistrup, Denmark, 2018. [Google Scholar]
- Dahliou, D.; Laarabi, B.; Barhdadi, A. Review on dew water effect on soiling of solar panels: Towards its enhancement or mitigation. Sustain. Energy Technol. Assess. 2022, 49, 101774. [Google Scholar] [CrossRef]
- Kabela, E.D.; Hornbuckle, B.K.; Cosh, M.H.; Anderson, M.C.; Gleason, M.L. Dew frequency, duration, amount, and distribution in corn and soybean during SMEX05. Agric. For. Meteorol. 2009, 149, 11–24. [Google Scholar] [CrossRef]
- Jacobs, A.F.G.; Heusinkveld, B.G.; Berkowicz, S.M. Dew deposition and drying in a desert system: A simple simulation model. J. Arid Environ. 1999, 42, 211–222. [Google Scholar] [CrossRef]
- Uclés, O.; Villagarcia, L.; Moro, M.J.; Canton, Y.; Domingo, F. Role of dewfall in the water balance of a semiarid coastal steppe ecosystem. Hydrol. Process. 2014, 28, 2271–2280. [Google Scholar] [CrossRef]
- Wang, L.; Kaseke, K.F.; Seely, M.K. Effects of non-rainfall water inputs on ecosystem functions. WIRES Water 2017, 4, e1179. [Google Scholar] [CrossRef]
- Charnès, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Malek, E.; McCurdy, G.; Giles, B. Dew contribution to the annual water balances in semi-arid desert valleys. J. Arid Environ. 1999, 42, 71–80. [Google Scholar] [CrossRef]
- Dou, Y.; Quan, J.; Jia, X.; Wang, Q.; Liu, Y. Near-Surface Warming Reduces Dew Frequency in China. Geophys. Res. Lett. 2021, 48, e2020GL091923. [Google Scholar] [CrossRef]
- Steinberger, Y.; Loboda, I.; Garner, W. The Influence of Autumn Dewfall on Spatial and Temporal Distribution of Nematodes in the Desert Ecosystem. J. Arid Environ. 1989, 16, 177–183. [Google Scholar] [CrossRef]
- Shure, D.J.; Lewis, A.J. Dew formation and stem flow on common ragweed (Ambrosia artemisiifolia). Ecology 1973, 54, 1152–1155. [Google Scholar] [CrossRef]
- Gerlein-Safdi, C.; Koohafkan, M.C.; Chung, M.; Rockwell, F.E.; Thompson, S.; Caylor, K.K. Dew deposition suppresses transpiration and carbon uptake in leaves. Agric. For. Meteorol. 2018, 259, 305–316. [Google Scholar] [CrossRef]
- Berry, Z.C.; Emery, N.C.; Gotsch, S.G.; Goldsmith, G.R. Foliar water uptake: Processes, pathways, and integration into plant water budgets. Plant Cell Environ. 2019, 42, 410–423. [Google Scholar] [CrossRef]
- Zhuang, Y.; Ratcliffe, S. Relationship between dew presence and Bassia dasyphylla plant growth. J. Arid Land 2012, 4, 11–18. [Google Scholar] [CrossRef][Green Version]
- Ben-Asher, J.; Alpert, P.; Ben-Zyi, A. Dew is a major factor affecting vegetation water use efficiency rather than a source of water in the eastern Mediterranean area. Water Resour. Res. 2010, 46, W10532. [Google Scholar] [CrossRef]
- Kidron, G.J.; Kronenfeld, R.; Starinsky, A.; Xiao, B.; Muselli, M.; Beysens, D. Even in a dew desert: Dewfall does not provide sufficient moisture for biocrust growth–Evidence from direct measurements and a meteorological model. J. Hydrol. 2023, 627, 130450. [Google Scholar] [CrossRef]
- Tomaszkiewicz, M.; Najm, M.A.; Beysens, D.; Alameddine, I.; El-Fadel, M. Dew as a Sustainable Non-Conventional Water Resource: A Critical Review. Environ. Rev. 2015, 23, 425–442. [Google Scholar] [CrossRef]
- Acker, K.; Moeller, D.; Auel, R.; Wieprecht, W.; Kalaß, D. Concentrations of nitrous acid, nitric acid, nitrite and nitrate in the gas and aerosol phase at a site in the emission zone during ESCOMPTE 2001 experiment. Atmos. Res. 2005, 74, 507–524. [Google Scholar] [CrossRef]
- Rubio, M.A.; Lissi, E.; Villena, G. Nitrite in rain and dew in Santiago City, Chile. Its possible impact on the early morning start of the photochemical smog. Atmos. Environ. 2002, 36, 293–297. [Google Scholar] [CrossRef]
- Rubio, M.A.; Lissi, E.; Villena, G. Factors determining the concentration of nitrite in dew from Santiago, Chile. Atmos. Environ. 2008, 42, 7651–7656. [Google Scholar] [CrossRef]
- Hamilton, W.J.; Seely, M.K. Fog basking by the Namib Desert beetle, Onymacris unguicularis. Nature 1976, 262, 284–285. [Google Scholar] [CrossRef]
- Seely, M.; Henschel, J.R.; Hamilton III, W.J. Long-term data show behavioural fog collection adaptations determine Namib Desert beetle abundance. S. Afr. J. Sci. 2005, 101, 570. [Google Scholar]
- Kaseke, K.F.; Wang, L. Fog and dew as potable water resources: Maximizing harvesting potential and water quality concerns. GeoHealth 2018, 2, 327–332. [Google Scholar] [CrossRef] [PubMed]
- Sharan, G.; Roy, A.K.; Royon, L.; Mongruel, A.; Beysens, D. Dew plant for bottling water. J. Clean. Prod. 2017, 155, 83–92. [Google Scholar] [CrossRef]
- N’Gobi, G.K.; Kounouhéwa, B.; Kouchadé, C.; Anago, R.; Beysens, D. Perception of Dew by Cereal Growers in Semi-Arid Climate (Guéné, North Benin). Int. J. Humanit. Soc. Sci. Educ. 2018, 5, 25–36. [Google Scholar]
- Randriatsitohaina, J.B.; Raniriketra, C.; Mara, T.; Champin, L.; Taïbi, A.N.; Razakamanana, T.; Fleurant, C. Vulnérabilité de Toliara face à l’insuffisance en eau, région Sud-Ouest de Madagascar. Madamines 2018, 1, 29–52. [Google Scholar]
- Sector Minister’s Meeting, The Madagascar Country Brief, 4–5 April 2019, San José, Costa Rica. Available online: https://www.google.com/url?q=https://www.sanitationandwaterforall.org/sites/default/files/migrate_default_content_files/Madagascar_Country_Brief.pdf&sa=U&ved=2ahUKEwiQt8OJ7fuGAxXdTkEAHSSQCXwQFnoECAoQAg&usg=AOvVaw2DOVht2B3_TxvaTP-bCaxc (accessed on 15 May 2024).
- Raholijao, N.; Arivelo, T.A.; Rakotomavo, Z.A.P.H.; Voahangin-dRakotoson, D.; Srinivasan, G.; Shanmugasundaram, J.; Dash, I.; Qiu, J. Les Tendances Climatiques et les Futurs Changements Climatiques à Madagascar-2019; Government of Madagascar: Antananarivo, Madagascar, 2019. Available online: https://www.primature.gov.mg/cpgu/wp-content/uploads/2019/11/Publication_FR_09_Sept_Version_Finale.pdf (accessed on 15 May 2024).
- Grouzis, M. Le Sud-Ouest de Madagascar. Paris, France: Institut de Recherche Pour le Développement. Rapport sur le Programme de Recherché de Gestion des Espaces Ruraux et Environnement à Madagascar (1996–2002). 2004. Available online: https://www.google.com/url?q=https://horizon.documentation.ird.fr/exl-doc/pleins_textes/divers16-08/010042918.pdf&sa=U&ved=2ahUKEwj1yrGUkfyGAxU7WEEAHQkACeAQFnoECAgQAg&usg=AOvVaw2XzsOVESwml5X7jzdKyUk3 (accessed on 15 June 2024).
- Hanisch, S.; Lohrey, C.; Buerkert, A. Dewfall and its ecological significance in semi-arid coastal south-western Madagascar. J. Arid Environ. 2015, 121, 24–31. [Google Scholar] [CrossRef]
- Muselli, M.; Lekouch, I.; Beysens, D. Physical and chemical characteristics of dew and rain in north-west Africa with focus on Morocco: Past and future evolution (2005–2100). Atmosphere 2022, 13, 1974. [Google Scholar] [CrossRef]
- Beysens, D. Estimating dew yield worldwide from a few meteo data. Atm. Res. 2016, 167, 146–155. [Google Scholar] [CrossRef]
- Communiqué de la Présidence de la République de Madagascar sur le Projet D’amélioration de L’accès en eau Potable, 15 June 2022. Available online: https://www.presidence.gov.mg/actualites/1604-madagascar-220-millions-de-dollars-pour-ameliorer-l-acces-a-l-eau-et-a-l’assainissement-de-base.html (accessed on 15 May 2024).
- Randriamarolaza, L.Y.A.; Aguilar, E.; Skrynyk, O.; Vicente-Serrano, S.M.; Domínguez-Castro, F. Indices for daily temperature and precipitation in Madagascar, based on quality-controlled and homogenized data, 1950–2018. Int. J. Clim. 2022, 42, 265–288. [Google Scholar] [CrossRef]
- Moriste, D. Biodiversité des Haies Vives Dans la Région de Toliara; Rapport de Licence; Faculté des Sciences, Université de Toliara: Toliara, Madagascar, 2010. [Google Scholar]
- Nations Online Project. 2022. Available online: https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.nationsonline.org%2Foneworld%2Fmap%2Fmadagascar_map.htm&psig=AOvVaw1MWvWQQTxAm1k8rFdjE65H&ust=1673779532637000&source=images&cd=vfe&ved=0CA8QjRxqFwoTCLi62NjwxvwCFQAAAAAdAAAAABAEhttps://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.nationsonline.org%2Foneworld%2Fmap%2Fmadagascar_map.htm&psig=AOvVaw1MWvWQQTxAm1k8rFdjE65H&ust=1673779532637000&source=images&cd=vfe&ved=0CA8QjRxqFwoTCLi62NjwxvwCFQAAAAAdAAAAABAE (accessed on 12 January 2023).
- Mapcarta. Available online: https://mapcarta.com/14494606https://mapcarta.com/14494606 (accessed on 15 February 2023).
- Weather Base. Available online: https://www.weatherbase.com/weather/weather-summary.php3?s=16176&cityname=Toliara,Madagascar (accessed on 4 February 2022).
- Rasoafaniry, A. Etude de la Contribution de la Rosée Sur L’Adduction en Eau Dans la Commune Urbaine de Toliara. Master’s Thesis, Ecole Supérieure Polytechnique d’Antananarivo, Antananarivo, Madagascar, 2022. [Google Scholar]
- ERA5-Land. Available online: https://confluence.ecmwf.int/plugins/servlet/mobile?contentId=140385202#content/view/140385202 (accessed on 1 December 2023).
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Zhou, J.L.; Guo, Z.M. A hybrid SNN-STLSTM method for human error assessment in the high-speed railway system. Adv. Eng. Inform. 2024, 60, 102408. [Google Scholar] [CrossRef]
- Alani, A.E.; Abraim, M.; Ghennioui, H.; Ghennioui, A.; Ikenbi, I.; Dahr, F.E. Short term solar irradiance forecasting using sky images based on a hybrid CNN–MLP model. Energy Rep. 2021, 7, 888–900. [Google Scholar] [CrossRef]
- Hunasigi, P.; Jedhe, S.; Mane, M.; Patil-Shinde, V. Multilayer perceptron neural network based models for prediction of the rainfall and reference crop evapotranspiration for sub-humid climate of Dapoli, Ratnagiri District, India. Acta Ecol. Sin. 2023, 43, 154–201. [Google Scholar] [CrossRef]
- Das, B.; Dursun, O.O.; Toraman, S. Prediction of air pollutants for air quality using deep learning methods in a metropolitan city. Urban Clim. 2022, 46, 101291. [Google Scholar] [CrossRef]
- Rodriguez, F.; Genn, M.; Fontan, L.; Galarza, A. Very short-term temperature forecaster using MLP and N-nearest stations for calculating key control parameters in solar photovoltaic generation. Sustain. Energy Technol. Assess. 2021, 45, 101085. [Google Scholar] [CrossRef]
- Lekouch, I.; Lekouch, K.; Muselli, M.; Mongruel, A.; Kabbachi, B.; Beysens, D. Rooftop dew, fog and rain collection in southwest Morocco and predictive dew modeling using neural networks. J. Hydrol. 2012, 448, 60–72. [Google Scholar] [CrossRef]
- Lindholm, A.; Wahlström, N.; Lindsten, F.; Schön, T.B. Supervised Machine Learning; Department of Information Technology, Uppsala University: Uppsala, Sweden, 2019; p. 112. [Google Scholar]
- Kassambara, A. Machine Learning Essentials: Practical Guide in R, 1st ed.; stdha.com/English; CreateSpace: Scotts Valley, CA, USA, 2018. [Google Scholar]
- Touzet, C. Les Réseaux de Neurones Artificiels, Introduction au Connexionnisme: Cours, Exercices et Travaux Pratiques. Ec2, 1992, Collection de l’EERIE. hal-01338010. Available online: https://amu.hal.science/hal-01338010/file/Les_reseaux_de_neurones_artificiels.pdf (accessed on 25 June 2024).
- Abadi, M. Réalisation d’un Réseau de Neurones “SOM” sur une Architecture Matérielle Adaptable Et Extensible à Base de Réseaux sur puce “NoC”. Université de Lorraine; Université du Centre (Sousse, Tunisie). 2018. Available online: https://tel.archives-ouvertes.fr/tel-01868313https://tel.archives-ouvertes.fr/tel-01868313 (accessed on 15 May 2024).
- Parizeau, M. Le Perceptron Multicouche ET Son Algorithme de Rétropropagation Des Erreurs; Département de génie électrique et de génie informatique, Université de Laval: Québec, QC, Canada, 2004. [Google Scholar]
- h2o: R Interface for the ‘H2O’ Scalable Machine Learning Platform. Available online: https://cran.r-project.org/web/packages/h2o/index.html (accessed on 15 May 2024).
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Tutorial for the nnfor R package. Available online: http://kourentzes.com/forecasting/2019/01/16/tutorial-for-the-nnfor-r-package/ (accessed on 15 May 2024).
- Kourentzes, N.; Barrow, D.K.; Crone, S.F. Neural network ensemble operators for time series forecasting. Expert Syst. Appl. 2014, 41, 4235–4244. [Google Scholar] [CrossRef]
- Buerkert, A. (Organic Plant Production and Agroecosystems Research in the Tropics and Subtropics. University of Kassel, Steinstrasse 19, D-37213 Witzenhausen, Germany). Private communication, 2023.
- Meunier, D.; Beysens, D. Dew, fog, drizzle and rain Water in Baku (Azerbaijan). Atmos. Res. 2016, 178, 65–72. [Google Scholar] [CrossRef][Green Version]
- Huang, B.; Su, T.; Zhi, R.; Zhang, Z.; Shen, H.; Wu, Y.; Feng, T. Synergistic effect of El Niño Southern oscillation and subtropical Indian Ocean Dipole on Southern China winter precipitation. Atmos. Res. 2023, 293, 106928. [Google Scholar] [CrossRef]
- IOD. 2023. Available online: http://la.climatologie.free.fr/iod/iod.htm (accessed on 1 December 2023).





| Sites | Latitude | Longitude | Elevation (m) asl | Distance from the Sea (km) | Köppen Geiger Climate |
|---|---|---|---|---|---|
| Toliara | 23°4 S | 43°7 E | 9 | 1 | Bsh |
| Ifaty | 23°1 S | 43°6 E | 80 | 1 | Bsh |
| Andremba | 24°0 S | 44°2 E | 260 | 60 | Bsh |
| Efoetsy | 24°1 S | 43°7 S | 10 | 2 | Bsh |
| Hot and Rainy Season | Cold and Dry Season | Mean Temp. (°C) | Mean Max Temp. (Jan.) (°C) | Mean Min Temp. (Jul.) (°C) | Mean Rain (mm·yr−1) * | Max Rain (mm·mth−1) * | Min Rain (mm·mth−1) * | Mean RH (%) $ | Max RH (%) $ | Min RH (%) $ |
|---|---|---|---|---|---|---|---|---|---|---|
| Nov.–Mar. | Apr.–Oct. | 23.9 | 27.8 | 20.6 | 342.9 | 73.7 | 5.1 | 77 | 100 | 12 |
| Sites | Year of Max. Yield | Year of Min. Yield | Sen’s Slope (×10−5 mm·mth−2) |
|---|---|---|---|
| Ifaty | 2000 | 2021 | −3.8 |
| Toliara | 2000 | 2021 | −2.4 |
| Andremba | 2000 | 2021 | - |
| Dew | Data | Mths. | Min (mm·mth−1) | Max (mm·mth−1) | Mean (mm·mth−1) | SD (mm·mth−1) | p-Value * | MK Meaningful Trend $ | Sen’s Slope (×10−5 mm·mth−2) | Sen’s Constant |
|---|---|---|---|---|---|---|---|---|---|---|
| Ifaty | Meas. | 391 | 0.322 | 3.795 | 1.678 | 0.488 | <0.0001 | Yes | −3.8 | 3.160 |
| Extrap. | 120 | 0.915 | 1.964 | 1.502 | 0.241 | 0.227 | No | −2.5 | 2.704 | |
| All | 511 | 0.322 | 3.795 | 1.637 | 0.449 | <0.0001 | Yes | −2.6 | 2.712 | |
| Toliara | Meas. | 391 | 0.128 | 2.885 | 1.157 | 0.401 | <0.0001 | Yes | −2.4 | 2.072 |
| Extrap. | 120 | 0.643 | 1.700 | 1.302 | 1.172 | 0.005 | Yes | 3.7 | −0.433 | |
| All | 511 | 0.128 | 2.885 | 1.191 | 0.366 | 0.165 | No | 0.5 | 1.008 | |
| Andremba | Meas. | 391 | 0.067 | 3.072 | 1.187 | 0.557 | 0.060 | No | −1.5 | 1.720 |
| Extrap. | 120 | 0.534 | 1.622 | 1.096 | 0.270 | 0.234 | No | −3.1 | 2.577 | |
| All | 511 | 0.067 | 3.072 | 1.165 | 0.506 | 0.055 | No | −0.9 | 1.513 |
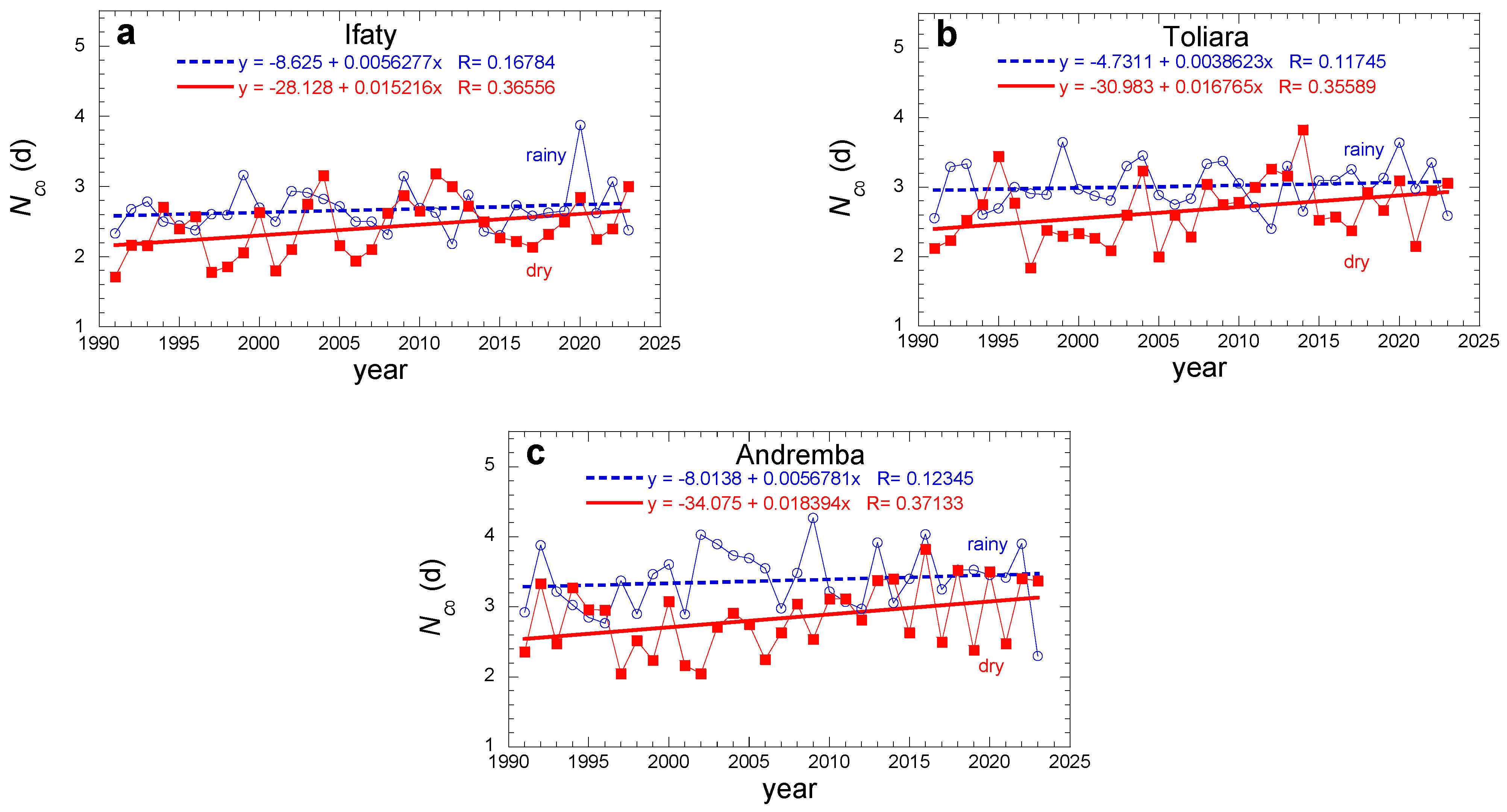
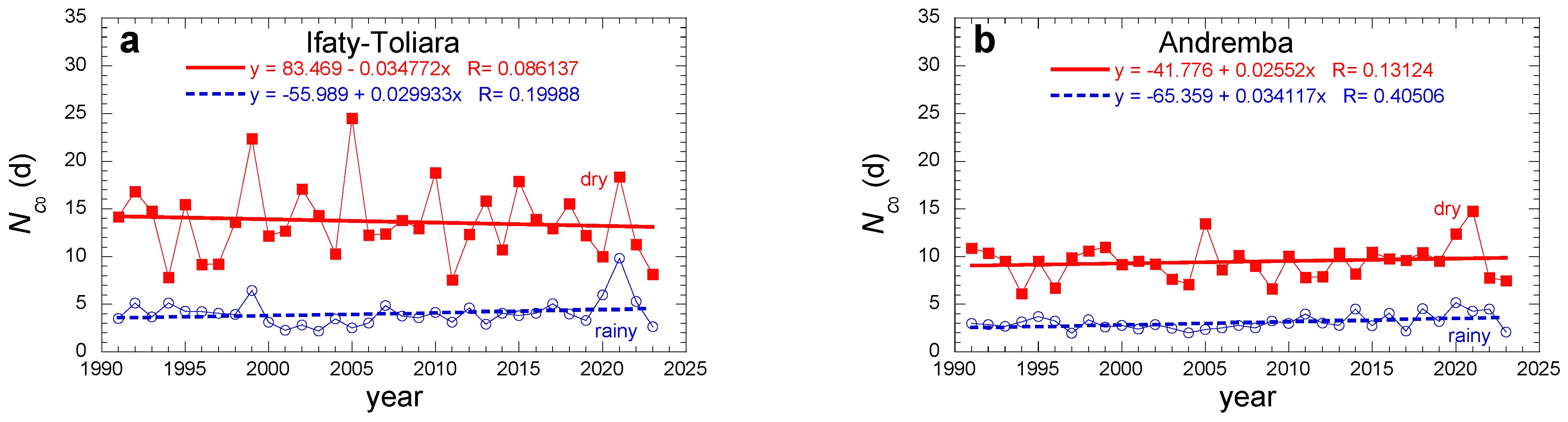
| No Dew Nb. Consecutive Days | Data | Min (d·yr−1) | Max (d·yr−1) | Mean (d·yr−1) | SD (d) | p-Value * | MK Meaningful Trend $ | Sen’s Slope (×10−6 d·yr−2) | Sen’s Constant |
|---|---|---|---|---|---|---|---|---|---|
| Ifaty | Rainy season | 2.179 | 3.875 | 2.67 | 0.324 | 0.721 | No | 3.9 | 2.643 |
| Dry season | 1.714 | 3.182 | 2.411 | 0.402 | 0.035 | Yes | 44 | 0.645 | |
| Toliara | Rainy season | 2.405 | 3.645 | 3.021 | 0.318 | 0.457 | No | 13 | 2.482 |
| Dry season | 1.842 | 3.824 | 2.664 | 0.456 | 0.031 | Yes | 53 | 0.554 | |
| Andremba | Rainy season | 2.3 | 4.269 | 3.382 | 0.445 | 0.285 | No | 25 | 2.364 |
| Dry season | 2.048 | 3.824 | 2.841 | 0.479 | 0.035 | Yes | 57 | 0.546 |
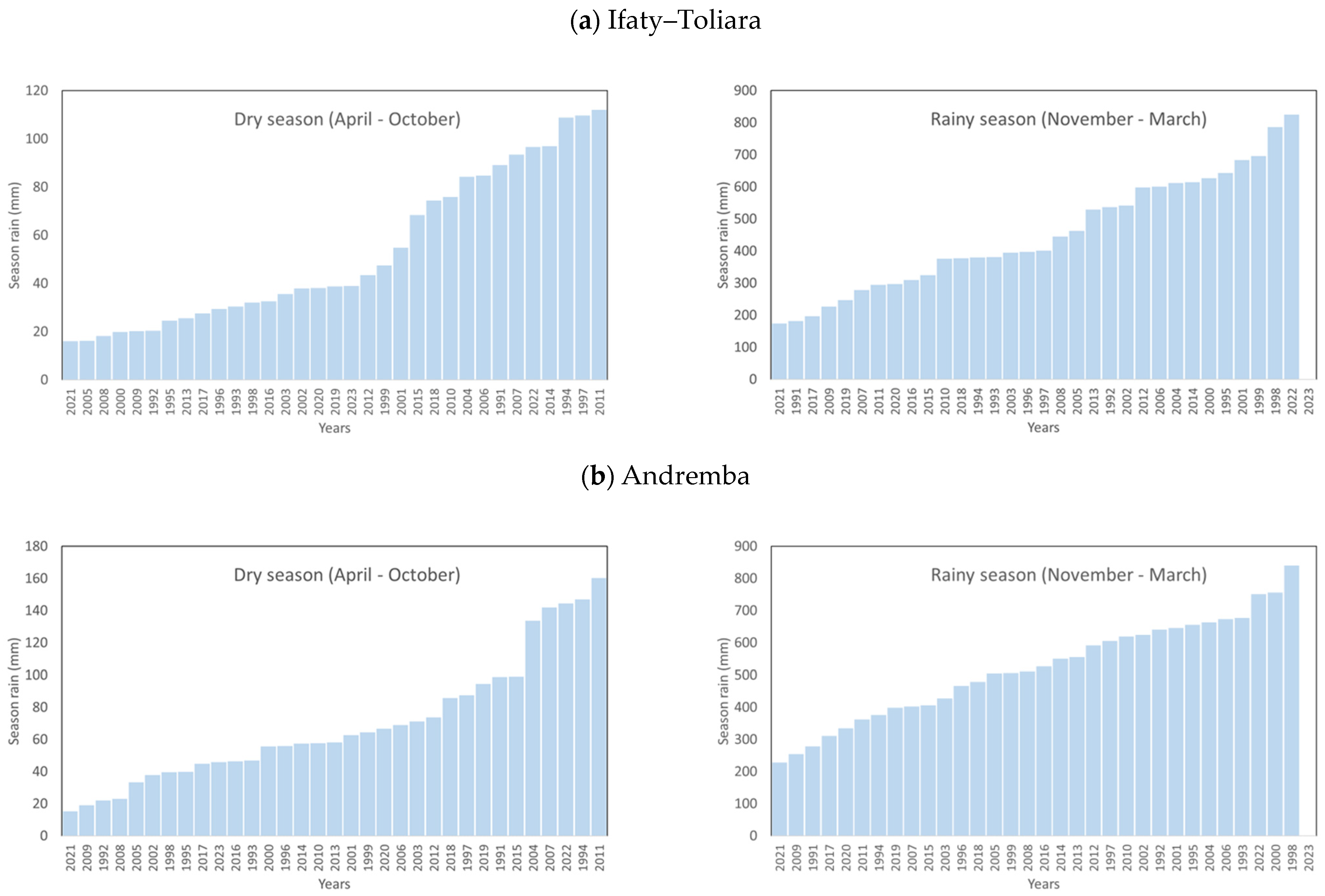
| Rain | Data | Mths. | Min (mm·mth−1) | Max (mm·mth−1) | Mean (mm·mth−1) | SD (mm·mth−1) | p-Value * | MK Meaningful Trend $ | Sen’s Slope (×10−5 mm·mth−2) | Sen’s Constant |
|---|---|---|---|---|---|---|---|---|---|---|
| Ifaty, Toliara | Meas. | 391 | 0 | 455.6 | 42.343 | 73.426 | 0.244 | No | −11.9 | 15.791 |
| Extrap. | 120 | 0 | 307.0 | 53.265 | 71.611 | 0.738 | No | 0 | 19.793 | |
| All | 511 | 0 | 455.6 | 44.907 | 73.081 | 0.496 | No | 5.1 | 10.790 | |
| Andremba | Meas. | 391 | 0 | 435.5 | 48.998 | 74.108 | 0.377 | No | −11.8 | 19.225 |
| Extrap. | 120 | 0 | 227.0 | 56.489 | 61.977 | 0.819 | No | 45.8 | 4.643 | |
| All | 511 | 0 | 435.5 | 50.757 | 71.457 | 0.102 | No | 27.0 | 6.937 |
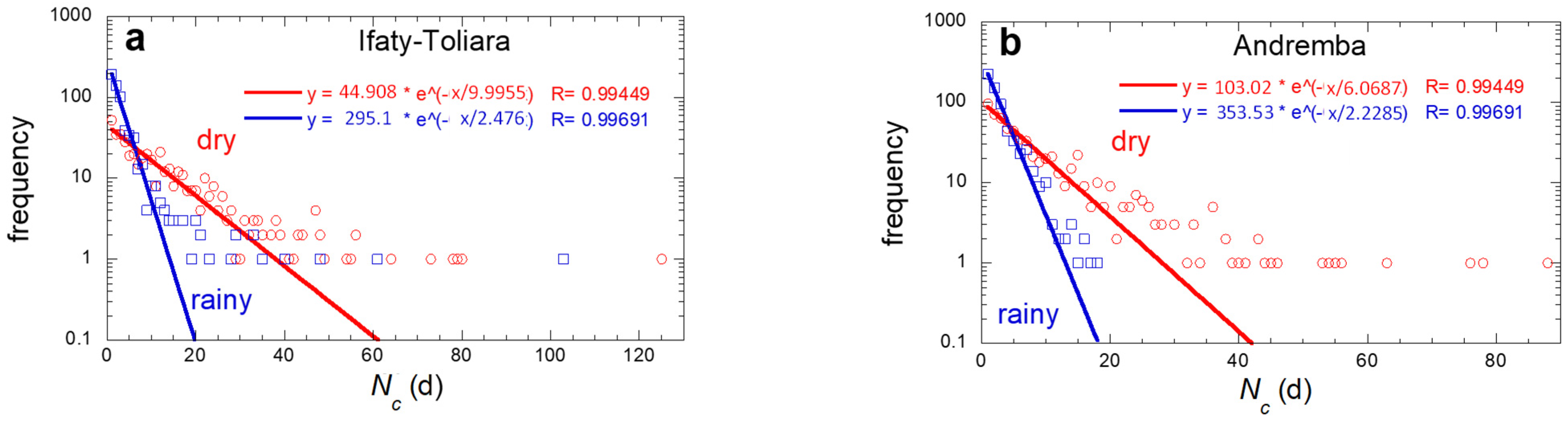
| No Rain Nb. Consecutive Days | Data | Min (d·yr−1) | Max (d·yr−1) | Mean (d·yr−1) | SD (d·yr−1) | p-Value * | MK Meaningful Trend $ | Sen’s Slope (×10−6 d·yr−2) | Sen’s Constant |
|---|---|---|---|---|---|---|---|---|---|
| Ifaty and Toliara | Rainy season | 2.174 | 9.833 | 4.086 | 1.448 | 0.653 | No | 28 | 2.738 |
| Dry season | 7.55 | 24.5 | 13.681 | 3.903 | 0.62 | No | 112 | 17.657 | |
| Andremba | Rainy season | 1.96 | 5.167 | 3.113 | 0.814 | 0.107 | No | 79 | −0.147 |
| Dry season | 6.115 | 14.77 | 9.443 | 1.880 | 0.889 | No | 10 | 9.174 |
| Yearly | Period | Ratio (% yr−1) | p-Value * | MK Meaningful Trend $ | Sen’s Slope (×10−6·yr−2) | Sen’s Constant | |||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | ||||||
| Ifaty | 1991–2023 | 2.114 | 7.34 | 4.317 | 1.24 | 0.698 | No | 29 | 2.841 |
| 2023–2033 | 1.986 | 3.687 | 2.75 | 0.49 | 0.161 | No | −156 | −10.358 | |
| 1991–2033 | 1.986 | 7.340 | 3.967 | 1.28 | 0.017 | Yes | −86 | 7.107 | |
| Toliara | 1991–2023 | 1.929 | 5.601 | 2.984 | 0.86 | 0.816 | No | 14 | 2.152 |
| 2023–2033 | 2.028 | 3.986 | 2.623 | 0.63 | 0.013 | Yes | 266 | −9.977 | |
| 1991–2033 | 1.929 | 5.601 | 2.914 | 0.81 | 0.818 | No | −5.6 | 2.883 | |
| Andremba | 1991–2023 | 1.571 | 4.064 | 2.523 | 0.59 | 0.975 | No | 1.6 | 2.427 |
| 2023–2033 | 1.571 | 2.532 | 2.277 | 0.28 | 1 | No | 6.7 | 2.037 | |
| 1991–2033 | 1.571 | 4.064 | 2.482 | 0.52 | 0.683 | No | −6.7 | 2.705 | |
| Dry Season | Period | Ratio (% yr−1) | p-Value * | MK Meaningful Trend $ | Sen’s Slope (×10−6·yr−2) | Sen’s Constant | |||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | ||||||
| Ifaty | 1991–2023 | 9.645 | 77.415 | 32.403 | 19.744 | 0.258 | No | −905 | 65.033 |
| 2023–2033 | 5.615 | 30.63 | 11.205 | 7.158 | 0.436 | No | 980 | −37.535 | |
| 1991–2033 | 5.615 | 77.415 | 27.209 | 19.924 | 0.001 | Yes | −1858 | 99.681 | |
| Toliara | 1991–2023 | 7.453 | 54.779 | 23.390 | 14.473 | 0.345 | No | −415 | 36.185 |
| 2023–2033 | 5.191 | 19.856 | 9.829 | 4.824 | 0.213 | No | 1308 | −53.281 | |
| 1991–2033 | 5.191 | 54.779 | 20.003 | 14.187 | 0.004 | Yes | −1069 | 62.949 | |
| Andremba | 1991–2023 | 4.689 | 42.802 | 15.662 | 10.054 | 0.209 | No | −560 | 35.022 |
| 2023–2033 | 5.379 | 19.477 | 14.785 | 3.907 | 0.35 | No | −630 | 45.47 | |
| 1991–2033 | 4.689 | 42.802 | 15.403 | 8.985 | 0.601 | No | −104 | 18.648 | |
| Rainy Season | Period | Ratio (% yr−1) | p-Value * | MK Meaningful Trend $ | Sen’s Slope (×10−6·yr−2) | Sen’s Constant | |||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | ||||||
| Ifaty | 1991–2023 | 0.954 | 4.615 | 2.063 | 0.817 | 0.588 | No | 24 | 1.113 |
| 2023–2033 | 1.165 | 1.991 | 1.465 | 0.257 | 0.283 | No | 90 | −2.815 | |
| 1991–2033 | 0.954 | 4.615 | 1.942 | 0.767 | 0.386 | No | −19 | 2.565 | |
| Toliara | 1991–2023 | 0.691 | 2.477 | 1.323 | 0.453 | 0.631 | No | 13 | 0.813 |
| 2023–2033 | 1.071 | 1.87 | 1.424 | 0.323 | 0.002 | Yes | 219 | −8.855 | |
| 1991–2033 | 0.691 | 2.477 | 1.353 | 0.428 | 0.153 | No | 24 | 0.34 | |
| Andremba | 1991–2023 | 0.768 | 1.957 | 1.234 | 0.264 | 0.329 | No | 15 | 0.622 |
| 2023–2033 | 0.921 | 1.339 | 1.028 | 0.13 | 0.371 | No | −30 | 2.407 | |
| 1991–2033 | 0.768 | 1.957 | 1.189 | 0.256 | 0.298 | No | −9.5 | 1.527 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasoafaniry, A.; Muselli, M.; Beysens, D. Dew and Rain Evolution from Climate Change in Semi-Arid South-Western Madagascar between 1991 and 2033 (Extrapolated). Atmosphere 2024, 15, 784. https://doi.org/10.3390/atmos15070784
Rasoafaniry A, Muselli M, Beysens D. Dew and Rain Evolution from Climate Change in Semi-Arid South-Western Madagascar between 1991 and 2033 (Extrapolated). Atmosphere. 2024; 15(7):784. https://doi.org/10.3390/atmos15070784
Chicago/Turabian StyleRasoafaniry, Adriana, Marc Muselli, and Daniel Beysens. 2024. "Dew and Rain Evolution from Climate Change in Semi-Arid South-Western Madagascar between 1991 and 2033 (Extrapolated)" Atmosphere 15, no. 7: 784. https://doi.org/10.3390/atmos15070784
APA StyleRasoafaniry, A., Muselli, M., & Beysens, D. (2024). Dew and Rain Evolution from Climate Change in Semi-Arid South-Western Madagascar between 1991 and 2033 (Extrapolated). Atmosphere, 15(7), 784. https://doi.org/10.3390/atmos15070784







