Abstract
In this study, a diagnostic model for evaporation ducts was established based on the Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) and the Naval Postgraduate School (NPS) models. Utilizing this model, four sensitivity tests were conducted over the South China Sea from 21 September to 5 October 2008, when four tropical cyclones affected the study domain. These tests were designed with different roughness schemes to investigate the impact mechanisms of wave processes on evaporation duct simulation under extreme weather conditions. The results indicated that wave processes primarily influenced the evaporation duct heights by altering sea surface roughness and dynamical factors. The indirect impacts of waves without dynamical factors were rather weak. Generally, a decrease in local roughness led to increased wind speed, decreased humidity, and a reduced air–sea temperature difference, resulting in the formation of evaporation ducts at higher altitudes. However, this affecting mechanism between roughness and evaporation ducts was also greatly influenced by changes in regional circulation. In the eastern open sea areas of the South China Sea, changes in evaporative ducts were more closely aligned with local impact mechanisms, whereas the changes in the central and western areas demonstrated greater complexity and fewer local impacts due to variations in regional circulation.
1. Introduction
The propagation of electromagnetic (EM) signals is significantly influenced by atmospheric refraction. Under specific conditions, abrupt vertical changes in refractivity can cause EM signals to become trapped at certain altitudes and extend beyond normal radio ranges. This phenomenon, known as an atmospheric duct, can occur in various atmospheric conditions. One specific type of atmospheric duct is the evaporation duct, which forms primarily above the sea surface, typically within altitudes of 30–40 m. Previous studies have indicated that the formation of the evaporation duct is associated with the rapid reduction in water vapor concentration within the first few meters above the sea surface due to evaporation [1,2].
The characteristics of the evaporation duct over a wind-roughened sea surface depend not only on the profiles of atmospheric variables within the altitudes of 30~40 m above the sea surface, but also on processes occurring at the air–sea interface, such as waves, air–sea thermal differences, and evaporation [3,4,5]. Among these influencing factors, the impact of dynamic ocean wave processes on changes in evaporation ducts is of considerable interest. This is because the shadowing effects over a rough sea surface have been shown to introduce additional uncertainties in the estimation of scattering and path loss for the propagation of EM signals [6,7].
Wave processes are recognized for their interaction with the upper atmosphere, notably by enhancing air–sea fluxes of heat, mass, and momentum [8,9]. Research suggests that even small waves can perturb atmospheric profiles near the sea surface, thereby influencing evaporation ducts [10,11].
To explore the impact of ocean waves on EM propagation and atmospheric ducts, several large-scale intensive observation experiments were conducted to gather data for validating numerical models’ simulations of rough sea surfaces [12,13,14]. For instance, the Rough Evaporation Duct (RED) experiment conducted in Oahu Island, Hawaii, revealed that waves distorted mean wind streamlines and vertical profiles of temperature and humidity, resulting in refractivity fluctuations with periods nearly matching those of wave phases [15]. However, it is regrettable that no significant effects on evaporation ducts were observed during the RED experiment period due to meteorological conditions.
Previous studies have explored the relationship between waves and evaporation ducts using field observations, reanalysis data, or numerical models [16,17,18]. For instance, Yang et al. examined the interannual variability of the evaporation duct over the South China Sea utilizing Climate Forecast System Reanalysis (CFSR) data [19]. They observed a strong correlation between regions of high surface wind, indicative of rough sea surfaces, and areas with elevated evaporation duct heights. While these studies have identified consistent changes between waves and evaporation ducts, the mechanisms by which waves affect changes in evaporation ducts still remain unclear. Additionally, there are a limited number of quantitative analysis studies focusing on the relationships between evaporation ducts and wave-induced roughness or changes in fluxes. One contributing factor to this research gap is the scarcity of vertical observations within the evaporation duct’s height.
Due to a lack of comprehensive vertical observation data within the marine atmospheric boundary layer, many studies investigating the mechanisms of evaporation ducts have relied on numerical weather models supplemented with empirical evaporation duct models [20,21,22]. Despite significant advancements in boundary-layer parameterizations, these numerical weather models have struggled to accurately represent processes occurring within the extremely shallow layer near the sea surface in evaporation duct simulations. Over the past few decades, several empirical models based on the Monin–Obukhov similarity theory have been developed to characterize the properties of evaporation ducts and have been widely validated for their reliability in subsequent studies [23,24,25].
Thanks to the comprehensive observational experiments mentioned previously, the effectiveness of numerical weather simulations combined with empirical evaporation duct models has been validated through hydro-meteorological and radar field observations [26,27]. For instance, Ulate et al. analyzed datasets from the Coupled Air-Sea Processes and Electromagnetic Ducting Research (CASPER) experiment and determined that the Coupled Ocean/Atmospheric Mesoscale Prediction System (COAMPS) performed admirably in both forecasting meteorological conditions and diagnosing evaporation ducts [28]. In extreme weather conditions, the changes in waves and atmospheric elements near the sea surface are more pronounced, which helps researchers delve deeper into the mechanisms of ocean-atmosphere interaction. However, there have been few studies on the variation of the evaporative duct phenomenon under extreme weather conditions in the past, making the response mechanism of the evaporative duct height to waves and roughness unclear. The establishment of a fully coupled ocean-atmosphere-wave model provides an excellent tool for studying this aspect. Unlike uncoupled atmospheric models, fully coupled ocean-atmosphere-wave models can account for dynamic interactions between atmospheric boundary layers and ocean upper layers, enhancing simulations of processes near the air–sea interface, particularly in extreme weather conditions and high seas [29,30,31,32]. These models enable sensitivity tests and investigations into the mechanisms linking wave processes and evaporation ducts. One such prominent coupled model, the Coupled Ocean-Atmosphere-Wave-Sediment Transport (COAWST), developed by Warner et al., has seen extensive application in operational forecasting and the study of air–sea interaction mechanisms [33,34,35,36,37,38].
In this study, we integrated the COAWST model with an empirical evaporation duct model—the Naval Postgraduate School (NPS) model, which is widely employed for practical duct estimation. Several simulation tests were conducted using the COAWST model, considering different aspects of wave processes, to examine the sensitivity of evaporation duct characteristics to these processes. A dataset of hydro-meteorological parameters gathered from an air–sea flux observation tower situated in the Yongxing Island, South China Sea, was employed, along with the reanalysis dataset, to validate the simulations.
2. Model and Data
2.1. COAWST Model
The COAWST model comprises three component models designed to represent the atmosphere, ocean, and wave environments [39]. The atmospheric component model employs the Weather Research and Forecasting (WRF) system with the Advanced Research WRF (ARW) dynamic core [40]. Utilizing various physical schemes, the WRF model facilitates simulations across different scales, from synoptic to mesoscale. The ocean component model is the Regional Ocean Modeling System (ROMS), capable of solving the three-dimensional Reynolds-averaged Navier–Stokes equations through hydrostatic and Boussinesq approximations [41]. The wave component model, Simulating Waves Nearshore (SWAN), operates as a spectral wave model, resolving the spectral density evolution equation [42].
The three component models communicate via the Model Coupling Toolkit (MCT), a parallelized tool designed for exchanging model state variables [43]. Furthermore, the Spherical Coordinate Remapping Interpolation Package (SCRIP) is utilized for grid interpolation across different coordinate systems of the component models [44].
During the variable exchange process, the WRF model receives Sea Surface Temperature (SST) data from the ROMS model while providing atmospheric pressure, temperature, relative humidity, surface winds, cloud fraction, precipitation, shortwave and longwave radiation back to the ROMS model. Utilizing these parameters, the ROMS model computes ocean surface stress and net heat fluxes using the COARE algorithm [45]. Furthermore, the ROMS model receives wave characteristics such as direction, height, length, period, percent breaking, energy dissipation, and bottom orbital velocity from the SWAN model while providing bathymetry, bottom elevation, sea surface height, and depth-averaged currents to the SWAN model.
In the atmosphere-wave exchange process, the WRF model furnishes surface winds at the 10 m level to the SWAN model for wave computation. Concurrently, the WRF model obtains wave height and length data to determine sea surface roughness. In the Mellor-Yamada Nakanishi Niino (MYNN) level 2.5 planetary boundary layer scheme, the surface roughness z0 is parameterized as:
where ca is the Charnok coefficient taken by 0.016, u* is the surface stress, g is gravity, and ʋ is the viscosity [46,47]. Within the COAWST model framework, modifications were made to the planetary boundary layer scheme, along with its corresponding surface scheme. Equation (1) was replaced with another one, which considered the wave effects and was described as:
In this formulation, Hwave is the significant wave height, while Lwave is the mean wavelength [48].
Based on previous evaluation studies of the COAWST model, the incorporation of wave processes was found to enhance the cooling effects of SST and mitigate changes in wind stress at the sea surface [49].
The COAWST model demonstrated excellent performance in simulating marine hydro-meteorological conditions. For instance, Sian et al. investigated the effects of air–sea coupling on the simulations of typhoons over the South China Sea. They found that the root mean square error of the 10 m wind speed from COAWST was reduced by 5.73% when compared to the WRF simulation [50]. Zheng et al. evaluated the simulation of super typhoon Megi (2010) from COAWST and found that the mean absolute errors of typhoon intensity decreased by approximately 36% compared to those of WRF [51].
Utilizing the hydro-meteorological outputs of COAWST near the sea surface, the NPS model enables the diagnosis of feature parameters associated with evaporation ducts.
2.2. NPS Model
The NPS bulk model, developed by the Naval Postgraduate School in the USA, is widely employed for conducting duct simulations [52,53]. This model utilizes hydro-meteorological variables such as wind speed, pressure, temperature, humidity, and SST at specific levels near the sea surface as inputs. Subsequently, it computes air temperature, humidity, and pressure profiles based on the Monin–Obukhov similarity theory. In this study, the scaling parameters at the sea surface were determined using version 3.0 of the COARE (Coupled Ocean Atmosphere Response Experiment) bulk model [54]. The modified atmospheric refractive index, M, is derived by
where T is air temperature in K, P is air pressure in hPa, e is water vapor pressure in hPa, and z is height above the sea surface in m. The evaporation duct height is determined based on the profile of M, identifying the height at which M reaches its minimum value.
Based on a range of propagation experiments and evaluation studies, the NPS model demonstrated superior accuracy in generating evaporation duct and atmospheric refractivity profiles [55]. Guo et al. employed marine observations over the South China Sea to validate the accuracy of the NPS model. They found the NPS performed better than the P-J (Paulus-Jeske) model when the duct height lies within the altitudes of 5 m to 20 m. Its mean absolute error of duct height was 1.45 m, which was 0.2 m lower than the P-J model, but its mean relative error was higher by 3.3% when the duct height was higher than 1 m [56].
2.3. Observation Data
The validation of the evaporation duct in this study utilized site observations obtained from the air–sea flux observation experiment conducted between 25 April and 7 October 2008. The experiment took place at a reef-based observation tower located at 16.83° N, 112.33° E, off the coast of Yongxing Island in the South China Sea [57,58]. The observation dataset encompasses Sea Surface Temperature (SST), wave data, and evaporation duct heights diagnosed from meteorological variables at three levels: 3.5 m, 7.0 m, and 10.5 m above mean sea level. This dataset is currently accessible upon request from the National Earth System Science Data Center, National Science & Technology Infrastructure of China (http://www.geodata.cn, accessed on 7 June 2024).
Furthermore, this study also utilized the ERA5 reanalysis data provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) to validate the duct diagnosis model established by COAWST and NPS. The dataset can be accessed online at https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 7 June 2024).
3. Methodology
3.1. Experimental Design
This study conducted one control test (CTL) and three sensitivity tests (T1, T2, and T3) with varied settings to assess the influence of wave coupling processes on simulated evaporation duct characteristics. For ease of comparison, the CTL was configured using the fully coupled option (WRF-ROMS-SWAN), wherein the surface roughness calculation adopted Equation (2), accounting for wave processes as previously described.
The T1 test was configured with the air–sea coupling option (WRF-ROMS), neglecting the wave process and determining surface roughness based on Equation (1). In contrast, the T2 test maintained the fully coupled option (WRF-ROMS-SWAN) but still employed Equation (1) for surface roughness calculation. Consequently, the wave model SWAN did not directly influence WRF dynamics in the T2 test. Compared to the T1 test, variations in the T2 tests only arose from indirect feedback mechanisms, such as SST or sea surface heat fluxes induced by wave processes.
The T3 test employed the same configurations as the CTL but incorporated a new roughness formulation from Drennan et al. to replace Equation (2) mentioned earlier [59]. This new formulation considers sea surface roughness as a function of wave age, which is described as
where Cwave is denoted as the wave celerity, and calculated by
where Twave is the peak wave period.
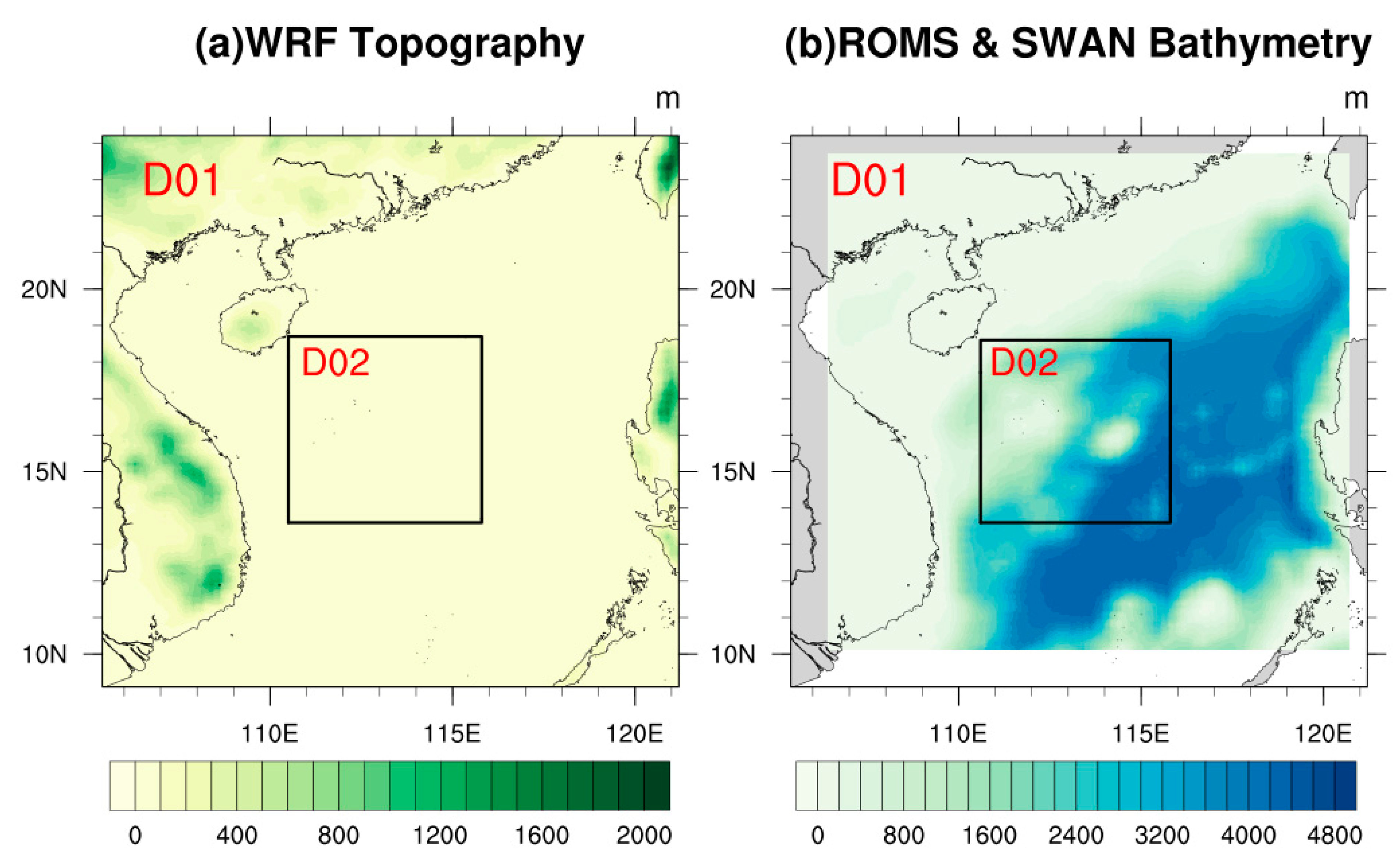
The study domain is centered around the observation tower location (16.83° N, 112.33° E) on Yongxing Island, South China Sea. Figure 1 illustrates the topography and bathymetry of the study domain. To achieve higher resolution, two sets of nested model grids were employed, designated as D01 and D02, respectively. The outer domain, D01, had a resolution of 18 km × 18 km. The inner domain, D02, featured a horizontal resolution of 6 km × 6 km and was selected for local change analysis. D02 is situated near the central part of the South China Sea, characterized by increasing water depth from northwest to southeast. Spatial distribution analysis in subsequent sections was based on results from the D01 domain, while results from the D02 domain were solely utilized for station validation and regional time series analysis.
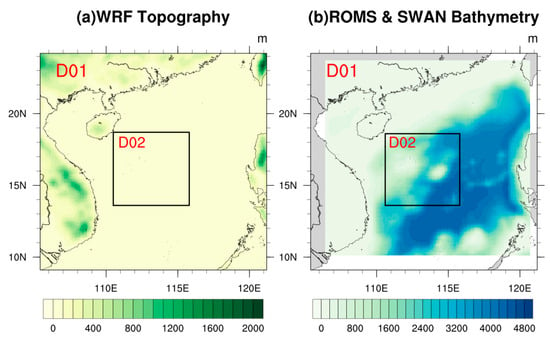
Figure 1.
(a) Topography for the WRF model; (b) bathymetry for the ROMS and SWAN model. The entire colored area is D01 domain and the area enclosed by the black frame is D02 domain.
3.2. Model Configuration
The default scheme options of COAWST were employed, with the exception of the surface roughness settings in the boundary layer scheme. The specific schemes employed are listed in Table 1.

Table 1.
Physical parameterization schemes employed by each component model of COAWST in the simulations.
The component models within COAWST—WRF, ROMS, and SWAN—exchanged variables every 1800 s, coordinated by the main program through the Model Coupling Toolkit (MCT). Main configuration parameters for the three component models of COAWST are presented in Table 2. The NCEP Climate Forecast System Reanalysis (CFSR) data, accessible at https://cfs.ncep.noaa.gov/cfsr/ (accessed on 7 June 2024), provided boundary forcing information for WRF model runs. Ocean reanalysis data from the Global Ocean Forecasting System (GOFS) 3.1, available at https://www.hycom.org/dataserver/gofs-3pt1/reanalysis (accessed on 7 June 2024), was employed to drive the ROMS model. In this study, the SWAN model was driven by outputs from WRF and ROMS and did not receive external forcing data.

Table 2.
Main configuration parameters for the sub-models in COAWST.
Prior to initiating the simulation tests, a 72 h spin-up period was implemented to achieve balanced hydro-meteorological conditions for subsequent simulations. Following the completion of the spin-up phase, the four tests were conducted from 21 September, 0:00 to 5 October, 0:00 UTC, 2008.
3.3. Studied Events
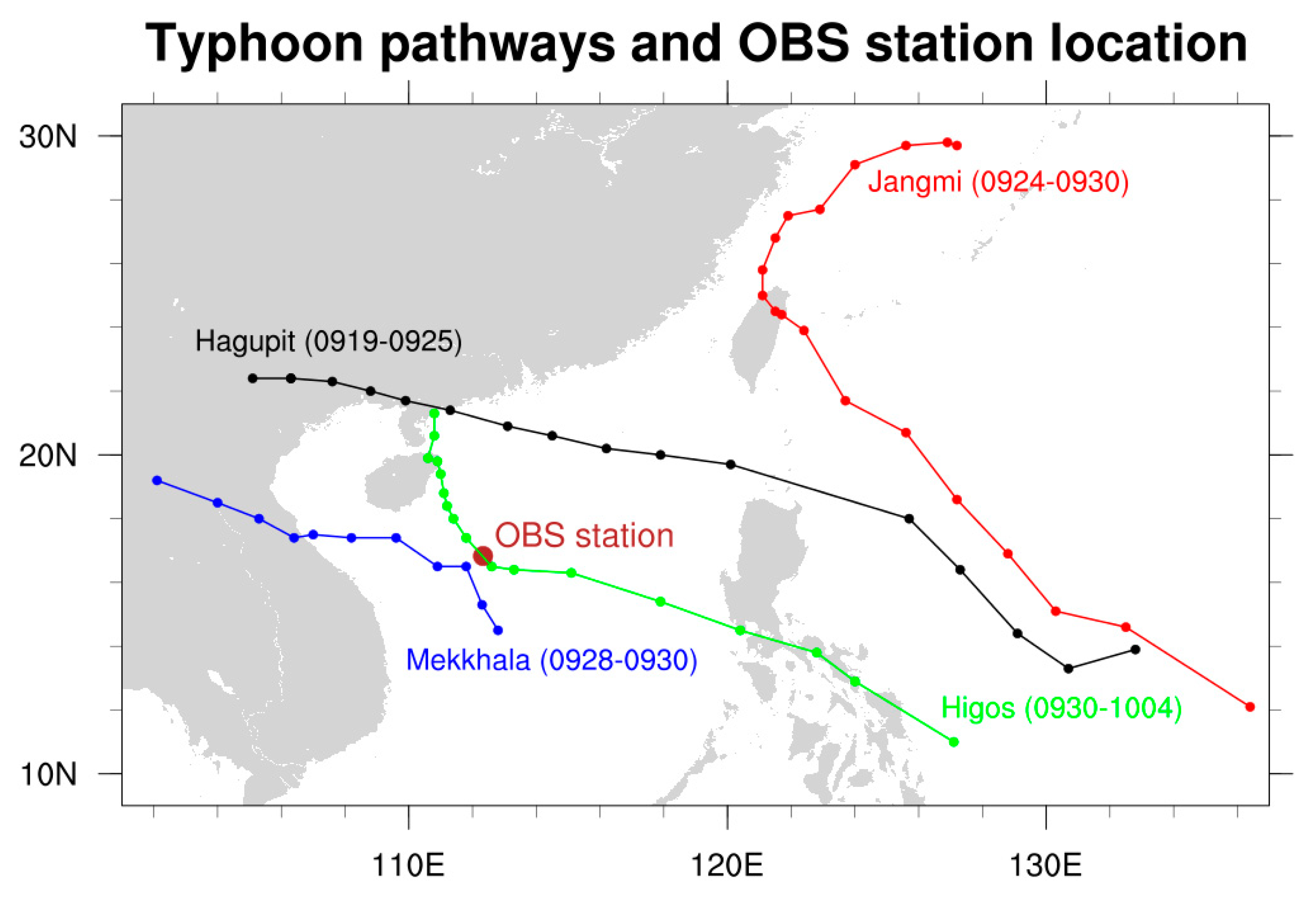
During the simulation period, the study domain was affected by tropical cyclones on four occasions within two weeks, resulting in local winds stronger than Beaufort force 6. Such a high frequency of extreme events was rare in the study domain, making it highly valuable for research. Under high sea state conditions, the differences in near-sea surface elements from each sensitivity test were more pronounced. Compared to simulations under normal weather conditions in other time periods, the higher differences were advantageous in highlighting changes in the main processes without being overshadowed by other processes. Detailed background information on these four TCs is provided in Table 3, compiled from the sorted observation dataset and the National Meteorological Center of China’s typhoon website (http://typhoon.nmc.cn, accessed on 7 June 2024). Additionally, Figure 2 illustrates the pathways of these four TCs in relation to the observation tower’s location.

Table 3.
Background information on TCs during the simulation period.
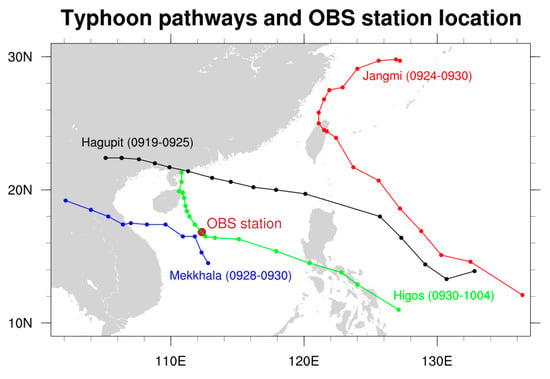
Figure 2.
The pathways of the four TCs during the simulation period with the location of observation tower in Yongxing Island, South China Sea.
4. Result
4.1. Model Validation of CTL Test
Table 4 presents various statistical indices, such as the temporal correlation coefficient, root-mean-square error (RMSE), and standard deviation, comparing the CTL results with ERA5 reanalysis data. The air temperature and relative humidity at 2 m level (T2m and RH2m) were selected as the variables for validation. These metrics demonstrate a close correspondence between the CTL and the ERA5 data. Moreover, the statistical indices across the D02 domain were slightly lower than those across the entire D01 domain, attributable to the smaller area and pronounced localized features.

Table 4.
Statistics of CTL across the D01 and D02 domain.
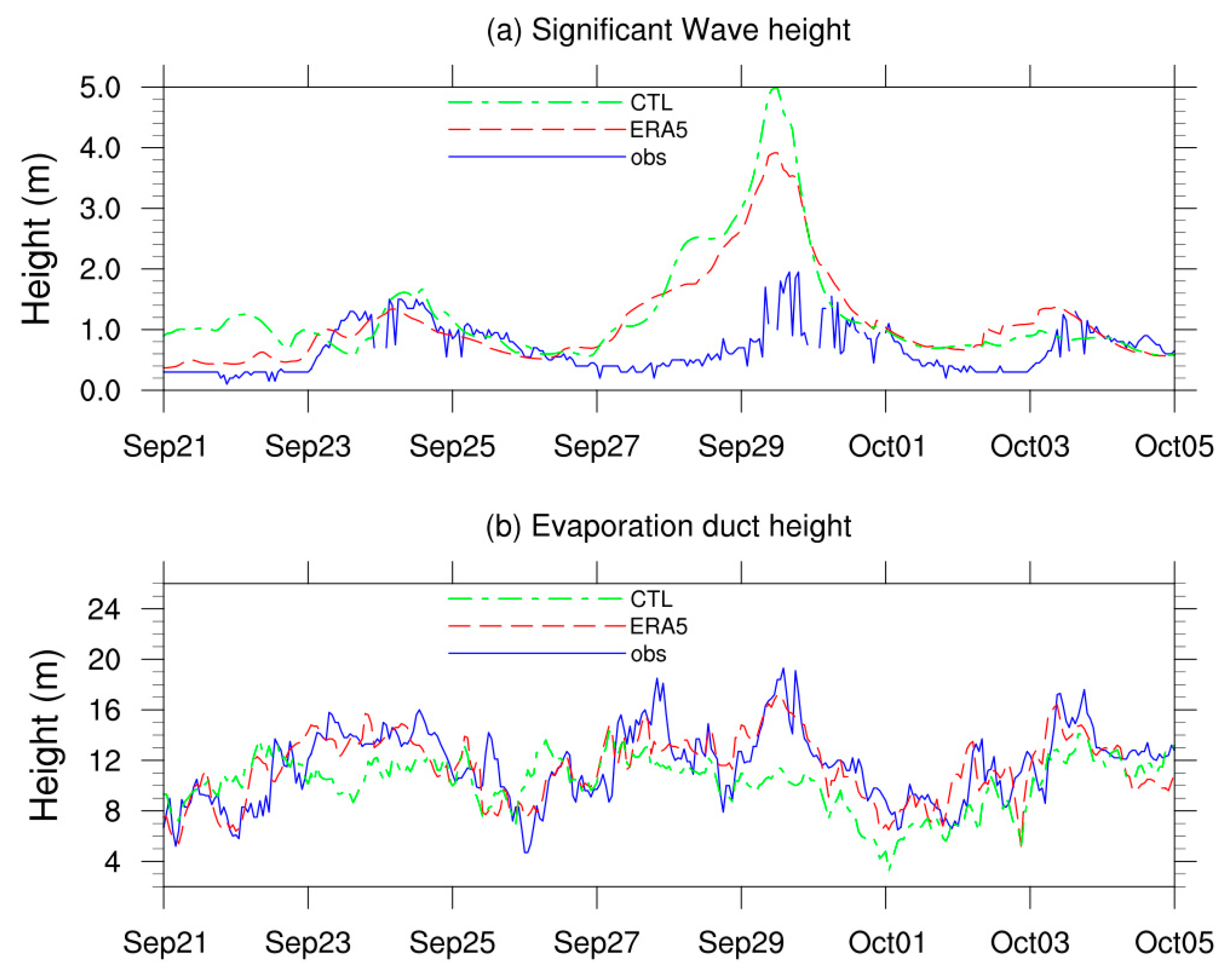
Figure 3 illustrates the hourly series of significant wave height and evaporation duct height at the observation tower location. As depicted in Figure 3a, the observed significant wave height exhibited three peaks during the simulation period, corresponding to the influence periods of Typhoons Hagupit, Mekkhala, and Higos, as listed in Table 1. Typhoon Jangmi, the most distant from the observation tower, caused short periods of windy weather but did not result in high waves. While the CTL aligned in magnitude with the ERA5 data, both indicated higher wave heights compared to the observations. The mean bias of wave height in the CTL was 0.59 m, slightly higher than the bias observed in the ERA5 data, which stood at 0.47 m. Notably, during the period surrounding 29 September, coinciding with Typhoon Mekkahala, the CTL simulated a higher intensity of the typhoon, with a maximum wave height bias exceeding 3 m. However, this bias rapidly decreased to within 1 m as Typhoon Mekkahala passed.
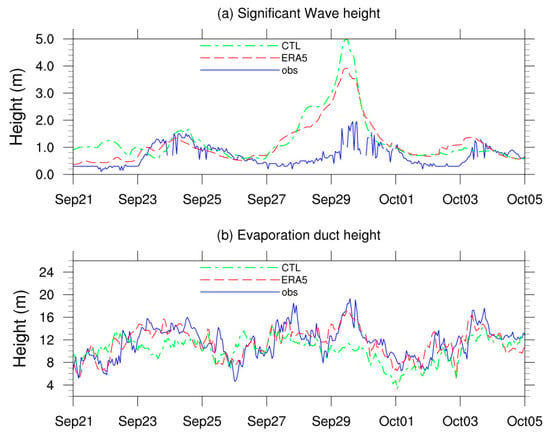
Figure 3.
The hourly series of (a) significant wave height and (b) evaporation duct height for the CTL, ERA5 data and station observation in Yongxing Island.
The evaporation duct series depicted in Figure 3b for both the CTL and ERA5 data were analyzed using the NPS model. The evaporation duct height series exhibited a general positive correlation with wave heights. Throughout the simulation period, the mean evaporation duct height derived from observations was 11.63 m, while ERA5 data and the CTL indicated heights of 11.47 m and 10.23 m, respectively. Despite the CTL showing slightly lower numerical values, its temporal variation closely resembled that of the observations.
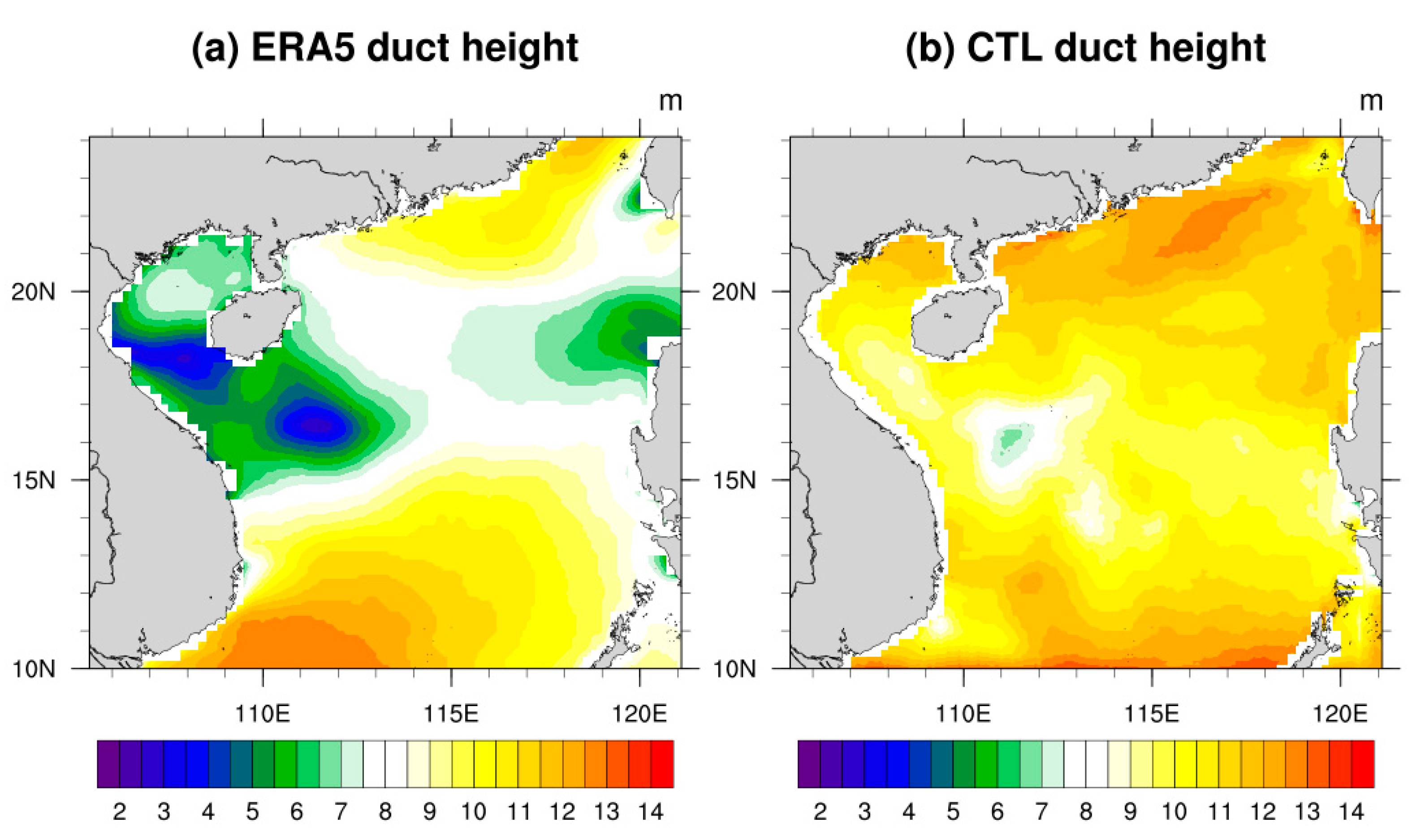
Additionally, alongside the time series, Figure 4 illustrates the mean spatial distributions of evaporation duct height across the D01 domain throughout the simulation period. In Figure 4a, the height distribution for the ERA5 data revealed two prominent high-value centers located in the northern and southern boundary regions of the South China Sea, with a mean height of 8.76 m. Conversely, in the western and eastern areas, the evaporation ducts tended to exhibit lower heights compared to other regions. Figure 4b shows the simulated duct heights for the CTL, which exhibit similar distributions, albeit with less pronounced spatial heterogeneity. The mean duct height over the domain was observed at 10.22 m, underscoring the efficacy of the duct diagnosis model established in this study for simulating evaporation ducts.
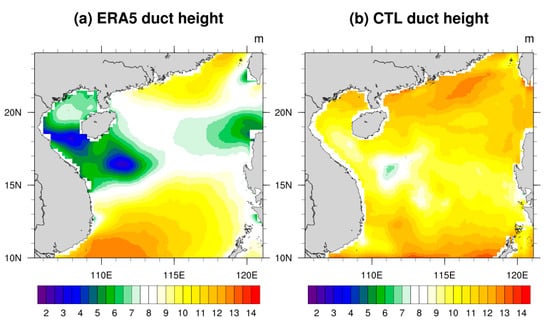
Figure 4.
The spatial distributions of mean evaporation duct height for (a) the ERA5 reanalysis data and (b) the CTL during the simulation period.
4.2. Spatial Distributions of Changes Resulted from Sensitivity Tests
To explore deeper into the impacts of wave processes on the evaporative duct under different roughness schemes, the subsequent section investigated the spatial distribution changes in three sensitivity tests relative to the CTL.
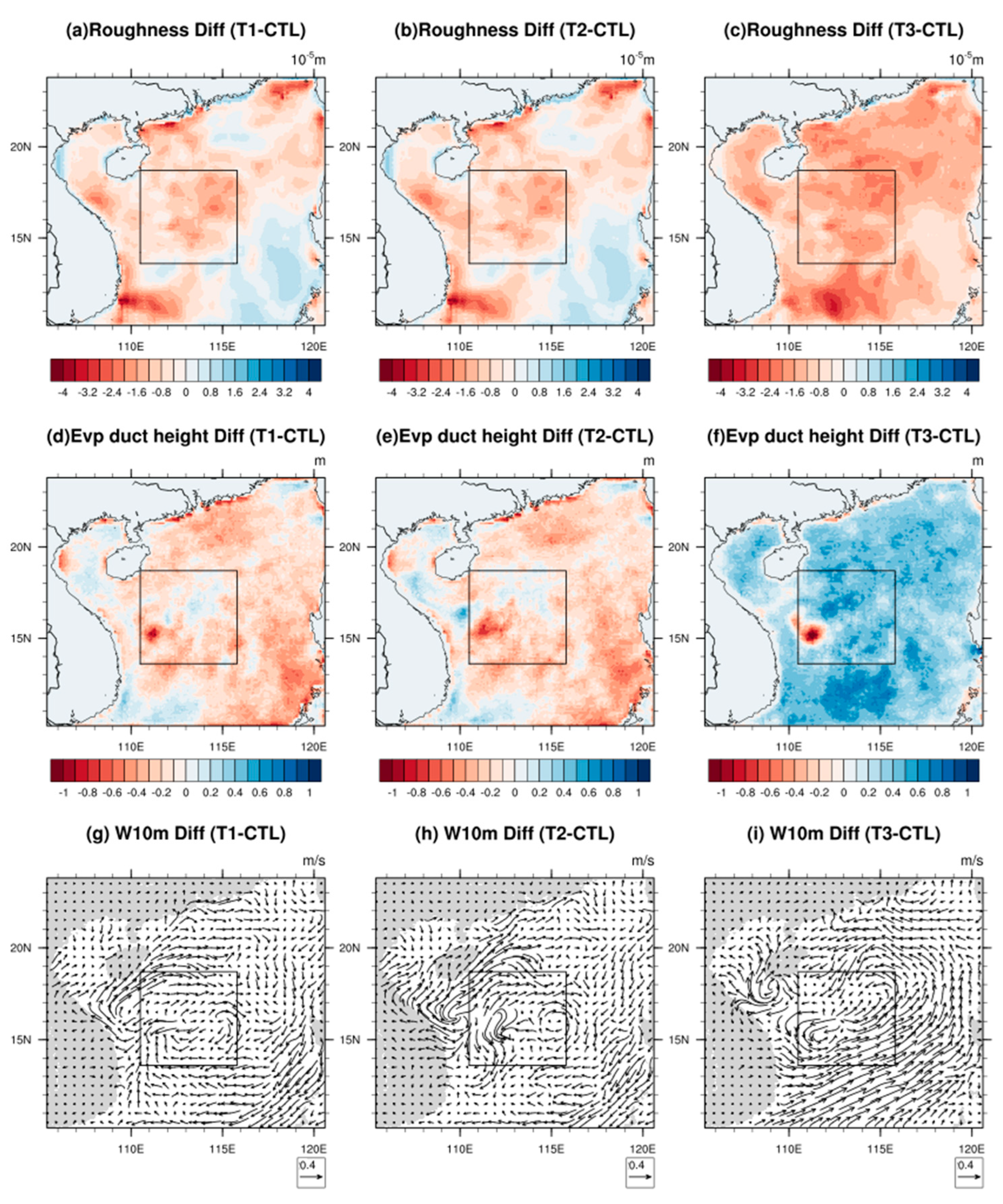
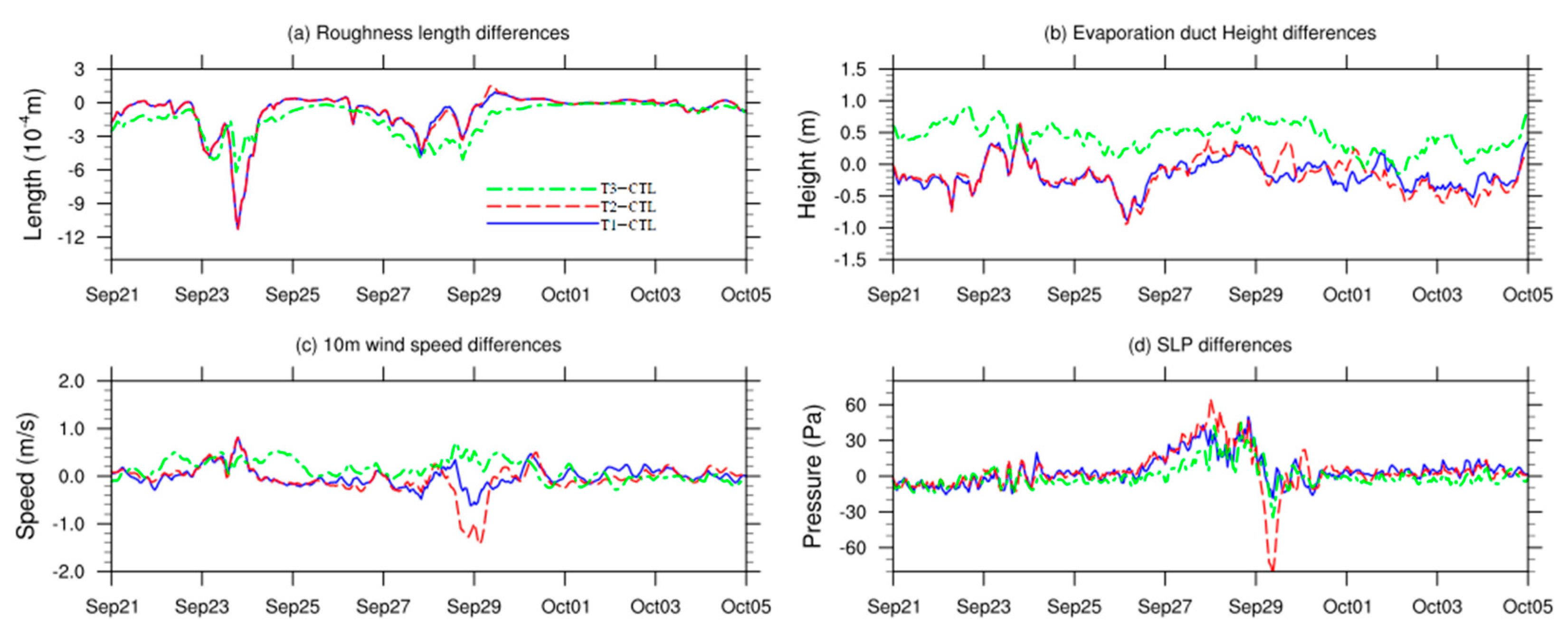
Figure 5 illustrates the spatial distributions of differences between the three sensitivity tests and the CTL. As depicted in Figure 5a–c, the simulated surface roughness in T1, T2, and T3 was generally lower than that in the CTL, with mean differences specifically measured at −0.24 × 10−5 m, −0.25 × 10−5 m, and −0.84 × 10−5 m, respectively. As per the experimental design, the T1 test did not factor in wave processes, while the T2 test included wave processes but still utilized Equation (1) for calculating surface roughness, as the T1 test did. Consequently, in the T2 test, wave processes solely influenced variables such as SST and currents without directly impacting the atmosphere. Thus, the difference in roughness between the T1 and T2 tests was marginal. A slight reduction in roughness in the T2 test compared to the T1 test was observed, suggesting that the indirect feedback from wave processes might further diminish roughness. In the T3 test, featuring an alternative roughness scheme accounting for wave age effects, the roughness lengths were notably lower than those in the CTL, indicating that Equation (4) resulted in the lowest roughness among the tests, and winds near the sea surface in the T3 test would encounter less resistance. Spatially, the T3 test demonstrated a reduction in roughness across the entire South China Sea region compared to the CTL. The T1 and T2 tests, which disregarded direct wave influences, exhibited a decrease in roughness over much of the central and western areas of the domain, albeit with a slight increase in roughness detected in the southeastern areas. These changes can further induce variations in near-surface wind fields, consequently influencing the distribution of heat and evaporative duct processes.
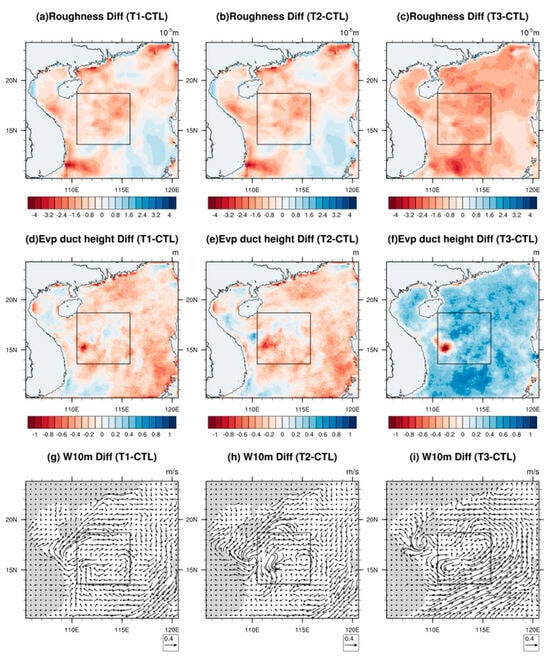
Figure 5.
The spatial distributions of mean roughness differences for (a) T1−CTL, (b) T2−CTL, (c) T3−CTL, mean evaporation duct height differences for (d) T1−CTL, (e) T2−CTL, (f) T3−CTL, and mean wind differences at 10 m level for (g) T1−CTL, (h) T2−CTL, (i) T3−CTL during the simulation period. The area enclosed by the black frame is D02 domain.
The distributions of evaporation duct height differences are depicted in Figure 5d–f. In the absence of wave processes, evaporation ducts were observed to form at lower levels, as evidenced by a mean duct height decrease of 0.13 m and 0.14 m in the T1 and T2 tests, respectively. In contrast, the mean duct heights in the T3 test (Figure 5f) exhibited an increase of 0.23 m across the domain. The spatial distributions of duct height differences in Figure 5d–f roughly corresponded with those in Figure 5a–c. Notably, in the southeastern part of the domain where surface roughness increases (Figure 5a,b), centers of negative duct height differences were identified there (Figure 5d,e). Conversely, stronger correlations were observed between the distributions in Figure 5c,f. Spatial correlation coefficients were computed by converting the 2-D spatial arrays into 1-D series and calculating the linear correlation coefficient. The coefficient values between Figure 5a–f were −0.46, −0.46, and −0.81. These negative correlations suggest that the initial decrease in surface roughness led to an increase in evaporation duct heights. The only difference between T3 and CTL lay in the roughness calculation, which exhibited the strongest correlations. However, differences among T1, T2, and CTLs were entangled with more intricate air–sea feedback, potentially weakening the correlations.
The wind discrepancies at the 10 m level among the three sensitivity tests and the CTL are illustrated in Figure 5g–i. Throughout the simulation period, influenced by the summer monsoon in the South China Sea, prevailing wind directions in the region the predominantly southerly and southwesterly. In the T1 and T2 tests, average wind speeds decreased by 0.14 m/s and 0.13 m/s, respectively. Increased roughness in the southeastern part of the domain primarily influenced wind differences there, predominantly leading to northerly winds, thereby somewhat diminishing the prevailing wind speeds. Conversely, in the western part of the domain, there was a noticeable strengthening of southwesterly winds. Consequently, both the T1 and T2 tests induced an anticyclonic difference within the domain, with its center roughly located in the central South China Sea within the designated black box labeled as D02. Compared to T1, the T2 test exhibited stronger differences in southwesterly winds in the western region, and more pronounced northerly wind differences were observed in the central sea area within the D02 domain, indicating a further reduction in prevailing wind speeds, consistent with decreased roughness.
The T3 test showed fundamentally opposite wind difference distributions, with an average wind speed increase of 0.23 m/s. Due to decreased roughness across the entire region, a significant enhancement of southwesterly winds was observed in the central and eastern parts of the South China Sea, driving the northward movement of warmer surface waters. Consequently, the D02 domain in the central South China Sea detected significant cyclonic differences, further impacting local processes such as evaporation and convection.
In general, wind speed changes resulting from wave parameterization exhibited a positive correlation with changes in evaporation duct height, with spatial correlation coefficients of 0.72, 0.66, and 0.82. In regions where wind speeds increased, evaporation duct height also increased, possibly due to enhanced moisture exchange facilitated by stronger winds, thereby impeding the formation of large humidity vertical gradients locally. Consequently, the inversion layer caused by evaporation (i.e., the height of the evaporation duct) could only form at higher altitudes further from the water surface.
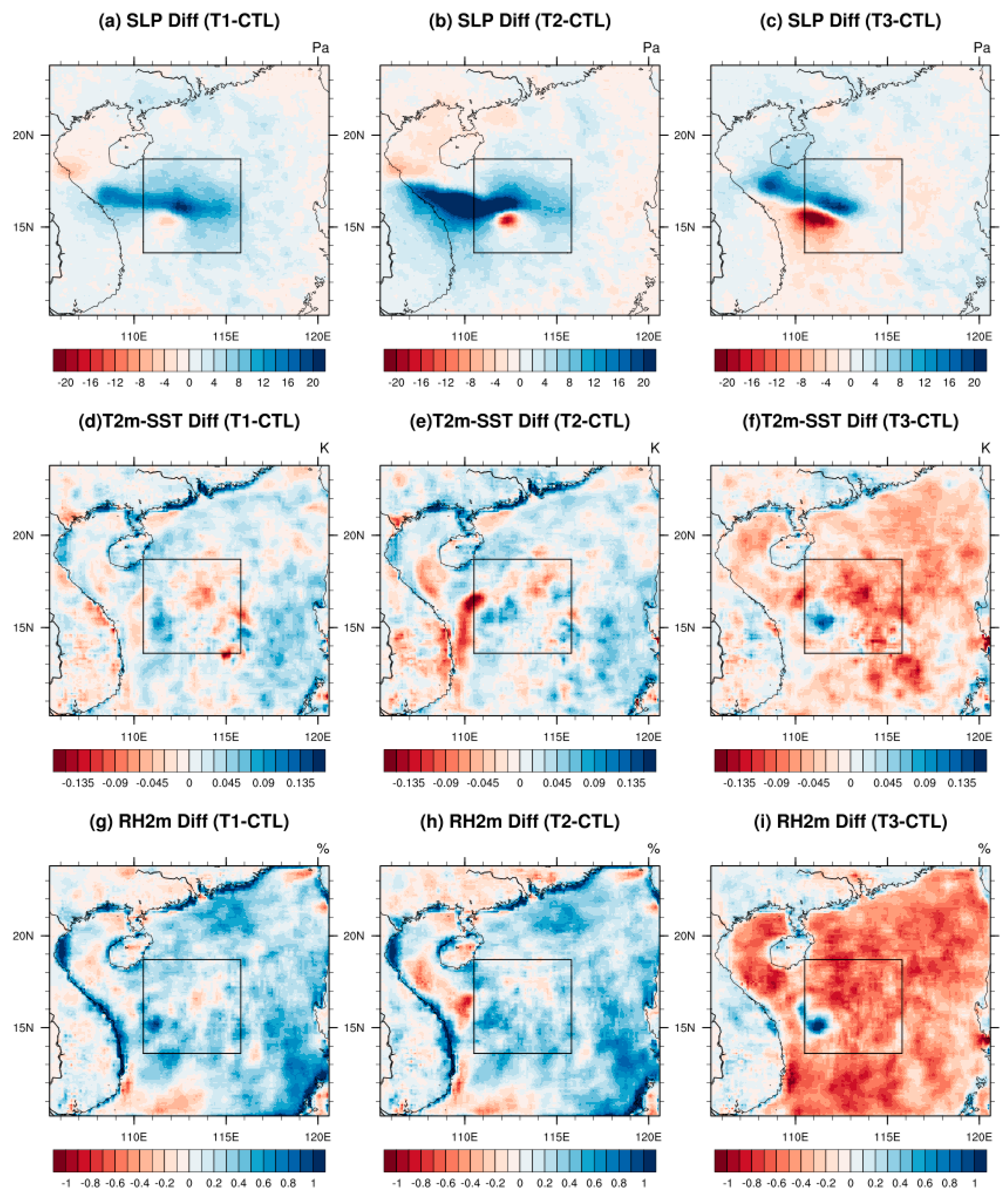
Figure 6 illustrates the spatial distribution of differences in sea level pressure (SLP), air–sea temperature difference, and RH2m. As depicted in Figure 6a–c, both the T1 and T2 tests showed an average increase in SLP of 1.54 Pa and 1.77 Pa, respectively, compared to the CTL within the domain. The center of pressure increase was situated in the central South China Sea, largely corresponding to the anticyclonic center of difference in sea surface wind shown in Figure 5. The pressure increase observed in the T2 test slightly exceeded that in the T1 test, attributed to a further reduction in roughness and prevailing wind speed within the D02 domain, along with the suppression of the rise of the anticyclonic center.
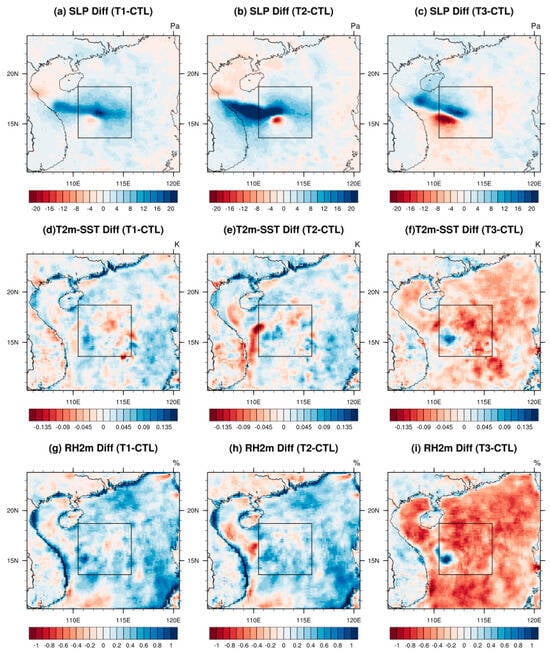
Figure 6.
The spatial distributions of mean SLP differences for (a) T1−CTL, (b) T2−CTL, (c) T3−CTL, mean differences of T2m minus SST for (d) T1−CTL, (e) T2−CTL, (f) T3−CTL, and mean RH2m differences for (g) T1−CTL, (h) T2−CTL, (i) T3−CTL during the simulation period.
In contrast, the T3 test, influenced by changes in cyclonic wind fields, demonstrated noticeable low-pressure differences in the western South China Sea, accompanied by relatively weaker high-pressure differences, resulting in a modest increase in SLP across the entire region, approximately 0.70 Pa. The spatial distributions of SLP exhibited relatively low correlation with evaporation duct heights, with correlation coefficients of −0.01, 0.09, and 0.03 between the three tests and CTL one.
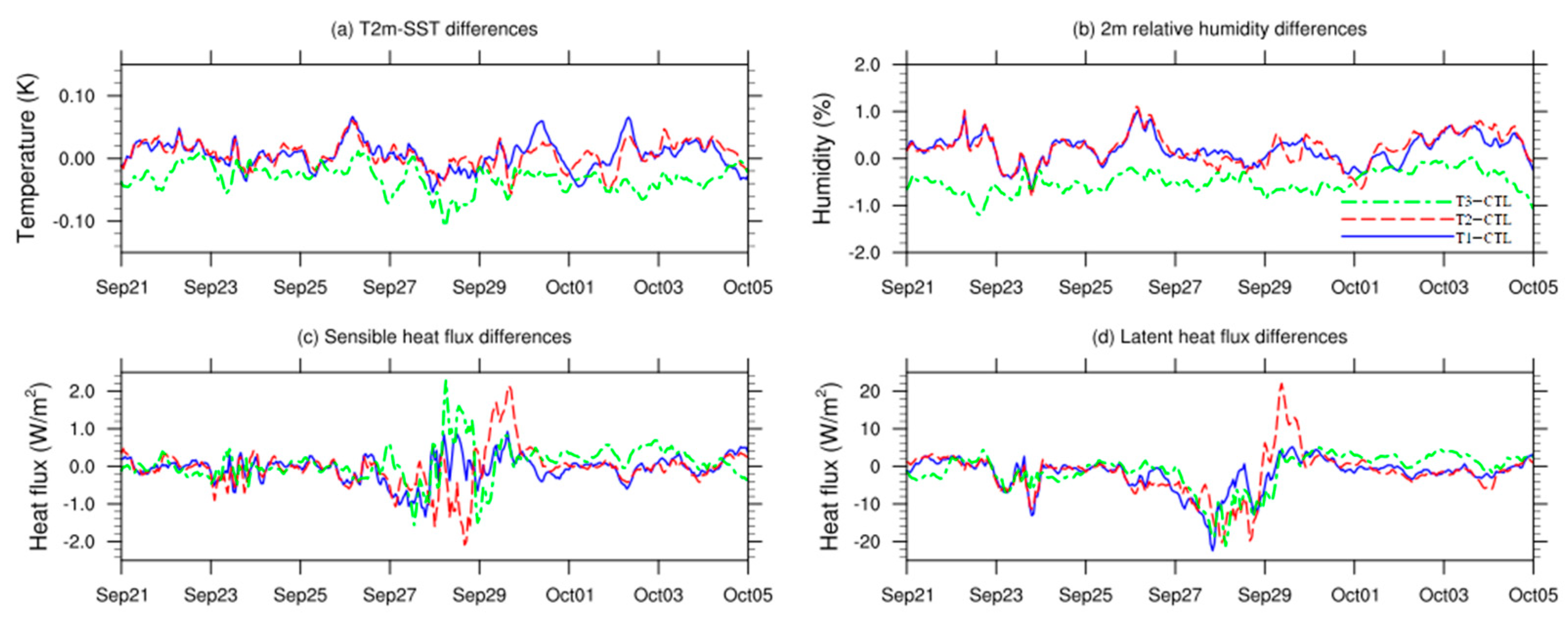
In the process of diagnosing evaporation ducts, it is important to note that their formation does not rely solely upon sea surface temperature (SST) or air temperature. Similar to the evaporation mechanism, the temperature contrast between the air and surface seawater plays a crucial role. As the air–sea temperature difference increases, there is a greater likelihood of temperature-inversion layers forming at lower levels. Figure 6d–f illustrate the disparities in air–sea temperature difference (T2m minus SST) among the three sensitivity tests and the CTL one.
Slight enhancements in the temperature difference between T2m and SST were observed in both the T1 and T2 tests, with mean increases of 0.011 K and 0.012 K, respectively. These findings suggest that without accounting for wave processes, the thermal differential between the air and sea surface would widen, favoring duct formation at lower altitudes. Although the T2 test exhibited no significant deviation from the T1 test in terms of regional averages, it showed a slightly stronger air–sea thermal difference.
Conversely, the T3 test showed a reduction in the air–sea temperature difference across most regions, with a mean value of −0.021 K. This implies that reduced roughness and higher wind speeds weakened the temperature gradient between the atmosphere and sea surface, thereby promoting the formation of evaporation ducts at higher altitudes. Regarding spatial correlation coefficients, the correlations between the air–sea temperature differences and changes in evaporation duct height were −0.40, −0.41, and −0.69, slightly lower than those between roughness and evaporation duct height alterations.
Figure 6g–i illustrate the changes in humidity at the 2 m level (RH2m). On average, humidity increased by 0.23%, 0.22%, and −0.28% across the three sensitivity tests. In the T1 and T2 tests, the absence of wave feedback and the reduction in roughness in most regions resulted in higher humidity, except for a decrease detected in the western part of the D02 domain. Within this area, the enhanced north wind difference in the T2 test (see Figure 5h) led to a more pronounced decrease in humidity compared to the T1 test.
In the T3 test, characterized by diminished roughness, increased wind speeds over the eastern parts of the South China Sea caused a decline in humidity, with an uptick observed only near the cyclonic divergence center in Figure 5i. Overall, the changes in RH2m across the three sensitivity tests exhibited an obvious negative correlation with alterations in evaporation duct height throughout the domain. When compared to changes in other elements, the correlation between humidity variation and evaporation duct height appeared to be the strongest, with values of −0.75, −0.74, and −0.89. Despite the primary focus of these sensitivity tests on dynamic element changes, this study uncovered that humidity’s correlation with evaporative duct heights surpassed that of wind speed and roughness. This underscores the significant role of humidity in the evaporation duct processes.
Moreover, the evaporation process near the sea surface is influenced not solely by changes in regional winds but also by local heat and moisture fluxes. Hence, Figure 7 illustrates the distributions of latent and sensible heat flux differences for the three sensitivity tests. Figure 7a–c depict the changes in sensible heat flux. Sensible heat fluxes in all tests exhibited varying degrees of increase, with an average value of approximately 0.033 W/m2, 0.012 W/m2, and 0.044 W/m2. Changes in sensible heat flux primarily arose from fluctuations in sea surface thermal conditions. Spatially, the alterations in sensible heat flux for the three tests displayed a similar distribution to SST changes (not depicted), predominantly driven by changes in wind fields leading to heat transport in ocean currents, with only a weak positive correlation observed with evaporation duct height changes (0.02, 0.05, and 0.22).
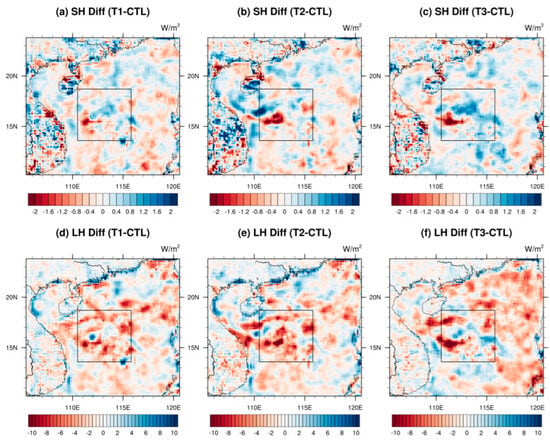
Figure 7.
The spatial distributions of mean sensible heat flux differences for (a) T1−CTL, (b) T2−CTL, (c) T3−CTL, mean latent heat flux for (d) T1−CTL, (e) T2−CTL, (f) T3−CTL during the simulation period.
The latent heat flux originates from the phase change energy during the sea surface evaporation process and is typically considered the energy-based description of evaporation. As depicted in Figure 7d–f, the latent heat fluxes for the three tests all demonstrated a certain decrease, with a regional average decrease of approximately 0.036 W/m2, 0.082 W/m2, and 0.918 W/m2. Generally, the latent heat flux is influenced by both the sea surface wind speed and the air–sea temperature difference. An increase in sea surface wind speed or air–sea temperature difference will stimulate more water evaporation from the sea surface, completing the transfer of heat from liquid seawater to gaseous water vapor. In this study, it appeared challenging for the changes in sea surface wind speed and air–sea temperature difference, induced by different parameterizations of roughness, to increase or decrease simultaneously. In the region of significant changes in wind speed in the eastern part of the South China Sea, the air–sea temperature difference was nearly opposite to the wind speed change. The changes in latent heat flux shown in Figure 7d–f bore more resemblance to the distribution of air–sea temperature differences in Figure 6d–f than to the distribution of wind speed changes. This also indicated that in the COAWST model, the air–sea temperature difference played a greater role in determining latent heat or evaporation processes. Overall, there was a weak negative correlation between the changes in latent heat flux and evaporation duct heights, with the spatial correlation coefficients of −0.20, −0.19, and −0.02. In regions where latent heat flux decreases (or evaporation processes are suppressed), evaporation duct heights are usually higher. Additionally, the disparities between the T2 and T1 tests suggested that the wave processes would further diminish the latent heat flux from the sea surface to the atmosphere through indirect feedback processes, consequently increasing the evaporation duct heights.
4.3. Vertical Profiles and Temporal Series of Differences
According to the spatial distributions observed in the South China Sea as described above, alterations in the general circulation were discovered to induce discrepancies or even opposing trends in surrounding areas compared to those in central regions. The computation of regional averages revealed that changes in the central region often became obscured by those occurring elsewhere. Hence, beyond examining spatial distributions, this study also focused on the D02 domain within the central South China Sea as a typical area for investigating the vertical distribution and temporal variations of near-surface atmospheric elements on a regional average scale. This approach facilitated a deeper exploration of the localized response of hydro-meteorological processes.
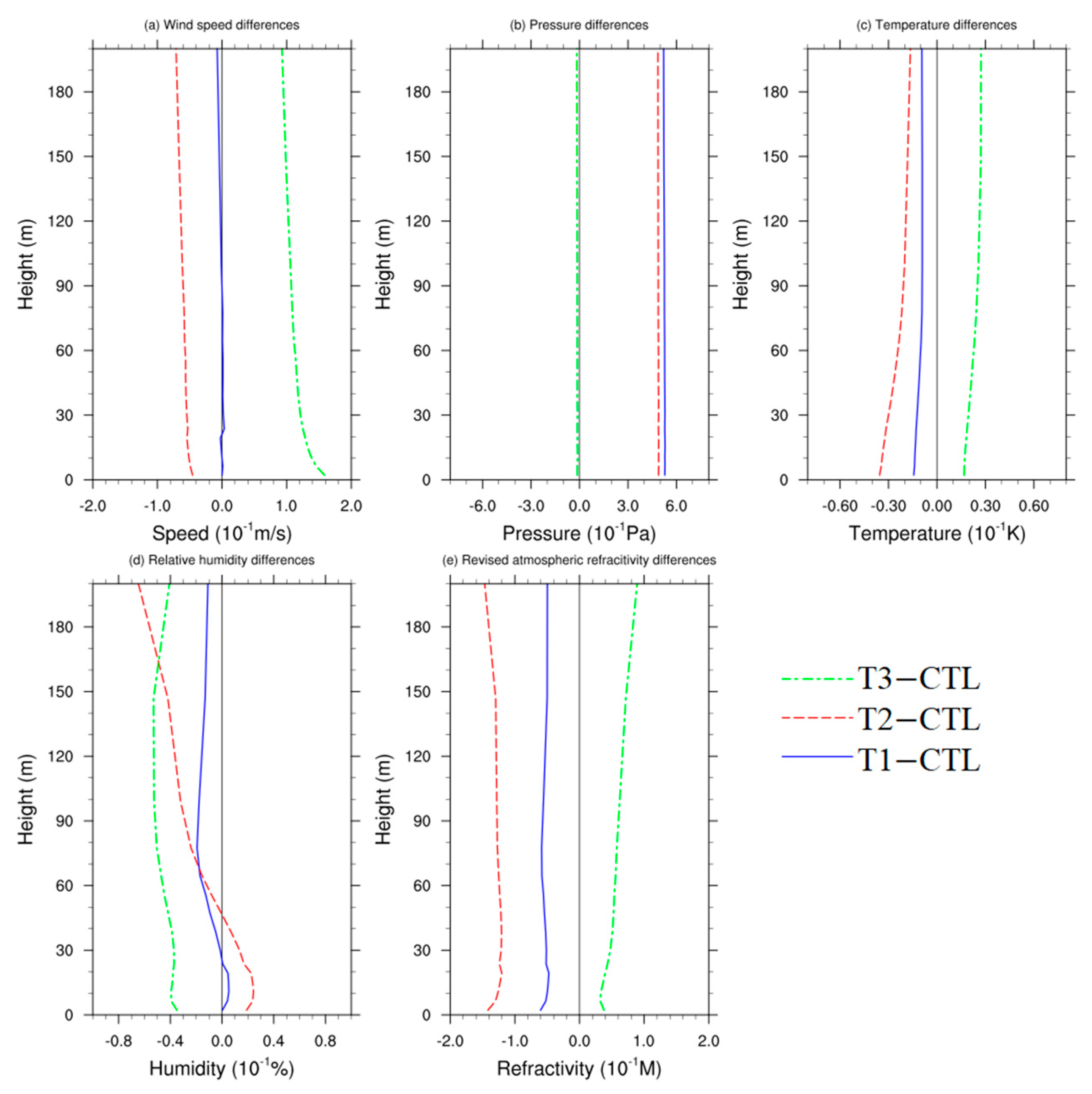
Figure 8 illustrates the discrepancy profiles of the revised atmospheric refractivity derived from the NPS model output, alongside wind speed, relative humidity, air temperature, and air pressure within the D02 domain across three sensitivity tests. To enhance clarity, the profiles in the figure were magnified tenfold. Although some spatial variability persisted within the D02 domain, the mean values were generally aligned with the regional distribution. Overall, vertical differences within 200 m were not pronounced across the three sensitivity tests.
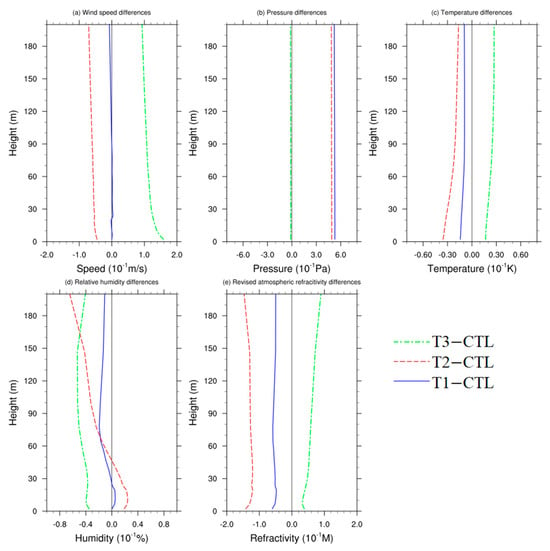
Figure 8.
The vertical profiles of (a) mean wind speed differences, (b) mean air pressure differences, (c) mean air temperature differences, (d) mean relative humidity differences, and (e) mean revised atmospheric refractivity differences for the three sensitivity tests within the D02 typical domain during the simulation period.
As for the wind speed differences depicted in Figure 8a, the T1 test exhibited minimal changes in wind speed compared to the CTL, whereas T2 showed a decline in wind speed, with this decrease amplifying as altitude increased. Conversely, the T3 test revealed a gradual attenuation of the wind speed difference over the sea surface as altitude increased. Regarding the pressure differences in Figure 8b, the vertical variation for each test was considerably smaller than the discrepancy among them, resulting in minimal observable changes within 200 m.
The differential temperature profiles averaged across the region (Figure 8c) revealed a distinct negative correlation with wind speed differences; as wind speed increased (or decreased), temperature differences decreased (or increased) correspondingly. For the T1 and T2 tests, the near-surface cold difference gradually diminished with altitude. Conversely, the T3 test exhibited a reverse trend, indicating that higher wind speeds induced more intense heat exchange, thereby reducing temperature differences.
The vertical humidity variances among the three tests (Figure 8d) showed notable discrepancies. The T3 test within the D02 domain exhibited an overall decline in humidity with minimal vertical fluctuation. Conversely, the T1 and T2 tests exhibited a tendency towards elevated humidity levels near the sea surface, gradually transitioning into a drier difference at higher altitudes. This transition notably amplified the vertical humidity gradient within the D02 domain, facilitating the formation of evaporation ducts at lower altitudes in this area.
Furthermore, the discrepancy profiles of the revised atmospheric refractivity were also depicted in Figure 8e. The vertical variances indicated an insignificant decreasing trend within the 200 m. However, the T3 test showed a slight increasing trend with altitude, without any noticeable abrupt changes.
In addition to the variations in vertical profiles, the temporal series of hydro-meteorological elements averaged over the D02 domain is also presented. Figure 9 illustrates the difference series in roughness, evaporation duct height, wind speed at the 10 m level, and SLP. As depicted in Figure 9a, the roughness differences among the three sensitivity tests were primarily negative, aligning with the spatial distribution shown in Figure 5d–f. Notably, during the simulation period, the South China Sea region encountered four typhoon events: Hagupit (19–25 September), Jangmi (24–30 September), Mekkhala (28–30 September), and Higos (30 September–4 October). Extreme weather fluctuations on 23–24 and 28–29 September had a particularly significant impact on roughness differences.
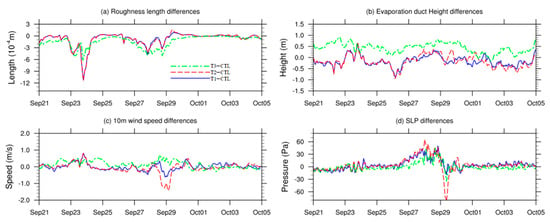
Figure 9.
The temporal series of (a) mean roughness length differences, (b) mean evaporation duct height differences, (c) mean wind speed differences at 10 m level, and (d) mean SLP differences for the three sensitivity tests within the D02 typical domain during the simulation period.
Specifically, due to the roughness calculations in the T1 and T2 tests, which solely considered variations in wind speed, a notable decrease in roughness occurred around 24 September due to the influence of wind speed. Conversely, the T3 test, which factored in changes in wind speed, wave height, and wave age, exhibited lower roughness changes compared to the other two tests for most of the period, except around 24 September.
Regarding evaporation duct height (Figure 9b), its positive difference peaks generally corresponded to the negative difference peaks in roughness. However, this negative correlation was not universally applicable, as changes in evaporation duct height were largely influenced by regional environmental alterations at the ocean surface.
Figure 9c depicts the difference in wind speed at the 10 m level. The regional wind speed variances in the T1 and T2 tests generally aligned, except around 29 September, when the simulated wind speed notably decreased in the T2 test, corresponding to the passage of Typhoon Mekkhala through the D02 domain. This suggests that the T2 test, which accounts for indirect wave feedback, was more sensitive to extreme weather events. Moreover, the T3 test showed elevated wind speed differences around 29 September, consistent with its lower roughness and higher evaporation duct height.
The SLP differences illustrated in Figure 9d exhibited a similar trend to the wind speed differences. Compared to the CTL, all three tests showed more pronounced variations in simulated pressure during the passage of Typhoon Mekkhala (28–30 September), while the influence of the other three typhoons on SLP changes in the D02 domain was less significant. Furthermore, in line with the spatial distribution, the changes in SLP did not demonstrate a clear correlation with evaporation duct height.
Similar to Figure 9, Figure 10 presents the temporal series of air–sea temperature difference, RH2m, sensible heat flux, and latent heat flux within the D02 domain. In Figure 10a, the series of air–sea temperature differences (T2m minus SST) is depicted. For the majority of the observation period, both the T1 and T2 tests exhibited an increase in air–sea temperature difference while the T3 test demonstrated the opposite trend. Notably, around 28 September, the air–sea temperature difference in the T3 test notably decreased, attributed to an intensified sensible heat exchange between the sea and the atmosphere.
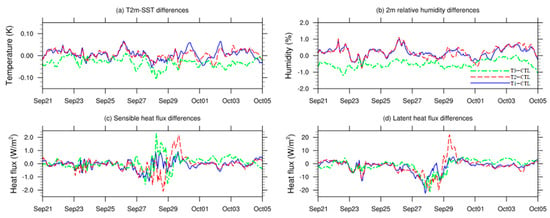
Figure 10.
The temporal series of (a) mean differences of T2m minus SST, (b) mean relative humidity differences at 2 m level, (c) mean sensible heat flux differences, and (d) mean latent heat flux differences for the three sensitivity tests within the D02 typical domain during the simulation period.
Regarding Figure 10b, which illustrates the variations in RH2m, both the T1 and T2 tests generally indicated an uptick in humidity within the D02 domain, whereas the T3 test showed a decrease in humidity. This average difference corresponded with the spatial distributions in Figure 6g–i. Specifically, the T1 and T2 tests exhibited wetter conditions, while the T3 test showed a negative average humidity difference during the simulation period.
Figure 10c,d depict the difference series of sensible heat flux and latent heat flux, respectively. Similar to the pressure dynamics, significant variations in sensible and latent heat flux were observed across all three sensitivity tests during the period of 28–30 September. Contrasting with the CTL, the T1 test, which excluded wave processes, showed a slight uptick in sensible heat and a notable decline in latent heat within the D02 region. This suggests that wave processes may enhance local air–sea heat exchange during extreme weather scenarios. Despite the absence of direct wave-atmosphere feedback in the T2 test, the indirect effects of ocean undercurrents influenced by waves resulted in even more pronounced flux alterations during extreme weather events. These significant flux adjustments align with the slight increase in evaporation duct height observed in the T2 test during this period. Conversely, the T3 test exhibited an increase in sensible heat flux and a decrease in latent heat flux during this period, with the heightened sensible heat flux closely corresponding to the decrease in air–sea temperature difference.
In summary, the temporal difference series of evaporation duct height demonstrated a strong correlation with variations in air–sea temperature difference and RH2m, consistent with their spatial distribution. Despite drastic changes in variables such as heat fluxes, SLP, and roughness within the D02 region during extreme weather events, the variation in evaporation duct height remained relatively stable. As depicted in the single-point time series of evaporation duct height in Figure 3, the empirically diagnosed evaporation duct persisted in relatively stable presence even during extreme weather conditions in this study.
5. Discussion
This study investigated the influence mechanisms of waves and roughness on the evaporation ducts over the sea surface under extreme weather conditions. It is worth noting that this study still had some limitations and uncertainties, primarily stemming from four aspects: data, model bias, experimental design, and result analysis.
First, in terms of data, the diagnosis of the evaporation duct height required multi-layer observational data within the altitude of 30~40 m above the sea surface, which was quite limited. The scarcity of site data posed challenges for model validation, and future studies should involve more field measurements to capture real-world variations in the evaporation duct, thereby enhancing the representativeness of simulation results.
Second, in terms of the model bias, the simulated wave heights were higher than the site observations, and the typhoon simulations were overly intense. Additionally, the simulated evaporation duct height exhibited a certain bias. During several extreme events in the simulation period, the temporal variations of evaporation duct height did not demonstrate drastic changes similar to other hydro-meteorological elements. This discrepancy was probably related to the applicability of the Monin–Obukhov similarity theory under extreme weather conditions. Since all evaporation duct models were established based on similarity theory, the ideal duct estimates derived from this theory may deviate from reality under highly unstable atmospheric stratification. This is a common challenge faced by all empirical evaporation duct models, necessitating further research in the fields of air–sea interaction and boundary layer meteorology.
Third, in terms of experimental design, the simulation period in this study was relatively short, affecting the representativeness of the conclusions. Hence, future studies should conduct longer simulations. The sensitivity tests in this study selected several mature roughness parameterization schemes, but the differences in the simulated roughness were not linear, posing difficulties in result analysis. Future studies should introduce more ideal simulations, artificially adjusting roughness changes uniformly, and compare them with simulations under real conditions to comprehensively investigate the responses of evaporation ducts. In addition, since this study focused on short-term weather simulation, the three-day spin-up for the simulation tests may not fully balance the deep ocean and soil variables. Therefore, we conducted another simulation test with the same settings as the CTL, running from September 15, 0:00 to October 5, 0:00 UTC. The first six days of simulations served as the spin-up period. When comparing this test with the CTL, there were almost no significant differences in the sea-surface elements between the two tests. This also indicated that the imbalance in deep ocean and soil variables was unlikely to affect atmospheric variables in a short time. In subsequent studies, conducting simulations several months in advance is necessary to achieve a more balanced initial state of the climate system.
Finally, in terms of result analysis, the simulations in the South China Sea indicated significant spatial variations in the evaporation duct across different areas. In the open sea areas of the eastern South China Sea, the mechanisms influencing the evaporation duct were relatively clearer, whereas in the central and western areas, the complex combined effects of land–sea distribution, local vertical activity, and regional circulation made the mechanism analysis very challenging, with many signal changes being obscured by other complex processes. Therefore, it is necessary to construct more sensitivity experiments in the future to clarify the response of evaporation duct processes to hydro-meteorological environmental changes within the study domain. The simulation results of this study further validated and refined previous research conclusions regarding the mechanisms of evaporation ducts and their relationship with waves and surface roughness. Most of these studies were made based on local site observational analysis or sensitivity tests under ideal conditions. For instance, Kulessa et al. found a clear positive correlation between evaporation duct height and wind speed and a negative correlation with humidity, based on experimental data from the Tropical Air-Sea Propagation Study along the coast of Queensland, Australia [13]. Ding et al. conducted sensitivity tests to analyze the relationship between significant wave height, wind speed, and evaporation duct height. The results indicated that although significant wave height and wind speed did not strictly correspond in terms of temporal variability, both variables exhibited a clear positive correlation with evaporation duct height [18,56]. Yang et al. diagnosed the distribution of evaporation ducts in the South China Sea based on reanalysis data and found a rough positive correlation between evaporation duct height and the distribution of wind speed and SST, but did not conduct further analysis on the influencing mechanisms [19]. These conclusions were further confirmed in the simulated tests of this study but were only limited to the open waters of the eastern South China Sea. There, the simulations showed that changes in evaporation duct height corresponded to the positive correlation observed in previous research with wind speed. However, in the nearshore central and western areas, this relationship was not fully established due to greater influences from coastal and regional circulations, making local impact mechanisms more easily obscured by processes in other regional circulations. The ocean is a fluid, and local hydro-meteorological changes can easily trigger a response in the overall climate system, resulting in local analyses in the marine environment being applicable only in certain cases and not fully suitable for the marine environments. Based on observational data from the Coastal Waves 96 experiment along the coast of California, Brooks obtained some results contrary to other studies referred to above [16]. He found that the areas of increasing wind speed roughly coincided with the areas of decreasing evaporation duct height, attributing it to the complexity of the climate system. The simulation results of this study also confirmed that in complex coastal areas, the distribution of evaporation duct height was able to exhibit patterns of change completely different from open waters. The root of the problem lay in determining the extent of local impacts in the formation process of evaporation ducts. The Monin–Obukhov similarity theory does not apply to all environments, so evaporation duct models based on similarity theory may exhibit discrepancies between actual patterns of change and theoretical predictions when the theory cannot accurately describe environmental changes.
6. Conclusions
In this study, a coupled diagnostic model for evaporation ducts was established by integrating the COAWST ocean-atmosphere model and the NPS evaporation duct model. By comparison with ERA5 reanalysis data and station observations from Yongxing Island, the model demonstrated excellent capabilities in simulating evaporation ducts and sea surface elements. To further investigate the influence of wave processes on evaporation duct variability under extreme weather conditions, this study modified the wave coupling methods and roughness parameterization schemes in this model and conducted one control test and three additional sensitivity tests.
Among them, the CTL adopted the fully coupled atmosphere, ocean, and wave coupling, along with the default roughness calculation method considering wind speed and wave height. The T1 test ignored wave processes, and roughness was only related to wind speed. The T2 test considered wave processes but used the roughness calculation method of the T1 test without considering wave height. The T3 test adopted the fully coupled scheme of CTL but modified the roughness calculation to a new method considering wave age. By comparing the changes in evaporation duct height and sea surface elements between the three sensitivity tests and the CTL, specific conclusions drawn from this study are as follows:
- (1)
- During the simulation period from 21 September to 5 October, the sea surface elements and evaporative duct simulated by the CTL maintained a high level of accuracy, suitable for further sensitivity mechanism studies. Compared with ERA5 data, the CTL exhibited RMSEs of less than 0.6 K and 5% for the air temperature and humidity at 2 m level within the entire domain, respectively. The spatial distribution pattern of evaporative duct heights closely resembled that of ERA5 data, with an average bias of approximately 2.0 m. In comparison with observations from the Yongxing Island station, the CTL simulated significantly higher wave heights around 29 September under the influence of Typhoon Mekkhala, but with bias within 1.0 m during other periods. Overall, the simulated evaporative duct heights were lower than the station observations, with an average bias of within 1.5 m.
- (2)
- Roughness variations exhibited a clear negative correlation with changes in evaporation duct heights. In the three sensitivity tests (T1, T2, and T3), evaporation duct heights typically rose within regions of decreased roughness when compared to the CTL. From a local process perspective, a decrease in the overall regional mean roughness generally led to an increase in wind speed and a decrease in the air–sea temperature difference. These changes in oceanic dynamics and thermodynamics further induce a decline in near-surface humidity, accompanied by a slight increase in sensible heat flux and a decrease in latent heat flux, thereby inhibiting surface evaporation. Under enhanced surface wind speeds and weakened evaporation processes, it became more challenging for temperature and humidity to establish vertical gradients near the sea surface, ultimately resulting in the formation of evaporative ducts at higher altitudes. The reverse held true as well. This localized mechanism can explain the majority of the response variations in meteorological and hydrological elements induced by roughness in this study. However, the dynamic atmosphere posed challenges for analysis using this local mechanism, as changes in regional atmospheric circulation rendered local impact mechanisms inapplicable to all regions, especially to the western and central regions near the land.
- (3)
- When investigating the mechanisms by which roughness and wave processes affect changes in evaporative duct heights, the influence of regional circulation changes cannot be overlooked alongside local processes. Within the South China Sea region, variations in surface wind fields induced by wave and roughness changes differed among the three sensitivity tests. The T1 and T2 tests exhibited weak anticyclonic differences, whereas the T3 test, conversely, presented regional cyclonic differences. The centers of cyclonic and anticyclonic differences in all three tests were located in the central region of the South China Sea, causing hydro-meteorological variations in the D02 domain to be not entirely consistent or even opposite to those in the coastal regions surrounding the South China Sea. Overall, in the open seas of the eastern South China Sea, the local impact mechanisms were more apparent. In contrast, the western and central regions of the South China Sea were greatly influenced by the continent, resulting in more chaotic wind field changes and highly nonlinear variations in each element, with relatively smaller local impacts.
- (4)
- The differences between the T1 and T2 tests indicated that, under the same roughness scheme, wave processes were able to indirectly affect atmospheric processes through sea surface temperature and heat flux. However, the magnitude of this influence was far smaller than the atmospheric motion changes induced by roughness variations. On a regional average scale, the indirect impact of waves on the atmosphere in the South China Sea manifested as decreased near-surface wind speeds, increased atmospheric pressure, and reduced humidity. These changes, to some extent, inhibited the sensible and latent heat fluxes from the ocean to the atmosphere, further lowering the average evaporation duct height.
- (5)
- In this study, wave processes primarily affected sea surface wind speed through changes in roughness, thereby influencing the evaporation duct process. Consequently, variations in roughness and wind speed exhibited a significant spatial correlation with changes in evaporation duct height. Additionally, among the other parameters required for evaporation duct diagnostics, humidity variation showed the highest spatial correlation with changes in evaporation duct height, even surpassing that of roughness and wind speed. The correlation between air–sea temperature difference and evaporation duct height was similar to that of roughness, while SLP was essentially unrelated to evaporation duct height.
- (6)
- For the typical D02 domain, the average variations in the T1 and T2 tests generally opposed those of the T3 test, consistent with the regional distribution. Within the 200 m altitude range, the most significant changes in humidity vertical gradient occurred. In T1 and T2 tests, there was a lower-level humidity increase accompanied by an upper-level humidity decrease, further enhancing the humidity gradient, which led to a decrease in evaporation duct height. In the T3 test, humidity decreased overall, with less pronounced vertical variability. Regarding the regional average time series, significant fluctuations were observed in all elements due to several typhoon events, with the most notable changes occurring around September 24th and 29th. Among the three sensitivity tests, the T1 and T2 tests, which lacked direct feedback from wave processes, exhibited stronger fluctuations compared to the CTL, particularly under extreme weather conditions. Conversely, the T3 test, which considered wave processes, showed smoother differences compared to the CTL.
Author Contributions
Project administration, J.Z.; writing—original draft preparation, Z.S.; software, W.W., X.L. and H.Z.; validation, J.W. and S.Y.; resources, H.Z. and M.S.; writing—review and editing, W.W., J.Z. and H.Z.; supervision, B.W. and Z.Q.; conceptualization, Z.S. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the “Pioneer and Leading Goose” R&D Program of Zhejiang (2022C03009), the National Natural Science Foundation of China (Grant nos. 42076195, 42206188), the Natural Science Foundation of Shandong province, China (ZR2022MD100), the Key R&D Plan of Shandong Province, China (2023CXPT015), the “Four Projects” of computer science (2021JC02002) and the basic research foundation (2023PY004, 2023JBZ02) in Qilu University of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to internal policy of Powerchina Huadong Engineering Corporation Limited.
Acknowledgments
All the authors thank the four anonymous reviewers and the editors for their contributions to this paper.
Conflicts of Interest
Authors Zhigang Shan, Niaojun Sun and Wei Wang were employed by the company Zhejiang Engineering Research Center of Marine Geotechnical Investigation Technology and Equipment, Zhejiang Huadong Geotechnical Investigation & Design Institute Corporation Ltd., Powerchina Huadong Engineering Corporation Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Babin, S.M.; Dockery, G.D. LKB–based evaporation duct model comparison with buoy data. J. Appl. Meteorol. 2002, 41, 434–446. [Google Scholar] [CrossRef]
- Woods, G.S.; Ruxton, A.; Huddlestone-Holmes, C.; Gigan, G. High–capacity, long–range, over ocean microwave link using the evaporation duct. IEEE J. Ocean. Eng. 2009, 34, 323–330. [Google Scholar] [CrossRef]
- Franklin, K.B.; Wang, Q.; Jiang, Q.; Shen, L. Understanding evaporation duct variabilities on turbulent eddy scales. J. Geophys. Res. Atmos. 2022, 127, e2022JD036434. [Google Scholar] [CrossRef]
- Mikhailov, M.S.; Permyakov, V.A.; Isakov, M.V. Influence of tropospheric ducts on radio propagation over sea surface. In Proceedings of the Progress in Electromagnetics Research Symposium, Toyama, Japan, 1–4 August 2018. [Google Scholar]
- Ortiz-Suslow, D.G.; Wang, Q.; Kalogiros, J.; Yamaguchi, R.; de Paolo, T.; Terrill, E.; Shearman, R.K.; Welch, P.; Savelyev, I. Interactions between nonlinear internal ocean waves and the atmosphere. Geophys. Res. Lett. 2019, 46, 9291–9299. [Google Scholar] [CrossRef]
- Benhmammouch, O.; Caouren, N.; Khenchaf, A. Influence of sea surface roughness on electromagnetic waves propagation in presence of evaporation duct. In Proceedings of the International Radar Conference, Bordeaux, France, 12–16 October 2009. [Google Scholar]
- Penton, S.E.; Hackett, E.E. Rough ocean surface effects on evaporation duct atmospheric refractivity inversions using genetic algorithms. Radio Sci. 2018, 53, 804–819. [Google Scholar] [CrossRef]
- Makin, V.K.; Mastenbroek, C. Impact of waves on air–sea exchange of sensible heat and momentum. Bound.-Layer Meteorol. 1996, 79, 279–300. [Google Scholar] [CrossRef]
- Fan, Y.; Ginis, I.; Hara, T. The effect of wind–wave–current interaction on air–sea momentum fluxes and ocean response in tropical cyclones. J. Phys. Oceanogr. 2009, 39, 1019–1034. [Google Scholar] [CrossRef]
- Hristov, T.; Miller, S. Wave–coherent fields in air flow over ocean waves: Identification of cooperative behavior buried in turbulence. Phys. Rev. Lett. 1998, 81, 5245–5248. [Google Scholar] [CrossRef]
- Hristov, T.; Miller, S.; Friehe, C. Dynamical coupling of wind and ocean waves through wave–induced air flow. Nature 2003, 422, 55–58. [Google Scholar] [CrossRef]
- Garrett, S.A.; Cook, D.E.; Marshall, R.E. The Seabreeze 2009 experiment: Investigating the impact of ocean and atmospheric processes on radar performance in the Bay of Plenty, New Zealand. Weather Clim. 2011, 31, 81–99. [Google Scholar] [CrossRef]
- Kulessa, A.S.; Barrios, A.; Claverie, J.; Garrett, S.; Haack, T.; Hacker, J.M.; Hansen, H.J.; Horgan, K.; Hurtaud, Y.; Lemon, C.; et al. The Tropical Air–sea Propagation Study (TAPS). Bull. Am. Meteorol. Soc. 2017, 98, 517–537. [Google Scholar] [CrossRef]
- Wang, Q.; Alappattu, D.P.; Billingsley, S.; Blomquist, B.; Burkholder, R.J.; Christman, A.J.; Creegan, E.D.; de Paolo, T.; Eleuterio, D.P.; Fernando, H.J.S.; et al. CASPER: Coupled Air–sea Processes and Electromagnetic Ducting Research. Bull. Am. Meteorol. Soc. 2018, 99, 1449–1471. [Google Scholar] [CrossRef]
- Anderson, K.; Brooks, B.; Caffrey, P.; Clarke, A.; Cohen, L.; Crahan, K.; Davidson, K.; De Jong, A.; De Leeuw, G.; Dion, D.; et al. The RED experiment: An assessment of boundary layer effects in a trade winds regime on microwave and infrared propagation over the Sea. Bull. Am. Meteorol. Soc. 2004, 85, 1355–1366. [Google Scholar] [CrossRef]
- Brooks, I.M. Air–sea interaction and spatial variability of the surface evaporation duct in a coastal environment. Geophys. Res. Lett. 2001, 28, 2009–2012. [Google Scholar] [CrossRef]
- Yang, C.; Guo, L.; Wu, Z. Investigation on global positioning system signal scattering and propagation over the rough sea surface. Chin. Phys. B 2010, 19, 245–253. [Google Scholar]
- Ding, J.; Fei, J.; Huang, X.; Cheng, X.; Hu, X.; Ji, L. Development and validation of an evaporation duct model. Part II: Evaluation and improvement of stability functions. J. Meteorol. Res. 2015, 29, 482–495. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, Q.; Shi, Y. Interannual variability of the evaporation duct over the South China Sea and its relations with regional evaporation. J. Geophys. Res. Ocean. 2017, 122, 6698–6713. [Google Scholar] [CrossRef]
- Burk, S.D.; Haack, T.; Rogers, L.T.; Wagner, L.J. Island wake dynamics and wake influence on the evaporation duct and radar propagation. J. Appl. Meteorol. 2003, 42, 349–367. [Google Scholar] [CrossRef]
- Jiao, L.; Zhang, Y. An evaporation duct prediction model coupled with the MM5. Acta Oceanol. Sin. 2015, 34, 46–50. [Google Scholar] [CrossRef]
- Wang, Q.; Burkholder, R.J. Modeling and measurement of ducted EM propagation over the Gulf Stream. In Proceedings of the IEEE International Symposium on Antennas and Propagation and USNC–URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019. [Google Scholar]
- Gunashekar, S.D.; Warrington, E.M.; Siddle, D.R. Long–term statistics related to evaporation duct propagation of 2 GHz radio waves in the English Channel. Radio Sci. 2010, 45, RS6010. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, D.; Huang, S.; Chen, J. Statistical estimations of atmospheric duct over the South China Sea and the tropical eastern Indian Ocean. Chin. Sci. Bull. 2013, 58, 2794–2797. [Google Scholar] [CrossRef]
- Saeger, J.T.; Grimes, N.G.; Rickard, H.E.; Hackett, E.E. Evaluation of simplified evaporation duct refractivity models for inversion problems. Radio Sci. 2015, 50, 1110–1130. [Google Scholar] [CrossRef]
- Fountoulakis, V.; Earls, C. Duct heights inferred from radar sea clutter using proper orthogonal bases. Radio Sci. 2016, 51, 1614–1626. [Google Scholar] [CrossRef]
- Han, J.; Wu, J.-J.; Zhu, Q.-L.; Wang, H.-G.; Zhou, Y.-F.; Jiang, M.-B.; Zhang, S.-B.; Wang, B. Evaporation duct height nowcasting in China’s Yellow Sea based on deep learning. Remote Sens. 2021, 13, 1577. [Google Scholar] [CrossRef]
- Ulate, M.; Wang, Q.; Haack, T.; Holt, T.; Alappattu, D.P. Mean offshore refractive conditions during the CASPER east filed campaign. J. Appl. Meteorol. Climatol. 2018, 58, 853–874. [Google Scholar] [CrossRef]
- Liobello, P.; Martucci, G.; Zampieri, M. Implementation of a coupled atmosphere–wave–ocean model in the Mediterranean Sea: Sensitivity of the short time scale evolution to the air–sea coupling mechanisms. Glob. Atmos. Ocean Syst. 2003, 9, 65–95. [Google Scholar]
- Chen, S.S.; Curcic, M. Ocean surface waves in Hurricane Ike (2008) and Superstorm Sandy (2012): Coupled model predictions and observations. Ocean Model. 2016, 103, 161–176. [Google Scholar] [CrossRef]
- Wahle, K.; Staneva, J.; Koch, W.; Fenogliomarc, L.; Hohagemann, H.T.M.; Stanev, E.V. An atmosphere–wave regional coupled model: Improving predictions of wave heights and surface winds in the southern North Sea. Ocean Sci. 2016, 13, 289–301. [Google Scholar] [CrossRef]
- Shahi, N.K.; Polcher, J.; Bastin, S.; Pennel, R.; Fita, L. Assessment of the spatio-temporal variability of the added value on precipitation of convection-permitting simulation over the Iberian Peninsula using the RegIPSL regional earth system model. Clim. Dyn. 2022, 59, 471–498. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Signell, R.P.; Harris, C.K.; Arango, H.G. Development of a three–dimensional, regional, coupled wave, current, and sediment–transport model. Comput. Geosci. 2008, 34, 1284–1306. [Google Scholar] [CrossRef]
- Liu, N.; Ling, T.; Wang, H.; Zhang, Y.; Gao, Z.; Wang, Y. Numerical simulation of typhoon Muifa (2011) using a Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) modeling system. J. Ocean U. China 2015, 14, 199–209. [Google Scholar] [CrossRef]
- Zambon, J.B.; He, R.; Warner, J.C. Investigation of hurricane Ivan using the coupled ocean–atmosphere–wave–sediment transport (COAWST) model. Ocean Dyn. 2014, 64, 1535–1554. [Google Scholar] [CrossRef]
- Xue, Z.; Zambon, J.B.; Yao, Z.; Liu, Y.; He, R. An integrated ocean circulation, wave, atmosphere, and marine ecosystem prediction system for the South Atlantic Bight and Gulf of Mexico. J. Oper. Oceanogr. 2015, 8, 80–91. [Google Scholar] [CrossRef]
- Ricchi, A.; Miglietta, M.M.; Falco, P.P.; Benetazzo, A.; Bonaldo, D.; Bergamasco, A.; Sclavo, M.; Carniel, S. On the use of a coupled ocean-atmosphere-wave model during an extreme cold air outbreak over the Adriatic Sea. Atmos. Res. 2016, 172–173, 48–65. [Google Scholar] [CrossRef]
- Rizza, U.; Canepa, E.; Ricchi, A.; Bonaldo, D.; Carniel, S.; Morichetti, M.; Passerini, G.; Santiloni, L.; Puhales, F.S.; Miglietta, M.M. Influence of wave state and sea spray on the roughness length: Feedback on Medicanes. Atmosphere 2018, 9, 301. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) modeling system. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Tachnical Note, NCAR/TN–475+STR; NCAR: Boulder, CO, USA, 2008. [Google Scholar]
- Shchepetkin, A.F.; McWilliams, J.C. The regional ocean modeling system: A split–explicit, free–surface, topography–following coordinates ocean model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third–generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Warner, J.C.; Perlin, N.; Skyllingstad, E.D. Using the model coupling toolkit to couple earth system models. Environ. Model. Softw. 2008, 23, 1240–1249. [Google Scholar] [CrossRef]
- Jones, P.W. A User’s Guide for SCRIP: A Spherical Coordinate Remapping and Interpolation Package; Theoretical Division, Los Alamos National Laboratory: Los Alamos, NM, USA, 1997. [Google Scholar]
- Fairall, C.W.; Bradley, E.F.; Rogers, D.P.; Edson, J.B.; Young, G.S. Bulk parameterization of air–sea fluxes for tropical ocean–global atmosphere Coupled–Ocean Atmosphere Response Experiment. J. Geophys. Res. Ocean. 1996, 101, 3747–3764. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor–Yamada level 3 model: Its numerical stability and application to a regional prediction of advection fog. Bound.-Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteorol. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Taylor, P.K.; Yelland, M.J. The dependence of sea surface roughness on the height and steepness of the waves. J. Phys. Oceanogr. 2001, 31, 572–590. [Google Scholar] [CrossRef]
- Olabarrieta, M.; Warner, J.C.; Armstrong, B.; Zambon, J.B.; He, R. Ocean–atmosphere dynamics during Hurricane Ida and Nor’Ida: An application of the coupled ocean–atmosphere–wave–sediment transport (COAWST) modeling system. Ocean Model. 2012, 43–44, 112–137. [Google Scholar] [CrossRef]
- Sian, K.; Dong, C.; Liu, H.; Wu, R.; Zhang, H. Effects of model coupling on Typhoon Kalmaegi (2014) simulation in the South China Sea. Atmosphere 2020, 11, 432. [Google Scholar] [CrossRef]
- Zheng, M.; Zhang, Z.; Zhang, W.; Fan, M.; Wang, H. Effects of ocean states coupling on the simulated Super Typhoon Megi (2010) in the South China Sea. Front. Mar. Sci. 2023, 10, 1105687. [Google Scholar] [CrossRef]
- Frederickson, P.A.; Davidson, K.L.; Anderson, K.D.; Doss-Hammel, S.M.; Tsintikidis, D. Air-sea interaction processes observed from buoy and propagation measurements during the RED experiment. In Proceedings of the 12th Conference on Interactions of the Sea and Atmosphere, American Meteorological Society, Long Beach, CA, USA, 8–13 February 2003. [Google Scholar]
- Frederickson, P.A.; Murphree, J.T.; Twigg, K.L.; Barrios, A. A modern global evaporation duct climatology. In Proceedings of the IEEE International Conference on Radar, Adelaide, Australia, 2–5 September 2008. [Google Scholar]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air–sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Ding, J.; Fei, J.; Huang, X.; Cheng, X.; Hu, X.; Ji, L. Development and validation of an evaporation duct model. part I: Model establishment and sensitivity experiments. J. Meteorol. Res. 2015, 29, 467–481. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, D.; Zhang, L.; Wang, H.; Kang, S. A comparison study of sensitivity on PJ and NPS models in China seas. J. Ocean Univ. China 2019, 18, 1022–1030. [Google Scholar] [CrossRef]
- Sun, Q.; Chen, J.; Yan, J.; Zhang, X.; Huang, L.; Wang, C.; Yao, H.; Zhao, X.; Chen, C. The variation characteristics of air–sea fluxes over the Xisha area before and after the onset of the South China Sea monsoon in 2008. Acta Oceanol. Sin. 2010, 32, 12–23. (In Chinese) [Google Scholar]
- Huang, L.; Wang, C.; Yan, J.; Sun, Q.; Yao, H.; Zhao, X.; Chen, C. Air–sea fluxes exchange and heat budget over the SCS Xisha seas during the period of 2008 summer monsoon. Acta Meteorol. Sin. 2012, 70, 492–505. (In Chinese) [Google Scholar]
- Drennan, W.M.; Taylor, P.K.; Yelland, M.J. Parameterizing the sea surface roughness. J. Phys. Oceanogr. 2005, 35, 835–848. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Hong, S.; Dudhia, J.; Chen, S. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Flather, R.A. A tidal model of the north-west European continental shelf. Mémoires De La Société R. Des Sci. De Liège 1976, 6, 141–164. [Google Scholar]
- Komen, G.J.; Hasselmann, S.; Hasselmann, K. On the existence of a fully developed wind–sea spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).