Interannual Fluctuations and Their Low-Frequency Modulation of Summertime Heavy Daily Rainfall Potential in Western Japan
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
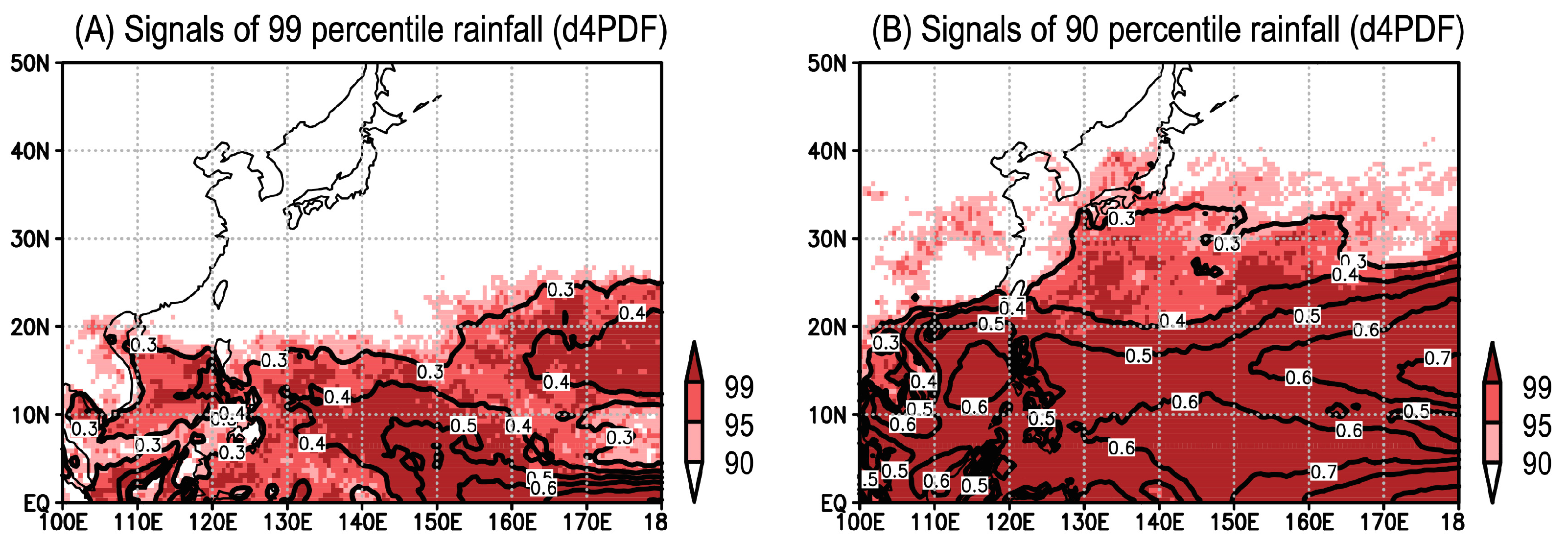
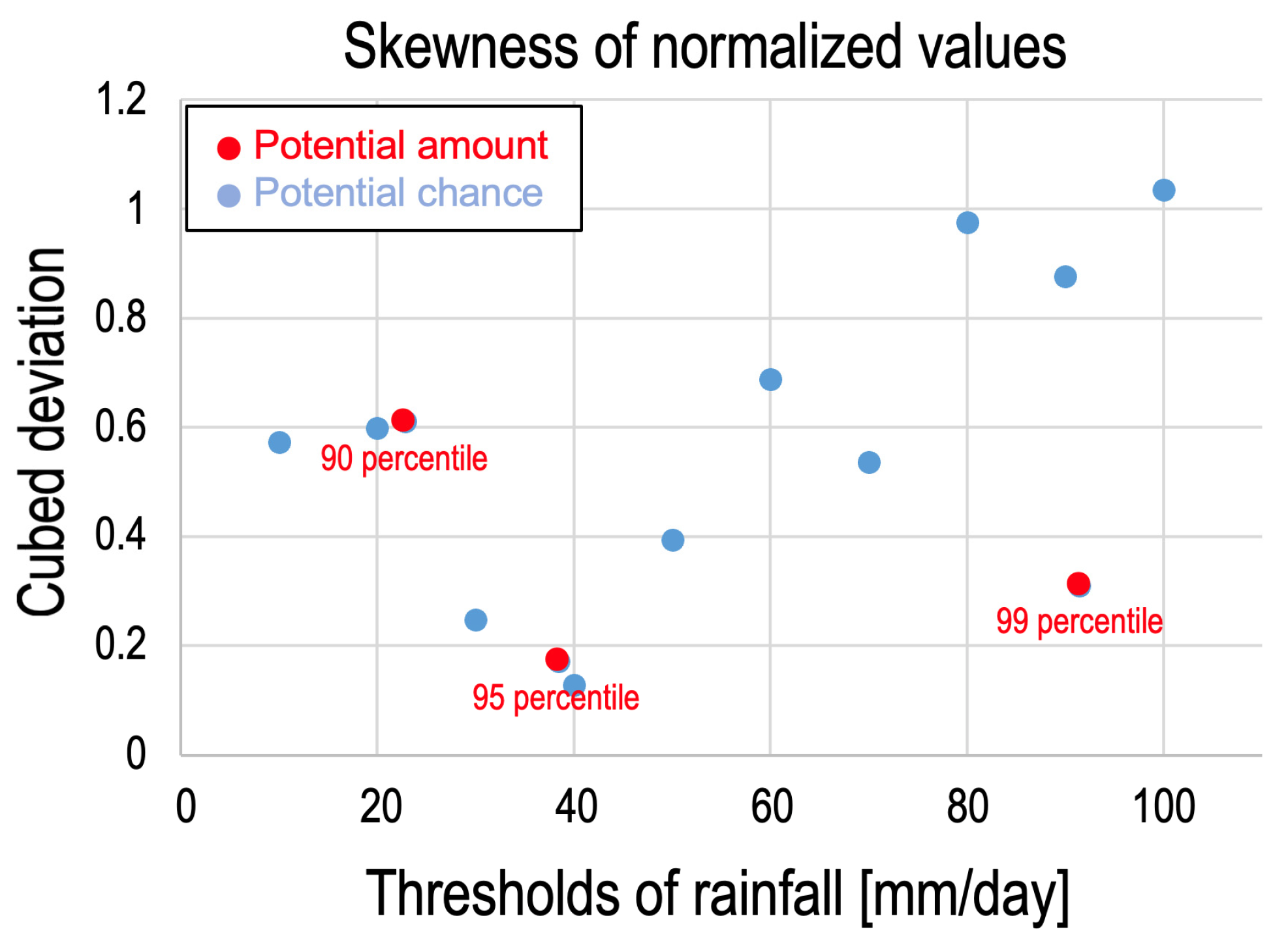
2.2. Methods
3. Results
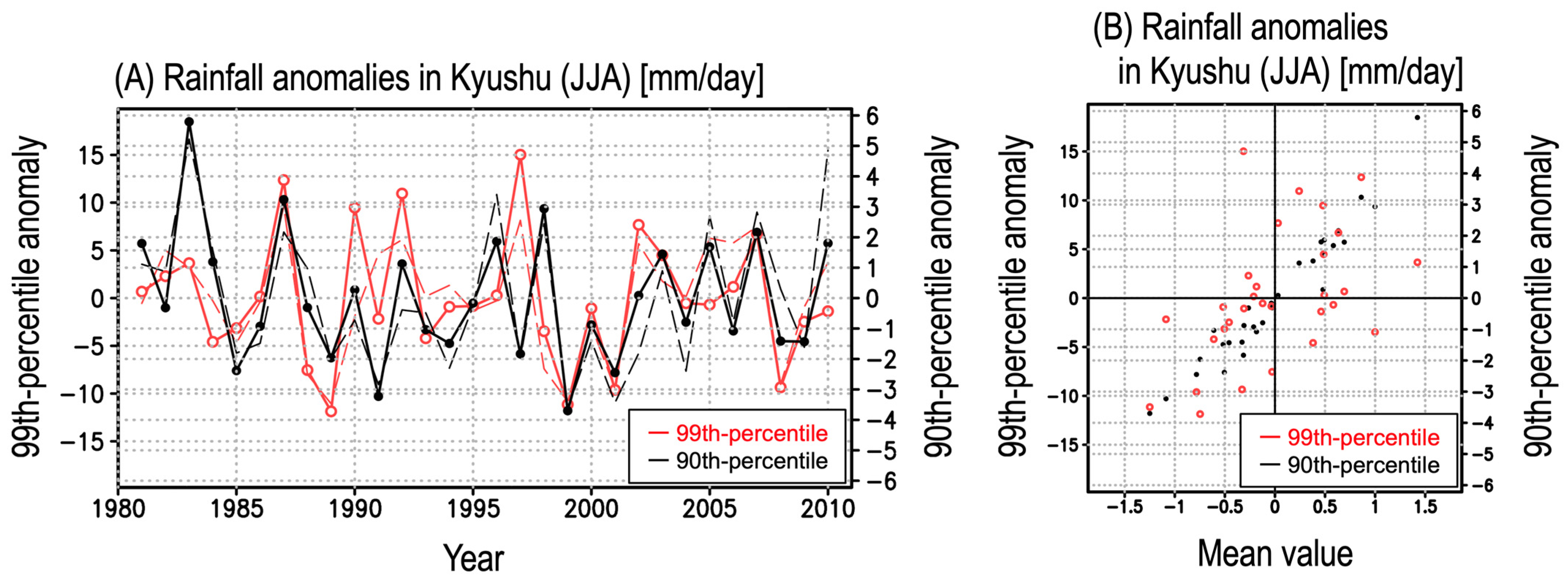
3.1. Interannual Fluctuations in Heavy Daily Rainfall Potential
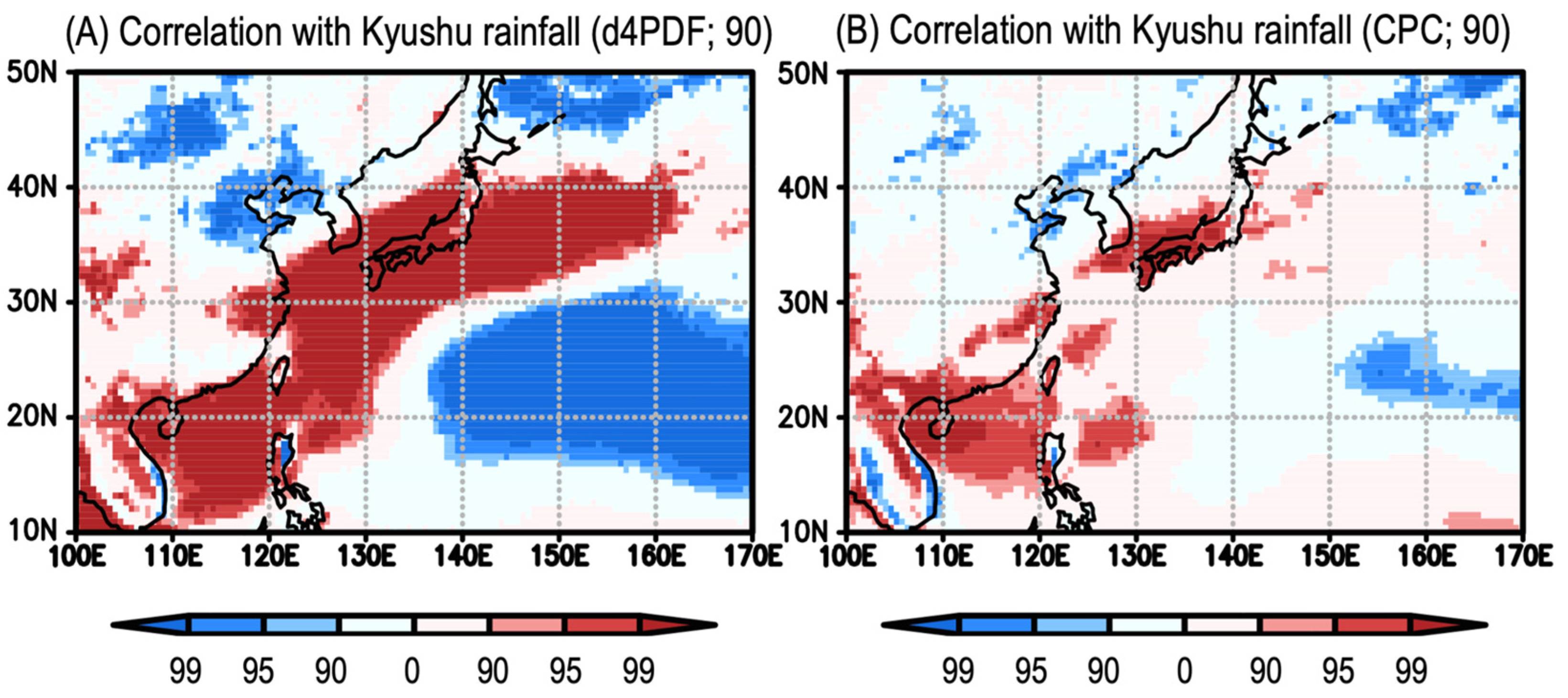
3.2. Low-Frequency Modulation in Influential SST Patterns
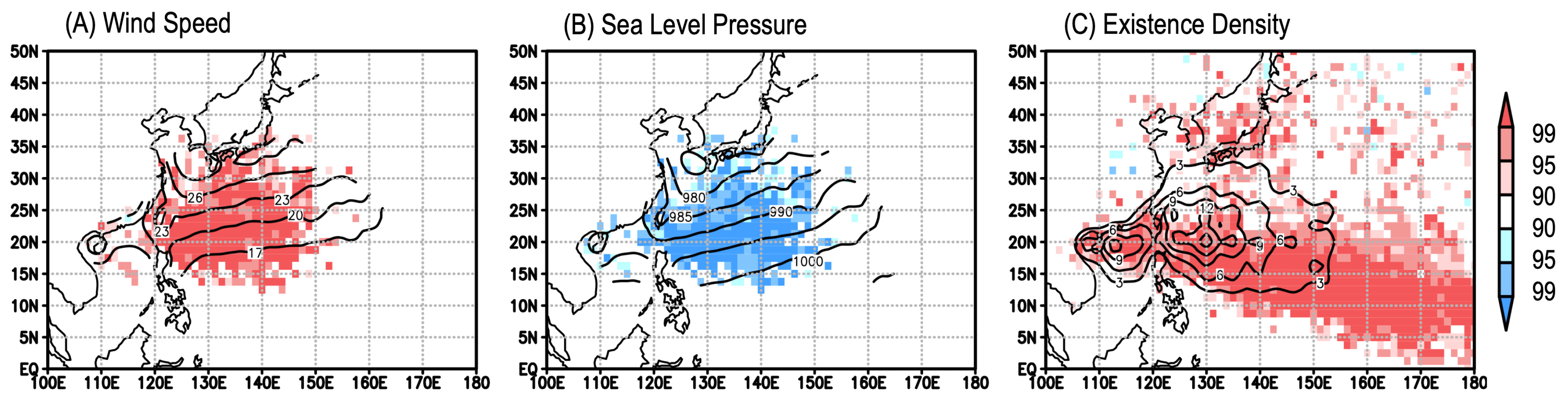
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meehl, G.A.; Hu, A.; Tebaldi, C. Decadal prediction in the Pacific region. J. Clim. 2010, 23, 2959–2973. [Google Scholar] [CrossRef]
- Meehl, G.A.; Goddard, L.; Boer, G.; Burgman, R.; Branstator, G.; Cassou, C.; Corti, S.; Danabasoglu, G.; Doblas-Reyes, F.; Hawkins, E.; et al. Decadal climate prediction: An update from the trenches. Bull. Am. Meteorol. Soc. 2013, 95, 243–267. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Andreu-Burillo, I.; Chikamoto, Y.; Garcia-Serrano, J.; Guemas, V.; Kimoto, M.; Mochizuki, T.; Rodrigues, L.R.L.; van Oldenborgh, G.J. Initialized near-term regional climate change prediction. Nat. Commun. 2013, 4, 1715. [Google Scholar] [CrossRef]
- Choi, J.; Son, S.-W.; Ham, Y.-G.; Lee, J.-Y.; Kim, H.-M. Seasonal-to-interannual prediction skills of near-surface air temperature in the CMIP5 decadal hindcast experiments. J. Clim. 2016, 29, 1511–1527. [Google Scholar] [CrossRef]
- Smith, D.M.; Eade, R.; Scaife, A.A.; Caron, L.P.; Danabasoglu, G.; DelSole, T.M.; Delworth, T.; Doblas-Reyes, F.J.; Dunstone, N.J.; Hermanson, L.; et al. Robust skill of decadal climate predictions. Npj Clim. Atmos. Sci. 2019, 2, 13. [Google Scholar] [CrossRef]
- Smith, D.M.; Scaife, A.A.; Eade, R.; Athanasiadis, P.; Bellucci, A.; Bethke, I.; Bilbao, R.; Borchert, L.F.; Caron, L.P.; Counillon, F.; et al. North Atlantic climate far more predictable than models imply. Nature 2020, 583, 796–800. [Google Scholar] [CrossRef]
- Kataoka, T.; Tatebe, H.; Koyama, H.; Mochizuki, T.; Ogochi, K.; Naoe, H.; Imada, Y.; Shiogama, H.; Kimoto, M.; Watanabe, M. Seasonal to decadal predictions with MIROC6: Description and basic evaluation. J. Adv. Model Earth Syst. 2020, 12, e2019MS002035. [Google Scholar] [CrossRef]
- Smith, D.M.; Cusack, S.; Colman, A.W.; Folland, C.K.; Harris, G.R.; Murphy, J.M. Improved surface temperature prediction for the coming decade from a global climate model. Science 2007, 317, 796–799. [Google Scholar] [CrossRef]
- Keenlyside, N.S.; Latif, M.; Jungclaus, J.; Kornblueh, L.; Roeckner, E. Advancing decadal-scale climate prediction in the North Atlantic sector. Nature 2008, 453, 84–88. [Google Scholar] [CrossRef]
- Yeager, S.G.; Robson, J.I. Recent progress in understanding and predicting Atlantic decadal climate variability. Curr. Clim. Change Rep. 2017, 3, 112–127. [Google Scholar] [CrossRef] [PubMed]
- Pohlmann, H.; Jungclaus, J.H.; Köhl, A.; Stammer, D.; Marotzke, J. Initializing decadal climate predictions with the GECCO oceanic synthesis: Effect on the North Atlantic. J. Clim. 2009, 22, 3926–3938. [Google Scholar] [CrossRef]
- Mochizuki, T.; Ishii, M.; Kimoto, M.; Chikamoto, Y.; Watanabe, M.; Nozawa, T.; Sakamoto, T.T.; Shiogama, H.; Awaji, T.; Sugiura, N.; et al. Pacific decadal oscillation hindcasts relevant to near-term climate prediction. Proc. Natl. Acad. Sci. USA 2010, 107, 1833–1837. [Google Scholar] [CrossRef] [PubMed]
- Takaya, Y.; Kosaka, Y.; Watanabe, M.; Maeda, S. Skillful predictions of the Asian summer monsoon one year ahead. Nat. Commun. 2021, 12, 2094. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.-Q.; Xie, S.-P.; Zhang, R. Historic Yangtze flooding of 2020 tied to extreme Indian Ocean conditions. Proc. Nat. Acad. Sci. USA 2021, 118, e2022255118. [Google Scholar] [CrossRef] [PubMed]
- Mizuta, R.; Murata, A.; Ishii, M.; Shiogama, H.; Hibino, K.; Mori, N.; Arakawa, O.; Imada, Y.; Yoshida, K.; Aoyagi, T.; et al. Over 5000 years of ensemble future climate simulations by 60 km global and 20 km regional atmospheric models. Bull. Am. Meteorol. Soc. 2017, 98, 1383–1398. [Google Scholar] [CrossRef]
- Fujita, M.; Mizuta, R.; Ishii, M.; Endo, H.; Sato, T.; Okada, Y.; Kawazoe, S.; Sugimoto, S.; Ishihara, K.; Watanabe, S. Precipitation changes in a climate with 2-K surface warming from large ensemble simulations using 60-km global and 20-km regional atmospheric models. Geophys. Res. Lett. 2020, 46, 435–442. [Google Scholar] [CrossRef]
- Hatsuzuka, D.; Sato, T.; Yoshida, K.; Ishii, M.; Mizuta, R. Regional projection of tropical-cyclone-induced extreme precipitation around Japan based on large ensemble simulations. Sci. Online Lett. Atmos. 2020, 16, 23–29. [Google Scholar] [CrossRef]
- Takabatake, D.; Inatsu, M. Summertime precipitation in Hokkaido and Kyushu, Japan in response to global warming. Clim. Dyn. 2022, 58, 1671–1682. [Google Scholar] [CrossRef]
- Kawase, H.; Murata, A.; Mizuta, R.; Sasaki, H.; Nosaka, M.; Ishii, M.; Takayabu, I. Enhancement of heavy daily snowfall in central Japan due to global warming as projected by large ensemble of regional climate simulations. Clim. Change 2016, 139, 265–278. [Google Scholar] [CrossRef]
- Hatsuzuka, D.; Sato, T. Future changes in monthly extreme precipitation in Japan using large-ensemble regional climate simulations. J. Hydrometeorol. 2019, 20, 563–574. [Google Scholar] [CrossRef]
- Mochizuki, T. Multi-year potential predictability of the wintertime heavy precipitation potentials in East Asia. Geophys. Res. Lett. 2024, 51, e2024GL108312. [Google Scholar] [CrossRef]
- Chikamoto, Y.; Timmermann, A.; Luo, J.-J.; Mochizuki, T.; Kimoto, M.; Watanabe, M.; Ishii, M.; Xie, S.-P.; Jin, F.-F. Skillful multi-year predictions of tropical trans-basin climate variability. Nat. Commun. 2015, 6, 6869. [Google Scholar] [CrossRef] [PubMed]
- McGregor, S.; Timmermann, A.; Stuecker, M.F.; England, H.; Merrifield, M.; Jin, F.F.; Chikamoto, Y. Recent walker circulation strengthening and Pacific cooling amplified by Atlantic warming. Nat. Clim. Change 2014, 4, 888–892. [Google Scholar] [CrossRef]
- Kawase, H.; Imada, Y.; Sasaki, H.; Nakaegawa, T.; Murata, A.; Nosaka, M.; Takayabu, I. Contribution of historical global warming to local-scale heavy precipitation in western Japan estimated by large ensemble high-resolution simulations. J. Geophys. Res. 2019, 124, 6093–6103. [Google Scholar] [CrossRef]
- Imada, Y.; Kawase, H. Potential seasonal predictability of the risk of local rainfall extremes estimated using high-resolution large ensemble simulations. Geophys. Res. Lett. 2021, 48, e2021GL096236. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. 2007, 112, C11007. [Google Scholar] [CrossRef]
- Kug, J.-S.; Jin, F.-F.; An, S.-I. Two types of El Niño events: Cold tongue El Niño and warm pool El Niño. J. Clim. 2009, 22, 1499–1515. [Google Scholar] [CrossRef]
- Song, J.; Klotzbach, P.J.; Duan, Y. Differences in western north Pacific tropical cyclone activity among three El Niño phases. J. Clim. 2020, 33, 7983–8002. [Google Scholar] [CrossRef]
- Xie, S.-P.; Hu, K.; Hafner, J.; Tokinaga, H.; Du, Y.; Huang, G.; Sampe, T. Indian Ocean capacitor effect on Indo-western Pacific climate during the summer following El Niño. J. Clim. 2009, 22, 730–747. [Google Scholar] [CrossRef]
- Xie, S.-P.; Kosaka, Y.; Du, Y.; Hu, K.; Chowdary, J.S.; Huang, G. Indo-western Pacific ocean capacitor and coherent climate anomalies in post-ENSO summer: A review. Adv. Atmos. Sci. 2016, 33, 411–432. [Google Scholar] [CrossRef]
- Panagoulia, D.; Bárdossy, A.; Lourmas, G. Diagnostic statistics of daily rainfall variability in an evolving climate. Adv. Geosci. 2006, 7, 349–354. [Google Scholar] [CrossRef]
- Fujiwara, K.; Kawamura, R. Appearance of a quasi-quadrennial variation in Baiu precipitation in southern Kyushu, Japan, after the beginning of this century. Sci. Online Lett. Atmos. 2022, 18, 181–186. [Google Scholar] [CrossRef]
- Yu, T.; Feng, J.; Chen, W.; Hu, K.; Chen, S. Enhanced tropospheric biennial oscillation of the East Asian summer monsoon since the late-1970s. J. Clim. 2022, 35, 1613–1628. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, C. On the relationship between ENSO and tropical cyclones in the western North Pacific during the boreal summer. Clim. Dyn. 2019, 52, 275–288. [Google Scholar] [CrossRef]
- Hirahara, S.; Ishii, M.; Fukuda, Y. Centennial-scale sea surface temperature analysis and its uncertainty. J. Clim. 2014, 27, 57–75. [Google Scholar] [CrossRef]
- Ishii, M.; Fukuda, Y.; Hirahara, S.; Yasui, S.; Suzuki, T.; Sato, K. Accuracy of global upper ocean heat content estimation expected from present observational data sets. Sci. Online Lett. Atmos. 2017, 13, 163–167. [Google Scholar] [CrossRef]
- Xie, P.; Yatagai, A.; Chen, M.; Hayasaka, T.; Fukushima, Y.; Liu, C.; Yang, S. A gauge-based analysis of daily precipitation over East Asia. J. Hydrometeorol. 2007, 8, 607–626. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. 2008, 113, D04110. [Google Scholar] [CrossRef]
- Yoshida, K.; Sugi, M.; Mizuta, R.; Murakami, H.; Ishii, M. Future changes in tropical cyclone activity in high-resolution large-ensemble simulations. Geophys. Res. Lett. 2017, 44, 9910–9917. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Hurrell, J.W. Decadal atmosphere-ocean variations in the Pacific. Clim. Dyn. 1994, 9, 303–319. [Google Scholar] [CrossRef]
- Chiang, J.C.H.; Vimont, D.J. Analogous Pacific and Atlantic meridional modes of tropical atmosphere–ocean variability. J. Clim. 2004, 17, 4143–4158. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, L.; Zhou, W. Interannual changes of tropical cyclone intensity in the western North Pacific. J. Meteorol. Soc. Jpn. 2011, 89, 243–253. [Google Scholar] [CrossRef]
- Zhang, W.; Graf, H.-F.; Leung, Y.; Herzog, M. Different El Niño types and tropical cyclone landfall in East Asia. J. Clim. 2012, 25, 6510–6523. [Google Scholar] [CrossRef]
- Wu, M.C.; Chang, W.L.; Leung, W.M. Impacts of El Niño-Southern Oscillation events on tropical cyclone landfalling activity in the western North Pacific. J. Clim. 2004, 17, 1419–1428. [Google Scholar] [CrossRef]
- Camargo, S.J.; Robertson, A.W.; Gaffney, S.J.; Smyth, P.; Ghil, M. Cluster analysis of typhoon tracks. Part II: Large-scale circulation and ENSO. J. Clim. 2007, 20, 3654–3676. [Google Scholar] [CrossRef]
- Yoshida, N.; Kawamura, R.; Kawano, T.; Mochizuki, T.; Iizuka, S. Remote dynamic and thermodynamic effects of typhoons on Meiyu–Baiu precipitation in Japan assessed with bogus typhoon experiments. Weather Clim. Extrem. 2023, 41, 100578. [Google Scholar] [CrossRef]
- Feng, J.; Lian, T.; Ying, J.; Li, J.; Li, G. Do CMIP5 models show El Nino diversity? J. Clim. 2019, 33, 1619–1641. [Google Scholar] [CrossRef]
- Mochizuki, T.; Watanabe, M. Observed and hindcasted subdecadal variability of the tropical Pacific climate. ICES J. Mar. Sci. 2019, 76, 1271–1279. [Google Scholar] [CrossRef]
- Mochizuki, T.; Watanabe, M. Atlantic impacts on subdecadal warming over the tropical Pacific in the 2000s. Front. Clim. 2022, 4, 1040352. [Google Scholar] [CrossRef]
- Xie, M.; Wang, C.; Chen, S. The role of the maritime continent SST anomalies in maintaining the Pacific–Japan pattern on decadal time scales. J. Clim. 2022, 35, 1079–1095. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.-P. The tropical Pacific as a key pacemaker of the variable rates of global warming. Nat. Geosci. 2016, 9, 669–673. [Google Scholar] [CrossRef]
- Meehl, G.A.; Hu, A.; Santer, B.D.; Xie, S.-P. Contribution of the Interdecadal Pacific Oscillation to twentieth-century global surface temperature trends. Nat. Clim. Change 2016, 6, 1005–1008. [Google Scholar] [CrossRef]
- Xie, S.-P.; Philander, S.G.H. A coupled ocean-atmosphere model of relevance to the ITCZ in the eastern Pacific. Tellus 1994, 46A, 340–350. [Google Scholar] [CrossRef]
- Kawamura, R.; Matsuura, T.; Iizuka, S. Role of equatorially asymmetric sea surface temperature anomalies in the Indian Ocean in the Asian summer monsoon and El Nino-Southern Oscillation coupling. J. Geophys. Res. 2001, 106, 4681–4693. [Google Scholar] [CrossRef]
- Chen, S.; Chen, W.; Xie, S.-P.; Yu, B.; Wu, R.; Wang, Z.; Lan, X.; Graf, H.-F. Strengthened impact of boreal winter North Pacific Oscillation on ENSO development in warming climate. Npj Clim. Atmos. Sci. 2024, 7, 69. [Google Scholar] [CrossRef]
- Eade, R.; Smith, D.; Scaife, A.; Wallace, E.; Dunstone, N.; Hermanson, L.; Robinson, N. Do seasonal-to-decadal climate predictions underestimate the predictability of the real world? Geophys. Res. Lett. 2014, 41, 5620–5628. [Google Scholar] [CrossRef]
- Kato, T. Statistical study of band-shaped rainfall systems, the Koshikijima and Nagasaki Lines, observed around Kyushu Island, Japan. J. Meteorol. Soc. Jpn. 2005, 83, 943–957. [Google Scholar] [CrossRef]
- Kato, T. Quasi-stationary band-shaped precipitation systems, named “Senjo-Kousuitai”, causing localized heavy rainfall in Japan. J. Meteorol. Soc. Jpn. 2020, 98, 485–509. [Google Scholar] [CrossRef]
- Kato, T. Interannual and diurnal variations in the frequency of heavy rainfall events in the Kyushu area, western Japan during the rainy season. Sci. Online Lett. Atmos. 2024, 20, 191–197. [Google Scholar] [CrossRef]
- Luo, J.-J.; Sasaki, W.; Masumoto, Y. Indian Ocean warming modulates Pacific climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 18701. [Google Scholar] [CrossRef]
- Mochizuki, T.; Kimoto, M.; Watanabe, M.; Chikamoto, Y.; Ishii, M. Interbasin effects of the Indian Ocean on Pacific decadal climate change. Geophys. Res. Lett. 2016, 43, 7168–7175. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Sun, X.G.; Yang, X.Q. Understanding the inter-decadal variability of East Asian summer monsoon precipitation: Joint influence of three oceanic signal. J. Clim. 2018, 31, 5485–5506. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C.L. Inactive period of western North Pacific tropical cyclone activity in 1998-2011. J. Clim. 2013, 26, 2614–2630. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mochizuki, T. Interannual Fluctuations and Their Low-Frequency Modulation of Summertime Heavy Daily Rainfall Potential in Western Japan. Atmosphere 2024, 15, 814. https://doi.org/10.3390/atmos15070814
Mochizuki T. Interannual Fluctuations and Their Low-Frequency Modulation of Summertime Heavy Daily Rainfall Potential in Western Japan. Atmosphere. 2024; 15(7):814. https://doi.org/10.3390/atmos15070814
Chicago/Turabian StyleMochizuki, Takashi. 2024. "Interannual Fluctuations and Their Low-Frequency Modulation of Summertime Heavy Daily Rainfall Potential in Western Japan" Atmosphere 15, no. 7: 814. https://doi.org/10.3390/atmos15070814
APA StyleMochizuki, T. (2024). Interannual Fluctuations and Their Low-Frequency Modulation of Summertime Heavy Daily Rainfall Potential in Western Japan. Atmosphere, 15(7), 814. https://doi.org/10.3390/atmos15070814







