Machine Learning to Characterize Biogenic Isoprene Emissions and Atmospheric Formaldehyde with Their Environmental Drivers in the Marine Boundary Layer
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description and Preprocessing
2.2. Isoprene Production Model
2.3. Machine Learning Methods
3. Results and Discussion
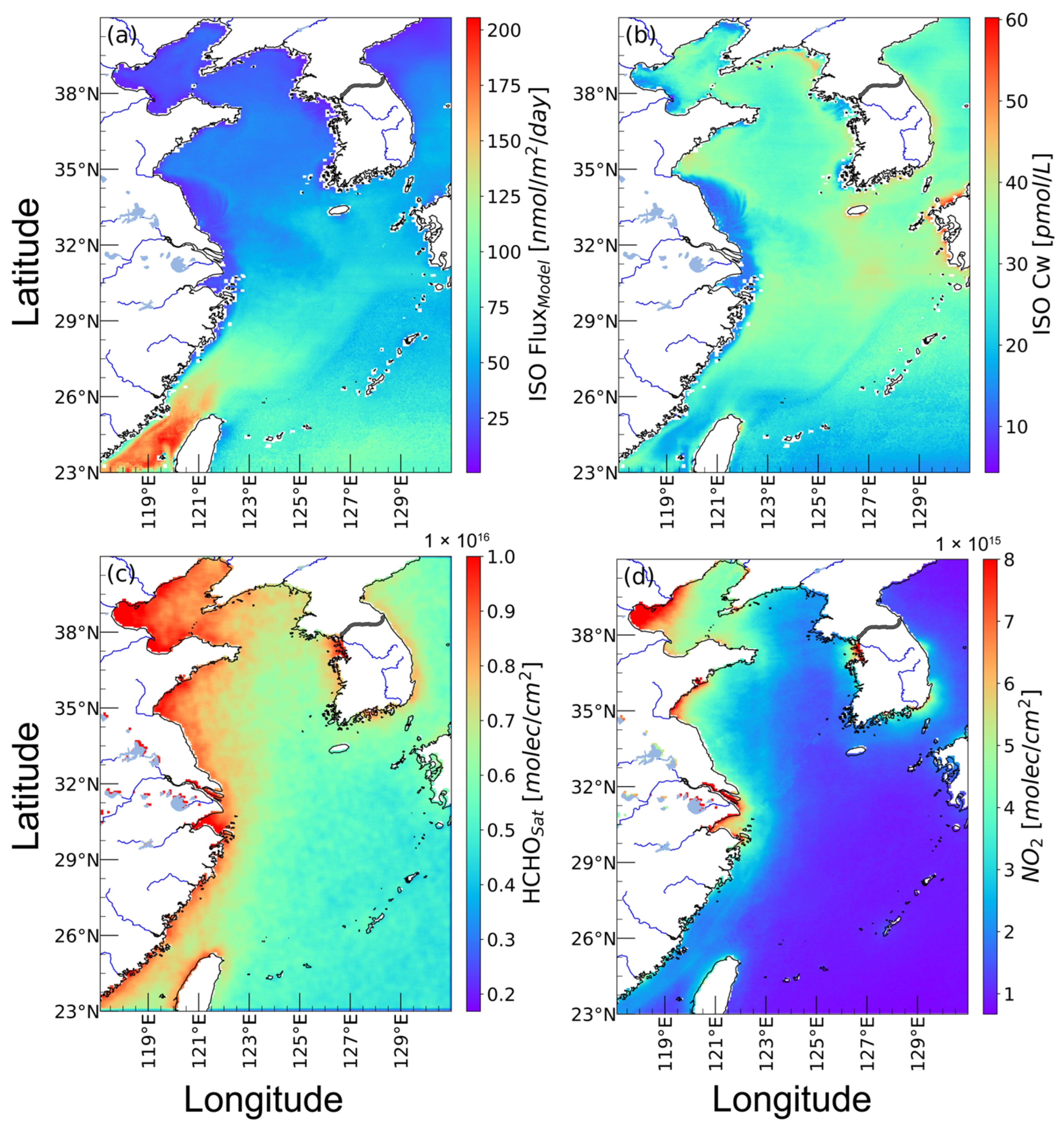
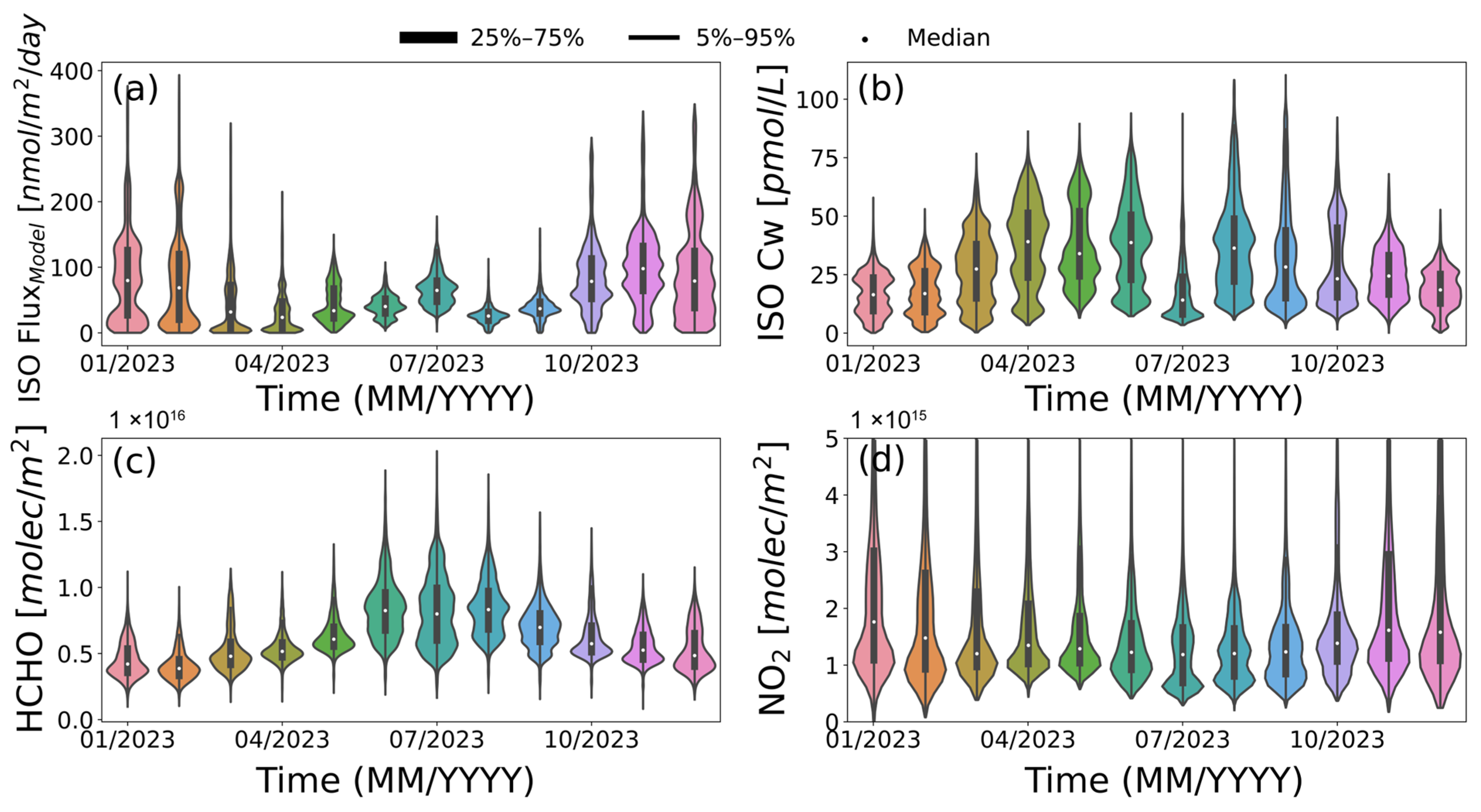
3.1. Spatiotemporal Distribution of Marine Biogenic Emissions and Trace Gas Components
3.2. Construction of ML Model and Analysis of Influencing Factor
3.2.1. Construction of ML Model for Isoprene Flux and HCHO
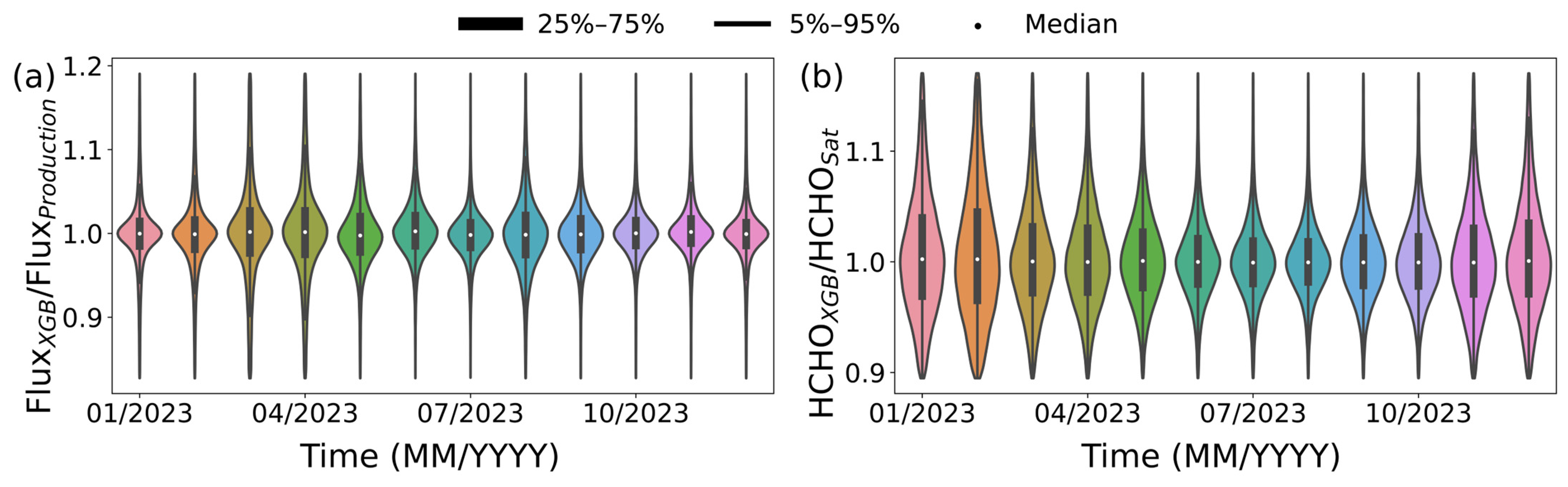
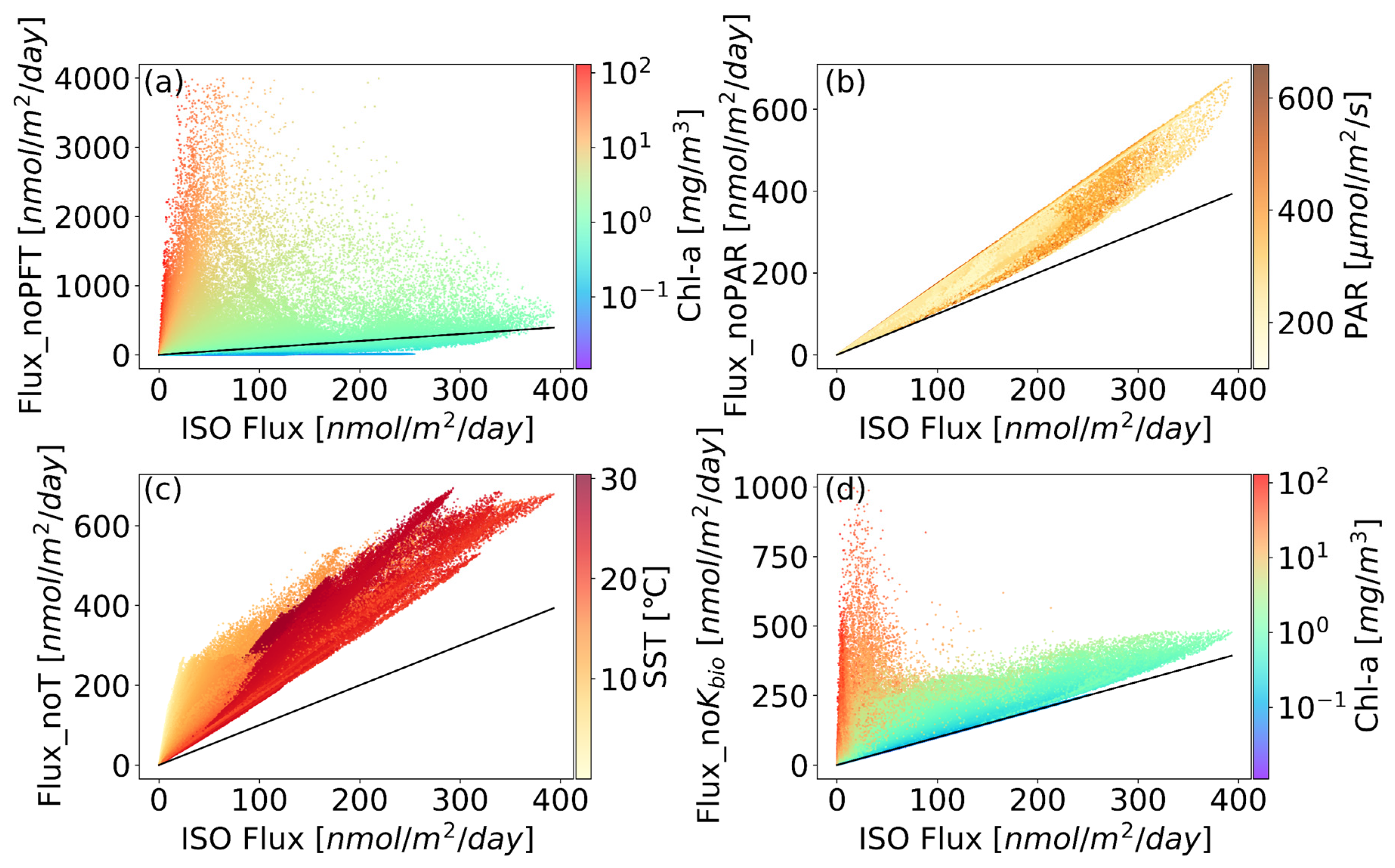
3.2.2. Assessment for Influencing Factors of Flux Based on Isoprene Production Model
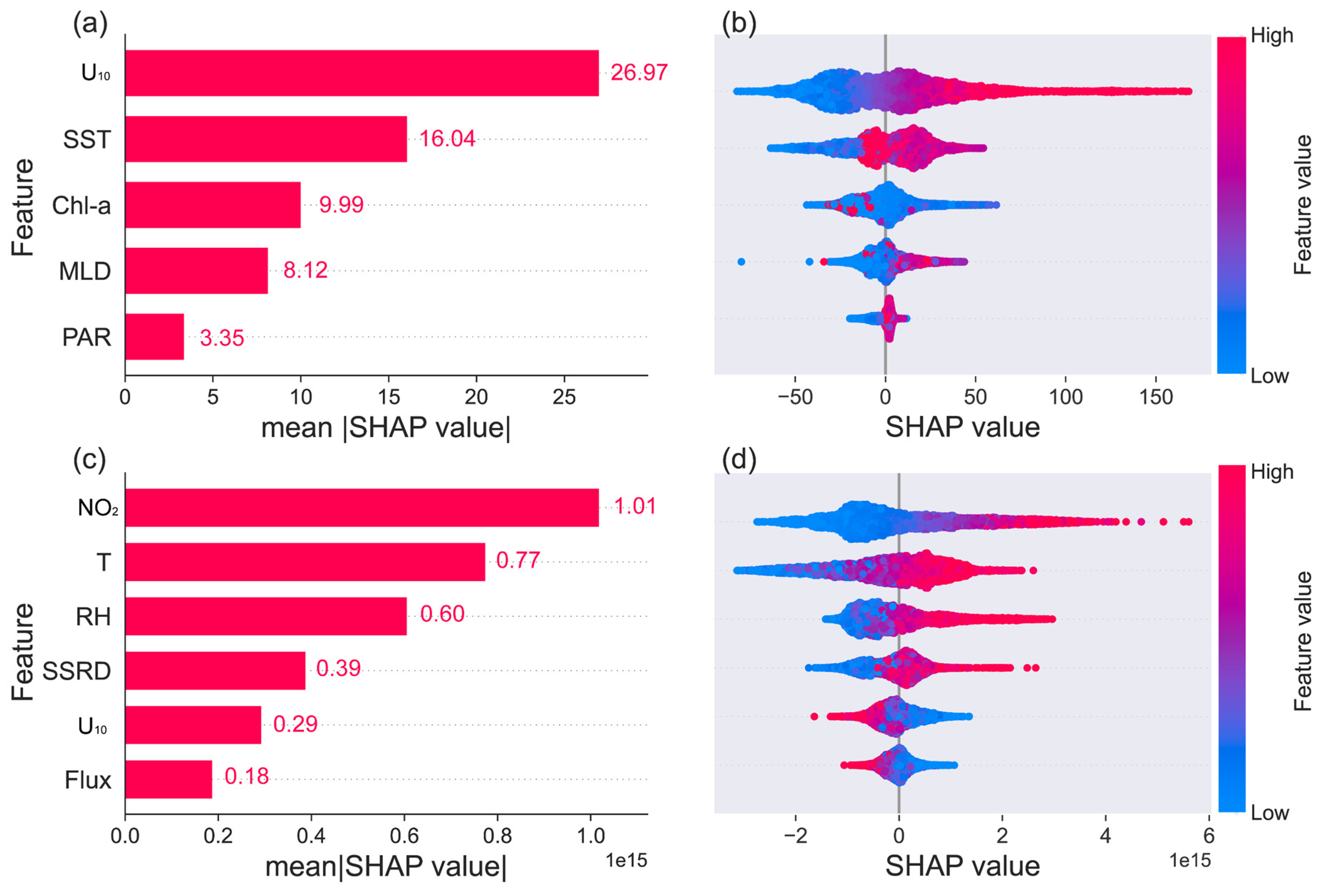
3.2.3. Assessment for Influencing Factors of Isoprene Flux and HCHO Based on XGBoost
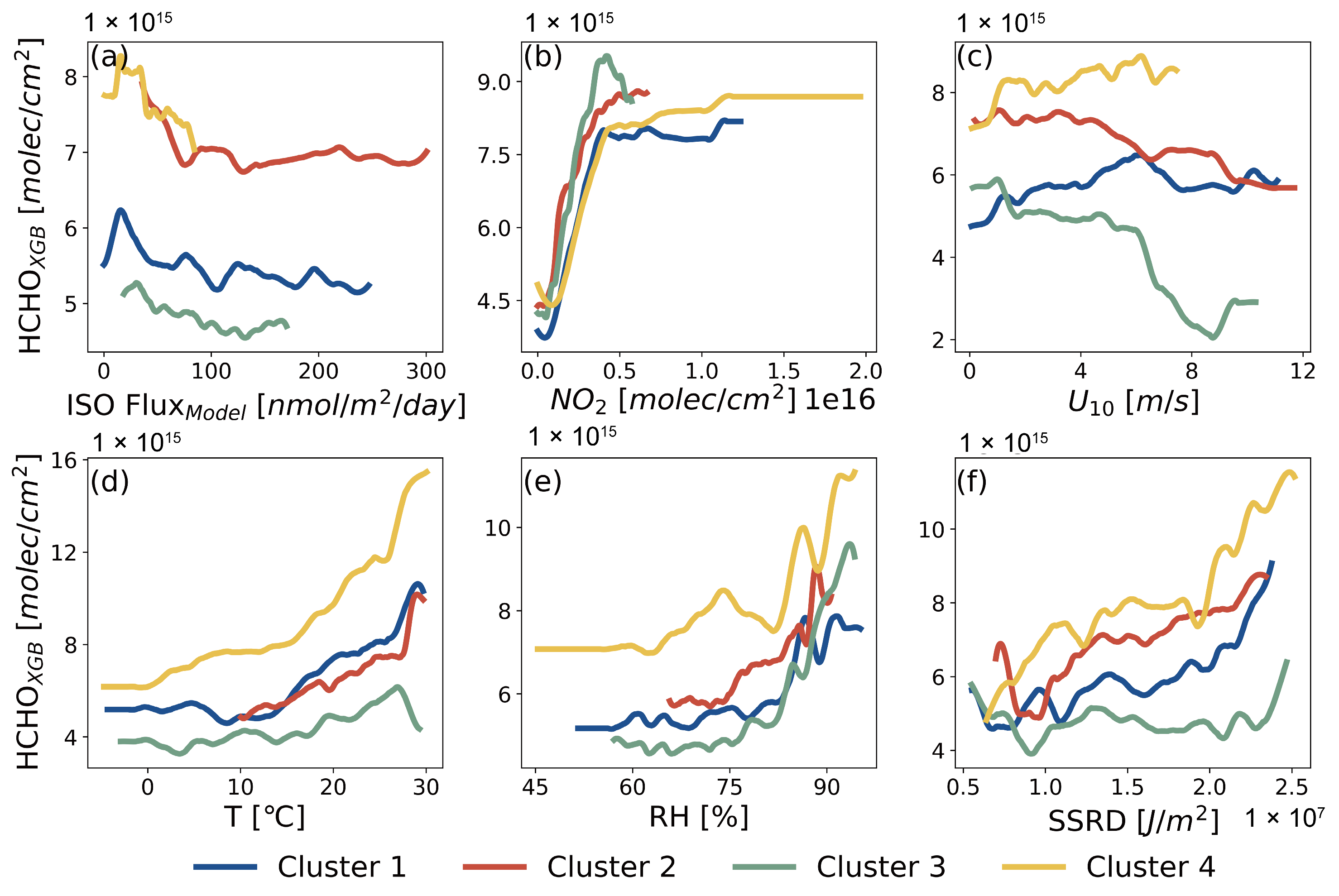
3.3. MBL HCHO under Different Air Masses Based on Clustering Methods
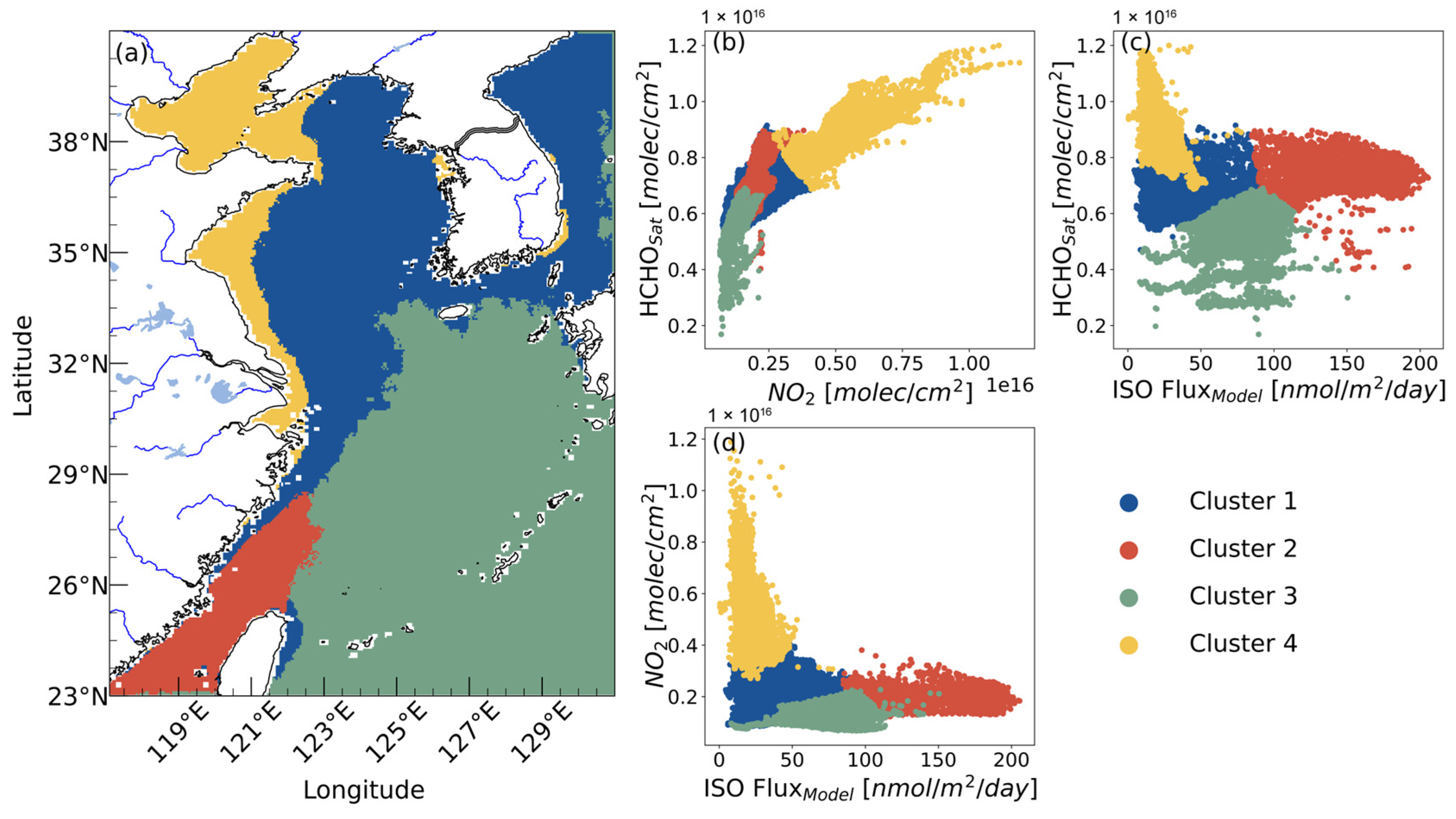
3.3.1. Comprehensive Clustering of Air Masses and Characterization of Air Mass Parameters
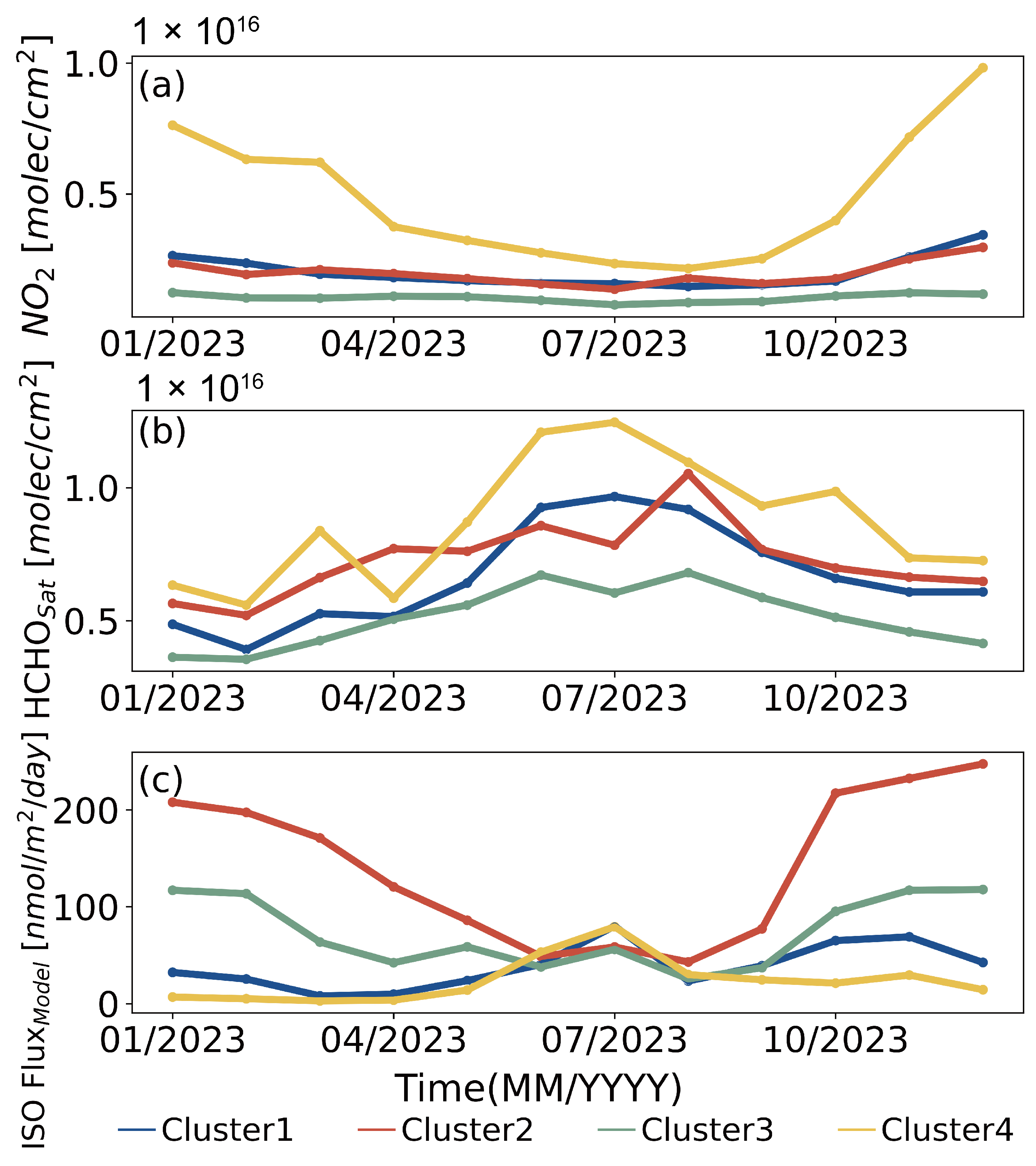
3.3.2. Impact of Isoprene on the MBL HCHO in Different Air Masses
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Huang, X.-F.; Han, Y.; Zhu, B.; He, L.-Y. Sources and Potential Photochemical Roles of Formaldehyde in an Urban Atmosphere in South China. J. Geophys. Res. Atmos. 2017, 122, 11934–11947. [Google Scholar] [CrossRef]
- Su, W.; Liu, C.; Hu, Q.; Zhao, S.; Sun, Y.; Wang, W.; Zhu, Y.; Liu, J.; Kim, J. Primary and Secondary Sources of Ambient Formaldehyde in the Yangtze River Delta Based on Ozone Mapping and Profiler Suite (OMPS) Observations. Atmos. Chem. Phys. 2019, 19, 6717–6736. [Google Scholar] [CrossRef]
- Li, D.; Wang, S.; Xue, R.; Zhu, J.; Zhang, S.; Sun, Z.; Zhou, B. OMI-Observed HCHO in Shanghai, China, during 2010–2019 and Ozone Sensitivity Inferred by an Improved HCHO/NO2 Ratio. Atmos. Chem. Phys. 2021, 21, 15447–15460. [Google Scholar] [CrossRef]
- Xue, R.; Wang, S.; Zhang, S.; Zhan, J.; Zhu, J.; Gu, C.; Zhou, B. Ozone Pollution of Megacity Shanghai during City-Wide Lockdown Assessed Using TROPOMI Observations of NO2 and HCHO. Remote Sens. 2022, 14, 6344. [Google Scholar] [CrossRef]
- Folberth, G.A.; Hauglustaine, D.A.; Lathière, J.; Brocheton, F. Interactive Chemistry in the Laboratoire de Météorologie Dynamique General Circulation Model: Model Description and Impact Analysis of Biogenic Hydrocarbons on Tropospheric Chemistry. Atmos. Chem. Phys. 2006, 6, 2273–2319. [Google Scholar] [CrossRef]
- Dawson, R.A.; Crombie, A.T.; Pichon, P.; Steinke, M.; McGenity, T.J.; Murrell, J.C. The Microbiology of Isoprene Cycling in Aquatic Ecosystems. Aquat. Microb. Ecol. 2021, 87, 79–98. [Google Scholar] [CrossRef]
- Gopikrishnan, G.S.; Kuttippurath, J. A Decade of Satellite Observations Reveal Significant Increase in Atmospheric Formaldehyde from Shipping in Indian Ocean. Atmos. Environ. 2021, 246, 118095. [Google Scholar] [CrossRef]
- Miller, M.A.; Mages, Z.; Zheng, Q.; Trabachino, L.; Russell, L.M.; Shilling, J.E.; Zawadowicz, M.A. Observed Relationships Between Cloud Droplet Effective Radius and Biogenic Gas Concentrations in Summertime Marine Stratocumulus Over the Eastern North Atlantic. Earth Space Sci. 2022, 9, e2021EA001929. [Google Scholar] [CrossRef]
- Chen, Z.; Schofield, R.; Keywood, M.; Cleland, S.; Williams, A.G.; Wilson, S.; Griffiths, A.; Xiang, Y. Observations of the Boundary Layer in the Cape Grim Coastal Region: Interaction with Wind and the Influences of Continental Sources. Remote Sens. 2023, 15, 461. [Google Scholar] [CrossRef]
- Li, Q.; Tham, Y.J.; Fernandez, R.P.; He, X.-C.; Cuevas, C.A.; Saiz-Lopez, A. Role of Iodine Recycling on Sea-Salt Aerosols in the Global Marine Boundary Layer. Geophys. Res. Lett. 2022, 49, e2021GL097567. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, Q.; Wang, S.; Zhang, M.; Zhang, Y.; Qiao, F. Enhanced Daytime Atmospheric Mercury in the Marine Boundary Layer in the South Oceans. Sci. Total Environ. 2023, 892, 164691. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.C.; Nicely, J.M.; Wolfe, G.M.; Hanisco, T.F.; Salawitch, R.J.; Canty, T.P.; Dickerson, R.R.; Apel, E.C.; Baidar, S.; Bannan, T.J.; et al. Formaldehyde in the Tropical Western Pacific: Chemical Sources and Sinks, Convective Transport, and Representation in CAM-Chem and the CCMI Models. J. Geophys. Res. Atmos. 2017, 122, 11201–11226. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Paulot, F.; Jacob, D.J.; Cohen, R.C.; Crounse, J.D.; Wennberg, P.O.; Keller, C.A.; Hudman, R.C.; Barkley, M.P.; Horowitz, L.W. Ozone and Organic Nitrates over the Eastern United States: Sensitivity to Isoprene Chemistry. J. Geophys. Res. Atmos. 2013, 118, 11256–11268. [Google Scholar] [CrossRef]
- Wang, S.; Apel, E.C.; Schwantes, R.H.; Bates, K.H.; Jacob, D.J.; Fischer, E.V.; Hornbrook, R.S.; Hills, A.J.; Emmons, L.K.; Pan, L.L.; et al. Global Atmospheric Budget of Acetone: Air-Sea Exchange and the Contribution to Hydroxyl Radicals. J. Geophys. Res. Atmos. 2020, 125, e2020JD032553. [Google Scholar] [CrossRef]
- Wolfe, G.M.; Kaiser, J.; Hanisco, T.F.; Keutsch, F.N.; de Gouw, J.A.; Gilman, J.B.; Graus, M.; Hatch, C.D.; Holloway, J.; Horowitz, L.W.; et al. Formaldehyde Production from Isoprene Oxidation across NOx Regimes. Atmos. Chem. Phys. 2016, 16, 2597–2610. [Google Scholar] [CrossRef] [PubMed]
- Chan Miller, C.; Jacob, D.J.; Marais, E.A.; Yu, K.; Travis, K.R.; Kim, P.S.; Fisher, J.A.; Zhu, L.; Wolfe, G.M.; Hanisco, T.F.; et al. Glyoxal Yield from Isoprene Oxidation and Relation to Formaldehyde: Chemical Mechanism, Constraints from SENEX Aircraft Observations, and Interpretation of OMI Satellite Data. Atmos. Chem. Phys. 2017, 17, 8725–8738. [Google Scholar] [CrossRef]
- Zhong, J.; Kumar, M.; Anglada, J.M.; Martins-Costa, M.T.C.; Ruiz-Lopez, M.F.; Zeng, X.C.; Francisco, J.S. Atmospheric Spectroscopy and Photochemistry at Environmental Water Interfaces. Annu. Rev. Phys. Chem. 2019, 70, 45–69. [Google Scholar] [CrossRef]
- Sprengnether, M.; Demerjian, K.L.; Donahue, N.M.; Anderson, J.G. Product Analysis of the OH Oxidation of Isoprene and 1,3-Butadiene in the Presence of NO. J. Geophys. Res. Atmos. 2002, 107, ACH 8-1–ACH 8-13. [Google Scholar] [CrossRef]
- Booge, D.; Marandino, C.A.; Schlundt, C.; Palmer, P.I.; Schlundt, M.; Atlas, E.L.; Bracher, A.; Saltzman, E.S.; Wallace, D.W.R. Can Simple Models Predict Large-Scale Surface Ocean Isoprene Concentrations? Atmos. Chem. Phys. 2016, 16, 11807–11821. [Google Scholar] [CrossRef]
- Booge, D.; Schlundt, C.; Bracher, A.; Endres, S.; Zäncker, B.; Marandino, C.A. Marine Isoprene Production and Consumption in the Mixed Layer of the Surface Ocean—A Field Study over Two Oceanic Regions. Biogeosciences 2018, 15, 649–667. [Google Scholar] [CrossRef]
- Li, X.-J.; Liang, H.-R.; Zhuang, G.-C.; Wu, Y.-C.; Li, S.-T.; Zhang, H.-H.; Montgomery, A.; Yang, G.-P. Annual Variations of Isoprene and Other Non-Methane Hydrocarbons in the Jiaozhou Bay on the East Coast of North China. J. Geophys. Res. Biogeosci. 2022, 127, e2021JG006531. [Google Scholar] [CrossRef]
- Qiao, W.-Z.; Wu, Y.-C.; Wang, P.; Wang, J.; Zhou, L.-M.; Li, S.-T.; Zhang, H.-H. Distribution Characteristics and Environmental Effects of Non-Methane Hydrocarbons in the East China Sea. Cont. Shelf Res. 2023, 261, 105023. [Google Scholar] [CrossRef]
- Li, J.-L.; Zhai, X.; Ma, Z.; Zhang, H.-H.; Yang, G.-P. Spatial Distributions and Sea-to-Air Fluxes of Non-Methane Hydrocarbons in the Atmosphere and Seawater of the Western Pacific Ocean. Sci. Total Environ. 2019, 672, 491–501. [Google Scholar] [CrossRef] [PubMed]
- Li, J.-L.; Zhang, H.-H.; Yang, G.-P. Distribution and Sea-to-Air Flux of Isoprene in the East China Sea and the South Yellow Sea during Summer. Chemosphere 2017, 178, 291–300. [Google Scholar] [CrossRef] [PubMed]
- Shaw, S.L.; Gantt, B.; Meskhidze, N. Production and Emissions of Marine Isoprene and Monoterpenes: A Review. Adv. Meteorol. 2010, 2010, 408696. [Google Scholar] [CrossRef]
- Luo, G.; Yu, F. A Numerical Evaluation of Global Oceanic Emissions of α-Pinene and Isoprene. Atmos. Chem. Phys. 2010, 10, 2007–2015. [Google Scholar] [CrossRef]
- Arnold, S.R.; Spracklen, D.V.; Williams, J.; Yassaa, N.; Sciare, J.; Bonsang, B.; Gros, V.; Peeken, I.; Lewis, A.C.; Alvain, S.; et al. Evaluation of the Global Oceanic Isoprene Source and Its Impacts on Marine Organic Carbon Aerosol. Atmos. Chem. Phys. 2009, 9, 1253–1262. [Google Scholar] [CrossRef]
- Baker, A.R.; Turner, S.M.; Broadgate, W.J.; Thompson, A.; McFiggans, G.B.; Vesperini, O.; Nightingale, P.D.; Liss, P.S.; Jickells, T.D. Distribution and Sea-Air Fluxes of Biogenic Trace Gases in the Eastern Atlantic Ocean. Glob. Biogeochem. Cycles 2000, 14, 871–886. [Google Scholar] [CrossRef]
- Broadgate, W.J.; Malin, G.; Küpper, F.C.; Thompson, A.; Liss, P.S. Isoprene and Other Non-Methane Hydrocarbons from Seaweeds: A Source of Reactive Hydrocarbons to the Atmosphere. Mar. Chem. 2004, 88, 61–73. [Google Scholar] [CrossRef]
- Broadgate, W.J.; Liss, P.S.; Penkett, S.A. Seasonal Emissions of Isoprene and Other Reactive Hydrocarbon Gases from the Ocean. Geophys. Res. Lett. 1997, 24, 2675–2678. [Google Scholar] [CrossRef]
- Conte, L.; Szopa, S.; Aumont, O.; Gros, V.; Bopp, L. Sources and Sinks of Isoprene in the Global Open Ocean: Simulated Patterns and Emissions to the Atmosphere. J. Geophys. Res. Ocean. 2020, 125, e2019JC015946. [Google Scholar] [CrossRef]
- Cui, L.; Xiao, Y.; Hu, W.; Song, L.; Wang, Y.; Zhang, C.; Fu, P.; Zhu, J. Enhanced Dataset of Global Marine Isoprene Emissions from Biogenic and Photochemical Processes for the Period 2001–2020. Earth Syst. Sci. Data 2023, 15, 5403–5425. [Google Scholar] [CrossRef]
- Palmer, P.I.; Marvin, M.R.; Siddans, R.; Kerridge, B.J.; Moore, D.P. Nocturnal Survival of Isoprene Linked to Formation of Upper Tropospheric Organic Aerosol. Science 2022, 375, 562–566. [Google Scholar] [CrossRef]
- Palmer, P.I.; Shaw, S.L. Quantifying Global Marine Isoprene Fluxes Using MODIS Chlorophyll Observations. Geophys. Res. Lett. 2005, 32, L09805. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, D. Geostationary Satellite Reveals Increasing Marine Isoprene Emissions in the Center of the Equatorial Pacific Ocean. NPJ Clim. Atmos. Sci. 2022, 5, 83. [Google Scholar] [CrossRef]
- Li, J.; An, X.; Li, Q.; Wang, C.; Yu, H.; Zhou, X.; Geng, Y. Application of XGBoost Algorithm in the Optimization of Pollutant Concentration. Atmos. Res. 2022, 276, 106238. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, Y.; Chang, H.H.; Meng, X.; Geng, G.; Lyapustin, A.; Liu, Y. Full-Coverage High-Resolution Daily PM2.5 Estimation Using MAIAC AOD in the Yangtze River Delta of China. Remote Sens. Environ. 2017, 199, 437–446. [Google Scholar] [CrossRef]
- Stern, R.; Builtjes, P.; Schaap, M.; Timmermans, R.; Vautard, R.; Hodzic, A.; Memmesheimer, M.; Feldmann, H.; Renner, E.; Wolke, R.; et al. A Model Inter-Comparison Study Focussing on Episodes with Elevated PM10 Concentrations. Atmos. Environ. 2008, 42, 4567–4588. [Google Scholar] [CrossRef]
- Yin, H.; Lu, X.; Sun, Y.; Li, K.; Gao, M.; Zheng, B.; Liu, C. Unprecedented Decline in Summertime Surface Ozone over Eastern China in 2020 Comparably Attributable to Anthropogenic Emission Reductions and Meteorology. Environ. Res. Lett. 2021, 16, 124069. [Google Scholar] [CrossRef]
- Silva, S.J.; Keller, C.A.; Hardin, J. Using an Explainable Machine Learning Approach to Characterize Earth System Model Errors: Application of SHAP Analysis to Modeling Lightning Flash Occurrence. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002881. [Google Scholar] [CrossRef]
- Qian, Q.F.; Jia, X.J.; Lin, H. Machine Learning Models for the Seasonal Forecast of Winter Surface Air Temperature in North America. Earth Space Sci. 2020, 7, e2020EA001140. [Google Scholar] [CrossRef]
- Lu, B.; Meng, X.; Dong, S.; Zhang, Z.; Liu, C.; Jiang, J.; Herrmann, H.; Li, X. High-Resolution Mapping of Regional VOCs Using the Enhanced Space-Time Extreme Gradient Boosting Machine (XGBoost) in Shanghai. Sci. Total Environ. 2023, 905, 167054. [Google Scholar] [CrossRef] [PubMed]
- Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in Water Resources Engineering: A Systematic Literature Review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Van Griensven Thé, J.; Gharabaghi, B. Spatiotemporal Air Pollution Forecasting in Houston-TX: A Case Study for Ozone Using Deep Graph Neural Networks. Atmosphere 2023, 14, 308. [Google Scholar] [CrossRef]
- Just, A.C.; Arfer, K.B.; Rush, J.; Dorman, M.; Shtein, A.; Lyapustin, A.; Kloog, I. Advancing Methodologies for Applying Machine Learning and Evaluating Spatiotemporal Models of Fine Particulate Matter (PM2.5) Using Satellite Data over Large Regions. Atmos. Environ. 2020, 239, 117649. [Google Scholar] [CrossRef] [PubMed]
- Kamińska, J.A. The Use of Random Forests in Modelling Short-Term Air Pollution Effects Based on Traffic and Meteorological Conditions: A Case Study in Wrocław. J. Environ. Manag. 2018, 217, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Chen, B.; Nie, Z.; Ren, Z.; Xu, B.; Tang, S. Estimation of Hourly Full-Coverage PM2.5 Concentrations at 1-Km Resolution in China Using a Two-Stage Random Forest Model. Atmos. Res. 2021, 248, 105146. [Google Scholar] [CrossRef]
- Wang, F.; Li, X.; Tang, X.; Sun, X.; Zhang, J.; Yang, D.; Xu, L.; Zhang, H.; Yuan, H.; Wang, Y.; et al. The Seas around China in a Warming Climate. Nat. Rev. Earth Environ. 2023, 4, 535–551. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Tang, H.; Shi, X.; Rivkin, R.B.; Legendre, L. Spatiotemporal Variations of Inorganic Nutrients along the Jiangsu Coast, China, and the Occurrence of Macroalgal Blooms (Green Tides) in the Southern Yellow Sea. Harmful Algae 2017, 63, 164–172. [Google Scholar] [CrossRef]
- Gao, S.; Wang, H.; Liu, G.; Li, H. Spatio-Temporal Variability of Chlorophyll a and Its Responses to Sea Surface Temperature, Winds and Height Anomaly in the Western South China Sea. Acta Oceanol. Sin. 2013, 32, 48–58. [Google Scholar] [CrossRef]
- Jin, X.; Zhu, Q.; Cohen, R.C. Direct Estimates of Biomass Burning NOx Emissions and Lifetimes Using Daily Observations from TROPOMI. Atmos. Chem. Phys. 2021, 21, 15569–15587. [Google Scholar] [CrossRef]
- Fujinawa, T.; Noguchi, K.; Kuze, A.; Richter, A.; Burrows, J.P.; Meier, A.C.; Sato, T.O.; Kuroda, T.; Yoshida, N.; Kasai, Y. Concept of Small Satellite UV/Visible Imaging Spectrometer Optimized for Tropospheric NO2 Measurements in Air Quality Monitoring. Acta Astronaut. 2019, 160, 421–432. [Google Scholar] [CrossRef]
- Xue, R.; Wang, S.; Li, D.; Zou, Z.; Chan, K.L.; Valks, P.; Saiz-Lopez, A.; Zhou, B. Spatio-Temporal Variations in NO2 and SO2 over Shanghai and Chongming Eco-Island Measured by Ozone Monitoring Instrument (OMI) during 2008–2017. J. Clean. Prod. 2020, 258, 120563. [Google Scholar] [CrossRef]
- Xue, R.; Wang, S.; Zhang, S.; He, S.; Liu, J.; Tanvir, A.; Zhou, B. Estimating City NOX Emissions from TROPOMI High Spatial Resolution Observations—A Case Study on Yangtze River Delta, China. Urban Clim. 2022, 43, 101150. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Japan. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Cheng, Y.; Dai, T.; Goto, D.; Chen, L.; Si, Y.; Murakami, H.; Yoshida, M.; Zhang, P.; Cao, J.; Nakajima, T.; et al. Improved Hourly Estimate of Aerosol Optical Thickness over Asian Land by Fusing Geostationary Satellites Fengyun-4B and Himawari-9. Sci. Total Environ. 2024, 923, 171541. [Google Scholar] [CrossRef] [PubMed]
- Kurihara, Y.; Murakami, H.; Kachi, M. Sea Surface Temperature from the New Japanese Geostationary Meteorological Himawari-8 Satellite. Geophys. Res. Lett. 2016, 43, 1234–1240. [Google Scholar] [CrossRef]
- Zhu, Z.; Gu, J.; Xu, B.; Shi, C. Characterization of Himawari-8/AHI to Himawari-9/AHI Infrared Observations Continuity. Int. J. Remote Sens. 2024, 45, 121–142. [Google Scholar] [CrossRef]
- Cummings, J.A. Operational Multivariate Ocean Data Assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3583–3604. [Google Scholar] [CrossRef]
- Cummings, J.A.; Smedstad, O.M. Variational Data Assimilation for the Global Ocean. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. II); Park, S.K., Xu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 303–343. ISBN 978-3-642-35088-7. [Google Scholar]
- Helber, R.W.; Townsend, T.L.; Barron, C.N.; Dastugue, J.M.; Carnes, M.R. Validation Test Report for the Improved Synthetic Ocean Profile (ISOP) System, Part I: Synthetic Profile Methods and Algorithm; Defense Technical Information Center: Fort Belvoir, VA, USA, 2013.
- Trott, C.B.; Metzger, E.J.; Yu, Z. Luzon Strait Mesoscale Eddy Characteristics in HYCOM Reanalysis, Simulation, and Forecasts. J. Ocean 2023, 79, 423–441. [Google Scholar] [CrossRef]
- Holte, J.; Talley, L.D.; Gilson, J.; Roemmich, D. An Argo Mixed Layer Climatology and Database. Geophys. Res. Lett. 2017, 44, 5618–5626. [Google Scholar] [CrossRef]
- de Souza, J.M.A.C.; Couto, P.; Soutelino, R.; Roughan, M. Evaluation of Four Global Ocean Reanalysis Products for New Zealand Waters–A Guide for Regional Ocean Modelling. N. Z. J. Mar. Freshw. Res. 2021, 55, 132–155. [Google Scholar] [CrossRef]
- He, S.; Wang, S.; Zhang, S.; Zhu, J.; Sun, Z.; Xue, R.; Zhou, B. Vertical Distributions of Atmospheric HONO and the Corresponding OH Radical Production by Photolysis at the Suburb Area of Shanghai, China. Sci. Total Environ. 2023, 858, 159703. [Google Scholar] [CrossRef]
- Shaw, S.L.; Chisholm, S.W.; Prinn, R.G. Isoprene Production by Prochlorococcus, a Marine Cyanobacterium, and Other Phytoplankton. Mar. Chem. 2003, 80, 227–245. [Google Scholar] [CrossRef]
- Bonsang, B.; Gros, V.; Peeken, I.; Yassaa, N.; Bluhm, K.; Zoellner, E.; Sarda-Esteve, R.; Williams, J. Isoprene Emission from Phytoplankton Monocultures: The Relationship with Chlorophyll-a, Cell Volume and Carbon Content. Environ. Chem. 2010, 7, 554–563. [Google Scholar] [CrossRef]
- Colomb, A.; Yassaa, N.; Williams, J.; Peeken, I.; Lochte, K. Screening Volatile Organic Compounds (VOCs) Emissions from Five Marine Phytoplankton Species by Head Space Gas Chromatography/Mass Spectrometry (HS-GC/MS). J. Environ. Monit. 2008, 10, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Hirata, T.; Hardman-Mountford, N.J.; Brewin, R.J.W.; Aiken, J.; Barlow, R.; Suzuki, K.; Isada, T.; Howell, E.; Hashioka, T.; Noguchi-Aita, M.; et al. Synoptic Relationships between Surface Chlorophyll-a and Diagnostic Pigments Specific to Phytoplankton Functional Types. Biogeosciences 2011, 8, 311–327. [Google Scholar] [CrossRef]
- Exton, D.A.; Suggett, D.J.; McGenity, T.J.; Steinke, M. Chlorophyll-Normalized Isoprene Production in Laboratory Cultures of Marine Microalgae and Implications for Global Models. Limnol. Oceanogr. 2013, 58, 1301–1311. [Google Scholar] [CrossRef]
- Gantt, B.; Meskhidze, N.; Kamykowski, D. A New Physically-Based Quantification of Marine Isoprene and Primary Organic Aerosol Emissions. Atmos. Chem. Phys. 2009, 9, 4915–4927. [Google Scholar] [CrossRef]
- Meskhidze, N.; Sabolis, A.; Reed, R.; Kamykowski, D. Quantifying Environmental Stress-Induced Emissions of Algal Isoprene and Monoterpenes Using Laboratory Measurements. Biogeosciences 2015, 12, 637–651. [Google Scholar] [CrossRef]
- Thomas, M.K.; Kremer, C.T.; Klausmeier, C.A.; Litchman, E. A Global Pattern of Thermal Adaptation in Marine Phytoplankton. Science 2012, 338, 1085–1088. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Berthon, J. Surface Pigments, Algal Biomass Profiles, and Potential Production of the Euphotic Layer: Relationships Reinvestigated in View of Remote-sensing Applications. Limnol. Oceanogr. 1989, 34, 1545–1562. [Google Scholar] [CrossRef]
- Wu, Y.-C.; Li, J.-L.; Wang, J.; Zhuang, G.-C.; Liu, X.-T.; Zhang, H.-H.; Yang, G.-P. Occurance, Emission and Environmental Effects of Non-Methane Hydrocarbons in the Yellow Sea and the East China Sea. Environ. Pollut. 2021, 270, 116305. [Google Scholar] [CrossRef] [PubMed]
- Simó, R.; Cortés-Greus, P.; Rodríguez-Ros, P.; Masdeu-Navarro, M. Substantial Loss of Isoprene in the Surface Ocean Due to Chemical and Biological Consumption. Commun. Earth Environ. 2022, 3, 1–8. [Google Scholar] [CrossRef]
- Wu, Y.-C.; Gao, X.-X.; Zhang, H.-H.; Liu, Y.-Z.; Wang, J.; Xu, F.; Zhang, G.-L.; Chen, Z.-H. Characteristics and Emissions of Isoprene and Other Non-Methane Hydrocarbons in the Northwest Pacific Ocean and Responses to Atmospheric Aerosol Deposition. Sci. Total Environ. 2023, 876, 162808. [Google Scholar] [CrossRef] [PubMed]
- Wanninkhof, R. Relationship between Wind Speed and Gas Exchange over the Ocean. J. Geophys. Res. 1992, 97, 7373. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Liu, J.; Ren, K.; Ming, T.; Qu, J.; Guo, W.; Li, H. Investigating the Effects of Local Weather, Streamflow Lag, and Global Climate Information on 1-Month-Ahead Streamflow Forecasting by Using XGBoost and SHAP: Two Case Studies Involving the Contiguous USA. Acta Geophys. 2023, 71, 905–925. [Google Scholar] [CrossRef]
- Lin, N.; Zhang, D.; Feng, S.; Ding, K.; Tan, L.; Wang, B.; Chen, T.; Li, W.; Dai, X.; Pan, J.; et al. Rapid Landslide Extraction from High-Resolution Remote Sensing Images Using SHAP-OPT-XGBoost. Remote Sens. 2023, 15, 3901. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar]
- Huang, K.; Zhu, Q.; Lu, X.; Gu, D.; Liu, Y. Satellite-Based Long-Term Spatiotemporal Trends in Ambient NO2 Concentrations and Attributable Health Burdens in China From 2005 to 2020. GeoHealth 2023, 7, e2023GH000798. [Google Scholar] [CrossRef]
- Zhang, W.; Ashraf, W.M.; Senadheera, S.S.; Alessi, D.S.; Tack, F.M.G.; Ok, Y.S. Machine Learning Based Prediction and Experimental Validation of Arsenite and Arsenate Sorption on Biochars. Sci. Total Environ. 2023, 904, 166678. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhai, X.; Zhang, H.; Yang, G. Temporal Variations in the Distribution and Sea-to-Air Flux of Marine Isoprene in the East China Sea. Atmos. Environ. 2018, 187, 131–143. [Google Scholar] [CrossRef]
- Kurihara, M.; Iseda, M.; Ioriya, T.; Horimoto, N.; Kanda, J.; Ishimaru, T.; Yamaguchi, Y.; Hashimoto, S. Brominated Methane Compounds and Isoprene in Surface Seawater of Sagami Bay: Concentrations, Fluxes, and Relationships with Phytoplankton Assemblages. Mar. Chem. 2012, 134–135, 71–79. [Google Scholar] [CrossRef]
- Shimada, T.; Chang, Y.; Lan, K.-W. Climatological Features of Surface Winds Blowing through the Taiwan Strait. Int. J. Climatol. 2016, 36, 4287–4296. [Google Scholar] [CrossRef]
- Yu, L.; Zhong, S.; Bian, X.; Heilman, W.E. Climatology and Trend of Wind Power Resources in China and Its Surrounding Regions: A Revisit Using Climate Forecast System Reanalysis Data. Int. J. Climatol. 2016, 36, 2173–2188. [Google Scholar] [CrossRef]
- Marvin, M.R.; Wolfe, G.M.; Salawitch, R.J.; Canty, T.P.; Roberts, S.J.; Travis, K.R.; Aikin, K.C.; de Gouw, J.A.; Graus, M.; Hanisco, T.F.; et al. Impact of Evolving Isoprene Mechanisms on Simulated Formaldehyde: An Inter-Comparison Supported by in Situ Observations from SENEX. Atmos. Environ. 2017, 164, 325–336. [Google Scholar] [CrossRef]
- Millet, D.B.; Jacob, D.J.; Turquety, S.; Hudman, R.C.; Wu, S.; Fried, A.; Walega, J.; Heikes, B.G.; Blake, D.R.; Singh, H.B.; et al. Formaldehyde Distribution over North America: Implications for Satellite Retrievals of Formaldehyde Columns and Isoprene Emission. J. Geophys. Res. Atmos. 2006, 111, D24S02. [Google Scholar] [CrossRef]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Bréon, F.M. Remote Sensing of Phytoplankton Groups in Case 1 Waters from Global SeaWiFS Imagery. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 1989–2004. [Google Scholar] [CrossRef]
- Tran, S.; Bonsang, B.; Gros, V.; Peeken, I.; Sarda-Esteve, R.; Bernhardt, A.; Belviso, S. A Survey of Carbon Monoxide and Non-Methane Hydrocarbons in the Arctic Ocean during Summer 2010. Biogeosciences 2013, 10, 1909–1935. [Google Scholar] [CrossRef]
- Ooki, A.; Nomura, D.; Nishino, S.; Kikuchi, T.; Yokouchi, Y. A Global-Scale Map of Isoprene and Volatile Organic Iodine in Surface Seawater of the Arctic, Northwest Pacific, Indian, and Southern Oceans. J. Geophys. Res. Ocean. 2015, 120, 4108–4128. [Google Scholar] [CrossRef]
- Hoppe, H.-G.; Gocke, K.; Koppe, R.; Begler, C. Bacterial Growth and Primary Production along a North–South Transect of the Atlantic Ocean. Nature 2002, 416, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Loi, C.L.; Wu, C.-C.; Liang, Y.-C. Prediction of Tropical Cyclogenesis Based on Machine Learning Methods and Its SHAP Interpretation. J. Adv. Model. Earth Syst. 2024, 16, e2023MS003637. [Google Scholar] [CrossRef]
- Marbach, T.; Beirle, S.; Platt, U.; Hoor, P.; Wittrock, F.; Richter, A.; Vrekoussis, M.; Grzegorski, M.; Burrows, J.P.; Wagner, T. Satellite Measurements of Formaldehyde Linked to Shipping Emissions. Atmos. Chem. Phys. 2009, 9, 8223–8234. [Google Scholar] [CrossRef]
- Ye, M.; Zhu, L.; Li, X.; Ke, Y.; Huang, Y.; Chen, B.; Yu, H.; Li, H.; Feng, H. Estimation of the Soil Arsenic Concentration Using a Geographically Weighted XGBoost Model Based on Hyperspectral Data. Sci. Total Environ. 2023, 858, 159798. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Li, X.; Sun, W.; Fang, X.; He, F.; Tu, J. Semi-Surrogate Modelling of Droplets Evaporation Process via XGBoost Integrated CFD Simulations. Sci. Total Environ. 2023, 895, 164968. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, N.; Girach, I.A.; Kompalli, S.K.; Murari, V.; Nair, P.R.; Babu, S.S.; Sahu, L.K. Sources and Distribution of Light NMHCs in the Marine Boundary Layer of the Northern Indian Ocean During Winter: Implications to Aerosol Formation. J. Geophys. Res. Atmos. 2024, 129, e2023JD039433. [Google Scholar] [CrossRef]
- Tripathi, N.; Sahu, L.K.; Singh, A.; Yadav, R.; Patel, A.; Patel, K.; Meenu, P. Elevated Levels of Biogenic Nonmethane Hydrocarbons in the Marine Boundary Layer of the Arabian Sea During the Intermonsoon. J. Geophys. Res. Atmos. 2020, 125, e2020JD032869. [Google Scholar] [CrossRef]


| Model | n_Estimators | Learning_Rate | Max_Depth | Gamma | Subsample | Colsample_Bytree | Reg_Alpha | Reg_Lambda |
|---|---|---|---|---|---|---|---|---|
| XGBFlux | 1900 | 0.086 | 5 | 0.21 | 0.97 | 0.81 | 0.14 | 0.52 |
| XGBHCHO | 1701 | 0.024 | 10 | 0.06 | 0.68 | 0.66 | 0.79 | 0.51 |
| Cluster | HCHO [molec/cm2] | NO2 [molec/cm2] | ISO Flux [nmol/m2/day] |
|---|---|---|---|
| Cluster 1 | 6.67 × 1015 ± 6.19 × 1014 | 2.03 × 1015 ± 6.18 × 1014 | 38.16 ± 12.95 |
| Cluster 2 | 7.29 × 1015 ± 6.11 × 1014 | 1.97 × 1015 ± 3.25 × 1014 | 142.28 ± 27.64 |
| Cluster 3 | 5.11 × 1015 ± 5.01 × 1014 | 1.04 × 1015 ± 2.09 × 1014 | 73.41 ± 15.51 |
| Cluster 4 | 8.68 × 1015 ± 7.26 × 1014 | 4.83 × 1015 ± 1.21 × 1014 | 24.08 ± 7.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Wang, S.; Xue, R.; Tan, Y.; Zhang, S.; Gu, C.; Zhou, B. Machine Learning to Characterize Biogenic Isoprene Emissions and Atmospheric Formaldehyde with Their Environmental Drivers in the Marine Boundary Layer. Atmosphere 2024, 15, 679. https://doi.org/10.3390/atmos15060679
Wang T, Wang S, Xue R, Tan Y, Zhang S, Gu C, Zhou B. Machine Learning to Characterize Biogenic Isoprene Emissions and Atmospheric Formaldehyde with Their Environmental Drivers in the Marine Boundary Layer. Atmosphere. 2024; 15(6):679. https://doi.org/10.3390/atmos15060679
Chicago/Turabian StyleWang, Tianyu, Shanshan Wang, Ruibin Xue, Yibing Tan, Sanbao Zhang, Chuanqi Gu, and Bin Zhou. 2024. "Machine Learning to Characterize Biogenic Isoprene Emissions and Atmospheric Formaldehyde with Their Environmental Drivers in the Marine Boundary Layer" Atmosphere 15, no. 6: 679. https://doi.org/10.3390/atmos15060679
APA StyleWang, T., Wang, S., Xue, R., Tan, Y., Zhang, S., Gu, C., & Zhou, B. (2024). Machine Learning to Characterize Biogenic Isoprene Emissions and Atmospheric Formaldehyde with Their Environmental Drivers in the Marine Boundary Layer. Atmosphere, 15(6), 679. https://doi.org/10.3390/atmos15060679







