El Niño–Southern Oscillation-Independent Regulation of Western North Pacific Tropical Cyclone Genesis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
- Definition of Pacific–Japan Index
- b.
- Wave-activity flux
- c.
- Dynamic TC genesis potential index
- d.
- Removing ENSO
- e.
- Extracting interannual signals
- f.
- Significance test
3. Result and Discussion
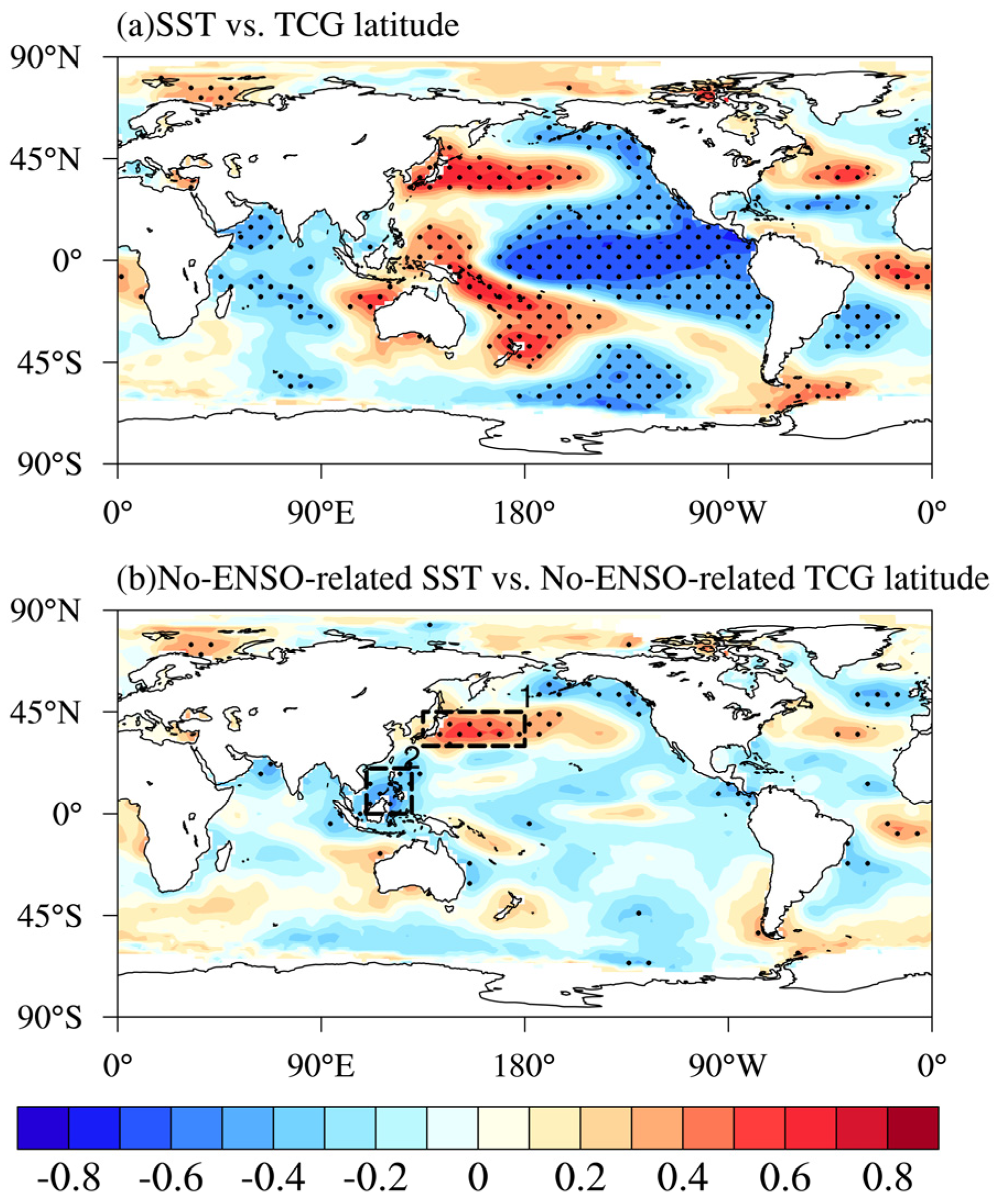
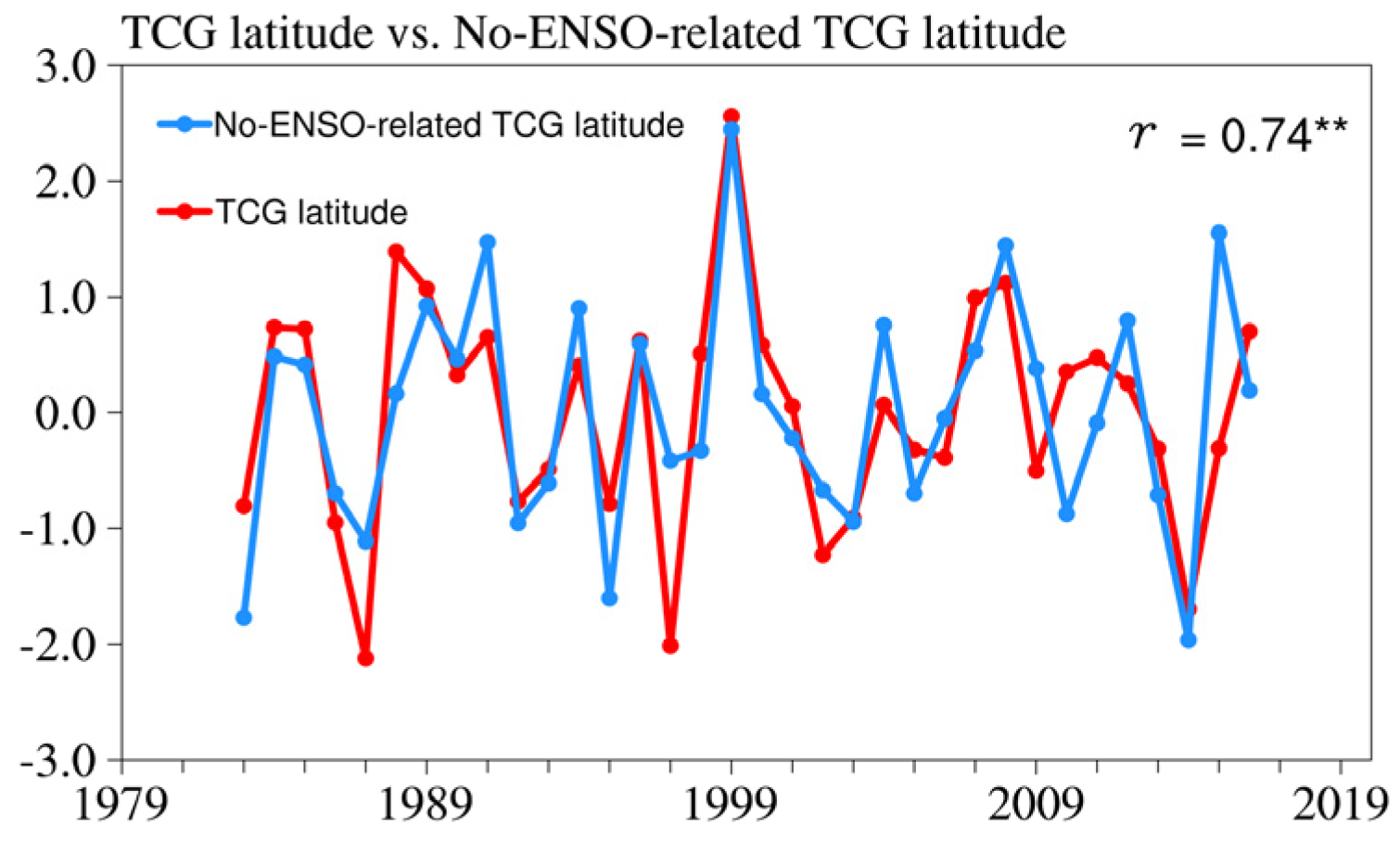
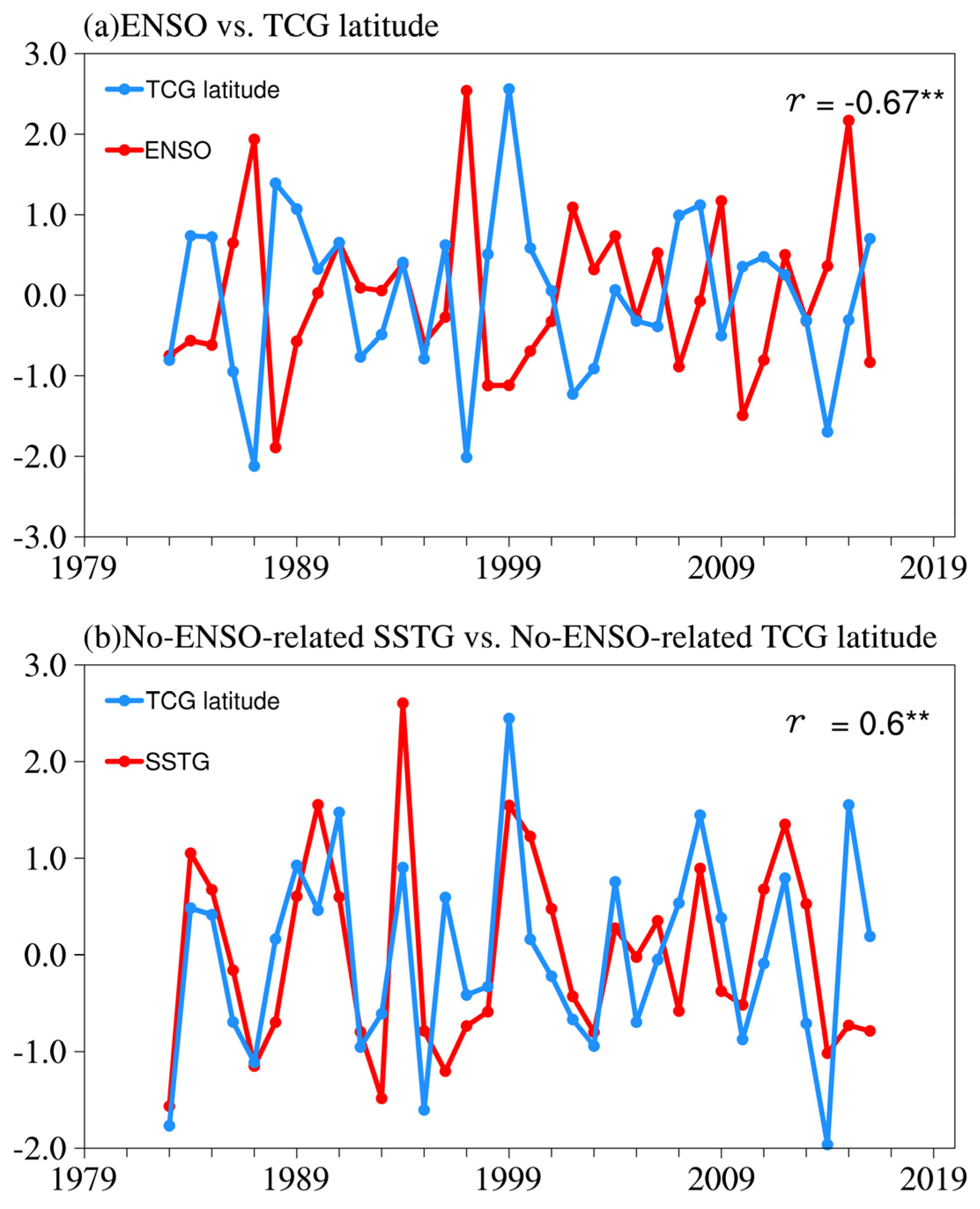
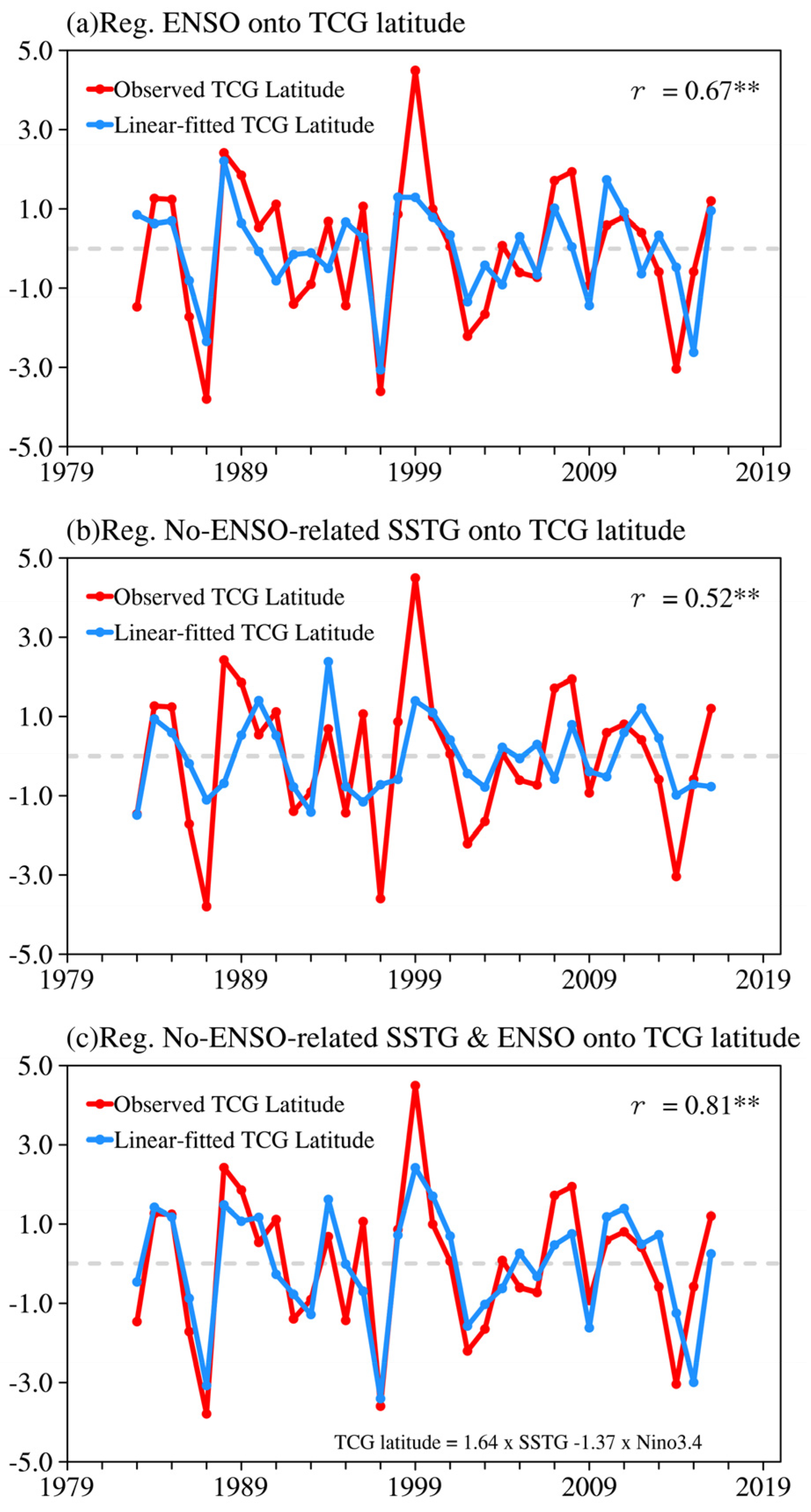
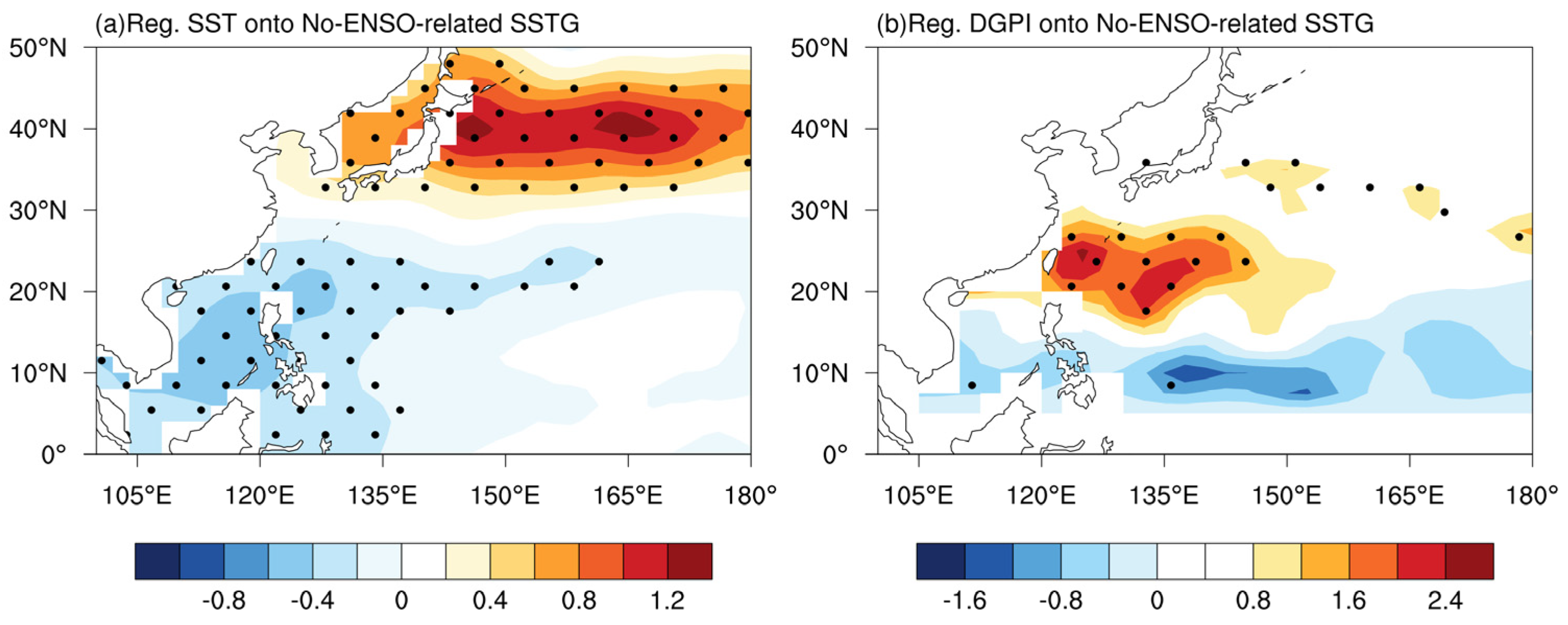
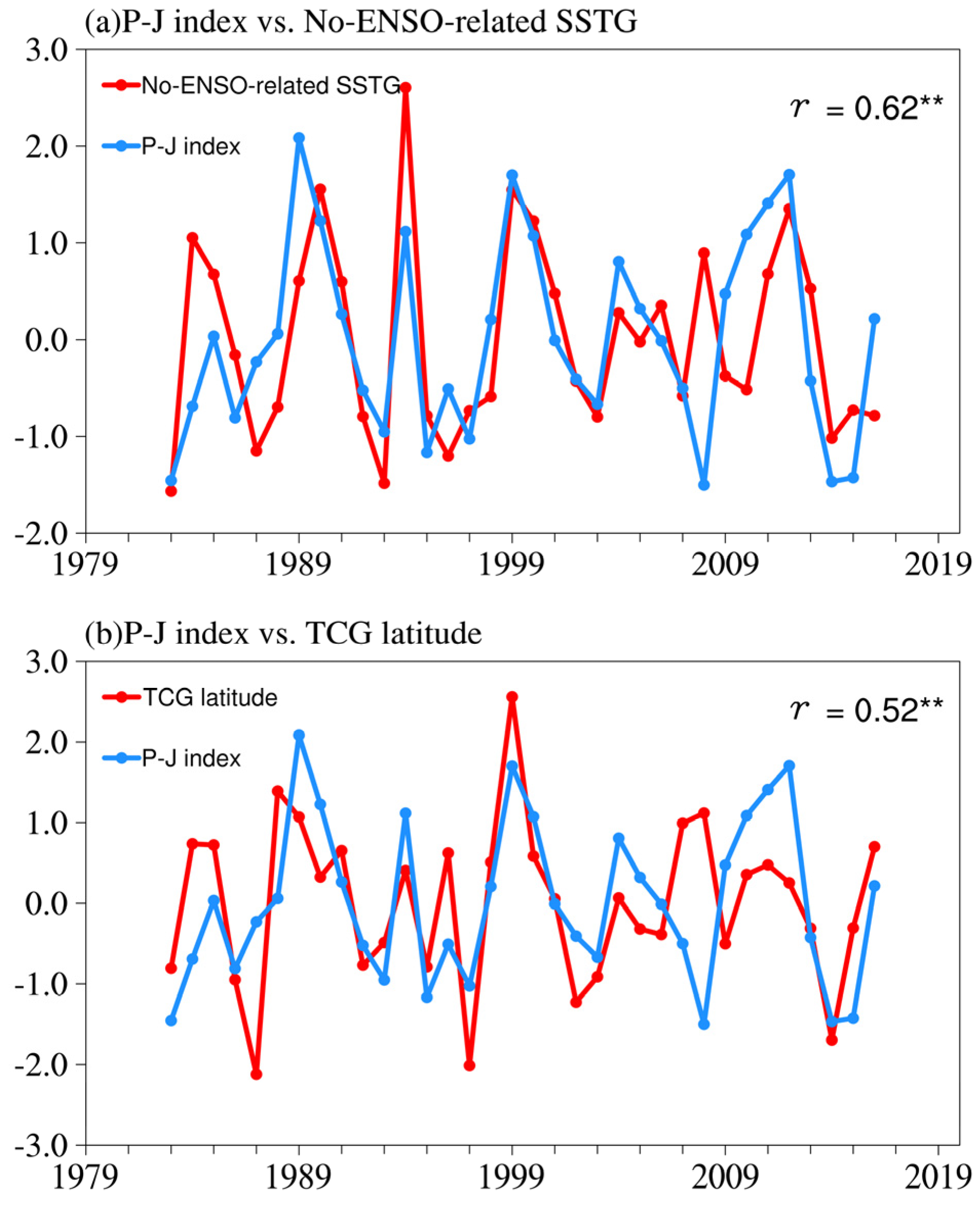
3.1. Relationship between ENSO-Independent SST and Interannual Variability in TCG Latitude
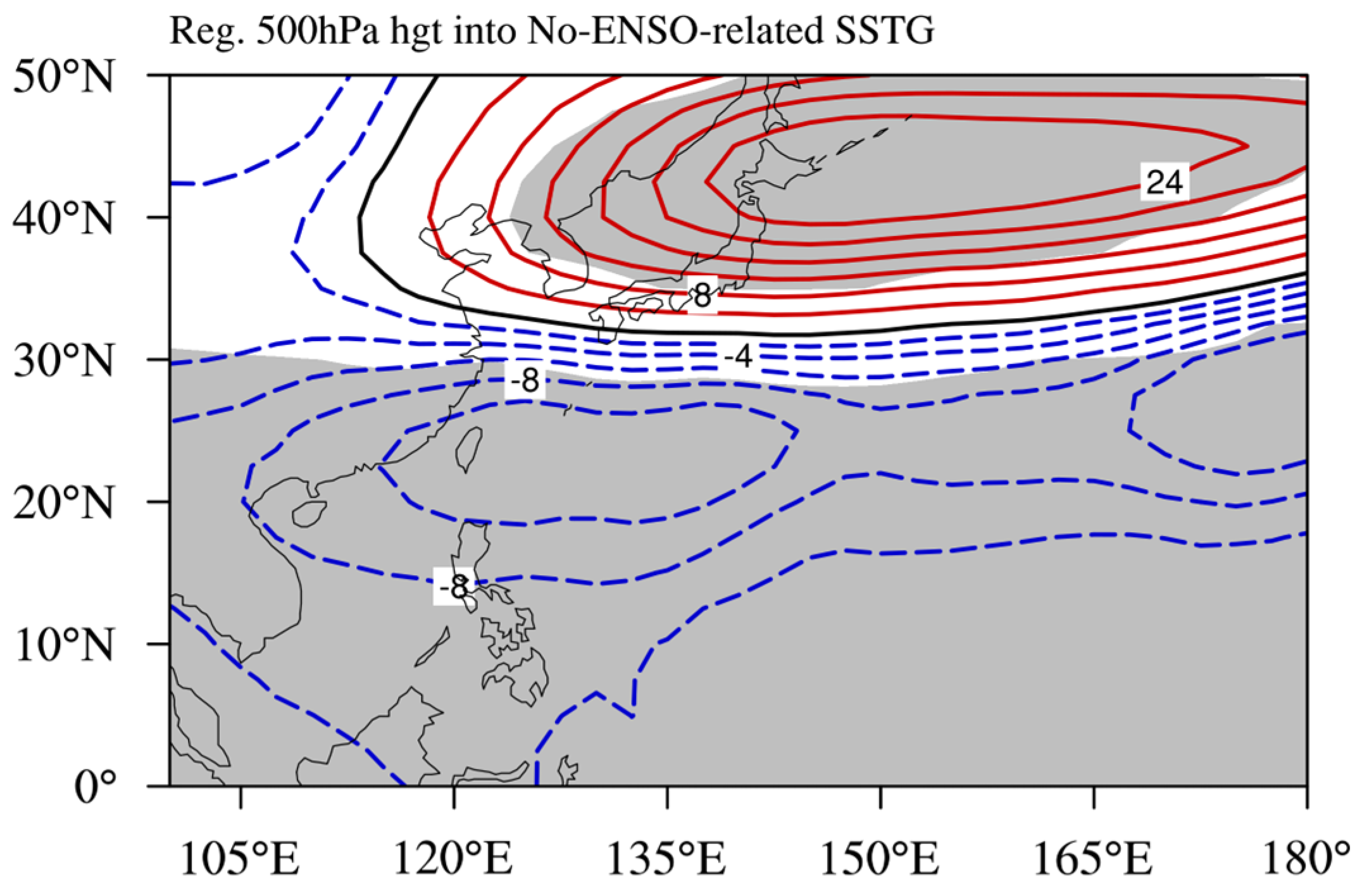
3.2. Possible Physical Mechanisms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gray, W.M. Global View of the Origin of Tropical Disturbances and Storms. Mon. Weather Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
- Schreck, C.J.; Knapp, K.R.; Kossin, J.P. The Impact of Best Track Discrepancies on Global Tropical Cyclone Climatologies using IBTrACS. Mon. Weather Rev. 2014, 142, 3881–3899. [Google Scholar] [CrossRef]
- Chan, J.C.L. Tropical Cyclone Activity in the Northwest Pacific in Relation to the El Niño/Southern Oscillation Phenomenon. Mon. Weather Rev. 1985, 113, 599–606. [Google Scholar] [CrossRef]
- Peduzzi, P.; Chatenoux, B.; Dao, H.; De Bono, A.; Herold, C.; Kossin, J.; Mouton, F.; Nordbeck, O. Global trends in tropical cyclone risk. Nat. Clim. Chang. 2012, 2, 289–294. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C.L. Inactive period of western North Pacific tropical cyclone activity in 1998–2011. J. Clim. 2013, 26, 2614–2630. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, C. Interdecadal modulation on the relationship between ENSO and typhoon activity during the late season in the western north Pacific. Clim. Dyn. 2016, 47, 315–328. [Google Scholar] [CrossRef]
- Roy, C.; Kovordányi, R. Tropical cyclone track forecasting techniques—A review. Atmos. Res. 2012, 104, 40–69. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, L.; Zhou, W. Assessing the influence of the ENSO on tropical cyclone prevailing tracks in the western North Pacific. Adv. Atmos. Sci. 2010, 27, 1361–1371. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, L.; Zhou, W. Interannual changes of tropical cyclone intensity in the western north Pacific. J. Meteorol. Soc. Jpn. Ser. II 2011, 89, 243–253. [Google Scholar] [CrossRef]
- Cai, Y.; Han, X.; Zhao, H.; Klotzbach, P.J.; Wu, L.; Raga, G.B.; Wang, C. Enhanced predictability of rapidly intensifying tropical cyclones over the western North Pacific associated with snow depth changes over the Tibetan Plateau. J. Clim. 2022, 35, 2093–2110. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Vitart, F.; Lang, S.T.K.; Magnusson, L.; Elsberry, R.L.; Elliott, G.; Kyouda, M.; Nakazawa, T. Global distribution of the skill of tropical cyclone activity forecasts on short-to medium-range time scales. Weather Forecast. 2015, 30, 1695–1709. [Google Scholar] [CrossRef]
- Kossin, J.P.; Emanuel, K.A.; Vecchi, G.A. The poleward migration of the location of tropical cyclone maximum intensity. Nature 2014, 509, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Daloz, A.S.; Camargo, S.J. Is the poleward migration of tropical cyclone maximum intensity associated with a poleward migration of tropical cyclone genesis? Clim. Dyn. 2018, 50, 705–715. [Google Scholar] [CrossRef]
- Zhao, H.; Duan, X.; Raga, G.B.; Klotzbach, P.J. Changes in characteristics of rapidly intensifying western North Pacific tropical cyclones related to climate regime shifts. J. Clim. 2018, 31, 8163–8179. [Google Scholar] [CrossRef]
- Wu, L.; Wang, C.; Wang, B. Westward shift of western North Pacific tropical cyclogenesis. Geophys. Res. Lett. 2015, 42, 1537–1542. [Google Scholar] [CrossRef]
- He, H.; Yang, J.; Gong, D.; Mao, R.; Wang, Y.; Gao, M. Decadal changes in tropical cyclone activity over the western North Pacific in the late 1990s. Clim. Dyn. 2015, 45, 3317–3329. [Google Scholar] [CrossRef]
- Korty, R.L.; Emanuel, K.A.; Huber, M.; Zamora, R.A. Tropical cyclones downscaled from simulations with very high carbon dioxide levels. J. Clim. 2017, 30, 649–667. [Google Scholar] [CrossRef]
- Kossin, J.P.; Emanuel, K.A.; Camargo, S.J. Past and projected changes in western North Pacific tropical cyclone exposure. J. Clim. 2016, 29, 5725–5739. [Google Scholar] [CrossRef]
- Bell, S.S.; Chand, S.S.; Tory, K.J.; Dowdy, A.J.; Turville, C.; Ye, H. Projections of southern hemisphere tropical cyclone track density using CMIP5 models. Clim. Dyn. 2019, 52, 6065–6079. [Google Scholar] [CrossRef]
- Shan, K.; Yu, X. Enhanced understanding of poleward migration of tropical cyclone genesis. Environ. Res. Lett. 2020, 15, 104062. [Google Scholar] [CrossRef]
- Song, J.; Klotzbach, P.J. What has controlled the poleward migration of annual averaged location of tropical cyclone lifetime maximum intensity over the western North Pacific since 1961? Geophys. Res. Lett. 2018, 45, 1148–1156. [Google Scholar] [CrossRef]
- Moon, I.-J.; Kim, S.-H.; Klotzbach, P.; Chan, J.C.L. Roles of interbasin frequency changes in the poleward shifts of the maximum intensity location of tropical cyclones. Environ. Res. Lett. 2015, 10, 104004. [Google Scholar] [CrossRef]
- Li, T.; Kwon, M.; Zhao, M.; Kug, J.; Luo, J.; Yu, W. Global warming shifts Pacific tropical cyclone location. Geophys. Res. Lett. 2010, 37, L21804. [Google Scholar] [CrossRef]
- Knutson, T.; Camargo, S.J.; Chan, J.C.L.; Emanuel, K.; Ho, C.-H.; Kossin, J.; Mohapatra, M.; Satoh, M.; Sugi, M.; Walsh, K.; et al. Tropical cyclones and climate change assessment: Part I: Detection and attribution. Bull. Am. Meteorol. Soc. 2019, 100, 1987–2007. [Google Scholar] [CrossRef]
- Lee, C.Y.; Camargo, S.J.; Sobel, A.H.; Tippett, M.K. Statistical–dynamical downscaling projections of tropical cyclone activity in a warming climate: Two diverging genesis scenarios. J. Clim. 2020, 33, 4815–4834. [Google Scholar] [CrossRef]
- Gray, W.M. Atlantic seasonal hurricane frequency. Part I: El Niño and 30 mb quasi-biennial oscillation influences. Mon. Weather Rev. 1984, 112, 1649–1668. [Google Scholar] [CrossRef]
- Wang, B.; Chan, J.C.L. How strong ENSO events affect tropical storm activity over the western North Pacific. J. Clim. 2002, 15, 1643–1658. [Google Scholar] [CrossRef]
- Camargo, S.J.; Sobel, A.H. Western North Pacific tropical cyclone intensity and ENSO. J. Clim. 2005, 18, 2996–3006. [Google Scholar] [CrossRef]
- Chia, H.H.; Ropelewski, C.F. The interannual variability in the genesis location of tropical cyclones in the northwest Pacific. J. Clim. 2002, 15, 2934–2944. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, W.; Li, C.; Wang, D. Effects of the East Asian summer monsoon on tropical cyclone genesis over the South China Sea on an interdecadal time scale. Adv. Atmos. Sci. 2012, 29, 249–262. [Google Scholar] [CrossRef]
- Li, R.C.Y.; Zhou, W. Changes in western Pacific tropical cyclones associated with the El Niño–Southern Oscillation cycle. J. Clim. 2012, 25, 5864–5878. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean 2007, 112. [Google Scholar] [CrossRef]
- Yu, J.Y.; Kao, H.Y. Decadal Changes of ENSO Persistence Barrier in SST and Ocean Heat Content Indices: 1958–2001. J. Geophys. Res. 2007, 112, D13106. [Google Scholar] [CrossRef]
- Wang, C.; Li, C.; Mu, M.; Duan, W. Seasonal modulations of different impacts of two types of ENSO events on tropical cyclone activity in the western North Pacific. Clim. Dyn. 2013, 40, 2887–2902. [Google Scholar] [CrossRef]
- Saji, N.H.; Yamagata, T. Possible impacts of Indian Ocean dipole mode events on global climate. Clim. Res. 2003, 25, 151–169. [Google Scholar] [CrossRef]
- Yoo, S.H.; Yang, S.; Ho, C.H. Variability of the Indian Ocean sea surface temperature and its impacts on Asian-Australian monsoon climate. J. Geophys. Res. Atmos. 2006, 111, D03108. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Q.; Xie, S.; Liu, Z.; Wu, L. Impact of the Indian Ocean SST basin mode on the Asian summer monsoon. Geophys. Res. Lett. 2007, 34, L02708. [Google Scholar] [CrossRef]
- Xie, S.P.; Hu, K.; Hafner, J.; Tokinaga, H.; Du, Y.; Huang, G.; Sampe, T. Indian Ocean capacitor effect on Indo–western Pacific climate during the summer following El Niño. J. Clim. 2009, 22, 730–747. [Google Scholar] [CrossRef]
- Du, Y.; Yang, L.; Xie, S.P. Tropical Indian Ocean influence on northwest Pacific tropical cyclones in summer following strong El Niño. J. Clim. 2011, 24, 315–322. [Google Scholar] [CrossRef]
- Gong, H.; Wang, L.; Chen, W.; Wu, R.; Huang, G.; Nath, D. Diversity of the Pacific–Japan pattern among CMIP5 models: Role of SST anomalies and atmospheric mean flow. J. Clim. 2018, 31, 6857–6877. [Google Scholar] [CrossRef]
- Tao, L.; Li, T.; Ke, Y.H.; Zhao, J.W. Causes of interannual and interdecadal variations of the summertime Pacific–Japan-like pattern over East Asia. J. Clim. 2017, 30, 8845–8864. [Google Scholar] [CrossRef]
- Choi, K.S.; Wu, C.C.; Cha, E.J. Change of tropical cyclone activity by Pacific-Japan teleconnection pattern in the western North Pacific. J. Geophys. Res. Atmos. 2010, 115, D19114. [Google Scholar] [CrossRef]
- Zhan, R.; Wang, Y.; Lei, X. Contributions of ENSO and East Indian Ocean SSTA to the interannual variability of Northwest Pacific tropical cyclone frequency. J. Clim. 2011, 24, 509–521. [Google Scholar] [CrossRef]
- Chen, G.; Tam, C.Y. Different impacts of two kinds of Pacific Ocean warming on tropical cyclone frequency over the western North Pacific. Geophys. Res. Lett. 2010, 37, L01803. [Google Scholar] [CrossRef]
- Jiayu, Z.; Wu, Q.; Guo, Y.; Zhao, S. The impact of summertime North Indian ocean SST on tropical cyclone genesis over the Western North Pacific. Sola 2016, 12, 242–246. [Google Scholar] [CrossRef]
- Camargo, S.J.; Emanuel, K.A.; Sobel, A.H. Use of a genesis potential index to diagnose ENSO effects on tropical cyclone genesis. J. Clim. 2007, 20, 4819–4834. [Google Scholar] [CrossRef]
- Wang, H.J.; Sun, J.Q.; Fan, K. Relationships between the North Pacific Oscillation and the typhoon/hurricane frequencies. Sci. China Ser. D Earth Sci. 2007, 50, 1409–1416. [Google Scholar] [CrossRef]
- Chu, P.S. Large-scale circulation features associated with decadal variations of tropical cyclone activity over the central North Pacific. J. Clim. 2002, 15, 2678–2689. [Google Scholar] [CrossRef]
- Huang, S.; Oey, L.Y. Land-falling typhoons are controlled by the meridional oscillation of the Kuroshio Extension. Clim. Dyn. 2019, 52, 2855–2867. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. Ncep–doe amip-ii reanalysis (r-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Huang, R.H.; Li, W.J. Influence of heat source anomaly over the western tropical Pacific on the subtropical high over East Asia and its physical mechanism. Chin. J. Atmos. Sci. 1988, 12, 107–116. [Google Scholar]
- Nitta, T. Long-term variations of cloud amount in the western Pacific region. J. Meteorol. Soc. Jpn. Ser. II 1986, 64, 373–390. [Google Scholar] [CrossRef]
- Wakabayashi, S.; Kawamura, R. Extraction of major teleconnection patterns possibly associated with the anomalous summer climate in Japan. J. Meteorol. Soc. Jpn. Ser. II 2004, 82, 1577–1588. [Google Scholar] [CrossRef]
- Takaya, K.; Nakamura, H. A formulation of a phase-independent wave-activity flux for stationary and migratory quasigeostrophic eddies on a zonally varying basic flow. J. Atmos. Sci. 2001, 58, 608–627. [Google Scholar] [CrossRef]
- Emanuel, K.; Nolan, D.S. Tropical cyclone activity and the global climate system. In Proceedings of the 26th Conference on Hurricanes and Tropical Meteorology, Miami, FL, USA, 3–7 May 2004; American Meteorology Society: Boston, MA, USA, 2004; Volume 10, pp. 240–241. [Google Scholar]
- Cao, J.; Zhao, H.; Wang, B.; Wu, L. Hemisphere-asymmetric tropical cyclones response to anthropogenic aerosol forcing. Nat. Commun. 2021, 12, 6787. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Wang, H.; Zhao, H.; Wang, B.; Wu, L.; Wang, C. Reversed and comparable climate impacts from historical anthropogenic aerosol and GHG on global-scale tropical cyclone genesis potential. Environ. Res. Lett. 2022, 17, 094027. [Google Scholar] [CrossRef]
- Murakami, H.; Wang, B. Patterns and frequency of projected future tropical cyclone genesis are governed by dynamic effects. Commun. Earth Environ. 2022, 3, 77. [Google Scholar] [CrossRef]
- Wang, B.; Murakami, H. Dynamic genesis potential index for diagnosing present-day and future global tropical cyclone genesis. Environ. Res. Lett. 2020, 15, 114008. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. A look at the relationship between the ENSO and the Indian Ocean dipole. J. Meteorol. Soc. Jpn. Ser. II 2003, 81, 41–56. [Google Scholar] [CrossRef]
- Shindell, D.; Faluvegi, G.J.N.G. Climate response to regional radiative forcing during the twentieth century. Nat. Geosci. 2009, 2, 294–300. [Google Scholar] [CrossRef]
- Li, C. Actions of typhoons over the western Pacific (including the South China Sea) and El Nino. Adv. Atmos. Sci. 1988, 5, 107–115. [Google Scholar] [CrossRef]
- Frank, W.M. Tropical cyclone formation. In A Global View of Tropical Cyclones; Office of Naval Research: Arlington, VA, USA, 1987; pp. 53–90. [Google Scholar]
- Chelton, D.B.; Esbensen, S.K.; Schlax, M.G.; Thum, N.; Freilich, M.H.; Wentz, F.J.; Gentemann, C.L.; McPhaden, M.J.; Schopf, P.S. Observations of coupling between surface wind stress and sea surface temperature in the eastern tropical Pacific. J. Clim. 2001, 14, 1479–1498. [Google Scholar] [CrossRef]
- Liu, T.W.; Xie, X.; Polito, P.S.; Xie, S.; Hashizume, H. Atmospheric manifestation of tropical instability wave observed by QuikSCAT and Tropical Rain Measuring Mission. Geophys. Res. Lett. 2000, 27, 2545–2548. [Google Scholar] [CrossRef]
- Hashizume, H.; Xie, S.P.; Liu, W.T.; Takeuchi, K. Local and remote atmospheric response to tropical instability waves: A global view from space. J. Geophys. Res. Atmos. 2001, 106, 10173–10185. [Google Scholar] [CrossRef]
- Ricchi, A.; Sangelantoni, L.; Redaelli, G.; Mazzarella, V.; Montopoli, M.; Miglietta, M.M.; Tiesi, A.; Mazzà, S.; Rotunno, R.; Ferretti, R. Impact of the SST and topography on the development of a large-hail storm event, on the Adriatic Sea. Atmos. Res. 2023, 296, 107078. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Summertime coupling between sea surface temperature and wind stress in the California Current System. J. Phys. Oceanogr. 2007, 37, 495–517. [Google Scholar] [CrossRef]
- Chelton, D.B. The impact of SST specification on ECMWF surface wind stress fields in the eastern tropical Pacific. J. Clim. 2005, 18, 530–550. [Google Scholar] [CrossRef]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. The effects of SST-induced surface wind speed and direction gradients on midlatitude surface vorticity and divergence. J. Clim. 2010, 23, 255–281. [Google Scholar] [CrossRef]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K.; Wentz, F.J. High-resolution satellite measurements of the atmospheric boundary layer response to SST variations along the Agulhas Return Current. J. Clim. 2005, 18, 2706–2723. [Google Scholar] [CrossRef]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. Observations of SST-induced perturbations of the wind stress field over the Southern Ocean on seasonal timescales. J. Clim. 2003, 16, 2340–2354. [Google Scholar] [CrossRef]
- Meroni, A.N.; Parodi, A.; Pasquero, C. Role of SST patterns on surface wind modulation of a heavy midlatitude precipitation event. J. Geophys. Res. Atmos. 2018, 123, 9081–9096. [Google Scholar] [CrossRef]
- Small, R.; Deszoeke, S.; Xie, S.; O’neill, L.; Seo, H.; Song, Q.; Cornillon, P.; Spall, M.; Minobe, S. Air–sea interaction over ocean fronts and eddies. Dyn. Atmos. Ocean. 2008, 45, 274–319. [Google Scholar] [CrossRef]
- Miyamoto, A.; Nakamura, H.; Miyasaka, T. Influence of the subtropical high and storm track on low-cloud fraction and its seasonality over the south Indian Ocean. J. Clim. 2018, 31, 4017–4039. [Google Scholar] [CrossRef]
- Frenger, I.; Gruber, N.; Knutti, R.; Münnich, M. Imprint of Southern Ocean eddies on winds, clouds and rainfall. Nat. Geosci. 2013, 6, 608–612. [Google Scholar] [CrossRef]
- Seo, H.; O’neill, L.W.; Bourassa, M.A.; Czaja, A.; Drushka, K.; Edson, J.B.; Fox-Kemper, B.; Frenger, I.; Gille, S.T.; Kirtman, B.P.; et al. Ocean mesoscale and frontal-scale ocean–atmosphere interactions and influence on large-scale climate: A review. J. Clim. 2023, 36, 1981–2013. [Google Scholar] [CrossRef]
- Small, R.J.; de Szoeke, S.; Xie, S.P.; O’Neill, L.; Seo, H.; Song, Q.; Cornillon, P.; Spall, M.; Minobe, S. Atmospheric response to ocean fronts and eddies: A Review. In Proceedings of the 15th Conference on Air-Sea Interaction, Portland, OR, USA, 20–24 August 2007. [Google Scholar]
- Rotunno, R.; Emanuel, K.A. An air–sea interaction theory for tropical cyclones. Part II: Evolutionary study using a nonhydrostatic axisymmetric numerical model. J. Atmos. Sci. 1987, 44, 542–561. [Google Scholar] [CrossRef]
- Zambon, J.B.; He, R.; Warner, J.C. Investigation of hurricane Ivan using the coupled ocean–atmosphere–wave–sediment transport (COAWST) model. Ocean. Dyn. 2014, 64, 1535–1554. [Google Scholar] [CrossRef]
- Everson DA, L.; Gan, M.A.; de Lima MOSCATIM, C. The role of latent and sensible heat fluxes in an explosive cyclogenesis over the South American East Coast. J. Meteorol. Soc. Jpn. 2011, 89, 637–663. [Google Scholar] [CrossRef]
- Carniel, S.; Benetazzo, A.; Bonaldo, D.; Falcieri, F.M.; Miglietta, M.M.; Ricchi, A.; Sclavo, M. Scratching beneath the surface while coupling atmosphere, ocean and waves: Analysis of a dense water formation event. Ocean Model. 2016, 101, 101–112. [Google Scholar] [CrossRef]
- Tous, M.; Romero, R.; Ramis, C. Surface heat fluxes influence on medicane trajectories and intensification. Atmos. Res. 2013, 123, 400–411. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a coupled ocean–atmosphere–wave–sediment transport (COAWST) modeling system. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- Huang, R.; Sun, F. Impacts of the tropical western Pacific on the East Asian summer monsoon. J. Meteorol. Soc. Jpn. Ser. II 1992, 70, 243–256. [Google Scholar] [CrossRef]
- Kosaka, Y.; Nakamura, H. Structure and dynamics of the summertime Pacific–Japan teleconnection pattern. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2006, 132, 2009–2030. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Wang, L.; Lin, Z. Characteristics, processes, and causes of the spatio-temporal variabilities of the East Asian monsoon system. Adv. Atmos. Sci. 2012, 29, 910–942. [Google Scholar] [CrossRef]
- Kim, J.S.; Li, R.C.Y.; Zhou, W. Effects of the Pacific-Japan teleconnection pattern on tropical cyclone activity and extreme precipitation events over the Korean peninsula. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Zhan, R.; Wang, Y.; Wu, C.C. Impact of SSTA in the east Indian Ocean on the frequency of northwest Pacific tropical cyclones: A regional atmospheric model study. J. Clim. 2011, 24, 6227–6242. [Google Scholar] [CrossRef]
- Tao, L.; Wu, L.; Wang, Y.; Yang, J. Influence of tropical Indian Ocean warming and ENSO on tropical cyclone activity over the western North Pacific. J. Meteorol. Soc. Jpn. Ser. II 2012, 90, 127–144. [Google Scholar] [CrossRef]
- Xie, M.; Wang, C.; Chen, S. The role of the Maritime Continent SST anomalies in maintaining the Pacific–Japan pattern on decadal time scales. J. Clim. 2022, 35, 1079–1095. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, T.; Li, T. Contrast of rainfall–SST relationships in the western North Pacific between the ENSO-developing and ENSO-decaying summers. J. Clim. 2009, 22, 4398–4405. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, D.; Zhao, H.; Liu, M.; Wang, R. El Niño–Southern Oscillation-Independent Regulation of Western North Pacific Tropical Cyclone Genesis. Atmosphere 2024, 15, 537. https://doi.org/10.3390/atmos15050537
Jian D, Zhao H, Liu M, Wang R. El Niño–Southern Oscillation-Independent Regulation of Western North Pacific Tropical Cyclone Genesis. Atmosphere. 2024; 15(5):537. https://doi.org/10.3390/atmos15050537
Chicago/Turabian StyleJian, Danlei, Haikun Zhao, Min Liu, and Ronghe Wang. 2024. "El Niño–Southern Oscillation-Independent Regulation of Western North Pacific Tropical Cyclone Genesis" Atmosphere 15, no. 5: 537. https://doi.org/10.3390/atmos15050537
APA StyleJian, D., Zhao, H., Liu, M., & Wang, R. (2024). El Niño–Southern Oscillation-Independent Regulation of Western North Pacific Tropical Cyclone Genesis. Atmosphere, 15(5), 537. https://doi.org/10.3390/atmos15050537








