Abstract
Prediction of fine particulate matter with particle size less than 2.5 µm (PM2.5) is an important component of atmospheric pollution warning and control management. In this study, we propose a deep learning model, namely, a spatiotemporal weighted neural network (STWNN), to address the challenge of poor long-term PM2.5 prediction in areas with sparse and uneven stations. The model, which is based on convolutional neural network–bidirectional long short-term memory (CNN–Bi-LSTM) and attention mechanisms and uses a geospatial data-driven approach, considers the spatiotemporal heterogeneity effec It is correct.ts of PM2.5. This approach effectively overcomes instability caused by sparse station data in forecasting daily average PM2.5 concentrations over the next week. The effectiveness of the STWNN model was evaluated using the Xinjiang Uygur Autonomous Region as the study area. Experimental results demonstrate that the STWNN exhibits higher performance (RMSE = 10.29, MAE = 6.4, R2 = 0.96, and IA = 0.81) than other models in overall prediction and seasonal clustering. Furthermore, the SHapley Additive exPlanations (SHAP) method was introduced to calculate the contribution and spatiotemporal variation of feature variables after the STWNN prediction model. The SHAP results indicate that the STWNN has significant potential in improving the performance of long-term PM2.5 prediction at the regional station level. Analyzing spatiotemporal differences in key feature variables that influence PM2.5 provides a scientific foundation for long-term pollution control and supports emergency response planning for heavy pollution events.
1. Introduction
Air pollution, a serious environmental problem, has been recognized as a major threat to human health and has received increasing attention worldwide [1]. According to statistics, 6.7 million people died globally in 2019 due to nonattainment pollutants, with 4.1 million deaths attributed to fine particulate matter [2]. Particulate matter with a diameter of less than 2.5 µm (PM2.5) is one of the major air pollutants; it penetrates deep into the human bronchial tubes and alveoli, harms the immune system, and leads to chronic respiratory diseases, lung cancer, and cardiovascular diseases [1,3]. Prediction of PM2.5 concentrations can effectively support environmental management and provides a basis for the development of rational decision-making programs.
Previous studies on PM2.5 prediction can be categorized into deterministic models, statistical models, and machine learning models. Deterministic models, also known as chemical transport models, predict PM2.5 concentrations by simulating the physical transport and chemical reactions of air pollutants, such as the incremental testing of the Community Multiscale Air Quality model [4] and the Weather Research and Forecasting model coupled with Chemistry [5]. However, these methods require abundant priori knowledge and relatively complex computations, leading to high uncertainties in the prediction results [6,7].
Statistical modeling, on the contrary, overcomes these limitations in PM2.5 prediction and has a certain degree of interpretability [8]. Linear models, such as linear regression [9,10] and multiple linear regression [11,12], were the primary methods for PM2.5 prediction. However, the models established in these studies are global regression models, indicating that the relationship between yield and explanatory variables is assumed to be spatially constant. In reality, this relationship is highly variable in time and space, especially in extensive areas, always influenced by natural and anthropogenic factors, i.e., spatial heterogeneity (or spatial non-stationarity) [13]. The phenomenon that an explanatory variable has different effects on model output over space is known as spatial heterogeneity [14]. The relationship of each feature variable with PM2.5 can be highly variable in varying geographical locations within the research area [15]. Therefore, scholars further proposed various spatial statistical regression models, such as the geographically weighted regression model [16], linear mixed effects model [17], two-stage model [18,19], and geographically and temporally weighted regression model [20]. The geographically weighted regression model effectively utilizes the spatial distribution characteristics of PM2.5, capturing spatial coefficient variations at the local scale. In addition to space, time is an important dimension that affects the relationship between PM2.5 and the feature variables [21]. Therefore, the geographically and temporally weighted regression model further considers the spatiotemporal heterogeneity and can capture the changing patterns of the data under different spatiotemporal conditions. These studies primarily focus on enhancing model accuracy by incorporating meteorological parameters and land use variables. However, by introducing random or local effects into the regression model, they tend to simplify the complex nonlinear relationships between variables, resulting in weak feature learning capabilities and limiting predictive performance [22].
Machine learning models can fit nonlinear relationships better than statistical models, such as random forest (RF) models [23,24] and neural networks [25,26]. However, the geographical and temporal features hidden in time series and spatial distributions have not been fully exploited [27]. In recent years, prediction models based on deep learning (DL) have achieved significant success in forecasting spatiotemporal data, using techniques such as convolutional neural networks (CNN) [28], general regression neural networks [29], and some models based on long short-term memory (LSTM) [30,31]. Most recurrent neural network models are based on time series, ignoring spatial heterogeneity and spatial correlation, which strongly affects the geographic objects (i.e., PM2.5) [32]. The DL model based on CNN–LSTM can effectively capture the spatial features of PM2.5 and the complex relationships among feature variables through CNN. Simultaneously, LSTM has an excellent advantage in dealing with time series, whereas bidirectional LSTM (Bi-LSTM), with bidirectional dependencies, further enhances the learning capacity for time series features. In addition, to better handle the complex correlated features between variables and PM2.5, the convolutional attention module (CBAM) is introduced into the model, providing enhancement from channel and spatial dimensions [33]. However, CBAM mainly captures global information, thereby limiting its performance in dealing with local spatial information to some extent. Most of the existing studies on hybrid DL models based on CNN–LSTM obtain data from densely populated areas with relatively uniform distributed monitoring station distribution (e.g., the Beijing–Tianjin–Hebei urban agglomeration, southeastern provinces in China, etc.) [34,35,36,37]. For the hybrid DL model designed for PM2.5 prediction in spatially large-scale study areas, although the enhanced ability to capture spatial features has led to a significant improvement in the prediction performance, the results remain unsatisfactory due to the sparse observation data in some areas [15,27,30,38,39].
In addition to the model structure, completing features related to PM2.5 is also important for the accurate forecast of PM2.5. The aerosol optical depth (AOD) data has been widely used for the estimation and inversion of surface PM2.5 concentration for its spatial continuity [40,41]. However, some areas frequently face substantial gaps in AOD product coverage during the autumn and winter seasons, and it is difficult to achieve a high level of prediction accuracy with the existing means of filling [42]. In the past, PM2.5 prediction studies in the Xinjiang Uygur Autonomous Region (hereinafter Xinjiang) often superimposed daily AOD data and averaged it to predict the annual or monthly average concentration of PM2.5, resulting in relatively low prediction accuracy [43,44,45,46]. Therefore, this study matched daily AOD data to sites for inclusion in the study of characteristic variables.
In summary, establishing a multi-station long-term PM2.5 prediction framework holds crucial value for regional pollution management and public health. Nevertheless, the spatiotemporal heterogeneity of PM2.5 poses a great challenge for accurate multi-station PM2.5 forecasting. Therefore, this study is dedicated to developing a spatiotemporal weighted neural network (STWNN) by aggregating neighborhood spatiotemporal information. It considers the impact of spatial heterogeneity and temporal dependency on PM2.5 to enhance the accuracy of PM2.5 long-term predictions (seven days). Considering Xinjiang, China as the study area, this study is dedicated to addressing the following objectives: (1) Analyze the spatiotemporal distribution characteristics of PM2.5 and identify its sources of pollution in Xinjiang; (2) compare the predictive performance of the STWNN with CNN–LSTM, CNN–Bi-LSTM, and CBAM–CNN–Bi-LSTM (CBAM+) under different temporal clustering scenarios; and (3) conduct a spatiotemporal analysis of errors and use the SHapley Additive exPlanations (SHAP) method to calculate the contribution distribution of feature variables within the STWNN, demonstrating its interpretability.
2. Study Area and Materials
2.1. Study Area
Xinjiang is located in northwestern China (73°40′ E~96°23′ E, 34°22′ N~49°10′ N), covering a total area of 1,664,900 km2. It is the largest provincial-level administrative region in China and accounts for approximately one-sixth of the nation’s total land area. The topography of Xinjiang is characterized by mountains and basins, with the Altai Mountains, Junggar Basin, Tianshan Mountains, Tarim Basin, and Kunlun Mountains, forming a “three mountains and two basins” landscape, in that order. The snow and glaciers from these mountain ranges converge to create over 500 rivers, predominantly distributed in the basins located to the north and south of the Tianshan Mountains. Xinjiang has a temperate continental climate characterized by substantial temperature variations and ample sunshine (annual sunshine duration ranging from 2500 to 3500 h). The climate is dry, marked by scarce precipitation (average annual precipitation of 150 mm). Influenced by the topography and spatial distribution of water resources, urban agglomerations in the region typically align in strip or ring formations, and the geographic distribution of environmental monitoring stations in Xinjiang is consistent with the distribution of cities (Figure 1). Cities and urban agglomerations play an important role in regional economic development, but air pollution has become an urgent problem in the region due to the intense human activities and fragile ecological environment.
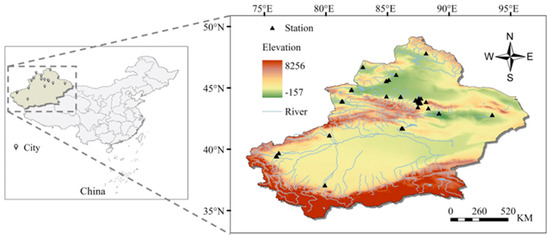
Figure 1.
Study area.
2.2. Data
The study data mainly consist of ground-based observed PM2.5 concentrations and satellite data products (AOD, meteorological data, and normalized vegetation index (NDVI)). Details of the specific data and sources (Table 1) used are as follows.

Table 1.
Details of major data sources in this research.
2.2.1. PM2.5
Ground-level concentrations of PM2.5 are crucial data for refining model parameters and assessing estimation outputs. The PM2.5 data utilized in this study were sourced from the China Environmental Monitoring Center (http://www.cnemc.cn/, accessed on 1 January 2023). Specifically, hourly PM2.5 data spanning from 1 January 2021 to 31 December 2021 were collected from 46 effective monitoring stations (Figure 1) within the Xinjiang region.
2.2.2. Feature Variables
AOD exhibits a strong correlation with near-surface PM2.5 concentrations and is widely used for estimating and inverting surface PM2.5 concentrations [47,48]. For this study, we obtained the MODIS Collection 6 MAIAC AOD product (MCD19A2 V6.1) from the Land Processes Distributed Active Archive Center (https://lpdaac.usgs.gov/, accessed on 3 August 2023) provided by the National Aeronautics and Space Administration. The data, generated daily at a one-kilometer resolution, include quality assurance measures to ensure retrieval quality.
The distribution and chemical–optical properties of PM2.5 are significantly influenced by meteorological conditions [49,50]. Therefore, six meteorological variables were selected from the European Center for Medium Weather Forecasting (https://www.ecmwf.int/, accessed on 4 August 2023) (Table 1) as follows: boundary layer height (BLH, m), dew point temperature (D2M, K), wind speed (WD, m/s), surface pressure (SP, Pa), air temperature (T2M, K), and precipitation (TP, m), each with a spatial resolution of 0.25° × 0.25°.
In addition to meteorological variables, changes in vegetation cover can induce local climate variations impacting PM2.5 concentrations [51]. Therefore, we also considered land cover type. In this study, the NDVI was used as an approximation of land cover type. NDVI data were obtained from the MODIS 16-day NDVI product (MOD13A2\MYD13A2) with a spatial resolution of 1 km and a temporal resolution of 16 days (https://lpdaac.usgs.gov/, accessed on 3 August 2023).
2.3. Data Preprocessing
Hourly observations of PM2.5 were averaged daily for daily estimation. After removing abandoned monitoring stations, there are a total of 46 valid stations in the Xinjiang region with a missing data rate of less than 5%. The Lagrange interpolation method was used to fill in the small amount of missing data in the valid station to encode the daily mean PM2.5 concentration values into a time series format for input into the time series module structure [52]. For the model fitting and testing, the multisource remote sensing products ((i.e., AOD, meteorological, NDVI) were initially preprocessed to remove nulls. Among them, the MODIS data are preprocessed by ENVI + IDL, including quality control, mean value calculation, same-day Mosaic, reprojection, coordinate system transformation, etc., and the NDVI is filled linearly using the interpolate method, resampling the temporal resolution to daily so that small variations are reflected daily. Subsequently, all raster predictor variables were uniformly resampled to the same spatial size (1 km) and the temporal interval (one day) using the bilinear interpolation method. Finally, the multisource data and ground station PM2.5 mass concentration data were matched temporally and spatially based on latitude, longitude, and time. To validate the model’s generalization ability, the dataset was partitioned into a training set (70%), a validation set (20%), and a test set (10%).
3. Methods
3.1. Flow Chart
The flow chart of this study is shown in Figure 2. First, all the data were preprocessed and coded into time series form, and then analyzed for correlation. Second, the spatiotemporal analysis of PM2.5 in Xinjiang was conducted, and all data were divided into four clusters (seasonal) in the temporal dimension. Finally, using these distinct clusters, different models were evaluated and compared in terms of training and validation performance, and the interpretability of the STWNN was verified.
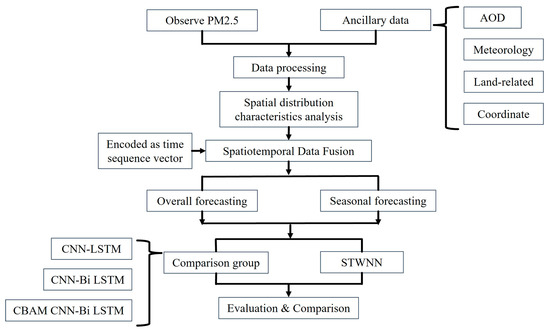
Figure 2.
Flow chart of PM2.5 concentrations prediction.
3.2. Spatiotemporal Analysis and Clustering
In the temporal dimension, we computed the mean and standard deviation of PM2.5 concentrations at various time scales and analyzed the variation characteristics on seasonal and monthly scales in Xinjiang. We used inverse distance weighted interpolation and Moran’s I statistics for the spatial dimension to analyze the spatial distribution characteristics of PM2.5 concentrations. The inverse distance weight interpolation was used to estimate the unknown points. The expressions are as follows:
where is the interpolated value of the unsampled point , is the eigenvalue of the sampled point , is the distance between the sampled point and the unsampled point, is the number of sampled points, and is the power exponent controlling the degree of distance influence, typically ranging from 1 to 3.
Moran’s I assesses the spatial correlation of a variable [53,54]. The global Moran’s I statistic indicates clustering presence or absence across all sample points. Local Moran’s I is a statistical metric identifying and assessing spatial patterns of PM2.5 hotspot areas. The formulas for the global and local Moran’s I statistics are as follows:
where is the global Moran’s I statistic, is the local Moran’s I statistic of sample point I, is the variance of all values, and are the values of sample points and , respectively, is the mean value of all sample points, is the spatial weight, and is the number of sample points.
Moran’s I statistic ranges from −1 to 1. A positive global Moran’s I indicates spatial positive correlation, whereas a negative value suggests negative correlation. When local Moran’s I is statistically significant, sample points can be categorized into high–high, high–low, low–high, and low–low clusters.
3.3. STWNN
The STWNN utilizes multi-temporal, multisource remote sensing products as inputs, aggregates domain spatial features based on spatial signals, enhances feature learning capabilities through an improved channel attention mechanism, and acquires temporal features using a Bi-LSTM structure to augment spatiotemporal features. Finally, the predicted PM2.5 concentrations for the upcoming week serve as the output. The modeling framework is segmented into spatial, attention, and temporal modules (Figure 3).
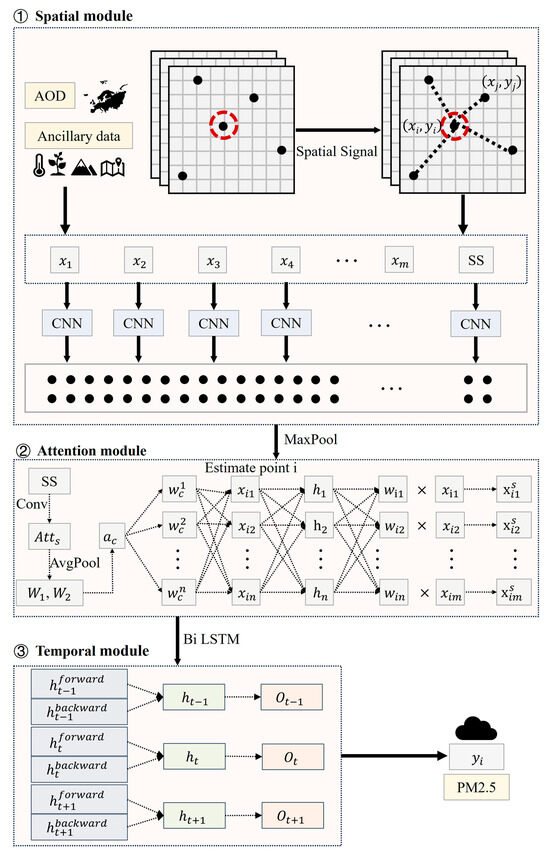
Figure 3.
Overall architecture of the STWNN model for PM2.5 estimation.
3.3.1. Spatial Module
Given the sparse and heterogeneous stations in Xinjiang, spatial clustering often leads to model overfitting due to fewer stations in some clusters, thereby increasing uncertainty and error. Therefore, this study is based on the STWNN (Figure 3) that captures local dependencies in limited spatial data to deal with spatial correlation and heterogeneity of spatial objects. To achieve this objective, the spatial signal (SS) is introduced in the spatial module [55]. The SS is calculated as follows:
where the SS considers the effect of neighboring observations near the target point and uses distance weighting to enhance or attenuate the effect of the nearer observations, is the PM2.5 concentration of point near the target data point , is the distance between points and , n is the number of the nearest points of point , and the adaptive nature of usually ensures sufficient local calibration when the samples are dense or sparse and is crucial for calculating spatial correlation. is defined as the Euclidean distance, calculated using the coordinates of point and point , as follows:
Subsequently, the SS at each time node “t” is encoded as a time series vector input to the CNN along with other feature variables to extract all feature variables and obtain the spatial dependencies of all stations. Meanwhile, the TimeDistributed layer is used to obtain more information about the historical time step of the time series data. This condition allows the CNN to overcome the limitation of using only previous data from a single point in time as an input, enabling the capture of long-term data features. The primary structure of the CNN encompasses an input layer, a convolutional layer, a pooling layer, a fully-connected layer, and an output layer. The information from the input layer is processed through feature transformation and extraction in the convolutional and pooling layers. This local information from the convolutional and pooling layers is further integrated by the fully connected layer and mapped to the output signal through the output layer. The feature mapping function is defined as follows:
where is the output value of the feature mapping in the row and column, is the value of the input matrix in the row and column, is the activation function, is the weight of the convolution kernel in the row and column, and is the bias of the convolution kernel.
3.3.2. Attention Module
The channel attention module amplifies the feature representation of a convolutional neural network by leveraging SS signals to emphasize the most informative features. Initially, the module generates channel attention weights for the model through two fully connected layers and a ReLU activation function. Furthermore, the SS is isolated from the input tensor, and a spatial attention map is produced via convolutional layers () and an activation function (sigmoid). This attention map comprises weights that quantify the importance of each spatial location in the SS signal, thereby capturing intricate relationships and dependencies between the input feature channels. Subsequently, the weights acquired through this process are propagated to other feature channels to obtain the adjusted SS signal. This approach not only preserves the information within the SS signal itself but also elevates the representation of the feature channels. The channel attention layer seamlessly integrates after the initial maximum pooling layer of the model, enabling the attention mechanism to refine the feature representation early in the network. This refinement profoundly impacts the subsequent layers, enhancing their ability to extract and process the most relevant information. The adjusted SS signal undergoes element-wise multiplication with the feature variables within the channel, yielding the final feature representation. This targeted feature refinement empowers the network to learn more robust and discriminative feature representations, ultimately translating into improved predictive performance. The weighting formula is as follows:
where is the spatial attention map, which is generated by SS; and are the weight matrices of the two fully connected layers; is the adjusted spatial signal, which is the channel attention weight; is the convolutional layer, and and are the activation functions.
3.3.3. Temporal Module
LSTM is a special type of recurrent neural network model that overcomes the phenomena of gradient explosion and vanishing in error back propagation and effectively captures long- and short-term information LSTM using an input layer, an output layer, and a series of memory blocks. Each LSTM block contains an oblivion gate , which determines how much information is retained from time step ; an input gate , which determines how much information is stored from the current time step ; a cell state , which updates the current cell state; and an output gate , which determines how much information from the current cell state is transferred to the output. The LSTM equation for time step can be expressed as follows:
where , , , and denote the vectors of the oblivion gate, input gate, output gate, and cell state, respectively; , , , and are the weights; , , , and denote the bias vectors of the corresponding gate state and cell state; and are the output vectors of the different time steps and , respectively; is the current input, and combines the two vectors into the output; and and are the activation functions.
Bi-LSTM is an extension of LSTM; it overcomes the shortcoming of LSTM in which the time series only flows forward and allows the time series to flow both forward and backward [56,57]. In Bi-LSTM, the output vector at time step t is expanded into two vectors: and . Combining these vectors from the oppostation time directions forms the final output vector [,], i.e., . The Bi-LSTM uses independent hidden layers in two directions; thus, each hidden layer can record past and future information. Therefore, Bi-LSTM can be regarded as a model with a built-in time weighting mechanism, it retrieves a more comprehensive set of PM2.5 features to improve the prediction of the network.
In this experiment, we use Keras, based on TensorFlow, to construct the proposed STWNN model. Table 2 displays the parameters utilized to train the prediction model.

Table 2.
STWNN model parameters setting.
3.4. Evaluation Indicators
Four metrics, the root mean square error (RMSE), the mean absolute error (MAE), the coefficient of determination (R2) and the index of agreement (IA), were selected to evaluate the model [34,35,58]. RMSE reflects the sensitivity of the model to errors, and MAE reflects the stability of the model. When both values are close to 0, the prediction result is improved. R2 indicates the prediction ability of the actual data, and IA indicates the similarity of the distribution between the actual and predicted values, and the value of the two variables spans [0,1]. Moreover, when the value is closer to 1, the prediction result is consistent with the distribution of the actual data. The formula is as follows:
3.5. Explainability Analysis of Deep Learning Models
This study introduces SHAP to quantify the influence of various feature variables on forecasting outcomes. It connects optimal credit allocation with local explanations by the classical Shapley values from game theory and the related extensions [59]. It aims to calculate the impact of different feature variables on the model output in each sample and show the positivity or negativity of the impact [60]. SHAP calculates distinct marginal contributions of feature variables considering all sequences of variables and ensuring equitable comparisons. The final feature contribution is the weighted average of marginal contributions for each feature variable when incorporated into the model. The formula is expressed as follows:
where y(x) is the predicted value of the model that includes some feature variables and F is the number of total subsets of input features.
4. Results
4.1. Variable Importance
The variable importance test refers to the computation of the importance of each variable in model design [61]. In this study, RF is introduced to quantify the importance of variables. Following the variable selection strategy [62], variables with importance scores below 2% are excluded. As shown in Figure 4, the importance scores of all variables in this research exceed 2%, positively contributing to the estimation accuracy of the model. The most crucial variable is AOD (33.69%), which exhibits a high correlation with PM2.5 concentrations. Meteorological variables also play a significant role in PM2.5, particularly BLH (21.05%). The thick temperature inversion layer and low precipitation and BLH increase the air stagnation, stabilizing the polluted air over the area without diffusion [63]. A relatively high relative humidity favors the formation of secondary aerosols, a vital component of PM2.5 [64]. In addition, the land-related variables of the NDVI (8.65%) exhibit a considerable impact.
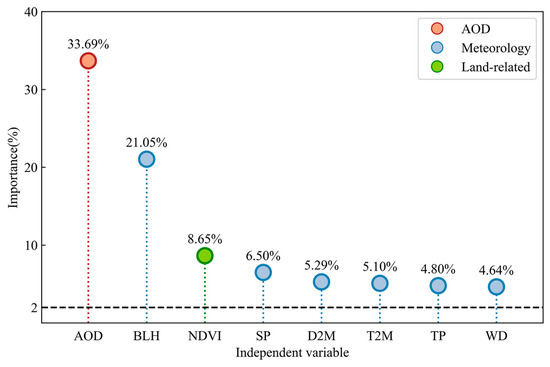
Figure 4.
Importance of independent variables selected for PM2.5 prediction.
4.2. Characteristics of Spatial and Temporal Distribution of PM2.5
In the time dimension, Figure 5 analyzes the annual, seasonal, and monthly changes in PM2.5 index. Figure 5a illustrates that the annual average PM2.5 concentration in Xinjiang was 44.42 in 2021, exceeding the national average (30). The PM2.5 levels exhibited significant seasonal differences (p < 0.001), following the order of spring, winter, summer, and autumn. Average PM2.5 concentrations in summer (26.98) and autumn (21.97) were below the national results, whereas those in spring (73.95) and winter (54.78) were notably higher. Figure 5b indicates that the monthly average PM2.5 concentrations in Xinjiang ranged from 15.93 to 86.61 in 2021, showing a U-shaped trend with higher values at the beginning and end of the year and lower values in the middle. Notably, June recorded the lowest average PM2.5 concentration (15.93), whereas January had the highest (86.61). These variations suggest that PM2.5 pollution concentrations in Xinjiang were generally excellent and stable during summer and autumn in 2021, with increased concentrations in spring and winter.
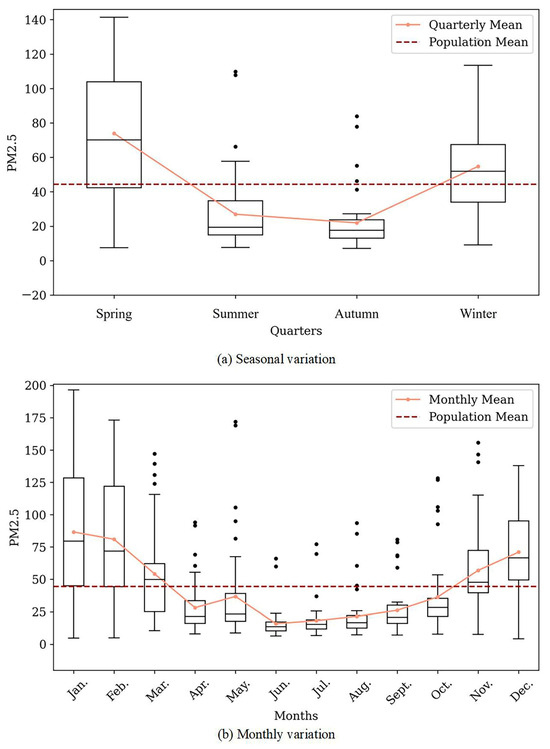
Figure 5.
Temporal distribution.
In the spatial dimension, Moran’s I statistical value of the annual mean PM2.5 concentrations at several stations in Xinjiang in 2021 was 0.71 (p < 0.001). Moreover, Moran’s I values for seasonal mean concentrations in summer (0.95), autumn (0.92), and winter (0.74) exceeded those for annual mean concentrations. This finding implies significant positive spatial correlation and aggregation of annual mean PM2.5 concentrations at multiple stations in Xinjiang. Seasonal datasets better reflected spatial aggregation changes. In addition, inverse distance weighting was applied to the mean PM2.5 concentrations for each season in 2021. During summer, autumn, and winter, Xinjiang exhibited a trend of higher PM2.5 concentrations in the southwest and lower concentrations in the northeast. Local Moran’s index statistics (Figure 6) indicate high–high clustering in the Kashgar (Ⅰ) and Hotan (Ⅱ) regions in southern Xinjiang during summer. Conversely, most areas in northern Xinjiang display low–low clustering in summer and autumn. Among them, the urban agglomeration on the northern slope of the Tianshan Mountain (Ⅲ) no longer follows this pattern in winter, showing elevated PM2.5 concentrations, gradually shifting to high–high clustering in spring.
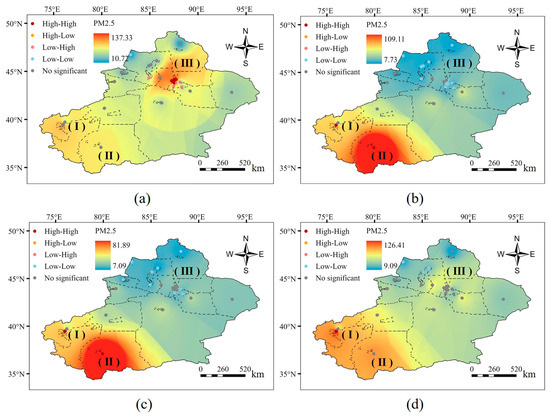
Figure 6.
Spatial and temporal distribution characteristics of seasonal PM2.5 using the localized Moran’s index. (a) Spring analysis, (b) summer analysis, (c) autumn analysis, and (d) winter analysis.
In summary, the region displayed significant spatiotemporal heterogeneity in PM2.5 concentrations. In northern Xinjiang, the large temperature difference between day and night during the summer and autumn seasons, coupled with intense solar radiation, led to a rapid rise in surface temperatures and heating of the near-surface air. This condition resulted in increased convection, unstable atmospheric stratification, and enhanced precipitation, facilitating the diffusion and deposition of air pollutants. Consequently, PM2.5 concentrations were generally lower in northern Xinjiang during summer and autumn. By contrast, emissions from operations such as mining and transportation of energy sources (e.g., oilfields and coal) in the core area of urban and industrial development on the northern slopes of the Tianshan Mountains contributed to rising PM2.5 concentrations in winter and spring. In addition, surface inversions caused by low surface temperatures in spring and winter hindered vertical convection, impeding pollutant diffusion. The widespread dusty weather in southern Xinjiang, influenced by cold air activities in spring, also had a significant impact on northern Xinjiang. In southern Xinjiang, the abundance of deserts brought a rich source of atmospheric pollutants, and the region, surrounded by mountains on three sides, caused floating dust to linger for an extended period, resulting in prolonged high concentrations of PM2.5. The primary sources of PM2.5 in southern Xinjiang were windy dust, supplemented by oil and gas combustion, and to a lesser extent, coal combustion emissions.
4.3. Model Fitting and Validation
4.3.1. Determination of Proximity Points Number N for SS
The determination of the proximity point number (n) is critical for assessing spatial correlation. Through multiple experiments (refer to Table 3), the optimal prediction performance was achieved when n = 3. Consequently, this study aggregated the spatiotemporal information from three stations near each sampling point. The features were spatially augmented using a distance-weighting method, enabling the model to effectively compute spatial correlation and achieve optimal performance.

Table 3.
Effect of number of adjacent points on model performance.
4.3.2. Overall Forecasting
The prediction accuracies of the four PM2.5 prediction models based on the relevant data in 2021 are shown in Figure 7. For single-day predictions, the MAE ranks in descending order are STWNN, CBAM+, CNN–Bi-LSTM, CNN–LSTM, and similarly in ascending order for IA. The RMSE follows the descending order of STWNN, CNN–Bi-LSTM, CBAM+, CNN–LSTM, and the same ascending order for R2. Among these models, STWNN (RMSE = 16.23, MAE = 8.43, R2 = 0.92, and IA = 0.78) exhibits the best predictive ability, whereas the original CNN–LSTM (RMSE = 24.09, MAE = 13.18, R2 = 0.78, IA = 0.73) performs the least favorably. The other models show improvements in predictive ability compared with the CNN–LSTM.
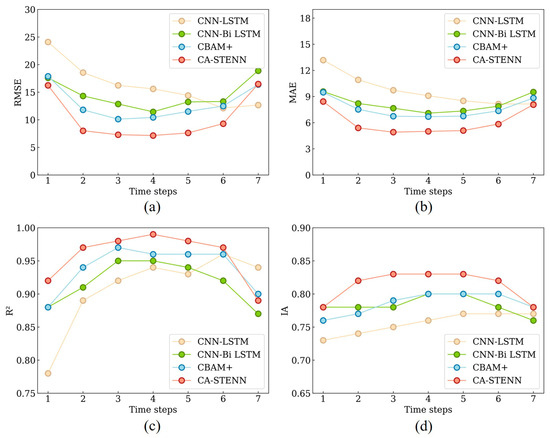
Figure 7.
Overall PM2.5 forecasting. (a) RMSE, (b) MAE, (c) R2, and (d) IA.
For multi-day forecasting, prediction accuracy generally increases and then decreases with the number of days, with models reaching peak accuracy around the fourth day (Figure 7). Averaging the prediction accuracies over the seven days, STWNN (RMSE = 10.29, MAE = 6.10, R2 = 0.96, and IA = 0.81) has the highest average prediction accuracy (Figure 8). Notably, STWNN (RMSE = 7.15, MAE = 4.19, R2 = 0.99, and IA = 0.83) has the highest prediction accuracy on the fourth day.
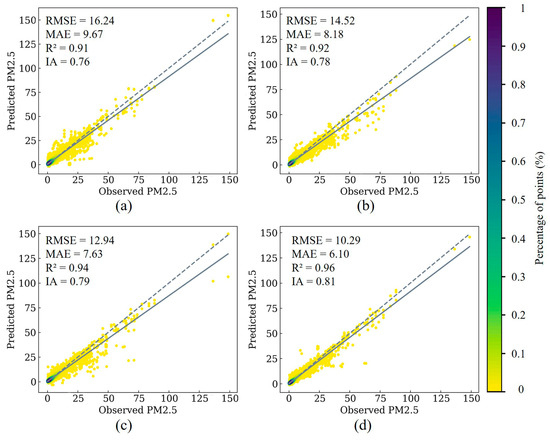
Figure 8.
Overall forecasting scatter plots for (a) CNN–LSTM, (b) CNN–Bi-LSTM, (c) CBAM+, and (d) STWNN. The color of points represents the percentage of the total number of points in this value range. A higher percentage indicates that more data points are within this value range. The average value of multi-step prediction evaluation results is provided (N = 34134).
In the experiment, the time step was set at 7, corresponding to one week. This value allows the model to capture cyclical changes effectively, leading to improved simulation accuracy for the first four to five days. However, for longer time spans, increased uncertainty in spatiotemporal features may result in overfitting and reduced prediction performance.
4.3.3. Seasonal Forecasting
Given the evident seasonal differences in PM2.5 concentrations within Xinjiang, the dataset is categorized into four clusters based on the seasons, leading to the establishment of a seasonal PM2.5 prediction model for each cluster (Figure 9). The multi-day prediction accuracy trend of the seasonal prediction model is approximately similar to that of the overall forecasting model, exhibiting an initial increase followed by a decrease (the highest accuracy is reached on the fourth to fifth day). Figure 9 illustrates a comparative analysis of seasonal prediction models utilizing four types of neural networks. Notably, some seasonal differences in prediction accuracy are found among the models, with autumn predictions displaying the most robust performance across all four models (CNN–LSTM (RMSE = 4.56, MAE = 2.7, R2 = 0.95, and IA = 0.87); CNN–Bi-LSTM (RMSE = 6, MAE = 3.28, R2 = 0.94, and IA = 0.86); CBAM+ (RMSE = 4.15, MAE = 2.69, R2 = 0.97, and IA = 0.89); STWNN (RMSE = 4.56, MAE = 2.38, R2 = 0.95, and IA = 0.89)). Examination of the model performance reveals that CNN–LSTM and CNN–Bi-LSTM consistently outperform the overall prediction across all four seasonal clustering predictions. CBAM+ excels in three seasonal clustering predictions (autumn, winter, and summer). By contrast, STWNN demonstrates comparable performance to the overall prediction in spring and summer clustering predictions, outperforming the overall prediction in autumn and winter (Table 4). Notably, in seasonal predictions, STWNN consistently outperforms other models across all seasonal clusters (spring (RMSE = 12.48, MAE = 5.71, R2 = 0.96, and IA = 0.85); summer (RMSE = 10.98, MAE = 5.68, R2 = 0.96, and IA = 0.81); autumn (RMSE = 4.56, MAE = 2.38, R2 = 0.95, and IA = 0.89); winter (RMSE = 7.99, MAE = 5.64, R2 = 0.96, and IA = 0.87)).
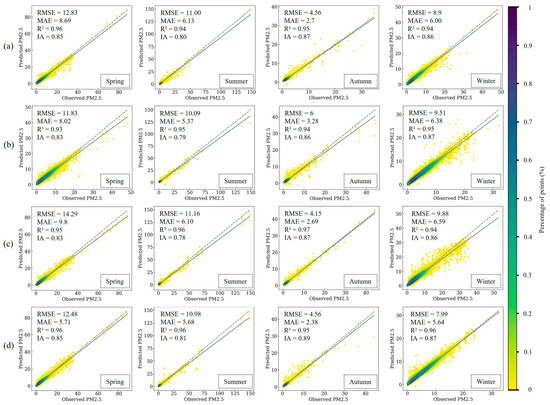
Figure 9.
Seasonal forecasting scatter plots for (a) CNN–LSTM, (b) CNN–Bi-LSTM, (c) CBAM+, and (d) STWNN. N = 7728.

Table 4.
Comparison of overall forecasting and seasonal forecasting by the STWNN model.
Seasonal forecasting, as observed in the experiments, generally outperforms the overall forecasting. This enhanced performance is likely attributed to pronounced seasonal variations in PM2.5 concentrations influenced by meteorological and anthropogenic factors. Season-specific models prove adept at capturing these unique patterns, resulting in more accurate predictions. Training distinct models for each season allows the network to learn season-specific features without being confounded by broader variations in annual data. This approach acknowledges that discretizing data across different seasons may limit the ability to perform accurate seasonal forecasting. In Xinjiang, autumn PM2.5 concentrations are generally low, leading to consistently small prediction errors. Conversely, in spring, the discrete and fluctuating nature of PM2.5 concentrations, especially with high values, hampers the model’s forecasting ability, resulting in larger errors. This limitation is likely linked to the frequent occurrence of dust storms during spring in the Xinjiang region.
4.4. Spatiotemporal Variation of Feature Variable Based on SHAP Values
On the basis of the results of the overall and seasonal forecasting, the distribution of each feature variable’s contribution to the PM2.5 forecasting is described from a global interpretability standpoint. This analysis considers station A (Altay 2708A) in the northern part of the northern frontier, station B (Urumqi 1494A) in the urban agglomeration on the northern slope of the Tianshan Mountain, and station C (Kashgar 2699A) located on the western edge of the Taklamakan Desert in the southern frontier (Figure 10a).
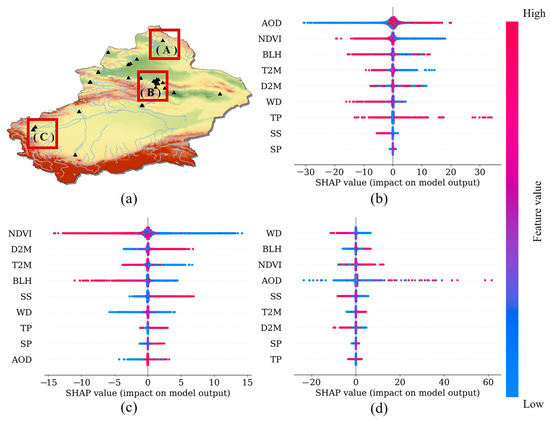
Figure 10.
SHAP values for nine factors when predicting PM2.5 concentrations in different regions throughout Xinjiang ((a) the location of the selected stations, (b) station A, (c) station B, and (d) station C).
4.4.1. Overall Forecasting
Figure 10 and Figure 11 illustrates the distribution of SHAP values for various feature variables at different stations concerning their contributions to PM2.5 in the overall predictions. Figure 10b indicates that station A is predominantly influenced by AOD (SHAP value = 1.14, contributing 39.83%), exerting a significantly positive impact on PM2.5. Elevated AOD levels forecasting increased vertical aerosol accumulation, resulting in atmospheric haziness and a subsequent increase in PM2.5 levels. The contributing factors as well as their corresponding SHAP values and percentage contributions are as follows: NDVI (SHAP value = 0.744 with a contribution of 26%), BLH (SHAP value = 0.296 with a contribution of 10.34%), T2M (SHAP value = 0.293 with a contribution of 10.24%), and D2M (SHAP value = 0.145 with a contribution of 5.07%). Figure 10c reveals that station B is mainly driven by the NDVI (SHAP value = 0.787 with a contribution of 58.08%), leading to a substantial negative impact on PM2.5. Therefore, relatively high vegetation cover promotes the absorption and deposition of PM2.5, resulting in a decrease in PM2.5 levels. Subsequent factors include D2M (SHAP value = 0.127 with a contribution of 9.37%), T2M (SHAP value = 0.127 with a contribution of 9.37%), BLH (SHAP value = 0.111 with a contribution of 8.19%), and SS (SHAP value = 0.088 with a contribution of 6.49%). Figure 10d indicates that station C is primarily influenced by WD (SHAP value = 0.154 with a contribution of 16.68%), resulting in a negative impact on PM2.5. Wind tends to bring abundant pollutants from the sand source given its proximity to the desert. The subsequent factors include BLH (SHAP value = 0.137 with a contribution of 14.84%), NDVI (SHAP value = 0.134 with a contribution of 14.52%), AOD (SHAP value = 0.131 with a contribution of 14.19%), and SS (SHAP value = 0.129 with a contribution of 13.98%). A relatively high SS value indicates a more substantial influence of surrounding stations on the focal point, with the positivity or negativity of the impact depending on the PM2.5 levels at the surrounding stations. This result aligns with the presented results in the figure. The contribution distribution of these aforementioned features indicates spatial heterogeneity between PM2.5 and the feature variables.
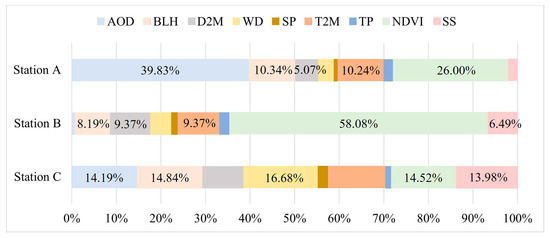
Figure 11.
Contribution of each factor predicting PM2.5 concentrations in different regions throughout Xinjiang.
4.4.2. Seasonal Forecasting
Apart from regional variations in key variables, seasonal differences in the impact of feature variables on PM2.5 are observed. Figure 12 displays the mean absolute SHAP values and contribution percentages of the top three contributing feature variables, where higher SHAP values indicate a greater influence on the dependent variable.
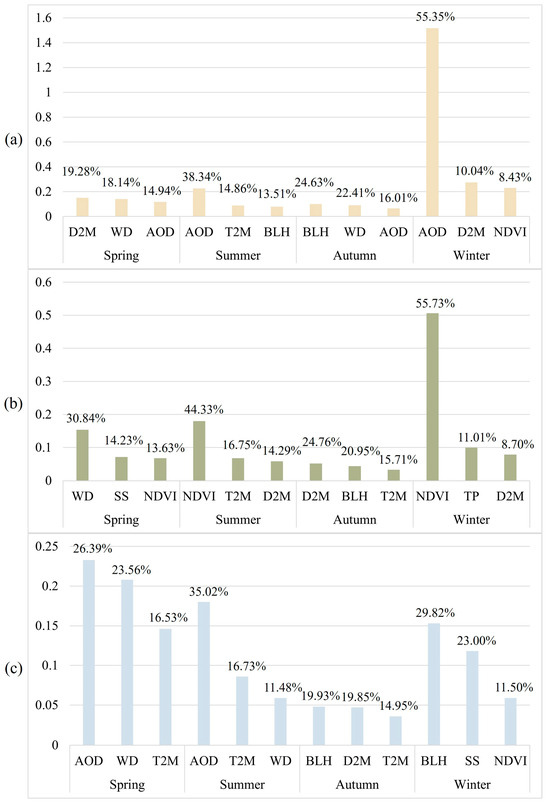
Figure 12.
Dominant factors affecting PM2.5 concentration and their SHAP values in different regions ((a) station A, (b) station B, and (c) station C) of Xinjiang in different seasons.
The Altay region, where station A is located, is in the northernmost part of Xinjiang and is recognized as a water-sustaining mountain grassland ecological function area with light PM2.5 pollution. In summer and winter, AOD remains the dominant factor, consistent with the overall predictions. However, spring and autumn exhibit different dominant factors and seasonal differences. In spring, D2M significantly influences PM2.5 at station A (SHAP value = 0.151 with a contribution of 19.28%), showing a negative impact. Subsequently, WD, and AOD contribute 18.14% and 14.94%, respectively. The region experiences dry and windy conditions in spring. Consequently, changes in D2M significantly affect aerosol wetting and condensation processes, thereby substantially influencing the PM2.5 concentrations. In summer, AOD has a major negative impact on the area where station A is located (SHAP value = 0.227 with a contribution of 38.34%), followed by T2M and BLH, contributing 14.86% and 13.51%, respectively. In autumn, BLH has a significant negative impact on station A (SHAP value = 0.100 with a contribution of 24.63%), followed by WD and AOD with contributions of 22.41% and 16.01%, respectively. The region experiences clear and cool conditions in autumn, with a usually larger boundary layer height, facilitating pollutant dispersion and resulting in reduced PM2.5 concentrations and relatively good air quality. In winter, AOD significantly influences station A, contributing 55.35% (SHAP value = 1.516), followed by D2M and NDVI contributing 10.04% and 8.43%, respectively. Moreover, in spring and autumn, the second and third contributing feature variables (WD and AOD, respectively) are consistent. Generally, higher wind speeds are believed to enhance aerosol diffusion and reduce AOD values [65].
Similar to station A, the dominant factor (NDVI) for station B in summer and winter aligns with the overall predictions, whereas the meteorological variables become dominant in spring and autumn, showing seasonal differences. In spring, WD significantly influences station B (SHAP value = 0.154 with a contribution of 30.84%), followed by SS and NDVI with contributions of 14.23% and 13.63%, respectively. The Urumqi region, where station B is located, is in the urban agglomeration of the northern slope of Tianshan Mountain. The region experiences the highest wind speed in spring, beneficial for reducing PM2.5 concentrations, negatively affecting the predictions. In summer, the NDVI has a major impact on station B (SHAP value = 0.18 with a contribution of 44.33%), followed by T2M and D2M with contributions of 16.75% and 14.29%, respectively. In autumn, humidity has a significant impact on station B (SHAP value = 0.052 with a contribution of 24.76%), followed by BLH and T2M with contributions of 20.95% and 15.71%, respectively. In winter, the NDVI significantly influences station B, contributing 55.73% (SHAP value = 0.506), followed by T2M and D2M with contributions of 11.01% and 8.7%, respectively. Abundant precipitation tends to bring moist water vapor, and high humidity conditions usually occur under low-pressure systems, jointly affecting PM2.5 nucleation, condensation, and coagulation, resulting in elevated PM2.5 concentrations [66].
Station C is located in the southwestern part of Kashgar, surrounded by mountains on three sides and the Taklamakan Desert to the east, where floating dust lingers for an extended period and is not easily dispersed. Because of the windy, sandy and floating dust weather in this area in spring and summer, AOD has a significant impact on station C in spring (SHAP value = 0.233 with a contribution of 26.39%) and summer (SHAP value = 0.180 with a contribution of 35.02%), followed by WD and T2M because of the windy, sandy, and floating dust weather in this area in spring and summer. In addition, BLH has a greater impact on the area, where station C is located in the autumn (SHAP value = 0.048 with a contribution of 19.93%), followed by D2M and T2M with contributions of 19.85% and 14.95%, respectively. In winter, BLH (SHAP value = 0.153 with a contribution of 29.82%) is also the largest dominant factor, followed by SS and NDVI, with contributions of 23.00% and 11.50%, respectively. These characteristics are consistent with the top five dominant factors with closer contributions in the overall prediction of the previous section.
5. Discussion
The STWNN model demonstrated that spatial signals in sparsely and unevenly distributed areas can enhance the predictive performance of PM2.5. STWNN strengthened its ability to capture spatial heterogeneity by incorporating spatial information into the model. In the overall forecasting, SS significantly improved the model’s predictive performance (RMSE = 10.29, MAE = 6.10, R2 = 0.96, and IA = 0.81), with STWNN emerging as the optimal PM2.5 prediction model in this study. Taking MAE as an example, the predictive errors of STWNN were decreased by 36.9% (CNN–LSTM), 25.4% (CNN–Bi-LSTM), and 20.1% (CBAM+) compared to other models. Autocorrelation analyses of the errors for each model in the overall forecasting were conducted, to investigate the spatiotemporal characteristics of the model performance. The results indicate that the errors are randomly distributed in the study area, signifying effective capturing of spatial heterogeneity by the models. Notably, for CNN–LSTM (0.081), CNN–Bi-LSTM (−0.126), CBAM+ (0.116), and STWNN (0.006), all p-values are less than 0.05. The degree of error aggregation of STWNN was evidently weaker than that of other models, demonstrating that STWNN was better at capturing spatiotemporal heterogeneity. In temporal clustering, there is a certain improvement found in predictive accuracy based on seasonal clustering. Taking MAE as an example, the prediction errors of STWNN decreased by 10.8% (spring), 11.3% (summer), 62.8% (autumn), and 11.9% (winter) compared to the overall forecasting. Model performance variations may stem from the relationships between PM2.5 and feature variables, temporal clustering methods, and model development techniques. Factors such as data volume, cluster discretization levels, and spatial correlation can also yield different prediction outcomes. Figure 13 provides the spatial distribution of model absolute errors for different temporal clusters under ideal spatiotemporal heterogeneity expression, further illustrating the adaptability of the model within the study area, and showing the superior performance of the STWNN. Comparing the four models, STWNN consistently outperforms others in all temporal clusters, with the model based on seasonal clustering surpassing the overall prediction.
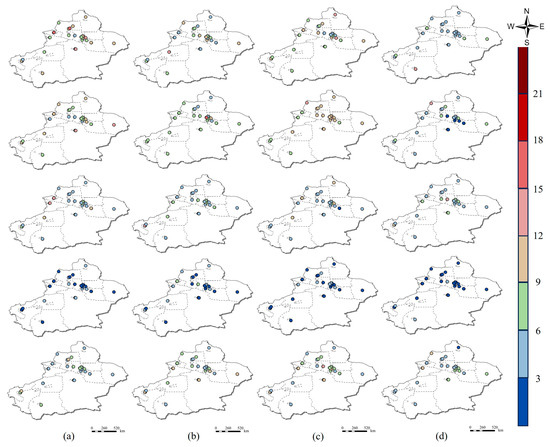
Figure 13.
Spatial distributions of MAE for (a) CNN–LSTM, (b) CNN–Bi-LSTM, (c) CBAM+, and (d) STWNN. Note: Images from top to bottom present the overall forecasting and seasonal forecasting (spring, summer, autumn, and winter).
In this study, RF analysis was used to assess the relative importance of various feature variables. However, this method inadequately conveys the spatial contribution of these variables to PM2.5. To address this issue, the SHAP model was added to conduct interpretative analysis on the STWNN prediction results, revealing the spatiotemporal variations in the driving patterns of feature variables in PM2.5 prediction in Xinjiang province. This approach concludes the intensity and spatiotemporal heterogeneity of the impact of different variables on PM2.5. The variable importance test and SHAP interpretation in this study indicate that AOD, BLH, and NDVI are the most influential variables in generating PM2.5 in Xinjiang. In addition, SHAP results highlight two main differences in the major feature variable of PM2.5 prediction in the study area: geographic location and seasonal variation. In summary, the results of this study encompass the support of early warning systems and the development of management measures to enhance air quality. For example, increasing urban green spaces in agglomerations and judicious use of artificial rain autumn can contribute to long-term PM2.5 reduction.
The proposed STWNN showed satisfactory accuracy in the PM2.5 prediction, but some shortcomings still exist. To enhance the model, considering integrating SS with time-related attention to enhance spatiotemporal features could be beneficial. Meanwhile, additional features, such as socioeconomic data, could be incorporated for more comprehensive information. Moreover, the study area can be refined to urban regions to enhance the spatial resolution (e.g., urban-level 500 m spatial coverage) and improve prediction accuracy and reliability. This will enable more accurate prediction and analysis of PM2.5 changes within cities, providing targeted support for urban air quality management and decision-making.
6. Conclusions
Previous studies on PM2.5 prediction often yielded less-than-ideal results in regions with sparse and unevenly distributed monitoring stations. This study introduces a DL model (STWNN) that integrates spatial signals into a recurrent neural network capable of handling time series. The model enhances feature representation through the SS in attention layer, considering spatial and temporal heterogeneity. The conclusions of this study are as follows:
- (1)
- Temporally, PM2.5 in Xinjiang exhibits significant seasonal variations, forming a U-shaped pattern on annual and monthly scales. Spatially, the annual average concentration of PM2.5 in Xinjiang shows a trend of being higher in the southwest and lower in the northeast. The PM2.5 concentration in this region demonstrates notable spatiotemporal variations.
- (2)
- STWNN demonstrates significantly improved predictive accuracy compared with most previous models (CNN–LSTM, CNN–Bi-LSTM, and CBAM+). Performance is relatively enhanced for seasonal predictions compared with the overall predictions. STWNN is considered the top-performing model for overall and seasonal predictions. Error pattern analysis further indicates that STWNN (0.006, p < 0.05) captures spatial heterogeneity, exhibiting strong spatiotemporal adaptability.
- (3)
- This study introduces SHAP methods for in-depth analysis of the STWNN prediction model, enhancing its interpretability and credibility. SHAP reveals the importance and spatiotemporal variation of key factors affecting PM2.5 predictions. Results indicate that AOD, BLH, and NDVI are the most influential feature variables in generating PM2.5 in Xinjiang.
The proposed STWNN model fully utilizes the spatiotemporal variations of PM2.5 and remote sensing data, providing daily PM2.5 products for regions with sparse monitoring stations. This is more suitable for daily public requirements and provides scientific support for government decision-making.
Author Contributions
Conceptualization, Y.W. and L.X.; methodology, Y.W. and Z.X.; software, Y.W.; validation, Y.W. and Z.X.; formal analysis, Y.W.; resources, J.W. and L.X.; data curation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, Z.X., J.W. and L.X.; visualization, Y.W.; funding acquisition, J.W. and L.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (grant No. 31760151), in part by the Third Xinjiang Comprehensive Scientific Expedition (grant No. 2021xjkk0801), and in part by Corps Science and Technology Program Projects (grant No. 2023CB008-23).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author or the first author. The data are not publicly available due to restrictions eg privacy or ethical.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, F.; Chen, Z. Cost of Economic Growth: Air Pollution and Health Expenditure. Sci. Total Environ. 2021, 755, 142543. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Tian, A.; Shi, Y.; Chen, B.; Ji, R.; Ge, J.; Su, X.; Pu, B.; Lei, L.; Ma, R.; et al. Associations of Long-Term Fine Particulate Matter Exposure with All-Cause and Cause-Specific Mortality: Results from the ChinaHEART Project. Lancet Reg. Health West. Pac. 2023, 41, 100908. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhou, Y.; Lu, J. Exploring the Relationship between Air Pollution and Meteorological Conditions in China under Environmental Governance. Sci. Rep. 2020, 10, 14518. [Google Scholar] [CrossRef] [PubMed]
- Foley, K.M.; Roselle, S.J.; Appel, K.W.; Bhave, P.V.; Pleim, J.E.; Otte, T.L.; Mathur, R.; Sarwar, G.; Young, J.O.; Gilliam, R.C.; et al. Incremental Testing of the Community Multiscale Air Quality (CMAQ) Modeling System Version 4.7. Geosci. Model Dev. 2010, 3, 205–226. [Google Scholar] [CrossRef]
- Tie, X.; Madronich, S.; Li, G.H.; Ying, Z.; Zhang, R.; Garcia, A.R.; Lee-Taylor, J.; Liu, Y. Characterizations of Chemical Oxidants in Mexico City: A Regional Chemical Dynamical Model (WRF-Chem) Study. Atmos. Environ. 2007, 41, 1989–2008. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, H.; Xu, X.; Han, M.; Zuo, P. A Balanced Social LSTM for PM2.5 Concentration Prediction Based on Local Spatiotemporal Correlation. Chemosphere 2022, 291, 133124. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.; Liao, J.; Yang, J.; Sun, W.; Nong, M.; Li, F. Multi-Hour and Multi-Site Air Quality Index Forecasting in Beijing Using CNN, LSTM, CNN-LSTM, and Spatiotemporal Clustering. Expert. Syst. Appl. 2021, 169, 114513. [Google Scholar] [CrossRef]
- Wang, J.; Wu, T.; Mao, J.; Chen, H. A Forecasting Framework on Fusion of Spatiotemporal Features for Multi-Station PM2.5. Expert. Syst. Appl. 2024, 238, 121951. [Google Scholar] [CrossRef]
- Schaap, M.; Apituley, A.; Timmermans, R.M.A.; Koelemeijer, R.B.A.; De Leeuw, G. Atmospheric Chemistry and Physics Exploring the Relation between Aerosol Optical Depth and PM 2.5 at Cabauw, the Netherlands. Atmos. Chem. Phys. 2009, 9, 909–925. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and Quantitative Evaluation of MODIS Satellite Sensor Data for Regional and Urban Scale Air Quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, Y.; Chang, H.H.; Meng, X.; Geng, G.; Lyapustin, A.; Liu, Y. Full-Coverage High-Resolution Daily PM2.5 Estimation Using MAIAC AOD in the Yangtze River Delta of China. Remote Sens. Environ. 2017, 199, 437–446. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Z.; Gong, W.; Zhu, Z.; Sun, K.; Wang, L.; Huang, Y.; Mao, F.; Shen, H.; Li, Z.; et al. Estimation of Ultrahigh Resolution PM2.5 Concentrations in Urban Areas Using 160 m Gaofen-1 AOD Retrievals. Remote Sens. Environ. 2018, 216, 91–104. [Google Scholar] [CrossRef]
- Feng, L.; Wang, Y.; Zhang, Z.; Du, Q. Geographically and Temporally Weighted Neural Network for Winter Wheat Yield Prediction. Remote Sens. Environ. 2021, 262, 112514. [Google Scholar] [CrossRef]
- O’SULLIVAN, D. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships, by A. S. Fotheringham, C. Brunsdon, and M. Charlton. Geogr. Anal. 2003, 35, 272–275. [Google Scholar] [CrossRef]
- Dai, Z.; Wu, S.; Wang, Y.; Zhou, H.; Zhang, F.; Huang, B.; Du, Z. Geographically Convolutional Neural Network Weighted Regression: A Method for Modeling Spatially Non-Stationary Relationships Based on a Global Spatial Proximity Grid. Int. J. Geogr. Inf. Sci. 2022, 36, 2248–2269. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Lyapustin, A.; Wang, Y.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G.; Estes, S.M.; Quattrochi, D.A.; Puttaswamy, S.J.; et al. Estimating Ground-Level PM2.5 Concentrations in the Southeastern United States Using MAIAC AOD Retrievals and a Two-Stage Model. Remote Sens. Environ. 2014, 140, 220–232. [Google Scholar] [CrossRef]
- Li, R.; Gong, J.; Chen, L.; Wang, Z. Estimating Ground-Level PM2.5 Using Fine-Resolution Satellite Data in the Megacity of Beijing, China. Aerosol Air Qual. Res. 2015, 15, 1347–1356. [Google Scholar] [CrossRef]
- Wu, J.; Yao, F.; Li, W.; Si, M. VIIRS-Based Remote Sensing Estimation of Ground-Level PM2.5 Concentrations in Beijing–Tianjin–Hebei: A Spatiotemporal Statistical Model. Remote Sens. Environ. 2016, 184, 316–328. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Lyapustin, A.; Wang, Y.; Liu, Y. 10-Year Spatial and Temporal Trends of PM2.5 Concentrations in the Southeastern US Estimated Using High-Resolution Satellite Data. Atmos. Chem. Phys. 2014, 14, 6301–6314. [Google Scholar] [CrossRef]
- He, Q.; Huang, B. Satellite-Based Mapping of Daily High-Resolution Ground PM2.5 in China via Space-Time Regression Modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, Z.; Hu, C.; Wang, K.; Ding, X. Geographically Weighted Neural Network Considering Spatial Heterogeneity for Landslide Susceptibility Mapping: A Case Study of Yichang City, China. Catena 2024, 234, 107590. [Google Scholar] [CrossRef]
- Liu, J.; Weng, F.; Li, Z. Satellite-Based PM2.5 Estimation Directly from Reflectance at the Top of the Atmosphere Using a Machine Learning Algorithm. Atmos. Environ. 2019, 208, 113–122. [Google Scholar] [CrossRef]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; de Hoogh, K.; de’ Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of Daily PM10 and PM2.5 Concentrations in Italy, 2013–2015, Using a Spatiotemporal Land-Use Random-Forest Model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Guo, J.; Zhang, X.; Tian, X.; Zhang, J.; Wang, Y.; Duan, J.; Li, X. Synergy of Satellite and Ground Based Observations in Estimation of Particulate Matter in Eastern China. Sci. Total Environ. 2012, 433, 20–30. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-Surface Fusion of Station Measurements and Satellite Observations for Mapping PM2.5 Distribution in China: Methods and Assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, B.; Huang, B.; Ma, Z.; Biswas, A.; Jiang, Y.; Shi, Z. Predicting Annual PM2.5 in Mainland China from 2014 to 2020 Using Multi Temporal Satellite Product: An Improved Deep Learning Approach with Spatial Generalization Ability. ISPRS J. Photogramm. Remote Sens. 2022, 187, 141–158. [Google Scholar] [CrossRef]
- Yang, J.; Yan, R.; Nong, M.; Liao, J.; Li, F.; Sun, W. PM2.5 Concentrations Forecasting in Beijing through Deep Learning with Different Inputs, Model Structures and Forecast Time. Atmos. Pollut. Res. 2021, 12, 101168. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T.; Shen, H.; Zhang, L. Mapping PM2.5 Concentration at a Sub-Km Level Resolution: A Dual-Scale Retrieval Approach. ISPRS J. Photogramm. Remote Sens. 2020, 165, 140–151. [Google Scholar] [CrossRef]
- Wang, W.; Mao, W.; Tong, X.; Xu, G. A Novel Recursive Model Based on a Convolutional Long Short-Term Memory Neural Network for Air Pollution Prediction. Remote Sens. 2021, 13, 1284. [Google Scholar] [CrossRef]
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long Short-Term Memory Neural Network for Air Pollutant Concentration Predictions: Method Development and Evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhou, Y.; Zhao, R.; Wang, N.; Biswas, A.; Shi, Z. High-Resolution Prediction of the Spatial Distribution of PM2.5 Concentrations in China Using a Long Short-Term Memory Model. J. Clean. Prod. 2021, 297, 126493. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Li, D.; Liu, J.; Zhao, Y. Prediction of Multi-Site PM2.5 Concentrations in Beijing Using CNN-Bi LSTM with CBAM. Atmosphere 2022, 13, 1719. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A Deep Cnn-Lstm Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Li, J.; Liu, L.; Guo, X.; Huang, L.; Hu, M. Application of CNN-LSTM Algorithm for PM2.5 Concentration Forecasting in the Beijing-Tianjin-Hebei Metropolitan Area. Atmosphere 2023, 14, 1392. [Google Scholar] [CrossRef]
- Ding, C.; Wang, G.; Zhang, X.; Liu, Q.; Liu, X. A Hybrid CNN-LSTM Model for Predicting PM2.5 in Beijing Based on Spatiotemporal Correlation. Environ. Ecol. Stat. 2021, 28, 503–522. [Google Scholar] [CrossRef]
- Wang, Z.; Li, R.; Chen, Z.; Yao, Q.; Gao, B.; Xu, M.; Yang, L.; Li, M.; Zhou, C. The Estimation of Hourly PM2.5 Concentrations across China Based on a Spatial and Temporal Weighted Continuous Deep Neural Network (STWC-DNN). ISPRS J. Photogramm. Remote Sens. 2022, 190, 38–55. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, L. A Locally Weighted Neural Network Constrained by Global Training for Remote Sensing Estimation of PM. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Xue, Y.; Li, Y.; Guang, J.; Tugui, A.; She, L.; Qin, K.; Fan, C.; Che, Y.; Xie, Y.; Wen, Y.; et al. Hourly PM2.5 Estimation over Central and Eastern China Based on Himawari-8 Data. Remote Sens. 2020, 12, 855. [Google Scholar] [CrossRef]
- Qi, Y.; Li, Q.; Karimian, H.; Liu, D. A Hybrid Model for Spatiotemporal Forecasting of PM 2.5 Based on Graph Convolutional Neural Network and Long Short-Term Memory. Sci. Total Environ. 2019, 664, 1–10. [Google Scholar] [CrossRef]
- Li, T.; Zhang, C.; Shen, H.; Yuan, Q.; Zhang, L. Real-Time and Seamless Monitoring of Ground-Level Pm2.5 Using Satellite Remote Sensing. arXiv 2018, arXiv:1803.03409. [Google Scholar] [CrossRef]
- Quan, W.; Xia, N.; Guo, Y.; Hai, W.; Song, J.; Zhang, B. PM2.5 Concentration Assessment Based on Geographical and Temporal Weighted Regression Model and MCD19A2 from 2015 to 2020 in Xinjiang, China. PLoS ONE 2023, 18, e0285610. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.Y.; Ding, J.; Ge, X.; Liu, J.; Xie, B.; Zhao, S.; Zhao, Q. Machine Learning Driven by Environmental Covariates to Estimate High-Resolution PM2.5 in Data-Poor Regions. PeerJ 2022, 10, e13203. [Google Scholar] [CrossRef] [PubMed]
- Ren, M.; Sun, W.; Chen, S. Combining Machine Learning Models through Multiple Data Division Methods for PM2.5 Forecasting in Northern Xinjiang, China. Environ. Monit. Assess. 2021, 193, 476. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, J.; Bai, Z.; Yang, W.; Zhang, H.; Mao, J.; Sun, Y.L.; Ma, Z.; Xiao, J.; Gao, S.; et al. Background Concentrations of PMs in Xinjiang, West China: An Estimation Based on Meteorological Filter Method and Eckhardt Algorithm. Atmos. Res. 2019, 215, 141–148. [Google Scholar] [CrossRef]
- Wang, J.; Christopher, S.A. Intercomparison between Satellite-Derived Aerosol Optical Thickness and PM2.5 Mass: Implications for Air Quality Studies. Geophys. Res. Lett. 2003, 30, 2095. [Google Scholar] [CrossRef]
- Li, R.; Mei, X.; Chen, L.; Wang, Z.; Jing, Y.; Wei, L. Influence of Spatial Resolution and Retrieval Frequency on Applicability of Satellite-Predicted Pm2.5 in Northern China. Remote Sens. 2020, 12, 736. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhao, C.; Kwan, M.-P.; Cai, J.; Zhuang, Y.; Zhao, B.; Wang, X.; Chen, B.; Yang, J.; et al. Influence of Meteorological Conditions on PM2.5 Concentrations across China: A Review of Methodology and Mechanism. Environ. Int. 2020, 139, 105558. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating Regional Spatial and Temporal Variability of PM2.5 Concentrations Using Satellite Data, Meteorology, and Land Use Information. Environ. Health Perspect. 2009, 117, 886–892. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Mao, W.; Yang, D.; Zhao, J.; Xu, J. Effects of Land-Use and Landscape Pattern on PM2.5 in Yangtze River Delta in China. Atmos. Pollut. Res. 2018, 9, 705–713. [Google Scholar] [CrossRef]
- Claridge, D.E.; Chen, H. Missing Data Estimation for 1–6 h Gaps in Energy Use and Weather Data Using Different Statistical Methods. Int. J. Energy Res. 2006, 30, 1075–1091. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena; Oxford University Press: Oxford, UK, 2014; Volume 11. [Google Scholar]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating Ground-Level PM2.5 by Fusing Satellite and Station Observations: A Geo-Intelligent Deep Learning Approach. Geophys. Res. Lett. 2017, 44, 11985–11993. [Google Scholar] [CrossRef]
- Xue, T.; Zheng, Y.; Tong, D.; Zheng, B.; Li, X.; Zhu, T.; Zhang, Q. Spatiotemporal Continuous Estimates of PM2.5 Concentrations in China, 2000–2016: A Machine Learning Method with Inputs from Satellites, Chemical Transport Model, and Ground Observations. Environ. Int. 2019, 123, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Shi, W.; Tian, J.; Qi, Z.; Li, B.; Hao, H.; Xu, B. Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification; Association for Computational Linguistics: New Brunswick, NJ, USA, 2016. [Google Scholar]
- Qin, D.; Yu, J.; Zou, G.; Yong, R.; Zhao, Q.; Zhang, B. A Novel Combined Prediction Scheme Based on CNN and LSTM for Urban PM2.5 Concentration. IEEE Access 2019, 7, 20050–20059. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Allen, P.G.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Yang, Y.; Mei, G.; Izzo, S. Revealing Influence of Meteorological Conditions on Air Quality Prediction Using Explainable Deep Learning. IEEE Access 2022, 10, 50755–50773. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Bender, A.; Bermejo, J.L.; Strobl, C. Random Forest Gini Importance Favours SNPs with Large Minor Allele Frequency: Impact, Sources and Recommendations. Brief. Bioinform. 2012, 13, 292–304. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Cribb, M. Reconstructing 1-Km-Resolution High-Quality PM2.5 Data Records from 2000 to 2018 in China: Spatiotemporal Variations and Policy Implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- Chen, S.; Tong, B.; Russell, L.M.; Wei, J.; Guo, J.; Mao, F.; Liu, D.; Huang, Z.; Xie, Y.; Qi, B.; et al. Lidar-Based Daytime Boundary Layer Height Variation and Impact on the Regional Satellite-Based PM2.5 Estimate. Remote Sens. Environ. 2022, 281, 113224. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, Q.; Zhang, Y.; He, K.B.; Wang, K.; Zheng, G.J.; Duan, F.K.; Ma, Y.L.; Kimoto, T. Heterogeneous Chemistry: A Mechanism Missing in Current Models to Explain Secondary Inorganic Aerosol Formation during the January 2013 Haze Episode in North China. Atmos. Chem. Phys. 2015, 15, 2031–2049. [Google Scholar] [CrossRef]
- Wang, J.; Ogawa, S. Effects of Meteorological Conditions on PM2.5 Concentrations in Nagasaki, Japan. Int. J. Environ. Res. Public. Health 2015, 12, 9089–9101. [Google Scholar] [CrossRef]
- Gao, S.; Cheng, X.; Yu, J.; Chen, L.; Sun, Y.; Bai, Z.; Xu, H.; Azzi, M.; Zhao, H. Meteorological Influences on PM2.5 Variation in China Using a Hybrid Model of Machine Learning and the Kolmogorov-Zurbenko Filter. Atmos. Pollut. Res. 2023, 14, 101905. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).