1. Introduction
Over the past few years, the climate crisis caused by the greenhouse effect has aroused continuous concern, and the existing scientific knowledge has realized the severity and urgency of the climate challenge. As the second largest greenhouse gas in the world, methane (CH
4) has emerged as a focal point in societal discourse, with increased scrutiny focused on its emission and the resulting alterations in atmospheric balance [
1,
2]. The IPCC Sixth Assessment Report from Working Group I [
3] reveals a global surface temperature warming of more than 1 °C in 2010–2019 compared to that of 1850–1900, with a radiative forcing from methane of 0.5 (0.3–0.8) °C. In contrast to carbon dioxide (CO
2), which has a lifespan of hundreds of years in the atmosphere, methane exhibits a considerably shorter average atmospheric lifespan of merely 11.8 years, approximately one-tenth that of carbon dioxide. Its global warming potential (GWP) is 84 times that of carbon dioxide over a 20-year period. Furthermore, beyond its role as a greenhouse gas, methane also plays a crucial role as a significant contributor to tropospheric ozone production and is intricately linked to the dynamics of air pollutants [
4]. Therefore, the mitigation of methane emissions holds the potential to curb excessive global warming and reduce environmental risks within a relatively short time frame.
In the 26th meeting of the Conference of the Parties to the UN Framework Convention on Climate Change (CoP26), numerous countries sponsored the Global Methane Pledge, which calls for a reduction of at least 30% of anthropogenic methane emissions by 2030 relative to 2020. The reduction of methane emissions has subsequently become a focal point in climate negotiations among major international stakeholders. Methane emissions come from diverse sources, which can be mainly categorized as natural or anthropogenic. Natural sources encompass wetlands [
5] and freshwater systems (lakes, ponds, reservoirs) [
6], which are located in predominantly anaerobic environments. Natural sources also include geology, wildfires, and termites [
7]. In addition, some studies have pointed out that heat wave events may linked to increased methane concentrations in polar permafrost regions. [
8]. The melting of permafrost may release an unknown amount of methane into the atmosphere, creating a positive climate feedback effect [
9,
10,
11].
Anthropogenic sources, on the other hand, are predominantly associated with animal husbandry, waste management, the oil and gas industry, and coal mining [
1]. Among these, the oil and gas industry stand out as the predominant contributor to methane emissions [
12], with a notable focus on point source emissions. Specifically, small facilities emit high concentrations of methane gas plumes [
13]. The surge in methane observed over the past three decades correlates closely with human activities [
3]. To a certain extent, this surge shows that taking emission reduction actions regarding anthropogenic methane offers certain feasibility in mitigating the greenhouse effect. Notably, undertaking abatement actions targeting methane emissions from coal mines and the oil and gas industry can achieve a “zero net cost” [
14]. Meanwhile, challenges arise in responding effectively to sporadic and unpredictable methane emissions resulting from incidents such as methane escapes, blowouts, and pipeline ruptures in the oil and gas industry, which are difficult to realistically and effectively observe using traditional means. The inherent uncertainty and complexity of methane emissions present formidable challenges to monitoring practices.
Currently, the monitoring of XCH
4 (the monitoring of the column-averaged dry air mixing ratio of CH
4) can be primarily categorized into land-based monitoring, space-based monitoring, and satellite-based monitoring [
15]. The fundamental international ground-based methane observation networks encompass the Total Carbon Column Observing Network (TCCON) [
16], the Network for the Detection of Atmospheric Composition Change (NDACC) [
17], and the Global Atmosphere Watch (GAW) program of the World Meteorological Organization (WMO) [
18]. While ground-based observations yield high-precision monitoring data [
19], the limited number and uneven distribution of methane monitoring stations present challenges in obtaining comprehensive, large-scale methane monitoring information. Space-based monitoring methods mainly include the Airborne Visible Infrared Imaging Spectrometer (AVIRIS) and the Airborne Visible InfraRed Imaging Spectrometer-Next Generation (VIRIS-NG) [
20,
21]. However, these instruments face limitations arising from factors like flight speed, impeding comprehensive and ubiquitous detection capabilities. At the same time, the devices experience a time lag, and disordered emissions cannot be monitored. On the contrary, satellite remote sensing enables multi-scale observations at specific spatial resolutions, thereby providing a crucial scientific foundation for understanding the circulation dynamics of methane within the earth’s system. In addition, discrepancies in methane emission data among different governments and sectors arise due to diverse observation methods, statistical approaches, and other factors [
22]; thus, the utilization of satellites for monitoring can achieve unified quantitative targets for global methane emissions. Consequently, satellites have become an important means of monitoring methane emissions and a powerful technical support for establishing top-down emission source inventories.
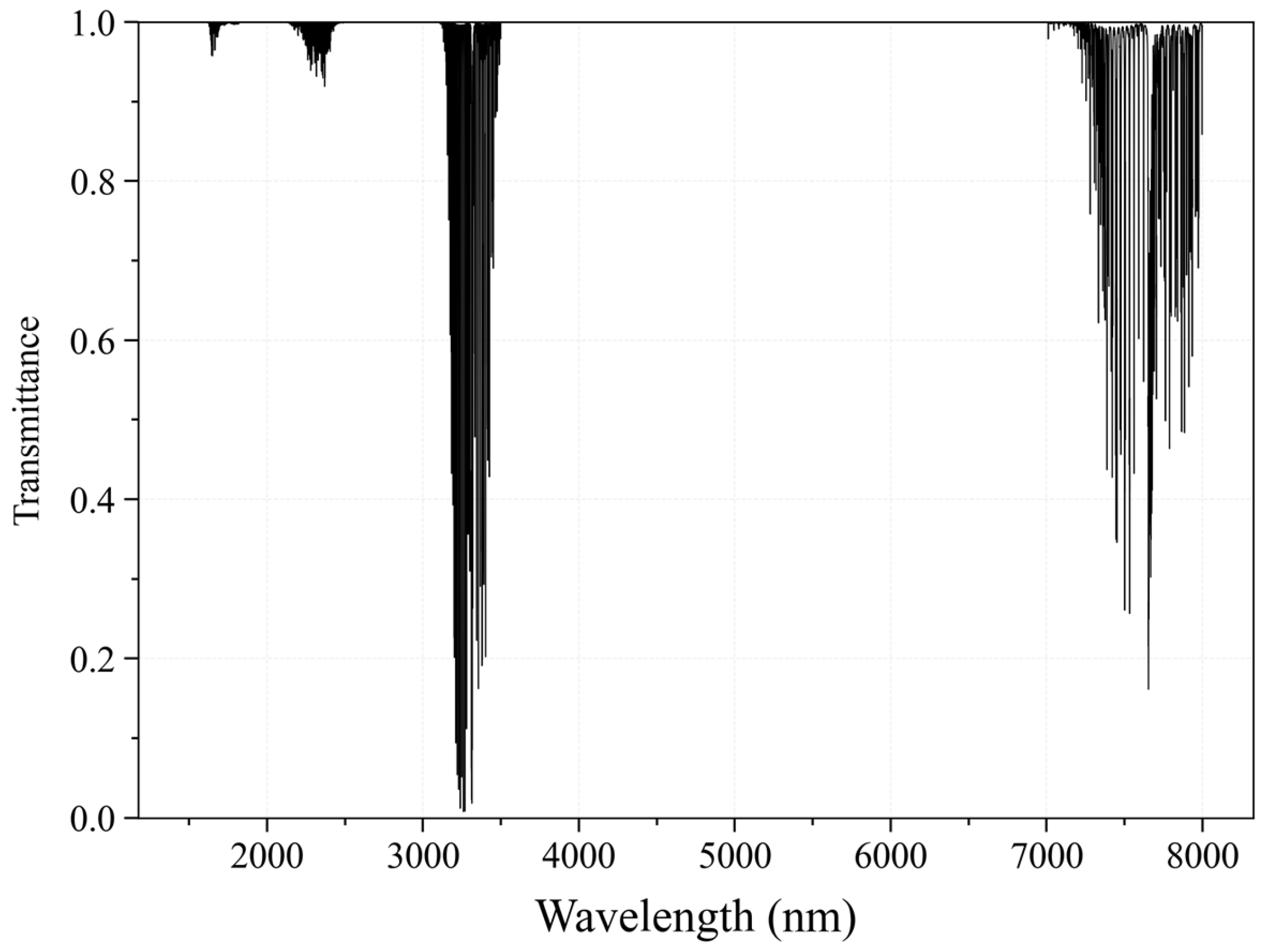
Methane exhibits absorption characteristics in both short wavelength infrared (SWIR) and thermal infrared (TIR) spectra, as shown in
Figure A1. In the SWIR spectrum, methane absorbs radiation primarily through fundamental vibrational transitions in its molecular bonds. These transitions are associated with relatively narrow absorption bands. Because of shorter wavelengths in SWIR spectrum there is a stronger interaction between the absorbed radiation and the methane concentration in the atmosphere, which results in a more consistent profile of vertical sensitivity [
23]. A more uniform vertical sensitivity thus helps to obtain surface information more efficiently. Meanwhile, emission sources are mostly concentrated at the surface, and information from SWIR spectrum can be used to investigate natural and anthropogenic methane emissions, which is crucial for understanding climate change and developing effective mitigation strategies [
24,
25].
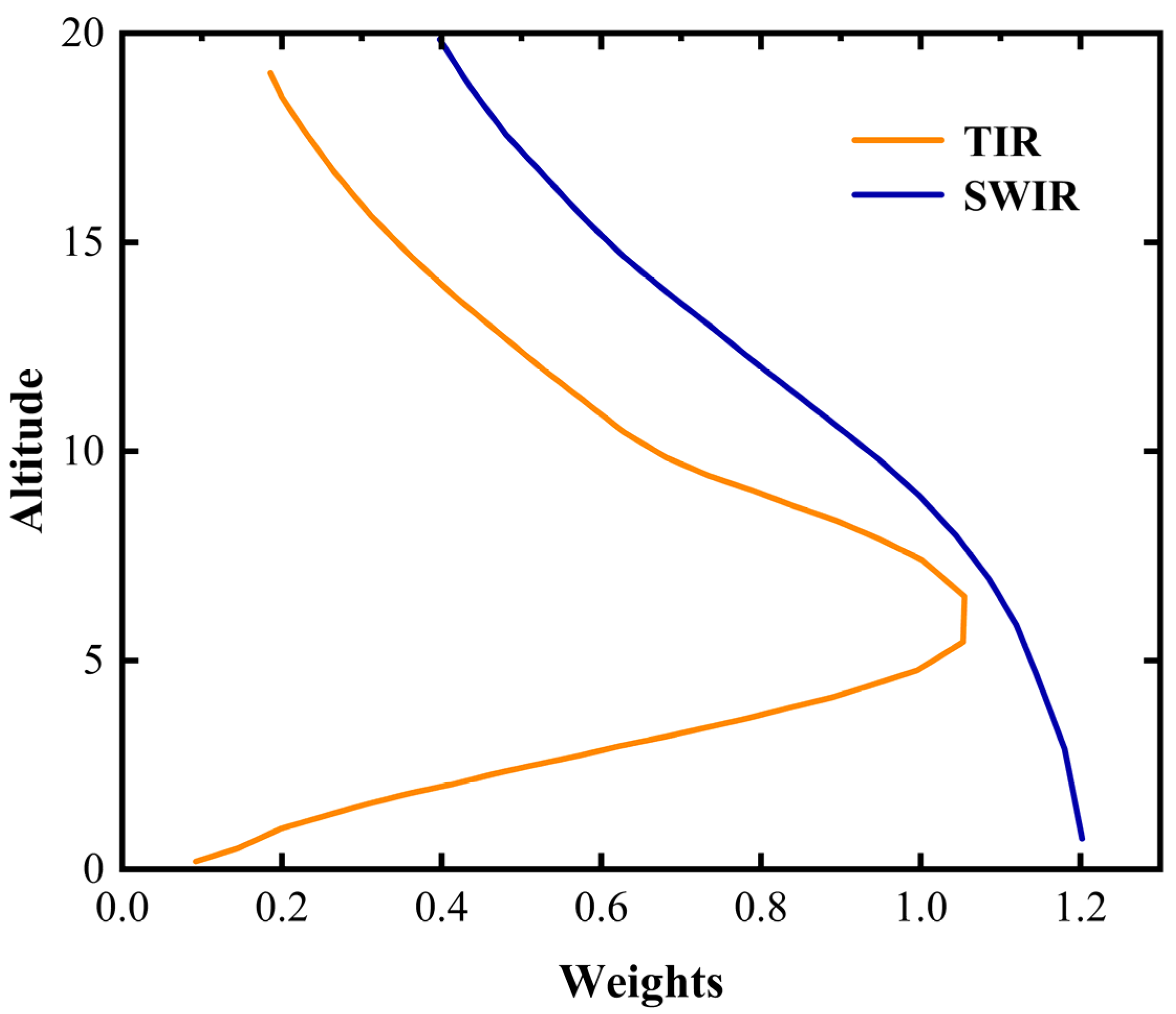
In the SWIR spectrum, methane exhibits strong absorption bands near 1.65 μm and 2.3 μm, affording distinct characterizations of methane information. Therefore, in recent years, the majority of methane remote sensing satellites have performed retrieval based on the SWIR spectrum. Meanwhile, methane also shows strong absorption bands in the TIR spectrum (near 3.3 μm and 7.66 μm), but information retrieved from this spectrum is primarily focused on the middle troposphere. The methane weight in different bands is shown in
Figure A2. In this paper, we will introduce the current main satellite remote sensing instruments and give a more detailed description of the retrieval algorithms used by the satellites. At the same time, a new satellite-based technology developed in recent years for the detection of methane point sources is introduced. Based on the current status of satellite development, we can predict future development trends regarding the two types of satellites and provide certain theoretical support for subsequent scientific research. This paper is organized as follows.
Section 2 will focus on introducing different types of satellites and their retrieval algorithms.
Section 3 presents specific quantification methods for methane point source emissions. Conclusions and the outlook for the future will be presented in
Section 4.
2. Introduction for Methane Remote Sensing Satellites
Presently, satellite methane remote sensing technology is undergoing rapid development and is widely used. According to different retrieval requirements, it can be divided into area flux mappers for climate change and point source imagers for methane point sources [
26]. Area flux mappers exhibit high-precision and low-bias detection capabilities, focusing on the retrieval of XCH
4; such instruments could achieve the global or large-regional scale remote sensing of methane distribution. Data from these devices is usually employed as a priori information for an atmospheric chemical transport model, enabling the discernment of changes in methane sources and sinks [
27,
28]. Additionally, these data also serve as valuable references for point source imagers, offering essential information on hotspot areas. Point source imagers are characterized by relatively low spectral resolution and specialize in achieving the quantitative estimation of single methane plume emissions through ultra-high spatial resolution, mainly focusing on small areas.
Due to differences in absorption band selection, area flux mappers can be further classified as SWIR methane remote sensing satellites and TIR methane remote sensing satellites.
Figure 1 illustrates the two distinct satellite remote sensing methods which developed round the beginning of the 21st century, based on the absorption properties of the TIR band, the distribution of upper tropospheric methane in large-scale regions was obtained [
29]. Subsequently, more SWIR methane remote sensing satellites have been launched, contributing to enhanced observation efficiency and improved detection accuracy. This advancement has resulted in the availability of more detailed methane research data. Based on area flux mappers, Maasakkers et al. [
30] estimated the methane emissions and performed its trend analysis in North America using GOSAT (the Greenhouse Gases Observing Satellite). Building upon GOSAT observation data, Zhang et al. [
31] optimized the hydroxyl (OH) concentration in the inversion model, leading to a more precise analysis of the factors governing atmospheric methane and the reasons behind its accelerated growth from 2010 to 2018. Moreover, numerous researchers worldwide have conducted atmospheric inversion and quantitative analyses of methane emissions in North America and China, drawing on data from TROPOMI (Tropospheric Monitoring Instrument). Their findings indicate that top-down emission inventory data based on satellite remote sensing were higher than the National Emissions Inventory reported by the United Nations [
32,
33,
34].
Regarding methane point source detection, satellites equipped with multispectral and hyperspectral imagers have been extensively employed for plume monitoring and quantification. Currently, research on methane point sources predominantly focuses on oil and gas industry regions, mainly in Europe, America, and the Middle East. For Asia, large methane emission events have also been detected in the Shanxi region of China and India, based on satellite detection [
35,
36]. Varon et al. [
37], for instance, harnessed the synergy between GHGSat-D (Greenhouse Gas Satellite-Demonstrator) and TROPOMI to achieve a more intricate tracing of methane point source emissions. Ehret et al. [
38] conducted a power-law analysis using multi-source satellite and airborne data, suggesting that high XCH
4 observed on a global scale may indicate relatively small but undetected methane emissions, and Cusworth et al. [
39] monitored a methane blowout event using multi-source satellites to capture the short-term dynamics of methane leakage. Irakulis-Loitxate et al. [
40] realized the quantitative attribution of methane point sources in the Permian Basin by using China’s hyperspectral satellites, such as Gaofen-5 (GF-5) and ZiYuan-1 (ZY-1), and pointed out that the inefficient flaring of new facilities in the region is the main reason for the large amount of methane emissions. Additionally, Irakulis-Loitxate et al. [
41] used the sun-glint mode to mitigate the effect of water vapor on methane retrieval and to achieve the monitoring quantification of methane point sources near the offshore Gulf of Mexico. Furthermore, satellites dedicated to methane point source detection play a crucial role in addressing international events. Jia et al. [
42] used Sentinel-2 to quantify the methane leakage event of the Nord Stream pipeline in 2022, pointing out that the emission rate of the methane leakage point is about 72
38 t/h, which provides a scientific reference for the quantitative estimation of the Nord Stream pipeline explosion event.
2.1. Satellite Retrieval Algorithms for Area Flux Mappers
Table 1 outlines the current major area flux mappers, showcasing the parameters of the global methane monitoring satellites. The world’s first global methane column concentration map was obtained by the retrieval of the GMI (green gas monitoring instrument) on board ADEOS (Advanced Earth Observing Satellite), which was launched in 1996. Subsequently, SCIAMACHY (scanning imaging absorption spectrometer for atmospheric cartography), on board Envisat (Environmental Satellite), became the first satellite instrument to use the SWIR band to detect atmospheric methane (2003–2009), achieving near-surface methane detection. GOSAT, developed by Japan as the first global greenhouse gas remote-sensing satellite, has been operating well since its launch in January 2009. Equipped with a TANSO-FTS (thermal and near-infrared sensor for carbon observations-Fourier transform spectrometer), GOSAT provides valuable data for investigating global methane sources and sinks, as well as their climate effects. The subsequent launch of GOSAT-2 in 2018 and the planned launch of GOSAT-GW (Global Observing Satellite for Greenhouse Gases and Water Cycle) in 2023 further expand the capabilities for observing methane and the water cycle.
TROPOMI, launched by the Copernicus Sentinel-5 Precursor in 2017, enhances spatial resolution for global methane distribution (5.5 × 7 km
2) and ensures global daily coverage. Among its advantages, TROPOMI can not only achieve remote sensing of global methane distribution but also monitor some methane point sources [
43,
44]. However, compared with the spatial resolution of within a hundred meters of the point source imagers, there are still many limitations in the performance of methane point source detection due to factors such as coarse spatial resolution and cloud coverage. Compared with GOSAT and TCCON data, TROPOMI data has been proven to provide higher data quality [
45,
46].
China’s Gaofen-5 satellite, equipped with GMI, has likewise contributed to global methane concentration monitoring. However, passive methane remote sensing satellites encounter some limitations. Since passive remote sensing obtains methane data based on reflected solar radiation information, the solar altitude angle, i.e., the influence of sunlight, is one of the important factors for detection. At the same time, there is no solar radiation at night, so it is difficult to achieve night detection. Winter in high latitudes is also affected by sunlight, and it is difficult for satellites to receive enough solar radiation under these conditions. Moreover, observation efficiency is adversely affected by interference from clouds and aerosols. Addressing these challenges, the scheduled launch of MERLIN (Methane Remote Sensing Lidar Mission) in 2028 will bridge these gaps through active methane remote sensing, thereby reducing uncertainties in exploring the global methane cycle.
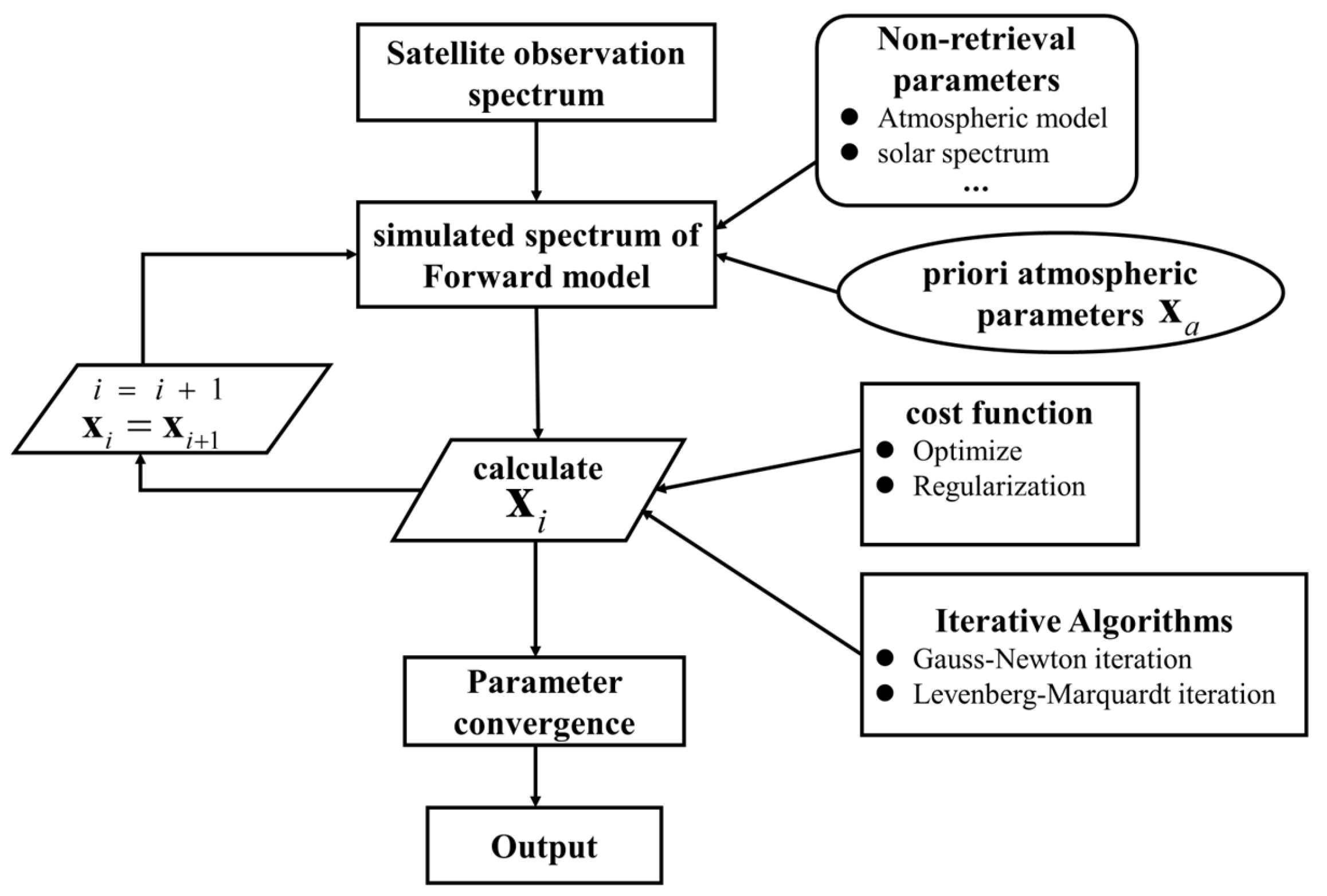
Currently, there are many differences in the satellite retrieval algorithms for area flux mappers. However, a majority of these algorithms are based on the SWIR spectrum and are dominated by physical models, as well as carbon dioxide proxy models. The algorithmic flow of most physical model-based methods is delineated in
Figure 2. In this process, known a priori atmospheric state parameters are utilized, and simulated spectra are generated by combining non-retrieval parameters (such as the atmospheric model, solar spectrum, etc.) into a retrieval model. Iterative calculations, often employing methods like the Gauss–Newton or Levenberg–Marquardt techniques, are then applied to minimize or regularize the cost function. When the iterative calculation converges the simulated values to the observed spectrum, the output value is the retrieval result. The physical model-based algorithms are widely used in area flux mappers [
47,
48,
49], but also in point source imagers like AVIRIS and AVIRIS-NG [
50]. Furthermore, point source imagers such as GHGSats rely on a physical model, allowing for the detection of methane plumes without considering scattering and thermal radiation. The carbon dioxide proxy method is retrieved, based on the presence of absorption bands around 1.65 for both CH
4 and CO
2. 2.1.1. Optimization Algorithms
The optimal estimation method (OEM) stands as a frequently employed algorithm for satellite retrieval. Assuming that the observed spectrum received by the satellite instrument is
, and the atmospheric state vector is
, considering an atmospheric model and simulating the observation spectrum by the forward model
, the atmospheric state can be expressed as [
51]:
where
represents the instrument noise error, and
represents the error caused by the forward model. In the forward model, the simulated top-of-atmosphere (TOA) radiation can be obtained from the radiative transfer model. The state vector
contains several elements, such as the vertical stratified column concentration of methane, the total column concentration of CO, the total column concentration of water vapor, and so forth. Neglecting the error, Equation (1) is linearized as:
Among these,
K is the Jacobian matrix, which represents the sensitivity of the forward model to the true value profile;
is the a priori parameter of the atmospheric state. This method implements retrieval based on Bayesian estimation of the atmospheric states. It combines observation data with model information through Bayesian estimation. Notably, this method requires prior information for the constraints.
where
is the probability distribution of the real atmospheric parameters, i.e., the known a priori information, and
is the probability distribution of the observed spectra. Given the state vector
, the probability distribution of
, that is, the theoretical observation error, and
represents the probability distribution of
obtained under the condition of observing spectrum
. It is assumed that in the real state, the vector
follows a Gaussian distribution:
where
is the vector covariance. Equation (4) is varied to give the following equation:
where
is an independent constant of
,
is the covariance matrix of the measurement error, and
is the a priori covariance matrix of the atmospheric parameters. Considering that the forward model is usually nonlinear, the methane information is obtained by minimizing the cost function, in which
is set to be:
Subsequently, the Gauss–Newton iteration method is employed to ascertain the optimal solution:
In addition, the Levenberg–Marquardt iterative method is extensively employed [
50]. The iterative process is illustrated by the following equation:
where
is the parameter that determines the step size of each iteration. It is worth noting that aerosols are not included in the real and simulated state vectors, as they are considered in the simulated forward model.
2.1.2. Regularization Algorithms
The RemoTeC (Remote sensing of greenhouse gases for carbon cycle modeling) fully physical retrieval algorithm, developed by the Netherlands Institute for Space Research (SRON), uses Philips–Tikhonov regularization to handle the objective function and employs Gauss-Newton iterative linearization for retrieval. This algorithm could reduce the impact of measurement noise on the retrieval state vector and does not require prior information to constrain the retrieval [
47]:
where
is the diagonal measurement error variance matrix, containing the noise estimates,
is the regularization parameter, and
is the diagonal weighting matrix with side constraints on the dimensionless data, ensuring that only the methane parameter and the scattering parameter play a role in the model. The data product of methane retrieval is given in the form of XCH
4. According to the retrieved state vector, it can be discerned as follows:
where
represents the dry air column (derived from meteorological elements, surface pressure, and water vapor profile). Simultaneously, to ensure the precision of the retrieval, the averaging kernel
needs to be used to describe its sensitivity to changes in the real methane profile:
The XCH
4 obtained from the retrieval is correlated with the true methane profile
as well as the a priori profile
:
The algorithm assumed a cloud-free and plane-parallel atmosphere, with thin-layer scattering. Lorente et al. [
46] upgraded the full physical algorithm in TROPOMI in terms of the regularization scheme, the selection of the spectral database, and the updating of the elevation maps. These enhancements have led to improved retrieval precision and, to some extent, have mitigated the influence of albedo.
2.1.3. Improved Retrieval Algorithm for Differential Absorption Spectroscopy
Differential optical absorption spectroscopy (DOAS) is designed to separate the high-frequency information (fast-changing part), caused by optical thickness change induced by rapidly varying molecular absorption characteristics of the wavelength, from the low-frequency information (slowly changing part), caused by Rayleigh scattering and Mie scattering. This method has been widely applied in the retrieval of various atmospheric components, and the absorption cross-section can be expressed as [
52]:
where
is the absorption cross-section obtained from low-frequency information, mainly attributable to Rayleigh and Mie scattering, and
is the fast-rotating part, primarily arising from various absorbing gas molecules.
Equation (14) represents the three main factors affecting radiation intensity in the atmosphere, which encompass the impacts induced by the rapid absorption of trace gases, Rayleigh scattering, and Mie scattering. Additionally,
is expressed as an effect caused by systemic and atmospheric turbulence, where
denotes the concentration of jth gas;
and
represent the extinction effects of Rayleigh scattering and Mie scattering, respectively.
To simplify the calculation, in this algorithm, the radiation change
caused by low-frequency information can be approximated by a polynomial. This is one of the commonly used methods to remove the influence of low-frequency information. Then, the differential optical thickness D′ can be expressed as:
while D′ can be obtained through observation. By combining multiple bands and performing least squares fitting of the gas absorption cross-section through differential absorption spectra, the gas concentration can be obtained. In addition, it is necessary to correct the integral of the gas concentration in the optical path. However, in the SWIR spectrum, the problem will become more complicated. In the next sub-section, we will explain this in detail.
Weighting Function Modified Differential Absorption Spectroscopy
In the NIR or SWIR spectrum, accurately approximating radiance becomes challenging when using the linear model of the Beer–Lambert relationship. The weighting function modified differential optical absorption spectroscopy retrieval algorithm (WFM-DOAS) is a modification of the DOAS algorithm, addressing the sensitivity of the infrared band absorption cross-section to temperature and pressure. In addition, there is a strong overlap of absorption lines in the same band for several gases. Moreover, atmospheric scattering complicates the optical flow, and it is not possible to express the absorption characteristics of gases in terms of a simple exponential function. This algorithm employs the gas column concentration weight function to replace the absorption cross-section reference spectrum and can only be used to retrieve the methane column concentration, but not the methane profile. SCIAMACHY uses this algorithm to realize methane column concentration detection. This method is based on the linear radiative transfer model
and the logarithm of the low-order polynomial
to fit the logarithm of the ratio of nadir radiation and the solar radiation spectrum [
53]:
The normalized linear radiative transfer model is:
where
is the atmospheric column concentration of methane obtained by retrieval,
is an estimate of methane obtained from irradiance simulation,
denotes the column concentration of the jth gas,
and the polynomial parameter
are obtained by a linearized least-squares fit of the observations to the model values, and
is a low-order polynomial used to represent the effect of low-frequency information, i.e., aerosol, ground albedo, cloud cover, etc. The column weight function
denotes the radiative derivative of the fitted parameter, which is the change in TOA caused by the change in total gas absorption. Additionally, the algorithm avoids time-consuming calculations for radiative transfer modeling by establishing a lookup table (LUT) method and assumes that the reference spectra are established under clear weather conditions in the U.S. Standard Atmosphere. Notably, the method does not require a priori information to constrain the column concentrations for retrieval. The WFM-DOAS method is more suitable for cloud-free conditions. However, for thin clouds, whose radiative properties are equivalent to those of aerosols, the low-order polynomials in the WFM-DOAS retrieval can be well-fitted.
Iterative Maximum A Posteriori Differential Absorption Spectrum Retrieval Algorithm
Based on the differential absorption algorithm, Frankenberg et al. [
54] introduced the iterative maximum a posteriori differential absorption spectral retrieval algorithm, denoted as IMAP-DOAS, which takes into account the nonlinearities caused by changes in atmospheric temperatures and pressure profiles, as well as spectral resolving ability. The algorithm was employed for determining the XCH
4 using data from the SCIAMACHY satellite [
54,
55]. Furthermore, it has found widespread application in point source imagers such as EnMAP (Environmental Mapping and Analysis Program) and PRSIMA (Precursore Iperspettrale della Missione applicativa) for determining methane point sources [
56].
The retrieval algorithm is grounded in the Beer–Lambert theorem and is coupled with an optimization algorithm to attain consistency between the observed and the simulated spectrum. The forward model of the IMAP-DOAS algorithm is:
where
is the high-resolution backscattered TOA radiation at wavelength
,
is the intensity of the incident radiation,
is the default optical thickness of a constant amount of gaseous elements in the U.S. Standard Atmosphere,
is the scaling factor of the default optical thickness in the optimal retrieval process,
denotes the kth polynomial, and
is a polynomial coefficient used to account for the low-frequency spectral variations. Similarly, since the forward model is nonlinear, the Gauss–Newton iteration is utilized to solve the optimal state vector solution, and the iteration process is shown below:
The algorithm optimizes the scaling factor relative to the a priori profile, setting the scaling factor to 1 for the initial estimate of the gas in two layers of vertical space.
Moreover, for the detection of methane point sources, Thorpe, Frankenberg, and Roberts [
57] proposed using a hybrid method involving IMAP-DOAS and singular value decomposition (SVD) to better characterize the underlying surface characteristics and atmospheric absorption. SVD is closely related to principal component analysis (PCA) and can effectively summarize high-dimensional data, providing the potential to reduce computing time (see
Section 2.1.5 for details).
2.1.4. Carbon Dioxide Proxy Method
This method is based on the existence of absorption bands around 1.6 μm (CO
2:1.61 μm, CH
4:1.65 μm) for both carbon dioxide and methane. It disregards the impact of scattering in the atmosphere in the retrieval and assumes that the optical paths of the target gas methane and the proxy gas carbon dioxide in the atmosphere are the same and are known a priori.
The parameter XCO
2 can be assimilated from the CarbonTracker dataset [
58], while
and
denote the vertical column density concentrations, respectively. CarbonTracker, an assimilative dataset initiated by the National Oceanic and Atmospheric Administration Earth System Research Laboratories (NOAA ESRL), is designed for the monitoring and estimation of global carbon emissions. The data assimilation set for monitoring and estimating global carbon emissions is coupled to an ensemble Kalman filter for assimilation using an atmospheric transport model. The assimilation process encompasses fossil combustion, heat sources, terrestrial biosphere, and oceanic exchanges, with diverse emission data derived from distinct emission inventories. The instantaneous fluxes, considering the four emission processes, can be expressed as follows:
Herein,
symbolizes the set of linear scale factors to be estimated in the interval
assimilation. This retrieval method also needs to first remove the effect of clouds, wherein clear-sky surface pressure is a prerequisite, relying specifically on the O
2-A band. Subsequently, this value is interpolated for comparison with air pressure data furnished by the European Centre for Medium-Range Weather Forecasts (ECMWF) at corresponding time and spatial coordinates. In instances where a discernible discrepancy of 20 hPa in pressure exists between the two datasets, the meteorological conditions are classified as overcast, precluding methane retrieval [
16]. Schepers et al. [
49] conducted a comparative analysis between the full physical methodology and the carbon dioxide proxy approach in the processing of GOSAT satellite data, highlighting the capability of both methods to replicate the variability trend. Furthermore, Lorente et al. [
46] pointed out that the carbon dioxide proxy method achieves the highest data output between the two. Since TROPOMI does not include the 1.6 μm absorption band, it cannot be retrieved using the carbon dioxide proxy method.
2.1.5. Singular Value Decomposition Retrieval Algorithm
This algorithm endeavors to diminish data from higher dimensions to lower dimensions, thereby simplifying the complexity of data processing and analysis. It accomplishes this by transforming a multitude of potentially pertinent vectors into a series of more concise, uncorrelated vectors, denoted as singular vectors—an approach closely aligned with principal component analysis (PCA). Both AIRS (atmospheric infrared sounder) and IASI (infrared atmospheric sounding interferometer) sensors achieve precise detection of atmospheric methane through the application of this algorithm.
The following is an
order matrix
, where the matrix
contains the left singular vectors and the matrix
contains the right singular vectors.
In this method, the retrieval of methane is based on the successful retrieval of various atmospheric parameters, including temperature profiles, water vapor profiles, surface temperature, albedo, and so on. These variables serve as inputs to the forward model.
Through the calculation of the difference of
between the radiance obtained from the simulation and the radiance in the absence of clouds, the resulting disparity can be employed for the determination of methane profiles
[
29,
59]:
In the provided equation,
presents the observed irradiance in the absence of clouds,
represents the observed irradiance under cloud-free conditions,
expresses the difference between the observed and simulated values in the spectral band, and
is the vector of methane differences from the initial profile on the different Lth vertical planes.
denotes the sensitivity of the irradiance in the spectral band to changes in methane on the Lth layer, and
denotes the error vector in the different spectral bands. Equation (23) can be solved by the singular value decomposition (SVD) of the sensitivity covariance matrix, which is obtained by weighting the precision and accuracy estimates obtained from the retrieval of the radiative transfer model, as well as the error and noise in the measurement. The variation of methane can be written as:
Here,
is the retrieval error matrix, and
denotes the background term.
is a diagonal matrix whose elements are
, and
serves as the damping variable. This retrieval method minimizes the dependence on the initial value profile and covariance matrix, and strongly relies on the signal-to-noise ratio of the observations. When processing real satellite data, we also need to combine optimization methods with dimensionality reduction to achieve the inversion of a large amount of hyperspectral data [
60].
2.1.6. Fast Atmospheric Trace Gas Retrieval
The fast atmospheric trace gas retrieval (FOCAL) algorithm was originally developed for the retrieval of the OCO-2 (Orbiting Carbon Observatory-2) satellite of the United States, offering an approximation to the analytical solution of the radiative transfer problem. This approximation focuses on multiple scattering from an optically thin scattering layer, resulting in reduced computational costs. Significantly, FOCAL has been adopted as the retrieval algorithm for the CO2M (Copernicus Anthropogenic Carbon Monitoring) satellite, which represents the next generation of greenhouse gas detection satellites under the European Space Agency (ESA). In this algorithm, it is assumed that the spectral signals generated by absorption within the scattering layer cannot be easily separated from the albedo and scattering signals; consequently, only the effect of extinction from scattering is considered [
61]:
It is assumed that the radiance reaching the satellite instrument consists of the following:
where
is the radiation directly dispersed from the scattering layer to the satellite,
denotes the direct radiation from the surface,
denotes the radiation from the surface subsequent to the scattering layer,
denotes the diffuse radiation from the surface,
denotes the diffuse radiation subsequent to the scattering layer, and
denotes the radiation from the solar-induced chlorophyll fluorescence. Assuming that the incident solar radiation is
, considering the Lambertian body, the above radiation components are part of the following equation:
The goal of the algorithm is not to retrieve the absorption within the scattering layer, but to approximate the optical thickness of the absorption as 0. Consequently, the albedo and the quantity of scattered radiation may exhibit slight deviations. Also, it is assumed that light is dispersed at the scattering layer in equal parts to the upper and lower hemispheres.
Subsequently, the methane concentration is modeled and resolved utilizing the observed spectra from satellite instruments, incorporating a priori information. In the model, three scattering-related vectors—scattering layer height
, scattering optical thickness
, and the Ångström exponent
, collectively termed as 3-Scat—are considered. This configuration ensures that the scattering information is exclusively derived from the absorption band of the target gas. The algorithm has been applied to the OCO-2 retrieval of CO
2, but also to the GOSAT retrieval of XCH
4, with good data quality [
62].
2.1.7. Integral Path Differential Absorption Algorithm
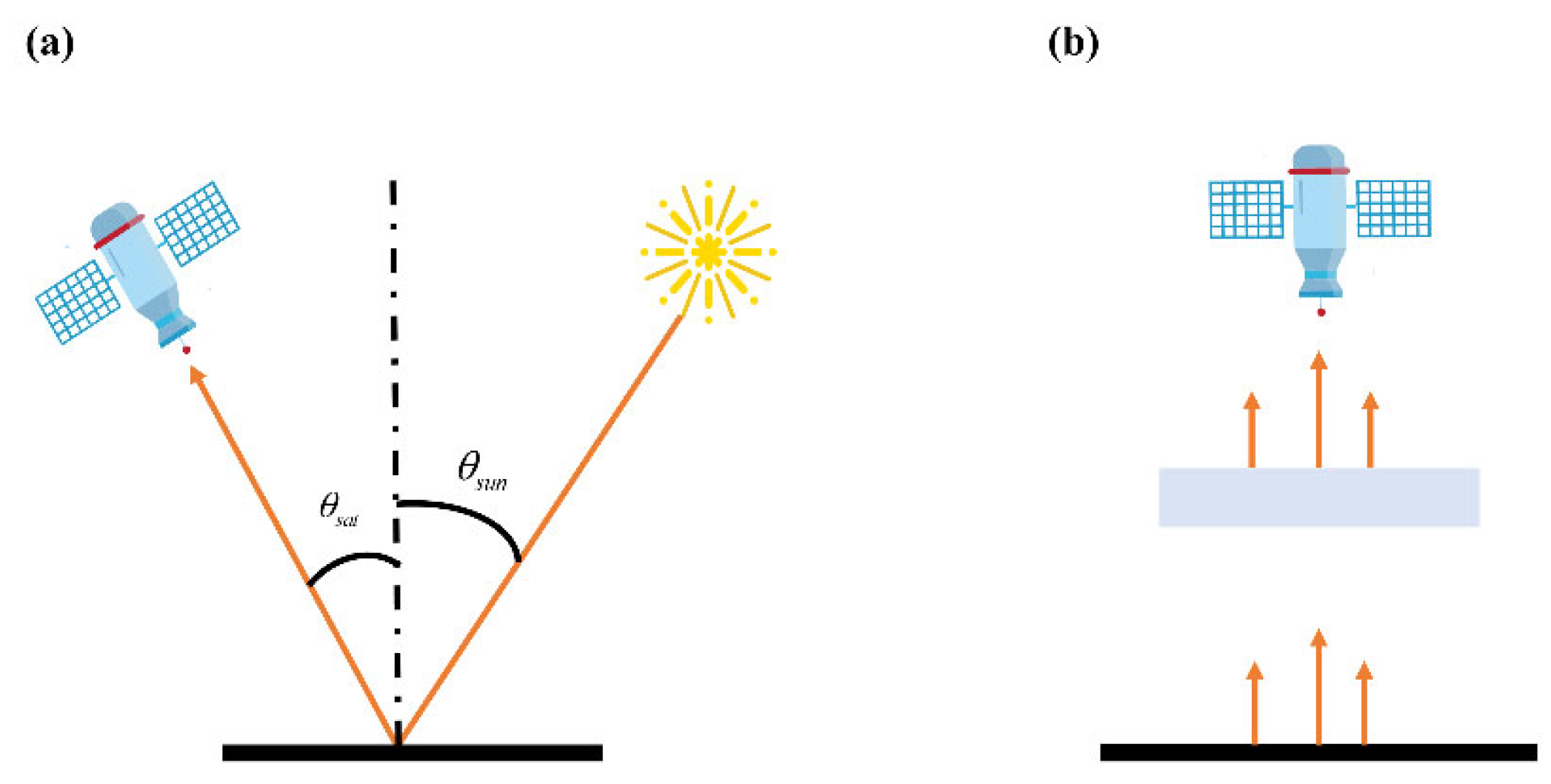
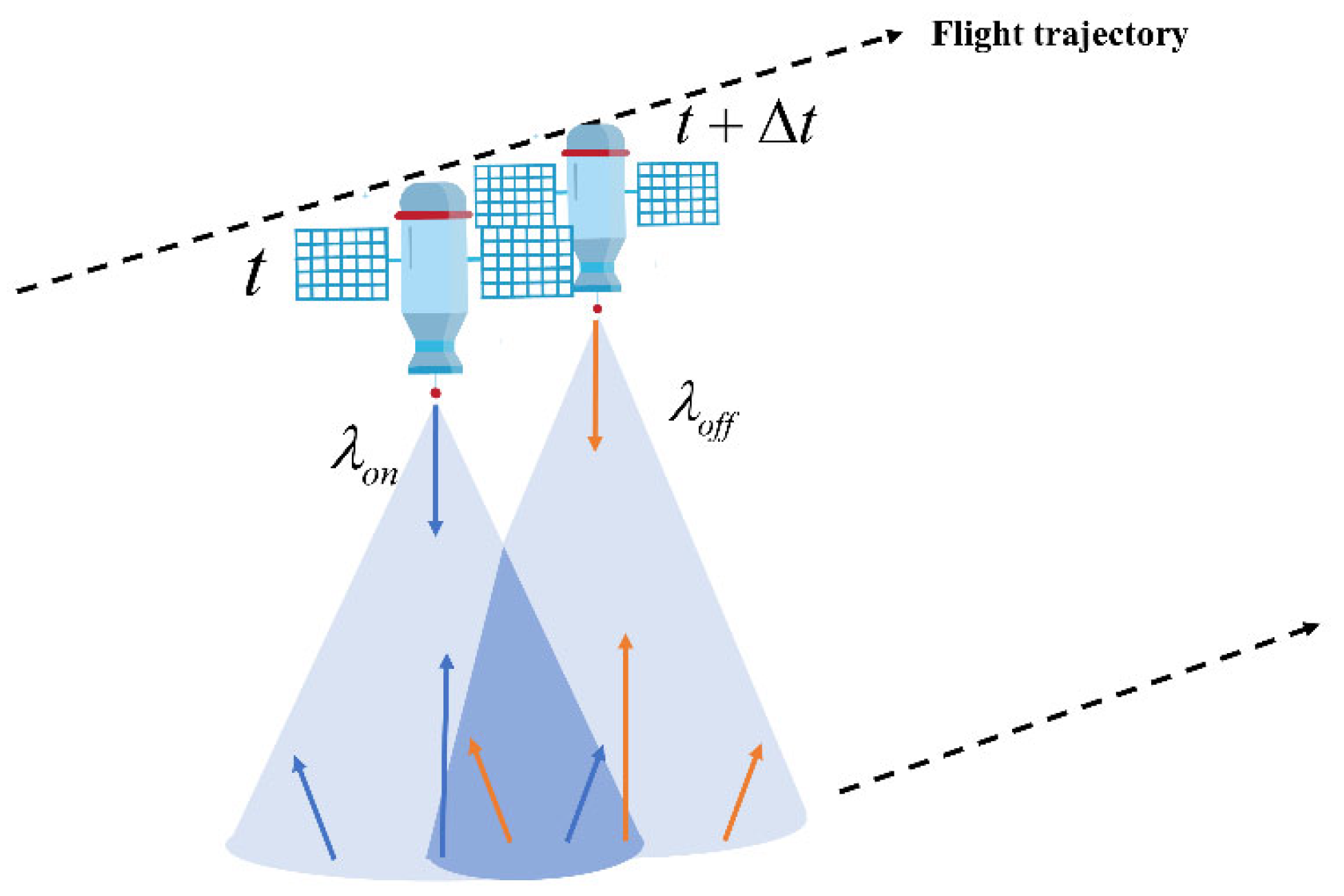
In contrast to passive remote sensing satellite retrieval, active remote sensing methane satellites operate independently of solar radiation or earth infrared radiation. Consequently, they possess the capability to monitor methane concentrations both day and night, throughout all seasons, and across all latitudes. The forthcoming MERLIN satellite planned to be launched in 2028 is equipped with lidar, which can complete the measurement based on the integrated path differential absorption method (IPDA). This satellite sensor emits laser pulses at two frequencies near 1.64 μm, referred to as online and offline frequencies. Specifically, the online frequency is strategically chosen within the trough of the 1.64 μm methane absorption line to enhance sensitivity to ground-level methane concentration changes. Simultaneously, the offline measurement serves as a reference frequency, positioned where methane absorption is negligible. Online and offline frequencies are emitted with a very short time delay (
), resulting in nearly identical optical path and surface scattering characteristics. The measurement process is illustrated in
Figure 3 [
63].
Following the Beer–Lambert law, the differential absorption optical thickness of methane can be given by the measured lidar signal
:
Among these, represent the measured lidar signals, respectively. is the measuring height, is the methane dry air mixing ratio at height , is the water vapor mixing ratio, is the air number density, and is the corresponding molecular absorption cross-section of online and offline results. The integration is carried out from the top of the atmosphere to the target altitude . The second term in the equation aggregates the contributions of other atmospheric components, particularly water vapor and carbon dioxide, in the form of differential optical depth (DAOD). It is noteworthy that the interference of water vapor can be further reduced by mitigation through the water vapor compensation mode. This mode is based on the idea of selecting an offline position within the water vapor absorption line so that the differential absorption of water vapor can be measured. Subsequently, the water vapor contribution relevant to the dry air mixture ratio calculation is then compensated.
Considering the hydrostatic equations, XCH
4 can be calculated from the measured DAOD:
where
is the weight function, characterized as a function of air pressure and temperature, and
is the gravitational acceleration.
and
are the masses of the dry air and water vapor molecules, and
is the water vapor mixing ratio compared to dry air, which describes the contribution of the atmosphere to the concentration of the trace gas mixing ratio columns at pressure
and temperature
.
In addition to the methane data acquired through retrieval, MERLIN is poised to furnish information about other climate-relevant parameters, encompassing cloud-top heights, surface retro-reflectivity, and potentially, canopy heights. The primary scientific objective of MERLIN is to contribute to the refinement of source and sink estimations through atmospheric inversion, thereby mitigating uncertainties in the global methane cycle. Moreover, alongside the two-pulse lidar, retrieval based on the ASCENDS (active sensing of CO
2 emission over nights, days, and seasons) data, multi-pulse lidar sounding has been realized [
64], and XCH
4 retrieval can be obtained based on the same retrieval theory.
2.2. Satellite Retrieval Algorithms for Point Source Imagers
Numerous studies have consistently demonstrated that methane point source emissions and their frequency exhibit a heavy-tailed distribution, wherein super point source emission events are characterized as low probability occurrences, but instances of super emissions do exist [
39,
65]. Therefore, effective monitoring of methane emission point sources can successfully promote the achievement of methane emission reduction objectives. Considering the challenges faced by area flux mappers in remotely sensing point source emissions, the advent of point source imagers has substantially bridged the gap in regards to methane monitoring. As far as the current point source imagers are concerned, they can be divided into multispectral remote sensing satellites (Landsat-8, Sentinel-2, etc.) and hyperspectral remote sensing satellites (PRISMA, EnMAP, GF-5, etc.). Notably, the GHGSats networking satellite is specifically designed for the detection and quantification of point source greenhouse gas emissions. Comprising six networking satellites, all equipped with wide-angle Fabry–Perot imagers (WAF-P), these satellites can sample the methane band near 1700 nm, facilitating the detection of methane column concentration in vertical space. Noteworthy among them are the GHGSat-D (Claire), launched in June 2016, and September 2020, as well as the GHGSat-C1 (Iris) satellites, capable of simultaneously monitoring methane and carbon dioxide. PRISMA was launched in March 2019 as the successor satellite of HypSEO (Hyperspectral Satellite for Earth Observation). The satellite is equipped with a hyperspectral camera that can achieve observations in near-infrared and short-wave infrared spectra. Its 2110–2450 nm band is suitable for methane monitoring and is currently widely used in methane point source detection. Moreover, visible short-wave infrared hyperspectral cameras, such as the Advanced Hyperspectral Imagers (AHSIs) aboard China’s GF-5 and ZY-1 satellites, exhibit significant promise for methane monitoring applications. The Sentinel-2 satellite, featuring a multispectral imager (MSI), currently comprises two identical satellites: Sentinel-2A, launched in June 2015, and Sentinel-2B, launched in March 2017. Furthermore, a third satellite, Sentinel-3C, is anticipated to be launched in 2024. The joint utilization of Sentinel-2A and Sentinel-2B has significantly reduced revisit times to approximately five days. Each satellite is equipped with an MSI covering 13 bands, from near-infrared to short-wave infrared, encompassing band-11 (1613.7 nm (S2A)/1610.4 nm (S2B)) and band-12 (2202.4 nm (S2A)/2185.7 nm (S2B)) in the SWIR spectrum. Launched in November 2013, Landsat-8 carries the Operational Land Imager (OLI), which covers the visible, near-infrared, and short-wave infrared bands, enabling detection of methane point sources, but the satellite has a revisit time of up to 16 days. Compared to the low revisit rate of Landsat-8, Worldview-3, which was launched in August 2014, this technology shows a very short revisit time (less than 1 day). In contrast, the WV110 (WorldView-110 camera) on board contains eight bands in the infrared band, with a spatial resolution of up to 3.7 m, enabling the detection of small methane point-source emissions that may not be easily revealed by other satellites [
36]. For point source imagers, the primary concept underlying retrieval involves transforming the three-dimensional spatial methane plume into a two-dimensional image and subsequently conducting retrieval based on the Beer–Lambert law. The current major point source imagers for methane detection are shown in
Table 2.
2.2.1. Retrieval Algorithms Based on Multispectral Imagers
In the case of multispectral imagers, even though the detailed analysis of SWIR spectral information may not be feasible, inferences regarding methane column concentration enhancement can still be derived from methane transmittance images. Furthermore, owing to the global coverage afforded by multispectral imagers, they exhibit distinct advantages in the detection of methane point sources. In this context, the main point of the retrieval for methane column concentration enhancement by multispectral imagers focuses on the calculation of the methane background concentration value, as well as the consideration only of the absorption of the gas. This section provides an overview of the current principal algorithms for multispectral imagers. The differences between the algorithms mainly focus on the solution of the background value, which is predominantly obtained by comparing the transmittance of the absorption band, with or without the presence of methane. The reference value can be approximated by other bands that are not sensitive to methane, or can be estimated by using the concentration values of the same band, during periods when no methane emission is occurring.
SBMP, MBSP, and MBMP Algorithms
It is recognized that band-11 and band-12 in the Sentinel-2 satellite are located near the methane absorption band. Varon et al. [
37] developed three retrieval algorithms for calculating the methane column concentration enhancement of intermittent point source emissions, namely the SBMP retrieval algorithm (single-band–multi-pass retrieval), the MBSP retrieval algorithm (multi-band–single-pass retrieval), and the MBMP retrieval algorithm (multi-band–multi-pass retrieval). In the context of the SBMP retrieval method, the albedo changes in band-12 caused by the presence or absence of a methane plume at the same location is analyzed, and then the methane column concentration enhancement (
) is derived. The variation in radiance can be expressed as follows:
where
is the proportional coefficient of the radiance changes at the same location on different days. The proportional coefficient can be obtained by the least squares fitting of the radiances of R
12 (with methane emissions) and the R′
12 (without methane emissions) in the target area. Further comparison with the absorption model is performed, as follows:
where
signifies the simulated value of spectral radiance, with and without methane emissions. Then the observed and simulated values are combined, and the objective function
is minimized through iteration to obtain
. Compared with Landsat-8 and Sentinel-2, Worldview-3 not only boasts higher spatial resolution but also encompasses a more extensive array of channels within the short-wave infrared band. Notably, these bands are characterized by narrower spectral widths compared to other satellites. Alternatively, estimation can be achieved through multiple linear regression involving various bands, albeit necessitating the elimination of redundant methane-sensitive absorption bands in the regression process [
36].
The MBSP retrieval method, on the other hand, utilizes the albedo difference between band-11 and band-12 in the single satellite pass for methane concentration enhancement measurements with an albedo change of:
In this equation,
is the fit of band-12 to the albedo of band-11. The absorption model, consequently, can be articulated as:
The method is based on the difference in albedo between the two bands, and the methane concentration enhancement can be derived through the optimization of the objective function .
Furthermore, the MBMP retrieval method synergistically integrates the strengths of the aforementioned two methods to more effectively mitigate the impact of artifacts. This algorithm can eliminate the absorption effect of the ground surface in the SWIR spectrum. Based on two satellite passes (with and without methane emission presence, respectively), the methane column concentration enhancement is solved using the difference in albedo in band-12 and band-11 at different times:
Through the practical application of the above methods, it was found that the retrieval capability of the algorithm depends, to a large extent, on the surface conditions. For most scenarios, the MBMP algorithm exhibits the highest retrieval precision. Simultaneously, it is observed that the primary source of error in the retrieval process stems from alterations in the albedo of the underlying surface.
Time Series Model
In the pursuit of methane plume retrieval using multispectral imagers, Ehret et al. [
38] calculated the background value of the target scene based on the time series changes of multiple satellite passes, subsequently deriving the column concentration enhancement of the methane plume. This method is rooted in the Beer–Lambert law, assuming an ideal atmospheric model, specifically, a pure atmospheric model, where only methane is considered. The existing methane leakage is represented by
, and the radiation intensity received by the sensor can be expressed as:
where
is the sensitivity function, while
denotes the surface albedo,
denotes the absorption coefficient, and AMF (air mass factor) denotes the radiative transfer path (
), as illustrated in
Figure 1.
The approach posits a stable and unchanging surface albedo using the ideal atmospheric model. It further assumes that the occurrence of methane emissions is a stochastic event, with no methane emissions during the remaining periods. On the basis of this assumption, the background concentration value of no methane emission at the target range can be estimated using long-term satellite transit scan images.
Specifically, this involves conducting a linear regression of methane concentrations observed in images predating the target date. If the observed radiation intensity at time
is denoted by
, then the calculation of the optimal weights
for the linear regression can be optimized as
, and the methane background concentration values for the target date can be expressed as a linear combination of
. Then, the methane concentration enhancement can be expressed by the optimization problem between the observed and simulated values as:
This method employs a time window of 30 days. However, in practical applications, the subsurface albedo of the target scene undergoes temporal variations. Consequently, an extended time window not only proves ineffective in enhancing methane plume detection precision, but may also introduce larger errors.
Transmittance Simplified Model
Sánchez-García et al. [
36] proposed an estimation of methane concentration enhancement based on methane plume transmittance. The primary foundation of this method lies in the assessment of the ratio of radiation from the methane-sensitive band to that from the methane-free band. The transmittance can be succinctly described as:
where
is the methane absorption cross-section. Various methods are employed to determine the transmittance for different satellites. For instance, in the context of the Sentinel-2 remote sensing satellite, Gorroño et al. [
66] expressed the transmittance as:
, which is similar to the MSMP retrieval method mentioned by [
37]. By segregating
in the equation to obtain
, the quantification of the methane plume can be achieved, which can then be transformed into the enhancement of the methane concentration:
2.2.2. Retrieval Algorithms Based on Hyperspectral Imagers
Compared to the multispectral imager, hyperspectral imagers have a shorter revisit time and a higher spectral resolution. A high revisit rate increases the coverage of the area, which in turn enhances the probability of the discovery of undetected plumes. Consider that in the SWIR spectrum, other gas components (carbon dioxide, water vapor, nitrous oxide) all absorb in this spectrum, while surface features also affect the entire spectrum. The higher the spectral resolution, the finer atmospheric methane absorption features which can be captured, and the more complete methane information which can be received by the sensors, thus mitigating the influence of various factors on the inversion results [
67].
Currently, physically driven and data-driven methods are widely employed in the retrieval of methane concentration enhancement by hyperspectral imagers. Physically driven methods hinge on the intricate interplay between subsurface features, atmospheric conditions, and radiative transfer. The detailed algorithmic process for these methods is expounded upon in
Section 2.1. On the other hand, data-driven methods utilize target information extracted from images to execute retrieval through statistical approaches. Data-driven methods do not need to take into account the influence of the background value, and at the same time, they show a higher computational efficiency than do physically driven methods. The data-driven methods are mainly based on the matched filter method.
Matched Filter
The matched filter method is a calculation in which the input spectral information can be expressed as perturbations in the average spectrum caused by changes in methane concentration. The algorithm searches for typical variations in each spatial pixel that maximize the signal-to-noise ratio and enhance the detection of the target, while whitening the data by considering the background covariance. This method is widely used in the retrieval of methane point sources. Grounded in the Beer–Lambert theorem, it undergoes Taylor first-order expansion linearization [
68]:
Here,
represents the absorption spectrum of methane, and
can be approximately replaced by the average radiance value
of the sensor. The target spectrum
is the disturbance of the background radiation signal caused by the enhanced methane column concentration. It can be obtained from radiative transfer model, the convolution of the instrument response function with the methane absorption spectrum is necessary in this process. Similarly, assuming that only methane is the single gas of interest and the absorption characteristics of methane will not change, the value of the methane column concentration enhancement can be obtained by applying the Gaussian logarithmic likelihood to the above formula and optimizing the target formula, as follows:
where
and
are the values recalculated for each reweighting iteration.
Foote et al. [
69] suggested that sparsification of the data and reflectance correction during the matched filter method can eliminate the effect of background, to some extent, and improve the detection precision. By introducing a re-weighted
minimization scheme onto the same matched filter, using the iterative shrinkage threshold algorithm (ISTA), then the solution for methane concentration enhancement becomes:
In addition, Pei et al. [
70] point out that the traditional matched filter algorithm is only applicable to point sources with small emissions, and they propose a logarithmic matched filter algorithm, i.e., using the logarithmic normal distribution as a substitute for the spectral background model. Based on this, the iterative computation of anomaly rejection can improve the inversion accuracy.
GHGSat Optimization Algorithm
GHGSats operates in “target” mode, a configuration in which the satellite’s attitude is controlled to prolong the duration of target observation compared to that inherent in the sky-bottom (downward pointing) mode. This extended viewing enhances the signal-to-noise ratio. Multiple 2D images are captured during each observation sequence, allowing ground targets to pass through the field of view, thus sampling the spectral information contained in the full extent of the image.
The satellite accomplishes the methane plume retrieval through the optimization method outlined in
Section 2.1.1, where the a priori information
used by GHGSats is the albedo parameter of LandSat-8 for the same scene, the a priori state vectors of CO
2 and water vapor concentration values from AIRS, and the proximity time methane concentration values from TROPOMI. It is worth noting that there are nearly 200,000 pixel points in the satellite’s field of view when performing Gauss–Newton iterations to minimize the cost function. This is difficult to achieve in practice for each pixel point in order to compute its forward model, as well as the Jacobi matrix. To address this issue, the algorithm is streamlined into two primary steps. Firstly, the full forward model and Gauss–Newton retrieval iteration are employed to estimate the scene-wide average state vector
. Then, the retrieval of each pixel is accomplished using the linearized forward model (LFM). The LFM model is shown below [
71]:
The first element of the state vector represents the surface reflectance, and the methane, carbon dioxide, and water vapor column densities in pixel can all be retrieved. The linearized forward model (LFM) consists of two terms: one contains Jacobian state vectors, proportional to surface reflectance (e.g., molecular column density), while the other contains Jacobian state vectors, unscaled by reflectivity. By calculating this model, the change in the state vector for each pixel is determined. This change can then be incorporated into the forward model and fitted with the actual spectrum to obtain the optimal state parameters. The primary advantage of using LFM is that the forward model and the Jacobian matrix each only need to be calculated once at the beginning of the retrieval of a tile. However, the disadvantage of this technique is that for nonlinear parameters in the forward model, retrieval using LFM will introduce systematic deviations away from the linearization point. Additionally, the premise of this algorithm is that the ground elevation is flat, and it ignores the impact of terrain on the retrieval.
2.3. Application of Deep Learning in the Retrieval Algorithm
For area flux mappers, the amount of data collected by the satellite is substantial, potentially leading to significant time requirements for data retrieval. Moreover, traditional methods in this domain depend heavily upon prior information and rely on specific physical assumptions. Contrary to traditional retrieval methods, deep learning eschews a priori assumptions regarding the statistical properties of the data. Furthermore, instead of using assumed knowledge, connections between inputs and outputs are inferred from the data. For the neural network method, for
inputs
in the network, the output
of a neuron is the weighted sum of its inputs transformed by its activation function
. This process can be expressed as:
where
is the weight,
is the deviation, and the activation function is usually a sigmoid or hyperbolic tangent function. The input layer consists of a group of neurons representing the input features (satellite observation spectrum). Each neuron in the hidden layer performs a weighted linear summation of the values of the previous layer, followed by an output obtained through a nonlinear activation function. The number of neurons in the input layer and output layer is determined by the input and output dimensions, respectively. For different problems, there is no specific method to determine the number of hidden layers and their neurons, which is usually selected through trial and error. The schematic diagram of the method flow is shown in
Figure 4. Fenwick, Boecsh, and Tyukin [
72] applied the neural network method to implement the retrieval of XCH
4 by TROPOMI, determining the optimal model parameters by comparing the number of different hidden layers. David, Bréon, and Chevallier [
73] demonstrated, through gas retrieval results, that a neural network trained on a representative dataset achieves slightly better precision than a full physics algorithm.
In the context of point source imagers, traditional methods for detecting methane point sources and quantifying emission rates are time-consuming, labor-intensive, and have a certain error rate due to the need for a large amount of human intervention. In recent years, deep learning has been used to detect and quantify point source emissions, reducing the interference of other factors, to a certain extent. Kumar et al. [
74] proposed a hybrid technique that combines the core concepts of traditional signal processing with deep learning, which helps in enhancing detection and removing the surface terrain confusion by learning the terrain and plume shapes, training the neural network to generate segmentation maps of methane plumes, and removing the artifacts. Kumar et al. [
75] introduced a new enhanced matched filter method integrated into a transformer-based convolutional neural network; this approach aims to classify detected surface types and artifacts to facilitate signal-to-noise separation. Groshenry et al. [
76] designed a plume transfer method, transferring Sentinel-2 images to PRISMA by modifying the plume distribution of Sentinel-2 to match the instrumental features of PRISMA, preserving the features of the original image to compensate for the relative scarcity of PRISMA images, and employing deep learning to achieve the retrieval of methane plumes.
While the multispectral remote sensing retrieval algorithms discussed in
Section 2.2.1 are capable of detecting methane plumes, they exhibit noticeable limitations. Firstly, the above three methods cannot eliminate artifacts caused by surface albedo and usually require manual verification; secondly, the retrieval of plumes relies on the time series of images. Vaughan et al. [
77] used Sentinel-2 satellite data to train a machine model and achieved the segmentation of methane plumes from a single image. The model was trained on Sentinel-2 images and manually annotated methane plume datasets spanning from 2017 to 2021, with a focus on areas containing super emission sources. The methane detection frame is formulated as a binary segmentation problem, classifying pixels as 1 if they are part of the methane plume and 0 otherwise; the MBMP algorithm is employed as an auxiliary tool for annotation. The detection model uses U-Net architecture, which is simple and flexible, for segmentation, taking the Sentinel-2 band as input, and the output is a probability prediction of whether the pixel is part of a methane plume [
78]. The potential application of this model lies in the automated monitoring of areas with known methane plumes. The evaluation of different scenes and pixels demonstrated overall high prediction quality. However, a drawback of the current model is that the output only provides a binary mask, rather than quantifying the methane concentration value for each tile.
4. Conclusions and Future Outlook
As methane has received increasing attention in recent years, the need for methane detection not only reflects changes in large-scale budgets, but also includes the impact of small-scale emissions. Satellite detection can accomplish the observation of atmospheric methane column concentration at different spatial scales. Satellite remote sensing detection of methane has also advanced from a global scale to high spatial resolution detection of individual plumes. This article provides an overview of the current major satellite methane remote sensing algorithms, and a simple description is shown in
Table A2.
A variety of algorithms based on the optimization algorithm methods, the most fundamental inversion methods, have been developed. At present, area flux mappers mainly rely on physical models and proxy algorithms. Founded on the spectral characteristics, instrument characteristics, and other factors of various satellites, different versions of the retrieval algorithm are derived based on the basic algorithm, notably, the NIES-FP, ACOS, UoL-FP, and RemoTeC retrieval algorithms. The NIES-FP retrieval algorithm, developed by NIES (the National Institute for Environmental Studies) in Japan, is the standard algorithm for processing GOSAT observation data. It utilizes two orthogonal polarization measurement spectra to generate a total intensity spectrum, reducing the impact of polarization. The algorithm is regularly updated, incorporating corrections for aerosol and other factors [
84].
The University of Leicester Full-Physics Retrieval Algorithm (UoL-FP), developed by the University of Leicester in the UK, is a classic algorithm for retrieving greenhouse gases. The algorithm uses principal component analysis to speed up the retrieval of radiative transfer flux and separates aerosols, classifying them into only two standards. This algorithm has been employed for products and services, in collaboration with the European Space Agency’s Climate Change Initiative (CCI) and the Copernicus Climate Change Service (C3S).
The RemoTeC algorithm serves as the standard for TROPOMI’s methane retrieval. It is based on regularization operations and performs line-by-line calculations of single scattering in the forward model. This algorithm is known for its speed, making it suitable for the large-width scanning characteristics of TROPOMI [
47].
Similarly, based on the optimization retrieval, NASA’s ACOS (Atmospheric CO2 Observations from Space) model is used for OCO-2 retrieval, employing an LUT for fast calculation by making scattering and absorption part of the forward modeling process. In addition, considering that surface pressure is directly related to the retrieval of greenhouse gases, the NIESFP, ACOS, and UoL-FP algorithms use the O2-A band to synchronously correct the surface pressure, while RemoTeC uses the equivalent surface pressure corrected by the surface height.
The theoretical basis of the physical algorithm is basically the same, and the accuracy of the retrieval results is also similar. Because it can more accurately simulate the atmospheric radiation transfer process, the physical algorithm has become the most accurate algorithm at this stage. Furthermore, although the classic DOAS algorithm is also suitable for the retrieval of various atmospheric components, it is based on the assumption that the absorption cross-section of the target component does not change with temperature and pressure. Consequently, it is particularly well-suited for the retrieval of ozone and other gases within the ultraviolet spectral band.
The IMAP-DOAS and WFM-DOAS algorithms address the nonlinear issues of atmospheric temperature, pressure profile sensitivity, and instrument spectral capabilities. The WFM-DOAS retrieval was originally used for SCIAMACHY to retrieve carbon dioxide and methane, and is also implemented for TROPOMI methane retrieval. This method involves replacing the absorption cross-section with a weighting function of the total gas column volume when performing the fitting of the differential absorption spectrum. Also, the algorithm allows retrieval at lower spectral resolution, but relies more on information such as temperature and pressure profiles and is more suitable for cloud-free scenarios [
85]. IMAP-DOAS can be used not only for regional retrieval, but also for methane point source retrieval. Both methods remove the scattering effect by fitting a low-order polynomial. Additionally, the carbon dioxide proxy method can achieve faster retrieval speed, but its retrieval precision is greatly affected by the precision of the proxy gas carbon dioxide, and is also limited by the selection of the methane retrieval absorption band. The applicability of the proxy method also requires the selection of the spectral band of the sensors, and the method is currently only applicable to instruments that can achieve retrieval through the weak absorption band of methane. Area flux mappers can achieve a retrieval precision of nearly less than 1%, based on the above inversion algorithm.
For point source imagers, a majority of algorithms ignore the impact of thermal radiation and scattering in the retrieval processes. Nonetheless, given the substantial concentration variations in methane plume emissions compared to the background, as mentioned in
Section 2.2, the point source retrieval algorithm can complete the retrieval of point sources with a certain absolute precision. In addition, the retrieval precision of point sources is largely influenced by the subsurface. In general, the more homogeneous the subsurface, the smaller the emissions that can be detected. The study in Ref. [
86] has achieved the detection of a small plume, with 180 kg/h of emissions, on a uniform sea surface. In addition to the influence of the retrieval algorithm, the detection thresholds of point source imagers are affected by a combination of other factors, such as instrument parameters [
67]. In addition, there is another point of interest for point source imagers, as the cost of such satellites is lower compared with that of area flux mappers. Considering that the GeoCarb (Geostationary Carbon Cycle Observatory) had been canceled owing to several factors, including cost and technology, the lower cost would make it easier to form constellations, thus further increasing the revisit rate. In recent years, with the rapid development of artificial intelligence, deep learning has also been widely used in gas inversion. Compared with traditional algorithms, which are computationally intensive and time-consuming, deep learning can better solve this problem and perform simulation calculations on nonlinear problems. In addition, deep learning can also be used to automatically monitor methane point sources and achieve the efficient segmentation of plumes. However, deep learning requires a large amount of data for training, and current algorithms are still immature.
The utilization of satellite remote sensing not only facilitates the long-term and large-scale observation of methane, leading to the establishment of a unified monitoring system, but it also enables the detection and quantification of anomalous methane point-source emissions by overcoming temporal and spatial constraints. Nevertheless, challenges persist in regards to methane point source detection due to instrument limitations and the impact of complex subsurface conditions. Additionally, current methane remote sensing satellites predominantly rely on passive observation methods, resulting in limited observation frequency. The absence of monitoring during nighttime and in polar regions leaves a significant number of methane emission areas unobserved. The upcoming launch of the MERLIN satellite in 2028 aims to address these limitations. By introducing nighttime observation capabilities, MERLIN will mitigate the impact of cloud cover on observations, increasing the number of effective observations, and enabling the monitoring of the permafrost areas. This satellite will play a crucial role in filling observational gaps in the monitoring of polar sources of methane emissions, enhancing our understanding of methane’s role in climate change, and reducing uncertainties regarding methane emission estimates. The MethaneSAT satellite, which has been launched in 2024, will focus on monitoring the oil and gas industry region, with a high revisit rate, carrying out remote sensing quantification of high-resolution large-scale point sources on a larger spatial scale.
In the future evolution of methane remote sensing satellites, a more integrated approach is essential, combining area flux mappers and point source imagers to establish diverse satellite networks for observation. The establishment of a unified monitoring mechanism for emission detection and assimilation datasets is also necessary. The synergy of active and passive satellites holds the potential to enhance detection precision, while the integration of geostationary satellites with polar orbiting satellites can significantly improve temporal resolution. The establishment of a network of observation satellites contributes to the development of a globally unified and continuous methane gas observation dataset. This network-centric approach ensures comprehensive coverage, minimizing observational gaps and fostering a more nuanced understanding of methane dynamics. Then, it can comprehensively observe the methane gas concentration and the temporal variations in sources and sinks in the context of the carbon-neutral background. This will provide strong support for the global carbon inventory, started in 2023, and reduce uncertainties in regards to national emission inventory reports.