Traffic Flow Prediction Research Based on an Interactive Dynamic Spatial–Temporal Graph Convolutional Probabilistic Sparse Attention Mechanism (IDG-PSAtt)
Abstract
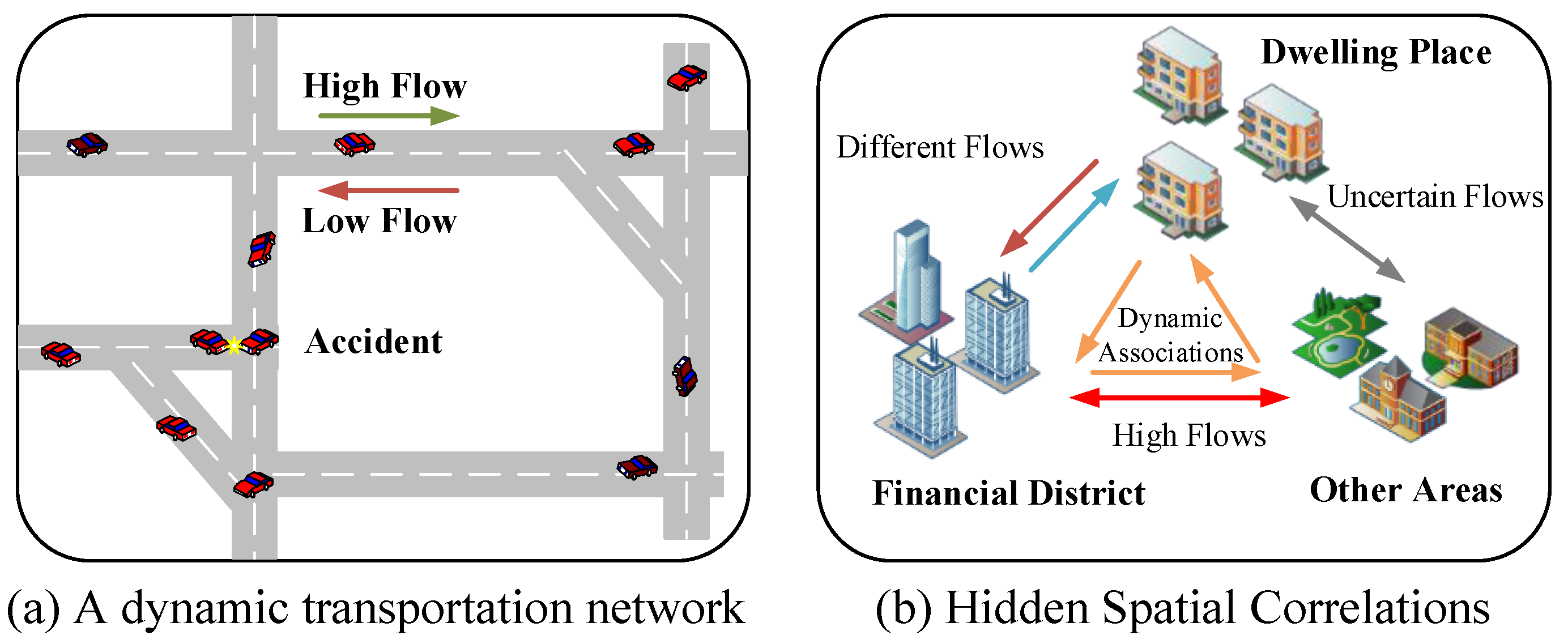
1. Introduction
- A traffic flow prediction model based on IDG-PSAtt is proposed; this model embeds a DGCN into an interactive learning structure and inherits the advantages of spatial–temporal convolution, as well as a ProbSSAtt block to capture long-range dynamic spatia–temporal features.
- A DGCN is constructed to capture spatial–temporal features; this network is generated via the fusion of an adaptive adjacency matrix and a learnable adjacency matrix, where the adaptive adjacency matrix captures the heterogeneity of the given traffic flow time series and the learnable adjacency matrix learns the dynamic correlations among the nodes of the road network.
- An ST-Conv block is designed, and the ProbSSAtt block is introduced; these blocks learn the hidden spatial features among various nodes and the complex spatial–temporal dependencies to improve the computational efficiency of the model.
- Several comparative experiments are conducted on two datasets and the results show that the IDG-PSAtt model achieves the best prediction performance in both cases when compared to the existing baseline methods.
- The traffic flow prediction model proposed in this paper can guide the transportation planning process, thus improving the transportation environment, enhancing the quality of residents’ travel, and promoting the sustainable development of cities.
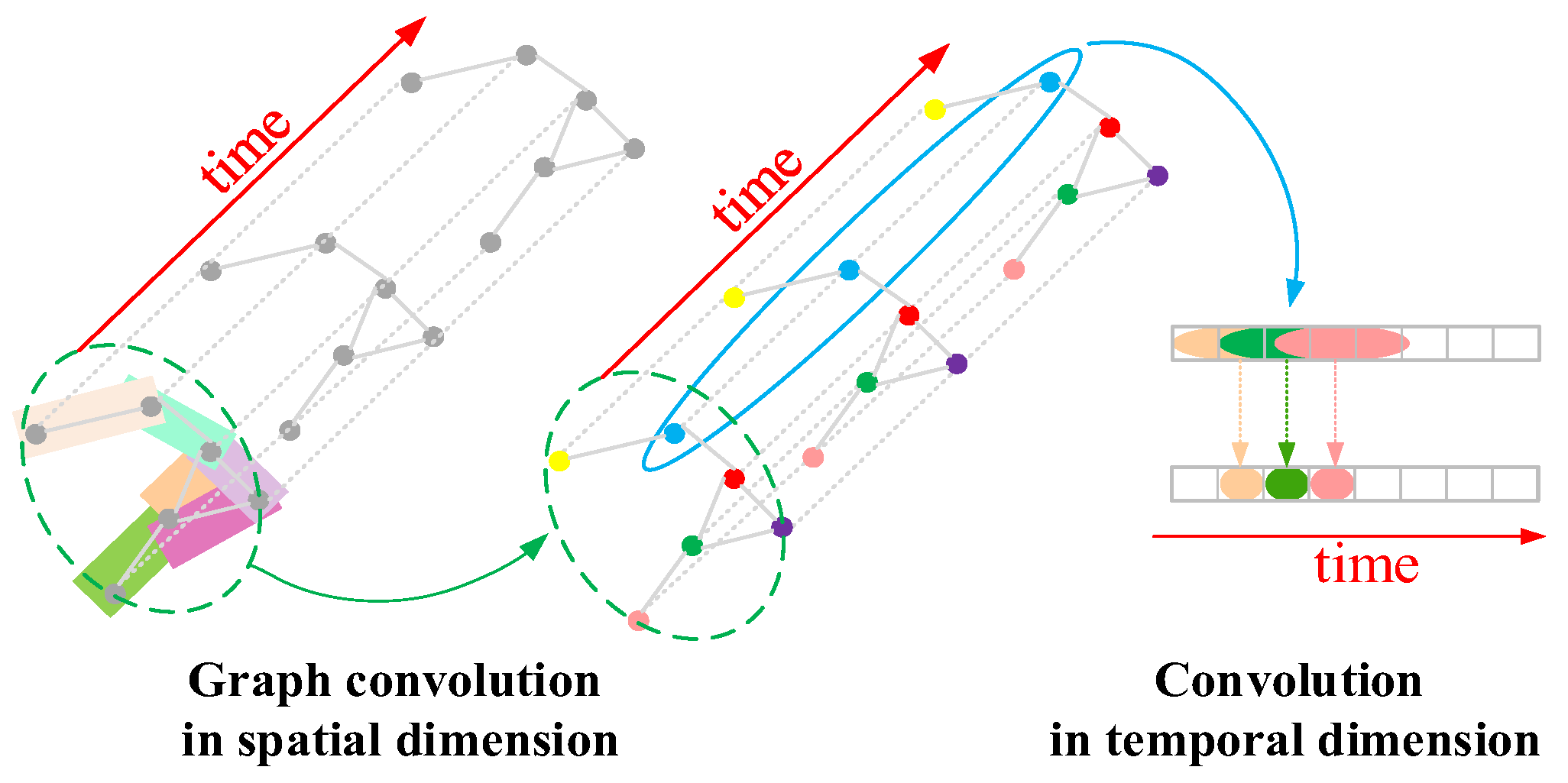
2. Methodology
2.1. Problem Definition
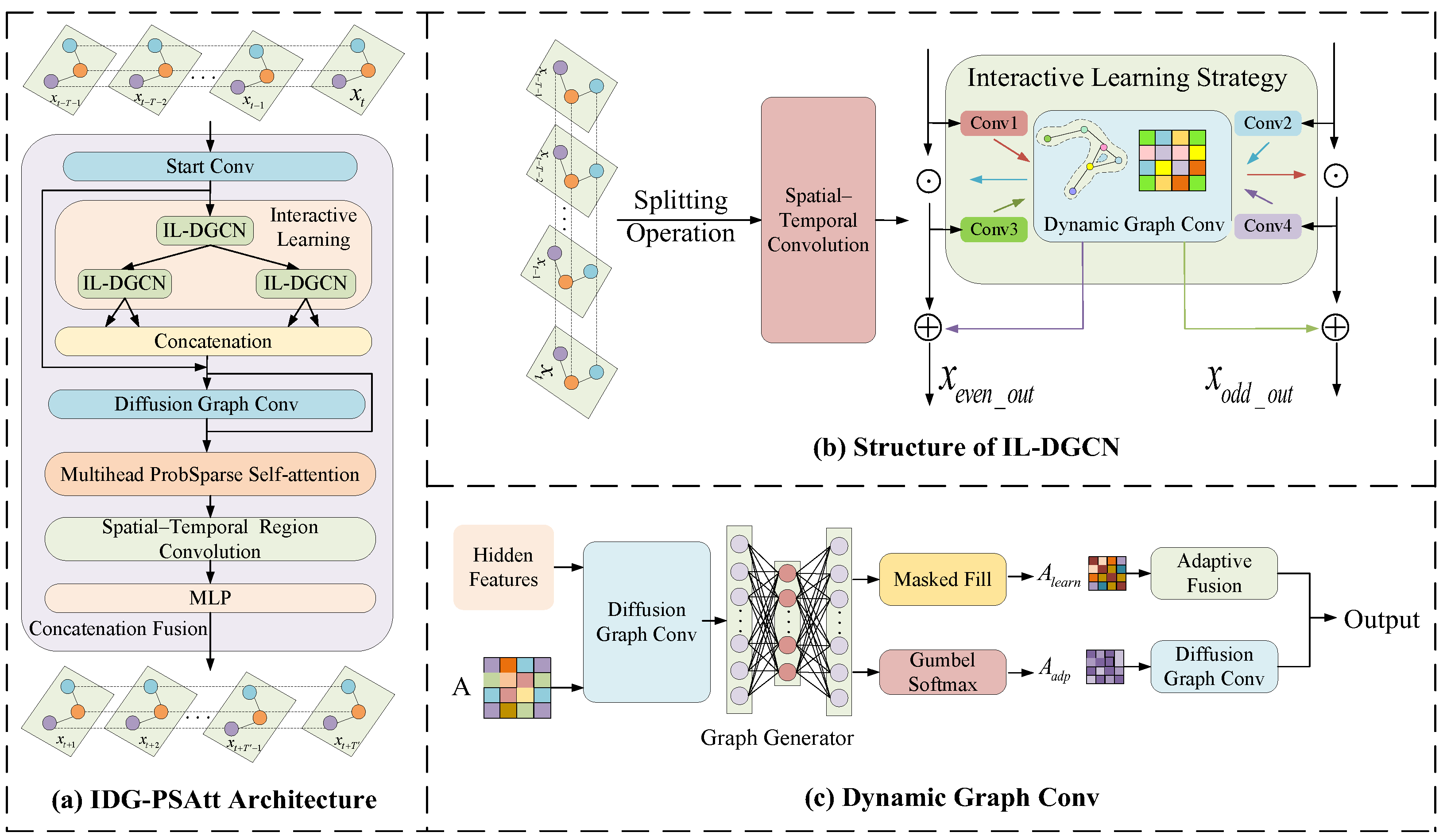
2.2. Framework of IDG-PSAtt
2.2.1. Interactive Learning
2.2.2. Dynamic Graph Convolution
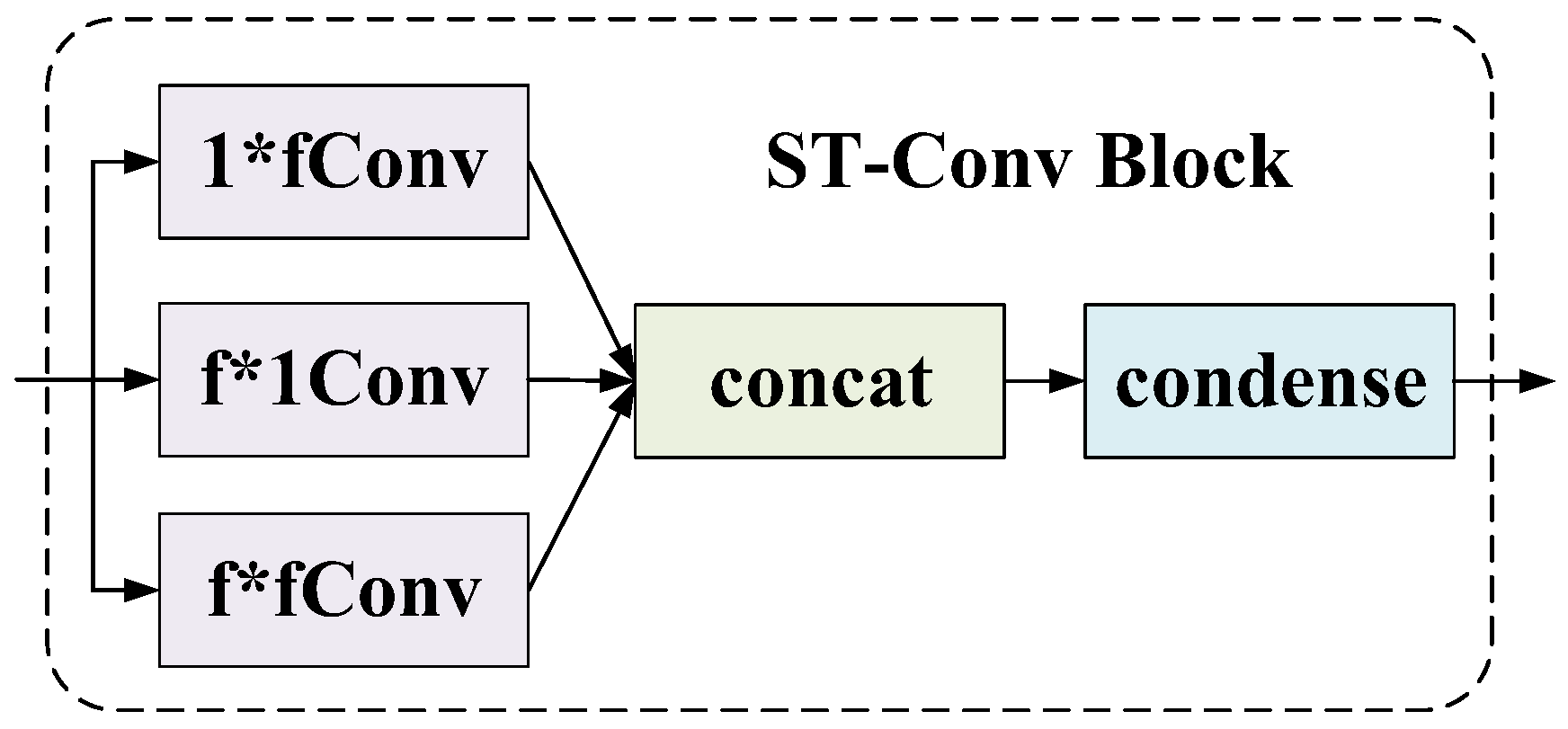
2.2.3. ST-Convolution Block
2.2.4. Subsubsection
2.3. Data Description
2.4. Evaluation Metrics
2.5. Baselines
- (1)
- HA [33]: The average values of the historical and current traffic flows are used as the prediction values for the next step. In the baseline method, the average of the past 12 time slices in the same period as a week ago is utilized to forecast the current time slice.
- (2)
- VAR [34]: This method represents vector autoregression.
- (3)
- SVR [35]: This is an extension of support vector machine (SVM) classification for regression problems. According to the grid search method, the insensitivity loss coefficient ε is set to 0.1 and the penalty factor C is set to 1.0.
- (4)
- FNN [7]: This is a two-hidden-layer feedforward neural network using L2 regularization.
- (5)
- ARIMA [36]: This is a popular model used in time series prediction tasks. The orders of the autoregression, difference, and moving average operations are the three crucial parameters for the ARIMA model, (p, d, q) is set to (4, 1, 1).
- (6)
- FC-LSTM [37]: This is a classic RNN that learns time series and makes predictions via fully connected neural networks, a single hidden layer with 64 hidden units is utilized.
- (7)
- WaveNet [38]: This is a CNN for predicting sequence data, there are 8 stacked layers with a specific dilation rate of [1, 2, 1, 2, 1, 2, 1, 2, 1, 2], and the hidden dimension is set to 64.
- (8)
- Graph WaveNet [3]: This network is constructed with a GCN and a gated temporal convolution layer (gated TCN), there are 8 stacked layers with a specific dilation rate of [1, 2, 1, 2, 1, 2, 1, 2, 1, 2], and the hidden dimension is set to 64.
- (9)
- STGCN [2]: This network employs graph convolutional layers and convolutional sequence layers, there are 2 spatiotemporal cells and the hidden dimension is set to 64.
- (10)
- ASTGCN [8]: This model employs an attention mechanism to capture spatiotemporal dynamic correlations, there are 2 spatiotemporal cells and the hidden dimension is set to 64.
- (11)
- STSGCN [16]: This model individually captures localized spatial and temporal correlations, the number of STSG layers is set to 3 and the hidden dimension is set to 64.
3. Results and Discussion
- (1)
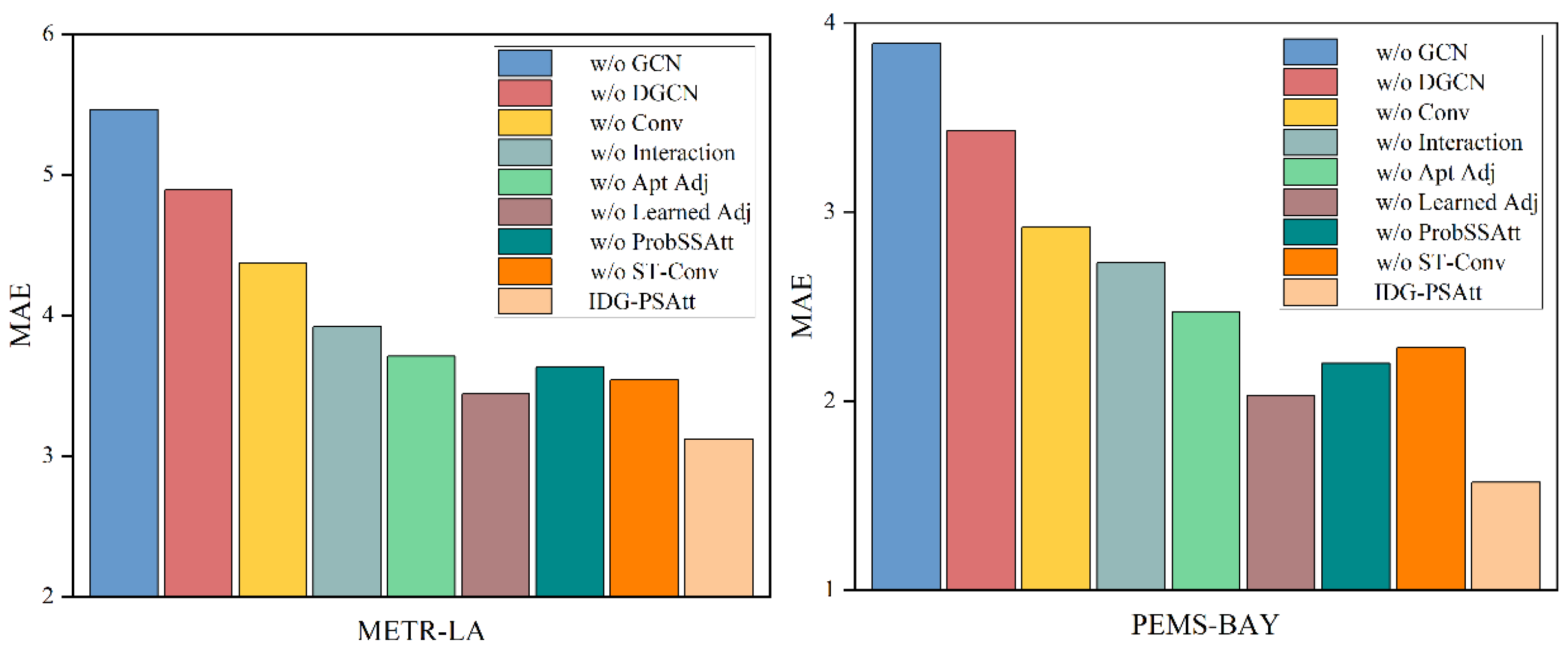
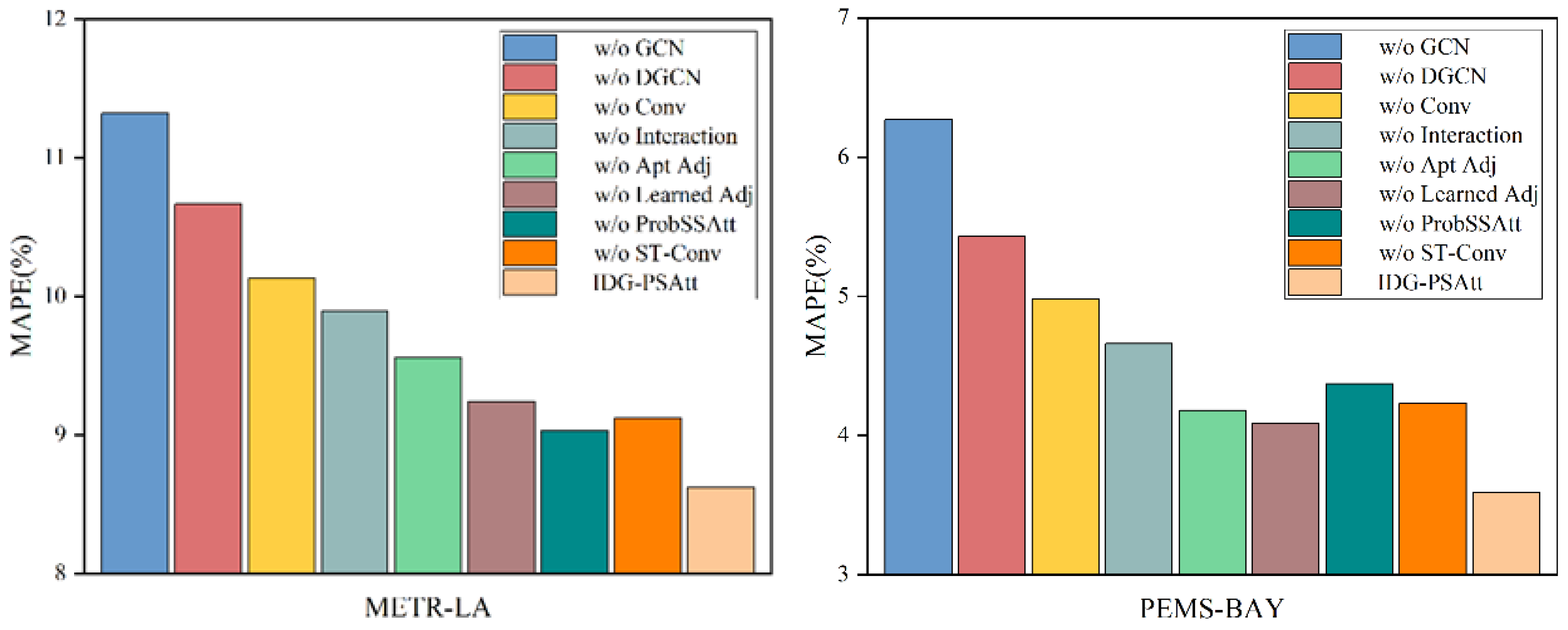
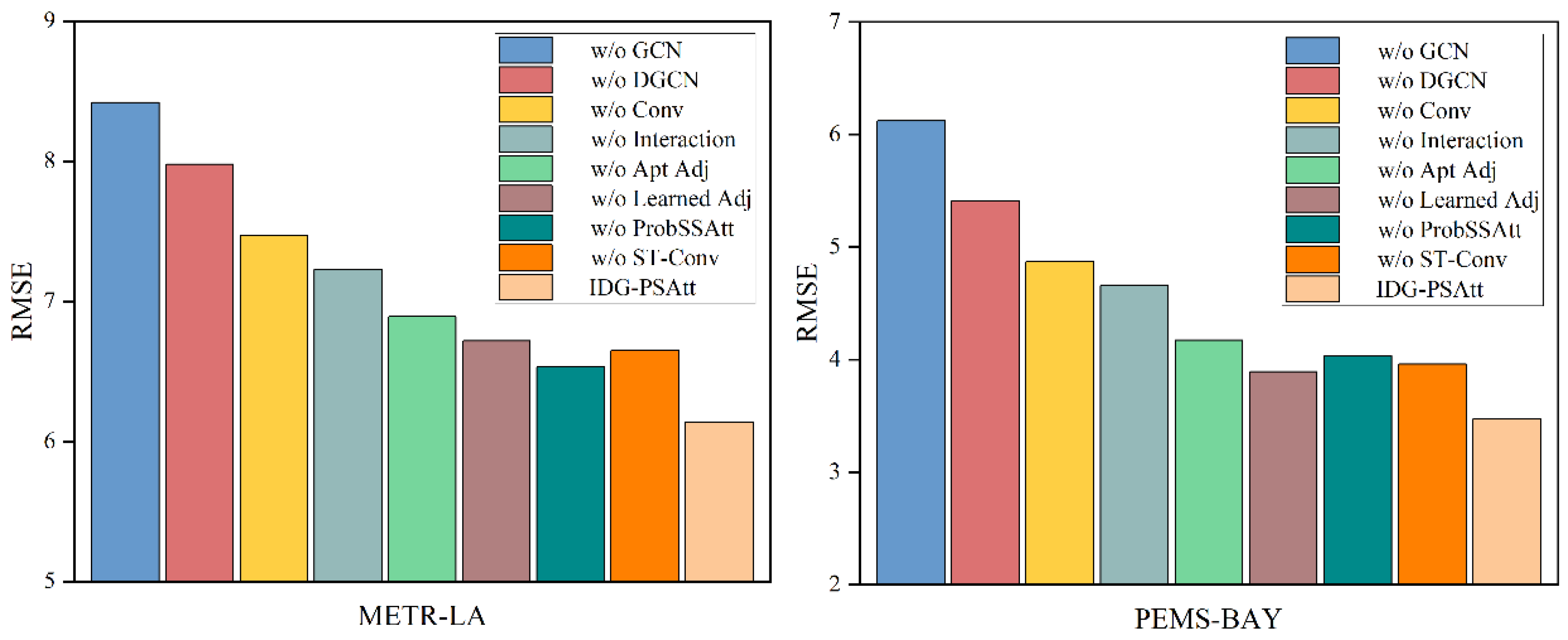
- Ablation Experiment
- (1)
- GCN w/o: Based on the IDG-PSAtt model, the GCN is removed.
- (2)
- DGCN w/o: Based on the IDG-PSAtt model, the DGCN is removed.
- (3)
- Conv w/o: The one-dimensional convolutional modules are removed from the interactive learning structures based on the IDG-PSAtt model.
- (4)
- Interaction w/o: Based on the IDG-PSAtt model, the interactive learning structures are removed.
- (5)
- Apt Adj w/o: Based on the IDG-PSAtt model, the adaptive adjacency matrix in the DGCN is removed.
- (6)
- Learned Adj w/o: Based on the IDG-PSAtt model, the graph generation structure is removed, and the adaptive adjacency matrix is retained.
- (7)
- ProbSSAtt w/o: Based on the IDG-PSAtt model, the ProbSSAtt block module is removed.
- (8)
- ST-Conv Block w/o: Based on the IDG-PSAtt model, the ST-Conv module is removed.
- (2)
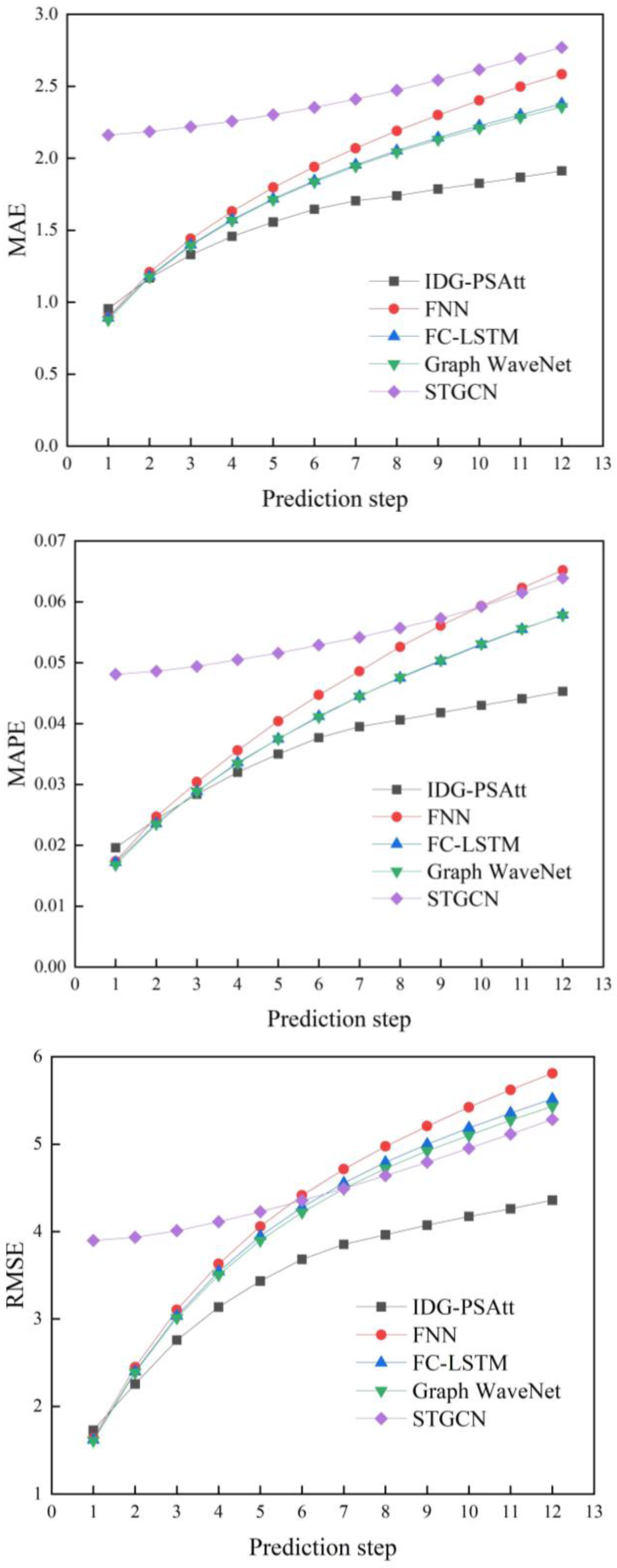
- Visual Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IDG-PSAtt | interactive dynamic spatial–temporal graph convolutional probabilistic sparse attention mechanism |
| IL-DGCN | interactive dynamic graph convolutional network |
| ST-Conv | spatial–temporal convolution |
| ProbSSAtt | probabilistic sparse self-attention |
| GCN | graph convolutional network |
| MAE | mean absolute error |
| RMSE | root mean square error |
| ITSs | intelligent transportation systems |
| STGCN | spatial–temporal graph convolutional network |
| GLUs | gated linear units |
| TCNs | temporal convolutional networks |
| GRU | gated recursive unit |
| RNN | artificial neural network |
| MLP | multilayer perceptron |
| MAPE | mean absolute percentage error |
| HA | historical average |
| VAR | vector autoregression |
| SVM | support vector machine |
| FNN | feedforward neural network |
| ARIMA | Autoregressive Integrated Moving Average Model |
| FC-LSTM | Fully Connected Long Short-Term Memory |
| STGCN | Spatiotemporal Graph Convolutional Network |
| ASTGCN | Attention-based Spatial–Temporal Graph Convolutional Network |
| STSGCN | Spatiotemporal Stream Graph Convolutional Network |
| Nomenclature | |
| graph | |
| the set of nodes | |
| the set of edges between the nodes | |
| denotes the initial adjacency matrix generated by the graph | |
| adjacency matrix | |
| future traffic flows | |
| historical time series | |
| denotes the observation value of graph at time | |
| denotes the number of feature channels | |
| denotes the length of the given historical time series | |
| denotes the length of the predicted future traffic series | |
References
- He, R.; Xiao, Y.; Lu, X.; Zhang, S.; Liu, Y. ST-3DGMR: Spatio-temporal 3D grouped multiscale ResNet network for region-based urban traffic flow prediction. Inf. Sci. 2023, 624, 68–93. [Google Scholar] [CrossRef]
- Li, D.; Lasenby, J. Spatiotemporal Attention-Based Graph Convolution Network for Segment-Level Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2022, 23, 8337–8345. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for Deep Spatial-Temporal Graph Modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar] [CrossRef]
- Zhang, Q.; Chang, J.; Meng, G.; Xiang, S.; Pan, C. Spatio-temporal graph structure learning for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 1177–1185. [Google Scholar] [CrossRef]
- Shao, Y.; Zhao, Y.; Yu, F.; Zhu, H.; Fang, J. The Traffic Flow Prediction Method Using the Incremental Learning-Based CNN-LTSM Model: The Solution of Mobile Application. Mob. Inf. Syst. 2021, 2021, 5579451. [Google Scholar] [CrossRef]
- Li, M.; Zhu, Z. Spatial-temporal fusion graph neural networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 4189–4196. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, D.G.; Yan, H.R.; Qiu, J.N.; Gao, J.X. A new method of data missing estimation with FNN-based tensor heterogeneous ensemble learning for internet of vehicle. Neurocomputing 2021, 420, 98–110. [Google Scholar] [CrossRef]
- Qi, J.; Zhao, Z.; Tanin, E.; Cui, T.; Nassir, N.; Sarvi, M. A Graph and Attentive Multi-Path Convolutional Network for Traffic Prediction. IEEE Trans. Knowl. Data Eng. 2022, 35, 6548–6560. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Wan, H.; Li, X.; Cong, G. Learning Dynamics and Heterogeneity of Spatial-Temporal Graph Data for Traffic Forecasting. IEEE Trans. Knowl. Data Eng. 2021, 34, 5415–5428. [Google Scholar] [CrossRef]
- Bai, L.; Yao, L.; Li, C.; Wang, X.; Wang, C. Adaptive graph convolutional recurrent network for traffic forecasting. Adv. Neural Inf. Process. Syst. 2020, 33, 17804–17815. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Chen, W.; Chen, L.; Xie, Y.; Cao, W.; Gao, Y.; Feng, X. Multirange attentive bicomponent graph convolutional network for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3529–3536. [Google Scholar] [CrossRef]
- Dong, C.; Shao, C.; Li, X. Short-Term Traffic Flow Forecasting of Road Network Based on Spatial-Temporal Characteristics of Traffic Flow. In Proceedings of the World Congress on Computer Science & Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, Y.; Wang, J.; Qin, J.; Liu, X.; Yin, H.; Huang, H. DAGCRN: Graph convolutional recurrent network for traffic forecasting with dynamic adjacency matrix. Expert Syst. Appl. 2023, 227, 120259. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Online, CA, USA, 6–10 July 2020; pp. 753–763. [Google Scholar] [CrossRef]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 914–921. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, W.; Chen, X.M. Bibliometric methods in traffic flow prediction based on artificial intelligence. Expert Syst. Appl. 2023, 228, 120421. [Google Scholar] [CrossRef]
- Huo, G.; Zhang, Y.; Wang, B.; Gao, J.; Hu, Y.; Yin, B. Hierarchical Spatio–Temporal Graph Convolutional Networks and Transformer Network for Traffic Flow Forecasting. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3855–3867. [Google Scholar] [CrossRef]
- Wang, S.; Pan, Y.; Zhang, J.; Zhou, X.; Cui, Z.; Hu, G.; Pan, Z. Robust and label efficient bi-filtering graph convolutional networks for node classification. Knowl.-Based Syst. 2021, 224, 106891. [Google Scholar] [CrossRef]
- Yu, W.; Huang, X.; Qiu, Y.; Zhang, S.; Chen, Q. GSTC-Unet: A U-shaped multi-scaled spatiotemporal graph convolutional network with channel self-attention mechanism for traffic flow forecasting. Expert Syst. Appl. 2023, 232, 120724. [Google Scholar] [CrossRef]
- Deng, L.; Zhang, X.; Tao, S.; Zhao, Y.; Wu, K.; Liu, J. A spatiotemporal graph convolution-based model for daily runoff prediction in a river network with non-Euclidean topological structure. Stoch. Environ. Res. Risk Assess. 2023, 37, 1457–1478. [Google Scholar] [CrossRef]
- Yan, B.; Wang, G.; Yu, J.; Jin, X.; Zhang, H. Spatial-Temporal Chebyshev Graph Neural Network for Traffic Flow Prediction in IoT-Based ITS. IEEE Internet Things J. 2022, 9, 9266–9279. [Google Scholar] [CrossRef]
- Tang, S.; Li, B.; Yu, H. ChebNet: Efficient and Stable Constructions of Deep Neural Networks with Rectified Power Units using Chebyshev Approximations. arXiv 2019, arXiv:1911.05467. [Google Scholar] [CrossRef]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Part C Emerg. Technol. 2020, 118, 102674. [Google Scholar] [CrossRef]
- Fukuda, S.; Uchida, H.; Fujii, H.; Yamada, T. Short-term Prediction of Traffic Flow under Incident Conditions using Graph Convolutional RNN and Traffic Simulation. IET Intell. Transp. Syst. 2020, 14, 936–946. [Google Scholar] [CrossRef]
- Liang, G.; Kintak, U.; Tiwari, P.; Nowaczyk, S.; Kumar, N. Semantics-Aware Dynamic Graph Convolutional Network for Traffic Flow Forecasting. IEEE Trans. Veh. Technol. 2023, 72, 7796–7809. [Google Scholar] [CrossRef]
- Chen, Z.; Lu, Z.; Chen, Q.; Zhong, H.; Zhang, Y.; Xue, J.; Wu, C. Spatial-temporal short-term traffic flow prediction model based on dynamical-learning graph convolution mechanism. Inf. Sci. 2022, 611, 522–539. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, X.; Wang, E.; Liu, W.; Yang, Y.; Yang, F. Dynamic traffic correlations based spatio-temporal graph convolutional network for urban traffic prediction. Inf. Sci. 2023, 621, 580–595. [Google Scholar] [CrossRef]
- Zheng, G.; Chai, W.K.; Katos, V. A dynamic spatial-temporal deep learning framework for traffic speed prediction on large-scale road networks. Expert Syst. Appl. 2022, 195, 116585. [Google Scholar] [CrossRef]
- Zheng, C.; Fan, X.; Wang, C.; Qi, J. Gman: A graph multi-attention network for traffic prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 1234–1241. [Google Scholar] [CrossRef]
- Khaled, A.; Elsir, A.M.T.; Shen, Y. TFGAN: Traffic forecasting using generative adversarial network with multi-graph convolutional network. Knowl. Based Syst. 2022, 249, 108990. [Google Scholar] [CrossRef]
- Huang, B.; Dou, H.; Luo, Y.; Li, J.; Wang, J.; Zhou, T. Adaptive Spatiotemporal Transformer Graph Network for Traffic Flow Forecasting by IoT Loop Detectors. IEEE Internet Things J. 2023, 10, 15. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, B.; Zhu, Y. Shor-term Traffic Speed Forecasting Based on Attention Convolutional Neural Network for Arterials. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 999–1016. [Google Scholar] [CrossRef]
- Divyam, S.A.; Singh, B. Comparative Study of Static VAR Compensation Techniques—Thyristor Switched Reactor and Thyristor Switched Capacitor. In Proceedings of the International Conference on Communication and Electronics Systems, Coimbatore, India, 10–12 June 2020. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H. Short-term traffic flow forecasting with spatial-temporal correlation in a hybrid deep learning framework. arXiv 2016, arXiv:1612.01022. [Google Scholar] [CrossRef]
- Yan, H.; Ma, X.; Pu, Z. Learning dynamic and hierarchical traffic spatiotemporal features with transformer. IEEE Trans. Intell. Transp. Syst. 2021, 23, 22386–22399. [Google Scholar] [CrossRef]
- Ishida, K.; Ercan, A.; Nagasato, T.; Kiyama, M.; Amagasaki, M. Use of 1D-CNN for input data size reduction of LSTM in Hourly Rainfall-Runoff modeling. arXiv 2021, arXiv:2111.04732. [Google Scholar] [CrossRef]
- Rio, J.; Momey, F.; Ducottet, C.; Alata, O. WaveNet based architectures for denoising periodic discontinuous signals and application to friction signals. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021; pp. 1580–1584. [Google Scholar] [CrossRef]
- Chen, J.; Yu, Y.; Guo, Q. Freeway traffic congestion reduction and environment regulation via model predictive control. Algorithms 2019, 12, 220. [Google Scholar] [CrossRef]
- Medina-Salgado, B.; Sánchez-DelaCruz, E.; Pozos-Parra, P.; Sierra, J.E. Urban traffic flow prediction techniques: A review. Sustain. Comput. Inform. Syst. 2022, 35, 100739. [Google Scholar] [CrossRef]
| Data | METR-LA | PEMS-BAY |
|---|---|---|
| Type | sequential | sequential |
| Attribute | speed | speed |
| Location | highways of Los Angeles | the Bay Area |
| Edges | 1515 | 2369 |
| Time Steps | 34,272 | 52,116 |
| Nodes | 207 | 325 |
| Data | Models | 15 min | 30 min | 60 min | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | ||
| METR-LA | HA | 4.56 | 8.92 | 13.00% | 4.56 | 8.92 | 13.00% | 4.56 | 8.92 | 13.00% |
| VAR | 4.42 | 7.89 | 10.20% | 5.41 | 9.13 | 12.7% | 6.52 | 10.11 | 15.80% | |
| SVR | 3.99 | 8.45 | 9.30% | 5.05 | 10.87 | 12.10% | 6.72 | 13.76 | 16.70% | |
| FNN | 3.99 | 7.94 | 9.90% | 4.23 | 8.17 | 12.90% | 4.49 | 8.69 | 14.00% | |
| ARIMA | 3.99 | 8.21 | 9.60% | 5.15 | 10.45 | 12.70% | 6.90 | 13.23 | 17.40% | |
| FC-LSTM | 3.44 | 6.30 | 9.60% | 3.77 | 7.23 | 10.90% | 4.37 | 8.69 | 13.20% | |
| WaveNet | 2.99 | 5.89 | 8.04% | 3.59 | 7.28 | 10.25% | 4.45 | 8.93 | 13.62% | |
| GWN | 2.98 | 5.90 | 7.92% | 3.59 | 7.29 | 10.26% | 4.43 | 8.97 | 13.64% | |
| STGCN | 2.88 | 5.74 | 7.62% | 3.47 | 7.24 | 9.57% | 4.59 | 9.40 | 12.70% | |
| ASTGCN | 4.86 | 9.27 | 9.21% | 5.43 | 10.61 | 10.13% | 6.51 | 12.52 | 11.64% | |
| STSGCN | 3.31 | 7.62 | 8.06% | 4.13 | 9.77 | 10.29% | 5.06 | 11.66 | 12.91% | |
| IDG-PSAtt | 2.77 | 5.28 | 7.24% | 3.15 | 6.24 | 8.73% | 3.62 | 7.38 | 10.52% | |
| PEMS-BAY | HA | 2.88 | 5.59 | 6.80% | 2.88 | 5.59 | 6.80% | 2.88 | 5.59 | 6.80% |
| VAR | 1.74 | 3.16 | 3.60% | 2.32 | 4.25 | 5.00% | 2.93 | 5.44 | 6.50% | |
| SVR | 1.85 | 3.59 | 3.80% | 2.48 | 5.18 | 5.50% | 3.28 | 7.08 | 8.00% | |
| FNN | 2.20 | 4.42 | 5.19% | 2.30 | 4.63 | 5.43% | 2.46 | 4.98 | 5.89% | |
| ARIMA | 1.62 | 3.30 | 3.50% | 2.33 | 4.76 | 5.40% | 3.38 | 6.50 | 8.30% | |
| FC-LSTM | 2.05 | 4.19 | 4.80% | 2.20 | 4.55 | 5.20% | 2.37 | 4.96 | 5.70% | |
| WaveNet | 1.39 | 3.01 | 2.91% | 1.83 | 4.21 | 4.16% | 2.35 | 5.43 | 5.87% | |
| GWN | 1.39 | 3.01 | 2.89% | 1.83 | 4.21 | 4.11% | 2.35 | 5.43 | 5.78% | |
| STGCN | 1.36 | 2.96 | 2.90% | 1.81 | 4.27 | 4.17% | 2.49 | 5.69 | 5.79% | |
| ASTGCN | 1.52 | 3.13 | 3.22% | 2.01 | 4.27 | 4.48% | 2.61 | 5.42 | 6.00% | |
| STSGCN | 1.44 | 3.01 | 3.04% | 1.83 | 4.18 | 4.17% | 2.26 | 5.21 | 5.40% | |
| IDG-PSAtt | 0.96 | 1.72 | 1.96% | 1.64 | 3.68 | 3.77% | 1.91 | 4.36 | 4.53% | |
| Dataset | Model | MAE | RMSE | MAPE |
|---|---|---|---|---|
| METR-LA | w/o GCN | 5.46 | 8.42 | 11.32% |
| w/o DGCN | 4.89 | 7.98 | 10.67% | |
| w/o Conv | 4.37 | 7.47 | 10.13% | |
| w/o Interaction | 3.92 | 7.23 | 9.89% | |
| w/o Apt Adj | 3.71 | 6.89 | 9.56% | |
| w/o Learned Adj | 3.44 | 6.72 | 9.24% | |
| w/o ProbSSAtt | 3.63 | 6.53 | 9.03% | |
| w/o ST-Conv | 3.54 | 6.65 | 9.12% | |
| IDG-PSAtt | 3.12 | 6.14 | 8.62% | |
| PEMS-BAY | w/o GCN | 3.89 | 6.12 | 6.27% |
| w/o DGCN | 3.43 | 5.41 | 5.43% | |
| w/o Conv | 2.92 | 4.87 | 4.98% | |
| w/o Interaction | 2.73 | 4.66 | 4.66% | |
| w/o Apt Adj | 2.47 | 4.17 | 4.18% | |
| w/o Learned Adj | 2.03 | 3.89 | 4.09% | |
| w/o ProbSSAtt | 2.20 | 4.03 | 4.37% | |
| w/o ST-Conv | 2.28 | 3.96 | 4.23% | |
| IDG-PSAtt | 1.57 | 3.47 | 3.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; He, Z.; Huang, Z.; Wang, J.; Yin, H. Traffic Flow Prediction Research Based on an Interactive Dynamic Spatial–Temporal Graph Convolutional Probabilistic Sparse Attention Mechanism (IDG-PSAtt). Atmosphere 2024, 15, 413. https://doi.org/10.3390/atmos15040413
Ding Z, He Z, Huang Z, Wang J, Yin H. Traffic Flow Prediction Research Based on an Interactive Dynamic Spatial–Temporal Graph Convolutional Probabilistic Sparse Attention Mechanism (IDG-PSAtt). Atmosphere. 2024; 15(4):413. https://doi.org/10.3390/atmos15040413
Chicago/Turabian StyleDing, Zijie, Zhuoshi He, Zhihui Huang, Junfang Wang, and Hang Yin. 2024. "Traffic Flow Prediction Research Based on an Interactive Dynamic Spatial–Temporal Graph Convolutional Probabilistic Sparse Attention Mechanism (IDG-PSAtt)" Atmosphere 15, no. 4: 413. https://doi.org/10.3390/atmos15040413
APA StyleDing, Z., He, Z., Huang, Z., Wang, J., & Yin, H. (2024). Traffic Flow Prediction Research Based on an Interactive Dynamic Spatial–Temporal Graph Convolutional Probabilistic Sparse Attention Mechanism (IDG-PSAtt). Atmosphere, 15(4), 413. https://doi.org/10.3390/atmos15040413






