Decomposition of Lorenz Trajectories Based on Space Curve Tangent Vector
Abstract
1. Introduction
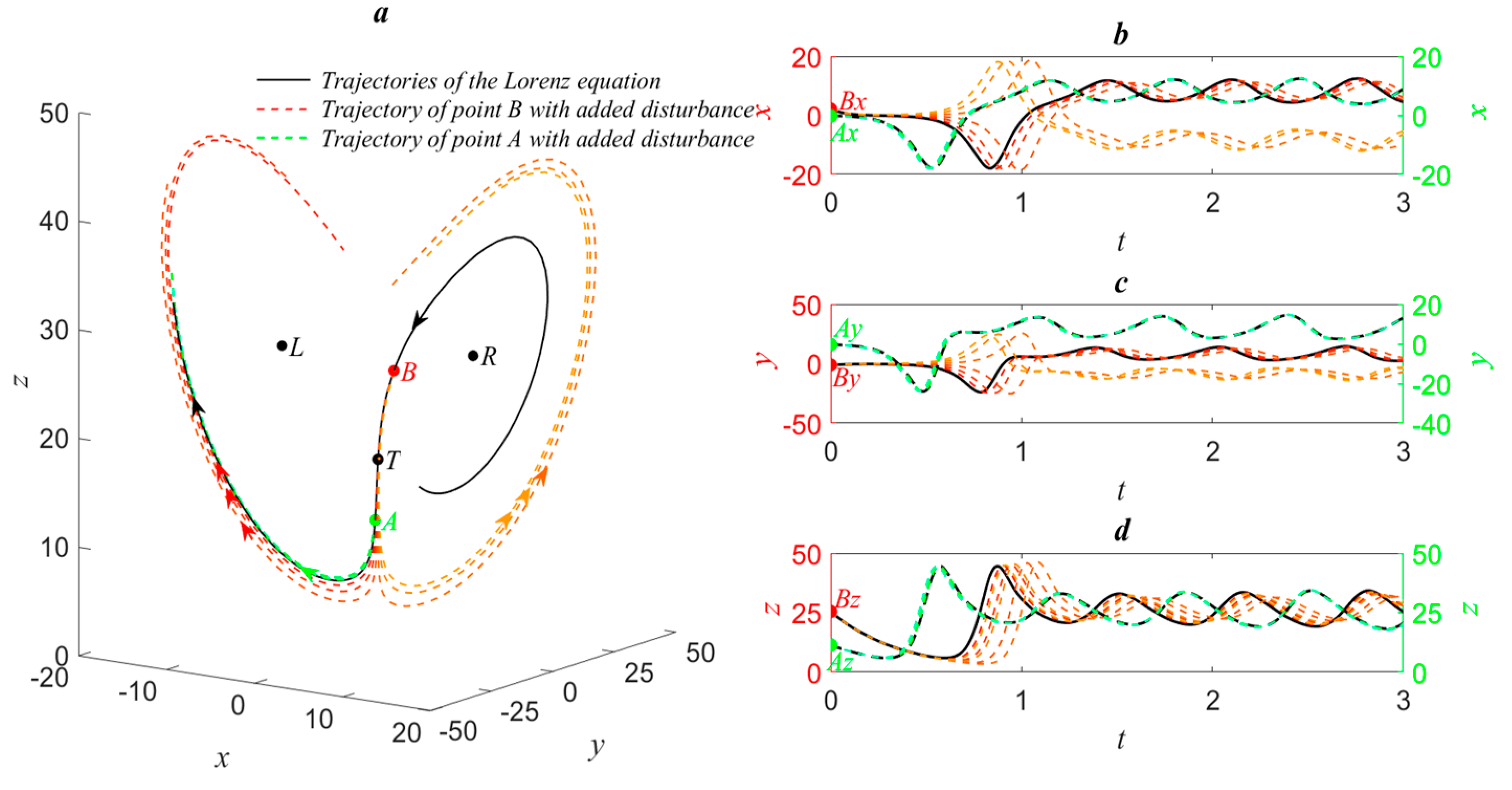
2. Perturbation Response of Point on Lorenz Trajectories
3. Decomposition of Lorenz Trajectories
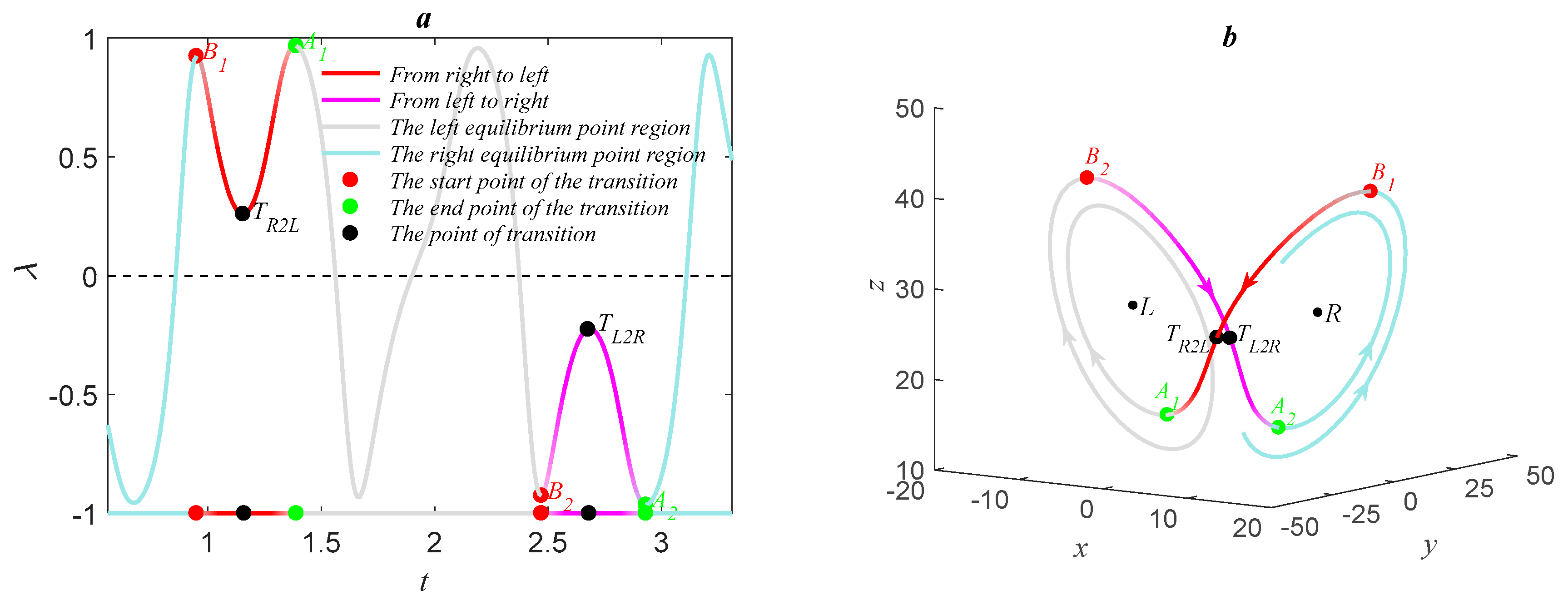
3.1. Determination of Transition Points on the Trajectories
3.2. Transition Time of Trajectories of the Lorenz Equation
3.3. Fitting of Trajectories and Transition Points
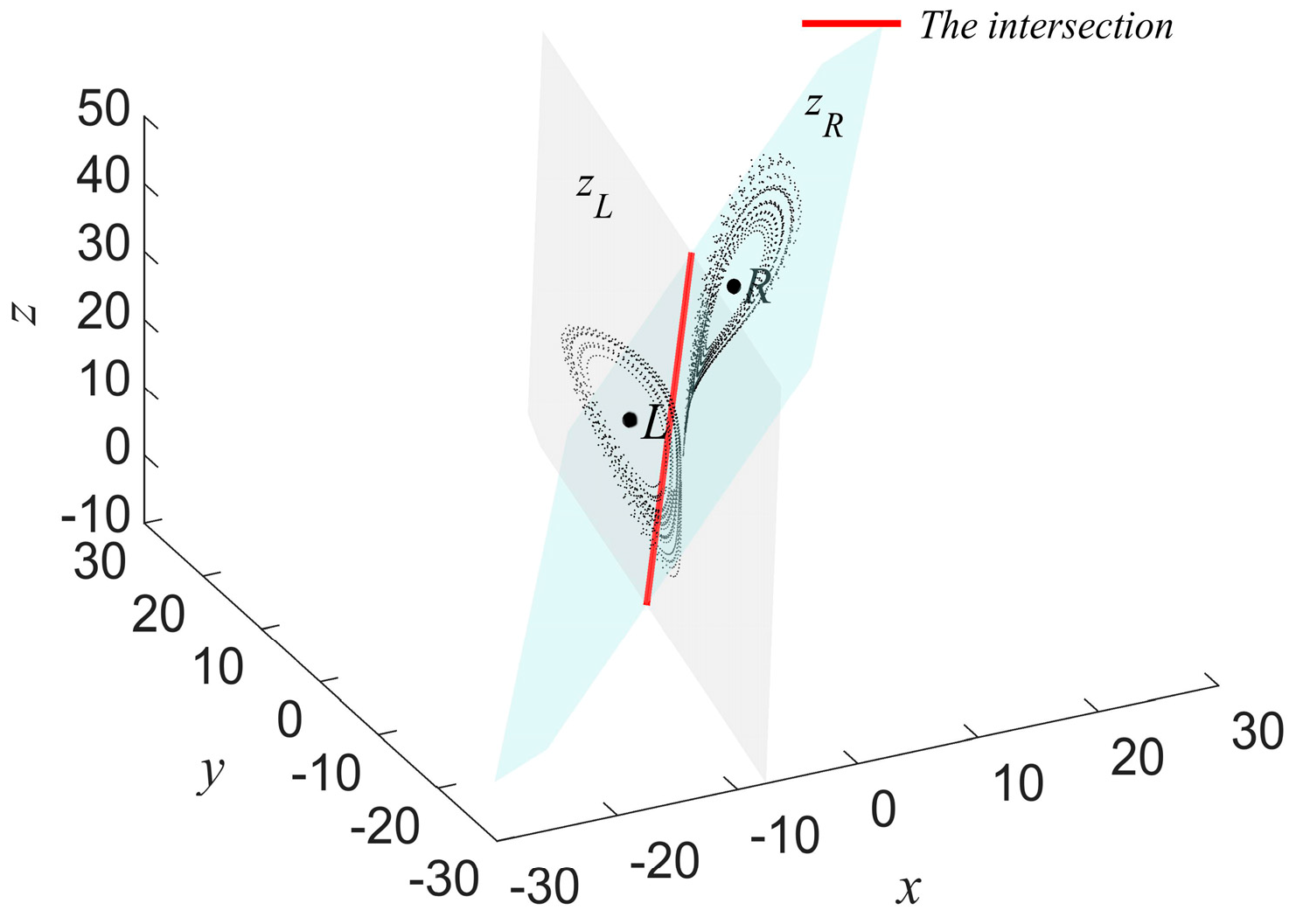
3.3.1. Linear Fitting of Trajectories in the Region of Left and Right Equilibrium Points
3.3.2. Fitting of Transition Points
4. Conclusions and Research Significance
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Bao, B.C.; Liu, Z.A. Hyperchaotic attractor coined from chaotic lu system. Chin. Phys. Lett. 2008, 25, 2396–2399. [Google Scholar] [CrossRef]
- Li, C.B.; Julien, C.S.; Wesley, T.; Zhu, H.Q. A new piecewise linear hyperchaotic circuit. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 977–981. [Google Scholar] [CrossRef]
- Sun, K.H.; Sprott, J.C. Dynamics of a simplified Lorenz system. Int. J. Bifurc. Chaos 2009, 19, 1357–1360. [Google Scholar] [CrossRef]
- Qiang, J. Hyperchaos generated from the Lorenz chaotic system and its control. Phys. Lett. A 2007, 366, 217–222. [Google Scholar] [CrossRef]
- He, W.P.; Feng, G.L.; Dong, W.J.; Li, J.P. On the predictability of the Lorenz system. Acta Phys. Sin. 2006, 55, 969–977. [Google Scholar] [CrossRef]
- Ding, R.Q.; Li, J.P. Study on the regularity of predictability limit of chaotic systems with different initial errors. Acta Phys. Sin. 2008, 57, 7494–7499. [Google Scholar] [CrossRef]
- Feng, G.L.; Wang, Q.G.; Hou, W.; Gong, Z.Q.; Zhi, R. Long-range correlation of extreme events in meterorological field. Acta Phys. Sin. 2009, 58, 2853–2861. [Google Scholar] [CrossRef]
- Li, J.P.; Ding, R.Q. Studies of predictability of single variable from multi-dimensional chaotic dynamical system. Chin. J. Atmos. Sci. 2009, 33, 551–556. [Google Scholar] [CrossRef]
- Shi, Z.; Ding, R.Q.; Li, J.P. Impacts of random error on the predictability of chaotic systems. Chin. J. Atmos. Sci. 2012, 36, 458–470. [Google Scholar] [CrossRef]
- Wang, Q.G.; Feng, G.L.; Zheng, Z.H.; Zhi, R.; Chou, J.F. The preliminary analysis of the procedures of extracting predicable components in numerical model of Lorenz system. Chin. J. Atmos. Sci. 2012, 36, 539–550. [Google Scholar] [CrossRef]
- Zhu, D.W.; Tu, L.L. Adaptive synchronization and parameter identification for Lorenz chaotic system with stochastic perturbations. Acta Phys. Sin. 2013, 62, 98–103. [Google Scholar] [CrossRef]
- Huai, X.W.; Li, J.P.; Ding, R.Q.; Feng, J.; Liu, D.Q. Quantifying local predictability of the Lorenz system using the nonlinear local Lyapunov exponent. Atmos. Ocean. Sci. Lett. 2017, 10, 372–378. [Google Scholar] [CrossRef]
- Li, B.S.; Ding, R.Q.; Li, J.P.; Zhong, Q.J. Predictability of forced Lorenz system. Acta Phys. Sin. 2017, 66, 35–42. [Google Scholar] [CrossRef]
- Liang, D.; Gu, B.; Ding, R.Q.; Li, J.P.; Zhong, Q.J. Comparative study of Lorenz model based ensemble forecasting and single forecasting. Acta Phys. Sin. 2018, 67, 74–82. [Google Scholar] [CrossRef]
- Da, C.J.; Shen, B.L.; Song, J.; Cairang, X.W.; Feng, G.L. Abrupt change detection method based on features of Lorenz trajectories. Atmosphere 2021, 12, 781. [Google Scholar] [CrossRef]
- Jia, H.Y.; Cheng, Z.Q.; Xue, W. Analysis and circuit implementation for the fractional-order Lorenz system. Acta Phys. Sin. 2013, 62, 56–62. [Google Scholar] [CrossRef]
- Ruan, J.Y.; Sun, K.H.; Mou, J. Memristor-based Lorenz hyper-chaotic system and its circuit implementation. Acta Phys. Sin. 2016, 65, 25–35. [Google Scholar] [CrossRef]
- Zhang, B.; Deng, F. Double-compound synchronization of six memristor-based Lorenz systems. Nonlinear Dyn. 2014, 77, 1519–1530. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Ouyang, Z.Q. Biological synergetics, Lorenz model and population dynamics. J. Biomath. 2003, 18, 218–223. [Google Scholar] [CrossRef]
- Ma, R.R.; Wu, J.; Wu, K.Z.; Pan, X.H. Adaptive fixed-time synchronization of Lorenz systems with application in chaotic finance systems. Nonlinear Dyn. 2022, 109, 3145–3156. [Google Scholar] [CrossRef]
- Hadamard, J.; Morse, P.M. Lectures on Cauchy’s problem in linear partial differential equations. Phys. Today 1953, 6, 18. [Google Scholar] [CrossRef]
- Dong, X.H.; Li, X.H.; Zhang, Y.F. Dissipativeness property in lattices of coupled nonidentical Lorenz equations. J. Henan Univ. Nat. Sci. 2008, 38, 346–348. [Google Scholar] [CrossRef]
- Wang, Q.G.; Zhi, R.; Zhang, Z.P. The research on long range correlation of Lorenz system. Acta Phys. Sin. 2008, 57, 5343–5350. [Google Scholar] [CrossRef]
- Ding, R.Q.; Li, J.P. Relationships between the limit of predictability and initial error in the uncoupled and coupled Lorenz models. Adv. Atmos. Sci. 2012, 29, 1078–1088. [Google Scholar] [CrossRef]
- Ren, H.L.; Chou, J.F.; Huang, J.P.; Zhang, P.Q. Theoretical basis and application of an analogue-dynamical model in the Lorenz system. Adv. Atmos. Sci. 2009, 26, 67–77. [Google Scholar] [CrossRef]
- Chiu, C.H.; Lin, W.W.; Peng, C.C. Asymptotic synchronization in lattices of coupled nonidentical Lorenz equations. Int. J. Bifurc. Chaos 2000, 10, 2717–2728. [Google Scholar] [CrossRef]
- Lorenz, E.N. A study of the predictability of a 28-variable atmospheric model. Tellus 1965, 17, 321–333. [Google Scholar] [CrossRef]
- Lorenz, E.N. Nondeterministic theories of climatic change. Quat. Res. 1976, 6, 495–506. [Google Scholar] [CrossRef]
- Casdagli, M. Nonlinear prediction of chaotic time series. Phys. D Nonlinear Phenom. 1989, 35, 335–356. [Google Scholar] [CrossRef]
- Palmer, T.N. A nonlinear dynamical perspective on climate prediction. J. Clim. 1999, 12, 575–591. [Google Scholar] [CrossRef]
- Feng, G.L.; Dai, X.G.; Wang, A.H.; Chou, J.F. On numerical predictability in the chaos system. Acta Phys. Sin. 2001, 50, 606–611. [Google Scholar] [CrossRef]
- Ren, H.L.; Dai, X.G.; Chou, J.F. Statistical analysis of the predictability of the chaotic solution series of Lorenz system. J. Lanzhou Univ. Nat. Sci. 2003, 39, 93–98. [Google Scholar] [CrossRef]
- Ding, R.Q.; Li, J.P. Nonlinear error dynamics and predictability study. Chin. J. Atmos. Sci. 2007, 31, 571–576. [Google Scholar] [CrossRef]
- Ding, R.Q.; Li, J.P. Comparison of the influences of initial error and model parameter error on the predictability of numerical forecast. Chin. J. Geophys. 2008, 51, 1007–1012. [Google Scholar] [CrossRef]
- He, W.P.; Feng, G.L.; Gao, X.Q.; Chou, J.F. Dynamics of the Lorenz system under quasiperiodic driving. Acta Phys. Sin. 2006, 55, 3175–3179. [Google Scholar] [CrossRef]
- Li, A.B.; Zhang, L.F.; Wang, Q.L.; Li, B.; Li, Z.Z.; Wang, Y.Q. Information theory in nonlinear error growth dynamics and its application to predictability: Taking the Lorenz system as an example. Sci. China Earth Sci. 2013, 56, 1413–1421. [Google Scholar] [CrossRef]
- Miao, J.H.; Liu, Z.Y. Control of Lorenz chaos. Acta Meteorol. Sin. 1999, 57, 751–757. [Google Scholar] [CrossRef]
- Yu, J.Z.; Su, N.; Vincent, T.L. Study on control of chaotic Lorenz system. Acta Phys. Sin. 1998, 47, 397–402. [Google Scholar] [CrossRef]
- Feng, G.L.; Gong, Z.Q.; Dong, W.J.; Li, J.P. Abrupt climate change detection based on heuristic segmentation algorithm. Acta Phys. Sin. 2005, 54, 5494–5499. [Google Scholar] [CrossRef]
- Hou, W.; Feng, G.L.; Dong, W.J.; Li, J.P. A technique for distinguishing dynamical species in the temperature time series of north China. Acta Phys. Sin. 2006, 55, 2663–2668. [Google Scholar] [CrossRef]
- Zhi, R.; Gong, Z.Q.; Wang, D.Y.; Feng, G.L. Analysis of the spatio-temporal characteristics of precipitation of China based on the power-law exponent. Acta Phys. Sin. 2006, 55, 6185–6191. [Google Scholar] [CrossRef]
- Bruno, E.; Demin, Y. Local Lyapunov exponents in chaotic systems. Phys. D Nonlinear Phenom. 1993, 65, 100–108. [Google Scholar] [CrossRef]
- Zhang, Y. New prediction of chaotic time series based on local Lyapunov exponent. Chin. Phys. B 2013, 22, 050502. [Google Scholar] [CrossRef]
- Da, C.J.; Mu, S.; Ma, D.S.; Yu, H.P.; Hou, W.; Gong, Z.Q. The theoretical study of the turning period in numerical weather prediction models based on the Lorenz equations. Acta Phys. Sin. 2014, 63, 442–455. [Google Scholar] [CrossRef]
- Fu, C.B.; Wang, Q. The definition and detection of the Abrupt Climatic Change. Chin. J. Atmos. Sci. 1992, 16, 482–493. [Google Scholar] [CrossRef]


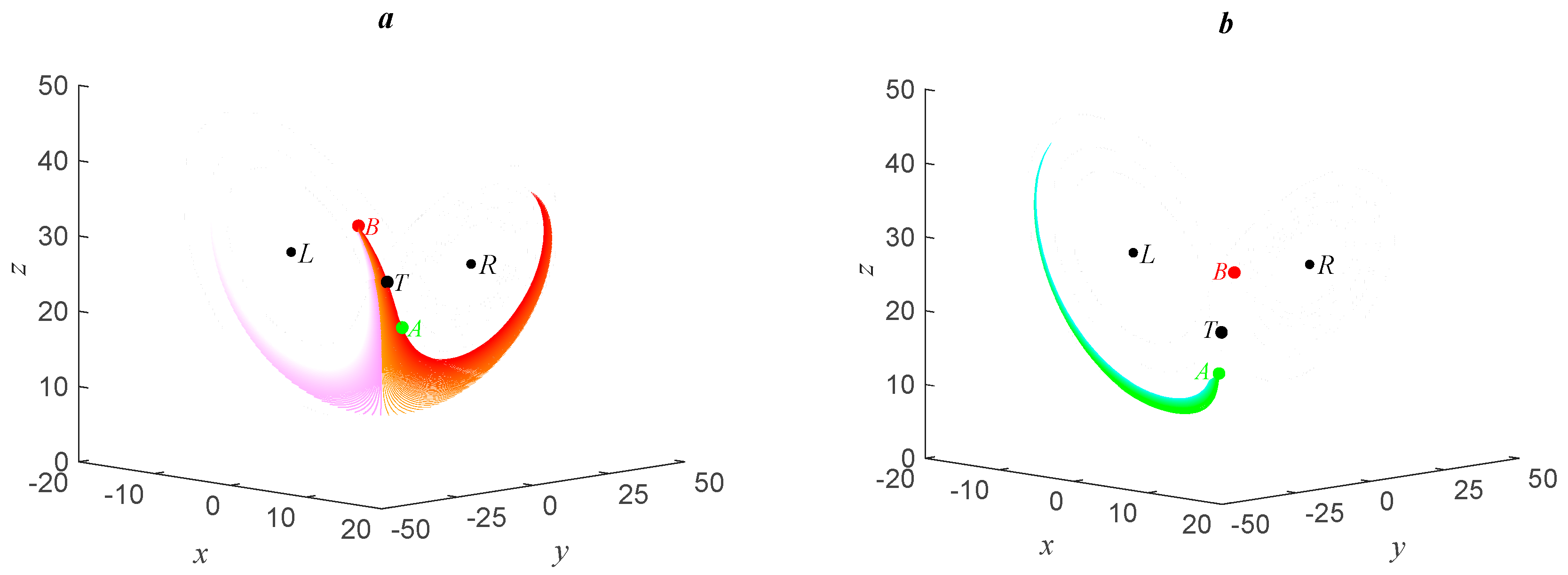
| BR2L | TR2L | AR2L | BL2R | TL2R | AL2R |
|---|---|---|---|---|---|
| 0.96 | 1.17 | 1.40 | 2.48 | 2.69 | 2.94 |
| 3.22 | 3.55 | 3.98 | 4.27 | 4.44 | 4.62 |
| 9.12 | 9.33 | 9.56 | 10.63 | 10.85 | 11.10 |
| 11.38 | 11.67 | 12.03 | 12.31 | 12.49 | 12.69 |
| 15.15 | 15.38 | 15.64 | 15.92 | 16.16 | 16.45 |
| 16.73 | 16.94 | 17.18 | 18.44 | 18.61 | 18.80 |
| 21.95 | 22.17 | 22.42 | 21.67 | 22.99 | 22.70 |
| 23.63 | 23.81 | 24.01 | 26.48 | 26.70 | 26.96 |
| 27.23 | 27.51 | 27.84 | 28.12 | 28.31 | 28.51 |
| 0 | 0.004 | 0.016 | 0.019 | 0.027 | 0.019 | 0.013 | 0.021 | 0.016 | 0.009 | ||
| 0.004 | 0 | 0.013 | 0.016 | 0.024 | 0.017 | 0.012 | 0.018 | 0.014 | 0.006 | ||
| 0.016 | 0.013 | 0 | 0.004 | 0.014 | 0.009 | 0.015 | 0.008 | 0.002 | 0.008 | ||
| 0.018 | 0.015 | 0.003 | 0 | 0.015 | 0.012 | 0.015 | 0.009 | 0.005 | 0.010 | ||
| 0.027 | 0.024 | 0.014 | 0.015 | 0 | 0.009 | 0.029 | 0.007 | 0.013 | 0.020 | ||
| 0.019 | 0.017 | 0.009 | 0.012 | 0.009 | 0 | 0.023 | 0.004 | 0.008 | 0.014 | ||
| 0.013 | 0.012 | 0.015 | 0.015 | 0.029 | 0.023 | 0 | 0.022 | 0.016 | 0.010 | ||
| 0.021 | 0.018 | 0.008 | 0.009 | 0.007 | 0.004 | 0.022 | 0 | 0.006 | 0.014 | ||
| 0.016 | 0.013 | 0.002 | 0.005 | 0.013 | 0.008 | 0.016 | 0.006 | 0 | 0.009 | ||
| 0.009 | 0.006 | 0.008 | 0.010 | 0.020 | 0.014 | 0.010 | 0.014 | 0.009 | 0 | ||
| 0 | 0.068 | 0.012 | 0.034 | 0.019 | 0.041 | 0.039 | 0.045 | 0.071 | 0.083 | ||
| 0.071 | 0 | 0.066 | 0.046 | 0.087 | 0.042 | 0.044 | 0.027 | 0.009 | 0.030 | ||
| 0.011 | 0.063 | 0 | 0.025 | 0.026 | 0.032 | 0.030 | 0.038 | 0.064 | 0.075 | ||
| 0.034 | 0.045 | 0.025 | 0 | 0.047 | 0.007 | 0.005 | 0.022 | 0.045 | 0.053 | ||
| 0.019 | 0.084 | 0.026 | 0.047 | 0 | 0.054 | 0.051 | 0.062 | 0.087 | 0.099 | ||
| 0.041 | 0.041 | 0.032 | 0.007 | 0.054 | 0 | 0.004 | 0.020 | 0.040 | 0.047 | ||
| 0.039 | 0.043 | 0.030 | 0.005 | 0.052 | 0.004 | 0 | 0.023 | 0.043 | 0.050 | ||
| 0.046 | 0.027 | 0.039 | 0.022 | 0.063 | 0.020 | 0.023 | 0 | 0.027 | 0.040 | ||
| 0.072 | 0.009 | 0.066 | 0.046 | 0.090 | 0.041 | 0.044 | 0.027 | 0 | 0.021 | ||
| 0.084 | 0.029 | 0.076 | 0.054 | 0.100 | 0.047 | 0.050 | 0.040 | 0.021 | 0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Hu, L.; She, H.; Fan, B.; Da, C. Decomposition of Lorenz Trajectories Based on Space Curve Tangent Vector. Atmosphere 2024, 15, 319. https://doi.org/10.3390/atmos15030319
Ma J, Hu L, She H, Fan B, Da C. Decomposition of Lorenz Trajectories Based on Space Curve Tangent Vector. Atmosphere. 2024; 15(3):319. https://doi.org/10.3390/atmos15030319
Chicago/Turabian StyleMa, Jingru, Lei Hu, Hongke She, Binghuai Fan, and Chaojiu Da. 2024. "Decomposition of Lorenz Trajectories Based on Space Curve Tangent Vector" Atmosphere 15, no. 3: 319. https://doi.org/10.3390/atmos15030319
APA StyleMa, J., Hu, L., She, H., Fan, B., & Da, C. (2024). Decomposition of Lorenz Trajectories Based on Space Curve Tangent Vector. Atmosphere, 15(3), 319. https://doi.org/10.3390/atmos15030319




