Assessment and Prediction of Future Climate Change in the Kaidu River Basin of Xinjiang under Shared Socioeconomic Pathway Scenarios
Abstract
1. Introduction
2. Study Area and Data
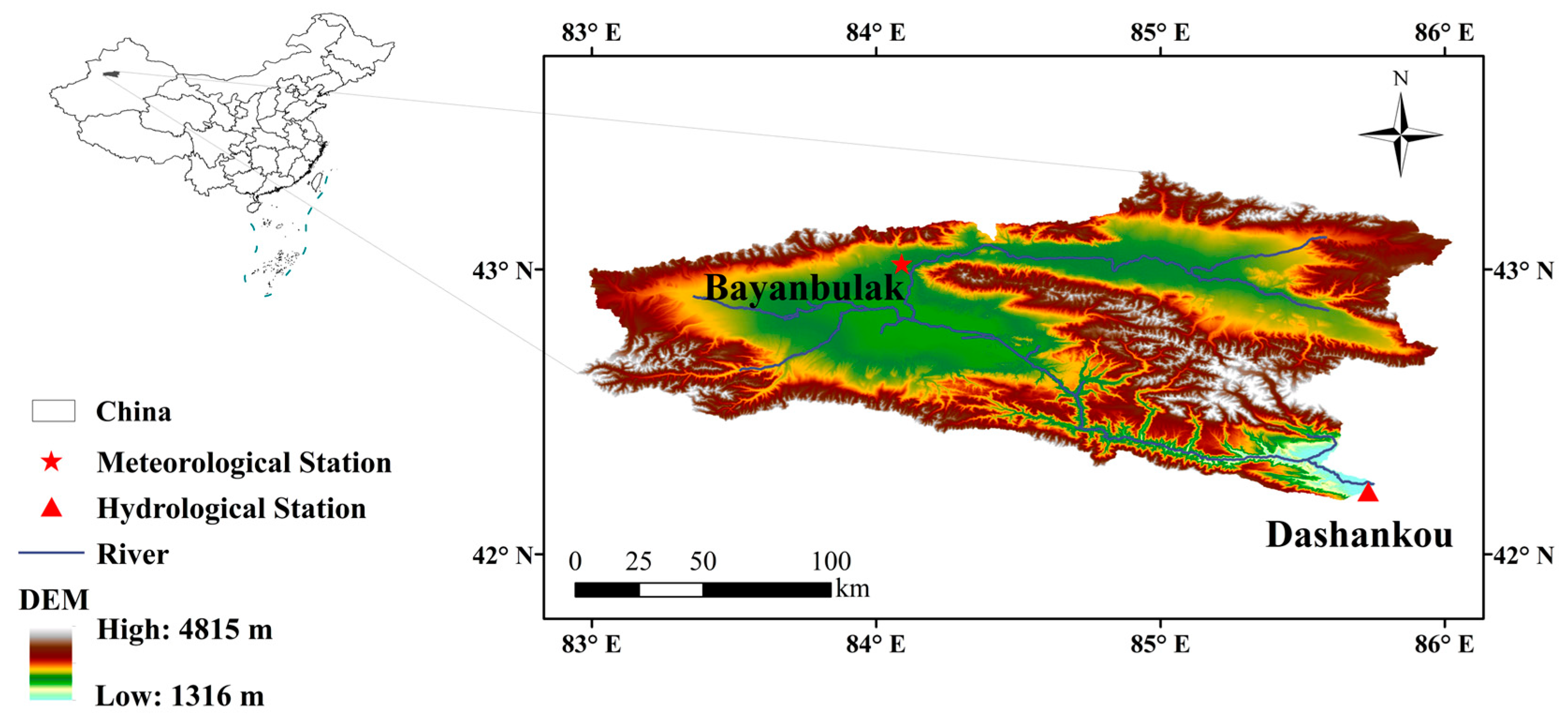
2.1. Study Area
2.2. Data
3. Methods
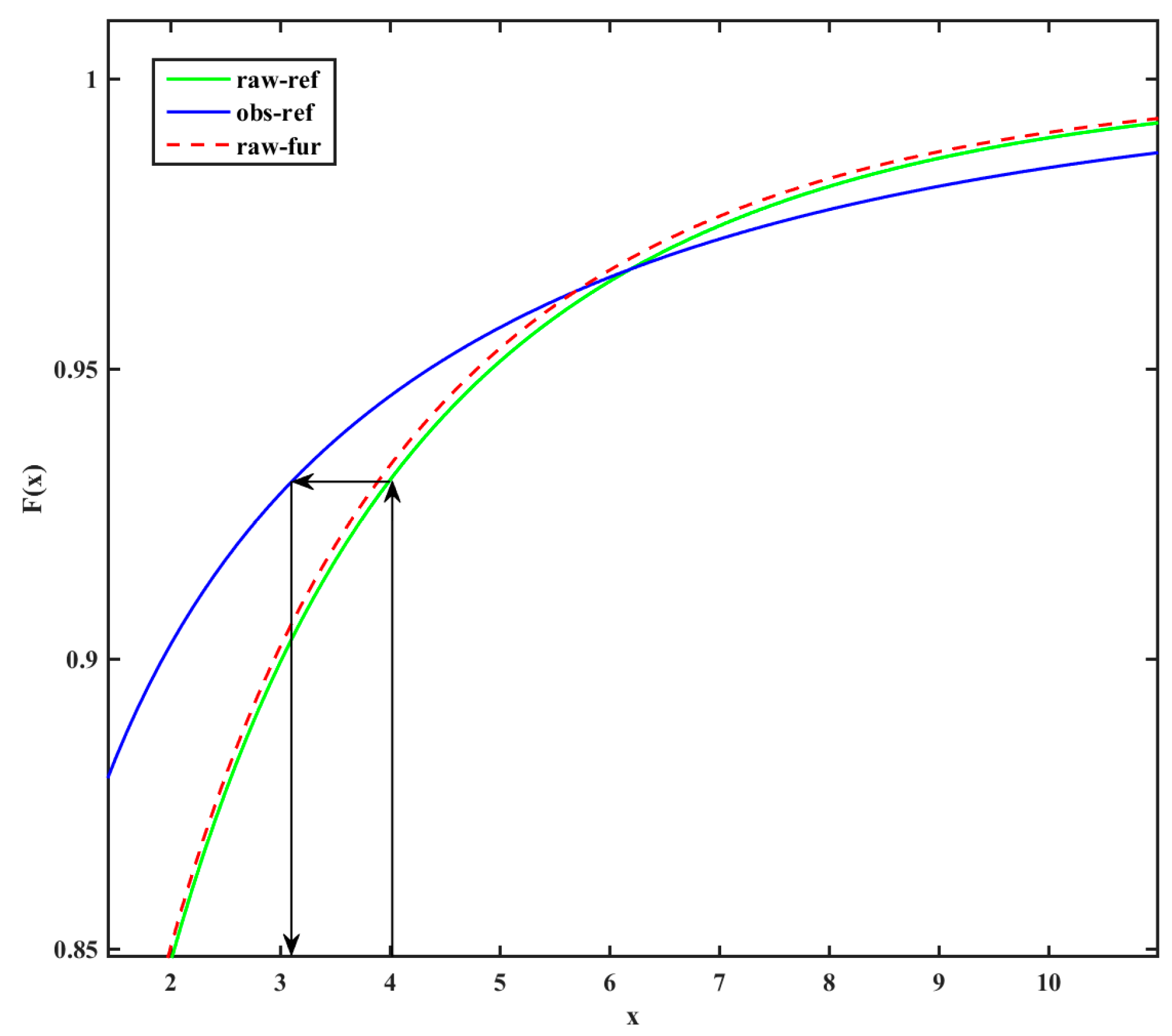
3.1. Bias Correction Methods
3.1.1. LS Method
3.1.2. DT Method
3.1.3. EQM Method
3.1.4. DM Method
3.1.5. LOCI Method
3.1.6. Combine Method
3.1.7. Evaluation Indicators
3.2. Extreme Climate Indicators
4. Results
4.1. Analysis of Bias Correction Methods
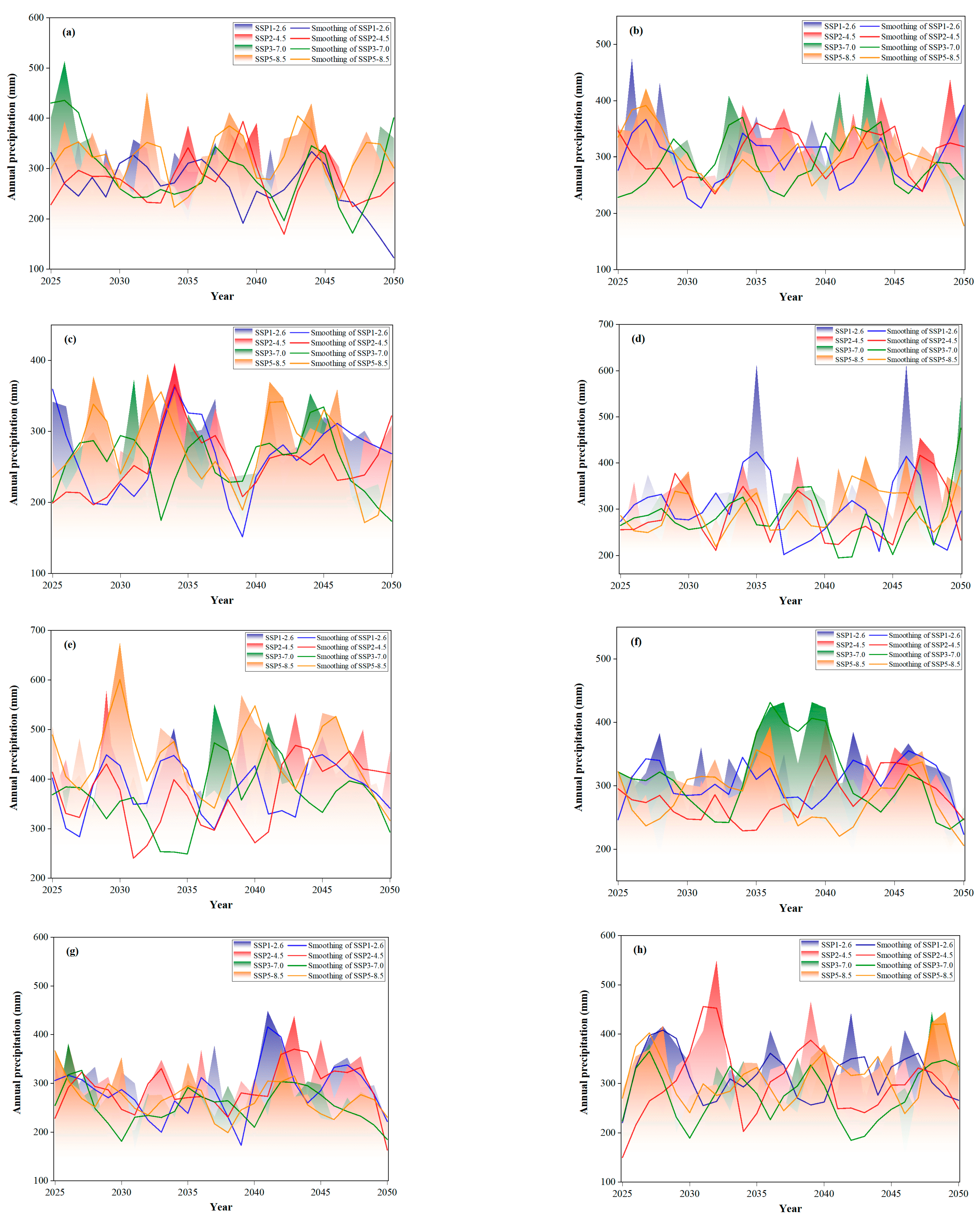
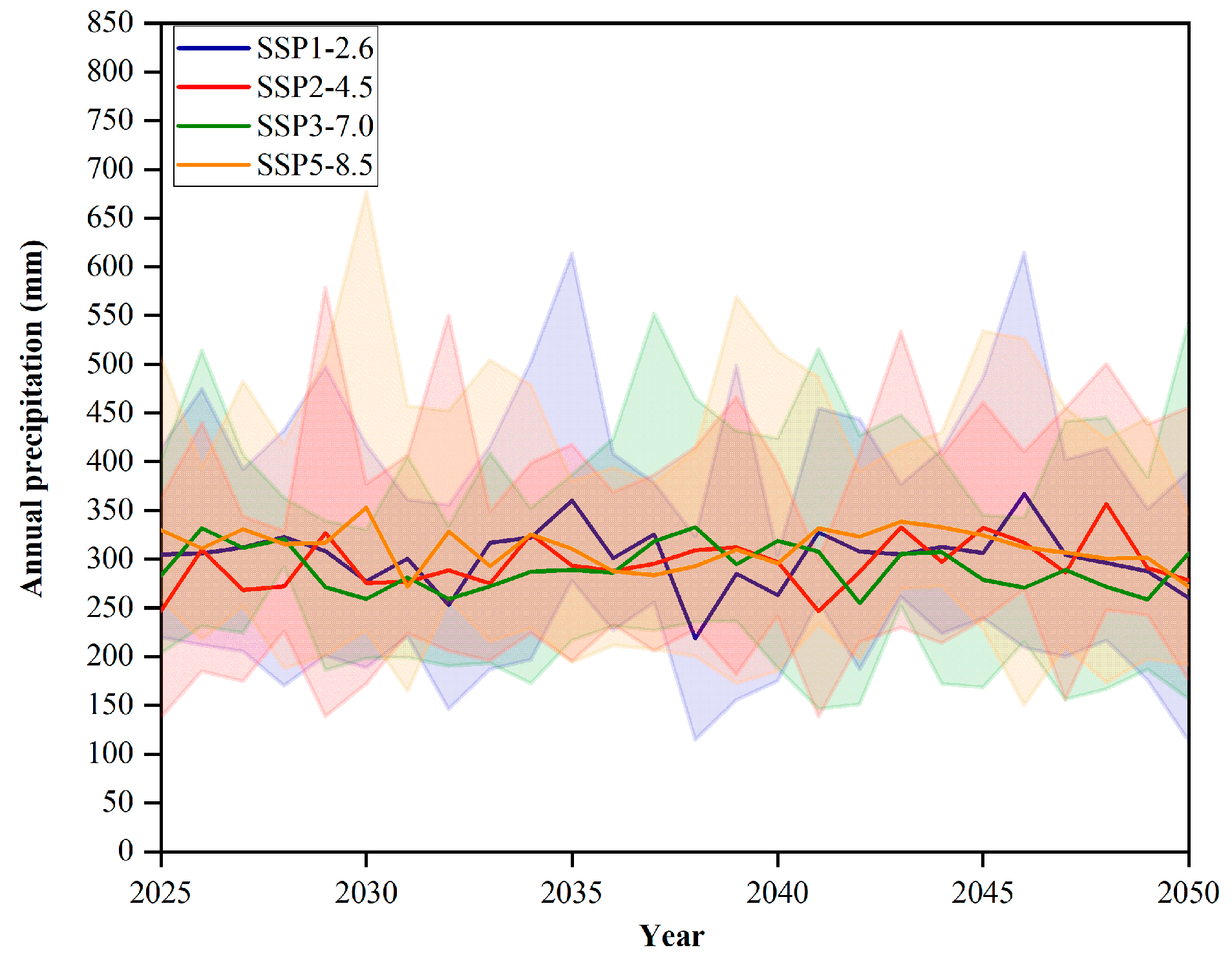
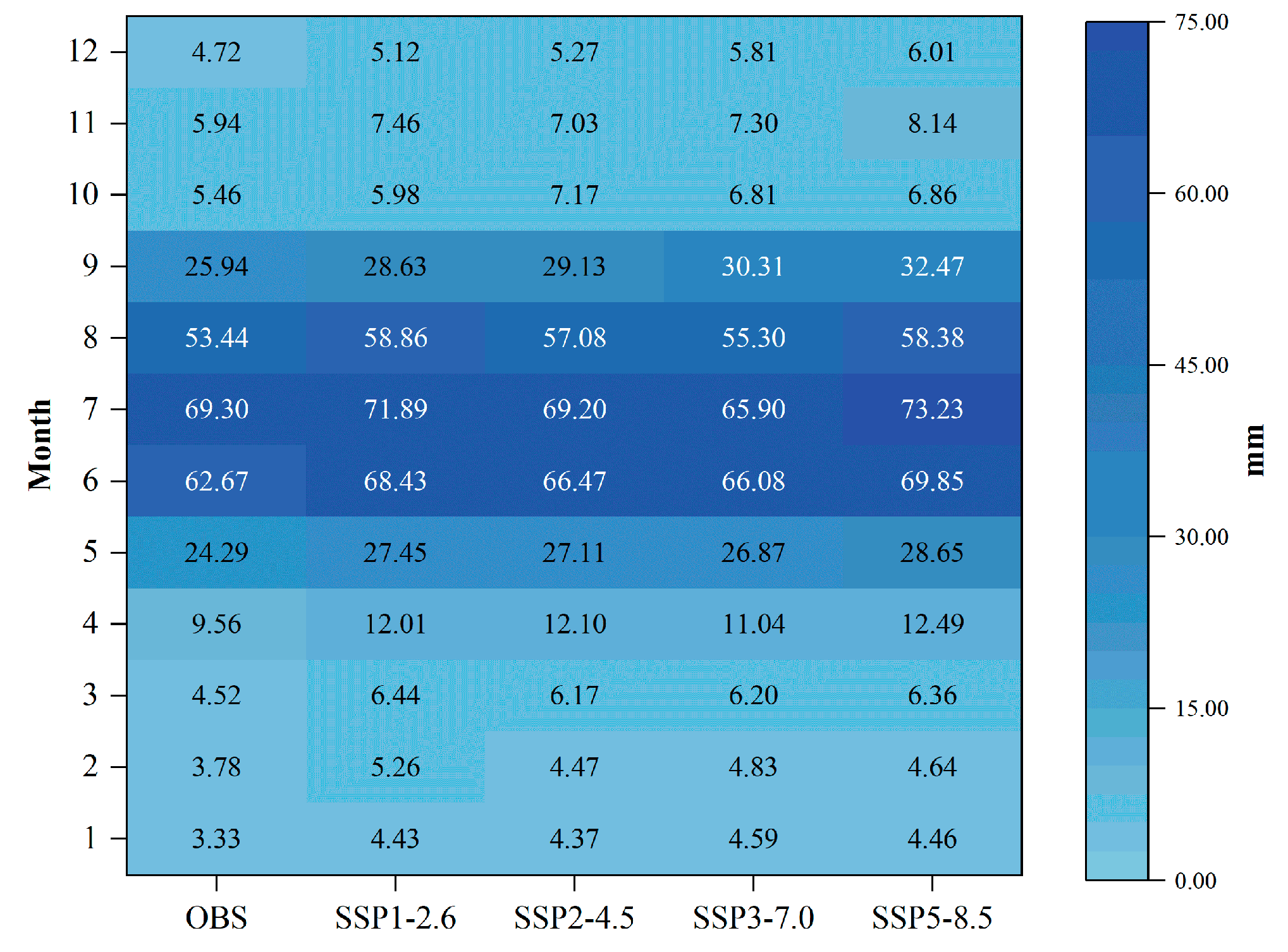
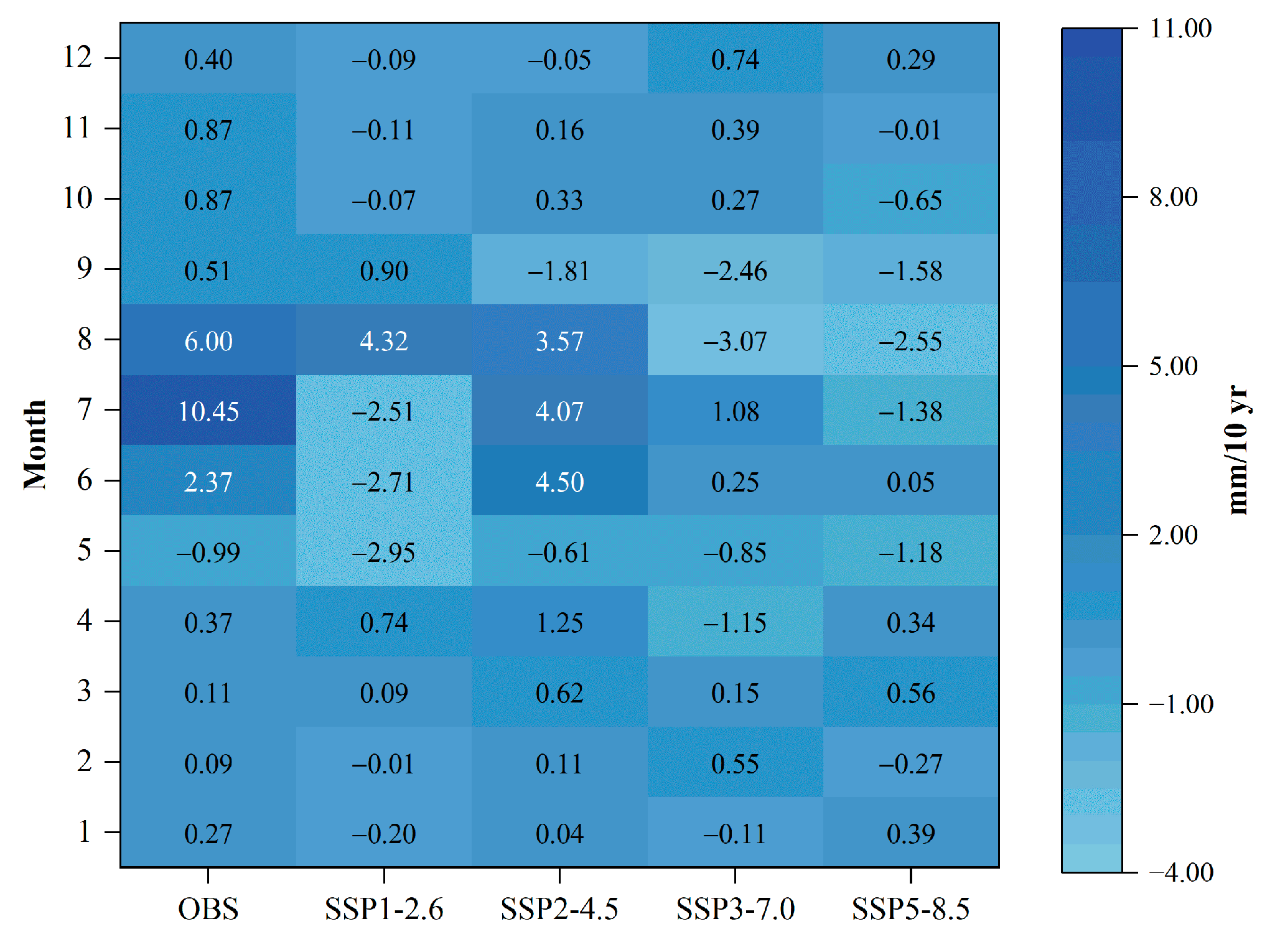
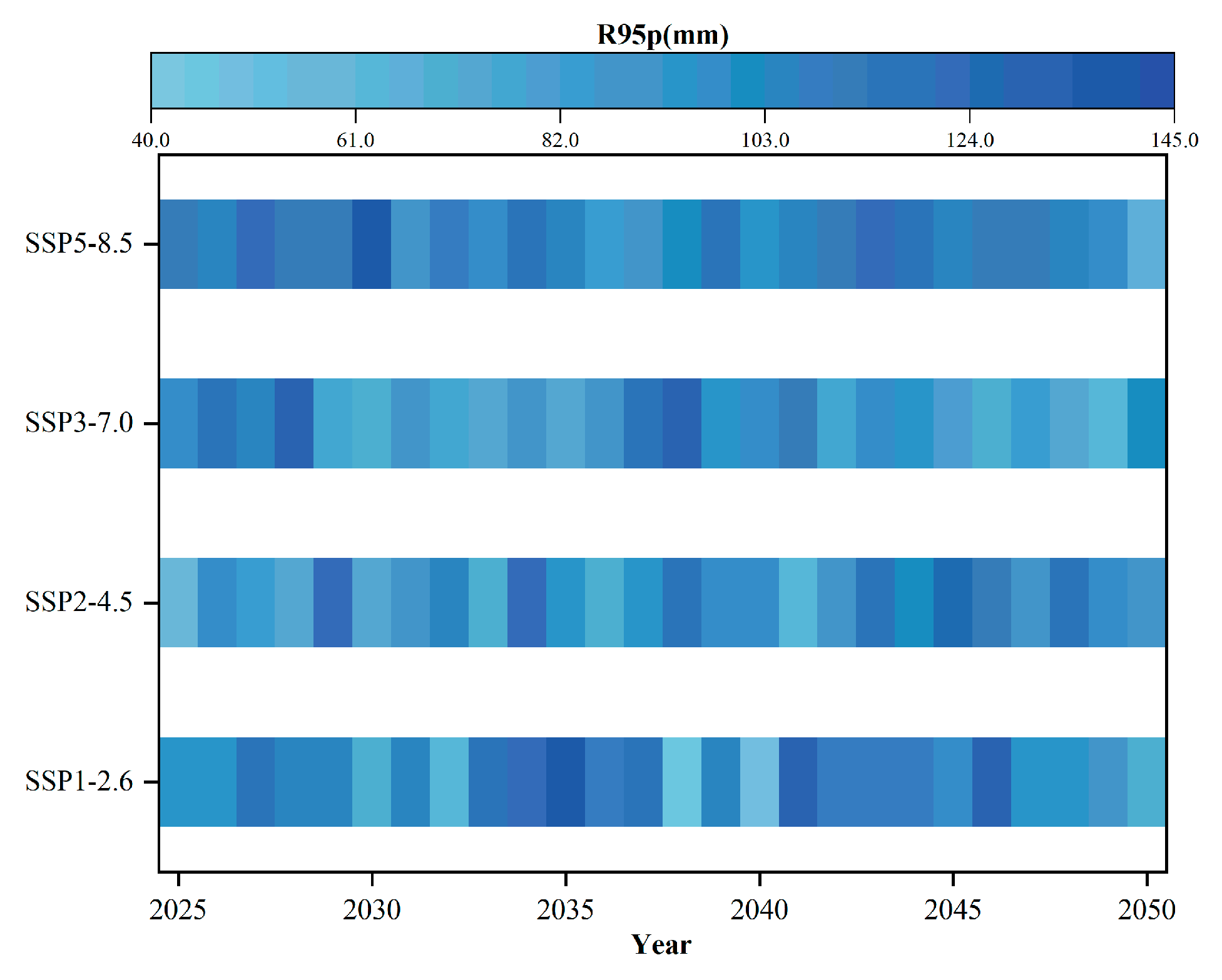
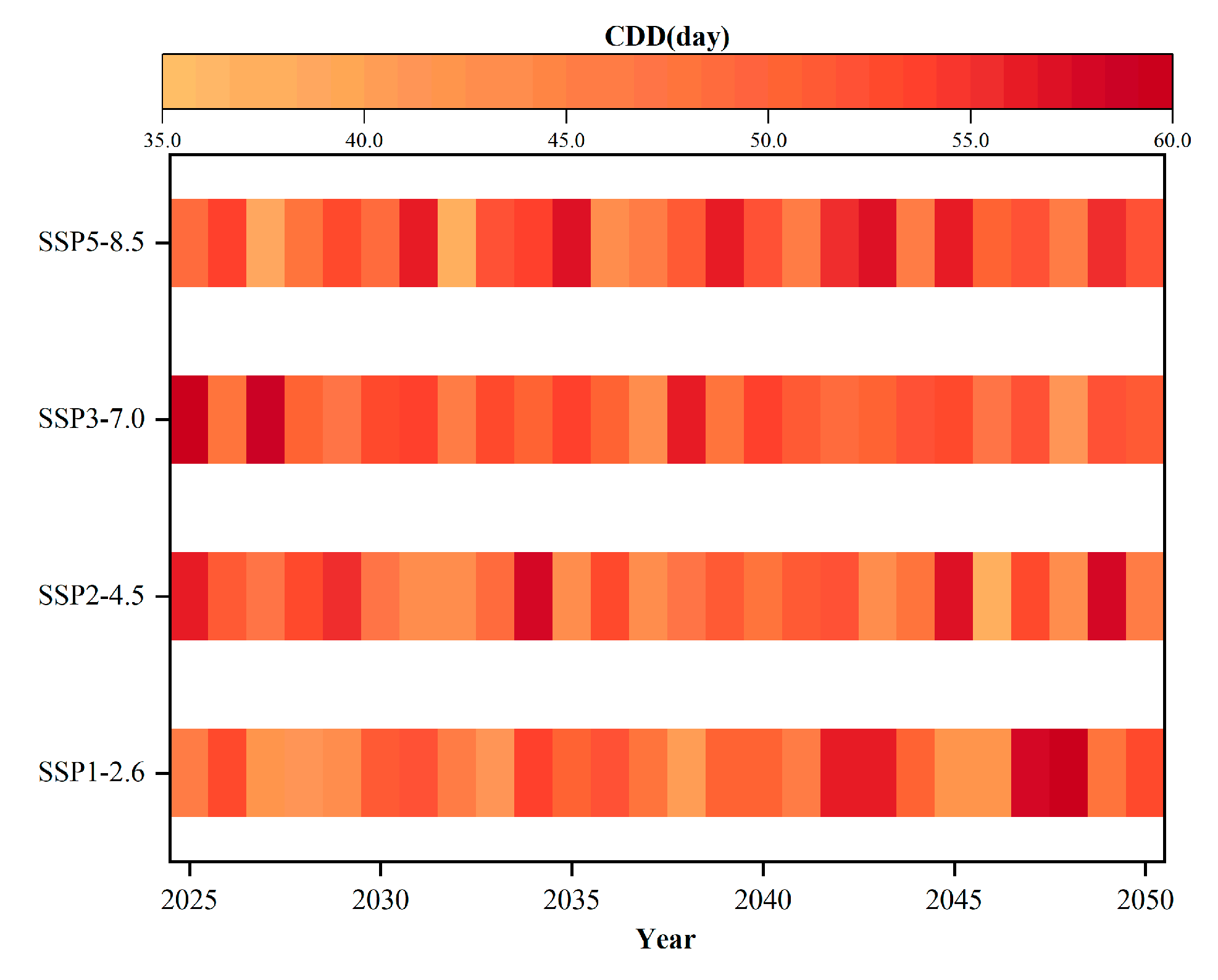
4.2. Precipitation Trend and Extreme Value Analysis
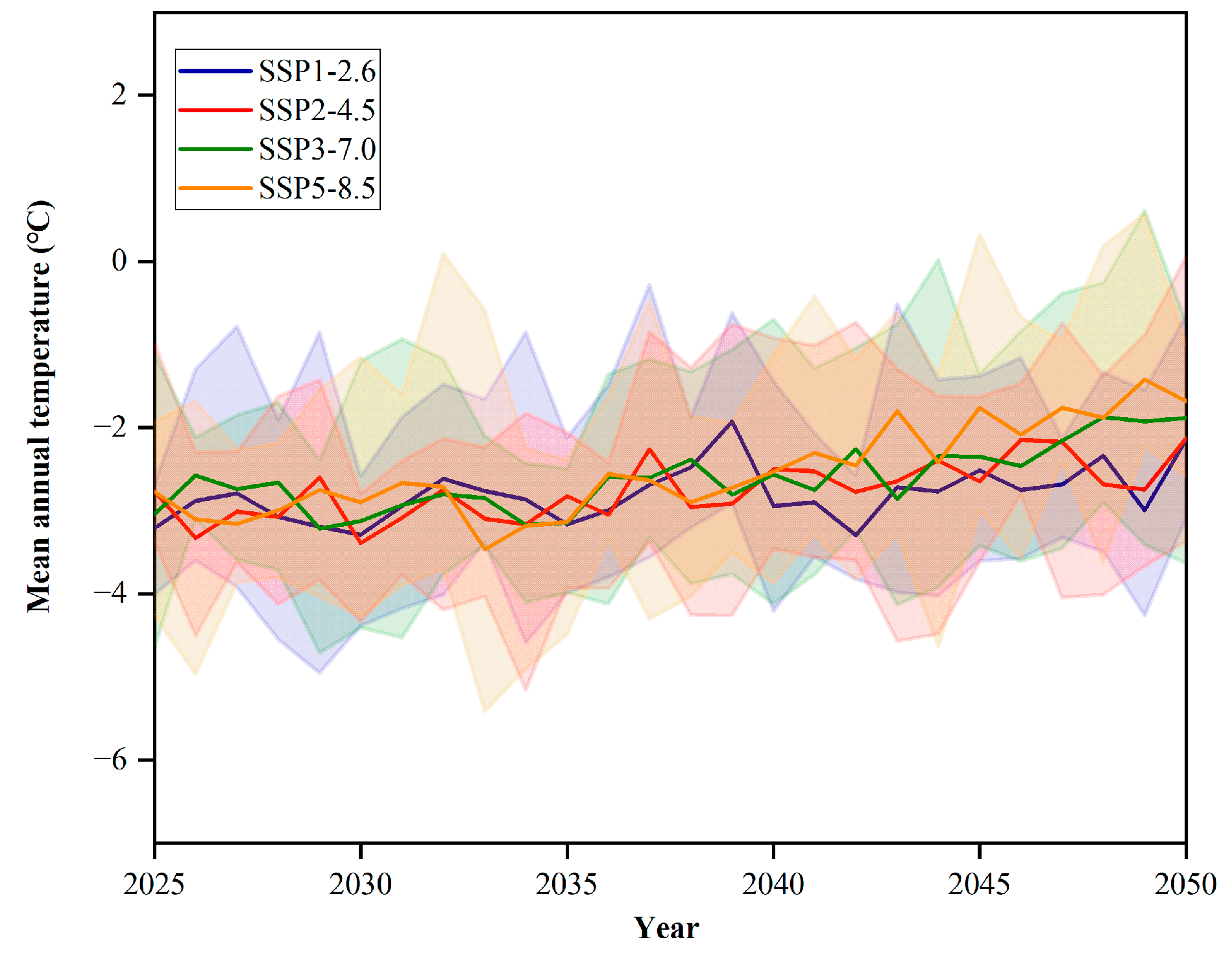
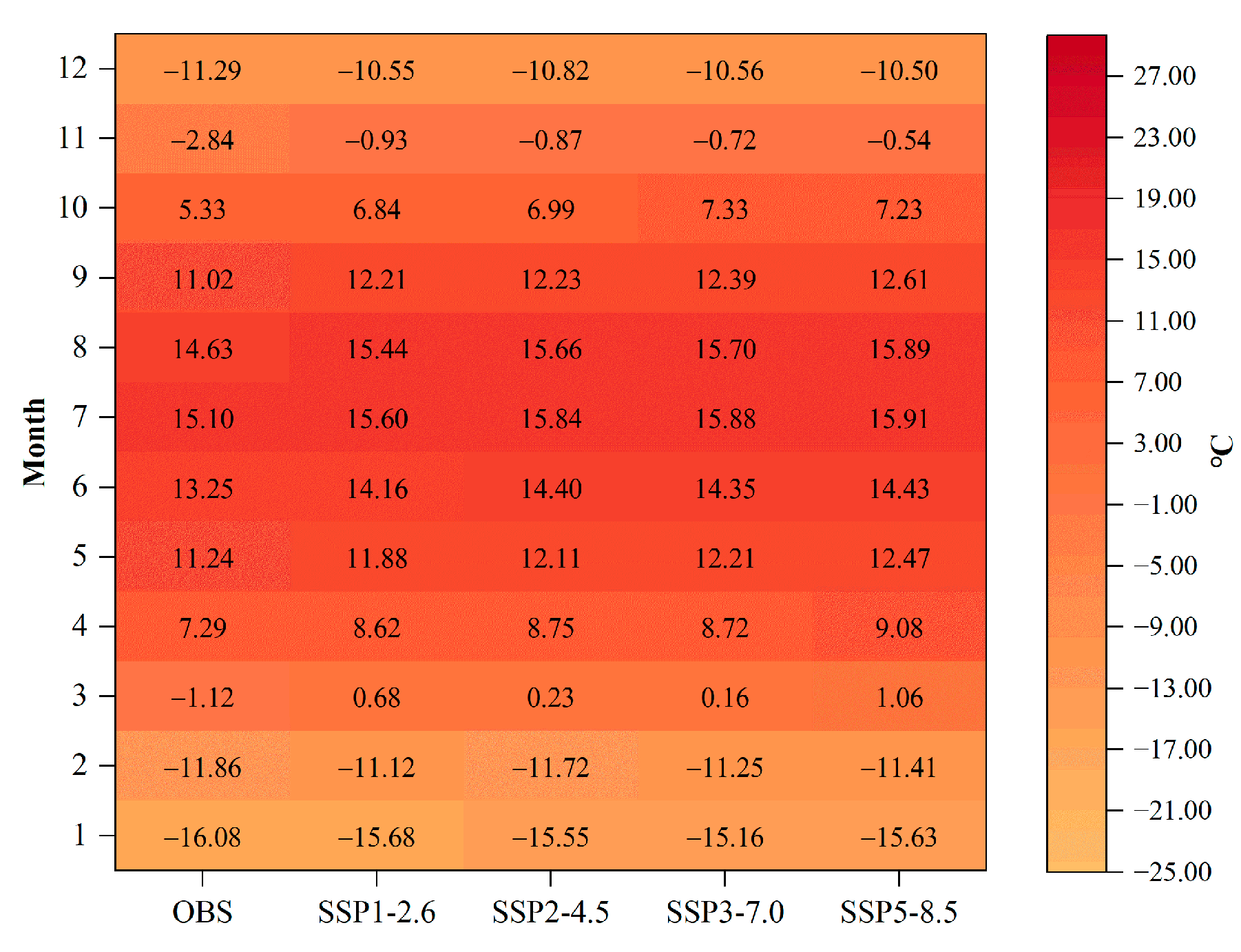
4.3. Temperature Trend and Extreme Value Analysis
5. Discussion
5.1. The Applicability of Bias Correction Methods for CMIP6 in the Arid Area of Northwest China
5.2. Future Changes of Extreme Climatic Events in River Basins
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Qin, D. Influence of climate change and human activity on water resources in arid region of Northwest China: An overview. Adv. Clim. Chang. Res. 2017, 8, 268–278. [Google Scholar] [CrossRef]
- Dong, L.; Xiong, L.; Yu, K.; Li, S. Research advances in effects of climate change and human activities on hydrology. Adv. Water Sci. 2012, 23, 278–285. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, S.; Xia, J.; Chen, Y.; Zhang, Y.; Cai, W.; Wang, W.; Wang, H.; Luo, X.; Chen, X. Risk assessment of water resource shortages in the Aksu River basin of northwest China under climate change. J. Environ. Manag. 2022, 305, 114394. [Google Scholar] [CrossRef]
- Liu, J.; Chen, H.; Tian, Z. Interpretation of IPCC AR6: Climate change and water security. Clim. Chang. Res. 2022, 18, 405–413. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, J.; Jin, C. Evaluation and projection of climate change in Jiangsu Province based on the CMIP5 multi-model ensemble mean datasets. J. Meteorol. Sci. 2019, 39, 739–746. [Google Scholar]
- Jose, D.M.; Dwarakish, G.S. Bias Correction and Trend Analysis of Temperature Data by a High-Resolution CMIP6 Model over a Tropical River Basin. Asia-Pac. J. Atmos. Sci. 2021, 58, 97–115. [Google Scholar] [CrossRef]
- Gleick, P.H. Climate change, hydrology, and water resources. Rev. Geophys. 1989, 27, 329–344. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, H.; Yang, K.; Jiang, R.; Yang, Y.; Wang, W.; Zhang, X. Projection of China’s future runoff based on the CMIP6 mid-high warming scenarios. Sci. China-Earth Sci. 2023, 66, 528–546. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Y.; Xu, C.; Yao, Y. Assessment of Precipitation Simulations in China by CMIP5 Multi-models. Progress. Inquisitiones De Mutat. Clim. 2014, 10, 217–225. [Google Scholar] [CrossRef]
- Sonali, P.; Kumar, D.N. Review of recent advances in climate change detection and attribution studies: A large-scale hydroclimatological perspective. J. Water Clim. Chang. 2020, 11, 1–29. [Google Scholar] [CrossRef]
- Jose, D.M.; Dwarakish, G.S. Uncertainties in predicting impacts of climate change on hydrology in basin scale: A review. Arab. J. Geosci. 2020, 13, 1037. [Google Scholar] [CrossRef]
- Yue, S.; Hu, S.; Mo, X.; Zhan, C.; Liu, S. Improved frequency-dependent bias correction method for GCM daily precipitation and its application in Yangtze River Basin. Geogr. Res. 2021, 40, 1432–1444. [Google Scholar] [CrossRef]
- Cao, L.; Fang, Y.; Jiang, T.; Luo, Y. Advances in Shared Socio-economic Pathways for Climate Change Research and Assessment. Progress. Inquisitiones De Mutat. Clim. 2012, 8, 74–78. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, J.; Li, N. Evaluation of CMIP6 HighResMIP models in Simulating Precipitation over Tibetan Plateau. Torrential Rain Disasters 2022, 41, 215–223. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, H. Assessment of warm season precipitation in the eastern slope of the Tibetan Plateau by CMIP6 models. Clim. Chang. Res. 2022, 18, 129–141. [Google Scholar] [CrossRef]
- Chokkavarapu, N.; Mandla, V.R. Comparative study of GCMs, RCMs, downscaling and hydrological models: A review toward future climate change impact estimation. SN Appl. Sci. 2019, 1, 1698. [Google Scholar] [CrossRef]
- Zhang, M.; Peng, D.; Hu, L. Research Progress on Statistical Downscaling Methods. South-North Water Transf. Water Sci. Technol. 2013, 11, 118–122. [Google Scholar]
- Liu, Y.; Guo, W.; Feng, J.; Zhang, K. A Summary of Methods for Statistical Downscaling of Meteorological Data. Adv. Earth Sci. 2011, 26, 837–847. [Google Scholar]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Yao, J.; Yang, Q.; Chen, Y.; Hu, W.; Liu, Z.; Zhao, L. Climate change in arid areas of Northwest China in past 50 years and its effects on the local ecological environment. Chin. J. Ecol. 2013, 32, 1283–1291. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Y.; Zhu, C.; Li, W. The concept and mode of ecosystem sustainable management in arid desert areas in northwest China. Acta Ecol. Sin. 2019, 39, 7410–7417. [Google Scholar]
- Chen, Y. Impacts of Climate Change on the Water Cycle Mechanism and Water Resources Security in the Arid Region of Northwest China. China Basic Sci. 2015, 17, 15–21+12. [Google Scholar]
- Cui, Z.; Tan, H.; Du, Q. A review on ecological water requirement in river basin. J. Cap. Norm. Univ. 2010, 31, 70–74+87. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Li, Z.; Liu, Y.; Huang, W.; Liu, X.; Feng, M. Analysis of the Impact of Global Climate change on Dryland Areas. Adv. Earth Sci. 2022, 37, 111–119. [Google Scholar] [CrossRef]
- Xie, Y.; Zhu, J. Hydrological Characteristics of Kaidou River Basin. J. China Hydrol. 2011, 31, 92–96. [Google Scholar]
- Qiu, H.; Liu, J. Study on Variation Characteristics of Runoff Kaidu River Over 60 Years. Yellow River 2016, 38, 22–26. [Google Scholar]
- Liu, Z.; Huang, Y.; Liu, T.; Bao, A.; Feng, X.; Xing, W.; Duan, Y.; Guo, C. Climate response of runoff variation in the source area of the Kaidu River. Arid. Zone Res. 2020, 37, 418–427. [Google Scholar]
- Sun, Y.; Liu, S.; Xing, K.; Xie, L.; Zheng, L.; Liu, Y. Quantitative Analysis of Discharge and Driving Factors in the Headwaters of Kaidu River over 60 Years. J. Hydroecol. 2023, 44, 10–18. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Riahi, K.; Ebi, K.L.; Hallegatte, S.; Carter, T.R.; Mathur, R.; van Vuuren, D.P. A new scenario framework for climate change research: The concept of shared socioeconomic pathways. Clim. Chang. 2014, 122, 387–400. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Ebi, K.L.; Kemp-Benedict, E.; Riahi, K.; Rothman, D.S.; van Ruijven, B.J.; van Vuuren, D.P.; Birkmann, J.; Kok, K.; et al. The roads ahead: Narratives for shared socioeconomic pathways describing world futures in the 21st century. Glob. Environ. Chang. 2017, 42, 169–180. [Google Scholar] [CrossRef]
- Riahi, K.; van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 2017, 42, 153–168. [Google Scholar] [CrossRef]
- Leander, R.; Buishand, T.A. Resampling of regional climate model output for the simulation of extreme river flows. J. Hydrol. 2007, 332, 487–496. [Google Scholar] [CrossRef]
- Mpelasoka, F.S.; Chiew, F.H.S. Influence of Rainfall Scenario Construction Methods on Runoff Projections. J. Hydrometeorol. 2009, 10, 1168–1183. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Block, P.J.; Souza Filho, F.A.; Sun, L.; Kwon, H.H. A Streamflow Forecasting Framework using Multiple Climate and Hydrological Models1. J. Am. Water Resour. Assoc. 2009, 45, 828–843. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Schoenau, G.J.; Kehrig, R.A. A Method for Calculating Degree-days to any Base Temperature. Energy Build 1990, 14, 299–302. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, Y.; Chen, Y.; Zhang, Q. Impact of Climate Change on the Hydrological Regime of the Yarkant River Basin, China: An Assessment Using Three SSP Scenarios of CMIP6 GCMs. Remote Sens. 2021, 14, 115. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, L.; Ma, M.; Wang, L.; Lin, H. Downscaling of temperature and precipitation in the Daling River Basin, Liaoning Province. Water Resour. Hydropower Eng. 2021, 52, 16–31. [Google Scholar]
- Zhang, M.; Xu, W.; Hu, Z.; Merz, C.; Ma, M.; Wei, J.; Guan, X.; Jiang, L.; Bao, R.; Wei, Y.; et al. Projection of future climate change in the Poyang Lake Basin of China under the global warming of 1.5–3 °C. Front. Environ. Sci. 2022, 10, 985145. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J.; Chen, Y.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Han, Z.; Tong, Y.; Gao, X.; Xu, Y. Correction based on quantile mapping for temperature simulated by the RegCM4. Clim. Chang. Res. 2018, 14, 331–340. [Google Scholar] [CrossRef]
- Mishra, V.; Bhatia, U.; Tiwari, A.D. Bias-corrected climate projections for South Asia from Coupled Model Intercomparison Project-6. Sci. Data 2020, 7, 338. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Tian, L.; Liu, T.; Bao, A.; Huang, Y. Application of CFSR Precipitation Dataset in Hydrological Model for Arid Mountainous Area: A Case Study in the Kaidu River Basin. Arid. Zone Res. 2017, 34, 755–761. [Google Scholar]
- Wang, S.; Ding, Y.; Jiang, F.; Wu, X.; Xue, J. Identifying hot spots of long-duration extreme climate events in the northwest arid region of China and implications for glaciers and runoff. Res. Cold Arid. Reg. 2022, 14, 347–360. [Google Scholar] [CrossRef]
- Wu, X.; Luo, M.; Meng, F.; Sa, C.; Yin, C.; Bao, Y. New characteristics of spatio-temporal evolution of extreme climate events in Xinjiang under the background of warm and humid climate. Arid. Zone Res. 2022, 39, 1695–1705. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Li, M.; Li, L.; Liu, F.; Liu, D.L.; Pulatov, B. Projection of precipitation extremes in China’s mainland based on the statistical downscaled data from 27 GCMs in CMIP6. Atmos. Res. 2022, 280, 106462. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, J.; Qi, J.; Liu, H.; Zhang, X.; Marek, G.W.; Yuan, C.; Ding, B.; Feng, P.; Liu, D.L.; et al. Evaluating the effects of single and integrated extreme climate events on hydrology in the Liao River Basin, China using a modified SWAT-BSR model. J. Hydrol. 2023, 623, 129772. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, Y.; Li, J.; Han, Z. Evaluation on the performance of CMIP6 global climate models with different horizontal resolution in simulating the precipitation over China. Clim. Chang. Res. 2021, 17, 730–743. [Google Scholar] [CrossRef]
- Xiang, J.; Zhang, L.; Deng, Y.; She, D.; Zhang, Q. Projection and evaluation of extreme temperature and precipitation in major regions of China by CMIP6 models. Eng. J. Wuhan Univ. 2021, 54, 46–57+81. [Google Scholar] [CrossRef]



| ID | Model Name | Country | Institution | Experiment | Resolution |
|---|---|---|---|---|---|
| A | BCC-CSM2-MR | China | Beijing Climate Center | r1i1p1f1 | 100 km |
| B | CAMS-CSM1-0 | China | Chinese Academy of Meteorological Sciences | r2i1p1f1 | 100 km |
| C | CAS-FGOALS-g3 | China | Chinese Academy of Sciences | r1i1p1f1 | 250 km |
| D | MPI-ESM1-2-HR | Germany | Max Planck Institute for Meteorology | r1i1p1f1 | 100 km |
| E | MRI-ESM2-0 | Japan | Meteorological Research Institute | r1i1p1f1 | 100 km |
| F | IPSL-CM6A-LR | France | Institut Pierre Simon Laplace | r1i1p1f1 | 250 km |
| G | GFDL-ESM4 | USA | Geophysical Fluid Dynamics Laboratory | r1i1p1f1 | 100 km |
| H | UKESM1-0-LL | UK | Met Office Hadley Centre | r1i1p1f2 | 250 km |
| No. | GCM | Method | Mean | Standard Deviation | Median | Percentile | Frequency of Wet Days | Intensity of Wet Days | RMSE | MAE | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 95% | 90% | 75% | ||||||||||
| 1 | Observed | 0.75 | 2.45 | 0.00 | 4.40 | 2.00 | 0.20 | 32.12 | 2.33 | |||
| 2 | BCC-CSM2-MR | raw | 1.00 | 2.06 | 0.19 | 4.70 | 2.89 | 1.06 | 57.58 | 1.73 | 3.19 | 1.47 |
| DT | 0.76 | 2.41 | 0.00 | 4.49 | 2.00 | 0.20 | 28.60 | 2.64 | 3.26 | 1.23 | ||
| LS | 0.75 | 2.41 | 0.06 | 3.77 | 1.77 | 0.42 | 43.89 | 1.68 | 3.27 | 1.19 | ||
| EQM | 0.74 | 2.45 | 0.00 | 4.35 | 1.96 | 0.18 | 27.42 | 2.68 | 3.29 | 1.21 | ||
| Gamma | 0.75 | 2.44 | 0.00 | 4.22 | 2.07 | 0.27 | 31.29 | 2.39 | 3.28 | 1.21 | ||
| LOCI | 0.74 | 2.47 | 0.00 | 4.00 | 1.97 | 0.33 | 32.36 | 2.28 | 3.31 | 1.21 | ||
| LOCI_QM | 0.74 | 2.45 | 0.00 | 4.35 | 1.96 | 0.18 | 27.42 | 2.68 | 3.29 | 1.21 | ||
| LOCI_Gamma | 0.76 | 2.44 | 0.00 | 4.28 | 2.14 | 0.26 | 29.88 | 2.53 | 3.28 | 1.22 | ||
| 3 | CAMS-CSM1-0 | raw | 1.33 | 2.68 | 0.13 | 6.92 | 4.35 | 1.31 | 52.31 | 2.52 | 3.72 | 1.82 |
| DT | 0.74 | 2.52 | 0.00 | 4.40 | 1.99 | 0.10 | 24.09 | 3.07 | 3.36 | 1.24 | ||
| LS | 0.75 | 3.17 | 0.02 | 3.30 | 1.07 | 0.27 | 35.65 | 2.07 | 3.86 | 1.27 | ||
| EQM | 0.89 | 2.44 | 0.00 | 4.35 | 1.95 | 1.20 | 39.47 | 2.25 | 3.24 | 1.24 | ||
| Gamma | 0.71 | 2.45 | 0.00 | 4.22 | 1.74 | 0.11 | 25.22 | 2.81 | 3.31 | 1.22 | ||
| LOCI | 0.59 | 2.07 | 0.04 | 3.07 | 1.27 | 0.15 | 43.46 | 1.35 | 3.09 | 1.12 | ||
| LOCI_QM | 0.89 | 2.44 | 0.00 | 4.35 | 1.95 | 1.20 | 39.47 | 2.25 | 3.24 | 1.24 | ||
| LOCI_Gamma | 0.81 | 2.42 | 0.00 | 4.17 | 1.76 | 0.72 | 40.27 | 2.00 | 3.26 | 1.23 | ||
| 4 | CAS-FGOALS-g3 | raw | 1.37 | 2.75 | 0.36 | 6.23 | 3.71 | 1.41 | 68.92 | 1.98 | 3.58 | 1.66 |
| DT | 0.77 | 2.55 | 0.00 | 4.50 | 2.05 | 0.20 | 28.50 | 2.70 | 3.34 | 1.24 | ||
| LS | 0.75 | 1.85 | 0.12 | 3.53 | 2.00 | 0.59 | 52.98 | 1.39 | 2.85 | 1.13 | ||
| EQM | 0.74 | 2.45 | 0.00 | 4.34 | 1.95 | 0.17 | 27.32 | 2.68 | 3.27 | 1.20 | ||
| Gamma | 0.73 | 2.49 | 0.01 | 3.81 | 1.72 | 0.28 | 32.82 | 2.20 | 3.30 | 1.19 | ||
| LOCI | 0.75 | 2.30 | 0.00 | 4.05 | 2.02 | 0.36 | 32.20 | 2.31 | 3.16 | 1.19 | ||
| LOCI_QM | 0.74 | 2.45 | 0.00 | 4.34 | 1.95 | 0.17 | 27.27 | 2.69 | 3.27 | 1.20 | ||
| LOCI_Gamma | 0.75 | 2.45 | 0.00 | 4.20 | 2.00 | 0.26 | 29.26 | 2.57 | 3.26 | 1.21 | ||
| 5 | MPI-ESM1-2-HR | raw | 2.19 | 4.12 | 0.03 | 11.14 | 7.51 | 2.72 | 46.00 | 4.76 | 5.08 | 2.64 |
| DT | 0.76 | 2.52 | 0.00 | 4.44 | 1.95 | 0.19 | 25.85 | 2.91 | 3.38 | 1.24 | ||
| LS | 0.75 | 3.00 | 0.01 | 3.36 | 1.22 | 0.30 | 36.24 | 2.05 | 3.75 | 1.25 | ||
| EQM | 0.82 | 2.44 | 0.00 | 4.33 | 1.95 | 0.55 | 35.82 | 2.26 | 3.28 | 1.23 | ||
| Gamma | 0.72 | 2.42 | 0.00 | 4.31 | 1.68 | 0.16 | 27.11 | 2.64 | 3.31 | 1.22 | ||
| LOCI | 0.66 | 2.27 | 0.04 | 3.51 | 1.43 | 0.16 | 45.72 | 1.43 | 3.22 | 1.16 | ||
| LOCI_QM | 0.82 | 2.44 | 0.00 | 4.33 | 1.95 | 0.55 | 35.84 | 2.26 | 3.28 | 1.23 | ||
| LOCI_Gamma | 0.80 | 2.41 | 0.00 | 4.29 | 1.70 | 0.58 | 41.81 | 1.91 | 3.28 | 1.23 | ||
| 6 | MRI-ESM2-0 | raw | 3.75 | 5.14 | 1.52 | 14.37 | 10.80 | 5.53 | 77.85 | 4.81 | 6.13 | 3.62 |
| DT | 0.81 | 2.68 | 0.00 | 4.67 | 2.09 | 0.20 | 28.19 | 2.84 | 3.47 | 1.27 | ||
| LS | 0.75 | 1.25 | 0.19 | 3.48 | 2.40 | 0.89 | 58.56 | 1.26 | 2.52 | 1.07 | ||
| EQM | 0.73 | 2.45 | 0.00 | 4.35 | 1.95 | 0.17 | 27.22 | 2.69 | 3.31 | 1.21 | ||
| Gamma | 0.76 | 2.23 | 0.00 | 4.44 | 2.14 | 0.33 | 33.35 | 2.26 | 3.13 | 1.20 | ||
| LOCI | 0.75 | 1.82 | 0.00 | 4.53 | 2.58 | 0.46 | 32.17 | 2.32 | 2.86 | 1.16 | ||
| LOCI_QM | 0.73 | 2.45 | 0.00 | 4.35 | 1.95 | 0.17 | 27.24 | 2.69 | 3.31 | 1.21 | ||
| LOCI_Gamma | 0.79 | 2.34 | 0.00 | 4.98 | 2.39 | 0.22 | 28.13 | 2.81 | 3.20 | 1.24 | ||
| 7 | IPSL-CM6A-LR | raw | 2.00 | 4.21 | 0.19 | 9.13 | 6.00 | 2.24 | 53.87 | 3.71 | 4.87 | 2.28 |
| DT | 0.78 | 2.51 | 0.00 | 4.53 | 2.08 | 0.20 | 28.33 | 2.72 | 3.32 | 1.24 | ||
| LS | 0.75 | 2.08 | 0.03 | 3.89 | 2.32 | 0.43 | 40.81 | 1.81 | 3.02 | 1.17 | ||
| EQM | 0.73 | 2.45 | 0.00 | 4.35 | 1.94 | 0.17 | 27.28 | 2.68 | 3.28 | 1.20 | ||
| Gamma | 0.76 | 2.44 | 0.00 | 4.06 | 2.29 | 0.23 | 28.80 | 2.62 | 3.27 | 1.21 | ||
| LOCI | 0.75 | 2.13 | 0.00 | 3.97 | 2.42 | 0.38 | 35.53 | 2.10 | 3.05 | 1.18 | ||
| LOCI_QM | 0.73 | 2.45 | 0.00 | 4.35 | 1.94 | 0.17 | 27.29 | 2.68 | 3.28 | 1.20 | ||
| LOCI_Gamma | 0.76 | 2.44 | 0.00 | 4.05 | 2.30 | 0.22 | 27.97 | 2.70 | 3.27 | 1.22 | ||
| 8 | GFDL-ESM4 | raw | 1.54 | 2.65 | 0.46 | 6.33 | 4.41 | 1.97 | 66.25 | 2.32 | 3.61 | 1.87 |
| DT | 0.78 | 2.52 | 0.00 | 4.62 | 2.06 | 0.20 | 28.23 | 2.75 | 3.33 | 1.25 | ||
| LS | 0.75 | 1.91 | 0.11 | 3.73 | 1.98 | 0.56 | 51.73 | 1.43 | 2.89 | 1.15 | ||
| EQM | 0.74 | 2.45 | 0.00 | 4.35 | 1.95 | 0.18 | 27.29 | 2.69 | 3.27 | 1.21 | ||
| Gamma | 0.75 | 2.44 | 0.00 | 4.06 | 1.95 | 0.32 | 32.88 | 2.26 | 3.26 | 1.21 | ||
| LOCI | 0.75 | 2.20 | 0.00 | 4.18 | 2.16 | 0.40 | 32.20 | 2.31 | 3.09 | 1.20 | ||
| LOCI_QM | 0.74 | 2.45 | 0.00 | 4.35 | 1.95 | 0.18 | 27.28 | 2.69 | 3.27 | 1.21 | ||
| LOCI_Gamma | 0.77 | 2.43 | 0.00 | 4.33 | 2.15 | 0.25 | 28.58 | 2.67 | 3.26 | 1.23 | ||
| 9 | UKESM1-0-LL | raw | 0.79 | 2.38 | 0.03 | 4.21 | 2.07 | 0.37 | 37.66 | 2.06 | 3.35 | 1.29 |
| DT | 0.75 | 2.38 | 0.00 | 4.48 | 2.00 | 0.20 | 29.69 | 2.50 | 3.26 | 1.21 | ||
| LS | 0.75 | 2.89 | 0.02 | 3.52 | 1.58 | 0.28 | 33.37 | 2.21 | 3.64 | 1.23 | ||
| EQM | 0.73 | 2.45 | 0.00 | 4.30 | 1.94 | 0.18 | 27.48 | 2.66 | 3.30 | 1.21 | ||
| Gamma | 0.76 | 2.44 | 0.00 | 4.11 | 2.09 | 0.33 | 33.35 | 2.27 | 3.29 | 1.21 | ||
| LOCI | 0.75 | 2.88 | 0.05 | 3.55 | 1.60 | 0.24 | 32.53 | 2.25 | 3.64 | 1.23 | ||
| LOCI_QM | 0.73 | 2.45 | 0.00 | 4.30 | 1.94 | 0.18 | 27.48 | 2.66 | 3.30 | 1.21 | ||
| LOCI_Gamma | 0.76 | 2.44 | 0.00 | 4.15 | 2.12 | 0.30 | 32.11 | 2.37 | 3.29 | 1.21 | ||
| 10 | Average | raw | 1.75 | 3.25 | 0.36 | 7.88 | 5.22 | 2.08 | 57.55 | 2.99 | 4.19 | 2.08 |
| DT | 0.77 | 2.51 | 0.00 | 4.52 | 2.03 | 0.19 | 27.69 | 2.77 | 3.34 | 1.24 | ||
| LS | 0.75 | 2.32 | 0.07 | 3.57 | 1.80 | 0.47 | 44.15 | 1.74 | 3.23 | 1.18 | ||
| EQM | 0.76 | 2.45 | 0.00 | 4.34 | 1.95 | 0.35 | 29.91 | 2.57 | 3.28 | 1.21 | ||
| Gamma | 0.74 | 2.42 | 0.00 | 4.15 | 1.96 | 0.25 | 30.60 | 2.43 | 3.27 | 1.21 | ||
| LOCI | 0.72 | 2.27 | 0.02 | 3.86 | 1.93 | 0.31 | 35.77 | 2.04 | 3.18 | 1.18 | ||
| LOCI_QM | 0.76 | 2.45 | 0.00 | 4.34 | 1.95 | 0.35 | 29.91 | 2.57 | 3.28 | 1.21 | ||
| LOCI_Gamma | 0.78 | 2.42 | 0.00 | 4.31 | 2.07 | 0.35 | 32.25 | 2.44 | 3.26 | 1.22 | ||
| No. | GCM | Method | Mean | Standard Deviation | Median | Percentile | RMSE | MAE | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 95% | 90% | 75% | ||||||||
| 1 | Observed | −4.24 | 14.04 | −0.20 | 12.30 | 11.00 | 8.10 | |||
| 2 | BCC-CSM2-MR | raw | 1.62 | 12.39 | 1.68 | 20.13 | 17.82 | 12.25 | 9.47 | 7.56 |
| DT | −4.25 | 14.03 | −0.21 | 12.22 | 10.97 | 8.03 | 6.33 | 4.70 | ||
| LS | −4.23 | 14.26 | −1.21 | 14.49 | 12.44 | 7.91 | 6.76 | 5.27 | ||
| EQM | −4.27 | 14.04 | −0.24 | 12.21 | 10.96 | 8.04 | 6.32 | 4.70 | ||
| Normal | −4.23 | 14.04 | −0.17 | 12.40 | 11.14 | 8.08 | 6.32 | 4.70 | ||
| 3 | CAMS-CSM1-0 | raw | 0.18 | 11.06 | 0.81 | 16.12 | 14.20 | 9.49 | 8.61 | 6.44 |
| DT | −4.23 | 14.04 | −0.21 | 12.27 | 10.98 | 8.07 | 6.32 | 4.70 | ||
| LS | −4.24 | 14.02 | −0.54 | 13.36 | 11.65 | 7.67 | 6.29 | 4.80 | ||
| EQM | −4.28 | 14.04 | −0.25 | 12.21 | 10.97 | 8.03 | 6.31 | 4.70 | ||
| Normal | −4.24 | 14.04 | −0.23 | 12.46 | 11.18 | 7.94 | 6.32 | 4.71 | ||
| 4 | CAS-FGOALS-g3 | raw | −1.81 | 11.58 | −1.68 | 15.15 | 13.35 | 8.68 | 7.82 | 5.85 |
| DT | −4.24 | 14.05 | −0.21 | 12.25 | 10.99 | 8.06 | 6.35 | 4.68 | ||
| LS | −4.23 | 14.03 | −0.55 | 13.22 | 11.74 | 7.99 | 6.30 | 4.78 | ||
| EQM | −4.27 | 14.04 | −0.24 | 12.21 | 10.97 | 8.04 | 6.32 | 4.66 | ||
| Normal | −4.23 | 14.04 | −0.02 | 12.40 | 11.18 | 8.05 | 6.32 | 4.65 | ||
| 5 | MPI-ESM1-2-HR | raw | −1.24 | 11.95 | −1.41 | 17.03 | 14.85 | 9.07 | 8.01 | 6.15 |
| DT | −4.25 | 14.05 | −0.26 | 12.21 | 10.98 | 8.07 | 6.31 | 4.67 | ||
| LS | −4.24 | 14.07 | −0.87 | 13.76 | 12.07 | 7.84 | 6.35 | 4.90 | ||
| EQM | −4.28 | 14.04 | −0.26 | 12.21 | 10.96 | 8.03 | 6.28 | 4.66 | ||
| Normal | −4.24 | 14.04 | −0.09 | 12.42 | 11.18 | 7.97 | 6.28 | 4.65 | ||
| 6 | MRI-ESM2-0 | raw | −2.99 | 9.91 | −2.87 | 11.51 | 10.02 | 5.97 | 7.56 | 5.68 |
| DT | −4.23 | 14.04 | −0.21 | 12.25 | 10.98 | 8.05 | 6.25 | 4.63 | ||
| LS | −4.24 | 13.79 | −0.65 | 13.01 | 11.61 | 8.05 | 5.77 | 4.43 | ||
| EQM | −4.28 | 14.04 | −0.26 | 12.21 | 10.97 | 8.04 | 6.23 | 4.62 | ||
| Normal | −4.24 | 14.04 | −0.10 | 12.40 | 11.18 | 8.09 | 6.22 | 4.63 | ||
| 7 | IPSL-CM6A-LR | raw | −6.76 | 11.93 | −6.02 | 10.70 | 8.93 | 2.46 | 8.31 | 6.54 |
| DT | −4.25 | 14.06 | −0.24 | 12.25 | 10.97 | 8.05 | 6.40 | 4.72 | ||
| LS | −4.24 | 14.26 | −0.27 | 13.39 | 11.83 | 7.73 | 6.81 | 5.12 | ||
| EQM | −4.28 | 14.04 | −0.25 | 12.21 | 10.96 | 8.04 | 6.38 | 4.71 | ||
| Normal | −4.24 | 14.04 | −0.01 | 12.37 | 11.27 | 7.81 | 6.40 | 4.72 | ||
| 8 | GFDL-ESM4 | raw | −3.58 | 10.33 | −2.93 | 11.41 | 9.62 | 5.47 | 7.51 | 5.76 |
| DT | −4.22 | 14.03 | −0.22 | 12.27 | 10.99 | 8.07 | 6.45 | 4.76 | ||
| LS | −4.23 | 13.86 | −0.56 | 13.30 | 11.62 | 7.76 | 6.08 | 4.69 | ||
| EQM | −4.27 | 14.04 | −0.24 | 12.21 | 10.96 | 8.04 | 6.44 | 4.76 | ||
| Normal | −4.23 | 14.04 | 0.07 | 12.36 | 11.07 | 8.00 | 6.44 | 4.76 | ||
| 9 | UKESM1-0-LL | raw | 2.18 | 12.01 | 4.07 | 18.37 | 16.81 | 12.82 | 8.96 | 7.24 |
| DT | −4.23 | 14.01 | −0.20 | 12.25 | 10.99 | 8.04 | 6.16 | 4.56 | ||
| LS | −4.23 | 13.84 | −0.60 | 13.13 | 11.65 | 7.98 | 5.83 | 4.47 | ||
| EQM | −4.27 | 14.02 | −0.22 | 12.20 | 10.96 | 8.02 | 6.14 | 4.55 | ||
| Normal | −4.23 | 14.03 | −0.04 | 12.24 | 11.11 | 8.07 | 6.14 | 4.55 | ||
| 10 | Average | raw | −1.55 | 11.40 | −1.04 | 15.05 | 13.20 | 8.28 | 8.28 | 6.40 |
| DT | −4.24 | 14.04 | −0.22 | 12.24 | 10.98 | 8.05 | 6.32 | 4.68 | ||
| LS | −4.23 | 14.02 | −0.66 | 13.46 | 11.83 | 7.87 | 6.27 | 4.81 | ||
| EQM | −4.27 | 14.04 | −0.25 | 12.21 | 10.96 | 8.03 | 6.30 | 4.67 | ||
| Normal | −4.23 | 14.04 | −0.07 | 12.38 | 11.17 | 8.00 | 6.30 | 4.67 | ||
| R-Month | Raw | DT | EQM | LS | Gamma | LOCI | LOCI_QM | LOCI_Gamma |
|---|---|---|---|---|---|---|---|---|
| R-Pr | 0.33 | 0.72 | 0.74 | 0.74 | 0.73 | 0.73 | 0.74 | 0.74 |
| R-Month | Raw | DT | EQM | LS | Normal |
|---|---|---|---|---|---|
| R-Tas | 0.94 | 0.97 | 0.97 | 0.97 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Wang, Y.; Fan, L.; Ding, J.; Chen, W. Assessment and Prediction of Future Climate Change in the Kaidu River Basin of Xinjiang under Shared Socioeconomic Pathway Scenarios. Atmosphere 2024, 15, 208. https://doi.org/10.3390/atmos15020208
Cao C, Wang Y, Fan L, Ding J, Chen W. Assessment and Prediction of Future Climate Change in the Kaidu River Basin of Xinjiang under Shared Socioeconomic Pathway Scenarios. Atmosphere. 2024; 15(2):208. https://doi.org/10.3390/atmos15020208
Chicago/Turabian StyleCao, Chenglin, Yi Wang, Lei Fan, Junwei Ding, and Wen Chen. 2024. "Assessment and Prediction of Future Climate Change in the Kaidu River Basin of Xinjiang under Shared Socioeconomic Pathway Scenarios" Atmosphere 15, no. 2: 208. https://doi.org/10.3390/atmos15020208
APA StyleCao, C., Wang, Y., Fan, L., Ding, J., & Chen, W. (2024). Assessment and Prediction of Future Climate Change in the Kaidu River Basin of Xinjiang under Shared Socioeconomic Pathway Scenarios. Atmosphere, 15(2), 208. https://doi.org/10.3390/atmos15020208





