Estimation of Radiation Exposure for Various Flights from Athens International Airport
Abstract
1. Introduction
2. Methods and Analysis
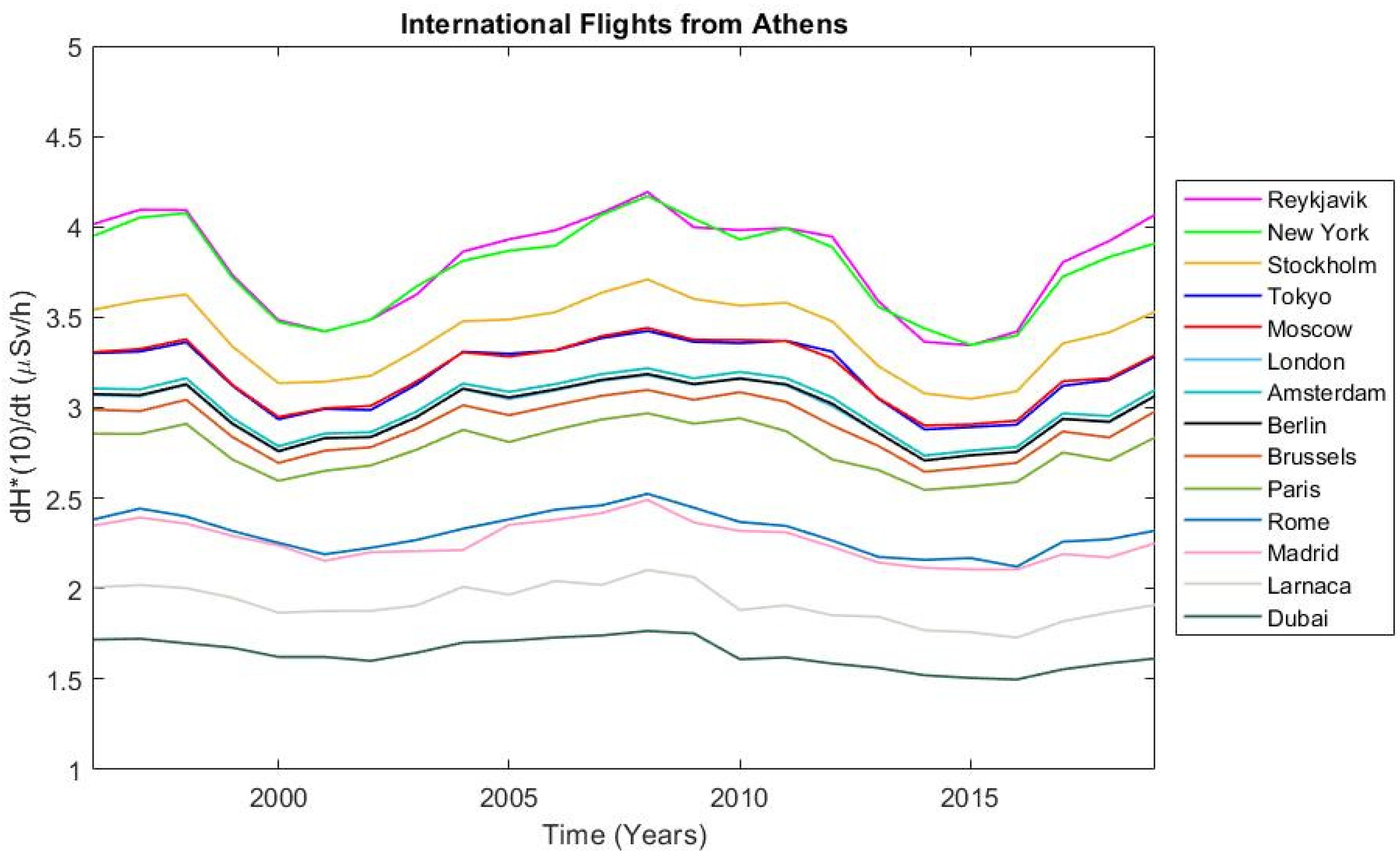
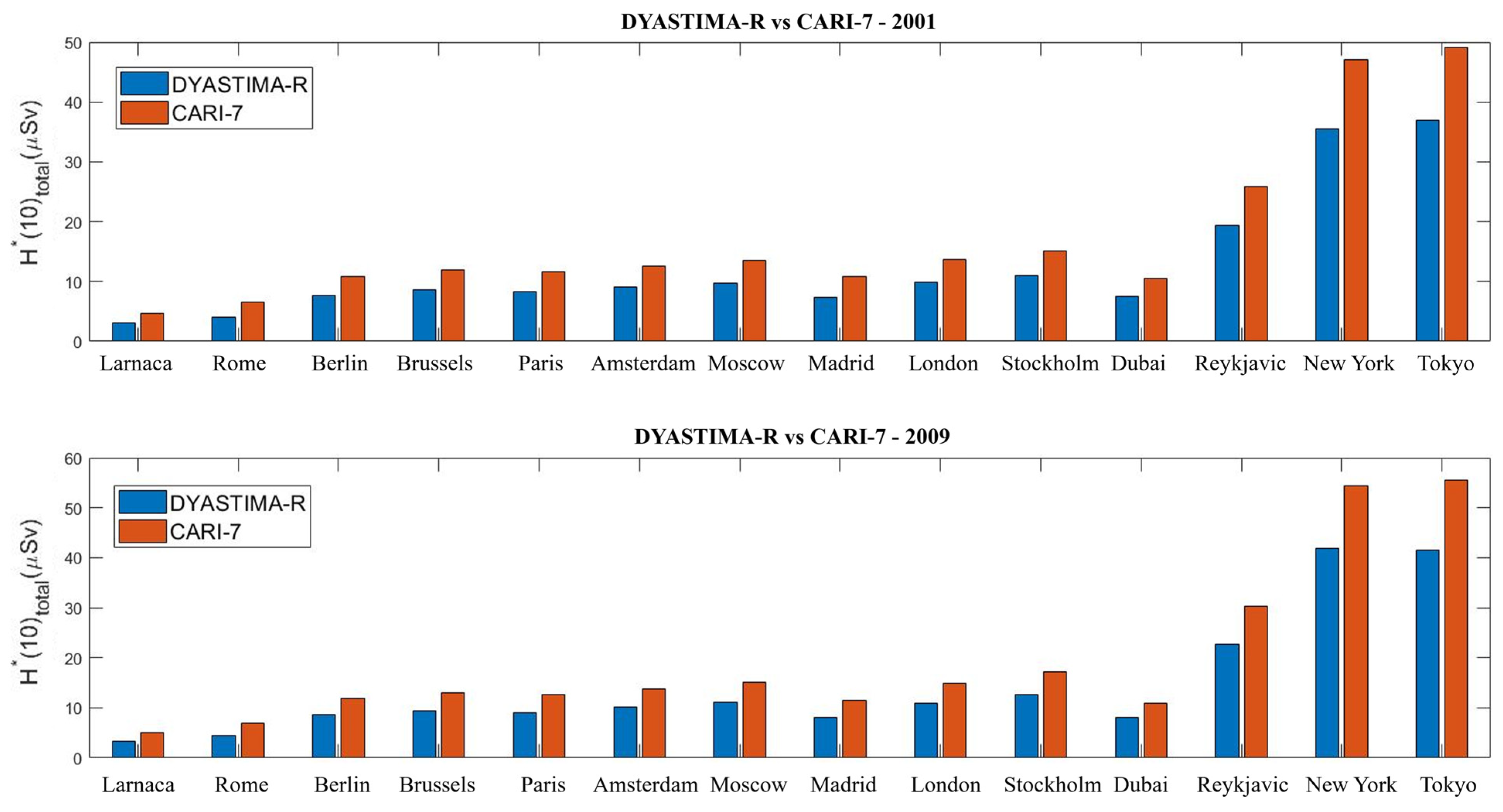
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuipers, S.; Venemans-Jellema, A.; Cannegieter, S.C.; van Haften, M.; Middeldorp, S.; Büller, H.R.; Rosendaal, F.R. The incidence of venous thromboembolism in commercial airline pilots: A cohort study of 2630 pilots. J. Thromb. Haemost. 2014, 12, 1260–1265. [Google Scholar] [CrossRef] [PubMed]
- Zeeb, H.; Hammer, G.P.; Blettner, M. Epidemiological investigations of aircrew: An occupational group with low-level cosmic radiation exposure. J. Radiol. Prot. 2012, 32, N15–N19. [Google Scholar] [CrossRef]
- Rafnsson, V.; Tulinius, H.; Jónasson, J.G.; Hrafnkelsson, J. Risk of breast cancer in female flight attendants: A population-based study (Iceland). Cancer Causes Control 2001, 12, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Mavromichalaki, H.; Gerontidou, M.; Paschalis, P.; Paouris, E.; Tezari, A.; Sgouropoulos, C.; Dierckxsens, M. Dierckxsens, Real-Time Detection of the Ground Level Enhancement on 10 September 2017 by A.Ne.Mo.S.: System Report. Space Weather 2018, 16, 1797–1805. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Kovaltsov, G.A.; Mironova, I.A.; Tylka, A.J.; Dietrich, W.F. Ionization effect of solar particle GLE events in low and middle atmosphere. Atmos. Meas. Tech. 2011, 11, 1979–1988. [Google Scholar] [CrossRef][Green Version]
- Miroshnichenko, L.I. Retrospective analysis of GLEs and estimates of radiation risks. J. Space Weather Space Clim. 2018, 8, A52. [Google Scholar] [CrossRef]
- Plainaki, C.; Laurenza, M.; Mavromichalaki, H.; Storini, M.; Gerontidou, M.; Kanellakopoulos, A.; Andriopoulou, M.; Belov, A.; Eroshenko, E.; Yanke, V. Derivation of relativistic SEP properties through neutron monitor data modeling. J. Phys. Conf. Ser. 2015, 632, 012076. [Google Scholar] [CrossRef]
- Vainio, R.; Valtonen, E.; Heber, B.; Malandraki, O.E.; Papaioannou, A.; Klein, K.L.; Vilmer, N. The first SEPServer event catalogue ~68-MeV solar proton events observed at 1 AU in 1996–2010. J. Space Weather Space Clim. 2013, 3, A12. [Google Scholar] [CrossRef]
- Mishev, A.L.; Koldobskiy, S.A.; Kocharov, L.G.; Usoskin, I.G. GLE # 67 Event on 2 November 2003: An Analysis of the Spectral and Anisotropy Characteristics Using Verified Yield Function and Detrended Neutron Monitor Data. Sol. Phys. 2021, 296, 1–18. [Google Scholar] [CrossRef]
- Linnersjo, A.; Hammar, N.; Dammström, B.-G.; Johansson, M.; Eliasch, H. Cancer incidence in airline cabin crew: Experience from Sweden. Occup. Environ. Med. 2003, 60, 810–814. [Google Scholar] [CrossRef]
- Beck, P. Aircraft crew radiation exposure in aviation altitudes during quiet and solar storm periods. In Space Weather; Lilensten, J., Ed.; Astrophysics and Space Science Library: Dordrecht, The Netherlands, 2007; Volume 344, pp. 241–266. [Google Scholar] [CrossRef]
- Beck, P.; Bartlett, D.; Lindborg, L.; McAulay, I.; Schnuer, K.; Schraube, H.; Spurny, F. Aircraft crew radiation workplaces: Comparison of measured and calculated ambient dose equivalent rate data using the EURADOS in-flight radiation data base. Radiat. Prot. Dosim. 2006, 118, 182–189. [Google Scholar] [CrossRef] [PubMed]
- Beck, P.; Bartlett, D.T.; Bilski, P.; Dyer, C.; Fluckiger, E.; Fuller, N.; Lantos, P.; Reitz, G.; Ruhm, W.; Spurny, F.; et al. Validation of modelling the radiation exposure due to solar particle events at aircraft altitudes. Radiat. Prot. Dosim. 2008, 131, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Bottollier-Depois, J.F.; Beck, P.; Latocha, M.; Mares, V.; Matthiä, D.; Rühm, W.; Wissmann, F. Comparison of Codes Assessing Radiation Exposure of Aircraft Crew due to Galactic Cosmic Radiation; Report 2012-03; European Radiation Dosimetry Group (EURADOS): Braunschweig, Germany, 2012; ISBN 978-3-943701-02-9. [Google Scholar]
- Bottollier-Depois, J.F.; Biau, A.; Blanchard, P.; Clairand, I.; Dessarps, P.; Lantos, P.; Saint-Lô, D.; Valero, M. Assessing exposure to cosmic radiation aboard aircraft: The SIEVERT system. Radioprotection 2003, 38, 357–366. [Google Scholar] [CrossRef]
- Bütikofer, R.; Flückiger, E.; Desorgher, L.; Moser, M. The extreme solar cosmic ray particle event on 20 January 2005 and its influence on the radiation dose rate at aircraft altitude. Sci. Total Environ. 2008, 391, 177–183. [Google Scholar] [CrossRef] [PubMed]
- Clairand, I.; Fuller, N.; Bottollier-Depois, J.-F.; Trompier, F. The SIEVERT system for aircrew dosimetry. Radiat. Prot. Dosim. 2009, 136, 282–285. [Google Scholar] [CrossRef]
- EC. Radiation Protection 156: Evaluation of the Implementation of Radiation Protection Measures for Aircrew; Directorate-General for Energy and Transport of the European Commission: Luxembourg, 2009; ISBN 978-92-79-08409-6. [Google Scholar]
- EC. Radiation Protection 173: Comparison of Codes Assessing Radiation Exposure of Aircraft Crew due to Galactic Cosmic Radiation; Directorate-General for Energy and Transport of the European Commission: Luxembourg, 2017; ISBN 978-92-79-27036-9. [Google Scholar]
- EC. Radiation Protection 140: Cosmic Radiation Exposure of Aircraft Crew—Compilation of Measured and Calculated Data; Directorate-General for Energy and Transport of the European Commission: Luxembourg, 2004; ISBN 92-894-8448-9. [Google Scholar]
- Guillaume, H.; Sébastien, A. Analysis of solar and galactic cosmic rays induced atmospheric ionizing radiation: Impacts for typical transatlantic ights and antarctica environment. JSM Environ. Sci. Ecol. 2017, 5, 9–44. [Google Scholar]
- Hubert, G.; Aubry, S. Analysis of Exposure to Solar and Galactic Cosmic Radiations of Flights Representative of the European International Air Traffic. Radiat. Res. 2018, 190, 271–281. [Google Scholar] [CrossRef]
- Lantos, P.; Fuller, N. Semi-Empirical Model to Calculate Potential Radiation Exposure on Board Airplane During Solar Particle Events. IEEE Trans. Plasma Sci. 2004, 32, 1468–1477. [Google Scholar] [CrossRef]
- Mares, V.; Yasuda, H. Aviation route doses calculated with EPCARD.Net and JISCARD EX. Radiat. Meas. 2010, 45, 1553–1556. [Google Scholar] [CrossRef]
- Shea, M.; Smart, D. Cosmic ray Implications for Human Health. Space Sci. Rev. 2000, 93, 187–205. [Google Scholar] [CrossRef]
- Perez, R. Methods for Spacecraft Avionics Protection Against Space Radiation in the Form of Single-Event Transients. IEEE Trans. Electromagn. Compat. 2008, 50, 455–465. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; The GEANT4 Collaboration. Recent developments in geant4. Nucl. Instrum. Methods Phys. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Tezari, A.; Paschalis, P.; Stassinakis, A.; Mavromichalaki, H.; Karaiskos, P.; Gerontidou, M.; Alexandridis, D.; Kanellakopoulos, A.; Crosby, N.; Dierckxsens, M. Radiation Exposure in the Lower Atmosphere during Different Periods of Solar Activity. Atmosphere 2022, 13, 166. [Google Scholar] [CrossRef]
- Tezari, A.; Stassinakis, A.N.; Paschalis, P.; Mavromichalaki, H.; Plainaki, C.; Kanellakopoulos, A.; Crosby, N.; Dierckxsens, M.; Karaiskos, P. Radiation Dosimetry Estimations in the Venusian Atmosphere during Different Periods of Solar Activity. Universe 2022, 8, 637. [Google Scholar] [CrossRef]
- Makrantoni, P.; Tezari, A.; Stassinakis, A.N.; Paschalis, P.; Gerontidou, M.; Karaiskos, P.; Georgakilas, A.G.; Mavromichalaki, H.; Usoskin, I.G.; Crosby, N.; et al. Estimation of Cosmic-Ray-Induced Atmospheric Ionization and Radiation at Commercial Aviation Flight Altitudes. Appl. Sci. 2022, 12, 5297. [Google Scholar] [CrossRef]
- Tezari, A.; Paschalis, P.; Mavromichalaki, H.; Karaiskos, P.; Crosby, N.; Dierckxsens, M. Assessing radiation exposure inside the earth’s atmosphere. Radiat. Prot. Dosim. 2020, 190, 427–436. [Google Scholar] [CrossRef]
- ISO 2533:1975ISO; Standard Atmosphere. International Organization for Standardization: Geneva, Switzerland, 2007.
- ISO 15390:2004ISO; Space Environment (Natural and Artificial)—Galactic Cosmic Ray Model. International Organization for Standardization: Geneva, Switzerland, 2004.
- OMERE Space Radiation Environment and Effects Tool: New Developments and New Interface. Available online: https://indico.esa.int/event/188/contributions/1622/attachments/1521/1753/OMERE_space_radiation_environment_and_effects_tool_Varotsou_07032017.pdf (accessed on 5 December 2023).
- Gerontidou, M.; Katzourakis, N.; Mavromichalaki, H.; Yanke, V.; Eroshenko, E. World grid of cosmic ray vertical cut-off rigidity for the last decade. Adv. Space Res. 2021, 67, 2231–2240. [Google Scholar] [CrossRef]
- Smart, D.F.; Shea, M.A. World grid of calculated cosmic ray vertical cut off_rigidities for epoch 1995.0. In Proceedings of the 30th International Cosmic Ray Conference, Merida, Mexico, 3–11 July 2007; Volume 1, pp. 733–736. [Google Scholar]
- Smart, D.F.; Shea, M.A. World grid of calculated cosmic ray vertical cut off rigidities for epoch 2000.0. In Proceedings of the 30th International Cosmic Ray Conference, Merida, Mexico, 3–11 July 2007; Volume 1, pp. 737–740. [Google Scholar]
- Smart, D.F.; Shea, M.A. Vertical geomagnetic cut off rigidities for epoch 2015. In Proceedings of the 36th International Cosmic Ray Conference, PoS(ICRC2019), Madison, WI, USA, 24 July–1 August 2019; Volume 1154, pp. 1–8. [Google Scholar]
- Mavromichalaki, H.; Belehaki, A.; Rafios, X.; Tsagouri, I. Hale-cycle effects in cosmic-ray intensity during the last four cycles. Astrophys. Space Sci. 1997, 246, 7–14. [Google Scholar] [CrossRef]
- ICRP. Radiological protection from cosmic radiation in aviation. icrp publication 132. Ann. ICRP 2016, 45, 1–48. [Google Scholar] [CrossRef]
- ICRU. Reference data for the validation of doses from cosmic-radiation exposure of aircraft crew. Report 84. J. Int. Comm. Radiat. Units Meas. 2010, 10, e1–e2. [Google Scholar] [CrossRef]
- Tezari, A.; Stassinakis, A.; Paschalis, P.; Mavromichalaki, H.; Gerontidou, M.; Karaiskos, P.; Kanellakopoulos, A.; Plainaki, C.; Crosby, N.; Dierckxsens, M. Estimation of the radiation exposure in the atmospheres of Earth, Venus and Mars with the software DYASTIMA. In Proceedings of the 44th COSPAR Scientific Assembly, Athens, Greece, 16–24 July 2022; Available online: https://www.cosparathens2022.org/.AbstractF2.3–0023-22 (accessed on 30 November 2023).
- Copeland, K. CARI-7A: Development and validation. Radiat. Prot. Dosim. 2017, 175, 419–431. [Google Scholar] [CrossRef]
- Sihver, L.; Ploc, O.; Puchalska, M.; Ova, I.A.; Ak, J.K.; Kyselova, D.; Shurshakov, V. Radiation environment at aviation altitudes and in space. Radiat. Prot. Dosim. 2015, 164, 477–483. [Google Scholar] [CrossRef] [PubMed]
- van der Ende, B.M.; Atanackovic, J.; Erlandson, A.; Bentoumi, G. Use of GEANT4 vs. MCNPX for the characterization of a boron-lined neutron detector. In Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment; Elsevier B.V.: Amsterdam, The Netherlands, 2016; Volume 820, pp. 40–47. ISSN 0168-9002. [Google Scholar]
- Latocha, M.; Beck, P.; Rollet, S. AVIDOS—A software package for European accredited aviation dosimetry. Radiat. Prot. Dosim. 2009, 136, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Mishev, A. Computation of radiation environment during ground level enhancements 65, 69 and 70 at equatorial region and flight altitudes. Adv. Space Res. 2014, 54, 528–535. [Google Scholar] [CrossRef]
- Mishev, A.; Adibpour, F.; Usoskin, I.; Felsberger, E. Computation of dose rate at flight altitudes during ground level enhancements no. 69, 70 and 71. Adv. Space Res. 2015, 55, 354–362. [Google Scholar] [CrossRef]
- Mishev, A.L.; Usoskin, I.G. Assessment of the Radiation Environment at Commercial Jet-Flight Altitudes During GLE 72 on 10 September 2017 Using Neutron Monitor Data. Space Weather 2018, 16, 1921–1929. [Google Scholar] [CrossRef]
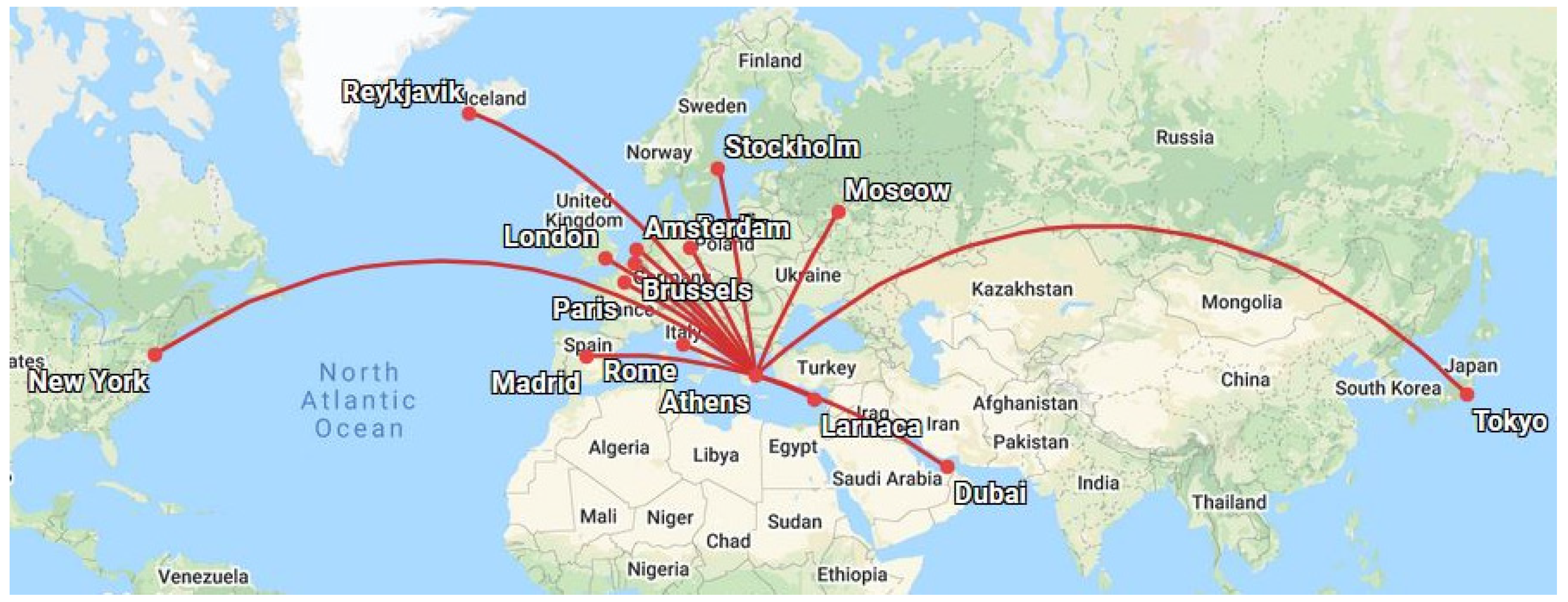

| City | Airport | ICAO | Geogr. Coordinates |
|---|---|---|---|
| Athens | Eleftherios Venizelos Airport | LGAV | 37:9° N; 23:9° E |
| Larnaca | Larnaca International Airport | LCLK | 34:9° N; 33:6° E |
| Rome | Leonardo Da Vinci—Fiumicino Airport | LIFR | 41:8° N; 12:2° E |
| Madrid | Adolfo Suarez Madrid—Barajas Airport | LEMD | 40:5° N; 3:6° W |
| Paris | Chales de Gaulle Airport | LFPG | 49:0° N; 2:5° E |
| Berlin | Berlin Tegel Airport | EDDT | 52:6° N; 13:3° E |
| Amsterdam | Amsterdam Airport Schiphol | EHAM | 52:3° N; 4:8° E |
| Brussels | Melsbroek Air Base | EBMB | 50:5° N; 4:3° E |
| London | Heathrow Airport | EGLL | 51:5° N; 0:5° W |
| Moscow | Sheremetyvo International Airport | UUEE | 56:0° N; 37:4° E |
| Stockholm | Stockholm Arlanda Airport | ESSA | 59:6° N; 17:9° E |
| Reykjavik | Reykjavik Airport | BIRK | 64:1° N; 21:9° W |
| Dubai | Dubai International Airport | OMDB | 25:3° N; 55:4° E |
| New York | JFK International Airport | KJFK | 40:6° N; 73:8° W |
| Tokyo | Narita International Airport | RJAA | 35:8° N; 140:4° E |
| Flight | Duration | Flight | Duration |
|---|---|---|---|
| Athens–Larnaca | 1 h 38 min | Athens–Madrid | 3 h 27 min |
| Athens–Rome | 1 h 49 min | Athens–London | 3 h 29 min |
| Athens–Berlin | 2 h 44 min | Athens–Stockholm | 3 h 30 min |
| Athens–Brussels | 3 h 6 min | Athens–Dubai | 4 h 35 min |
| Athens–Paris | 3 h 7 min | Athens–Reykiavik | 5 h 41 min |
| Athens–Amsterdam | 3 h 11 min | Athens–New York | 10 h 22 min |
| Athens–Moscow | 3 h 16 min | Athens–Tokyo | 12 h 21 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tezari, A.; Stassinakis, A.N.; Makrantoni, P.; Paschalis, P.; Alexandridis, D.; Gerontidou, M.; Mavromichalaki, H.; Karaiskos, P.; Crosby, N.; Dierckxsens, M. Estimation of Radiation Exposure for Various Flights from Athens International Airport. Atmosphere 2024, 15, 149. https://doi.org/10.3390/atmos15020149
Tezari A, Stassinakis AN, Makrantoni P, Paschalis P, Alexandridis D, Gerontidou M, Mavromichalaki H, Karaiskos P, Crosby N, Dierckxsens M. Estimation of Radiation Exposure for Various Flights from Athens International Airport. Atmosphere. 2024; 15(2):149. https://doi.org/10.3390/atmos15020149
Chicago/Turabian StyleTezari, Anastasia, Argyris N. Stassinakis, Panagiota Makrantoni, Pavlos Paschalis, Dimitris Alexandridis, Maria Gerontidou, Helen Mavromichalaki, Pantelis Karaiskos, Norma Crosby, and Mark Dierckxsens. 2024. "Estimation of Radiation Exposure for Various Flights from Athens International Airport" Atmosphere 15, no. 2: 149. https://doi.org/10.3390/atmos15020149
APA StyleTezari, A., Stassinakis, A. N., Makrantoni, P., Paschalis, P., Alexandridis, D., Gerontidou, M., Mavromichalaki, H., Karaiskos, P., Crosby, N., & Dierckxsens, M. (2024). Estimation of Radiation Exposure for Various Flights from Athens International Airport. Atmosphere, 15(2), 149. https://doi.org/10.3390/atmos15020149







