Improving Solar Radiation Prediction in China: A Stacking Model Approach with Categorical Boosting Feature Selection
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection and Processing
2.2. Evaluation of Model Input Characteristics
2.2.1. CatBoost Feature Selection Algorithm
2.2.2. Shapley Additive Explanation
2.3. Learner Selection for Stacking
2.3.1. Support Vector Regression (SVR)
2.3.2. Artificial Neural Networks (ANNs)
2.3.3. K-Nearest Neighbor (KNN)
2.3.4. Bayesian Ridge Regression (Bayesian)
2.3.5. Extreme Gradient Boosting (XGBoost)
2.3.6. Elastic Network Regression (ElasticNet)
2.3.7. Stacking
2.4. Performance Evaluation
3. Results and Discussion
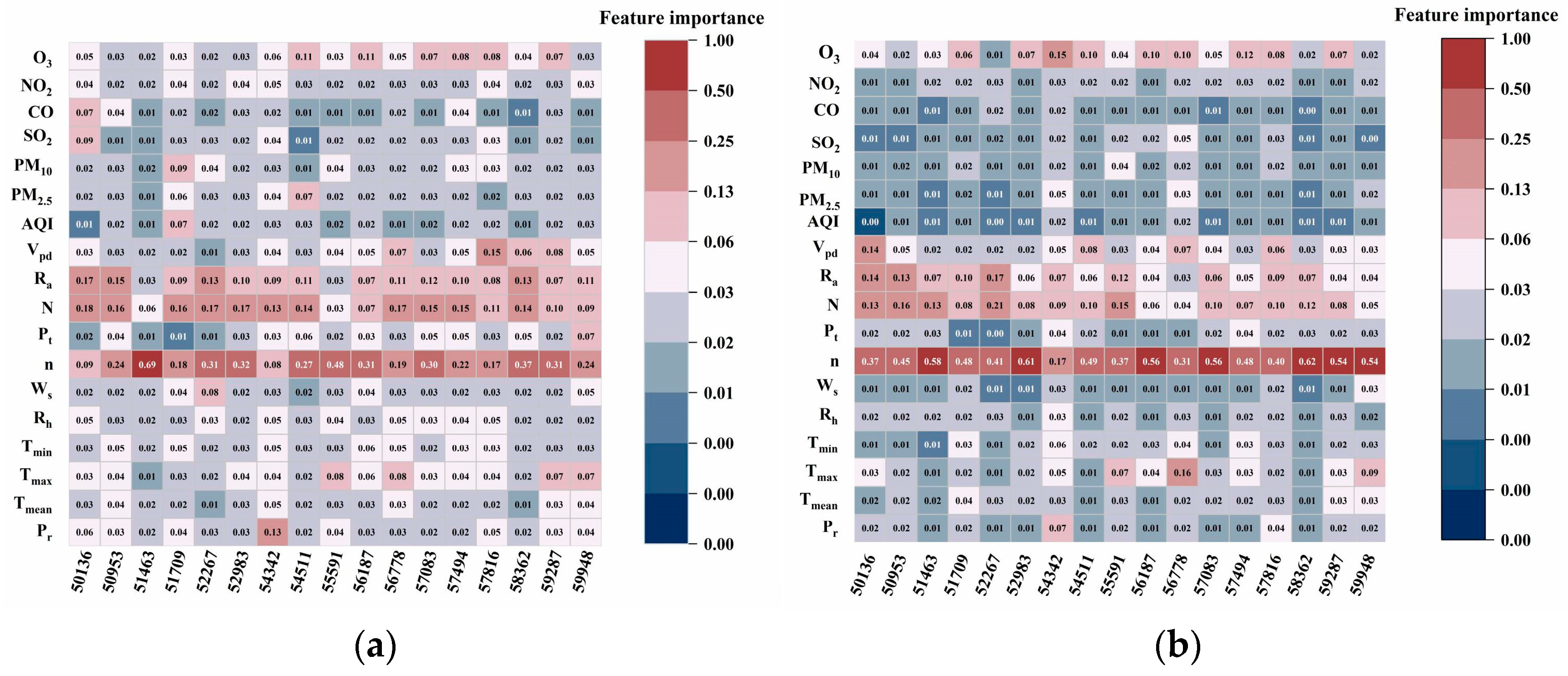
3.1. Selection Results of the CatBoost Feature Selection Algorithm
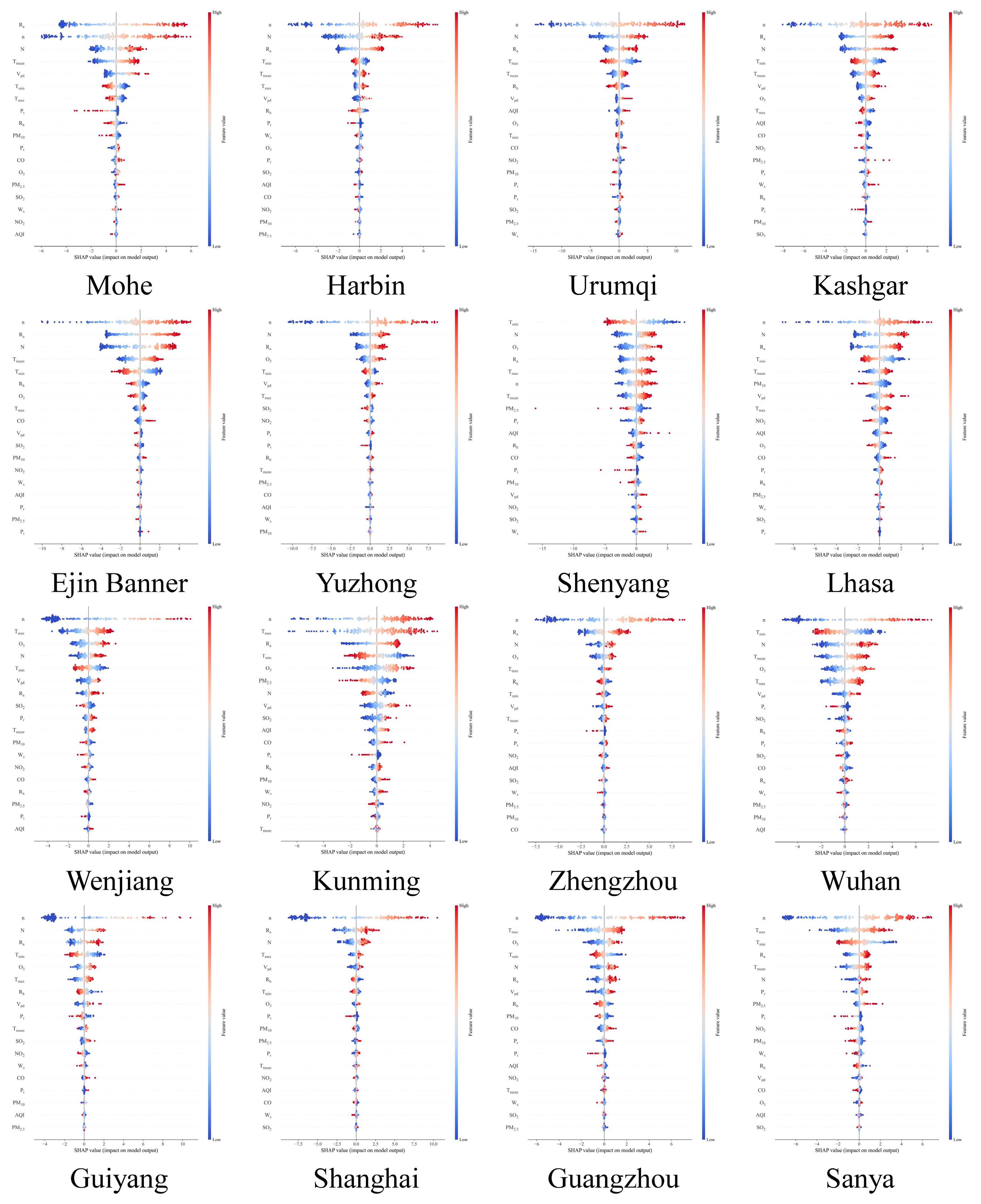
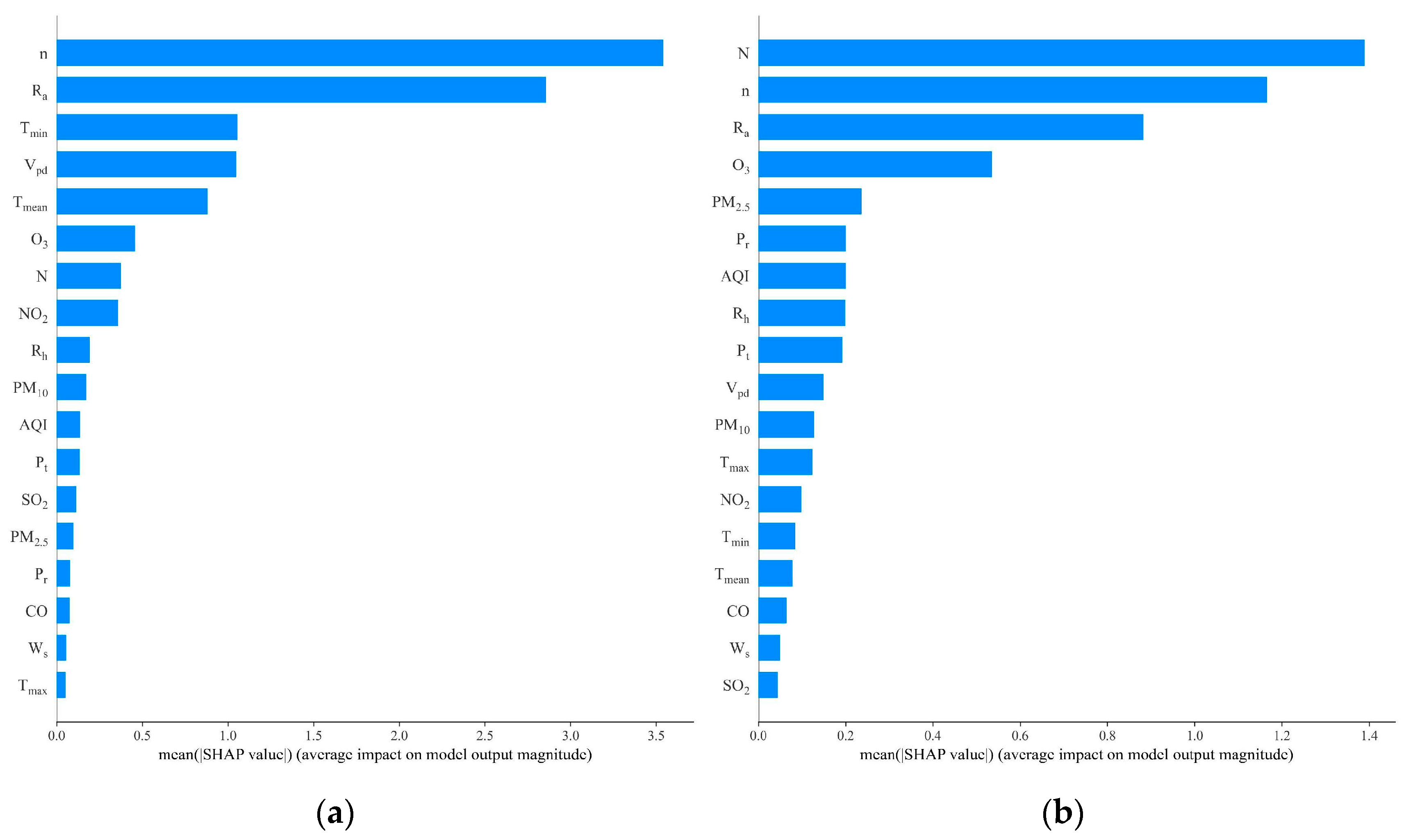
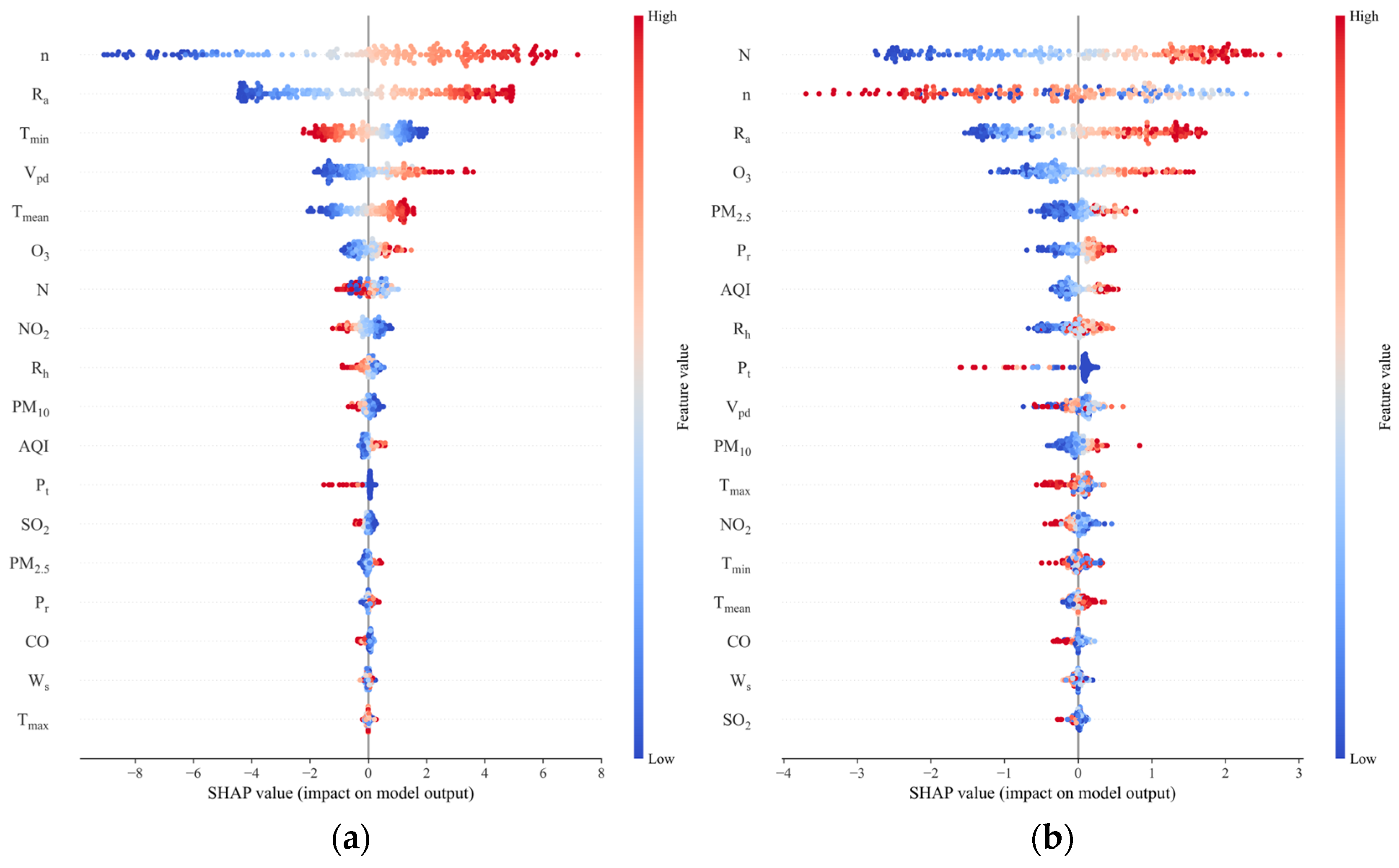
3.2. Shapley Additive Explanation (SHAP) Analysis
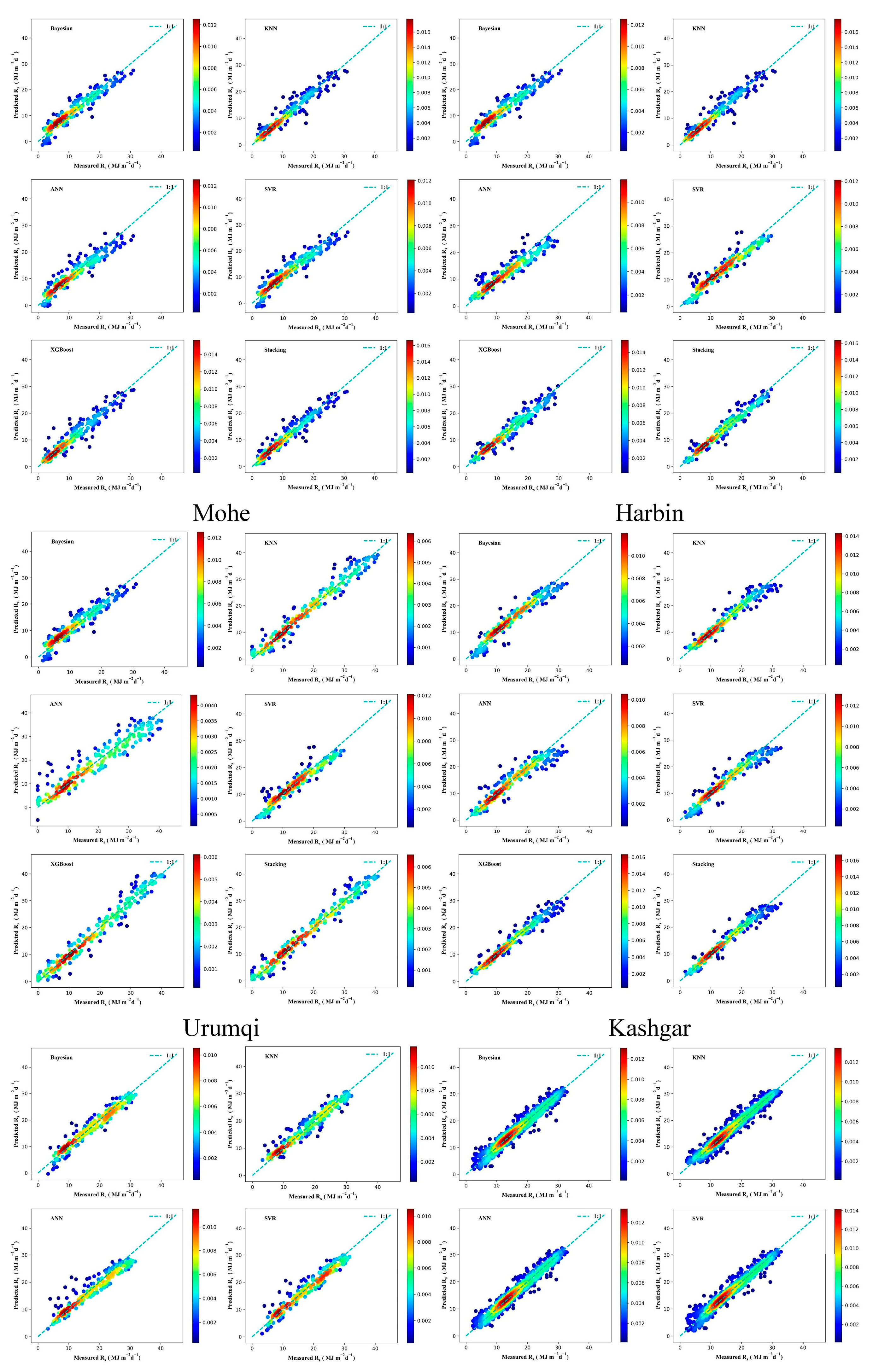
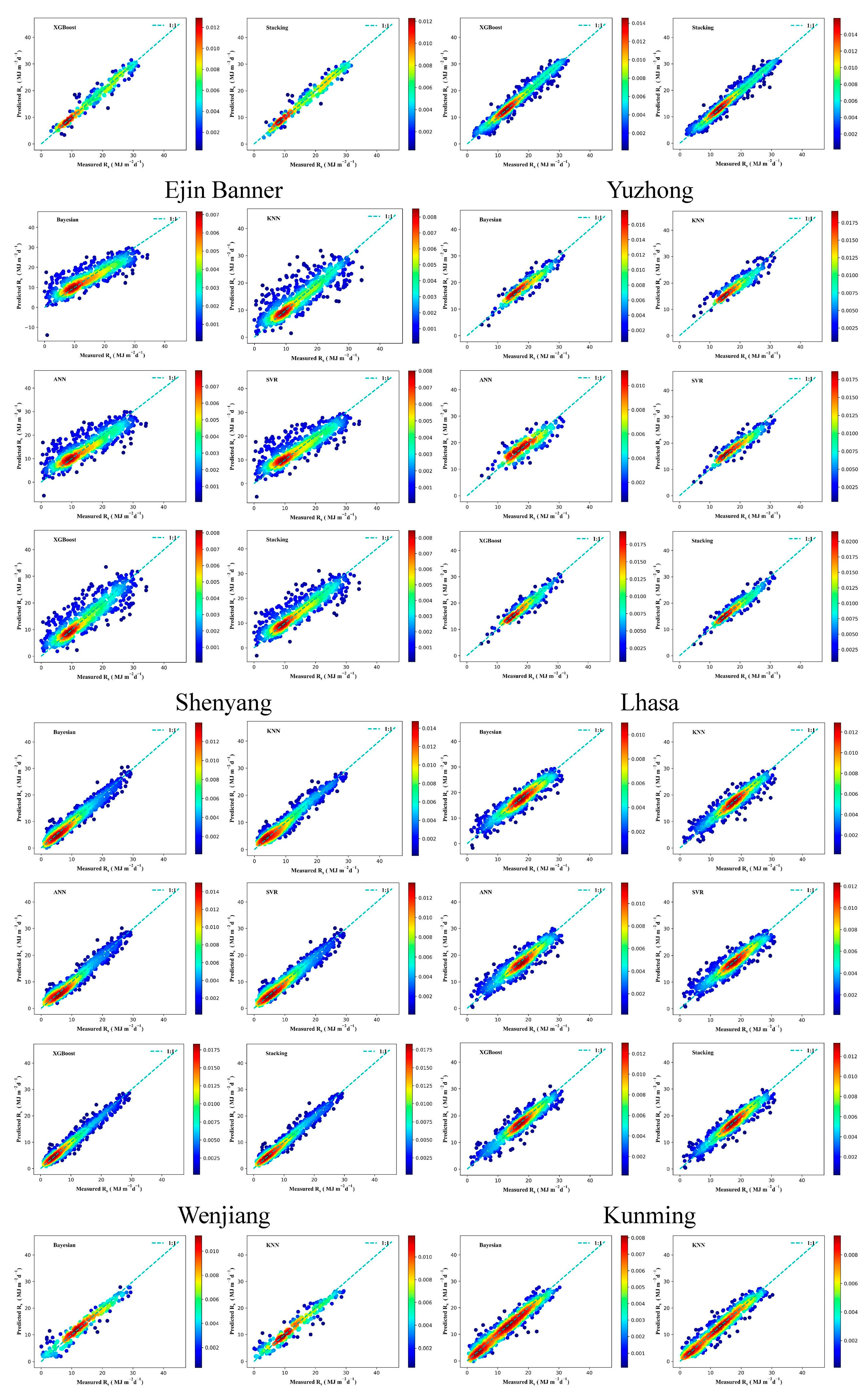
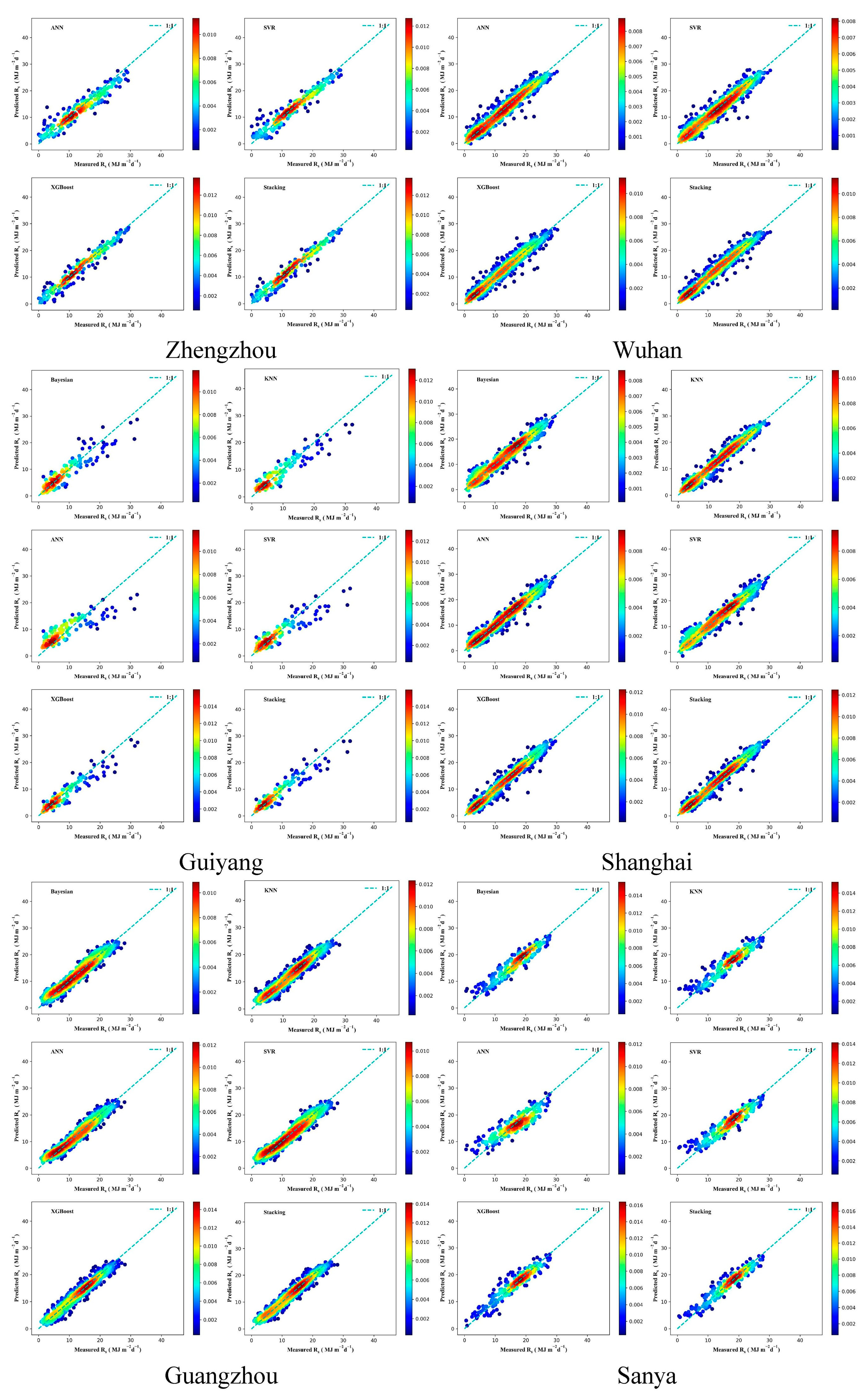
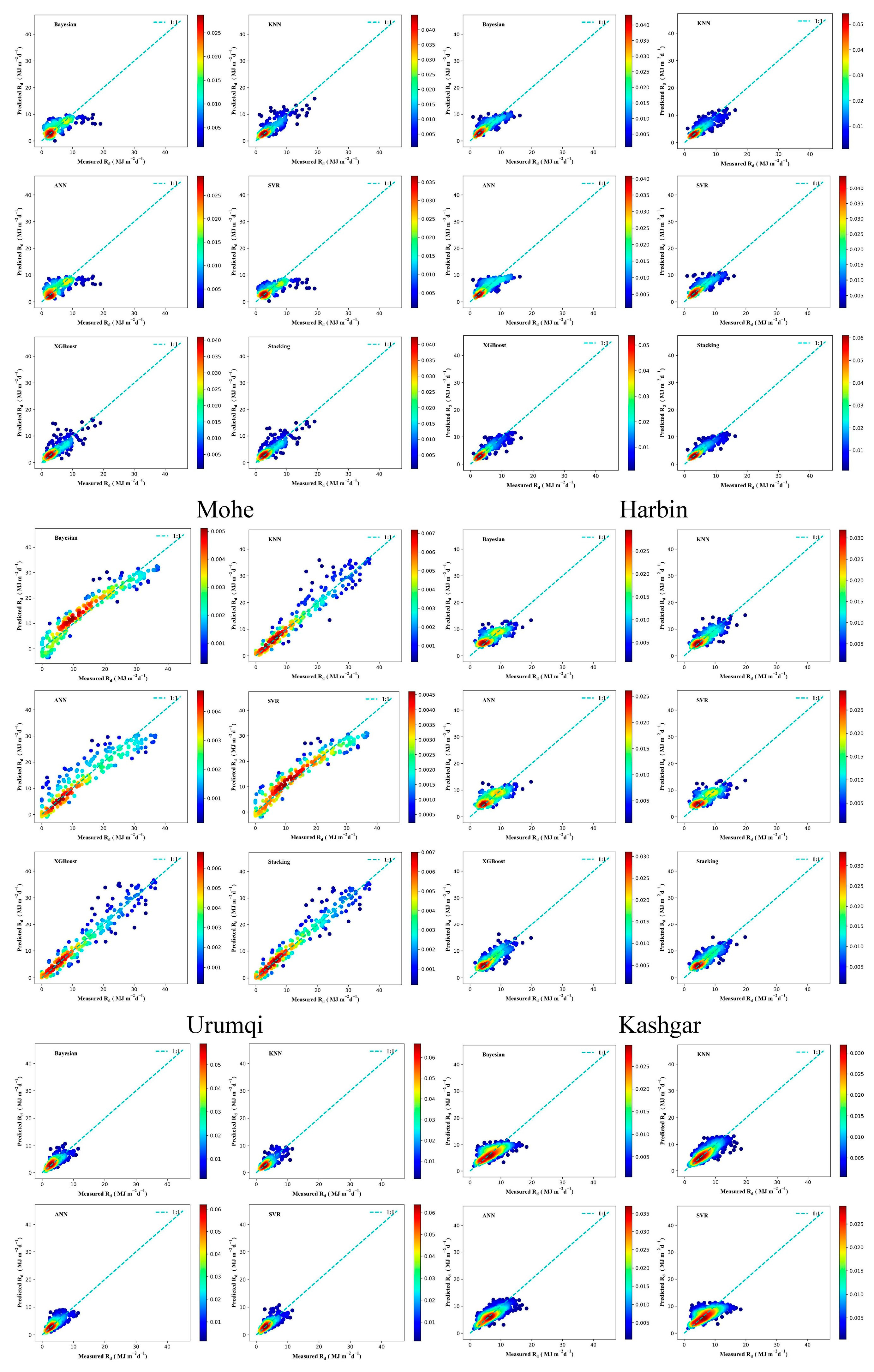
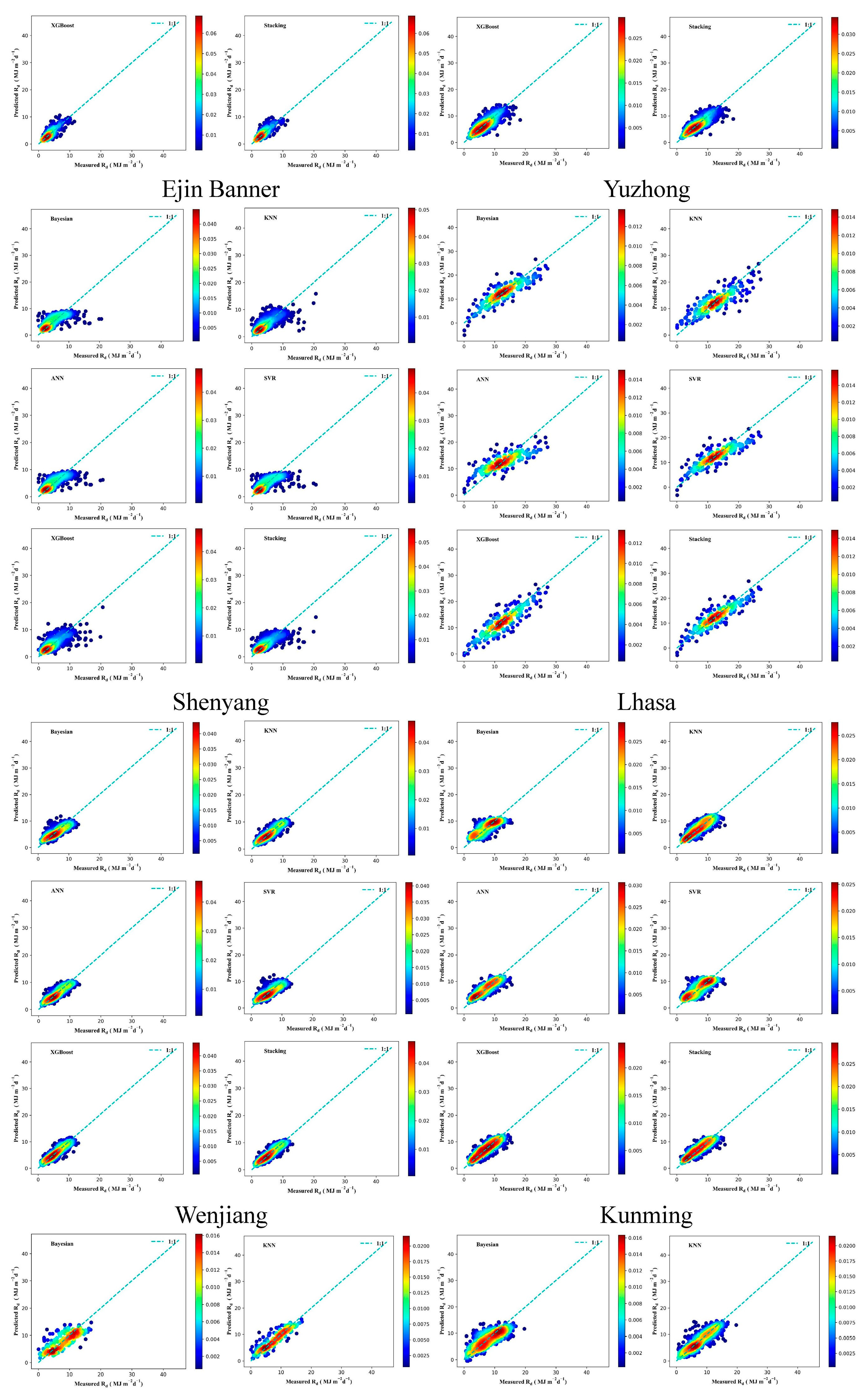
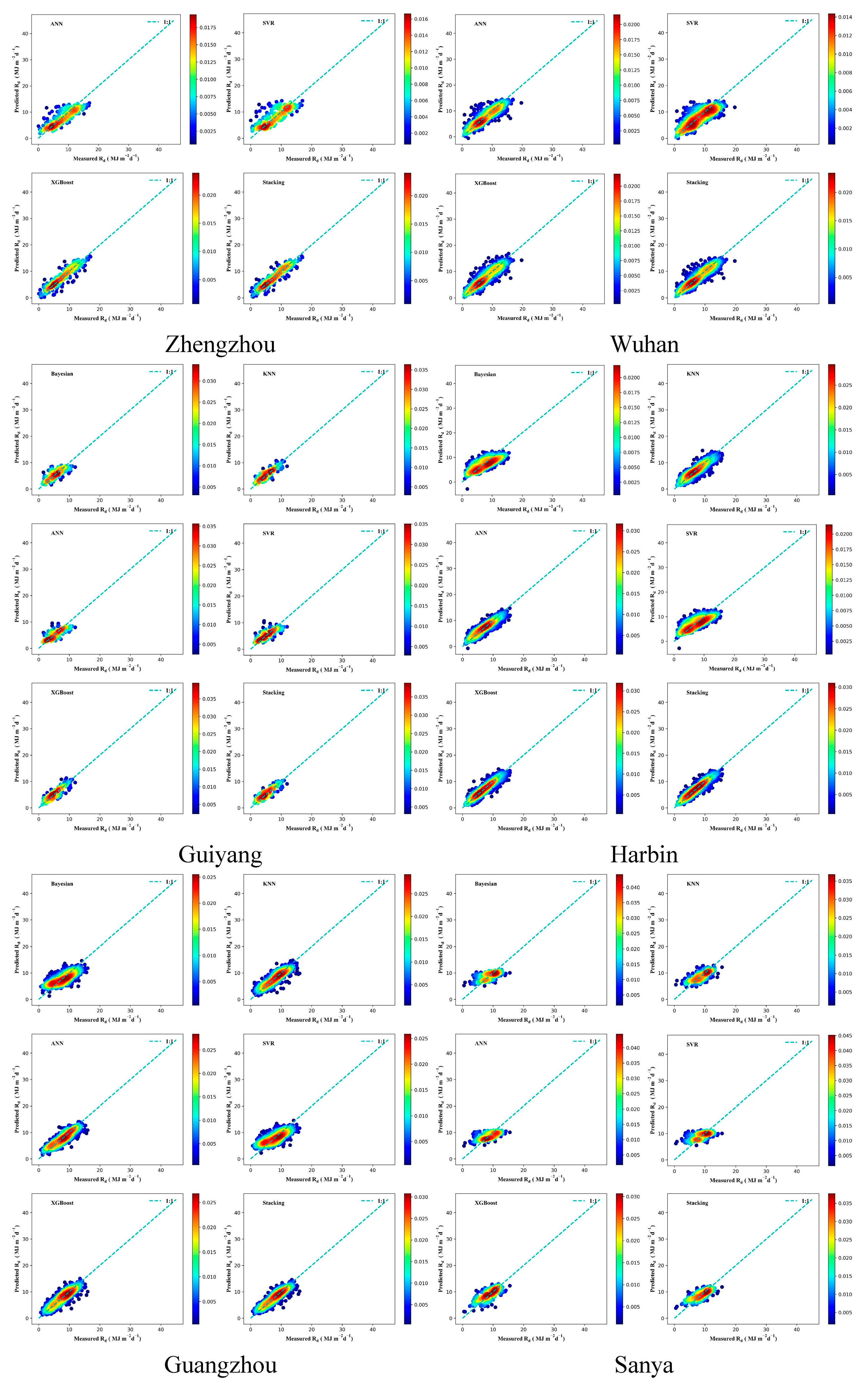
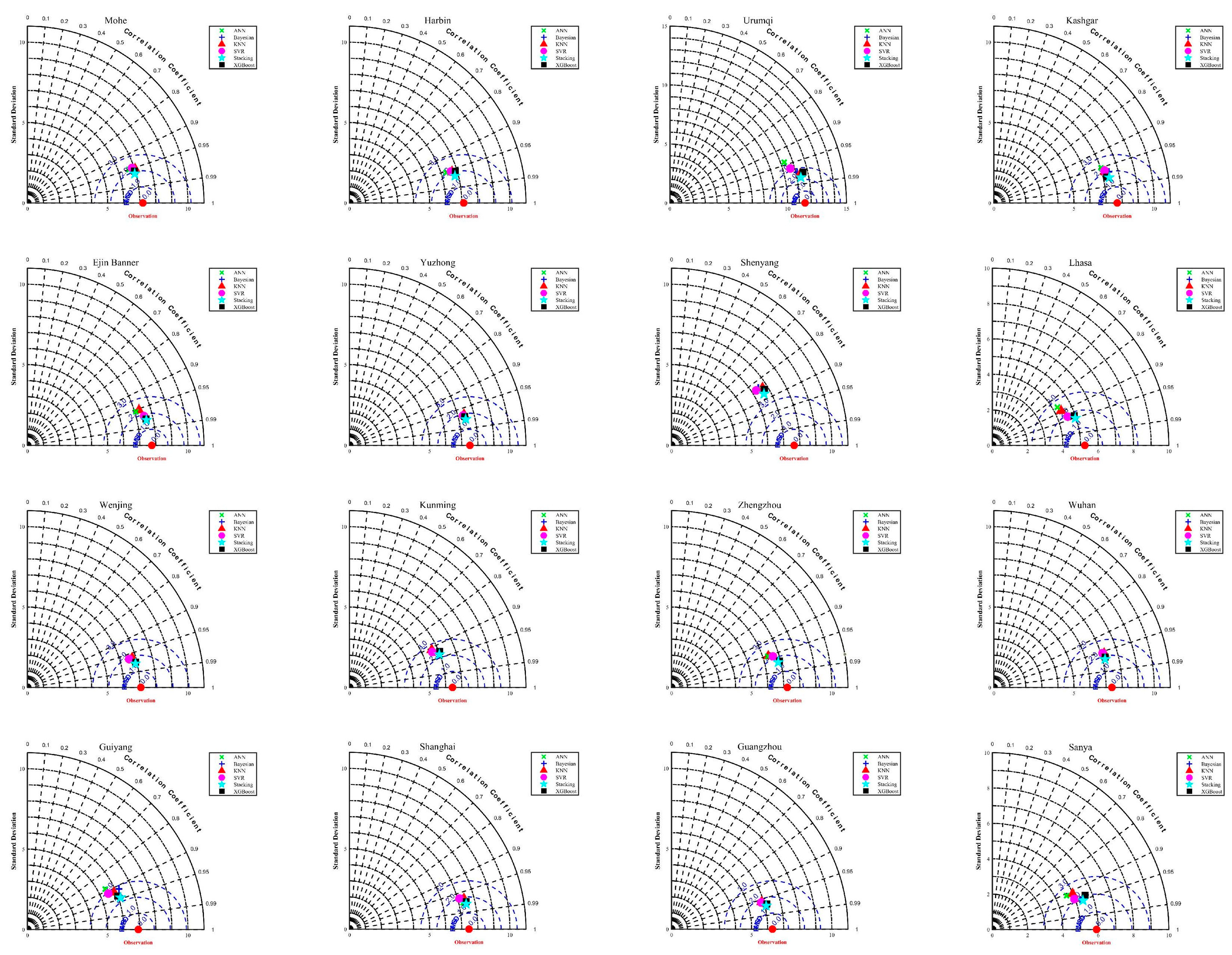
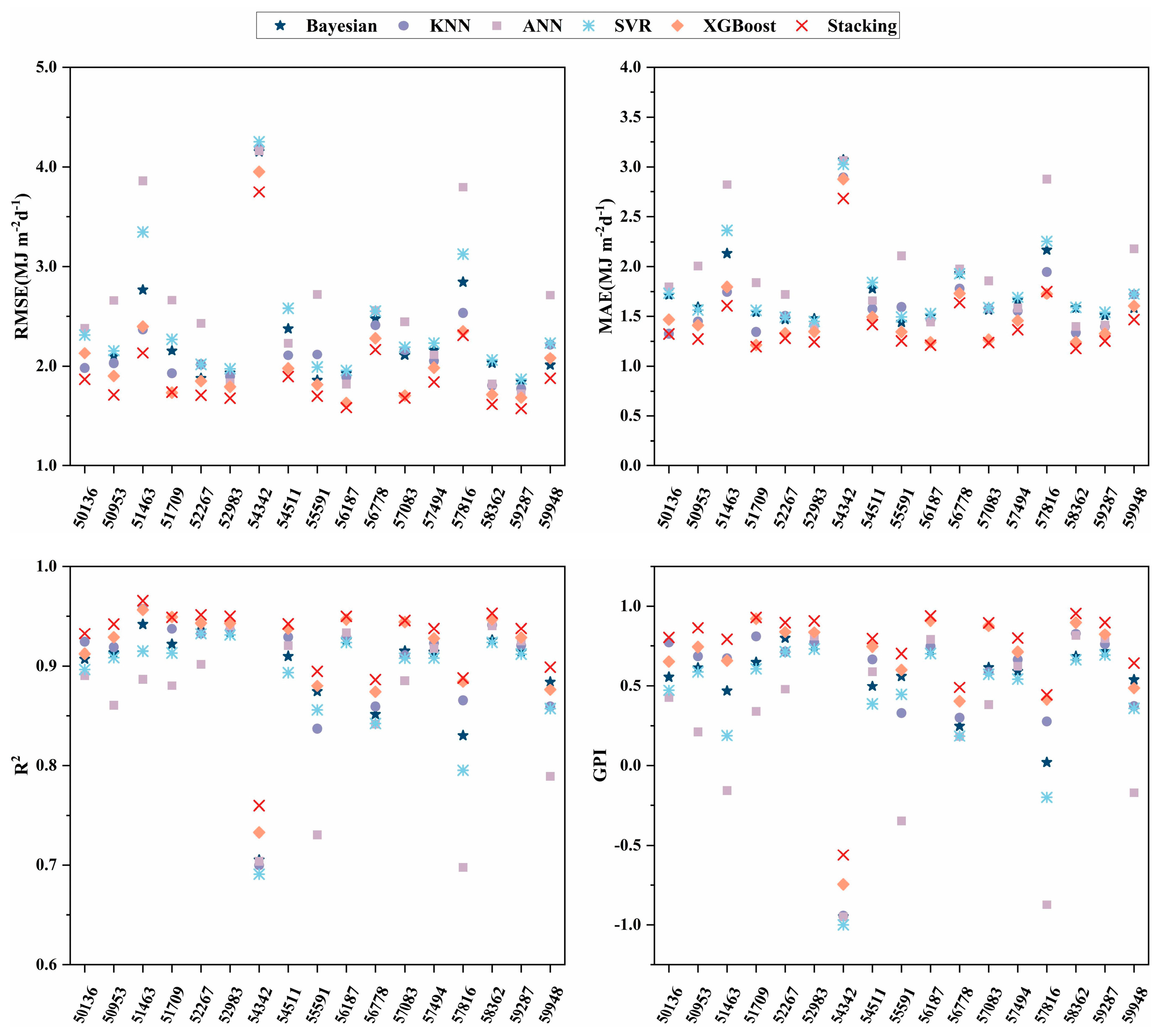
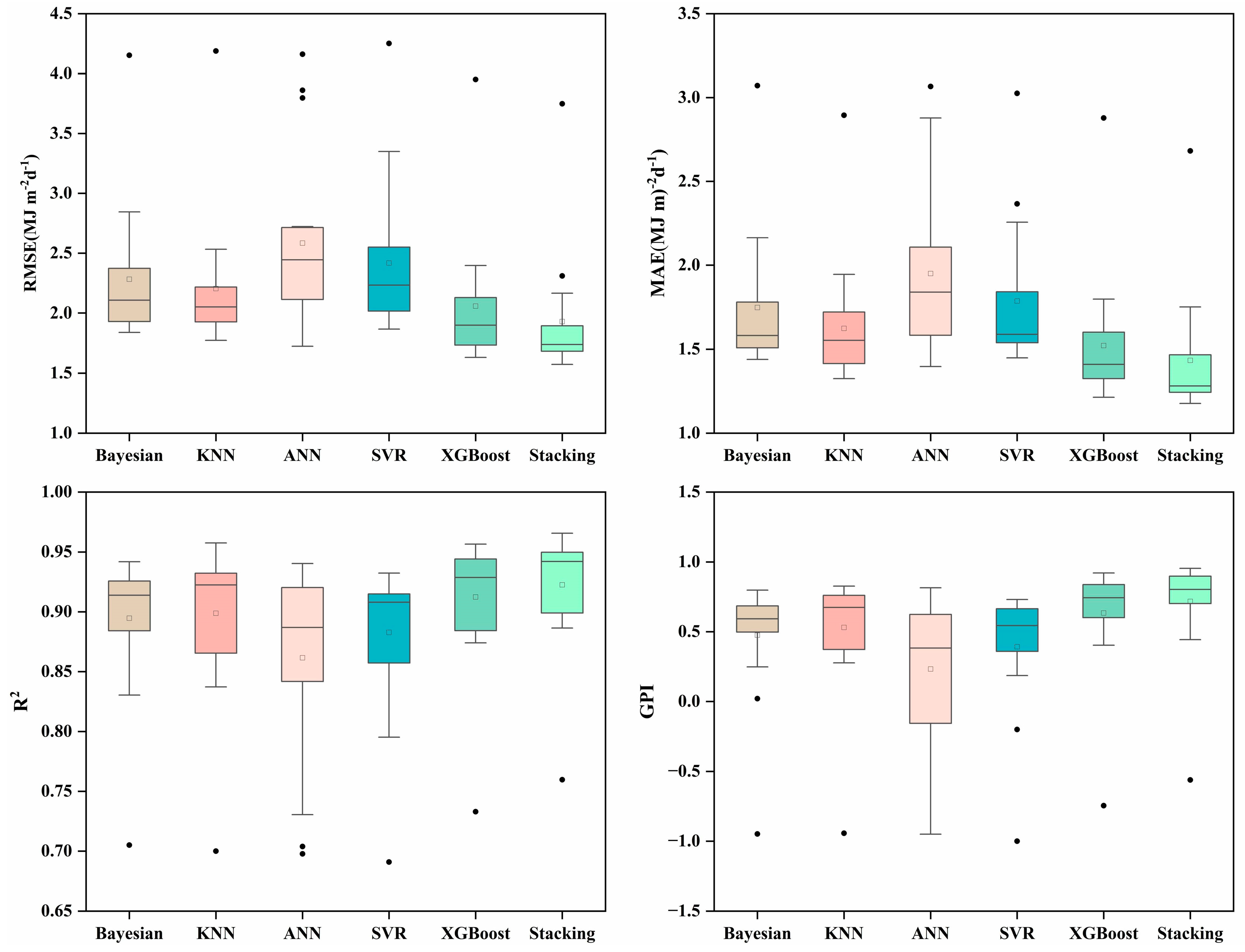
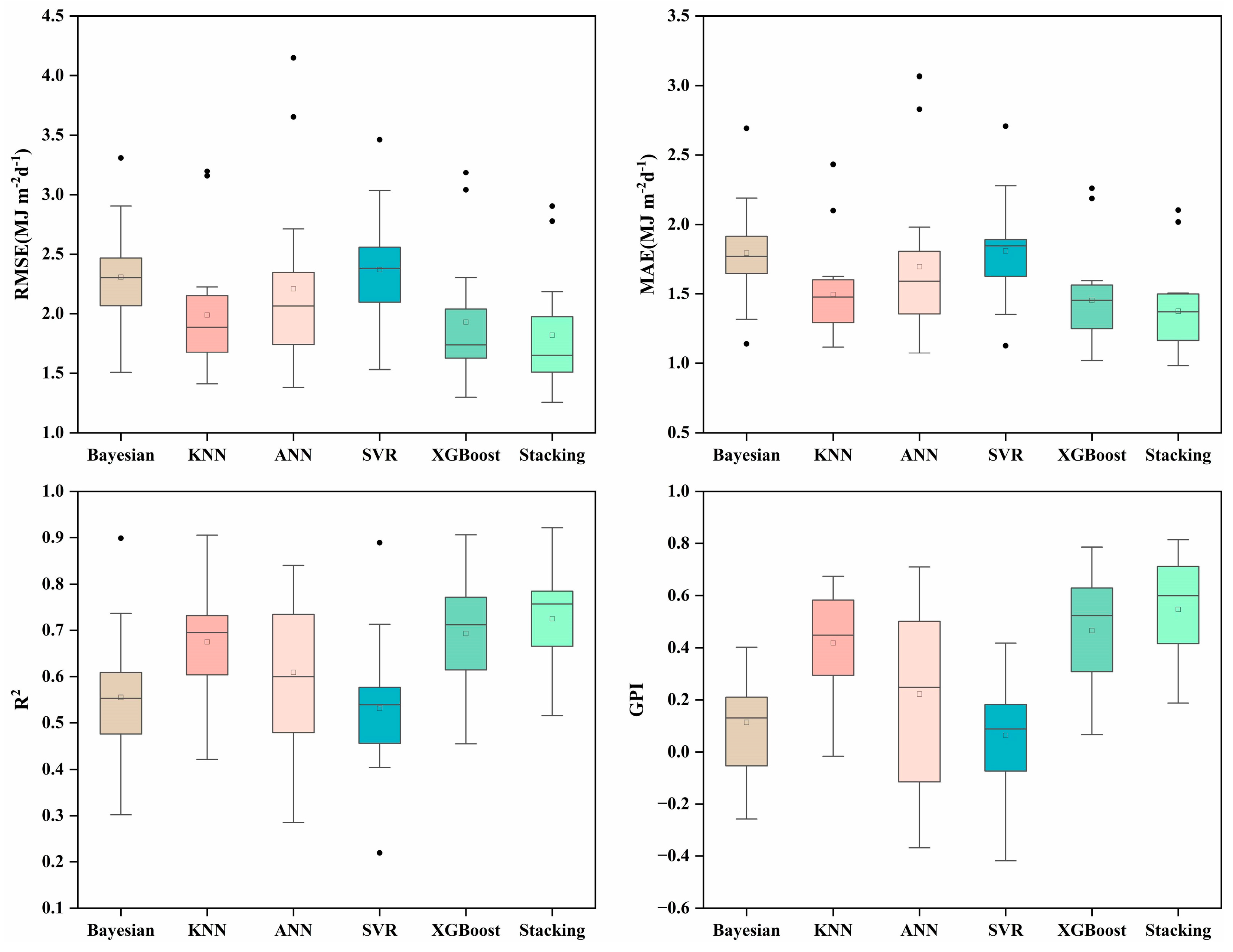
3.3. Performance of Different ML Models in Radiation Estimation
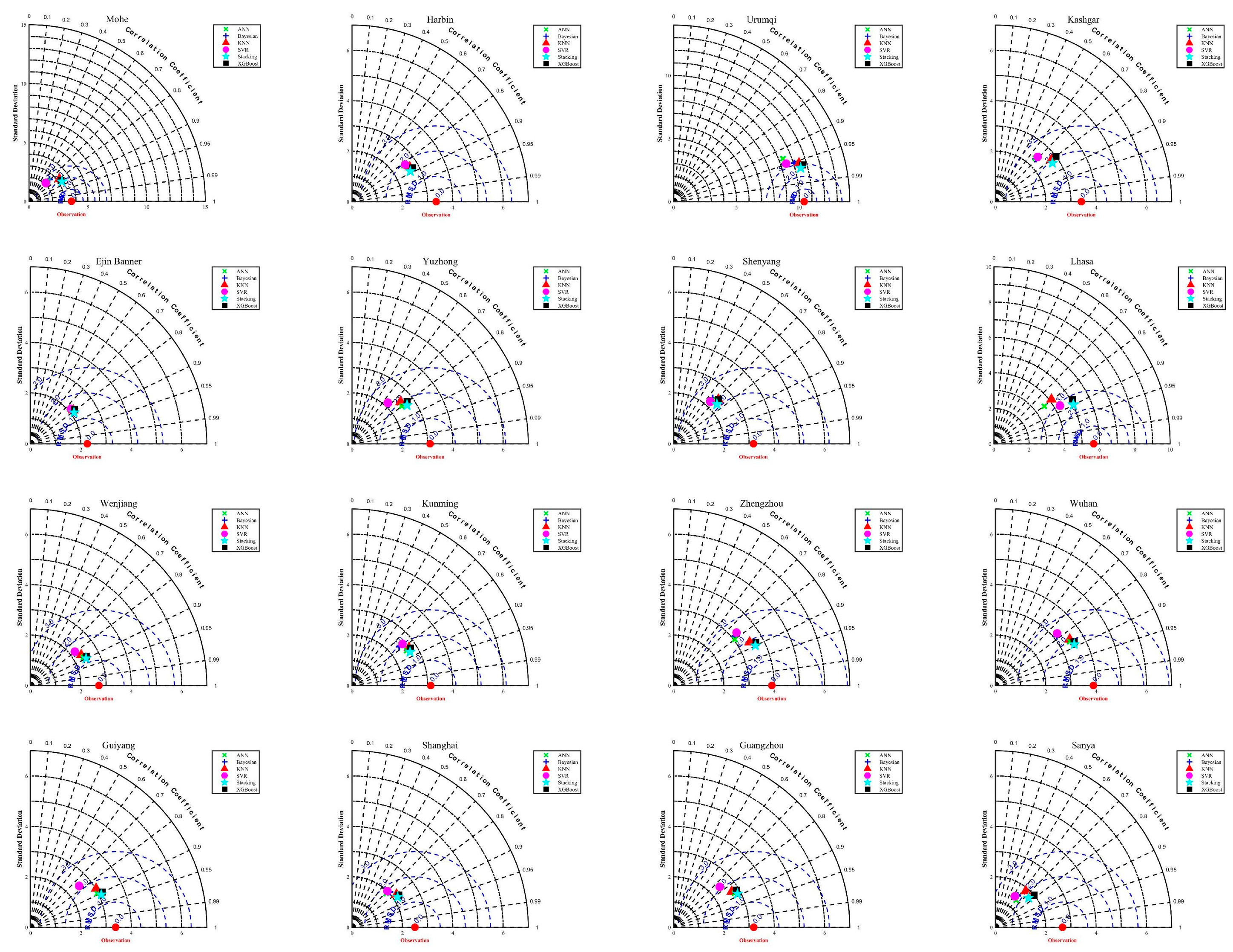
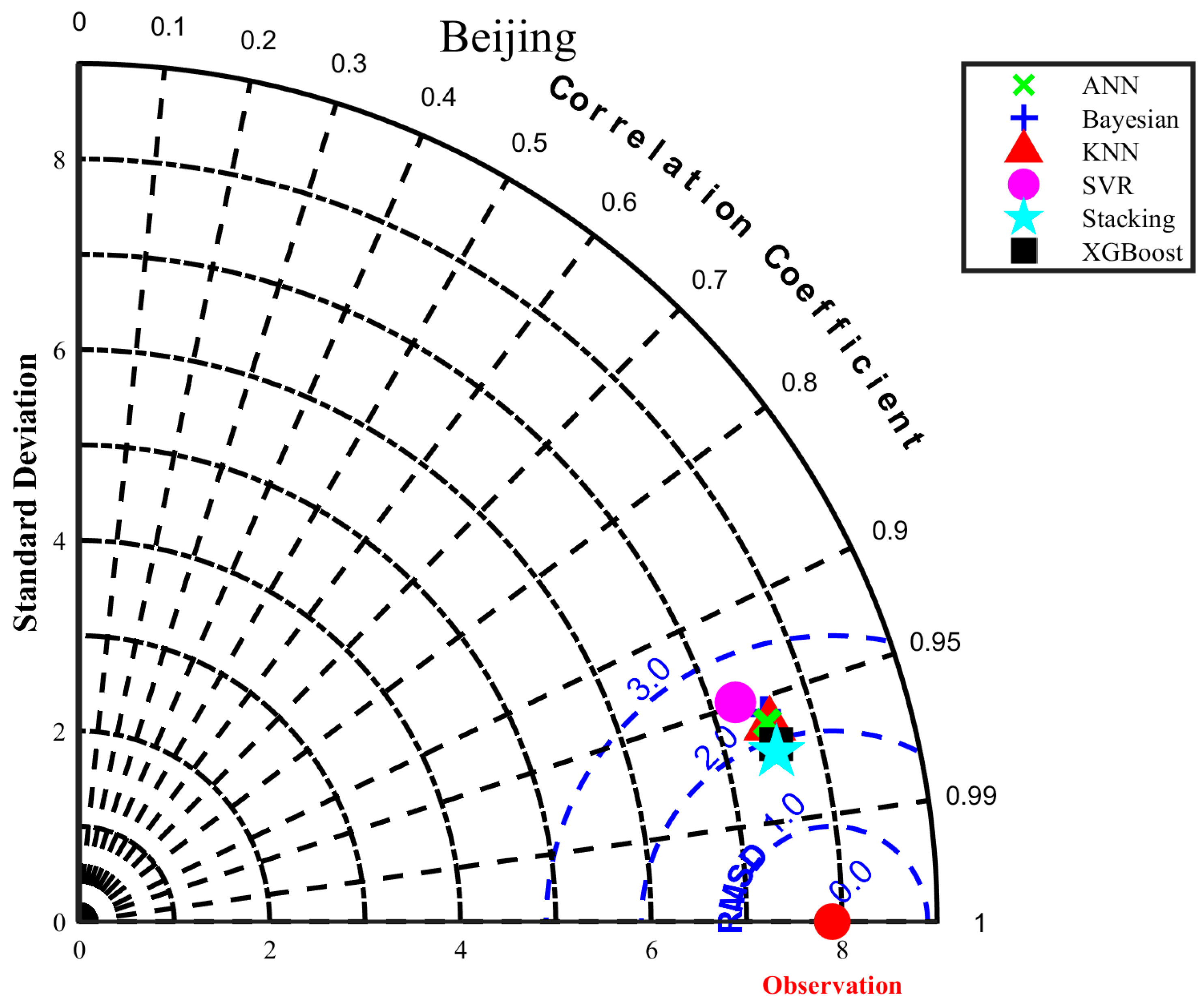
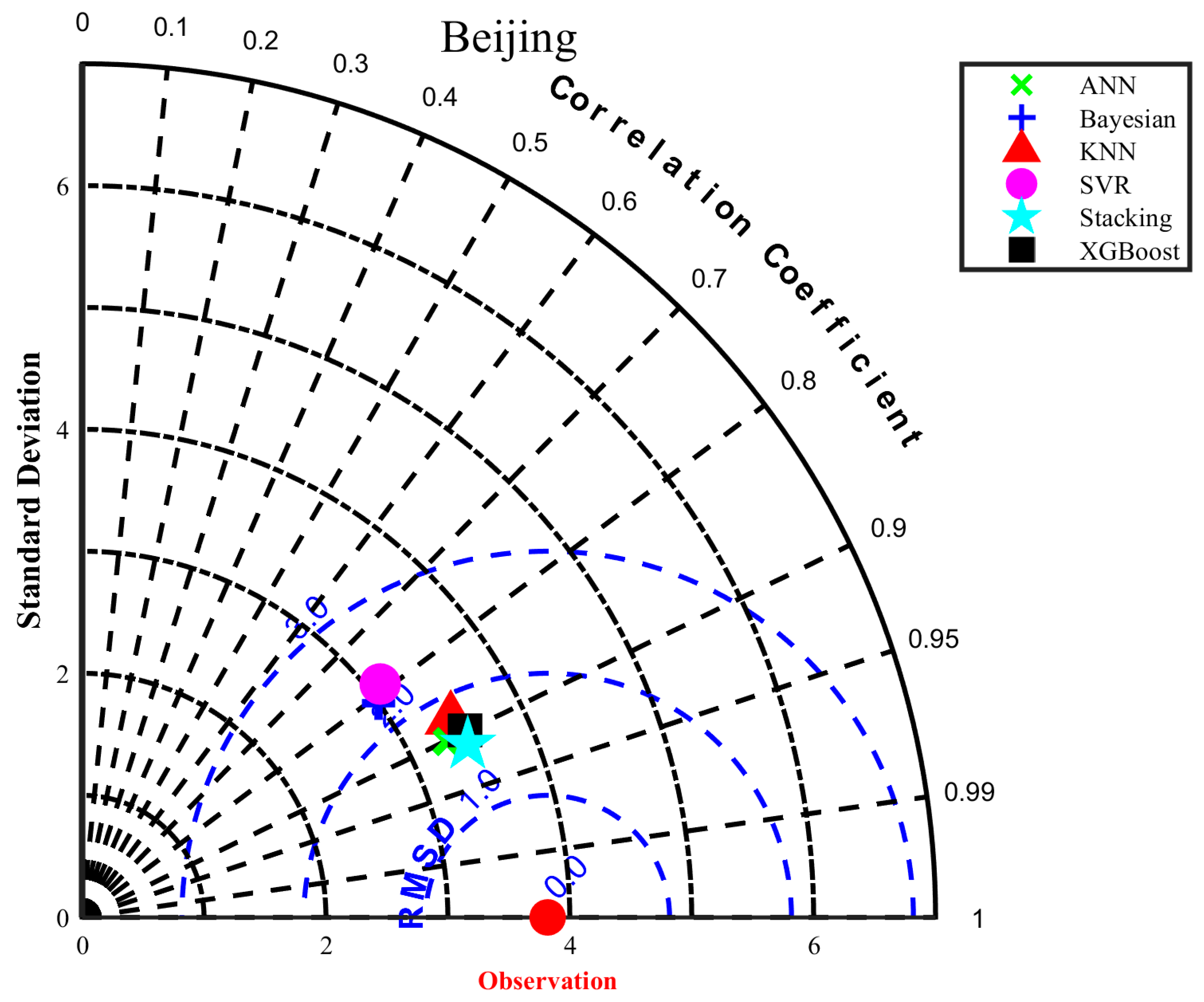
3.4. Solar Radiation Performance of the Stacking Model in Different Regions
4. Conclusions
- (1)
- Among the meteorological factors, n and its related characteristics (Ra and N) have the greatest influence on the prediction of solar radiation (Rs, Rd), whereas O3 has the greatest influence on the air pollution data. The most important feature is n, and the higher its value, the greater the influence on the radiation prediction. Regarding air pollution characteristics, a larger O3 value implies a greater effect on radiation prediction.
- (2)
- Compared with base learners, the proposed stacking model performs optimally with a mean improvement range of 5.70%–25.25% for RMSE, 5.31%–26.48% for MAE, and 1.12%–36.24% for R2, thus highlighting the necessity of ensemble learning model construction.
- (3)
- This study provides a reference for selecting predicted radiation input characteristics in different climatic regions in China. Notably, the accuracy of the proposed stacking model in coastal areas (Shanghai and Guangzhou) is better than that in inland regions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AQI | air quality index |
| CO | carbon monoxide |
| GPI | global performance index |
| MAE | mean absolute error |
| n | sunshine duration |
| N | maximum sunshine duration |
| NO2 | nitrogen dioxide |
| O3 | ozone |
| Pr | air pressure |
| Pt | precipitation |
| R2 | coefficient of determination |
| Ra | extra-terrestrial solar radiation |
| Rd | diffuse solar radiation |
| Rh | relative humidity |
| RMSE | root mean square error |
| Rs | global solar radiation |
| SO2 | sulfur dioxide |
| Tmax | maximum temperature |
| Tmean | mean temperature |
| Tmin | minimum temperature |
| Vpd | vapor pressure deficit |
| Ws | wind speed |
Appendix A
| Station | Selected Features | |
|---|---|---|
| Rs | Rd | |
| Mohe | ‘n’, ‘Ra’, ‘Vpd’, ‘N’, ‘O3’, ‘Tmax’, ‘Pt’, ‘Rh’, ‘Pr’ | ‘N’, ‘Ra’, ‘SO2’, ‘n’, ‘CO’, ‘Pr’, ‘O3’, ‘Rh’, ‘NO2’ |
| Harbin | ‘n’, ‘N’, ‘Ra’, ‘Vpd’, ‘Tmean’, ‘O3’, ‘Pt’, ‘Rh’, ‘Tmax’ | ‘n’, ‘N’, ‘Ra’, ‘Tmin’, ‘Pt’, ‘Tmean’, ‘Tmax’, ‘CO’, ‘Pr’ |
| Urumqi | ‘n’, ‘N’, ‘Ra’, ‘O3’, ‘Pt’, ‘Rh’, ‘NO2’, ‘Vpd’, ‘Tmean’ | ‘n’, ‘N’, ‘Ra’, ‘O3’, ‘NO2’, ‘Rh’, ‘Ws’, ‘Pr’, ‘Tmin’ |
| Kashgar | ‘n’, ‘Ra’, ‘N’, ‘O3’, ‘Tmean’, ‘Tmin’, ‘Rh’, ‘Vpd’, ‘Ws’ | ‘n’, ‘N’, ‘Ra’, ‘PM10’, ‘AQI’, ‘PM2.5’, ‘Tmin’, ‘Ws’, ‘NO2’ |
| Ejin Banner | ‘n’, ‘N’, ‘Ra’, ‘NO2’, ‘Rh’, ‘Tmean’, ‘Vpd’, ‘CO’, ‘SO2’ | ‘n’, ‘N’, ‘Ra’, ‘Ws’, ‘PM10’, ‘Rh’, ‘PM2.5’, ‘Pr’, ‘SO2’ |
| Yuzhong | ‘n’, ‘N’, ‘O3’, ‘Ra’, ‘Tmax’, ‘Vpd’, ‘Tmin’, ‘Tmean’, ‘CO’ | ‘n’, ‘N’, ‘Ra’, ‘Tmax’, ‘NO2’, ‘Tmin’, ‘Vpd’, ‘Pt’, ‘CO’ |
| Shenyang | ‘n’, ‘O3’, ‘N’, ‘Ra’, ‘Pr’, ‘Tmin’, ‘PM2.5’, ‘Vpd’, ‘Tmax’ | ‘Pr’, ‘N’, ‘Ra’, ‘n’, ‘O3’, ‘NO2’, ‘Tmean’, ‘Tmin’, ‘Rh’ |
| Beijing | ‘n’, ‘N’, ‘O3’, ‘Vpd’, ‘Ra’, ‘Tmin’, ‘Pt’, ‘NO2’, ‘Rh’ | ‘n’, ‘N’, ‘Ra’, ‘O3’, ‘PM2.5’, ‘Pt’, ‘Rh’, ‘Vpd’, ‘NO2’ |
| Lhasa | ‘n’, ‘N’, ‘Ra’, ‘Tmax’, ‘PM10’, ‘O3’, ‘Tmean’, ‘Vpd’, ‘Rh’ | ‘n’, ‘Tmax’, ‘PM10’, ‘Rh’, ‘Pr’, ‘Vpd’, ‘N’, ‘O3’, ‘Tmean’ |
| Wenjiang | ‘n’, ‘O3’, ‘N’, ‘Tmax’, ‘Ra’, ‘Vpd’, ‘Tmin’, ‘SO2’, ‘PM10’ | ‘n’, ‘O3’, ‘N’, ‘Ra’, ‘Tmin’, ‘Tmax’, ‘Vpd’, ‘Ws’, ‘Pt’ |
| Kunming | ‘n’, ‘Tmax’, ‘O3’, ‘Vpd’, ‘SO2’, ‘Tmin’, ‘N’, ‘PM2.5’, ‘Ra’ | ‘n’, ‘N’, ‘Ra’, ‘Tmax’, ‘Vpd’, ‘Tmin’, ‘Rh’, ‘O3’, ‘Tmean’ |
| Zhengzhou | ‘n’, ‘N’, ‘Ra’, ‘O3’, ‘Vpd’, ‘Tmax’, ‘Tmean’, ‘Pt’, ‘NO2’ | ‘n’, ‘N’, ‘Ra’, ‘O3’, ‘Pt’, ‘Tmax’, ‘Rh’, ‘Vpd’, ‘SO2’ |
| Wuhan | ‘n’, ‘O3’, ‘N’, ‘Ra’, ‘Pt’, ‘Tmin’, ‘Tmax’, ‘Vpd’, ‘NO2’ | ‘n’, ‘N’, ‘Ra’, ‘O3’, ‘Pt’, ‘Vpd’, ‘CO’, ‘Rh’, ‘Tmax’ |
| Guiyang | ‘n’, ‘N’, ‘Ra’, ‘O3’, ‘Vpd’, ‘Pr’, ‘Tmin’, ‘SO2’, ‘Tmean’ | ‘n’, ‘Vpd’, ‘N’, ‘Ra’, ‘O3’, ‘Rh’, ‘Pr’, ‘Tmax’, ‘NO2’ |
| Shanghai | ‘n’, ‘N’, ‘Ra’, ‘Vpd’, ‘Pt’, ‘O3’, ‘Tmax’, ‘Tmean’, ‘Pr’ | ‘n’, ‘N’, ‘Ra’, ‘Vpd’, ‘Pt’, ‘O3’, ‘PM2.5’, ‘Pr’, ‘PM10’ |
| Guangzhou | ‘n’, ‘N’, ‘O3’, ‘Ra’, ‘Vpd’, ‘Tmean’, ‘Tmax’, ‘Rh’, ‘Pt’ | ‘n’, ‘N’, ‘Ra’, ‘Vpd’, ‘Pt’, ‘O3’, ‘PM2.5’, ‘Pr’, ‘PM10’ |
| Sanya | ‘n’, ‘Tmax’, ‘N’, ‘Ra’, ‘Ws’, ‘Tmean’, ‘Vpd’, ‘Tmin’, ‘Pt’ | ‘n’, ‘Ra’, ‘N’, ‘Tmax’, ‘Pt’, ‘Vpd’, ‘Ws’, ‘Pr’, ‘Tmean’ |
| Station | Model | Rs | Rd | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (MJ m−2 d−1) | MAE (MJ m−2 d−1) | R2 | GPI | Rank | RMSE (M Jm−2 d−1) | MAE (MJ m−2 d−1) | R2 | GPI | Rank | ||
| Mohe | Bayesian | 2.1918 | 1.7144 | 0.9071 | 0.5563 | 64 | 2.7046 | 1.9142 | 0.4392 | −0.1873 | 96 |
| KNN | 1.9807 | 1.3251 | 0.9241 | 0.7711 | 28 | 2.1523 | 1.4765 | 0.6449 | 0.3683 | 50 | |
| ANN | 2.3784 | 1.7955 | 0.8906 | 0.4265 | 75 | 2.7138 | 1.9335 | 0.4354 | −0.1958 | 97 | |
| SVR | 2.3133 | 1.7336 | 0.8965 | 0.4724 | 71 | 2.7881 | 1.8902 | 0.4040 | −0.2662 | 99 | |
| XGBoost | 2.1291 | 1.4671 | 0.9123 | 0.6532 | 50 | 2.2428 | 1.5118 | 0.6144 | 0.3079 | 52 | |
| Stacking | 1.8686 | 1.3225 | 0.9325 | 0.8029 | 20 | 2.0729 | 1.4494 | 0.6706 | 0.4179 | 39 | |
| Harbin | Bayesian | 2.0972 | 1.5900 | 0.9132 | 0.6140 | 55 | 1.9911 | 1.4315 | 0.6453 | 0.3905 | 45 |
| KNN | 2.0296 | 1.4477 | 0.9187 | 0.6868 | 43 | 1.7722 | 1.2932 | 0.7190 | 0.5618 | 28 | |
| ANN | 2.6591 | 2.0056 | 0.8605 | 0.2122 | 87 | 2.1163 | 1.5929 | 0.5993 | 0.2476 | 57 | |
| SVR | 2.1542 | 1.5628 | 0.9084 | 0.5886 | 60 | 1.9804 | 1.3846 | 0.6491 | 0.4184 | 38 | |
| XGBoost | 1.9013 | 1.4095 | 0.9287 | 0.7435 | 33 | 1.7395 | 1.2146 | 0.7293 | 0.6141 | 19 | |
| Stacking | 1.7134 | 1.2734 | 0.9421 | 0.8639 | 12 | 1.6492 | 1.1659 | 0.7567 | 0.6764 | 12 | |
| Urumqi | Bayesian | 2.7671 | 2.1300 | 0.9419 | 0.4683 | 72 | 3.3087 | 2.6906 | 0.8984 | 0.2571 | 56 |
| KNN | 2.3679 | 1.7471 | 0.9575 | 0.6740 | 45 | 3.1970 | 2.0990 | 0.9051 | 0.4400 | 37 | |
| ANN | 3.8613 | 2.8224 | 0.8869 | −0.1551 | 92 | 4.1473 | 3.0654 | 0.8403 | −0.1159 | 92 | |
| SVR | 3.3488 | 2.3650 | 0.9149 | 0.1885 | 88 | 3.4619 | 2.7063 | 0.8887 | 0.1903 | 63 | |
| XGBoost | 2.3976 | 1.7975 | 0.9564 | 0.6590 | 49 | 3.1848 | 2.1865 | 0.9058 | 0.3991 | 43 | |
| Stacking | 2.1316 | 1.6042 | 0.9655 | 0.7917 | 25 | 2.9038 | 2.0177 | 0.9217 | 0.5027 | 32 | |
| Kashgar | Bayesian | 2.1529 | 1.5410 | 0.9218 | 0.6486 | 51 | 2.4672 | 1.9025 | 0.4783 | −0.0732 | 90 |
| KNN | 1.9285 | 1.3431 | 0.9372 | 0.8094 | 19 | 2.1505 | 1.6264 | 0.6037 | 0.2387 | 60 | |
| ANN | 2.6621 | 1.8388 | 0.8804 | 0.3406 | 82 | 2.5345 | 1.9817 | 0.4495 | −0.1522 | 95 | |
| SVR | 2.2693 | 1.5594 | 0.9131 | 0.6072 | 56 | 2.4775 | 1.8891 | 0.4739 | −0.0730 | 89 | |
| XGBoost | 1.7351 | 1.2141 | 0.9492 | 0.9210 | 4 | 2.0379 | 1.5694 | 0.6441 | 0.3352 | 51 | |
| Stacking | 1.7402 | 1.1964 | 0.9489 | 0.9293 | 3 | 1.9745 | 1.4958 | 0.6659 | 0.3889 | 46 | |
| Ejin Banner | Bayesian | 1.8779 | 1.4681 | 0.9413 | 0.7982 | 22 | 1.5072 | 1.1420 | 0.5530 | 0.3980 | 44 |
| KNN | 2.0167 | 1.5041 | 0.9323 | 0.7136 | 39 | 1.5122 | 1.1182 | 0.5500 | 0.4052 | 41 | |
| ANN | 2.4295 | 1.7217 | 0.9018 | 0.4803 | 70 | 1.5234 | 1.1510 | 0.5433 | 0.3800 | 48 | |
| SVR | 2.0163 | 1.4906 | 0.9323 | 0.7138 | 38 | 1.5298 | 1.1286 | 0.5394 | 0.3852 | 47 | |
| XGBoost | 1.8504 | 1.3298 | 0.9430 | 0.8375 | 13 | 1.4453 | 1.0650 | 0.5889 | 0.4861 | 34 | |
| Stacking | 1.7101 | 1.2810 | 0.9513 | 0.8974 | 9 | 1.3756 | 1.0100 | 0.6276 | 0.5676 | 27 | |
| Yuzhong | Bayesian | 1.9320 | 1.4760 | 0.9338 | 0.7507 | 30 | 2.3032 | 1.7705 | 0.4478 | −0.0532 | 88 |
| KNN | 1.8964 | 1.4146 | 0.9362 | 0.7728 | 27 | 1.9778 | 1.4778 | 0.5928 | 0.2936 | 54 | |
| ANN | 1.8332 | 1.4079 | 0.9404 | 0.8116 | 18 | 1.9612 | 1.4817 | 0.5996 | 0.3014 | 53 | |
| SVR | 1.9735 | 1.4485 | 0.9309 | 0.7309 | 34 | 2.3815 | 1.8120 | 0.4096 | −0.1275 | 93 | |
| XGBoost | 1.7937 | 1.3454 | 0.9429 | 0.8356 | 14 | 1.9725 | 1.4856 | 0.5950 | 0.2929 | 55 | |
| Stacking | 1.6804 | 1.2441 | 0.9499 | 0.9079 | 6 | 1.8468 | 1.3773 | 0.6449 | 0.4160 | 40 | |
| Shenyang | Bayesian | 4.1527 | 3.0711 | 0.7051 | −0.9483 | 100 | 2.3879 | 1.6394 | 0.4344 | −0.0844 | 91 |
| KNN | 4.1885 | 2.8946 | 0.7000 | −0.9434 | 99 | 2.2269 | 1.5212 | 0.5081 | 0.1522 | 70 | |
| ANN | 4.1614 | 3.0661 | 0.7039 | −0.9502 | 101 | 2.3477 | 1.5913 | 0.4533 | −0.0029 | 85 | |
| SVR | 4.2514 | 3.0254 | 0.6909 | −1.0000 | 102 | 2.4509 | 1.6019 | 0.4042 | −0.1493 | 94 | |
| XGBoost | 3.9516 | 2.8782 | 0.7330 | −0.7450 | 97 | 2.3046 | 1.5955 | 0.4732 | 0.0665 | 81 | |
| Stacking | 3.7482 | 2.6814 | 0.7597 | −0.5614 | 96 | 2.1878 | 1.4982 | 0.5253 | 0.1877 | 64 | |
| Beijing | Bayesian | 2.3739 | 1.7793 | 0.9097 | 0.4979 | 67 | 2.3646 | 1.7941 | 0.6165 | 0.1828 | 65 |
| KNN | 2.1076 | 1.5725 | 0.9288 | 0.6669 | 46 | 1.7896 | 1.3066 | 0.7803 | 0.6426 | 15 | |
| ANN | 2.2310 | 1.6586 | 0.9202 | 0.5896 | 59 | 1.8379 | 1.3631 | 0.7683 | 0.5984 | 23 | |
| SVR | 2.5790 | 1.8408 | 0.8934 | 0.3871 | 78 | 2.4842 | 1.7709 | 0.5767 | 0.1301 | 73 | |
| XGBoost | 1.9783 | 1.4928 | 0.9373 | 0.7461 | 32 | 1.7378 | 1.2575 | 0.7929 | 0.6840 | 11 | |
| Stacking | 1.8961 | 1.4168 | 0.9424 | 0.7953 | 24 | 1.6405 | 1.1985 | 0.8154 | 0.7444 | 5 | |
| Lhasa | Bayesian | 1.8594 | 1.4395 | 0.8742 | 0.5609 | 63 | 2.9043 | 2.1891 | 0.7368 | 0.1671 | 69 |
| KNN | 2.1159 | 1.5922 | 0.8372 | 0.3301 | 83 | 3.1569 | 2.4330 | 0.6890 | −0.0161 | 86 | |
| ANN | 2.7218 | 2.1076 | 0.7305 | −0.3469 | 95 | 3.6526 | 2.8312 | 0.5837 | −0.3688 | 101 | |
| SVR | 1.9900 | 1.4940 | 0.8560 | 0.4455 | 73 | 3.0334 | 2.2771 | 0.7129 | 0.0884 | 78 | |
| XGBoost | 1.8151 | 1.3435 | 0.8802 | 0.6014 | 57 | 3.0388 | 2.2588 | 0.7118 | 0.0883 | 79 | |
| Stacking | 1.7011 | 1.2535 | 0.8947 | 0.7020 | 41 | 2.7780 | 2.1024 | 0.7592 | 0.2428 | 58 | |
| Wenjiang | Bayesian | 1.9252 | 1.5010 | 0.9258 | 0.7241 | 35 | 1.6984 | 1.3169 | 0.6088 | 0.4025 | 42 |
| KNN | 1.8894 | 1.4664 | 0.9285 | 0.7474 | 31 | 1.4109 | 1.1182 | 0.7300 | 0.6746 | 13 | |
| ANN | 1.8219 | 1.4432 | 0.9335 | 0.7909 | 26 | 1.3805 | 1.0739 | 0.7415 | 0.7014 | 9 | |
| SVR | 1.9572 | 1.5264 | 0.9233 | 0.7031 | 40 | 1.7294 | 1.3526 | 0.5944 | 0.3713 | 49 | |
| XGBoost | 1.6322 | 1.2413 | 0.9467 | 0.9095 | 5 | 1.2996 | 1.0189 | 0.7710 | 0.7714 | 4 | |
| Stacking | 1.5830 | 1.2111 | 0.9498 | 0.9394 | 2 | 1.2589 | 0.9811 | 0.7851 | 0.8055 | 2 | |
| Kunming | Bayesian | 2.4756 | 1.9301 | 0.8515 | 0.2480 | 86 | 2.0656 | 1.6469 | 0.5633 | 0.2106 | 62 |
| KNN | 2.4103 | 1.7799 | 0.8592 | 0.3005 | 84 | 1.7261 | 1.3115 | 0.6951 | 0.5189 | 31 | |
| ANN | 2.5556 | 1.9765 | 0.8418 | 0.1826 | 90 | 1.7430 | 1.3557 | 0.6891 | 0.5013 | 33 | |
| SVR | 2.5512 | 1.9286 | 0.8423 | 0.1862 | 89 | 2.0952 | 1.6264 | 0.5507 | 0.1824 | 66 | |
| XGBoost | 2.2803 | 1.7327 | 0.8740 | 0.4028 | 77 | 1.7173 | 1.3221 | 0.6982 | 0.5231 | 30 | |
| Stacking | 2.1655 | 1.6358 | 0.8864 | 0.4908 | 68 | 1.6212 | 1.2413 | 0.7310 | 0.6037 | 20 | |
| Zhengzhou | Bayesian | 2.1074 | 1.5631 | 0.9149 | 0.6162 | 54 | 2.5686 | 1.9922 | 0.5672 | 0.0419 | 83 |
| KNN | 2.1584 | 1.5784 | 0.9107 | 0.5885 | 61 | 1.8867 | 1.3968 | 0.7665 | 0.5797 | 26 | |
| ANN | 2.4454 | 1.8581 | 0.8854 | 0.3826 | 79 | 2.3237 | 1.8028 | 0.6458 | 0.2387 | 59 | |
| SVR | 2.1919 | 1.5861 | 0.9079 | 0.5743 | 62 | 2.6730 | 2.0114 | 0.5313 | −0.0500 | 87 | |
| XGBoost | 1.7064 | 1.2659 | 0.9442 | 0.8755 | 11 | 1.7201 | 1.2745 | 0.8059 | 0.6944 | 10 | |
| Stacking | 1.6830 | 1.2375 | 0.9457 | 0.8960 | 10 | 1.6387 | 1.2315 | 0.8238 | 0.7406 | 6 | |
| Wuhan | Bayesian | 2.1617 | 1.6598 | 0.9138 | 0.5922 | 58 | 2.4688 | 1.9253 | 0.5975 | 0.1197 | 75 |
| KNN | 2.0503 | 1.5531 | 0.9225 | 0.6653 | 47 | 2.0680 | 1.5262 | 0.7176 | 0.4480 | 36 | |
| ANN | 2.1136 | 1.5833 | 0.9176 | 0.6240 | 53 | 2.0640 | 1.5253 | 0.7187 | 0.4500 | 35 | |
| SVR | 2.2333 | 1.6909 | 0.9080 | 0.5443 | 65 | 2.5581 | 1.9822 | 0.5679 | 0.0467 | 82 | |
| XGBoost | 1.9836 | 1.4564 | 0.9274 | 0.7139 | 37 | 1.9261 | 1.4523 | 0.7550 | 0.5367 | 29 | |
| Stacking | 1.8406 | 1.3651 | 0.9375 | 0.7989 | 21 | 1.8608 | 1.3714 | 0.7714 | 0.5988 | 22 | |
| Guiyang | Bayesian | 2.8445 | 2.1639 | 0.8303 | 0.0200 | 91 | 1.8099 | 1.3897 | 0.4760 | 0.1750 | 68 |
| KNN | 2.5333 | 1.9454 | 0.8654 | 0.2771 | 85 | 1.4346 | 1.1220 | 0.6708 | 0.5820 | 25 | |
| ANN | 3.7968 | 2.8784 | 0.6977 | −0.8734 | 98 | 1.8045 | 1.4026 | 0.4791 | 0.1812 | 67 | |
| SVR | 3.1248 | 2.2558 | 0.7953 | −0.1992 | 94 | 1.8442 | 1.3974 | 0.4560 | 0.1374 | 71 | |
| XGBoost | 2.3494 | 1.7264 | 0.8843 | 0.4144 | 76 | 1.3859 | 1.0940 | 0.6928 | 0.6302 | 16 | |
| Stacking | 2.3101 | 1.7507 | 0.8881 | 0.4431 | 74 | 1.3464 | 1.0684 | 0.7100 | 0.6684 | 14 | |
| Shanghai | Bayesian | 2.0299 | 1.5825 | 0.9258 | 0.6848 | 44 | 2.2584 | 1.8567 | 0.5533 | 0.1297 | 74 |
| KNN | 1.8070 | 1.3368 | 0.9412 | 0.8271 | 15 | 1.6760 | 1.2782 | 0.7540 | 0.6188 | 17 | |
| ANN | 1.8217 | 1.3967 | 0.9402 | 0.8152 | 17 | 1.5510 | 1.2025 | 0.7893 | 0.7105 | 8 | |
| SVR | 2.0611 | 1.5891 | 0.9235 | 0.6648 | 48 | 2.2541 | 1.8447 | 0.5550 | 0.1336 | 72 | |
| XGBoost | 1.7172 | 1.2426 | 0.9469 | 0.8976 | 8 | 1.4645 | 1.1032 | 0.8122 | 0.7855 | 3 | |
| Stacking | 1.6160 | 1.1773 | 0.9530 | 0.9542 | 1 | 1.4217 | 1.0770 | 0.8230 | 0.8135 | 1 | |
| Guangzhou | Bayesian | 1.8411 | 1.5085 | 0.9145 | 0.7142 | 36 | 2.1980 | 1.7564 | 0.5240 | 0.1089 | 76 |
| KNN | 1.7749 | 1.3943 | 0.9205 | 0.7609 | 29 | 1.6496 | 1.2628 | 0.7319 | 0.5947 | 24 | |
| ANN | 1.7249 | 1.4105 | 0.9249 | 0.7957 | 23 | 1.6422 | 1.2846 | 0.7343 | 0.6006 | 21 | |
| SVR | 1.8690 | 1.5391 | 0.9119 | 0.6943 | 42 | 2.2258 | 1.7745 | 0.5119 | 0.0820 | 80 | |
| XGBoost | 1.6858 | 1.3248 | 0.9283 | 0.8226 | 16 | 1.6252 | 1.2496 | 0.7398 | 0.6142 | 18 | |
| Stacking | 1.5737 | 1.2529 | 0.9375 | 0.8980 | 7 | 1.5092 | 1.1474 | 0.7756 | 0.7123 | 7 | |
| Sanya | Bayesian | 2.0116 | 1.5810 | 0.8841 | 0.5400 | 66 | 2.2276 | 1.7637 | 0.3020 | −0.2575 | 98 |
| KNN | 2.2169 | 1.7200 | 0.8592 | 0.3728 | 80 | 2.0277 | 1.6016 | 0.4216 | 0.0126 | 84 | |
| ANN | 2.7130 | 2.1768 | 0.7892 | −0.1700 | 93 | 2.2544 | 1.8058 | 0.2851 | −0.3018 | 100 | |
| SVR | 2.2331 | 1.7238 | 0.8572 | 0.3592 | 81 | 2.3561 | 1.8536 | 0.2191 | −0.4186 | 102 | |
| XGBoost | 2.0795 | 1.6019 | 0.8761 | 0.4856 | 69 | 1.9681 | 1.5654 | 0.4551 | 0.0904 | 77 | |
| Stacking | 1.8783 | 1.4672 | 0.8989 | 0.6438 | 52 | 1.8562 | 1.5052 | 0.5153 | 0.2148 | 61 | |



References
- Acikgoz, H. A novel approach based on integration of convolutional neural networks and deep feature selection for short-term solar radiation forecasting. Appl. Energy 2022, 305, 117912. [Google Scholar] [CrossRef]
- Sohrabi Geshnigani, F.; Golabi, M.R.; Mirabbasi, R.; Tahroudi, M.N. Daily solar radiation estimation in Belleville station, Illinois, using ensemble artificial intelligence approaches. Eng. Appl. Artif. Intell. 2023, 120, 105839. [Google Scholar] [CrossRef]
- Ajith, M.; Martínez-Ramón, M. Deep learning based solar radiation micro forecast by fusion of infrared cloud images and radiation data. Appl. Energy 2021, 294, 117014. [Google Scholar] [CrossRef]
- Mayer, M.J. Benefits of physical and machine learning hybridization for photovoltaic power forecasting. Renew. Sustain. Energy Rev. 2022, 168, 112772. [Google Scholar] [CrossRef]
- Amiri, B.; Gómez-Orellana, A.M.; Gutiérrez, P.A.; Dizène, R.; Hervás-Martínez, C.; Dahmani, K. A novel approach for global solar irradiation forecasting on tilted plane using Hybrid Evolutionary Neural Networks. J. Clean. Prod. 2021, 287, 125577. [Google Scholar] [CrossRef]
- Shao, C.; Yang, K.; Tang, W.; He, Y.; Jiang, Y.; Lu, H.; Fu, H.; Zheng, J. Convolutional neural network-based homogenization for constructing a long-term global surface solar radiation dataset. Renew. Sustain. Energy Rev. 2022, 169, 112952. [Google Scholar] [CrossRef]
- Yang, D.; Gueymard, C.A. Ensemble model output statistics for the separation of direct and diffuse components from 1-min global irradiance. Sol. Energy 2020, 208, 591–603. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhang, Q.; Zhao, L.; Gong, D. Comparison of artificial intelligence and empirical models for estimation of daily diffuse solar radiation in North China Plain. Int. J. Hydrogen Energy 2017, 42, 14418–14428. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Gandhi, O.; Srinivasan, D. Can we justify producing univariate machine-learning forecasts with satellite-derived solar irradiance? Appl. Energy 2020, 259, 114122. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.; Wang, D.; Liu, Y. A multi-step ahead global solar radiation prediction method using an attention-based transformer model with an interpretable mechanism. Int. J. Hydrogen Energy 2023, 48, 15317–15330. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Zhu, C.; Zou, L.; Zhang, M.; Feng, L.; Cao, Q. Predicting surface solar radiation using a hybrid radiative Transfer–Machine learning model. Renew. Sustain. Energy Rev. 2023, 173, 113105. [Google Scholar] [CrossRef]
- Gao, Y.; Li, P.; Yang, H.; Wang, J. A solar radiation intelligent forecasting framework based on feature selection and multivariable fuzzy time series. Eng. Appl. Artif. Intell. 2023, 126, 106986. [Google Scholar] [CrossRef]
- Xue, X. Prediction of daily diffuse solar radiation using artificial neural networks. Int. J. Hydrogen Energy 2017, 42, 28214–28221. [Google Scholar] [CrossRef]
- Yang, D. Correlogram, predictability error growth, and bounds of mean square error of solar irradiance forecasts. Renew. Sustain. Energy Rev. 2022, 167, 112736. [Google Scholar] [CrossRef]
- Huang, C.; Shi, H.; Yang, D.; Gao, L.; Zhang, P.; Fu, D.; Chen, Q.; Yuan, Y.; Liu, M.; Hu, B.; et al. Retrieval of sub-kilometer resolution solar irradiance from Fengyun-4A satellite using a region-adapted Heliosat-2 method. Sol. Energy 2023, 264, 112038. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Casillas-Pérez, D.; Salcedo-Sanz, S. Boosting solar radiation predictions with global climate models, observational predictors and hybrid deep-machine learning algorithms. Appl. Energy 2022, 316, 119063. [Google Scholar] [CrossRef]
- Bailek, N.; Bouchouicha, K.; Al-Mostafa, Z.; El-Shimy, M.; Aoun, N.; Slimani, A.; Al-Shehri, S. A new empirical model for forecasting the diffuse solar radiation over Sahara in the Algerian Big South. Renew. Energy 2018, 117, 530–537. [Google Scholar] [CrossRef]
- De Souza, J.L.; Lyra, G.B.; Dos Santos, C.M.; Ferreira, R.A., Jr.; Tiba, C.; Lyra, G.B.; Lemes, M.A.M. Empirical models of daily and monthly global solar irradiation using sunshine duration for Alagoas State, Northeastern Brazil. Sustain. Energy Technol. Assess. 2016, 14, 35–45. [Google Scholar] [CrossRef]
- Uçkan, İ.; Khudhur, K.M. Improving of global solar radiation forecast by comparing other meteorological parameter models with sunshine duration models. Environ. Sci. Pollut. Res. 2022, 29, 37867–37881. [Google Scholar] [CrossRef]
- Alizamir, M.; Shiri, J.; Fard, A.F.; Kim, S.; Gorgij, A.D.; Heddam, S.; Singh, V.P. Improving the accuracy of daily solar radiation prediction by climatic data using an efficient hybrid deep learning model: Long short-term memory (LSTM) network coupled with wavelet transform. Eng. Appl. Artif. Intell. 2023, 123, 106199. [Google Scholar] [CrossRef]
- Yang, D. Reconciling solar forecasts: Probabilistic forecast reconciliation in a nonparametric framework. Sol. Energy 2020, 210, 49–58. [Google Scholar] [CrossRef]
- Hassan, M.A.; Khalil, A.; Kaseb, S.; Kassem, M.A. Potential of four different machine-learning algorithms in modeling daily global solar radiation. Renew. Energy 2017, 111, 52–62. [Google Scholar] [CrossRef]
- Feng, Y.; Gong, D.; Zhang, Q.; Jiang, S.; Zhao, L.; Cui, N. Evaluation of temperature-based machine learning and empirical models for predicting daily global solar radiation. Energy Convers. Manag. 2019, 198, 111780. [Google Scholar] [CrossRef]
- Zhao, S.; Wu, L.; Xiang, Y.; Dong, J.; Li, Z.; Liu, X.; Tang, Z.; Wang, H.; Wang, X.; An, J.; et al. Coupling meteorological stations data and satellite data for prediction of global solar radiation with machine learning models. Renew. Energy 2022, 198, 1049–1064. [Google Scholar] [CrossRef]
- Dong, J.; Wu, L.; Liu, X.; Fan, C.; Leng, M.; Yang, Q. Simulation of Daily Diffuse Solar Radiation Based on Three Machine Learning Models. Comput. Model. Eng. Sci. 2020, 123, 49–73. [Google Scholar] [CrossRef]
- Lee, J.; Wang, W.; Harrou, F.; Sun, Y. Reliable solar irradiance prediction using ensemble learning-based models: A comparative study. Energy Convers. Manag. 2020, 208, 112582. [Google Scholar] [CrossRef]
- Ganaie, M.A.; Hu, M.H.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Ensemble solar forecasting using data-driven models with probabilistic post-processing through GAMLSS. Sol. Energy 2020, 208, 612–622. [Google Scholar] [CrossRef]
- Al-Hajj, R.; Assi, A.; Fouad, M. Short-Term Prediction of Global Solar Radiation Energy Using Weather Data and Machine Learning Ensembles: A Comparative Study. J. Sol. Energy Eng. 2021, 143, 051003. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Y.; Yuan, Q.; Yue, L.; Zhang, L. Spatiotemporal estimation of 6-hour high-resolution precipitation across China based on Himawari-8 using a stacking ensemble machine learning model. J. Hydrol. 2022, 609, 127718. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Zeng, W.; Wang, X.; Zou, H. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: A review and case study in China. Renew. Sustain. Energy Rev. 2019, 100, 186–212. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Zhang, F.; Ma, X.; Wu, L. Predicting daily diffuse horizontal solar radiation in various climatic regions of China using support vector machine and tree-based soft computing models with local and extrinsic climatic data. J. Clean. Prod. 2020, 248, 119264. [Google Scholar] [CrossRef]
- Abreu, E.F.M.; Gueymard, C.A.; Canhoto, P.; Costa, M.J. Performance assessment of clear-sky solar irradiance predictions using state-of-the-art radiation models and input atmospheric data from reanalysis or ground measurements. Sol. Energy 2023, 252, 309–321. [Google Scholar] [CrossRef]
- Buster, G.; Bannister, M.; Habte, A.; Hettinger, D.; Maclaurin, G.; Rossol, M.; Sengupta, M.; Xie, Y. Physics-guided machine learning for improved accuracy of the National Solar Radiation Database. Sol. Energy 2022, 232, 483–492. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Chen, Y.; Wang, D.; Wang, Y.; Zhu, Y. Comparison of support vector machine and copula-based nonlinear quantile regression for estimating the daily diffuse solar radiation: A case study in China. Renew. Energy 2020, 146, 1101–1112. [Google Scholar] [CrossRef]
- Sun, H.; Gui, D.; Yan, B.; Liu, Y.; Liao, W.; Zhu, Y.; Lu, C.; Zhao, N. Assessing the potential of random forest method for estimating solar radiation using air pollution index. Energy Convers. Manag. 2016, 119, 121–129. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, B.; Huang, W.; Liu, J.; Weng, W.; Lan, W. Multi-label feature selection based on label correlations and feature redundancy. Knowl.-Based Syst. 2022, 241, 108256. [Google Scholar] [CrossRef]
- Liu, X.; Tang, H.; Ding, Y.; Yan, D. Investigating the performance of machine learning models combined with different feature selection methods to estimate the energy consumption of buildings. Energy Build. 2022, 273, 112408. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and CatBoost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Mitrentsis, G.; Lens, H. An interpretable probabilistic model for short-term solar power forecasting using natural gradient boosting. Appl. Energy 2022, 309, 118473. [Google Scholar] [CrossRef]
- Bas, J.; Zou, Z.; Cirillo, C. An interpretable machine learning approach to understanding the impacts of attitudinal and ridesourcing factors on electric vehicle adoption. Transp. Lett. 2022, 15, 30–41. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Ding, S.; Huang, W.; Xu, W.; Wu, Y.; Zhao, Y.; Fang, P.; Hu, B.; Lou, L. Improving kitchen waste composting maturity by optimizing the processing parameters based on machine learning model. Bioresour. Technol. 2022, 360, 127606. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluating the effect of air pollution on global and diffuse solar radiation prediction using support vector machine modeling based on sunshine duration and air temperature. Renew. Sustain. Energy Rev. 2018, 94, 732–747. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Li, L.; Qiao, J.; Yu, G.; Wang, L.; Li, H.Y.; Liao, C.; Zhu, Z. Interpretable tree-based ensemble model for predicting beach water quality. Water Res. 2022, 211, 118078. [Google Scholar] [CrossRef]
- Zhou, H.; Deng, Z.; Xia, Y.; Fu, M. A new sampling method in particle filter based on Pearson correlation coefficient. Neurocomputing 2016, 216, 208–215. [Google Scholar] [CrossRef]
- Ghimire, S.; Bhandari, B.; Casillas-Pérez, D.; Deo, R.C.; Salcedo-Sanz, S. Hybrid deep CNN-SVR algorithm for solar radiation prediction problems in Queensland, Australia. Eng. Appl. Artif. Intell. 2022, 112, 104860. [Google Scholar] [CrossRef]
- Talib, A.; Park, S.; Im, P.; Joe, J. Grey-box and ANN-based building models for multistep-ahead prediction of indoor temperature to implement model predictive control. Eng. Appl. Artif. Intell. 2023, 126, 107115. [Google Scholar] [CrossRef]
- Markovics, D.; Mayer, M.J. Comparison of machine learning methods for photovoltaic power forecasting based on numerical weather prediction. Renew. Sustain. Energy Rev. 2022, 161, 112364. [Google Scholar] [CrossRef]
- Xin, Y. Evolving artificial neural networks. Proc. IEEE 1999, 87, 1423–1447. [Google Scholar] [CrossRef]
- Nguyen, B.; Morell, C.; De Baets, B. Large-scale distance metric learning for k-nearest neighbors regression. Neurocomputing 2016, 214, 805–814. [Google Scholar] [CrossRef]
- Saqib, M. Forecasting COVID-19 outbreak progression using hybrid polynomial-Bayesian ridge regression model. Appl. Intell. 2021, 51, 2703–2713. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA; pp. 785–794. [Google Scholar]
- Lv, M.; Li, H. Nonlinear Chirp Component Decomposition: A Method Based on Elastic Network Regression. IEEE Trans. Instrum. Meas. 2021, 70, 3515813. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Yang, D.; van der Meer, D. Post-processing in solar forecasting: Ten overarching thinking tools. Renew. Sustain. Energy Rev. 2021, 140, 110735. [Google Scholar] [CrossRef]
- Kadingdi, F.; Ayawah, P.; Azure, J.; Bruno, K.; Kaba, A.; Frimpong, S. Stacked Generalization for Improved Prediction of Ground Vibration from Blasting in Open-Pit Mine Operations. Min. Metall. Explor. 2022, 39, 2351–2363. [Google Scholar] [CrossRef]
- Yang, D. The future of solar forecasting in China. J. Renew. Sustain. Energy 2023, 15, 052301. [Google Scholar] [CrossRef]
- Qiu, R.; Liu, C.; Cui, N.; Gao, Y.; Li, L.; Wu, Z.; Jiang, S.; Hu, M. Generalized Extreme Gradient Boosting model for predicting daily global solar radiation for locations without historical data. Energy Convers. Manag. 2022, 258, 115488. [Google Scholar] [CrossRef]
- He, C.; Liu, J.; Xu, F.; Zhang, T.; Chen, S.; Sun, Z.; Zheng, W.; Wang, R.; He, L.; Feng, H.; et al. Improving solar radiation estimation in China based on regional optimal combination of meteorological factors with machine learning methods. Energy Convers. Manag. 2020, 220, 113111. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Tong, C.W.; Alam, K.A.; Petković, D. Potential of adaptive neuro-fuzzy system for prediction of daily global solar radiation by day of the year. Energy Convers. Manag. 2015, 93, 406–413. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Ma, X.; Zhou, H.; Zhang, F. Hybrid support vector machines with heuristic algorithms for prediction of daily diffuse solar radiation in air-polluted regions. Renew. Energy 2020, 145, 2034–2045. [Google Scholar] [CrossRef]
- Labani, M.; Moradi, P.; Ahmadizar, F.; Jalili, M. A novel multivariate filter method for feature selection in text classification problems. Eng. Appl. Artif. Intell. 2018, 70, 25–37. [Google Scholar] [CrossRef]
- Liu, D.L.; Scott, B.J. Estimation of solar radiation in Australia from rainfall and temperature observations. Agric. For. Meteorol. 2001, 106, 41–59. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Ma, J.; Yu, Z.; Qu, Y.; Xu, J.; Cao, Y. Application of the XGBoost Machine Learning Method in PM2.5 Prediction: A Case Study of Shanghai. Aerosol Air Qual. Res. 2020, 20, 128–138. [Google Scholar] [CrossRef]
- Patel, S.K.; Surve, J.; Katkar, V.; Parmar, J.; Al-Zahrani, F.A.; Ahmed, K.; Bui, F.M. Encoding and Tuning of THz Metasurface-Based Refractive Index Sensor with Behavior Prediction Using XGBoost Regressor. IEEE Access 2022, 10, 24797–24814. [Google Scholar] [CrossRef]
- Jia, D.; Yang, L.; Lv, T.; Liu, W.; Gao, X.; Zhou, J. Evaluation of machine learning models for predicting daily global and diffuse solar radiation under different weather/pollution conditions. Renew. Energy 2022, 187, 896–906. [Google Scholar] [CrossRef]
- Wang, L.; Lu, Y.; Zou, L.; Feng, L.; Wei, J.; Qin, W.; Niu, Z. Prediction of diffuse solar radiation based on multiple variables in China. Renew. Sustain. Energy Rev. 2019, 103, 151–216. [Google Scholar] [CrossRef]
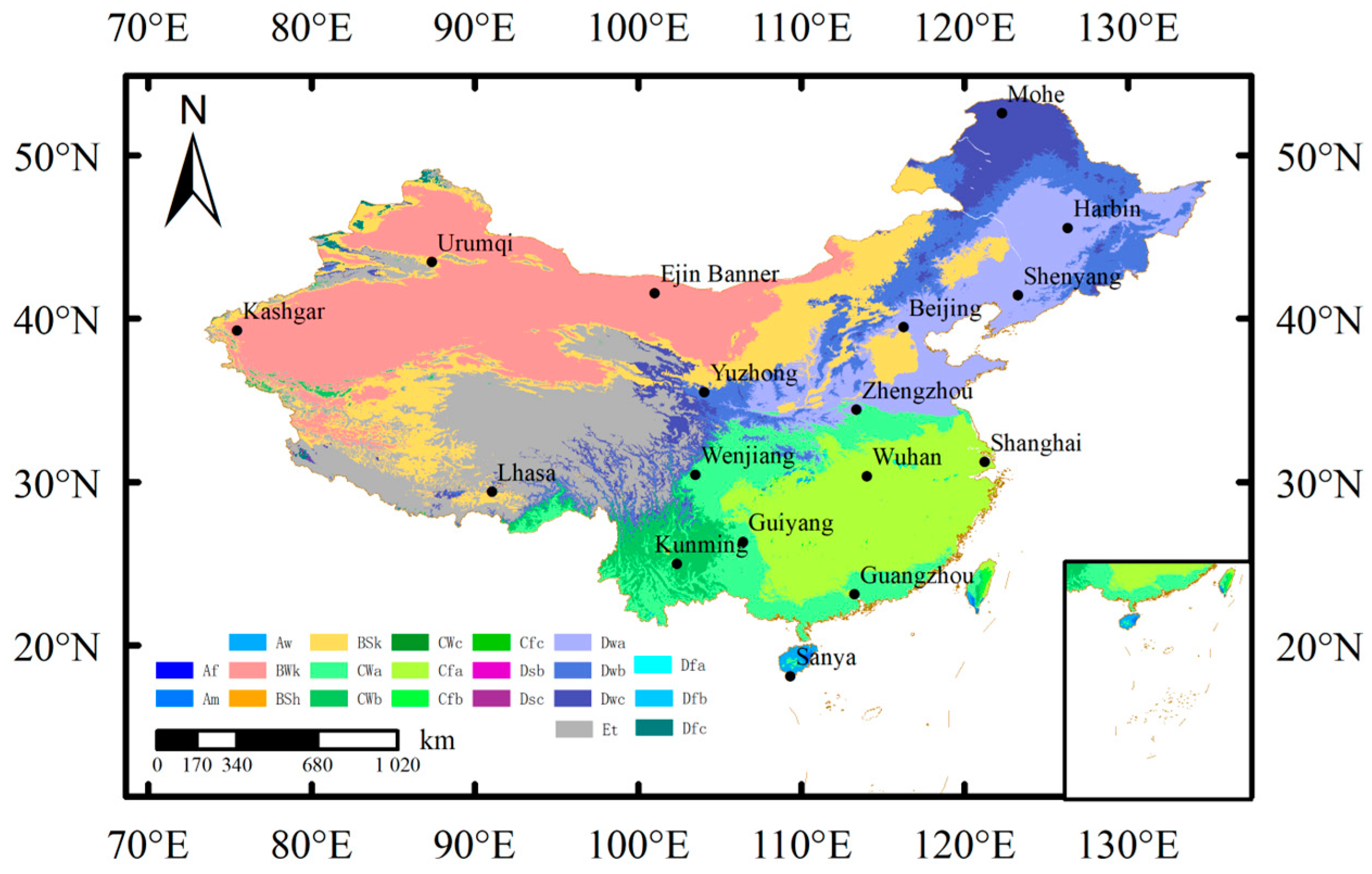





| ID | Station | Latitude (°N) | Longitude (°E) | Altitude (m) | Climatic Zone | Koppen–Geiger Climate |
|---|---|---|---|---|---|---|
| 50136 | Mohe | 52.58 | 122.31 | 438.5 | TMZ | Dw |
| 50953 | Harbin | 45.56 | 126.34 | 118.3 | TMZ | Dw |
| 51463 | Urumqi | 43.47 | 87.39 | 1930 | TCZ | Bs |
| 51709 | Kashgar | 39.29 | 75.45 | 1385.6 | TCZ | Bw |
| 52267 | Ejin Banner | 41.57 | 101.04 | 940.5 | TCZ | Bw |
| 52983 | Yuzhong | 35.52 | 104.09 | 1874.1 | TMZ | Dw |
| 54342 | Shenyang | 41.44 | 123.31 | 49.0 | TMZ | Dw |
| 54511 | Beijing | 39.48 | 116.28 | 45.8 | TMZ | Bs |
| 55591 | Lhasa | 29.40 | 91.08 | 8658 | MPZ | Bs |
| 56187 | Wenjiang | 30.45 | 103.52 | 548.9 | SMZ | Cf |
| 56778 | Kunming | 25.00 | 102.39 | 1888.1 | SMZ | Cf |
| 57083 | Zhengzhou | 34.43 | 113.39 | 110.4 | TMZ | Dw |
| 57494 | Wuhan | 30.36 | 114.03 | 23.6 | SMZ | Cf |
| 57816 | Guiyang | 26.35 | 106.44 | 1223.8 | SMZ | Cf |
| 58362 | Shanghai | 31.24 | 121.27 | 2.8 | SMZ | Cf |
| 59287 | Guangzhou | 23.13 | 113.29 | 70.7 | TPMZ | Cf |
| 59948 | Sanya | 18.13 | 109.35 | 5.0 | TPMZ | Aw |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Wang, Y.; Li, Z.; Zhao, L.; Shi, Y.; Xing, X.; Chen, S. Improving Solar Radiation Prediction in China: A Stacking Model Approach with Categorical Boosting Feature Selection. Atmosphere 2024, 15, 1436. https://doi.org/10.3390/atmos15121436
Ding Y, Wang Y, Li Z, Zhao L, Shi Y, Xing X, Chen S. Improving Solar Radiation Prediction in China: A Stacking Model Approach with Categorical Boosting Feature Selection. Atmosphere. 2024; 15(12):1436. https://doi.org/10.3390/atmos15121436
Chicago/Turabian StyleDing, Yuehua, Yuhang Wang, Zhe Li, Long Zhao, Yi Shi, Xuguang Xing, and Shuangchen Chen. 2024. "Improving Solar Radiation Prediction in China: A Stacking Model Approach with Categorical Boosting Feature Selection" Atmosphere 15, no. 12: 1436. https://doi.org/10.3390/atmos15121436
APA StyleDing, Y., Wang, Y., Li, Z., Zhao, L., Shi, Y., Xing, X., & Chen, S. (2024). Improving Solar Radiation Prediction in China: A Stacking Model Approach with Categorical Boosting Feature Selection. Atmosphere, 15(12), 1436. https://doi.org/10.3390/atmos15121436










