Examine the Role of Indo-Pacific Sea Surface Temperatures in Recent Meteorological Drought in Sudan
Abstract
1. Introduction
2. Data and Methodology
2.1. Study Site Description
2.2. Data
2.2.1. Precipitation
2.2.2. Wind and Mean Sea Level Pressure (MSLP)
2.3. Methods
2.3.1. Climatic Indices
2.3.2. The Standardized Precipitation Index (SPI)
2.3.3. Anomaly
2.3.4. The Empirical Orthogonal Function (EOF)
2.3.5. Pearson’s Correlation Coefficient (PCC)
2.3.6. Composite Analysis (CA)
2.3.7. Trend Analysis
3. Results and Discussion
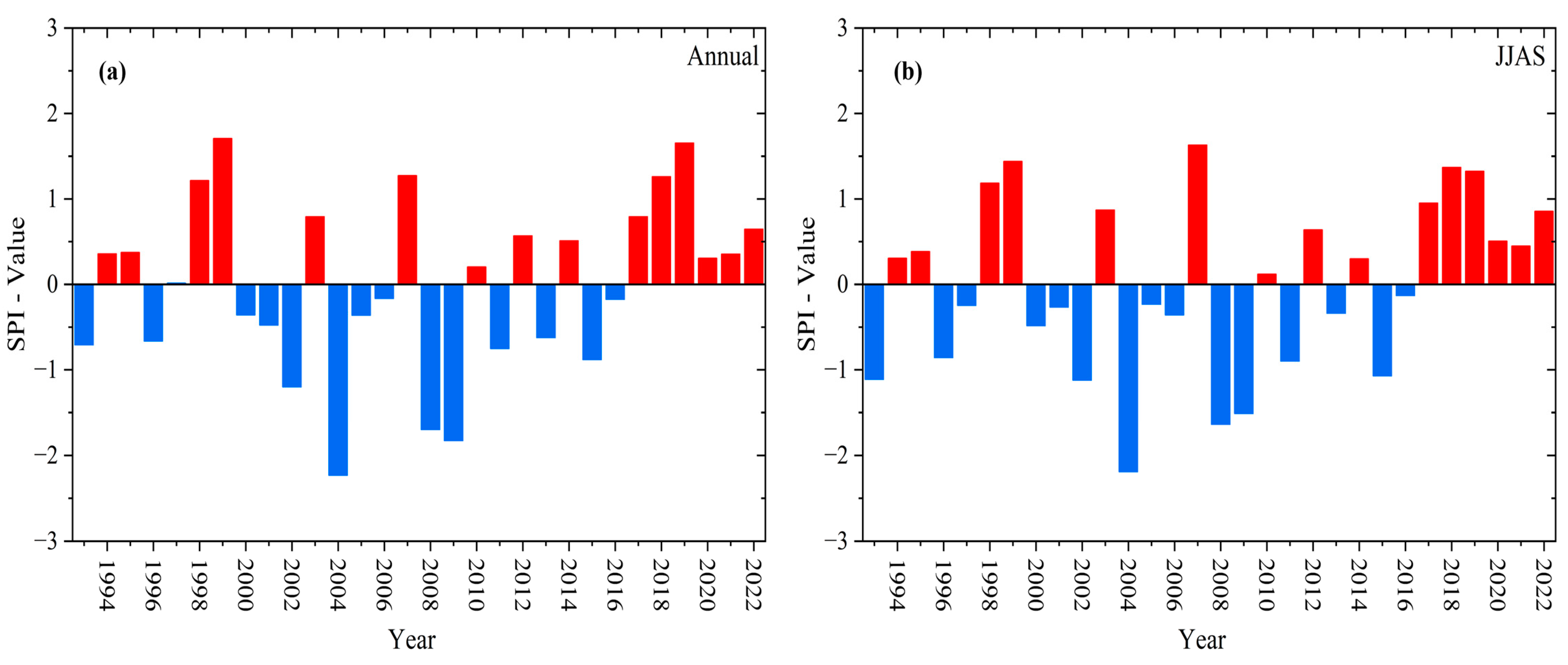
3.1. The Standardized Precipitation Index (SPI)
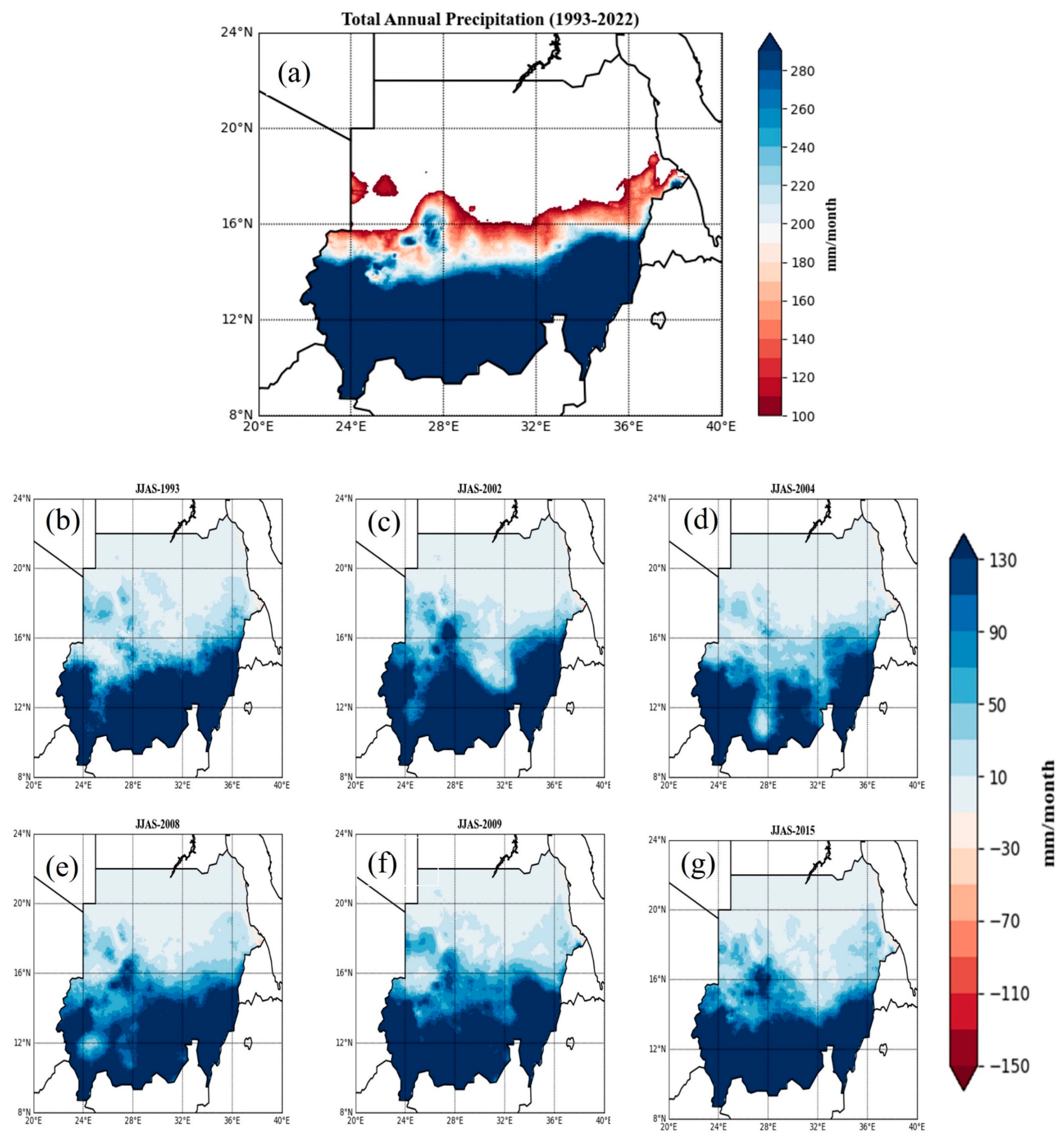
3.2. Anomaly
3.3. Trend
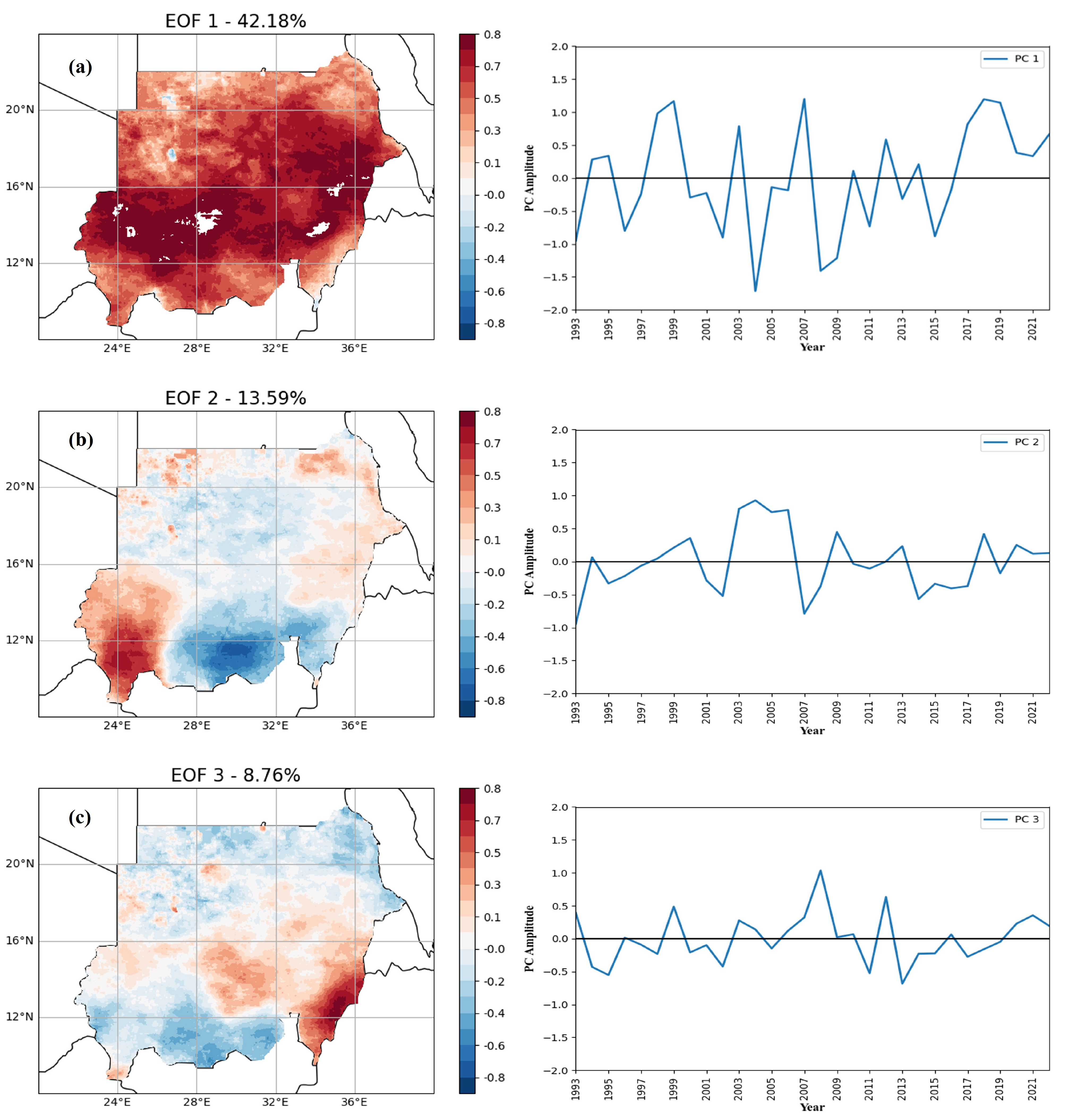
3.4. The Empirical Orthogonal Function (EOF)
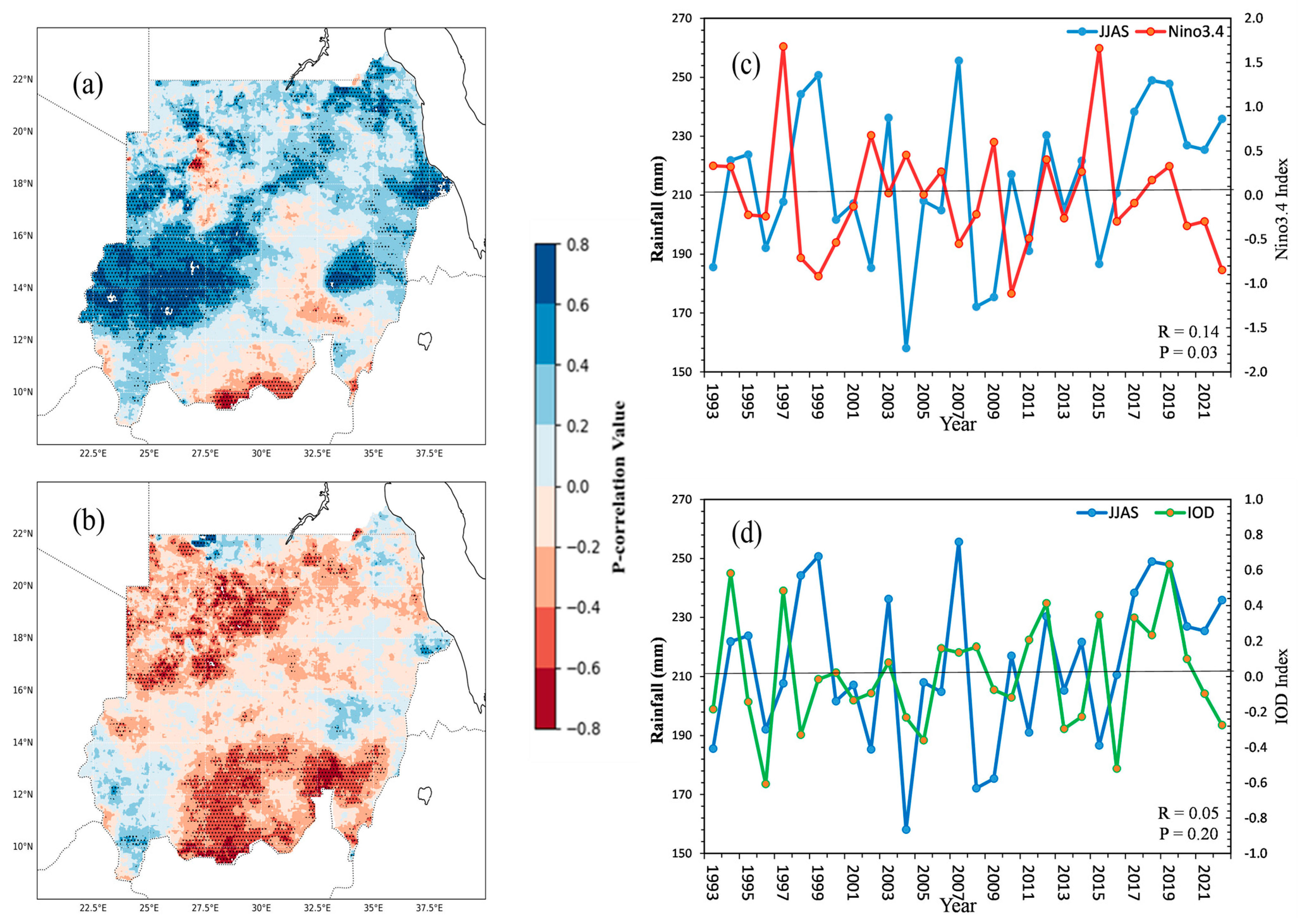
3.5. The Linkage with Indo-Pacific Oceans Temperatures
3.6. Composite Analysis
4. Conclusions
- The SPI during these 30 years highlighted a persistent challenge for Sudan, with frequent and prolonged drought conditions. Specifically, 2002, 2004, 2008, and 2009 were notable drought occurrences. In particular, 2004 is an exceptionally dry year, indicating extreme drought conditions across the region.
- The analysis of the anomaly from mean precipitation in SDN during the selected years (1993, 2002, 2004, 2008, 2009, and 2015) provided insights into drought patterns and their spatial effects. This reveals that the northern regions of SDN, including KH, AJ, and North and South Darfur (western region), consistently experienced drought with varying degrees and extent of impact.
- The Sequential Mann–Kendall and Mann–Kendall trend tests revealed a clear trend of increasing rainfall levels for both JJAS (June, July, August, and September) and annual rainfall after 2016. Before 2016, the rainfall revealed a decreasing trend. The increase in annual precipitation after 2016 was more pronounced than the increase in JJAS rainfall, indicating a potential change in the climate and precipitation dynamics in the region.
- The EOF analysis revealed spatial patterns of rainfall variations in the investigated region. The first EOF mode (42.2%) is the most influential in determining wet and dry conditions during the JJAS season.
- The association with Indo-Pacific Ocean temperatures indicated a strong positive correlation between ENSO, suggesting that negative El Niño Southern Oscillation (ENSO) events may have contributed to the observed dry conditions. Furthermore, a weak positive influence of IOD on JJAS precipitation was observed, as was the first EOF mode in Sudan, which had a significant impact on precipitation amount.
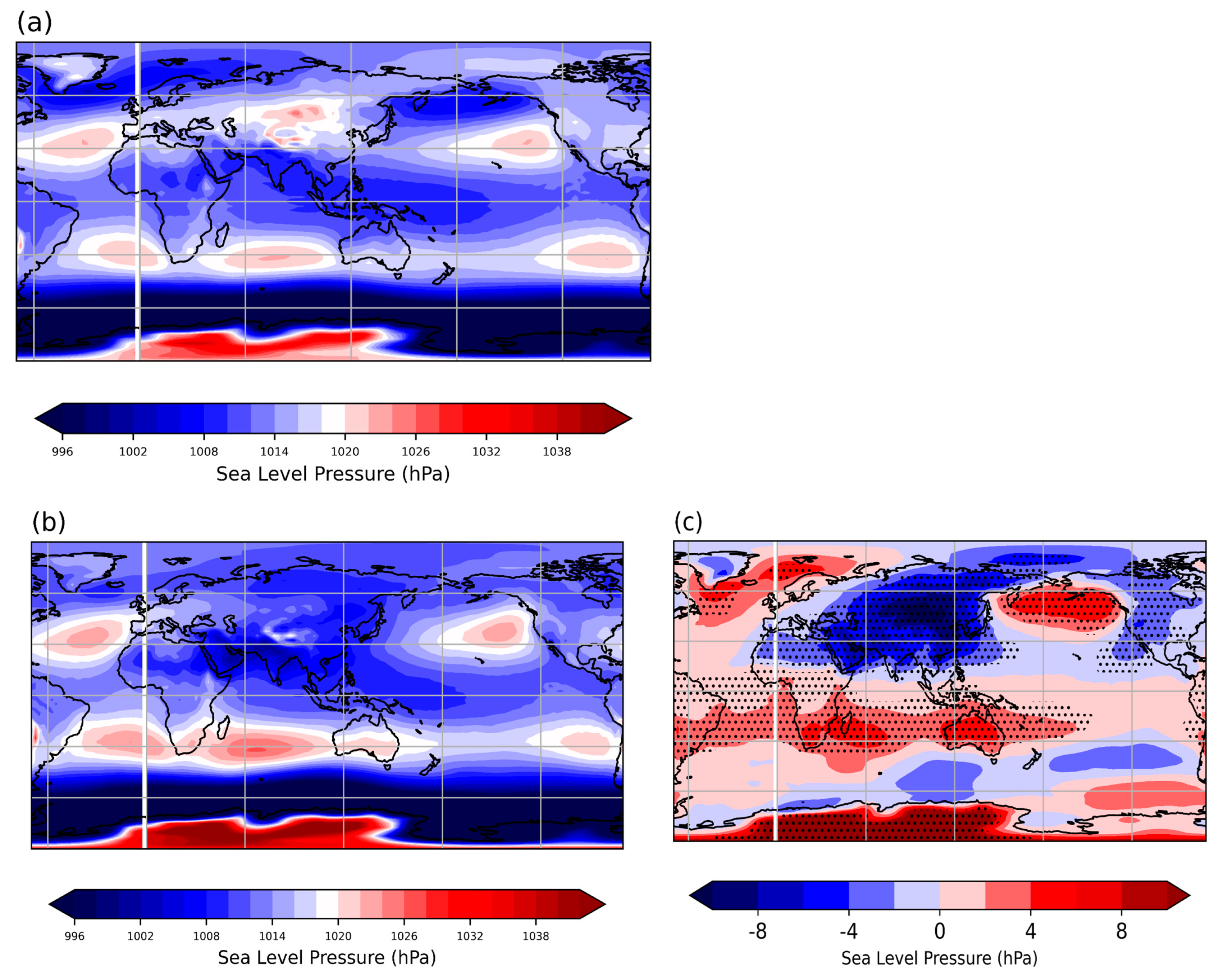
- Composite analysis: (a) The wind circulation patterns, particularly the TEJ, AEJ, SJ and WAM, exert a significant influence on the rainfall patterns across Sudan. The most important of these are the strength and interaction of TEJ and AEJ, which have the strongest correlation with precipitation variability. Additional research is essential to fully understand the effect of wind circulation patterns on precipitation in SDN. (b) The analysis of the pressure systems highlights the significant influence of subtropical high-pressure fluctuations in both hemispheres on the flow of the ITCZ over SDN. It is noteworthy that significant changes in the location and intensity of these high-pressure systems, coupled with the effects of oceanic high- and low-pressure systems, have a direct and measurable impact on precipitation patterns in the region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kallis, G. Droughts. Annu. Rev. Environ. Resour. 2008, 33, 85–118. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Y.; Liu, Y. An Approach to Tracking Meteorological Drought Migration. Water Resour. Res. 2019, 55, 3266–3284. [Google Scholar] [CrossRef]
- Zhao, R.; Yang, S.; Sun, H.; Zhou, L.; Li, M.; Xing, L.; Tian, R. Extremeness Comparison of Regional Drought Events in Yunnan Province, Southwest China: Based on Different Drought Characteristics and Joint Return Periods. Atmosphere 2023, 14, 1153. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Fischer, T.; Wang, Y.; Kundzewicz, Z.W.; Zhai, J.; Sun, H.; Wang, A.; Zeng, X.; Wang, G.; et al. Drought losses in China might double between the 1.5 °C and 2.0 °C warming. Proc. Natl. Acad. Sci. USA 2018, 115, 10600–10605. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal Drought Prediction: Advances, Challenges, and Future Prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- FAO. The Impact of Disasters and Crises on Agriculture and Food Security: 2021; FAO: Rome, Italy, 2021. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.; Li, Y.; Feng, K.; Zhang, Z.; Tian, Q.; Zhu, X.; Yang, H. Dynamic variation of meteorological drought and its relationships with agricultural drought across China. Agric. Water Manag. 2022, 261, 107301. [Google Scholar] [CrossRef]
- Ji, Y.; Fu, J.; Lu, Y.; Liu, B. Three-dimensional-based global drought projection under global warming tendency. Atmos. Res. 2023, 291, 106812. [Google Scholar] [CrossRef]
- Gebremeskel, G.; Tang, Q.; Sun, S.; Huang, Z.; Zhang, X.; Liu, X. Droughts in East Africa: Causes, impacts and resilience. Earth-Sci. Rev. 2019, 193, 146–161. [Google Scholar] [CrossRef]
- Seager, R.; Hoerling, M.; Schubert, S.; Wang, H.; Lyon, B.; Kumar, A.; Nakamura, J.; Henderson, N. Causes of the 2011 to 2014 California drought. J. Clim. 2015, 28, 6997–7024. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Kumar, A.; Leung, R.; Mariotti, A.; Mo, K.; Schubert, S.; Seager, R. Causes and predictability of the 2012 great plains drought. Bull. Am. Meteorol. Soc. 2014, 95, 269–282. [Google Scholar] [CrossRef]
- Dutra, E.; Magnusson, L.; Wetterhall, F.; Cloke, H.L.; Balsamo, G.; Boussetta, S.; Pappenberger, F. The 2010–2011 drought in the Horn of Africa in ECMWF reanalysis and seasonal forecast products. Int. J. Climatol. 2013, 33, 1720–1729. [Google Scholar] [CrossRef]
- Peterson, T.C.; Heim, R.R., Jr.; Hirsch, R.; Kaiser, D.P.; Brooks, H.; Diffenbaugh, N.S.; Dole, R.M.; Giovannettone, J.P.; Guirguis, K.; Karl, T.R.; et al. Monitoring and Understanding Changes in Heat Waves, Cold Waves, Floods, and Droughts in the United States: State of Knowledge. Bull. Am. Meteorol. Soc. 2013, 94, 821–834. [Google Scholar] [CrossRef]
- Nielsen-Gammon, J.W. The 2011 Texas Drought. Tex. Water J. 2012, 3, 59–95. [Google Scholar] [CrossRef]
- Hussien, A. Analysis of the Drought Impact as an Extreme Climatic Event in Sudan. J. Geosci. Environ. Prot. 2024, 12, 38–47. [Google Scholar] [CrossRef]
- Laki, S.L. Desertification in the Sudan: Causes, effects and policy options. Int. J. Sustain. Dev. World Ecol. 1994, 1, 198–205. [Google Scholar] [CrossRef]
- Mbogo, I. Drought Conditions and Management Strategies in Kenya; Namibia Meteorological Services: Windhoek, Namibia, 2014; pp. 1–9. [Google Scholar]
- Teklu, T.; Von Braum, J.; Zaki, E. Drought and famine relationships in Sudan: Policy implications. Res. Rep.-Int. Food Policy Res. Inst. 1991, 88, 1–3. [Google Scholar] [CrossRef]
- Von Braun, J.; Rose, B. Research report drought and family relationship: Sudan. 1991. Available online: https://www.researchgate.net/publication/5057065_Drought_and_Famine_Relationships_in_Sudan_Policy_Implications (accessed on 2 October 2024).
- Wilhite, D.A. Managing drought risk in a changing climate. Clim. Res. 2016, 70, 99–102. [Google Scholar] [CrossRef]
- Li, T.; Lv, A.; Zhang, W.; Liu, Y. Spatiotemporal Characteristics of Watershed Warming and Wetting: The Response to Atmospheric Circulation in Arid Areas of Northwest China. Atmosphere 2023, 14, 151. [Google Scholar] [CrossRef]
- Yin, H.; Wu, Z.; Fowler, H.J.; Blenkinsop, S.; He, H.; Li, Y. The Combined Impacts of ENSO and IOD on Global Seasonal Droughts. Atmosphere 2022, 13, 1673. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Clark, E.A.; Wood, A.W.; Hamlet, A.F.; Lettenmaier, D.P. Twentieth-century drought in the conterminous United States. J. Hydrometeorol. 2005, 6, 985–1001. [Google Scholar] [CrossRef]
- Liang, X.S. The Liang-Kleeman information flow: Theory and applications. Entropy 2013, 15, 327–360. [Google Scholar] [CrossRef]
- Schubert, S.D.; Stewart, R.E.; Wang, H.; Barlow, M.; Berbery, E.H.; Cai, W.; Hoerling, M.P.; Kanikicharla, K.K.; Koster, R.D.; Lyon, B.; et al. Global meteorological drought: A synthesis of current understanding with a focus on SST drivers of precipitation deficits. J. Clim. 2016, 29, 3989–4019. [Google Scholar] [CrossRef]
- IMasih; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef]
- Haile, G.G.; Tang, Q.; Leng, G.; Jia, G.; Wang, J.; Cai, D.; Sun, S.; Baniya, B.; Zhang, Q. Long-term spatiotemporal variation of drought patterns over the Greater Horn of Africa. Sci. Total Environ. 2020, 704, 135299. [Google Scholar] [CrossRef] [PubMed]
- Kalisa, W.; Zhang, J.; Igbawua, T.; Ujoh, F.; Ebohon, O.J.; Namugize, J.N.; Yao, F. Spatio-temporal analysis of drought and return periods over the East African region using Standardized Precipitation Index from 1920 to 2016. Agric. Water Manag. 2020, 237, 106195. [Google Scholar] [CrossRef]
- Doi, T.; Behera, S.K.; Yamagata, T. On the Predictability of the Extreme Drought in East Africa during the Short Rains Season. Geophys. Res. Lett. 2022, 49, e2022GL100905. [Google Scholar] [CrossRef]
- Funk, C.; Harrison, L.; Shukla, S.; Pomposi, C.; Galu, G.; Korecha, D.; Husak, G.; Magadzire, T.; Davenport, F.; Hillbruner, C.; et al. Examining the role of unusually warm Indo-Pacific sea-surface temperatures in recent African droughts. Q. J. R. Meteorol. Soc. 2018, 144, 360–383. [Google Scholar] [CrossRef]
- Mahmoud, S.H.; Gan, T.Y.; Allan, R.P.; Li, J.; Funk, C. Worsening drought of Nile basin under shift in atmospheric circulation, stronger ENSO and Indian Ocean dipole. Sci. Rep. 2022, 12, 8049. [Google Scholar] [CrossRef]
- Osman, Y.Z.; Shamseldin, A.Y. Qualitative rainfall prediction models for central and southern Sudan using El Nino-southern oscillation and Indian Ocean sea surface temperature indices. Int. J. Climatol. 2002, 22, 1861–1878. [Google Scholar] [CrossRef]
- Alriah, M.A.A.; Bi, S.; Shahid, S.; Nkunzimana, A.; Ayugi, B.; Ali, A.; Bilal, M.; Teshome, A.; Sarfo, I.; Elameen, A.M. Summer monsoon rainfall variations and its association with atmospheric circulations over Sudan. J. Atmos. Sol.-Terr. Phys. 2021, 225, 105751. [Google Scholar] [CrossRef]
- Elramlawi, H.R.; Mohammed, H.I.; Elamin, A.W.; Abdallah, O.A.; Taha, A.A.A.M. Adaptation of Sorghum (Sorghum bicolor L. Moench) Crop Yield to Climate Change in Eastern Dryland of Sudan. In Handbook of Climate Change Resilience; Filho, W.L., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 2549–2573. [Google Scholar] [CrossRef]
- Alriah, M.A.A.; Bi, S.; Nkunzimana, A.; Elameen, A.M.; Sarfo, I.; Ayugi, B. Multiple gridded-based precipitation products’ performance in Sudan’s different topographical features and the influence of the Atlantic Multidecadal Oscillation on rainfall variability in recent decades. Int. J. Climatol. 2022, 42, 9539–9566. [Google Scholar] [CrossRef]
- Philip, S.; Kew, S.F.; van Oldenborgh, G.J.; Otto, F.; O’keefe, S.; Haustein, K.; King, A.; Zegeye, A.; Eshetu, Z.; Hailemariam, K.; et al. Attribution analysis of the Ethiopian drought of 2015. J. Clim. 2018, 31, 2465–2486. [Google Scholar] [CrossRef]
- de Waal, A. Peace and the security sector in Sudan, 2002–2011. Afr. Secur. Rev. 2017, 26, 180–198. [Google Scholar] [CrossRef]
- Santos, J.d.S.; de Oliveira-Júnior, J.F.; Costa, M.d.S.; Cardoso, K.R.A.; Shah, M.; Shahzad, R.; da Silva, L.F.F.F.; Romão, W.M.d.O.; Singh, S.K.; Mendes, D.; et al. Effects of extreme phases of El Niño–Southern Oscillation on rainfall extremes in Alagoas, Brazil. Int. J. Climatol. 2023, 43, 7700–7721. [Google Scholar] [CrossRef]
- Chapman, B.; Rosemond, K. Seasonal climate summary for the southern hemisphere (autumn 2018): A weak La Niña fades, the austral autumn remains warmer and drier. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 328–352. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J.R. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Available online: https://api.semanticscholar.org/CorpusID:129950974 (accessed on 15 March 2022).
- Edwards, D.C.; McKee, T.B. Thesis Characteristics of 20th Century Drought in the United States at Multiple Time Scales; Department of Atmospheric Science, Colorado State University: Fort Collins, CO, USA, 1997; Volume 298, p. 155. [Google Scholar]
- Zhang, Z.; Xu, C.Y.; Yong, B.; Hu, J.; Sun, Z. Understanding the changing characteristics of droughts in Sudan and the corresponding components of the hydrologic cycle. J. Hydrometeorol. 2012, 13, 1520–1535. [Google Scholar] [CrossRef]
- Awange, J.L.; Khandu; Schumacher, M.; Forootan, E.; Heck, B. Exploring hydro-meteorological drought patterns over the Greater Horn of Africa (1979-2014) using remote sensing and reanalysis products. Adv. Water Resour. 2016, 94, 45–59. [Google Scholar] [CrossRef]
- Guenang, G.M.; Kamga, F.M. Computation of the standardized precipitation index (SPI) and its use to assess drought occurrences in Cameroon over recent decades. J. Appl. Meteorol. Climatol. 2014, 53, 2310–2324. [Google Scholar] [CrossRef]
- Ugwu, E.B.I.; Ugbor, D.O.; Agbo, J.U.; Alfa, A. Analyzing rainfall trend and drought occurences in Sudan Savanna of Nigeria. Sci. Afr. 2023, 20, e01670. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Svoboda; Hayes, M.; Wood, D. Standradized Precipitation Index User Guide; WMO: Geneva, Switzerland, 2012. [Google Scholar]
- Wilks, D.S. Preface. In Statistical Methods in the Atmospheric Sciences; International Geophysics Series; Academic Press: Cambridge, MA, USA, 2006; Volume 59. [Google Scholar] [CrossRef]
- Nicholson, S.E. Climate and climatic variability of rainfall over eastern Africa. Rev. Geophys. 2017, 55, 590–635. [Google Scholar] [CrossRef]
- dar, J.; dar, A.Q. Spatio-temporal variability of meteorological drought over India with footprints on agricultural production. Environ. Sci. Pollut. Res. 2021, 28, 55796–55809. [Google Scholar] [CrossRef] [PubMed]
- Rayner, N.a. A Manual for EOF and SVD. J. Geophys. Res. 1997, 108, 4407. [Google Scholar] [CrossRef]
- Oktaviani, F.; Miftahuddin; Setiawan, I. Cross-correlation Analysis between Sea Surface Temperature Anomalies and Several Climate Elements in the Indian Ocean. Parameter J. Stat. 2021, 1, 13–20. [Google Scholar] [CrossRef]
- Mclean, L.D.; Guilford, J.P.; Fruchter, B. Fundamental Statistics in Psychology and Education. 1943. Available online: https://api.semanticscholar.org/CorpusID:145224068 (accessed on 2 October 2024).
- Bayable, G.; Gashaw, T. Spatiotemporal variability of agricultural drought and its association with climatic variables in the Upper Awash Basin, Ethiopia. SN Appl. Sci. 2021, 3, 465. [Google Scholar] [CrossRef]
- Colman, A.W.; Graham, R.J.; Davey, M.K. Direct and indirect seasonal rainfall forecasts for East Africa using global dynamical models. Int. J. Climatol. 2020, 40, 1132–1148. [Google Scholar] [CrossRef]
- Kipkogei, O.; Mwanthi, A.M.; Mwesigwa, J.B.; Atheru, Z.K.K.; Wanzala, M.A.; Artan, G. Improved seasonal prediction of rainfall over East Africa for application in agriculture: Statistical downscaling of CFSv2 and GFDL-FLOR. J. Appl. Meteorol. Climatol. 2017, 56, 3229–3243. [Google Scholar] [CrossRef]
- Ogwang, B.A.; Ongoma, V.; Xing, L.; Ogou, F.K. Influence of mascarene high and Indian Ocean dipole on East African extreme weather events. Geogr. Pannonica 2015, 19, 64–72. [Google Scholar] [CrossRef]
- Omondi, P.; Ogallo, L.A.; Anyah, R.; Muthama, J.M.; Ininda, J. Linkages between global sea surface temperatures and decadal rainfall variability over Eastern Africa region. Int. J. Climatol. 2013, 33, 2082–2104. [Google Scholar] [CrossRef]
- Welhouse, L.J.; Lazzara, M.A.; Keller, L.M.; Tripoli, G.J.; Hitchman, M.H. Composite analysis of the effects of ENSO events on Antarctica. J. Clim. 2016, 29, 1797–1808. [Google Scholar] [CrossRef]
- Nkunzimana, A.; Shuoben, B.; Guojie, W.; Alriah, M.A.A.; Sarfo, I.; Zhihui, X.; Vuguziga, F.; Ayugi, B.O. Assessment of drought events, their trend and teleconnection factors over Burundi, East Africa. Theor. Appl. Climatol. 2021, 145, 1293–1316. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Ongoma, V.; Chen, H. Temporal and spatial variability of temperature and precipitation over East Africa from 1951 to 2010. Meteorol. Atmos. Phys. 2017, 129, 131–144. [Google Scholar] [CrossRef]
- Tan, C.; Yang, J.; Li, M. Temporal-spatial variation of drought indicated by SPI and SPEI in Ningxia Hui Autonomous Region, China. Atmosphere 2015, 6, 1399–1421. [Google Scholar] [CrossRef]
- Esit, M.; Yuce, M. Comprehensive evaluation of trend analysis of extreme drought events in the Ceyhan River Basin, Turkey. Meteorol. Hydrol. Water Manag. 2022, 11, 22–43. [Google Scholar] [CrossRef]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal drought analysis by the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Jain, S.K.; Kumar, V. Trend analysis of rainfall and temperature data for India. Curr. Sci. 2012, 102, 37–49. [Google Scholar]
- Mohmmed, A.; Zhang, K.; Kabenge, M.; Keesstra, S.; Cerdà, A.; Reuben, M.; Elbashier, M.M.; Dalson, T.; Ali, A.A. Analysis of drought and vulnerability in the North Darfur region of Sudan. Land Degrad. Dev. 2018, 29, 4424–4438. [Google Scholar] [CrossRef]
- Alriah, M.A.A.; Bi, S.; Nkunzimana, A.; Elameen, A.M.; Sarfo, I.; Ayugi, B. Assessment of observed changes in drought characteristics and recent vegetation dynamics over arid and semiarid areas in Sudan. Theor. Appl. Climatol. 2024, 155, 3541–3561. [Google Scholar] [CrossRef]
- Ngarukiyimana, J.P.; Fu, Y.; Yang, Y.; Ogwang, B.A.; Ongoma, V.; Ntwali, D. Dominant atmospheric circulation patterns associated with abnormal rainfall events over Rwanda, East Africa. Int. J. Climatol. 2018, 38, 187–202. [Google Scholar] [CrossRef]
- Ongoma, V.; Chen, H.; Omony, G.W. Variability of extreme weather events over the equatorial East Africa, a case study of rainfall in Kenya and Uganda. Theor. Appl. Climatol. 2018, 131, 295–308. [Google Scholar] [CrossRef]
- Sian, K.T.C.L.K.; Dosio, A.; Ayugi, B.O.; Hagan, D.F.T.; Kebacho, L.L.; Ongoma, V. Dominant modes of precipitation over Africa, and their associated atmospheric circulations from observations. Int. J. Climatol. 2023, 43, 4603–4618. [Google Scholar] [CrossRef]
- Ndomeni, C.W.; Cattani, E.; Merino, A.; Levizzani, V. An observational study of the variability of East African rainfall with respect to sea surface temperature and soil moisture. Q. J. R. Meteorol. Soc. 2018, 144, 384–404. [Google Scholar] [CrossRef]
- Endris, H.S.; Lennard, C.; Hewitson, B.; Dosio, A.; Nikulin, G.; Artan, G.A. Future changes in rainfall associated with ENSO, IOD and changes in the mean state over Eastern Africa. Clim. Dyn. 2019, 52, 2029–2053. [Google Scholar] [CrossRef]
- El Gamri, T.; Saeed, A.B.; Abdalla, A. Rainfall of the Sudan: Characteristics and Prediction. J. Fac. Arts Univ. Khartoum 2021, 27, 17–35. [Google Scholar] [CrossRef]
- Kebacho, L. Large-scale circulations associated with recent interannual variability of the short rains over East Africa. Meteorol. Atmos. Phys. 2022, 134, 10. [Google Scholar] [CrossRef]
- Kebacho, L.L.; Sarfo, I. Why Eastern Africa was not dry during the 2020 short rainy season despite La Niña and a negative Indian Ocean Dipole: Interplay between the Madden-Julian Oscillation and La Niña in modulating short rain. Theor. Appl. Climatol. 2023, 153, 1191–1201. [Google Scholar] [CrossRef]
- Hulme, M.; Tosdevin, N. The Tropical easterly Jet and Sudan rainfall: A review. Theor. Appl. Climatol. 1989, 39, 179–187. [Google Scholar] [CrossRef]
- Mishra, S.K.; Tandon, M.K. A combined barotropic-baroclinic instability study of the upper tropospheric tropical easterly jet. J. Atmos. Sci. 1983, 40, 2708–2723. [Google Scholar] [CrossRef][Green Version]
- Druyan, L.M.; Koster, R.D. Sources of Sahel Precipitation for Simulated Drought and Rainy Seasons. J. Clim. 1989, 2, 1438–1446. [Google Scholar] [CrossRef]
- Lélé, M.I.; Lamb, P.J. Variability of the Intertropical Front (ITF) and rainfall over the West African Sudan-Sahel zone. J. Clim. 2010, 23, 3984–4004. [Google Scholar] [CrossRef]
- Agustí-Panareda, A.; Beljaars, A.; Cardinali, C.; Genkova, I.; Thorncroft, C. Impacts of assimilating AMMA soundings on ECMWF analyses and forecasts. Weather Forecast. 2010, 25, 1142–1160. [Google Scholar] [CrossRef]
- Vizy, E.K.; Cook, K.H. Connections between the summer east African and Indian rainfall regimes. J. Geophys. Res. Atmos. 2003, 108, 4510. [Google Scholar] [CrossRef]



| Parameters | Annual | JJAS |
|---|---|---|
| S | 115 | 89 |
| Z | 2.3 | 1.59 |
| P | 0.04 | 0.11 |
| Significance | Significantly increasing trend | Insignificantly |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, A.H.A.; Zhang, X.; Alriah, M.A.A. Examine the Role of Indo-Pacific Sea Surface Temperatures in Recent Meteorological Drought in Sudan. Atmosphere 2024, 15, 1194. https://doi.org/10.3390/atmos15101194
Mohammed AHA, Zhang X, Alriah MAA. Examine the Role of Indo-Pacific Sea Surface Temperatures in Recent Meteorological Drought in Sudan. Atmosphere. 2024; 15(10):1194. https://doi.org/10.3390/atmos15101194
Chicago/Turabian StyleMohammed, Awad Hussien Ahmed, Xiaolin Zhang, and Mohamed Abdallah Ahmed Alriah. 2024. "Examine the Role of Indo-Pacific Sea Surface Temperatures in Recent Meteorological Drought in Sudan" Atmosphere 15, no. 10: 1194. https://doi.org/10.3390/atmos15101194
APA StyleMohammed, A. H. A., Zhang, X., & Alriah, M. A. A. (2024). Examine the Role of Indo-Pacific Sea Surface Temperatures in Recent Meteorological Drought in Sudan. Atmosphere, 15(10), 1194. https://doi.org/10.3390/atmos15101194







