Backward Integration of Nonlinear Shallow Water Model: Part I: Solitary Rossby Waves
Abstract
1. Introduction
2. Basic Equations and Numerical Model
3. Backward Integration
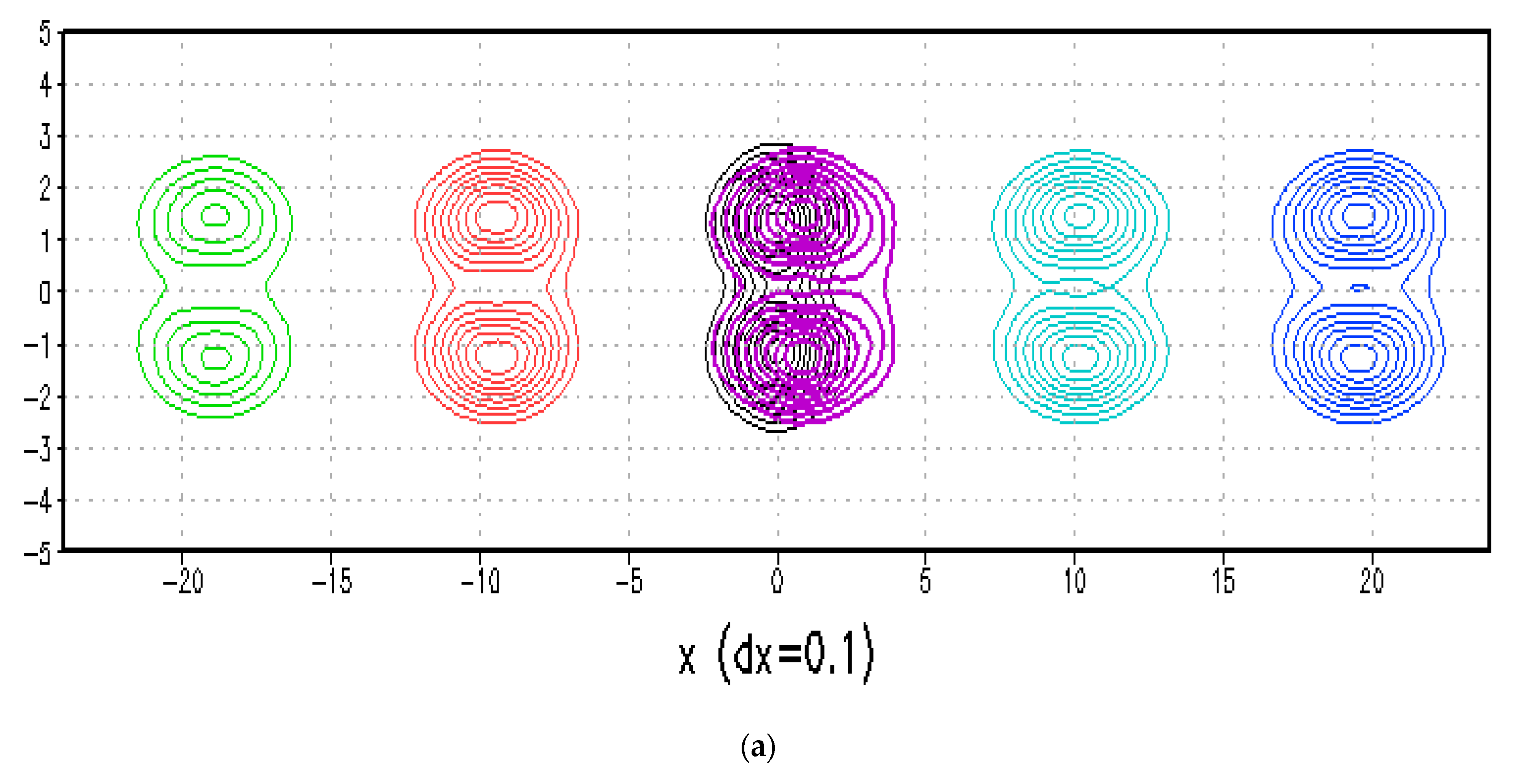
4. Initial Conditions and Numerical Results
4.1. Initial Condition of Solitary Rossby Wave in Forward Integration
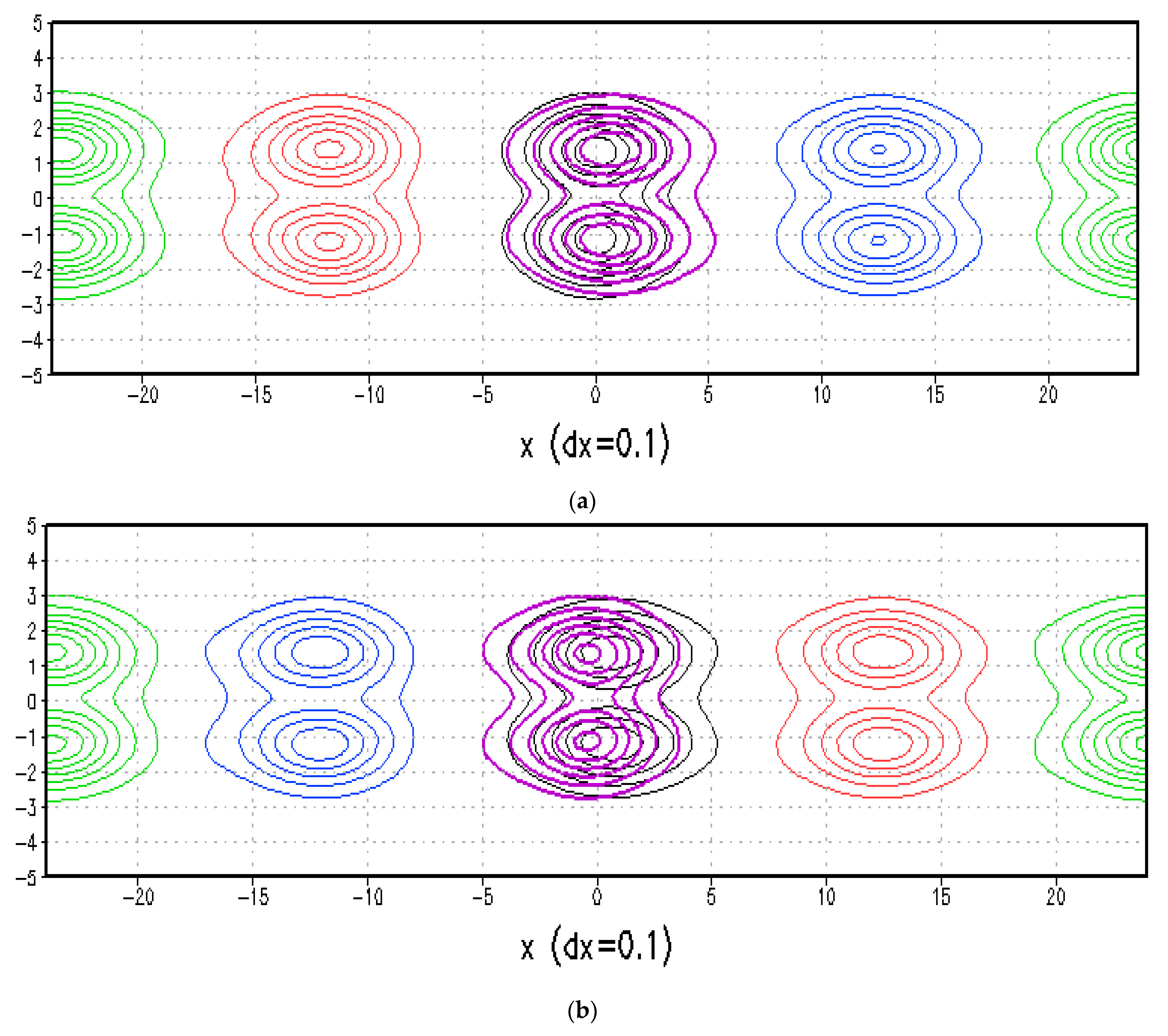
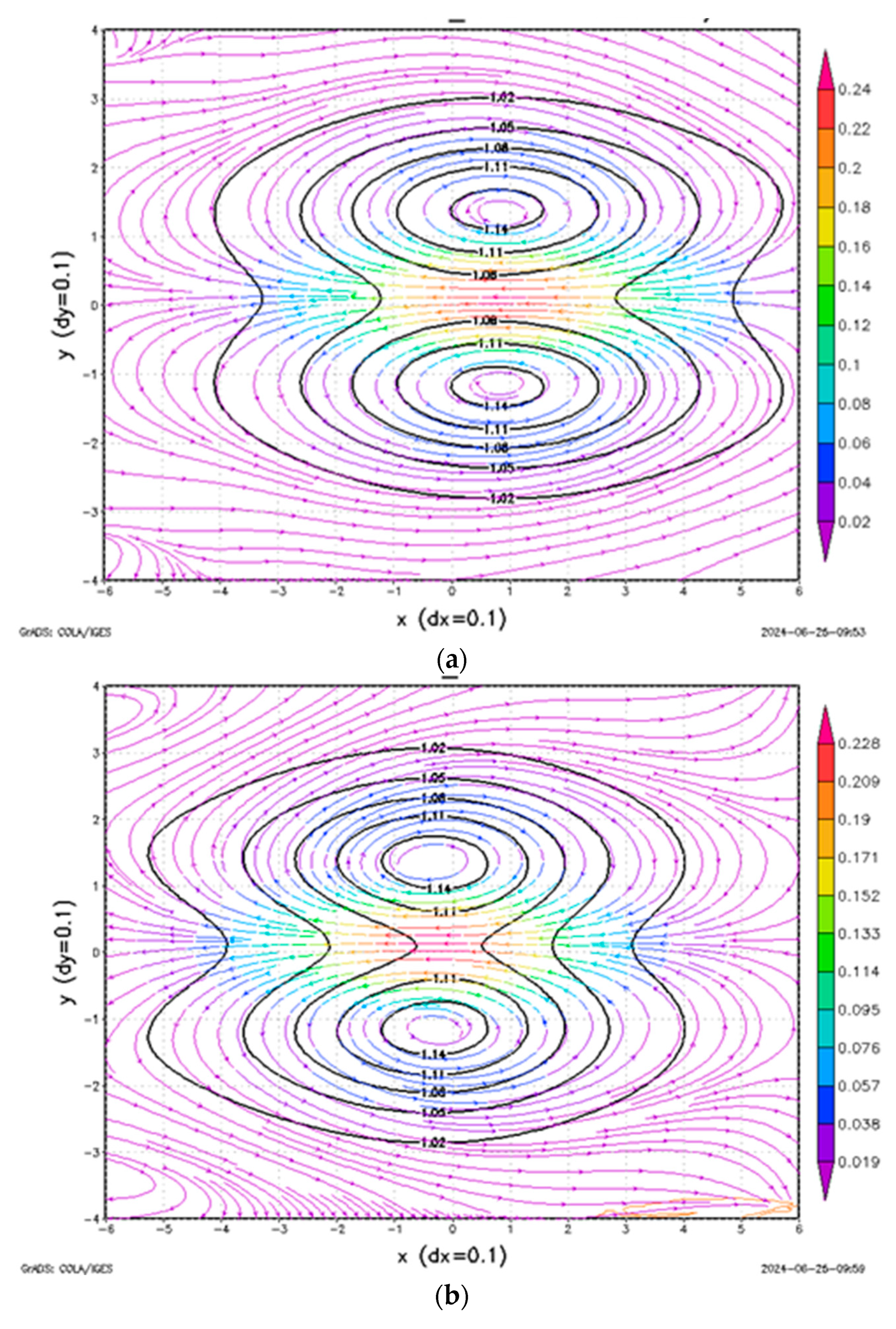
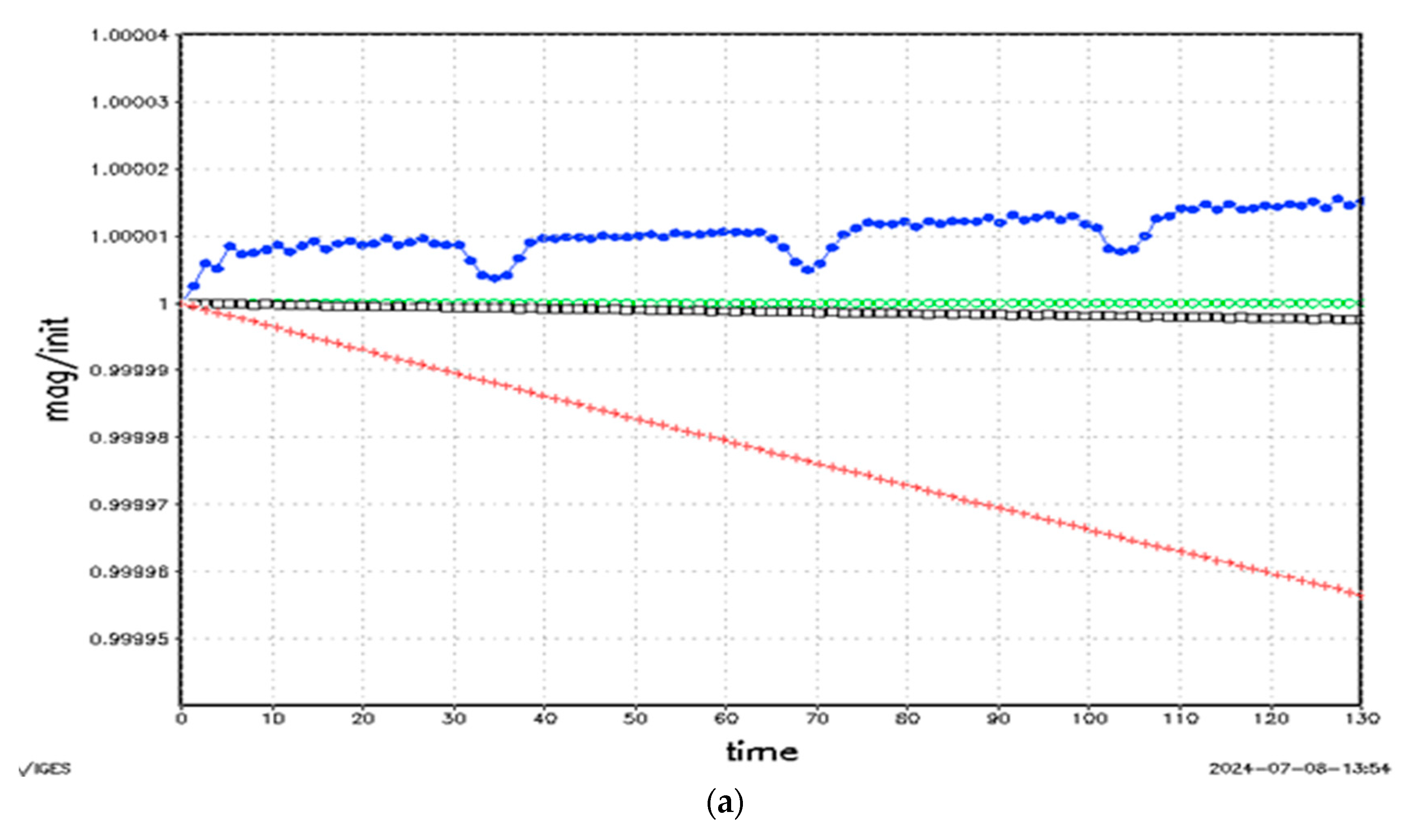
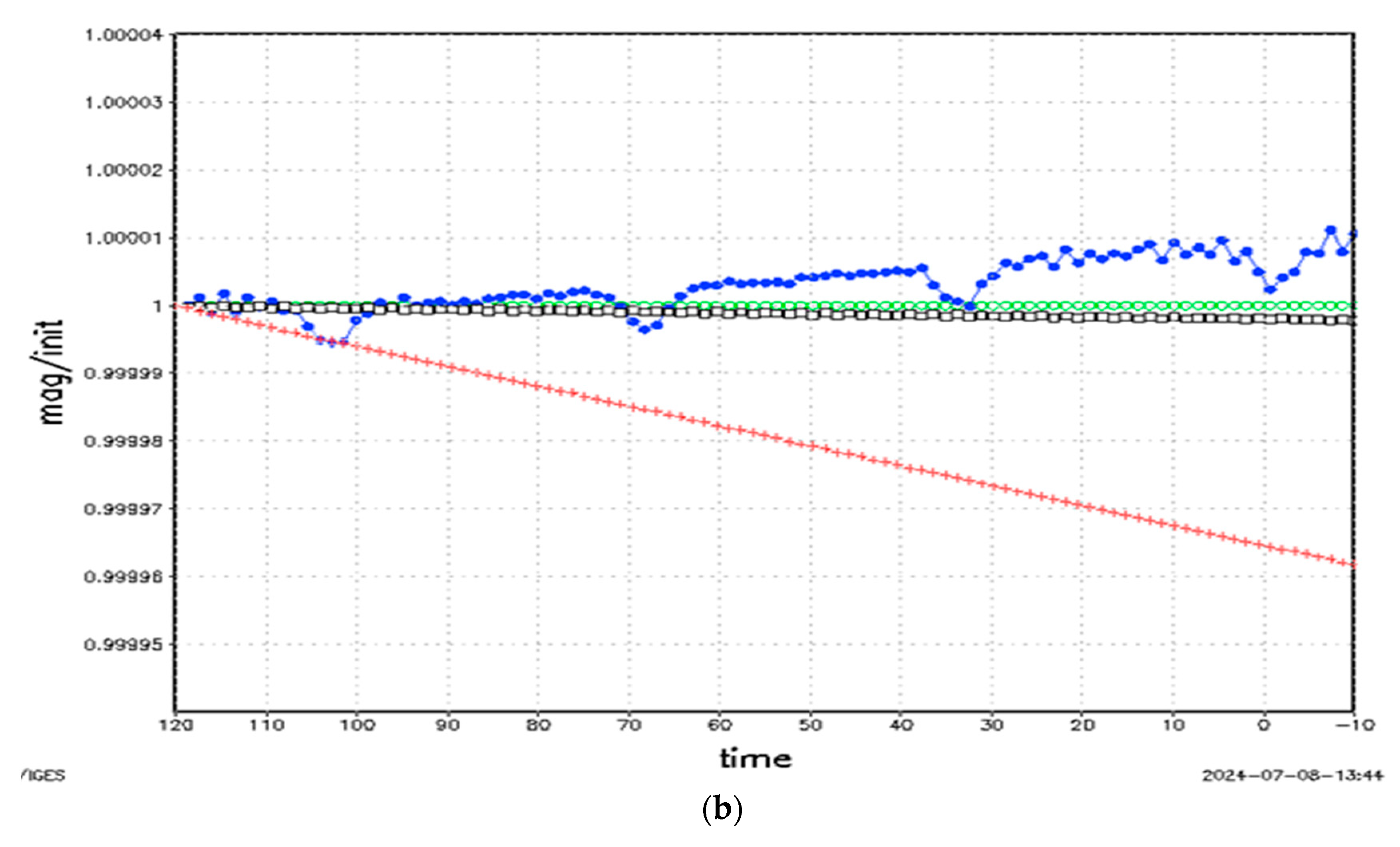
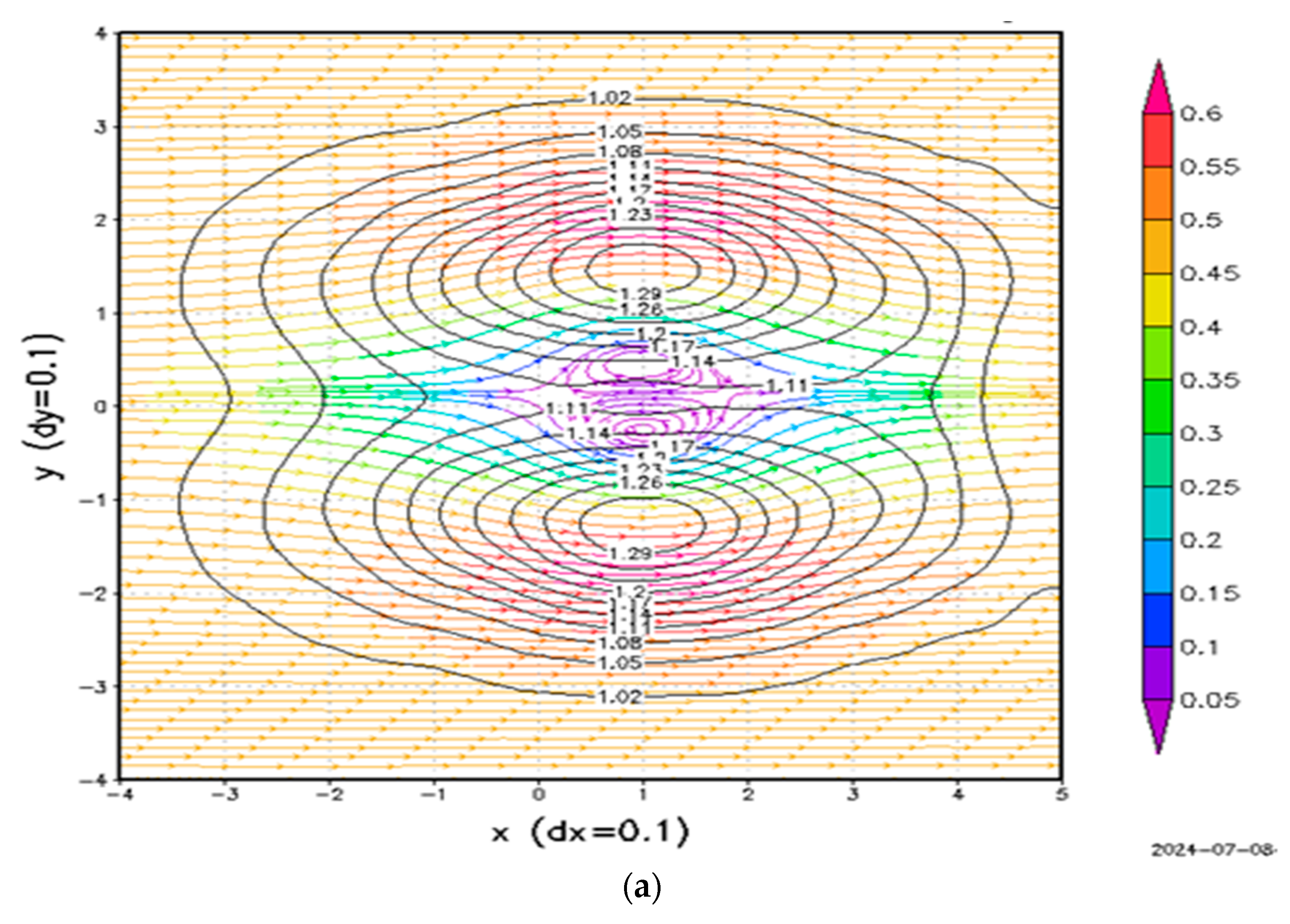
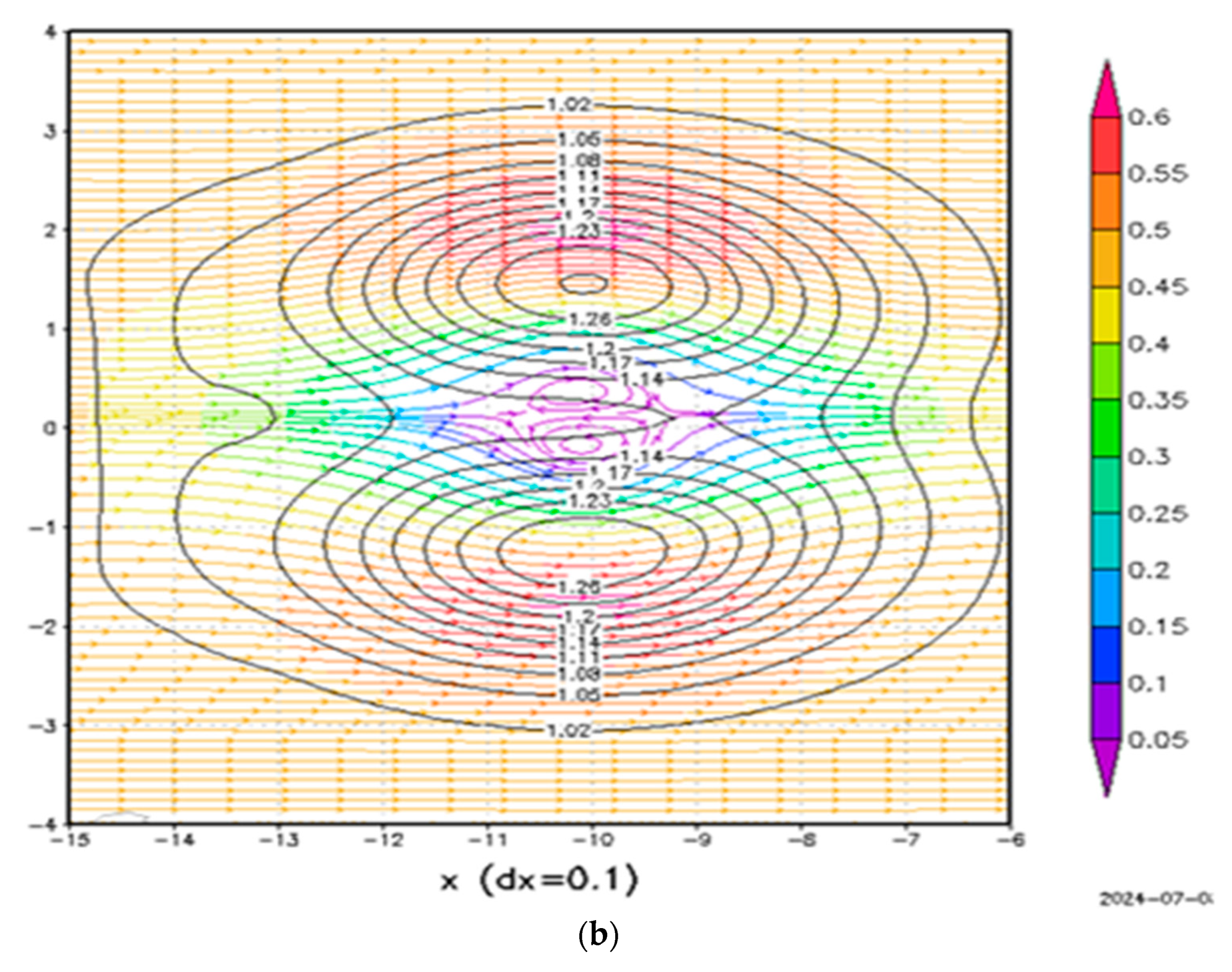
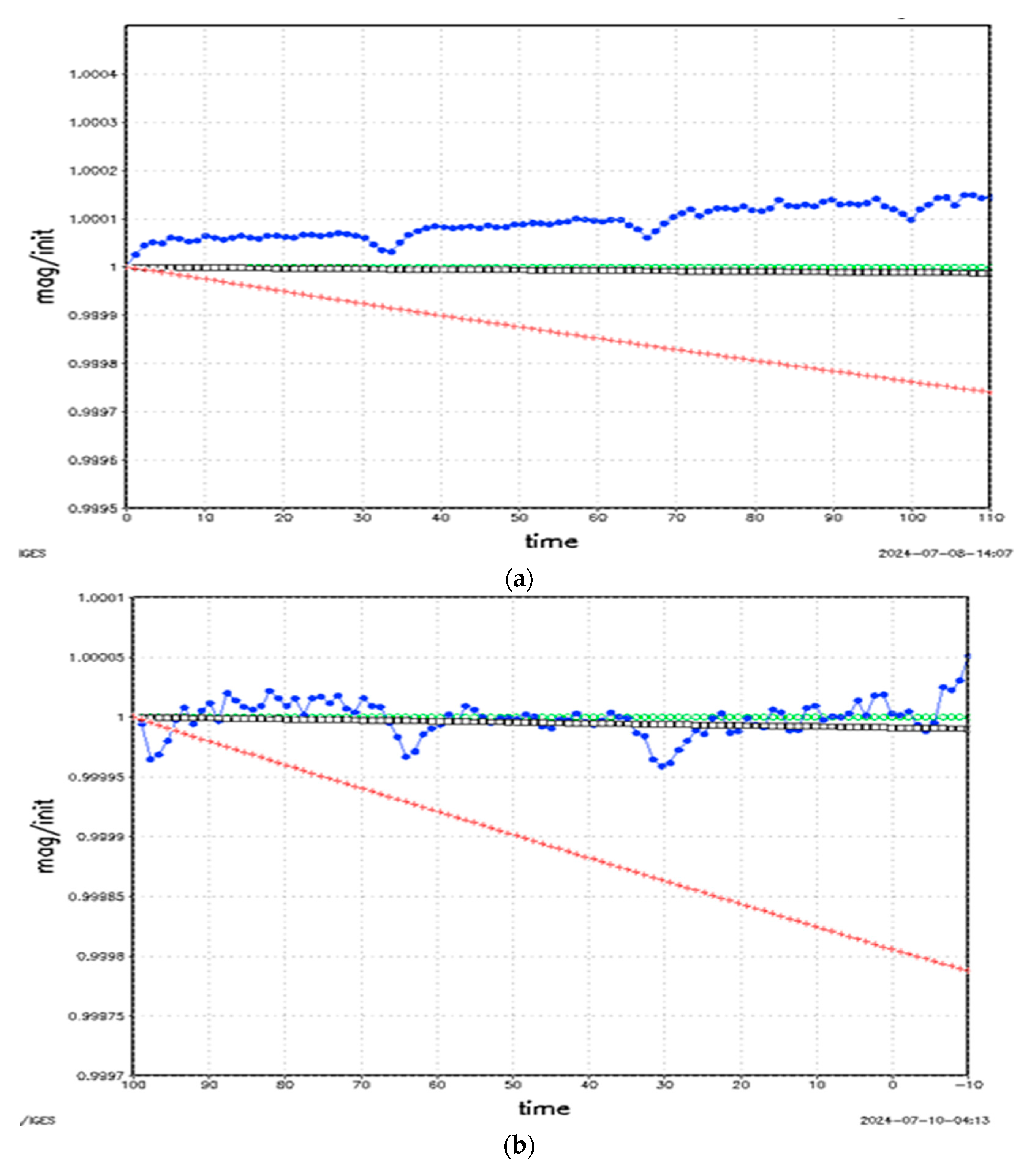
4.2. Result with B = 0.395 and CB = 0.395
4.3. Results with B = 0.6 and CB = 0.476
5. Discussion
6. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, W.Y. Instability in Leapfrog and Forward-Backward Schemes: Part II: Numerical Simulation of Dam Break. J. Comput. Fluids 2011, 45, 70–76. [Google Scholar] [CrossRef][Green Version]
- Pine, D.J.; Gollub, J.P.; Brady, J.F.; Leshansky, A.M. Chaos and threshold for irreversibility in sheared suspensions. Nature 2005, 438, 15. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G. Low Reynolds Number Flows and Reversibility. 1967. Available online: http://web.mit.edu/hml/notes.html (accessed on 25 September 2024).
- Wikipedia. Taylor–Couette Flow. Available online: https://en.wikipedia.org/wiki/Taylor%E2%80%93Couette_flow (accessed on 25 September 2024).
- Wikipedia. Navier–Stokes Equations. Available online: https://en.wikipedia.org/wiki/Navier%E2%80%93Stokes_equations (accessed on 25 September 2024).
- Haltiner, G.J.; Williams, R.T. Numerical Prediction and Dynamic Meteorology, 2nd ed.; Wiley: Hoboken, NJ, USA, 1980; p. 477. [Google Scholar]
- Fourier, J.B.J. Theorie Analytique de la Chaleur; Didot: Paris, France, 1822; pp. 499–508. [Google Scholar]
- Sun, W.Y.; Sun, O.M. Backward Integration of Diffusion Equation. Aerosol Air Qual. Res. 2017, 17, 278–289. [Google Scholar] [CrossRef]
- Eckhardt, B.; Hascoët, E. Breaking time reversal symmetry by viscous dephasing. Phys. Rev. E 2005, 72, 037301. [Google Scholar] [CrossRef]
- Fang, L.; Bos, W.J.T.; Liang, S.; Bertoglio, J.-P.; Shao, L. Time reversibility of Navier-Stokes turbulence and its implication for subgrid scale models. J. Turbul. 2012, 13, 639777. [Google Scholar] [CrossRef][Green Version]
- Kalnay, E.; Park, S.K.; Pu, Z.X.; Gao, J. Application of the Quasi-Inverse Method to Data Assimilation. Mon. Wea. Rev. 2000, 128, 864–875. [Google Scholar] [CrossRef][Green Version]
- Sun, W.Y. Instability in leapfrog and forward-backward Schemes. Mon. Wea. Rev. 2010, 138, 1497–1501. [Google Scholar] [CrossRef][Green Version]
- Lorenc, A.C. Analysis Methods for Numerical Weather Prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Sasaki, Y. Some basic formalisms in numerical variational analysis. Mon. Wea. Rev. 1970, 98, 875–883. [Google Scholar] [CrossRef]
- Le Dimet, F.; Talagrand, O. Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects. Tellus A. 1986, 38A, 97–110. [Google Scholar] [CrossRef]
- Johnson, C.; Nichols, N.K.; Hoskins, B.J. Very Large Inverse Problems in Atmosphere and Ocean Modelling; Numerical Analysis Report 5/04; Department of Mathematics, University of Reading: Reading, UK, 2005. [Google Scholar] [CrossRef]
- Huang, S.; Xiang, J.; Du, H.; Cao, X. Inverse problems in atmospheric science and their application. J. Phys. Conf. Ser. 2005, 12, 45–57. [Google Scholar] [CrossRef]
- Pu, Z.-X.; Kalnay, E.; Sela, J.; Szunyogh, I. Sensitivity of forecast errors to initial conditions with a quasi-inverse linear model. Mon. Wea. Rev. 1997, 125, 2479–2503. [Google Scholar] [CrossRef]
- Nabi, S.; Grover, P.; Caulfield, C. Robust preconditioned one-shot methods and direct-adjoint-looping for optimizing Reynolds-averaged turbulent flows. Comput. Fluids 2022, 238, 105390. [Google Scholar] [CrossRef]
- O’Connor, L.; Lecoanet, D.; Anders, E.H.; Augustson, K.C.; Burns, K.J.; Vasil, G.M.; Oishi, J.S.; Brown, B.P. Iterative methods for Navier-Stokes inverse problems. Phys Rev. E. 2024, 109, 045108. [Google Scholar] [CrossRef] [PubMed]
- Keller, J.J. Inverse Euler equation. Z. Angew. Math. Phys. 1966, 49, 363–383. [Google Scholar] [CrossRef]
- Kaus, B.J.P.; Podadchikov, Y.Y. Forward and Reverse Modeling of the Three-Dimensional Viscous Rayleigh-Taylor Instability. Geo. Res. Lett. 2001, 6, 1095–1098. [Google Scholar] [CrossRef]
- Sun, W.Y. Diffusion modeling in a convective boundary layer. Atmos. Environ. 1989, 23, 1205–1217. [Google Scholar]
- Sun, W.Y.; Sun, O.M.T. Numerical Simulation of Rossby Wave in Shallow Water. Comput. Fluids 2013, 76, 116–127. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai sur la Theorie des Eaux Courantes. Memoires Presentes par Divers Savants a L’academie des Sciences de L’institut National de France; XXIII, Imprimerie Nationale: Paris, France, 1877; pp. 1–680. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. London Edinburgh Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Larichev, V.D.; Reznik, G.M. On two-dimensional solitary Rossby waves. Dokl. Akad. Nauk. SSSR 1976, 231, 1077–1079. [Google Scholar]
- Boyd, J.P. Equatorial solitary waves. Part-1: Rossby solitons. J Phys Ocean. 1980, 10, 1699–1717. [Google Scholar] [CrossRef]
- Boyd, J.P. Equatorial solitary waves. Part 3: Westward-traveling motions. J Phys Ocean. 1985, 15, 46–54. [Google Scholar] [CrossRef]
- Muccino, J.C.; Bennett, A.F. Generalized inversion of the Korteweg–de Vries equation. Dyn. Atmos. Ocean. 2002, 35, 227–263. [Google Scholar] [CrossRef]
- Sun, W.Y.; Oh, T.J. Vortex Merger in Shallow Water Model. Asia-Pac. J. Atmos. Sci. 2022, 58, 533–547. [Google Scholar] [CrossRef]
- Sun, W.Y. Challenges and Progress in Computational Geophysical Fluid Dynamics in Recent Decades. Atmosphere 2023, 14, 1324. [Google Scholar] [CrossRef]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Sun, W.Y. Numerical experiments for advection equation. J. Comput. Phys. 1993, 108, 264–271. [Google Scholar] [CrossRef]
- Craig, W. An existence theory for water waves and the Boussinesq and Korteweg–de Vries scaling limits. Comm. Partial. Differ. Equ. 1985, 10, 787–1003. [Google Scholar] [CrossRef]
- Segur, H. Lecture 5: Waves in Shallow Water, Part I: The Theory; WHOI-2010-01 2009 Program of Study: Geophysical Fluid Dynamics, Nonlinear Waves; Woods Hole Oceanographic Institution: Falmouth, MA, USA, 2009; pp. 39–51. [Google Scholar]
- Drazin, P.G. Solitons; Lecture Note Series 85; Cambridge University Press London Mathematical Society: London, UK, 1983; ISSN 0076-0552. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics—The Finite Volume Method; Longman Scientific & Technical: New York, NY, USA, 1995; p. 257. [Google Scholar]
- Sun, W.Y.; Yeh, K.S. A general semi-Lagrangian advection scheme employing forward trajectories. J. R. Meteorol. Soc. 1997, 123, 2463–2476. [Google Scholar]
- Sun, W.Y. An efficient forward semi-Lagrangian model. Terr. Atmos. Ocean. Sci. 2024, 35, 1–6. [Google Scholar] [CrossRef]
- Oh, T.J. The Development and Testing of Characteristic-Based Semi-Lagrangian Two-Dimensional Shallow Water Equations Model. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2007. Available online: https://docs.lib.purdue.edu/dissertations/AAI3278686/ (accessed on 20 December 2020).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.-Y. Backward Integration of Nonlinear Shallow Water Model: Part I: Solitary Rossby Waves. Atmosphere 2024, 15, 1161. https://doi.org/10.3390/atmos15101161
Sun W-Y. Backward Integration of Nonlinear Shallow Water Model: Part I: Solitary Rossby Waves. Atmosphere. 2024; 15(10):1161. https://doi.org/10.3390/atmos15101161
Chicago/Turabian StyleSun, Wen-Yih. 2024. "Backward Integration of Nonlinear Shallow Water Model: Part I: Solitary Rossby Waves" Atmosphere 15, no. 10: 1161. https://doi.org/10.3390/atmos15101161
APA StyleSun, W.-Y. (2024). Backward Integration of Nonlinear Shallow Water Model: Part I: Solitary Rossby Waves. Atmosphere, 15(10), 1161. https://doi.org/10.3390/atmos15101161





