High-Resolution Daily PM2.5 Exposure Concentrations in South Korea Using CMAQ Data Assimilation with Surface Measurements and MAIAC AOD (2015–2021)
Abstract
1. Introduction
2. Measurement Data from Surface and Satellite
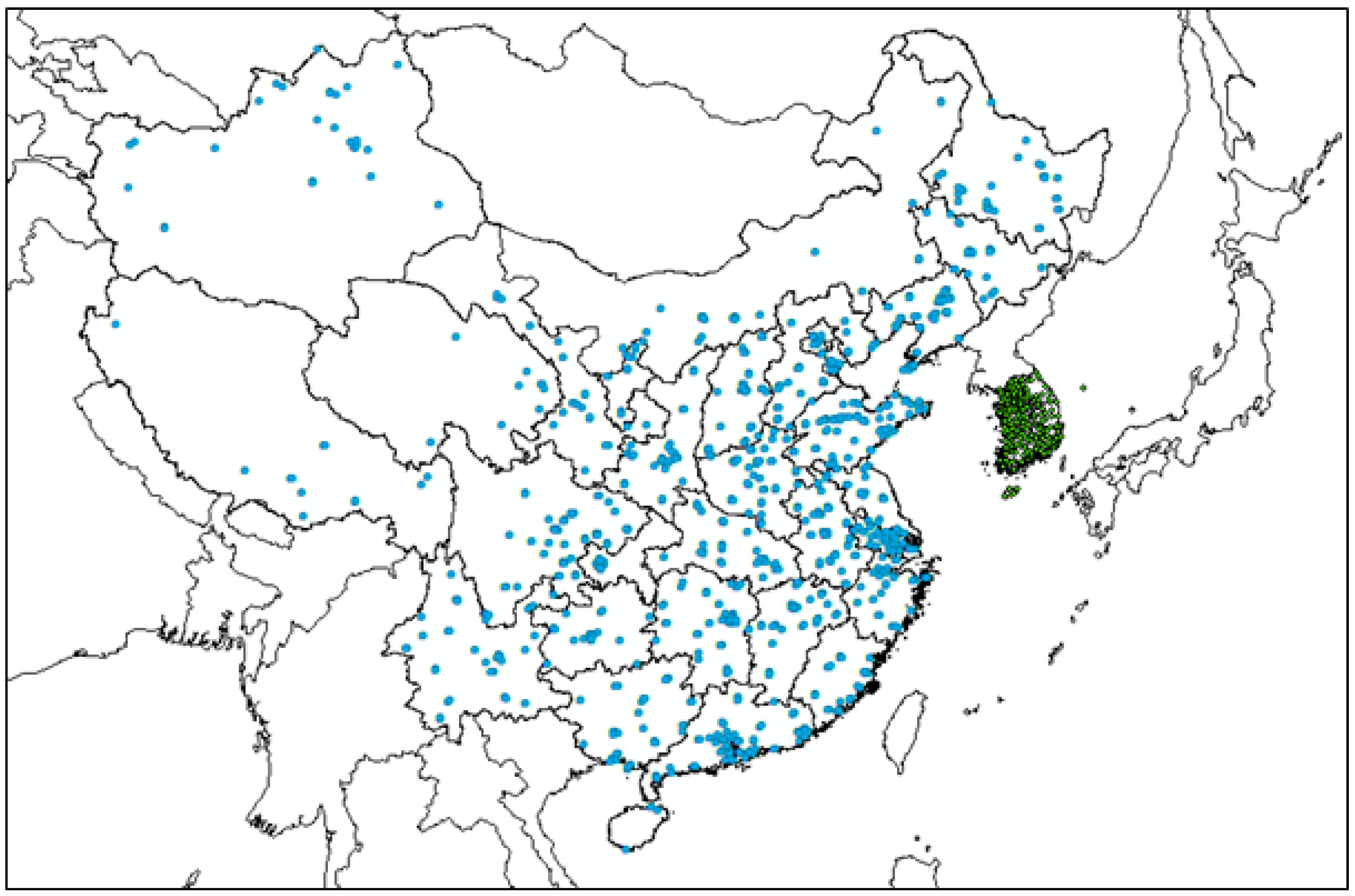
2.1. Air Quality Measurement Data
2.2. AOD and NDVI Satellite Observation Data
3. Chemical Transport Model with Data Assimilation
4. Results
4.1. Multiple Regression Analysis
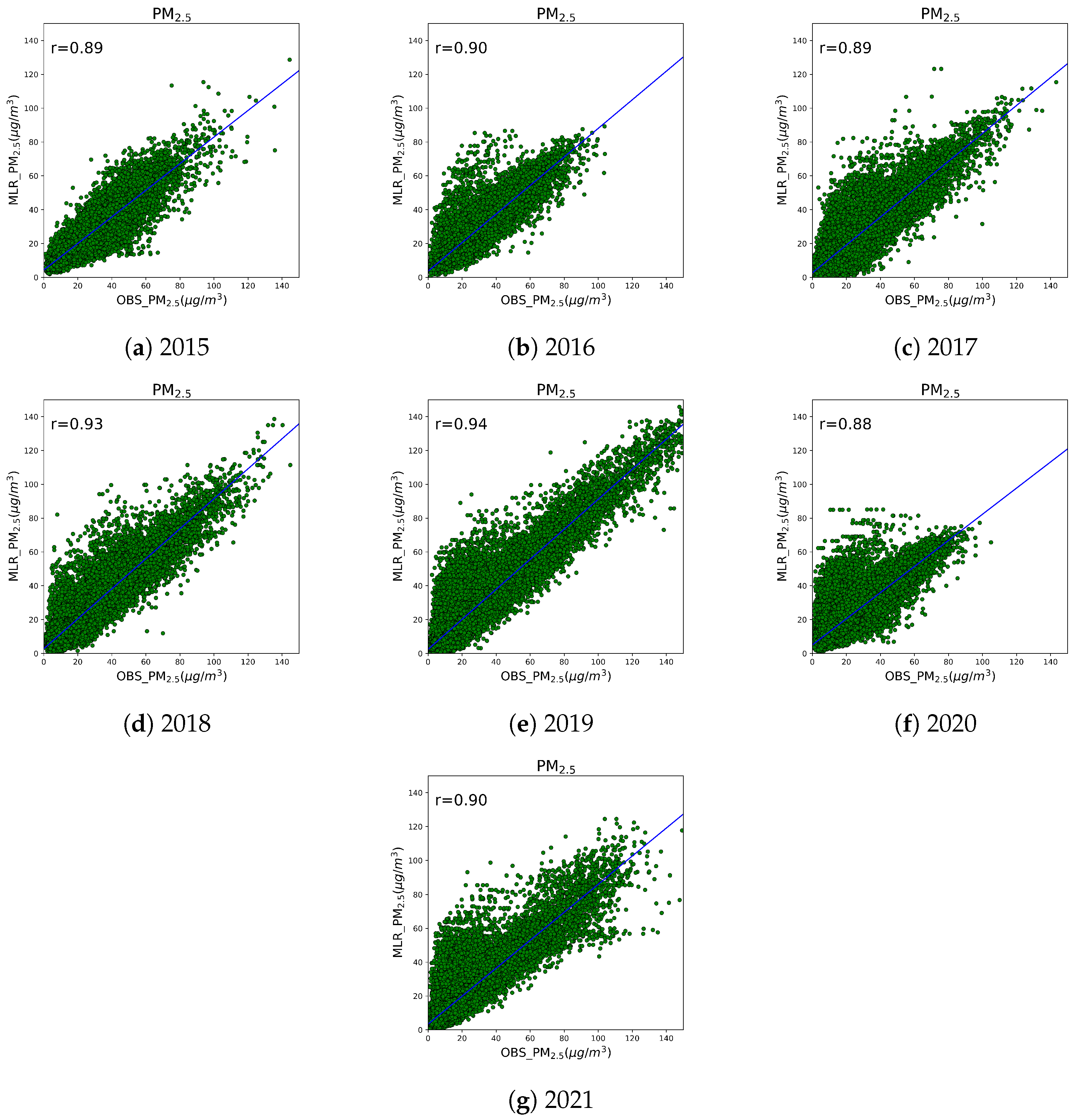
4.2. Evaluation of Reanalyzed Data Using Multiple Regression Analysis
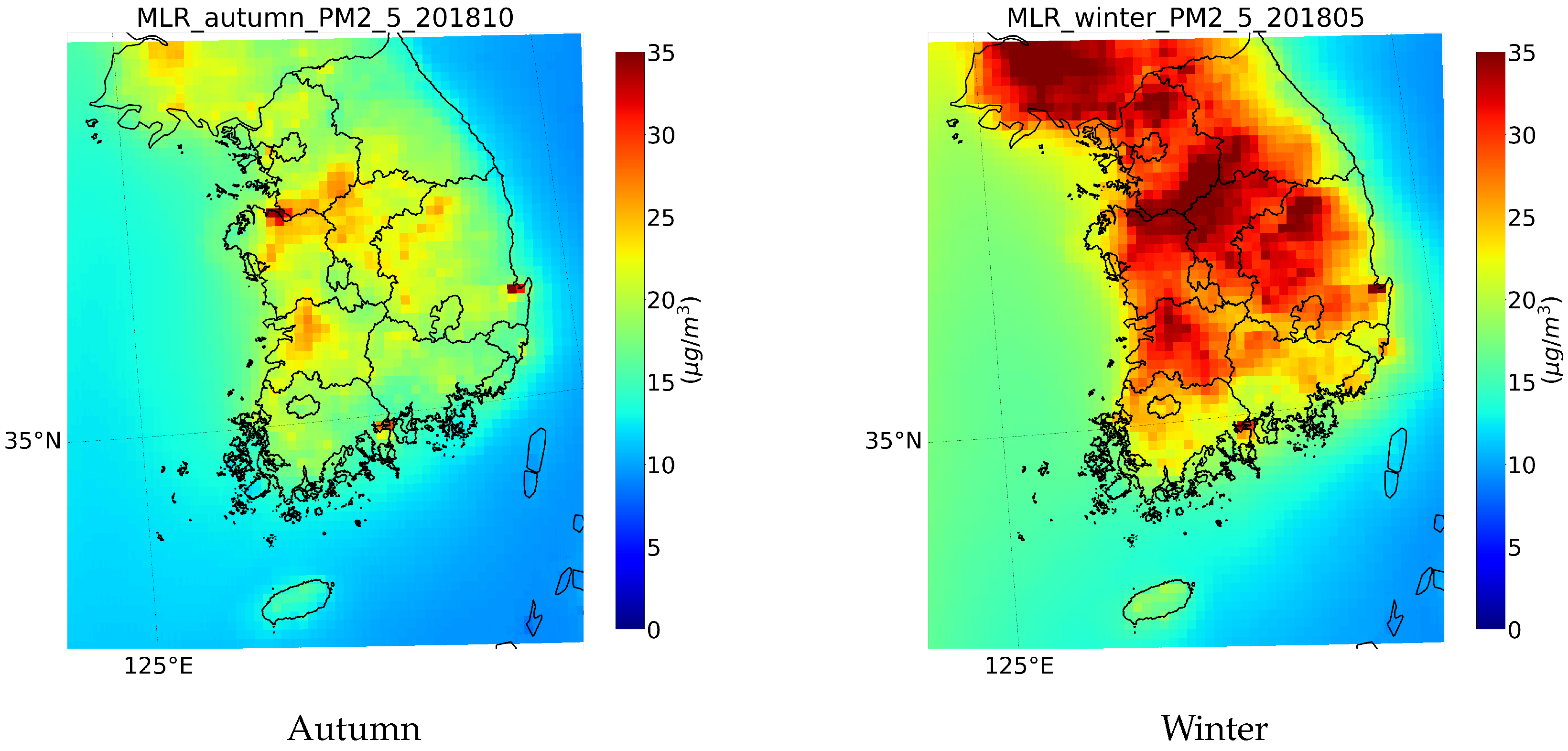
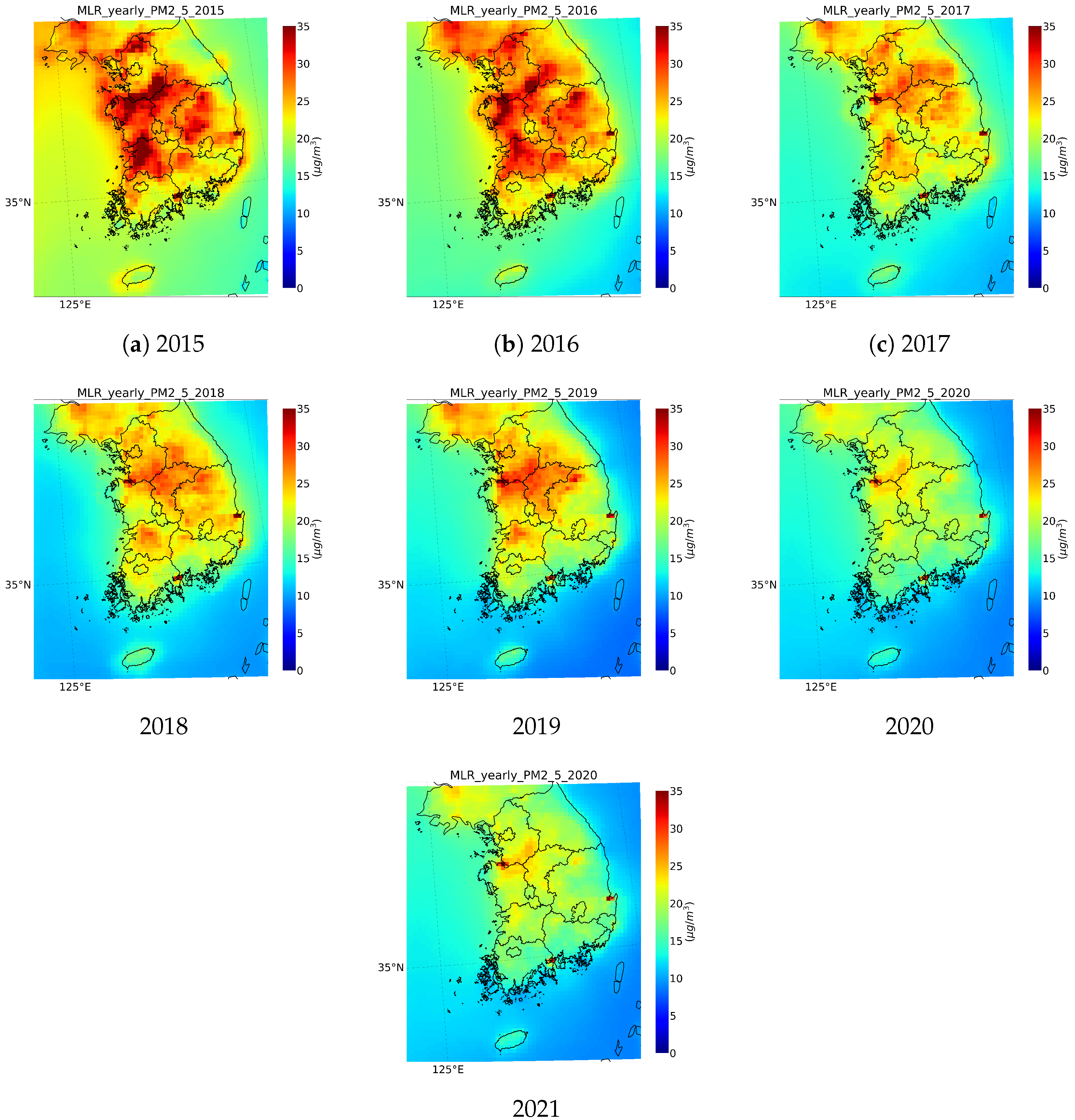
4.3. Spatial Distribution of Seasonal and Annual Average PM2.5 Concentrations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pope, C.A., III; Lefler, J.S.; Ezzati, M.; Higbee, J.D.; Marshall, J.D.; Kim, S.Y.; Bechle, M.; Gilliat, K.S.; Vernon, S.E.; Robinson, A.L.; et al. Mortality Risk and Fine Particulate Air Pollution in a Large, Representative Cohort of U.S. Adults. Environ. Health Perspect. 2019, 127, 77007. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Ambient Air Pollution: A Global Assessment of Exposure and Burden of Disease. 2016. Available online: https://www.who.int/publications/i/item/9789241511353 (accessed on 11 August 2024).
- Hwang, M.J.; Cheong, H.K.; Kim, J.H.; Koo, Y.S.; Yun, H.Y. Ambient air quality and subjective stress level using Community Health Survey data in Korea. Epidemiol. Health 2018, 40, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Oh, I.H.; Park, J.H.; Cheong, H.K. Premature Deaths Attributable to Long-term Exposure to Ambient Fine Particulate Matter in the Republic of Korea. J. Korean Med. Scil. Atmos. Environ. 2018, 33, e251. [Google Scholar] [CrossRef]
- Lim, H.; Kown, H.J.; Lim, J.A.; Choi, J.H.; Ha, M.; Hwang, S.S.; Choi, W.J. Short-term Effect of Fine Particulate Matter on Children’s Hospital Admissions and Emergency Department Visits for Asthma: A Systematic Review and Meta-analysis. J. Prev. Med. Public Health 2016, 49, 205–219. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kim, H.; Lee, J.T. Effect of air pollutant emission reduction policies on hospital visits for asthma in Seoul, Korea; Quasi-experimental study. Environ. Int. 2019, 132, 104954. [Google Scholar] [CrossRef]
- Beckerman, B.S.; Jerrett, M.; Martin, R.V.; Donkelaar, A.V.; Ross, Z.; Burnett, R.T. Application of the deletion substitution addition algorithm to selecting land use regression models for interpolating air pollution measurements in California. Atmos. Environ. 2013, 77, 142–149. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Meng, X.; Fang, Y.; Ge, Y.; Wang, J. Estimation of PM2.5 concentrations at a high spatiotemporal resolution using constrained mixed-effect bagging models with MAIAC aerosol optical depth. Remote Sens. Environ. 2018, 217, 573–586. [Google Scholar] [CrossRef]
- Chamependal, A.; Kanevski, M.; Huguenot, P.E. Air Pollution Mapping Using Nonlinear Land Use Regression Models. In Computational Science and Its Applications—ICCSA 2014; Lecutre Notes in Computer Science; Springer: Cham, Switzerland, 2014; pp. 682–690. [Google Scholar]
- Beloconia, A.; Chrysoulakis, N.; Lyapustin, A.; Utzinger, J.; Vounatsou, P. Bayesian geostatistical modelling of PM10 and PM2.5 surface level concentrations in Europe using high resolution satellite derived products. Environ. Int. 2018, 121, 57–70. [Google Scholar] [CrossRef]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; de Hoogh, K.; de’ Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013-2015, using a spatiotemporal land use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef]
- Ndiaye, A.; Shen, Y.; Kyriakou, K.; Karssenberg, D.; Schimitz, O.; Flukiger, B.; Hoogh, K.; Hoek, G. Hourly land-use regression modeling for NO2 and PM2.5 in the Netherlands. Environ. Res. 2024, 256, 119233. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Li, S.; Cao, W.; Ren, H.; Knibbs, L.D.; Abramson, M.J.; Guo, Y. Spatiotemporal patterns of PM10 concentrations over China during 2005–2016 A satellite-based estimation using the random forests approach. Environ. Pollut. 2018, 242, 605–613. [Google Scholar] [CrossRef]
- Xue, T.; Zheng, Y.; Tong, D.; Zheng, B.; Li, X.; Zhu, T.; Zhang, Q. Spatiotemporal continuous estimates of PM2.5 concentrations in China, 2000-2016:A machine learning method with inputs from satellites, chemical transport model, and ground observations. Environ. Int. 2022, 123, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Fiore, A.M.; Curci, G.; Lyapustin, A.; Civerolo, K.; Ku, M.; van Donkelaar, A.; Martin, R.V. Assessing uncertainties of a geophysical approach to estimate surface fine particulate matter distributions from satellite-observed aerosol optical depth. Atmos. Chem. Phys. 2019, 19, 295–313. [Google Scholar] [CrossRef]
- Wang, F.; Yao, S.; Luo, H.; Huang, B. Estimating High-Resolution PM2.5 Concentrations by Fusing Satellite AOD and Smartphone Photographs Using a Convolutional Neural Network and Ensemble Learning. Remote Sens. 2022, 14, 1515. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, J.H.; Im, J.H.; Song, C.K.; Choi, M.J.; Kim, J.; Lee, S.G.; Park, R.J.; Kim, S.M.; Yoon, J.M.; et al. Estimation of spatially continuous daytime particulate matter concentrations under all sky conditions through the synergistic use of satellite-based AOD and numerical models. Sci. Total. Environ. 2020, 713, 136516. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.S.; Lee, K.H.; Kim, S.M.; Yu, J.H.; Jeong, S.T.; Yeom, J.M. Hourly Ground-Level PM2.5 Estimation Using Geostationary Satellite and Reanalysis Data via Deep Learning. Remote Sens. 2021, 13, 2121. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, S.H.; Lee, M.I.; Kim, G.H.; Im, J.H.; Song, C.K. Air Quality Forecasts Improved by Combining Data Assimilation and Machine Learning with Satellite AOD. Geophys. Res. Lett. 2022, 49, e2021GL096066. [Google Scholar] [CrossRef]
- Tang, B.; Stanier, C.O.; Carmichael, G.R.; Gao, M. Ozone, nitrogen dioxide, and PM2.5 estimation from observation-model machine learning fusion over S. Korea: Influence of observation density, chemical transport model resolution, and geostationary remotely sensed AOD. Atmosphere 2024, 331, 120603. [Google Scholar] [CrossRef]
- Cho, S.Y.; Park, H.Y.; Son, J.S.; Chang, L.S. Development of the Global to Mesoscale Air Quality Forecast and Analysis System (GMAF) and Its Application to PM2.5 Forecast in Korea. Atmosphere 2021, 12, 411. [Google Scholar] [CrossRef]
- Lyapustin, A.; Martonchik, J.; Wang, Y.; Laszlo, I.; Korkin, S. Multiangle implementation of atmospheric correction (MAIAC): 1. Radiative transfer basis and look-up tables. J. Geophys. Res. Atmos. 2011, 116, D03210. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y. MCD19A2 V006 [Data set]. MODIS/Terra+Aqua Land Aerosol Optical Depth Daily L2G Global 1km SIN Grid. In NASA EOSDIS Land Processes DAAC; NASA: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Koo, Y.S.; Choi, D.R.; Yun, H.Y.; Yun, G.W.; Lee, J.B. A Development of PM Concentration Reanalysis Method using CMAQ with Surface Data Assimilation and MAIAC AOD in Korea. Korean J. Atmos. Environ. 2020, 16, 558–573. [Google Scholar] [CrossRef]
- Choi, D.R.; Yun, H.Y.; Koo, Y.S. A Development of Air Quality Forecasting System with Data Assimilation using Surface Measurements in East Asia. JKOSAE 2019, 35, 60–85. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatc atmospheric model for weather reasearch and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Borge, R.; Lopez, J.; Lumbereas, J.; Narros, A.; Rodriguez, E. Influence of boundary conditions on CMAQ simulations over the Iberian Peninsula. Atmos. Environ. 2010, 44, 2681–2695. [Google Scholar] [CrossRef]
- Byun, D.W.; Ching, J.K.S. Science Algorithms of the EPA Models-3 Community Multiscale Air Quality (CMAQ) Modeling System; EPA: Washington, DC, USA, 1998.
- Byun, D.W.; Schere, K.L. Review of the governing equations, computational algorithm and other components of the Models-3 Community Multi-scale Air Quality (CMAQ) modeling system. ASME 2006, 59, 51–77. [Google Scholar]
- Woo, J.H.; Kim, Y.H.; Kim, H.K.; Choi, K.C.; Eum, J.H.; Lee, J.B.; Lim, J.H.; Kim, J.Y.; Seong, M.A. Development of the CREATE Inventory in Support of Integrated Climate and Air Quality Modeling for Asia. Sustainability 2020, 12, 7930. [Google Scholar] [CrossRef]
- Lee, D.; Lee, Y.; Jang, K.; Yoo, C.; Kang, K.; Lee, J.; Jung, S.; Park, J.; Lee, S.; Han, J.; et al. Korean National Emissions Inventory System and 2007 Air Pollutant Emissions. Asian J. Atmos. Environ. 2011, 5, 278–291. [Google Scholar] [CrossRef]
- Cressman, G.P. An Operational Objective Analysis System, An Operational Objective Analysis System. Mon. Weather. Rev. 1959, 87, 364–374. [Google Scholar] [CrossRef]
- Pun, K.; Seigneur, C. Using CMAQ interpolate among CASTNET measurements. In Proceedings of the CMAS Conference, Chapel Hill, NC, USA, 16–18 October 2006; Available online: https://www.cmascenter.org/conference/2006/abstracts/pun_session7.pdf (accessed on 11 August 2024).
- Cohen, J. The Earth is Round (p < .05). Am. Psychol. 1994, 49, 997–1003. [Google Scholar]
- Ioannidis, J.P.A. Why most published research findings are false. Remote Sens. PLoS Med. 2005, 2, e124. [Google Scholar] [CrossRef]
- Koo, Y.S.; Kim, S.T.; Cho, J.S.; Jang, Y.K. Performance evaluation of the updated air quality forecasting system for Seoul predicting PM10. Atmos. Environ. 2012, 58, 56–69. [Google Scholar] [CrossRef]
- Koo, Y.S.; Choi, D.R.; Kwon, H.Y.; Jang, Y.K.; Han, J.S. Improvement of PM10 prediction in East Asia using inverse modeling. Atmos. Environ. 2015, 106, 318–328. [Google Scholar] [CrossRef]
- Koo, Y.S.; Yun, H.Y.; Choi, D.R.; Han, J.S.; Lee, J.B.; Lim, Y.J. An analysis of chemical and meteorological characteristics of haze events in the Seoul metropolitan area during January 12–18, 2013. Atmos. Environ. 2018, 178, 87–100. [Google Scholar] [CrossRef]


| Satellite Data | Description | CMAQ and WRF Model Data | Description |
|---|---|---|---|
| MODIS AOD | MAIAC MCD19 AOD | M_PM10 | assimilated PM10 |
| MODIS NDVI | MAIAC MOD13 NDVI | M_PM2.5 | assimilated PM2.5 |
| M_TEMP | WRF prediction | ||
| M_PLB | WRF prediction | ||
| M_RH | WRF prediction | ||
| M_WS | WRF prediction | ||
| M_PRSFC | WRF prediction |
| Predictor | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
|---|---|---|---|---|---|---|---|
| M_PM2.5 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| M_PBL | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| M_WS | 0.000 | 0.000 | 0.000 | 0.000 | 0.134 | 0.248 | 0.000 |
| M_SPRES | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| M_TEMP | 0.000 | 0.073 | 0.000 | 0.000 | 0.000 | 0.003 | 0.009 |
| M_RH | 0.000 | 0.156 | 0.000 | 0.000 | 0.415 | 0.000 | 0.000 |
| AOD | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| NDVI | 0.008 | 0.000 | 0.000 | 0.015 | 0.000 | 0.000 | 0.000 |
| Type | Year | MLR Equations |
|---|---|---|
| MLR (With AOD and NDVI) | 2015 | |
| 2016 | ||
| 2017 | ||
| 2018 | ||
| 2019 | ||
| 2020 | ||
| 2021 |
| Type | Year | MLR Equations |
|---|---|---|
| MLR (Without AOD and NDVI) | 2015 | |
| 2016 | ||
| 2017 | ||
| 2018 | ||
| 2019 | ||
| 2020 | ||
| 2021 |
| Year | R | R2 | IOA | RMSE | MB | NMB |
|---|---|---|---|---|---|---|
| 2015 | 0.89 | 0.79 | 0.94 | 6.58 | −1.16 | −4.54 |
| 2016 | 0.90 | 0.82 | 0.95 | 5.66 | −0.40 | −1.54 |
| 2017 | 0.89 | 0.79 | 0.94 | 6.90 | −1.78 | −7.13 |
| 2018 | 0.93 | 0.87 | 0.96 | 5.52 | 0.14 | 0.62 |
| 2019 | 0.94 | 0.88 | 0.97 | 5.73 | −0.23 | −1.01 |
| 2020 | 0.88 | 0.77 | 0.93 | 5.68 | 0.71 | 3.80 |
| 2021 | 0.90 | 0.82 | 0.95 | 5.60 | 0.28 | 1.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.-G.; Lee, J.-Y.; Lee, J.-B.; Lim, J.-H.; Yun, H.-Y.; Choi, D.-R. High-Resolution Daily PM2.5 Exposure Concentrations in South Korea Using CMAQ Data Assimilation with Surface Measurements and MAIAC AOD (2015–2021). Atmosphere 2024, 15, 1152. https://doi.org/10.3390/atmos15101152
Kang J-G, Lee J-Y, Lee J-B, Lim J-H, Yun H-Y, Choi D-R. High-Resolution Daily PM2.5 Exposure Concentrations in South Korea Using CMAQ Data Assimilation with Surface Measurements and MAIAC AOD (2015–2021). Atmosphere. 2024; 15(10):1152. https://doi.org/10.3390/atmos15101152
Chicago/Turabian StyleKang, Jin-Goo, Ju-Yong Lee, Jeong-Beom Lee, Jun-Hyun Lim, Hui-Young Yun, and Dae-Ryun Choi. 2024. "High-Resolution Daily PM2.5 Exposure Concentrations in South Korea Using CMAQ Data Assimilation with Surface Measurements and MAIAC AOD (2015–2021)" Atmosphere 15, no. 10: 1152. https://doi.org/10.3390/atmos15101152
APA StyleKang, J.-G., Lee, J.-Y., Lee, J.-B., Lim, J.-H., Yun, H.-Y., & Choi, D.-R. (2024). High-Resolution Daily PM2.5 Exposure Concentrations in South Korea Using CMAQ Data Assimilation with Surface Measurements and MAIAC AOD (2015–2021). Atmosphere, 15(10), 1152. https://doi.org/10.3390/atmos15101152








