Abstract
Pilots commonly undergo training to effectively manage instances of wind shear (WS) during both the landing and takeoff stages. Nevertheless, in exceptional circumstances, there may be instances of severe wind shear (SWS) surpassing a magnitude of 30 knots, leading to adverse effects on the operation of taking off and landing aircraft. This phenomenon can lead to the execution of aborted landing maneuvers and deviations from the intended glide path. This study utilized the explainable boosting machine (EBM), an advanced machine learning (ML) model known for its transparency, to predict the severity of WS occurrences and analyze the underlying factors. The dataset consisted of 21,392 data points from 2018 to 2022 acquired from two Doppler light detection and ranging (LiDAR) systems installed at Hong Kong International Airport (HKIA). Initially, the Doppler LiDAR data received data treatment in order to address the issue of data imbalance. Subsequently, utilizing the processed data, the hyperparameters of EBM were optimized using the Bayesian optimization technique. The EBM model underwent subsequent training and evaluation, wherein its performance metrics were computed and compared with those of an alternative glass-box model including decision tree (DT) and counterpart black-box models, namely, random forest (RF) and extreme gradient boosting (XGBoost). The EBM model trained on synthetic minority oversampling technique (SMOTE)-treated data demonstrated superior performance in comparison with the alternative models, as indicated by its higher geometric mean (0.77), balanced accuracy (0.78), and Matthews’ correlation coefficient (0.169). Furthermore, the EBM exhibited enhanced predictive performance and facilitated a comprehensive analysis of individual and pairwise factor interactions in the prediction of WS severity. This enabled the assessment of the factors that contributed to the instances of SWS in the proximity of airport runways.
1. Introduction
Wind shear (WS) is defined by the International Civil Aviation Organization (ICAO) as a minimum of 15 knots of consistent headwind or tailwind variation occurring within 1600 feet of the ground [1]. Typically, pilots acquire training on handling this phenomenon. Nevertheless, rare instances exist in which severe wind shear (SWS) can manifest, surpassing 30 knots in magnitude [2]. The SWS phenomenon is of a critical safety nature as it possesses a tendency to induce aircraft to stray from their established flight course, thus putting incoming and departing aircraft in jeopardy as shown in Figure 1. Flight disruptions such as delays, cancellations, and catastrophes can transpire under particularly extreme circumstances [3,4,5,6].
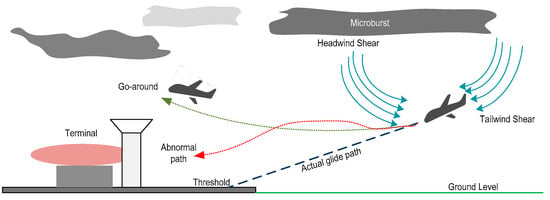
Figure 1.
Effect of WS on the aircraft’s final approach.
Various airports across the globe have recorded numerous instances of SWS [7,8,9]. Prompt notifications of WS are of paramount significance due to the potential for SWS to negatively impact aircraft as well as airport operations. Hong Kong International Airport (HKIA) is widely recognized as one of the airports that exhibit a significant susceptibility to weather-related disruptions, particularly WS and aviation turbulence [10,11]. The location of HKIA is in the northern region of Lantau Island, known for its undulating landscape that includes mountain peaks reaching heights exceeding 900 m and valleys descending to around 300 m. Therefore, the requirement of a reliable approach for predicting WS and turbulence is crucial in the context of achieving accurate and efficient alerts, in addition to guaranteeing the safety of civil aviation.
Researchers have utilized various numerical modeling strategies, such as large-eddy simulations (LESs) [12,13], computational fluid dynamics (CFD) [14,15], and numerical weather prediction (NWP) [11], to forecast or simulate WS as well as turbulence phenomena. However, the aforementioned studies primarily examined individual or isolated instances of WS events. There has been a dearth of comprehensive and enduring assessments pertaining to the efficacy of numerical models in accurately predicting WS severity. The study of quantifying the WS severity in the closest vicinity of airport runways and analyzing the factors that contribute to its happening is a highly intricate and challenging domain within the realm of civil aviation safety. In recent times, machine learning (ML) algorithms have witnessed substantial advancements [16,17,18]. They have gained significant popularity and proven to be extremely useful in various areas of transportation [19,20] and meteorological research [21,22]. This field of study falls at the junction of statistics and computer science. The utilization of ML models is of paramount significance in tackling all of the challenges that arise when building statistical models from large-scale datasets, necessitating the implementation of computational techniques. However, a notable limitation of ML models is their inherent “black-box” characteristic [23]. While they may offer superior performance, they fall short in delivering a comprehensive interpretation.
On the contrary, a recent development in the field is the explainable boosting machine (EBM) [24], a contemporary “glass-box” model designed with inherent interpretability as an important attribute. This implies that the generated explanations possess a dual characteristic of precision and comprehensibility for human comprehension [25,26]. This strategy takes advantage of a tree-based, cyclic gradient-boosting mechanism. It is a general additive model that incorporates automatic interaction detection. In regard to reliability, EBM has exhibited similar performance to advanced ML models [27,28,29].
In an effort to transition from black-box models to glass-box models, this study aimed to provide an EBM technique for WS severity prediction and interpretation of the contributing factors. WS data were compiled from Doppler light detection and ranging (LiDAR) systems located at HKIA in order to retrieve a number of factors. Our intent was to formulate a binary classification problem in which SWS events were rare instances that were designated as the minority class, while non-severe WS (NSWS) were designated as the majority class. Consequently, prior to training the model, the imbalanced WS data were addressed using the synthetic minority oversampling technique (SMOTE) [30], support vector machine—synthetic minority oversampling technique (SVM-SMOTE) [31], and adaptive synthetic oversampling (ADASYN) [32]. Similarly, during the training–validation stage, the hyperparameters of the EBM model were also required to be optimized to achieve better performance. In this study, we employed the Bayesian optimization technique [33] to fine-tune the hyperparameters of the EBM model.
This study is, to the best of our knowledge, the first practical application of a glass-box approach for the purpose of predicting and interpreting the WS severity in close proximity to airport runways. The outcomes of our study would provide pilots, air traffic controllers, and other policymakers in the realm of civil aviation with a better understanding of the factors that contribute to the occurrence of SWS. Through the implementation of aviation safety standards, the provision of comprehensive pilot training, and the acquisition of appropriate equipment, it becomes feasible to develop preventive strategies aimed at efficiently handling SWS events. Figure 2 depicts the comprehensive research framework. The subsequent sections of the article are organized in the following form: Section 2 provides a comprehensive account of various aspects, including the study location, the intricate specifications of the Doppler LiDAR system employed for acquiring WS data, a theoretical description of the EBM framework, an overview of Bayesian optimization, and a discussion of the performance measures employed in the study. Section 3 presents the outcomes derived from the EBM model and its subsequent comparison with other advanced ML models. Furthermore, an interpretation of the EBM model is also provided. Section 4 of the paper is specifically allocated to the presentation of the conclusions and recommendations.
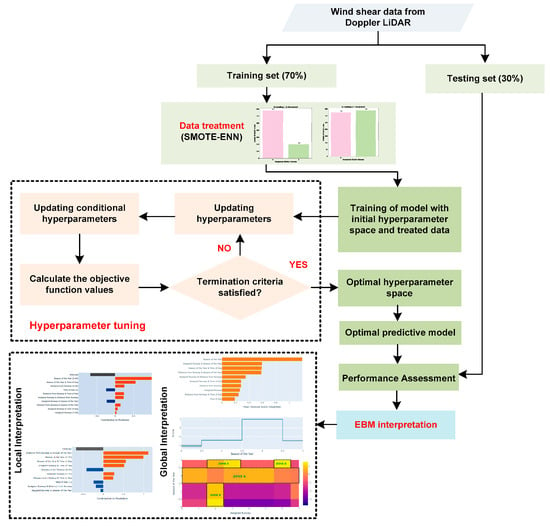
Figure 2.
Schematic flowchart of EBM-based WS severity modeling and interpretation.
2. Materials and Methods
2.1. Study Location and Data Retrieval from HKIA-Based Doppler LiDAR
HKIA is located on Lantau Island of Hong Kong. This island is bordered by water on all three of its sides. In the southern region of the HKIA lies a mountainous terrain characterized by elevated plateaus that exceed an altitude of 900 m relative to sea level, as shown in Figure 3. As HKIA is highly susceptible to the WS occurrences, therefore, this study utilized WS data collected from two long-range Doppler LiDAR systems [34] at HKIA. The Doppler LiDAR system had the capability to estimate the magnitude of WS events and provide information on their specific occurrence locations. The Doppler LiDAR’s radial resolution, referred to as the physical range gate, was 100 m, while its operational wavelength was approximately 1.5 microns in the infrared spectrum. The maximum achievable radial velocity was around 40 m/s [35]. Under ideal weather conditions and without any impediments like low clouds, it was possible to observe objects within a radius that ranged from 10 to 15 km. Doppler LiDAR systems have the capability to be tailored to conduct glide path scans with regard to landing and takeoff paths, alongside regular fixed-elevation scans known as plan position indicators. In order to achieve the intended objective, it was crucial to align the vertical (elevation) and horizontal (azimuth) shifts of the laser scanner’s head. The estimation of WS over each runway could be conducted by utilizing radial velocity data obtained from glide path scans. The typical time required to scan each runway was approximately 1 min. The northern Doppler LiDAR system handled various configurations of the northern runway, namely, 07LA, 25RA, 07LD, and 25RD. Similarly, the southern Doppler LiDAR system examined the configurations of the southern runway, namely, 25LA, 07LA, 07RD, and 25LD, as depicted in Figure 4.
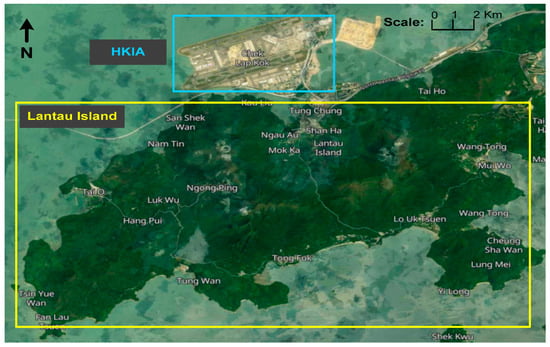
Figure 3.
Location of Lantau Island of Hong Kong and HKIA at the northern region of Lantau Island.
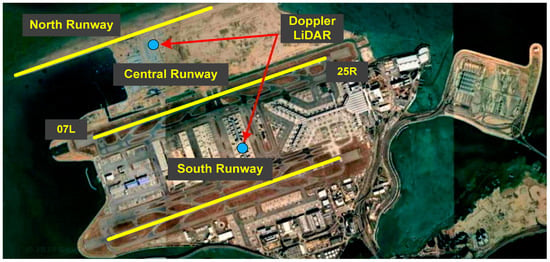
Figure 4.
Location of Doppler LiDAR systems at HKIA.
Figure 5 displays an example of a visual representation of a radial velocity plot that was obtained through the utilization of a plan position indicator (PPI) scan of the southern runway Doppler LiDAR. The scan was performed with an azimuth angle of 3° in relation to the horizon. A significant expanse of winds was observed to be flowing in a direction opposite to the prevailing east-southeast airflow, situated in the western and southern regions relative to the specified coordinates. This area was located at a distance of three nautical miles (equivalent to 5.6 km) in the west-southwest direction from the westernmost point of the southern runway. The depicted region is visually characterized by its green hue.
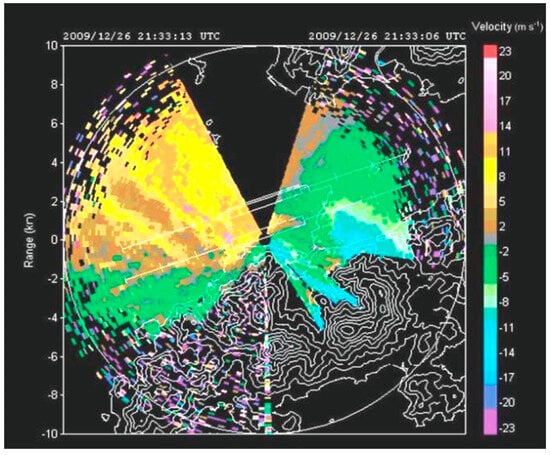
Figure 5.
WS at the south runway detected by the HKIA-based Doppler LiDAR system.
It is imperative to comprehend that the precise horizontal encounter location of the WS was also of paramount importance. As depicted in Figure 6, the areas where WS events took place were denoted by the aviation terminology of RWY, MD, or MF. The encounter locations of WS events at specific horizontal distances from the runway threshold, such as 1 nautical mile (1MF) and 2 nautical miles (2MF) from the approaching and departing end of the runway, are depicted in Figure 6. Table 1 illustrates the sample WS data obtained from HKIA-based Doppler LiDAR.
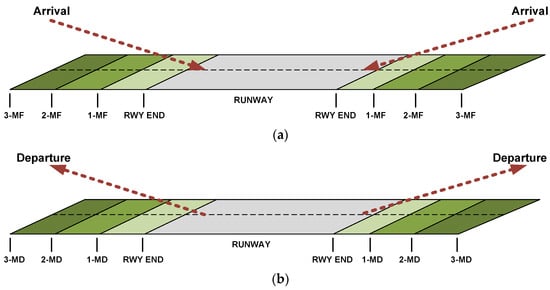
Figure 6.
WS encounter locations. (a) WS occurrence distances at the arrival. (b) WS occurrences distance at the departure.

Table 1.
Sample of HKIA-based Doppler LiDAR WS data points.
2.2. Developing a Binary Classification Problem
To develop a WS severity model, a substantial quantity of WS data was necessary. In light of the provided context, the initial step involved acquiring the WS data from HKIA-based Doppler LiDAR systems. Subsequently, a filtering procedure was implemented to classify the WS events into two distinct categories: severe wind speed (SWS) and non-severe wind speed (NSWS). More specifically, as shown in Table 1, a WS event that had an absolute magnitude equal to or greater than 30 knots was classified as SWS, whereas all other WS events were designated as NSWS. The binary classification problem entailed assigning a value of 1 to the occurrence of the “SWS” event and a value of 0 to the occurrence of “NSWS,” as demonstrated in Equation (1).
The other factors, including the season of the year, the time of the day, the assigned runway for operation, and the WS occurring distance from the runway threshold, were coded by means of the label encoding technique [36]. It is a commonly employed method in ML modeling to transform categorical factors into numerical representations, enabling their utilization in models that exclusively accept numerical data. Table 2 illustrates the label encoding of different factors that were considered in the EBM modeling.

Table 2.
Label encoding of data extracted from HKIA-based Doppler LiDAR system.
2.3. Explainable Boosting Machine: An ML-Based Glass-Box Model
EBM is a contemporary glass-box model that is inherently interpretable and is based upon the general additive model (GAM), incorporating supplementary pairwise interactions. The functional form of the EBM is denoted as Equation (2) for each th data point within the Doppler LiDAR dataset .
where
- : Link function, representing identity function for regression and logit function for classification
- Intercept term
- Shape or smooth function
During the training of an explainable boosting machine (EBM) model, a “round-robin loop” is used where each factor is addressed sequentially. This loop ensures that the order in which the factors are considered does not affect the final outcome. A smaller learning rate is employed to gradually update the model as each factor is incorporated. The iterations continue until all the factors have been taken into account. Therefore, in the initial iteration, the response factor is provided as
Similarly, the second iteration is given as follows:
The process persists until the th iteration is attained. By summing all of the other functions associated with a particular factor, one can ascertain its overall objective, that is,
EBM generates a table of versus for each factor, which is then used to generate the plot of score versus . This narrative aids in comprehending the correlation between factor and factor , as well as the individual impact of each factor on the predictive ability of factor .
However, EBM does not conclude at this point. Furthermore, this approach considers the interactions among the factors within a two-dimensional scheme. A model that incorporates two-dimensional interaction can be effectively interpreted by representing the outcomes of these interactions as heat maps on a two-dimensional plane. Hence, the ultimate manifestation of EBM, which encompasses the intercept, individual effects, and interaction effect, can be mathematically expressed as Equation (3).
Typically, the detection of interaction terms necessitates a substantial computational capacity, especially when dealing with huge datasets. The challenge is addressed by EBM through the implementation of a two-stage construction strategy and the utilization of FAST [37] to effectively rank the pairwise interactions. The strategy is divided into two discrete phases. The initial stage entails the development of an ideal additive model by employing solely one-dimensional elements. In the next phase, the one-dimensional functions are stabilized, and models are developed to account for pairwise interactions in the remaining variation. Specifically, the highest-T interaction pairs are selected using the FAST algorithm, and a model is fitted using these pairs on the residual . The value of the T is computed based on the available computing power.
The final outcome in EBM is determined by aggregating the individual contributions of each factor. This approach allows for a clear and intuitive understanding of the contributions made by distinct factors and interaction terms. The additional training cost incurred by EBM due to the modularity of the prediction results in a slower performance compared with similar ML strategies. Nevertheless, the prediction process remains unaffected by this as it only requires basic arithmetic operations within the factor functions. Indeed, this characteristic renders the EBM strategy one of the most expeditious predictive models to deploy. The learning mechanism of EBM models is visualized in Figure 7.
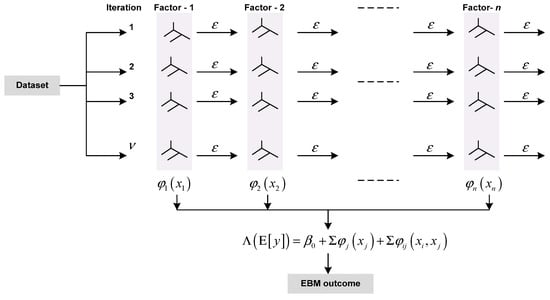
Figure 7.
Learning mechanism of EBM framework.
2.4. Bayesian Optimization
The process of hyperparameter tuning through trial and error is laborious and frequently yields sub-optimal outcomes. Therefore, it is imperative to employ robust tuning approaches, particularly when the objective of optimization is to locate the highest value at the point of sampling for an unfamiliar function as shown by Equation (4).
In the present context, the symbol is employed to denote the sampling point, whereas it signifies the search space of said sampling point . The function represents an unspecified objective function, and denotes the location at which this objective function is to be optimized for maximum value. The Bayesian optimization consists of two primary steps.
- First, the Bayesian optimization attempts to construct a surrogate function for by randomly selecting a subset of data points. In this study, the surrogate function was updated using a Gaussian process (GP) to create the posterior distribution over . The use of GP was justified by its high flexibility, robustness, accuracy, and analytical traceability.
- Initially, the Bayesian optimization procedure endeavors to create a surrogate function for the target function, denoted as , by employing a random selection process to choose a subset of data points. The surrogate function in this study was enhanced through the utilization of GP in order to generate the posterior distribution over . The utilization of GP was justified due to its notable attributes such as high flexibility, robustness, accuracy, and analytical traceability. Subsequently, the posterior distribution obtained from the initial step is employed to derive an acquisition function that serves the dual purpose of exploring unexplored regions within the search space and exploiting regions that have already been identified as yielding optimal outcomes. The processes of exploration and exploitation are ongoing, and the surrogate model continues to be updated with new findings until an established until the termination criterion is met. The primary aim is to enhance the performance of the acquisition function, particularly the expected improvement metric, for the purpose of identifying the subsequent sampling point.
2.5. Performance Measures
The performance of the EBM model in terms of its predictive and classifying abilities can be assessed by confusion matrix as shown in Figure 8. The four indicators including true position , false positive , true negative , and false negative were obtained from the confusion matrix and were then used to obtain various performance measures including precision, recall, geometric mean (G-mean), balanced accuracy (BA), and Matthews’ correlation coefficient (MCC). In addition, the area under the receiver operating characteristic (AU-ROC) curve was also obtained. The mathematical expressions for these performance measure are shown in Equations (5)–(9).
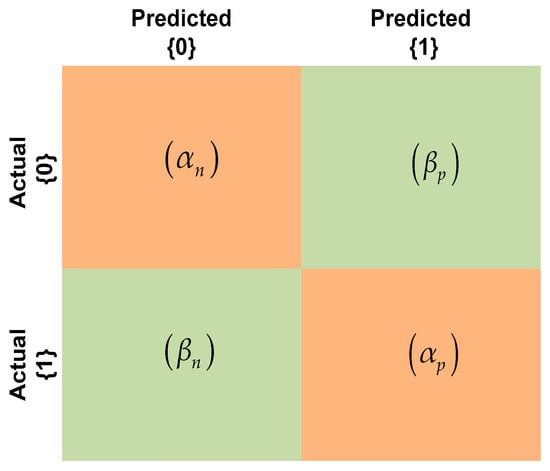
Figure 8.
Confusion matrix.
3. Results and Discussion
The WS data obtained from two Doppler LiDAR systems stationed at HKIA were originally subjected to a data cleaning process and examined for the existence of any missing values. Following this, we partitioned the data into distinct training–validation (70%) and testing datasets (30%). In the course of the present research, both the positive and negative classes were denoted as “SWS” and “NSWS,” respectively. Nevertheless, a class imbalance existed between the “SWS” and “NSWS” classes. A total of 21,392 data points of WS have been acquired from Doppler LiDAR. Examining these data points revealed that 2956 data points corresponded to SWS incidents, while the remaining data points represented NSWS events. To address the issue of data imbalance, various treatment procedures, such as SMOTE, SVM-SMOTE, and ADASYN, were applied to the training dataset prior to model training. Figure 9 illustrates the distribution of each class (SWS and NSWS) both with and without data treatments.
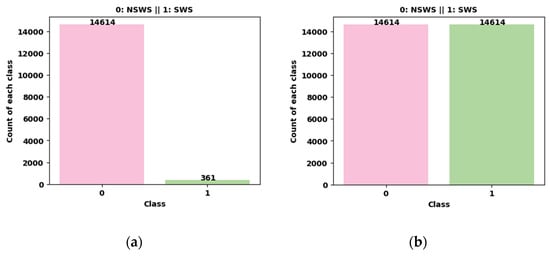
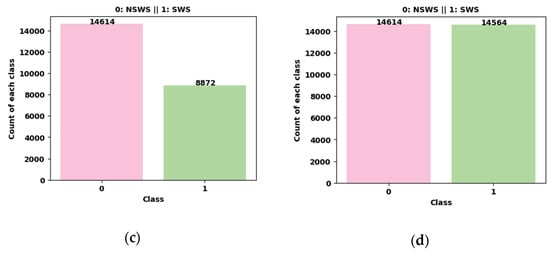
Figure 9.
Doppler LiDAR training data treatment. (a) Untreated/original data. (b) SMOTE-treated training data. (c) SVM-SMOTE-treated training data. (d) ADASYN-treated training data.
3.1. Optimal Hyperparameters via Bayesian Optimization
Following the data treatment process, the subsequent stage involved the hyperparameter adjusting of the EBM model, as well as other competitor models such as XGBoost and RF. These models were trained on distinct treated datasets. This stage held significance because of its potential impact on the performance of generalization, its ability to mitigate over-fitting, and its capacity to reduce the complexity of the model. In order to acquire the optimal hyperparameters, a Bayesian optimization technique was utilized, with the objective of maximizing the “G-mean” value. Bayesian optimization was implemented in conjunction with a 10-fold cross-validation strategy in the present study. The approach entailed the random division of the training set into ten subsets, wherein nine subsets were utilized for training and one subset was designated for testing in each iteration. The hyperparameters’ optimal values are shown in Table 3.

Table 3.
Hyperparameters optimized using Bayesian optimization.
It is essential to emphasize that to assure consistency in the tuning of hyperparameters for various data treatments, the search space for all hyperparameters remained unchanged. As an example, the search space for the learning_rate parameter ranged from 0.01 to 0.2, the max_depth parameter ranged from 3 to 10, the n_estimators parameter ranged from 100 to 1500, and the max_leaves parameter ranged from 3 to 10. It is important to note that the remaining hyperparameters were disregarded in the process of Bayesian optimization due to their lack of substantial contribution toward enhancing the performance.
3.2. Predictive Performance of EBM and Comparative Analysis
The confusion matrix values for various treated data were utilized to derive the classification outcomes, including true positive, true negative, false positive, and false negative (refer to Table 4). These results were utilized in the computation of the evaluation measures with the purpose of enabling the comparison of different models. Measures such as precision, recall, G-mean, BA, and MCC have been commonly employed in the field of imbalanced classification problems [38,39]. Table 5 presents the indicators computed for different data treatments. The findings revealed that the utilization of the EBM model, trained on data that had undergone SMOTE treatment, resulted in better performance compared with alternative models. This was evidenced by higher values of G-mean (0.77), BA (0.78), and MCC (0.169). The values given above demonstrated the highest scores among all evaluated competing models.

Table 4.
Comparison of confusion matrix outcomes of EBM and other competitive models.

Table 5.
Performance measures of EBM and other competitors with different data treatment strategies.
Furthermore, ROC curves were generated to ascertain the AU-ROC values for each model, as depicted in Figure 10. Both SMOTE+EBM and SVM-SMOTE+EBM attained the higher AU-ROC value (0.854). The strategy with the lowest AU-ROC (0.72) was demonstrated by ADASYN + RF. The SMOTE+EBM model may be interpreted in light of the aforementioned observation with the aim to examine a number of factors that lead to the occurrence of SWS.
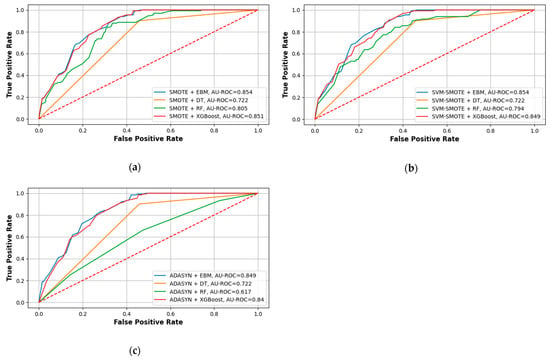
Figure 10.
ROC curves for EBM and other competitive models. (a) ROC curves based on SMOTE-treated training data. (b) ROC curves based on SVM-SMOTE-treated training data. (c) ROC curves based on ADASYN-treated training data.
3.3. Uncertainty Analysis of EBM Model
In addition to performance measures, it is important to conduct uncertainty analysis of EBM model. A bar graph as well as computed statistical indicators for uncertainty analysis of EBM model is shown in Figure 11. The results obtained from the bar graph of uncertainty analysis of an EBM provide insights into the level of uncertainty associated with the EBM model’s predictions for each instance in the testing dataset. The uncertainties were calculated using the entropy measure. Entropy is basically a measure of the impurity or unpredictability of a probability distribution. Higher entropy indicates higher uncertainty. The resulting uncertainties represent a numerical value for each instance, indicating the level of uncertainty associated with the EBM model’s prediction for that instance. A higher uncertainty value suggests that the model is less confident in its prediction for that particular instance. By plotting the uncertainties as a bar graph, we can visually analyze the distribution of uncertainty across the instances in the dataset. The x-axis represents the instances, and the y-axis represents the uncertainty values. The bar chart allowed us to compare and identify instances with higher or lower uncertainty.
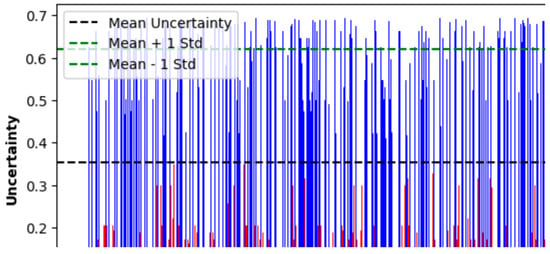
Figure 11.
Uncertainties (as entropy) of EBM model for testing data.
In addition to the visual analysis by using the bar graph, we obtained statistical indicators including the mean and standard deviation. We obtained the mean uncertainty value of 0.354, which suggested that on average, the EBM model’s predictions had a moderate level of uncertainty. The bars in red indicate the uncertainty values of each instance that is lower than the mean uncertainty. This indicates that the proposed model was reasonably confident in its predictions for most instances, but there was still some degree of uncertainty present. Similarly, the standard deviation of 0.267 indicates a slight variability of the uncertainty values around the mean. Overall, it was demonstrated that the EBM model’s predictions had a moderate level of uncertainty, with some instances having higher or lower uncertainty compared with the average.
3.4. EBM Interpretation
The comprehensive interpretation of EBM allows for an assessment of the impact of various combinations of factors on the predicted severity of WS outcomes. Figure 12 presents the contribution of each individual factor in predicting WS severity as well as individual and pairwise interaction of important factors (Global Interpretation). Figure 12a revealed that when considering individual factor, it is evident that the season of the year played the most contributing role. In the context of pairwise interaction, it can be observed that the season of the year and the assigned runway factor contributed the most to predicting WS severity.
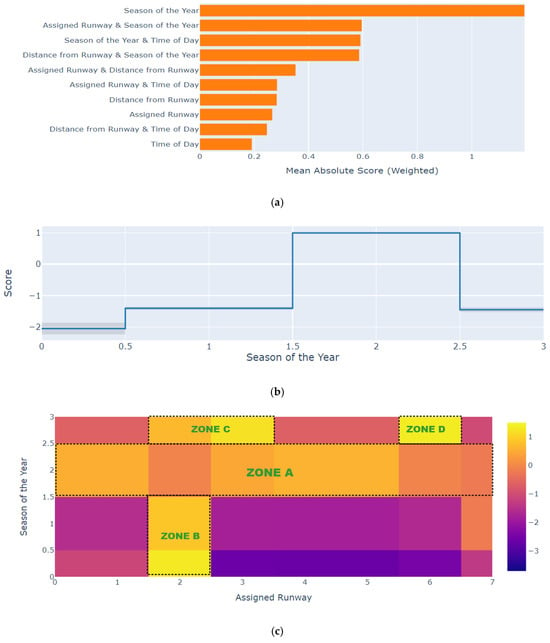
Figure 12.
Global Interpretation of SMOTE+EBM model. (a) Importance plot. (b) Shape function plot for the season of the year. (c) Heat map for the interaction of season of the year and assigned runway.
Similarly, Figure 12b is the shape function of the season of the year factor generated from the outputs of the SMOTE+EBM model. The higher score is indicated by the summer month (coded as 2). This implied that SWS events were more likely to occur during the summer. The potential cause may be attributed to the summer monsoon, which originates from the south or southwest but undergoes deflection due to the upstream terrain at HKIA [40]. Likewise, the months of winter and autumn exhibited a notable decrease in SWS events, rendering them comparatively tranquil periods [41].
The heat map (Figure 12c) illustrates the relationship between the season of the year and the assigned runway. Distinct zones were assigned to several significant sections of the heat map. Zone A depicts the period of summer (coded as 2) and all the assigned runways of HKIA. The transition from the hue yellow to orange signified an increase in the score, indicating that during the summer months, all runways were susceptible to SWS events. The occurrence of strong winds and subsequent heavy sea breezes and terrain-induced wind shear occurrences in Hong Kong during the summer season may be attributed to the influence of the monsoon. Zone B demonstrated a significant susceptibility of runway 07RA (coded as 2) to occurrences of SWS events during the winter and spring seasons. Likewise, zone C and zone D indicated that runways 07RA (coded as 2), 07RD (coded as 3), and 25LA (coded as 6) were susceptible to SWS events during the autumn season. These results are also consistent with previous studies [42,43].
In addition, local interpretation of the SMOTE+EBM model was also conducted. It allowed us to gain insights into how a specific instance was being predicted by the SMOTE+EBM model. It also helped to understand which factors were driving the prediction for that particular instance. For this purpose, we considered two randomly selected instances that were correctly classified as SWS.
Figure 13 displays bar graphs that represent the contribution of each feature to the prediction and classification of the corresponding ith instance. The EBM’s local interpretation strategy is notable for its ability to accurately determine the influence of individual factor on the outcome by presenting it as a probability. For example, in the case of instance #23 (Figure 13a), there was a 95% chance that the event was an SWS event. In this instance, the pairwise interaction of factors (distance from runway and season of the year) and the individual factor (season of the year = 2, which indicates summer) resulted most in the likelihood of SWS events. Similarly, for instance #137 (Figure 13b), the EBM showed that there was an 86% chance that the event was an SWS event. In this instance, the individual factor (season of the year) was the most influential, followed by pairwise interaction of factors (season of the year and time of the day).
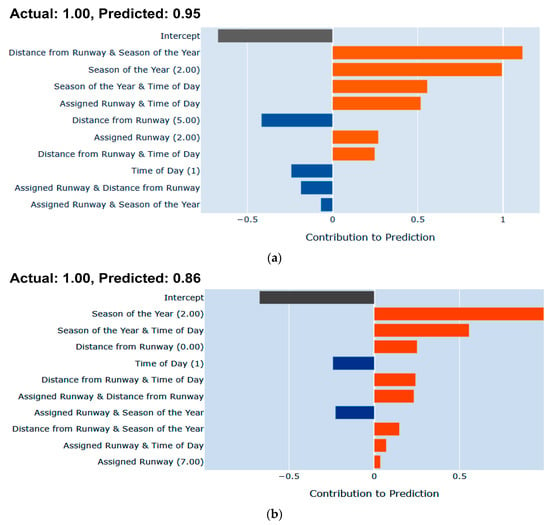
Figure 13.
Local interpretation by SMOTE+EBM. (a) Correct classification of a random instance (i = 23) as SWS. (b) Correct classification of a random instance (i = 137) as SWS.
3.5. Limitation of the Research
The limitations of the current research were as follows:
- In this study, we employed different input factors extracted from the Doppler LiDAR system of HKIA to estimate the WS severity. However, it is pertinent to note that forthcoming studies may encompass additional factors, including the atmospheric pressure and temperature, that will be derived from HKIA’s weather reports.
- The main focus of the study centered on the application of EBM and other advanced ML models to forecast the severity of WS. Future research endeavors may explore the integration of additional advanced deep learning (DL) algorithms, such as wide and deep networks (WDNs) and deep and cross networks (DCNs), among others.
- The severity of WS was a notable factor of interest in this current study. The incorporation of aviation turbulence as a complementary wind attribute for future research also merits serious consideration.
4. Conclusions and Recommendation
This study introduced an EBM framework, primarily an ML-based glass-box model, for the prediction of WS severity in close proximity to airport runways. The proposed model exhibited a comparable level of precision to its black-box counterparts, such as XGBoost and RF models, while also possessing the characteristics of explainability and inherent comprehensibility. Various factors were extracted from the Doppler LiDAR systems based at HKIA, including the magnitude of WS events, the season and time of day of WS occurrences, the location of WS encounters, and the assigned runway. Furthermore, in order to address the issue of data imbalance, the training data received treatment using the SMOTE, SVM-SMOTE, and ADASYN strategies before the modeling process. Subsequently, the Bayesian optimization technique was used to optimize the hyperparameters of the EBM model, as well as its counterparts XGBoost and RF, using the augmented data. The evaluation of the EBM, XGBoost, and RF models was conducted using a holdout approach with testing data. Based on the findings of this study, it was possible to draw the following conclusions:
- The performance of the EBM model differed slightly but was comparable to the XGBoost and RF models.
- The finely tuned EBM model trained on SMOTE-treated data performed better by achieving higher precision (0.98), recall (0.70), G-mean (0.77), BA (0.78), MCC (0.169), and AU-ROC values (0.854).
- The RF model trained on ADASYN-treated data demonstrated a poor performance as indicated by the precision (0.97), recall (0.53), G-mean (0.59), BA (0.59), MCC (0.105), and AU-ROC values (0.617).
- The EBM model also showed effectiveness in the interpretation of various factors. In terms of the individual factor contribution, the season of the year contributed most to predicting the WS severity. Similarly, in terms of pairwise interaction, the season of the year and the assigned runway pair contributed most to the occurrence of SWS events.
- The interpretation via the SMOTE+EBM model revealed most of the SWS events occurred in the summer months, and all runways were prone to the occurrence of SWS. However, runway 07 RA was significantly susceptible to SWS in winter and spring, and runways 07RA, 07RD, and 25LA were susceptible to SWS events in summer.
The EBM framework possesses the capability to be utilized for a comprehensive assessment of WS severity at different airports worldwide. Undoubtedly, this tool holds significant value for researchers engaged in the realm of civil aviation safety.
Author Contributions
Conceptualization, A.K.; data curation, P.-W.C.; formal analysis, A.K. and F.C.; funding acquisition, F.C.; investigation, J.Z. and H.A.; methodology, A.K.; project administration, P.-W.C. and H.A.; supervision, P.-W.C. and F.C.; validation, J.Z.; writing—original draft, A.K.; writing—review and editing, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The present study received financial support from the National Natural Science Foundation of China (Grant No. 52250410351), the National Foreign Expert Project (Grant No. QN2022133001L), the Shanghai Municipal Science and Technology Major Project (2021SHZDZX0100), and the Xiaomi Young Talent Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are unavailable due to privacy. The data presented in this study are available on request from the corresponding author.
Acknowledgments
We express our gratitude to our colleagues at the Hong Kong Observatory of Hong Kong International Airport for providing Doppler LiDAR data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Airport Council International. World Airport Traffic Forecast 2017–2040; Airport Council International: Montreal, QC, Canada, 2017. [Google Scholar]
- Chan, P. Severe wind shear at Hong Kong International airport: Climatology and case studies. Meteorol. Appl. 2017, 24, 397–403. [Google Scholar] [CrossRef]
- Council, N.R. Low-Altitude Wind Shear and Its Hazard to Aviation; National Academies Press: Washington, DC, USA, 1983. [Google Scholar]
- Onwuadiochi, I.; Ijioma, M.; Ezenwaji, E.E.; Obikwelu, M.C. Effects of wind shear on flight operations in Sam Mbakwe Airport, Imo State, Nigeria. Trop. Built Environ. J. 2020, 7, 39–49. [Google Scholar]
- Schänzer, G.; Krüger, J. Delayed Pilot Response in Windshear. Technische Univ, Flight Simulation: Where are the Challenges? In Proceedings of the Agard Conference Proceedings 577, Braunschweig, Germany, 22–25 May 1995. [Google Scholar]
- Taszarek, M.; Kendzierski, S.; Pilguj, N. Hazardous weather affecting European airports: Climatological estimates of situations with limited visibility, thunderstorm, low-level wind shear and snowfall from ERA5. Weather Clim. Extrem. 2020, 28, 100243. [Google Scholar] [CrossRef]
- Boilley, A.; Mahfouf, J.-F. Wind shear over the Nice Côte d’Azur airport: Case studies. Nat. Hazards Earth Syst. Sci. 2013, 13, 2223–2238. [Google Scholar] [CrossRef]
- Ratnasari, Y.; Trilaksono, N.; Septiadi, D. Causes and impact of extreme Low Level Wind Shear (LLWS) event at Soekarno-Hatta International Airport. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Yogyakarta, Indonesia/Online, 23–24 April 2022; p. 012011. [Google Scholar]
- Zhang, H.; Wu, S.; Wang, Q.; Liu, B.; Yin, B.; Zhai, X. Airport low-level wind shear lidar observation at Beijing Capital International Airport. Infrared Phys. Technol. 2019, 96, 113–122. [Google Scholar] [CrossRef]
- Carruthers, D.; Ellis, A.; Hunt, J.; Chan, P. Modelling of wind shear downwind of mountain ridges at Hong Kong International Airport. Meteorol. Appl. 2014, 21, 94–104. [Google Scholar] [CrossRef]
- Hon, K.-K. Predicting low-level wind shear using 200-m-resolution NWP at the Hong Kong International Airport. J. Appl. Meteorol. Climatol. 2020, 59, 193–206. [Google Scholar] [CrossRef]
- Wang, S.; De Roo, F.; Thobois, L.; Reuder, J. Characterization of terrain-induced turbulence by large-eddy simulation for air safety considerations in airport siting. Atmosphere 2022, 13, 952. [Google Scholar] [CrossRef]
- Misaka, T.; Yoshimura, R.; Obayashi, S.; Kikuchi, R. Large-Eddy Simulation of Wake Vortices at Tokyo/Haneda International Airport. J. Aircr. 2023, 60, 1819–1831. [Google Scholar] [CrossRef]
- Han, Y.; Liu, X.; Lu, X.; Li, H.; Wu, R. The 3D modeling and radar simulation of low-altitude wind shear via computational fluid dynamics method. In Proceedings of the 2016 Integrated Communications Navigation and Surveillance (ICNS), Herndon, VA, USA, 19–21 April 2016; pp. 4D3-1–4D3-9. [Google Scholar]
- Robinson, D.C.; Collins, D.; Brett, J.; Klewicki, J.; Murray, P. Airport building development: Towards a framework for managing building-induced wind shear and turbulence risks. J. Airpt. Manag. 2017, 11, 369–385. [Google Scholar]
- Laato, S.; Birkstedt, T.; Mäantymäki, M.; Minkkinen, M.; Mikkonen, T. AI governance in the system development life cycle: Insights on responsible machine learning engineering. In Proceedings of the 1st International Conference on AI Engineering: Software Engineering for AI, Pittsburgh, PA, USA, 16–24 May 2022; pp. 113–123. [Google Scholar]
- Patra, P.; Disha, B.; Kundu, P.; Das, M.; Ghosh, A. Recent advances in machine learning applications in metabolic engineering. Biotechnol. Adv. 2023, 62, 108069. [Google Scholar] [CrossRef] [PubMed]
- Thai, H.-T. Machine learning for structural engineering: A state-of-the-art review. Structures 2022, 38, 448–491. [Google Scholar] [CrossRef]
- Khawar, H.; Soomro, T.R.; Kamal, M.A. Machine learning for internet of things-based smart transportation networks. In Machine Learning for Societal Improvement, Modernization, and Progress; IGI Global: Hershey, PA, USA, 2022; pp. 112–134. [Google Scholar]
- Yuan, T.; Da Rocha Neto, W.; Rothenberg, C.E.; Obraczka, K.; Barakat, C.; Turletti, T. Machine learning for next-generation intelligent transportation systems: A survey. Trans. Emerg. Telecommun. Technol. 2022, 33, e4427. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Bi, J.; Liu, Y. A machine learning model to estimate ground-level ozone concentrations in California using TROPOMI data and high-resolution meteorology. Environ. Int. 2022, 158, 106917. [Google Scholar] [CrossRef] [PubMed]
- Wood, D.A. Local integrated air quality predictions from meteorology (2015 to 2020) with machine and deep learning assisted by data mining. Sustain. Anal. Model. 2022, 2, 100002. [Google Scholar] [CrossRef]
- Rudin, C. Why black box machine learning should be avoided for high-stakes decisions, in brief. Nat. Rev. Methods Primers 2022, 2, 81. [Google Scholar] [CrossRef]
- Nori, H.; Jenkins, S.; Koch, P.; Caruana, R. Interpretml: A unified framework for machine learning interpretability. arXiv 2019, arXiv:1909.09223. [Google Scholar]
- Maxwell, A.E.; Sharma, M.; Donaldson, K.A. Explainable boosting machines for slope failure spatial predictive modeling. Remote Sens. 2021, 13, 4991. [Google Scholar] [CrossRef]
- Nori, H.; Caruana, R.; Bu, Z.; Shen, J.H.; Kulkarni, J. Accuracy, interpretability, and differential privacy via explainable boosting. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 8227–8237. [Google Scholar]
- Khattak, A.; Chan, P.-w.; Chen, F.; Peng, H. Explainable Boosting Machine for Predicting Wind Shear-Induced Aircraft Go-around based on Pilot Reports. KSCE J. Civ. Eng. 2023, 27, 4115–4129. [Google Scholar] [CrossRef]
- Konstantinov, A.V.; Utkin, L.V. Interpretable machine learning with an ensemble of gradient boosting machines. Knowl. Based Syst. 2021, 222, 106993. [Google Scholar] [CrossRef]
- Sarica, A.; Quattrone, A.; Quattrone, A. Explainable boosting machine for predicting Alzheimer’s disease from MRI hippocampal subfields. In Brain Informatics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 341–350. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Cooper, E.W.; Kamei, K. Borderline over-sampling for imbalanced data classification. Int. J. Knowl. Eng. Soft Data Paradig. 2011, 3, 4–21. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Chan, P.W.; Shao, A.M. Depiction of complex airflow near Hong Kong International Airport using a Doppler LIDAR with a two-dimensional wind retrieval technique. Meteorol. Z. 2007, 16, 491–504. [Google Scholar] [CrossRef]
- Chan, P. Aviation applications of the pulsed Doppler LIDAR–Experience in Hong Kong. Open Atmos. Sci. J. 2009, 3, 138–146. [Google Scholar] [CrossRef]
- Jia, B.-B.; Zhang, M.-L. Multi-dimensional classification via sparse label encoding. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 4917–4926. [Google Scholar]
- Lou, Y.; Caruana, R.; Gehrke, J.; Hooker, G. Accurate intelligible models with pairwise interactions. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 623–631. [Google Scholar]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Gan, C.; Zhao, K.; Lin, X.; Quan, Z.; Wang, Z.-J. A novel model for imbalanced data classification. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 6680–6687. [Google Scholar]
- Hon, K.K.; Chan, P.W. Historical analysis (2001–2019) of low-level wind shear at the Hong Kong International Airport. Meteorol. Appl. 2022, 29, e2063. [Google Scholar] [CrossRef]
- Chan, P.; Hon, K. Observation and numerical simulation of terrain-induced windshear at the Hong Kong International Airport in a planetary boundary layer without temperature inversions. Adv. Meteorol. 2016, 2016, 1454513. [Google Scholar] [CrossRef]
- Stocker, J.; Johnson, K.; Jackson, R.; Smith, S.; Connolly, D.; Carruthers, D.; Chan, P.-W. Hong Kong Airport Wind Shear Now-Casting System Development and Evaluation. Atmosphere 2022, 13, 2094. [Google Scholar] [CrossRef]
- Chan, P.; Lai, K.; Li, Q. Performance of large-eddy simulations for capturing low-level wind shear at the Hong Kong International Airport for a whole wind-shear (spring) season. Meteorol. Z. 2023, 32, 383–394. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).