Standardized Precipitation and Evapotranspiration Index Approach for Drought Assessment in Slovakia—Statistical Evaluation of Different Calculations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Methodology of SPEI Calculation
2.4. Choice of the Optimal Probability Density Function of D
- Normality of final SPEI index;
- The number of cases when distribution parameter fitting failed (the number of no-solution cases);
- The number of SPEI extremes.
3. Results and Discussion
3.1. The Influence of Modification of Statistical Distribution on the Final SPEI Value
3.2. Choice of the Optimal Probability Density Function of D
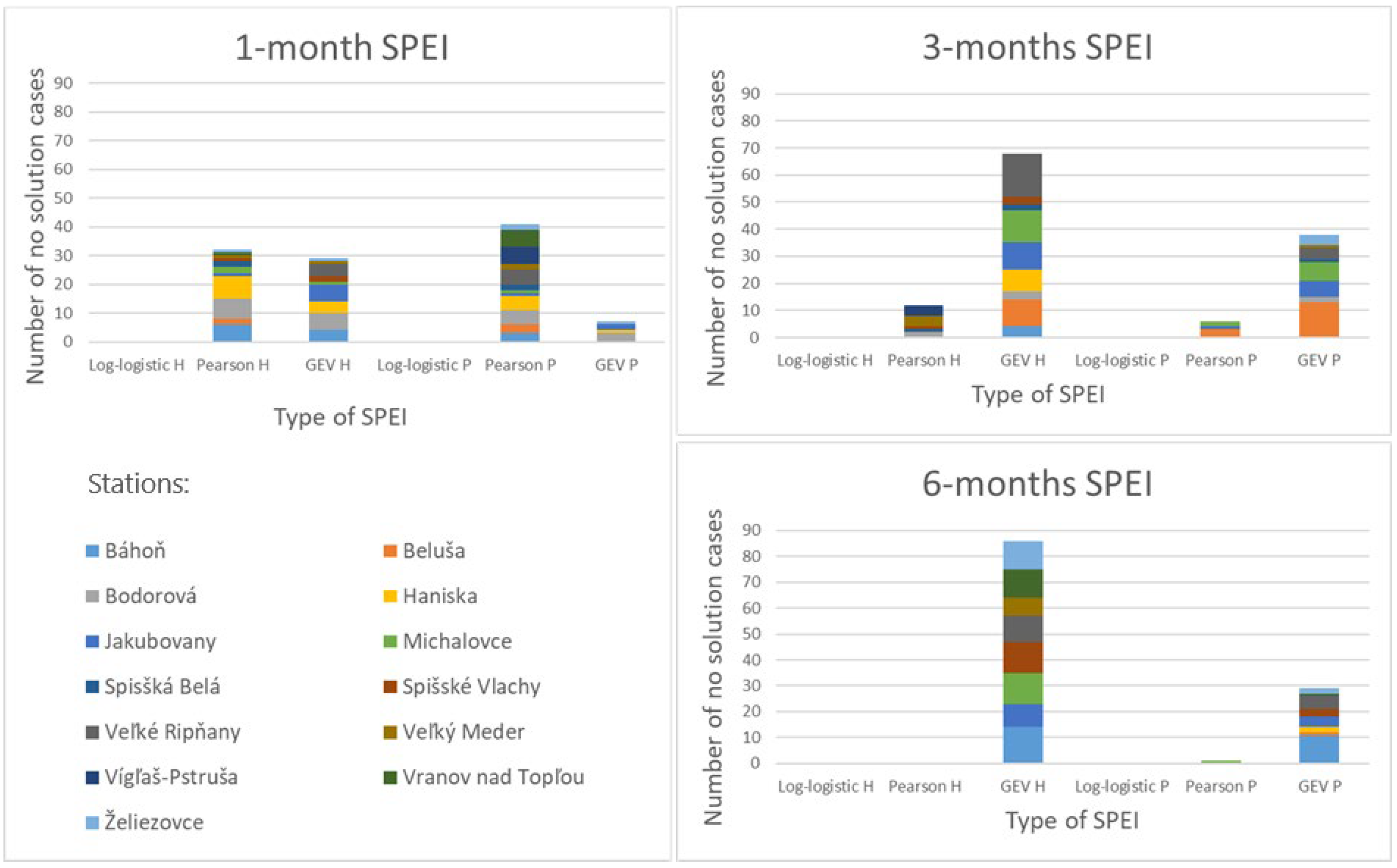
3.2.1. The Number of No-Solution Cases for Parameter Fitting
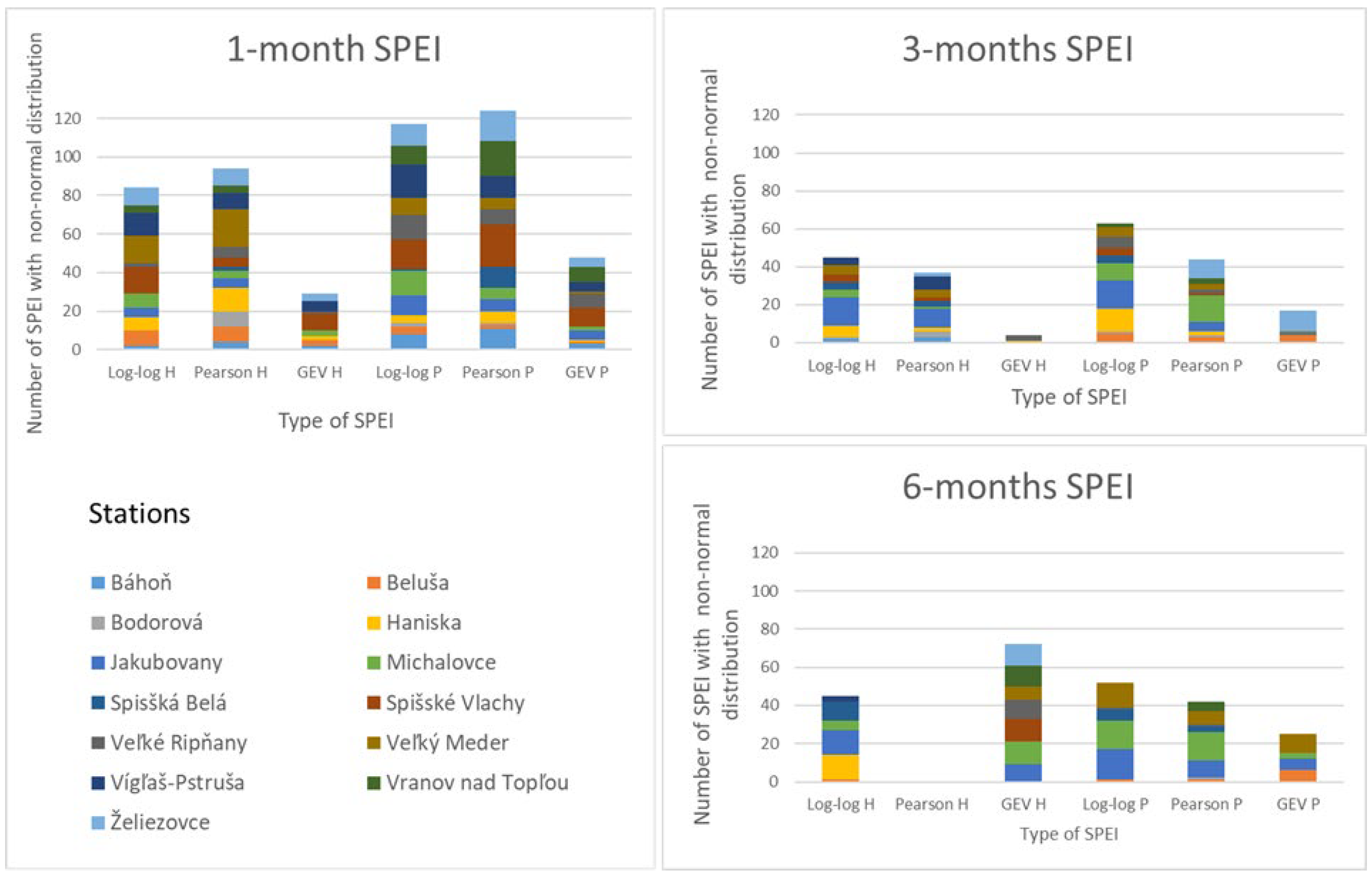
3.2.2. Shapiro–Wilk (S-W) Normality Test of the Final SPEI Index
3.2.3. The Number of SPEI Extremes
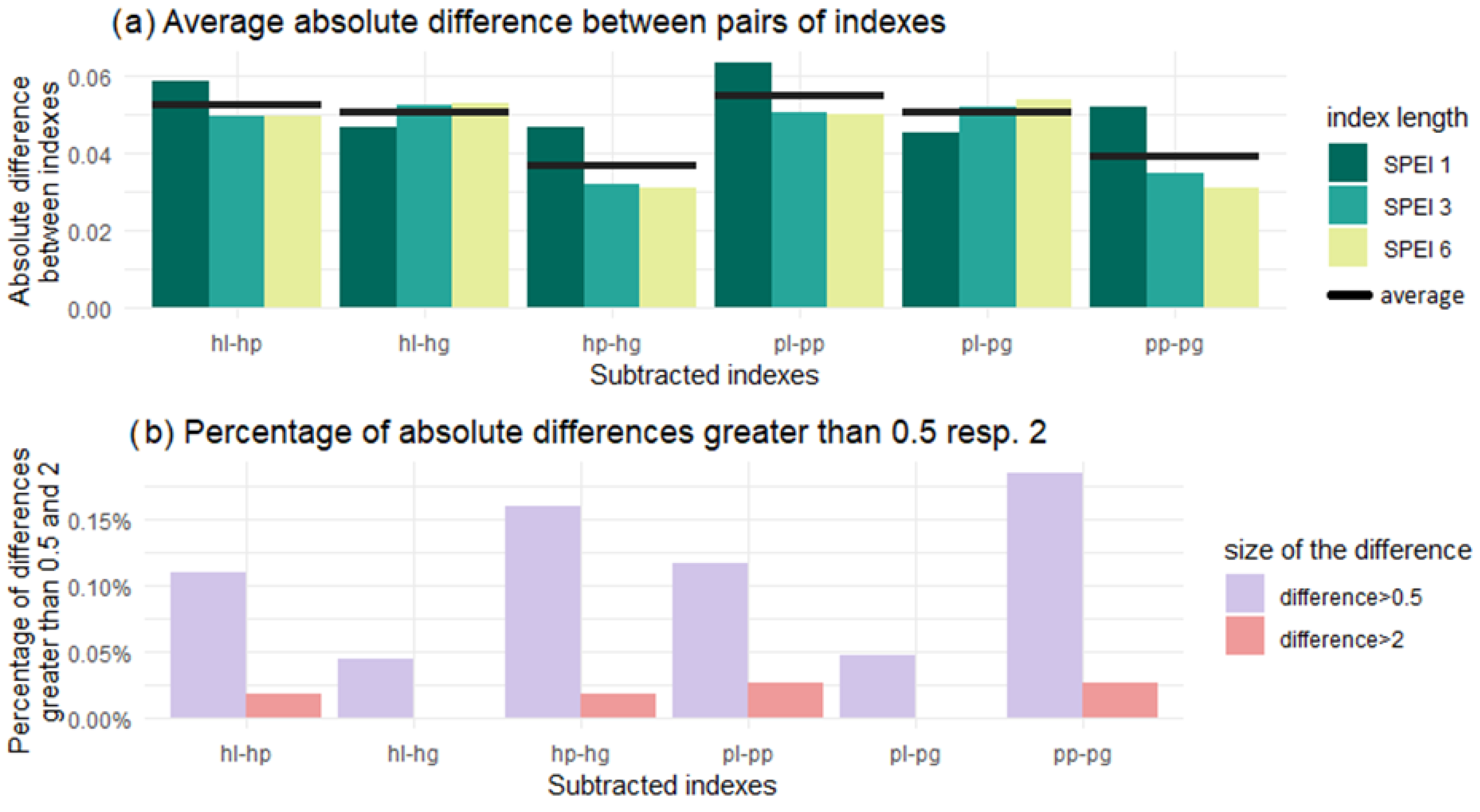
3.3. Comparison of Analysed Indices and Discussion
4. Conclusions
- (a)
- Absolute difference testing:
- (b)
- The number of no-solution cases and the number of inappropriate fits:
- (c)
- SPEI extremes:
- (d)
- Final comment
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faško, P.; Markovič, L.; Bochníček, O.; Pecho, J. Decadal Changes in Snow Cover Characteristics in Slovakia over the Period 1921–2020. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020. [Google Scholar]
- Dančová, M.; Chovancová, Ľ.; Hinerová, A.; Malatinská, L.; Thumová, L.; Špalková, V.; Škultéty, J.; Gnida, M.; Pavlovič, V.; Szemešová, J.; et al. The Eight National Communication of the Slovak Republic on Climate Change: Under the United Nations Framework Convention on Climate Change and the Kyoto Protocol; Ministry of Environment of the Slovak Republic: Bratislava, Slovakia, 2023. [Google Scholar]
- Trnka, M.; Balek, J.; Štěpánek, P.; Zahradníček, P.; Možný, M.; Eitzinger, J.; Žalud, Z.; Formayer, H.; Turňa, M.; Nejedlík, P.; et al. Drought Trends over Part of Central Europe between 1961 and 2014. Clim. Res. 2016, 70, 143–160. [Google Scholar] [CrossRef]
- Nikolova, N.; Nejedlík, P.; Lapin, M. Temporal Variability and Spatial Distribution of Drought Events in the Lowlands of Slovakia. Geofizika 2016, 33, 119–135. [Google Scholar] [CrossRef]
- Sönmez, K.F.; Komuscu, U.A.; Erkan, A.; Turgu, E. An Analysis of Spatial and Temporal Dimension of Drought Vulnerability in Turkey Using the Standardized Precipitation Index. Nat. Hazards 2005, 35, 243–264. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized Precipitation Evapotranspiration Index (SPEI) Revisited: Parameter Fitting, Evapotranspiration Models, Tools, Datasets and Drought Monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, A. CMIP6 Model-Projected Hydroclimatic and Drought Changes and Their Causes in the Twenty-First Century. J. Clim. 2022, 35, 897–921. [Google Scholar] [CrossRef]
- Trnka, M.; Hlavinka, P.; Semenov, M.A. Adaptation Options for Wheat in Europe Will Be Limited by Increased Adverse Weather Events under Climate Change. J. R. Soc. Interface 2015, 12, 20150721. [Google Scholar] [CrossRef]
- Balting, D.F.; AghaKouchak, A.; Lohmann, G.; Ionita, M. Northern Hemisphere Drought Risk in a Warming Climate. NPJ Clim. Atmos. Sci. 2021, 4, 61. [Google Scholar] [CrossRef]
- Hlásny, T.; Csaba, M.; Seidl, R.; Kulla, L.; Merganičová, K.; Trombik, J.; Dobor, L.; Barcza, Z.; Konôpka, B. Climate Change Increases the Drought Risk in Central European Forests: What Are the Options for Adaptation? Lesn. Cas. 2014, 60, 5–18. [Google Scholar] [CrossRef]
- Petrík, P.; Grote, R.; Gömöry, D.; Kurjak, D.; Petek-Petrik, A.; Lamarque, L.J.; Sliacka-Konôpková, A.; Mukarram, M.; Debta, H.; Fleischer, P., Jr. The Role of Provenance for the Projected Growth of Juvenile European Beech under Climate Change. Forest 2023, 14, 26. [Google Scholar] [CrossRef]
- Potopová, V.; Trifan, T.; Trnka, M.; De Michele, C.; Semerádová, D.; Fischer, M.; Meitner, J.; Musiolková, M.; Muntean, N.; Clothier, B. Copulas Modelling of Maize Yield Losses–Drought Compound Events Using the Multiple Remote Sensing Indices over the Danube River Basin. Agric. Water Manag. 2023, 280, 108217. [Google Scholar] [CrossRef]
- Török, P.; Dembicz, I.; Dajić-Stevanović, Z.; Kuzemko, A. Grasslands of Eastern Europe. In Encyclopedia of the World’s Biomes; Elsevier: Amsterdam, The Netherlands, 2020; pp. 703–713. ISBN 9780128160978. [Google Scholar]
- McKee, T.B.; Nolan, D.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Labudová, L.; Labuda, M.; Takáč, J. Comparison of SPI and SPEI Applicability for Drought Impact Assessment on Crop Production in the Danubian Lowland and the East Slovakian Lowland. Theor. Appl. Climatol. 2017, 128, 491–506. [Google Scholar] [CrossRef]
- Ionita, M.; Nagavciuc, V. Changes in Drought Features at the European Level over the Last 120 Years. Nat. Hazards Earth Syst. Sci. 2021, 21, 1685–1701. [Google Scholar] [CrossRef]
- Moorhead, J.E.; Gowda, P.H.; Singh, V.P.; Porter, D.O.; Marek, T.H.; Howell, T.A.; Stewart, B.A. Identifying and Evaluating a Suitable Index for Agricultural Drought Monitoring in the Texas High Plains. J. Am. Water Resour. Assoc. 2015, 51, 807–820. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Droogers, P.; Allen, R.G. Estimating Reference Evapotranspiration Under Inaccurate Data Conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Sienz, F.; Bothe, O.; Fraedrich, K. Monitoring and Quantifying Future Climate Projections of Dryness and Wetness Extremes: SPI Bias. Hydrol. Earth Syst. Sci. 2012, 16, 2143–2157. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S. Comment on ‘Candidate Distributions for Climatological Drought Indices (SPI and SPEI)’ by James H. Stagge et al. Int. J. Climatol. 2016, 36, 2120–2131. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Response to Comment on ‘Candidate Distributions for Climatological Drought Indices (SPI and SPEI)’. Int. J. Climatol. 2016, 36, 2132–2138. [Google Scholar] [CrossRef]
- Bezdan, J.; Bezdan, A.; Blagojević, B.; Mesaroš, M.; Pejić, B.; Vranešević, M.; Pavić, D.; Nikolić-Đorić, E. SPEI-Based Approach to Agricultural Drought Monitoring in Vojvodina Region. Water 2019, 11, 1481. [Google Scholar] [CrossRef]
- Blauhut, V.; Gudmundsson, L.; Stahl, K. Towards Pan-European Drought Risk Maps: Quantifying the Link between Drought Indices and Reported Drought Impacts. Environ. Res. Lett. 2015, 10, 014008. [Google Scholar] [CrossRef]
- Potopová, V.; Štěpánek, P.; Možný, M.; Türkott, L.; Soukup, J. Performance of the Standardised Precipitation Evapotranspiration Index at Various Lags for Agricultural Drought Risk Assessment in the Czech Republic. Agric. For. Meteorol. 2015, 202, 26–38. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.; Barbosa, P. European Drought Climatologies and Trends Based on a Multi-Indicator Approach. Glob. Planet. Change 2015, 127, 50–57. [Google Scholar] [CrossRef]
- Dukat, P.; Bednorz, E.; Ziemblińska, K.; Urbaniak, M. Trends in Drought Occurrence and Severity at Mid-Latitude European Stations (1951–2015) Estimated Using Standardized Precipitation (SPI) and Precipitation and Evapotranspiration (SPEI) Indices. Meteorol. Atmos. Phys. 2022, 134, 1–21. [Google Scholar] [CrossRef]
- Oikonomou, P.D.; Karavitis, C.A.; Tsesmelis, D.E.; Kolokytha, E.; Maia, R. Drought Characteristics Assessment in Europe over the Past 50 Years. Water Resour. Manag. 2020, 34, 4757–4772. [Google Scholar] [CrossRef]
- Melo, M.; Lapin, M.; Pecho, J. Climate in the Past and Present in the Slovak Landscapes—The Central European Context. In Landscapes and Landforms of Slovakia. World Geomorphological Landscapes; Springer: Berlin/Heidelberg, Germany, 2022; pp. 27–44. [Google Scholar]
- Repel, A.; Zeleňáková, M.; Jothiprakash, V.; Hlavatá, H.; Blišťan, P.; Gargar, I.; Purcz, P. Long-Term Analysis of Precipitation in Slovakia. Water 2021, 13, 952. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Stagge, J.H. SCI: Standardized Climate Indices Such as SPI, SRI or SPEI. V.1.0-2. 2016. Available online: https://cran.r-project.org/web/packages/SCI/index.html (accessed on 1 August 2023).
- Yimer, E.A.; Van Schaeybroeck, B.; Van de Vyver, H.; van Griensven, A. Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia. Atmosphere 2022, 13, 364. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]


| Moisture Category | SPEI |
|---|---|
| Extremely wet | ≥2 |
| Very wet | 1.50 to 1.99 |
| Moderately wet | 1.00 to 1.49 |
| Near normal | −0.99 to 0.99 |
| Moderately dry | −1.00 to −1.49 |
| Severely dry | −1.50 to −1.99 |
| Extremely dry | ≤−2 |
| Station | Altitude [m] | Tmax Jan. [°C] | Tmax July [°C] | Tmin Jan. [°C] | Tmin July [°C] | R Why [mm] | PET Why [mm] | |
|---|---|---|---|---|---|---|---|---|
| 1 | Báhoň | 159 | 2.55 | 27.75 | −3.25 | 15.46 | 307.95 | 754.21 |
| 2 | Beluša | 248 | 1.62 | 26.38 | −4.97 | 13.03 | 408.28 | 758.44 |
| 3 | Bodorová | 485 | 1.03 | 24.89 | −5.69 | 12.28 | 343.98 | 708.09 |
| 4 | Haniska | 200 | 0.68 | 26.28 | −5.15 | 14.38 | 407.84 | 717.32 |
| 5 | Jakubovany | 385 | −0.12 | 25.14 | −5.94 | 12.69 | 441.51 | 703.82 |
| 6 | Michalovce | 123 | 0.81 | 27.00 | −4.50 | 15.04 | 389.48 | 730.78 |
| 7 | Spišská Belá | 628 | −0.05 | 23.35 | −8.30 | 10.70 | 456.84 | 678.71 |
| 8 | Spišské Vlachy | 430 | 0.37 | 25.31 | −8.17 | 11.52 | 470.63 | 763.28 |
| 9 | Veľké Ripňany | 188 | 1.97 | 27.27 | −4.56 | 13.47 | 317.03 | 801.01 |
| 10 | Veľký Meder | 112 | 2.86 | 27.75 | −3.22 | 14.83 | 313.82 | 786.23 |
| 11 | Vígľaš | 340 | 1.09 | 26.19 | −6.96 | 11.50 | 394.04 | 802.74 |
| 12 | Vranov nad Topľou | 164 | 0.73 | 26.86 | −4.73 | 14.29 | 426.92 | 749.29 |
| 13 | Želiezovce | 130 | 2.25 | 28.21 | −4.42 | 14.40 | 329.45 | 824.76 |
| Potential Evapotranspiration | ||
|---|---|---|
| Distribution | Hargreaves | Penman–Monteith |
| Log-logistic | hl | pl |
| Pearson III | hp | pp |
| Generalized extreme value | hg | pg |
| Distribution | Number of Missing Indices Caused by Parameters Fitting Issues | Percent [%] |
|---|---|---|
| Log-logistic | 0 | 0.00 |
| Pearson III | 3588 | 0.32 |
| Generalized extreme value | 10,023 | 0.90 |
| Distribution | Number of Missing Indices Caused by Non-Normal Distribution | Percent [%] |
|---|---|---|
| Log-logistic | 15,834 | 1.43 |
| Pearson III | 14,664 | 1.32 |
| Generalized extreme value | 5070 | 0.46 |
| Number of Eliminated Indices Due to Three Criteria | |||||
|---|---|---|---|---|---|
| Elimination criterion → | 1. Parameters fitting issues | 2. Non-normal distribution | 3. Unlikely extremes (|SPEI| > 6) | Total | Percentage of eliminated indices [%] |
| Distribution ↓ | |||||
| Log-logistic | 0 | 15,834 | 0 | 15,834 | 1.43 |
| Pearson III | 3588 | 14,664 | 0 | 18,252 | 1.64 |
| GEV | 10,023 | 5070 | 0 | 15,093 | 1.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slavková, J.; Gera, M.; Nikolova, N.; Siman, C. Standardized Precipitation and Evapotranspiration Index Approach for Drought Assessment in Slovakia—Statistical Evaluation of Different Calculations. Atmosphere 2023, 14, 1464. https://doi.org/10.3390/atmos14091464
Slavková J, Gera M, Nikolova N, Siman C. Standardized Precipitation and Evapotranspiration Index Approach for Drought Assessment in Slovakia—Statistical Evaluation of Different Calculations. Atmosphere. 2023; 14(9):1464. https://doi.org/10.3390/atmos14091464
Chicago/Turabian StyleSlavková, Jaroslava, Martin Gera, Nina Nikolova, and Cyril Siman. 2023. "Standardized Precipitation and Evapotranspiration Index Approach for Drought Assessment in Slovakia—Statistical Evaluation of Different Calculations" Atmosphere 14, no. 9: 1464. https://doi.org/10.3390/atmos14091464
APA StyleSlavková, J., Gera, M., Nikolova, N., & Siman, C. (2023). Standardized Precipitation and Evapotranspiration Index Approach for Drought Assessment in Slovakia—Statistical Evaluation of Different Calculations. Atmosphere, 14(9), 1464. https://doi.org/10.3390/atmos14091464








