Abstract
To assess the performance and scalability of the Unified Forecast System (UFS) Short-Range Weather (SRW) application, case studies are chosen to cover a wide variety of forecast applications. Here, model forecasts of Hurricane Barry (July 2019) are examined and analyzed. Several versions of the Global Forecast System (GFS) and Rapid Refresh Forecast System (RRFS) physics suites are run in the UFS-SRW at grid spacings of 25 km, 13 km, and 3 km. All model configurations produce significant track errors of up to 350 km at landfall. The track errors are investigated, and several commonalities are seen between model configurations. A westerly bias in the environmental steering flow surrounding the tropical cyclone (TC) is seen across forecasts, and this bias is coincident with a warm sea surface temperature (SST) bias and overactive convection on the eastern side of the forecasted TC. Positive feedback between the surface winds, latent heating, moisture, convection, and TC intensification is initiated by this SST bias. The asymmetric divergent flow induced by the excess convection results in all model TC tracks being diverted to the east as compared to the track derived from reanalysis. The large differences between runs using the same physics packages at different grid spacing suggest a deficiency in the scalability of these packages with respect to hurricane forecasting in vertical wind shear.
1. Introduction
The accurate forecasting of TCs is of vital socioeconomic importance because even small errors in the hurricane track or intensity forecasts can result in drastic differences in the impact of these storms. TC forecasting involves complex, nonlinear physical interactions between the environmental conditions, the ocean surface, and the TC itself, and understanding and accurately modeling all of these relationships is crucial to a skillful forecast [1]. The UFS is a community-based, coupled comprehensive Earth system modeling system intended to help bridge the gap between research and operational forecasting by facilitating the implementation of research innovations not currently included in operational applications. The UFS is intended to span predictive scales from hours to years, and several applications have been and continue to be developed for various temporal and spatial scales. The UFS-SRW application [2] is employed for this study. This application is an atmosphere–land coupled limited area configuration of the UFS, focusing on time scales from minutes to days. While the UFS-SRW is primarily being used for research and development purposes, the operational instantiation of the UFS-SRW, the RRFS, is slated for US operations in 2024. For this reason, the UFS-SRW must provide timely and accurate forecasts for a variety of meteorological phenomena spanning a large range of spatiotemporal scales. Selecting a fixed resolution for a particular application poses a significant challenge to determine a grid spacing that can accurately represent the phenomena of interest while still being efficient enough to run in operations. Thus, evaluating the performance of operationally relevant physics packages available in the UFS-SRW at various grid spacings provides critical information to model physics developers as they strive to unify physics parameterizations across the various applications.
The focus of this work is a case study representing the forecasting challenge of TC evolution in a strongly sheared environment. Hurricane Barry was a Category 1 hurricane that made landfall over Intracoastal City, Louisiana on 14 July 2019. Due to the strong northerly wind shear that was prevalent throughout the TC development, this system was slow to intensify and was associated with an unusually asymmetric distribution of convective activity and precipitation [3]. The operational Global Forecast System (GFS) track error for Hurricane Barry was substantial, predicting landfall some 200 km to the east of Intracoastal City at the 72 h lead time [3]. Because of this, Hurricane Barry is a prime candidate for identifying the shortcomings in operationally relevant physics suites and investigating what effect (if any) the model grid spacing and resolved convection have on the development and evolution of TC forecasts run with the UFS-SRW, and whether and why the maturing physics suites might improve upon the forecasted track.
TC motion in vertical wind shear is generally controlled by the environmental steering flow and by vertical coupling mechanisms, such as diabatic heating due to convective processes and the vertical advection of potential vorticity [4,5,6,7]. Generally, convection tends to organize the downshear of a TC developing in a sheared environment, with a mesoscale subsidence in the upshear region [8]. Here, downshear and upshear refer to the regions about the TC center that the vertical shear vector points toward and away from, respectively. Chen and Gopalakrishnan (2014) [9] showed in a case study of Hurricane Earl that as the TC intensified, the warm subsiding air from the upshear region was advected into the upper levels of the TC center, thus amplifying the warm core and accelerating intensification. In addition, they showed that when convective bursts were concentrated in the downshear-left (DSL) and upshear-left (USL) regions relative to the TC center, the upper-level convective-scale subsidence about that convective burst superposes on the mesoscale subsidence region as it is advected into the TC core. This subsidence warms the lower-level TC core more rapidly and further accelerates intensification [9,10].
This concentration of convection in the DSL and USL TC center-relative quadrants should also be expected to introduce a track tendency toward that region due to the asymmetric divergent flow at the TC center [4,11,12,13,14], which tends to move the TC track toward the region of maximum convection; moreover, this effect also tends to reduce the TC vertical tilt. The vertical shear itself also induces a left-of-shear motion tendency due to the upper-level displacement of an anticyclonic potential vorticity anomaly [4,15,16]. There are several other physical mechanisms that have been demonstrated to affect the TC intensification and track forecasting, many of which are not fully understood [17]. Environmental wind shear [18,19,20], vertical tilt of the TC vortex [4], and convective to mesoscale processes that affect precipitation and inner core heating [21,22,23,24,25] have all been shown to play important roles in the forecasting of TC evolution. Nonlinear interactions between these processes mean that small errors in any of them can cause the errors to grow and alter the TC track and intensity forecast.
This case study of Hurricane Barry investigates the systematic errors in several versions of the Common Community Physics Package (CCPP) [26,27] physics suites within the UFS-SRW at multiple grid spacings. The objective is to identify the shortcomings within those physics suites and to investigate the scalability of the physics with respect to the representation of a TC in the presence of vertical shear. We find consistent errors in the forecast evolution of convection and intensity that all contribute nonlinearly to both each other and to the forecast track error. Section 2 discusses the model configuration, physics suites, and verification datasets used here, as well as the diagnostic methods used to demonstrate those shortcomings. Section 3 shows systematic errors in various fields related to the TC motion tendencies discussed in Section 1. The conclusions drawn from these fields are discussed in Section 4.
2. Data and Methods
2.1. Model Description, Physics Suites, and Verification Datasets
The experiments conducted in this study used the Finite-Volume Cubed Sphere (FV3) atmospheric dynamic core within the UFS-SRW application. The regional forecast domain spanned the tropical and subtropical North Atlantic Ocean and the eastern continental United States (Figure 1). The initial and boundary conditions for the atmosphere were generated from the operational GFS analysis and GFS forecast fields, respectively. The runs did not utilize data assimilation or ocean coupling. As in the operational GFS, the evolution of SST is controlled by the near-surface sea temperature (NSST) parameterization, which attempts to mimic the diurnal cycle of SST.
Figure 1.
The domain used in the UFS-SRW runs. Lakes and ocean points are colored blue while land points show elevation in meters corresponding to the color axis on the right. White areas are not defined.
Several physics suites available within the CCPP were tested at the following three different horizontal grid spacings: 25 km, 13 km, and 3 km. These grid spacings target resolutions typically used for subseasonal-to-seasonal (25 km), medium-range (13 km), and convection-permitting (3 km) forecast applications. The individual physics parameterizations included in each physics suite are shown in Table 1. Detailed information about each parameterization is provided by Zhang et al. (2021) [26] and references therein. Each physics suite in Table 1 represents an incremental version tested during the pre-implementation process, leading to the final version implemented in operations (e.g., GFSv16). Physics suites beginning with GFS indicate suites intended for the operational GFS, whereas physics suites beginning with GSD represent suites developed at NOAA Global Systems Laboratory for use in the operational Rapid Refresh (RAP) and High-Resolution Rapid Refresh (HRRR) models. The intention of performing runs with the various physics suites is to create a variety of possible forecast solutions that can be used to understand the environmental and TC inner core characteristics associated with “good” and “bad” track forecasts in this case. We do not attempt to attribute variations in forecast performance to specific differences between physics suites, since several of the suites differ in more than one way (Table 1). Additional forecast diversity is obtained by disabling the cumulus parameterization at 3 km in the GFSv16beta and GSD_noMY physics suites (GFSv16beta 3 km NoConv and GSD_noMY 3 km NoConv). These additional runs also quantify the sensitivity of the track forecast to whether a cumulus scheme is used. All of the runs were initialized at 06 UTC 11 July 2019 and had a forecast length of 72 h, except for the GSDv0 and GSD_noMY 3 km runs, which only ran for 56 and 59 h, respectively, due to computer resource limitations. This did not impact the results, however, because the analysis focuses on the pre-landfall evolution of the TC, and every run extended well past landfall.

Table 1.
Parameterizations included in each physics suite used in this study.
For verification of large-scale fields, including the environmental flow, latent heating, and SST, the latest version of the European Centre for Medium-Range Weather Forecasts Atmospheric Reanalysis (ERA5), is used [28]. The reanalysis is available at hourly intervals at 0.25° grid spacing. For verification of convection, satellite-derived precipitation data from the Integrated Multi-satellitE Retrievals for the Global Precipitation Measurement (IMERG) [29] are used as proxy. This product is available at half-hourly intervals with 0.1° grid spacing. These half-hourly data are accumulated for the hour prior to each forecast verification time to match the hourly frequency of the composite reflectivity data from the model forecasts. As an additional convection verification source, Stage IV radar-derived precipitation [30] is used as a proxy as well. These data are available at 4 km resolution at hourly intervals. The observed Hurricane Barry track data used for this study are taken from the data repository of tropical cyclone tracks referenced in Bourdin et al. (2022) [31], using the TRACK algorithm based on Hodges et al. (1994) [32] as applied to ERA5 data. These data are provided at 6 hourly intervals and so is linearly interpolated in time to hourly frequency. Throughout this manuscript, this track data are simply referred to as the ERA5 hurricane track.
For SST verification, in addition to ERA5, the NOAA/NESDIS/NCEI Daily Optimum Interpolation SST, version 2.1 dataset (DOISST) [33] and the NASA/JPL Multi-scale Ultra-High-Resolution SST analysis (MURSST) [34] is used. DOISST is derived from combined in situ ship and buoy measurements as well as satellite retrievals and is provided at 1/4° resolution. MURSST is available on a global 0.01° grid and is derived from multiple satellite and in situ sources with internal correction applied for biases between datasets. Each of these sources of observational SST are available at daily intervals.
2.2. Methods
Accurate identification of the TC location in the model output is crucial to this study. For this, the Geophysical Fluid Dynamics Laboratory (GFDL) vortex tracker software [35] is used to analyze the forecast variable fields at several vertical levels to track the TC position throughout the duration of each forecast. The steering flow is determined using the Optimal Steering Layer (OSL) method developed by Galarneau and Davis (2013) [36]. In this method, the steering flow is calculated by first removing the winds directly associated with the existence of the TC by subtracting the irrotational and nondivergent winds from the full wind field at radii ranging from 1° to 8°. Then, the pressure-weighted mean wind field with the TC removed is calculated from 850 hPa to various levels ranging from 800 to 200 hPa at 50 hPa intervals. This creates a matrix of mean environmental flow values that vary by TC removal radius and layer thickness. By comparing this complete matrix to the change in TC position between ±12 h from the forecast time in question, the velocity associated with the TC removal radius and layer thickness that most closely matches the TC motion is determined to be the steering flow velocity at that time. Because the determination of the TC motion requires ±12 h of information, the steering flow cannot be determined using this method during the first or last 12 h of the forecast.
3. Results
3.1. GFS Physics Suites
Figure 2 shows the ERA5 track and the track forecast from each GFS physics suite for Hurricane Barry. These runs reproduce the east-of-track bias seen in the operational GFS. The GFDL-MP tracks exhibit the most extreme errors of roughly 350 km at landfall. These forecasts diverge from ERA5 earlier in the runs than the other GFS suites, with a sharp northward recurve occurring around 24 h at 89°W longitude. For the GFSv15.2 suite, the forecast tracks begin to diverge northeastward from ERA5 around 30 h, and a few hours later the 25 km run turns west again, reducing the track error. By landfall, this westward motion has reduced the track error in the 25 km run by roughly 75 km compared to the 13 km and 3 km runs. The GFSv16beta track forecasts are very similar to those of GFSv15.2, making landfall in the same spatiotemporal location for each grid spacing. The GFSv16beta NoConv sensitivity test shows that disabling the cumulus parameterization makes the 3 km run perform comparably to the 25 km run. This is likely attributable to the superposition of the resolved and parameterized convective activity that could occur with the cumulus parameterization active at this resolution.
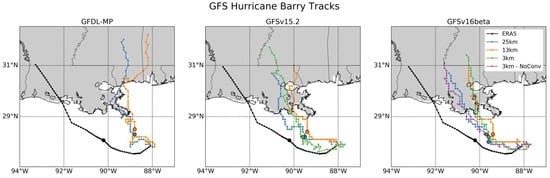
Figure 2.
TC track forecasts from each GFS physics suite tested at each grid spacing: 25 km (blue), 13 km (orange), and 3 km (green). The ERA5 track is shown in black. The violet track in the GFSv16beta plot represents the 3 km sensitivity experiment with the cumulus convection scheme disabled. Scatter points denote each hour of the run, and hour 30 of each forecast is denoted by an especially large point.
The TC track is controlled by the steering flow, computed here as described in Section 2.2. Figure 3 shows the steering flow for each of the GFS physics suite runs, with ERA5 included for verification. The zonal component (solid lines) of the ERA5 steering flow is quite consistent, holding steady around −2 m/s for the duration of the forecast. The meridional component (dashed lines), in contrast, increases steadily as the TC recurves northward, as expected. The GFDL-MP runs show a large eastward error in the steering flow, consistent with the large eastward track error in these runs; however, the meridional flow verifies well with ERA5. The absolute steering flow error in the GFDL-MP runs is fairly consistent around 1 m/s. A similar behavior is seen in the GFSv15.2 and GFSv16beta runs at 25 km and 13 km grid spacing, with the westerly component of the steering flow weaker than observed, while the meridional component verifies well, resulting in an overall slow error in the steering flow magnitude. In the 3 km runs, especially for GFSv16beta, the steering flow in both directions verifies well for the first several hours of the forecast, after which these diverge from ERA5 and tend toward the steering flow of the other runs (around 24 h for GFSv15.2 and around 32 h for GFSv16beta).
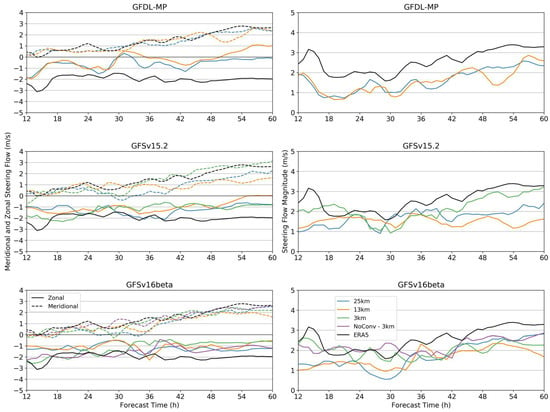
Figure 3.
Time series of the environmental steering flow around the TC. A 3 h rolling time average is applied to the hourly data to reduce noise. The figures on the left show the meridional (dashed lines) and zonal (solid lines) flow determined by the OSL method described in Section 2.2. On the right is the magnitude of the steering flow. The 25 km (blue), 13 km (orange), and 3 km (green) runs for each physics suite are compared with ERA5 (black) for verification. The GFSv16beta NoConv sensitivity run is shown in violet.
Table 2 shows the mean error of the OSL depth and removal radius to which each TC is sensitive. Here, a positive removal radius error means the simulated TC is sensitive to a larger removal radius than is ERA5, while if the depth error is positive, it means the simulated TC is sensitive to a deeper steering layer than ERA5. For GFSv16beta 25 km and 3 km NoConv, two of the best track forecasts in all the simulations, we find the post-recurve behavior to be the most important period for differentiation from the other runs (Figure 2). These runs’ OSL depth match ERA5 quite well, despite the relatively significant error in the pre-recurve period. For GFDL-MP, we see quite poor track forecasts, despite the relatively small error in the OSL parameters. This suggests that for these runs, the environmental winds themselves are erroneous (particularly in the zonal direction, see Figure 3), rather than just the layer to which the TC is sensitive. Nearly all of these runs show sensitivity to a deeper steering layer than ERA5, suggesting these TCs are deepening prematurely. Little such coherent patterns are seen relating the removal radius to track fidelity, though the simulated TCs are found nearly universally to be sensitive to environmental winds from a smaller removal radius than ERA5.

Table 2.
GFS physics runs mean error for OSL depth and removal radius, as compared to ERA5.
As discussed in Section 1, the TC motion tends toward the region of maximum convection and diabatic heating, which is the result of the coupled interactions between the convection and vertical wind shear. Figure 4 shows the composite reflectivity at 30 h from each GFS physics run, along with the simultaneous hourly accumulated IMERG and Stage IV precipitation for verification. The convection at 30 h is shown because it is around this time that the modeled TC tracks tend to recurve sharply to the north and diverge from ERA5, except for the GFDL-MP runs, which diverge earlier. Figure 4 shows strong disagreement between the observational data and the UFS-SRW, with each forecast run showing significant convection wrapping into the USL (northeast) TC-relative quadrant and the IMERG data showing precipitation largely confined to the region directly south of the TC center. The Stage IV data include this region of precipitation directly south of the TC center, but with a substantially reduced magnitude. One possible explanation of this discrepancy is that the radar-based precipitation estimates have previously been found to be underestimated at long range [37], and this region lies at the edge of the radar’s range. Stage IV also shows significant precipitation to the northeast of the TC, though most of this is displaced ~200 km from the TC center. GFDL-MP depicts the most convection in the USL quadrant, and this convection is also located within 50 km of the TC center, allowing it to more efficiently affect the intensification of the model TC [9].
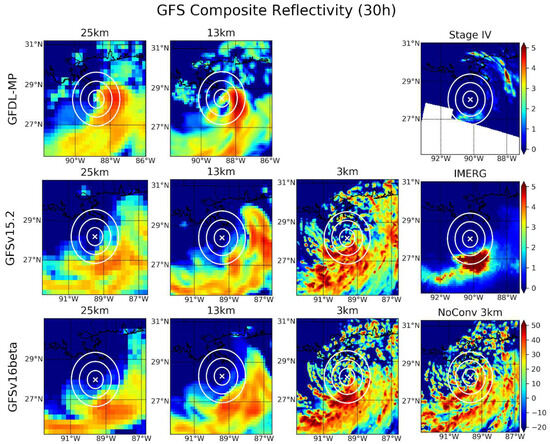
Figure 4.
TC-centered composite reflectivity (dB) at 30 h for the GFS physics suite runs with IMERG and Stage IV derived precipitation (mm/hr) for verification. The white cross indicates the TC center, and each concentric white circle indicates a 50, 100, and 150 km radius about the center. The whited out area in the Stage IV data are not defined due to being beyond the range of the radar from which these data are estimated.
For both GFSv15.2 and GFSv16beta, only the weak convection is seen wrapping into the USL quadrant in the 25 km run, while more is seen in the 13 km run. In the GFSv15.2 3 km run, there is a patch of heavy convection directly to the east of the TC center, while in the GFSv16beta 3 km run, the convection is largely confined to the region south of the TC, with some convection wrapping into the USL quadrant. The NoConv run of GFSv16beta shows similar behavior, though the convection to the south-southeast of the TC is concentrated into rain bands rather than the more aggregated convective region seen in the 3 km control.
To investigate the source of this excess convection, the surface latent heat flux (LHF) into the atmosphere at 30 h is shown in Figure 5. From this figure, it is clear that all of the GFS physics runs produce excess LHF to the east and especially northeast of the TC center. The magnitude of the LHF error and its proximity to the TC center are also roughly correlated with the extent of the track error that eventually develops in each run. Regions of excessive LHF contribute to areas of erroneous convection as the fluxes contribute to a positive feedback loop reminiscent of a wind-induced surface heat exchange (WISHE) process [38,39]. The GFDL-MP runs show the most extreme LHF error, and even by this time show the largest track errors as well. The GFSv16beta 25 km run shows only a slight LHF error to the east of the TC, and eventually shows the least track error seen in the GFS runs. In the GFSv16beta NoConv run at 3 km grid spacing, LHF is substantially reduced, especially within 100 km of the TC center, where differences of around 200 W/m2 emerge. That these reductions in LHF occur in the sensitivity experiment that results in one of the best track forecasts lends credence to the hypothesis that these processes are causally linked in the model through a WISHE process.
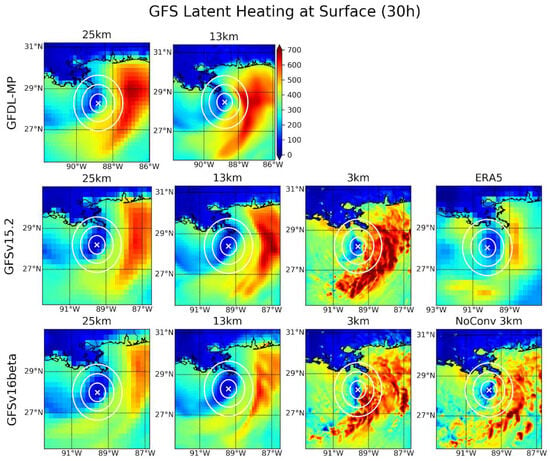
Figure 5.
TC-centered surface latent heating (W/m2) into the atmosphere at 30 h for the GFS physics suite runs, with ERA5 for verification. The white cross indicates the TC center and each concentric white circle indicates a 50, 100, and 150 km radius about the center. The color bar shown for GFDL-MP 13 km applies to all results shown in this figure.
What is the origin of this LHF error? Figure 6 shows the SST at the initialization time and at 18 h into the forecast. A slight warm SST error to the northeast of the TC is seen at 18 h when comparing the GFSv16beta 3 km run to DOISST, while this error is considerably stronger and more widespread in ERA5 and MURSST. This error is collocated with the LHF error seen in ERA5. Although only the GFSv16beta 3 km run is shown here, the SST field varies very little between physics suites and grid spacing. The NSST parameterization used in all these runs cannot represent the cold wake that typically develops to the right of the TC track in the Northern Hemisphere. Despite the forecasts being initialized with a SST field with a cool error, a warm error is present by 18 h, since the SST evolves very little during the forecast. In both ERA5 and the forecasts, the latent heating to the east of the storm is driven by the intensifying low-level winds, concentrated to the south of the TC center due to the sheared environment. In the model forecasts, the convection is far more active and closer to the TC center than that seen in the IMERG and Stage IV precipitation datasets. This convection is initially the most active in the southern semicircle, but it soon develops upshear due to the cyclonic winds of the TC. Once the convective bursts become concentrated in the downshear-left (southeast) and upshear-left (northeast) quadrants, the TC intensifies more efficiently in that the intensification is more extreme than if the convective bursts were located in different TC-relative regions. In ERA5 (and in reality), this process is attenuated because LHF and convective activity tend to cool the underlying ocean, as demonstrated in Figure 6. However, in the UFS-SRW forecasts, the SST effectively does not cool, and thus a positive-feedback loop is established because it is not dampened by the SST response. The next subsection will show similar features in the GSD physics runs, while Section 4 includes more in-depth discussion of this feedback loop.
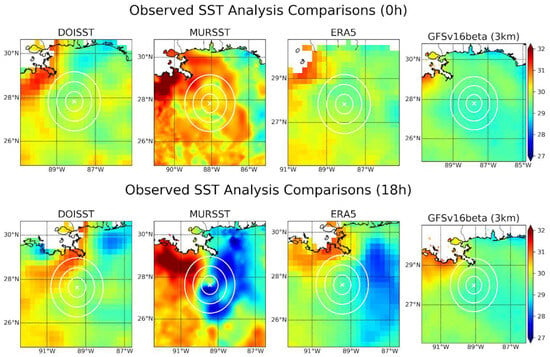
Figure 6.
TC-centered sea-surface temperature (°C) at 0 h (top) and 18 h (bottom) for the GFSv16beta 3 km run compared with DOISST, MURSST, and ERA5 reanalysis for verification. Although only one run is shown here, the SST field is virtually identical for all of the model forecasts considered in this study, regardless of physics suite or grid spacing.
3.2. GSD Physics Suites
In this section, it is shown that the runs using the GSD physics suites result in similar errors as the GFS suites. Figure 7 shows the TC track in these runs, along with ERA5. All the TCs in the GSD runs spend several hours moving erratically before getting caught in the prevailing steering flow around 15 h, after which they move northwestward. For GSDv0, the 25 km and 13 km tracks follow a very similar path to that seen in the GFDL-MP runs at the same grid spacings. However, the 3 km run shows significantly less error than the other grid spacings and is comparable to the least erroneous GFS runs (GFSv15.2 25 km, GFSv16beta 25 km, and GFSv16beta NoConv). GSD_noMY creates similar tracks for the 25 km and 13 km runs, but the 3 km run shows greatly reduced east-of-track error of around 75 km at landfall. For GSD_Noah, the 3 km run is the least erroneous of all the forecasts with any physics suite, making landfall around 30 km to the east of ERA5.

Figure 7.
As with Figure 2, but for the GSD physics suites. The bolded scatter point here designates forecast hour 15 h, as several runs diverge from ERA5 around this time.
Here, the NoConv run with the convection parameterization disabled, which does not improve the track forecast and, in fact, results in a slight degradation at later forecast times. The 25 km run with this suite is slightly improved over the other GSD suites, and the 13 km run shows slight improvement as well, splitting the difference between the 3 km runs and the 25 km run. Figure 8 shows the steering flow as calculated using the method described in Section 2.2. Regardless of the physics version, the 25 km runs show very similar behavior, with severely underestimated environmental zonal winds resulting in a strong slow error in the steering flow magnitude. A similar, though less extreme error, is seen in the GSD_Noah and GSD_noMY 13 km runs, as well as in the GSDv0 3 km run. In general, the meridional flow verifies much better than the zonal flow and is consistent with the eastward track error despite similar landfall times of each TC. The GSD_Noah and GSD_noMY 3 km runs (including the NoConv run), which result in the best track forecasts of all the physics suites and versions tested here. The 3 km runs with convection turned on show too strong zonal flow and, therefore, steering flow magnitude until around 26 h, while the NoConv run shows a slight slow error in the zonal flow and steering flow magnitude.
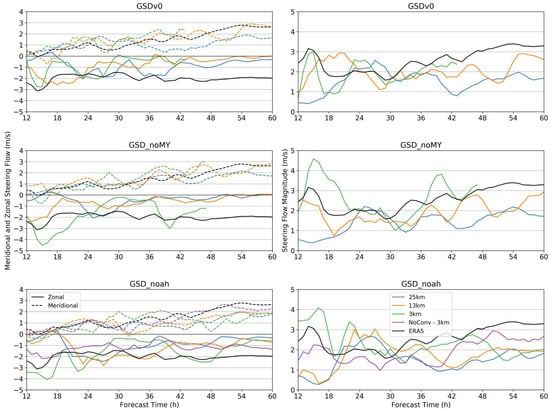
Figure 8.
As with Figure 3, but for the GSD physics suite runs.
Table 3 shows the OSL depth and removal radius for the GSD physics runs. With the exception of the pre-recurve GSD_noMY 13 km run, we find all TCs to be sensitive to a much deeper steering layer than ERA5. This, along with the early and stronger recurve, suggest even more premature intensification and deepening than in the GFS runs, despite the relative fidelity of the GSD 3 km runs. For the GSD_noMY 3 km and GSD_Noah 3 km NoConv runs, which result in the best track forecast across all runs, significantly reduced error in OSL depth is seen after recurve, suggesting that, although these TCs do intensify prematurely, their ultimate depth is on par with observations. The GSDv0 3 km run results in a similar, though a more erroneous track forecast, even though a far greater depth error is seen post-recurve. In that run, however, significantly reduced removal radius error is seen post-recurve, indicating that this TC may be too deep, but of similar size to the TC in ERA5. All other runs show erroneous OSL depth and removal radius post-recurve consistent with their more erroneous track forecasts. To investigate whether the GSD suites exhibit the same WISHE-like positive feedback that ostensibly contributes to the track errors in the GFS forecasts, the composite reflectivity and IMERG precipitation for verification at 15 h are shown in Figure 9. Each run using the GSD suites show very similar convective distributions, particularly in the USL and DSL quadrants. At this time, the IMERG data show only small areas of aggregated precipitation, at 100–150 km from the TC center, while the forecasts show significant wrapping of convection into the TC center, suggesting the same premature intensification and convective concentration exhibited by the GFS physics forecasts. The 3 km runs, including the NoConv run, show some intense convection to the southwest of the TC center as well, which may contribute to the relative fidelity of these forecasts by offsetting the USL/DSL convection, which would tend to contribute to asymmetric potential vorticity generation. Furthermore, because the steering flow magnitude shows a more significant slow error in the 25 km and 13 km runs compared to the 3 km runs, forecasts at those grid spacings may be more susceptible to motion tendencies induced by the convection error [6].

Table 3.
As with Table 2, but for GSD physics runs.
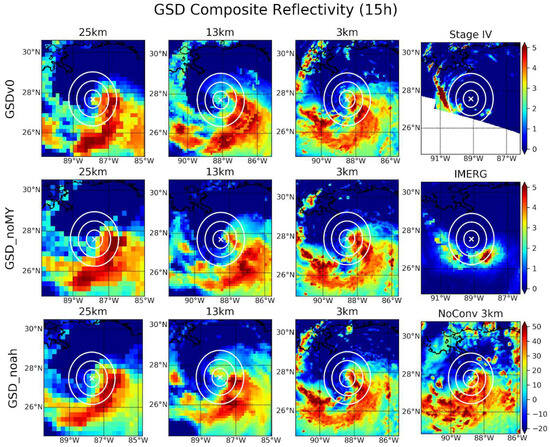
Figure 9.
As with Figure 4, except for the GSD physics suite runs and at forecast hour 15 h.
The next step in the WISHE feedback is the latent heating into the atmosphere, which is shown at 15 h in Figure 10. As with the GFS suites, we see a strong latent heating error to the east of the developing TC in most of the GSD physics runs. However, unlike the GFS forecasts, this error is largest in the 25 and 13 km runs, with smaller LHF in the 3 km runs. Interestingly, though the GSD_Noah 13 km run shows less track error than any other GSD 25- or 13 km run, it also exhibits the largest LHF error. This highlights the complexity of this nonlinear interaction and how slightly different physics packages can interact in slightly different ways to produce quite different results. Nevertheless, Figure 10 demonstrates that the LHF error is present in differing degrees in all UFS-SRW runs with GSD physics suites as well. Thus, the hypothesis that the previously described WISHE feedback is responsible for the premature intensification and the systematic east-of-track bias seen in the UFS-SRW and the operational UFS is supported. As with the GFS suites, the proximate cause of these feedbacks and errors is the insufficient representation of the cold wake effect of a passing TC, as shown in Figure 6 for GFSv16beta 3 km. The SST distribution in all UFS-SRW runs considered here, with all physics suites, is virtually identical to that shown in Figure 6, providing support for our hypothesis.
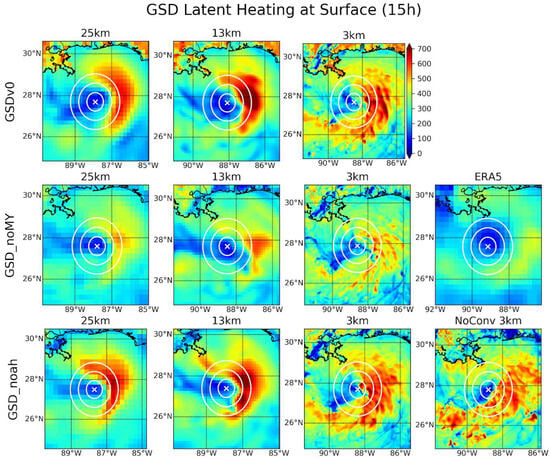
Figure 10.
As with Figure 5, except for the GSD physics suite runs and at forecast hour 15 h.
4. Discussion
The purpose of this study is to investigate the scalability of various CCPP physics suites within the UFS-SRW with respect to the case study of Hurricane Barry (2019), which developed in a strongly sheared environment. This particular event was chosen to investigate the strong east-of-track bias seen in the operational GFS for this event to identify shortcomings in the model physics. Regarding the physics scalability, we find that although the general large-scale pattern is similar throughout the runs at each grid spacing, significant differences in the forecast fields emerge, which result in differences in the TC tracks at landfall of several hundred kilometers in some cases. Here, we posit that these differences are strongly influenced by a WISHE-like positive feedback loop, which begins with strengthening winds due to the developing TC. These winds drive latent heating of the atmosphere near the ocean surface, resulting in convective activity as this heat is deposited into the atmosphere. In the model forecasts, the SST does not cool realistically in response to this latent heating and convection. Therefore, the ocean continues to pump heat unabated into the atmosphere, driving further latent heating and convection as the run continues. The convection tends to affect the local potential vorticity by driving an excess of asymmetrical diabatic heating in that region, thus causing the TC track to deflect toward that convection [6]. In addition, the cyclonic motion of the TC advects the convection into the regions that most efficiently intensify the developing TC (USL and DSL), as the convective-scale subsidence about these convective bursts superimposes on the mesoscale subsidence due to the sheared environment, thus carrying warm, relatively dry air into the midlevel TC core [9]. Finally, due to the premature intensification of the TC, the low-level winds now show a strong intensity error, and the feedback loop is complete.
The steering flow velocity is generally underestimated, excepting the GSD_Noah and GSD_noMY 3 km runs. This slow steering flow makes the TC track more susceptible to influence by asymmetric diabatic heating [5,6,7], thus magnifying the influence of the already excessive convection to the east of the TC center that is present due to the warm SST bias there. Due to the premature intensification of these TCs, they show sensitivity to a deeper OSL depth than ERA5. The 3 km GSD runs show stronger steering flow than the other runs considered here (which verifies more closely with ERA5). Because of this, despite similar errors in convection and latent heating developing in these runs as well, the TC tracks in the 3 km GSD runs are less influenced by the excess diabatic heating.
Why, then, is the steering flow more accurately represented in these runs? Figure 11 shows the 850 hPa geopotential height at 12 h for a few cases chosen to demonstrate some more general differences seen in these runs. In particular, these runs show roughly the most (GFDL-MP 13 km and GSD_noMY 25 km) and least (GFSv16beta 25 km and GSD_Noah 3 km) track error within their respective physics suite family. While all show a systematic negative bias in the 850 hPa geopotential height, the spatial distribution of that bias is very important in determining the effect on the steering flow. In GFDL-MP 13 km, a large negative error forms well to the north of the developing TC, extending south from the Great Lakes region. This geopotential height error would tend to impart a northeastward error on the steering flow due to cyclonic anomalies in the environmental wind field, consistent with the TC track behavior in that case. A very similar 850 hPa height field and track error is present in GFDL-MP 25 km (not shown). This strong geopotential error is not seen in GFSv16beta 25 km, but a different negative error to the east of the developing TC is present. This would tend to impart a southward anomaly on the environmental flow about the TC, thus slowing the steering flow, which is predominantly southeasterly. A similar result is found for GSD_noMY 25 km, but the effect on the steering flow magnitude is not as strong in this case due to the smaller error in the geopotential height field. Despite this, GFSv16beta 25 km shows significantly less track error than the GSD_noMY 25 km run, highlighting the complexity of the nonlinear problem presented here. Finally, in GSD_Noah 3 km, there is a strong negative error in the 850 hPa height directly to the southwest of the developing TC in that case. This would impart a southeasterly anomaly on the environmental wind field, thus strengthening the steering flow. Therefore, the convective error that develops in this case does not affect the track as strongly as in other cases, resulting in the highest fidelity track forecast of all the UFS-SRW runs.
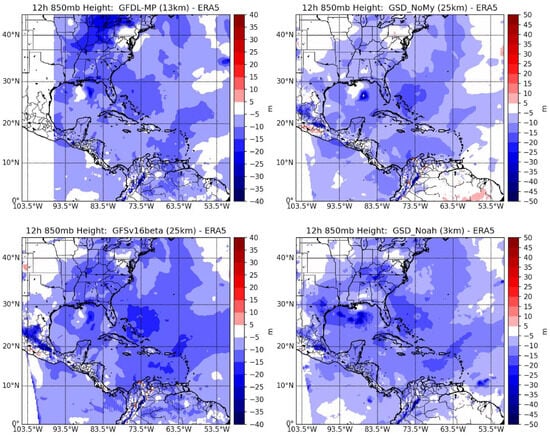
Figure 11.
850 hPa geopotential height difference at 12 h between GFDL-MP 13 km (top left), GFSv16beta 25 km (bottom left), GSD_noMY 25 km (top right), GSD_Noah 3 km (bottom right) and ERA5. These cases are chosen as demonstrative examples of features common to forecasts with similar track errors.
5. Conclusions
Clearly, slightly different physical interactions within the model can result in dramatically different outcomes with respect to the track forecast, demonstrating the complexity of the problem and the differing behavior of the tested physics suites’ scalability. For the GFS suites, some of the best track forecasts are found in the 25 km simulations, with only the 3 km NoConv run of the GFSv16beta physics rivaling the 25 km. For the GSD suites, we see exactly the opposite (and more expected) behavior; that is, improving the track forecasts with increasing resolution. As to why this might be happening, we are left to speculate and recommend future studies to investigate this issue. Many of the physics suites tested here differ in more than one way with respect to their internal parameterizations, making it difficult to make conclusions about their contributions to the track forecast simulations. The differing cumulus, PBL, and cloud microphysics schemes likely all contribute to this differing behavior in nonlinear ways. Ongoing development of these schemes is necessary to improve their scalability, coinciding with continued testing and verification to isolate the contribution of the various parameterizations to the errors in the environmental winds, latent heating, and intensification demonstrated in this study. Evaluations utilizing this model’s hierarchy approach of isolating the individual parameterizations and interactions at a process-level using tools such as a single-column model, as in Chen et al. (2021) [40], would provide an ideal tool for such a future study.
Though these track forecast errors can be at least partially traced back to the erroneous ocean forcing, i.e., the warm SST bias, the SST bias alone does not fully explain the right-of-track error seen in these forecasts, as this error is still present in the operational model forecasts at this initialization time using the fully coupled Hurricane Weather Research and Forecasting (HWRF) model [41]. Furthermore, although the SST bias is consistent in both the spatial location and magnitude throughout all these cases, this anomalous ocean forcing results in widely differing effects across physics suites and grid spacings, suggesting cascading differences in physical behavior as well. An improved parameterization or a fully coupled ocean model that more accurately represents the formation and evolution of cold wakes would likely improve the UFS-SRW performance but is not sufficient to explain the forecast errors. Sensitivity studies with fully coupled models should be performed in the future to isolate the contribution from the SST bias. There are no formal plans to implement two-way ocean coupling within the UFS-SRW; therefore, testing using the UFS Hurricane Application should be considered. Parallel efforts testing GFS-based physics suites within the UFS-SRW for Hurricane Florence (2018) have revealed similar results in the track forecasts at different scales [42]. The persistent finding that hundreds of kilometers at landfall differentiate track forecasts resulting from runs with the same physics but different grid spacing exemplifies the effort that still needs to be made to improve the scalability of these physics suites and the performance of this forecasting system.
Author Contributions
Conceptualization, N.D.L., K.M.N. and E.A.K.; data curation, K.M.N. and E.A.K.; formal analysis, N.D.L.; funding acquisition, K.M.N. and E.A.K.; investigation, N.D.L.; methodology, N.D.L., K.M.N. and E.A.K.; project administration, K.M.N. and E.A.K.; software, N.D.L. and K.M.N.; supervision, K.M.N.; validation, N.D.L.; writing—original draft, N.D.L.; writing—review and editing, K.M.N. and E.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
E.A.K. was supported by funding from NOAA Award Number NA17OAR4320101. The authors acknowledge the NOAA Research and Development High Performance Computing Program (http://rdhpcs.noaa.gov, accessed on 25 July 2023) for providing computational and storage resources that have contributed to the research results reported within this paper. The DTC is funded by NOAA, the U.S. Air Force, the National Center for Atmospheric Research (NCAR), and the National Science Foundation (NSF).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in this study have been archived on the High-Performance Storage System (HPSS) at the NOAA Environmental Security Computing Center (NESCC). An existing NOAA High Performance Computing account is required to access HPSS and to obtain the data. The authors are willing to share the data location on HPSS with those who have access and may be able to make data subsets available to those who do not have access on a case-by-case basis. Due to the large size of the model output files and the lack of an appropriate public-facing institutional repository, the authors are unable to make the data publicly available at this time.
Acknowledgments
Special thanks to Michelle Harrold for her help with the IMERG satellite data, Tracy Hertneky for contributions including the post-processing of model output, and Weiwei Li for her insights into the physics framework and steering flow analysis utilized here.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.; Rao, Y.; Tan, Z.-M.; Schönemann, D. A Statistical Analysis of the Effects of Vertical Wind Shear on Tropical Cyclone Intensity Change over the Western North Pacific. Mon. Weather Rev. 2015, 143, 3434–3453. [Google Scholar] [CrossRef]
- UFS Development Team. Unified Forecast System (UFS) Short-Range Weather (SRW) Application (v1.0.0); Zenodo: Geneva, Switzerland, 2021. [CrossRef]
- Cangialosi, J.P.; Hagen, A.B.; Berg, R. Tropical Cyclone Report: Hurricane Barry. National Hurricane Center. 2019. Available online: https://www.nhc.noaa.gov/data/tcr/AL022019_Barry.pdf (accessed on 5 July 2023).
- Wang, Y.; Holland, G.J. Tropical Cyclone Motion and Evolution in Vertical Shear. J. Atmos. Sci. 1996, 53, 3313–3332. [Google Scholar] [CrossRef]
- Wu, L.; Wang, B. A Potential Vorticity Tendency Diagnostic Approach for Tropical Cyclone Motion. Mon. Weather Rev. 2000, 128, 1899–1911. [Google Scholar] [CrossRef]
- Chan, J.C.L.; Ko, F.M.F.; Lei, Y.M. Relationship between Potential Vorticity Tendency and Tropical Cyclone Motion. J. Atmos. Sci. 2002, 59, 1317–1336. [Google Scholar] [CrossRef]
- Chan, J. The physics of tropical cyclone motion. Annu. Rev. Fluid Mech. 2005, 37, 99–128. [Google Scholar] [CrossRef]
- Jones, S.C. The evolution of vortices in vertical shear. I: Initially barotropic vortices. Q. J. R. Meteorol. Soc. 1995, 121, 821–851. [Google Scholar] [CrossRef]
- Chen, H.; Gopalakrishnan, S.G. A Study on the Asymmetric Rapid Intensification of Hurricane Earl (2010) Using the HWRF System. J. Atmos. Sci. 2014, 72, 531–550. [Google Scholar] [CrossRef]
- Reasor, P.D.; Eastin, M.D.; Gamache, J.F. Rapidly Intensifying Hurricane Guillermo (1997). Part I: Low-Wavenumber Structure and Evolution. Mon. Weather Rev. 2009, 137, 603–631. [Google Scholar] [CrossRef]
- Wang, Y.; Holland, G.J. The Beta Drift of Baroclinic Vortices. Part I: Adiabatic Vortices. J. Atmos. Sci. 1996, 53, 411–427. [Google Scholar] [CrossRef]
- Wang, Y.; Holland, G.J. The Beta Drift of Baroclinic Vortices. Part II: Diabatic Vortices. J. Atmos. Sci. 1996, 53, 3737–3756. [Google Scholar] [CrossRef]
- Willoughby, H.E. Linear Motion of a Shallow-Water, Barotropic Vortex. J. Atmos. Sci. 1988, 45, 1906–1928. [Google Scholar] [CrossRef]
- Willoughby, H.E. Linear Motion of a Shallow-Water Barotropic Vortex as an Initial-Value Problem. J. Atmos. Sci. 1992, 49, 2015–2031. [Google Scholar] [CrossRef]
- Wu, C.-C.; Emanuel, K.A. Interaction of a Baroclinic Vortex with Background Shear: Application to Hurricane Movement. J. Atmos. Sci. 1993, 50, 62–76. [Google Scholar] [CrossRef]
- Flatau, M.; Schubert, W.H.; Stevens, D.E. The Role of Baroclinic Processes in Tropical Cyclone Motion: The influence of Vertical Tilt. J. Atmos. Sci. 1994, 51, 2589–2601. [Google Scholar] [CrossRef]
- Kaplan, J.; DeMaria, M.; Knaff, J.A. A Revised Tropical Cyclone Rapid Intensification Index for the Atlantic and Eastern North Pacific Basins. Weather Forecast. 2010, 25, 220–241. [Google Scholar] [CrossRef]
- Gray, W.M. Global View of the Origin of Tropical Disturbances and Storms. Mon. Weather Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
- Merrill, R.T. Environmental Influences on Hurricane Intensification. J. Atmos. Sci. 1988, 45, 1678–1687. [Google Scholar] [CrossRef]
- Demaria, M.; Kaplan, J. Sea Surface Temperature and the Maximum Intensity of Atlantic Tropical Cyclones. J. Clim. 1994, 7, 1324–1334. [Google Scholar] [CrossRef]
- Schubert, W.H.; Hack, J.J. Inertial Stability and Tropical Cyclone Development. J. Atmos. Sci. 1982, 39, 1687–1697. [Google Scholar] [CrossRef]
- Willoughby, H.E.; Clos, J.A.; Shoreibah, M.G. Concentric Eye Walls, Secondary Wind Maxima, and The Evolution of the Hurricane vortex. J. Atmos. Sci. 1982, 39, 395–411. [Google Scholar] [CrossRef]
- Kossin, J.P.; Schubert, W.H. Mesovortices, Polygonal Flow Patterns, and Rapid Pressure Falls in Hurricane-Like Vortices. J. Atmos. Sci. 2001, 58, 2196–2209. [Google Scholar] [CrossRef]
- Eastin, M.D.; Gray, W.M.; Black, P.G. Buoyancy of Convective Vertical Motions in the Inner Core of Intense Hurricanes. Part I: General Statistics. Mon. Weather Rev. 2005, 133, 188–208. [Google Scholar] [CrossRef]
- Eastin, M.D.; Gray, W.M.; Black, P.G. Buoyancy of Convective Vertical Motions in the Inner Core of Intense Hurricanes. Part II: Case Studies. Mon. Weather Rev. 2005, 133, 209–227. [Google Scholar] [CrossRef]
- Zhang, M.; Bernardet, L.; Firl, G.; Heinzeller, D.; Carson, L. Scientific Documentation for the Common Community Physics Package Version 5. 2021. Available online: https://dtcenter.ucar.edu/GMTB/v5.0.0/sci_doc (accessed on 5 July 2023).
- Heinzeller, D.; Bernardet, L.; Firl, G.; Zhang, M.; Sun, X.; Ek, M. The Common Community Physics Package (CCPP) Framework v6. Geosci. Model Dev. 2023, 16, 2235–2259. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, K.; Hsu, K.; Joyce, R.; Xie, P. Integrated Multi-satellitE Retrievals for GPM (IMERG), Version 4.4. NASA’s Precipitation Processing Center. 2014. Available online: https://giovanni.gsfc.nasa.gov/giovanni/ (accessed on 1 August 2022).
- Du, J. NCEP/EMC 4KM Gridded Data (GRIB) Stage IV Data. Version 1.0 (Version 1.0) [GRIB-2: Gridded Binary Edition 2 (GRIB)]. UCAR/NCAR—Earth Observing Laboratory. 2011. Available online: https://data.eol.ucar.edu/dataset/21.093 (accessed on 28 June 2023). [CrossRef]
- Bourdin, S.; Fromang, S.; Dulac, W.; Cattiaux, J.; Chauvin, F. Intercomparison of Four Algorithms for Detecting Tropical Cyclones Using ERA5. Geosci. Model Dev. 2022, 15, 6759–6786. Available online: https://zenodo.org/record/6424432 (accessed on 22 June 2023). [CrossRef]
- Hodges, K.I. A General Method for Tracking Analysis and Its Application to Meteorological Data. Mon. Weather Rev. 1994, 122, 2573–2586. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, B.; Zhang, H.-M. Improvements of the Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 2923–2939. Available online: https://www.ncei.noaa.gov/erddap/griddap/ (accessed on 2 February 2023). [CrossRef]
- Chin, T.M.; Vazquez-Cuervo, J.; Armstrong, E.M. A Multi-Scale High-Resolution Analysis of Global Sea Surface Temperature. Remote Sens. Environ. 2017, 200, 154–169. Available online: https://cmr.earthdata.nasa.gov/virtual-directory/collections/C1996881146-POCLOUD/ (accessed on 13 July 2023). [CrossRef]
- Biswas, M.; Stark, D.; Carson, L. GFDL Vortex Tracker Users Guide Version 3.9a. 2018. Available online: https://dtcenter.org/sites/default/files/community-code/gfdl/standalone_tracker_UG_v3.9a.pdf (accessed on 5 July 2023).
- Galarneau, T.J.; Davis, C.A. Diagnosing Forecast Errors in Tropical Cyclone Motion. Mon. Weather Rev. 2013, 141, 405–430. [Google Scholar] [CrossRef]
- Kitchen, M.; Jackson, P.M. Weather Radar Performance at Long Range—Simulated and Observed. J. Appl. Meteorol. Climatol. 1993, 32, 975–985. [Google Scholar] [CrossRef]
- Zhang, F.; Emanuel, K. On the Role of Surface Fluxes and WISHE in Tropical Cyclone Intensification. J. Atmos. Sci. 2016, 73, 2011–2019. [Google Scholar] [CrossRef]
- Emanuel, K.A. An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-State Maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Chen, X.; Bryan, G.H.; Zhang, J.A.; Cione, J.J.; Marks, F.D. A Framework for Simulating the Tropical Cyclone Boundary Layer Using Large-Eddy Simulation and Its Use in Evaluating PBL Parameterizations. J. Atmos. Sci. 2021, 78, 3559–3574. [Google Scholar] [CrossRef]
- Hurricane Analysis and Forecast System. 2023. Available online: https://www.emc.ncep.noaa.gov/hurricane/HFSA/index.php (accessed on 24 July 2023).
- Li, W. Analysis of Hurricane Florence as a Case Study of UFS-SRW Performance; NCAR: Boulder, CO, USA, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).