Numerical Simulation Calculation of Thermal Discharge Water Diffusion in Coastal Nuclear Power Plants
Abstract
:1. Introduction
2. Materials and Methods
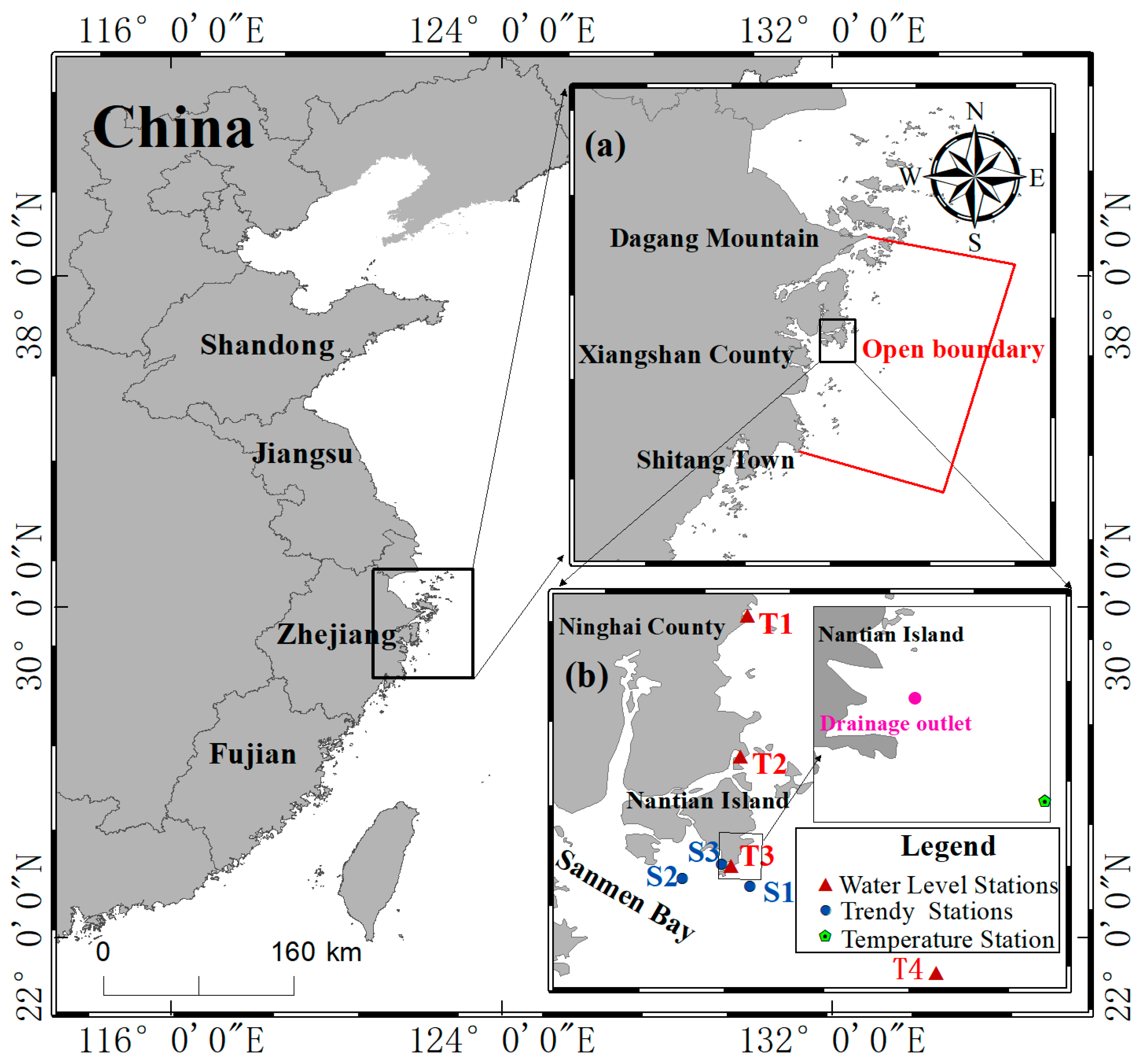
2.1. Overview of the Study Area
2.2. Model Introduction
2.2.1. Control Equation
- (1)
- MIKE fluid dynamics equation (Equations (1)–(3)) [42]:
- (2)
- MIKE temperature transport equation (Equations (4) and (5)):
- (3)
- Boundary control conditions
2.2.2. The Difference between the Temperature–Salinity Module and the ECO Module
3. Model Setup and Verification
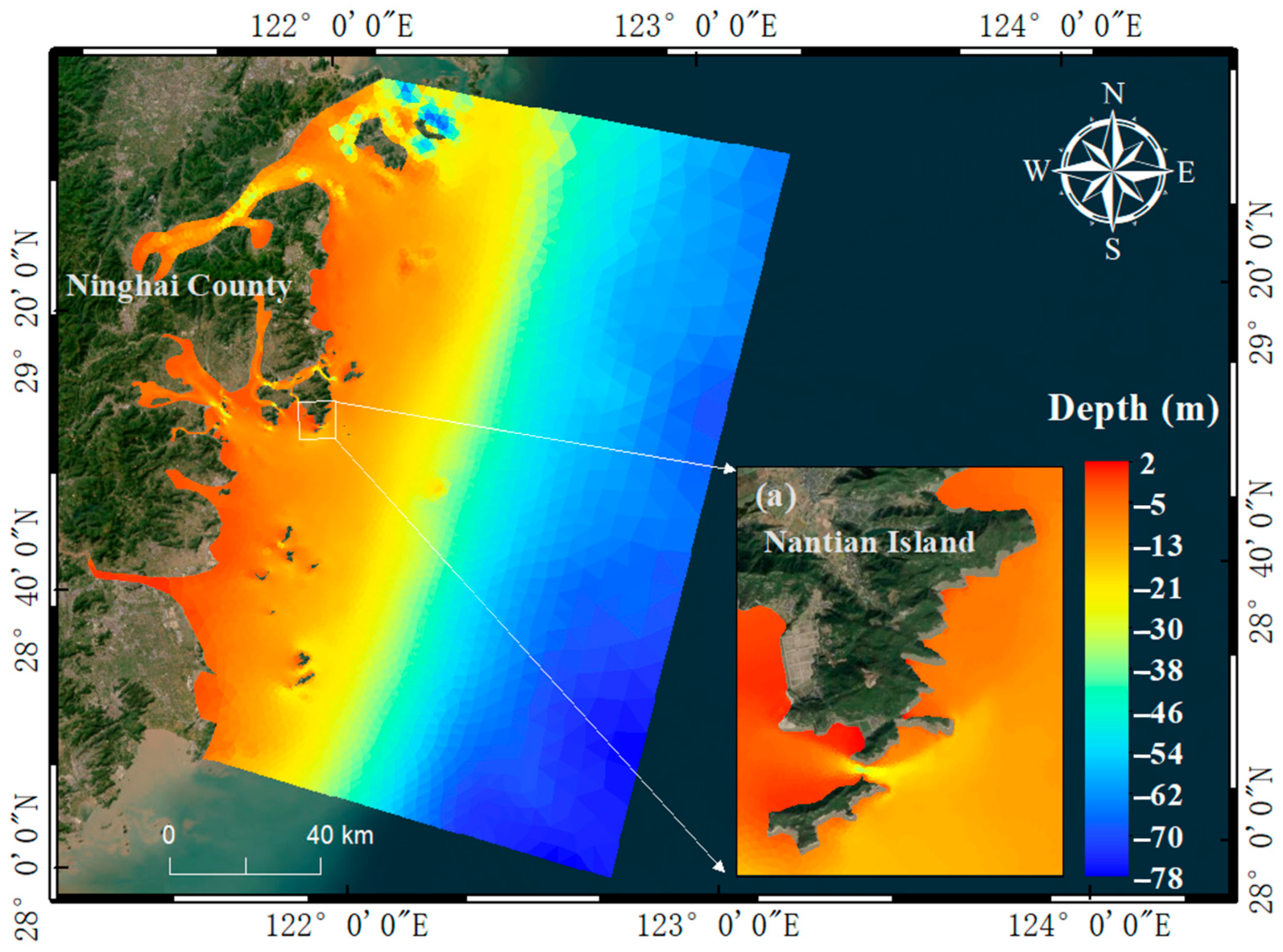
3.1. Grid and Water Depth Settings
3.2. Model-Driven Conditions
3.3. Model Parameter Configuration
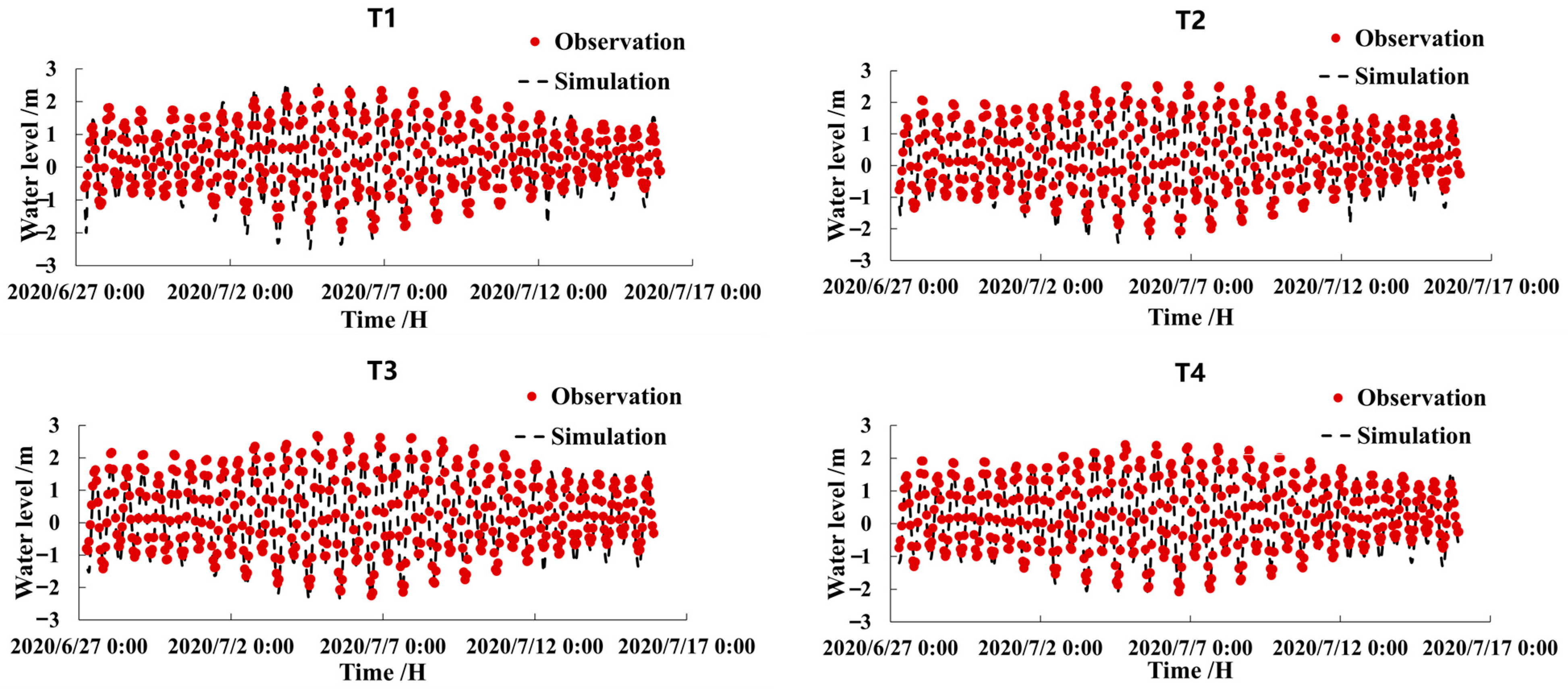
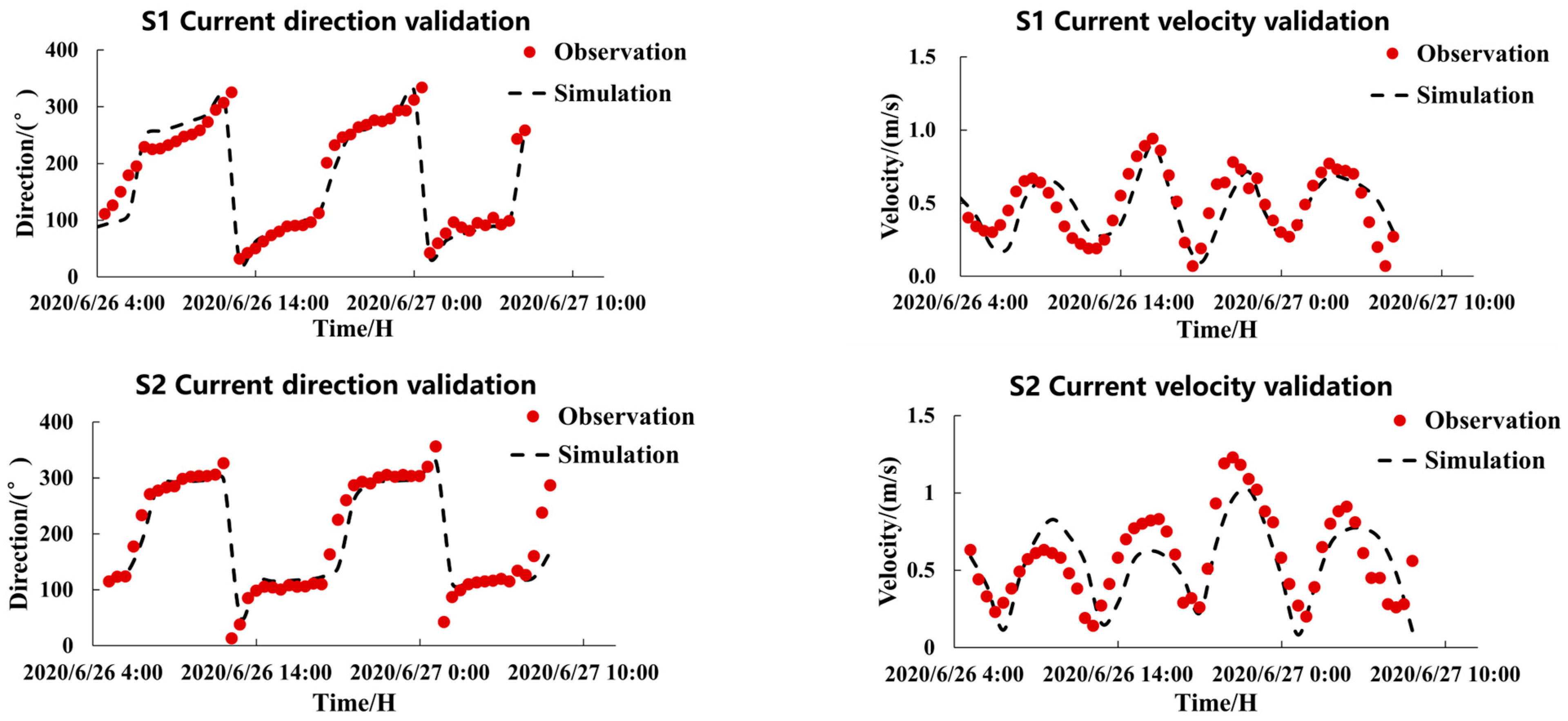
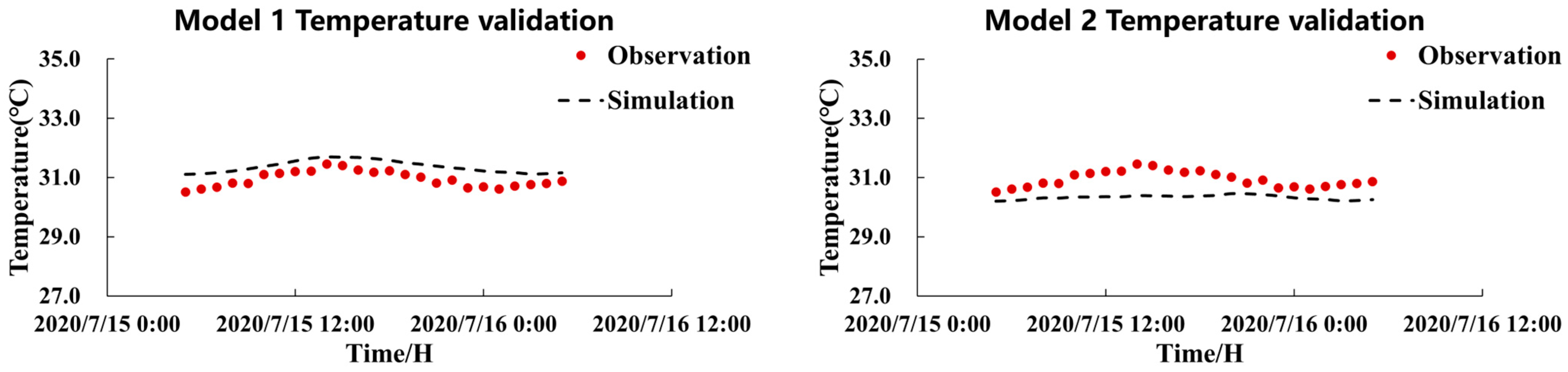
3.4. Model Validation
4. Results and Analysis
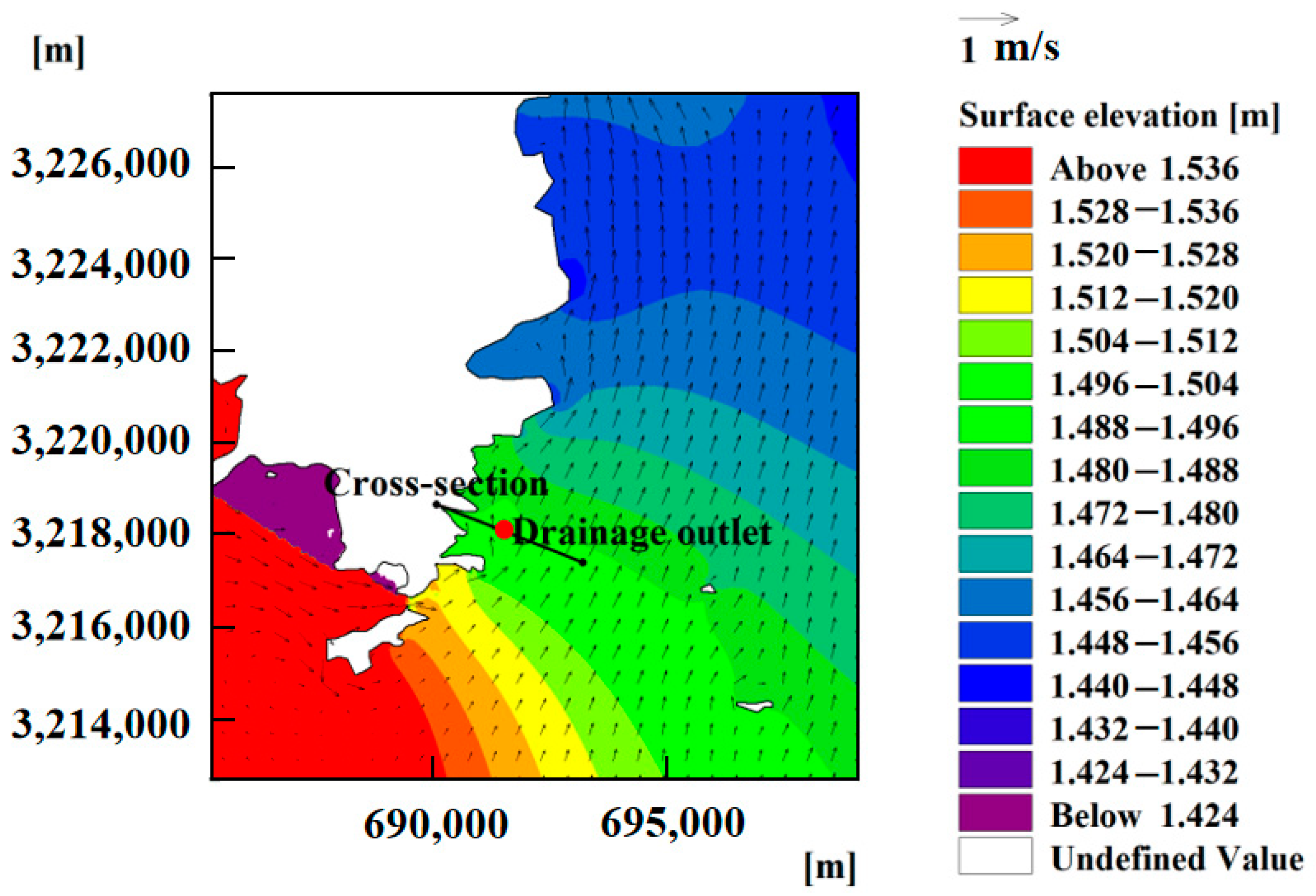
4.1. Hydrodynamic Characteristics
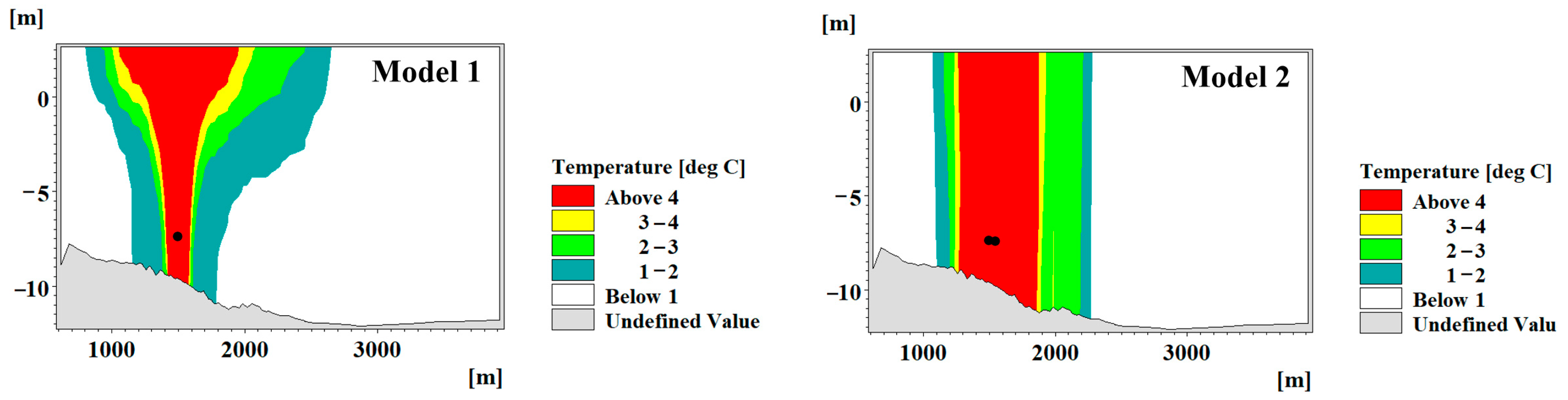
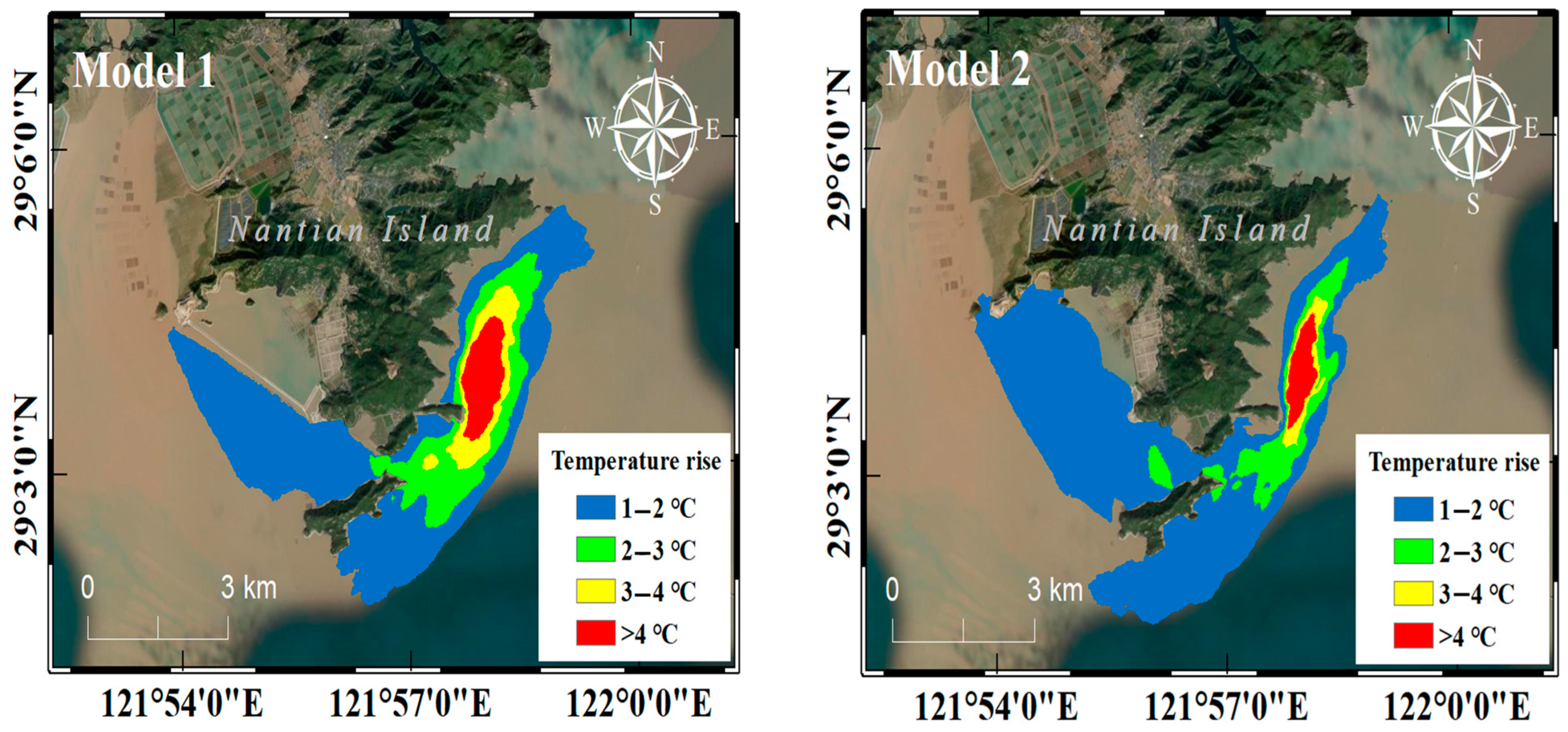
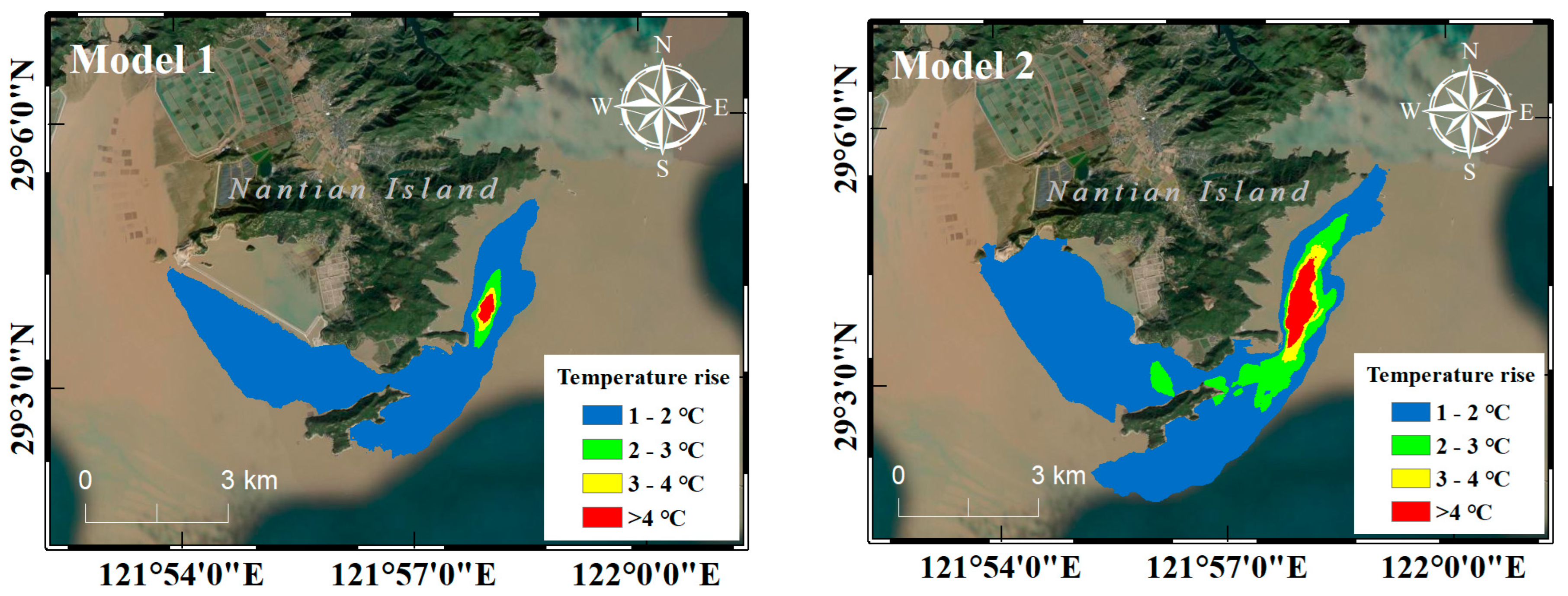
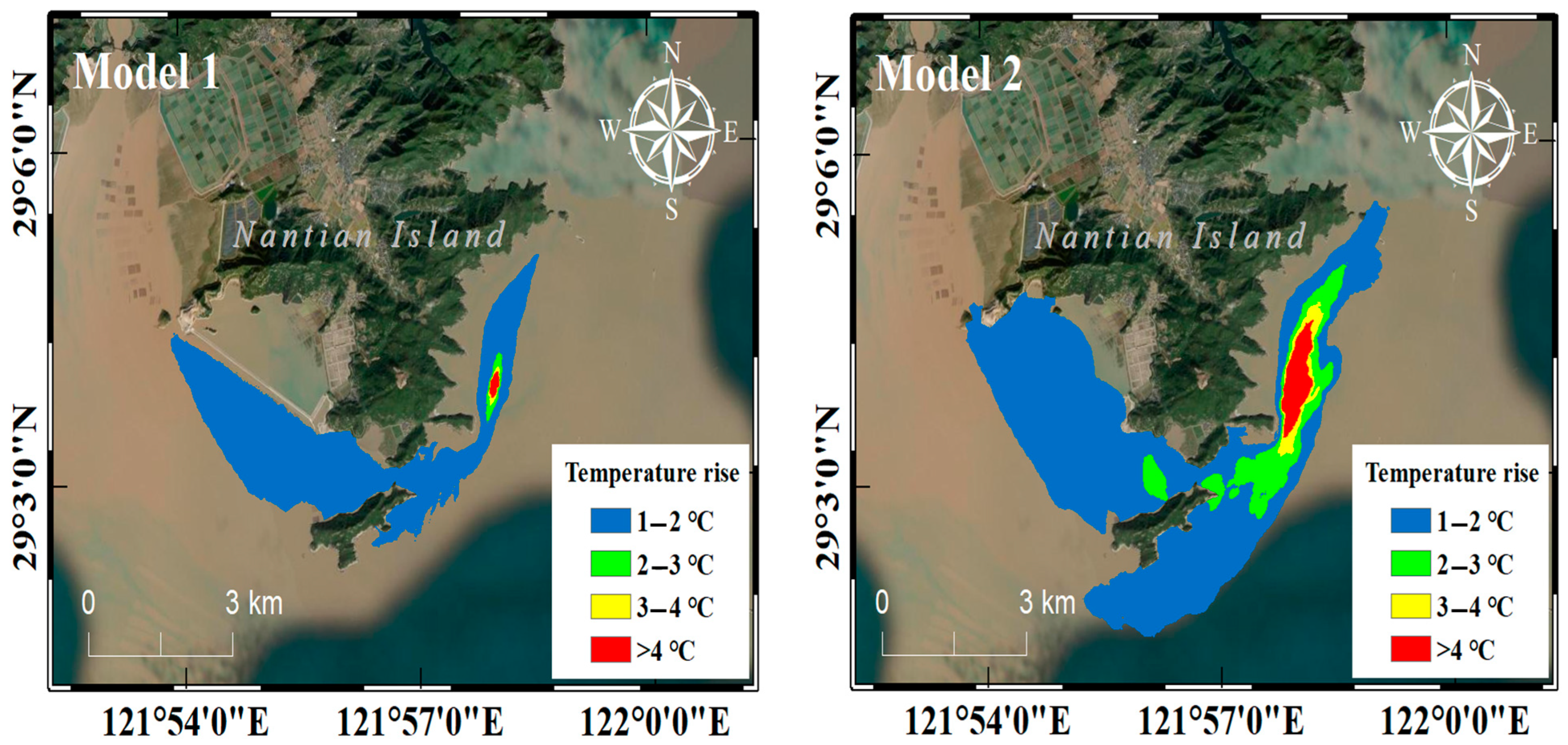
4.2. Cross-Sectional Temperature Rise Distribution
4.3. Planar Temperature Rise Distribution
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, J.; Yan, Q.; Chen, B.; Du, P. Ecological impact of thermal discharge from coastal power plants on plankton biomass in Xiangshan Bay. J. Shanghai Ocean Univ. 2015, 24, 894–905. [Google Scholar]
- Ye, Y.; Chen, K.; Zhou, Q.; Xiang, P.; Huo, Y.; Lin, M. Impacts of Thermal Discharge on Phytoplankton in Daya Bay. J. Coast. Res. 2019, 83, 135–147. [Google Scholar] [CrossRef]
- Qu, C.; Song, J.; Li, N. Causes of jellyfish blooms and their influence on marine environment. Chin. J. Appl. Ecol. 2014, 25, 3701–3712. [Google Scholar]
- Ben Mariem, H.; Chaieb, M. Climate change impacts on the distribution of stipa tenacissima l. Ecosystems in North African arid zone-a case study in Tunisia. Appl. Ecol. Environ. Res. 2017, 15, 67–82. [Google Scholar] [CrossRef]
- Duan, M.; Liu, Z.; Yan, D.; Peng, W.; Baghban, A. Application of lssvm algorithm for estimating higher heating value of biomass based on ultimate analysis. Energy Sources Part A-Recovery Util. Environ. Eff. 2018, 40, 709–715. [Google Scholar] [CrossRef]
- Li, Z.; Han, C.; Wei, D. Empirical research on the relationship between natural gas consumption and economic growth in the Northeast Asia. Energy Environ. 2018, 29, 216–231. [Google Scholar]
- Kumar, R.; Dewan, A. Computational Models for Turbulent Thermal Plumes: Recent Advances and Challenges. Heat Transf. Eng. 2014, 35, 367–383. [Google Scholar] [CrossRef]
- Kowalski, E.; Mazierski, J. Effects of cooling water discharges from a power plant on reservoir water quality. Oceanol. Hydrobiol. Stud. 2008, 37, 107–118. [Google Scholar] [CrossRef]
- Durán-Colmenares, A.; Barrios-Piña, H.; Ramírez-León, H. Numerical modeling of water thermal plumes emitted by thermal power plants. Water 2016, 8, 482. [Google Scholar] [CrossRef]
- Nikulenkov, A.M.; Dvornikov, A.Y.; Rumynin, V.G.; Ryabchenko, V.A.; Vereschagina, E.A. Assessment of allowable thermal load for a river reservoir subject to multi-source thermal discharge from operating and designed beloyarsk NPP Units (South Ural, Russian Federation). Environ. Model. Assess. 2017, 22, 609–623. [Google Scholar] [CrossRef]
- Poornima, E.H.; Rajadurai, M.; Rao, T.S.; Anupkumar, B.; Rajamohan, R.; Narasimhan, S.V.; Rao, V.N.R.; Venugopalan, V.P. Impact of thermal discharge from a tropical coastal power plant on phytoplankton. J. Therm. Biol. 2005, 30, 307–316. [Google Scholar] [CrossRef]
- Chuang, Y.; Yang, H.; Lin, H. Effects of a thermal discharge from a nuclear power plant on phytoplankton and periphyton in subtropical coastal waters. J. Sea Res. 2009, 61, 197–205. [Google Scholar] [CrossRef]
- Bedri, Z.; Bruen, M.; Dowley, A. Bartholomew asterson, Environmental consequences of a power plant shut-down: A three-dimensional water quality model of Dublin Bay. Mar. Pollut. Bull. 2013, 71, 117–128. [Google Scholar] [CrossRef]
- Cheng, Y.; Hao, Q. Effects of Topography on Diffusion of Thermal Discharge in Power Plant. Procedia Environ. Sci. 2011, 11, 618–623. [Google Scholar]
- Wang, S.; Chen, F.; Zhang, W. Numerical Investigation of Temperature Distribution of Thermal Discharge in a River-Type Reservoir. Pol. J. Environ. Stud. 2019, 28, 3909–3917. [Google Scholar] [CrossRef]
- Feng, L.; Chen, B.; Hayat, T.; Alsaedi, A.; Ahmad, B. Modelling the influence of thermal discharge under wind on algae. Phys. Chem. Earth 2015, 79–82, 108–114. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, D.; Wang, Z.; Lai, X. Numerical Simulation of Thermal Discharge Based on FVM Method. J. Ocean Univ. China 2006, 5, 7–11. [Google Scholar]
- Gaeta, M.G.; Samaras, A.; Archetti, R.; Lamberti, A. Numerical Investigation of Thermal Discharge to Coastal Areas Using Telemac-3d: A Case Study for South Italy. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Roy, P.; Rao, I.N.; Martha, T.R.; Kumar, K.V. Discharge water temperature assessment of thermal power plant using remote sensing techniques. Energy Geosci. 2022, 3, 172–181. [Google Scholar] [CrossRef]
- Martyanov, S.; Ryabchenko, V. Bottom sediment resuspension in the easternmost Gulf of Finland in the Baltic Sea: A case study based on three–dimensional modeling. Cont. Shelf Res. 2016, 117, 126–137. [Google Scholar] [CrossRef]
- Shi, H.Y.; Li, Q.J.; Sun, J.C.; Gao, G.D.; Sui, Y.; Qiao, S.W.; You, Z.J. Variation of Yellow River runoff and its influence on salinity in Laizhou Bay. J. Ocean Univ. China 2020, 19, 1235–1244. [Google Scholar] [CrossRef]
- Kolluru, V.S.; Buchak, E.M.; Brinkmann, P.E. Hydrodynamic modeling of coastal lng cooling water discharge. J. Energy Eng. 2012, 129, 16–31. [Google Scholar] [CrossRef]
- Lowe, S.A.; Schuepfer, F.; Dunning, D.J. Case study: Three-dimensional hydrodynamic model of a power plant thermal discharge. J. Hydraul. Eng. 2009, 135, 247–256. [Google Scholar] [CrossRef]
- Kitazawa, D.; Yang, J. Numerical analysis of water circulation and thermohaline structures in the Caspian Sea. J. Mar. Sci. Technol. 2012, 17, 168–180. [Google Scholar] [CrossRef]
- Goyal, R.; Rathod, P. Hydrodynamic Modelling for Salinity of Singapore Strait and Johor Strait using MIKE 3FM. In Proceedings of the 2nd International Conference on Environmental Science and Development, Xiamen, China, 25–27 May 2011. [Google Scholar]
- Serio, F.D.; Meftah, M.B.; Mossa, M. Monitoring and modelling of coastal currents and wastewater discharge: A case study. Geo-Eco-Mar. 2014, 20, 1–15. [Google Scholar]
- Saeed, S.; Hosseini, S.-S.; Hosseini, S.A.; Nasimi, S. Numerical simulation of temperature, salinity and density in the Caspian Sea using MIKE 3. J. Biol. Today’s World 2012, 1, 51–62. [Google Scholar]
- Gayathri, R.; Rao, V.R.; Rao, V.D.; Kumaresan, D. A 3D Numerical Modelling Study on Temperature and Salinity Structure along Coastal Waters of Kochi during Northeast Monsoon. J. Coast. Res. 2020, 89, 32. [Google Scholar] [CrossRef]
- Zhang, B.; Ping, J.; Liu, Z.; Jing, Z. Numerical Simulation of Thermal Discharge with Different Heat Exchange Methods on Water Surface. In Proceedings of the 2015 8th International Conference on Intelligent Computation Technology and Automation (ICICTA), Nanchang, China, 14–15 June 2015; pp. 597–600. [Google Scholar]
- Lin, J.; Zhang, S.; Gong, F. Numerical simulation study on site selection evaluation of marine ranching zone in Xiangshan Bay: Effects of thermal water discharged from coastal power plants. J. Shanghai Ocean Univ. 2012, 21, 816–824. [Google Scholar]
- Ahsan, Q.; Li, H.; Blumberg, A.F.; Piehler, G.R. Addressing practical environmental permitting issues through the use of sophisticated 3-d hydrothermal models. Power-Gen Int. 2002, 12, 10–12. [Google Scholar]
- Sojisuporn, P. Application of numerical model to thermal plume dispersion from power plant at kanom, thailand. In Proceedings of the Seventh OMISAR Workshop on Ocean Models, Singapore, 30 September–2 October 2002. [Google Scholar]
- Chen, X.Y.; Zhu, J.; Han, L.X. Defining methods of the heat transfer coefficient and its analysis of sensitiveness. Water Sci. Eng. Technol. 2007, 5, 9–13. [Google Scholar]
- Yu, L.; Yu, J. Numerical research on flow and thermal transport in cooling pool of electrical power station using three depth-averaged turbulence models. Water Sci. Eng. 2009, 2, 1–12. [Google Scholar]
- Wang, C.; Cai, L.; Wu, Y.; Ouyang, Y. Numerical simulation of the impact of an integrated renovation project on the Maowei Sea hydrodynamic environment. Sci. Rep. 2021, 11, 17059. [Google Scholar] [CrossRef]
- Cao, D.; Shen, Y.; Su, M.; Yu, C. Numerical simulation of hydrodynamic environment effects of the reclamation project of Nanhui tidal flat in Yangtze Estuary. J. Hydrodyn. 2019, 31, 603–613. [Google Scholar] [CrossRef]
- Sharbaty, S. Comparison of MIKE 3 Model and Princeton Ocean Model in Wind driven Current patterns under same conditions for the Caspian Sea. Can. J. Comput. Math. Nat. Sci. Eng. Med. 2012, 3, 60–66. [Google Scholar]
- Shi, H.Y.; Li, Q.J.; You, Z.J.; Yang, L.Z.; Fu, Y.C. Study on water exchange capacity of Fangcheng Bay in dry and wet season based on MIKE3 model. Desalin. Water Treat. 2021, 219, 287–296. [Google Scholar] [CrossRef]
- Bui, L.T.; Pham, H.T.H. Linking hydrological, hydraulic and water quality models for river water environmental capacity assessment. Sci. Total Environ. 2023, 857, 159490. [Google Scholar] [CrossRef]
- Cao, L.; Liu, Y. Optimization design and research of simulation system for urban green ecological rainwater by genetic algorithm. J. Supercomput. 2022, 78, 11318–11344. [Google Scholar] [CrossRef]
- Meza-Padilla, R.; Enriquez, C.; Appendini, C.M. Rapid assessment tool for oil spill planning and contingencies. Mar. Pollut. Bull. 2021, 166, 112196. [Google Scholar] [CrossRef]
- Gao, J.L.; Shi, H.B.; Zang, J.; Liu, Y.Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean. Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Munk, W.H.; Anderson, E.R. Notes on a theory of the thermocline. J. Mar. Res. 1948, 7, 276–295. [Google Scholar]
- Laguna-Zarate, L.; Barrios-Piña, H.; Ramírez-León, H.; García-Díaz, R.; Becerril-Piña, R. Analysis of Thermal Plume Dispersion into the Sea by Remote Sensing and Numerical Modeling. J. Mar. Sci. Eng. 2021, 9, 1437. [Google Scholar] [CrossRef]
- Willmott, C. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Parshakova, Y.N.; Lyubimova, T.P. Computer modelling of technogenic thermal pollution zones in large water bodies. J. Phys. Conf. Ser. 2018, 01, 955. [Google Scholar] [CrossRef]
- Yan, F.; Han, L.; Chen, R.; Zhang, L.; Chen, Q. Water temperature modeling and water temperature stratification pattern of reservoir based on the three-dimensional environment fluid dynamics code model. Adv. Mater. Res. 2014, 1073–1076, 2321–2326. [Google Scholar] [CrossRef]
- Yang, M.; Wang, M.; Zhang, F.; Lai, R. Numerical simulation and experimental study of three-dimensional density-stratified flow. IOP Conf. Ser. Mater. Sci. Eng. 2019, 472, 012080. [Google Scholar] [CrossRef]


| Model | Model 1 | Model 2 |
|---|---|---|
| Temperature and Salt Module | ECO Module | |
| Diffusion coefficient | k−ε turbulence models | |
| Coriolis force coefficient | ||
| Summer surface heat exchange amount | Latent heat flux: 20 W/m2 °C | Comprehensive heat dissipation of water surface: 45 W/m2 °C |
| Sensible heat flux: 12 W/m2 °C | ||
| Long-wave radiation flux: −17 W/m2 °C | ||
| Short-wave radiation flux: 30 W/m2 °C | ||
| Water surface temperature | 30 °C | |
| Air temperature | 32 °C | |
| Wind speed | 3.32 m/s | |
| power plant discharge volume | 150 m3/s | |
| Drainage temperature rise | 8.2 °C | |
| Evaluation Items | Site Name | Skill Value | Model Evaluation | Pearson Correlation Coefficient |
|---|---|---|---|---|
| Water level | T1 | 0.5 | Very good | 1.0 |
| T2 | 0.5 | Very good | 0.9 | |
| T3 | 0.6 | Very good | 1.0 | |
| T4 | 0.6 | Very good | 1.0 | |
| Flow velocity | S1 | 0.9 | Excellent | 0.8 |
| S2 | 0.8 | Excellent | 0.8 | |
| S3 | 0.9 | Excellent | 0.8 | |
| Flow direction | S1 | 1.0 | Excellent | 1.0 |
| S2 | 1.0 | Excellent | 1.0 | |
| S3 | 0.9 | Excellent | 0.9 | |
| Temperature | Model 1 | 0.8 | Excellent | 0.7 |
| Model 2 | 0.6 | Excellent | 0.5 |
| Model | 1 °C | 2 °C | 3 °C | 4 °C |
|---|---|---|---|---|
| Model 1 | 0.031864 | 0.017612 | 0.012696 | 0.009568 |
| Model 2 | 0.033712 | 0.028649 | 0.022336 | 0.016069 |
| 0.001848 | 0.011037 | 0.009641 | 0.006501 |
| Model | Tide Type | Vertical Position | 1 °C | 2 °C | 3 °C | 4 °C |
|---|---|---|---|---|---|---|
| Model 1 | Summer half-moon tide | Surface layer | 17.75 | 5.89 | 2.62 | 1.31 |
| Mid-layer | 12.16 | 0.55 | 0.23 | 0.13 | ||
| Bottom layer | 8.53 | 0.17 | 0.09 | 0.05 | ||
| Model 2 | Summer half-moon tide | Surface layer | 18.91 | 2.89 | 1.20 | 0.71 |
| Mid-layer | 18.89 | 2.82 | 1.17 | 0.70 | ||
| Bottom layer | 18.76 | 2.70 | 1.13 | 0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Shi, H.; Zhan, C.; Zhu, J.; Wang, Q.; Li, G. Numerical Simulation Calculation of Thermal Discharge Water Diffusion in Coastal Nuclear Power Plants. Atmosphere 2023, 14, 1371. https://doi.org/10.3390/atmos14091371
Zhang X, Shi H, Zhan C, Zhu J, Wang Q, Li G. Numerical Simulation Calculation of Thermal Discharge Water Diffusion in Coastal Nuclear Power Plants. Atmosphere. 2023; 14(9):1371. https://doi.org/10.3390/atmos14091371
Chicago/Turabian StyleZhang, Xuri, Hongyuan Shi, Chao Zhan, Jun Zhu, Qing Wang, and Guoqing Li. 2023. "Numerical Simulation Calculation of Thermal Discharge Water Diffusion in Coastal Nuclear Power Plants" Atmosphere 14, no. 9: 1371. https://doi.org/10.3390/atmos14091371
APA StyleZhang, X., Shi, H., Zhan, C., Zhu, J., Wang, Q., & Li, G. (2023). Numerical Simulation Calculation of Thermal Discharge Water Diffusion in Coastal Nuclear Power Plants. Atmosphere, 14(9), 1371. https://doi.org/10.3390/atmos14091371








