Characteristic Analysis of the 10–30-Day Intraseasonal Oscillation over Mid-High-Latitude Eurasia in Boreal Summer
Abstract
1. Introduction
2. Data and Methodology
3. Results
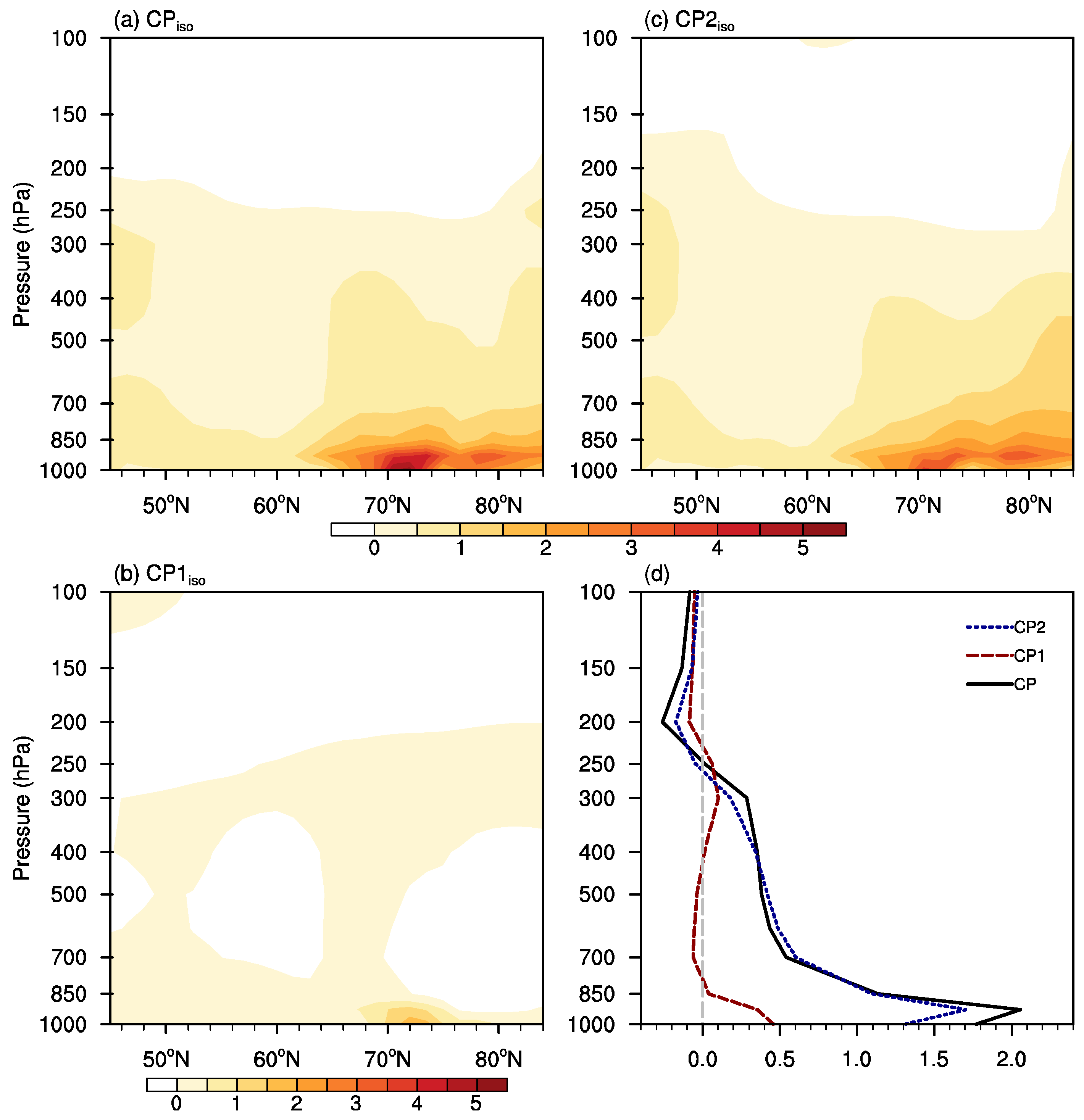
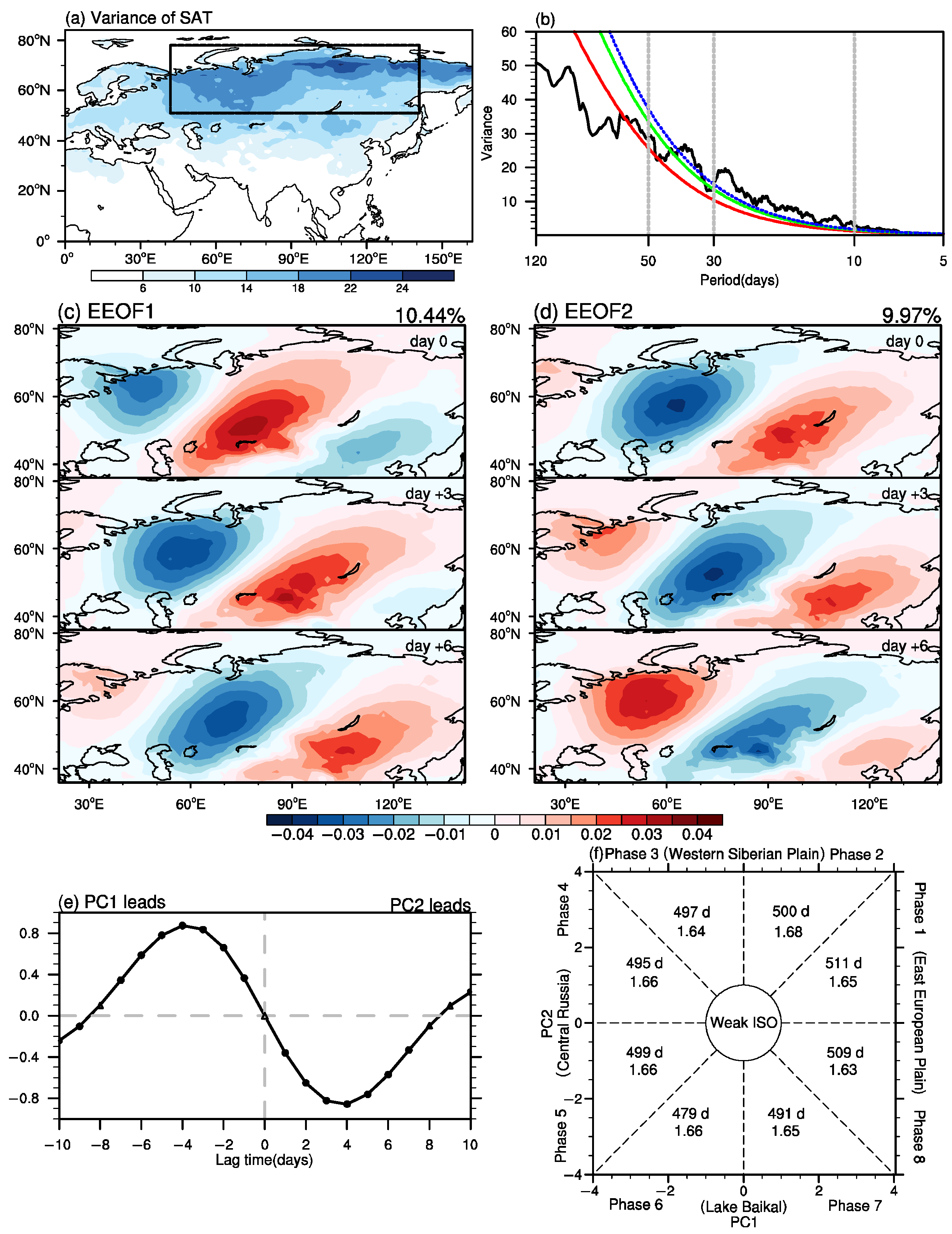
3.1. Evolution Features of the Leading ISO Mode
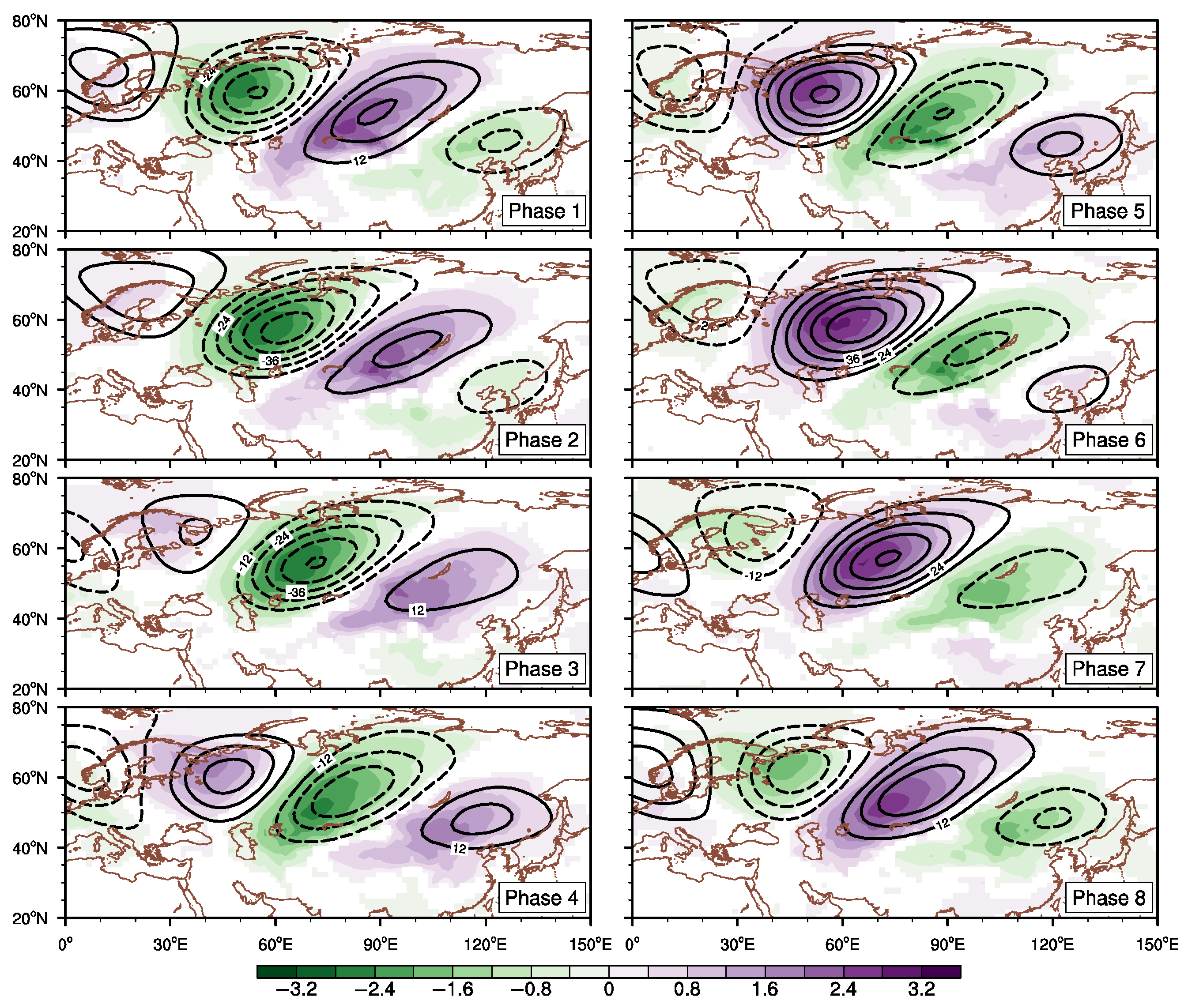
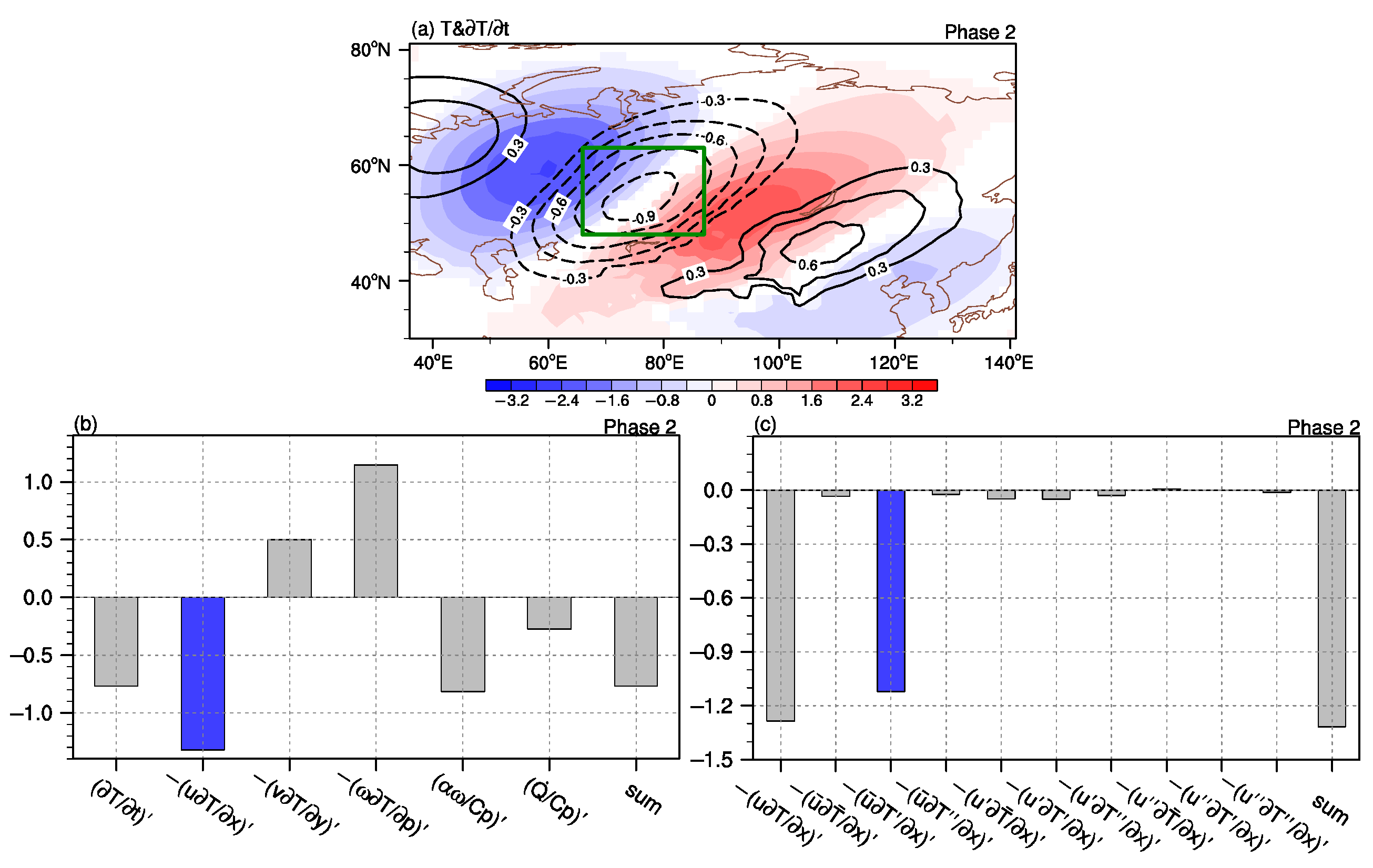
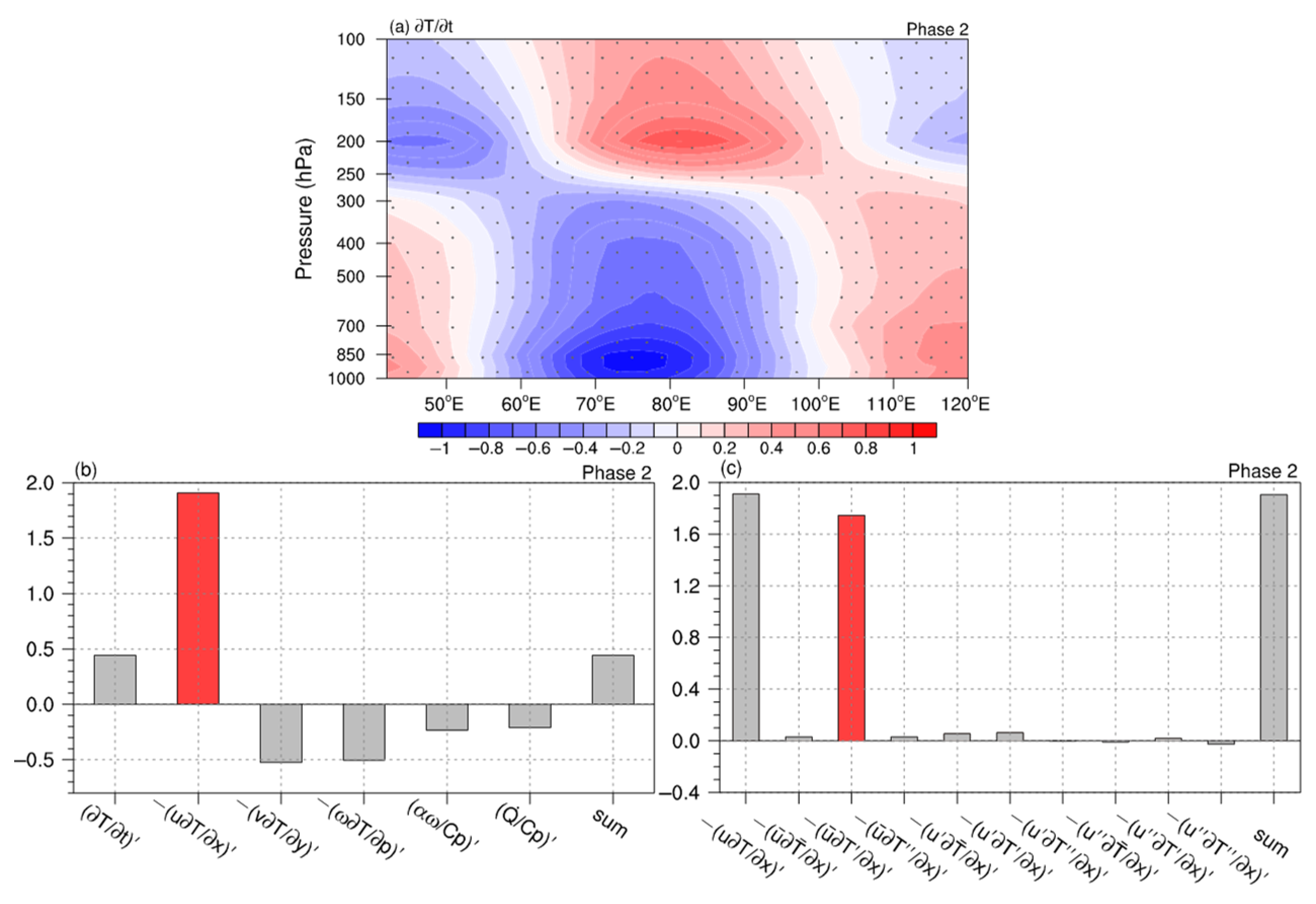
3.2. Cause of the Southeastward-Propagating T Anomaly
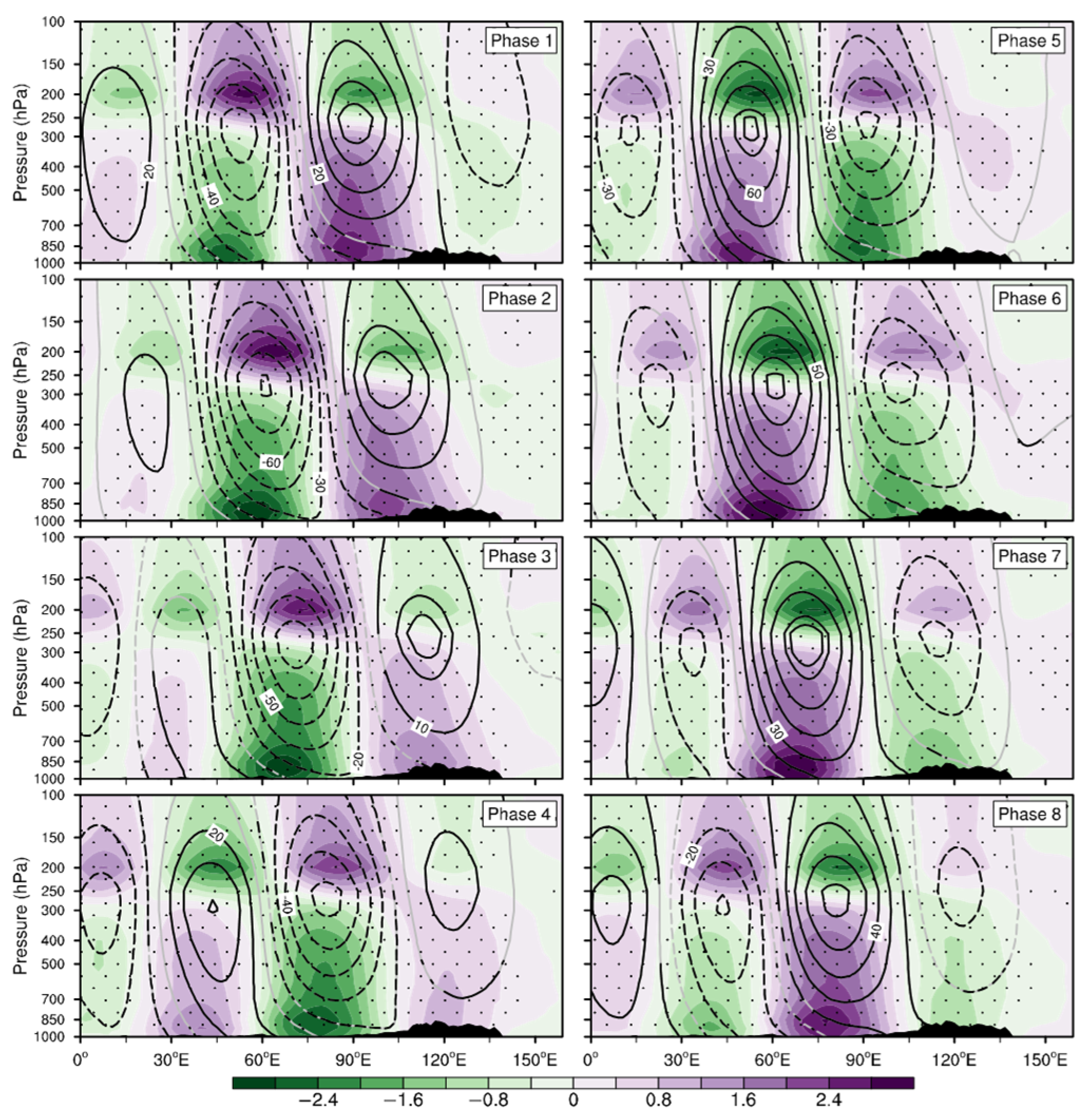
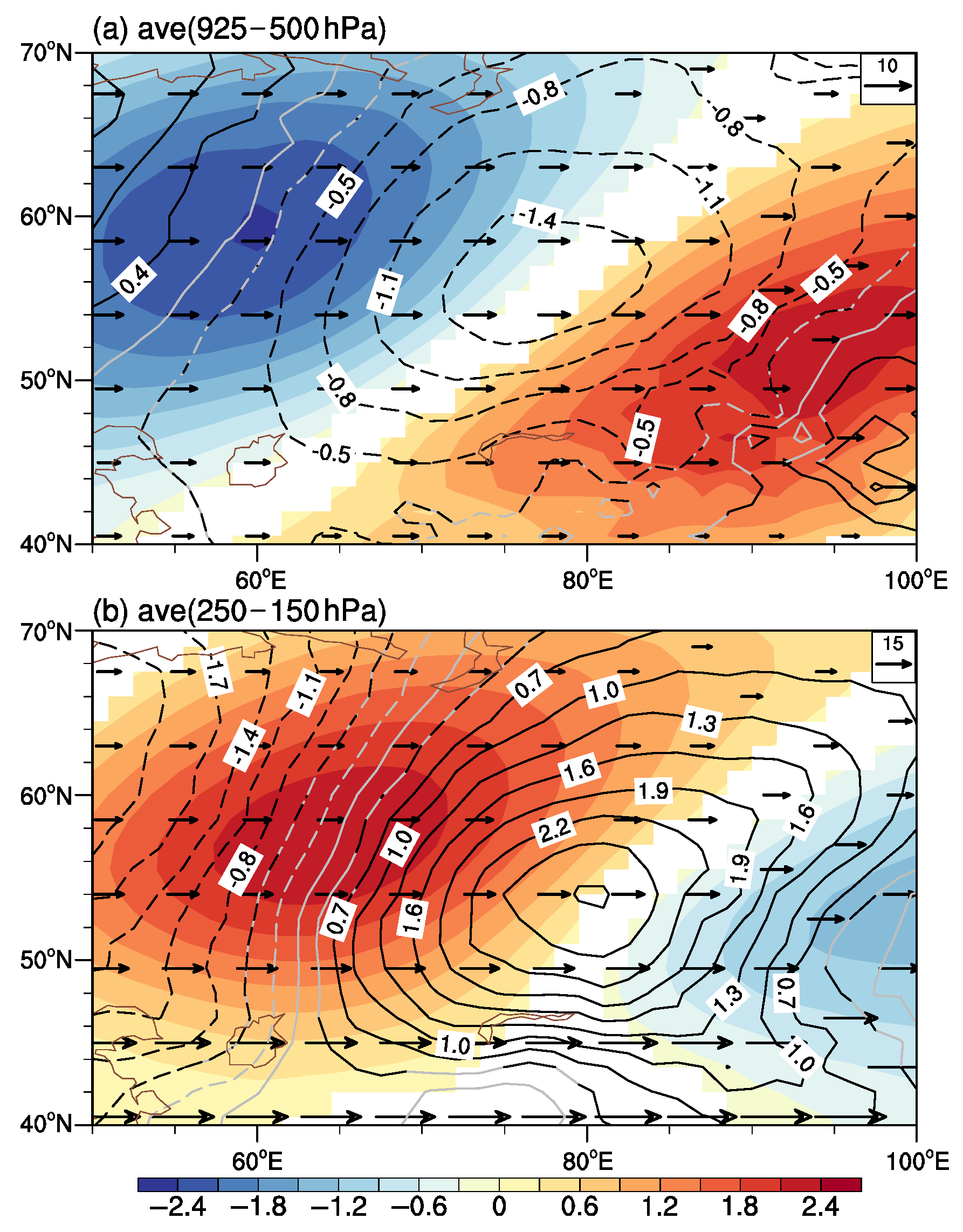
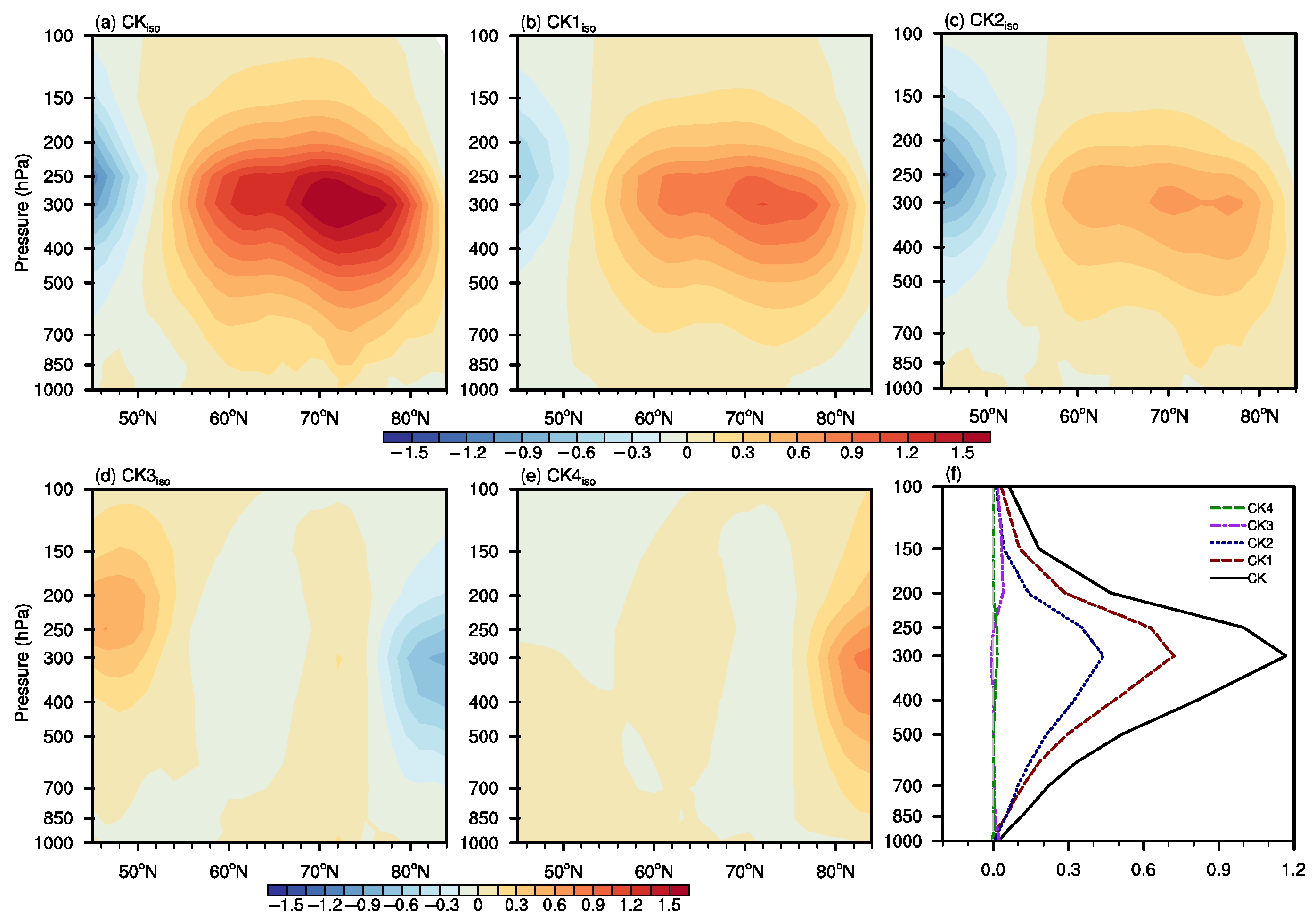
3.3. Energy Conversion Diagnosis for Southeastward Propagation
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lo, F.; Hendon, H.H. Empirical Extended-Range Prediction of the Madden-Julian Oscillation. Mon. Weather. Rev. 2000, 128, 2528–2543. [Google Scholar] [CrossRef]
- Seo, K.H.; Wang, W.; Gottschalck, J.; Zhang, Q.; Schemm, J.K.E.; Higgins, W.R.; Kumar, A. Evaluation of MJO Forecast Skill from Several Statistical and Dynamical Forecast Models. J. Clim. 2009, 22, 2372–2388. [Google Scholar] [CrossRef]
- Li, W.; Hsu, P.; He, J.; Zhu, Z.; Zhang, W. Extended-Range Forecast of Spring Rainfall in Southern China Based on the Madden-Julian Oscillation. Meteorol. Atmos. Phys. 2016, 128, 331–345. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, T. Extended-Range Forecasting of Chinese Summer Surface Air Temperature and Heat Waves. Clim. Dyn. 2018, 50, 2007–2021. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S. The Impact of Mid-High-Latitude Eurasian ISO on Soil Moisture Anomaly in North China during Boreal Summer. Clim. Dyn. 2023, 61, 185–201. [Google Scholar] [CrossRef]
- Zhu, Z.; Wu, J.; Huang, H. The Influence of 10–30-day boreal summer intraseasonal oscillation on the extended-range forecast skill of extreme rainfall over southern China. Clim. Dyn. 2023. [Google Scholar] [CrossRef]
- Hall, J.D.; Matthews, A.J.; Karoly, D.J. The Modulation of Tropical Cyclone Activity in the Australian Region by the Madden-Julian Oscillation. Mon. Weather Rev. 2001, 129, 2970–2982. [Google Scholar]
- Zhao, C.; Li, T. Basin Dependence of the MJO Modulating Tropical Cyclone Genesis. Clim. Dyn. 2019, 52, 6081–6096. [Google Scholar]
- Qian, Y.; Hsu, P.C.; Kazuyoshi, K. New Real-Time Indices for the Quasi-Biweekly Oscillation over the Asian Summer Monsoon Region. Clim. Dyn. 2019, 53, 2603–2624. [Google Scholar] [CrossRef]
- Lorenz, D.J.; Hartmann, D.L. The Effect of the MJO on the North American Monsoon. J. Clim. 2006, 19, 333–343. [Google Scholar] [CrossRef]
- Li, X.; Gollan, G.; Greatbatch, R.J.; Lu, R. Intraseasonal Variation of the East Asian Summer Monsoon Associated with the Madden-Julian Oscillation. Atmos. Sci. Lett. 2018, 19, e794. [Google Scholar] [CrossRef]
- Hsu, P.C.; Qian, Y.; Liu, Y.; Murakami, H.; Gao, Y. Role of Abnormally Enhanced MJO over the Western Pacific in the Formation and Subseasonal Predictability of the Record-Breaking Northeast Asian Heatwave in the Summer of 2018. J. Clim. 2020, 33, 3333–3349. [Google Scholar] [CrossRef]
- Schreck, C.J. Global Survey of the MJO and Extreme Precipitation. Geophys. Res. Lett. 2021, 48, e2021GL094691. [Google Scholar] [CrossRef]
- Qian, Y.; Hsu, P.C.; Wang, H.; Duan, M. Distinct Influential Mechanisms of the Warm Pool Madden-Julian Oscillation on Persistent Extreme Cold Events in Northeast China. Atmos. Ocean. Sci. Lett. 2022, 15, 100226. [Google Scholar] [CrossRef]
- Deng, L.; Li, T.; Liu, J.; Peng, M. Factors Controlling the Interannual Variations of MJO Intensity. J. Meteorol. Res. 2016, 30, 328–340. [Google Scholar] [CrossRef]
- Wang, L.; Li, T.; Maloney, E.; Wang, B. Fundamental Causes of Propagating and Nonpropagating MJOs in MJOTF/GASS Models. J. Clim. 2017, 30, 3743–3769. [Google Scholar] [CrossRef]
- Wang, B.; Chen, G.; Liu, F. Diversity of the Madden-Julian Oscillation. Sci. Adv. 2019, 5, eaax0220. [Google Scholar] [CrossRef]
- Huang, K.; Pegion, K. The Roles of Westward-Propagating Waves and the QBO in Limiting MJO Propagation. J. Clim. 2022, 35, 6031–6049. [Google Scholar] [CrossRef]
- Anderson, J.R.; Rosen, R.D. The Latitude-Height Structure of 40–50 Day Variations in Atmospheric Angular Momentum. J. Atmos. Sci. 1983, 40, 1584–1591. [Google Scholar] [CrossRef]
- Kikuchi, K.; Wang, B. Global Perspective of the Quasi-Biweekly Oscillation. J. Clim. 2009, 22, 1340–1359. [Google Scholar] [CrossRef]
- Wang, L.; Li, T.; Zhou, T.; Rong, X. Origin of the Intraseasonal Variability over the North Pacific in Boreal Summer. J. Clim. 2013, 26, 1211–1229. [Google Scholar] [CrossRef]
- Yang, S.; Wu, B.; Zhang, R.; Zhou, S. Relationship between an Abrupt Drought-Flood Transition over Mid-Low Reaches of the Yangtze River in 2011 and the Intraseasonal Oscillation over Mid-High Latitudes of East Asia. Acta. Meteorol. Sin. 2013, 27, 129–143. [Google Scholar] [CrossRef]
- Yang, S.; Wu, B.; Zhang, R.; Zhou, S. The Zonal Propagating Characteristics of Low-Frequency Oscillation over the Eurasian Mid-High Latitude in Boreal Summer. Sci. China Earth Sci. 2013, 56, 1566–1575. [Google Scholar] [CrossRef]
- Xiu, J.; Jiang, X.; Zhang, R.; Guan, W.; Chen, G. An Intraseasonal Mode Linking Wintertime Surface Air Temperature over Arctic and Eurasian Continent. J. Clim. 2022, 35, 2675–2696. [Google Scholar] [CrossRef]
- Yang, S.; Li, T. The Role of Intraseasonal Variability at Mid-high Latitudes in Regulating Pacific Blockings during Boreal Winter. Int. J. Climatol. 2017, 37, 1248–1256. [Google Scholar] [CrossRef]
- Yang, S.; Wen, X.; Gao, M. Relation of Mid-High-Latitude Eurasian ISO to Ural Blocking Frequency and Their Co-Effect on Extreme Hot Events during Boreal Summer. Atmosphere 2022, 13, 2041. [Google Scholar] [CrossRef]
- Yang, J.; Bao, Q.; Wang, B.; He, H.; Gao, M.; Gong, D. Characterizing Two Types of Transient Intraseasonal Oscillations in the Eastern Tibetan Plateau Summer Rainfall. Clim. Dyn. 2017, 48, 1749–1768. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, Z.; Cui, J.; Yang, Y. Regulation of the Intraseasonal Oscillation over Mid-to-High Latitude Eurasia on Winter Surface Air Temperature over China. Dyn. Atmos. Oceans 2019, 86, 63–72. [Google Scholar] [CrossRef]
- Yang, S.; Li, T. Intraseasonal Variability of Air Temperature over the Mid-High Latitude Eurasia in Boreal Winter. Clim. Dyn. 2016, 47, 2155–2175. [Google Scholar] [CrossRef]
- Jiao, Y.; Wu, R. Propagation and Influence on Tropical Precipitation of Intraseasonal Variation over Mid-Latitude East Asia in Boreal Winter. Atmos. Ocean. Sci. Lett. 2019, 12, 155–161. [Google Scholar] [CrossRef]
- Yang, H.; Li, C. The Relation between Atmospheric Intraseasonal Oscillation and Summer Severe Flood and Drought in the Changjiang—Huaihe River Basin. Adv. Atmos. Sci. 2003, 20, 540–553. [Google Scholar]
- Zhu, T.; Yang, J. Two Types of Mid-High-Latitude Low-Frequency Intraseasonal Oscillations near the Ural Mountains during Boreal Summer. J. Clim. 2021, 34, 4279–4296. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Duchon, C.E. Lanczos Filtering in One and Two Dimensions. J. Appl. Meteor. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Weare, B.C.; Nasstrom, J.S. Examples of Extended Empirical Orthogonal Function Analyses. Mon. Weather Rev. 1982, 110, 481–485. [Google Scholar] [CrossRef]
- Suhas, E.; Neena, J.M.; Goswami, B.N. An Indian Monsoon Intraseasonal Oscillations (MISO) Index for Real Time Monitoring and Forecast Verification. Clim. Dyn. 2013, 40, 2605–2616. [Google Scholar] [CrossRef]
- Holton, J.R. An Introduction to Dynamic Meteorology; Academic Press: London, UK, 1992; p. 511. [Google Scholar]
- Yanai, M.; Esbensen, S.; Chu, J.H. Determination of Bulk Properties of Tropical Cloud Clusters from Large-Scale Heat and Moisture Budgets. J. Atmos. Sci. 1973, 30, 611–627. [Google Scholar] [CrossRef]
- Varotsos, C.; Efstathiou, M.; Tzanis, C. Scaling Behaviour of the Global Tropopause. Atmos. Chem. Phys. 2009, 9, 677–683. [Google Scholar] [CrossRef]
- Efstathiou, M.N.; Varotsos, C.A. On the Altitude Dependence of the Temperature Scaling Behaviour at the Global Troposphere. Int. J. Remote Sens. 2010, 31, 343–349. [Google Scholar] [CrossRef]
- Hsu, P.C.; Li, T. Role of the Boundary Layer Moisture Asymmetry in Causing the Eastward Propagation of the Madden-Julian Oscillation. J. Clim. 2012, 25, 4914–4931. [Google Scholar] [CrossRef]
- Hoskins, B.J.; James, I.N.; White, G.H. The Shape, Propagation and Mean-Flow Interaction of Large-Scale Weather Systems. J. Atmos. Sci. 1983, 40, 1595–1612. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Wheeler, M.C.; Hendon, H.H. An All-Season Real-Time Multivariate MJO Index: Development of an Index for Monitoring and Prediction. Mon. Weather Rev. 2004, 132, 1917–1932. [Google Scholar] [CrossRef]
- Du, Y.; Lu, R. Wave Trains of 10–30-Day Meridional Wind Variations over the North Pacific during Summer. J. Clim. 2021, 34, 9267–9277. [Google Scholar] [CrossRef]
- Yao, S.; Liu, Y. The Zonal Wind Intraseasonal Oscillation in the Exit Region of the East Asian Subtropical Westerly Jet in Winter and Its Thermodynamic Mechanism. Atmosphere 2022, 13, 395. [Google Scholar] [CrossRef]
- Xu, P.; Wang, L.; Vallis, G.K.; Geen, R.; Screen, J.A.; Wu, P.; Ding, S.; Huang, P.; Chen, W. Amplified Waveguide Teleconnections Along the Polar Front Jet Favor Summer Temperature Extremes Over Northern Eurasia. Geophys. Res. Lett. 2021, 48, e2021GL093735. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Y. Evolution of Eurasian teleconnection pattern and its relationship to climate anomalies in China. Clim. Dyn. 2015, 44, 1017–1028. [Google Scholar] [CrossRef]
- Renwick, J.A.; Revell, M.J. Blocking over the South Pacific and Rossby wave propagation. Mon. Weather Rev. 1999, 127, 2233–2247. [Google Scholar] [CrossRef]
- Jiang, X.; Lau, N.-C. Intraseasonal teleconnection between North American and Western North Pacific monsoons with 20-day time scale. J. Clim. 2008, 21, 2664–2679. [Google Scholar] [CrossRef][Green Version]
- Zhao, P.; Cao, Z.; Chen, J. A summer teleconnection pattern over the extratropical Northern Hemisphere and associated mechanisms. Clim. Dyn. 2010, 35, 523–534. [Google Scholar] [CrossRef]
- Wang, Y.; Lupo, A.R. An extratropical air-sea interaction over the North Pacific in association with a preceding El Niño episode in early summer. Mon. Weather Rev. 2009, 137, 3771–3785. [Google Scholar] [CrossRef]
- Wang, Y.; Lupo, A.R.; Qin, J. A response in the ENSO cycle to an extratropical forcing mechanism during the El Niño to La Niña transition. Tellus A Dyn. Meteorol. Oceanogr. 2013, 65, 22431. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yang, S. Characteristic Analysis of the 10–30-Day Intraseasonal Oscillation over Mid-High-Latitude Eurasia in Boreal Summer. Atmosphere 2023, 14, 1372. https://doi.org/10.3390/atmos14091372
Liu Y, Yang S. Characteristic Analysis of the 10–30-Day Intraseasonal Oscillation over Mid-High-Latitude Eurasia in Boreal Summer. Atmosphere. 2023; 14(9):1372. https://doi.org/10.3390/atmos14091372
Chicago/Turabian StyleLiu, Yashu, and Shuangyan Yang. 2023. "Characteristic Analysis of the 10–30-Day Intraseasonal Oscillation over Mid-High-Latitude Eurasia in Boreal Summer" Atmosphere 14, no. 9: 1372. https://doi.org/10.3390/atmos14091372
APA StyleLiu, Y., & Yang, S. (2023). Characteristic Analysis of the 10–30-Day Intraseasonal Oscillation over Mid-High-Latitude Eurasia in Boreal Summer. Atmosphere, 14(9), 1372. https://doi.org/10.3390/atmos14091372