Construction and Research of Ultra-Short Term Prediction Model of Solar Short Wave Irradiance Suitable for Qinghai–Tibet Plateau
Abstract
1. Introduction
2. Data
2.1. Overview of the Study Area
2.2. Data Sources
2.3. Data Characteristics
2.3.1. Seasonal Characteristics
2.3.2. Diurnal Variation Characteristics
3. Methodology
3.1. Persistence Model
3.2. ARIMA Prediction Model
3.3. RF Prediction Model
3.3.1. Data Transformation and Feature Extraction
3.3.2. Model Optimization
3.4. LSTM Prediction Model
3.5. Model Evaluation
4. Results and Analysis
4.1. Impact of Training Set on Model
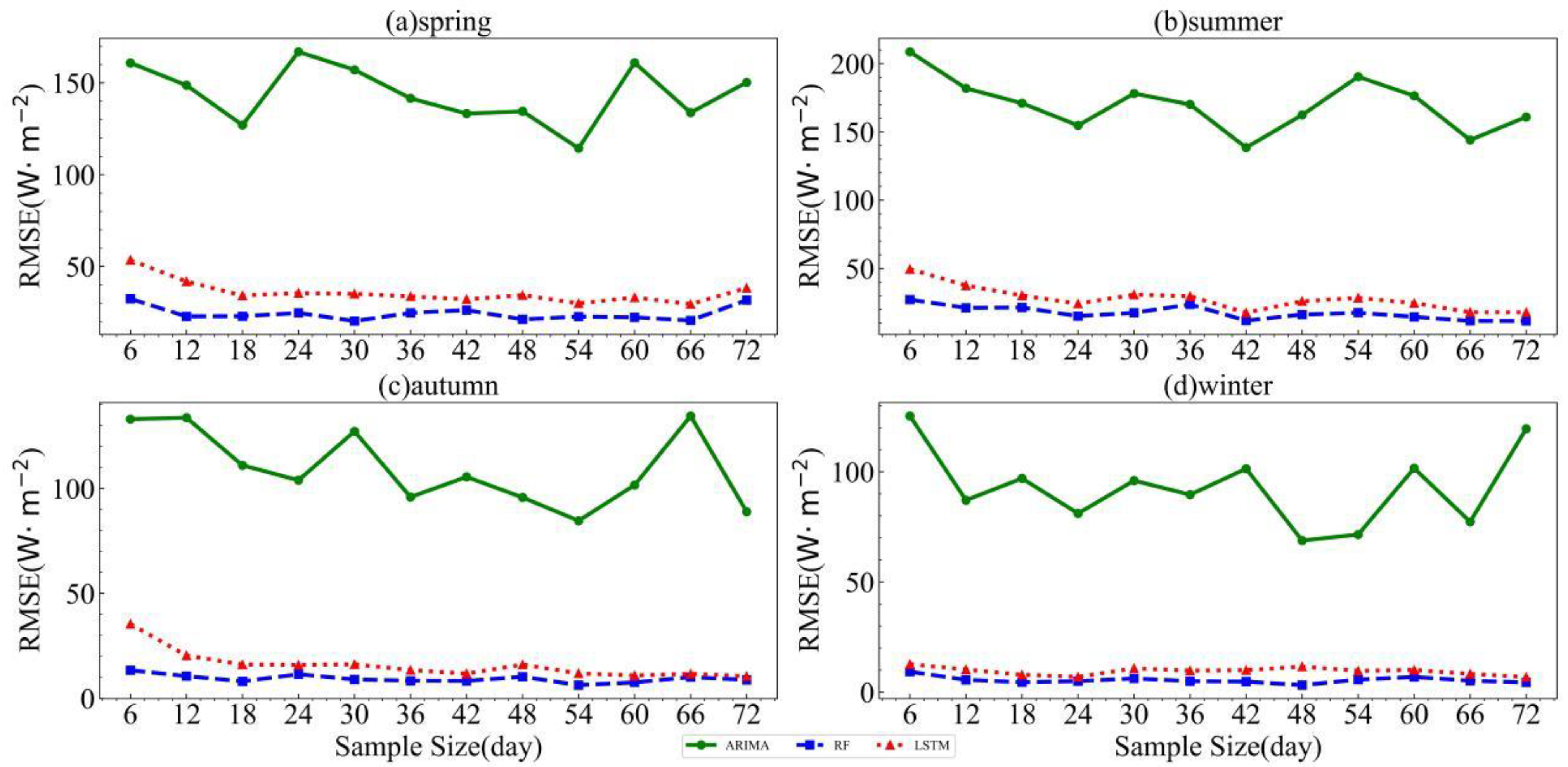
4.1.1. ARIMA Model
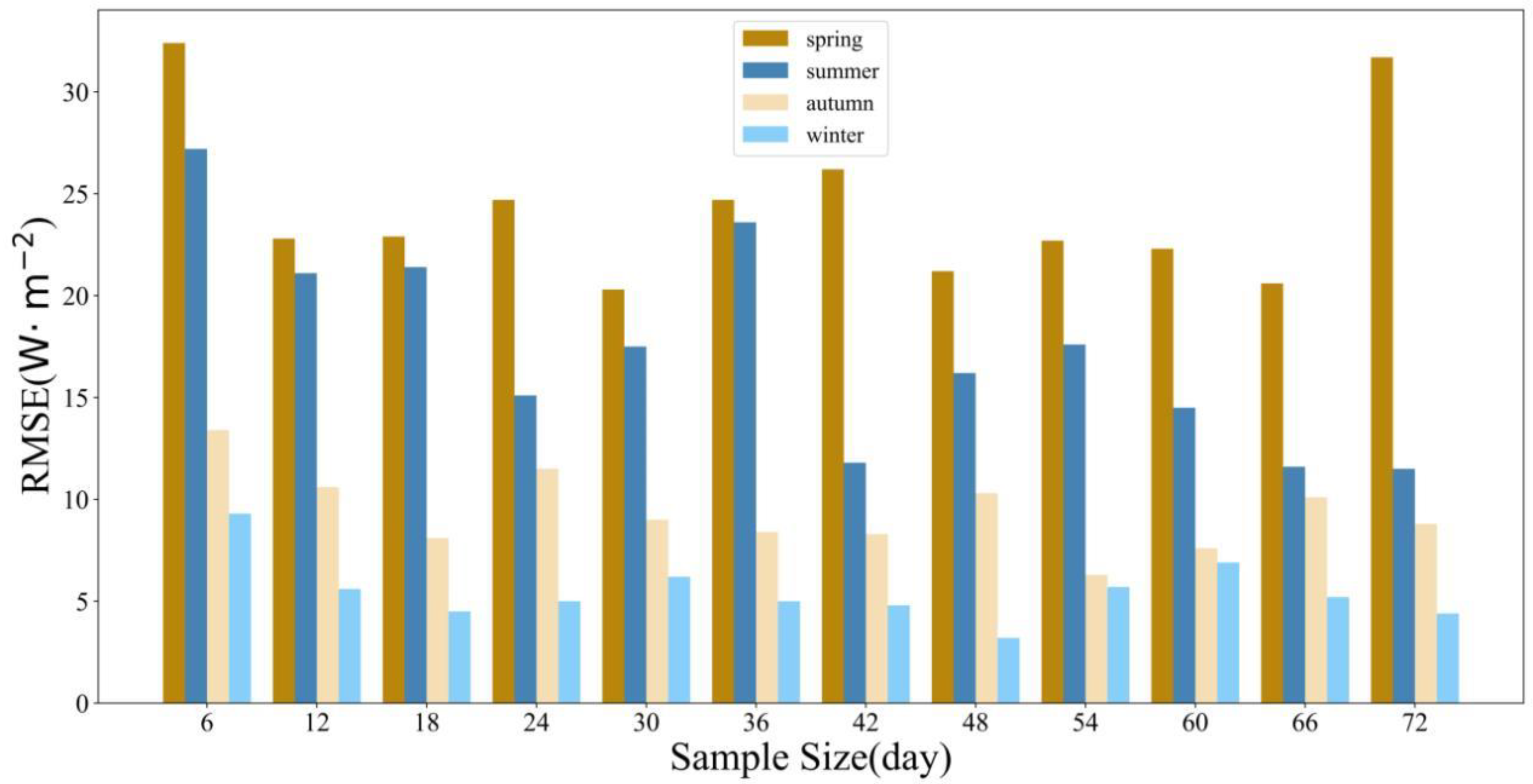
4.1.2. RF Model
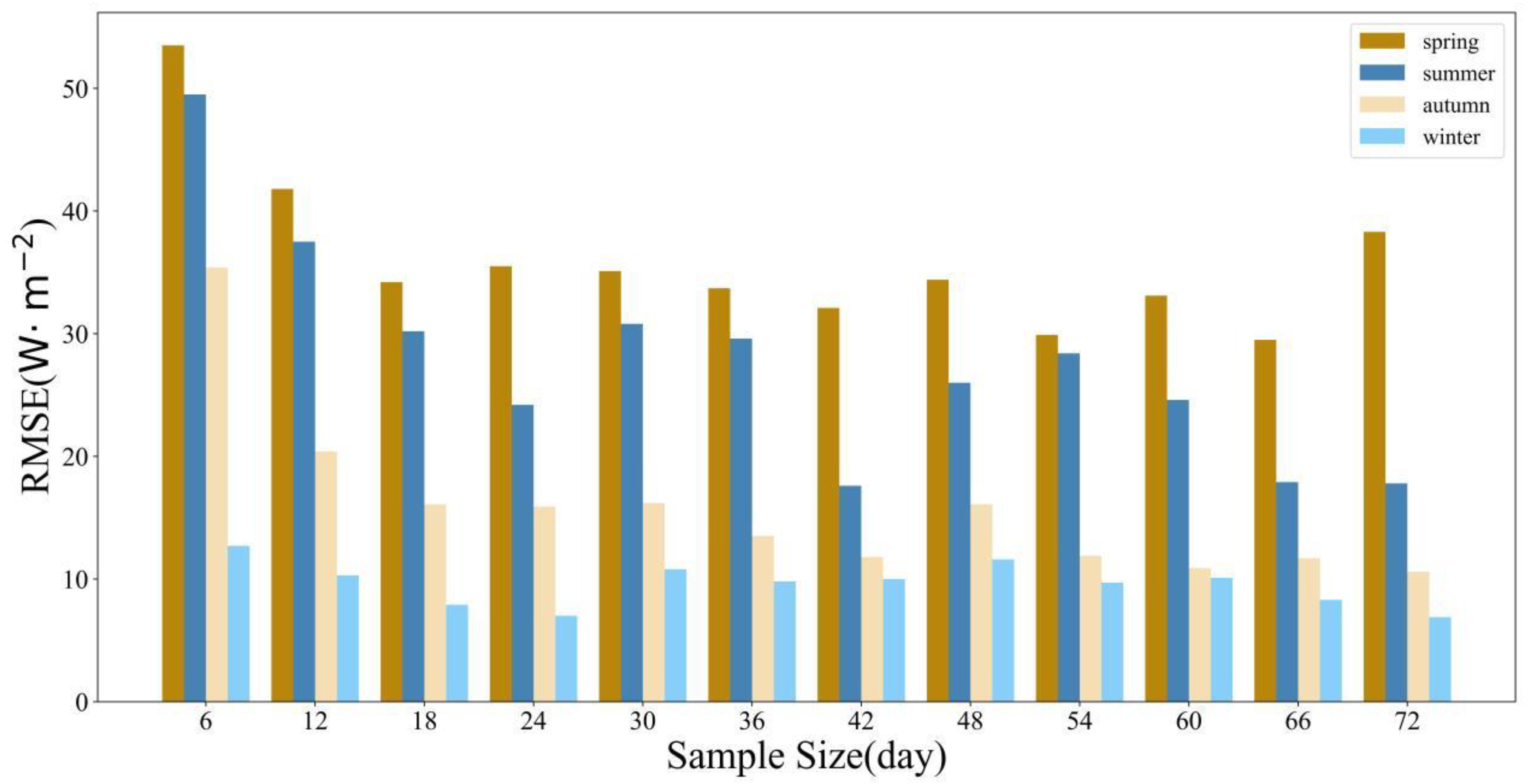
4.1.3. LSTM Model
4.1.4. Comparison between Models
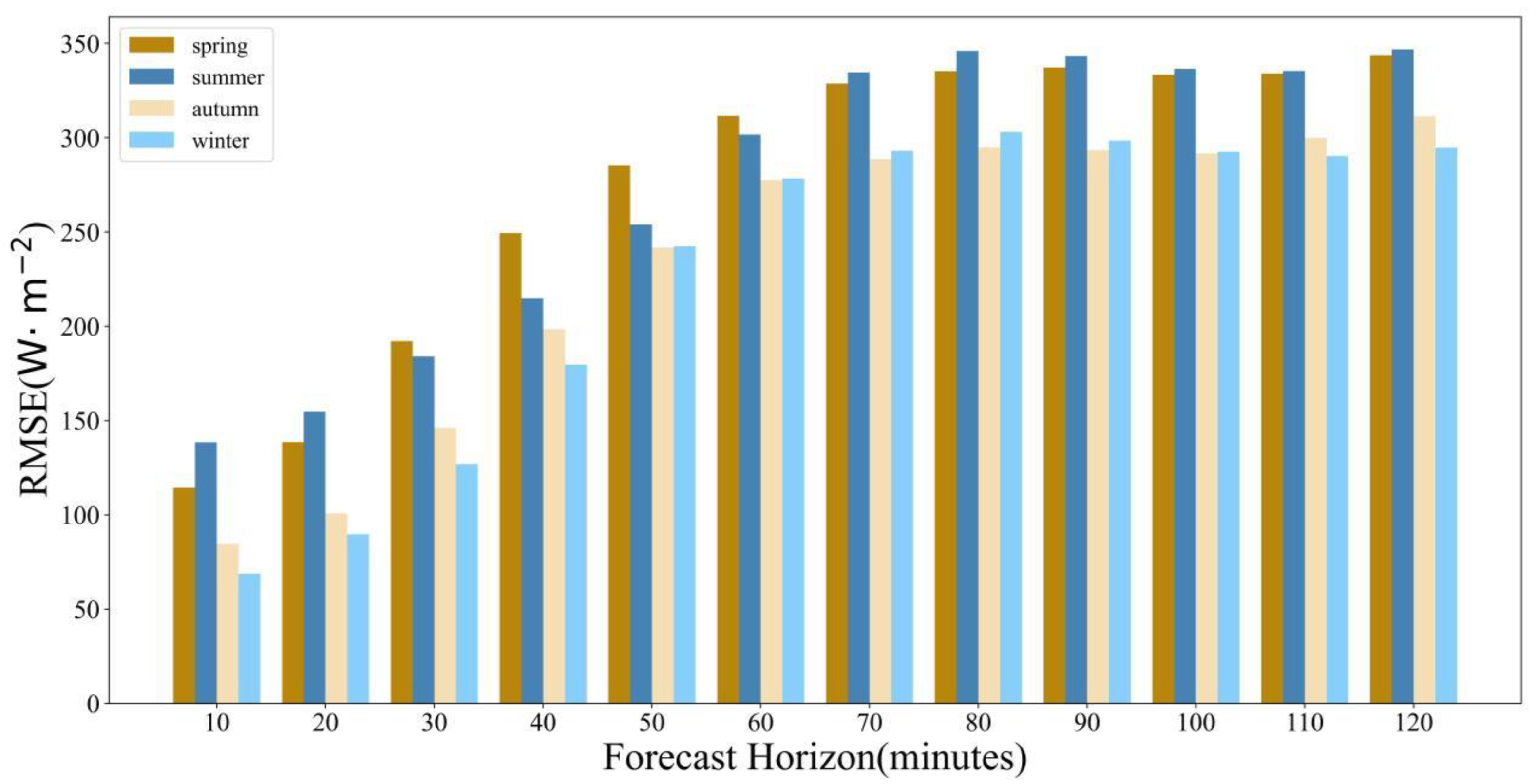
4.2. Impact of Forecast Horizon on Model
4.2.1. ARIMA Model
4.2.2. RF Model
4.2.3. LSTM Model
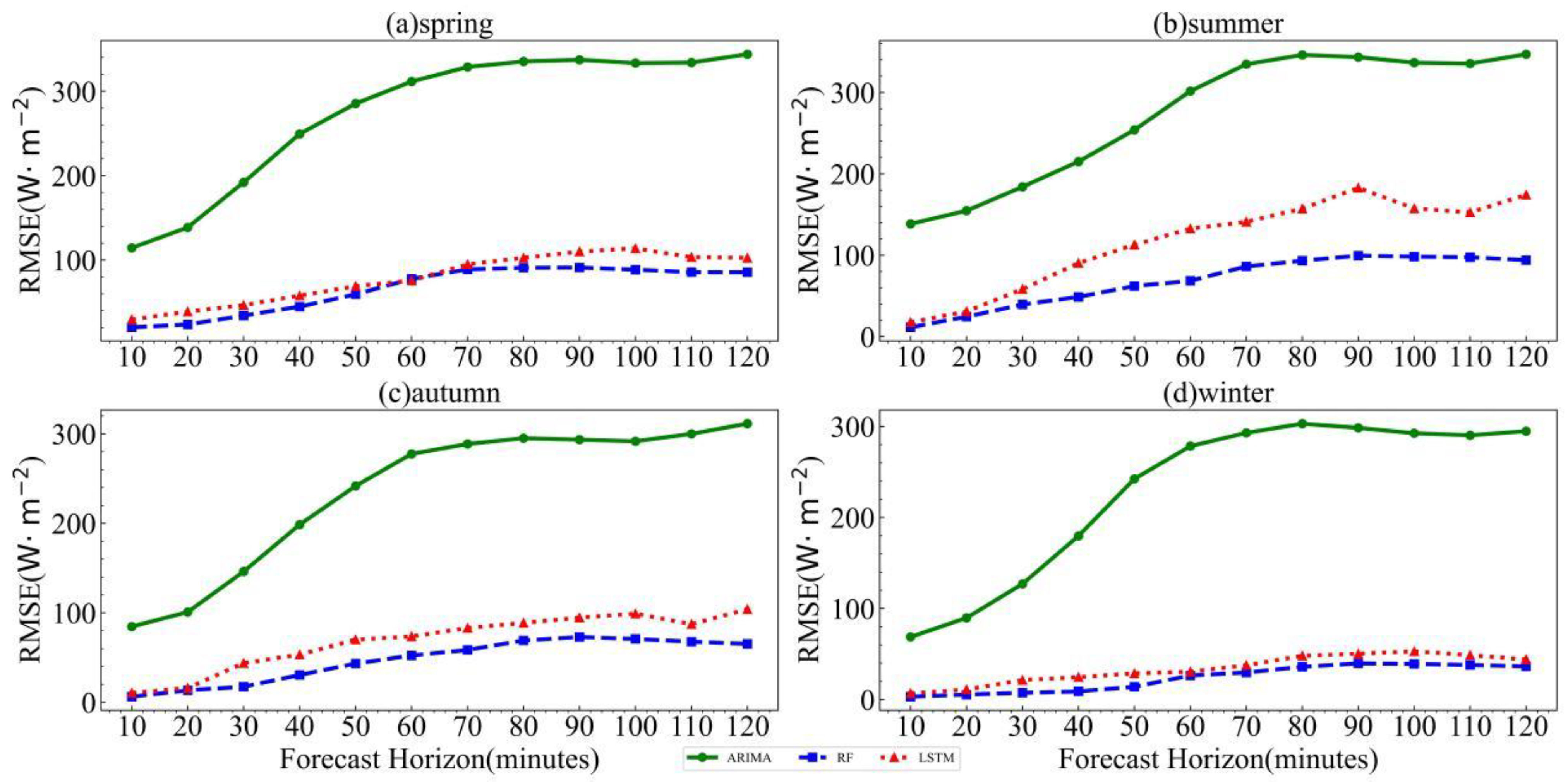
4.2.4. Comparison between Models
5. Conclusions
- Using the persistence model as a reference model, radiation forecasting was performed based on the ARIMA, RF, and LSTM models. Across all seasons, the accuracy of the ARIMA model was lower than that of the persistence model, but the RF and LSTM models exhibited higher accuracy than the persistence model.
- The prediction accuracy of the ARIMA, RF, and LSTM models for solar irradiance was significantly influenced by the sample size and distribution of the training set. When the sample size was the same, the accuracy of each model varied greatly across different seasons with different numerical distributions. Spring and summer had larger errors, while winter had the smallest errors. When the seasons were the same, i.e., when the numerical distributions of the training set were the same, the accuracy of each model differed significantly under different sample sizes. Overall, the LSTM model required a larger training set sample for learning and fitting compared to the RF and ARIMA models. When selecting training sets with equal sample sizes for the same season, the RF model exhibited the smallest prediction error, while the ARIMA model had the largest error.
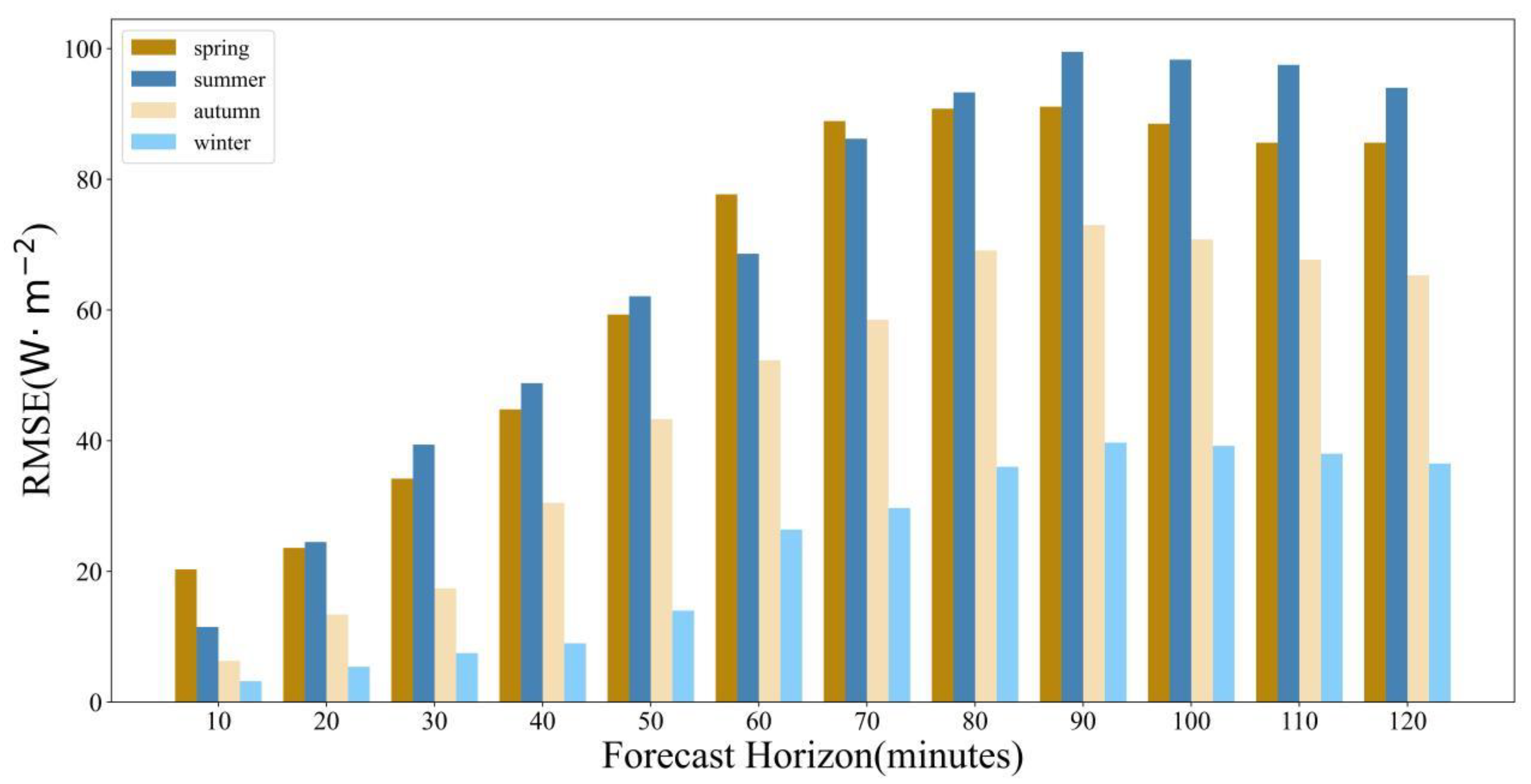
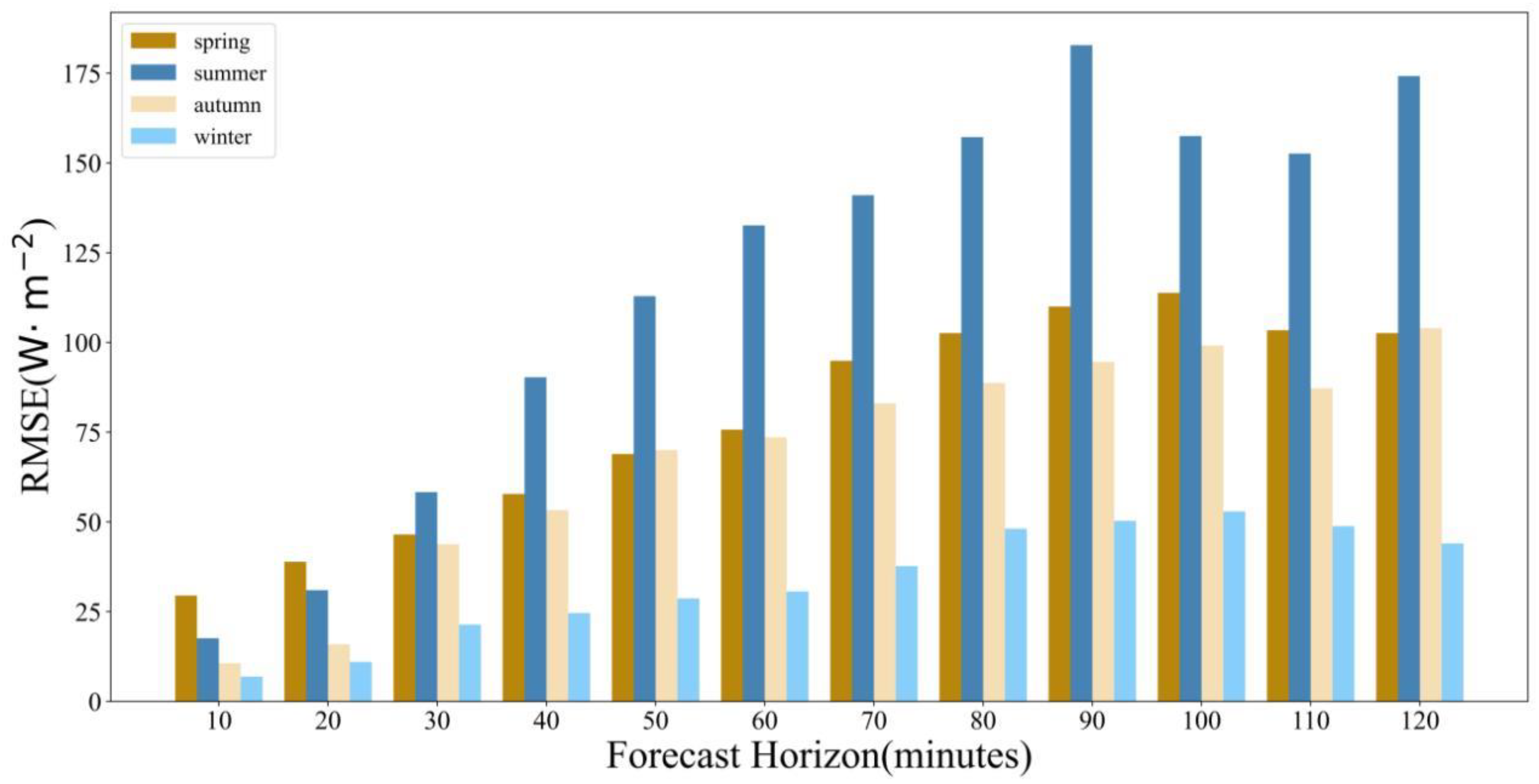
- In the prediction of solar irradiance, the forecast horizon has a significant impact on the prediction accuracy of each model. When the horizon was the same, the accuracy of each model varied greatly across different seasons, with overall prediction errors being the largest in summer and the smallest in winter. When the seasons were the same, as the forecast horizon increased, the prediction errors of all models gradually increased, reaching a peak at 80–100 min and then experiencing a slight decrease. When both the season and forecast horizon were the same, RF had the highest accuracy, with an RMSE lower than ARIMA by 65.6–258.3 W/m2 and lower than LSTM by 3.7–83.3 W/m2.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korachagaon, I.; Bapat, V.N. Predicting global solar radiation for South America. J. Renew. Sustain. Energy 2012, 4, 43101. [Google Scholar] [CrossRef]
- Urban, F.; Geall, S.; Wang, Y. Solar PV and solar water heaters in China: Different pathways to low carbon energy. Renew. Sustain. Energy Rev. 2016, 64, 531–542. [Google Scholar] [CrossRef]
- Chu, Y.; Pedro, H.T.C.; Li, M.; Coimbra, C.F.M. Real-time forecasting of solar irradiance ramps with smart image processing. Sol. Energy 2015, 114, 91–104. [Google Scholar] [CrossRef]
- Anvari-Moghaddam, A.; Monsef, H.; Rahimi-Kian, A.; Nance, H. Feasibility study of a novel methodology for solar radiation prediction on an hourly time scale: A case study in Plymouth, United Kingdom. J. Renew. Sustain. Energy 2014, 6, 33107. [Google Scholar] [CrossRef]
- Dou, C.; Qi, H.; Luo, W.; Zhang, Y. Elman neural network based short-term photovoltaic power forecasting using association rules and kernel principal component analysis. J. Renew. Sustain. Energy 2018, 10, 43501. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Liu, C.; Mi, Z.; Hodge, B.; Shafie-khah, M.; Catalão, J.P.S. Image phase shift invariance based cloud motion displacement vector calculation method for ultra-short-term solar PV power forecasting. Energy Convers. Manag. 2018, 157, 123–135. [Google Scholar] [CrossRef]
- Moreno-Muñoz, A.; de la Rosa, J.J.G.; Posadillo, R.; Pallarés, V.; Pallarés, V. Short term forecasting of solar radiation. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June 2008–2 July 2008. [Google Scholar]
- Martín, L.; Zarzalejo, L.F.; Polo, J.; Navarro, A.; Marchante, R.; Cony, M. Prediction of global solar irradiance based on time series analysis: Application to solar thermal power plants energy production planning. Sol. Energy 2010, 84, 1772–1781. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Sol. Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Ferrari, S.; Fina, A.; Lazzaroni, M.; Piuri, V.; Cristaldi, L.; Faifer, M.; Poli, T. Illuminance Prediction through Statistical Models. In Proceedings of the 2012 IEEE Workshop on Environmental Energy and Structural Monitoring Systems (EESMS), Perugia, Italy, 28 September 2012; pp. 90–96. [Google Scholar]
- Yang, D.; Jirutitijaroen, P.; Walsh, W.M. Hourly solar irradiance time series forecasting using cloud cover index. Sol. Energy 2012, 86, 3531–3543. [Google Scholar] [CrossRef]
- Das, S. Short term forecasting of solar radiation and power output of 89.6 kWp solar PV power plant. Mater. Today Proc. 2021, 39, 1959–1969. [Google Scholar] [CrossRef]
- Riihimaki, L.D.; Li, X.; Hou, Z.; Berg, L.K. Improving prediction of surface solar irradiance variability by integrating observed cloud characteristics and machine learning. Sol. Energy 2021, 225, 275–285. [Google Scholar] [CrossRef]
- Sun, H.; Gui, D.; Yan, B.; Liu, Y.; Liao, W.; Zhu, Y.; Lu, C.; Zhao, N. Assessing the potential of random forest method for estimating solar radiation using air pollution index. Energy Convers. Manag. 2016, 119, 121–129. [Google Scholar] [CrossRef]
- Fouilloy, A.; Voyant, C.; Notton, G.; Motte, F.; Paoli, C.; Nivet, M.; Guillot, E.; Duchaud, J. Solar irradiation prediction with machine learning: Forecasting models selection method depending on weather variability. Energy 2018, 165, 620–629. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, Z.; Gui, K.; Yan, X.; Gao, M.; Luo, M.; Geng, H.; Liao, T.; Li, X.; An, J.; et al. Daily Global Solar Radiation in China Estimated From High-Density Meteorological Observations: A Random Forest Model Framework. Earth Space Sci. 2020, 7, e2019EA001058. [Google Scholar] [CrossRef]
- Hou, N.; Zhang, X.; Zhang, W.; Wei, Y.; Jia, K.; Yao, Y.; Jiang, B.; Cheng, J. Estimation of Surface Downward Shortwave Radiation over China from Himawari-8 AHI Data Based on Random Forest. Remote Sens. 2020, 12, 181. [Google Scholar] [CrossRef]
- Villegas-Mier, C.; Rodriguez-Resendiz, J.; Álvarez-Alvarado, J.; Jiménez-Hernández, H.; Odry, Á. Optimized Random Forest for Solar Radiation Prediction Using Sunshine Hours. Micromachines 2022, 13, 1406. [Google Scholar] [CrossRef]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Yang, S.; Lu, X. Optimal load dispatch of community microgrid with deep learning based solar power and load forecasting. Energy 2019, 171, 1053–1065. [Google Scholar] [CrossRef]
- Huynh, A.N.; Deo, R.C.; An-Vo, D.; Ali, M.; Raj, N.; Abdulla, S. Near Real-Time Global Solar Radiation Forecasting at Multiple Time-Step Horizons Using the Long Short-Term Memory Network. Energies 2020, 13, 3517. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, C.; Li, Q.; Tai, Y.; Gao, B.; Shi, J. A Comparison of Hour-Ahead Solar Irradiance Forecasting Models Based on LSTM Network. Math. Probl. Eng. 2020, 2020, 4251517. [Google Scholar] [CrossRef]
- SORKUN, M.C.; DURMAZ İNCEL, Ö.; PAOLI, C. Time series forecasting on multivariate solar radiation data using deep learning (LSTM). Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 211–223. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Zhang, T.; Han, Y.; Zhou, X.; Xie, Y.; Yoo, S. Use of physics to improve solar forecast: Part II, machine learning and model interpretability. Sol. Energy 2022, 244, 362–378. [Google Scholar] [CrossRef]
- Gao, Y.; Miyata, S.; Akashi, Y. Multi-step solar irradiation prediction based on weather forecast and generative deep learning model. Renew. Energy 2022, 188, 637–650. [Google Scholar] [CrossRef]
- Bou-Rabee, M.A.; Naz, M.Y.; Albalaa, I.E.; Sulaiman, S.A. BiLSTM Network-Based Approach for Solar Irradiance Forecasting in Continental Climate Zones. Energies 2022, 15, 2226. [Google Scholar] [CrossRef]
- Alizamir, M.; Shiri, J.; Fard, A.F.; Kim, S.; Gorgij, A.D.; Heddam, S.; Singh, V.P. Improving the accuracy of daily solar radiation prediction by climatic data using an efficient hybrid deep learning model: Long short-term memory (LSTM) network coupled with wavelet transform. Eng. Appl. Artif. Intel. 2023, 123, 106199. [Google Scholar] [CrossRef]
- Paletta, Q.; Arbod, G.; Lasenby, J. Benchmarking of deep learning irradiance forecasting models from sky images—An in-depth analysis. Sol. Energy 2021, 224, 855–867. [Google Scholar] [CrossRef]
- He, K.; Zhao, W.; Liu, X.; Liu, J. Sensitivity Analysis of Training Set for Machine Learning Model in Surface Temperature Reconstruction under Cloud Cover. J. Remote Sens. 2021, 25, 1722–1734. [Google Scholar]
- Lauret, P.; Voyant, C.; Soubdhan, T.; David, M.; Poggi, P. A benchmarking of machine learning techniques for solar radiation forecasting in an insular context. Sol. Energy 2015, 112, 446–457. [Google Scholar] [CrossRef]
- Zhou, M.; Xue, X. Observational Analysis and Dynamic Study of the Atmospheric Boundary Layer on the Qinghai-Tibet Plateau; China Meteorological Press: Beijing, China, 2000. [Google Scholar]
- King, J.C. Longwave atmospheric radiation over Antarctica. Antarct. Sci. 1996, 8, 105–109. [Google Scholar] [CrossRef]
- YANG, D.; WANG, W.; XIA, X. Related articles that may interest you. Adv. Atmos. Sci. 2022, 8, 1239–1251. [Google Scholar] [CrossRef]
- Box, G.P.; Jenkins, G. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1994; p. 13. [Google Scholar]
- Fara, L.; Bartok, B.; Galbeaza Moraru, A.; Oprea, C.; Sterian, P.; Diaconu, A.; Fara, S. New results in forecasting of photovoltaic systems output based on solar radiation forecasting. J. Renew. Sustain. Energy 2013, 5, 41821. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Panamtash, H.; Zhou, Q.; Hong, T.; Qu, Z.; Davis, K.O. A copula-based Bayesian method for probabilistic solar power forecasting. Sol. Energy 2020, 196, 336–345. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Li, F.; Wang, S.; Wei, J. Long term rolling prediction model for solar radiation combining empirical mode decomposition (EMD) and artificial neural network (ANN) techniques. J. Renew. Sustain. Energy 2018, 10, 013704. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J.U. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Yu, L.; Qu, J.; Gao, F.; Tian, Y. A Novel Hierarchical Algorithm for Bearing Fault Diagnosis Based on Stacked LSTM. Shock Vib. 2019, 2019, 2756284. [Google Scholar] [CrossRef]
- Yang, Z.; Mourshed, M.; Liu, K.; Xu, X.; Feng, S. A novel competitive swarm optimized RBF neural network model for short-term solar power generation forecasting. Neurocomputing 2020, 397, 415–421. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Chu, Y.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid intra-hour DNI forecasts with sky image processing enhanced by stochastic learning. Sol. Energy 2013, 98, 592–603. [Google Scholar] [CrossRef]
- Yang, D.; Alessandrini, S.; Antonanzas, J.; Antonanzas-Torres, F.; Badescu, V.; Beyer, H.G.; Blaga, R.; Boland, J.; Bright, J.M.; Coimbra, C.F.M.; et al. Verification of deterministic solar forecasts. Sol. Energy 2020, 210, 20–37. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Short-term solar power forecast with deep learning: Exploring optimal input and output configuration. Sol. Energy 2019, 188, 730–741. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Monyei, C.G. On the global solar radiation prediction methods. J. Renew. Sustain. Energy 2016, 8, 23702. [Google Scholar] [CrossRef]
- Paliari, I.; Karanikola, A.; Kotsiantis, S. A Comparison of the Optimized LSTM, XGBOOST and ARIMA in Time Series Forecasting. In Proceedings of the 2021 12th International Conference on Information, Intelligence, Systems & Applications (IISA), Chania Crete, Greece, 12–14 July 2021; pp. 1–7. [Google Scholar]
- Yang, H.; Kurtz, B.; Nguyen, D.; Urquhart, B.; Chow, C.W.; Ghonima, M.; Kleissl, J. Solar irradiance forecasting using a ground-based sky imager developed at UC San Diego. Sol. Energy 2014, 103, 502–524. [Google Scholar] [CrossRef]
- Zhang, J.; Verschae, R.; Nobuhara, S.; Lalonde, J. Deep photovoltaic nowcasting. Sol. Energy 2018, 176, 267–276. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Chu, Y.; Pedro, H.T.C.; Nonnenmacher, L.; Inman, R.H.; Liao, Z.; Coimbra, C.F.M. A Smart Image-Based Cloud Detection System for Intrahour Solar Irradiance Forecasts. J. Atmos. Ocean. Technol. 2014, 31, 1995–2007. [Google Scholar] [CrossRef]
- Wu, L.; Chen, T.; Ciren, N.; Wang, D.; Meng, H.; Li, M.; Zhao, W.; Luo, J.; Hu, X.; Jia, S.; et al. Development of a Machine Learning Forecast Model for Global Horizontal Irradiation Adapted to Tibet Based on Visible All-Sky Imaging. Remote Sens. 2023, 15, 2340. [Google Scholar] [CrossRef]


| Spring | Summer | Autumn | Winter | |
|---|---|---|---|---|
| max | 1687 | 1713 | 1487 | 1292 |
| mean | 551 | 579 | 457 | 413 |
| std | 360 | 376 | 325 | 293 |
| Sping | Summer | Autumn | Winter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max | Mean | Std | Max | Mean | Std | Max | Mean | Std | Max | Mean | Std | |
| 8 | 569 | 123 | 110 | 569 | 143 | 108 | 355 | 42 | 58 | 56 | 0.1 | 7 |
| 9 | 970 | 339 | 154 | 909 | 315 | 179 | 699 | 211 | 113 | 418 | 103 | 83 |
| 10 | 1167 | 565 | 201 | 1198 | 525 | 245 | 1093 | 432 | 161 | 625 | 335 | 102 |
| 11 | 1592 | 750 | 235 | 1377 | 684 | 283 | 1316 | 616 | 195 | 831 | 537 | 117 |
| 12 | 1151 | 816 | 308 | 1584 | 787 | 344 | 1452 | 725 | 253 | 1138 | 683 | 146 |
| 13 | 1538 | 852 | 351 | 1713 | 863 | 357 | 1452 | 770 | 288 | 1161 | 730 | 195 |
| 14 | 1687 | 781 | 379 | 1710 | 857 | 386 | 1487 | 691 | 311 | 1292 | 696 | 216 |
| 15 | 1544 | 657 | 362 | 1598 | 769 | 389 | 1421 | 630 | 290 | 1174 | 599 | 232 |
| 16 | 1465 | 559 | 320 | 1436 | 609 | 346 | 1291 | 480 | 245 | 1104 | 453 | 201 |
| 17 | 1212 | 387 | 237 | 1180 | 508 | 281 | 1091 | 308 | 177 | 985 | 293 | 151 |
| 18 | 792 | 230 | 149 | 887 | 314 | 203 | 720 | 124 | 114 | 557 | 115 | 99 |
| ARIMA | RF | LSTM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| 6 d | 160.9 | 208.6 | 133.0 | 125.3 | 32.4 | 27.2 | 13.4 | 9.3 | 53.5 | 49.5 | 35.4 | 12.7 |
| 12 d | 148.7 | 181.9 | 133.7 | 87.1 | 22.8 | 21.1 | 10.6 | 5.6 | 41.8 | 37.5 | 20.4 | 10.3 |
| 18 d | 127.0 | 171.0 | 111.0 | 97.0 | 22.9 | 21.4 | 8.1 | 4.5 | 34.2 | 30.2 | 16.1 | 7.9 |
| 24 d | 166.9 | 154.7 | 103.9 | 81.1 | 24.7 | 15.1 | 11.5 | 5.0 | 35.5 | 24.2 | 15.9 | 7.0 |
| 30 d | 157.1 | 178.1 | 127.2 | 96.0 | 20.3 | 17.5 | 9.0 | 6.2 | 35.1 | 30.8 | 16.2 | 10.8 |
| 36 d | 141.6 | 170.1 | 95.9 | 89.6 | 24.7 | 23.6 | 8.4 | 5.0 | 33.7 | 29.6 | 13.5 | 9.8 |
| 42 d | 133.3 | 138.5 | 105.5 | 101.4 | 26.2 | 11.8 | 8.3 | 4.8 | 32.1 | 17.6 | 11.8 | 10.0 |
| 48 d | 134.5 | 162.4 | 95.7 | 68.8 | 21.2 | 16.2 | 10.3 | 3.2 | 34.4 | 26.0 | 16.1 | 11.6 |
| 54 d | 114.4 | 190.4 | 84.6 | 71.5 | 22.7 | 17.6 | 6.3 | 5.7 | 29.9 | 28.4 | 11.9 | 9.7 |
| 60 d | 161.0 | 176.4 | 101.6 | 101.6 | 22.3 | 14.5 | 7.6 | 6.9 | 33.1 | 24.6 | 10.9 | 10.1 |
| 66 d | 133.8 | 144.1 | 134.5 | 77.3 | 20.6 | 11.6 | 10.1 | 5.2 | 29.5 | 17.9 | 11.7 | 8.3 |
| 72 d | 150.3 | 160.9 | 88.9 | 119.5 | 31.7 | 11.5 | 8.8 | 4.4 | 38.3 | 17.8 | 10.6 | 6.9 |
| ARIMA | RF | LSTM | ||||
|---|---|---|---|---|---|---|
| p | q | Estimators | Max-Depth | Unit1 | Unit2 | |
| spring | 4 | 3 | 19 | 13 | 40 | 60 |
| summer | 3 | 2 | 16 | 13 | 52 | 63 |
| autumn | 3 | 3 | 25 | 10 | 63 | 67 |
| winter | 5 | 8 | 25 | 14 | 40 | 40 |
| Spring/Day | Summer/Day | Autumn/Day | Winter/Day | |
|---|---|---|---|---|
| ARIMA | 54 | 42 | 54 | 48 |
| RF | 30 | 72 | 54 | 48 |
| LSTM | 66 | 42 | 72 | 72 |
| ARIMA | RF | LSTM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| 10 min | 114.4 | 138.5 | 84.6 | 68.8 | 20.3 | 11.5 | 6.3 | 3.2 | 29.5 | 17.6 | 10.6 | 6.9 |
| 20 min | 138.6 | 154.6 | 100.8 | 89.7 | 23.6 | 24.5 | 13.4 | 5.4 | 38.9 | 31.0 | 15.9 | 11.0 |
| 30 min | 192.1 | 184.0 | 146.1 | 127.0 | 34.2 | 39.4 | 17.4 | 7.5 | 46.5 | 58.3 | 43.8 | 21.4 |
| 40 min | 249.4 | 215.0 | 198.5 | 179.7 | 44.8 | 48.8 | 30.5 | 9.0 | 57.8 | 90.3 | 53.3 | 24.6 |
| 50 min | 285.4 | 253.9 | 241.7 | 242.4 | 59.3 | 62.1 | 43.3 | 14.0 | 68.9 | 112.9 | 70.0 | 28.7 |
| 60 min | 311.5 | 301.6 | 277.5 | 278.3 | 77.7 | 68.6 | 52.3 | 26.4 | 75.7 | 132.6 | 73.6 | 30.6 |
| 70 min | 328.7 | 334.6 | 288.6 | 292.9 | 88.9 | 86.2 | 58.5 | 29.7 | 94.9 | 141.0 | 83.1 | 37.7 |
| 80 min | 335.3 | 346.0 | 295.0 | 303.0 | 90.8 | 93.3 | 69.1 | 36.0 | 102.6 | 157.2 | 88.7 | 48.1 |
| 90 min | 337.2 | 343.3 | 293.4 | 298.4 | 91.1 | 99.5 | 73.0 | 39.7 | 110.0 | 182.8 | 94.6 | 50.3 |
| 100 min | 333.4 | 336.5 | 291.6 | 292.5 | 88.5 | 98.3 | 70.8 | 39.2 | 113.8 | 157.5 | 99.1 | 52.9 |
| 110 min | 334 | 335.4 | 299.9 | 290.2 | 85.6 | 97.5 | 67.7 | 38.0 | 103.4 | 152.6 | 87.2 | 48.8 |
| 120 min | 343.8 | 346.8 | 311.3 | 294.8 | 85.6 | 94.0 | 65.3 | 36.5 | 102.6 | 174.2 | 104.0 | 44.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, H.; Wu, L.; Li, H.; Song, Y. Construction and Research of Ultra-Short Term Prediction Model of Solar Short Wave Irradiance Suitable for Qinghai–Tibet Plateau. Atmosphere 2023, 14, 1150. https://doi.org/10.3390/atmos14071150
Meng H, Wu L, Li H, Song Y. Construction and Research of Ultra-Short Term Prediction Model of Solar Short Wave Irradiance Suitable for Qinghai–Tibet Plateau. Atmosphere. 2023; 14(7):1150. https://doi.org/10.3390/atmos14071150
Chicago/Turabian StyleMeng, Huimei, Lingxiao Wu, Huaxia Li, and Yixin Song. 2023. "Construction and Research of Ultra-Short Term Prediction Model of Solar Short Wave Irradiance Suitable for Qinghai–Tibet Plateau" Atmosphere 14, no. 7: 1150. https://doi.org/10.3390/atmos14071150
APA StyleMeng, H., Wu, L., Li, H., & Song, Y. (2023). Construction and Research of Ultra-Short Term Prediction Model of Solar Short Wave Irradiance Suitable for Qinghai–Tibet Plateau. Atmosphere, 14(7), 1150. https://doi.org/10.3390/atmos14071150





