Numerical and Experimental Analysis of an Earth–Air Heat Exchanger
Abstract
1. Introduction
2. Methodology
2.1. Considerations and Equations
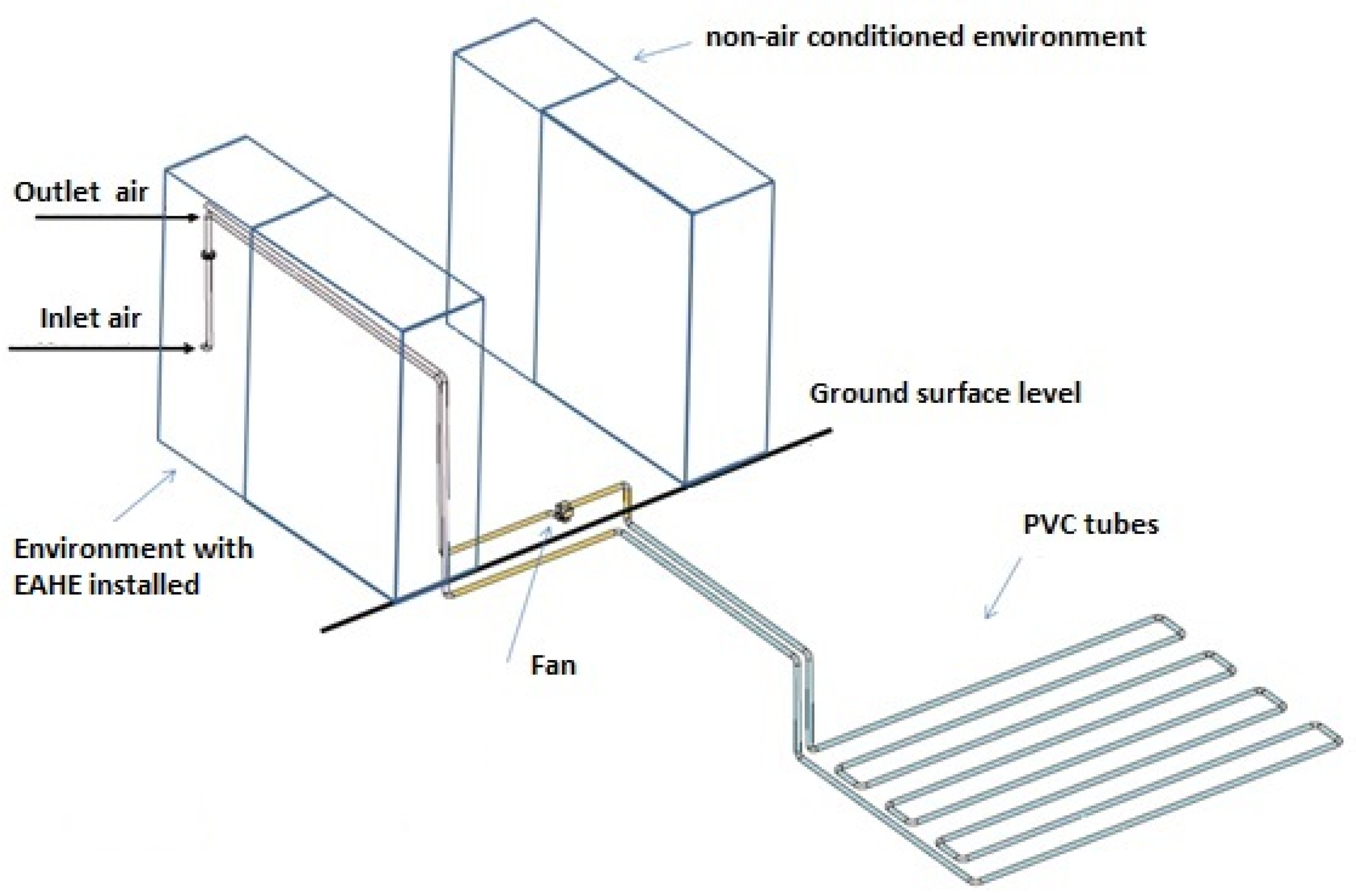
2.2. Geometry, Mesh, and Boundary Conditions
2.3. Experimental Apparatus
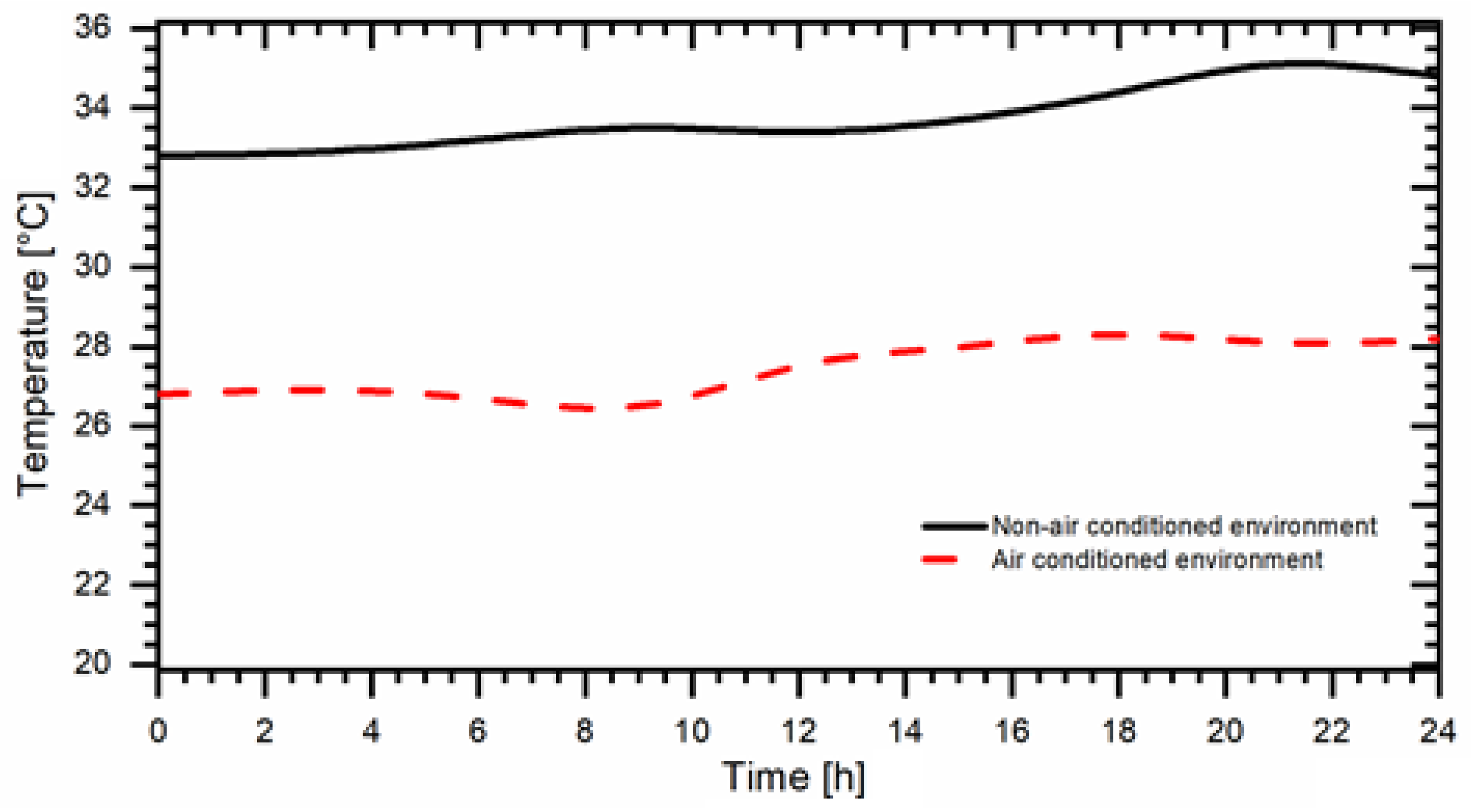
2.4. Indoor Environments
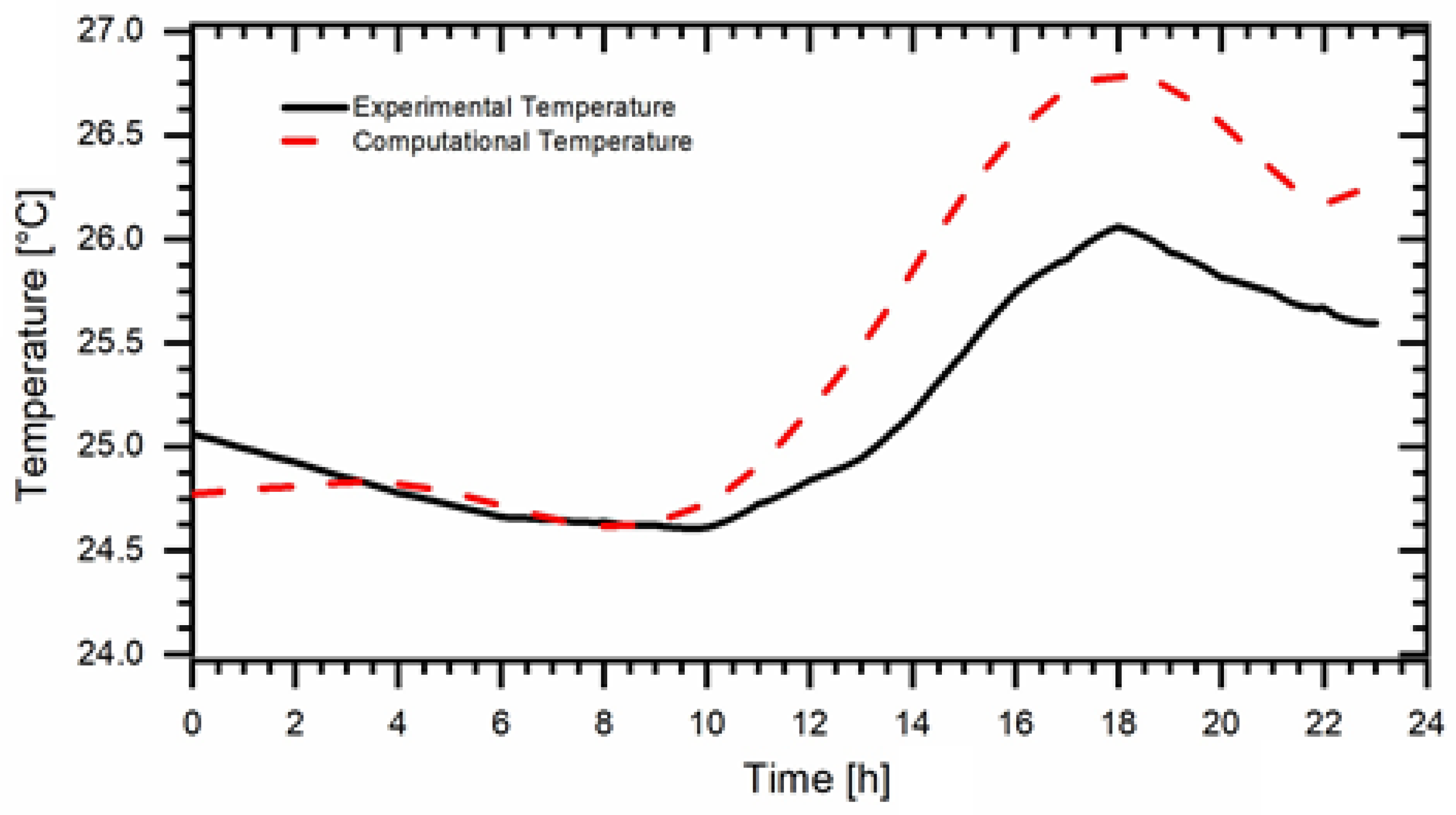
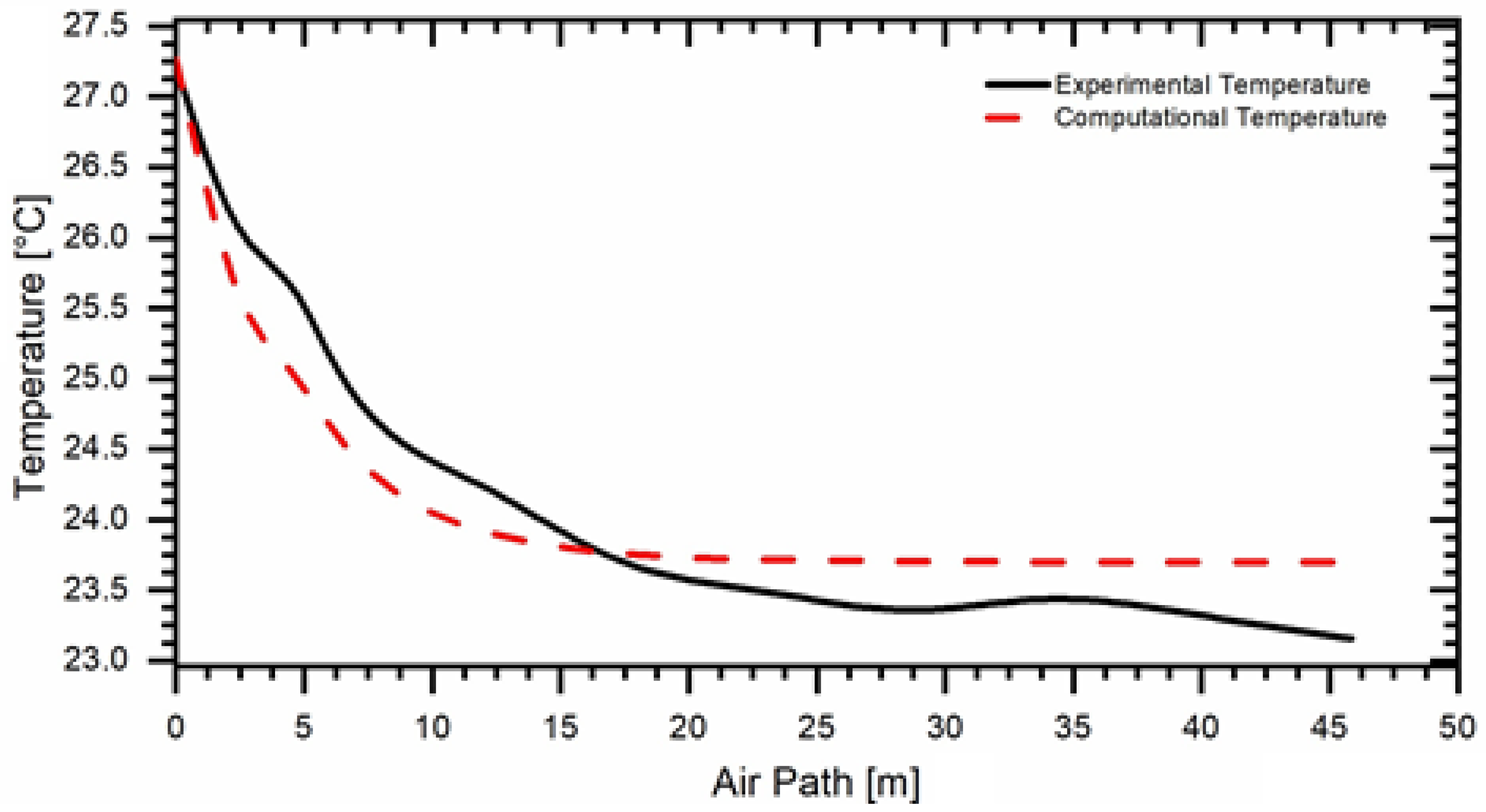
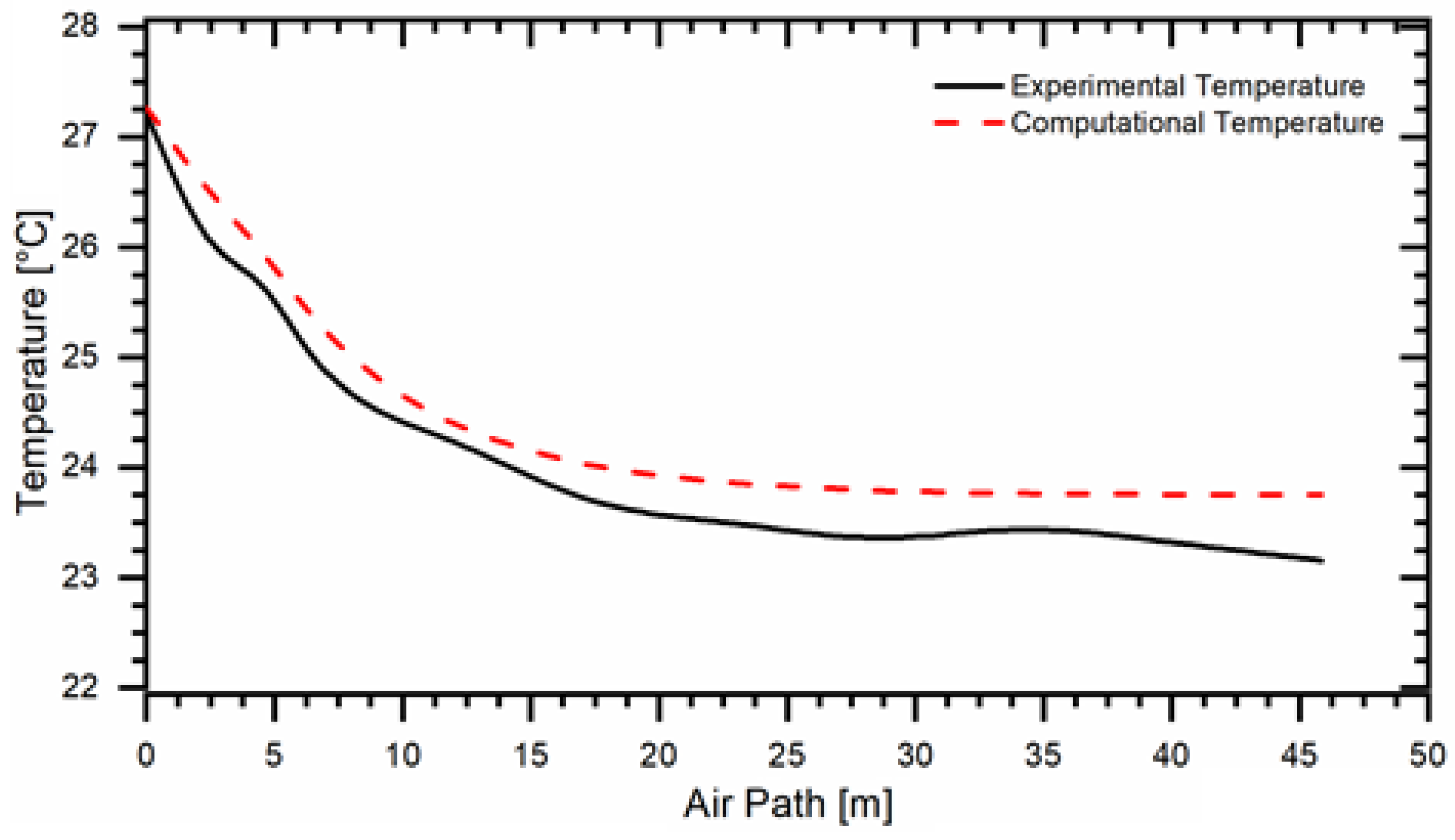
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| heat transferred [J/m3] | |
| thermal conductivity [W/(m.K)] | |
| constant 1 (turbulence model) [-] | |
| constant 2 (turbulence model) [-] | |
| constant 3 (turbulence model) [-] | |
| turbulent viscosity constant [-] | |
| turbulent Kinetic Energy [J/kg] | |
| internal energy [J/kg] | |
| specific mass [kg/m3] | |
| turbulent Prandtl number for [-] | |
| turbulent Prandtl number for 𝜖 [-] | |
| fluid static pressure [N/m2] | |
| turbulent energy dissipation [m2/s3] | |
| transfer rate of mechanical energy in the fluid deformation process due to viscosity [W/m3] | |
| coefficient of thermal conductivity [W/(m.K)] | |
| temperature [K] | |
| time [s] | |
| vector speed [m/s] | |
| dynamic viscosity [kg/(m.s)] | |
| turbulent viscosity [kg/(m.s)] | |
| turbulent kinetic energy [J] | |
| turbulent kinetic energy generation due to buoyancy generation due to mean velocity [J] |
References
- Brasil, Ministério de Minas e Energia, Balanço Energético Nacional. 2021. Available online: https://www.epe.gov.br/pt/publicacoes-dados-abertos/publicacoes/balanco-energetico-nacional-2021 (accessed on 3 December 2021).
- Vaz, J.; Sattler, M.A.; dos Santos, E.D.; Isoldi, L.A. Experimental and numerical analysis of an earth–air heat exchanger. Energy Build. 2011, 43, 2476–2482. [Google Scholar] [CrossRef]
- Maoz, M.; Ali, S.; Muhammad, N.; Amin, A.; Sohaib, M.; Basit, A.; Ahmad, T. Parametric Optimization of Earth to Air Heat Exchanger Using Response Surface Method. Sustainability 2019, 11, 3186. [Google Scholar] [CrossRef]
- Greco, A.; Masselli, C. The Optimization of the Thermal Performances of an Earth to Air Heat Exchanger for an Air Conditioning System: A Numerical Study. Energies 2020, 13, 6414. [Google Scholar] [CrossRef]
- Peña, S.A.P.; Ibarra, J.E.J. Potential Applicability of Earth to Air Heat Exchanger for Cooling in a Colombian Tropical Weather. Buildings 2021, 11, 219. [Google Scholar] [CrossRef]
- Abadie, M.O.; Santos, G.H.; Freire, R.Z.; Mendes, N. Heating and Cooling Potential of Buried Pipes in South Brazil. Braz. Soc. of Mechanical Sciences and Engineering—ABCM. In Proceedings of the 11th Brazilian Congress of Thermal Sciences and Engineering—ENCIT 2006, CIT06-0459, Curitiba, Brazil, 5–8 December 2006. [Google Scholar]
- Serageldin, A.A.; Abdelrahman, A.K.; Ookawara, S. Earth-Air Heat Exchanger thermal performance in Egyptian conditions: Experimental results, mathematical model, and Computational Fluid Dynamics simulation. Energy Convers. Manag. 2016, 122, 25–38. [Google Scholar] [CrossRef]
- Elminshawy, N.A.; Siddiqui, F.R.; Farooq, Q.U.; Addas, M.F. Experimental investigation on the performance of earth-air pipe heat exchanger for different soil compaction levels. Appl. Therm. Eng. 2017, 124, 1319–1327. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Z.; Liu, Z.; Qin, D.; Zhou, J.; Zhang, G. Performance Analysis of Earth-air Heat Exchangers in Hot Summer and Cold Winter Areas. Procedia Eng. 2017, 205, 1672–1677. [Google Scholar] [CrossRef]
- Menhoudj, S.; Mokhtari, A.M.; Benzaama, M.H.; Maalouf, C.; Lachi, M.; Makhlouf, M. Study of the Energy Performance of an Earth—Air Heat Exchanger for Refreshing Buildings in Algeria. Energy Build. 2018, 158, 1602–1612. [Google Scholar] [CrossRef]
- Li, H.; Ni, L.; Yao, Y.; Sun, C. Experimental investigation on the cooling performance of an Earth to Air Heat Exchanger (EAHE) equipped with an irrigation system to adjust soil moisture. Energy Build. 2019, 196, 280–292. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, Z.; Yang, T.; Li, S.; El Mankibi, M.; Roccamena, L.; Qin, D.; Zhang, G. Experimental investigation of a vertical earth-to-air heat exchanger system. Energy Convers. Manag. 2019, 183, 241–251. [Google Scholar] [CrossRef]
- Congedo, P.M.; Lorusso, C.; Baglivo, C.; Milanese, M.; Raimondo, L. Experimental validation of horizontal air-ground heat exchangers (HAGHE) for ventilation systems. Geothermics 2019, 80, 78–85. [Google Scholar] [CrossRef]
- Tang, L.; Liu, Z.; Zhou, Y.; Qin, D.; Zhang, G. Study on a Dynamic Numerical Model of an Underground Air Tunnel System for Cooling Applications—Experimental Validation and Multidimensional Parametrical Analysis. Energies 2020, 13, 1236. [Google Scholar] [CrossRef]
- Hegazi, A.; Abdelrehim, O.; Khater, A. Parametric optimization of earth-air heat exchangers (EAHEs) for central air conditioning. Int. J. Refrig. 2021, 129, 278–289. [Google Scholar] [CrossRef]
- Hacini, K.; Benatiallah, A.; Abdelkade, H.; Harrouz, A.; Belatrache, D. Efficiency assessment of an earth-air heat exchanger system for passive cooling in three different regions: The Algerian case. FME Trans. 2021, 49, 1035–1046. [Google Scholar] [CrossRef]
- Vivas, G.A.V.; Guerra, D.R.S. Modelagem computacional do trocador de calor solo-ar adaptado às condições climáticas de Belém. Ambiente Construído 2021, 21, 359–381. [Google Scholar] [CrossRef]
- Nejad, M.N.; Saffarian, M.R.; Nejad, M.B. Investigating the possibility of using the underground tunnel for air-conditioning in Tehran. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 473. [Google Scholar] [CrossRef]
- Qi, D.; Zhao, C.; Li, S.; Chen, R.; Li, A. Numerical Assessment of Earth to Air Heat Exchanger with Variable Humidity Conditions in Greenhouses. Energies 2021, 14, 1368. [Google Scholar] [CrossRef]
- Zeitoun, W.; Lin, J.; Siroux, M. Energetic and Exergetic Analyses of an Experimental Earth–Air Heat Exchanger in the Northeast of France. Energies 2023, 16, 1542. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, M.; Zhou, Y.; He, Y.; Zhang, L.; Zhang, G.; Chen, D. A state-of-the-art review on shallow geothermal ventilation systems with thermal performance enhancement system classifications, advanced technologies and applications. Energy Built Environ. 2023, 4, 148–168. [Google Scholar] [CrossRef]
- Amanowicz, Ł.; Ratajczak, K.; Dudkiewicz, E. Recent Advancements in Ventilation Systems Used to Decrease Energy Consumption in Buildings—Literature Review. Energies 2023, 16, 1853. [Google Scholar] [CrossRef]
- Michalak, P. Impact of Air Density Variation on a Simulated Earth-to-Air Heat Exchanger’s Performance. Energies 2022, 15, 3215. [Google Scholar] [CrossRef]
- Tannehill, J.C.; Anderson, D.A.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer; CRC Press: Washington, DC, USA, 1997; pp. 249–272. [Google Scholar]
- Misra, R.; Bansal, V.; Das Agrawal, G.; Mathur, J.; Aseri, T.K. CFD analysis based parametric study of derating factor for Earth Air Tunnel Heat Exchanger. Appl. Energy 2013, 103, 266–277. [Google Scholar] [CrossRef]
- Vasconcellos, D.P.; Santos, G. Thermal performance and geometric optimization of an earth-pipe-air heat exchanger (EPAHE) in different soils. In Proceedings of the 17th Brazilian Congress of Thermal Sciences and Engineering—Encit, Águas de Lindóia, SP, Brazil, 25–28 November 2018. [Google Scholar]
- Shojaee, S.M.N.; Malek, K. Earth-to-air heat exchangers cooling evaluation for different climates of Iran. Sustain. Energy Technol. Assess. 2017, 23, 111–120. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary-Layer Climatology; Methuen Co.: New York, NY, USA, 1987; p. 435. [Google Scholar]





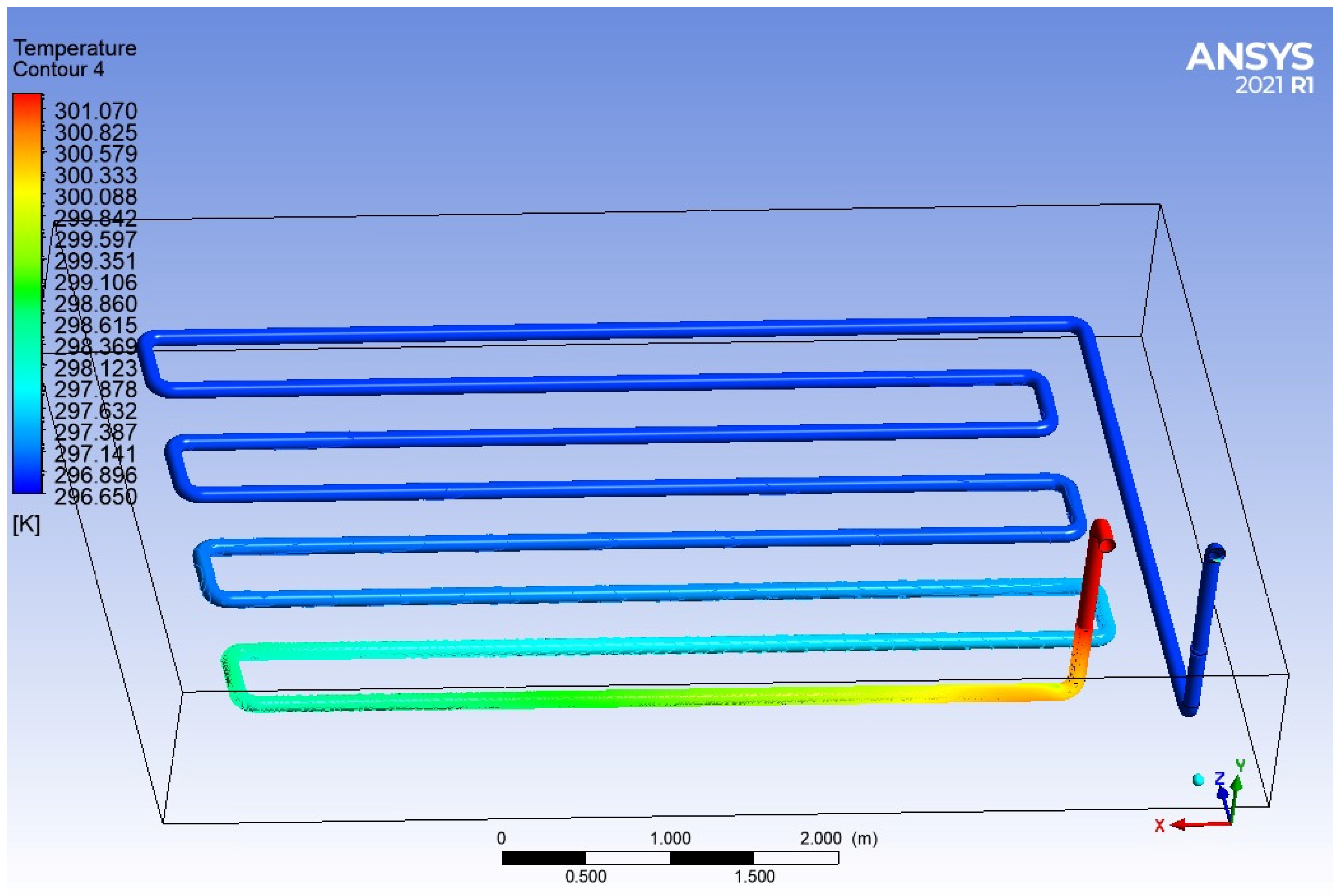
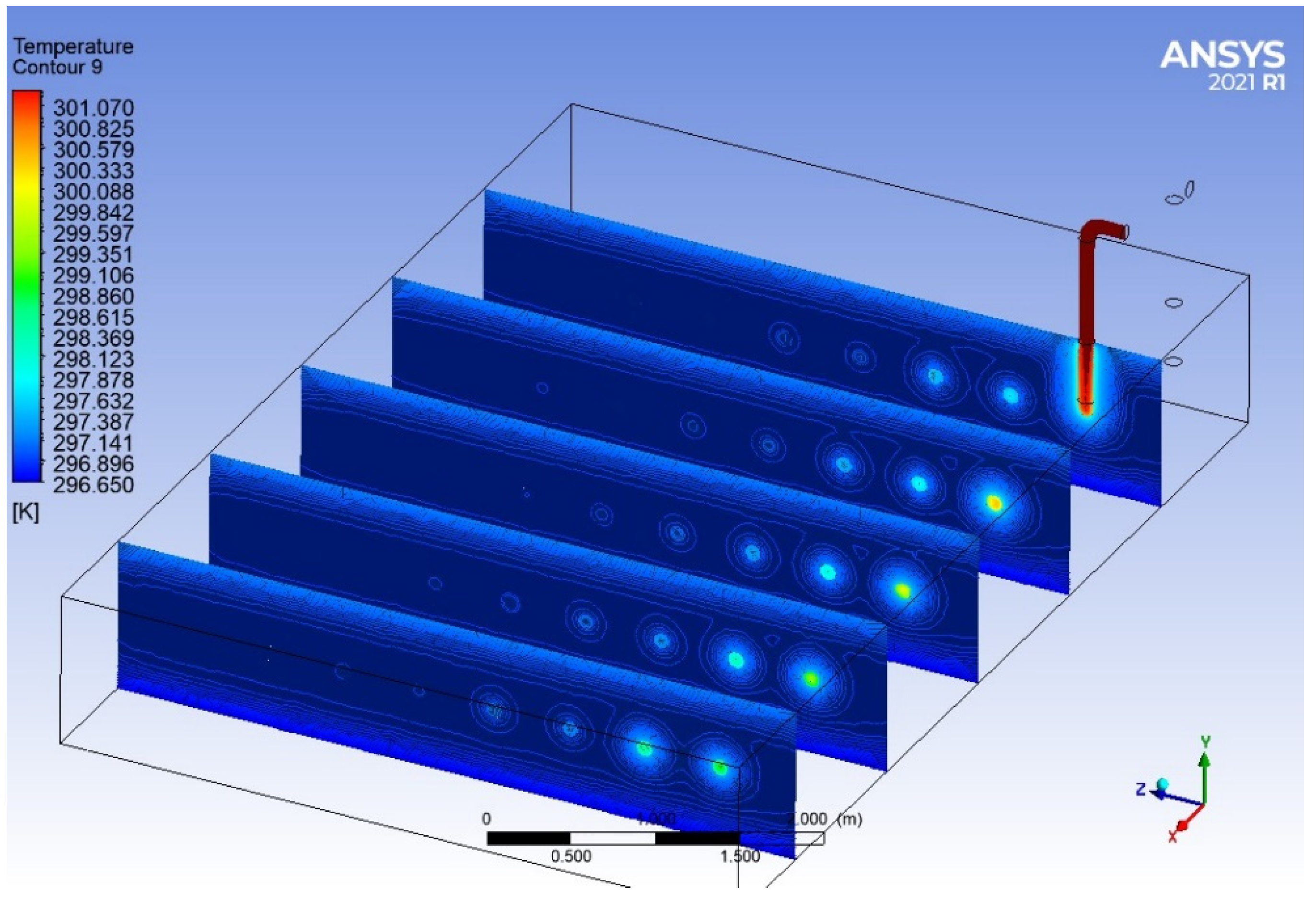
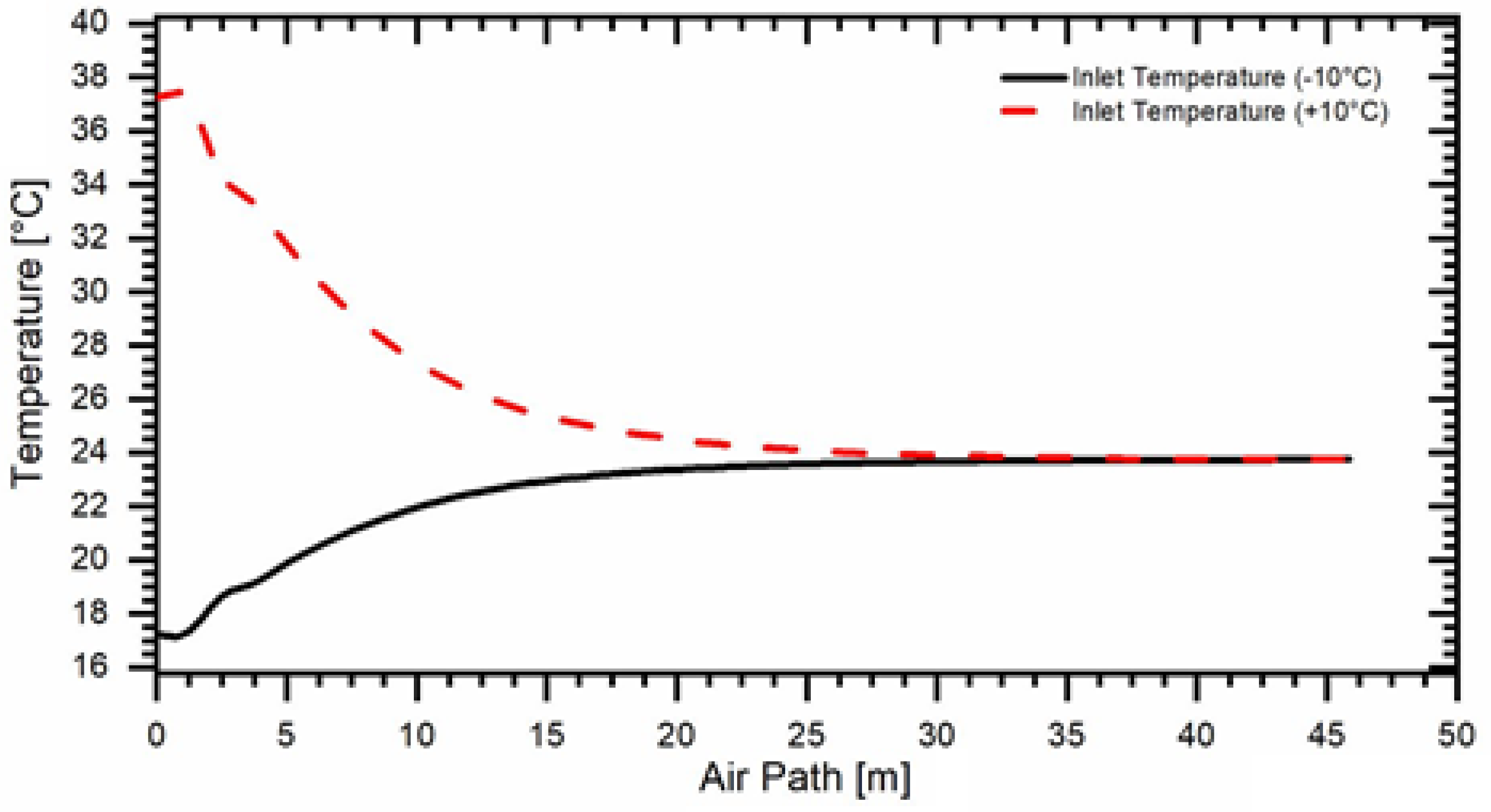
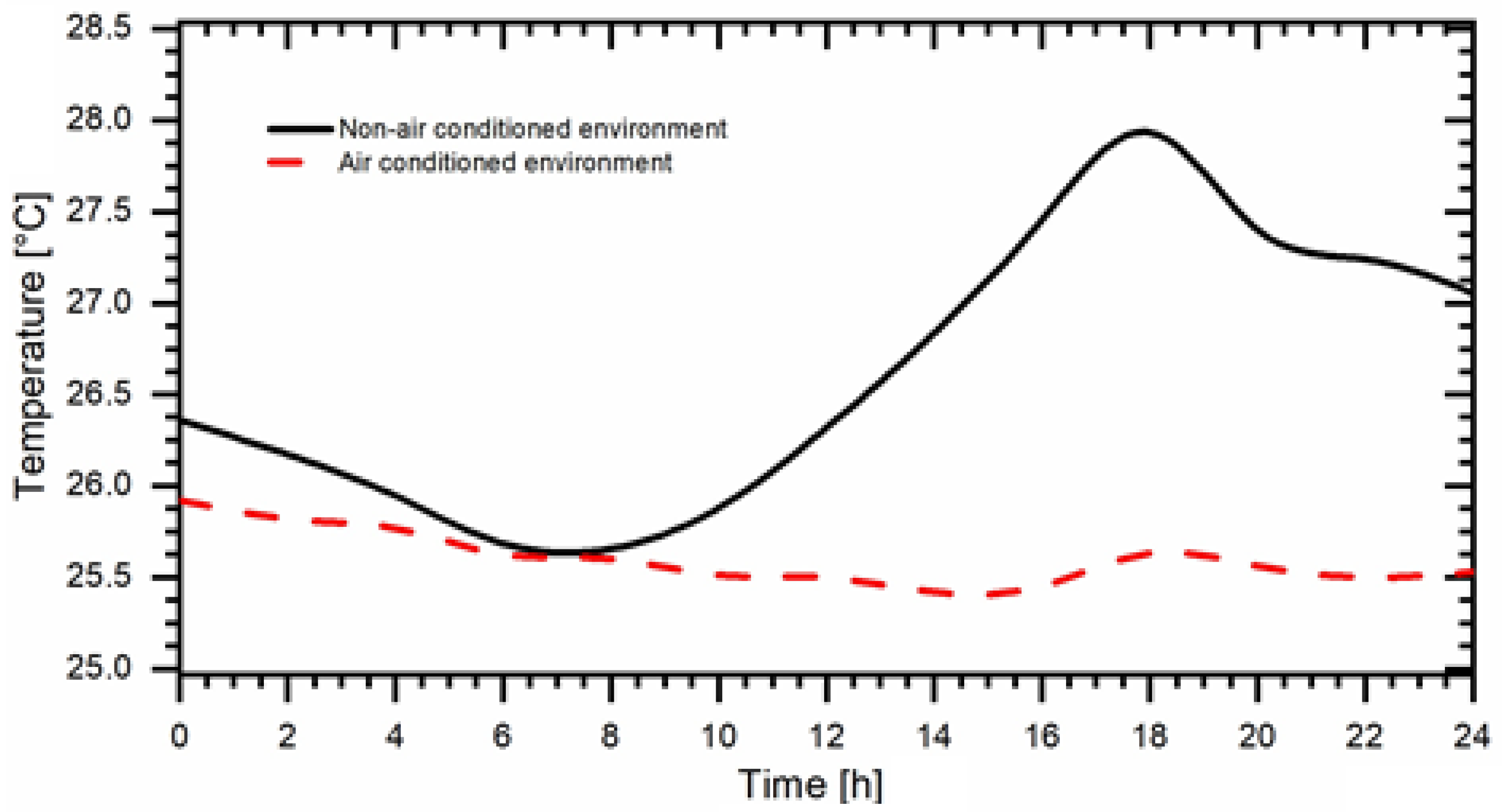
| Number of Steps | Distance between Pipes [m] | Installation Depth [m] | Pipe Diameter [m] | Total Length [m] |
|---|---|---|---|---|
| 8 | 0.5 | 1.5 | 0.1 | 48.20 |
| Mesh | Total Number of Elements | Max. Difference between Values [%] |
|---|---|---|
| Mesh used in simulations | 3,683,460 | 3.72 |
| Air domain | 4,019,658 | 3.78 |
| Air domain | 3,236,785 | 3.97 |
| Air and soil domains | 4,529,629 | 3.78 |
| Air and soil domains | 1,959,346 | 4.16 |
| Material | Density [kg/m3] | Specific Heat [J/kg.K] | Thermal Conductivity [W/m.K] | Viscosity [kg/m.s] |
|---|---|---|---|---|
| Air | 1.225 | 1006.4 | 0.0242 | 1.7894 × 10−5 |
| Soil | 2050 | 1840 | 0.52 | - |
| Parameter | Instrument | Uncertainty | Unit |
|---|---|---|---|
| Solar Irradiance | Pyranometer | ±3% | W/m2 |
| Temperature | Type K Thermocouple | ±0.25 | °C |
| Air velocity | Meteorological Station | ±0.3% | m/s |
| Power | Data Acquisition System | ±1.0% | W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diedrich, C.H.; Santos, G.H.d.; Carraro, G.C.; Dimbarre, V.V.; Alves, T.A. Numerical and Experimental Analysis of an Earth–Air Heat Exchanger. Atmosphere 2023, 14, 1113. https://doi.org/10.3390/atmos14071113
Diedrich CH, Santos GHd, Carraro GC, Dimbarre VV, Alves TA. Numerical and Experimental Analysis of an Earth–Air Heat Exchanger. Atmosphere. 2023; 14(7):1113. https://doi.org/10.3390/atmos14071113
Chicago/Turabian StyleDiedrich, Carlos Henrique, Gerson Henrique dos Santos, Gustavo Chaves Carraro, Victor Vaurek Dimbarre, and Thiago Antonini Alves. 2023. "Numerical and Experimental Analysis of an Earth–Air Heat Exchanger" Atmosphere 14, no. 7: 1113. https://doi.org/10.3390/atmos14071113
APA StyleDiedrich, C. H., Santos, G. H. d., Carraro, G. C., Dimbarre, V. V., & Alves, T. A. (2023). Numerical and Experimental Analysis of an Earth–Air Heat Exchanger. Atmosphere, 14(7), 1113. https://doi.org/10.3390/atmos14071113







