Projection and Analysis of Floods in the Upper Heihe River Basin under Climate Change
Abstract
1. Introduction
2. Materials and Methods
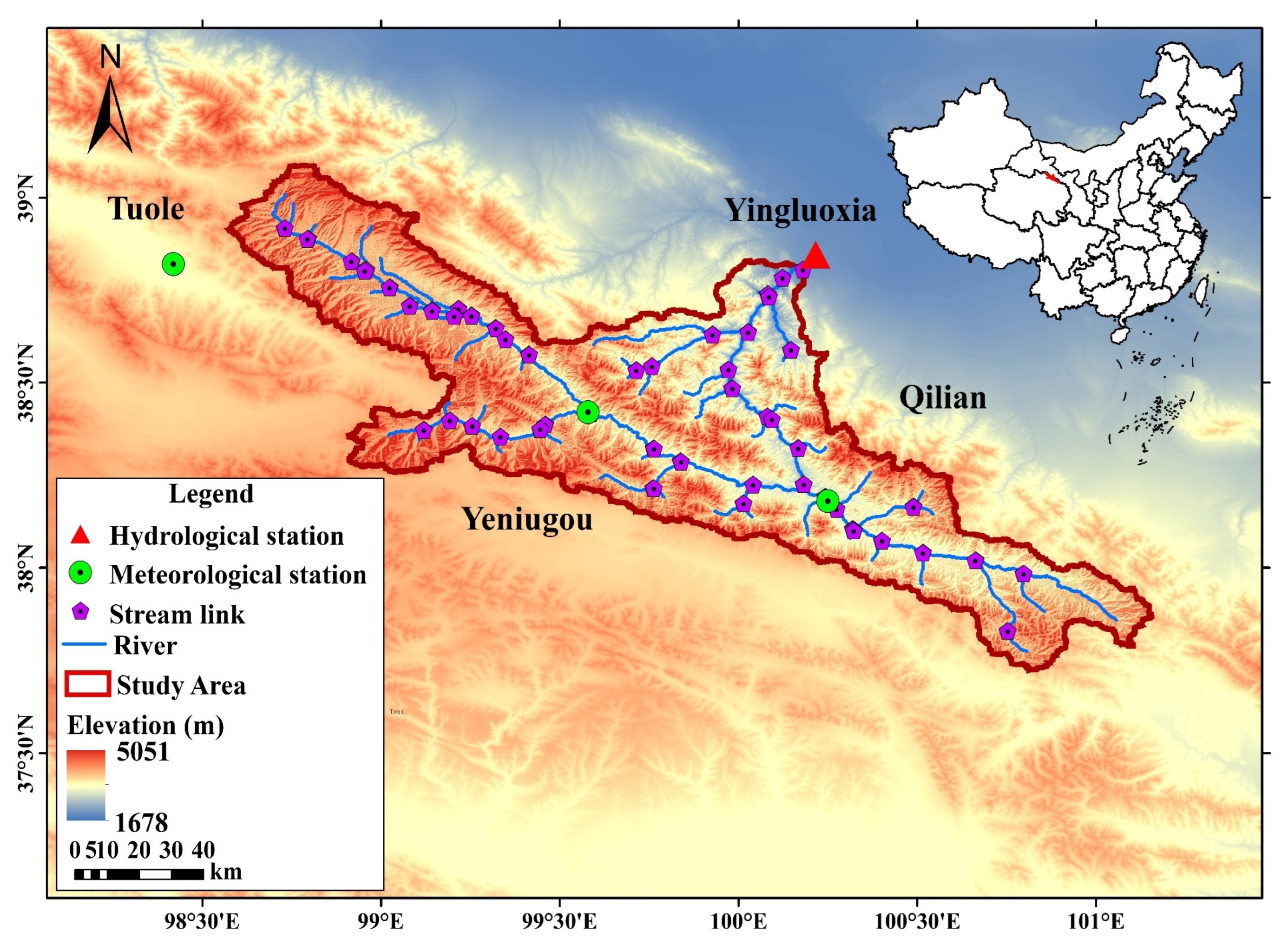
2.1. Study Area
2.2. Historical Data
2.3. Future Meteorological Data
2.4. SWAT Model
2.5. Model Calibration, Validation, and Performance Evaluation
2.6. Bias Correction of GCMs
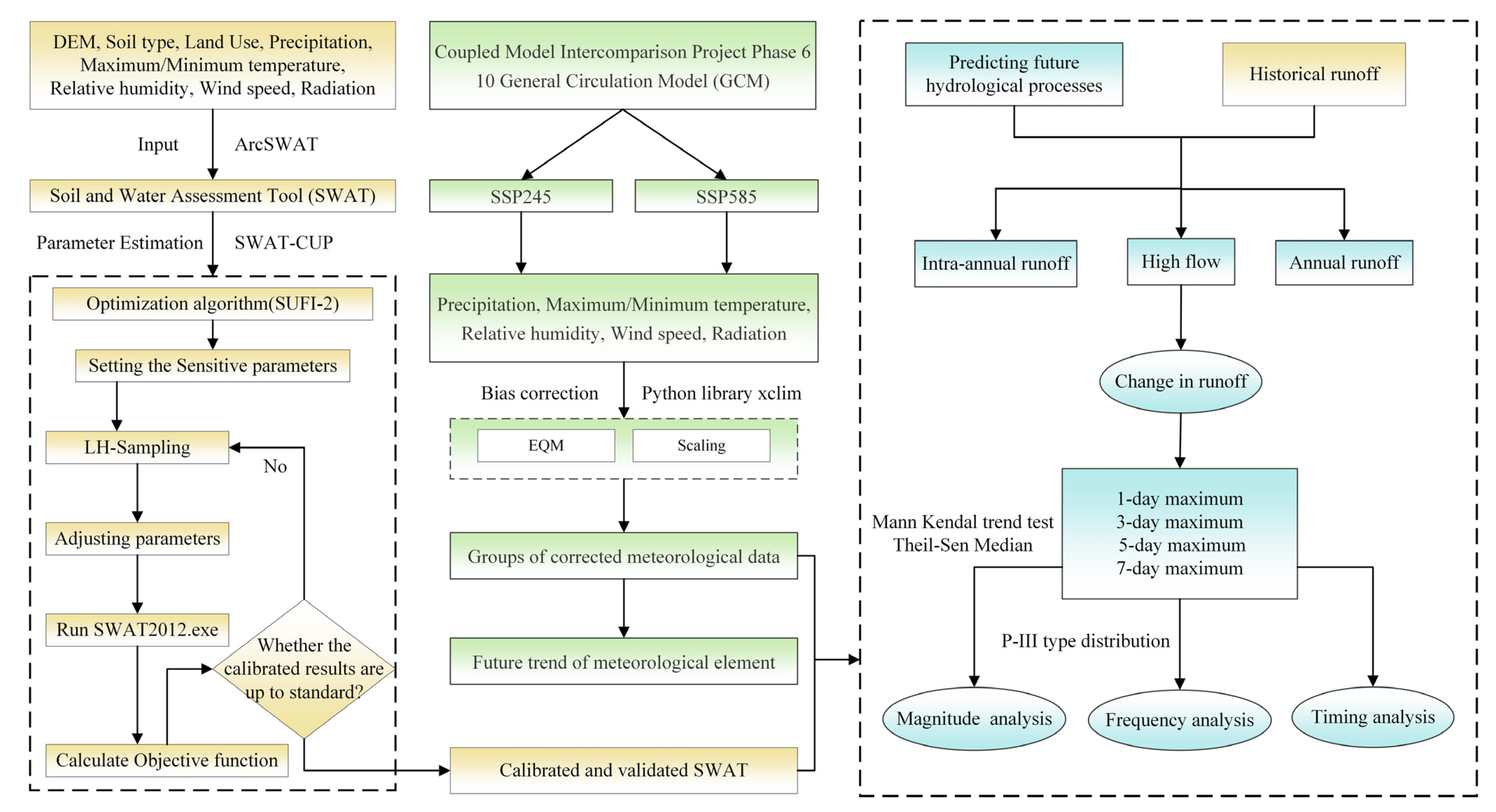
2.7. Framework
3. Results
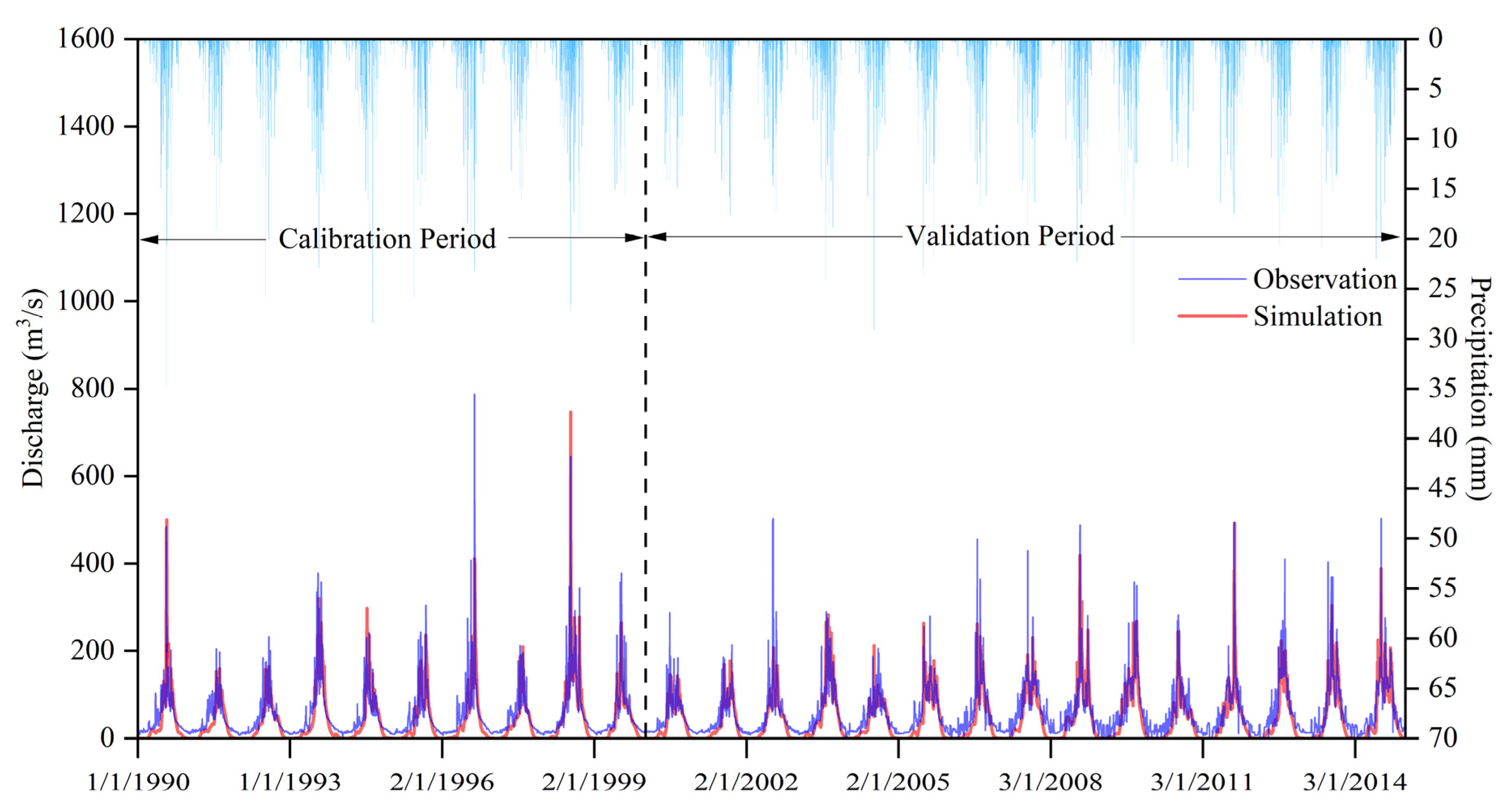
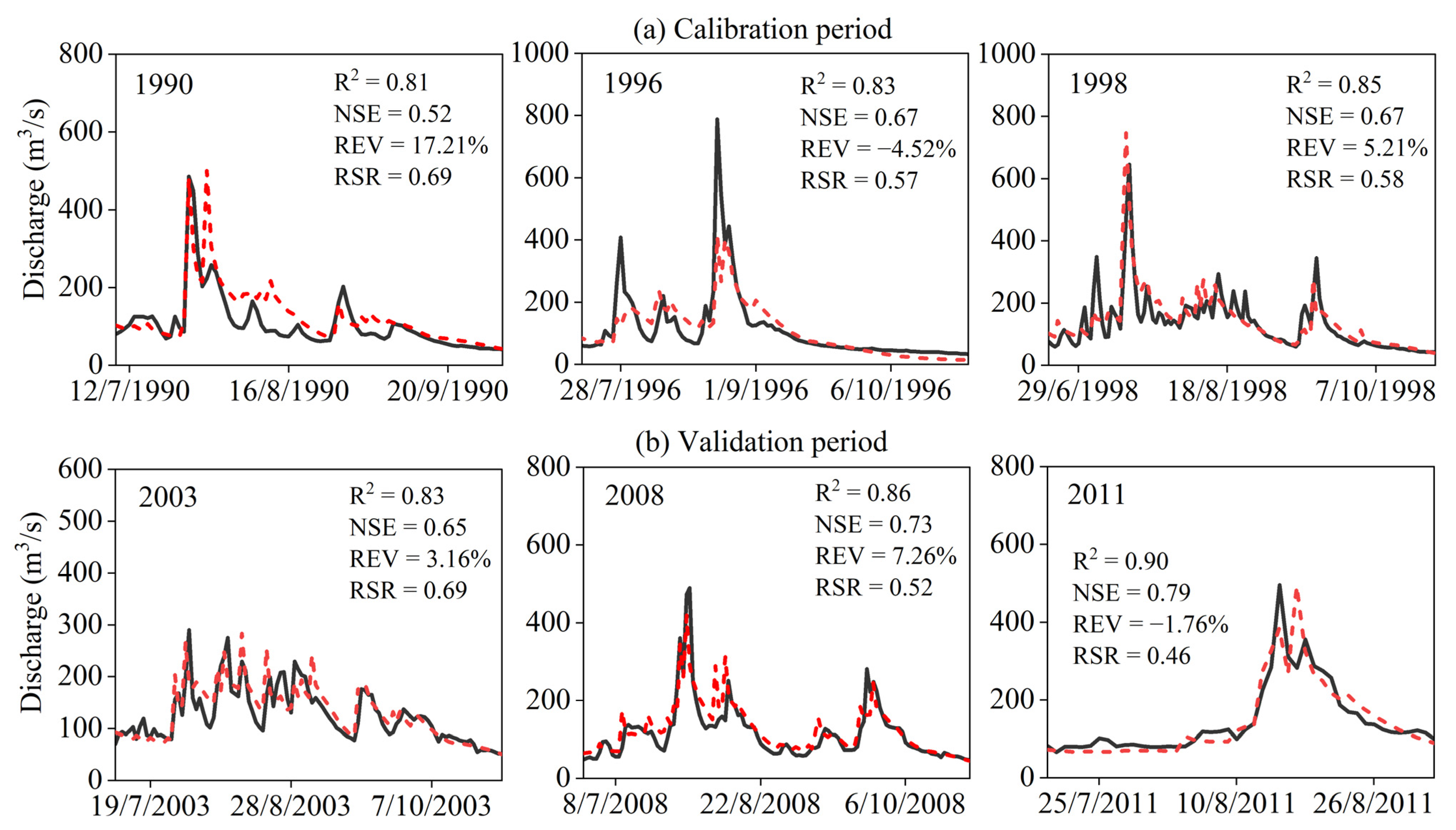
3.1. SWAT Model Calibration and Validation
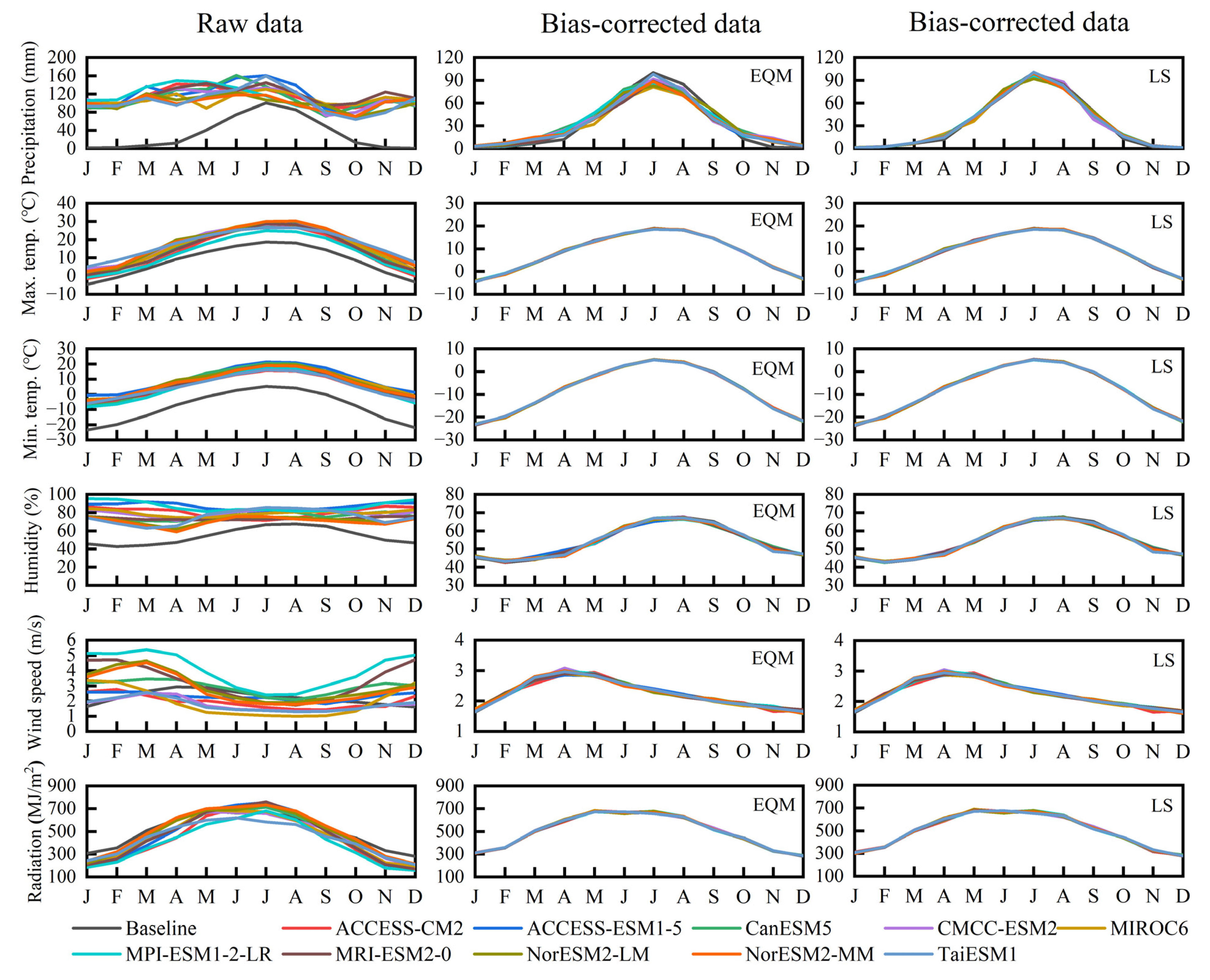
3.2. Bias Correction of GCM Outputs
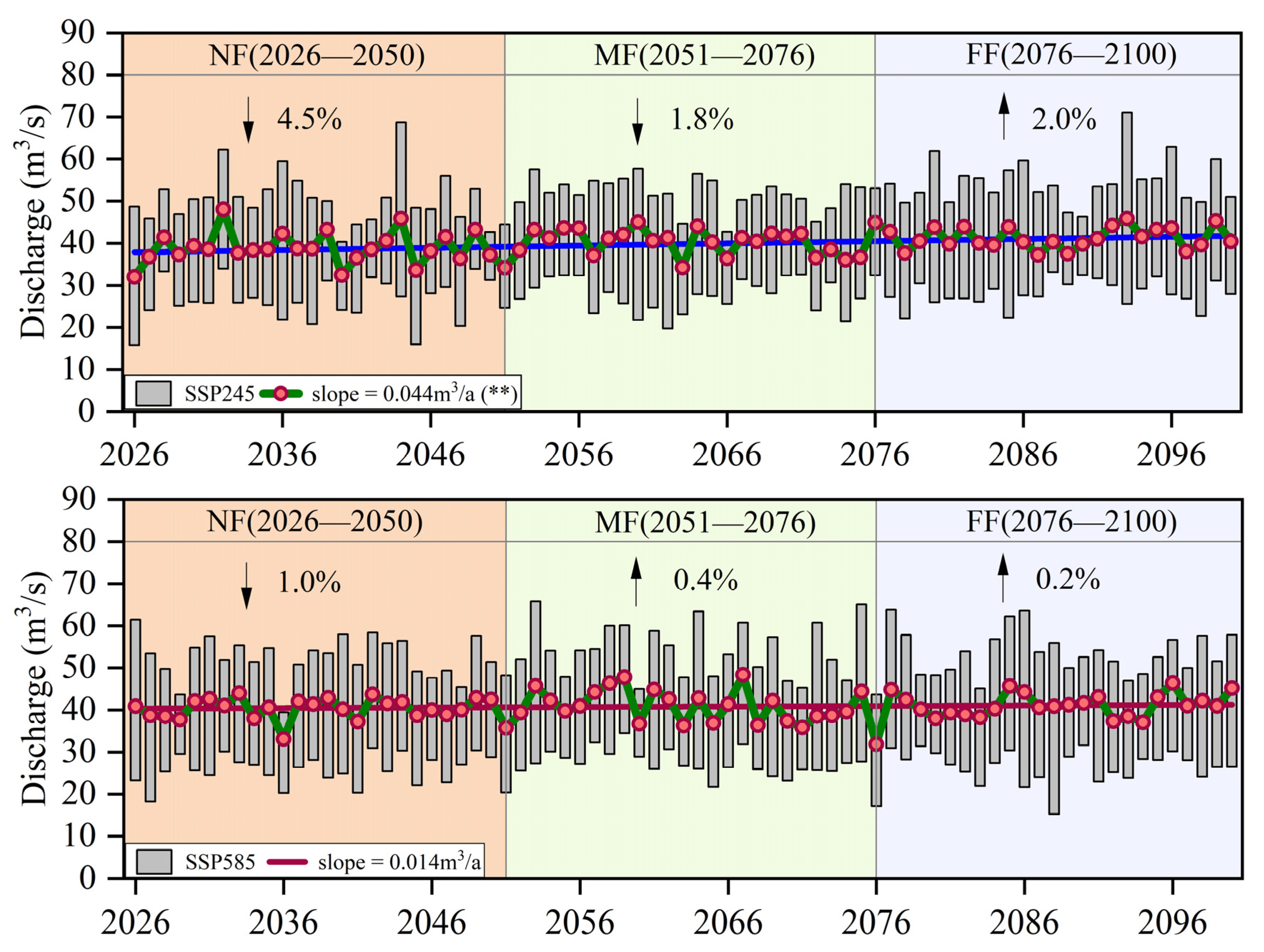
3.3. Runoff Projection
3.3.1. Annual and Intra-Annual Runoff
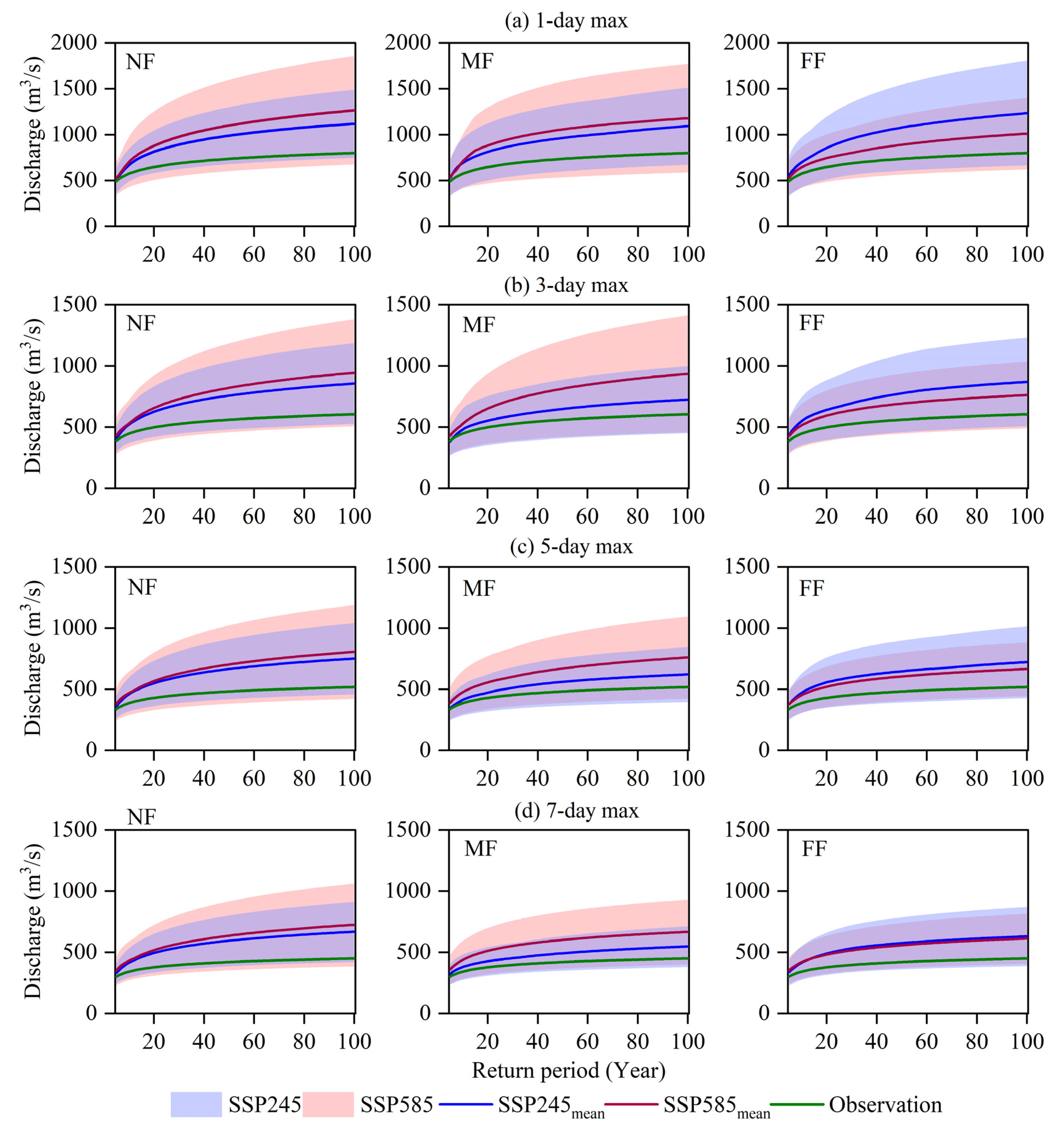
3.3.2. Magnitude of Floods
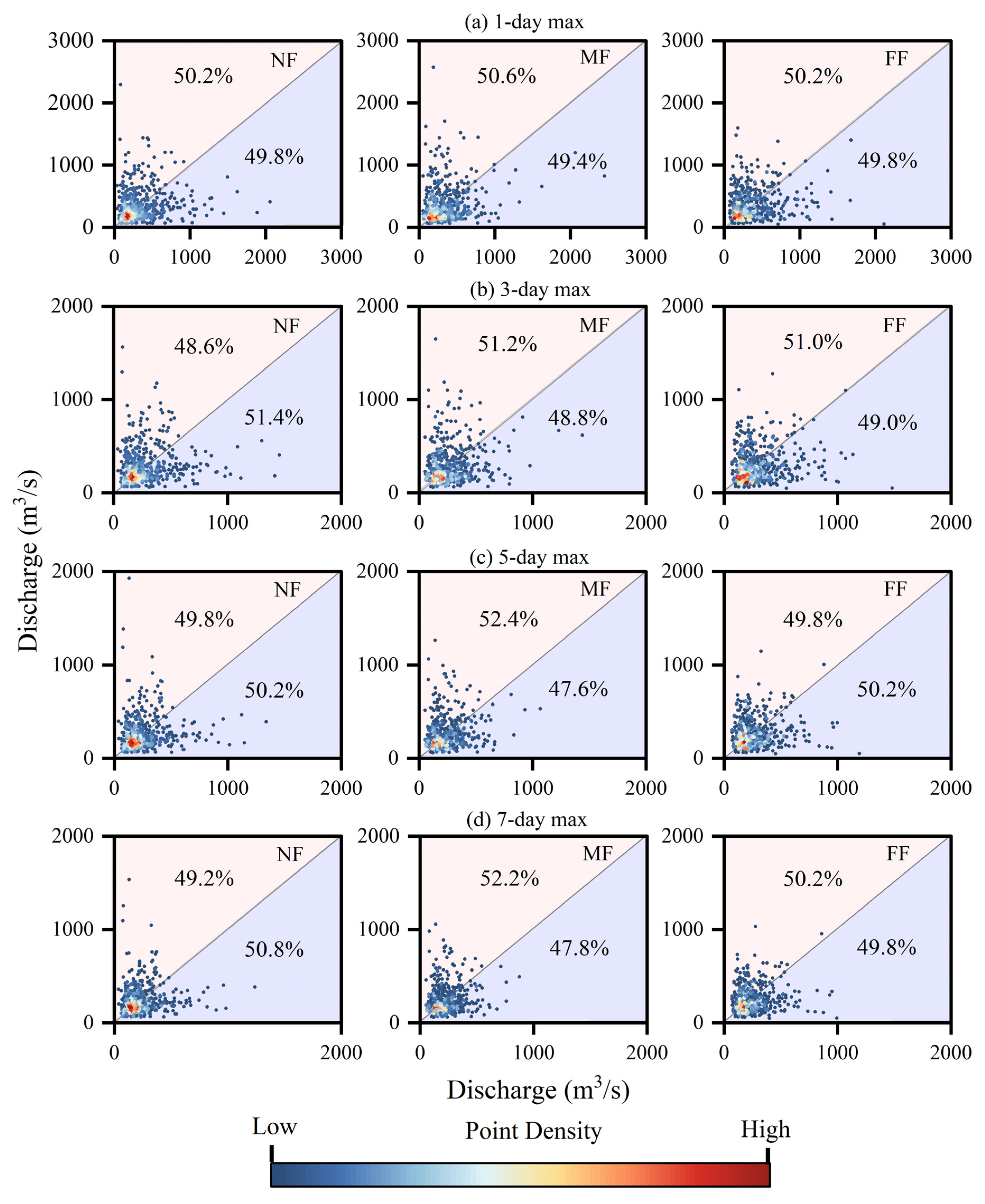
3.3.3. Frequency of Floods
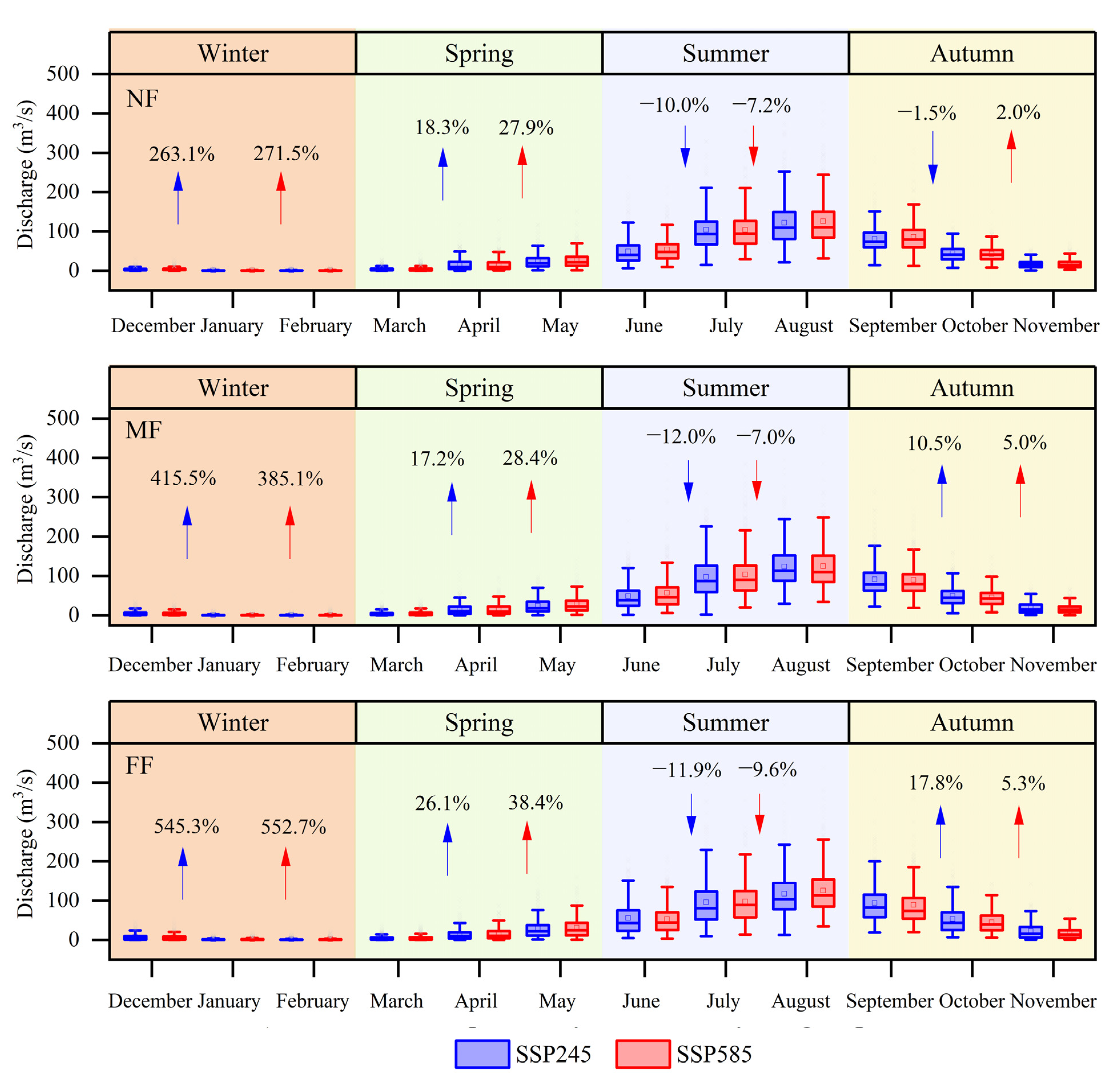
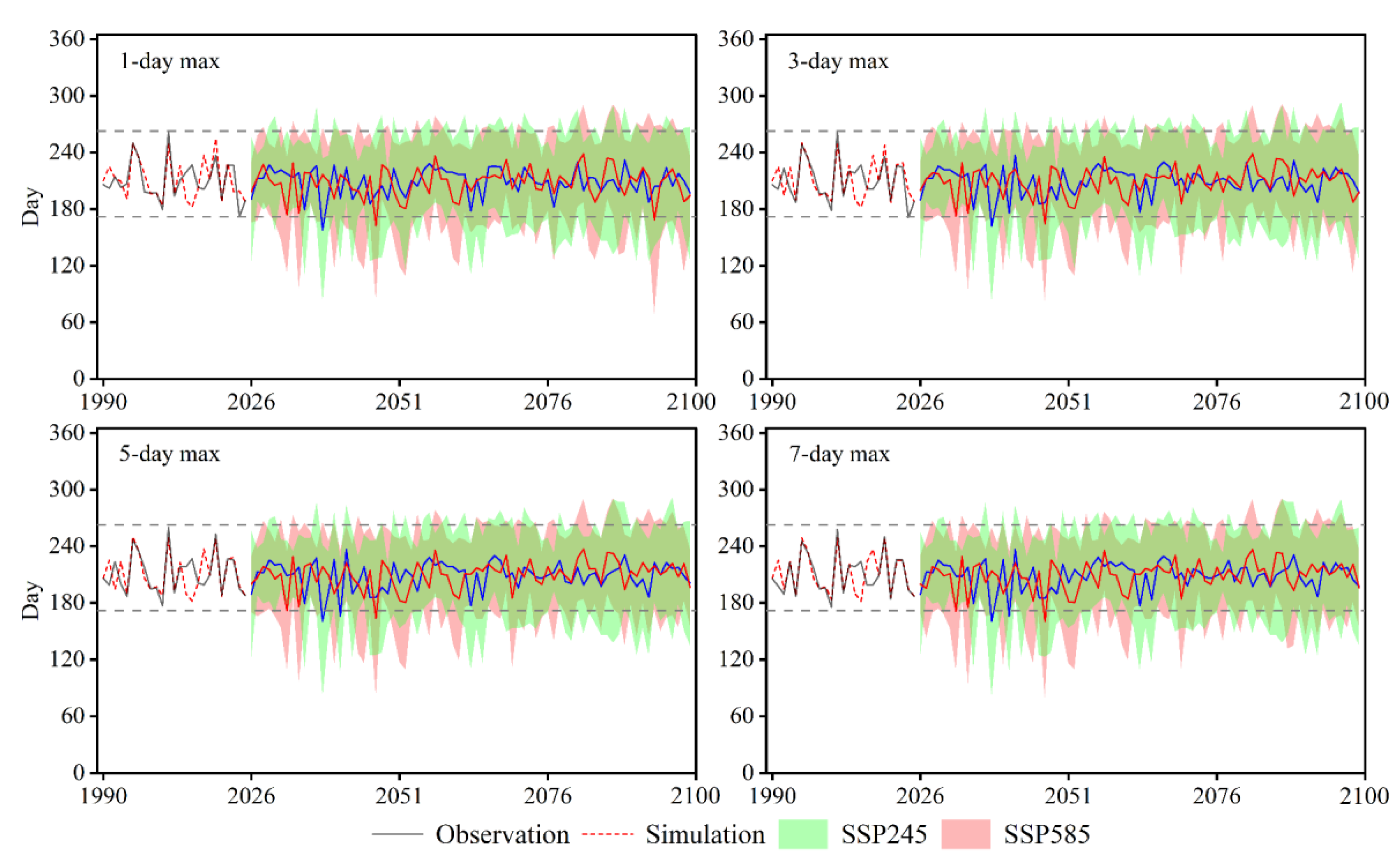
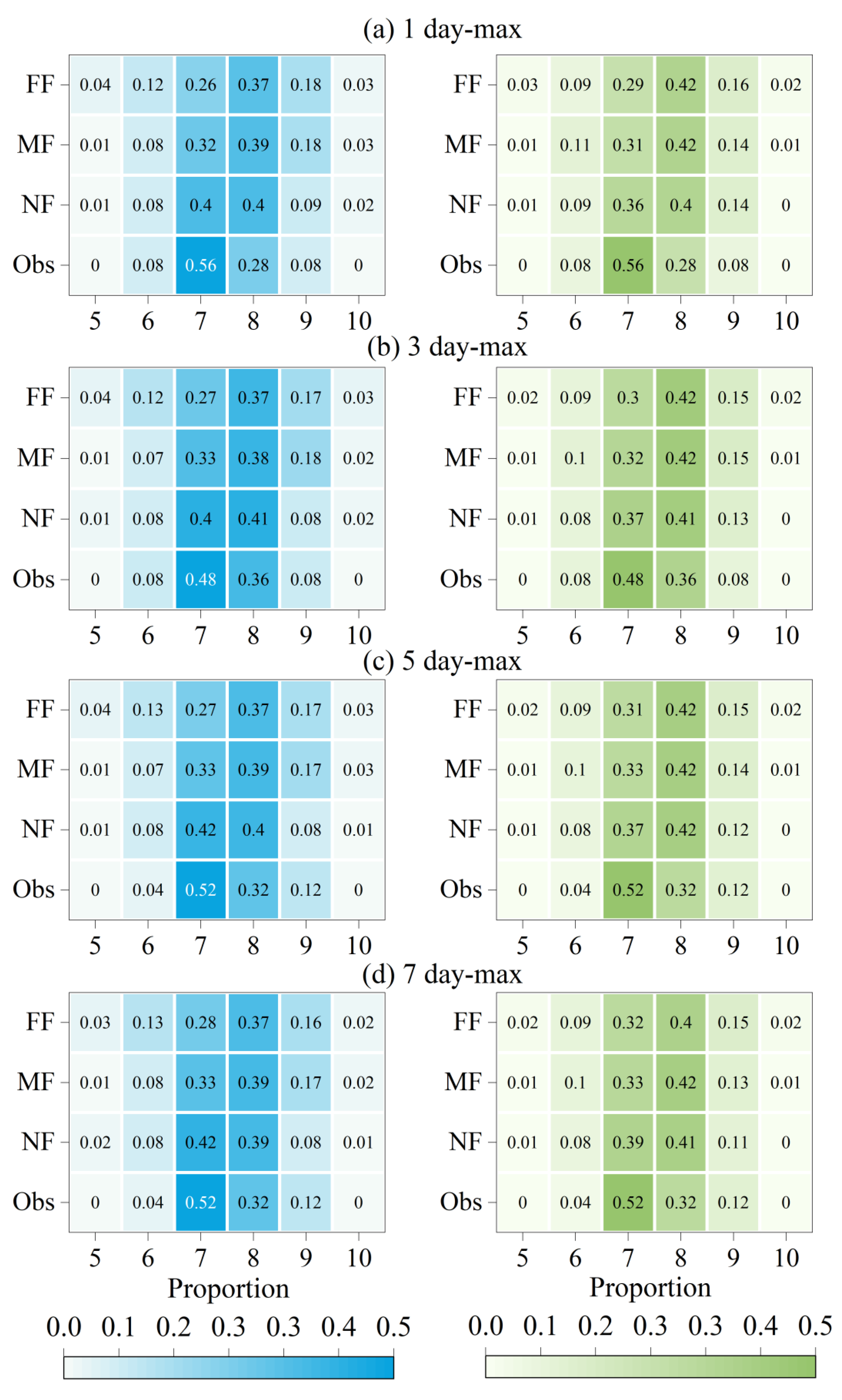
3.3.4. Timing of Floods
4. Discussion
4.1. Impacts of Climate Change on Annual and Intra-Annual Runoff
4.2. Impact of Climate Change on Floods
5. Conclusions
- (1)
- Climate change will affect the annual and intra-annual runoff in the basin. The change in the annual average runoff will be −4.5% (NF), −1.8% (MF), and +2.0% (FF) under the SSP245 scenario and −1.0% (NF), +0.4% (MF), and +0.2% (FF) under the SSP585 scenario. Winter and spring runoff is projected to increase due to more precipitation and snowmelt, whereas summer runoff is projected to decrease due to less rainfall and snowmelt and more evapotranspiration.
- (2)
- The MMEA’s projections show that the basin will experience higher flood magnitudes in the future. The 1-day maximum flow is expected to increase the most under the SSP245 and SSP585 scenarios (61.9% and 66.4%, respectively) compared to the historical period. The 3-day, 5-day, and 7-day maximum flow rates are also projected to increase under both scenarios, with increases ranging from 18.7% to 38.5%.
- (3)
- The flood frequency is projected to increase in the future, particularly in the NF period. The 1-day maximum flow is expected to increase by 44.72% and 63.72% under the SSP245 and SSP585 scenarios, respectively.
- (4)
- The flood timing is also expected to change, with the highest probability occurring from July to August. Additionally, there will be more flood events occurring in other months in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood Risk and Climate Change: Global and Regional. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Barredo, J.I. Natural Hazards and Earth System Sciences Normalised Flood Losses in Europe: 1970–2006. Hazards Earth Syst. Sci. 2009, 9, 97–104. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Woods, R.A.; Hutton, C.J.; Sivapalan, M. Dominant Flood Generating Mechanisms across the United States. Geophys. Res. Lett. 2016, 43, 4382–4390. [Google Scholar] [CrossRef]
- Mitigation of Climate Change Climate Change 2022 Working Group III Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2022; ISBN 9789291691609.
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM Precipitation to the Station Scale Using Statistical Transformations – A Comparison of Methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Felfelani, F.; Satoh, Y.; Boulange, J.; Burek, P.; Gädeke, A.; Gerten, D.; Gosling, S.N.; Grillakis, M.; Gudmundsson, L.; et al. Global Terrestrial Water Storage and Drought Severity under Climate Change. Nat. Clim. Chang. 2021, 11, 226–233. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, S.; Xia, J.; Zhan, C.; Cai, W.; Wang, W.; Luo, X.; Chen, N.; Li, J. Analysis of Drought and Flood Alternation and Its Driving Factors in the Yangtze River Basin under Climate Change. Atmos. Res. 2022, 270, 105536. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Li, K.; Yang, Y.; Liu, J.; Liu, Z.; Han, C. Trends and Variability in Flood Magnitude: A Case Study of the Floods in the Qilian Mountains, Northwest China. Atmosphere 2023, 14, 557. [Google Scholar] [CrossRef]
- Ekolu, J.; Dieppois, B.; Sidibe, M.; Eden, J.M.; Tramblay, Y.; Villarini, G.; Peña-Angulo, D.; Mahé, G.; Paturel, J.E.; Onyutha, C.; et al. Long-Term Variability in Hydrological Droughts and Floods in Sub-Saharan Africa: New Perspectives from a 65-Year Daily Streamflow Dataset. J. Hydrol. 2022, 613, 128359. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, Z.; Cui, Y.; Su, Y.; Tang, Y.; Luo, S.; Liu, L.; Zhou, Y.; Dong, J.; Wang, W.; et al. Prediction of Drought/Flood Intensities Based on a 500-Year Time Series in Three Different Climate Provinces of China. Reg. Environ. Chang. 2022, 22, 80. [Google Scholar] [CrossRef]
- Tabari, H.; Abghari, H.; Hosseinzadeh Talaee, P. Temporal Trends and Spatial Characteristics of Drought and Rainfall in Arid and Semiarid Regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Konisky, D.M.; Hughes, L.; Kaylor, C.H. Extreme Weather Events and Climate Change Concern. Clim. Chang. 2016, 134, 533–547. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Jiapaer, G.; Ndayisaba, F.; Jiang, L.; Kurban, A.; De Maeyer, P. Spatial and Temporal Characteristics of Droughts in Central Asia during 1966–2015. Sci. Total Environ. 2018, 624, 1523–1538. [Google Scholar] [CrossRef]
- Zhao, Y.; Weng, Z.; Chen, H.; Yang, J. Analysis of the Evolution of Drought, Flood, and Drought-Flood Abrupt Alternation Events under Climate Change Using the Daily SWAP Index. Water 2020, 12, 1969. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, P.; Zhang, Y.; Cheng, L.; Song, J.; Fu, G.; Wang, Y.; Liu, Q.; Lyu, S.; Qi, S.; et al. Long-Term Baseflow Responses to Projected Climate Change in the Weihe River Basin, Loess Plateau, China. Remote Sens. 2022, 14, 5097. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Schellnhuber, H.-J. Floods in the IPCC TAR Perspective. Nat. Hazards 2004, 31, 111–128. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, P.; Zhang, R.; Zhao, J.; Si, W.; Fang, Y.; Zhang, N. The Changing Precipitation Storm Properties under Future Climate Change. Hydrol. Res. 2023, 54, 580–590. [Google Scholar] [CrossRef]
- Eingrüber, N.; Korres, W. Climate Change Simulation and Trend Analysis of Extreme Precipitation and Floods in the Mesoscale Rur Catchment in Western Germany until 2099 Using Statistical Downscaling Model (SDSM) and the Soil & Water Assessment Tool (SWAT Model). Sci. Total Environ. 2022, 838, 155775. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Li, H.; Li, K.; Liu, J.; Liu, G. Detection and Attribution of Trends in Flood Frequency under Climate Change in the Qilian Mountains, Northwest China. J. Hydrol. Reg. Stud. 2022, 42, 101153. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Zhao, B.; Ma, T.; Lu, W.; Santisirisomboon, J. Future Changes in High and Low Flows under the Impacts of Climate and Land Use Changes in the Jiulong River Basin of Southeast China. Atmosphere 2022, 13, 150. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, Y.; Chen, Y.; Zhang, Q. Impact of Climate Change on the Hydrological Regime of the Yarkant River Basin, China: An Assessment Using Three SSP Scenarios of CMIP6 GCMs. Remote Sens. 2022, 14, 115. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Dahri, Z.H.; Querner, E.P.; Khan, A.; Hofstra, N. Impact of Climate Change on Flood Frequency and Intensity in the Kabul River Basin. Geosciences 2018, 8, 114. [Google Scholar] [CrossRef]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying Uncertainty Sources in an Ensemble of Hydrological Climate-Impact Projections. Water Resour. Res. 2013, 49, 1523–1536. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall Uncertainty Study of the Hydrological Impacts of Climate Change for a Canadian Watershed. Water Resour. Res. 2011, 47, W12509. [Google Scholar] [CrossRef]
- Wilby, R.L.; Harris, I. A Framework for Assessing Uncertainties in Climate Change Impacts: Low-Flow Scenarios for the River Thames, UK. Water Resour. Res. 2006, 42, W02419. [Google Scholar] [CrossRef]
- Addor, N.; Rössler, O.; Köplin, N.; Huss, M.; Weingartner, R.; Seibert, J. Robust Changes and Sources of Uncertainty in the Projected Hydrological Regimes of Swiss Catchments. Water Resour. Res. 2014, 50, 7541–7562. [Google Scholar] [CrossRef]
- Chegwidden, O.S.; Nijssen, B.; Rupp, D.E.; Arnold, J.R.; Clark, M.P.; Hamman, J.J.; Kao, S.C.; Mao, Y.; Mizukami, N.; Mote, P.W.; et al. How Do Modeling Decisions Affect the Spread Among Hydrologic Climate Change Projections? Exploring a Large Ensemble of Simulations Across a Diversity of Hydroclimates. Earths Future 2019, 7, 623–637. [Google Scholar] [CrossRef]
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of High Streamflow Extremes in Climate Change Studies: How Do We Calibrate Hydrological Models? Hydrol. Earth Syst. Sci. 2022, 26, 3863–3883. [Google Scholar] [CrossRef]
- Beckers, J.; Smerdon, B.; Wilson, M. FORREX. Review of Hydrologic Models for Forest Management and Climate Change Applications in British Columbia and Alberta. Forrex Ser. 2009, 25, 29–38. [Google Scholar]
- Nikam, B.R.; Garg, V.; Jeyaprakash, K.; Gupta, P.K.; Srivastav, S.K.; Thakur, P.K.; Aggarwal, S.P. Analyzing Future Water Availability and Hydrological Extremes in the Krishna Basin under Changing Climatic Conditions. Arab. J. Geosci. 2018, 11, 581. [Google Scholar] [CrossRef]
- Jackson, B.; Mcintyre, N.; Pechlivanidis, I.G.; Jackson, B.M.; Mcintyre, N.R.; Wheater, H.S. Catchment Scale Hydrological Modelling: A Review of Model Types, Calibration Approaches and Uncertainty Analysis Methods in the Context of Recent Developments in Technology and Applications. Artic. Glob. NEST Int. J. 2011, 13, 193–214. [Google Scholar] [CrossRef]
- The CMIP6 Landscape. Nat. Clim. Chang. 2019, 9, 727. [CrossRef]
- Pascoe, C.; Lawrence, B.N.; Guilyardi, E.; Juckes, M.; Taylor, K.E. Documenting Numerical Experiments in Support of the Coupled Model Intercomparison Project Phase 6 (CMIP6). Geosci. Model Dev. 2020, 13, 2149–2167. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q.; Wang, J.; Feng, Y.; Shao, Q. Impacts of Projected Climate Change on Runoff in Upper Reach of Heihe River Basin Using Climate Elasticity Method and GCMs. Sci. Total Environ. 2020, 716, 137072. [Google Scholar] [CrossRef]
- Zhang, A.; Liu, W.; Yin, Z.; Fu, G.; Zheng, C. How Will Climate Change Affect the Water Availability in the Heihe River Basin, Northwest China? J. Hydrometeorol. 2016, 17, 1517–1542. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Li, Z.; Lv, X. Responses of Runoff and Its Extremes to Climate Change in the Upper Catchment of the Heihe River Basin, China. Atmosphere 2023, 14, 539. [Google Scholar] [CrossRef]
- Jiménez-Navarro, I.C.; Jimeno-Sáez, P.; López-Ballesteros, A.; Pérez-Sánchez, J.; Senent-Aparicio, J. Impact of Climate Change on the Hydrology of the Forested Watershed That Drains to Lake Erken in Sweden: An Analysis Using Swat+ and Cmip6 Scenarios. Forests 2021, 12, 1803. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, L.; Xu, Z. An Integrated Modelling Approach Inmountainous Watershed of Heihe River Basin, Northwest China. Nat. Resour. 2014, 5, 90–98. [Google Scholar] [CrossRef]
- Song, X.; Liu, Y.; Zhong, F.; Deng, X.; Qi, Y.; Zhang, J.; Zhang, R.; Zhang, Y. Payment Criteria and Mode for Watershed Ecosystem Services: A Case Study of the Heihe River Basin, Northwest China. Sustainability 2020, 12, 6177. [Google Scholar] [CrossRef]
- Zhang, A.; Zheng, C.; Wang, S.; Yao, Y. Analysis of Streamflow Variations in the Heihe River Basin, Northwest China: Trends, Abrupt Changes, Driving Factors and Ecological Influences. J. Hydrol. Reg. Stud. 2015, 3, 106–124. [Google Scholar] [CrossRef]
- Luo, K.; Tao, F.; Deng, X.; Moiwo, J.P. Changes in Potential Evapotranspiration and Surface Runoff in 1981–2010 and the Driving Factors in Upper Heihe River Basin in Northwest China. Hydrol. Process. 2017, 31, 90–103. [Google Scholar] [CrossRef]
- Shang, X.; Jiang, X.; Jia, R.; Wei, C. Land Use and Climate Change Effects on Surface Runoff Variations in the Upper Heihe River Basin. Water 2019, 11, 344. [Google Scholar] [CrossRef]
- Shi, Z.; Dong, X. Study on Natural Disasters in Heihe River Basin in Historical Period. J. Dunhuang Stud. 2018, 102, 141–145. [Google Scholar] [CrossRef]
- Ren, Z.; Lu, Y.; Yang, D. Drought and Flood Disasters and Rebuilding of Precipitation Sequence in Heihe River Basin in the Past 2000 Years. J. Arid Land Resour. Environ. 2010, 24, 91–95. [Google Scholar] [CrossRef]
- Xia, T.; Zhang, Z. An Analysis of Drought and Flood Disasters in the Heihe River Basin Based on Historical Documents. J. Glaciol. Geocryol. 2017, 39, 490–497. [Google Scholar]
- Sharafati, A.; Pezeshki, E. A Strategy to Assess the Uncertainty of a Climate Change Impact on Extreme Hydrological Events in the Semi-Arid Dehbar Catchment in Iran. Theor. Appl. Clim. 2020, 139, 389–402. [Google Scholar] [CrossRef]
- Kumar, D.; Bhattacharjya, R.K. Evaluating Two GIS-Based Semi-Distributed Hydrological Models in the Bhagirathi-Alkhnanda River Catchment in India. Water Policy 2020, 22, 991–1014. [Google Scholar] [CrossRef]
- Teklay, A.; Dile, Y.T.; Asfaw, D.H.; Bayabil, H.K.; Sisay, K. Impacts of Climate and Land Use Change on Hydrological Response in Gumara Watershed, Ethiopia. Ecohydrol. Hydrobiol. 2021, 21, 315–332. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical Bias Correction for Daily Precipitation in Regional Climate Models over Europe. Theor. Appl. Clim. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Gutjahr, O.; Heinemann, G. Comparing Precipitation Bias Correction Methods for High-Resolution Regional Climate Simulations Using COSMO-CLM: Effects on Extreme Values and Climate Change Signal. Theor. Appl. Clim. 2013, 114, 511–529. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Van Deursen, W. Estimates of Future Discharges of the River Rhine Using Two Scenario Methodologies: Direct versus Delta Approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Amengual, A.; Homar, V.; Romero, R.; Alonso, S.; Ramis, C. A Statistical Adjustment of Regional Climate Model Outputs to Local Scales: Application to Platja de Palma, Spain. J. Clim. 2012, 25, 939–957. [Google Scholar] [CrossRef]
- Wilcke, R.A.I.; Mendlik, T.; Gobiet, A. Multi-Variable Error Correction of Regional Climate Models. Clim. Chang. 2013, 120, 871–887. [Google Scholar] [CrossRef]
- Déqué, M. Frequency of Precipitation and Temperature Extremes over France in an Anthropogenic Scenario: Model Results and Statistical Correction According to Observed Values. Glob. Planet. Chang. 2007, 57, 16–26. [Google Scholar] [CrossRef]
- Steinman, B.A.; Mann, M.E.; Miller, S.K. Atlantic and Pacific Multidecadal Oscillations and Northern Hemisphere Temperatures. Science 2015, 347, 988–991. [Google Scholar] [CrossRef]
- Lin, K.; Lv, F.; Chen, L.; Singh, V.P.; Zhang, Q.; Chen, X. Xinanjiang Model Combined with Curve Number to Simulate the Effect of Land Use Change on Environmental Flow. J. Hydrol. 2014, 519, 3142–3152. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Xu, C.Y.; Zhang, J.; Ye, C. Hydrological Design of Nonstationary Flood Extremes and Durations in Wujiang River, South China: Changing Properties, Causes, and Impacts. Math. Probl. Eng. 2013, 2013, 52746. [Google Scholar] [CrossRef]
- Gao, C.; Booij, M.J.; Xu, Y.P. Development and Hydrometeorological Evaluation of a New Stochastic Daily Rainfall Model: Coupling Markov Chain with Rainfall Event Model. J. Hydrol. 2020, 589, 125337. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wu, F.; Zhan, J.; Su, H.; Yan, H.; Ma, E. Scenario-Based Impact Assessment of Land Use/Cover and Climate Changes on Watershed Hydrology in Heihe River Basin of Northwest China. Adv. Meteorol. 2015, 2015, 410198. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Fan, Y.; Wang, H.; Deng, H. Progress and Prospects of Climate Change Impacts on Hydrology in the Arid Region of Northwest China. Environ. Res. 2015, 139, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, R.; Han, C.; Yang, Y.; Liu, J.; Liu, Z.; Song, Y. Changes in River Discharge in Typical Mountain Permafrost Catchments, Northwestern China. Quat. Int. 2019, 519, 32–41. [Google Scholar] [CrossRef]
- Piniewski, M.; Szczes’niak, M.; Huang, S.; Kundzewicz, Z.W. Projections of Runoff in the Vistula and the Odra River Basins with the Help of the SWAT Model. Hydrol. Res. 2018, 49, 303–317. [Google Scholar] [CrossRef]
- Islam, S.A.; Bari, M.A.F.; Anwar, A.H.M. Hydrologic Impact of Climate Change on Murray-Hotham Catchment of Western Australia: A Projection of Rainfall-Runoff for Future Water Resources Planning. Hydrol. Earth Syst. Sci. 2014, 18, 3591–3614. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes toward Earlier Streamflow Timing across Western North America. J. Clim. 2005, 18, 1136–1155. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes in Snowmelt Runoff Timing in Western North America under a “Business as Usual” Climate Change Scenario. Clim. Chang. 2004, 62, 217–232. [Google Scholar] [CrossRef]
- Laiti, L.; Mallucci, S.; Piccolroaz, S.; Bellin, A.; Zardi, D.; Fiori, A.; Nikulin, G.; Majone, B. Testing the Hydrological Coherence of High-Resolution Gridded Precipitation and Temperature Data Sets. Water Resour. Res. 2018, 54, 1999–2016. [Google Scholar] [CrossRef]
- Chan, W.C.H.; Thompson, J.R.; Taylor, R.G.; Nay, A.E.; Ayenew, T.; MacDonald, A.M.; Todd, M.C. Uncertainty Assessment in River Flow Projections for Ethiopia’s Upper Awash Basin Using Multiple GCMs and Hydrological Models. Hydrol. Sci. J. 2020, 65, 1720–1737. [Google Scholar] [CrossRef]
- Vetter, T.; Reinhardt, J.; Flörke, M.; van Griensven, A.; Hattermann, F.; Huang, S.; Koch, H.; Pechlivanidis, I.G.; Plötner, S.; Seidou, O.; et al. Evaluation of Sources of Uncertainty in Projected Hydrological Changes under Climate Change in 12 Large-Scale River Basins. Clim. Chang. 2017, 141, 419–433. [Google Scholar] [CrossRef]

| Data Type | Data Source | Resolution |
|---|---|---|
| Digital Elevation Model | https://www.gscloud.cn (accessed on 26 March 2021). | 90 m |
| Land-use data in 2000 | https://www.resdc.cn/DOI/DOI.aspx?DOIID=54 (accessed on 19 April 2021). | 1 km |
| Soil type | http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/en/ (accessed on 19 April 2021)). | 1 km |
| Type of Stations | Site Name | Longitude and Latitude | Data Description |
|---|---|---|---|
| Meteorological stations | Tuole | 98.42° E, 38.82° N | Daily air pressure, wind speed, average temperature, maximum temperature, minimum temperature, relative humidity, precipitation, sunshine hours, with a time span of 1987–2014 |
| Yeniugou | 99.58° E, 38.42° N | ||
| Qilian | 100.25° E, 38.18° N | ||
| Hydrological stations | Yingluoxia | 100.18° E, 38.82° N | Daily runoff data with a time span of 1987–2014 |
| Name of GCM | Country | Resolution | Frequency |
|---|---|---|---|
| ACCESS-CM2 | Australia | 1.875° × 1.25° | daily |
| ACCESS-ESM1-5 | Australia | 1.875° × 1.25° | daily |
| CanESM5 | Canadian | 2.8125° × 2.8125° | daily |
| CMCC-ESM2 | Italy | 1.25° × 0.9375° | daily |
| MIROC6 | Japan | 1.40625° × 1.40625° | daily |
| MPI-ESM1-2-LR | Germany | 1.875° × 1.875° | daily |
| MRI-ESM2-0 | Japan | 1.125° × 1.125° | daily |
| NorESM2-LM | Norway | 2.5° × 1.875° | daily |
| NorESM2-MM | Norway | 1.25° × 0.9375° | daily |
| TaiESM | Taipei | 1.25° × 0.9375° | daily |
| Parameter | Description | Range | Calibration Results |
|---|---|---|---|
| v__SFTMP.bsn | Snowfall temperature | [−5, 5] | 4.6587 |
| v__SMTMP.bsn | Snow melt base temperature | [−5, 5] | 3.2865 |
| v__SURLAG.bsn | Surface runoff lag time | [1, 24] | 15.2123 |
| v__ALPHA_BF.gw | Baseflow alpha factor | [0, 1] | 0.2937 |
| r__CN2.mgt | Initial SCS CN II value | [−0.5, 0.5] | 0.1681 |
| v__ESCO.hru | Soil evaporation compensation factor | [0.01, 1] | 0.3156 |
| r__SOL_K.sol | The soil layer’s available water capacity | [−0.7, 0.7] | 0.5842 |
| r__SOL_AWC.sol | Saturated hydraulic conductivity | [−0.7, 0.7] | 0.6123 |
| v__GWQMN.gw | Threshold depth of water in the shallow aquifer required for return flow to occur | [0, 5000] | 3046.6331 |
| v__GW_REVAP.gw | Groundwater “revap” coefficient | [0.02, 0.2] | 0.0874 |
| v__CH_K2.rte | Effective hydraulic conductivity | [0, 100] | 59.0481 |
| v__CH_N2.rte | Manning’s nvalue for main channel | [0, 0.3] | 0.2455 |
| Period | R2 | NSE | PBIAS | RSR |
|---|---|---|---|---|
| Calibration | 0.87 | 0.68 | −23.81% | 0.56 |
| Validation | 0.89 | 0.71 | −26.31% | 0.54 |
| GCMs | Methods | Precipitation | Max.temp | Mix.temp | Humidity | Wind Speed | Radiation |
|---|---|---|---|---|---|---|---|
| ACCESS-CM2 | Historical | 4.00 | 7.11 | 13.31 | 0.28 | 1.27 | 5.61 |
| Eqm | 1.60 | 4.09 | 3.88 | 0.14 | 1.12 | 3.87 | |
| LS | 1.62 | 4.69 | 4.54 | 0.11 | 1.16 | 4.67 | |
| ACCESS-ESM1-5 | Historical | 4.14 | 9.19 | 18.22 | 0.33 | 1.21 | 5.37 |
| Eqm | 1.64 | 4.09 | 3.89 | 0.13 | 1.12 | 3.88 | |
| LS | 1.59 | 4.55 | 4.25 | 0.10 | 1.09 | 4.64 | |
| CanESM5 | Historical | 3.91 | 8.43 | 15.65 | 0.25 | 1.46 | 5.44 |
| Eqm | 1.69 | 4.12 | 3.88 | 0.14 | 1.12 | 3.89 | |
| LS | 1.57 | 4.98 | 5.20 | 0.12 | 1.08 | 5.18 | |
| CMCC-ESM2 | Historical | 3.86 | 10.02 | 15.05 | 0.27 | 1.09 | 5.89 |
| Eqm | 1.70 | 4.09 | 3.95 | 0.14 | 1.12 | 3.92 | |
| LS | 1.56 | 4.52 | 4.56 | 0.11 | 0.96 | 5.75 | |
| MIROC6 | Historical | 4.07 | 8.65 | 16.23 | 0.27 | 1.46 | 5.80 |
| Eqm | 1.59 | 4.09 | 3.94 | 0.14 | 1.12 | 3.97 | |
| LS | 1.68 | 4.36 | 4.06 | 0.11 | 1.06 | 5.61 | |
| MPI-ESM1-2-LR | Historical | 4.09 | 6.42 | 13.59 | 0.34 | 2.31 | 6.44 |
| Eqm | 1.68 | 4.19 | 3.95 | 0.14 | 1.12 | 3.95 | |
| LS | 1.63 | 4.76 | 4.69 | 0.11 | 1.09 | 5.64 | |
| MRI-ESM2-0 | Historical | 4.23 | 8.11 | 15.16 | 0.23 | 1.81 | 5.76 |
| Eqm | 1.59 | 4.17 | 3.99 | 0.14 | 1.13 | 3.85 | |
| LS | 1.64 | 4.76 | 4.77 | 0.13 | 1.01 | 5.37 | |
| NorESM2-LM | Historical | 3.70 | 10.00 | 16.51 | 0.22 | 1.51 | 5.54 |
| Eqm | 1.66 | 4.10 | 3.88 | 0.14 | 1.11 | 3.88 | |
| LS | 1.58 | 4.68 | 4.49 | 0.13 | 0.99 | 5.47 | |
| NorESM2-MM | Historical | 3.73 | 10.15 | 15.90 | 0.21 | 1.43 | 5.49 |
| Eqm | 1.64 | 4.09 | 3.88 | 0.14 | 1.11 | 3.89 | |
| LS | 1.60 | 4.76 | 4.50 | 0.13 | 1.00 | 5.39 | |
| TaiESM1 | Historical | 3.77 | 9.89 | 13.65 | 0.24 | 1.10 | 6.31 |
| Eqm | 1.66 | 4.23 | 4.02 | 0.14 | 1.12 | 3.98 | |
| LS | 1.58 | 4.80 | 5.20 | 0.13 | 0.96 | 6.32 |
| Time Scale | SSP245 | SSP585 | ||||
|---|---|---|---|---|---|---|
| Trend | p-Value | Change Rate (%) | Trend | p-Value | Change Rate (%) | |
| 1-day max | ↑ | 0.127 | 61.9% | ↑ | 0.855 | 66.4% |
| 3-day max | ↑ | 0.141 | 34.3% | ↑ | 0.742 | 38.5% |
| 5-day max | ↑ | 0.154 | 22.6% | ↑ | 0.694 | 26.2% |
| 7-day max | ↑ | 0.188 | 18.7% | ↑ | 0.577 | 22.5% |
| Time Scale | Future Period | 30-Year Flood | 50-Year Flood | 80-Year Flood | 100-Year Flood | ||||
|---|---|---|---|---|---|---|---|---|---|
| SSP245 | SSP585 | SSP245 | SSP585 | SSP245 | SSP585 | SSP245 | SSP585 | ||
| 1-day max | NF | 32.34% | 46.10% | 37.97% | 54.04% | 42.64% | 60.72% | 44.72% | 63.72% |
| MF | 16.45% | 39.01% | 20.03% | 44.97% | 24.31% | 52.16% | 24.31% | 52.16% | |
| FF | 29.95% | 19.91% | 34.15% | 23.07% | 37.64% | 25.68% | 39.19% | 26.83% | |
| Mean | 26.25% | 35.01% | 30.72% | 40.69% | 34.86% | 46.19% | 36.07% | 47.57% | |
| 3-day max | NF | 30.68% | 36.97% | 35.96% | 42.79% | 40.37% | 47.66% | 42.34% | 49.84% |
| MF | 12.39% | 32.98% | 15.30% | 37.98% | 17.71% | 42.16% | 18.79% | 44.02% | |
| FF | 27.66% | 22.29% | 31.63% | 25.57% | 34.93% | 28.29% | 36.39% | 29.50% | |
| Mean | 23.58% | 30.75% | 27.63% | 35.45% | 31.00% | 39.37% | 32.51% | 41.12% | |
| 5-day max | NF | 31.17% | 34.58% | 36.12% | 39.66% | 40.25% | 43.92% | 42.10% | 45.82% |
| MF | 11.38% | 32.23% | 13.78% | 36.74% | 15.77% | 40.49% | 16.66% | 42.16% | |
| FF | 27.05% | 23.26% | 30.61% | 26.28% | 33.58% | 28.78% | 34.90% | 29.89% | |
| Mean | 23.20% | 30.02% | 26.84% | 34.23% | 29.87% | 37.73% | 31.22% | 39.29% | |
| 7-day max | NF | 33.35% | 36.34% | 38.32% | 41.38% | 42.49% | 45.62% | 44.35% | 47.51% |
| MF | 14.41% | 35.67% | 16.88% | 40.32% | 18.94% | 44.20% | 19.86% | 45.93% | |
| FF | 29.99% | 28.29% | 33.71% | 31.64% | 36.82% | 34.43% | 38.21% | 35.67% | |
| Mean | 25.92% | 33.43% | 29.64% | 37.78% | 32.75% | 41.42% | 34.14% | 43.04% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Li, Z.; Li, X.; Li, Z. Projection and Analysis of Floods in the Upper Heihe River Basin under Climate Change. Atmosphere 2023, 14, 1083. https://doi.org/10.3390/atmos14071083
Ye Y, Li Z, Li X, Li Z. Projection and Analysis of Floods in the Upper Heihe River Basin under Climate Change. Atmosphere. 2023; 14(7):1083. https://doi.org/10.3390/atmos14071083
Chicago/Turabian StyleYe, Yingtao, Zhanling Li, Xintong Li, and Zhanjie Li. 2023. "Projection and Analysis of Floods in the Upper Heihe River Basin under Climate Change" Atmosphere 14, no. 7: 1083. https://doi.org/10.3390/atmos14071083
APA StyleYe, Y., Li, Z., Li, X., & Li, Z. (2023). Projection and Analysis of Floods in the Upper Heihe River Basin under Climate Change. Atmosphere, 14(7), 1083. https://doi.org/10.3390/atmos14071083






