Statistics of the Inertial Energy Transfer Range in d-Dimensional Turbulence (2 ≤ d ≤ 3) in a Lagrangian Renormalized Approximation

Abstract

Statistics in the inertial energy transfer range (IETR) of d-dimensional turbulence ( $2\le d\le 3$) are studied using a Lagrangian renormalized approximation (LRA). The LRA suggests that the energy spectrum in the IETR is given by $K_d{\left|\overline{\epsilon }\right|}^{2/3}{k}^{-5/3}$, where $K_d$ is a constant and $\overline{\epsilon }$ is the energy flux across wave-number k; the energy transfer is forward for $d_c<d\le 3$ but inverse for $2\le d<d_c$, where $d_c\approx 2.065$; at $d=d_c$, $K_d$ diverges and the skewness of the longitudinal velocity difference vanishes; and the d-dependence of the two-time Lagrangian velocity correlation spectra under appropriate normalization is weak in the IETR.

1. Introduction

It was at an IUTAM Symposium held at Kyoto on 1983 when the second author (Y.K.) first met Jack Herring, while it was in 1990 at Boulder when the first author (T.G.) first met him. Since then, both authors have had chances to enjoy discussions with Jack, including during the workshops of the Geophysical Turbulence Program at the National Center for Atmospheric Research and his visits to Nagoya. The discussions covered various topics, but particularly statistical theories of turbulence. Our common interests included the spectral closure theories, in particular two-point two-time closure approximations. We were inspired by his works, especially those on spectral closure approaches. The discussions with him have been friendly and stimulating.

In this paper, we consider the application of a spectral closure approach to turbulence in the d space dimension with $2\le d\le 3$. In practice, we use a spectral closure theory based on a view point of Lagrangian renormalization. The closure theory is called Lagrangian renormalized approximation (LRA) [1] here. The LRA is a two-point two-time Lagrangian closure approximation free from any adjustment parameter, and similar in this sense to the abridged Lagrangian-history direct-interaction approximation (ALHDIA) of Kraichnan [2] and strain-based ALHDIA of Kraichnan and Herring [3] and Herring and Kraichnan [4]. The equations of the LRA are simpler than those of the ALHDIA and strain-based ALHDIA.

In general, the dynamics of a fluid may be fundamentally different in different space dimension. For example, vortex stretching plays important dynamic roles in three, but not two, dimensions. It is not surprising that, given such observations, the statistics of turbulence may differ fundamentally in different space dimensions. Indeed, studies so far suggest that energy in the so-called inertial energy cascade range is transferred in opposite directions in two and three dimensions, i.e., from large to small eddies (scales) (forward) in three dimensions, but from small to large scales (backward or inverse) in two dimensions, if the turbulence has a sufficiently large Reynolds number $Re$. One may ask: What happens in spaces of noninteger dimension d between two and three dimensions?

It is difficult to realize turbulence in such noninteger dimension by experiments or numerical simulation, so that one might think that such a question is purely academic. However, the history of the statistical mechanics of critical phenomena suggests that understanding the physics of noninteger dimension may improve our understanding of physics in three (and two) dimensions, as noted by Fournier and Frisch [5] in a pioneering study of turbulence in noninteger dimension. The study of turbulence in noninteger dimension via a closure-theoretical approach may extend the field of the applications of spectral closures in which both Jack Herring and the authors were/are interested.

In this paper, we begin by considering the homogeneous and isotropic turbulences (HIT) of an incompressible fluid that obeys the Navier–Stokes (NS) equation in integer dimensions d with $d=2,3,4\cdots$. After reviewing certain exact relations in physical and wave-vector spaces of d-dimension in Section 2, we briefly review, in Section 3, the LRA equations for HIT in d-dimensions, following Gotoh et al. [6]. In the LRA equations, the parameter d representing the space dimension plays a key role. The dimension d is limited to integers in Section 2 and Section 3. In Section 4, we take a bold step; we relax d to allow noninteger values. Assuming that the LRA equations are applicable to noninteger values d, we analyze (in Section 4) the statistics in the wavenumber range wherein the energy flux across wavenumber k is independent of k. Here, we refer to this range as the inertial energy transfer range (IETR). A particular attention is paid to statistics associated with Lagrangian two-point two-time velocity correlation and the skewness factor of the longitudinal velocity increment in the ITER; two-time statistics are, in general, not captured in single time closures such as the eddy-damped quasinormal Markovian (EDQNM) approximation [7] used in [5,8].

2. Exact Relations

2.1. Navier–Stokes Equation in d-Dimension with $d=2,3,4\cdots$

We begin with the NS equation for an incompressible fluid

$$\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\nu \mathsf{\Delta }{u}_i+f_i^{ext},$$

(1)

and the incompressibility condition

$$\frac{\partial u_i}{\partial x_i}=0,$$

(2)

in d-dimensional space ($d=2,3,4\cdots$) where $u_i,x_i$ and $f_i^{ext}$ are the components of the velocity u, the position x, and the external force in the i-th Cartesian direction ($i=1,2,3,\cdots ,d$), respectively, t is the time, p is the pressure divided by the constant fluid density, and $\nu$ is the kinematic viscosity. Throughout, we employ the summation convention for repeated indices.

Multiplying Equation (1) by $u_i$ and taking the summation over i gives

$$\begin{array}{ccc}\hfill & \hfill & \frac{\partial }{\partial t}\frac{1}{2}{u}_i^2+\frac{\partial }{\partial x_j}\left[\left(\frac{1}{2}{u}_i^2+p\right)u_j\right]\hfill \\ \hfill & =\hfill & \nu \frac{\partial }{\partial x_j}\left(u_i\frac{\partial u_i}{\partial x_j}\right)-\nu \frac{\partial u_j}{\partial x_i}\frac{\partial u_j}{\partial x_i}+u_i{f}_i^{ext},\hfill \end{array}$$

(3)

under the incompressibility condition Equation (2). Integrating Equation (1) over the fluid domain V, one obtains

$$\frac{\partial }{\partial t}{\int }_V\frac{1}{2}{u}_i^2\left(\mathit{x}\right)d\mathit{x}=-{\int }_V[\epsilon \left(\mathit{x}\right)-{\epsilon }_f\left(\mathit{x}\right)]d\mathit{x},$$

(4)

where the energy dissipation rate $\epsilon \left(x\right)$ and energy injection rate ${\epsilon }_f\left(x\right)$ at position x are defined by

$$\epsilon \left(\mathit{x}\right)=\nu \frac{\partial u_j}{\partial x_i}\frac{\partial u_j}{\partial x_i},$$

(5)

$${\epsilon }_f\left(\mathit{x}\right)=u_i\left(\mathit{x}\right)f_i^{e\mathit{x}t}\left(\mathit{x}\right),$$

(6)

and the integration over the boundary surface of the domain V is assumed to be negligible. This assumption can be justified under the assumption of periodic boundary conditions, for example.

2.2. Spectral Relations

In homogeneous and isotropic turbulence (HIT), the single-time two-point velocity correlation $〈u_i(\mathit{x},t){\mathit{u}}_j({\mathit{x}}^{\prime },t)〉$ depends on x and ${\mathit{x}}^{\prime }$ only via $\mathit{r}\equiv \mathit{x}-{\mathit{x}}^{\prime }$, and its Fourier transform $Q_{ij}(\mathit{k},t)$ with respect to r may be written in the form

$$Q_{ij}(\mathit{k},t)=\frac{1}{d-1}{P}_{ij}\left(\mathit{k}\right)Q(k,t),$$

(7)

where $Q(k,t)$ depends on k only via $k\equiv \left|k\right|$ and $P_{ij}\left(\mathit{k}\right)\equiv {\delta }_{ij}-k_i{k}_j/k^2$. The Fourier transform $\widehat{\mathit{u}}\left(\mathit{k}\right)$ of $\mathit{u}\left(\mathit{r}\right)$ with respect to r is related to $\mathit{u}\left(\mathit{r}\right)$ by

$$\mathit{u}\left(\mathit{r}\right)=\int \widehat{\mathit{u}}\left(\mathit{k}\right)e^{i\mathit{k}·\mathit{r}}{d}^d\mathit{k},$$

(8)

in which the integration is over the entire k-space. The total energy $E\left(t\right)$ is given by

$$E\left(t\right)=\frac{〈{\mathit{u}}^2\left(t\right)〉}{2}={\int }_0^{\infty }E(k,t)dk,$$

(9)

where the energy spectral density $E(k,t)$ is defined as

$$E(k,t)=\frac{1}{2}{S}_d{k}^{d-1}Q(k,t),S_d=\frac{2{\pi }^{d/2}}{\Gamma (d/2)},$$

(10)

and $S_d$ is the surface area of a d-dimensional sphere of unit radius. The brackets $\langle \rangle$ indicate an appropriate average such as the ensemble or space average.

According to the NS equation, Equation (1), the energy spectrum $E(k,t)$ obeys

$$\left(\frac{\partial }{\partial t}+2\nu k^2\right)E(k,t)=T(k,t)+W(k,t),$$

(11)

where $W(k,t)$ is the energy injected by the external force $f_i^{ext}$. $T(k,t)$ is the so-called energy transfer function that represents the energy transfer attributable to nonlinear triad interactions in the wave-vector space. The energy conservation by the nonlinear term in the NS equation implies that

$${\int }_0^{\infty }T(k,t)dk=0.$$

(12)

The so-called energy flux across k is defined by

$$\Pi (k,t)={\int }_k^{\infty }T(k^{\prime },t)d{k}^{\prime }=-{\int }_0^{k}T(k^{\prime },t)d{k}^{\prime }.$$

(13)

The average energy dissipation rate per unit mass is given by

$$〈\epsilon 〉=2\nu {\int }_0^{\infty }{k}^{2}E\left(k\right)dk,$$

(14)

and the average energy injection rate per unit mass is given by

$$〈{\epsilon }_f〉={\int }_0^{\infty }W\left(k\right)dk.$$

(15)

Here and hereinafter, we omit the time-arguments at will.

2.3. Statistics in the Inertial Energy Transfer Ranges of Wave-Vector and Physical Spaces

Equations (11) and (13) imply that

$$\Pi (k,t)={\int }_k^{\infty }\left[\frac{\partial }{\partial t}E(k^{\prime },t)+2\nu k^{2}E(k^{\prime },t)-W(k^{\prime },t)\right]d{k}^{\prime }.$$

(16)

Suppose that $Re$ is very large, so that $T(k^{\prime },t)$, i.e., the sum of the three terms in the integrand of Equation (16) is negligibly small (in an appropriate sense) over a certain range of $k^{\prime }$, say $k_{\mathcal{L}}\ll k^{\prime }\ll k_{\ell }$. Equation (16) then implies that the energy flux $\Pi \left(k\right)$ is almost constant independent of k, and we may therefore approximate it as

$$\Pi \left(k\right)=\overline{\epsilon },$$

(17)

over the range wherein we have set the constant to $\overline{\epsilon }$. We assume here that the time dependence of $\overline{\epsilon }$ is negligible.

As shown in Appendix A, if such a range k is sufficiently wide, we obtain the approximation

$$D_{LLL}\left(r\right)=-\frac{12\overline{\epsilon }}{d(d+2)}r,$$

(18)

over the corresponding range of r, i.e., $\ell \equiv (1/k_{\ell })\ll r\ll \mathcal{L}$ ($\equiv 1/k_{\mathcal{L}}$), where $D_{LLL}=〈u_r^3〉$ is the third-order structure function of the longitudinal velocity increment $u_r=(r/r)·(u(x+r)-u\left(x\right))$. We call this range inertial energy transfer range (IETR), and the wave-number range $k_{\mathcal{L}}\ll k\ll k_{\ell }$ is called the IET wave-number range (simply, IETR). The relation (18) with $\overline{\epsilon }=〈\epsilon 〉$ can be derived from a generalization of the Kármán–Howarth–Kolmogorov (KHK) equation for $d=3$ to any arbitrary integer $d>0$ for freely decaying turbulence with $f_i^{ext}=0$ [9,10,11].

For freely decaying turbulence in three dimensions ($d=3$), Equation (18) with $\overline{\epsilon }=〈\epsilon 〉$ gives Kolmogorov’s 4/5-th law [12],

$$D_{LLL}\left(r\right)=-\frac{4}{5}\overline{\epsilon }r.$$

(19)

Kolmogorov noted that under the assumption that the skewness S of $u_r$ defined by

$$S\equiv \frac{D_{LLL}\left(r\right)}{{\left[D_{LL}\left(r\right)\right]}^{3/2}},$$

(20)

is constant, Equation (19) gives

$$D_{LL}\left(r\right)=C_3{\left(\overline{\epsilon }r\right)}^{2/3},$$

(21)

where $D_{LL}\equiv 〈u_r^2〉$, $C_3={\left[-4/\left(5S\right)\right]}^{2/3}$ is a nondimensional constant, and we have used $\overline{\epsilon }>0$. A similar statement holds true for $d\ne 3$, i.e., if the skewness factor is constant, then Equation (18) gives

$$D_{LL}\left(r\right)=C_d\left(\right|\overline{\epsilon }{\left|r\right)}^{2/3},$$

(22)

where $C_d$ is a nondimensional constant, but may depend on d. Here, we use $|\overline{\epsilon }|$ instead of $\overline{\epsilon }$ to allow the possibility that $\overline{\epsilon }$ may be negative.

In spectral space, Equation (21) gives

$$E\left(k\right)=K_d{\left|\overline{\epsilon }\right|}^{2/3}{k}^{-5/3},$$

(23)

provided that the IETR is sufficiently wide, where $K_d$ is a nondimensional constant that may depend on d. Straightforward algebra shows that $C_d$ is related to $K_d$ by

$$C_d=2.56\Gamma (d/2)K_d/\Gamma (d/2+4/3),$$

(24)

where $\Gamma$ is the gamma function [6]. Equations (18), (20), (22) and (24) then give

$$S^{\left(d\right)}=-\frac{12}{d(d+2)}\begin{array}{c}\hfill \frac{\overline{\epsilon }}{|\overline{\epsilon }|}\end{array}{\left(\frac{\Gamma (d/2+4/3)}{2.56\Gamma (d/2)}\right)}^{3/2}{K}_d^{-3/2},$$

(25)

where we have replaced S in Equation (20) by $S^{\left(d\right)}$.

3. LRA Equations in Integer Dimension $\mathbf{d}$

3.1. LRA Equations

One of the main interests in the study of turbulence is how to theoretically predict the transfer $T(k,t)$. Extensive studies have been made on this problem. Readers may refer to, for example, the review by Zhou [13] for a recent and comprehensive review of the studies.

The LRA is one of the closure theories that give approximations for the transfer $T(k,t)$ [1]. Let $Q_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,s)$ be the two-time two-point Lagrangian velocity correlation defined by

$$Q_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,s)\equiv 〈v_i(\mathit{x},s|t)v_j({\mathit{x}}^{\prime },s|s)〉,(t\ge s)$$

(26)

and $G_{ij}(\mathit{x},x^{\prime },t,s)$ is the Lagrangian response function defined by

$$G_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,s)\equiv 〈\delta v_i(\mathit{x},s|t)/\delta f_j({\mathit{x}}^{\prime },s)〉,(t\ge s)$$

(27)

where $v(\mathit{x},s|t)$ is the generalized velocity defined as the fluid velocity at time t of the fluid particle that was at position x at time s, $\delta f_i(\mathit{x},t)$ is an infinitesimal force term added to the right-hand side of Equation (1), and $\delta /\delta$ denotes functional differentiation. Since $v(\mathit{x},t|t)$ is just the Eulerian velocity $u(\mathit{x},t)$, we have $Q_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,t)=〈u_i(\mathit{x},t)u_j({\mathit{x}}^{\prime },t)〉$.

In statistically homogeneous turbulence, $Q_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,s)$ and $G_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,s)$ depend on x and ${\mathit{x}}^{\prime }$ only via $\mathit{r}\equiv \mathit{x}-{\mathit{x}}^{\prime }$. Let the Fourier transforms with respect to r of $Q_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,s)$ and $G_{ij}(\mathit{x},{\mathit{x}}^{\prime },t,s)$ after an appropriate normalization be, respectively, $Q_{ij}(\mathit{k},t,s)$ and $G_{ij}(\mathit{k},t,s)$. The LRA gives a closed set of equations for $P_{im}\left(\mathit{k}\right)Q_{mj}(\mathit{k},t,s)$ and $P_{im}\left(\mathit{k}\right)G_{mj}(\mathit{k},t,s)$. (Since the pressure in Equation (1) kills the compressible part of $\delta f_i$, it is shown that $P_{im}\left(k\right)G_{mj}(k,t,s)=P_{im}\left(k\right)G_{mn}(k,t,s)P_{nj}\left(k\right)$. The latter expression instead of the former was used in Kaneda (1981)). In HIT, they may be written in the form

$$\begin{array}{ccc}& & P_{im}\left(\mathit{k}\right)Q_{mj}(\mathit{k},t,s)=\frac{1}{d-1}{P}_{ij}\left(\mathit{k}\right)Q(k,t,s),\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& & P_{im}\left(\mathit{k}\right)G_{mj}(\mathit{k},t,s)=P_{ij}\left(\mathit{k}\right)G(k,t,s),\hfill \end{array}$$

(29)

where $Q(k,t,s)$ and $G(k,t,s)$ depend on k only via k. Since $\mathit{v}(\mathit{x},t|t)=\mathit{u}(\mathit{x},t)$, as noted above, and the fluid is incompressible, we have $P_{im}\left(\mathit{k}\right)Q_{mj}(\mathit{k},t,t)=Q_{ij}(\mathit{k},t,t)=Q_{ij}(\mathit{k},t)$, where $Q_{ij}(\mathit{k},t)$ is the Fourier transform of $〈u_i(\mathit{x},t){\mathit{u}}_j({\mathit{x}}^{\prime },t)〉$ with respect to $\mathit{r}\equiv \mathit{x}-{\mathit{x}}^{\prime }$. For $t=s$, Equation (28) with $Q(k,t,t)=Q(k,t)$ therefore reduces to Equation (7). The same closure equations as those in the LRA were derived by Kida and Goto [14] for $d=3$.

We quote here the LRA equations for $T(k,t)$, $Q(k,t,s)$ and $G(k,t,s)$ in integer dimension $d\ge 2$ from Gotoh et al. [6] as follows. Readers may refer to their paper for the details of the derivation, and to Kaneda [15] for the basic ideas and properties of the LRA.

The single time correlation $Q(k,t)\equiv Q(k,t,t)$ obeys

$$\left(\frac{\partial }{\partial t}+2\nu k^2\right)Q(k,t)=T_Q(k,t)+W_Q(k,t),$$

(30)

where

$$\begin{array}{cc}\hfill T_Q(k,t)=& 2N_d{k}^{4-d}\int {\int }_{\Delta }dpdq{\left(pq\right)}^{d-2}{(1-x^2)}^{\frac{d-3}{2}}{b}_{kpq}^{\left(d\right)}\hfill \\ \hfill & \times {\int }_{-\infty }^t{G}_d(k,t,s)G_d(p,t,s)G_d(q,t,s)Q(q,s)\left[Q(p,s)-Q(k,s)\right]ds,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill W_Q(k,t)=& \frac{1}{S_d{k}^{d-1}}W(k.t),\hfill \end{array}$$

(32)

and

$$\begin{array}{ccc}& & b_{kpq}^{\left(d\right)}=d{\left(\frac{p}{k}\right)}^2(1-x^2)+\frac{p}{k}(2z^3-3z-xy),\hfill \end{array}$$

(33)

$$\begin{array}{ccc}& & N_d=\frac{S_{d-1}}{{(d-1)}^2},\hfill \end{array}$$

(34)

$\int {\int }_{\mathsf{\Delta }}dpdq$ denotes the integral over the domain of $p,q$ such that $(k,p,q)$ can be the length of the sides of a triangle, and $(x,y,z)$ denotes the cosines of the interior angles opposite the triangle sides $(k,p,q)$, respectively. Here, we assume that the time t is large enough, so that we may let the lower bound of the time integral in Equation (31) be $-\infty$.

The Lagrangian two-time velocity correlation $Q(k,t,s)$ satisfies the fluctuation–dissipation relation

$$Q(k,t,s)=G_d(k,t,s)Q(k,s,s),t\ge s$$

(35)

and the Lagrangian response function $G_d(k,t,s)$ satisfies $G_d(k,s,s)=1$ and

$$\left(\frac{\partial }{\partial t}+\nu k^2+{\mu }_d(k,t,s)\right)G_d(k,t,s)=0,t\ge s$$

(36)

where

$$\begin{array}{ccc}& & {\mu }_d(k,t,s)={\int }_0^{\infty }dpkp{J}_d\left(\frac{p}{k}\right){\int }_s^t{G}_d(p,t,s^{\prime })E(p,s^{\prime })d{s}^{\prime },\hfill \end{array}$$

(37)

$$\begin{array}{l}{J}_d\left(x\right)=M_d{\widehat{J}}_d\left(x\right),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {\widehat{J}}_d\left(x\right)& ={\widehat{J}}_d(1/x)\hfill \\ & =\left\{\begin{array}{cc}xF(1,-d/2,d/2+2,x^2),\hfill & x\le 1\hfill \\ \frac{1}{x}F(1,-d/2,d/2+2,1/x^2),\hfill & x>1\hfill \end{array}\right.\hfill \end{array}$$

(39)

$$\begin{array}{ccc}& & M_d=\frac{4S_{d-1}}{{(d-1)}^2{S}_d}B\left(\frac{d+3}{2},\frac{1}{2}\right),\hfill \end{array}$$

(40)

F is Gauss’ hypergeometric function and B is the beta function. Here, we omit terms that disappear when $f_i^{ext}=0$.

According to Equation (31), the energy flux is given by

$$\begin{array}{cc}\hfill & {\Pi }_d(k,t)=S_d{N}_d{\int }_k^{\infty }d{k}^{\prime }\int {\int }_{\Delta }dpdq{k}^{\prime 3}{\left(pq\right)}^{d-2}{(1-x^2)}^{\frac{d-3}{2}}{b}_{k^{\prime }pq}^{\left(d\right)}\hfill \\ \hfill & \times {\int }_{-\infty }^t{G}_d(k^{\prime },t,s)G_d(p,t,s)G_d(q,t,s)Q(q,s)\left[Q(p,s)-Q(k,s)\right]ds,\hfill \end{array}$$

(41)

in the LRA. It can be confirmed that, as in three dimensions, the detailed balance and the energy conservation by the nonlinear term in the NS equation hold in the LRA in any integer dimensions $(\ge 2)$.

3.2. LRA Equations in the IETR

A simple dimensional analysis using the idea of Kolmogorov’s similarity theory [16] suggests that $E\left(k\right)$ and $G_d(k,t,s)$ in the IETR, where Equation (17) holds, are given by the following similarity forms:

$$\begin{array}{ccc}& & E\left(k\right)=K_d{\left|\overline{\epsilon }\right|}^{2/3}{k}^{-5/3},G_d(k,t,s)=G_d(k,\tau )=g_d\left(\sigma \right),\hfill \\ & & \tau =t-s,\sigma =\gamma |\overline{\epsilon }{|}^{1/3}{k}^{2/3}\tau ,\gamma =\sqrt{M_d{K}_d},\hfill \end{array}$$

(42)

where $K_d$ is the Kolmogorov constant in d-dimension. Here and hereafter we assume the statistical stationarity in the IETR.

The LRA equations are confirmed to be consistent with the similarity forms in Equation (42). Upon substitution of the similarity forms (42) of Equation (10) into Equation (37), the integral converges appropriately at small and large wave-number limits. Via substitution, one can reduce Equation (36) to

$$\begin{array}{ccc}& & \frac{d{g}_d\left(\sigma \right)}{d\sigma }+\left({\int }_0^{\infty }dx{x}^{-2/3}{\widehat{J}}_d\left(x\right){\int }_0^{\sigma }d\xi g_d\left(x^{2/3}\xi \right)\right)g_d\left(\sigma \right)=0.\hfill \end{array}$$

(43)

Similarly, by substituting the similarity forms, one can reduce the expression Equation (41) for the energy flux in the IETR to

$${\Pi }_d\left(k\right)=\left|\overline{\epsilon }\right|K_d^{3/2}\frac{4d{S}_{d-1}}{{(d-1)}^2{S}_d\sqrt{M_d}}{A}_d,$$

(44)

where

$$\begin{array}{ccc}& & A_d={\int }_0^{1}dulog\left(1/u\right){\int }_{max(u,|1-u\left|\right)}^{u+1}dv{\Theta }_d(1,u,v){\overline{D}}_d(1,u,v),\hfill \end{array}$$

(45)

$$\begin{array}{ccc}& & {\overline{D}}_d(1,u,v)={(1-x^2)}^{\frac{d-3}{2}}{u}^{-8/3}\left[({\overline{b}}_{1uv}^{\left(d\right)}+{\overline{b}}_{1vu}^{\left(d\right)})v^{-8/3}-({\overline{b}}_{1uv}^{\left(d\right)}{u}^{d+2/3}{v}^{-8/3}+{\overline{b}}_{1vu}^{\left(d\right)}{v}^{d-2})\right],\hfill \end{array}$$

(46)

$$\begin{array}{ccc}& & b_{1uv}^{\left(d\right)}=d{\overline{b}}_{1uv}^{\left(d\right)}=d\left(u^2(1-x^2)+\frac{u}{d}(2z^3-3z-xy)\right),\hfill \end{array}$$

(47)

and ${\Theta }_d$ is the triple relaxation time defined by

$${\Theta }_d(1,u,v)={\int }_0^{\infty }{g}_d\left(s\right)g_d\left(u^{2/3}s\right)g_d\left(v^{2/3}s\right)ds.$$

(48)

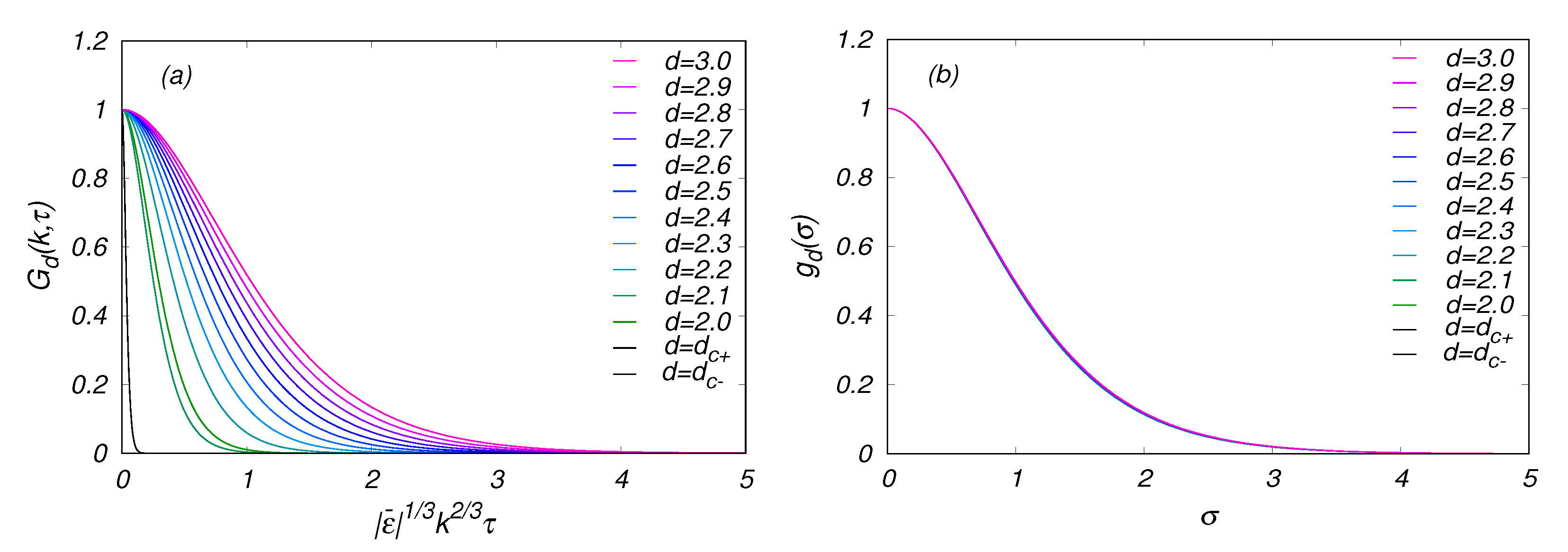
4. Statistics in the IETR for $\mathbf{2}\le \mathbf{d}\le \mathbf{3}$

Up to this point, we have assumed that the space dimension d is an integer, and we derived the relations in Section 2 and Section 3. We now take the bold step of assuming that we can continue to use Equation (25) and the LRA equations in a noninteger dimension d with $2<d<3$. If so, we can solve Equation (43) to obtain $g_d$ numerically for any noninteger dimension d, in $2<d<3$, in the same way as in Refs. [17,18,19]. Note that Expression (9) in Ref. [18] for a damping factor $\eta$ is too small by a factor of 2; thus, some factors must be corrected. For example, C ($K_2$ in the present notation) is too small by a factor of $2^{1/3}$, and, thus, should be $C=7.41$.

Figure 1a shows the response function $G_d(k,t-s)$ plotted against $|\overline{\epsilon }{|}^{1/3}{k}^{2/3}\tau$ for $d=2.0,2.1,\cdots ,3$ and $d_{c\pm }=d_c\pm 0.0001$, where $d_c\approx 2.065$. The function $G_d$ decays more rapidly as d decreases from 3 and rapidly moves to zero just above and below $d_c$. However, it decays more slowly as d changes from $d_c$ to 2. Figure 1b shows that the values of $g_d$ as a function of $\sigma =\sqrt{M_d{K}_d}{\left|\overline{\epsilon }\right|}^{1/3}{k}^{2/3}\tau$ are almost independent of d. Given the fluctuation–dissipation relation (35), this implies that the normalized two-point two-time Lagrangian-correlation spectrum $Q(k,t,s)/Q(k,s,s)$ is also almost independent of d under an appropriate normalization of time.

Substituting the values of $g_d$ thus obtained and integrating Equation (41) numerically, we derive estimates of $K_d$ for the given d, as in previous studies. The numerical code used in this study is based on that of Ref. [6]. The values of $K_d$ thus obtained are plotted in Figure 2a,b. It is seen that $K_d$ as a function of d tends to $K_2=7.43$ for $d=2$ and $K_3=1.73$ for $d=3$, respectively, and diverges at a point $d_c$. These numerical estimates, $7.43$ and $1.73$, are in agreement with the estimates $7.41$ and $1.72$ [6,14,17,18,19] within a difference of less than $0.6\%$.

It is numerically clear that $A_d$ is positive, so ${\Pi }_d$ given by Equation (44) is, thus, also positive; the energy transfer is forward at $d_c<d\le 3$ but negative (backward) at $2\le d<d_c$. If one assumes $A_d\propto (d-d_c)$ at small $|d-d_c|$, we obtain $K_d\propto {|d-d_c|}^{\sigma }$ with $\sigma =-2/3$, which is in good agreement with the numerical result of Figure 2b and agrees also with that of Fouriner and Frisch [5], who argued that $K_d$ diverges at $d=d_{FF}$ and the exponent is $-2/3$, on the basis of the EDQNM approximation, where $d_{FF}\approx 2.05$, which is very close to $d_c=2.065$ noted above. In the EDQNM approximation in Fouriner and Frisch [5], $\Pi \left(k\right)$ in the IETR is given by Equation (44) but with $G_d(k,\tau )$ in Equation (42) replaced by $G_{EDQNM}(k,\tau )=exp(-{\mu }_k\tau )$, and $1/{\mu }_k$ represents the local eddy turnover time and is given by

$${\mu }_k={\lambda }_d{\left({\int }_0^k{r}^{2}E\left(r\right)dr\right)}^{1/2},$$

(49)

and ${\lambda }_d$ is an adjusting parameter. The critical dimension $d_{FF}$ is seen to be independent of the choice of ${\lambda }_d$.

Substitution of the values of $K_d$ thus obtained from Equation (25) gives the values of the skewness factor $S^{\left(d\right)}$, which are plotted in Figure 3. It is seen that $S^{\left(d\right)}$ decreases as d decreases from $d=3$, and changes its sign at $d=d_c$ where $K_d$ diverges.

5. Discussion

The overlap of the curves of $g_d$ for different d in Figure 1b is impressive. This implies that the time dependence of the normalized Lagrangian two-point two-time correlation $Q_d(k,t,s)/Q_d(k,s,s)$ and that of the Lagrangian response function $G_d(k,t,s)$ under an appropriate normalization of time are insensitive to the difference in the space dimension. It would be interesting to explore the physics behind the overlap and implications thereof.

The skewness $S^{\left(d\right)}$ of the velocity increment must be 0 if the statistics of the velocity field are Gaussian. Hence, $S^{\left(d\right)}$ is a measure of the degree of the non-Gaussianity of the turbulence statistics. The results in Section 4 show that $S^{\left(d\right)}$ monotonically approaches the Gaussian value, i.e., 0, with the departure of the dimension d from 3, in the range $d_c<d<3$, and increases from 0 in the range $2<d<d_c$.

Recently studies have been made on turbulence in noninteger space dimensions $d<3$ using a fractal Fourier decimation model; see, for example, [20,21,22,23,24,25], and references cited therein. Studies so far made suggest that the non-Gaussianity of small-scale statistics depends on the space dimension d. In this respect, the results in Section 4 noted above are consistent with this, although the model used here is based on continuation of the LRA at integer dimensions to noninteger dimension $2<d<3$; this differs from the decimation model. It would be interesting to apply the LRA to the decimation model to see if the LRA can well capture the influence of d on the statistics related to the skewness $S^{\left(d\right)}$ in the model.