Abstract
The results of temperature measurements in the lower thermosphere at altitudes of 90–130 km by the method of resonant scattering of radio waves on artificial periodic inhomogeneities (APIs) of the ionospheric plasma are presented. These inhomogeneities are created when the ionosphere is exposed to powerful HF radio emission. The temperature profile was obtained from measurements of the relaxation time of the API scattered signal. The data processes and the method of the temperature determination are given in detail. The height and temporal resolutions of the API technique are of the order of 1 km and 15 s, respectively, making it possible to study both fast and slow processes in the lower thermosphere. Large temperature variability at altitudes of 90–130 km during the day and from day to day, due to the propagation of atmospheric waves, has been confirmed. The temporal variations of the atmospheric parameters take place with periods from 15 min to some hours. There are often height profiles of the temperature with the wave-like variations and with the vertical scale of about 4–10 km. The irregular temperature profiles were observed above 100 km.
1. Introduction
The region of the lower thermosphere, which covers heights of 90–130 km, is an intermediate region between the mesosphere and the upper thermosphere and is an area of intense dynamics. Atmospheric waves of different space–time scales propagate in the lower thermosphere. At these heights, developed turbulence, horizontal and vertical movements of the neutral environment and ionospheric plasma exist [1,2,3,4,5,6]. These and other atmospheric phenomena affect the temperature of the lower thermosphere and its altitude profile. Temperature perturbations in turn affect the rate of atmospheric chemical reactions. These circumstances determine the relevance of measuring the temperature of the mesosphere and lower thermosphere (MLT). Until now, information about the temperature behavior of the lower thermosphere is insufficient. At the same time, such information is important for establishing patterns and the role of dynamic factors in the formation of the thermal regime of the lower thermosphere for the development and improvement of the atmospheric model.
Studies of the MLT region show that the altitude profile of the temperature varies from day to day and in different seasons [7,8,9]. The temperature variability above the mesopause level is clearly seen in measurements taken by the method of falling spheres from meteorological rockets [3,10,11]. It has been found that temperature variations at a particular height can reach 50 K. Such variations can be caused by the propagation of internal gravity waves (IGWs) [6]. Rocket measurements are sporadic and rarely above 90 km.
A large amount of data on the temperature of the MLT region was obtained from measurements of the night glow in different atmospheric emissions [3,9,12,13]. The monograph [13] provides detailed information on methods for studying the upper atmosphere based on the measurement of atmospheric emissions, which are considered as an indicator of its structure and dynamics. In [12], based on 417 nights of lidar observations in the period from 1990 to 1999 in Fort Collins, Colorado (41° N, 105° W), the results of temperature measurements at altitudes of 80–110 km and the idea of a two-level mesopause were proposed. Phenomena in the MLT region caused by gravity wave breaking and associated with dynamic instability were studied using Na lidar and an Advanced Mesosphere Temperature Mapper over Logan, UT (41.7° N, 111.8° W) [14,15]. In [16], spectral characteristics of atmospheric waves in the MLT using lidar observation at Andes were studied.
In [17], the altitude profiles of the temperature near Andenes, Norway (69° N, 16° E) obtained with sodium lidar in the altitude range of 80–110 km are discussed. The results of temperature measurements at altitudes of 92–120 km on the EISCAT incoherent scatter radar are given in [18,19,20]. In general, there is a lack of experimental data at altitudes of 100–130 km since most of the measurements refer to lower altitudes. We are trying, to some extent, to compensate for the lack of measurement data on the temperature of the lower thermosphere by applying our method, which is based on the creation of artificial periodic inhomogeneities in the ionospheric plasma [21]. Note that although our proposed method is based on the impact on the ionosphere by a powerful HF radio emission with the creation of inhomogeneities, the temperature is measured at the stage of their relaxation, that is, in a natural undisturbed environment.
The remaining sections of this paper are as follows. Section 2 presents a brief description of the method for determining the temperature of the lower thermosphere based on the API technique. Section 3 includes a description of the experiments and a data processing technique. Section 4 gives examples of vertical profiles of time temperature variations obtained by the API technique. Section 5 discusses their features and compares the vertical temperature profiles obtained by the API method with model profiles. Finally, Section 6 contains conclusions.
2. API Technique and Observations
In the monography [21] and review [22], we have already touched upon the method of measuring the parameters of the neutral atmosphere by the API technique. APIs are formed in the field of a powerful standing wave that occurs when the ionosphere is disturbed by a powerful HF radio emission. They were first observed at the “Zimenki” heating facility (56.16° N, 44.3° E) in 1975 [23]. For many years, the API method has been developed on the basis of the SURA mid-latitude heating facility (56.15° N, 46.11° E). Experimental and theoretical studies of the ionosphere by the API technique have shown that its application makes it possible to determine more than a dozen parameters of the ionosphere and the neutral atmosphere and to obtain a large amount of data on the dynamics and parameters of the ionized and neutral components of the Earth’s atmosphere in the altitude range from 50–60 km to the height of the F layer maximum. Methods have been developed for determining many parameters of the ionosphere and the neutral atmosphere at these heights, including some aeronomic parameters of the D region and the sporadic E layer (Es) [21]. In [22], a brief review of studies of the Earth’s ionosphere at heights of the mesosphere and lower thermosphere by the API method is presented, including the measurement of many parameters of neutral and plasma components.
APIs are formed as a result of uneven plasma heating in the field of a standing radio wave when a powerful wave is reflected from the ionosphere. The main features of API formation are in detail in [21]. Note that, in different regions of the ionosphere, the formation of inhomogeneities is due to different physical processes. In the D region (height 60–90 km), the temperature dependence of the coefficient of attachment of electrons to neutral molecules plays a key role in the API formation. In the E region (height 90–150 km), APIs are formed due to the diffusion redistribution of plasma under the action of an excess pressure of electron gas, and in region F (height 150–350 km), they are formed under the action of a ponderomotive force on the ionospheric plasma. Irregularities scatter probe radio waves, and when the Bragg scattering condition is satisfied, the relatively high intensity of the backscattered signal is due to the in-phase summation of waves from each inhomogeneity [21]. Scattering of probe radio waves by APIs has resonant properties, that is, if the frequencies and polarizations of high-power and probe radio waves are equal, the amplitude of the signal scattered by inhomogeneities is 10–100 times higher than the level of natural noise. Therefore, the method was called the method of resonant scattering of probe radio waves on APIs. Many experiments using the SURA facility were carried out in order to determine the parameters of the ionosphere and the neutral atmosphere from the measured characteristics of API scattered signals. One of these parameters is the neutral temperature in the lower thermosphere. For this purpose, the height profile of the relaxation time of the signal scattered by inhomogeneities is used. For comparison, we used one of the widely used popular models of the neutral atmosphere, MSIS-E-90 [24].
For API formation, we used a powerful transmitter (heating facility) that creates an electromagnetic field that disturbs the ionospheric plasma. The SURA facility is also used as a source of probing pulses for diagnostics of the ionosphere. Using different time schemes for the emission of high-power and probe radio waves, it is possible to study the API rise and decay (relaxation) processes [21,22,25,26]. Figure 1a shows the time schedule for studying the API rise and decay.
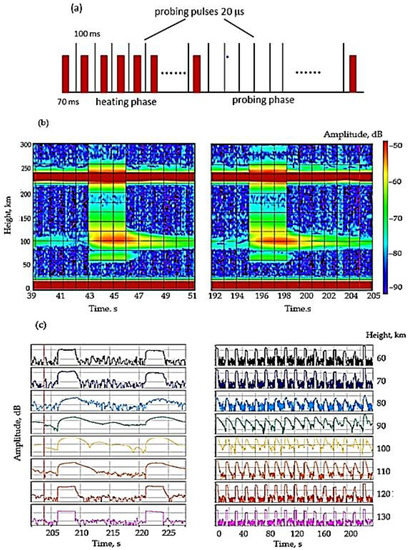
Figure 1.
Quasi-continuous schedule heating of the SURA facility used for API formation and diagnostics (a) allows studying the processes of API development and relaxation. Height–time–amplitude plots illustrating the API rise and decay (b) on time 16:03:12 and 16:38:50 and amplitudes of API scattered signal on time at the eight heights from 60 to 130 km for two and sixteen sessions on time 16:00:50 and 16:04:50 of the observation on 2 September 2021. (c) The SURA facility emitted high-power radio waves at a frequency of 4.3 MHz.
The transmitters of the SURA facility emit a heating pulse with a duration of 70 ms with a period of 100 ms with short daps, in which a short probing pulse with a duration of 20 μs is emitted. This mode of radiation lasts two or three minutes. After this time, the transmitters emit probe pulses with a repetition period of 100 ms. Such a mode of radiation of the transmitters of the facility is called quasi-continuous or “with tie-ins” mode. Figure 1b shows “effective height–time–amplitude” plots illustrating the API rise and decay on 2 September 2021 at 16:00:38 LT (left panel) and 16:03:12 LT (right panel). Amplitudes of API scattered signals at eight heights from 60 to 130 km for observations for a session of 4 min and two 15 s sessions are shown in Figure 1c. During the heating period, one can see the development of the API signal scattered in the F region in the altitude range of 160–270 km below the height of the specular reflection of the probe radio wave. The horizontal stripes at the top of Figure 1b are specular reflections of the probing radio wave. Figure 1c shows the growth and decrease in the amplitude of the scattered signal during the development and destruction of inhomogeneities. The relaxation or decay time is determined when the amplitude of the scattered signal decreases by e times. In this example, the rise and relaxation times in the E region reached 1–1.5 s. These values of API time scales are typical for the E region, when ambipolar diffusion dominates in their formation and relaxation [21]. The API echoes of the F region developed and disappeared typically in less than 30–300 ms after the heater switching. Sometimes, after the end of the impact on the ionosphere, the relaxation of the scattered signal in the E layer lasted for about 2–3 s.
Figure 2a shows a time diagram for studying only the process of API relaxation. It implements a continuous heating mode for several seconds, followed by switching the heating installation to a pulsed diagnostic mode with the emitting of short 30 μs pulses. In both cases of continuous and quasi-continuous heating, the receiving unit of the partial reflection setup receives the signal scattered by inhomogeneities and registers its amplitude and phase during the entire period of their relaxation [21,25,26]. The signal-to-noise ratio is 10–100 at altitudes of 60–130 km.
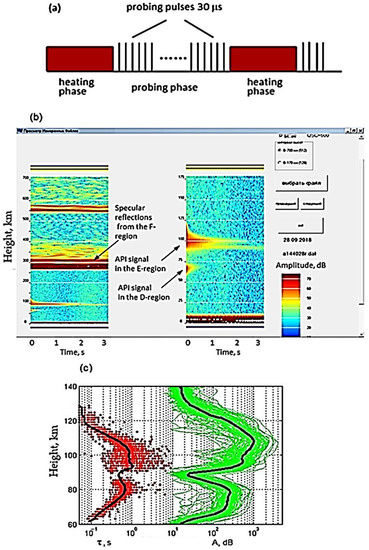
Figure 2.
Continuous schedule heating of the SURA facility used for API diagnostics at the relaxation stage: (a) an example of visualization of API scattered signals (b) and their dependences of the relaxation time and amplitude during 30 min on 18:00–18:30 LT 10 August 2010 (c).
Figure 2b shows an example of a real-time visualization of the scattered signal in height and time in the range of effective heights h = 0–700 km (left panel) and h = 0–175 km (right panel) after heating is stopped at the stage of inhomogeneity relaxation. The horizontal strip is a specular reflection of the probe wave from the F layer of the ionosphere. The amplitude of the API scattered signal in the D region (60–75 km) and E layer (90–125 km) gradually decreases on the API relaxation stage. The time of their relaxation is determined by the decrease in the amplitude by a factor of e. Figure 2c shows the height profiles of the amplitude and relaxation time of the scattered signal for 10 August 2010 only during API relaxation. The curves are data averaged over 5 min at each altitude. In this example, the diffusion law of relaxation is satisfied in the altitude range of 100–120 km. Under a height of 100 km, atmospheric turbulence begins to affect, destroying inhomogeneities faster than diffusion, and the relaxation time of the scattered signal decreases. At an altitude of 92 km, a local increase in the amplitude of the scattered signal is caused by a low sporadic E layer. At the same altitude, a local maximum of the relaxation time is observed. For heights of the D region, the amplitude and relaxation time change with altitude in full accordance with the temperature dependence of the electron detachment coefficient [21].
3. Methodology and Data Processing
Regular experiments by the API technique in order to determine the most important parameters of the ionosphere and the neutral atmosphere have been carried out since the mid-1980s of the last century. They cover more than three cycles of solar activity and include three partial eclipses of the Sun and all four seasons of the year. As a rule, the experiments were carried out from sunrise to sunset in the daytime, which is due to the need to reflect a powerful radio wave from the ionosphere for the API formation. It so happened that we mainly have data for a calm geomagnetic field or its weak disturbance.
3.1. Methodology
The results of temperature determination under various ionospheric conditions are contained in [21,27,28,29,30,31,32]. In this article, we will mainly present the results of temperature measurements in recent years including experiments conducted in September 2021. The experiments were carried out using the SURA heating facility to create and diagnose inhomogeneities. The transmitters of the facility emitted a powerful X- or O-mode with a frequency of 4.3 MHz or 4.7 MHz into zenith. The effective radiated power was 100–120 MW. API scattered signals were received by the antenna of the partial reflections setup and their quadrature components were recorded [26]. The height and time resolutions were typically 0.7–1.4 km and 15 s, respectively. In the experiments of 2021, the altitude step of data recording was 150 m.
After the end of heating of the ionospheric plasma by the powerful radio emission of the SURA facility in the indicated altitude range, the APIs relax under the action of ambipolar diffusion [21]. In this event, the relaxation time τ is given by formula
where D is the coefficient of ambipolar diffusion, kB is the Boltzmann constant, K = 4πn/λ is the wavenumber of a standing wave in plasma, λ is the length of the emitted powerful radio wave and n is the refractive index, Mi· and νim are the average mass of ions and the frequency of collisions of ions with molecules, and the temperatures of Ti ions and Te electrons are equal to the neutral temperature T at the heights of the lower thermosphere. By measuring the height dependence τ(h) and assuming that T = const in a small height interval, the temperature is determined by the formula
Here, H is the atmospheric height scale determined from the dependence τ(h), and M is the average molecular weight. The frequency of ion–molecular collisions is proportional to the density of the atmosphere and is defined as νim = βρ/M with a proportionality coefficient equal to β = 0.38·10−10 cm3s−1 [33].
It is important to note that this temperature determination methodology is applicable in the absence of a sporadic E layer and atmospheric turbulence. However, the main requirement is that the environment is isothermal within the scattering volume, which makes it possible to determine the atmospheric height scale H and then the temperature.
The sporadic E layer increases the relaxation time due to an increase of the masses of ions, which are often positive metal ions, for example, Fe+ (56 aem) and Ca+ (40 aem) [34,35,36]. Atmospheric turbulence destroys APIs faster than ambipolar diffusion, and the relaxation time decreases in this case. Such events are excluded from data analysis.
3.2. Data Processing
Formula (1) clearly shows that τ depends on the refractive index n of the powerful wave and, accordingly, on the electron concentration N. Thus, the first thing to do is to get the profile N(z) versus true height z. The best option is to measure N(z). The API method makes it possible to do this [37,38,39]. The electron density profiles measured by the API technique were used in most of our experiments. When this was not possible, we used the profile reconstructed from the oblique sounding ionogram during the period of experiments or the model N(z) profile calculated according to the International Reference Ionosphere (IRI model) [40]. After the height profile of the electron density is obtained, the data are processed according to the following algorithm. First, the relaxation times τ(h,t) are calculated depending on the effective height h and time t by reducing the amplitude of the received signal by e times when the powerful effect is turned off. For this, the dependence of the scattered signal amplitude on time is approximated by the function ln A(t) = ln A0–t/τ, where A0 is the signal amplitude at the moment of heating termination and τ is the API relaxation time.
Our long-term studies of the ionosphere by the API technique have shown that the relaxation time of the scattered signal fluctuates in height and in time [23,32,39,41]. Altitude profiles of the relaxation time τ(h) for 30 min of measurements are shown in Figure 2c. Each profile was obtained within one fifteen-second measurement session. At the height of the lower thermosphere, the relaxation time decreases with increasing height due to the effect of ambipolar diffusion on the relaxation process of inhomogeneities after the end of the SURA facility operation. It can be seen in Figure 2c that the profile τ(h) changes with time. These variations of τ are especially pronounced near the turbopause level, which in this example is close to 100 km. The local maximum of the amplitude and relaxation time of the scattered signal at a height of 95 km is due to the sporadic E layer [21,36].
An example of temporal variations in the relaxation time of the API scattered signal τ(h,t) is shown in Figure 3 for three heights of the lower thermosphere. Figure 3 shows a decrease in the values of τ with height, which should be carried out in accordance with the diffusion nature of the API relaxation. One can also see the influence of atmospheric waves with a period of 10–20 min to 3 h. The increase of the relaxation time to 3.5–4.5 s during 14:45 to 15:35 is due to the influence of the sporadic E layer due to the growth of Mi and due to the appearance of heavy positive metal ions (see Formula (1)). Such data were discarded.
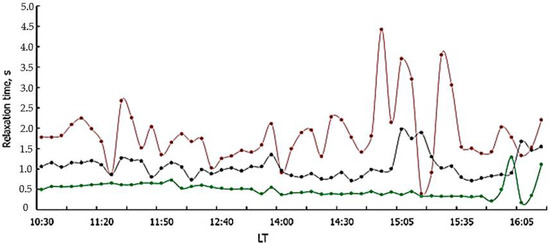
Figure 3.
Temporal dependence of the relaxation time for three altitudes, i.e., 100.8 km (in red), 105 km (in black) and 112 km (in green) on 25 October 2018. Wavelike variations are caused by the propagation of atmospheric waves (see also [42,43,44,45,46]).
We assume that the features of the height-temporal variation of the relaxation time also cause the features of temperature variations.
As a result of the fact that the relaxation time experiences significant altitude–temporal variations, to determine the temperature, it is necessary to average τ(h,t) over a time interval of 3–5 min and an altitude range of 1–4 km, when the isothermal approximation Te = Ti = T. In fact, a moving average procedure for height and time averaging is applied. The next step calculates the refractive index of the wave based on the profile N(z) and determines the true heights z corresponding to the actual heights h. Next, a linear regression procedure is used for the function ln(τn2) = –bz + a, where b = 1/H over a small height interval of 4–5 km. The height scale of the atmosphere H is determined from the interval of averaging over several neighboring values of τ, and according to formula 2, the temperature T of the lower thermosphere is calculated in the height range of 90–130 km. Every value of the temperature refers to the middle of the vertical averaging interval. Figure 4 shows examples of applying the linear regression procedure for the ln(τ·n2) function depending on the height. Figure 4a,b refer to the averaging of height data over the 4 km range. As an example, Figure 4c shows the application of linear regression for the entire range of heights on 2 September 2021 in the 15:00–15:04 session.
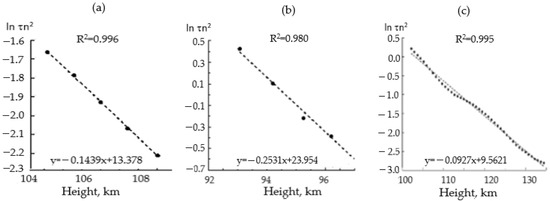
Figure 4.
Examples of applying of the linear regression procedure to the experimental function ln (τn2) versus the height: (a) and (b) show two sessions on 4 October 2007 over 4 km smoothing interval and (c) over the entire altitude interval on 2 September 2021.
In Figure 4, experimental data are shown by dots. On each plot, the straight dotted line is the regression one. The regression equations and the coefficient of determination R2 are shown. Almost all data are clustered around the regression line, which means a good approximation of the data. Determining the value of the atmosphere scale from the regression equations b = 1/H, we obtain the values H = 6.95 km and 4 km for Figure 4a,b and H = 5.5 km for Figure 4c. As a result of applying this processing algorithm, we obtain an altitude temperature profile in the height range of 90–130 km. The instrumental and statistical errors of temperature measurement in the aggregate do not exceed 5–10% [26,27].
4. Results
In this section, we present new examples of altitude temperature profiles obtained in recent years and the results of temperature measurements in experiments in September 2021.
4.1. Temperature Profiles
Figure 5 and Figure 6 show the height profiles T(z) (temperatures T versus true height z) obtained in different years in experiments by the API technique according to the above algorithm. Several characteristic types of T(z) can be distinguished. The first of these is relatively smooth profiles with a minimum or maximum at a certain height. Such profiles are shown in Figure 5a,c,e and Figure 6d. Another group of smooth monotonic profiles includes profiles without a pronounced extremum, shown in Figure 5b and Figure 6c. Finally, the largest group is the irregular temperature profiles shown in Figure 5d,f–h and Figure 6a,b. Note that the profiles shown in Figure 6 were obtained by the averaging of the relaxation time over the altitude range of 0.75 km.
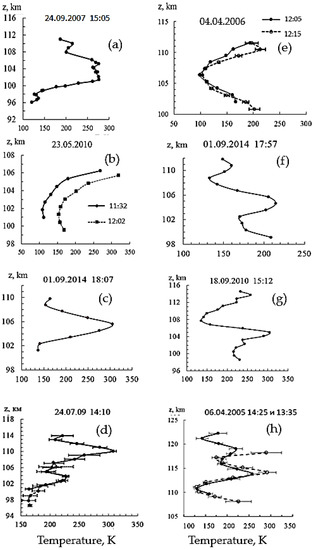
Figure 5.
Temperature profiles on the height of the lower thermosphere measured by the API technique (a–h). Smooth profiles with a minimum or maximum at a certain height (a,c,e); smooth monotonic profiles includes profiles without a pronounced extremum (b); the irregular temperature profiles (d,f,g,h). In the (d,h) panels, the bars show the temperature measurement errors.
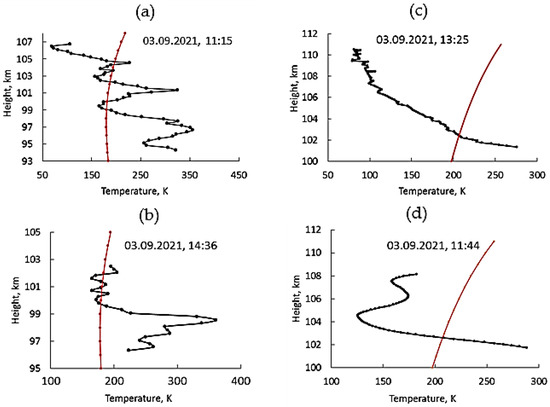
Figure 6.
Height temperature profiles in the lower thermosphere measured by the API technique on 3 September 2021 (a–d). Smooth profiles with a minimum or maximum at a certain height (d); smooth monotonic profiles includes profiles without a pronounced extremum (c); the irregular temperature profiles (a,b). The red lines show the vertical temperature profiles calculated according to the MSIS-E-90 model.
Note that Figure 5 shows the temperature profiles calculated using real electron density profiles N(z) measured by the API technique. The method of the N(z) measurement is described in detail in [37,38]. The temperature profiles shown in Figure 6 were obtained using the vertical electron density profile calculated according to the IRI-2016 model specifically for the measurement time [40].On some profiles, a negative temperature gradient from 10 to 20 K or more can form; for example, dT/dz =–14 K on the bottom part of Figure 5e. Often after this, the profile is transformed into a similar one shown in Figure 5d,h.
Figure 7 shows T(z) profiles obtained on 2 September 2021 with a scattered signal data recording step over a height of 150 m. To calculate the refractive index n, we used the height profiles of the electron density obtained according to the IRI-2016 model [40]. To calculate the temperature, the relaxation times were first averaged over the height range of 0.75 km. Then, the temperature calculation procedure described in Section 3 was applied. The application of vertical smoothing averages small-scale variations, but it does not affect the main features of the T(z) profile. All T(z) profiles shown in Figure 7 belong to the group of irregular profiles. Here, in Figure 7, the solid lines show the temperature profiles calculated according to the MSIS-E-90 model [24]. Note that, in general, at altitudes from 94 to 120 km, the temperature varied from 100 to 300 K, sometimes reaching 350 K. In some sessions, T values below 100 K were obtained, as shown in Figure 8e,f.
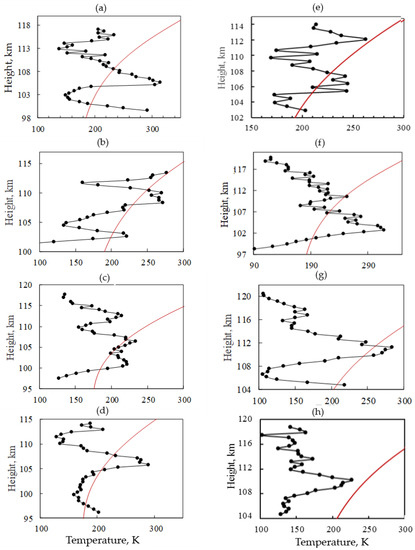
Figure 7.
Temperature profiles on the height of the lower thermosphere measured by the API technique on 2 September 2021 (a–h). Red lines show the temperature profiles calculated according to the MSIS-E-90 model.
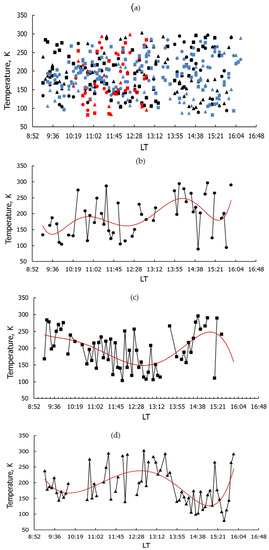
Figure 8.
Altitudinal temperature dependences in the daytime from 25 October to 26 October 2018 at three altitudes of 100 km, 105 km and 112 km (a); the same dependences only for 25 October: (b) for a height of 100 km, (c) for a height of 105 km, and (d) for a height of 112 km.
Consider the main features of the temperature profiles shown in Figure 7. One can see small-scale height temperature variations of the order of 0.7 km. Note that the original non-height-averaged temperature profiles (not presented in the article) are even more “jagged”. One can see undulating quasi-periodic height variation with a height period of 5–12 km. It is natural to assume that such variations as the alternation of temperature minima and maxima are due to the propagation of IGWs with a vertical wavelength of the same order.
As noted above, a feature of many temperature profiles is the existence of deep, pronounced temperature minima at altitudes of 103–107 km and 110–112 km. The value of the temperature minimum varied within 130–170 K. On the other hand, pronounced temperature maxima could be observed at these altitudes, reaching 230 K and 320 K in magnitude. Deep temperature variations are observed at neighboring altitudes. Therefore, for example, at altitudes of 105–106 km (Figure 7a), the temperature difference was 140 K, and at altitudes of 111–112 (Figure 7b), it was 50 K.
We compared the obtained vertical temperature profiles with those calculated using the MSIS-E-90 model. The input parameters in the model were set for each specific measurement session. It can be seen that, in almost all cases, the results of temperature measurements by the API technique are grouped with respect to the model profile only in a small altitude range of about 10 km. There are also cases, such as those shown in Figure 7h, where the measured and model profiles do not intersect. In Figure 7g, the intersection of the measured and model profiles occurs only at a height of 110–112 km.
4.2. Temperature Temporal Variation
The temperature of the lower thermosphere changes with time. Here, we consider the features of temporal temperature variations during the day. It is known that the influence of atmospheric waves on the mesosphere and lower thermosphere is very strong. There is a huge amount of information about this, obtained by various research methods [5,6,7,8,9,10,11,12,47,48,49]. In studies of the mesosphere and lower thermosphere using the API technique, we found the manifestation of wave motions and atmospheric turbulence in the altitude–time dependences of the amplitude and relaxation time of the scattered signal. A typical example of the effect of atmospheric waves on the relaxation time τ(t,z) is shown in Figure 3. The most typical wave periods were 10–15 min, 30–45 min, as well as 60 min and 4–6 h. Such periods of time variations are inherent in IGWs. Similar manifestations of atmospheric waves in the form of IGW were found by us in the altitude–time variations in the temperature and density, the velocity of the vertical motion of the plasma and the neutral component, the turbulent velocity and the level of the turbopause [21,22,30,31,32,36,43,44,45,46,50].
Figure 8a shows temporal temperature variations at three altitudes during the daytime on 24–26 October 2018. Different labels mark the temperature values at different altitudes: triangles refer to 100 km, squares to 105 km, and circles to 112 km. Temperature measurements on 24 October 2018 are shown in blue, 25 October in red and 26 October in black. Figure 8 shows that during these three days, there was a large scatter of temperature values from 85 K to 300 K. The average temperature at altitudes of 100–112 km was 190 K. Figure 8b,c,d show temperature versus time for 26 October 2018 only, for altitudes of 100 km, 105 km, and 112 km, respectively. The red line on the figures shows a polynomial trend of the 6th order. This is one of the simplest ways to estimate the periods of wave-like variations.
In Figure 8, along with temperature variations of 20–50 K, in some time intervals, deep fast T variations reaching 150 K are visible. The average temperatures exceeded the median values at an altitude of 100 km by 15 K (190 and 175 K, respectively), at an altitude of 105 km by 3 K (196 and 193 K, respectively), and practically did not differ from each other at an altitude of 112 km and was 190 K. This is indirect evidence that the height of 110 km is close to the turbulent region of the lower thermosphere.
5. Discussion
We demonstrated in Section 4 that the time–altitude dependences of temperature vary with height and time. The results strongly suggest that atmospheric waves, including IGWs, manifested in these variations. The basis for this statement is our long-term studies of the ionosphere by the API technique [21,22,30,31,32,39,43,44,45,46,50,51,52,53,54]. We estimated IGW parameters such as its horizontal wavelength kx and its period Twave. To do this, we used the dispersion relation for IGW, the vertical velocity of the environment Vz from our measurements of a phase of the scattered signal, and the vertical wavelength kz from height temperature profiles [54].
Assuming that the horizontal velocity Vx and the wavelength kx are much larger than the vertical ones, we can obtain the following estimates . For Vz = 0.5 m/s, λz = 5 km and Brunt-Väisälä frequency ωg = 10−2 Hz (Brunt-Väisälä period Tg = 8 min), we obtained λx = 50 km and Twave = 3.5 h. Regarding wave-like variations with such a period, we have repeatedly recorded in time variations of the amplitude and relaxation time of the scattered signal, temperature, vertical and turbulent velocities [21,22,30,31,32,39,43,44,45,46,50,51,52,53,54,55]. The temporal temperature variations observed in these experiments were undulating with a period from 5 min to several hours, which is typical for IGW.
In [32,42], examples of experimental height temperature profiles T(z) with a negative altitude gradient and subsequent development of disturbances in atmospheric parameters are presented and discussed. It is shown that the instability of the environment associated with a significant decrease of the temperature with a height increasing plays an important role in the temperature variations of the neutral component. In the approximation of a linear altitude dependence of temperature, a sufficient condition for the development of an instability is the fulfillment of the condition dT/dz < –(10–12) K/m. Based on the analysis of a large volume of time–altitude dependences of temperature and regular vertical motion velocity, it was concluded that when IGW propagates above 100 km, convective instabilities can be observed, which ensure the transfer of energy from the turbulent region to the lower thermosphere [42]. Excitation of IGW of different periods and associated instabilities should lead to environment turbulization. We found that in an atmosphere disturbed by waves below the turbopause level, turbulent velocities up to 5–7 m/s can be observed [32].
In many temperature profiles, minima of the temperature above 100 km were observed. Such profiles are shown in Figure 5, Figure 6 and Figure 8. Minima can appear as a result of the influence of various processes. They can arise due to the shift of the mesopause from 89–90 km to the region of heights above 90 km. There may also be a two-level mesopause effect, often occurring at equinoxes. In this case, the second temperature minimum appears near 100 km, as was shown in [55]. Probably, this effect can be observed not only at the equinox.
Temperature profiles with a deeper minimum of the temperature are shown in Figure 5 and Figure 8. They can probably be identified as temperature inversions. Temperature inversions were observed by lidars at altitudes between 70 and 90 km [56]. It was possible that they could also take place at above 100 km in the lower thermosphere [47]. The temperature gradients on the lower branch of these profiles exceeded the adiabatic gradient. These temperature profiles can be created through a wide variety of circumstances. In particular, they can be created when the heat flow upwards from the region of IGW dissipation occurs. Heating can contribute to an increase in temperature at the bottom of the profile. This is probably a consequence of the existence of these molecular or ionic layers, which are observed at these heights from time to time, and this can also affect temperature profile variations [4].
6. Conclusions
We have presented some results of temperature measurements in the lower thermosphere. The API technique makes it possible to determine the temperature of the lower thermosphere and to study its altitude–temporal features. The height and temporal resolutions are of the order of 1 km and 15 s, respectively, which makes it possible to study both fast and slow processes in the lower thermosphere. Large temperature variability at altitudes of 90–130 km during the day and from day to day, due to the propagation of atmospheric waves, has been confirmed.
The IGW manifestation in the temperature variations of the lower thermosphere has been confirmed. In the altitude–time variations of the amplitude and relaxation time of the scattered signal, as well as the temperature of the atmosphere, manifestations of wave-like motions of various periods are constantly present. IGWs are the most probable cause of them since parameter variations occur with character periods of these waves. The wave periods ranged from 5 min to several hours. The maximum duration of measurements was 10 h in summer.
Figure 5, Figure 6 and Figure 7 show that the vertical temperature profiles are highly variable. Among the large number of profiles obtained, one can find smooth monotonous profiles, profiles with a temperature minimum or maximum, and profiles with an irregular temperature change with height. On the basis of our previous studies, we concluded that irregularity can be associated with processes occurring in the lower thermosphere and mesosphere. One of them is atmospheric turbulence, which affects temperature below the turbopause level. This level is often at altitudes of 100–110 km. Other processes are atmospheric waves, including IGW with a vertical wave scale of 4–10 km and hydrodynamic instabilities, for example, a convective one, which can lead to an irregular shape of the height temperature profile.
We have found that the altitude temperature profiles differ for the most part from those calculated according to the MSIS-E-90 model. One of the reasons is the averaged nature of the model, in which it is not possible to take into account fast and small-scale variations in atmospheric parameters. Another reason for the differences is the use of a real electron density profile in the determining of the temperature by the API technique, which includes the dynamics of the ionosphere, including small-scale changes in the height profile of the electron density. The lower limit of measuring of the temperature of the lower thermosphere by the API technique is determined by the turbopause level, and the upper one depends on the diffusion nature of the relaxation of inhomogeneities.
On the whole, it can be concluded that the results of temperature measurements by the API method at altitudes of 90–130 km give a more complex picture of its variations than we assumed previously.
Author Contributions
Conceptualization, N.V.B. and G.I.G.; methodology, N.V.B.; software, E.E.K.; validation, N.V.B., G.I.G. and E.E.K.; formal analysis, N.V.B.; investigation, N.V.B. and I.N.Z.; resources, N.V.B., E.E.K. and I.N.Z.; data curation, N.V.B., E.E.K. and I.N.Z.; writing—original draft preparation, N.V.B.; writing—review and editing, N.V.B. and G.I.G.; visualization, N.V.B. and I.N.Z.; supervision, N.V.B.; project administration, N.V.B.; funding acquisition, N.V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Science Foundation grant number 20-17-00050.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The results were obtained using the equipment of the SURA heating facility http://www.nirfi.unn.ru/stend-sura/ accessed on 1 February 2022. The work of the SURA facility is supported by the project No. FSWR-2023-0038 of the state task of the Ministry of Education and Science of Russia. We are grateful to reviewers for the insightful comments and valuable suggestions on the improvement of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gossard, E.E.; Hooke, W.H. Waves in the Atmosphere; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 1975; 456p. [Google Scholar]
- Hines, C.O. Internal atmospheric gravity waves at atmospheric heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Lubken, F.-J.; von Zahn, U.; Manson, A.; Meek, C.; Hoppe, P.; Schmidlin, F.J.; Stegman, J.; Murtagh, D.P.; Ruster, R.; Schmidt, G.; et al. Means state densities, temperatures and winds during MAC/SINE and MAC/EPSILON campaign. J. Atmos. Terr. Phys. 1990, 52, 955–970. [Google Scholar] [CrossRef]
- Delgado, R.; Friedman, J.S.; Fentzke, J.T.; Raizada, S.; Tepley, C.A.; Zhou, Q. Sporadic metal atom and ion layers and their connection to chemistry and thermal structure in the mesopause region at Arecibo. J. Atmos. Sol. Terr. Phys. 2012, 74, 11–23. [Google Scholar] [CrossRef]
- Offermann, D.; Jarisch, M.; Oberheide, J.; Gusev, O.; Wohltmann, I.; Russel, J.M., III; Mlynczak, M.G. Global wave activity from upper stratosphere to lower thermosphere: A new turbopause concept. J. Atmos. Sol. Terr. Phys. 2006, 68, 1709–1729. [Google Scholar] [CrossRef]
- Tsuda, T.; Kato, S.; Yokol, T.; Inoue, T.; Yamamoto, M.; VanZand, T.E.; Fukao, S.; Sato, T. Gravity waves in the mesosphere observed with the middle and upper atmosphere radar. Radio Sci. 1990, 26, 1005–1018. [Google Scholar] [CrossRef]
- Offermann, D.; Goussev, O.; Kalicinsky, C.; Koppmann, R.; Matthes, K.; Schmidt, H.; Steinbrecht, W.; Wintel, J. A case study of multi-annual temperature oscillations in the atmosphere: Middle Europe. J. Atmos. Sol.-Terr. Phys. 2015, 135, 1–11. [Google Scholar] [CrossRef]
- Beig, G. Long-term trends in the temperature of the mesosphere/lower thermosphere region: 2. Solar response. J. Geophys. Res. Atmos. 2011, 116, A00H12. [Google Scholar] [CrossRef]
- Perminov, V.I.; Semenov, A.I.; Medvedeva, I.V.; Zheleznov, Y.A. Variability of mesopause temperature from the hydroxyl airglow observations over mid-latitudinal sites, Zvenigorod and Tory, Russia. Adv. Space Res. 2014, 54, 2511–2517. [Google Scholar] [CrossRef]
- Mertens, C.J.; Schmidlin, F.J.; Goldberg, R.A.; Remsberg, E.E.; Pesnell, W.D.; Russell, J.M.; Mlynczak, M.G.; López-Puertas, M.; Wintersteiner, P.P.; Picard, R.H.; et al. SABER observations of mesospheric temperatures and comparisons with falling sphere measurements taken during 2002 summer MaCWAVE campaign. Geophys. Res. Lett. 2004, 31, L03105. [Google Scholar] [CrossRef]
- Schmidlin, F.J. The inflatable sphere: A technique for the accurate measurement of middle atmosphere temperatures. J. Geophys. Res. 1991, 96, 22673–22682. [Google Scholar] [CrossRef]
- She, C.Y.; Chen, S.; Hu, Z.; Vance, J.D.; Vasoli, V.; White, M.A.; Yu, J.; Krueger, D.A. Eight-year climatology of nocturnal temperature and sodium density in the mesopause region (80–105 km) over Fort Collins, CO (41 N, 105 W). Geophys. Res. Lett. 2000, 27, 3289–3292. [Google Scholar] [CrossRef]
- Khomich, V.Y.; Semenov, A.I.; Shefov, N.N. Airglow as an Indicator of Upper Atmospheric Structure and Dynamics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Cai, X.; Yuan, T.; Zhao, Y.; Pautet, P.-D.; Taylor, M.J.; Pendleton, W.R. A coordinated investigation of the gravity wave breaking and the associated dynamical instability by a Na lidar and an Advanced Mesosphere Temperature Mapper over Logan, UT (41.7° N, 111.8° W). J. Geophys. Res. Space Phys. 2014, 119, 6852–6864. [Google Scholar] [CrossRef]
- Yuan, T.; Pautet, P.-D.; Zhao, Y.; Cai, X.; Criddle, N.R.; Taylor, M.J.; Pendleton, W.R. Coordinated investigation of midlatitude upper mesospheric temperature inversion layers and the associated gravity wave forcing by Na lidar and Advanced Mesospheric Temperature Mapper in Logan, Utah. J. Geophys. Res. Atmos. 2014, 119, 3756–3769. [Google Scholar] [CrossRef]
- Huang, K.M.; Liu, H.; Liu, A.Z.; Zhang, S.D.; Huang, C.M.; Gong, Y.; Ning, W.H. Investigation on spectral characteristics of gravity waves in the MLT using lidar observations at Andes. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028918. [Google Scholar] [CrossRef]
- Neuber, R.; von der Gathen, P.; von Zahn, U. Altitude and temperature of the mesopause at 69° N latitude in Winter. J. Geophys. Res. 1988, 93, 11093–11101. [Google Scholar] [CrossRef]
- Kirkwood, S. Lower thermosphere mean temperatures, densities and winds measured by EISCAT: Seasonal and solar cycle effects. J. Geophys. Res. 1996, 101, 5133–5148. [Google Scholar] [CrossRef]
- Nozawa, S.; Kawahara, T.D.; Saito, N.; Hall, C.M.; Tsuda, T.T.; Kawabata, T.; Wada, S.; Brekke, A.; Takahashi, T.; Fujiwara, H.; et al. Variations of the neutral temperature and sodium density between 80 and 107 km above Tromsø during the winter of 2010–2011 by a new solid-state sodium lidar. JGR Space Phys. 2014, 119, 441–451. [Google Scholar] [CrossRef]
- Kofman, W.; Lathuillere, C.; Pibaret, B. Neutral atmosphere studies in the altitude range 90–110 km using EISCAT. J. Atmos. Terr. Phys. 1986, 48, 837–847. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Benediktov, E.A.; Tolmacheva, A.V.; Bakhmet’eva, N.V. Ionospheric Research by Means of Artificial Periodic Irregularities; Copernicus GmbH: Katlenburg-Lindau, Germany, 2002. [Google Scholar]
- Bakhmetieva, N.V.; Grigoriev, G.I. Study of the Mesosphere and Lower Thermosphere by the Method of Creating Artificial Periodic Irregularities of the Ionospheric Plasma. Atmosphere 2022, 13, 1346. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Benediktov, E.A.; Getmantsev, G.G.; Ignat’ev, Y.A.; Komrakov, G.P. Scattering of radio waves from the artificially perturbed F region of the ionosphere (Engl. Translation). JETP Lett. 1975, 22, 243–244. [Google Scholar]
- Available online: https://ccmc.gsfc.nasa.gov/modelweb/models/msis_vitmo.php (accessed on 15 December 2022).
- Frolov, V.L.; Bakhmet’eva, N.V.; Belikovich, V.V.; Vertogradov, G.G.; Vertogradov, V.G.; Komrakov, G.P.; Kotik, D.S.; Mityakov, N.A.; Polyakov, S.V.; Rapoport, V.O.; et al. Modification of the Earth’s ionosphere by high power high frequency radio waves. Phys.-Uspekhi. 2007, 50, 315–324. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Vyakhirev, V.V.; Kalinina, E.E. Studies of the ionosphere using partial reflections. Geomag. Aeron. 2004, 44, 170–174. [Google Scholar]
- Belikovich, V.V.; Benediktov, E.A.; Goncharov, N.P.; Tolmacheva, A.V. Diagnostics of the ionosphere and neutral atmosphere at E-region heights using artificial periodic inhomogeneities. J. Atmos. Sol.-Terr. Phys. 1997, 59, 2447–2460. [Google Scholar] [CrossRef]
- Benediktov, E.A.; Belikovich, V.V.; Tolmacheva, A.K. Some results of measurement of atmospheric temperature and density using artificial periodic inhomogeneities of the ionospheric plasma. Radiophys. Quantum Electron. 1998, 41, 229–235. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Belikovich, V.V. Measurements of the temperature and density of the upper atmosphere using artificial periodic irregularities during the summer seasons of 1999–2002. Int. J. Geomagn. Aeron. 2004, 5, GI1008. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Bakhmetieva, N.V.; Grigoriev, G.I.; Kalinina, E.E. The main results of the long-term measurements of the neutral atmosphere parameters by the artificial periodic irregularities techniques. Adv. Space Res. 2015, 56, 1185–1193. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Vyakhirev, V.D.; Grigoriev, G.I.; Egerev, M.N.; Kalinina, E.E.; Tolmacheva, A.V.; Zhemyakov, I.N.; Vinogradov, G.R.; Yusupov, K.M. Dynamics of the mesosphere and lower thermosphere based on results of observations on the SURA facility. Geomag. Aeron. 2020, 60, 96–111. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigoriev, G.I.; Vinogradov, G.R.; Zhemyakov, I.N.; Kalinina, E.E.; Pershin, A.V. Parameters of Atmospheric Turbulence and the Dynamics of the Lower Ionosphere in Studies at the SURA Facility. Geomag. Aeron. 2021, 61, 871–887. [Google Scholar] [CrossRef]
- Banks, P.M.; Kockarts, G. Aeronomy, Part A.; Academic Press: Cambridge, MA, USA; University of California: Los Angeles, CA, USA, 1973. [Google Scholar]
- Huuskonen, A.; Nygren, T.; Jalonen, L.L.; Bjorn, N.; Hansen, T.L.; Brekke, A. Ion composition in sporadic E layers measured by the EISCAT UHF radar. J. Geophys. Res. 1988, 93, 14603. [Google Scholar] [CrossRef]
- Kopp, E. On the abundance of metal ions in the lower ionosphere. J. Geophys. Res. Space Phys. 1997, 102, 9967–9974. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Egerev, M.N.; Tolmacheva, A.V. Artificial periodic irregularities, wave phenomena in the lower ionosphere, and the sporadic E layer. Radiophys. Quantum Electron. 2010, 53, 69–81. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Bakhmeteva, N.V.; Kalinina, E.E.; Tolmacheva, A.V. A New method for determination of the electron number density in the E region of the ionosphere from relaxation times of artificial periodic inhomogeneities. Radiophys. Quantum Electron. 2006, 49, 669–674. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Bakhmet’eva, N.V.; Vyakhirev, V.D.; Bubukina, V.N.; Kalinina, E.E. Altitude–time variations in electron number density in the ionospheric E layer. Radiophys. Quantum Electron. 2011, 54, 365–375. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Vyakhirev, V.D.; Kalinina, E.E.; Komrakov, G.P. Earth’s lower ionosphere during partial solar eclipses according to observations near Nizhny Novgorod. Geomagn. Aeron. 2017, 57, 58–71. [Google Scholar] [CrossRef]
- Available online: https://ccmc.gsfc.nasa.gov/modelweb/models/iri2016_vitmo.php (accessed on 15 December 2022).
- Bakhmetieva, N.V.; Grigoriev, G.I.; Tolmacheva, A.V.; Zhemyakov, I.N. Investigations of Atmospheric Waves in the Earth Lower Ionosphere by Means of the Method of the Creation of the Artificial Periodic Irregularities of the Ionospheric Plasma. Atmosphere 2019, 10, 450. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Grigoriev, G.I.; Bakhmetieva, N.V. The variations of the atmospherical parameters on measurements using the artificial periodic irregularities of plasma. Russ. J. Phys. Chem. B. 2013, 7, 663–669. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigor’ev, G.I.; Tolmacheva, A.V. Artificial periodic irregularities, hydrodynamic instabilities, and dynamic processes in the mesosphere-lower thermosphere. Radiophys. Quantum Electron. 2011, 53, 623–637. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigor’ev, G.I.; Tolmacheva, A.V.; Kalinina, E.E. Atmospheric turbulence and internal gravity waves examined by the method of artificial periodic irregularities. Russ. J. Phys. Chem. B. 2018, 12, 510–521. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Benediktov, E.A.; Bubukina, V.N.; Goncharov, N.P.; Ignat’ev, Y.A. Investigation of acoustic gravity waves in the upper atmosphere by the artificial periodic inhomogeneities method at Nizhny Novgorod. Radiophys. Quantum Electron. 1996, 39, 224–228. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Bakhmetieva, N.V.; Grigoriev, G.I.; Egerev, M.N. Turbopause range measured by the method of the artificial periodic irregularities. Adv. Space Res. 2019, 64, 1968–1974. [Google Scholar] [CrossRef]
- Liu, X.; Maura, J.; Hagan, E.; Roble, R.G. Local mean state changes due to gravity wave breaking modulated by the diurnal tide. J. Geophys. Res. 2000, 105, 12381–12396. [Google Scholar] [CrossRef]
- Hauchecorne, A.; Chanin, M.L.; Wilson, R. Mesospheric temperature inversion and gravity wave breaking. Geophys. Res. Lett. 1987, 14, 933–936. [Google Scholar] [CrossRef]
- Rauthe, M.; Gerding, M.; Höffner, J.; Lübken, F.J. Lidar temperature measurements of gravity waves over Kühlungsborn (54° N) from 1 to 105 km: A winter-summer comparison. J. Geophys. Res. Atmos. 2006, 111, D24108. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Zhemyakov, I.N. Vertical plasma motions in the dynamics of the mesosphere and lower thermosphere of the Earth. Russ. J. Phys. Chem. B. 2022, 16, 990–1007. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigor’ev, G.I.; Tolmacheva, A.V.; Kalinina, E.E.; Egerev, M.N. Internal gravity waves in the lower thermosphere with linear temperature profile: Theory and experiment. Radiophys. Quantum Electron. 2017, 60, 103–112. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigoriev, G.I.; Kalinina, E.E. Acoustic gravity waves with a heterogeneous temperature profile of the neutral component in the earth’s atmosphere. Russ. J. Phys. Chem. B. 2022, 16, 499–507. [Google Scholar] [CrossRef]
- Grigor’ev, G.I.; Bakhmetieva, N.V.; Tolmacheva, A.V.; Kalinina, E.E. Relaxation time of artificial periodic irregularities of the ionospheric plasma and diffusion in the inhomogeneous atmosphere. Radiophys. Quantum Electron. 2013, 56, 187–196. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Belikovich, V.V.; Grigor’ev, G.I.; Tolmacheva, A.V. Effect of acoustic gravity waves on variations in the lower-ionosphere parameters as observed using artificial periodic inhomogeneities. Radiophys. Quantum Electron. 2002, 45, 211–219. [Google Scholar] [CrossRef]
- She, C.Y.; von Zahn, U. The concept of two-level mesopause: Support through new lidar observations. J. Geophys. Res. 1998, 103, 5855–5863. [Google Scholar] [CrossRef]
- Szewczyk, A.; Strelnikov, B.; Rapp, M.; Strelnikova, I.; Baumgarten, G.; Kaifler, N.; Dunker, T.; Hoppe, U.-P. Simultaneous observations of a mesospheric inversion layer and turbulence during the ECOMA-2010 rocket campaign. Ann. Geophys. 2013, 31, 775–785. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).