Impact of Soil Moisture in the Monsoon Region of South America during Transition Season
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Global Model
2.2. Numerical Experiments
2.3. Production of a New Soil Moisture Field
2.4. Reference Datasets
2.5. Land–Atmosphere Coupling Metrics
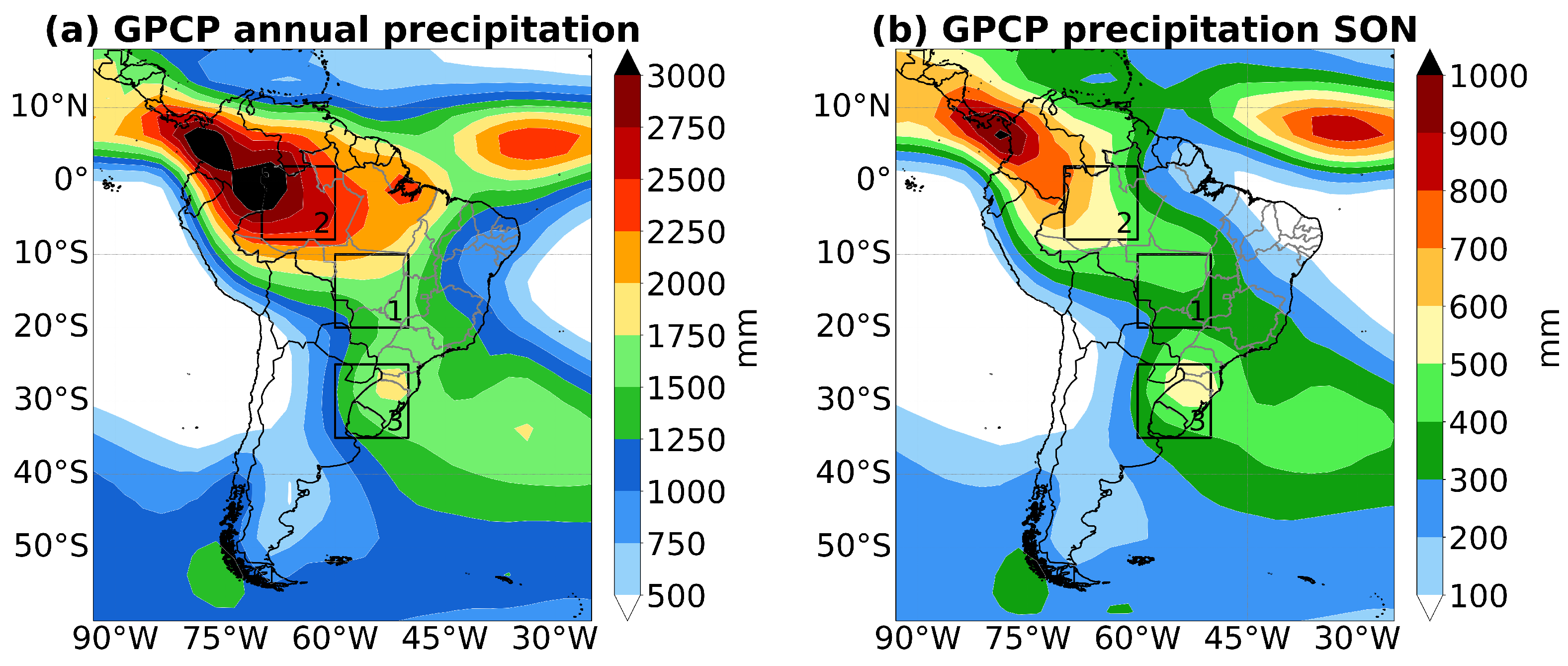
2.6. Areas of Interest
3. Results
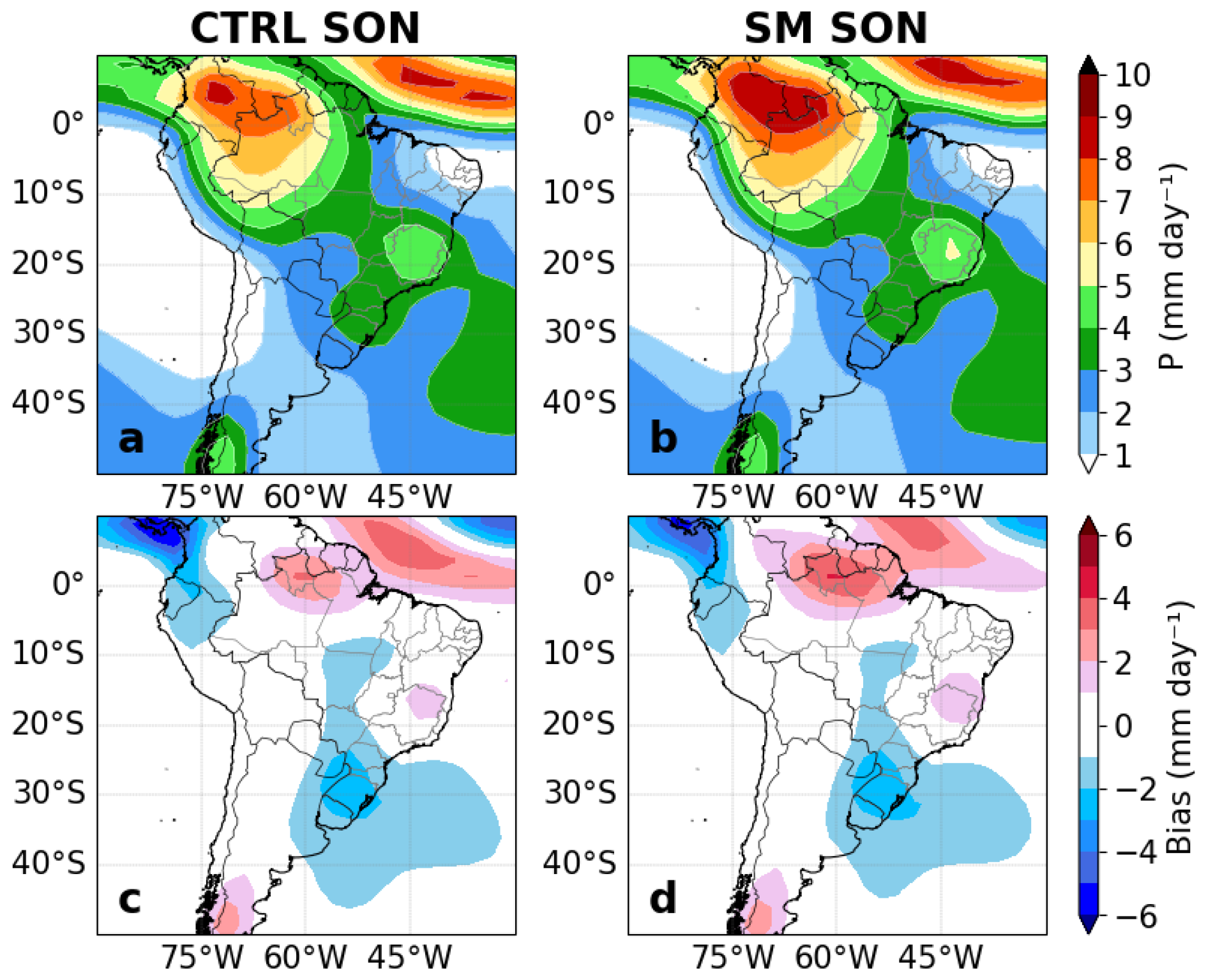
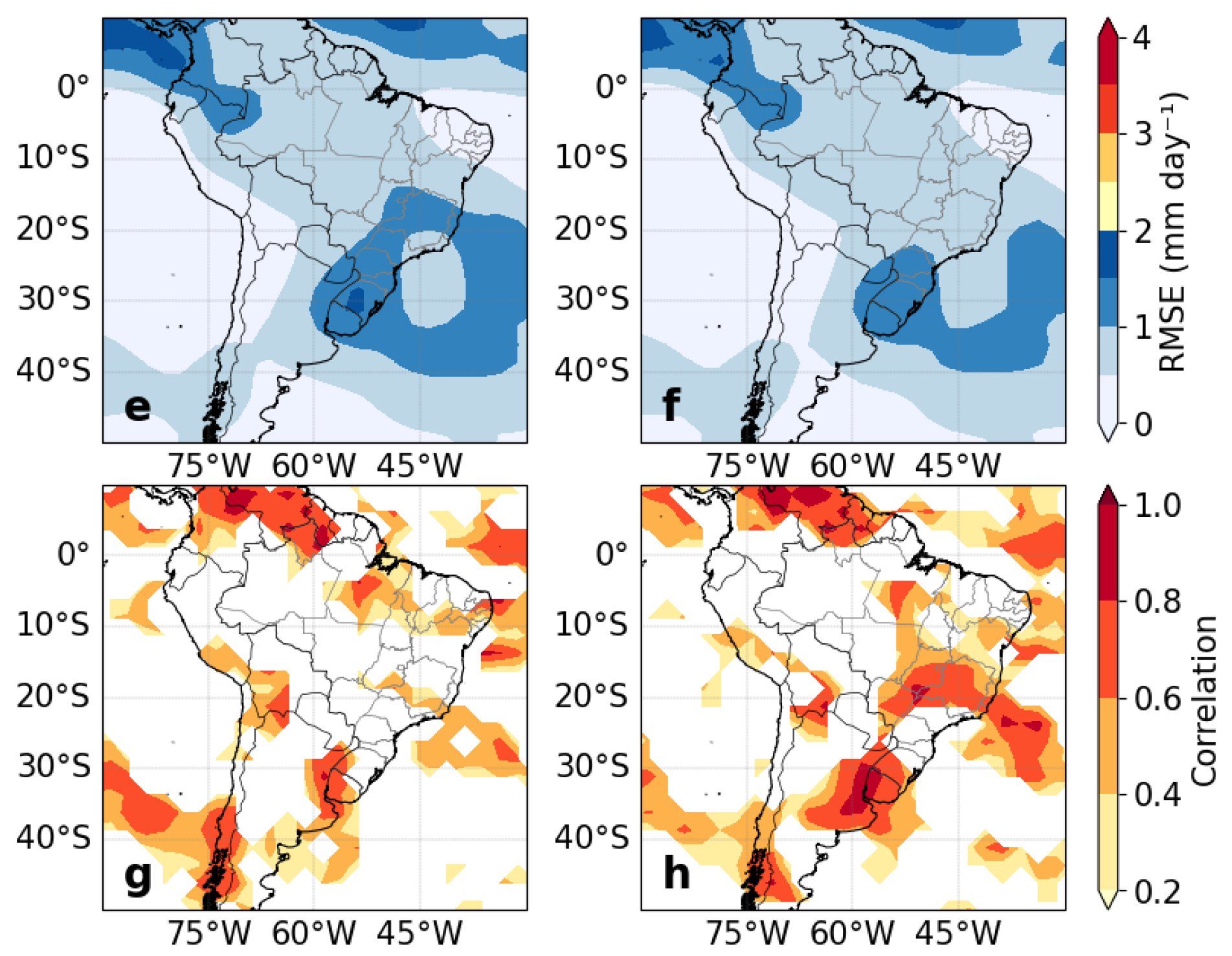
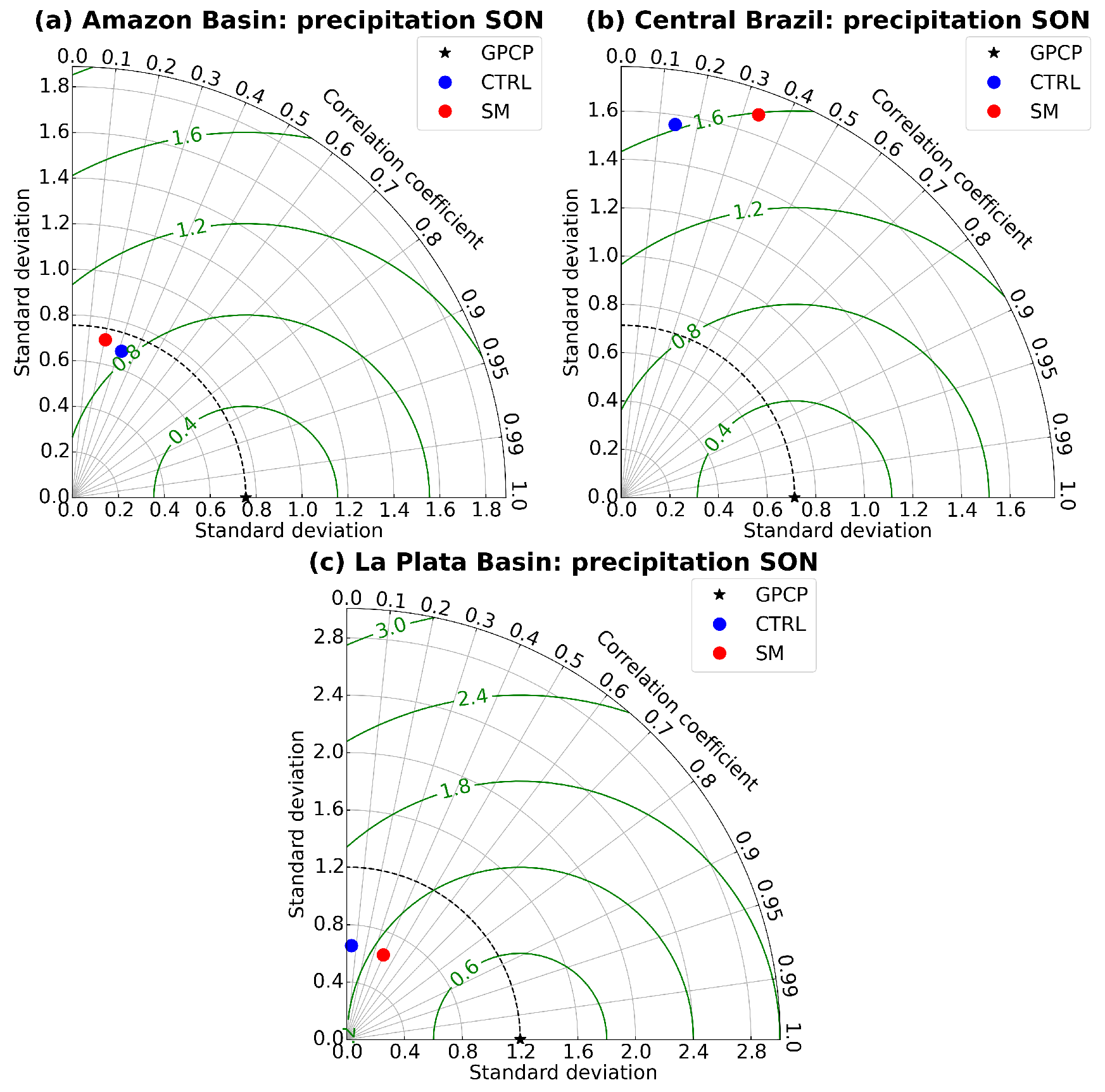
3.1. Forecast Ability for Precipitation
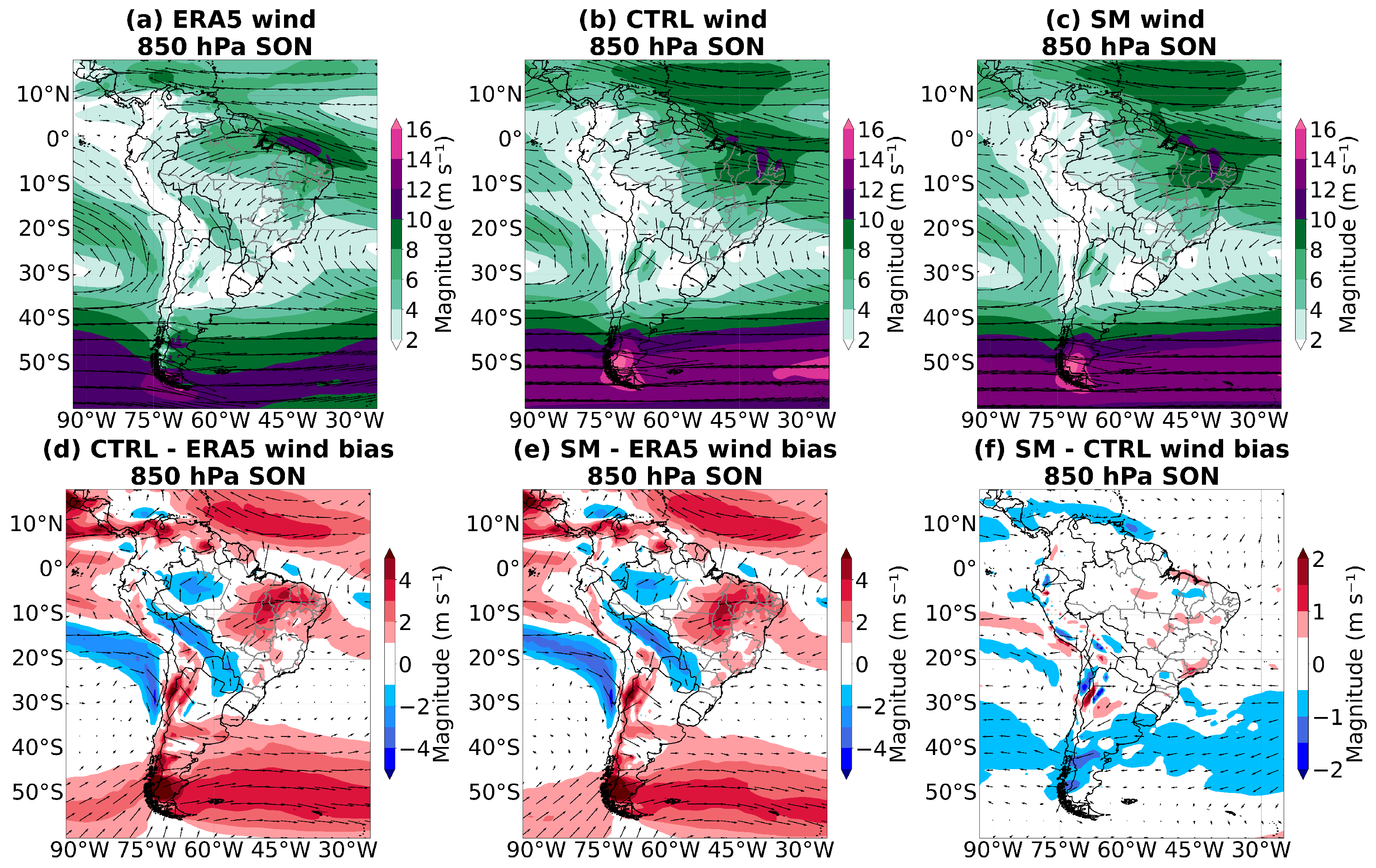
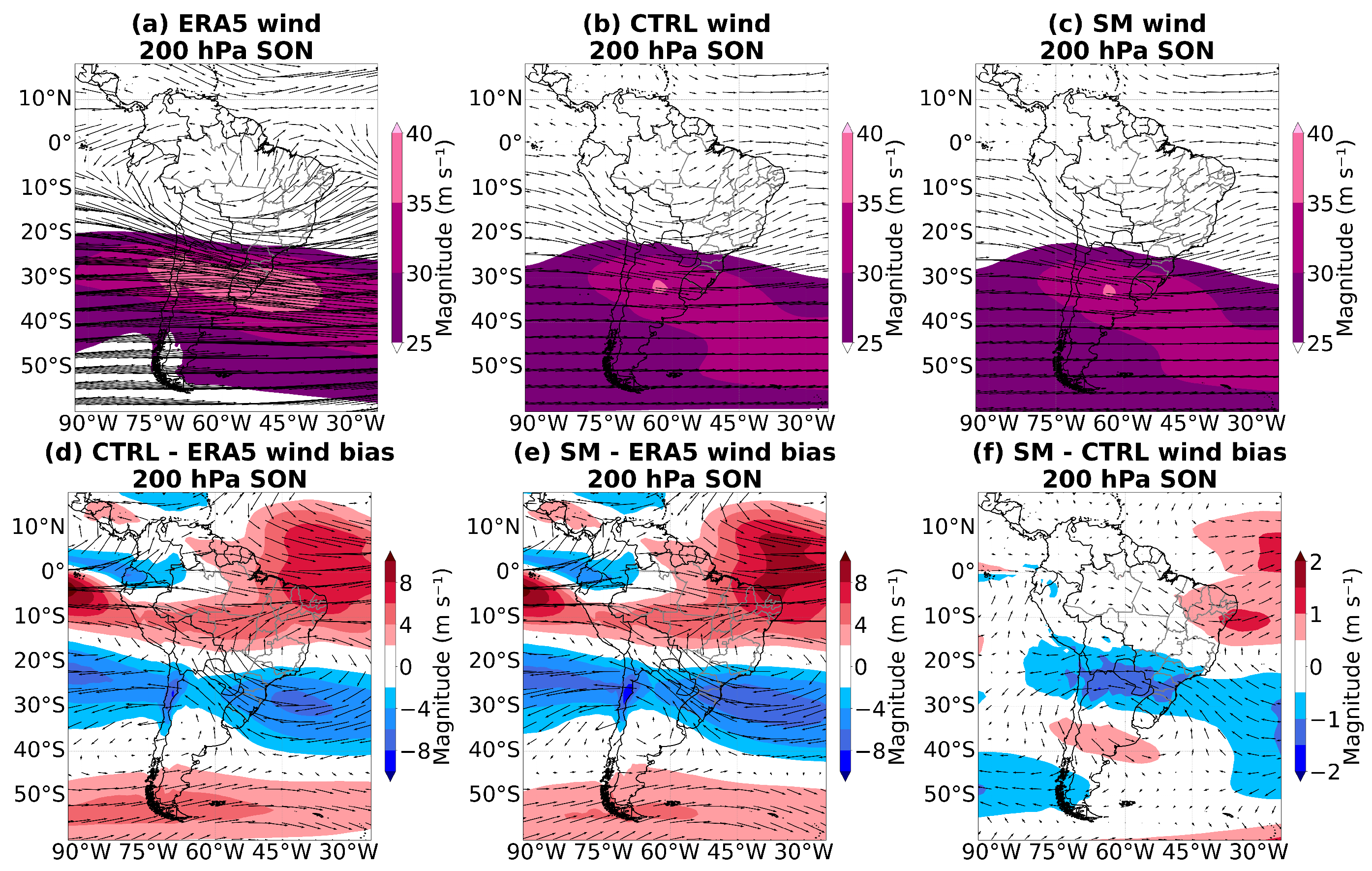
3.2. Circulation at Low and High Levels
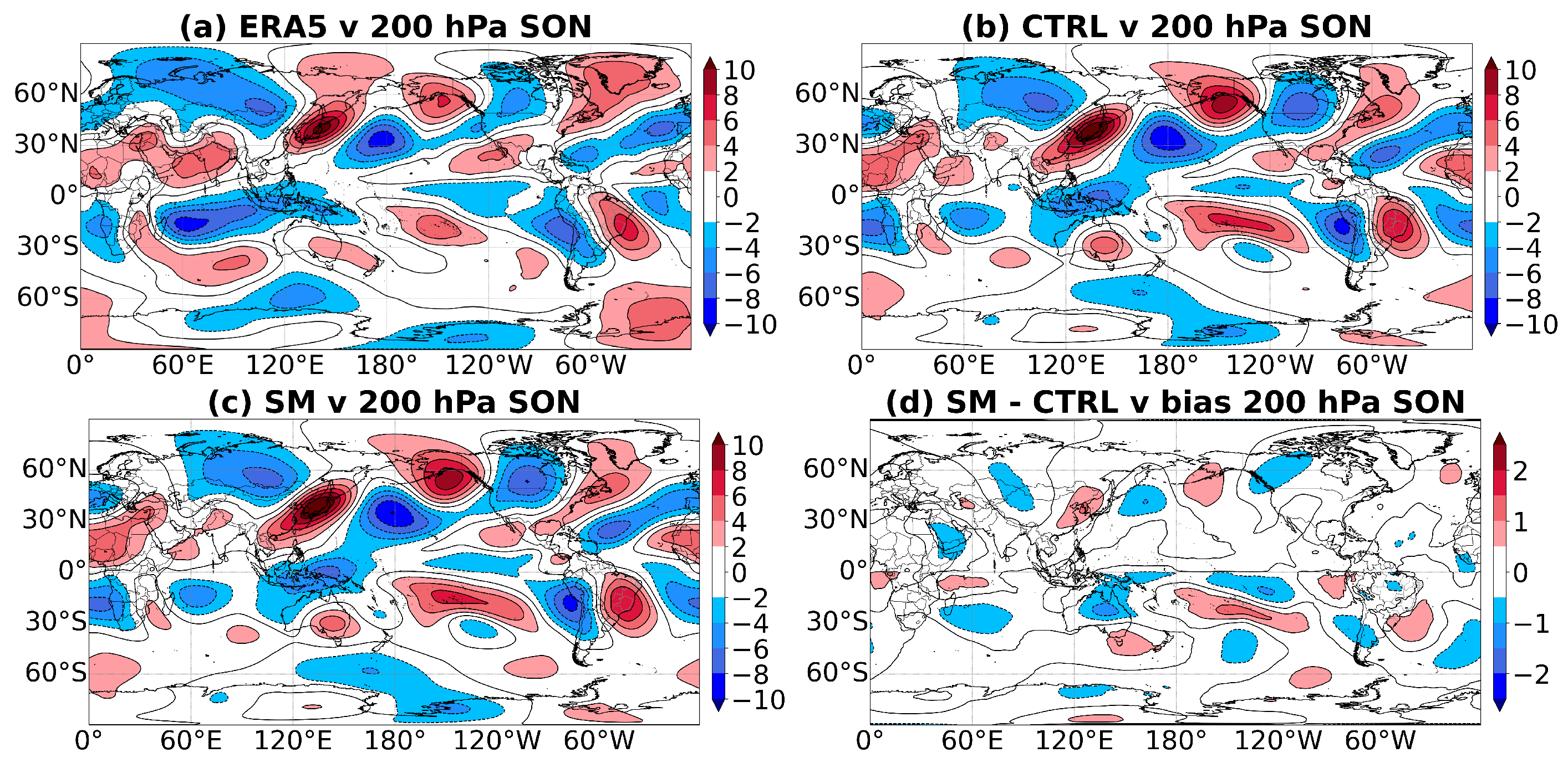
3.3. Meridional Wind Component
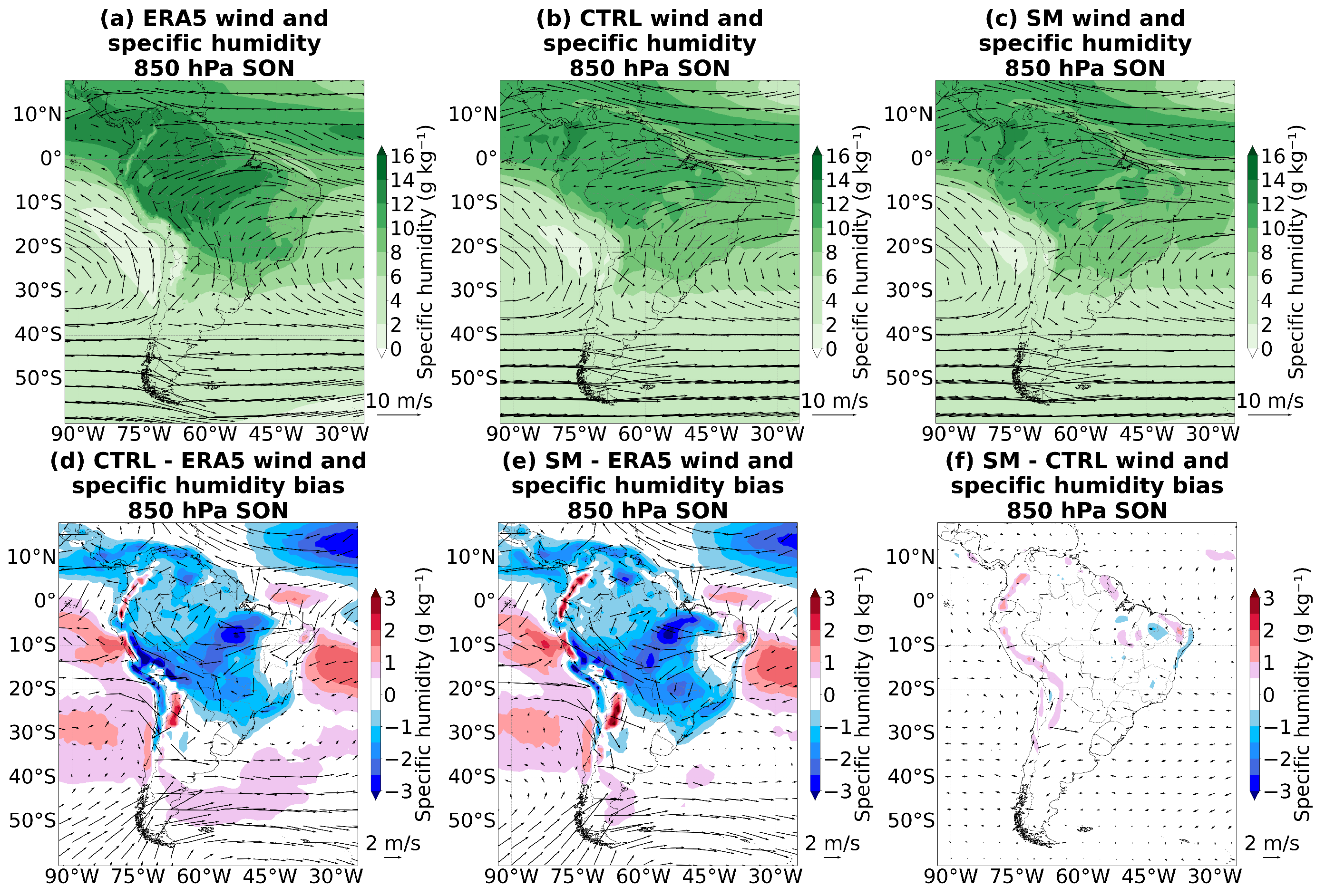
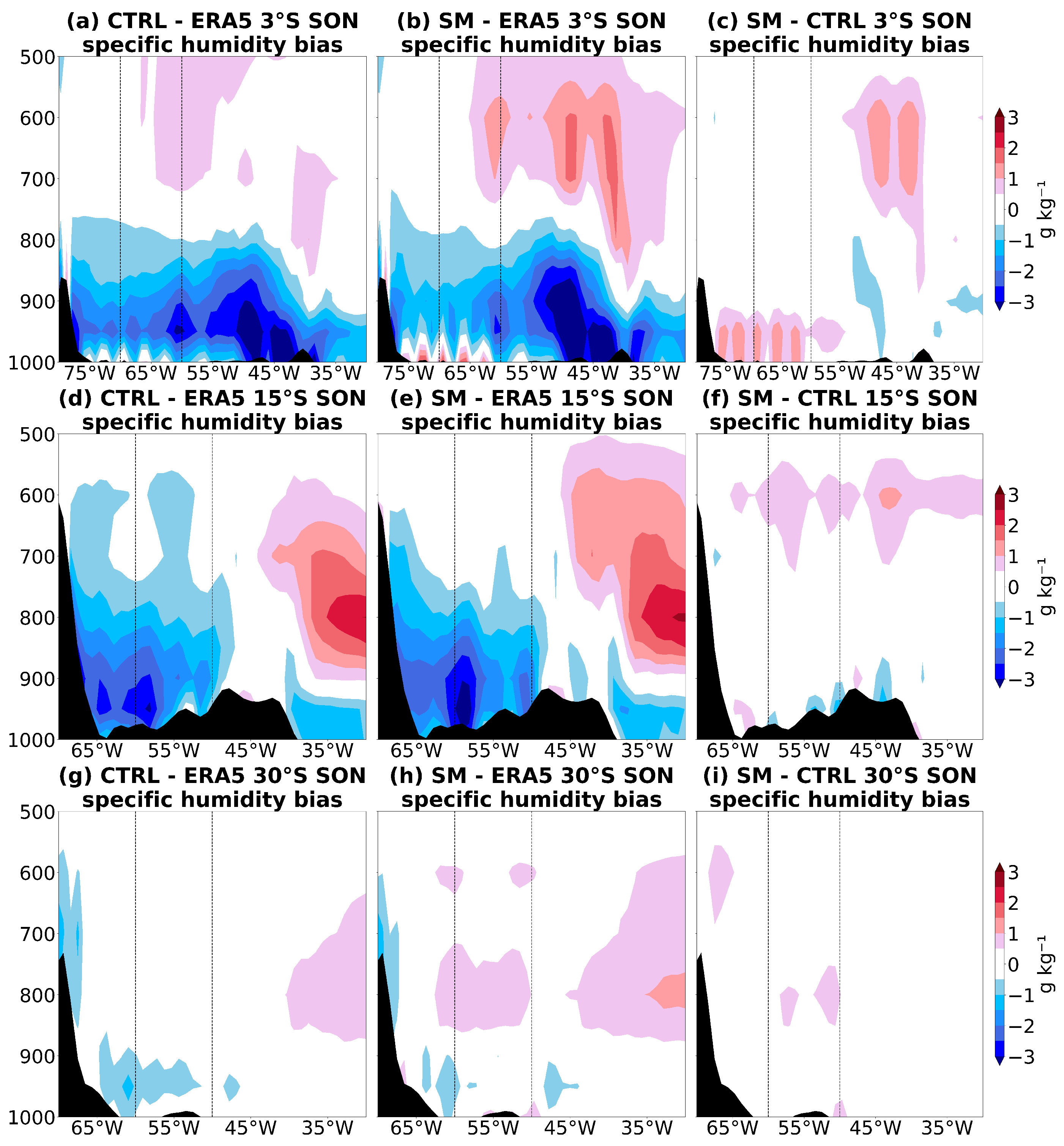
3.4. Humidity Distribution
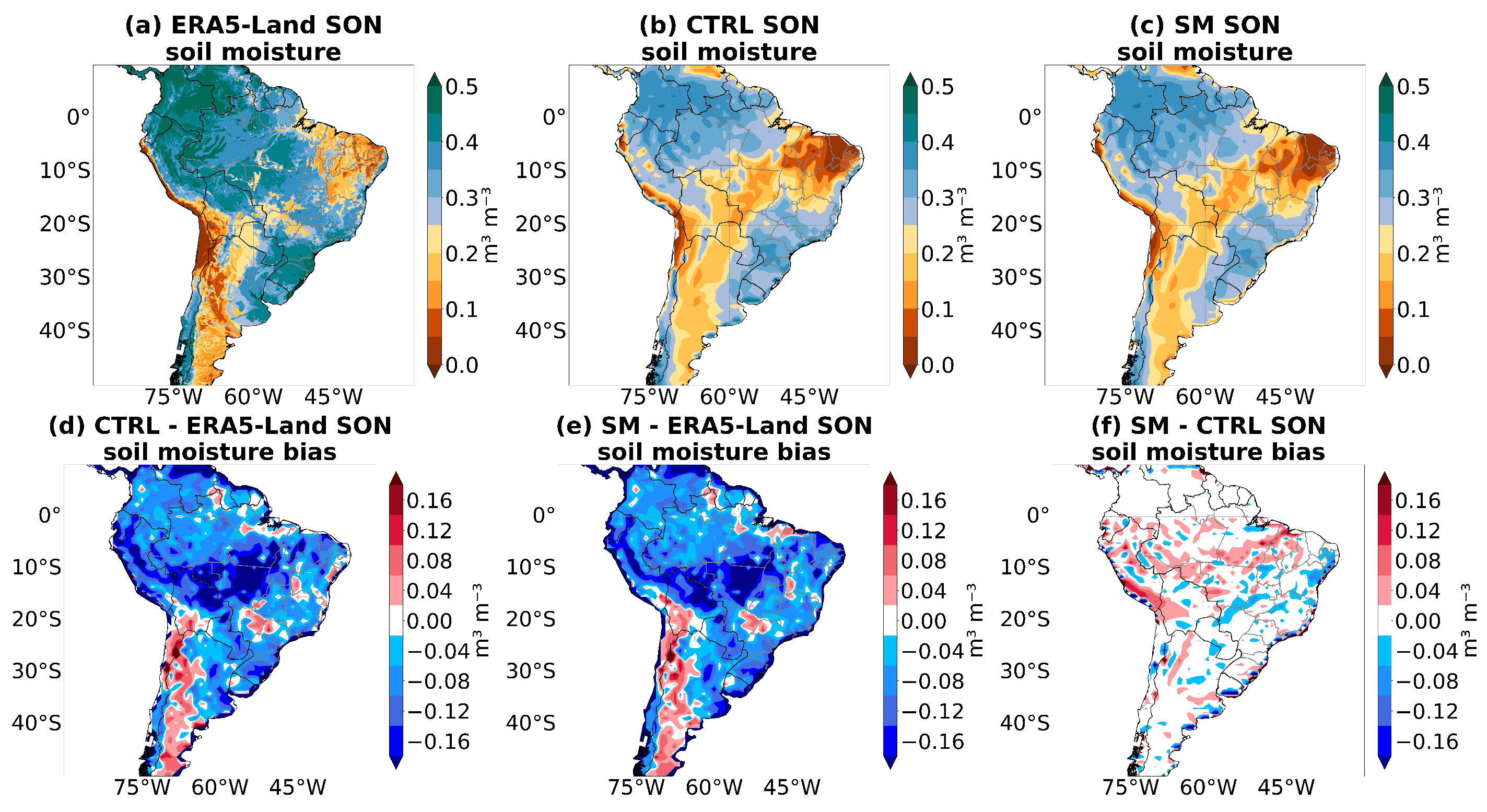
3.5. Soil Moisture
3.6. Surface Temperature
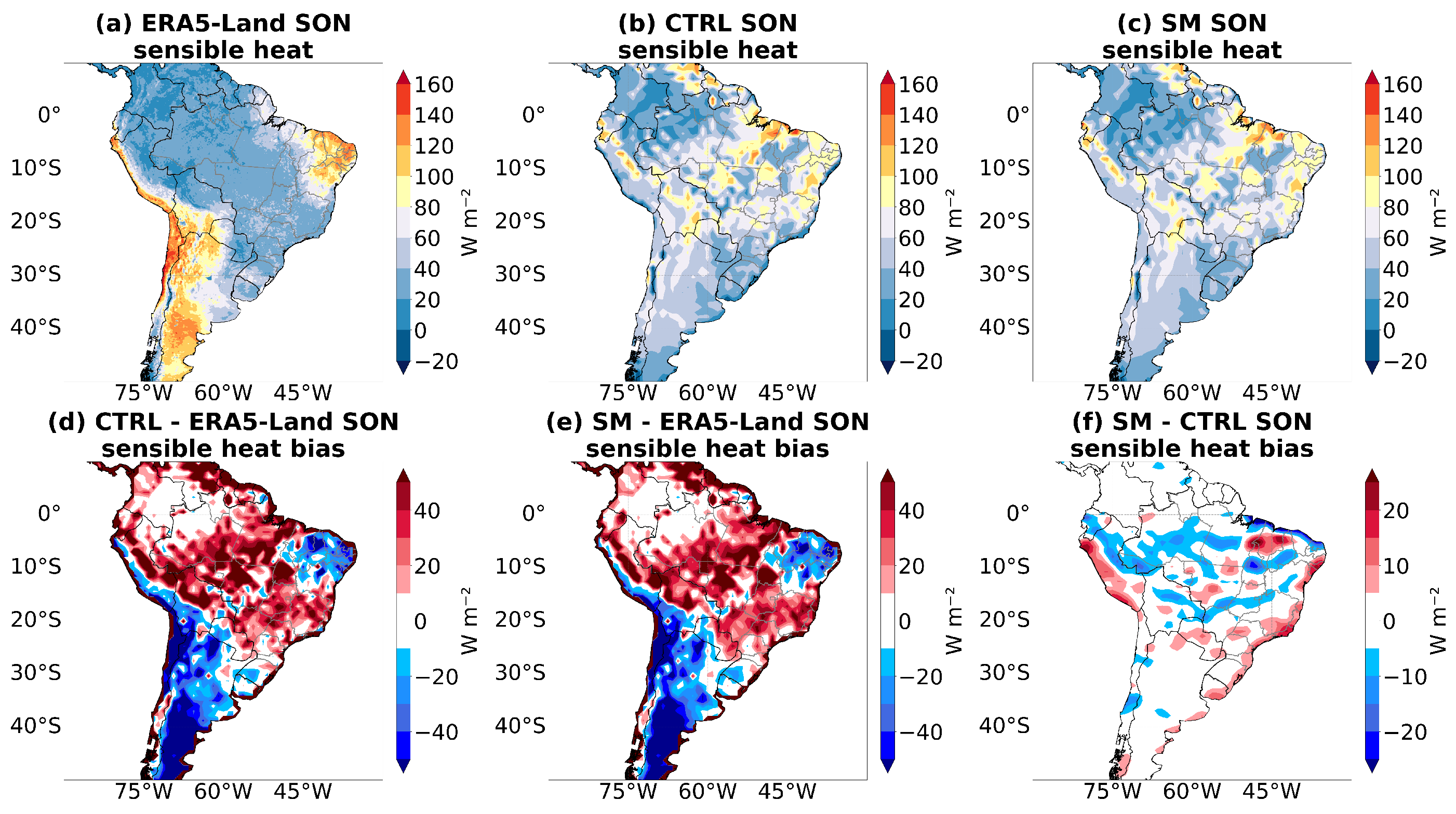
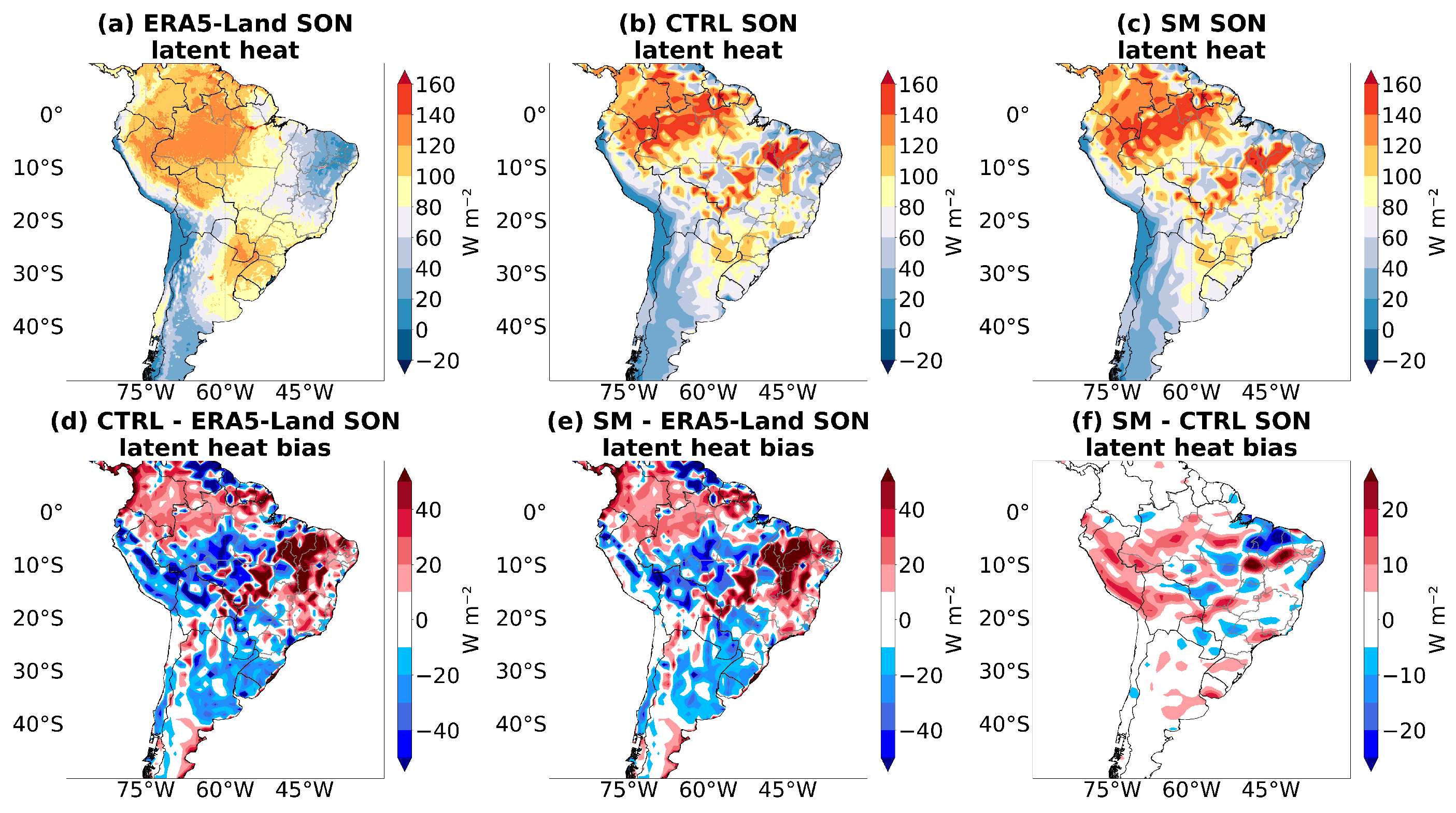
3.7. Surface Heat Fluxes
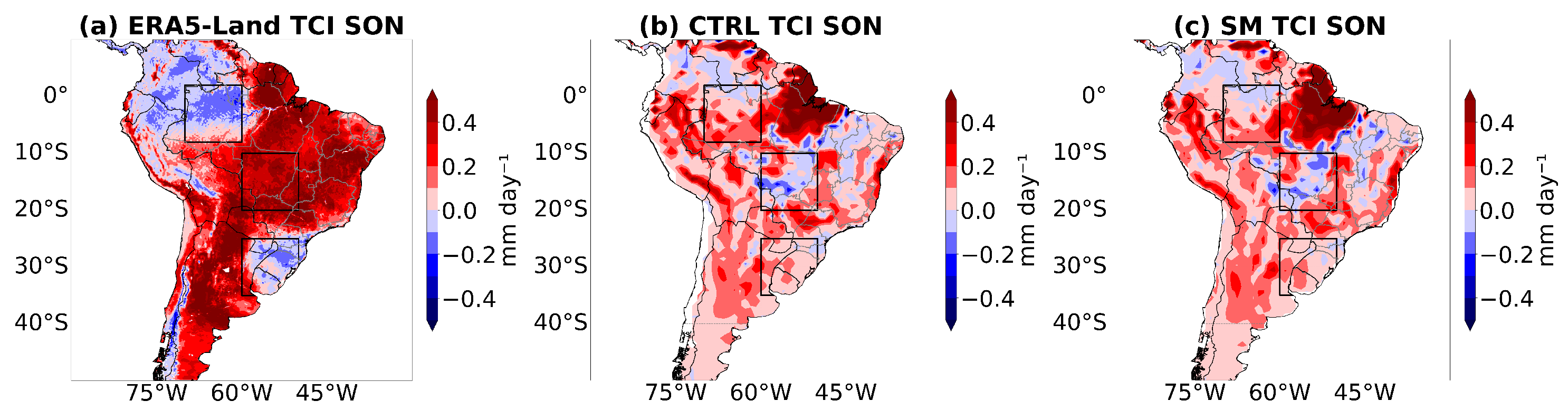
3.8. Land–Atmosphere Interactions
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGCM | Atmospheric General Circulation Model |
| BAM | Brazilian global Atmospheric Model |
| BAM CTRL | BAM Control experiment |
| BAM SM | BAM Soil Moisture experiment |
| CERES | Clouds and the Earth’s Radiant Energy System |
| CPTEC | Centro de Previsão de Tempo e Estudos Climáticos |
| CTRL | Control |
| DJF | December, January, and February |
| ENSO | El Niño Southern Oscillation |
| ET | Evapotranspiration |
| GDAS | Global Data Assimilation System |
| GDP | Gross Domestic Product |
| GLDAS | Global Land Data Assimilation System |
| GPCP | Global Precipitation Climatology Project |
| GPM | Global Precipitation Measurement mission |
| IBIS | Integrated Biosphere Simulator |
| IMERG | Integrated Multi-satellite Retrievals for GPM |
| INPE | Instituto Nacional de Pesquisas Espaciais |
| ITCZ | Intertropical Convergence Zone |
| LDAS | Land Data Assimilation Systems |
| LIS | Land Information System |
| P | Precipitation |
| RMSE | Root-Mean-Squared Error |
| SACZ | South American Convergence Zone |
| SALDAS | South American Land Data Assimilation System |
| SAMS | South American Monsoon System |
| SM | Soil Moisture |
| SON | September, October, and November |
| SST | Sea Surface Temperature |
| T | Surface temperature |
| TCI | Terrestrial Coupling Index |
| T_ET | Temperature–Evapotranspiration Metric |
| TL | Two-Legged coupling metric |
| ZG | Zeng’s Gamma |
References
- Balanço Energético Nacional 2021: Ano Base 2020. Available online: https://www.epe.gov.br/sites-pt/publicacoes-dados-abertos/publicacoes/PublicacoesArquivos/publicacao-675/topico-638/BEN2022.pdf (accessed on 1 November 2022).
- PIB DO AGRONEGÓCIO BRASILEIRO. Available online: https://www.cepea.esalq.usp.br/br/pib-do-agronegocio-brasileiro.aspx (accessed on 1 November 2022).
- Stockdale, T.; Alves, O.; Boer, G.; Deque, M.; Ding, Y.; Kumar, A.; Kumar, K.; Landman, W.; Mason, S.; Nobre, P.; et al. Understanding and Predicting Seasonal-to-Interannual Climate Variability—The Producer Perspective. Procedia Environ. Sci. 2010, 1, 55–80. [Google Scholar] [CrossRef]
- Folland, C.K.; Colman, A.W.; Rowell, D.P.; Davey, M.K. Predictability of North East Brazil rainfall and real-time forecast skill, 1987–1998. J. Clim. 2001, 14, 1937–1958. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Lidard-Peters, C.; Balsamo, G. Land-Atmosphere Interactions and the Water Cycle; World Meteorological Organization: Geneve, Switzerland, 2015. [Google Scholar]
- Halder, S.; Dirmeyer, P.A.; Marx, L.; Kinter, J.L. Impact of Land Surface Initialization and Land-Atmosphere Coupling on the Prediction of the Indian Summer Monsoon with the CFSv2. Front. Environ. Sci. 2018, 5, 92. [Google Scholar] [CrossRef]
- Douville, H.; Conil, S.; Tyteca, S.; Voldoire, A. Soil moisture memory and West African monsoon predictability: Artefact or reality? Clim. Dyn. 2007, 28, 723–742. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.P.; Yamada, T.J.; Balsamo, G.; Berg, A.A.; Boisserie, M.; Dirmeyer, P.A.; Doblas-Reyes, F.J.; Drewitt, G.; Gordon, C.T.; et al. Contribution of land surface initialization to subseasonal forecast skill: First results from a multi-model experiment. Geophys. Res. Lett. 2010, 6, 1–6. [Google Scholar] [CrossRef]
- Mattos, J.G.Z. A análise do Acoplamento de Processos de Superfície Continental e Atmosfera e o Impacto da Assimilação de Dados no Modelo Global do CPTEC/INPE; Doutorado em Meteorologia, Instituto Nacional de Pesquisas Espaciais (INPE): São José dos Campos, Brazil, 2016.
- de Gonçalves, L.G.G.; Shuttleworth, W.J.; Burke, E.J.; Houser, P.; Toll, D.L.; Rodell, M.; Arsenault, K. Toward a South America Land Data Assimilation System: Aspects of land surface model spin-up using the Simplified Simple Biosphere. J. Geophys. Res. 2006, 111, 1–13. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowakczyk, E.; Lawrence, D.; et al. Regions of Strong Coupling Between Soil Moisture and Precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Wang, G.; Mei, R.; Yu, Z.; Yu, M. Impact of initial soil moisture anomalies on climate mean and extremes over Asia. J. Geophys. Res. Atmos. 2014, 119, 529–545. [Google Scholar] [CrossRef]
- Guo, Z.; Dirmeyer, P.A.; Koster, R.D.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalkczyk, E.; Lawrence, D.; et al. GLACE: The Global Land-Atmosphere Coupling Experiment. Part II: Analysis. J. Hydrometeor. 2006, 7, 611–625. [Google Scholar] [CrossRef]
- Zhou, J.; Lau, K.-M. Does a Monsoon Climate Exist over South America? J. Clim. 1998, 11, 1020–1040. [Google Scholar] [CrossRef]
- Gan, M.A.; Kouski, V.E.; Repelewski, C.F. The South America Monsoon Circulation and Its Relationship to Rainfall over West-Central Brazil. J. Clim. 2004, 17, 47–66. [Google Scholar] [CrossRef]
- Jones, C.; Carvalho, L.M.V. Active and Break Phases in the South American Monsoon System. J. Clim. 2002, 15, 905–914. [Google Scholar] [CrossRef]
- Moon, S.; Ha, K. Early Indian Summer Monsoon Onset Driven by Low Soil Moisture in the Iranian Desert. Geophys. Res. Lett. 2019, 46, 10568–10577. [Google Scholar] [CrossRef]
- Collini, E.A.; Berbery, E.; Barros, V.R.; Pyle, M.E. How Does Soil Moisture Influence the Early Stages of the South American Monsoon? J. Clim. AMS 2008, 21, 195–213. [Google Scholar] [CrossRef]
- Grimm, A.M.; Pal, J.S.; Giorgi, F. Connection between Spring Conditions and Peak Summer Monsoon Rainfall in South America: Role of Soil Moisture, Surface Temperature, and Topography in Eastern Brazil. J. Clim. 2007, 20, 5929–5945. [Google Scholar] [CrossRef]
- Koster, R.D.; Sud, Y.C.; Guo, Z.; Dirmeyer, P.A.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Davies, H.; et al. GLACE: The Global Land–Atmosphere Coupling Experiment. Part I: Overview. J. Hydrometeor. 2006, 7, 590–610. [Google Scholar] [CrossRef]
- Baker, J.C.A.; de Souza, C.; Kubota, P.Y.; Buermann, W.; Coelho, C.A.S.; Andrews, M.B.; Gloor, M.; Garcia-Carreras, L.; Figueroa, S.N.; Spracklen, D.V. An Assessment of Land–Atmosphere Interactions over South America Using Satellites, Reanalysis, and Two Global Climate Models. J. Hydrometeor. 2021, 22, 905–922. [Google Scholar] [CrossRef]
- Cavalcanti, I.F.; Marengo, J.A.; Satyamurty, P.; Nobre, C.A.; Trosnikov, I.; Bonatti, J.P.; Manzi, A.O.; Tarasova, T.; Pezzi, L.P.; D’almeida, C.; et al. Global Climatological Features in a Simulation Using the CPTEC–COLA AGCM. J. Clim. 2002, 15, 2965–2988. [Google Scholar] [CrossRef]
- Figueroa, S.N.; Bonatti, J.P.; Kubota, P.Y.; Grell, G.A.; Morrison, H.; Barros, S.R.M.; Fernez, J.P.R.; Ramirez, E.; Siqueira, L.; Luzia, G.; et al. The Brazilian Global Atmospheric Model (BAM): Performance for Tropical Rainfall Forecasting and Sensitivity to Convective Scheme and Horizontal Resolution. Weather Forecast. 2016, 31, 1547–1572. [Google Scholar] [CrossRef]
- Guimarães, B.S.; Coelho, C.A.S.; Woolnough, S.J.; Kubota, P.Y.; Bastarz, P.Y.; Figueroa, S.N.; Bonatti, J.P.; de Souza, D.C. Configuration and hindcast quality assessment of a Brazilian global sub-seasonal prediction system. Q. J. R. Meteorol. Soc. 2020, 146, 1067–1084. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; de Souza, D.C.; Kubota, P.Y.; Costa, S.M.S.; Menezes, L.; Guimarães, B.S.; Figueroa, S.N.; Bonatti, J.P.; Cavalcanti, I.F.A.; Sampaio, G.; et al. Evaluation of climate simulations produced with the Brazilian global atmospheric model version 1.2. Clim. Dyn. 2002, 56, 873–898. [Google Scholar] [CrossRef]
- Kubota, P.Y. Variabiliade de Energia Armazenada na Superfície e seu Impacto na Definição do Padrão de Precipitação na América do Sul; Doutorado em Meteorologia, Instituto Nacional de Pesquisas Espaciais (INPE): São José dos Campos, Brazil, 2012.
- Willmott, C.J.; Rowe, C.M.; Mintz, Y. Climatology of the terrestrial seasonal water cycle. J. Clim. 1985, 5, 589–606. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Han, J.; Pan, H. Revision of Convection and Vertical Diffusion Schemes in the NCEP Global Forecast System. Weather Forecast. 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Tiedke, M.A. Comprehensive Mass Flux Scheme for Cumulus Parameterization in Large–Scale Models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Morrison, H.; Curry, J.A.; Khvorostyanov, V.I. A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models. Part I: Description. J. Atmos. Sci. 2005, 62, 1665–1677. [Google Scholar] [CrossRef]
- Chou, M.D.; Suarez, M.J.; Liang, X.; Yan, M.M. Technical Report Series on Global Modeling and Data Assimilation Vol. 19: A Thermal Infrared Radiation Parameterization for Atmospheric Studies; NASA: Washington, DC, USA, 2001.
- Chou, M.D.; Suarez, M.J. Technical Report Series on Global Modeling and Data Assimilation Vol. 15: A Solar Radiation Parameterization for Atmospheric Studies; NASA: Washington, DC, USA, 1999.
- Tarasova, T.A.; Fomin, B.A. Solar Radiation Absorption due to Water Vapor: Advanced Broadband Parameterizations. J. Appl. Meteorol. 2000, 39, 1947–1951. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Park, S. A New Moist Turbulence Parameterization in the Community Atmosphere Model. J. Clim. 2009, 22, 3422–3448. [Google Scholar] [CrossRef]
- de Gonçalves, L.G.G.; Shuttleworth, W.J.; Vila, D.; Larroza, E.; Bottino, M.J.; Herdies, D.L.; Aravéquia, J.A.; de Mattos, J.G.Z.; Toll, D.L.; Rodell, M.; et al. The South American Land Data Assimilation System (SALDAS) 5-yr Retrospective Atmospheric Forcing Datasets. J. Hydrometeor. 2009, 10, 999–1010. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Tian, Y.; Houser, P.R.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.L.; Doty, B.; Dirmeyer, P.; et al. Land information system: An interoperable framework for high resolution land surface modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-Year High-Resolution Global Dataset of Meteorological Forcings for Land Surface Modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Kleist, D.T.; Parrish, D.F.; Derber, J.C.; Treadon, R.; Wu, W.-S.; Lord, S. Introduction of the GSI into the NCEP Global Data Assimilation system. Weather Forecast. 2009, 24, 1691–1705. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG); NASA: Washington, DC, USA, 2019.
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-of-atmosphere (toa) Edition-4.0 Data Product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosolivich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979-Present); NASA: Washington, DC, USA, 2003.
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Sabater, J.M.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Dirmeyer, P.A. The terrestrial segment of soil moisture–climate coupling. Geophys. Res. Lett. 2011, 38, 16. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Luthi, D.; Litschi, M.; Schar, C. Land-atmosphere coupling and climate change in Europe. Nature 2006, 443, 205–209. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Zeng, X.; Barlage, M.; Castro, C.; Fling, K. Comparison of Land–Precipitation Coupling Strength Using Observations and Models. J. Hydrometeor. 2010, 11, 979–994. [Google Scholar] [CrossRef]
- Betts, A.K. Understanding hydrometeorology using global models. Bull. Am. Meteorol. Soc. 2004, 85, 1673–1688. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Wang, Z.; Mbuh, M.J.; Norton, H.E. Intensified land surface control on boundary layer growth in a changing climate. Geophys. Res. Lett. 2014, 41, 1290–1294. [Google Scholar] [CrossRef]
- Figueroa, S.N.; Nobre, C.A. Precipitation distribution over central and western tropical South America. Climanálise 1990, 5, 36–45. [Google Scholar]
- Herdies, D.L.; da Silva, A.; Silva Dias, M.A.; Nieto Ferreira, R. Moisture budget of the bimodal pattern of the summer circulation over South America. J. Geophys. Res. Atmos. 2002, 107, LBA 42-1–LBA 42-10. [Google Scholar] [CrossRef]
- Reboita, M.S.; Gan, M.A.; da Rocha, R.P.; Ambrizzi, T. Regimes de precipitação na América do Sul: Uma revisão bibliográfica. Rev. Bras. Meteorol. 2010, 25, 185–204. [Google Scholar] [CrossRef]
- Pinault, J.-L. Regions Subject to Rainfall Oscillation in the 5–10 Year Band. Climate 2018, 6, 2. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; de Souza, D.C.; Kubota, P.Y.; Cavalcanti, I.F.A.; Baker, J.C.A.; Figueroa, S.N.; Firpo, M.A.F.; Guimarães, B.S.; Costa, S.M.S.; Gonçalves, L.J.M.; et al. Assessing the representation of south american monsoon features in brazil and u.k. climate model simulations. Clim. Resil. Sustain. 2022, 1, 1. [Google Scholar] [CrossRef]







| Spatial resolution | T0126L042 |
| Initial condition | ERA–Interim [29] |
| SST and ozone | ERA–Interim [29] |
| Dynamics | Eulerian (spectral) [23] |
| Deep convection | Simplified Arakawa and Schubert [30] |
| Shallow convection | Tiedke [31] |
| Microphysics | Morrison [32] |
| Longwave radiation | CLIRAD–LW [33] |
| Shortwave radiation | CLIRAD–SW [34] modified by Tarasova et al. [35] |
| Planetary boundary layer | Moist diffusion scheme [36] |
| Land surface | IBIS–CPTEC [26] |
| Soil moisture | Willmott’s climatology [27] |
| SST | Persistent SST anomaly |
| Ensemble | 15 members |
| Initialization | July |
| Lead-time | SON |
| Period | 11 years |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arsego, V.B.M.; de Gonçalves, L.G.G.; Arsego, D.A.; Figueroa, S.N.; Kubota, P.Y.; de Souza, C.R. Impact of Soil Moisture in the Monsoon Region of South America during Transition Season. Atmosphere 2023, 14, 804. https://doi.org/10.3390/atmos14050804
Arsego VBM, de Gonçalves LGG, Arsego DA, Figueroa SN, Kubota PY, de Souza CR. Impact of Soil Moisture in the Monsoon Region of South America during Transition Season. Atmosphere. 2023; 14(5):804. https://doi.org/10.3390/atmos14050804
Chicago/Turabian StyleArsego, Vivian Bauce Machado, Luis Gustavo Gonçalves de Gonçalves, Diogo Alessandro Arsego, Silvio Nilo Figueroa, Paulo Yoshio Kubota, and Carlos Renato de Souza. 2023. "Impact of Soil Moisture in the Monsoon Region of South America during Transition Season" Atmosphere 14, no. 5: 804. https://doi.org/10.3390/atmos14050804
APA StyleArsego, V. B. M., de Gonçalves, L. G. G., Arsego, D. A., Figueroa, S. N., Kubota, P. Y., & de Souza, C. R. (2023). Impact of Soil Moisture in the Monsoon Region of South America during Transition Season. Atmosphere, 14(5), 804. https://doi.org/10.3390/atmos14050804






