Optimization of Photoacoustic Cell for Trace Acetylene Detection in Transformer Oil
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Principle of the PA Effect
2.2. Simulation Model Establishment and Verification
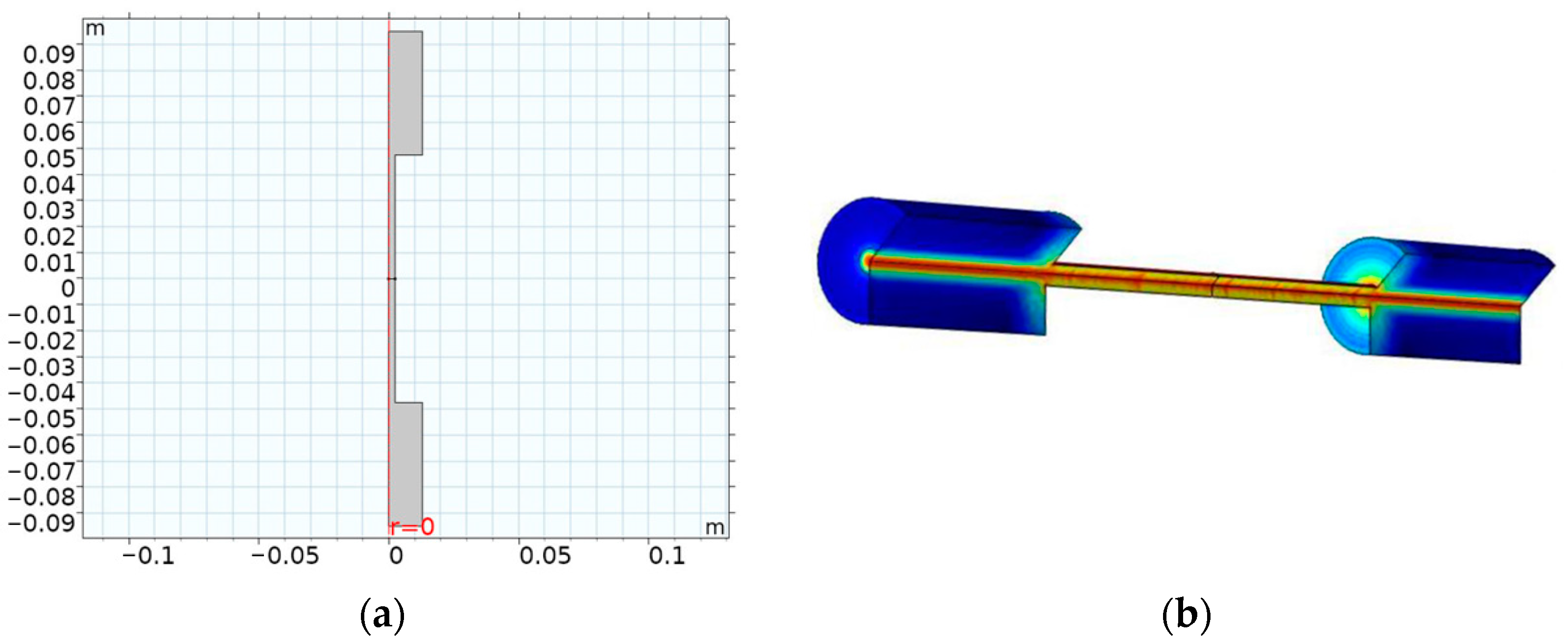
2.2.1. Simulation Model Establishment of the PA Cell
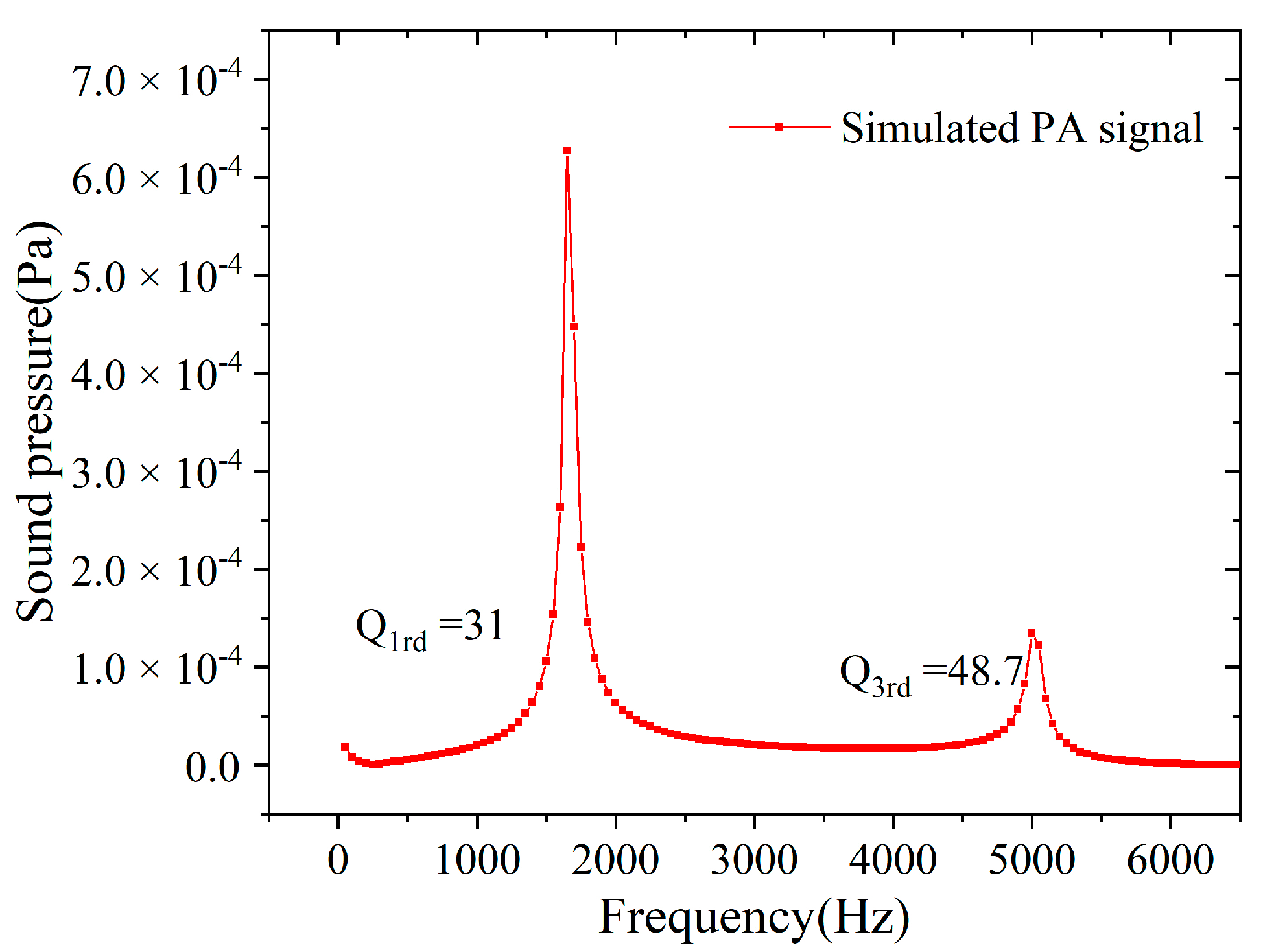
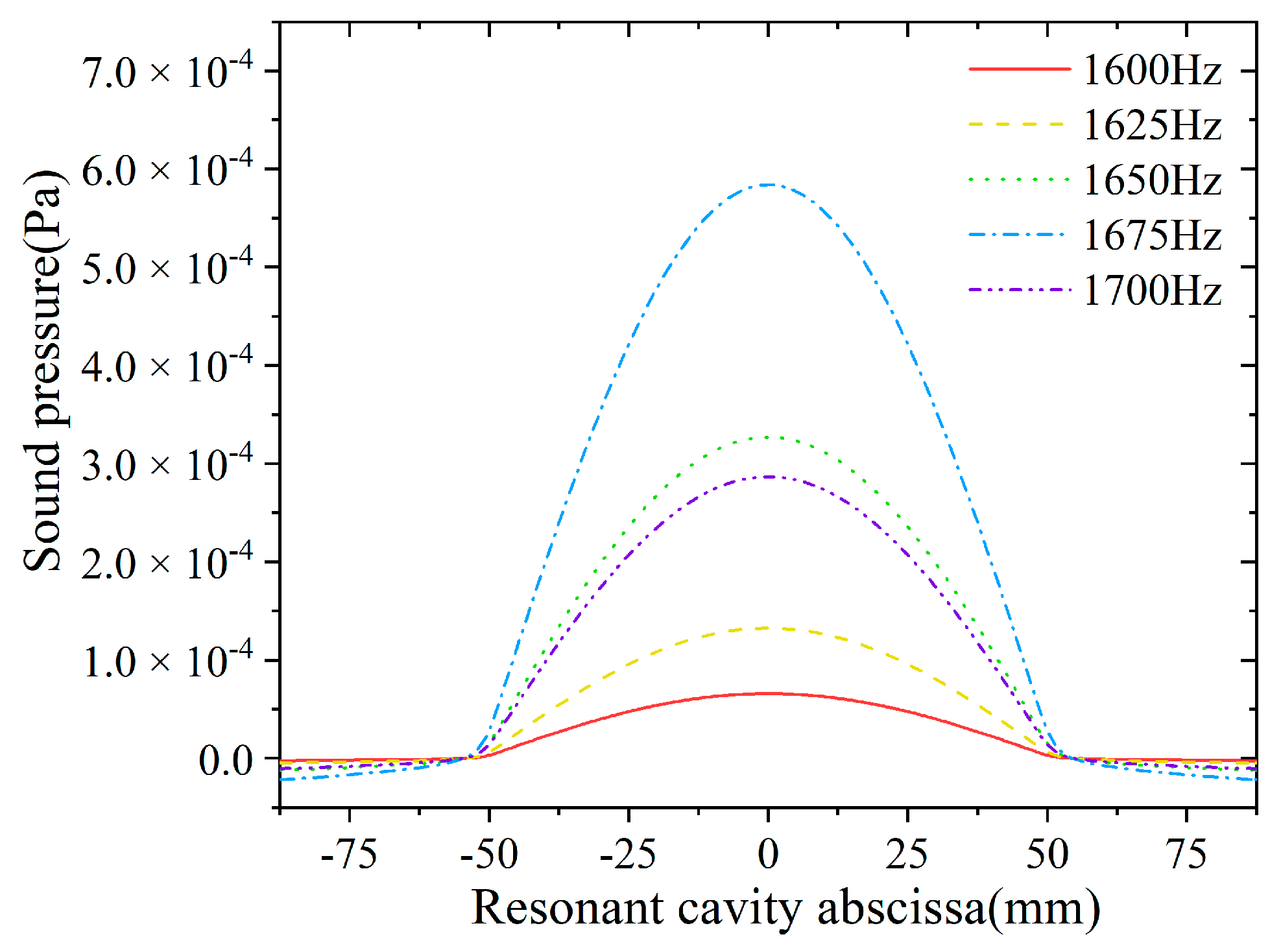
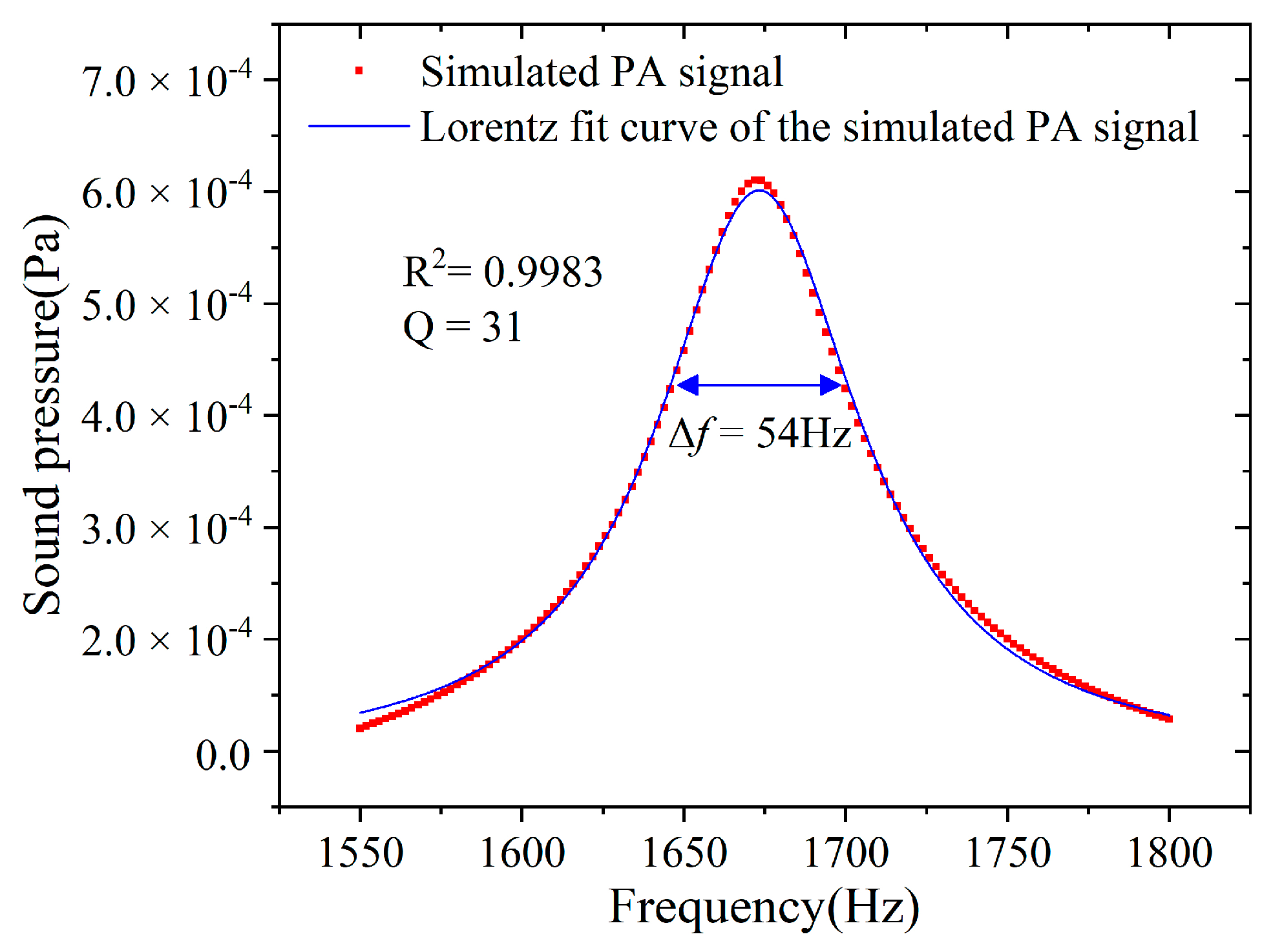
2.2.2. Simulation Model Verification of the PA Cell
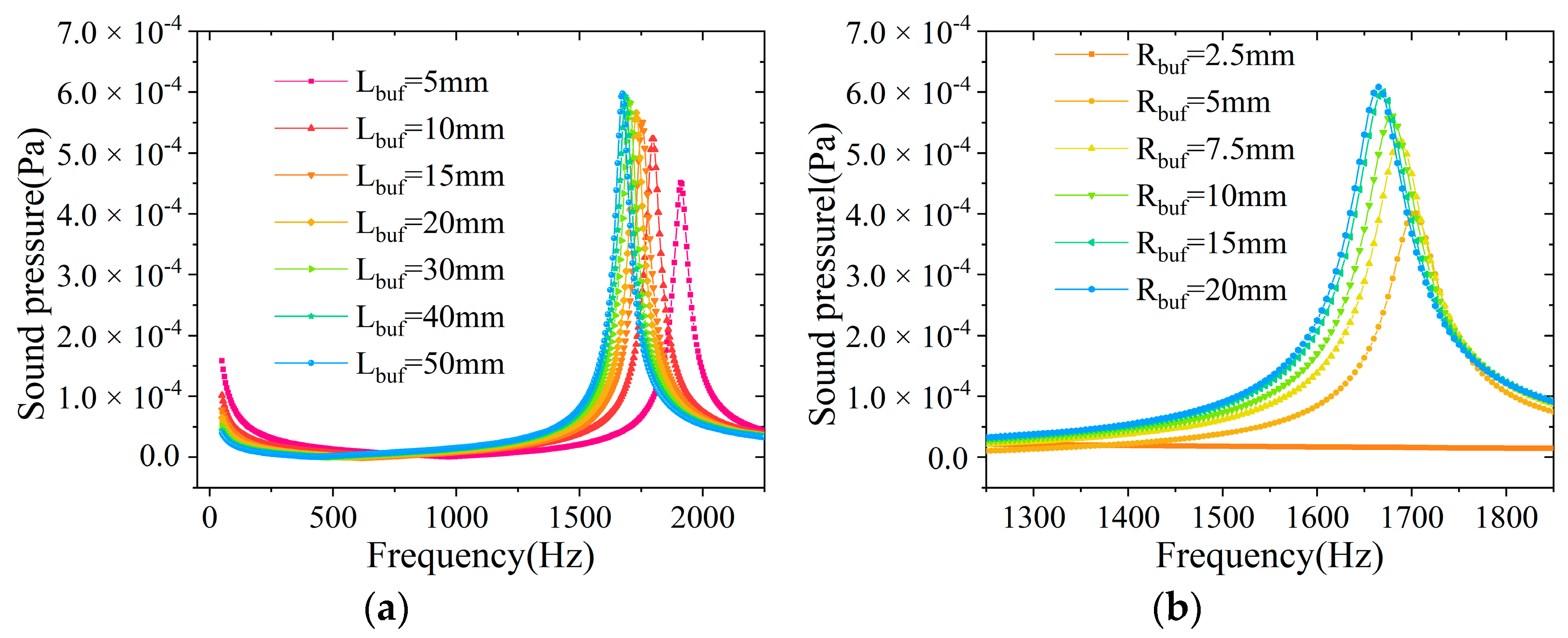
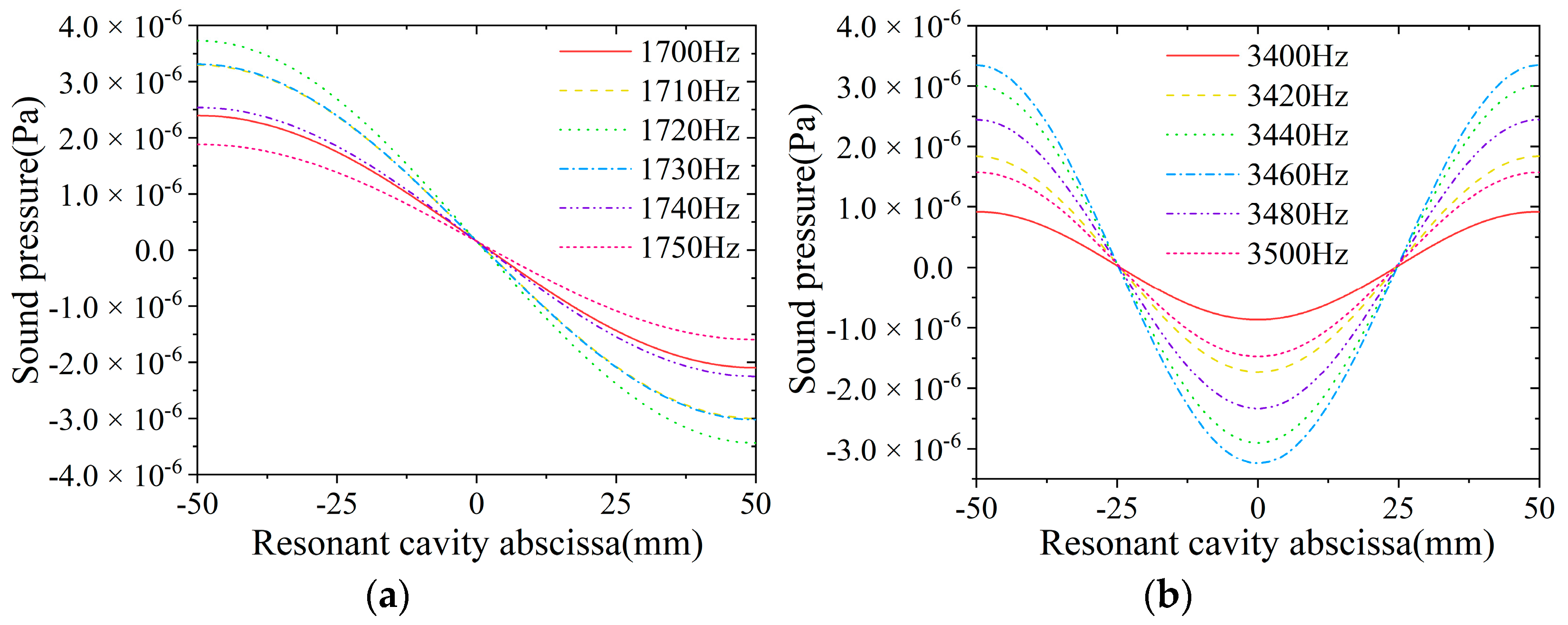
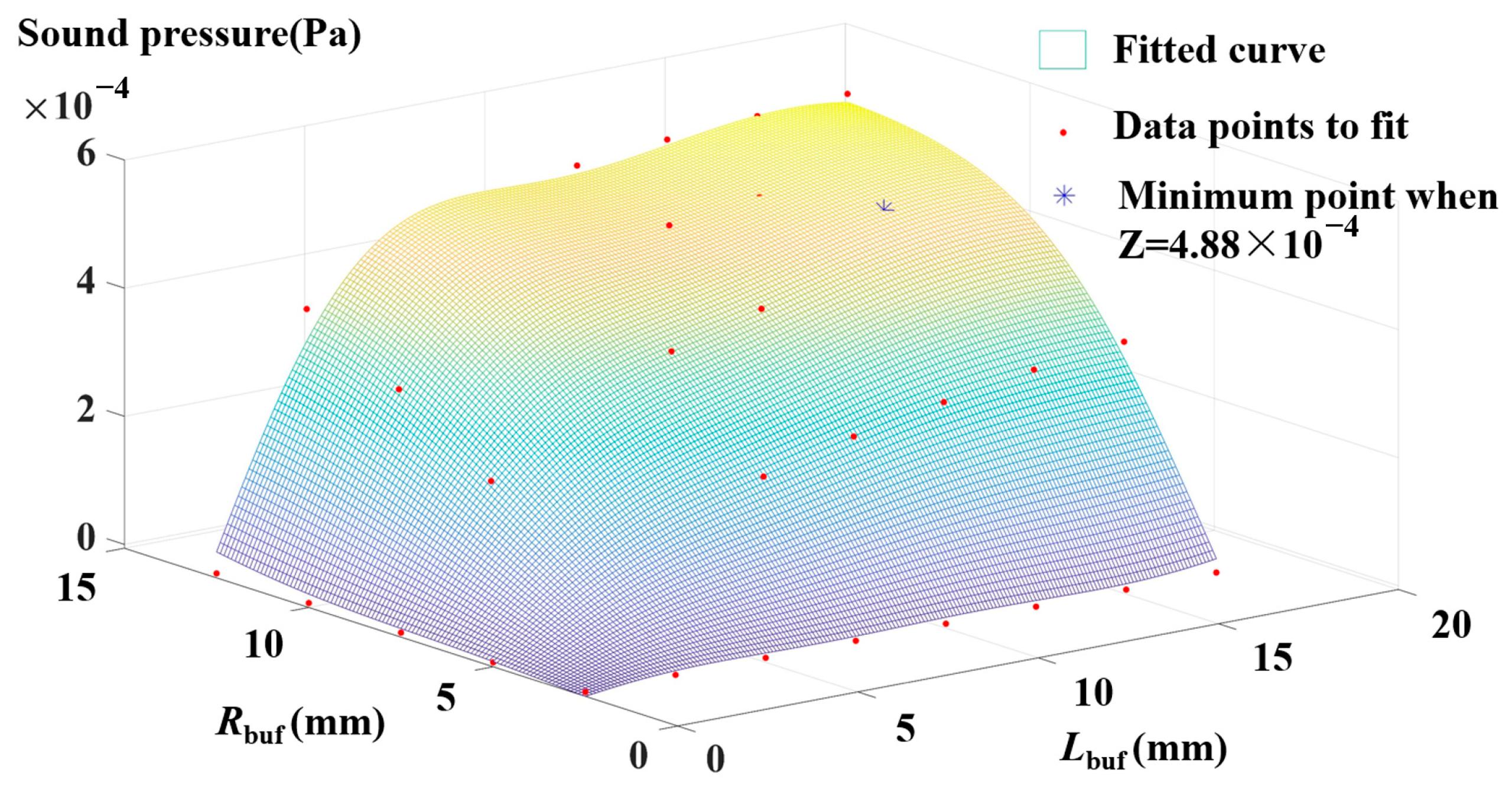
2.3. Simulation Optimization of the PA Cell
2.4. Photoacoustic Spectroscopy Gas Detection with the Optimized PA Cell
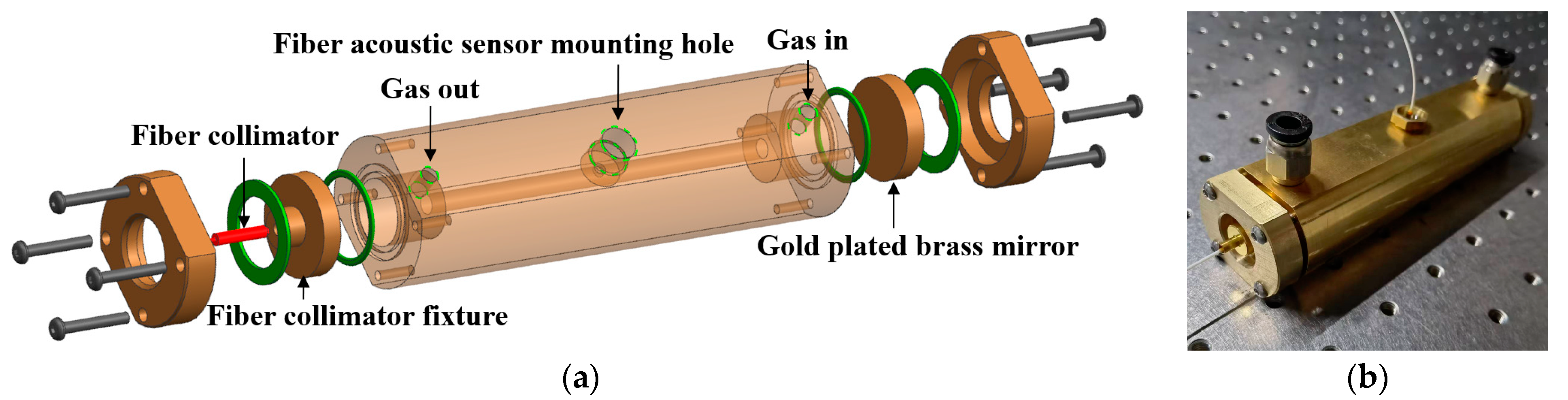
2.4.1. Design and Fabrication of the Optimized Buffer Chamber PA Cell
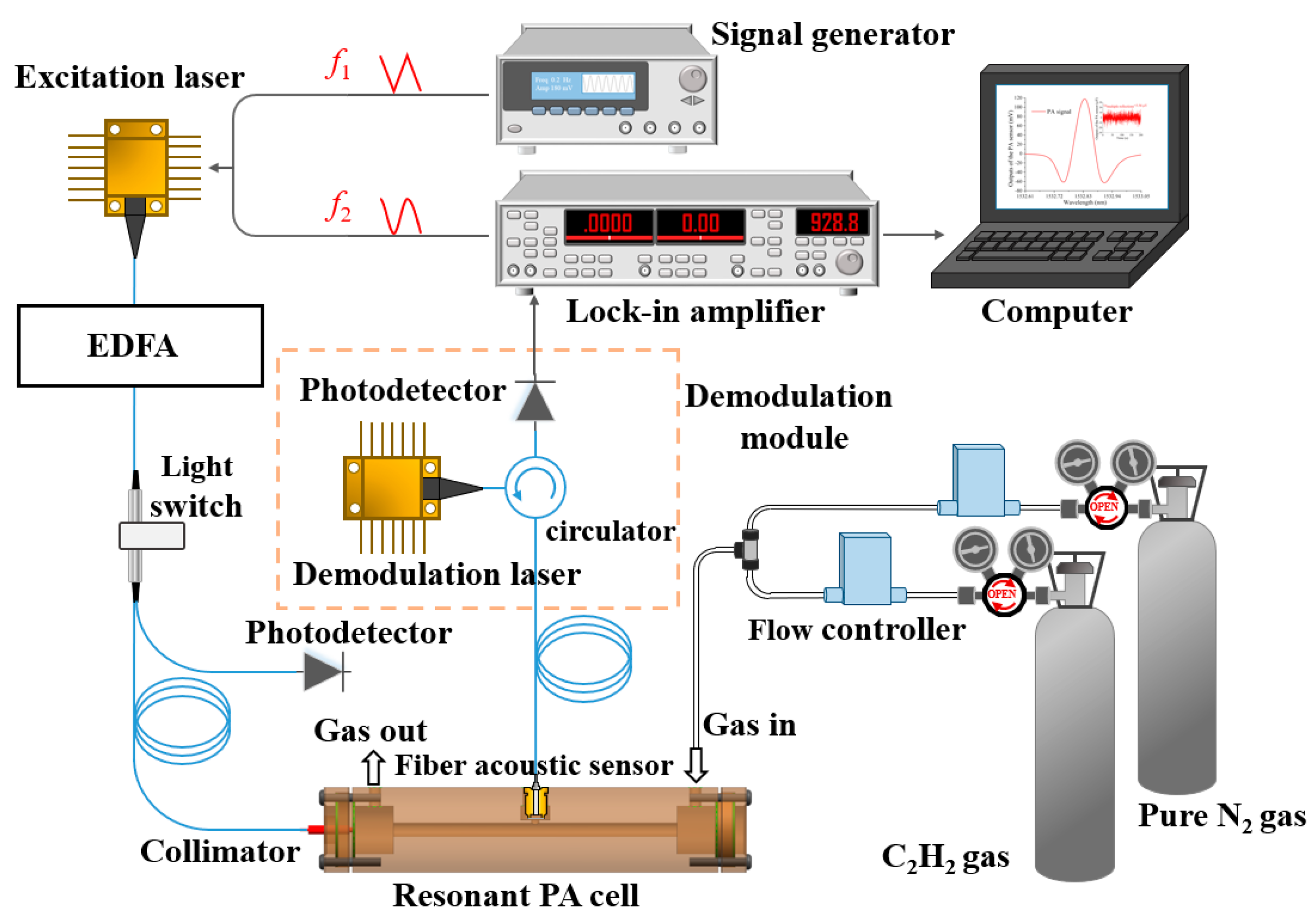
2.4.2. Construction of a Dual-Resonance Photoacoustic Spectroscopy Gas Detection System
3. Results
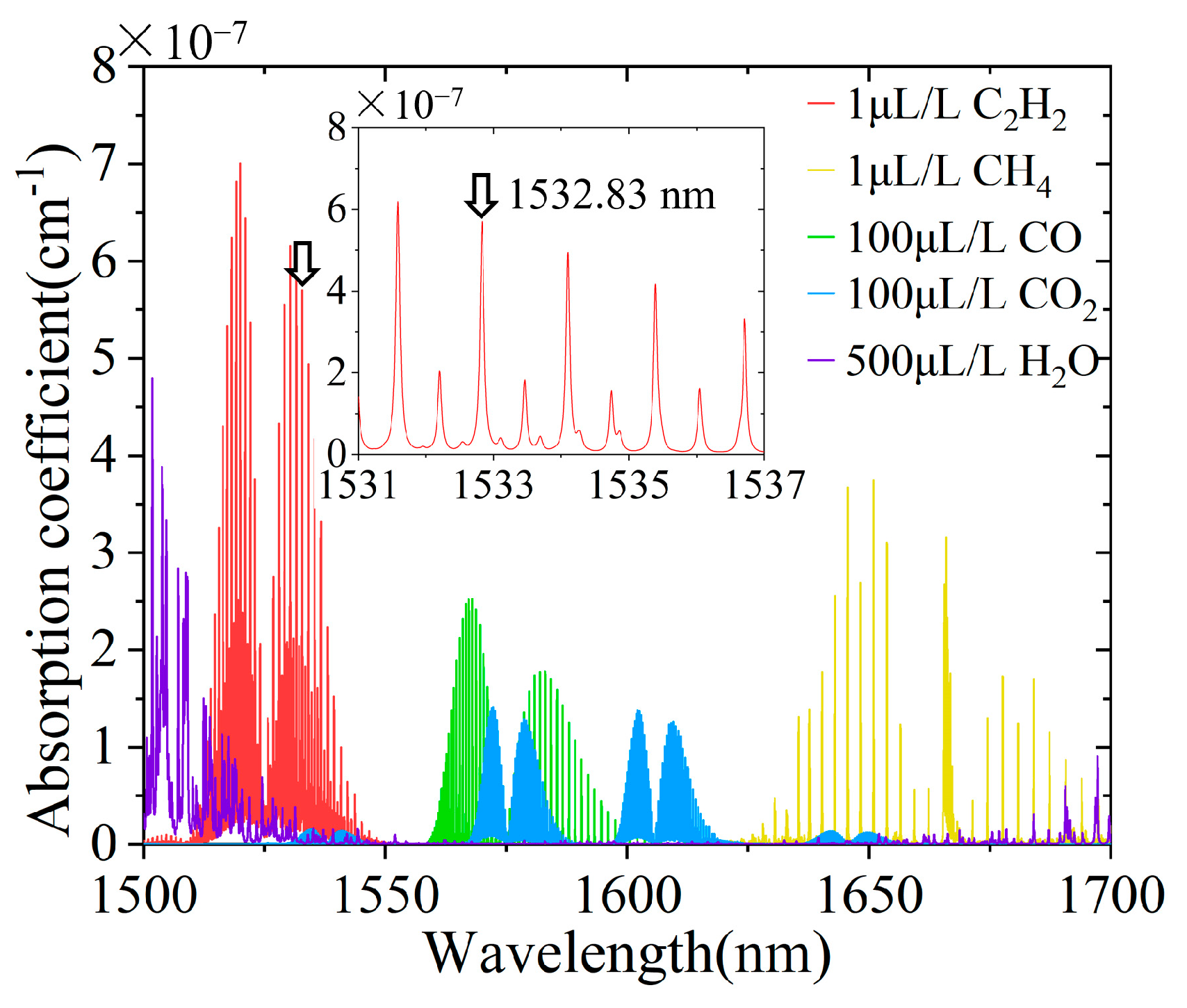
3.1. The Absorption Lines of C2H2
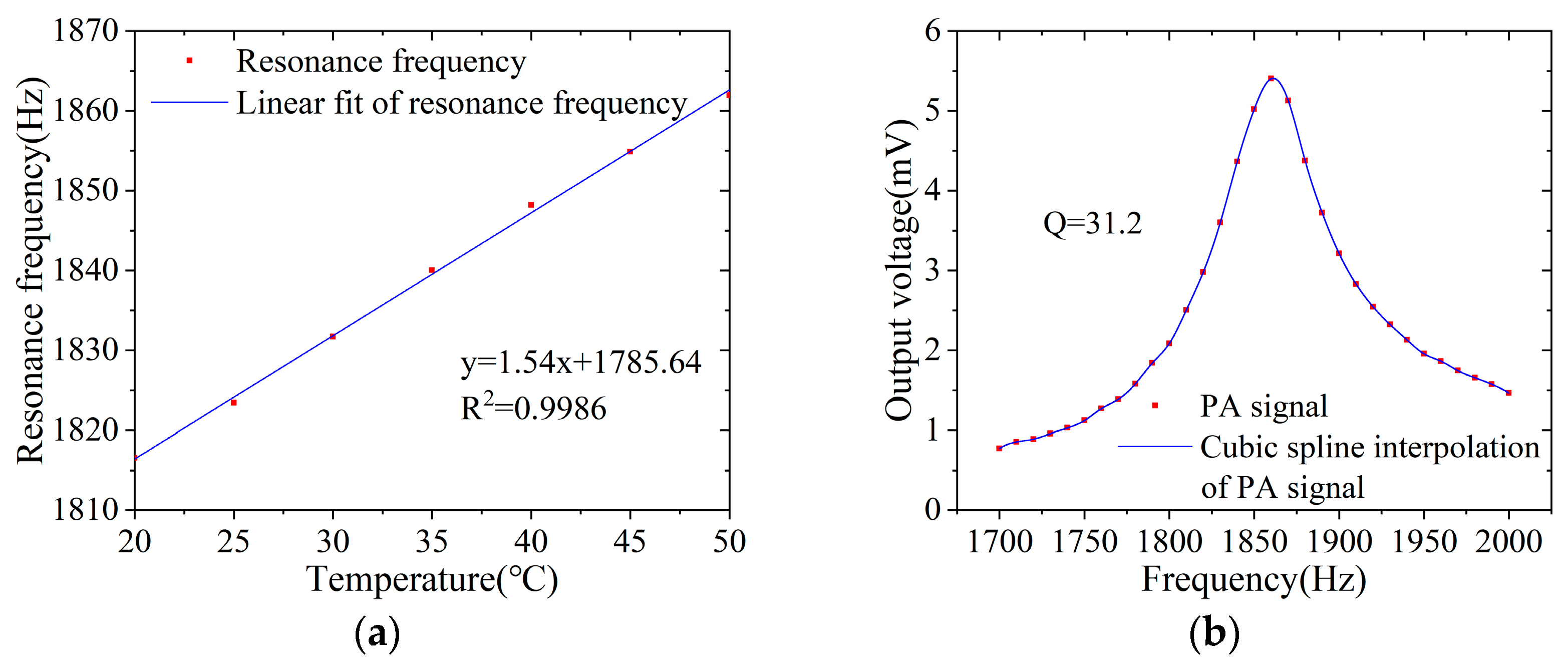
3.2. Resonant Frequency Measurement of the PA Cell
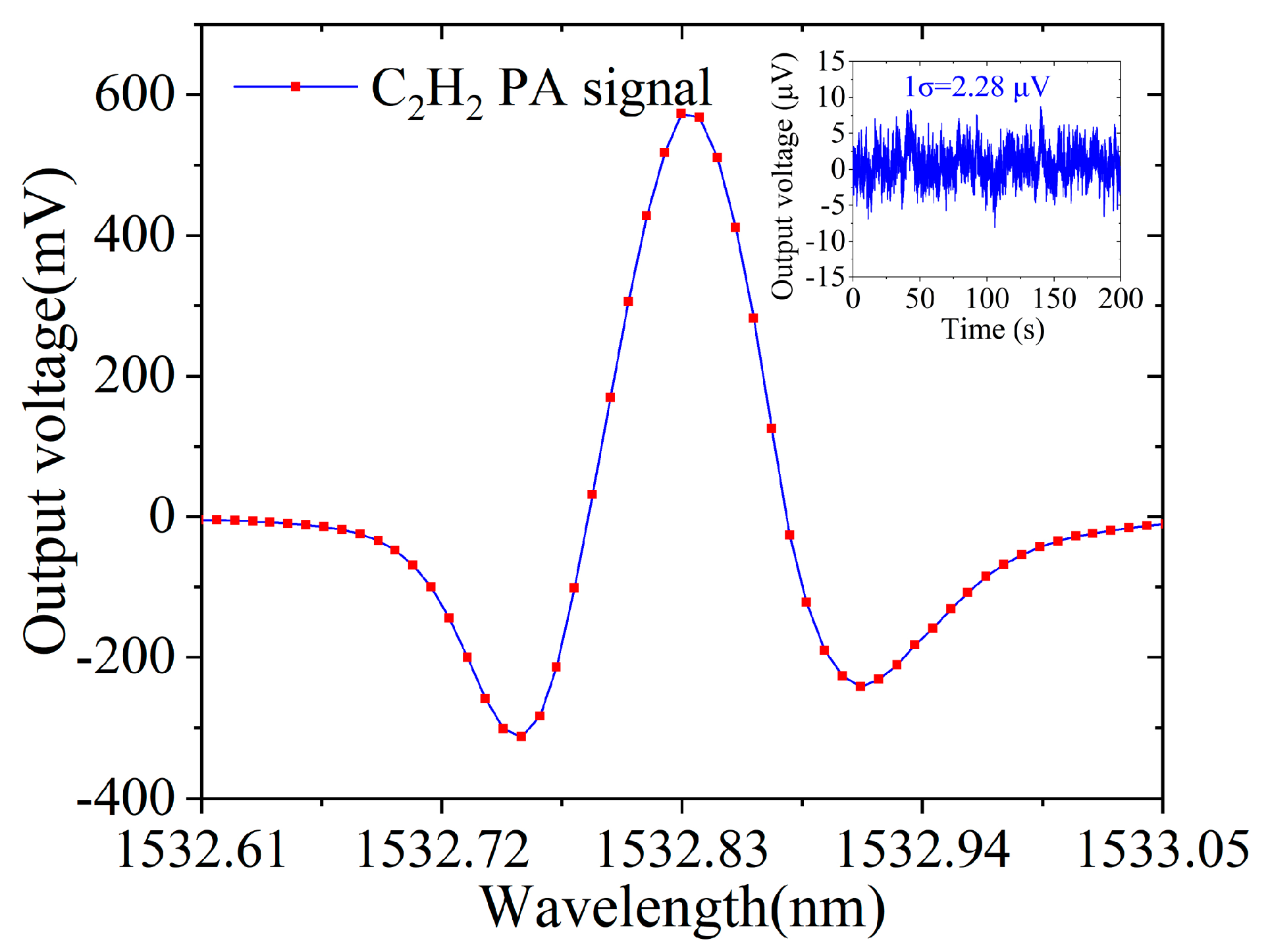
3.3. Gas Detection
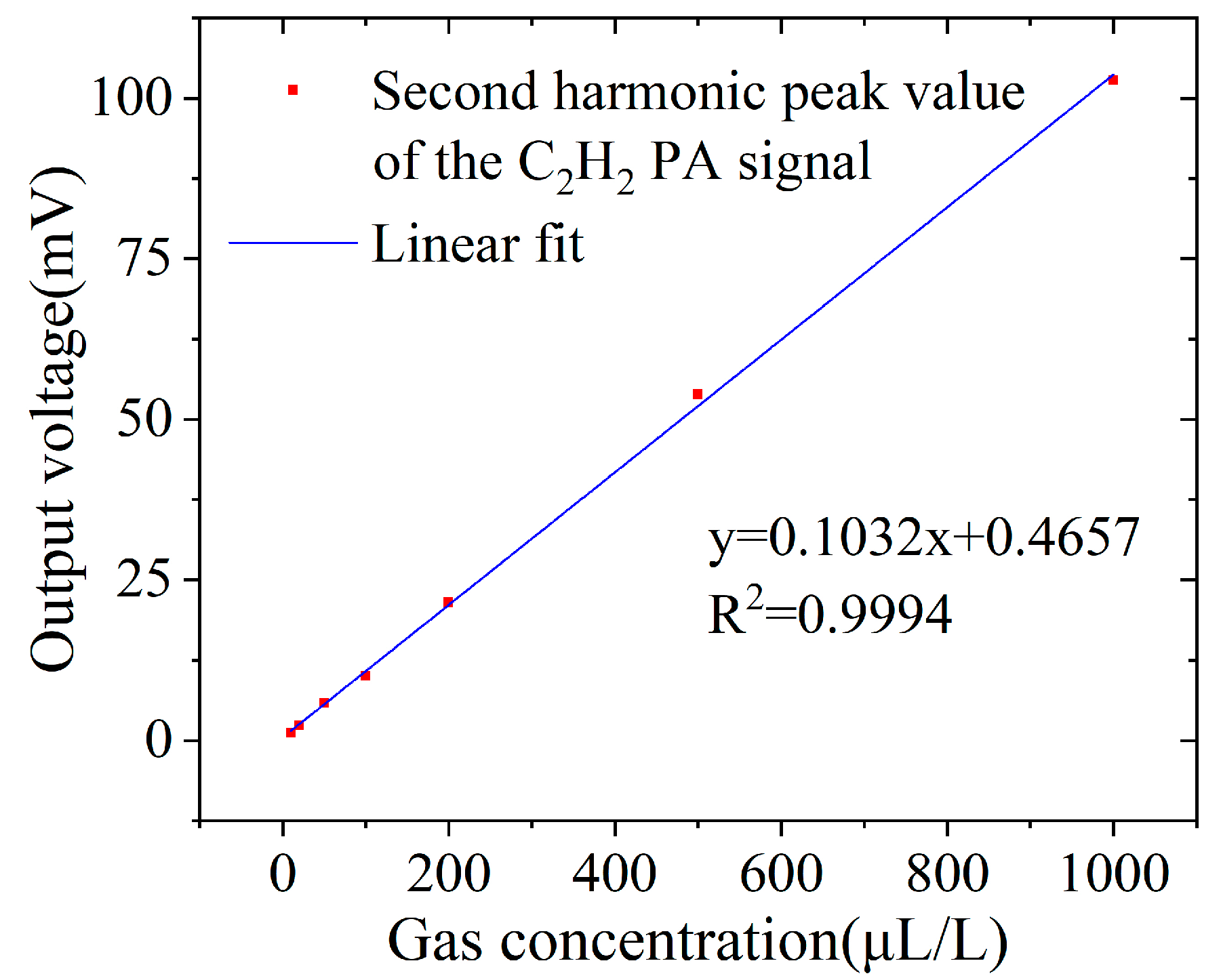
3.3.1. Detection Limit
3.3.2. Measuring Range
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bakar, N.A.; Abu-Siada, A.; Islam, S. A review of dissolved gas analysis measurement and interpretation techniques. IEEE Electr. Insul. Mag. 2014, 30, 39–49. [Google Scholar] [CrossRef]
- de Faria, H., Jr.; Costa, J.G.S.; Olivas, J.L.M. A review of monitoring methods for predictive maintenance of electric power transformers based on dissolved gas analysis. Renew. Sust. Energy Rev. 2015, 46, 201–209. [Google Scholar] [CrossRef]
- Bustamante, S.; Manana, M.; Arroyo, A.; Castro, P.; Laso, A.; Martinez, R. Dissolved Gas Analysis Equipment for Online Monitoring of Transformer Oil: A Review. Sensors 2019, 19, 4057. [Google Scholar]
- Wu, Z.Y.; Gong, Y.H.; Yu, Q.X. Photoacoustic spectroscopy detection and extraction of discharge feature gases in transformer oil based on 1.5 mu tunable fiber laser. Infrared Phys. Technol. 2013, 58, 86–90. [Google Scholar] [CrossRef]
- Gong, Z.F.; Chen, K.; Yang, Y.; Zhou, X.L.; Yu, Q.X. Photoacoustic spectroscopy based multi-gas detection using high-sensitivity fiber-optic low-frequency acoustic sensor. Sens. Actuator B-Chem. 2018, 260, 357–363. [Google Scholar] [CrossRef]
- Zhou, S.; Iannuzzi, D. Immersion photoacoustic spectrometer (iPAS) for arcing fault detection in power transformers. Opt. Lett. 2019, 44, 3741–3744. [Google Scholar] [PubMed]
- Tomberg, T.; Vainio, M.; Hieta, T.; Halonen, L. Sub-parts-per-trillion level sensitivity in trace gas detection by cantilever-enhanced photo-acoustic spectroscopy. Sci. Rep. 2018, 8, 1848. [Google Scholar] [CrossRef]
- Zhou, S.; Slaman, M.; Iannuzzi, D. Demonstration of a highly sensitive photoacoustic spectrometer based on a miniaturized all-optical detecting sensor. Opt. Express 2017, 25, 17541–17548. [Google Scholar]
- Gong, Z.; Chen, Y.; Gao, T.; Chen, K.; Jiao, Y.; Guo, M.; Zhang, B.; Liu, S.; Mei, L.; Peng, W.; et al. Parylene-C diaphragm-based low-frequency photoacoustic sensor for space-limited trace gas detection. Opt. Lasers Eng. 2020, 134, 106288. [Google Scholar] [CrossRef]
- Guo, M.; Chen, K.; Li, C.X.; Xu, L.; Zhang, G.Y.; Wang, N.; Li, C.Y.; Ma, F.X.; Gong, Z.F.; Yu, Q.X. High-Sensitivity Silicon Cantilever-Enhanced Photoacoustic Spectroscopy Analyzer with Low Gas Consumption. Anal. Chem. 2022, 94, 1151–1157. [Google Scholar] [CrossRef]
- Bijnen, F.G.C.; Reuss, J.; Harren, F.J.M. Geometrical optimization of a longitudinal resonant photoacoustic cell for sensitive and fast trace gas detection. Rev. Sci. Instrum. 1996, 67, 2914–2923. [Google Scholar] [CrossRef]
- Miklos, A.; Hess, P.; Bozoki, Z. Application of acoustic resonators in photoacoustic trace gas analysis and metrology. Rev. Sci. Instrum. 2001, 72, 1937–1955. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Wang, J.W.; Li, L.A.; Yu, Q.X. An all-optical photoacoustic spectrometer for trace gas detection. Sens. Actuator B-Chem. 2011, 153, 214–218. [Google Scholar] [CrossRef]
- Cheng, G.; Cao, Y.; Liu, K.; Cao, Y.N.; Chen, J.J.; Gao, X.M. Numerical calculation and optimization of photoacoustic cell for photoacoustic spectrometer. Acta Phys. Sin. 2019, 68, 074202. [Google Scholar] [CrossRef]
- Cheng, G.; Cao, Y.N.; Tian, X.; Liu, K.; Cheng, J.J. Calculation and Evaluation of Acoustic and Flow Field Characteristics of Trapezoid Compound Photoacoustic Cell. Acta Photonica Sin. 2021, 50, 0230001. [Google Scholar]
- Gong, Z.F.; Gao, T.L.; Mei, L.; Chen, K.; Chen, Y.W.; Zhang, B.; Peng, W.; Yu, Q.X. Ppb-level detection of methane based on an optimized T-type photoacoustic cell and a NIR diode laser. Photoacoustics 2021, 21, 100216. [Google Scholar] [CrossRef]
- Gong, Z.F.; Wu, G.J.; Jiang, X.; Li, H.E.; Gao, T.L.; Guo, M.; Ma, F.X.; Chen, K.; Mei, L.; Peng, W.; et al. All-optical high-sensitivity resonant photoacoustic sensor for remote CH4 gas detection. Opt. Express 2021, 29, 13600–13609. [Google Scholar] [CrossRef]
- Jin, H.W.; Luo, P.; Dou, J.; Bai, H.C. Study on neural network algorithm for detecting respirable dust in photoacoustic cavity. AIP Adv. 2021, 11, 125307. [Google Scholar] [CrossRef]
- Yin, X.K.; Gao, M.; Miao, R.Q.; Zhang, L.; Zhang, X.S.; Liu, L.X.; Shao, X.P.; Tittel, F.K. Near-infrared laser photoacoustic gas sensor for simultaneous detection of CO and H2S. Opt. Express 2021, 29, 34258–34268. [Google Scholar] [CrossRef]
- Cheng, H.; Zeng, F.; Zhang, X.; Tang, J.; Zhang, Y. The effect of the photoacoustic Field-Photoacoustic cell coupling term on the performance of the gas detection system. Opt. Laser Technol. 2022, 153, 108211. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Q.Y.; Yin, X.Y. Photoacoustic spectroscopy for detection of trace C2H2 using ellipsoidal photoacoustic cell. Opt. Commun. 2021, 487, 126764. [Google Scholar] [CrossRef]
- Zhao, N.; Zhao, D.; Ma, L.G.; Wang, B. Study on a photoacoustic spectroscopy trichloromethane gas detection method based on an arched photoacoustic cavity. Anal. Methods 2022, 14, 1507–1514. [Google Scholar] [CrossRef]
- Yin, X.; Dong, L.; Wu, H.; Gao, M.; Zhang, L.; Zhang, X.; Liu, L.; Shao, X.; Tittel, F.K. Compact QEPAS humidity sensor in SF6 buffer gas for high-voltage gas power systems. Photoacoustics 2022, 25, 100319. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Li, H.; Zhao, X.; Gao, M.; Cheng, K.; Shao, X.; Wu, H.; Dong, L.; Yin, X. Trace photoacoustic SO2 gas sensor in SF6 utilizing a 266 nm UV laser and an acousto-optic power stabilizer. Opt. Express 2023, 31, 6974–6981. [Google Scholar] [CrossRef]
- Yang, T.; Liu, R.; Yao, Y.; Luo, W.; Zhou, K.; Jin, L. Photoacoustic Spectroscopy for Detection of Trace CH4 using Optimized Photoacoustic Cell. In Proceedings of the 2022 IEEE International Conference on High Voltage Engineering and Applications (ICHVE), Chongqing, China, 25–29 September 2022; pp. 1–4. [Google Scholar]
- Bell, A.G. On the production and reproduction of sound by light. Am. J. Sci. 1880, 3, 305–324. [Google Scholar] [CrossRef]
- Bell, A.G. Upon the production of sound by radiant energy. Science 1881, 2, 242–253. [Google Scholar] [CrossRef]
- Zoltan, B.; Andrea, P.; Gabor, S. Photoacoustic Instruments for Practical Applications: Present, Potentials, and Future Challenges. Appl. Spectrosc. Rev. 2011, 46, 1–37. [Google Scholar]
- Dumitras, D.C.; Dutu, D.C.; Matei, C.; Magureanu, A.M.; Petrus, M.; Popa, C. Laser photoacoustic spectroscopy: Principles, instrumentation, and characterization. J. Optoelectron. Adv. Mater. 2007, 9, 3655–3701. [Google Scholar]
- Karbach, A.; Hess, P. High Precision Acoustic Spectroscopy by Laser Excitation of Resonator Modes. J. Chem. Phys. 1985, 83, 1075–1084. [Google Scholar] [CrossRef]
- Song, K.; Cha, H.; Kapitanov, V.; Ponomarev, Y.N.; Rostov, A.; Courtois, D.; Parvitte, B.; Zeninari, V. Differential Helmholtz Resonant Photoacoustic Cell for Spectroscopy and Gas Analysis with Room-Temperature Diode Lasers. Appl. Phys. B 2002, 75, 215–227. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, B.; Chen, K.; Guo, M.; Liu, S.; Chen, Y.W.; Gong, Z.F.; Yu, Q.X.; Chen, Z.Q.; Liao, M.F. Miniaturized multi-pass cell based photoacoustic gas sensor for parts-per-billion level acetylene detection. Sens. Actuator A-Phys. 2020, 308, 112013. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Benner, D.C.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R. The HITRAN2012 Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Li, C.G.; Dong, L.; Zheng, C.T.; Lin, J.; Wang, Y.D.; Tittel, F.K. Ppbv-Level Ethane Detection Using Quartz-Enhanced Photoacoustic Spectroscopy with a Continuous-Wave, Room Temperature Interband Cascade Laser. Sensors 2018, 18, 723. [Google Scholar] [CrossRef] [PubMed]
- Kuusela, T.; Kauppinen, J. Photoacoustic gas analysis using interferometric cantilever microphone. Appl. Spectrosc. Rev. 2007, 42, 443–474. [Google Scholar] [CrossRef]
- Hardy, H.C.; Telfair, D.; Pielemeier, W.H. The velocity of sound in air. J. Acoust. Soc. Am. 1942, 13, 226–233. [Google Scholar] [CrossRef]
- Guo, M.; Chen, K.; Gong, Z.F.; Yu, Q.X. Trace ammonia detection based on near-infrared fiber-optic cantilever-enhanced photoacoustic spectroscopy. Photonic Sens. 2019, 9, 293–301. [Google Scholar] [CrossRef]
- Chen, K.; Yu, Q.X.; Gong, Z.F.; Guo, M.; Qu, C. Ultra-high sensitive fiber-optic Fabry-Perot cantilever enhanced resonant photoacoustic spectroscopy. Sens. Actuator B-Chem. 2018, 268, 205–209. [Google Scholar] [CrossRef]
- Chen, K.; Deng, H.; Guo, M.; Luo, C.; Liu, S.; Zhang, B.; Ma, F.X.; Zhu, F.; Gong, Z.F.; Peng, W.; et al. Tube-cantilever double resonance enhanced fiber-optic photoacoustic spectrometer. Opt. Laser Technol. 2020, 123, 105894. [Google Scholar] [CrossRef]
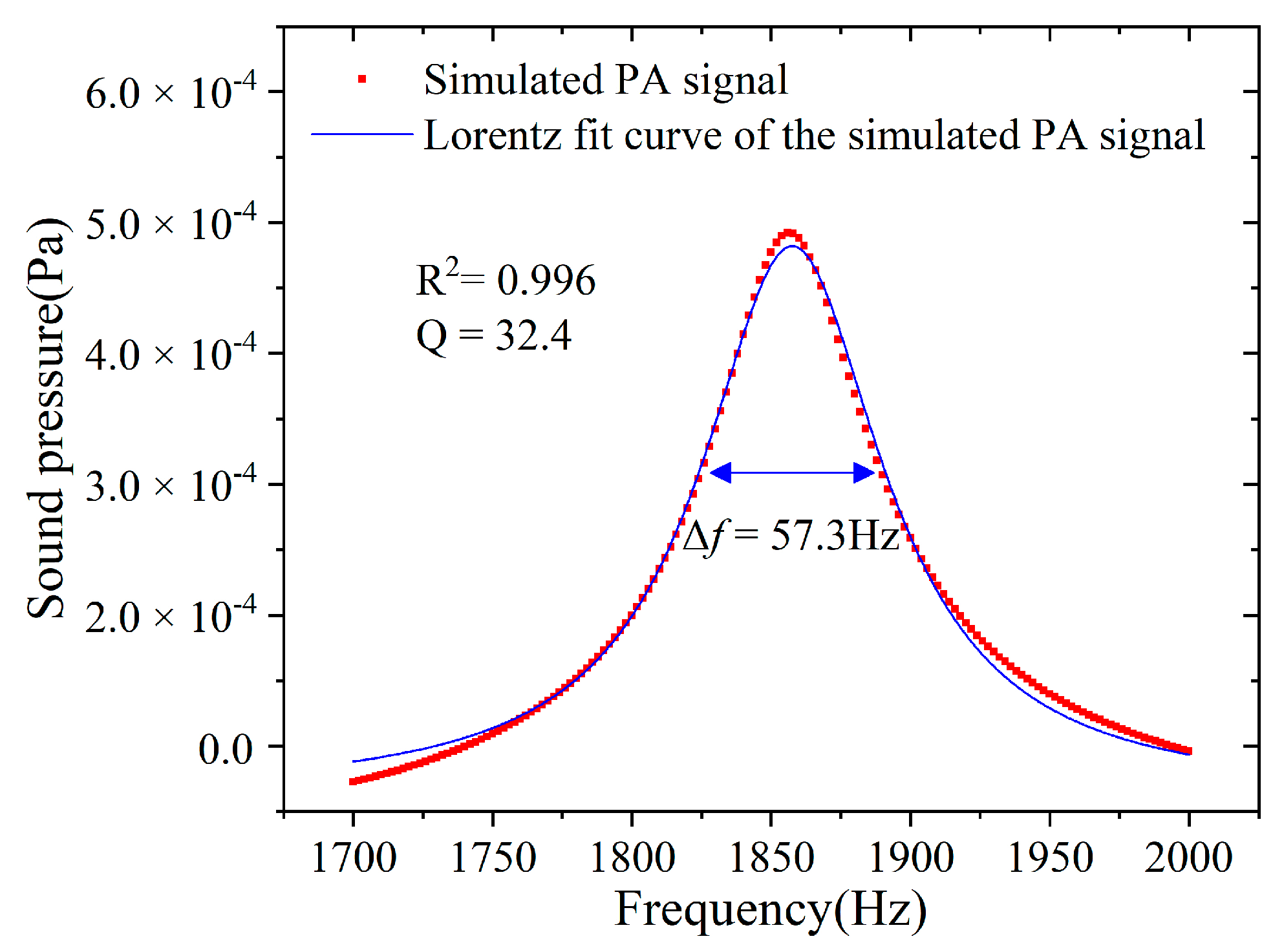
| Resonance Frequency (Hz) | Quality Factor | Cell Constant (Pa∙cm/W) | |
|---|---|---|---|
| Analytical parameters | 1673.96 | 32.4 | 3918.5 |
| Simulated parameters | 1673.3 | 31 | 3734.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Zhou, K.; Jin, L.; Liu, R.; Chen, W. Optimization of Photoacoustic Cell for Trace Acetylene Detection in Transformer Oil. Atmosphere 2023, 14, 801. https://doi.org/10.3390/atmos14050801
Yang T, Zhou K, Jin L, Liu R, Chen W. Optimization of Photoacoustic Cell for Trace Acetylene Detection in Transformer Oil. Atmosphere. 2023; 14(5):801. https://doi.org/10.3390/atmos14050801
Chicago/Turabian StyleYang, Tianhe, Kai Zhou, Lei Jin, Rui Liu, and Weigen Chen. 2023. "Optimization of Photoacoustic Cell for Trace Acetylene Detection in Transformer Oil" Atmosphere 14, no. 5: 801. https://doi.org/10.3390/atmos14050801
APA StyleYang, T., Zhou, K., Jin, L., Liu, R., & Chen, W. (2023). Optimization of Photoacoustic Cell for Trace Acetylene Detection in Transformer Oil. Atmosphere, 14(5), 801. https://doi.org/10.3390/atmos14050801






