A Metamodel-Based Optimization of Physical Parameters of High Resolution NWP ICON-LAM over Southern Italy
Abstract
1. Introduction—Background and Motivations
2. ICON-LAM: Model Description and Set Up
- v0snow is the factor in the terminal velocity for snow and is used in the grid scale clouds and precipitation parametrization;
- tkmmin is the scaling factor for minimum vertical diffusion coefficient (proportional to Richardson number, ) for momentum;
- tkhmin controls the minimum value for the turbulence coefficient (proportional to Richardson number, ) for heat and moisture;
- rlam_heat is a scaling factor of the laminar boundary layer for heat (scalars), with larger values corresponding to larger laminar resistance.
| Name | Parametrization | Min. | Max. | Baseline | Description |
|---|---|---|---|---|---|
| v0snow [ - ] | Microphysics | 10 | 30 | 30 | Snow vertical velocity |
| tkhmin [/s] | Vertical turbulent diffusion | 0.1 | 2.0 | 0.5 | Heat diffusion coefficient |
| tkmmin [/s] | Vertical turbulent diffusion | 0.1 | 2.0 | 0.75 | Momentum diffusion coefficient |
| rlam_heat [ - ] | Soil and vegetation processes | 0.05 | 20.0 | 10.0 | Heat laminar resistance factor |
3. Domains and Observational Data
4. The Test Cases Considered
5. Methodology
5.1. Post-Processing of ICON Results
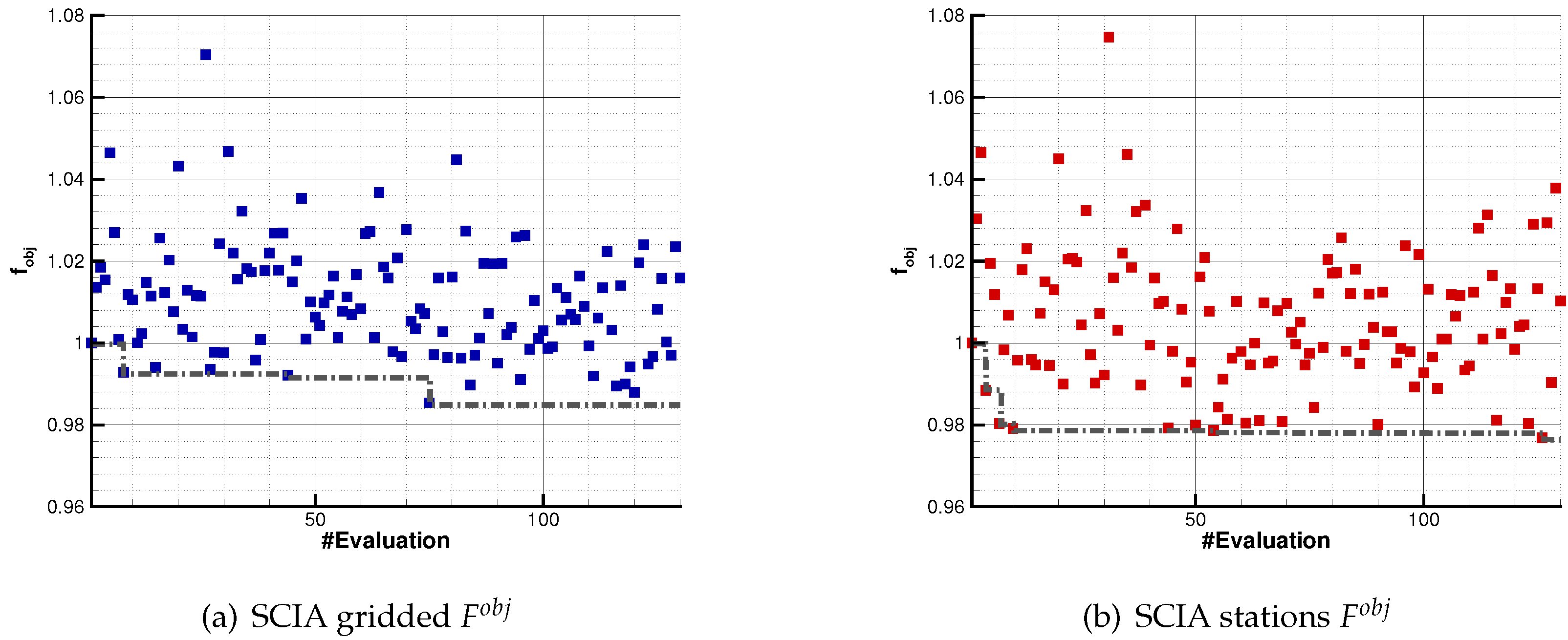
5.2. Objective Target Function
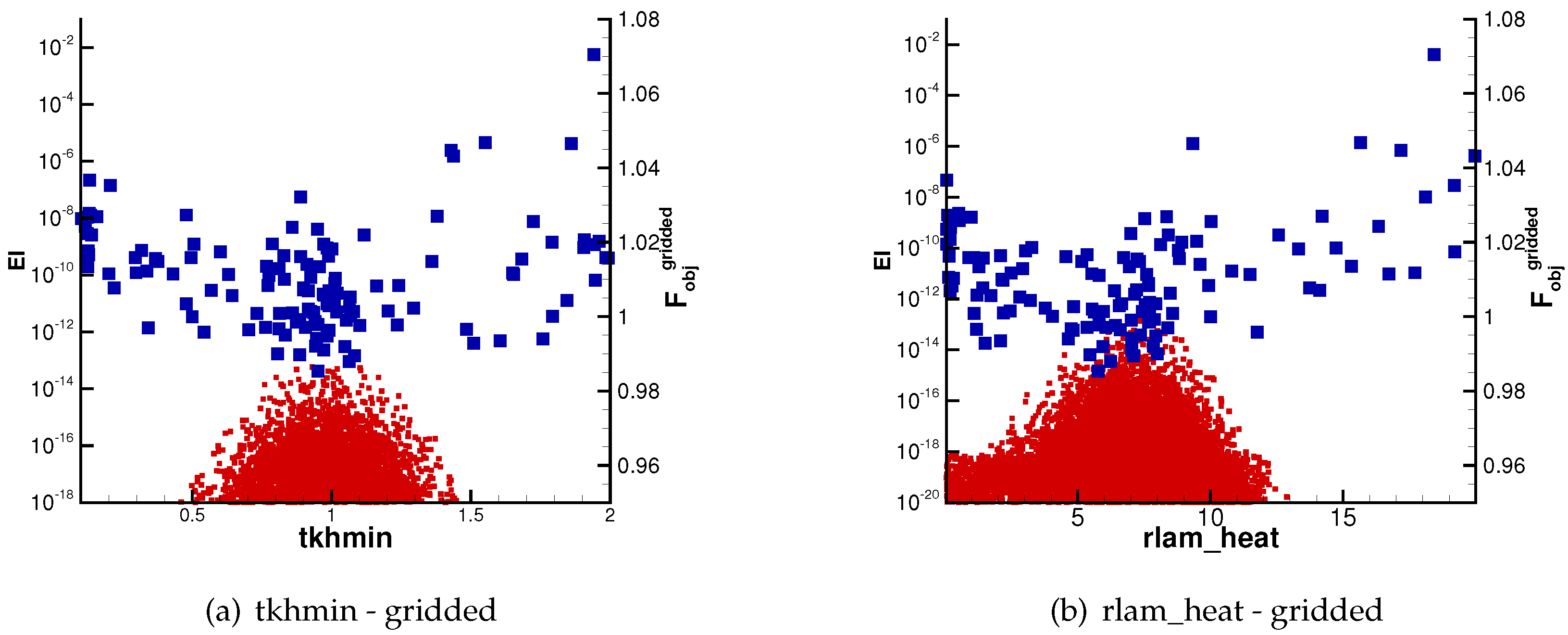
5.3. Automatic Calibration
6. Results
6.1. Domain Selection: Results
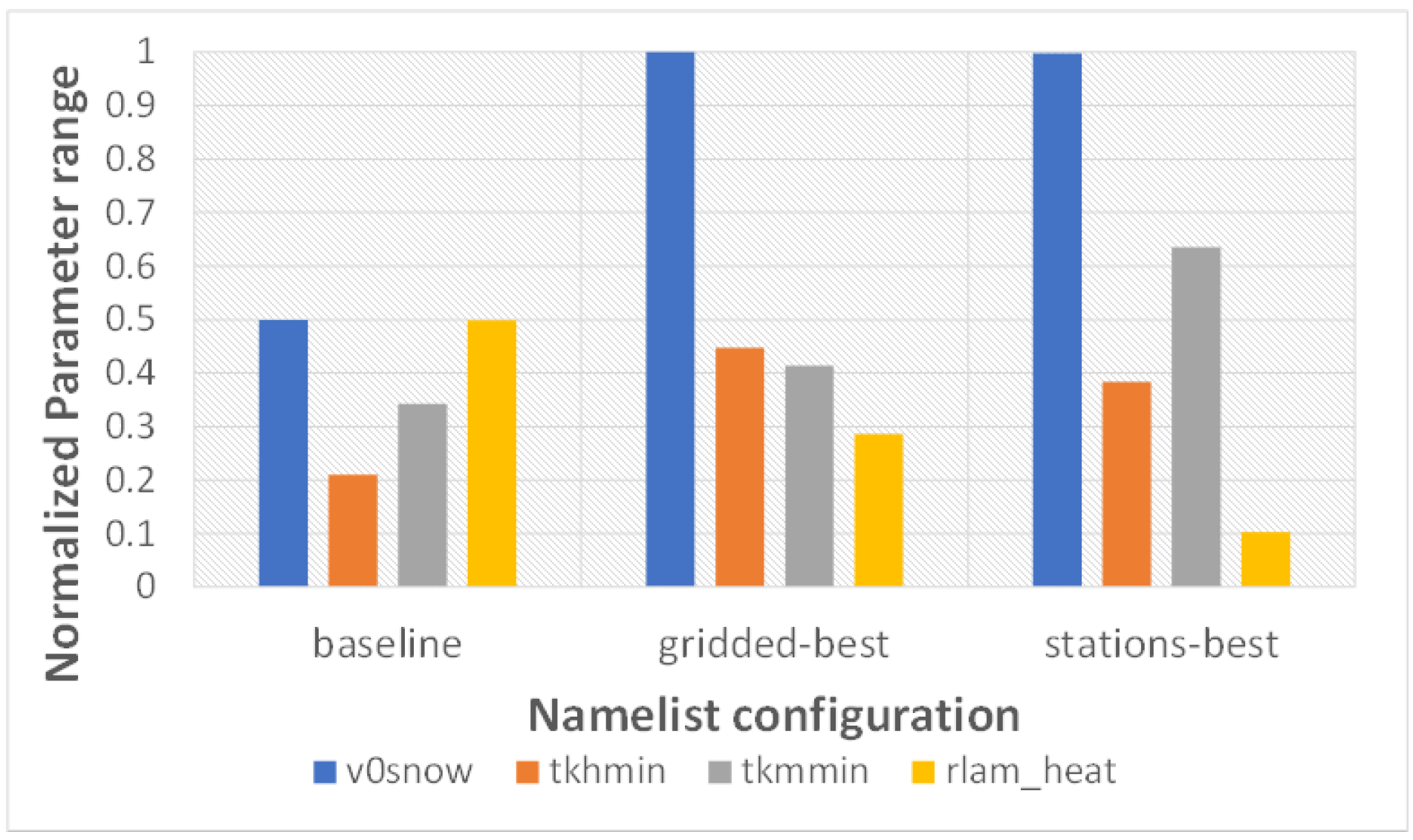
6.2. Automatic Calibration: Results
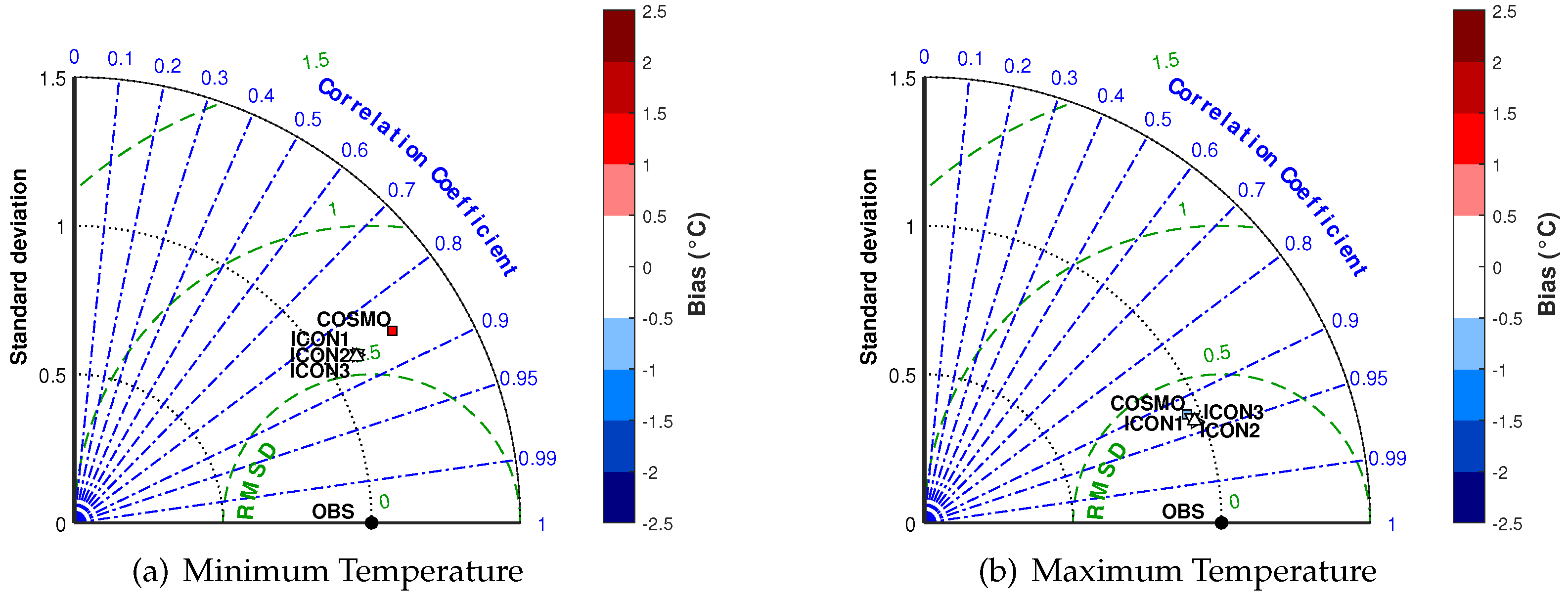
6.2.1. Analysis of Results against Grid Dataset
6.2.2. Analysis of Results against Station Data
6.3. Model Validation
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, Q.; Di, Z.; Quan, J.; Wang, C.; Gong, W.; Gan, Y.; Ye, A.; Miao, C.; Miao, S.; Liang, X.; et al. Automatic Model Calibration: A New Way to Improve Numerical Weather Forecasting. Bull. Am. Meteorol. Soc. 2017, 98, 959–970. [Google Scholar] [CrossRef]
- Neelin, J.D.; Bracco, A.; Luo, H.; McWilliams, J.C.; Meyerson, J.E. Considerations for parameter optimization and sensitivity in climate models. Proc. Natl. Acad. Sci. USA 2010, 107, 21349–21354. [Google Scholar] [CrossRef] [PubMed]
- Bellprat, O.; Kotlarski, S.; Lüthi, D.; De Elía, R.; Frigon, A.; Laprise, R.; Schär, C. Objective calibration of regional climate models: Application over Europe and North America. J. Clim. 2016, 29, 819–838. [Google Scholar] [CrossRef]
- Voudouri, A.; Avgoustoglou, E.; Carmona, I.; Levi, Y.; Bucchignani, E.; Kaufmann, P.; Bettems, J.M. Objective Calibration of Numerical Weather Prediction Model: Application on Fine Resolution COSMO Model over Switzerland. Atmosphere 2021, 12, 1358. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. Atmos. 2008, 113, D06104. [Google Scholar] [CrossRef]
- Chiandussi, G.; Codegone, M.; Ferrero, S.; Varesio, F. Comparison of multi-objective optimization methodologies for engineering applications. Comput. Math. Appl. 2012, 63, 912–942. [Google Scholar] [CrossRef]
- Gong, W.; Duan, Q.; Li, J.; Wang, C.; Di, Z.; Ye, A.; Miao, C.; Dai, Y. Multiobjective adaptive surrogate modeling-based optimization for parameter estimation of large, complex geophysical models. Water Resour. Res. 2016, 52, 1984–2008. [Google Scholar] [CrossRef]
- Zängl, G.; Reinert, D.; Rípodas, P.; Baldauf, M. The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Q. J. R. Meteorol. Soc. 2015, 141, 563–579. [Google Scholar] [CrossRef]
- De Lucia, C.; Bucchignani, E.; Mastellone, A.; Adinolfi, M.; Montesarchio, M.; Cinquegrana, D.; Mercogliano, P.; Schiano, P. A Sensitivity Study on High Resolution NWP ICON-LAM Model over Italy. Atmosphere 2022, 13, 540. [Google Scholar] [CrossRef]
- Desiato, F.; Lena, F.; Toreti, A. SCIA: A system for a better knowledge of the Italian climate. Boll. Geofis. Teor. Appl. 2007, 48, 351–358. [Google Scholar]
- Avgoustoglou, E.; Voudouri, A.; Khain, P.; Grazzini, F.; Bettems, J.M. Design and Evaluation of Sensitivity Tests of COSMO Model Over the Mediterranean Area. In Perspectives on Atmospheric Sciences; Karacostas, T., Bais, A., Nastos, P.T., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 49–54. [Google Scholar]
- Bucchignani, E.; Voudouri, A.; Mercogliano, P. A Sensitivity Analysis with COSMO-LM at 1 km Resolution over South Italy. Atmosphere 2020, 11, 430. [Google Scholar] [CrossRef]
- Seth, A.; Giorgi, F. The effects of domain choice on summer precipitation simulation and sensitivity in a regional climate model. J. Clim. 1998, 11, 2698–2712. [Google Scholar] [CrossRef]
- Goswami, P.; Shivappa, H.; Goud, S. Comparative analysis of the role of domain size, horizontal resolution and initial conditions in the simulation of tropical heavy rainfall events. Meteorol. Appl. 2012, 19, 170–178. [Google Scholar] [CrossRef]
- Leduc, M.; Laprise, R. Regional climate model sensitivity to domain size. Clim. Dyn. 2009, 32, 833–854. [Google Scholar] [CrossRef]
- Song, I.S.; Byun, U.Y.; Hong, J.; Park, S.H. Domain-size and top-height dependence in regional predictions for the Northeast Asia in spring. Atmos. Sci. Lett. 2018, 19, e799. [Google Scholar] [CrossRef]
- Jones, D.; Schonlau, M.; Welch, W. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.; Mitchell, T.; Wynn, H. Design and Analysis of a Computer Experiments. Stat. Sci. 1989, 4, 409–435. [Google Scholar] [CrossRef]
- McKay, M.; BeckMan, R.; Conover, W. A comparison of three methods for selecting values of input variables in the analisys of output from a computer code. Technometrics 1979, 21–22, 239–245. [Google Scholar]
- Voudouri, A.; Khain, P.; Carmona, I.; Avgoustoglou, E.; Bettems, J.; Grazzini, F.; Bellprat, O.; Kaufmann, P.; Bucchignani, E. Calibration of COSMO Model, Priority Project CALMO, Final Report. COSMO Technical Report. 2017. Available online: http://www.cosmo-model.org/content/model/cosmo/techReports/docs/techReport32.pdf (accessed on 16 May 2022).
- Voudouri, A.; Khain, P.; Carmona, I.; Bellprat, O.; Grazzini, F.; Avgoustoglou, E.; Bettems, J.; Kaufmann, P. Objective calibration of numerical weather prediction models. Atmos. Res. 2017, 190, 128–140. [Google Scholar] [CrossRef]
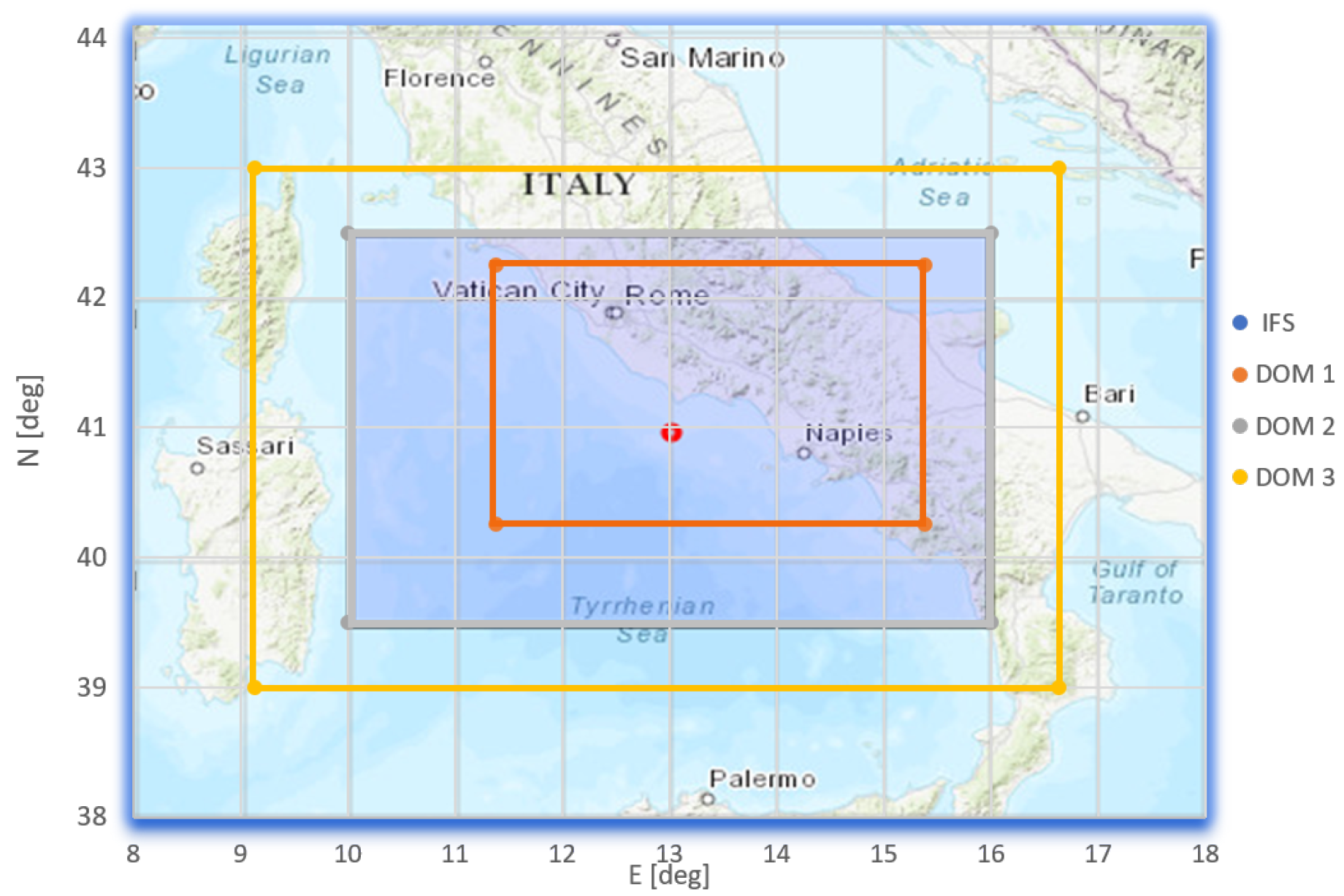
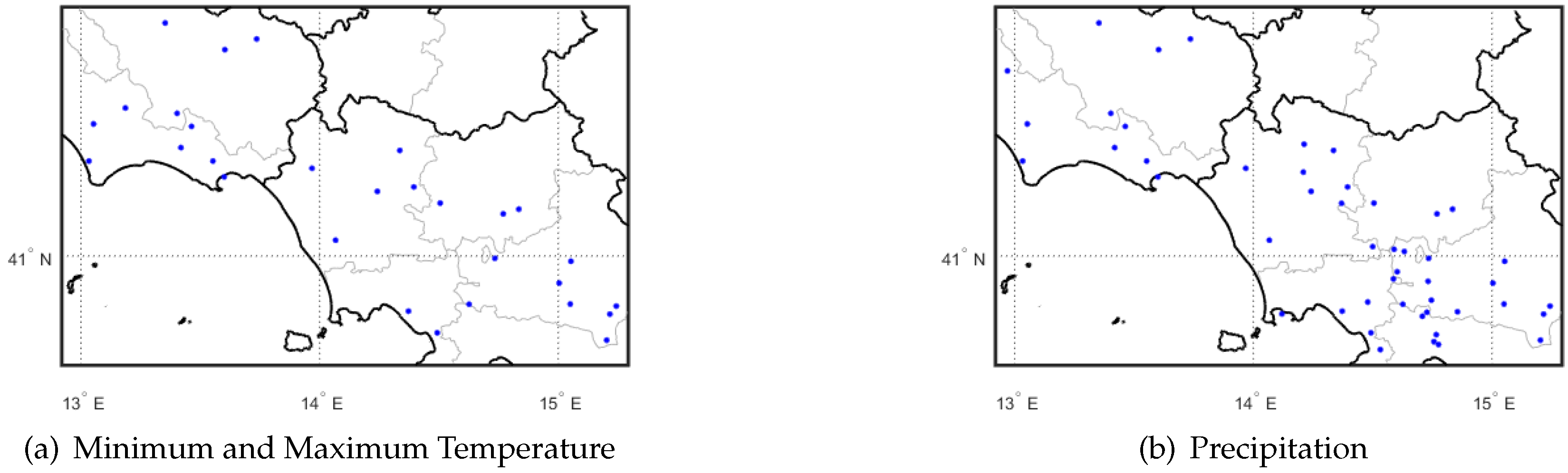
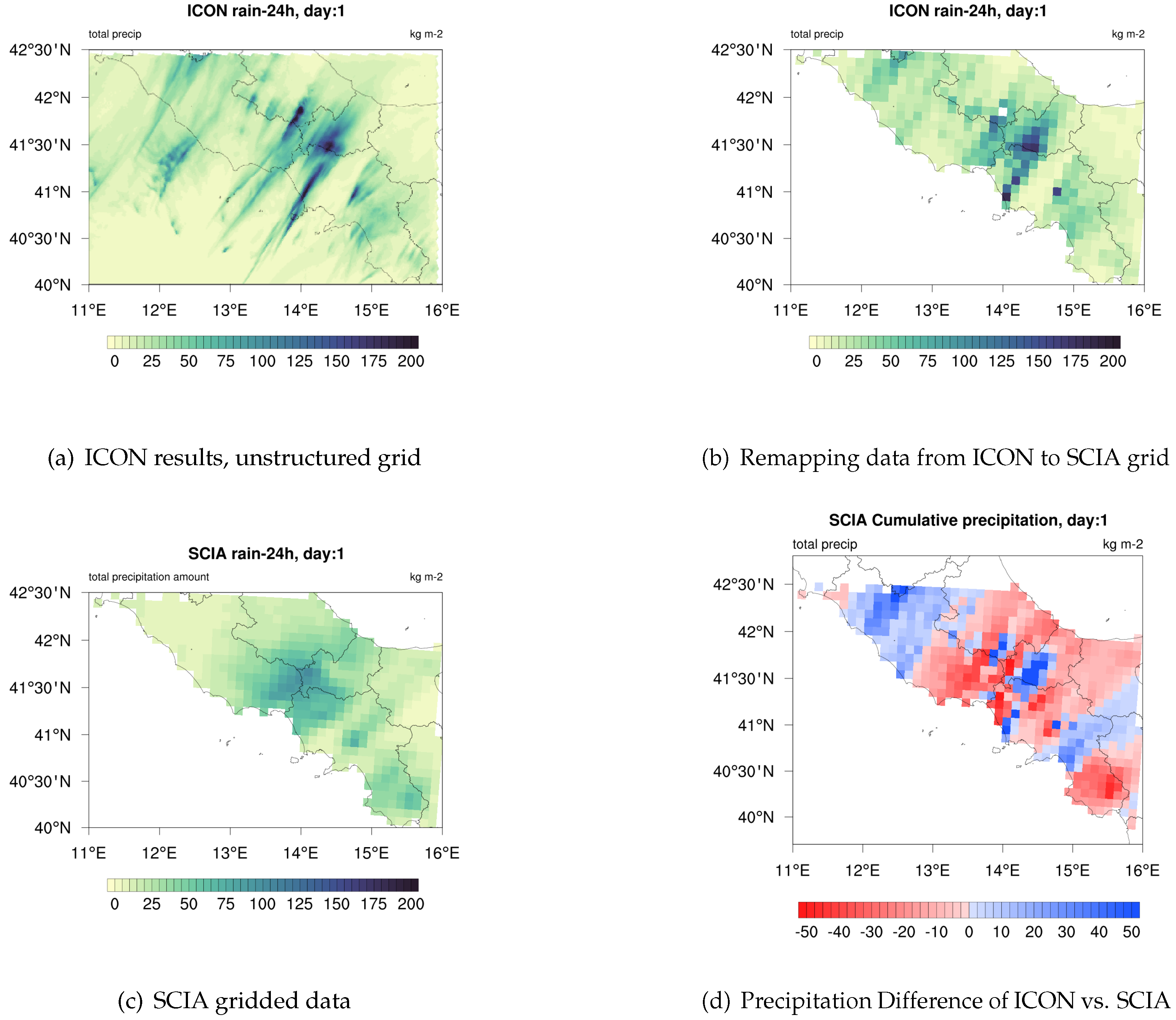

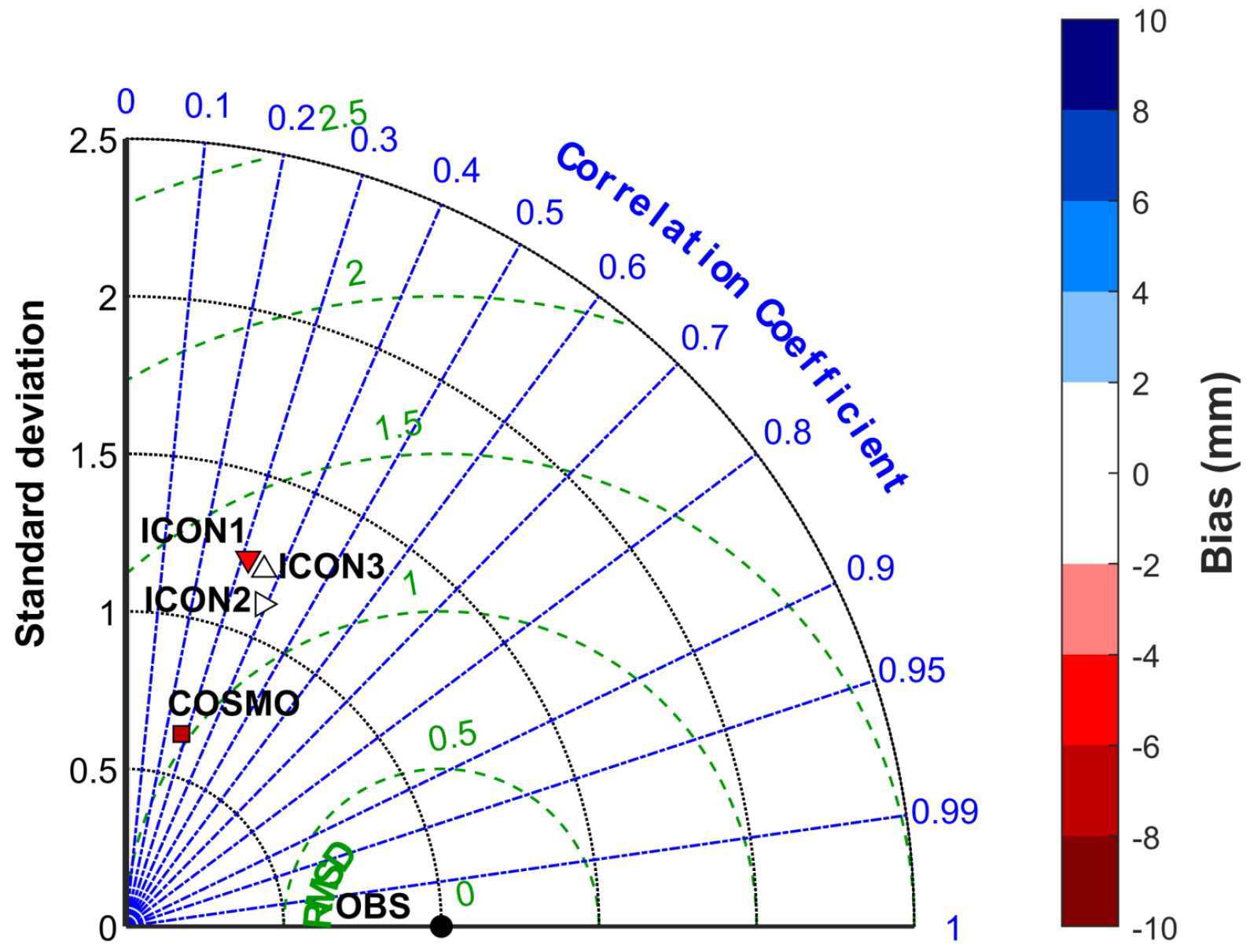

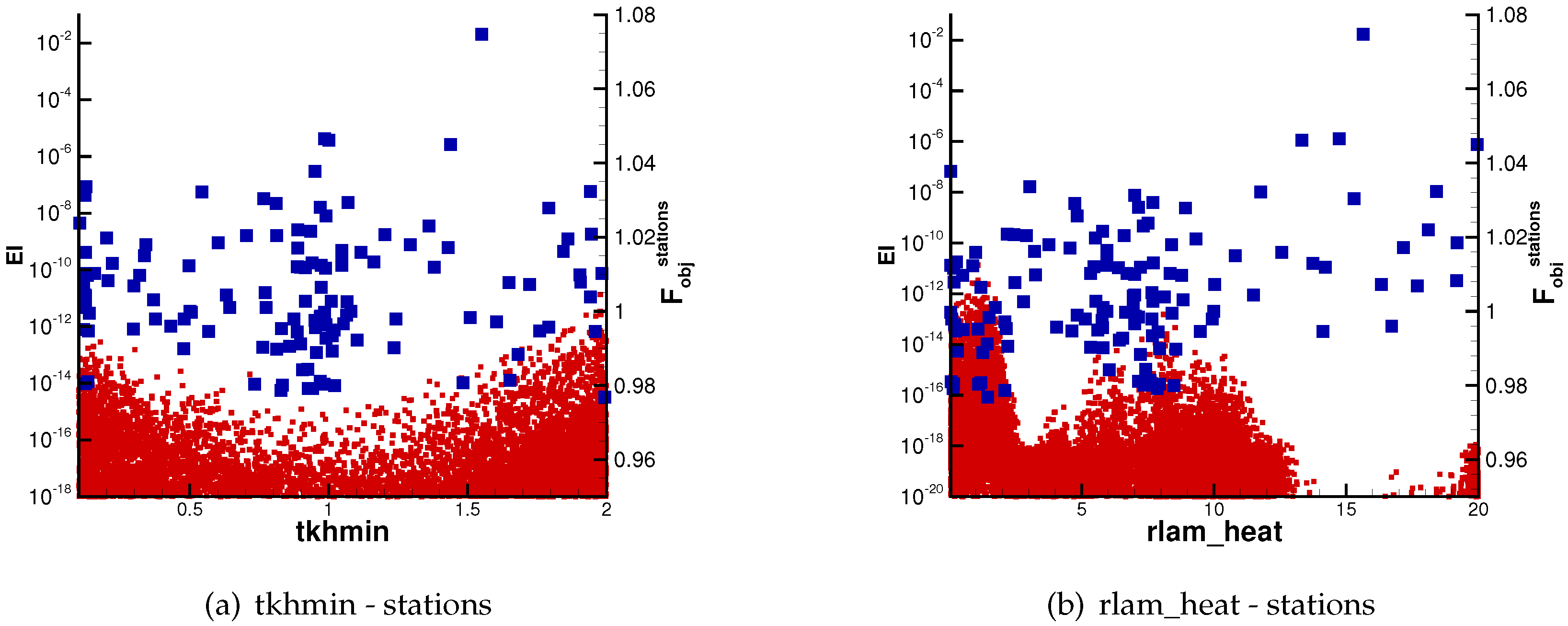
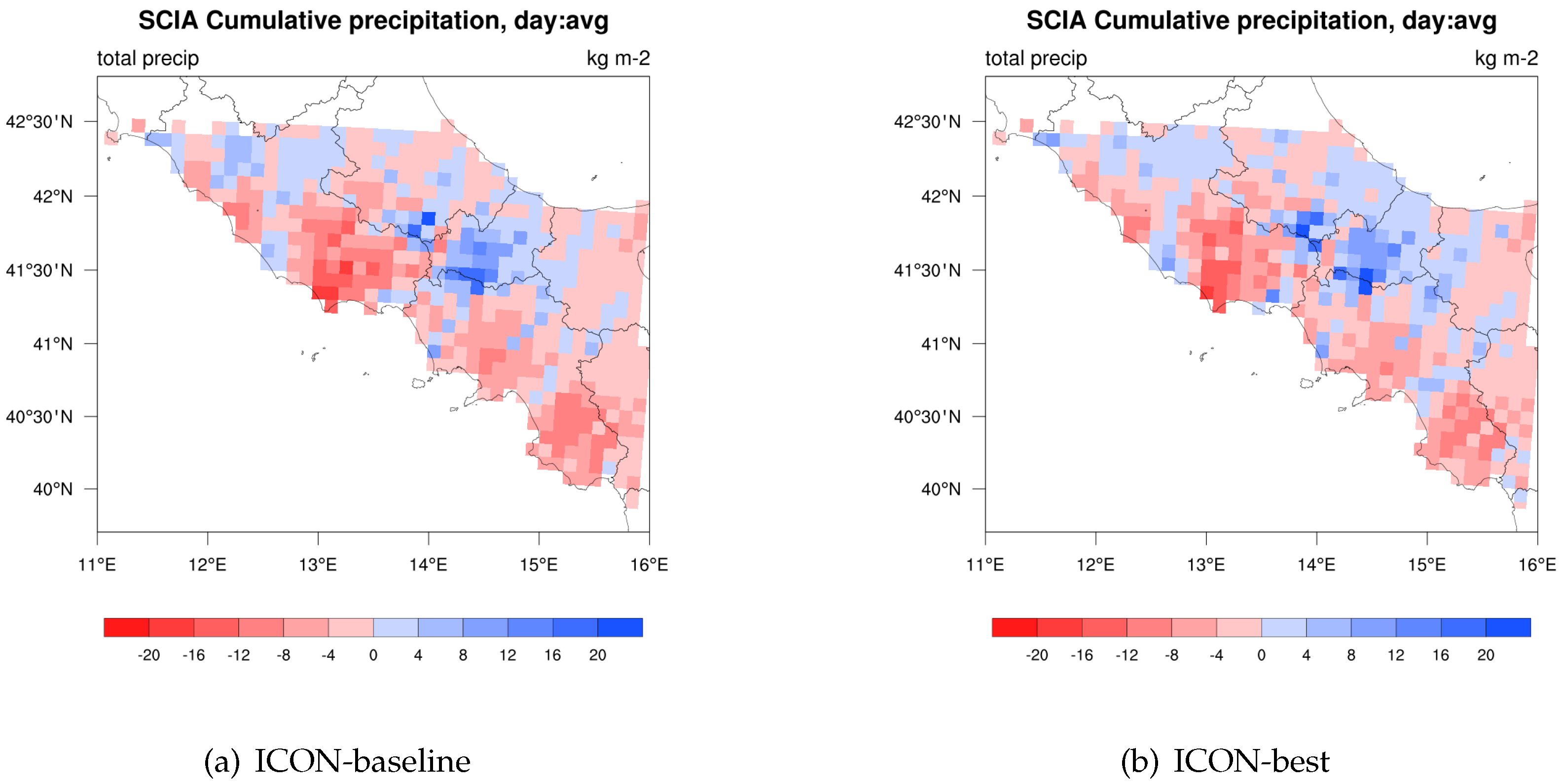
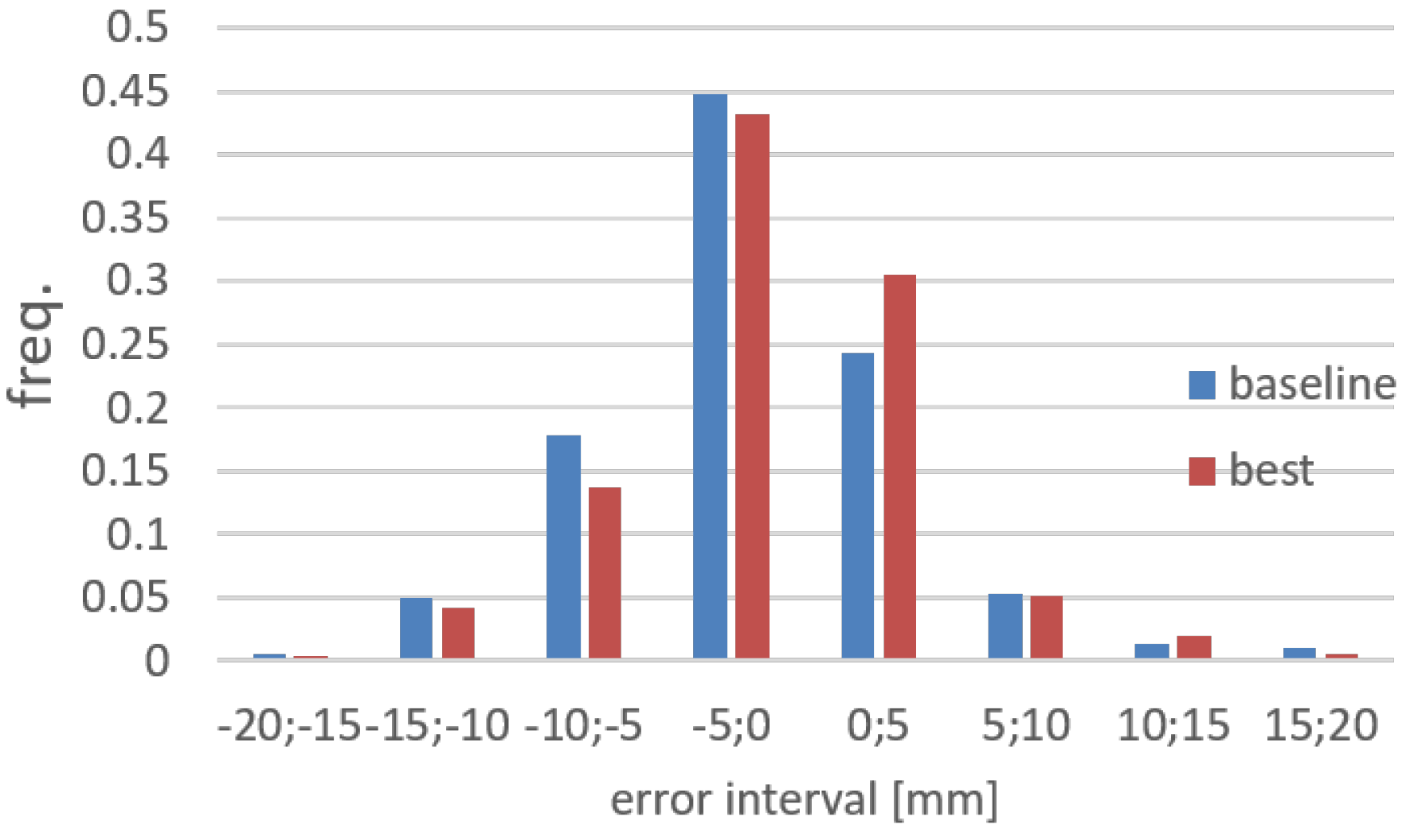
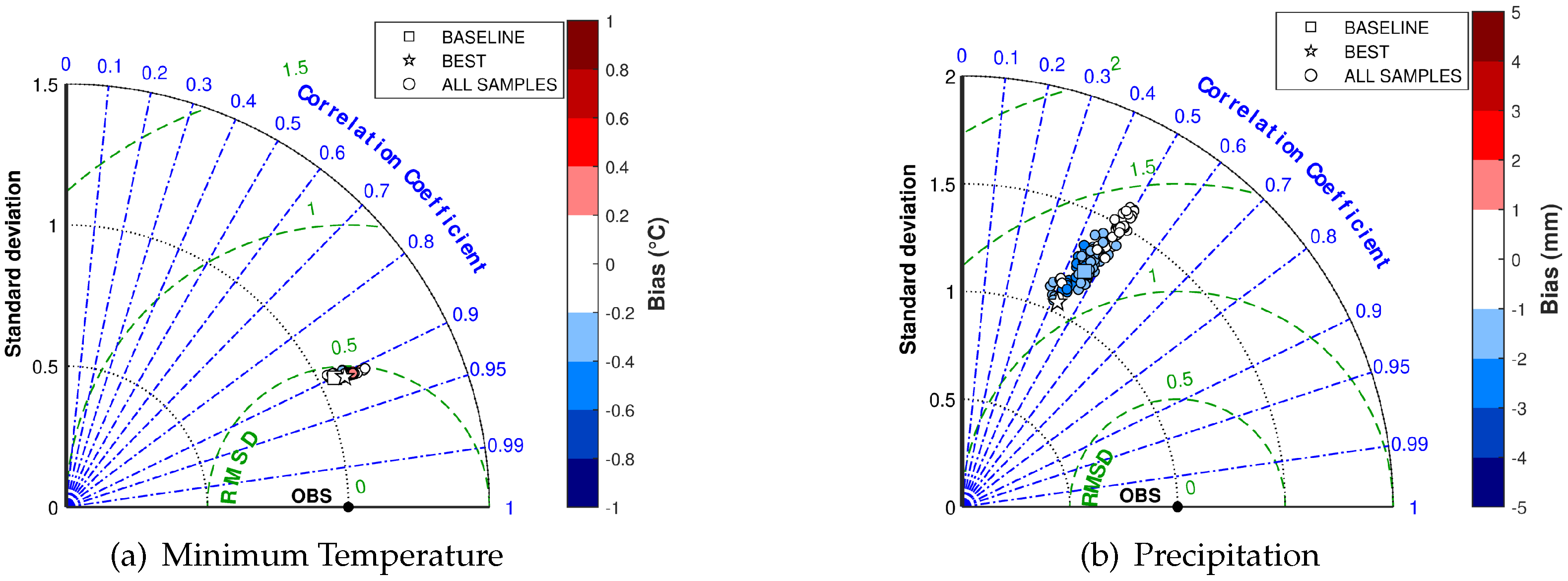



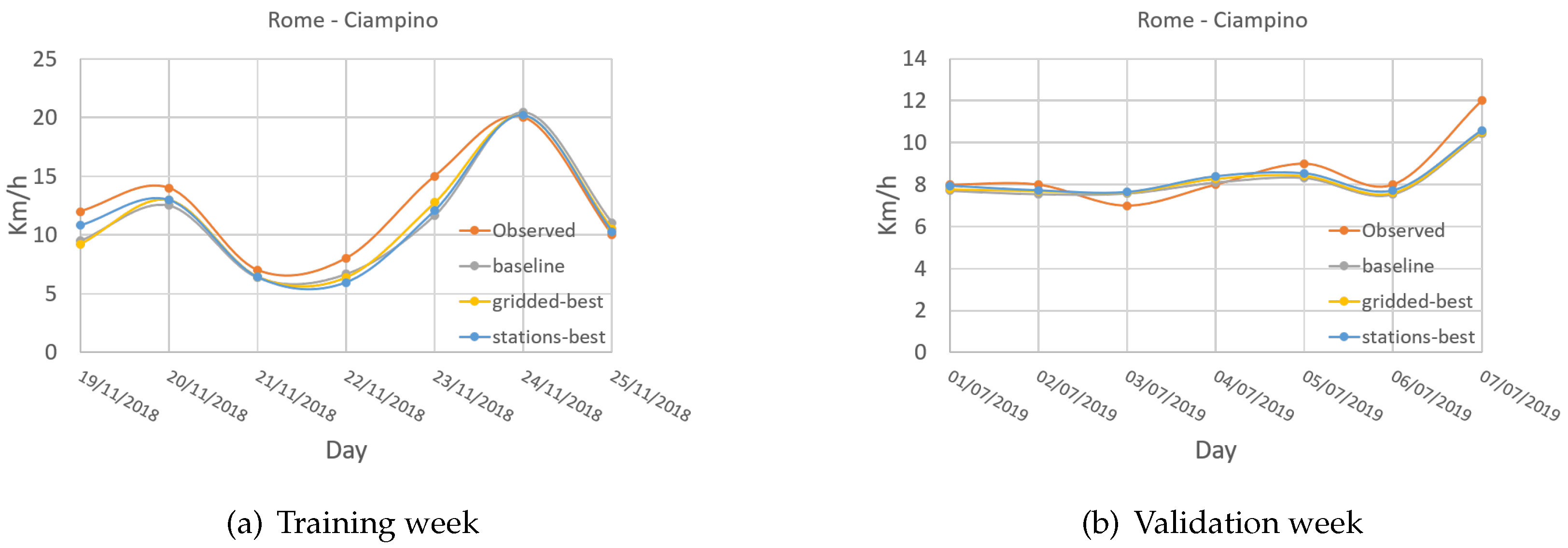

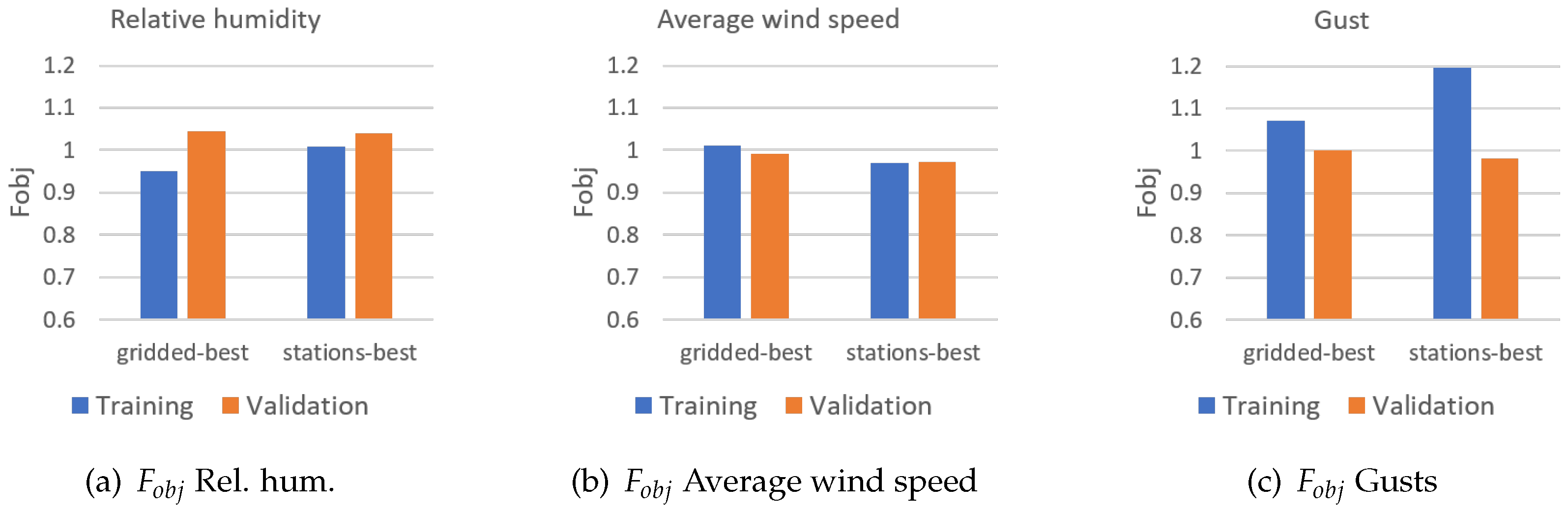
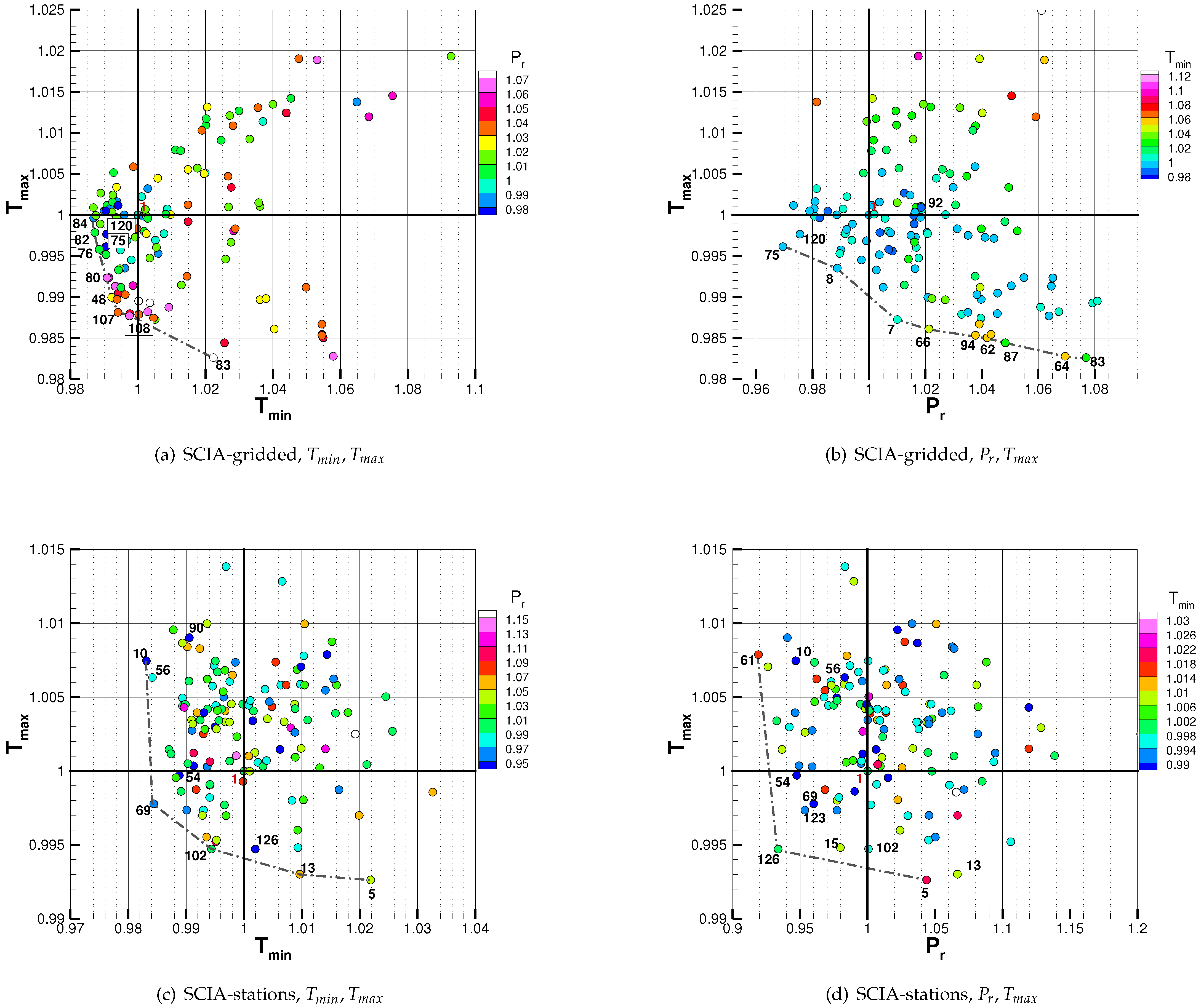
| Domain Label | Cells | Lon [deg E] | Lat [deg N] |
|---|---|---|---|
| DOM1 | 49,192 | 11.36–15.41 | 40.23–42.28 |
| DOM2 | 110,216 | 9.97–16.03 | 39.47–43.03 |
| DOM3 | 182,968 | 3.71–23.88 | 33.99–49.13 |
| v0snow | tkhmin | tkmmin | rlam-heat | ||
|---|---|---|---|---|---|
| Baseline | 20.00 | 0.500 | 0.750 | 10.00 | 1.000 |
| Gridded | 29.99 | 0.951 | 0.886 | 5.771 | 0.9854 |
| Stations | 29.94 | 0.829 | 1.307 | 2.089 | 0.9768 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cinquegrana, D.; Zollo, A.L.; Montesarchio, M.; Bucchignani, E. A Metamodel-Based Optimization of Physical Parameters of High Resolution NWP ICON-LAM over Southern Italy. Atmosphere 2023, 14, 788. https://doi.org/10.3390/atmos14050788
Cinquegrana D, Zollo AL, Montesarchio M, Bucchignani E. A Metamodel-Based Optimization of Physical Parameters of High Resolution NWP ICON-LAM over Southern Italy. Atmosphere. 2023; 14(5):788. https://doi.org/10.3390/atmos14050788
Chicago/Turabian StyleCinquegrana, Davide, Alessandra Lucia Zollo, Myriam Montesarchio, and Edoardo Bucchignani. 2023. "A Metamodel-Based Optimization of Physical Parameters of High Resolution NWP ICON-LAM over Southern Italy" Atmosphere 14, no. 5: 788. https://doi.org/10.3390/atmos14050788
APA StyleCinquegrana, D., Zollo, A. L., Montesarchio, M., & Bucchignani, E. (2023). A Metamodel-Based Optimization of Physical Parameters of High Resolution NWP ICON-LAM over Southern Italy. Atmosphere, 14(5), 788. https://doi.org/10.3390/atmos14050788








