Three-Dimensional Simulation of Corona Discharge in a Double-Needle System during a Thunderstorm
Abstract
1. Introduction
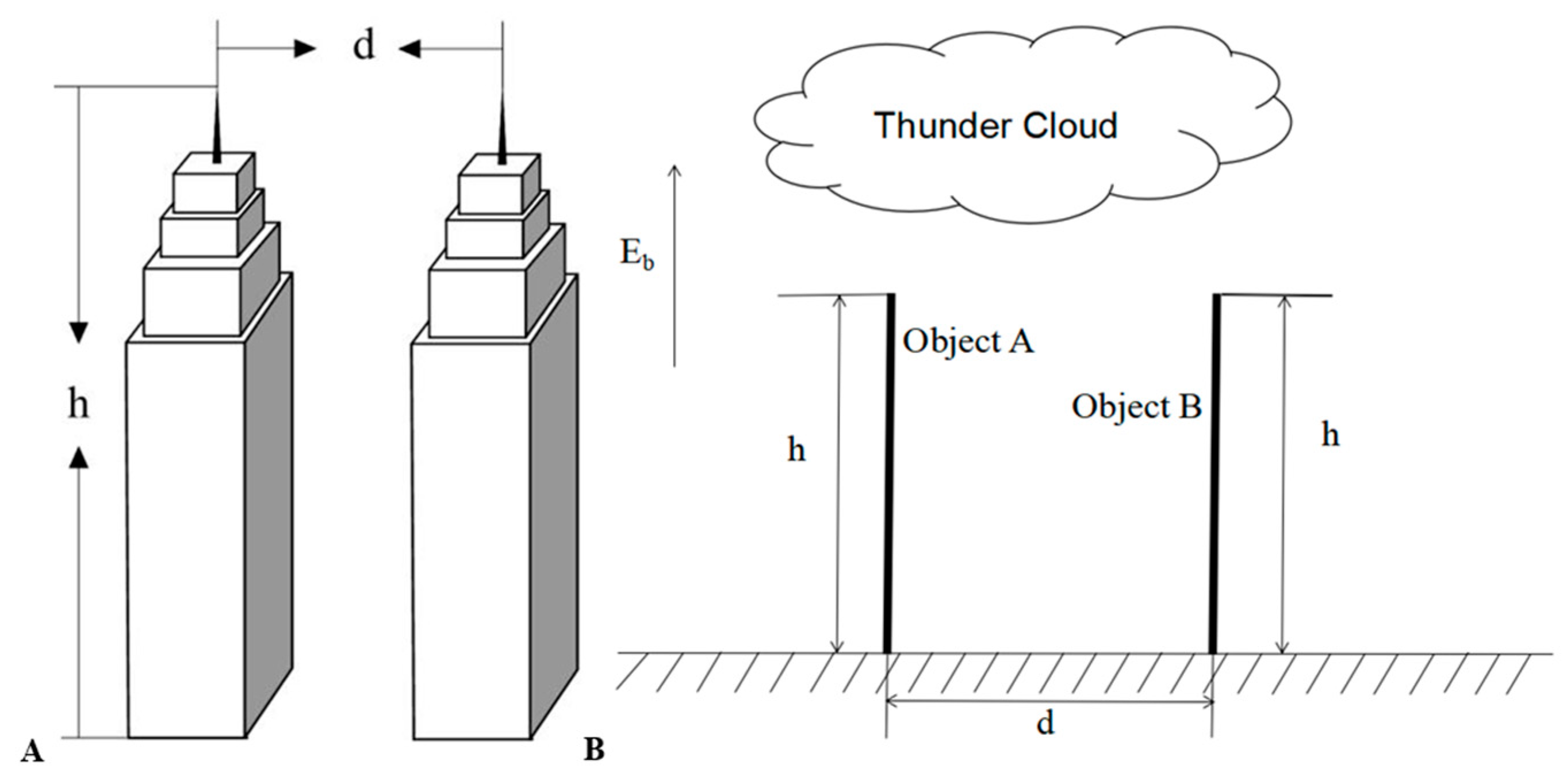
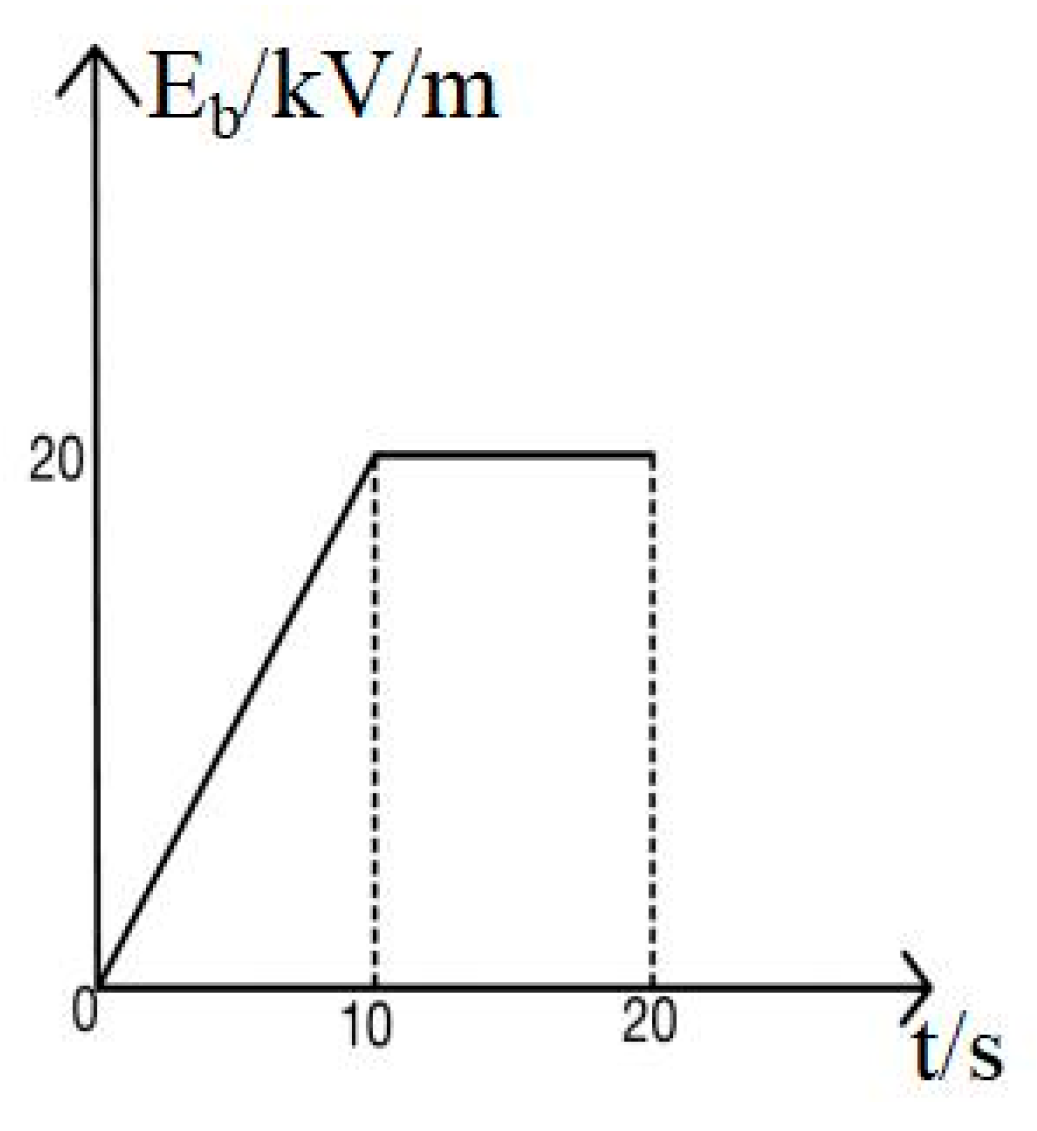
2. Model Settings
3. Simulation Results and Analysis
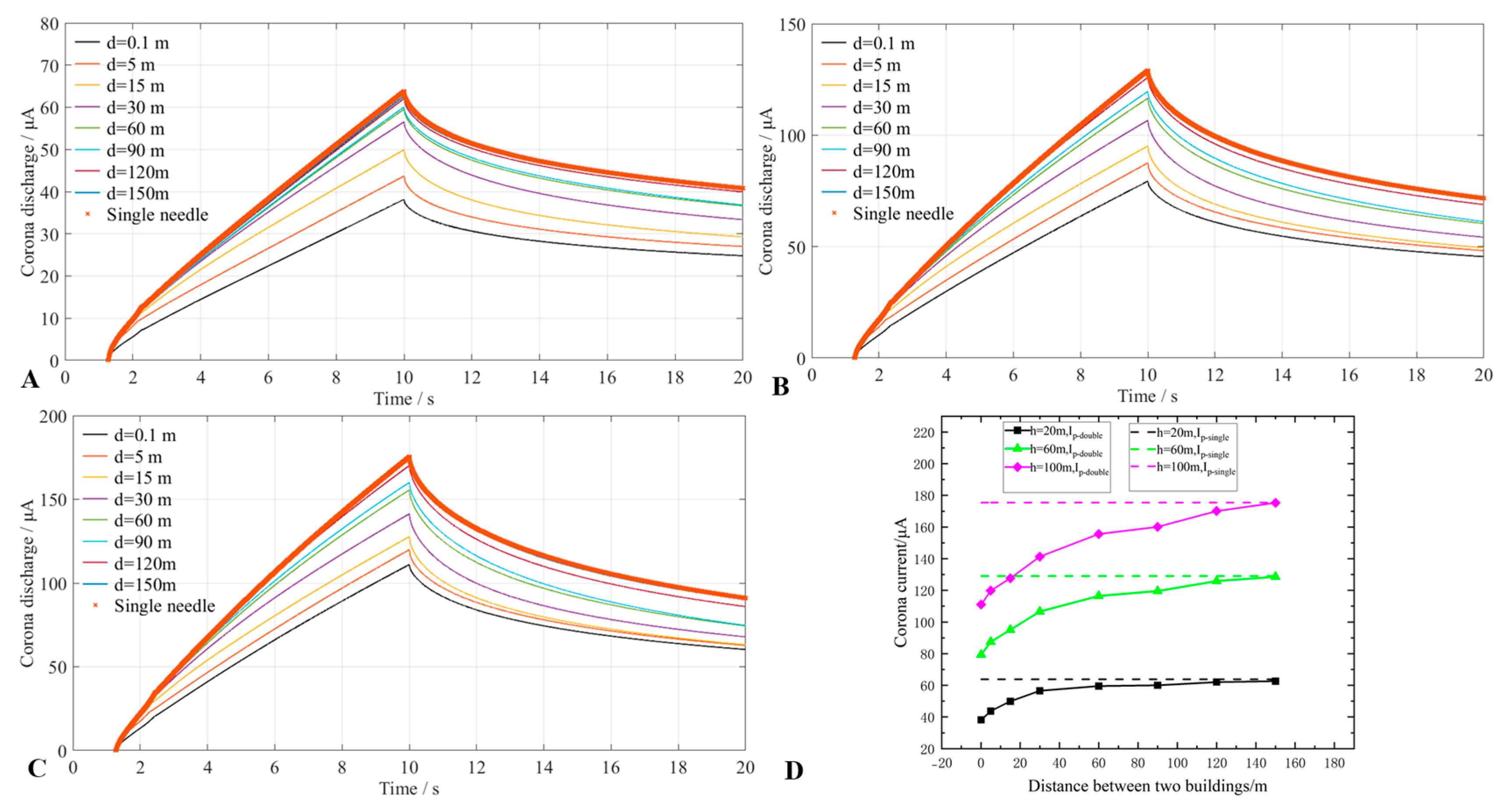
3.1. Corona Current in a Double-Needle System with Different Geometric Characteristics
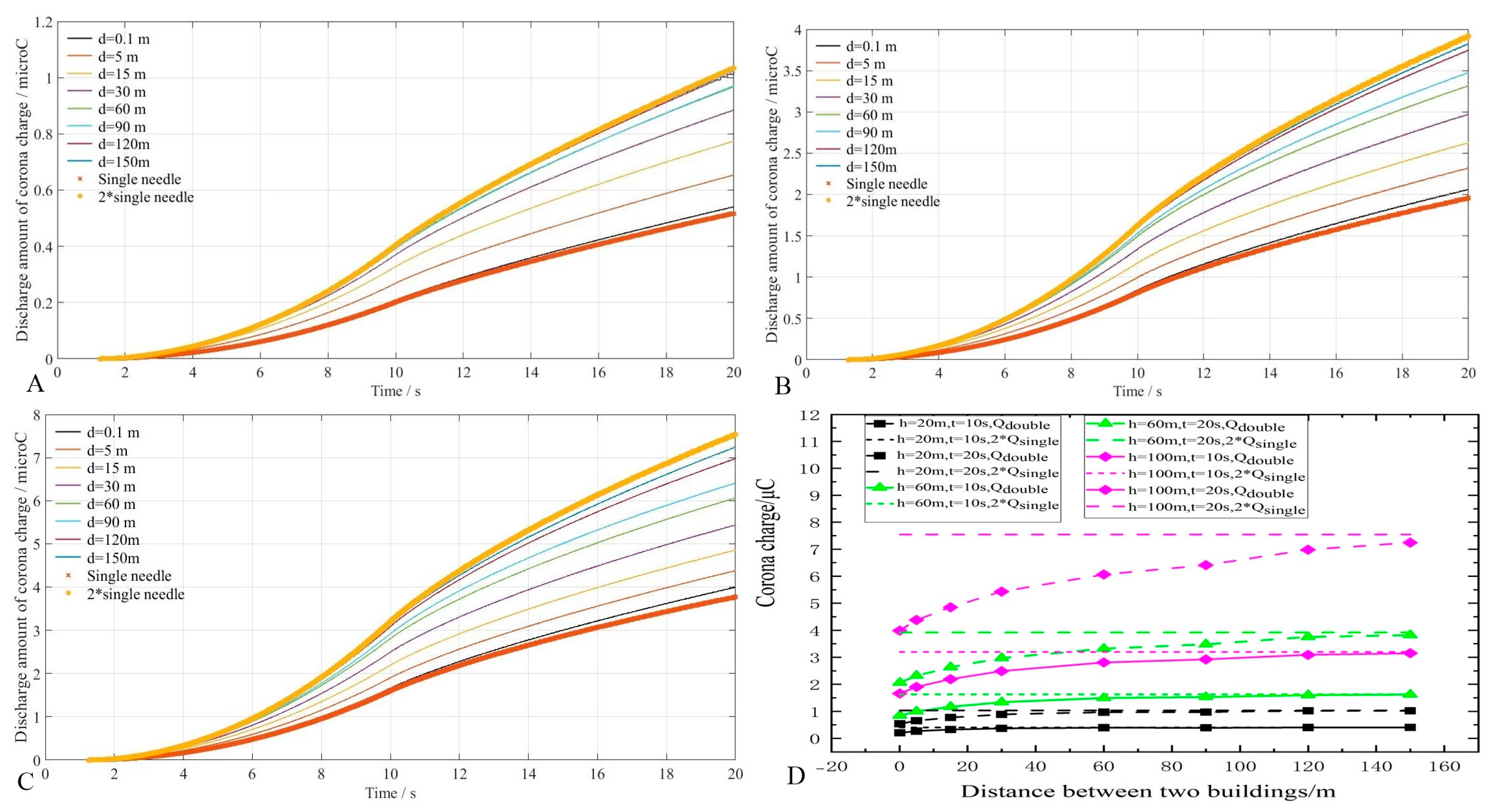
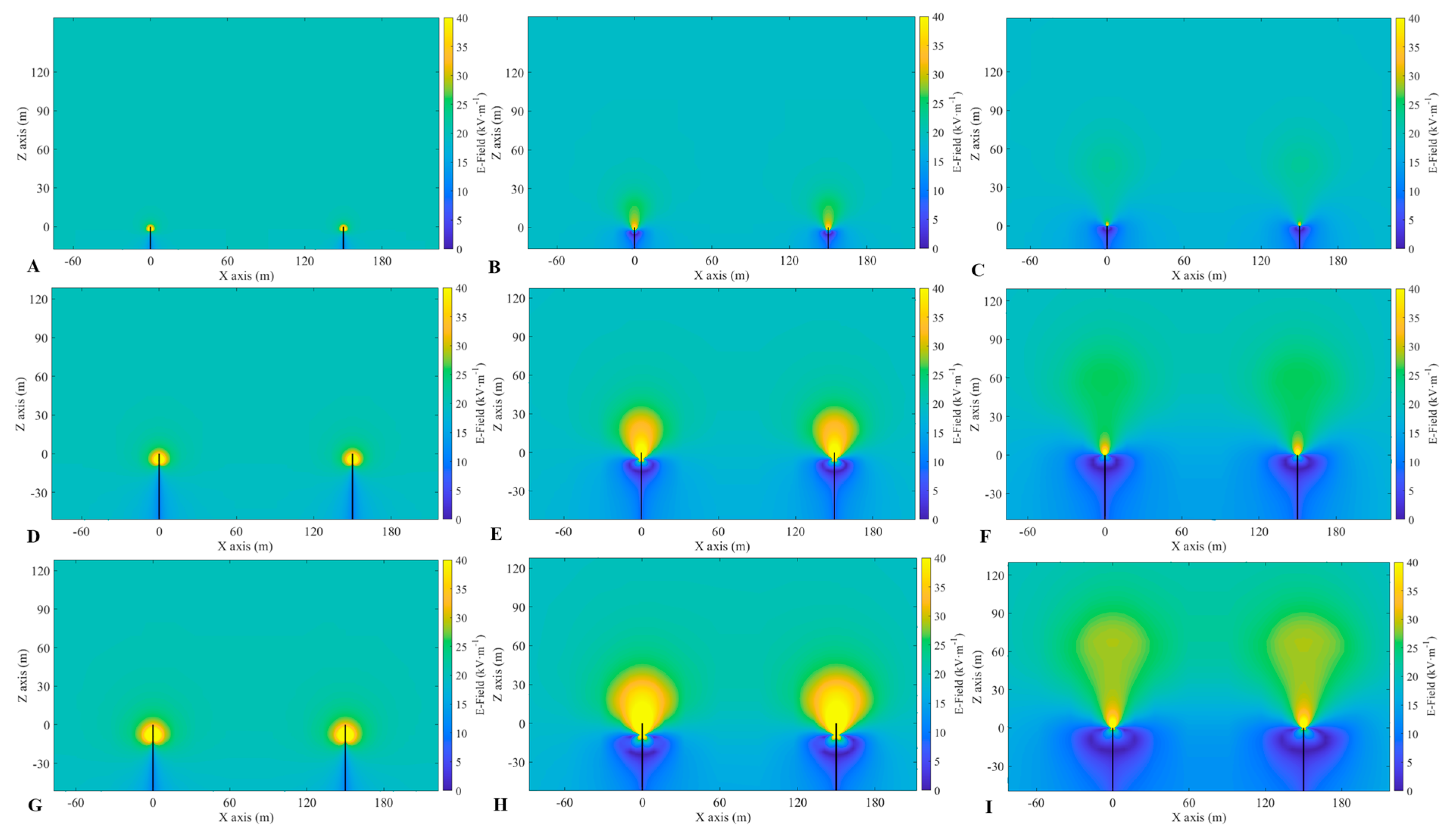
3.2. Corona Charges in a Double-Needle System with Different Geometric Characteristics
4. Result
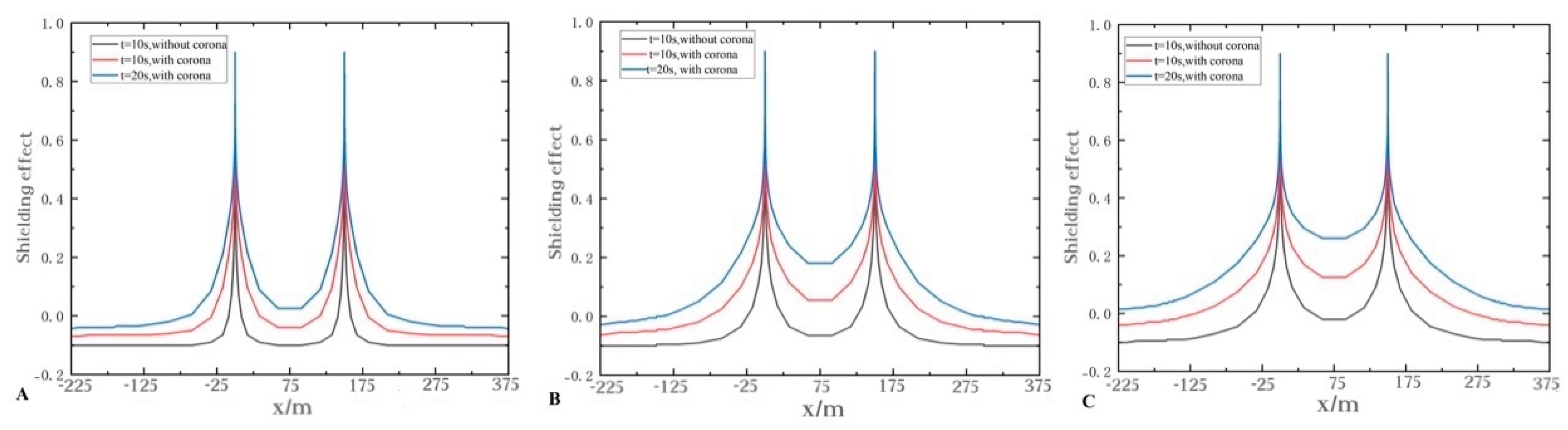
Shielding Effect of a Double-Needle System on the Ground Electric Field with and without Corona Discharge
5. Conclusions and Discussion
- (1)
- By comparing the corona-current variation characteristics of the double-needle system with different geometric characteristics, it was found that the corona current at each tip of the equal-height double-needle system is consistent with that of an independent lightning rod under the same thunderstorm electric field. With increasing d, Ip-double approaches Ip-single gradually, and for the double-needle system with different heights, the required d conditions for Ip-double ≈ Ip-single are different. For example, for h = 20 m, the required d is ca. 120 m, but for h = 60 m and 100 m, the required d exceeds 150 m, with the value for h = 60 m being less than that for h = 100 m;
- (2)
- For d = 0.1 m, Qdouble is almost equal to Qsingle. When d is increased to a certain value, Qdouble is almost equal to 2Qsingle. For Qdouble ≈ Qsingle, the required value of d increases with both h and t: at t = 10 s, d should be 60 m for the 20 m high double-needle system, 90 m for the 60 m high one, and 120 m for the 100 m high one, and the corresponding values of d are less at t = 20 s;
- (3)
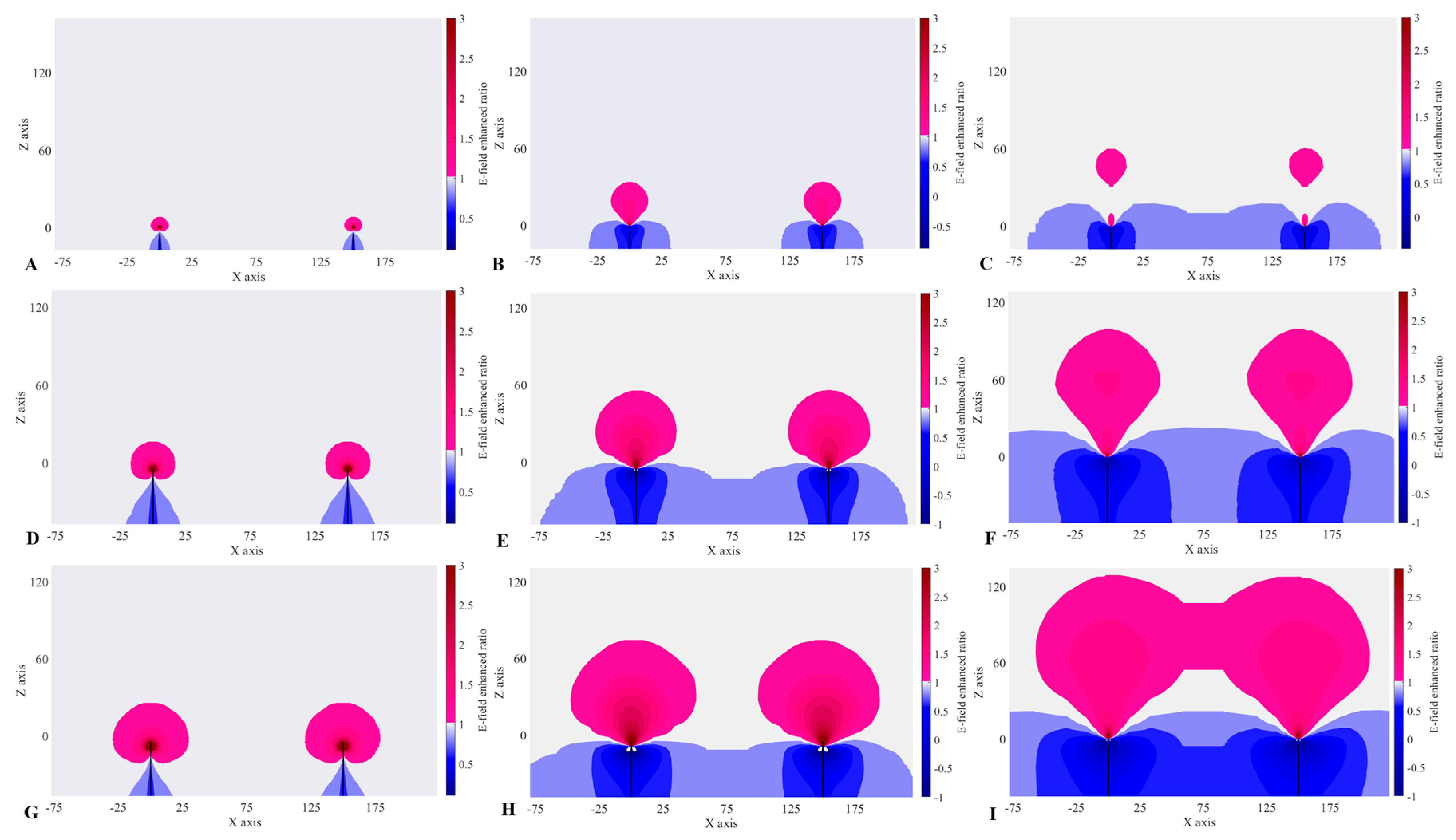
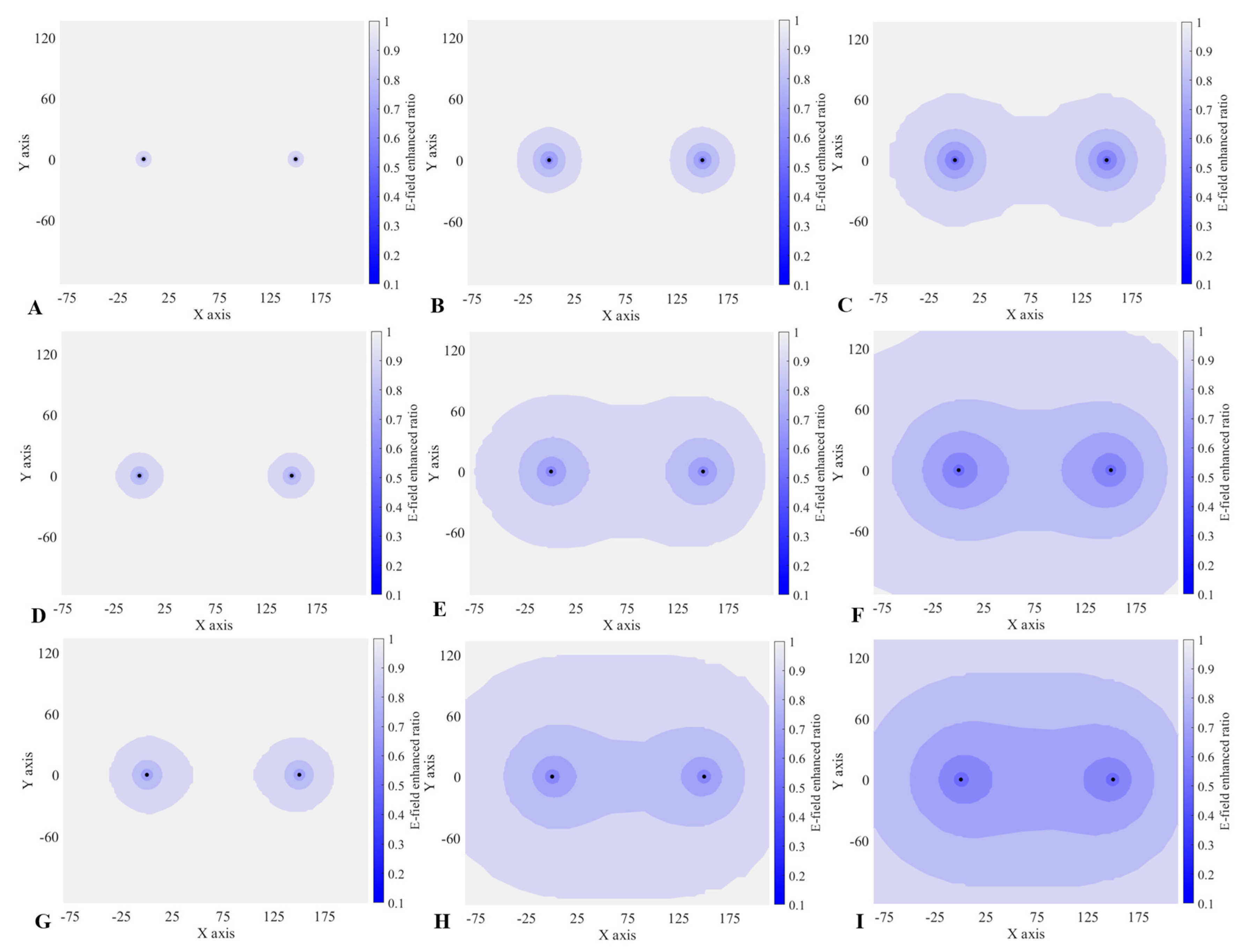
- The greater the value of t, the stronger the shielding effect of corona charges on the ground electric field and the larger the shielding range between the two needles of the double-needle system. However, the higher the value of h, the smaller the CD shielding range on the ground;
- (4)
- Herein, the shielding effect of CD on the ground electric field in the double-needle system was studied by comparing the cases of CD and no CD, and the conclusions are as follows. With CD, the shielding effect on the ground electric field is increased, and the higher the value of h, the greater the increase. The range of the CD shielding effect of the 20 m high double-needle system on the ground electric field is about 70 m, which is 8.8 times that without CD. However, the range of the CD shielding effect of the 100 m high double-needle system is about 150 m, which is just 1.5 times that without CD.
Author Contributions
Funding
Conflicts of Interest
References
- Bazelyan, E.M.; Raizer, Y.P.; Aleksandrov, N.L.; D’Alessandro, F. Corona processes and lightning attachment: The effect of wind during thunderstorms. Atmos. Res. 2009, 94, 436–447. [Google Scholar] [CrossRef]
- Bazelyan, E.M.; Raizer, Y.P.; Aleksandrov, N.L. The effect of space charge produced by corona at ground level on lightning attachment to high objects. Atmos. Res. 2015, 153, 74–86. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, X.; Zhu, J.; Shi, Z.; Zhang, D. Influence on simulation accuracy of atmospheric electric field around a building by space resolution. Atmos. Res. 2013, 138, 301–307. [Google Scholar] [CrossRef]
- Tan, Y.; Liang, Z.; Shi, Z.; Zhu, J.; Guo, X. Numerical simulation of the effect of lower positive charge region in thunderstorms on different types of lightning. Sci. China Earth Sci. 2014, 57, 2125–2134. [Google Scholar] [CrossRef]
- Mazur, V.; Ruhnke, L.H. Model of electric charges in thunderstorms and associated lightning. J. Geophys. Res. Atmos. 1998, 103, 23299–23308. [Google Scholar] [CrossRef]
- Soula, S. Transfer of electrical space charge from corona between ground and thundercloud: Measurements and modeling. J. Geophys. Res. Atmos. 1994, 99, 10759–10765. [Google Scholar] [CrossRef]
- Pérez-Invernón, F.J.; Malagón-Romero, A. Editorial for the Special Issue “Advances in Atmospheric Electricity”. Atmosphere 2022, 13, 1829. [Google Scholar] [CrossRef]
- Romanovskii, O.A.; Kharchenko, O.V. Atmospheric and Ocean Optics: Atmospheric Physics III. Atmosphere 2022, 13, 1912. [Google Scholar] [CrossRef]
- Soler, S.; Pérez-Invernón, F.J.; Gordillo-Vázquez, F.J.; Luque, A.; Li, D.; Malagón-Romero, A.; Neubert, T.; Chanrion, O.; Reglero, V.; Navarro-Gonzalez, J.; et al. Blue optical observations of narrow bipolar events by ASIM suggest corona streamer activity in thunderstorms. J. Geophys. Res. Atmos. 2020, 125, e2020JD032708. [Google Scholar] [CrossRef]
- Becerra, M. Corona discharges and their effect on lightning attachment revisited: Upward leader initiation and downward leader interception. Atmos. Res. 2014, 149, 316–323. [Google Scholar] [CrossRef]
- Yuan, S.; Jiang, R.; Qie, X.; Wang, D.; Sun, Z.; Liu, M. Characteristics of Upward Lightning on the Beijing 325 m Meteorology Tower and Corresponding Thunderstorm Conditions. J. Geophys. Res. Atmos. 2017, 122, 12093–12105. [Google Scholar] [CrossRef]
- Bao, R.; Zhang, Y.; Ma, B.J.; Zhang, Z.; He, Z. An Artificial Neural Network for Lightning Prediction Based on Atmospheric Electric Field Observations. Remote Sens. 2022, 14, 4131. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Zou, M.; Wang, J.; Li, Y.; Tan, Y.; Feng, Y.; Zhang, H.; Zhu, S. Advances in Lightning Monitoring and Location Technology Research in China. Remote Sens. 2022, 14, 1293. [Google Scholar] [CrossRef]
- Goelian, N.; Lalande, P.; Bondiou-Clergerie, A.; Bacchiega, G.; Gazzani, A.; Gallimberti, I. A simplified model for the simulation of positive-spark development in long air gaps. J. Phys. D Appl. Phys. 1997, 30, 2441–2452. [Google Scholar] [CrossRef]
- Bazelyan, E.M.; Drabkin, M.M. Scientific and technical basis for preventing lightning strikes to earthbound objects. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491), Toronto, ON, Canada, 13–17 July 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 4, pp. 2201–2208. [Google Scholar]
- Rizk, F.A. Analysis of space charge generating devices for lightning protection: Performance in slow varying fields. IEEE Trans. Power Deliv. 2010, 25, 1996–2006. [Google Scholar] [CrossRef]
- Chalmers, J.A. Atmospheric Electricity, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1976; pp. 451–499. [Google Scholar]
- Aubrecht, L.; Koller, J.; Stanek, Z. Onset voltages of atmospheric corona discharges on coniferous trees. J. Atmos. Sol. Terr. Phys. 2001, 63, 1901–1906. [Google Scholar] [CrossRef]
- Aubrecht, L.; Stanek, Z.; Koller, J. Corona discharge on coniferous trees-spruce and pine. Europhys. Lett. 2001, 53, 304. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Bazelyan, E.M.; Carpenter, R.B., Jr.; Drabkin, M.M.; Raizer, Y.P. The effect of coronae on leader initiation and development under thunderstorm conditions and in long air gaps. J. Phys. D Appl. Phys. 2001, 34, 3256. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Bazelyan, E.M.; Drabkin, M.M.; Carpenter, R.B.; Raizer, Y.P. Corona discharge at the tip of a tall object in the electric field of a thundercloud. Plasma Phys. Rep. 2002, 28, 953–964. [Google Scholar] [CrossRef]
- Bazelyan, E.M.; Raizer, Y.P.; Aleksandrov, N.L. Corona initiated from grounded objects under thunderstorm conditions and its influence on lightning attachment. Plasma Sources Sci. Technol. 2008, 17, 24015. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Bazelyan, E.M.; Raizer, Y.P. The effect of a corona discharge on a lightning attachment. Plasma Phys. Rep. 2005, 31, 75–91. [Google Scholar] [CrossRef]
- Bazelyan, E.M.; Raizer, Y.P.; Aleksandrov, N.L. Non-stationary corona around multi-point system in atmospheric electric field: I. Onset electric field and discharge current. J. Atmos. Sol. Terr. Phys. 2014, 109, 80–90. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Q. Effects of geometrical parameters of two height-unequal adjacent objects on corona discharges from their tips during a thunderstorm. Atmos. Res. 2017, 190, 113–120. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Q.; Zhang, J. Improvement of corona discharge model and its application on simulating corona discharge in the presence of wind. Math. Prob. Eng. 2017, 2017, 9853439. [Google Scholar] [CrossRef]
- Guo, X.; Ji, Z.; Gao, Y.; Ding, J.; Zhang, L. 3D corona discharge model and its use in the presence of wind during a thunderstorm. Front. Environ. Sci. 2022, 10, 2–8. [Google Scholar] [CrossRef]
- Peek, F.W. Dielectric Phenomena in High Voltage Engineering; McGraw-Hill Book Company, Inc.: New York, NY, USA; London, UK, 1920. [Google Scholar]
- Cristina, S.; Dinelli, G.; Feliziani, M. Numerical computation of corona space charge and VI characteristic in DC electrostatic precipitators. IEEE Trans. Ind. Appl. 1991, 27, 147–153. [Google Scholar] [CrossRef]
- Caron, A.; Dascalescu, L. Numerical modeling of combined corona-electrostatic fields. J. Electrostat. 2004, 61, 43–55. [Google Scholar] [CrossRef]
- Nouri, H.; Zebboudj, Y. Analysis of positive corona in wire-to-plate electrostatic precipitator. Eur. Phys. J. Appl. Phys. 2010, 49, 11001. [Google Scholar] [CrossRef]
- Becerra, M. Glow corona generation and streamer inception at the tip of grounded objects during thunderstorms: Revisited. J. Phys. D Appl. Phys. 2013, 46, 135205. [Google Scholar] [CrossRef]
- Qie, X.S.; Soula, S.; Chauzy, S. Numerical calculation of evolution of corona ions produced from the ground under thunderstorm. Chin. J. Geophys. 1996, 39, 43–51. (In Chinese) [Google Scholar]
- Becerra, M.; Cooray, V.; Soula, S.; Chauzy, S. Effect of the space charge layer created by corona at ground level on the inception of upward lightning leaders from tall towers. J. Geophys. Res. Atmos. 2007, 112, 1103–1118. [Google Scholar] [CrossRef]
- Qie, X.; Soula, S.; Chauzy, S. Influence of ion attachment on the vertical distribution of the electric field and charge density below a thunderstorm. Ann. Geophys. 1994, 12, 1218–1228. [Google Scholar] [CrossRef]
- Willett, J.C.; Davis, D.A.; Laroche, P. An experimental study of positive leaders initiating rocket-triggered lightning. Atmos. Res. 1999, 51, 189–219. [Google Scholar] [CrossRef]
- Pierce, E.T. Atmospheric electricity and earthquake prediction. Geophys. Res. Lett. 1976, 3, 185–188. [Google Scholar] [CrossRef]
- Antunes de Sá, A.; Marshall, R.; Sousa, A.; Viets, A.; Deierling, W. An array of low-cost, high-speed, autonomous electric field mills for thunderstorm research. Earth Space Sci. 2020, 7, e2020EA001309. [Google Scholar] [CrossRef] [PubMed]
- Soula, S.; Chauzy, S. Multilevel measurement of the electric field underneath a thundercloud: 2. Dynamical evolution of a ground space charge layer. J. Geophys. Res. Atmos. 1991, 96, 22327–22336. [Google Scholar] [CrossRef]
- Standler, R.B.; Winn, W.P. Effects of coronae on electric fields beneath thunderstorms. Q. J. R. Meteorol. Soc. 1979, 105, 285–302. [Google Scholar] [CrossRef]
| h [m] | d [m] | Qsingle at t = 10 s, q1 [µC] | Qdouble at t = 10 s, q2 [µC] | Qdouble at t = 20 s, q3 [µC] | Qdouble at t = 20 s, q4 [µC] | ΔQ1 = 2q1 − q2 [µC] | ΔQ2 = 2q3 − q4 [µC] |
|---|---|---|---|---|---|---|---|
| 20 | 90 | 0.202 | 0.391 | 0.517 | 0.971 | 0.013 | 0.063 |
| 120 | 0.202 | 0.401 | 0.517 | 1.022 | 0.003 | 0.012 | |
| 150 | 0.202 | 0.404 | 0.517 | 1.022 | 0 | 0.012 | |
| 60 | 90 | 0.813 | 1.53 | 1.96 | 3.48 | 0.096 | 0.44 |
| 120 | 0.813 | 1.60 | 1.96 | 3.75 | 0.026 | 0.17 | |
| 150 | 0.813 | 1.62 | 1.96 | 3.82 | 0.006 | 0.10 | |
| 100 | 90 | 1.60 | 2.92 | 3.77 | 6.41 | 0.28 | 1.13 |
| 120 | 1.60 | 3.09 | 3.77 | 6.98 | 0.11 | 0.56 | |
| 150 | 1.60 | 3.15 | 3.77 | 7.24 | 0.05 | 0.30 |
| h/m | x1/m | x2/m | x2/x1 | x3/m | y1/m | y2/m | y2/y1 | y3/m | p1/m | p2/m | p2/p1 | p3/m |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 8 | 70 | 8.8 | 150 | 4 | 30 | 7.5 | 62 | 1 | 5 | 5 | 10 |
| 60 | 53 | 150 | 2.8 | 150 | 17 | 80 | 4.7 | 150 | 3 | 10 | 3.3 | 40 |
| 100 | 100 | 150 | 1.5 | 150 | 33 | 150 | 4.5 | 150 | 5 | 14 | 2.8 | 62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Zhang, L.; Ji, Z.; Gao, Y.; Wang, Z.; Zhao, N. Three-Dimensional Simulation of Corona Discharge in a Double-Needle System during a Thunderstorm. Atmosphere 2023, 14, 789. https://doi.org/10.3390/atmos14050789
Guo X, Zhang L, Ji Z, Gao Y, Wang Z, Zhao N. Three-Dimensional Simulation of Corona Discharge in a Double-Needle System during a Thunderstorm. Atmosphere. 2023; 14(5):789. https://doi.org/10.3390/atmos14050789
Chicago/Turabian StyleGuo, Xiufeng, Ling Zhang, Ziyu Ji, Yue Gao, Zhaoxia Wang, and Nian Zhao. 2023. "Three-Dimensional Simulation of Corona Discharge in a Double-Needle System during a Thunderstorm" Atmosphere 14, no. 5: 789. https://doi.org/10.3390/atmos14050789
APA StyleGuo, X., Zhang, L., Ji, Z., Gao, Y., Wang, Z., & Zhao, N. (2023). Three-Dimensional Simulation of Corona Discharge in a Double-Needle System during a Thunderstorm. Atmosphere, 14(5), 789. https://doi.org/10.3390/atmos14050789






