Use of Assimilation Analysis in 4D-Var Source Inversion: Observing System Simulation Experiments (OSSEs) with GOSAT Methane and Hemispheric CMAQ
Abstract
1. Introduction
2. Methodology
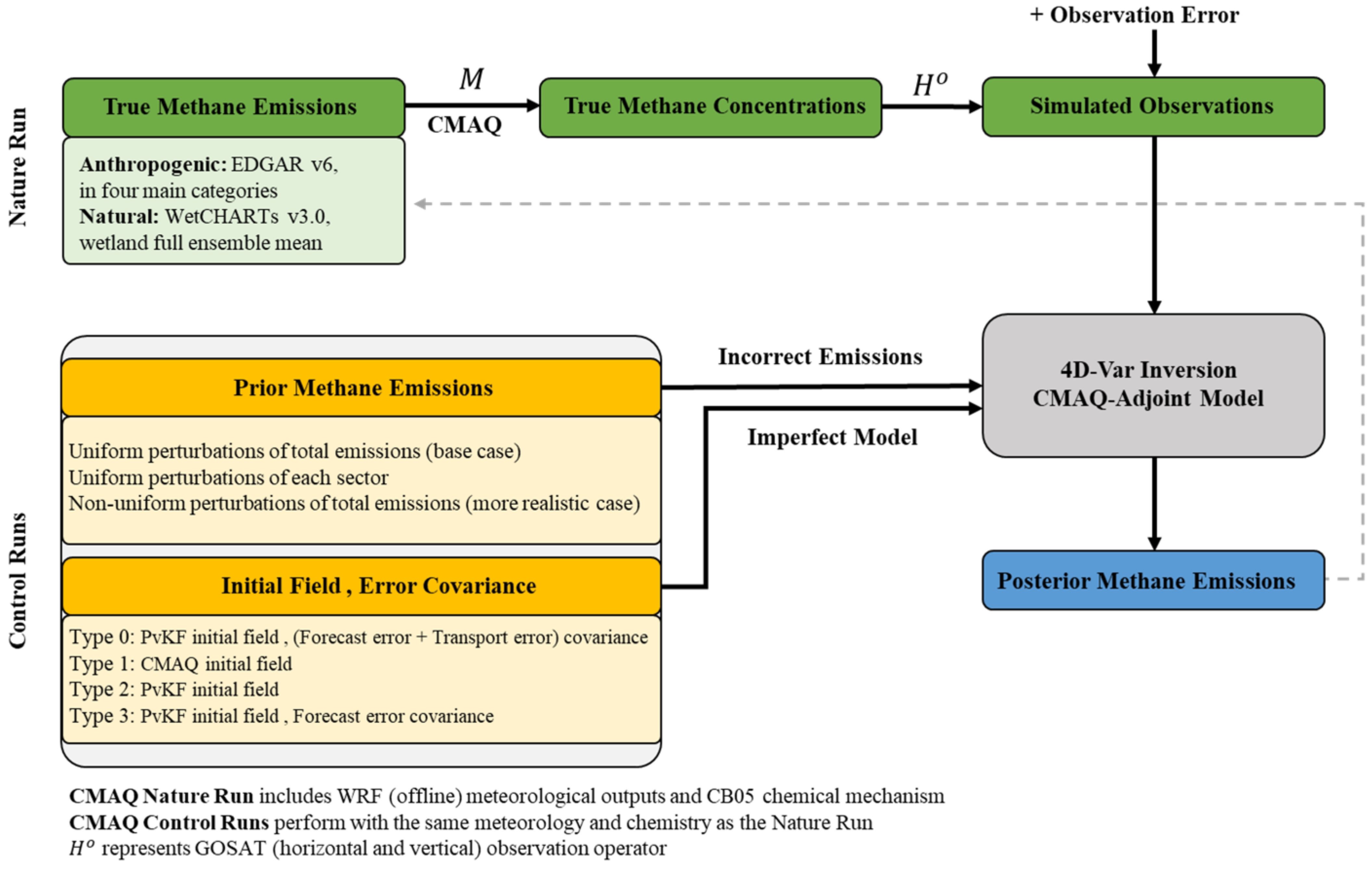
2.1. Satellite and Pseudo Observations
2.2. Chemical Transport Model and Methane Prior Emissions
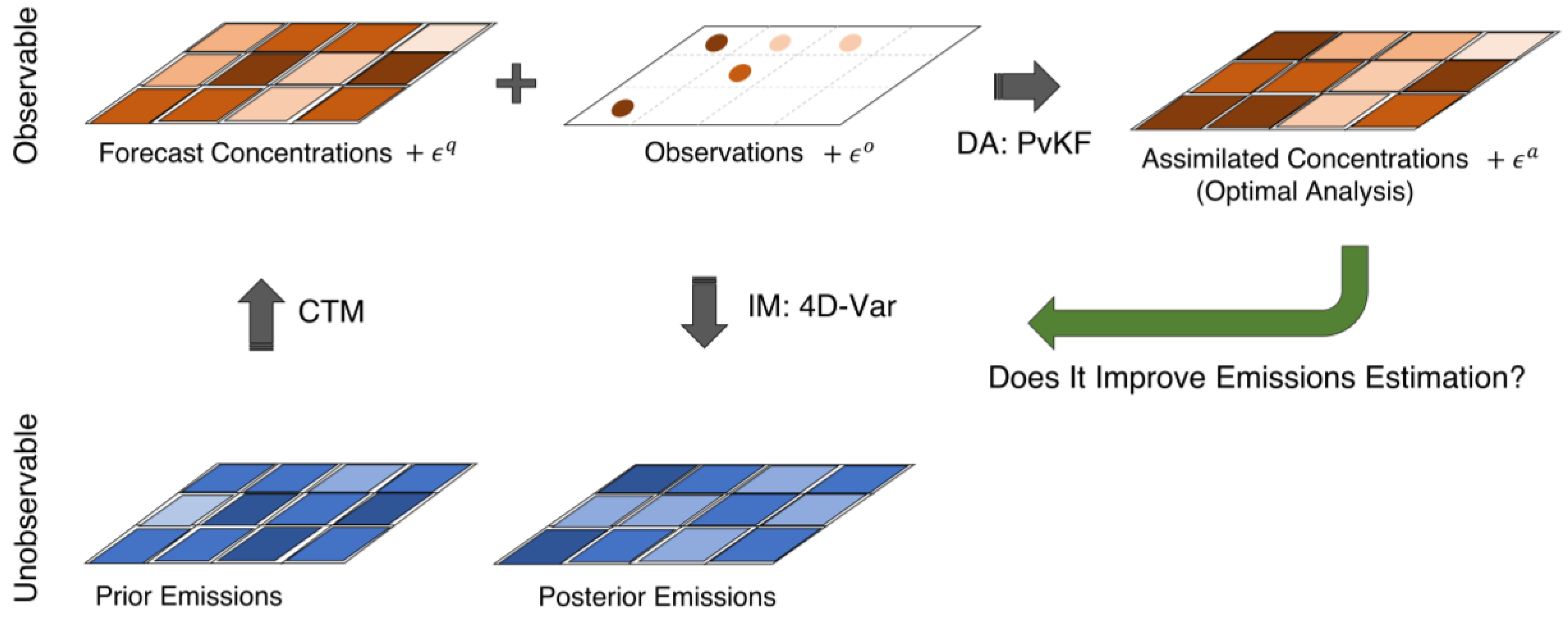
2.3. Overview of the Assimilation and Inversion Systems
2.3.1. PvKF Assimilation
2.3.2. 4D-Var Inversion
2.4. Using PvKF Assimilation Analysis in 4D-Var Inversion: The Formulation
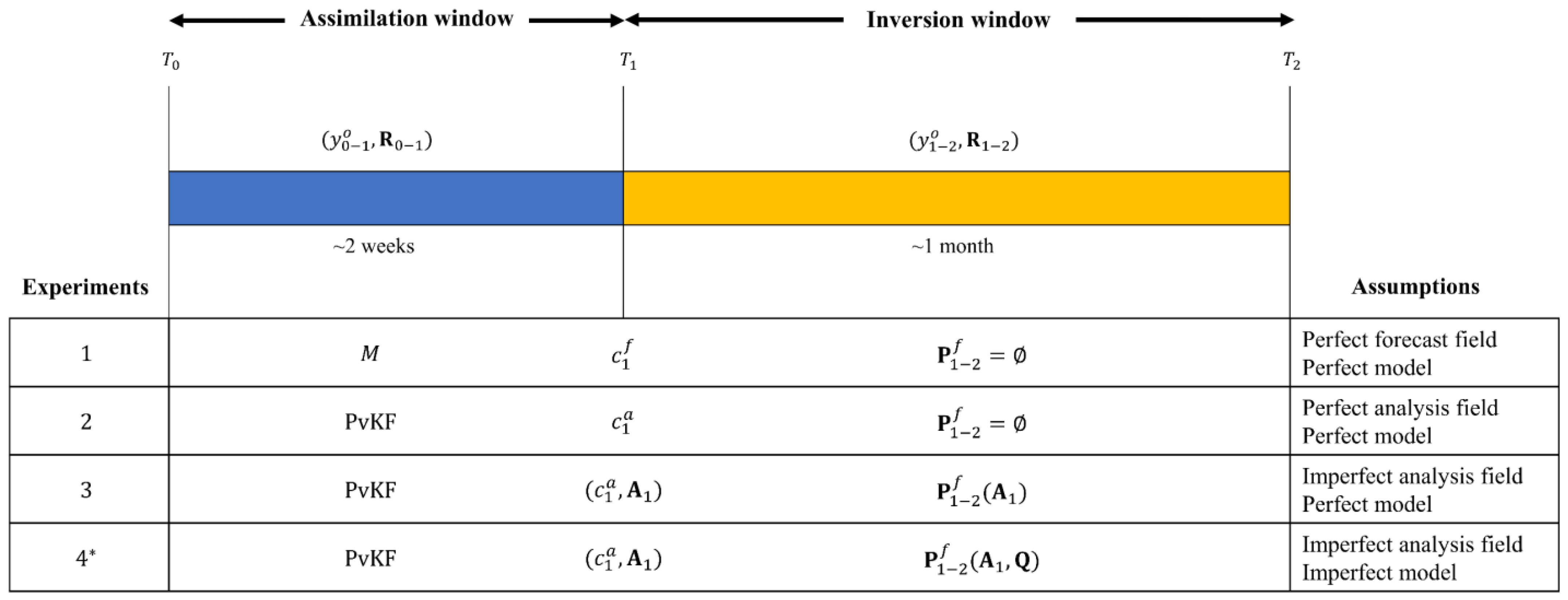
| Type | Cost Function | |
|---|---|---|
| Type 0 *: | (7) | |
| Type 1: | (8) | |
| Type 2: | (9) | |
| Type 3: | (10) |
2.5. Description of the OSSE Experiments
2.5.1. Perturbation Tests
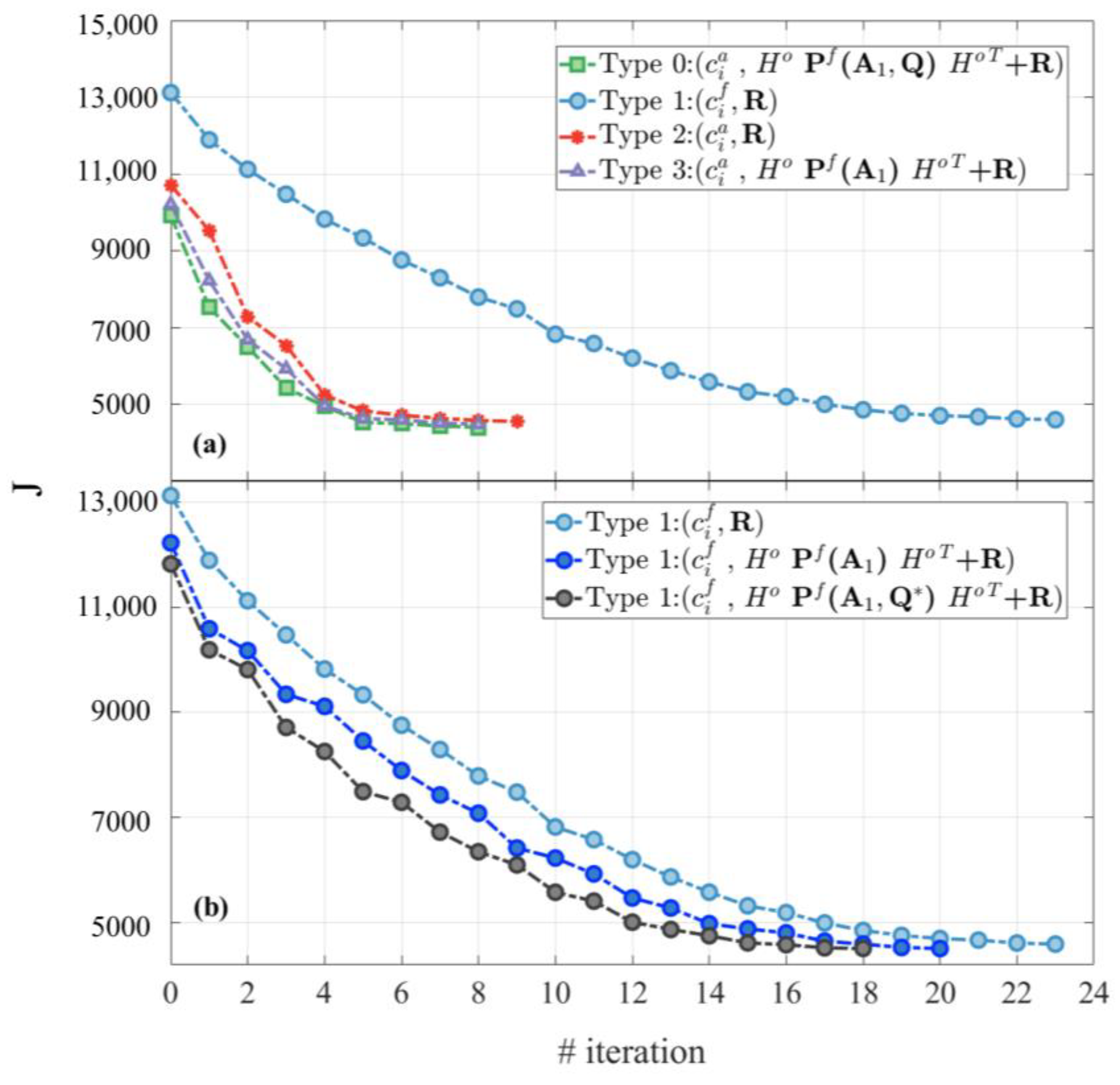
2.5.2. Experimenting with Different Cost Functions
3. Role of Assimilation in Improving Inversion Results
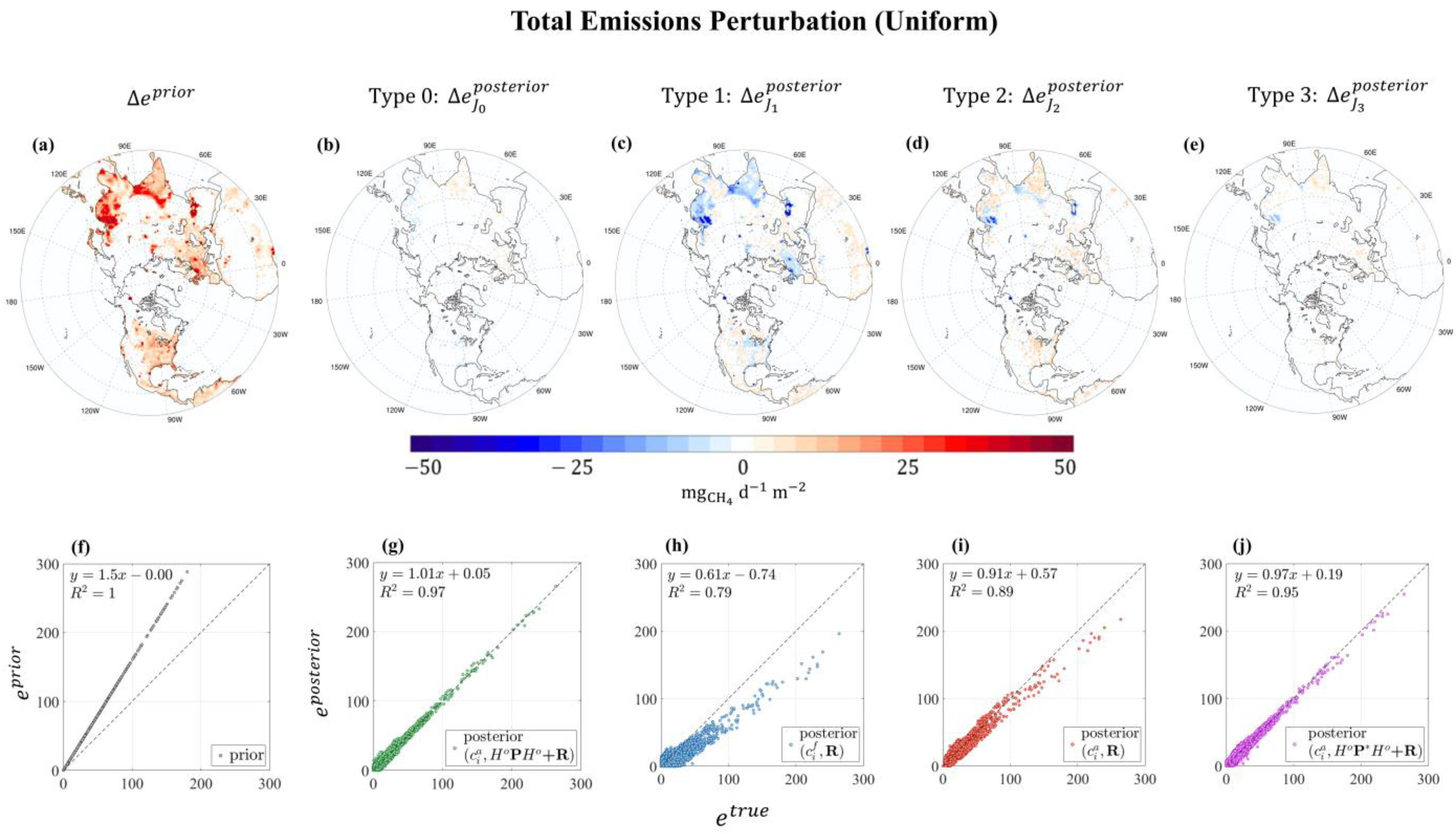
3.1. Perturbation of Total Emissions
3.2. Perturbation of Each Sector
3.3. More Realistic Perturbations
4. Additional Discussions for the Proposed System
4.1. Statistical Implications
4.2. Implications for Model Error
4.3. Computational Timing of Inversions
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Aspects of Matrix Inversion

Appendix B. Approximation of Modelling Error Due to Violation of Diffusion

References
- Staniaszek, Z.; Griffiths, P.T.; Folberth, G.A.; O’Connor, F.M.; Abraham, N.L.; Archibald, A.T. The role of future anthropogenic methane emissions in air quality and climate. Npj Clim. Atmos. Sci. 2022, 5, 8. [Google Scholar] [CrossRef]
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S.; Patra, P.K.; et al. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Nisbet, E.G.; Jones, A.E.; Pyle, J.A.; Skiba, U. Rising methane: Is there a methane emergency? Preface. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 4. [Google Scholar] [CrossRef] [PubMed]
- Worden, J.R.; Cusworth, D.H.; Qu, Z.; Yin, Y.; Zhang, Y.; Bloom, A.A.; Ma, S.; Byrne, B.K.; Scarpelli, T.; Maasakkers, J.D.; et al. The 2019 methane budget and uncertainties at 1° resolution and each country through Bayesian integration Of GOSAT total column methane data and a priori inventory estimates. Atmos. Chem. Phys. 2022, 22, 6811–6841. [Google Scholar] [CrossRef]
- Dlugokencky. NOAA/GML. 2022. Available online: www.esrl.noaa.gov/gmd/ccgg/trends_ch4/ (accessed on 31 August 2022).
- Minx, J.C.; Lamb, W.F.; Andrew, R.M.; Canadell, J.G.; Crippa, M.; Dobbeling, N.; Forster, P.M.; Guizzardi, D.; Olivier, J.; Peters, G.P.; et al. A comprehensive and synthetic dataset for global, regional, and national greenhouse gas emissions by sector 1970-2018 with an extension to 2019. Earth Syst. Sci. Data 2021, 13, 5213–5252. [Google Scholar] [CrossRef]
- Brasseur, G.P.; Jacob, D.J. Modeling of Atmospheric Chemistry; Cambridge University Press: New York, NY, USA, 2017; p. 606. [Google Scholar]
- Ganesan, A.L.; Schwietzke, S.; Poulter, B.; Arnold, T.; Lan, X.; Rigby, M.; Vogel, F.R.; van der Werf, G.R.; Janssens-Maenhout, G.; Boesch, H.; et al. Advancing Scientific Understanding of the Global Methane Budget in Support of the Paris Agreement. Glob. Biogeochem. Cycles 2019, 33, 1475–1512. [Google Scholar] [CrossRef]
- Palmer, P.I.; Feng, L.; Lunt, M.F.; Parker, R.J.; Bosch, H.; Lan, X.; Lorente, A.; Borsdorff, T. The added value of satellite observations of methane forunderstanding the contemporary methane budget. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 21. [Google Scholar] [CrossRef]
- Jacob, D.J.; Varon, D.J.; Cusworth, D.H.; Dennison, P.E.; Frankenberg, C.; Gautam, R.; Guanter, L.; Kelley, J.; McKeever, J.; Ott, L.E.; et al. Quantifying methane emissions from the global scale down to point sources using satellite observations of atmospheric methane. Atmos. Chem. Phys. Discuss. 2022, 2022, 9617–9646. [Google Scholar] [CrossRef]
- Dlugokencky, E.J.; Nisbet, E.G.; Fisher, R.; Lowry, D. Global atmospheric methane: Budget, changes and dangers. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2058–2072. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Karstens, U.; Manning, A.J.; Saunois, M.; Tsuruta, A.; Berchet, A.; Vermeulen, A.T.; Arnold, T.; Janssens-Maenhout, G.; Hammer, S.; et al. Inverse modelling of European CH4 emissions during 2006–2012 using different inverse models and reassessed atmospheric observations. Atmos. Chem. Phys. 2018, 18, 901–920. [Google Scholar] [CrossRef]
- Maasakkers, J.D.; Jacob, D.J.; Sulprizio, M.P.; Scarpelli, T.R.; Nesser, H.; Sheng, J.X.; Zhang, Y.Z.; Lu, X.; Bloom, A.A.; Bowman, K.W.; et al. 2010–2015 North American methane emissions, sectoral contributions, and trends: A high-resolution inversion of GOSAT observations of atmospheric methane. Atmos. Chem. Phys. 2021, 21, 4339–4356. [Google Scholar] [CrossRef]
- Houweling, S.; Bergamaschi, P.; Chevallier, F.; Heimann, M.; Kaminski, T.; Krol, M.; Michalak, A.M.; Patra, P. Global inverse modeling of CH4 sources and sinks: An overview of methods. Atmos. Chem. Phys. 2017, 17, 235–256. [Google Scholar] [CrossRef]
- Wecht, K.J.; Jacob, D.J.; Sulprizio, M.P.; Santoni, G.W.; Wofsy, S.C.; Parker, R.; Bosch, H.; Worden, J. Spatially resolving methane emissions in California: Constraints from the CalNex aircraft campaign and from present (GOSAT, TES) and future (TROPOMI, geostationary) satellite observations. Atmos. Chem. Phys. 2014, 14, 8173–8184. [Google Scholar] [CrossRef]
- Frankenberg, C.; Aben, I.; Bergamaschi, P.; Dlugokencky, E.J.; van Hees, R.; Houweling, S.; van der Meer, P.; Snel, R.; Tol, P. Global column-averaged methane mixing ratios from 2003 to 2009 as derived from SCIAMACHY: Trends and variability. J. Geophys. Res. Atmos. 2011, 116, 12. [Google Scholar] [CrossRef]
- Prather, M.J.; Zhua, X.; Strahan, S.E.; Steenrod, S.D.; Rodriguez, J.M. Quantifying errors in trace species transport modeling. Proc. Natl. Acad. Sci. USA 2008, 105, 19617–19621. [Google Scholar] [CrossRef] [PubMed]
- Locatelli, R.; Bousquet, P.; Saunois, M.; Chevallier, F.; Cressot, C. Sensitivity of the recent methane budget to LMDz sub-grid-scale physical parameterizations. Atmos. Chem. Phys. 2015, 15, 9765–9780. [Google Scholar] [CrossRef]
- Turner, A.J.; Jacob, D.J.; Benmergui, J.; Brandman, J.; White, L.; Randles, C.A. Assessing the capability of different satellite observing configurations to resolve the distribution of methane emissions at kilometer scales. Atmos. Chem. Phys. 2018, 18, 8265–8278. [Google Scholar] [CrossRef]
- Kopacz, M.; Jacob, D.J.; Fisher, J.A.; Logan, J.A.; Zhang, L.; Megretskaia, I.A.; Yantosca, R.M.; Singh, K.; Henze, D.K.; Burrows, J.P.; et al. Global estimates of CO sources with high resolution by adjoint inversion of multiple satellite datasets (MOPITT, AIRS, SCIAMACHY, TES). Atmos. Chem. Phys. 2010, 10, 855–876. [Google Scholar] [CrossRef]
- Janardanan, R.; Maksyutov, S.; Tsuruta, A.; Wang, F.J.; Tiwari, Y.K.; Valsala, V.; Ito, A.; Yoshida, Y.; Kaiser, J.W.; Janssens-Maenhout, G.; et al. Country-Scale Analysis of Methane Emissions with a High-Resolution Inverse Model Using GOSAT and Surface Observations. Remote Sens. 2020, 12, 375. [Google Scholar] [CrossRef]
- Lu, X.; Jacob, D.J.; Wang, H.L.; Maasakkers, J.D.; Zhang, Y.Z.; Scarpelli, T.R.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Nesser, H.; et al. Methane emissions in the United States, Canada, and Mexico: Evaluation of national methane emission inventories and 2010–2017 sectoral trends by inverse analysis of in situ (GLOBALVIEWplus CH4 ObsPack) and satellite (GOSAT) atmospheric observations. Atmos. Chem. Phys. 2022, 22, 395–418. [Google Scholar] [CrossRef]
- Locatelli, R.; Bousquet, P.; Chevallier, F.; Fortems-Cheney, A.; Szopa, S.; Saunois, M.; Agusti-Panareda, A.; Bergmann, D.; Bian, H.; Cameron-Smith, P.; et al. Impact of transport model errors on the global and regional methane emissions estimated by inverse modelling. Atmos. Chem. Phys. 2013, 13, 9917–9937. [Google Scholar] [CrossRef]
- Saad, K.M.; Wunch, D.; Deutscher, N.M.; Griffith, D.W.T.; Hase, F.; De Maziere, M.; Notholt, J.; Pollard, D.F.; Roehl, C.M.; Schneider, M.; et al. Seasonal variability of stratospheric methane: Implications for constraining tropospheric methane budgets using total column observations. Atmos. Chem. Phys. 2016, 16, 14003–14024. [Google Scholar] [CrossRef]
- Stanevich, I.; Jones, D.B.A.; Strong, K.; Keller, M.; Henze, D.K.; Parker, R.J.; Boesch, H.; Wunch, D.; Notholt, J.; Petri, C.; et al. Characterizing model errors in chemical transport modeling of methane: Using GOSAT XCH4 data with weak-constraint four-dimensional variational data assimilation. Atmos. Chem. Phys. 2021, 21, 9545–9572. [Google Scholar] [CrossRef]
- Stanevich, I.; Jones, D.B.A.; Strong, K.; Parker, R.J.; Boesch, H.; Wunch, D.; Notholt, J.; Petri, C.; Warneke, T.; Sussmann, R.; et al. Characterizing model errors in chemical transport modeling of methane: Impact of model resolution in versions v9-02 of GEOS-Chem and v35j of its adjoint model. Geosci. Model Dev. 2020, 13, 3839–3862. [Google Scholar] [CrossRef]
- Tremolet, Y. Model-error estimation in 4D-Var. Q. J. R. Meteorol. Soc. 2007, 133, 1267–1280. [Google Scholar] [CrossRef]
- Tremolet, Y. Accounting for an imperfect model in 4D-Var. Q. J. R. Meteorol. Soc. 2006, 132, 3127. [Google Scholar] [CrossRef]
- Zhang, Y.; Jacob, D.J.; Maasakkers, J.D.; Sulprizio, M.P.; Sheng, J.-X.; Gautam, R.; Worden, J. Monitoring global tropospheric OH concentrations using satellite observations of atmospheric methane. Atmos. Meas. Technol. 2018, 18, 15959–15973. [Google Scholar] [CrossRef]
- Bousserez, N.; Henze, D.K.; Rooney, B.; Perkins, A.; Wecht, K.J.; Turner, A.J.; Natraj, V.; Worden, J.R. Constraints on methane emissions in North America from future geostationary remote-sensing measurements. Atmos. Chem. Phys. 2016, 16, 6175–6190. [Google Scholar] [CrossRef]
- Elbern, H.; Strunk, A.; Schmidt, H.; Talagrand, O. Emission rate and chemical state estimation by 4-dimensional variational inversion. Atmos. Chem. Phys. 2007, 7, 3749–3769. [Google Scholar] [CrossRef]
- Basu, S.; Guerlet, S.; Butz, A.; Houweling, S.; Hasekamp, O.; Aben, I.; Krummel, P.; Steele, P.; Langenfelds, R.; Torn, M.; et al. Global CO2 fluxes estimated from GOSAT retrievals of total column CO2. Atmos. Chem. Phys. 2013, 13, 8695–8717. [Google Scholar] [CrossRef]
- Deng, F.; Jones, D.B.A.; Henze, D.K.; Bousserez, N.; Bowman, K.W.; Fisher, J.B.; Nassar, R.; O’Dell, C.; Wunch, D.; Wennberg, P.O.; et al. Inferring regional sources and sinks of atmospheric CO2 from GOSAT XCO2 data. Atmos. Chem. Phys. 2014, 14, 3703–3727. [Google Scholar] [CrossRef]
- Voshtani, S.; Menard, R.; Walker, T.W.; Hakami, A. Assimilation of GOSAT Methane in the Hemispheric CMAQ.; Part I: Design of the Assimilation System. Remote Sens. 2022, 14, 371. [Google Scholar] [CrossRef]
- Pannekoucke, O.; Menard, R.; El Aabaribaoune, M.; Plu, M. A methodology to obtain model-error covariances due to the discretization scheme from the parametric Kalman filter perspective. Nonlinear Process. Geophys. 2021, 28, 1–22. [Google Scholar] [CrossRef]
- Skachko, S.; Menard, R.; Errera, Q.; Christophe, Y.; Chabrillat, S. EnKF and 4D-Var data assimilation with chemical transport model BASCOE (version 05.06). Geosci. Model Dev. 2016, 9, 2893–2908. [Google Scholar] [CrossRef]
- Skachko, S.; Errera, Q.; Menard, R.; Christophe, Y.; Chabrillat, S. Comparison of the ensemble Kalman filter and 4D-Var assimilation methods using a stratospheric tracer transport model. Geosci. Model Dev. 2014, 7, 1451–1465. [Google Scholar] [CrossRef]
- Voshtani, S.; Menard, R.; Walker, T.W.; Hakami, A. Assimilation of GOSAT Methane in the Hemispheric CMAQ; Part II: Results Using Optimal Error Statistics. Remote Sens. 2022, 14, 375. [Google Scholar] [CrossRef]
- Yu, X.Y.; Millet, D.B.; Henze, D.K. How well can inverse analyses of high-resolution satellite data resolve heterogeneous methane fluxes? Observing system simulation experiments with the GEOS-Chem adjoint model (v35). Geosci. Model Dev. 2021, 14, 7775–7793. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Jacob, D.J.; Lu, X.; Maasakkers, J.D.; Scarpelli, T.R.; Sheng, J.X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Chang, J.F.; et al. Attribution of the accelerating increase in atmospheric methane during 2010–2018 by inverse analysis of GOSAT observations. Atmos. Chem. Phys. 2021, 21, 3643–3666. [Google Scholar] [CrossRef]
- Turner, A.J.; Frankenberg, C.; Kort, E.A. Interpreting contemporary trends in atmospheric methane. Proc. Natl. Acad. Sci. USA 2019, 116, 2805–2813. [Google Scholar] [CrossRef]
- Turner, A.J.; Jacob, D.J.; Wecht, K.J.; Maasakkers, J.D.; Lundgren, E.; Andrews, A.E.; Biraud, S.C.; Boesch, H.; Bowman, K.W.; Deutscher, N.M.; et al. Estimating global and North American methane emissions with high spatial resolution using GOSAT satellite data. Atmos. Chem. Phys. 2015, 15, 7049–7069. [Google Scholar] [CrossRef]
- Bousserez, N.; Henze, D.K. Optimal and scalable methods to approximate the solutions of large-scale Bayesian problems: Theory and application to atmospheric inversion and data assimilation. Q. J. R. Meteorol. Soc. 2018, 144, 365–390. [Google Scholar] [CrossRef]
- Byun, D.; Schere, K.L. Review of the governing equations, computational algorithms, and other components of the models-3 Community Multiscale Air Quality (CMAQ) modeling system. Appl. Mech. Rev. 2006, 59, 51–77. [Google Scholar] [CrossRef]
- Alexe, M.; Bergamaschi, P.; Segers, A.; Detmers, R.; Butz, A.; Hasekamp, O.; Guerlet, S.; Parker, R.; Boesch, H.; Frankenberg, C.; et al. Inverse modelling of CH4 emissions for 2010–2011 using different satellite retrieval products from GOSAT and SCIAMACHY. Atmos. Chem. Phys. 2015, 15, 113–133. [Google Scholar] [CrossRef]
- Cressot, C.; Chevallier, F.; Bousquet, P.; Crevoisier, C.; Dlugokencky, E.J.; Fortems-Cheiney, A.; Frankenberg, C.; Parker, R.; Pison, I.; Scheepmaker, R.A.; et al. On the consistency between global and regional methane emissions inferred from SCIAMACHY, TANSO-FTS, IASI and surface measurements. Atmos. Chem. Phys. 2014, 14, 577–592. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Houweling, S.; Segers, A.; Krol, M.; Frankenberg, C.; Scheepmaker, R.; Dlugokencky, E.; Wofsy, S.; Kort, E.; Sweeney, C. Atmospheric CH4 in the first decade of the 21st century: Inverse modeling analysis using SCIAMACHY satellite retrievals and NOAA surface measurements. J. Geophys. Res. Atmos. 2013, 118, 7350–7369. [Google Scholar] [CrossRef]
- Kuze, A.; Suto, H.; Nakajima, M.; Hamazaki, T. Thermal and near infrared sensor for carbon observation Fourier-transform spectrometer on the Greenhouse Gases Observing Satellite for greenhouse gases monitoring. Appl. Opt. 2009, 48, 6716–6733. [Google Scholar] [CrossRef]
- Butz, A.; Guerlet, S.; Hasekamp, O.; Schepers, D.; Galli, A.; Aben, I.; Frankenberg, C.; Hartmann, J.-M.; Tran, H.; Kuze, A.; et al. Toward accurate CO2 and CH4 observations from GOSAT. Geophys. Res. Lett. 2011, 38, 1–6. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schneising, O.; Hewson, W.; Detmers, R.G.; Boesch, H.; Hasekamp, O.P.; Aben, I.; Bovensmann, H.; Burrows, J.P.; et al. Global satellite observations of column-averaged carbon dioxide and methane: The GHG-CCI XCO2 and XCH4 CRDP3 data set. Remote Sens. Environ. 2017, 203, 276–295. [Google Scholar] [CrossRef]
- Mathur, R.; Xing, J.; Gilliam, R.; Sarwar, G.; Hogrefe, C.; Pleim, J.; Pouliot, G.; Roselle, S.; Spero, T.L.; Wong, D.C.; et al. Extending the Community Multiscale Air Quality (CMAQ) modeling system to hemispheric scales: Overview of process considerations and initial applications. Atmos. Chem. Phys. 2017, 17, 12449–12474. [Google Scholar] [CrossRef]
- Olsen, E.; Fetzer, E.; Hulley, G.; Manning, E.; Blaisdell, J.; Iredell, L.; Susskind, J.; Warner, J.; Wei, Z.; Blackwell, W. AIRS/AMSU/HSB version 6 level 2 product user guide. USA NASA-JPL Technol. Rep. 2013, 1, 760. [Google Scholar]
- CMAQ Tutorials. Available online: https://www.epa.gov/cmaq/cmaq-documentation (accessed on 14 October 2021).
- Crippa, M.; Solazzo, E.; Huang, G.L.; Guizzardi, D.; Koffi, E.; Muntean, M.; Schieberle, C.; Friedrich, R.; Janssens-Maenhout, G. High resolution temporal profiles in the Emissions Database for Global Atmospheric Research. Sci. Data 2020, 7, 121. [Google Scholar] [CrossRef]
- Wang, F.J.; Maksyutov, S.; Tsuruta, A.; Janardanan, R.; Ito, A.; Sasakawa, M.; Machida, T.; Morino, I.; Yoshida, Y.; Kaiser, J.W.; et al. Methane Emission Estimates by the Global High-Resolution Inverse Model Using National Inventories. Remote Sens. 2019, 11, 2489. [Google Scholar] [CrossRef]
- Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Lo Vullo, E.; Solazzo, E.; Monforti-Ferrario, F.; Olivier, J.; Vignati, E. EDGAR v6.0 Greenhouse Gas Emissions. Available online: http://data.europa.eu/89h/97a67d67-c62e-4826-b873-9d972c4f670b (accessed on 5 November 2021).
- Bloom, A.A.; Bowman, K.W.; Lee, M.; Turner, A.J.; Schroeder, R.; Worden, J.R.; Weidner, R.; McDonald, K.C.; Jacob, D.J. A global wetland methane emissions and uncertainty dataset for atmospheric chemical transport models (WetCHARTs version 1.0). Geosci. Model Dev. 2017, 10, 2141–2156. [Google Scholar] [CrossRef]
- UNC. Community Modeling and Analysis System CMAS [WWW Document]. SMOKE v3.6 User’s Man. Available online: https://www.cmascenter.org/smoke/ (accessed on 2 November 2021).
- IPCC. The Physical Science Basis; IPCC; Cambridge Univ Press: New York, NY, USA, 2013; p. 2013. [Google Scholar]
- Cohn, S.E. Dynamics of short-term univariate forecast error covariances. Mon. Weather Rev. 1993, 121, 3123–3149. [Google Scholar] [CrossRef]
- Menard, R.; Cohn, S.E.; Chang, L.P.; Lyster, P.M. Assimilation of stratospheric chemical tracer observations using a Kalman filter. Part I: Formulation. Mon. Weather Rev. 2000, 128, 2654–2671. [Google Scholar] [CrossRef]
- Menard, R.; Deshaies-Jacques, M. Evaluation of Analysis by Cross-Validation. Part I: Using Verification Metrics. Atmosphere 2018, 9, 86. [Google Scholar] [CrossRef]
- Hakami, A.; Henze, D.K.; Seinfeld, J.H.; Singh, K.; Sandu, A.; Kim, S.T.; Byun, D.W.; Li, Q.B. The adjoint of CMAQ. Environ. Sci. Technol. 2007, 41, 7807–7817. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.L.; Russell, M.G.; Hakami, A.; Capps, S.L.; Turner, M.D.; Henze, D.K.; Percell, P.B.; Resler, J.; Shen, H.; Russell, A.G.; et al. A multiphase CMAQ version 5.0 adjoint. Geosci. Model Dev. 2020, 13, 2925–2944. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.D.; Henze, D.K.; Hakami, A.; Zhao, S.L.; Resler, J.; Carmichael, G.R.; Stanier, C.O.; Baek, J.; Sandu, A.; Russell, A.G.; et al. Differences Between Magnitudes and Health Impacts of BC Emissions Across the United States Using 12 km Scale Seasonal Source Apportionment. Environ. Sci. Technol. 2015, 49, 4362–4371. [Google Scholar] [CrossRef]
- Chen, Y.L.; Shen, H.Z.; Kaiser, J.; Hu, Y.T.; Capps, S.L.; Zhao, S.L.; Hakami, A.; Shih, J.S.; Pavur, G.K.; Turner, M.D.; et al. High-resolution hybrid inversion of IASI ammonia columns to constrain US ammonia emissions using the CMAQ adjoint model. Atmos. Chem. Phys. 2021, 21, 2067–2082. [Google Scholar] [CrossRef]
- Hakami, A.; Henze, D.K.; Seinfeld, J.H.; Chai, T.; Tang, Y.; Carmichael, G.R.; Sandu, A. Adjoint inverse modeling of black carbon during the Asian Pacific Regional Aerosol Characterization Experiment. J. Geophys. Res. Atmos. 2005, 110, 17. [Google Scholar] [CrossRef]
- Sandu, A.; Daescu, D.N.; Carmichael, G.R.; Chai, T.F. Adjoint sensitivity analysis of regional air quality models. J. Comput. Phys. 2005, 204, 222–252. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.H.; Nocedal, J.; Zhu, C.Y. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Hansen, P.C. The L-curve and its use in the numerical treatment of inverse problems. In Computational Inverse Problems in Electrocardiology; Johnston, P., Ed.; Advances in Computational Bioengineering Series; WIT: Boston, MA, USA, 2000; Volume 5, pp. 119–142. [Google Scholar]
- Bergamaschi, P.; Corazza, M.; Karstens, U.; Athanassiadou, M.; Thompson, R.L.; Pison, I.; Manning, A.J.; Bousquet, P.; Segers, A.; Vermeulen, A. Top-down estimates of European CH4 and N2O emissions based on four different inverse models. Atmos. Chem. Phys. 2015, 16, 715–736. [Google Scholar] [CrossRef]
- Lahoz, W.A.; Schneider, P. Data assimilation: Making sense of Earth Observation. Front. Environ. Sci. 2014, 2, 16. [Google Scholar] [CrossRef]
- Basu, S.; Lan, X.; Dlugokencky, E.; Michel, S.; Schwietzke, S.; Miller, J.B.; Bruhwiler, L.; Oh, Y.; Tans, P.P.; Apadula, F.; et al. Estimating Emissions of Methane Consistent with Atmospheric Measurements of Methane and δ13C of Methane. Atmos. Chem. Phys. Discuss. 2022, 2022, 15351–15377. [Google Scholar] [CrossRef]
- Wu, X.R.; Elbern, H.; Jacob, B. The assessment of potential observability for joint chemical states and emissions in atmospheric modelings. Stoch. Environ. Res. Risk Assess. 2022, 36, 1743–1760. [Google Scholar] [CrossRef]
- Tandeo, P.; Ailliot, P.; Bocquet, M.; Carrassi, A.; Miyoshi, T.; Pulido, M.; Zhen, Y.C. A Review of Innovation-Based Methods to Jointly Estimate Model and Observation Error Covariance Matrices in Ensemble Data Assimilation. Mon. Weather Rev. 2020, 148, 3973–3994. [Google Scholar] [CrossRef]
- Maasakkers, J.D.; Jacob, D.J.; Sulprizio, M.P.; Scarpelli, T.R.; Nesser, H.; Sheng, J.X.; Zhang, Y.Z.; Hersher, M.; Bloom, A.A.; Bowman, K.W.; et al. Global distribution of methane emissions, emission trends, and OH concentrations and trends inferred from an inversion of GOSAT satellite data for 2010–2015. Atmos. Chem. Phys. 2019, 19, 7859–7881. [Google Scholar] [CrossRef]
- Qu, Z.; Jacob, D.J.; Shen, L.; Lu, X.; Zhang, Y.Z.; Scarpelli, T.R.; Nesser, H.; Sulprizio, M.P.; Maasakkers, J.D.; Bloom, A.A.; et al. Global distribution of methane emissions: A comparative inverse analysis of observations from the TROPOMI and GOSAT satellite instruments. Atmos. Chem. Phys. 2021, 21, 14159–14175. [Google Scholar] [CrossRef]
- Orbe, C.; Waugh, D.W.; Yang, H.; Lamarque, J.F.; Tilmes, S.; Kinnison, D.E. Tropospheric transport differences between models using the same large-scale meteorological fields. Geophys. Res. Lett. 2017, 44, 1068–1078. [Google Scholar] [CrossRef]
- Daley, R. Estimating model-error covariances for application to atmospheric data assimilation. Mon. Weather Rev. 1992, 120, 1735–1746. [Google Scholar] [CrossRef]
- Daley, R. Estimating the wind-field from chemical-constituent observations—Experiments with a one-dimensional extended kalman filter. Mon. Weather Rev. 1995, 123, 181–198. [Google Scholar] [CrossRef]
- Pannekoucke, O.; Ricci, S.; Barthelemy, S.; Menard, R.; Thual, O. Parametric Kalman filter for chemical transport models. Tellus Ser. Dyn. Meteorol. Oceanogr. 2016, 68, 14. [Google Scholar] [CrossRef]
- Menard, R.; Skachko, S.; Pannekoucke, O. Numerical discretization causing error variance loss and the need for inflation. Q. J. R. Meteorol. Soc. 2021, 147, 3498–3520. [Google Scholar] [CrossRef]
- Gilpin, S.; Matsuo, T.; Cohn, S.E. Continuum Covariance Propagation for Understanding Variance Loss in Advective Systems. SIAM/ASA J. Uncertain. Quantif. 2022, 10, 886–914. [Google Scholar] [CrossRef]
- Strang, G.; Borre, K. Linear Algebra, Geodesy, and GPS; Wellesley-Cambridge Press: Wellesley, MA, USA, 1997. [Google Scholar]
- Houtekamer, P.L.; Mitchell, H.L. A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 2001, 129, 123–137. [Google Scholar] [CrossRef]
- Cohn, S.E.; da Silva, A.; Guo, J.; Sienkiewicz, M.; Lamich, D. Assessing the effects of data selection with the DAO physical-space statistical analysis system. Mon. Weather Rev. 1998, 126, 2913–2926. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000; Volume 2. [Google Scholar]
- Migliorini, S. Information-based data selection for ensemble data assimilation. Q. J. R. Meteorol. Soc. 2013, 139, 2033–2054. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Menon, D. Matrix inversion using Cholesky decomposition. In Proceedings of the 2013 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 26–28 September 2013; pp. 70–72. [Google Scholar]
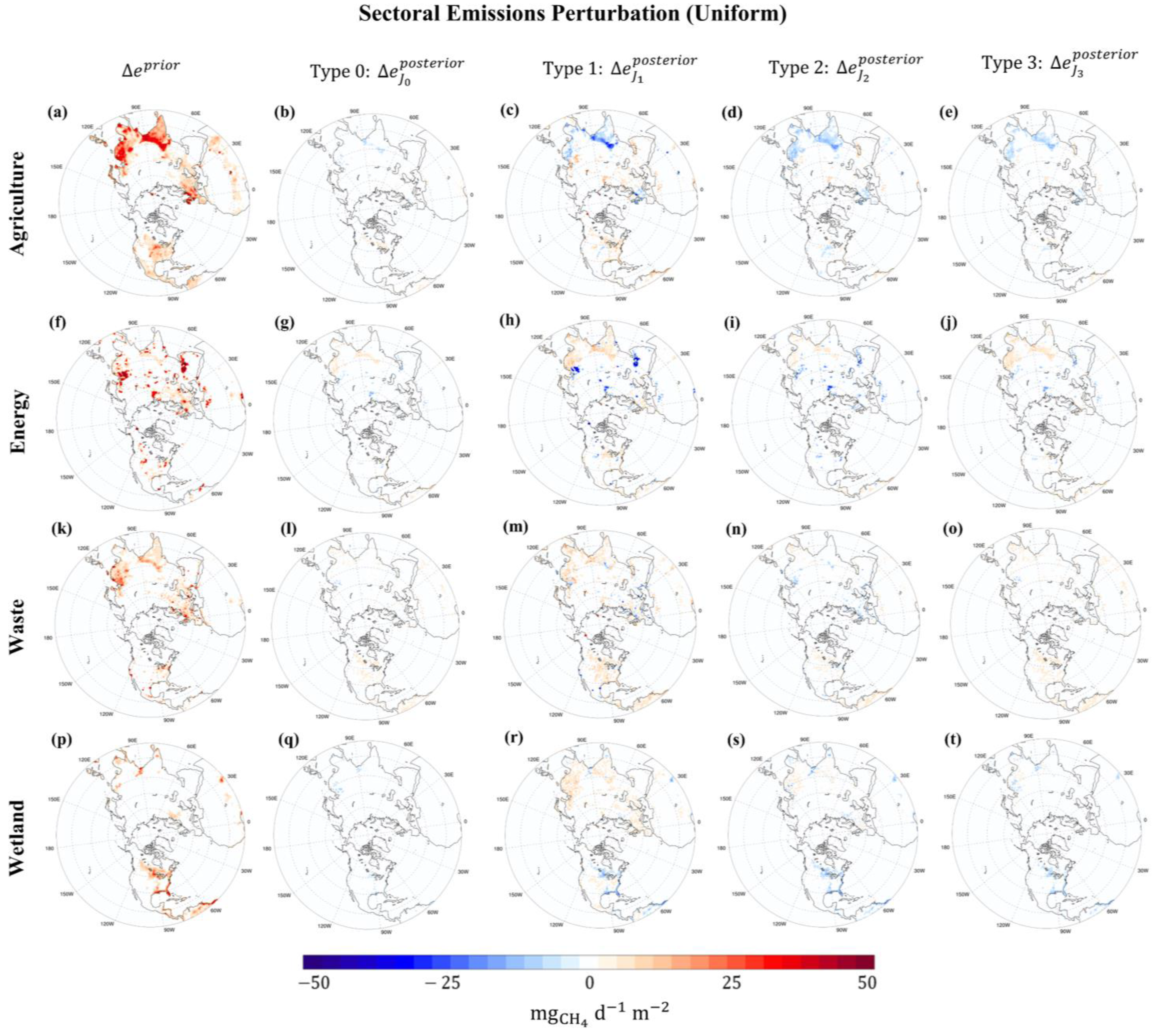
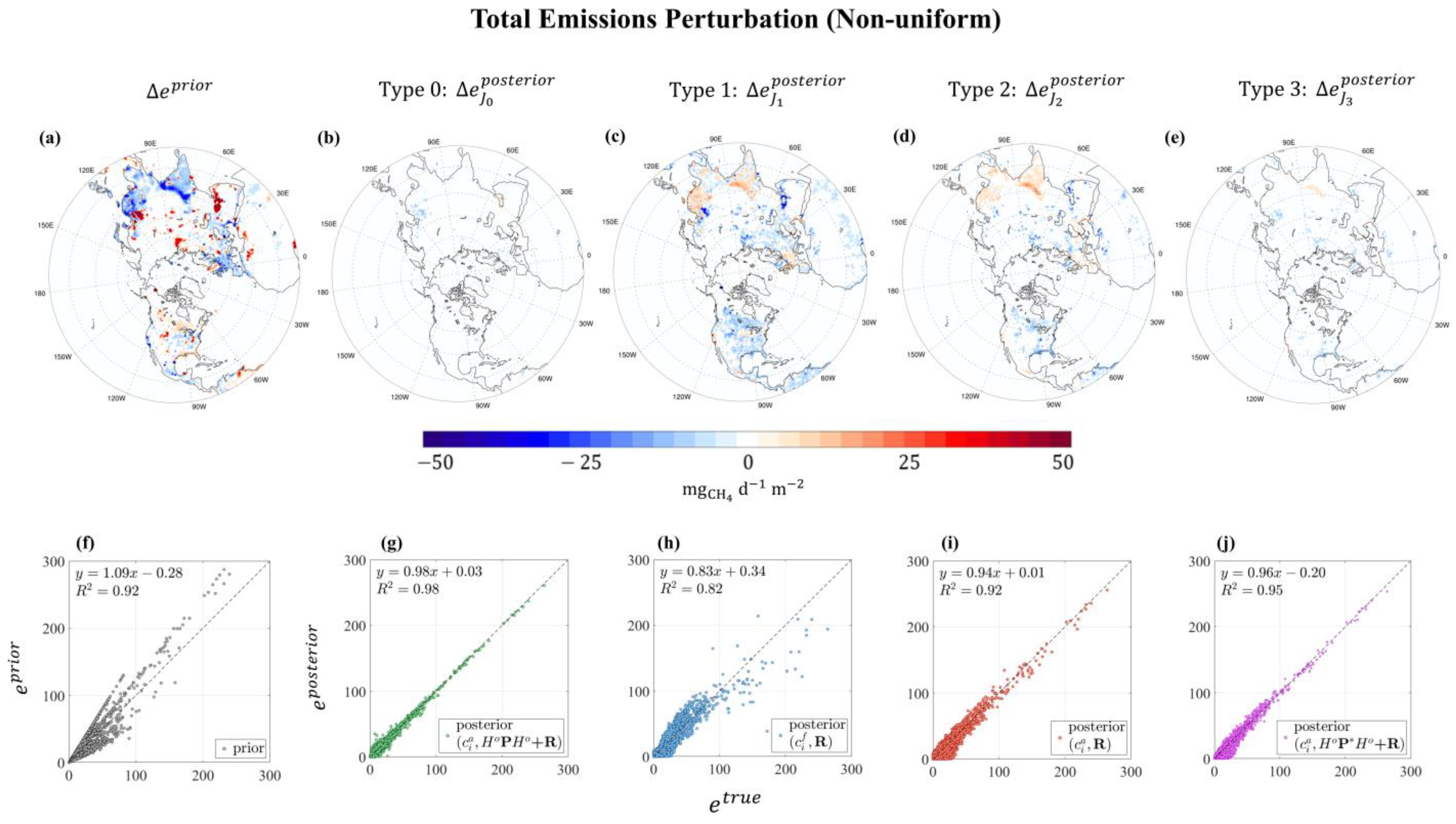
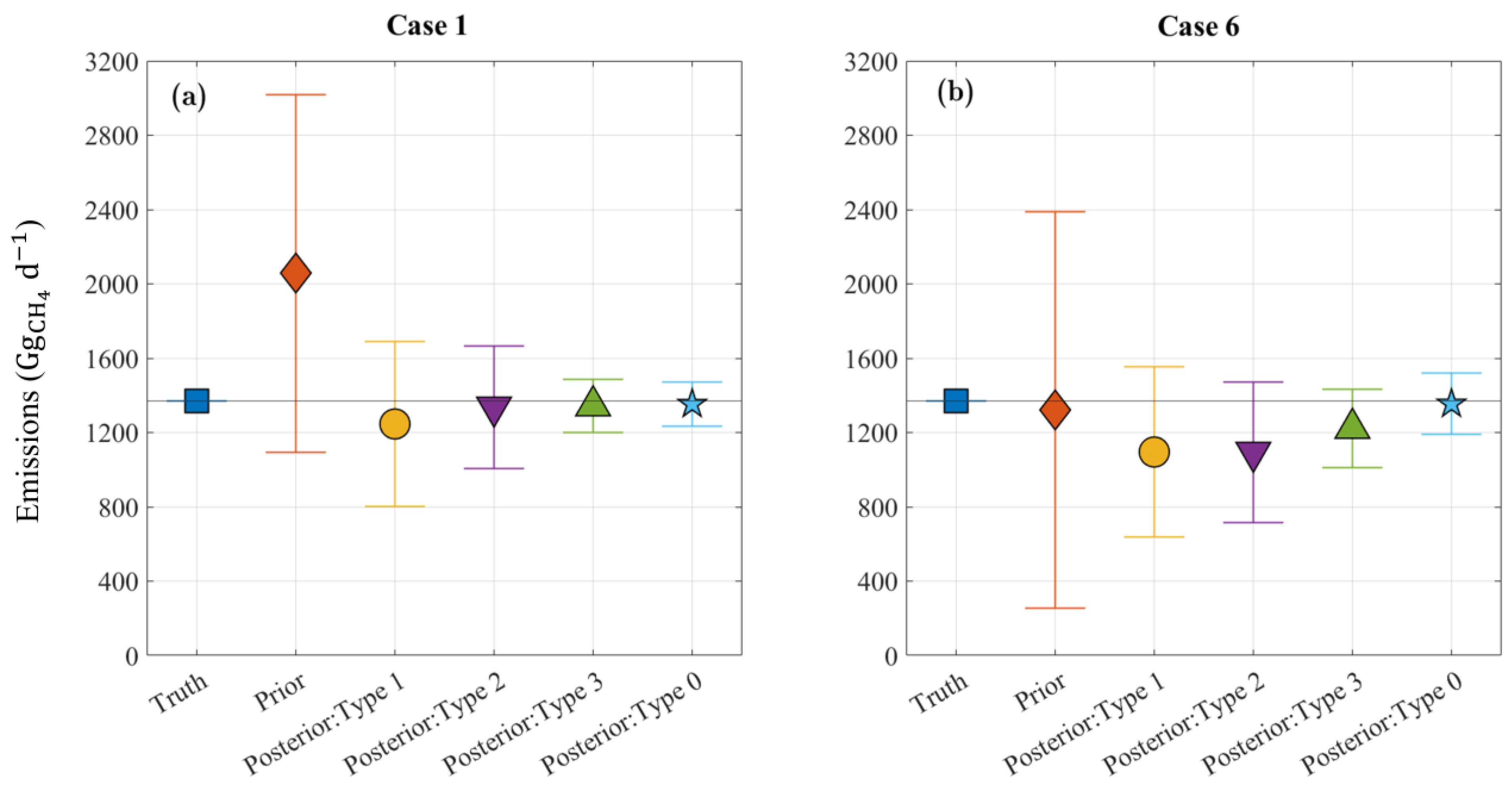
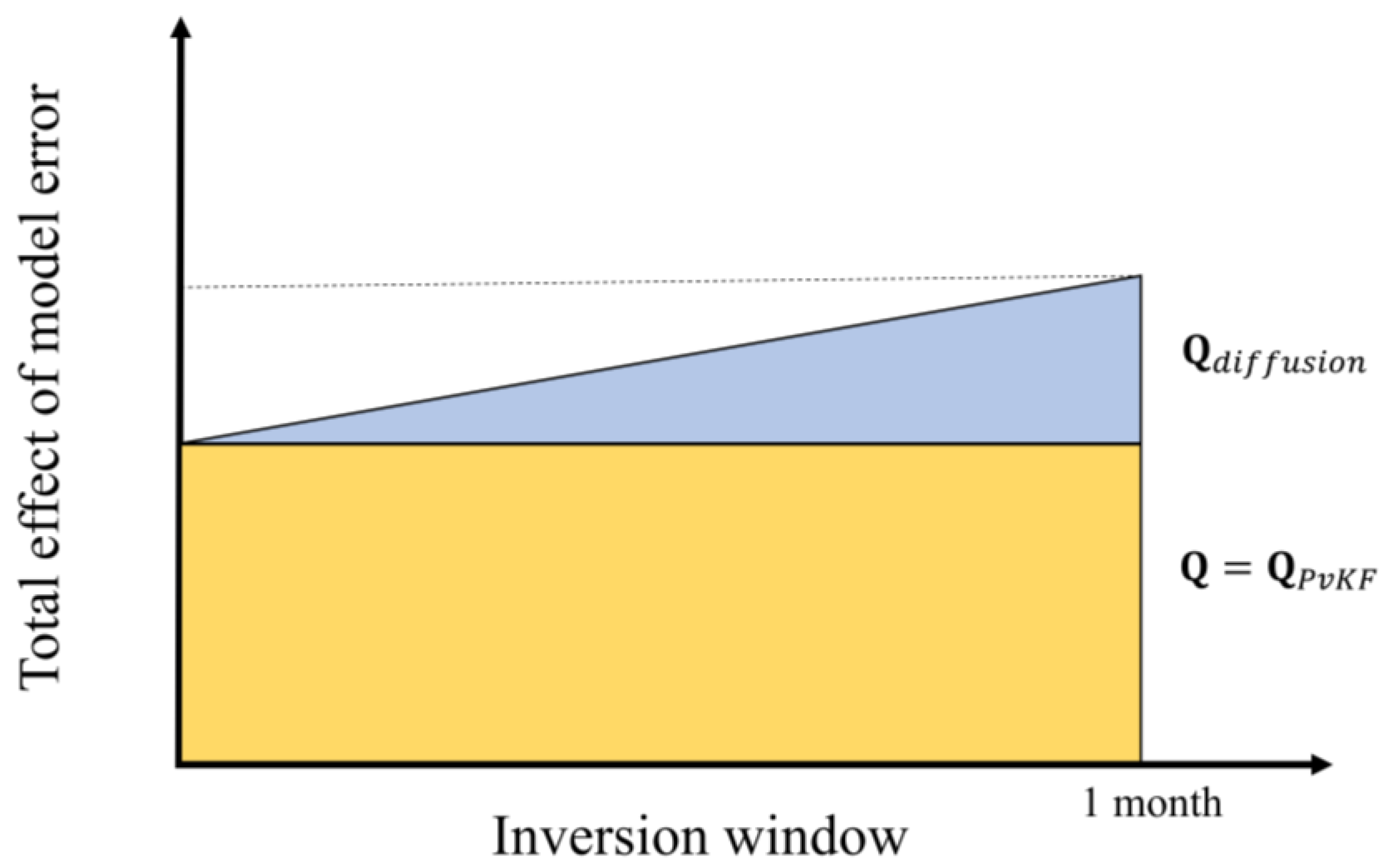
| Anthropogenic | Natural | ||
|---|---|---|---|
| Agriculture | Energy | Waste | Wetland |
| 386.42 (28.2%) | 303.65 (22.1%) | 196.9 (14.4%) | 483.81 (35.3%) |
| Agriculture Soil [93.830] Agriculture waste burning [8.582] Enteric fermentation a [249.04] Manure management [34.96] | Aviation b (all types) [0.013] Chemical process [0.526] Combustion manufacturing [1.454] Energy for building [28.247] Fossil fuel fire [0.409] Coal [89.05] Gas [97.246] Oil [73.233] Iron-steel production [0.298] Oil refineries [11.935] Power industry [0.876] Off-road [0.020] Road transportation [0.175] Shipping [0.167] | Solid waste incineration [33.997] Solid waste c [74.114] Water waste handling [88.79] | Wetland [483.81] |
| Cost Function | Type 0: | Type 1: | Type 2: | Type 3: | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Perturbation | NMB | NME | R | NMB | NME | R | NMB | NME | R | NMB | NME | R | |
| Case 1: All sectors/Uniform | +0.02 | 0.06 | 0.98 | −0.39 | 0.57 | 0.88 | −0.11 | 0.29 | 0.94 | −0.03 | 0.10 | 0.97 | |
| Case 2: Agriculture/Uniform | +0.01 | 0.04 | 0.99 | −0.07 | 0.28 | 0.96 | −0.05 | 0.12 | 0.93 | 0.00 | 0.06 | 0.95 | |
| Case 3: Energy/Uniform | +0.03 | 0.03 | 0.98 | −0.18 | 0.31 | 0.95 | −0.09 | 0.22 | 0.94 | +0.03 | 0.03 | 0.97 | |
| Case 4: Waste/Uniform | +0.02 | 0.02 | 0.99 | +0.11 | 0.45 | 0.94 | −0.03 | 0.10 | 0.95 | −0.02 | 0.03 | 0.98 | |
| Case 5: Wetland/Uniform | −0.01 | 0.01 | 0.99 | −0.06 | 0.11 | 0.99 | −0.05 | 0.09 | 0.99 | −0.05 | 0.04 | 0.99 | |
| Case 6: All sectors/Non-uniform | −0.02 | 0.05 | 0.99 | +0.22 | 0.37 | 0.90 | −0.07 | 0.19 | 0.92 | −0.05 | 0.11 | 0.95 | |
| Case 7: All sectors/Non-uniform | −0.04 | 0.06 | 0.98 | −0.10 | 0.35 | 0.87 | −0.10 | 0.19 | 0.93 | −0.04 | 0.07 | 0.96 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voshtani, S.; Ménard, R.; Walker, T.W.; Hakami, A. Use of Assimilation Analysis in 4D-Var Source Inversion: Observing System Simulation Experiments (OSSEs) with GOSAT Methane and Hemispheric CMAQ. Atmosphere 2023, 14, 758. https://doi.org/10.3390/atmos14040758
Voshtani S, Ménard R, Walker TW, Hakami A. Use of Assimilation Analysis in 4D-Var Source Inversion: Observing System Simulation Experiments (OSSEs) with GOSAT Methane and Hemispheric CMAQ. Atmosphere. 2023; 14(4):758. https://doi.org/10.3390/atmos14040758
Chicago/Turabian StyleVoshtani, Sina, Richard Ménard, Thomas W. Walker, and Amir Hakami. 2023. "Use of Assimilation Analysis in 4D-Var Source Inversion: Observing System Simulation Experiments (OSSEs) with GOSAT Methane and Hemispheric CMAQ" Atmosphere 14, no. 4: 758. https://doi.org/10.3390/atmos14040758
APA StyleVoshtani, S., Ménard, R., Walker, T. W., & Hakami, A. (2023). Use of Assimilation Analysis in 4D-Var Source Inversion: Observing System Simulation Experiments (OSSEs) with GOSAT Methane and Hemispheric CMAQ. Atmosphere, 14(4), 758. https://doi.org/10.3390/atmos14040758






