Mechanics of Particle Motion in a Standing Wave Electric Curtain: A Numerical Study
Abstract
1. Introduction
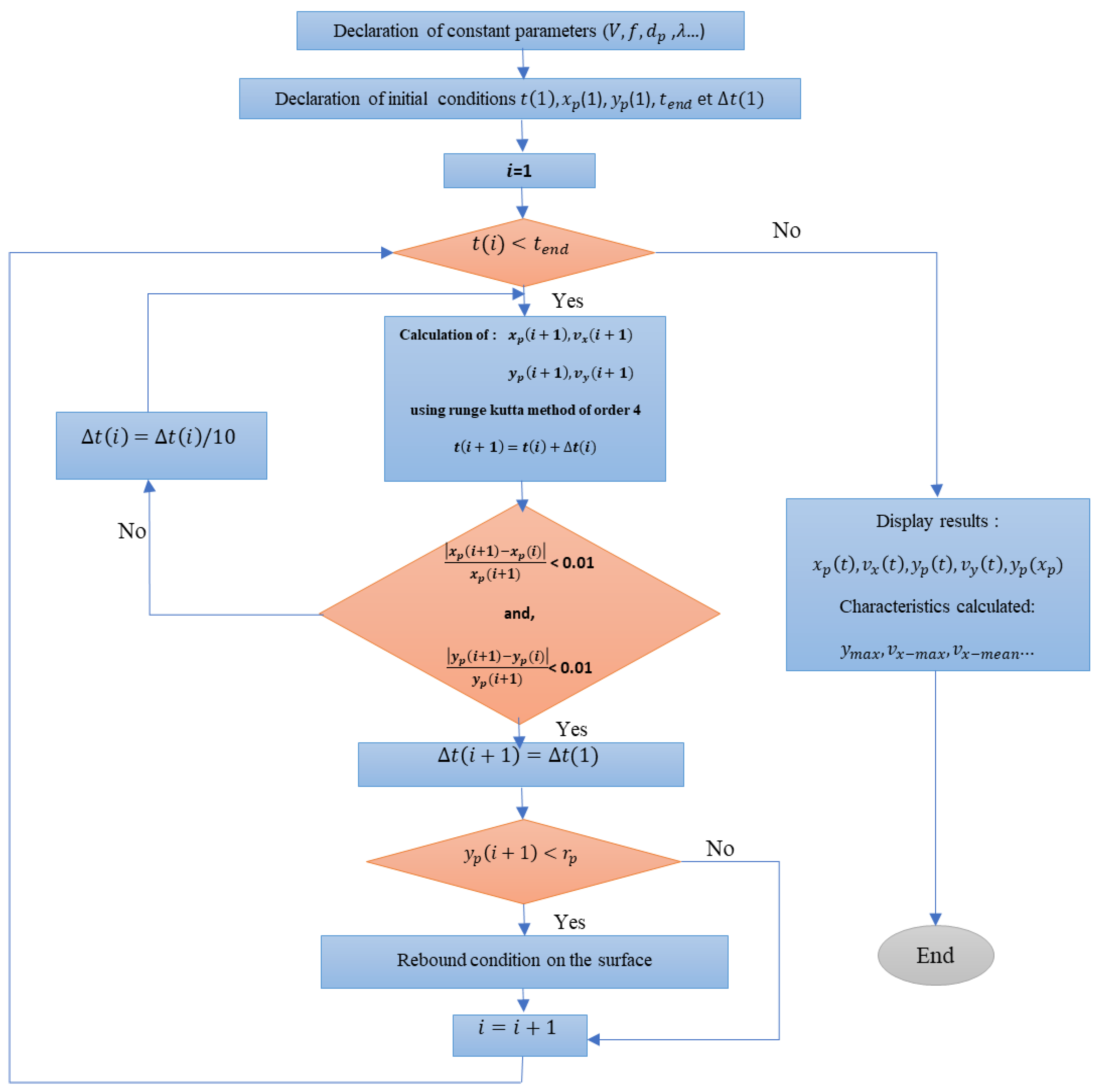
2. Numerical Model
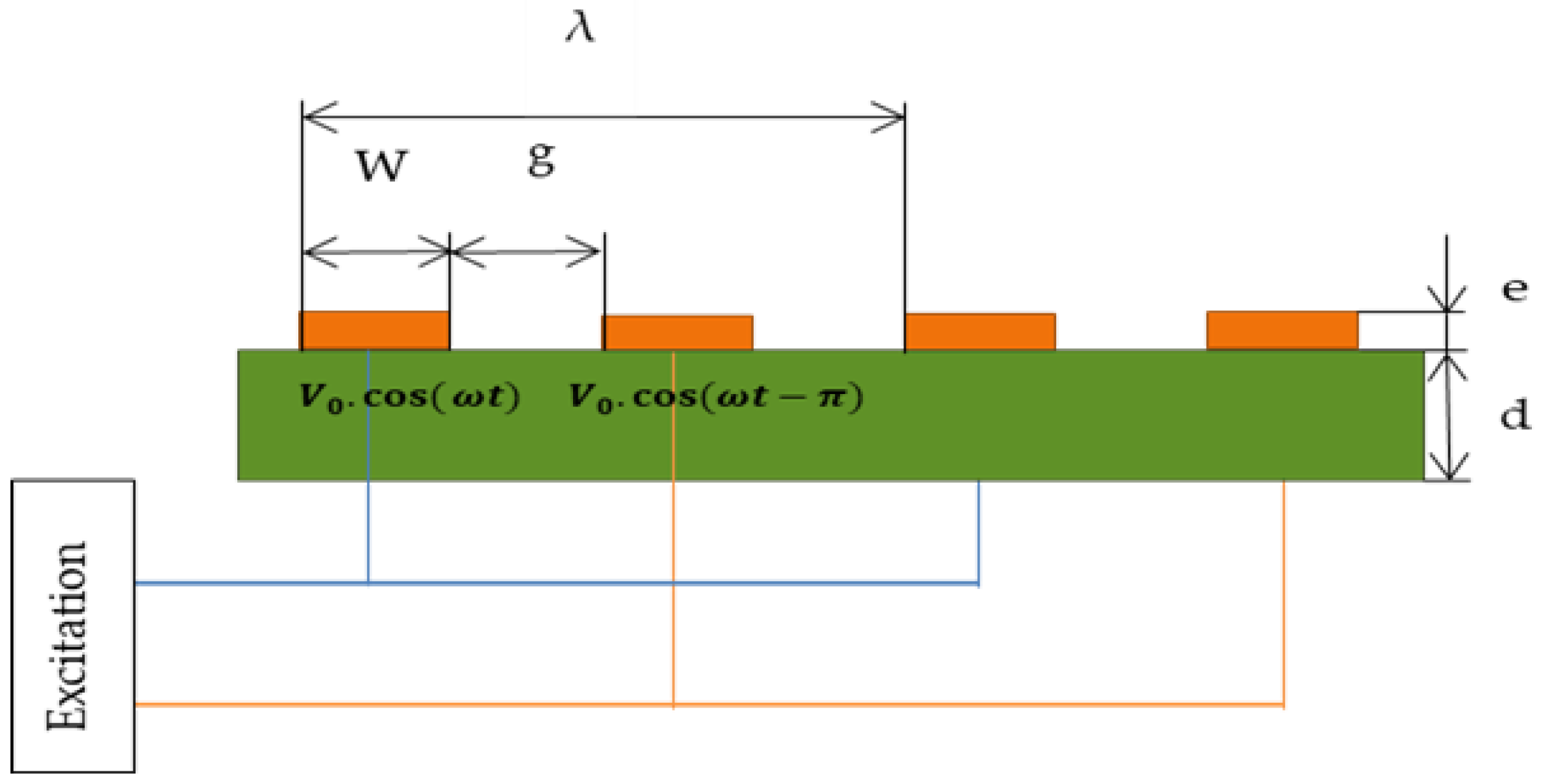
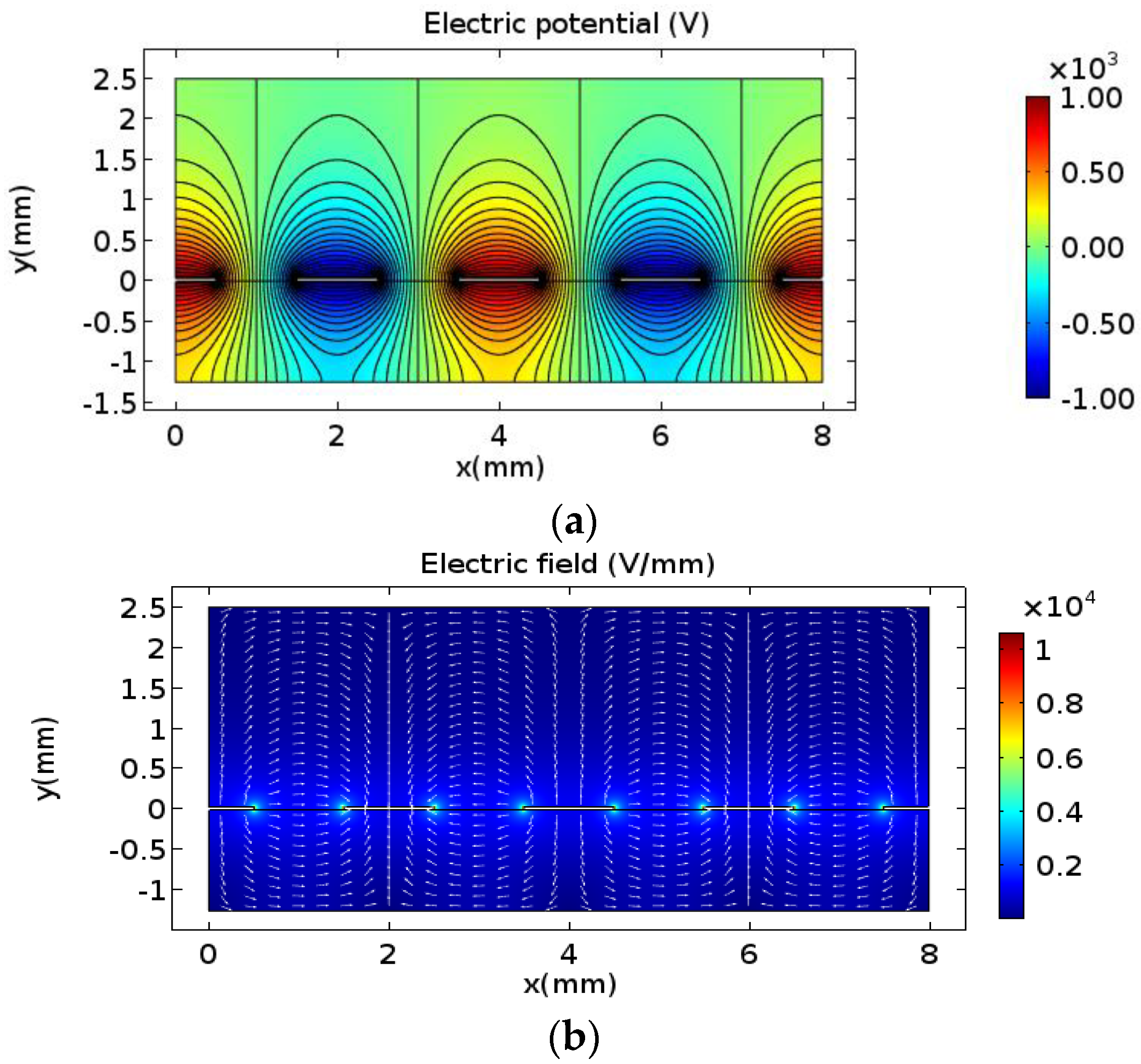
2.1. Electric Field and Electric Potential Distribution
2.2. Motion-Governing Equations
- The particle keeps its initial charge during movement. There is no charge exchange between the particle and the conveyor surface;
- The resolution of the problem is two-dimensional space ();
- The simulation is executed for one single particle, neglecting mechanical and electrical interactions between particles;
- The electrodes are extremely thin, so their thickness is neglected, and there is no dielectric barrier;
- At the surface, an elastic collision condition with a restitution coefficient of one is considered. This means that when the particle hits the surface, its velocity along the normal axis is inverted: .
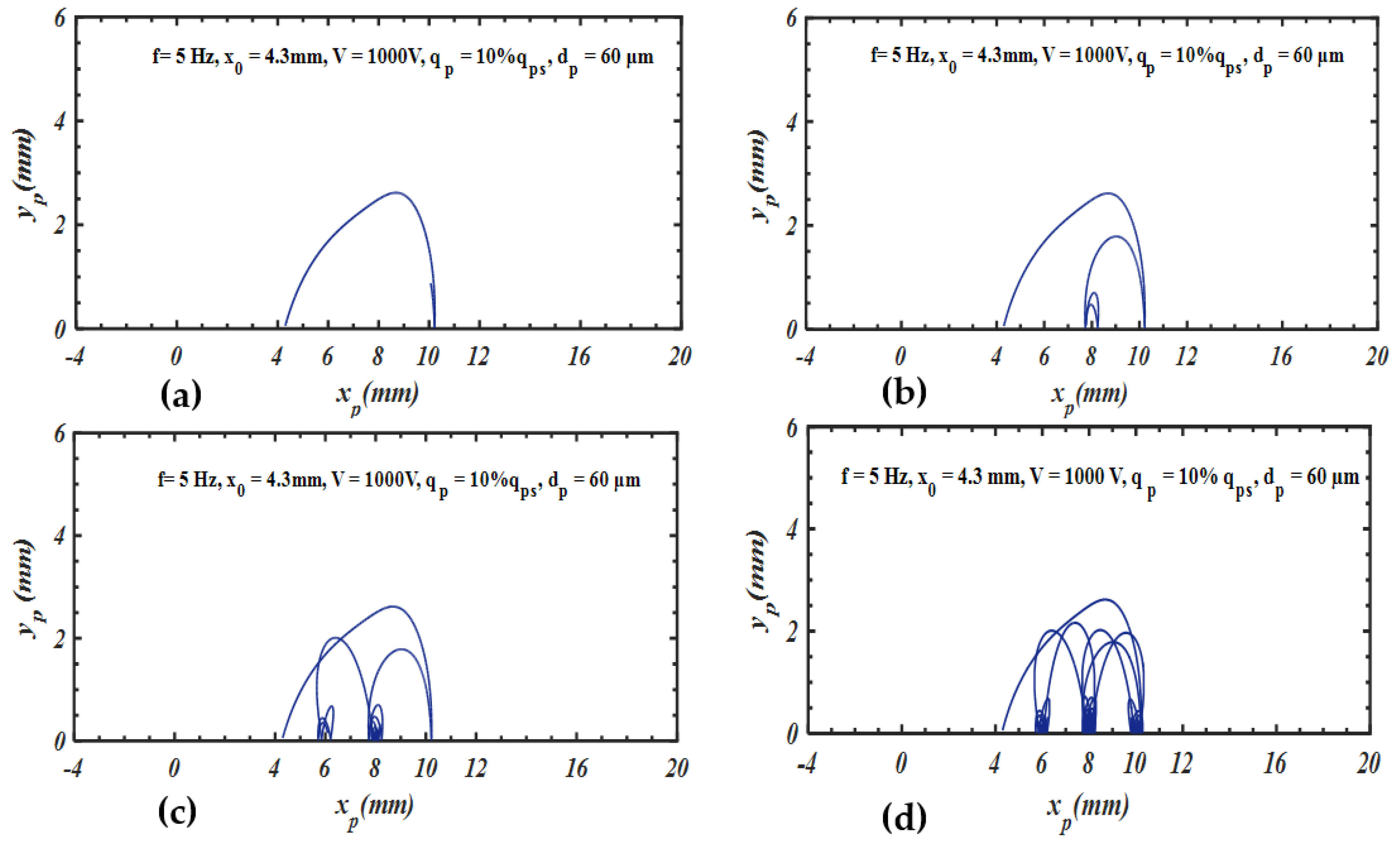
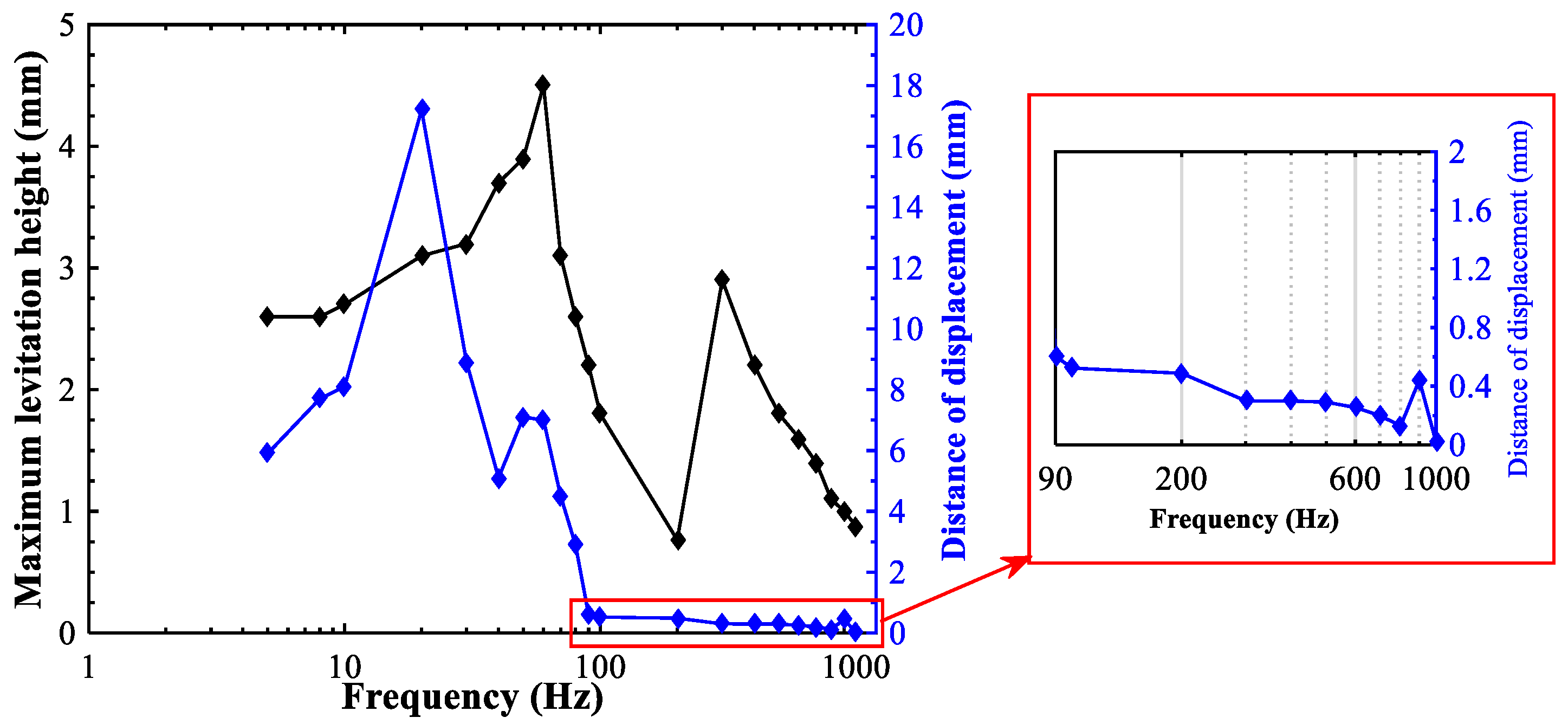
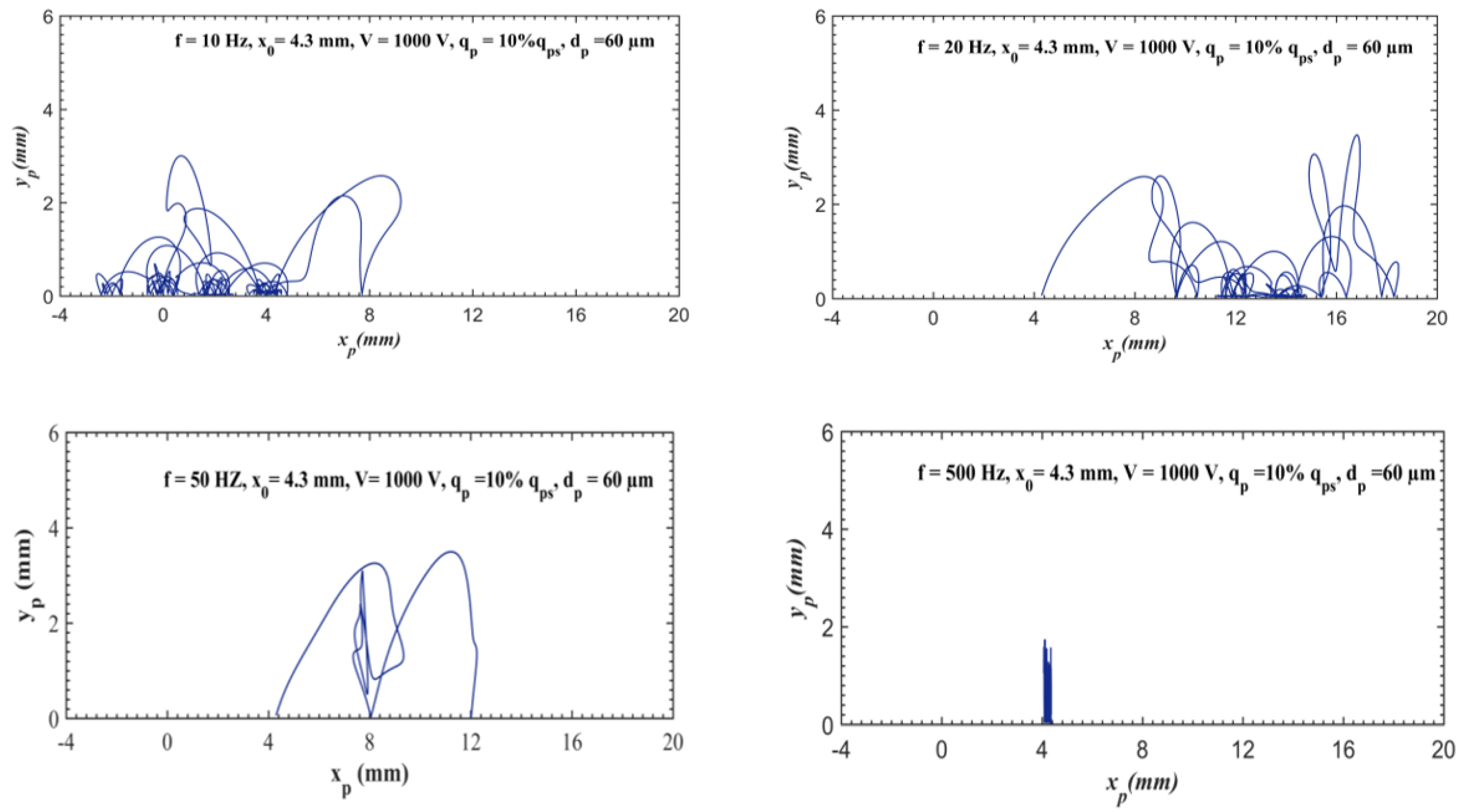
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarver, T.; Al-Qaraghuli, A.; Kazmerski, L.L. A comprehensive review of the impact of dust on the use of solar energy: History, investigations, results, literature, and mitigation approaches. Renew. Sustain. Energy Rev. 2013, 22, 698–733. [Google Scholar] [CrossRef]
- Deb, D.; Brahmbhatt, N.L. Review of yield increase of solar panels through soiling prevention, and a proposed water-free automated cleaning solution. Renew. Sustain. Energy Rev. 2018, 82, 3306–3313. [Google Scholar] [CrossRef]
- Kawamoto, H.; Shibata, T. Electrostatic cleaning system for removal of sand from solar panels. J. Electrost. 2014, 73, 65–70. [Google Scholar] [CrossRef]
- Yu, Y.; Cilliers, J. A review of particle transport and separation by electrostatic traveling wave methods. J. Electrost. 2022, 119, 103735. [Google Scholar] [CrossRef]
- Chang, J.-S.; Kelly, A.J.; Crowley, J.M. Handbook of Electrostatic Processes; M. Dekker: New York, NY, USA, 1995. [Google Scholar]
- Masuda, S.; Fujibayashi, K.; Ishida, K.; Inaba, H. Confinement and transportation of charged aerosol clouds via electric curtain. Electr. Eng. Jpn. 1972, 92, 43–52. [Google Scholar] [CrossRef]
- Masuda, S.; Matsumoto, Y. Theoretical characteristics of standing-wave electric curtains. Electr. Eng. Jpn. 1973, 93, 71–77. [Google Scholar] [CrossRef]
- Masuda, S.; Matsumoto, Y.; Akutsu, K. Characteristics of standing-wave, ring-type electric curtain. experimental study. Electr. Eng. Jpn. 1973, 93, 48–53. [Google Scholar] [CrossRef]
- Adams, J.G.; Cline, B.L.; Contaxes, N.A.; Johnson, R.D.; Seaman, H.; Srepel, V.; Tatom, F.B. Lunar Dust Degradation Effects and Removal/Prevention Concepts; Volume 2—Detailed Results Final Report; Northrop Space Laboratories: Huntsville, AL, USA, 1967. [Google Scholar]
- Masuda, S.; Washizu, M.; Iwadare, M. Separation of small particles suspended in liquid by nonuniform traveling field. IEEE Trans. Ind. Appl. 1987, IA-23, 474–480. [Google Scholar] [CrossRef]
- Masuda, S.; Fujibayashi, K.; Ishida, K. Electrodynamical behavior of charged aerosol particles in non-uniform alternating fields and its application in dust control. Staub-Reinhaltungs Luft 1970, 30, 449–456. [Google Scholar]
- Melcher, J.R.; Warren, E.P.; Kotwal, R.H. Theory for pure-traveling-wave boundary guided transport of tribo-electrified particles. Part. Sci. Technol. 1989, 7, 1–21. [Google Scholar] [CrossRef]
- Melcher, J.R.; Warren, E.P. Theory for finite-phase traveling-wave boundary-guided transport of triboelectrified particles. IEEE Trans. Ind. Appl. 1989, 25, 949–955. [Google Scholar] [CrossRef]
- Schmidlin, F.W. Modes of traveling wave particle transport and their applications. J. Electrost. 1995, 34, 225–244. [Google Scholar] [CrossRef]
- Kawamoto, H.; Hasegawa, N.; Seki, K. Traveling wave transport of particles and particle size classification. Trans. Jpn. Soc. Mech. Eng. Ser. 2003, C 69, 1216–1221. [Google Scholar] [CrossRef]
- Kawamoto, H.; Seki, K.; Kuromiya, N. Mechanism of travelling-wave transport of particles. J. Phys. D Appl. Phys. 2006, 39, 1249–1256. [Google Scholar] [CrossRef]
- Kawamoto, H. Electrostatic transport and manipulation of lunar soil and dust. AIP Conf. Proc. 2008, 969, 203–212. [Google Scholar]
- Horenstein, M.N.; Mazumder, M.K.; Sumner, R.C.; Stark, J.; Abuhamed, T.; Boxman, R. Modeling of trajectories in an electrodynamic screen for obtaining maximum particle removal efficiency. IEEE Trans. Ind. Appl. 2013, 49, 707–713. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Onck, P.; Toonder, J.D. A concise review of microfluidic particle manipulation methods. Microfluid. Nanofluid. 2020, 24, 24. [Google Scholar] [CrossRef]
- Gu, J.; Zhang, G.; Wang, Q.; Wang, C.; Liu, Y.; Yao, W.; Lyu, J. Experimental study on particles directed transport by an alternating travelling-wave electrostatic field. Powder Technol. 2022, 397, 117107. [Google Scholar] [CrossRef]
- Zouaghi, A.; Zouzou, N. Impact of spatial harmonic waves on dielectric particles displacement in standing and traveling wave electric fields. J. Electrost. 2019, 98, 25–33. [Google Scholar] [CrossRef]
- Zouaghi, A.; Zouzou, N.; Dascalescu, L. Assessment of forces acting on fine particles on a traveling-wave electric field conveyor: Application to powder manipulation. Powder Technol. 2019, 343, 375–382. [Google Scholar] [CrossRef]
- Chesnutt, J.K.; Marshall, J.S. Simulation of particle separation on an inclined electric curtain. IEEE Trans. Ind. Appl. 2013, 49, 1104–1112. [Google Scholar] [CrossRef]
- Hemstreet, J.M. Velocity distribution on the Masuda panel. J. Electrost. 1985, 17, 245. [Google Scholar] [CrossRef]
- Sims, R.A.; Biris, A.S.; Wilson, J.D.; Yurteri, C.U.; Mazumder, M.K.; Calle, C.I.; Buhler, C.R. Development of a transparent self-cleaning dust shield for solar panels. In Proceedings of the ESA-IEEE Joint Meeting on Electrostatics, Little Rock, AR, USA, 24–27 June 2003. [Google Scholar]
- Atten, P.; Pang, H.L.; Reboud, J.L. Study of dust removal by standing wave electric curtain for application to solar cells on Mars. IEEE Trans. Ind. Appl. 2009, 45, 75–86. [Google Scholar] [CrossRef]
- Kawamoto, H. Electrostatic cleaning equipment for dust removal from soiled solar panels. J. Electrostat. 2019, 98, 11–16. [Google Scholar] [CrossRef]
- Kawamoto, H.; Guo, B. Improvement of an electrostatic cleaning system for removal of dust from solar panels. J. Electrost. 2018, 91, 28–33. [Google Scholar] [CrossRef]
- Altıntaş, M.; Arslan, S. The study of dust removal using electrostatic cleaning system for solar panels. Sustainability 2021, 13, 9454. [Google Scholar] [CrossRef]
- Sun, Q.; Yang, N.; Cai, X.; Hu, G. Mechanism of dust removal by a standing wave electric curtain. Sci. China: Phys. Mech. Astron. 2012, 55, 1018–1025. [Google Scholar] [CrossRef]
- Pauthenier, M.; Moreau-Hanot, M. La charge des particules sphériques dans un champ ionisé. J. Phys. Radium 1932, 3, 590–613. [Google Scholar] [CrossRef]
- Duff, J.D. Dielectrophoretic Precipitation of Airborne Particles. Master’s Thesis, University of Louisville, Louisville, KY, USA, 2013. [Google Scholar]
- Taylor, D.M.; Secker, P.E. Industrial Electrostatics: Fundamentals and Measurements; Research Studies Press: Boston, MA, USA, 1994. [Google Scholar]
- Zouaghi, A.; Zouzou, N. Numerical modeling of particle motion in traveling wave solar panels cleaning device. J. Electrost. 2021, 110, 103552. [Google Scholar] [CrossRef]
- Rabinovich, Y.I.; Adler, J.J.; Ata, A.; Singh, R.K.; Moudgil, B.M. Adhesion between nanoscale rough surfaces: II. Measurement and comparison with theory. J. Colloid Interface Sci. 2000, 232, 17–24. [Google Scholar] [CrossRef]
- Zouaghi, A. Manipulation de Particules Diélectriques Micrométriques par Ondes Electrostatiques Progressives et Stationnaires. Études Théorique, Expérimentale et Numérique. Ph.D. Thesis, Poitiers University, Poitiers, France, 2019. [Google Scholar]


| Parameters | Values | Units |
|---|---|---|
| Amplitude of the applied voltage waveforms, | 1000 | V |
| Lamda, 𝜆 | / | |
| Particle radius, | 30 | µm |
| Particle relative permittivity, | 3.4 | / |
| Permittivity of the vacuum, | / | |
| Dynamic viscosity of the air, | ||
| Hamaker constant, (in the vacuum) | Of the order of | J |
| Shortest distance between the particle and the substrate, | Of the order of | M |
| Quadratic mean value of the surface roughness, | ≈3 | Nm |
| Mean distance between the peaks of the asperities, | ≈20 | Nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bechkoura, H.; Zouzou, N.; Kachi, M. Mechanics of Particle Motion in a Standing Wave Electric Curtain: A Numerical Study. Atmosphere 2023, 14, 681. https://doi.org/10.3390/atmos14040681
Bechkoura H, Zouzou N, Kachi M. Mechanics of Particle Motion in a Standing Wave Electric Curtain: A Numerical Study. Atmosphere. 2023; 14(4):681. https://doi.org/10.3390/atmos14040681
Chicago/Turabian StyleBechkoura, Hana, Noureddine Zouzou, and Miloud Kachi. 2023. "Mechanics of Particle Motion in a Standing Wave Electric Curtain: A Numerical Study" Atmosphere 14, no. 4: 681. https://doi.org/10.3390/atmos14040681
APA StyleBechkoura, H., Zouzou, N., & Kachi, M. (2023). Mechanics of Particle Motion in a Standing Wave Electric Curtain: A Numerical Study. Atmosphere, 14(4), 681. https://doi.org/10.3390/atmos14040681







