Climate Elasticity of Annual Runoff: Observation in Fifteen Forested Catchments on a Latitudinal Gradient in East Asia
Abstract
1. Introduction
2. Data and Methodology
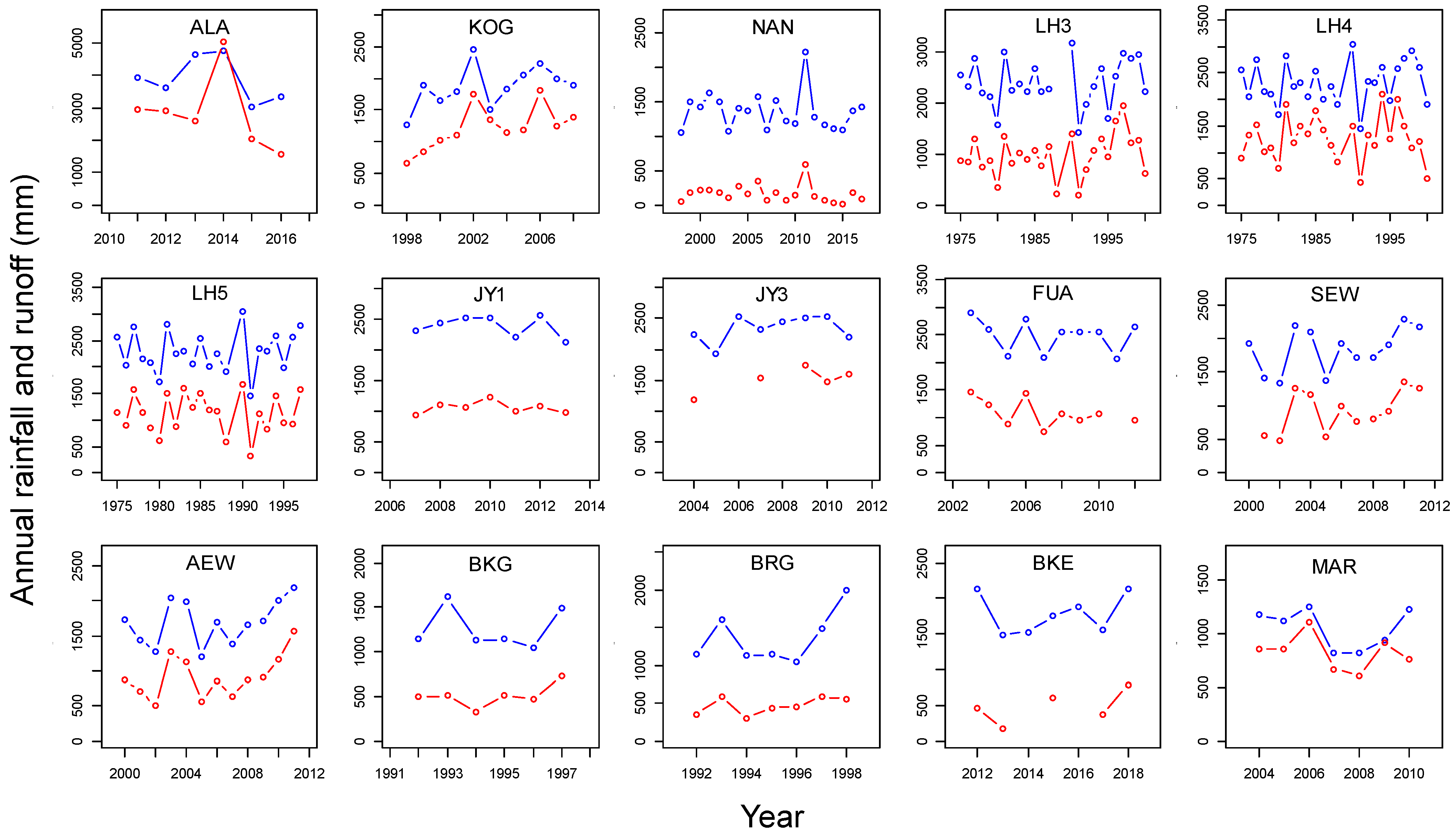
2.1. Data
2.2. Analysis
3. Results & Discussion
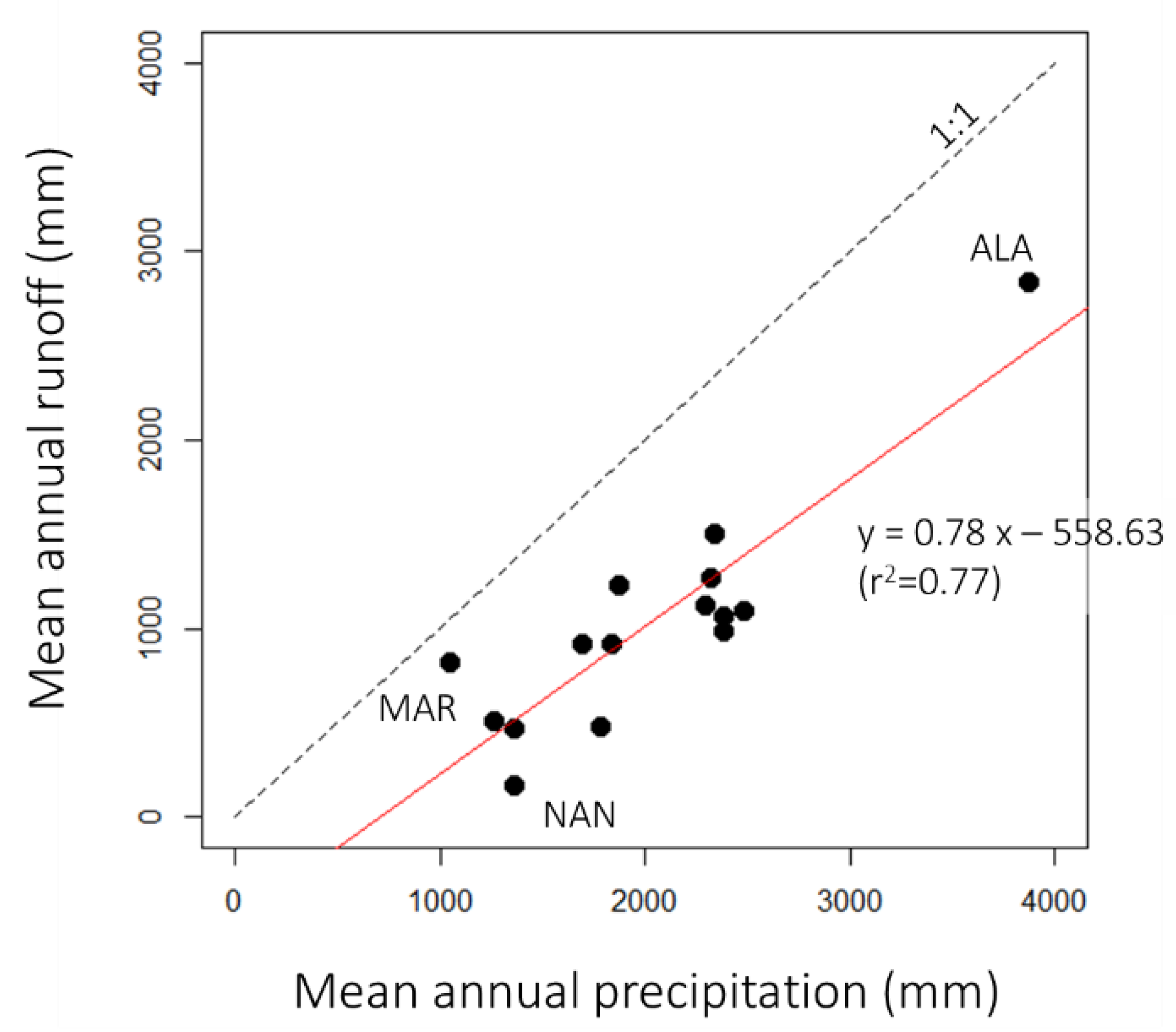
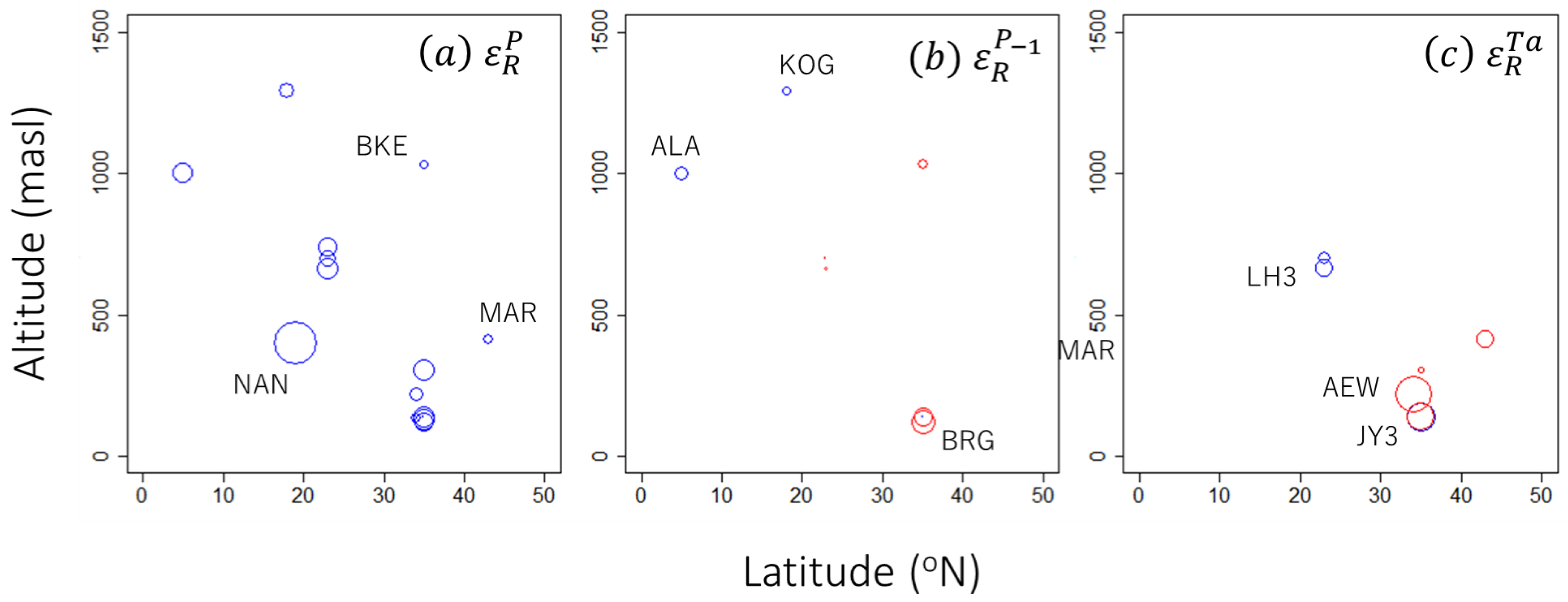
3.1. Overall Water Balances and Selected Elasticity Models
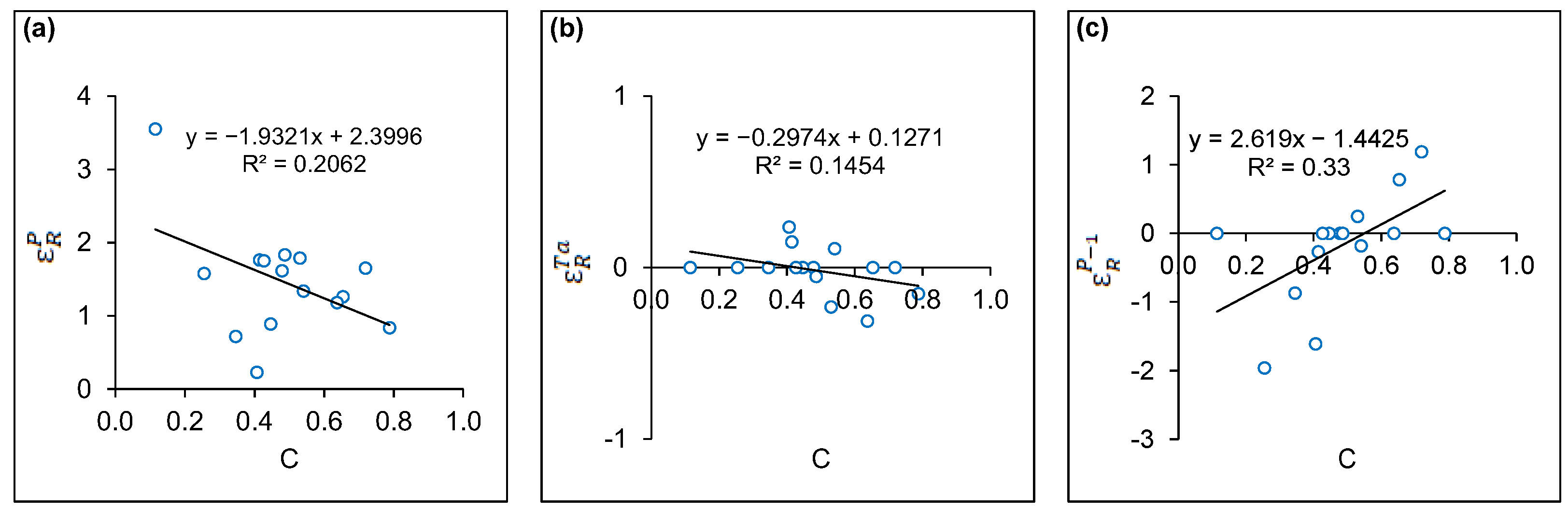
3.2. Annual Rainfall in the Current Year
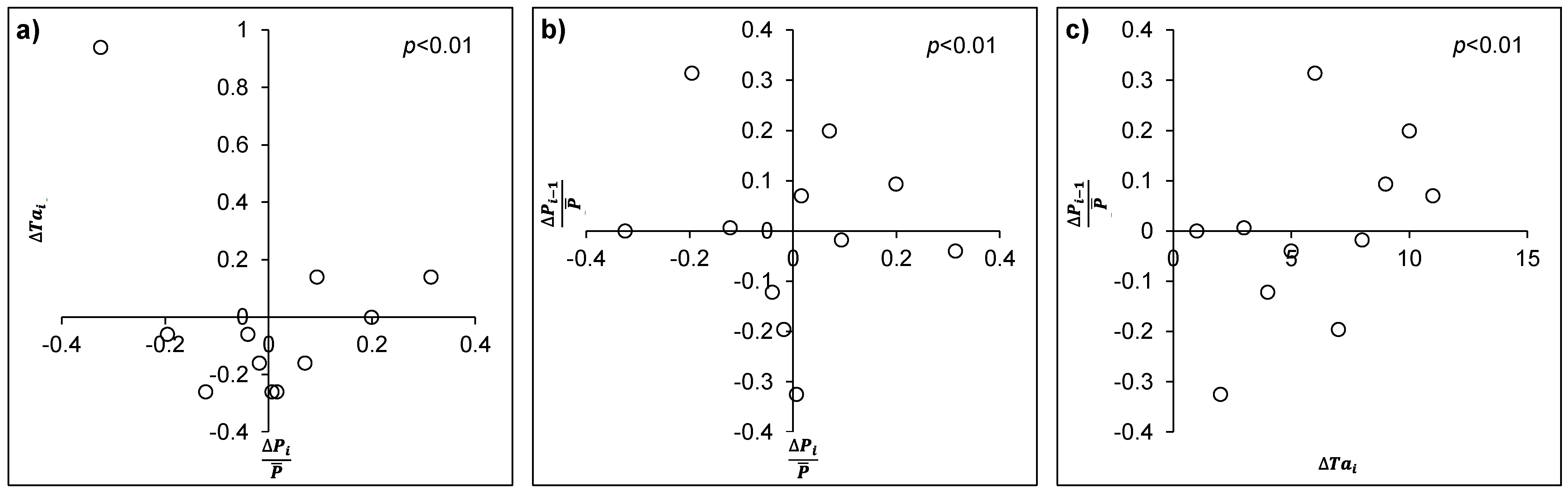
3.3. Annual Mean Air Temperature
3.4. Annual Rainfall in the Previous Year
4. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | Catchment | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ALA | KOG | NAN | LH3 | LH4 | LH5 | JY1 | JY3 | FUA | SEW | AEW | BMG | BRG | BKE | MAR | |
| M1 | |||||||||||||||
| 1.74 | 1.22 ** | 3.55 *** | 1.71 *** | 1.25 *** | 1.62 *** | 0.89 | 0.94 | 1.75 ** | 1.81 *** | 1.75 *** | 0.76 | 0.72 * | 1.99 | 0.78 | |
| SE | −0.69 | −0.32 | −0.35 | −0.25 | −0.3 | −0.24 | −0.37 | −0.96 | −0.4 | −0.07 | −0.13 | −0.51 | −0.27 | −0.93 | −0.33 |
| R2 | 0.56 | 0.59 | 0.84 | 0.68 | 0.41 | 0.69 | 0.49 | 0.19 | 0.71 | 0.99 | 0.94 | 0.31 | 0.54 | 0.54 | 0.48 |
| Adj. R2 | 0.47 | 0.55 | 0.84 | 0.66 | 0.39 | 0.67 | 0.4 | −0.01 | 0.67 | 0.99 | 0.93 | 0.17 | 0.46 | 0.42 | 0.39 |
| n | 6 | 11 | 20 | 24 | 25 | 22 | 7 | 5 | 9 | 11 | 12 | 6 | 7 | 5 | 7 |
| M2 | |||||||||||||||
| \ | 1.01 * | 3.59 *** | 1.71 *** | 1.20 *** | 1.62 *** | 0.88 | 1.18 | 1.76 ** | 1.83 *** | 1.80 *** | 0.76 | 1.00 ** | 1.9 | 0.84 | |
| SE | \ | −0.37 | −0.38 | −0.19 | −0.29 | −0.25 | −0.38 | −0.46 | −0.42 | −0.07 | −0.1 | −0.57 | −0.25 | −0.65 | −0.33 |
| \ | −0.04 | 0.03 | 0.15 *** | 0.10 * | 0 | 0.1 | −0.31 * | 0.03 | −0.05 | −0.21 * | −0.02 | −0.19 | 0.49 | −0.15 | |
| SE | \ | −0.18 | −0.13 | −0.04 | −0.05 | −0.04 | −0.12 | −0.08 | −0.12 | −0.04 | −0.07 | −0.18 | −0.08 | −0.21 | −0.14 |
| R2 | \ | 0.54 | 0.85 | 0.82 | 0.51 | 0.69 | 0.55 | 0.86 | 0.71 | 0.99 | 0.97 | 0.31 | 0.77 | 0.83 | 0.58 |
| Adj. R2 | \ | 0.43 | 0.83 | 0.8 | 0.46 | 0.65 | 0.37 | 0.77 | 0.63 | 0.99 | 0.96 | −0.04 | 0.67 | 0.72 | 0.41 |
| n | \ | 10 | 20 | 24 | 25 | 22 | 7 | 5 | 9 | 11 | 12 | 6 | 7 | 5 | 7 |
| M3 | |||||||||||||||
| 1.65 | 1.26 ** | 3.59 *** | 1.74 *** | 1.43 *** | 1.84 *** | 1.06 | 0.28 | 1.94 ** | 1.81 *** | 1.74 *** | 0.39 | 0.72 ** | 1.58 | 0.77 | |
| SE | −0.62 | −0.28 | −0.38 | −0.27 | −0.32 | −0.33 | −0.49 | −0.88 | −0.49 | −0.07 | −0.13 | −0.48 | −0.11 | −0.46 | −0.37 |
| 1.19 | 0.78 ** | −0.05 | −0.35 | −0.03 | 0.14 | 0.32 | 0.51 | 0.3 | 0.04 | 0.19 | −1.06 | −0.87 ** | −1.96 | 0.08 | |
| SE | −0.67 | −0.23 | −0.37 | −0.25 | −0.17 | −0.17 | −0.57 | −0.75 | −0.43 | −0.07 | −0.15 | −0.52 | −0.16 | −0.47 | −0.37 |
| R2 | 0.79 | 0.78 | 0.84 | 0.71 | 0.49 | 0.68 | 0.52 | 0.26 | 0.73 | 0.99 | 0.95 | 0.71 | 0.94 | 0.98 | 0.48 |
| Adj. R2 | 0.64 | 0.73 | 0.82 | 0.68 | 0.44 | 0.64 | 0.32 | −0.48 | 0.65 | 0.98 | 0.94 | 0.51 | 0.91 | 0.97 | 0.27 |
| n | 5 | 10 | 19 | 22 | 23 | 20 | 7 | 4 | 9 | 11 | 11 | 5 | 6 | 4 | 7 |
| M4 | |||||||||||||||
| \ | 0.98 * | 3.67 *** | 1.77 *** | 1.34 *** | 1.86 *** | 0.92 | 1.54 | 2.11* | 1.83 *** | 1.79 *** | 0.23 | 0.76 * | 1.43 | 0.87 | |
| SE | \ | −0.35 | −0.44 | −0.2 | −0.31 | −0.34 | −0.58 | −0.75 | −0.62 | −0.07 | −0.07 | −0.37 | −0.16 | −0.57 | −0.37 |
| \ | 0.67 * | −0.02 | −0.27 | −0.18 | 0.14 | 0.07 | 0.43 | 0.64 | 0.05 | 0.25 * | −1.61 | −0.80 * | −1.87 | −0.18 | |
| SE | \ | −0.24 | −0.39 | −0.19 | −0.18 | −0.17 | −0.76 | −0.43 | −0.8 | −0.07 | −0.08 | −0.49 | −0.24 | −0.56 | −0.45 |
| \ | 0.13 | 0.06 | 0.15 *** | 0.11 | −0.02 | 0.09 | −0.47 | −0.11 | −0.05 | −0.23 ** | 0.24 | −0.03 | 0.11 | −0.2 | |
| SE | \ | −0.26 | −0.14 | −0.04 | −0.06 | −0.05 | −0.17 | −0.21 | −0.21 | −0.05 | −0.05 | −0.13 | −0.07 | −0.16 | −0.19 |
| R2 | \ | 0.74 | 0.84 | 0.84 | 0.57 | 0.68 | 0.55 | 0.88 | 0.74 | 0.99 | 0.99 | 0.89 | 0.95 | 0.99 | 0.59 |
| Adj. R2 | \ | 0.61 | 0.81 | 0.82 | 0.5 | 0.63 | 0.22 | 0.52 | 0.61 | 0.98 | 0.98 | 0.73 | 0.89 | 0.96 | 0.29 |
| n | \ | 9 | 19 | 22 | 23 | 20 | 7 | 4 | 9 | 11 | 11 | 5 | 6 | 4 | 7 |
Appendix B
References
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of Mean Annual Evapotranspiration to Vegetation Changes at Catchment Scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Bonan, G.B. Forests and Global Change. In Forest Hydrology and Biogeochemistry. Ecological Studies; Levia, D., Carlyle-Moses, D., Tanaka, T., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 216, ISBN 978-94-007-1363-5. [Google Scholar]
- Kumar, A.; Mishra, S.; Bakshi, S.; Upadhyay, P.; Thakur, T.K. Response of Eutrophication and Water Quality Drivers on Greenhouse Gas Emissions in Lakes of China: A Critical Analysis. Ecohydrology 2023, 16, e2483. [Google Scholar] [CrossRef]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere, 4th ed.; Academic Press: Cambridge, MA, USA, 2013; pp. 1–401. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- AR5 Climate Change 2014: Mitigation of Climate Change—IPCC. Available online: https://www.ipcc.ch/report/ar5/wg3/ (accessed on 18 January 2023).
- Schaake, J.S. From Climate to Flow. In Climate Change and US Water Resources; Waggoner, P.E., Ed.; John Wiley: New York, NY, USA, 1990; pp. 177–206. ISBN 9780471618386. [Google Scholar]
- Sankarasubramanian, A.; Vogel, R.M.; Limbrunner, J.F. Climate Elasticity of Streamflow in the United States. Water Resour. Res. 2001, 37, 1771–1781. [Google Scholar] [CrossRef]
- Chiew, F.H.S. Estimation of Rainfall Elasticity of Streamflow in Australia. Hydrol. Sci. J. 2010, 51, 613–625. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Sivapalan, M. Assessing the Impact of Climate Variability on Catchment Water Balance and Vegetation Cover. Hydrol. Earth Syst. Sci. 2012, 16, 43–58. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D. Derivation of Climate Elasticity of Runoff to Assess the Effects of Climate Change on Annual Runoff. Water Resour. Res. 2011, 47, 7526. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Chiew, F.H.S. A Two-Parameter Climate Elasticity of Streamflow Index to Assess Climate Change Effects on Annual Streamflow. Water Resour. Res. 2007, 43, W11419. [Google Scholar] [CrossRef]
- Ma, H.; Yang, D.; Tan, S.K.; Gao, B.; Hu, Q. Impact of Climate Variability and Human Activity on Streamflow Decrease in the Miyun Reservoir Catchment. J. Hydrol. 2010, 389, 317–324. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Zou, S.; Deng, C. Projection of Future Runoff Change Using Climate Elasticity Method Derived from Budyko Framework in Major Basins across China. Glob. Planet. Chang. 2018, 162, 120–135. [Google Scholar] [CrossRef]
- Amrit, K.; Mishra, S.K.; Pandey, R.P.; Himanshu, S.K.; Singh, S. Standardized Precipitation Index-Based Approach to Predict Environmental Flow Condition. Ecohydrology 2019, 12, e2127. [Google Scholar] [CrossRef]
- Himanshu, S.K.; Pandey, A.; Madolli, M.J.; Palmate, S.S.; Kumar, A.; Patidar, N.; Yadav, B. An Ensemble Hydrologic Modeling System for Runoff and Evapotranspiration Evaluation over an Agricultural Watershed. J. Indian Soc. Remote Sens. 2023, 51, 177–196. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Viney, N.R.; Chen, S.; Wu, J.Q. Impacts of Climate Variability on Stream-Flow in the Yellow River. Hydrol. Process. 2007, 21, 3431–3439. [Google Scholar] [CrossRef]
- Sun, S.; Chen, H.; Ju, W.; Song, J.; Zhang, H.; Sun, J.; Fang, Y. Effects of Climate Change on Annual Streamflow Using Climate Elasticity in Poyang Lake Basin, China. Theor. Appl. Climatol. 2013, 112, 169–183. [Google Scholar] [CrossRef]
- Zhou, Y.; Lai, C.; Wang, Z.; Chen, X.; Zeng, Z.; Chen, J.; Bai, X. Quantitative Evaluation of the Impact of Climate Change and Human Activity on Runoff Change in the Dongjiang River Basin, China. Water 2018, 10, 571. [Google Scholar] [CrossRef]
- Trewartha, G.T.; Horn, L.H. An Introduction to Climate; McGraw-Hill: New York, NY, USA, 1980; p. 416. [Google Scholar]
- Trewartha, G.T. An Introduction to Climate; McGraw-Hill: New York, NY, USA, 1968; p. 408. [Google Scholar]
- Lai, Y.J.; Tanaka, N.; Im, S.; Kuraji, K.; Tantasirin, C.; Tuankrua, V.; Majuakim, L.; Cleophas, F.; Mahali, M.B. Climate Classification of Asian University Forests under Current and Future Climate. J. For. Res. 2020, 25, 136–146. [Google Scholar] [CrossRef]
- Mahali, M.; Kuraji, K.; Majuakim, L. Hydro-Meteorological Monitoring & Research in Crocker Range Park, Sabah Malaysia. In Proceedings of the 7th Symposium of Asian University Forest Consortium, Furano, Japan, 11–14 October 2016. [Google Scholar]
- Shiraki, K.; Tanaka, N.; Chatchai, T.; Suzuki, M. Water Budget and Rainfall to Runoff Processes in a Seasonal Tropical Watershed in Northern Thailand. Hydrol. Res. Lett. 2017, 11, 149–154. [Google Scholar] [CrossRef]
- Cheng, J.D.; Yan, C.S.; Yeh, J.L. Baseflow and Storage Relationships for Small Forested Watersheds (English Summary). Taiwan J. For. Sci. 2001, 16, 161–173. [Google Scholar]
- Committee, Hydrology and Water Quality Division: Fundamental Data Development. Report of the Hydrological Observation and Chemical Analysis of Water Quality in the University of Tokyo Forests; The University of Tokyo: Tokyo, Japan, 2019; Volume 63. [Google Scholar]
- Im, S.; Lee, J.; Kuraji, K.; Lai, Y.J.; Tuankrua, V.; Tanaka, N.; Gomyo, M.; Inoue, H.; Tseng, C.W. Soil Conservation Service Curve Number Determination for Forest Cover Using Rainfall and Runoff Data in Experimental Forests. J. For. Res. 2020, 25, 204–213. [Google Scholar] [CrossRef]
- Im, S.; Yang, H.; Eu, S.; Li, Q. Long-Term Monitoring Programs of Watershed Hydrology in the University Forests, SNU. In Proceedings of the 7th Symposium of Asian University Forest Consortium, Furano, Japan, 11–14 October 2016. [Google Scholar]
- Andréassian, V.; Coron, L.; Lerat, J.; Le Moine, N. Climate Elasticity of Streamflow Revisited—An Elasticity Index Based on Long-Term Hydrometeorological Records. Hydrol. Earth Syst. Sci. 2016, 20, 4503–4524. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Peel, M.C.; Mcmahon, T.A.; Siriwardena, L.W. Precipitation Elasticity of Streamflow in Catchments across the World. In Climate Variability and Change—Hydrological Impacts, Proceedings of the Fifth FRIEND World Conference, Havana, Cuba, 27 November–1 December 2006; IAHS Press: Wallingford, UK, 20 November 2006; Volume 308, pp. 256–262. [Google Scholar]
- Zhang, Y.; Viglione, A.; Blöschl, G. Temporal Scaling of Streamflow Elasticity to Precipitation: A Global Analysis. Water Resour. Res. 2022, 58, e2021WR030601. [Google Scholar] [CrossRef]
- Seymenov, K. Climate Elasticity of Annual Streamflow in Northwest Bulgaria. In Smart Geography: 100 Years of the Bulgarian Geographical Society; Springer: Cham, Switzerland, 2020; pp. 105–115. [Google Scholar] [CrossRef]
- Hisada, S.; Senge, M.; Ito, K.; Maruyama, T. Comparison of Characteristic of Water Balance between Evergreen Coniferous and Deciduous Broad-Leaved Forests. IDRE J. 2011, 271, 1–7. [Google Scholar] [CrossRef]
- Tanaka, N.; Kume, T.; Yoshifuji, N.; Tanaka, K.; Takizawa, H.; Shiraki, K.; Tantasirin, C.; Tangtham, N.; Suzuki, M. A Review of Evapotranspiration Estimates from Tropical Forests in Thailand and Adjacent Regions. Agric. For. Meteorol. 2008, 148, 807–819. [Google Scholar] [CrossRef]
- Kumagai, O.; Porporato, A. Strategies of a Bornean Tropical Rainforest Water Use as a Function of Rainfall Regime: Isohydric or Anisohydric? Plant Cell Environ. 2012, 35, 61–71. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhao, P.; Zhang, Z.; Ouyang, L.; Zhao, X.; Zhu, L.; Cao, C.; Zeng, L. Enhanced Isohydric Behavior Decoupled the Whole-Tree Sap Flux Response to Leaf Transpiration under Nitrogen Addition in a Subtropical Forest. Forests 2022, 13, 1847. [Google Scholar] [CrossRef]
- Mrad, A.; Sevanto, S.; Domec, J.C.; Liu, Y.; Nakad, M.; Katul, G. A Dynamic Optimality Principle for Water Use Strategies Explains Isohydric to Anisohydric Plant Responses to Drought. Front. For. Glob. Chang. 2019, 2, 49. [Google Scholar] [CrossRef]
- Sinha, J.; Sharma, A.; Khan, M.; Goyal, M.K. Assessment of the Impacts of Climatic Variability and Anthropogenic Stress on Hydrologic Resilience to Warming Shifts in Peninsular India. Sci. Rep. 2018, 8, 13833. [Google Scholar] [CrossRef] [PubMed]
| Catchment | Abbreviation | State/Province, Country | Climatic Zone (*) | Longitude | Latitude |
|---|---|---|---|---|---|
| Gunung Alab | ALA | Sabah, Malaysia | Cfb | 116°21′ | 5°49′ |
| Kog Ma D Watershed | KOG | Chiangmai, Thailand | Cfa | 98°54′ | 18°49′ |
| Nan Watershed Research Station | NAN | Nan, Thailand | Aw | 100°00′ | 19°00′ |
| Lienhuachih Watershed 3 | LH3 | Nantou, Taiwan | Cwa | 120°54′ | 23°55′ |
| Lienhuachih Watershed 4 | LH4 | Nantou, Taiwan | Cwa | 120°54′ | 23°56′ |
| Lienhuachih Watershed 5 | LH5 | Nantou, Taiwan | Cwa | 120°54′ | 23°56′ |
| Jyugei No.1 | JY1 | Shizuoka, Japan | Cfa | 138°50′ | 34°41′ |
| Jyugei No. 3 | JY3 | Shizuoka, Japan | Cfa | 138°51′ | 34°42′ |
| Fukuroyamasawa Watershed A | FUA | Chiba, Japan | Cfa | 140°06′ | 35°12′ |
| Shirasaka Experimental Watershed | SEW | Aichi, Japan | Doa | 137°10′ | 35°13′ |
| Ananomiya Experimental Watershed | AEW | Aichi, Japan | Doa | 137°06′ | 35°15′ |
| Bukmoongol | BKG | Jeollanam, Korea | Doa | 127°36′ | 35°02′ |
| Baramgol | BRG | Jeollanam, Korea | Da | 127°36′ | 35°02′ |
| Bakemonosawa | BKE | Saitama, Japan | Dcb | 138°49′ | 35°54′ |
| Maruyamazawa | MAR | Hokkaido, Japan | Dcb | 142°34′ | 43°15′ |
| Catchment (Abbreviation) | Altitudinal Range (masl) | Area (ha) | Forest Type | Bedrock |
|---|---|---|---|---|
| ALA | 1000–1970 | 8.5 | Evergreen broad-leaved | Paleogene sedimentary rocks |
| KOG | 1290–1440 | 8.6 | Evergreen broad-leaved | Mesozoic granite |
| NAN | 400–800 | 61,200.0 | Deciduous broad-leaved including irrigated croplands and villages | Paleozoic siltstone |
| LH3 | 666–781 | 4.1 | Evergreen broad-leaved | Paleogene sandstone and shale |
| LH4 | 728–797 | 5.9 | Chinese fir (plantation) | Paleogene sandstone and shale |
| LH5 | 735–788 | 8.4 | Evergreen broad-leaved | Paleogene sandstone and shale |
| JY1 | 133–320 | 7.3 | Evergreen broad-leaved | Neogene andesite |
| JY3 | 220–335 | 1.6 | Camphor laurel (plantation) | Neogene andesite |
| FUA | 129–225 | 0.8 | Japanese cedar and cypress (plantation) | Neogene sandstone and mudstone |
| SEW | 304–629 | 88.5 | Deciduous broad-leaved with evergreen conifers | Cretaceous granite |
| AEW | 140–218 | 13.9 | Deciduous broad-leaved with evergreen pine | Cretaceous granite |
| BKG | 120–341 | 16.0 | Pine mixed with Japanese cedar | Precambrian granite gneiss |
| BRG | 140–359 | 15.7 | Mixed pine forest | Precambrian granite gneiss |
| BKE | 1030–1640 | 41.1 | Deciduous broad-leaved | Paleo-Mesozoic sandstone and mudstone |
| MAR | 415–810 | 220.0 | Deciduous broad-leaved | Quaternary tuff |
| Catchment (Abbreviation) | P (mm) | R (mm) | Ta (°C) | Data Period |
|---|---|---|---|---|
| ALA | 3873 (±641) | 2841 (±1094) | 16 | 2011−2016 |
| KOG | 1870 (±316) | 1229 (±328) | 19.9 (±0.34) | 1998−2008 |
| NAN | 1362 (±266) | 169 (±127) | 26 (±0.59) | 1998−2017 |
| LH3 | 2386 (±443) | 984 (±402) | 21.2 (±0.97) | 1975−1988 and 1990−2000 |
| LH4 | 2320 (±390) | 1268 (±414) | 21.2 (±0.97) | 1975−1988 and 1990−2000 |
| LH5 | 2297 (±379) | 1122 (±361) | 21.3 (±0.98) | 1975−1988 and 1990−1997 |
| JY1 | 2385 (±157) | 1063 (±89) | 15.4 (±0.21) | 2007−2013 |
| JY3 | 2338 (±198) | 1503 (±187) | 15.4 (±0.31) | 2007 and 2009−2011 |
| FUA | 2485 (±276) | 1089 (±234) | 13.9 (±0.35) | 2004, 2003−2010, and 2012 |
| SEW | 1838 (±317) | 916 (±300) | 13.1 (±0.27) | 2001−2011 |
| AEW | 1693 (±306) | 919 (±299) | 13.1 (±0.27) | 2000−2011 |
| BKG | 1261 (±212) | 510 (±117) | 14 (±0.49) | 1992−1997 |
| BRG | 1365 (±322) | 467 (±108) | 14.2 (±0.65) | 1992−1998 |
| BKE | 1783 (±258) | 475 (±203) | 8.6 (±0.50) | 2012−2013, 2015, and 2017−2018 |
| MAR | 1051 (±175) | 823 (±155) | 5.9 (±0.39) | 2004−2010 |
| Catchment (Abbreviation) | Model | Coefficients * | C | Adjusted R2 | ||
|---|---|---|---|---|---|---|
| ALA | M3 | 1.655 | 1.189 | − | 0.719 | 0.644 |
| KOG | M3 | 1.263 | 0.784 | − | 0.654 | 0.727 |
| NAN | M1 | 3.550 | − | − | 0.114 | 0.837 |
| LH3 | M4 | 1.765 | −0.269 | 0.150 | 0.414 | 0.819 |
| LH4 | M4 | 1.339 | −0.179 | 0.110 | 0.541 | 0.501 |
| LH5 | M1 | 1.616 | − | − | 0.479 | 0.671 |
| JY1 | M1 | 0.890 | − | − | 0.446 | 0.400 |
| JY3 | M2 | 1.182 | − | −0.311 | 0.637 | 0.774 |
| FUA | M1 | 1.752 | − | − | 0.427 | 0.675 |
| SEW | M2 | 1.833 | − | −0.051 | 0.486 | 0.986 |
| AEW | M4 | 1.789 | 0.247 | −0.229 | 0.530 | 0.985 |
| BKG | M4 | 0.229 | −1.611 | 0.236 | 0.406 | 0.728 |
| BRG | M3 | 0.720 | −0.871 | − | 0.346 | 0.914 |
| BKE | M3 | 1.581 | −1.963 | − | 0.255 | 0.969 |
| MAR | M2 | 0.839 | − | −0.153 | 0.788 | 0.407 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanaka, N.; Lai, Y.-J.; Im, S.; Mahali, M.B.; Tuankrua, V.; Kuraji, K.; Cleophas, F.; Tantasirin, C.; Gomyo, M.; Tseng, C.-W.; et al. Climate Elasticity of Annual Runoff: Observation in Fifteen Forested Catchments on a Latitudinal Gradient in East Asia. Atmosphere 2023, 14, 629. https://doi.org/10.3390/atmos14040629
Tanaka N, Lai Y-J, Im S, Mahali MB, Tuankrua V, Kuraji K, Cleophas F, Tantasirin C, Gomyo M, Tseng C-W, et al. Climate Elasticity of Annual Runoff: Observation in Fifteen Forested Catchments on a Latitudinal Gradient in East Asia. Atmosphere. 2023; 14(4):629. https://doi.org/10.3390/atmos14040629
Chicago/Turabian StyleTanaka, Nobuaki, Yen-Jen Lai, Sangjun Im, Maznah Binti Mahali, Venus Tuankrua, Koichiro Kuraji, Fera Cleophas, Chatchai Tantasirin, Mie Gomyo, Chun-Wei Tseng, and et al. 2023. "Climate Elasticity of Annual Runoff: Observation in Fifteen Forested Catchments on a Latitudinal Gradient in East Asia" Atmosphere 14, no. 4: 629. https://doi.org/10.3390/atmos14040629
APA StyleTanaka, N., Lai, Y.-J., Im, S., Mahali, M. B., Tuankrua, V., Kuraji, K., Cleophas, F., Tantasirin, C., Gomyo, M., Tseng, C.-W., Shiraki, K., Hotta, N., Asano, Y., Inoue, H., & Nainar, A. (2023). Climate Elasticity of Annual Runoff: Observation in Fifteen Forested Catchments on a Latitudinal Gradient in East Asia. Atmosphere, 14(4), 629. https://doi.org/10.3390/atmos14040629








