Investigating the Inter-Relationships among Multiple Atmospheric Variables and Their Responses to Precipitation

Abstract

In this study, a comprehensive investigation into the inter-relationships among twelve atmospheric variables and their responses to precipitation was conducted. These variables include two Global Navigation Satellite Systems (GNSS) tropospheric products, eight weather variables and two time-varying parameters. Their observations and corresponding precipitation record over the period 2008–2019 were obtained from a pair of GNSS/weather stations in Hong Kong. Firstly, based on the correlation and regression analyses, the cross-relationships among the variables were systematically analyzed. Typically, the variables of precipitable water vapor (PWV), zenith total delay (ZTD), temperature, pressure, wet-bulb temperature and dew-point temperature have closer cross-correlativity. Next, the responses of these variables to precipitation of different intensities were investigated and some precursory information of precipitation contained in these variables was revealed. The lead times of using ZTD and PWV to detect heavy precipitation are about 8 h. Finally, by using the principal component analysis, it is shown that heavy precipitation can be effectively detected using these variables, among which, ZTD, PWV and cloud coverage play more prominent roles. The research findings can not only increase the utilization and uptake of atmospheric variables in the detection of precipitation, but also provide clues in the development of more robust precipitation forecasting models.

1. Introduction

In recent decades, affected by the warming of the planet, an increasing number of natural disasters caused by severe weather events and climatic hazards have seriously endangered the safety of human lives and assets. Among all hazardous phenomena, heavy precipitation occurs the most frequently [1,2]. Regarding its formation process, warmer surface runoffs and oceans continuously increase the amount of water that evaporates into the atmosphere, which also facilitates the movement of moisture-laden air and water vapor [3,4]. Then, the water vapor condenses into cloud droplets and precipitation particles during a convergence upward motion process, and finally with diffusional and collisional growths, they fall as raindrops [5,6]. In terms of the enormous influences brought by heavy precipitation, it is closely linked with the occurrences of flood events, soil erosion, landslide, crop damage and other disastrous phenomena [7]. Furthermore, according to the statistics, over 32% of natural disasters which happened in the Chinese mainland over the period of 1900–2011 were also caused by heavy precipitation [8]. Consequently, these facts all indicate that the accurate forecasting and monitoring of precipitation, especially heavy precipitation, is of great significance for disaster prevention and mitigation.

In view of this, nowadays, various types of new models have been developed to conduct precipitation forecasts. Generally, all existing models can be classified into three categories. The first category consists of operational numerical weather prediction (NWP) models. With the use of high accuracy meteorological data through the advanced data assimilation technique, NWP models can accurately predict the occurrences of precipitation dozens of hours ahead of the event [9,10,11,12,13]. For example, Rohm et al. [10] adopted the four-dimensional variational assimilation method to effectively assimilate Global Navigation Satellite System (GNSS) data, radiosonde profiles and surface synoptic observations into the model. Their results showed that precipitation forecasts have significant improvements when starting from a 9 h lead time. Sun et al. [11] assimilated radiosonde and uncrewed aerial vehicle observations into an NWP model to improve the performance of the model. Saito et al. [12] also took the NWP model run at the Japan Meteorological Agency to perform an experiment for assimilating precipitable water vapor (PWV) derived from GNSS observations to improve the accuracy of heavy precipitation prediction. The second category are the conventional extrapolation models, e.g., threshold-based and anomaly-based models, which adopt a set of predefined rules obtained from the analysis of historical data to detect precipitation in future scenarios [14,15,16,17]. For example, Zhao et al. [16] proposed a threshold-based rainfall forecasting model using the predictors of PWV, zenith total delay (ZTD) and their derivatives as predictors. Results indicated that the mean correct prediction rate was above 95%. Li et al. [17] employed fourteen predictors derived from PWV and ZTD, which took the overall variation features contained in their time series into account, to establish an anomaly-based heavy precipitation detection model. Results showed that its true detection rate and false alarm ratio were 99.1% and 22.4%, respectively. The third category comprises the models developed based on the neural network-based approach, which have drawn increasing attention over the past few years [18,19]. Based on their advanced techniques for extracting relationships/rules from a large amount of geospatial data, these models have also been effectively applied to heavy precipitation prediction [20,21,22,23,24]. For example, Sangiorgio et al. [21] proposed to use the advanced deep neural network to detect the onset of heavy precipitation, and results indicated that with the use of ZTD and other weather variables, the performance resulting from the deep neural network model was improved by over 3%. Li et al. [24] used the back propagation neural network algorithm, which was driven by seven atmospheric variables, to detect heavy precipitation. Results showed that the correct detection rate and false alarm rate were 94.5% and 20.8%, respectively.

Although a great number of models have been proposed, it can also be found that all the models cannot achieve better results or even successfully operate without the incorporation of various types of atmospheric variables sensed by different techniques [25,26]. This is mainly because high accuracy meteorological data are the backbone of all the operational NWP models; in terms of extrapolation models, all the predetermined conditions that can trigger a weather event should be obtained from the monitoring and analysis of the long-term series of atmospheric variables; for the neural network-based models, it is important to select effective variables to be used as their model inputs, as they are data-driven approaches. Consequently, these all highlight a pressing need to understand the intrinsic nature of different atmospheric variables and refine the existing models for the detection of precipitation events. In other words, the correct recognition of effective atmospheric variables and their rational use are the premises of achieving better precipitation prediction results, which is also the main motivation of this study.

Despite the fact that a large number of advanced techniques can be used to sense atmospheric variables, currently, the most common method is the use of in-situ weather stations. Although their spatial resolution still needs to be improved, according to statistics, over 10,000 meteorological stations maintained by the World Meteorological Organization are employed all over the world at the current stage [27]. Various types of meteorological variables (of different temporal resolution) and weather event records can be accurately obtained from these stations. Apart from this, satellite remote sensing technology, e.g., meteorological satellite-based sensing techniques and space/ground-based GNSS atmospheric sounding techniques, has undergone unprecedented development in recent years. Among these techniques, ground-based GNSS atmospheric sounding, as a deep fusion of the conventional GNSS-based navigation and satellite-based remote sensing technique, has opened up new opportunities for the monitoring of atmospheric variables and severe weather events [28,29,30,31,32]. According to a report released by the United Kingdom Met Office, the influences brought by per observation of various types of variables in global NWP were carefully evaluated, and the ground-based GNSS data were even ranked the second most influential [33]. Moreover, most of the aforementioned models also tend to incorporate ground-based GNSS observations. Therefore, apart from the weather data, this study also gives particular attention to ground-based GNSS atmospheric products to take advantage of the cutting-edge sounding technique.

As a final point, even though some previous studies have also conducted some analyses of different types of atmospheric data, their deficiencies mainly lie in the following aspects, which can also be regarded as the main contributions of this study.

• General perspective. The previous data analyses are generally preliminary analyses, and their main focuses are on developing models for precipitation detection rather than comprehensively analyzing their relationships [24,34].
• Variable selection. The variables adopted in previous studies are based on their actual situations and data availability. For example, if a study were focused on only using GNSS products for precipitation forecasts, the weather variables probably would not be contained and evaluated [14,16]. However, this study collected nearly all the commonly used weather and GNSS data, as well as some essential statistical parameters to form a more complete analysis. In addition, previous studies mainly focused on the time series data itself, while this study also extends this application by moving the original time series from their corresponding time epochs, thereby providing a more accurate investigation of the precipitation precursory information contained in the adopted time series.
• Analytical method. The analytical methods used in previous studies are rather unitary. For example, correlation analysis is often used as a preliminary analysis in neural network-based studies [35], regression analysis is often adopted in the simple fitting or prediction of variables [36] and composite analysis is often utilized to reveal a correlation between two time series for exploring the large-scale impacts of teleconnections from modes of atmospheric variability [37,38]. In this study, not only are the methods of correlation, regression, mean value and principal component analyses used, but also their improved and revised forms are adopted, thereby making it more applicable to analyze the responses of various variables to precipitation events.
• Target event. The target meteorological events in previous studies vary greatly [39,40,41], while in this study, we only focus on precipitation. In addition, to obtain some findings about precipitation of different intensities, the observed precipitation amount record is classified into the three intensities of slight, moderate and heavy precipitation according to the hourly amount.
• Seasonal characteristics. This study also divides the whole study period into four parts, representing the four seasons, thus capturing the seasonal features contained in the variables and precipitation record.

Therefore, the aims and objectives of this study are mainly to: (1) analyze the cross-relationships among weather and GNSS variables; (2) investigate the responses of the selected variables to precipitation and then figure out the precursory information of precipitation contained in the variables; and (3) test the effectiveness of using all the variables to detect the occurrence of precipitation of different intensities. The research findings from this study not only have the potential to increase the utilization and uptake of different atmospheric variables in the detection of precipitation, but also could provide some useful clues and guidance in the development of more robust and reliable models for precipitation forecasts.

2. Data Acquisition

Considering the focus of this study, the datasets adopted to conduct this systematic analysis should be obtained over a rather long-term period. This could help to better fetch and categorize some existing and notable features contained in the whole dataset from an all-round perspective. Furthermore, more types of atmospheric variables should also be obtained to find some more general phenomena. For these reasons, in the study, the variables were obtained at a pair of co-located GNSS-weather stations employed in the Hong Kong region, i.e., the HKSC-King’s Park (KP) stations, over a 12-year period (2008–2019). As stated in [42], the geographic coordinates of the HKSC and KP stations are (22.32° N, 114.14° E) and (22.31° N, 114.17° E), respectively, and they have a horizontal distance of 3.29 km and a vertical difference of 45 m. What needs to be illustrated is that if the distance between a GNSS and a weather station is within a few kilometers in the horizontal direction, they can be regarded as “co-located”. Based on our previous findings and the mechanisms of GNSS data retrieval, these horizontal and vertical offsets would not affect the experiments conducted in this study [42,43]. It must also be noted that the selection of the study period from 2008 to 2019 is because high-quality GNSS observations can only be obtained from mid-2007 in the context of Hong Kong. In addition, the exclusion of data from 2020 to the present is on account of the acknowledged fact that human activities may exert certain impacts on the environment and atmosphere [44,45]. In the context of the widespread coronavirus pandemic since 2020, to avoid the findings to be influenced by uncommon and irregular circumstances, the dataset collected during the densely populated study region over the past few years were ignored. Specifically, this is due to the possible reduction in carbon dioxide production that may be associated with the warming of the planet and atmospheric conditions.

The datasets used in this study can be divided into three main categories: weather variables, GNSS atmospheric products and statistical time-varying parameters.

Table 1. Twelve types of variables adopted in this study.

Classification	No. of Variable	Type of Variable	Temporal Resolution	Time Period
Weather variable	8	dry-bulb temperature, dew point temperature, wet-bulb temperature, solar radiation, cloud cover, pressure, wind speed and wind direction	Hourly	12-year period 2008–2019
GNSS atmospheric product	2	ZTD and PWV
Statistical time-varying parameter	2	day-of-year and hour-of-day

lists the twelve types of variables adopted in this study.

2.1. Weather Variables

In this study, eight types of weather variables were adopted, including dry-bulb temperature (T), dew point temperature (DPT), wet-bulb temperature (WBT), pressure (P), solar radiation (SR), cloud cover (cloud), wind speed (W_s) and wind direction (W_d). The selection of these variables is because these variables are proven to be associated with precipitation or atmospheric humidity, most of which are also employed in operational NWP models. Among the variables, T and P are the most commonly used in most existing studies towards the field of meteorology. Derived from the values of T and relative humidity, DPT has the ability to better indicate the moisture content of the air. WBT is measured from the use of a standard mercury-in-glass thermometer with its bulb wrapped in wet muslin. With regard to the other variables, SR indicates the electromagnetic radiation emitted by the sun [46]. It should be mentioned that, based on the characteristics of this observation, only the SR values over the period from 6 am to 8 pm per day can be provided. The observations corresponding to the other epochs (hours) were marked as “zero” in this study to form a complete time series. Cloud cover refers to the fraction of the sky obscured by clouds on average [47], the value of which is expressed as a percentage. Since sunlight can be blocked by clouds, the value of cloud cover is obviously correlated to that of SR. Lastly, W_s and W_d measurements were also included to figure out their impacts on the formation of rainfall events. In this study, the time series of the eight variables over the whole study period were all obtained at the KP station.

2.2. GNSS Atmospheric Products

As mentioned in Section 1, the GNSS atmospheric sounding technique has been widely used to serve the meteorological community in recent years, and the most commonly used variables are ZTD and PWV. Despite additional error sources that may be introduced into PWV in the conversion process from ZTD, PWV can be taken as an effective indicator of the atmosphere’s water vapor content, and it has proven to be closely linked with the formation and evolution of precipitation events [48,49,50]. Therefore, for a systematic data analysis as conducted in this study, the two types of variables should both be carefully evaluated. The data processing procedure for retrieving ZTD and PWV time series at the HKSC station over the 12-year study period is discussed as follows.

Firstly, the Bernese GNSS software V5.2 was used to retrieve ZTD and other geodetic variables (e.g., tropospheric gradients and site coordinates) from GNSS raw observations [51,52]. During the whole process, the strategies adopted also include the Vienna Mapping Function 1 [53], the double-difference approach, the cut-off angle of 3° and the International GNSS Service Finals clocks and orbits [54,55]. In addition, in accordance with the International Earth Rotation and Reference Systems Service Conventions 2010 [56], the phase wind-up effects, the solid Earth and ocean pole tide, as well as the relativistic delays were all modeled in fine detail. It must also be noted that the temporal resolution of the retrieved GNSS products was 5 min. However, to be consistent with the collected hourly weather variables, ZTDs obtained corresponding to their observation epochs, i.e., hourly ZTD values, were adopted in the following experiments.

Secondly, the total delay in the zenith direction is composed of the two parts of zenith hydrostatic delay (ZHD) and zenith wet delay (ZWD), representing dry and wet components in the troposphere, respectively. It is acknowledged that the ZHD can be accurately obtained by using the Saastamoinen model [57]. Then, by simply subtracting ZHD component from ZTD estimate, the ZWD value can be obtained.

Thirdly, the PWV estimate can be directly converted from the obtained ZWD by using a conversion factor, which is a function of the weighted mean temperature along the zenith direction [28,29,30,58]:

$$PWV=\prod \times ZWD=\frac{{10}^6\times ZWD}{{\rho }_{water}{R}_w\left[\frac{k_3}{T_m}+k_2-k_1\times \left(\frac{R_d}{R_w}\right)\right]},$$

(1)

where $\prod$ denotes the empirical conversion factor; ${\rho }_{water}$ refers to the density of liquid water (g/m³); $R_d$ and $R_w$ represent the specific gas constants of dry air and water vapor, respectively; the notations of k₁, k₂ and k₃ represent the refractivity constant values given in [29]; and $T_m$ is the weighted mean temperature along the vertical direction over the site, which plays an important role in the determination of the conversion factor. Specifically, the accuracy of PWV estimates is largely affected by the error sources of $T_m$ and ZWD [59,60,61]. Therefore, in this study, $T_m$ is determined by using a linear model proposed by Chen [62], based on eight-year weather measurements obtained in the context of Hong Kong. Therefore, taking each of the above steps, the ZTD and PWV time series at the HKSC site over the whole study period can be obtained. In addition, the accuracy of PWV estimates obtained at the HKSC station over the study period was evaluated by using sounding profiles as the reference. As stated in [43], the HKSC station is the closest GNSS station to the only radiosonde station employed in the Hong Kong area, with a 2.9 km horizontal distance and a 3.8 m height difference. By evaluating 8766 pairs (twice per day) of PWV estimates obtained from GNSS and sounding profiles over the 12-year period, results indicated that the root mean square error between the two time series were 1.63 mm, which is acceptable for the meteorological community. More detailed information in terms of the whole retrieval and quality control processes can be found in our previous studies [43,63].

2.3. Statistical Time-Varying Parameters

It is acknowledged that GNSS atmospheric products and weather variables all possess obvious fast-changing characteristics. The additional inclusion of the parameters of day-of-year (DOY) and hour-of-day (HOD) is to effectively capture the time-varying features of these variables and precipitation records. In addition, the reason why the two parameters are described as statistical is because their values can be simply counted rather than observed. For example, the value of DOY is the same as that of the Julian Date, thus its data ranges are 1–365 and 1–366 in common and leap years, respectively. Similarly, the parameter of HOD generally possesses the same value as the Coordinated Universal Time, representing the actual time on any certain date. Therefore, to conduct a comprehensive investigation on the response of variables to precipitation events, these statistical time-varying parameters are extremely indispensable.

2.4. Precipitation Record

Apart from all the above-mentioned variables, to investigate the responses of different variables to precipitation, the hourly precipitation amount record over the 12-year period was also collected at the KP station. According to the standard provided by the World Meteorological Organization [64], by evaluating the record of precipitation amount, precipitation events can be classified into different intensities, including slight, moderate and heavy.

Table 2. Definition of different precipitation intensities, as well as the number of epochs corresponding to each intensity and their percentages of occurrence.

Intensity	Range	No. of Epochs	Percentage
Slight	r < 2.5 mm/h	6091	70.0%
Moderate	2.5 mm/h ≤ r < 10 mm/h	1886	21.7%
Heavy/Intense	10 mm/h ≤ r	722	8.3%

Note: the notation of r represents hourly precipitation amount.

lists the detailed definitions for differentiating the three types of precipitation intensity. In addition, the number of epochs corresponding to each intensity and their respective percentages of occurrence over the whole study period are also displayed.

It can be seen from this table that precipitation events occurred at a total of 8699 epochs over the study period, in which the slight, moderate and heavy precipitation events account for 70.0%, 21.7% and 8.3%, respectively. Please note, since all the variables and records were obtained on an hourly basis, that a total of 105,192 samples for each variable should have been collected over the 12-year study period. However, it is universally acknowledged that only few operational weather stations have a complete unbroken record of information. The data gaps are more likely to have been caused by equipment downtimes. With regard to the stations adopted in this study, 101,462 hourly estimates are available over the whole 12-year study period. Therefore, the overall data availability ratio is 96.5% (101,462/105,192), which is optimal in comparison to any other pairs of co-located GNSS-weather stations employed in the Hong Kong region. This not only substantiates the superiority of using the HKSC-KP stations, but also confirms the availability of the selected dataset for the following experiments.

3. Methodology

In this study, various types of analytical methods were adopted to systematically analyze the relationships among the twelve variables, as well as their responses to precipitation events. According to the temporal resolution of these variables and the total duration of the study period, some commonly used analytical methods, e.g., the Mann-Kendall and Pettitt tests, were not applicable. Therefore, after a careful selection, the basic methods utilized in this study mainly include the correlation analysis, regression analysis, mean value analysis and principal component analysis (PCA).

3.1. Correlation Analysis

With regard to the correlation analysis, the most representative metrics include the Pearson correlation coefficient (PCC) [65] and the Spearman’s rank correlation coefficient (SCC) [66]. Between them, the PCC is the most widely used, which is also colloquially referred to as “correlation coefficient (denoted by r)”. It is often adopted to estimate linear correlation between two sets of time series, and its calculation equation can be expressed as [65]:

$$PCC=\frac{{\sum }_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\sum }_{i=1}^n{(X_i-\overline{X})}^2}\sqrt{{\sum }_{i=1}^n{(Y_i-\overline{Y})}^2}},$$

(2)

where n is the total number of samples in the whole time series; the subscription i is the index of a sample data; X_i and Y_i denote the i-th samples of the selected two time series; $\overline{X}$ and $\overline{Y}$ are the average values of the two sets of time series. As can be seen from the equation, PCC is a normalized measurement of the covariance, which is generally employed to test the dependence of two time series [65]. The value of PCC result is in the range between −1 and 1. Although the values of 1 and −1 both represent perfect linear correlations, the two circumstances indicate a positive and a negative correlation relationship, respectively. Another extreme case, i.e., the PCC value of 0, implies that there is no linear correlation between the tested time series. Moreover, by evaluating the absolute values of PCC, some detailed interpretation principles were also developed in [67], in which several correlation levels have been carefully categorized.

It is noted that in the calculation of PCC, which mainly evaluates the linear relationship between two continuous variables, many types of correlations contained in the two series are arbitrarily ignored, which is the main reason to use another type of correlation coefficient, i.e., SCC, in this study. The other motivation for adopting SCC lies in the fact that this study focuses on the time series data of the twelve variables, hence their rankings over the whole study period should not be overlooked in analyzing their inter-relationships. The monotonic relationships between each two series should also be tested. As mentioned in [24], since SCC has the ability to quantify the extent of statistical independence between the rankings of two time series, it has been effectively used in various applications [68,69,70]. SCC is calculated as [66]:

$$SCC=\frac{{\sum }_{i=1}^n({{rg}_X}_i-\overline{{rg}_X})({{rg}_Y}_i-\overline{{rg}_Y})}{\sqrt{{\sum }_{i=1}^n{({{rg}_X}_i-\overline{{rg}_X})}^2}\sqrt{{\sum }_{i=1}^n{({{rg}_Y}_i-\overline{{rg}_Y})}^2}},$$

(3)

It can be seen from Equation (3) that the calculation mechanism of SCC is almost the same as that of PCC; however, the time series data incorporated in Equations (2) and (3) are different. Since SCC is based on the ranked values for each variable rather than the raw data, hence ${rg}_X$ and ${rg}_Y$ refer to the ranks of the time series of X and Y (as shown in Equation (2)), respectively. In other words, to construct the time series of ${rg}_X$ and ${rg}_Y$, the original series of X and Y should be reorganized according to their rankings over the whole period. The definitions of the other notations (e.g., n and i) are the same as those defined in Equation (2). In the same way as PCC, the value of SCC is also in the range of [−1, 1], while the main difference is about the interpretation of the positive and negative signs. In terms of the SCC value, its plus-minus signs indicate the correlation direction. To be clear, the result with a plus sign shows that the two series have the same variation trend, i.e., increase or decrease simultaneously; the SCC value with a minus sign reveals that the variation trends of the two series are diametrically opposed. The closer the SCC value is to 1 or −1, the larger the tendency is between the two variables.

3.2. Regression Analysis

In most cases, given a dataset containing at least two sets of time series, their relationships (linear, multi-linear and nonlinear) can be inferred using regression analysis [71]. According to Freund et al. [72], regression analysis can also be taken as an effective tool for the forecasting of variables, background fields and weather phenomena, the mechanism of which is very much similar to the cutting-edge machine learning approach. For example, in our previous study [36], it was simply utilized to obtain a high accuracy potential evapotranspiration difference. In this study, the primary reason for using this method is to make it act as an extension of the above-introduced correlation analysis. Therefore, despite the most common form of regression analysis, i.e., linear regression, this study mainly focuses on using a broader range of non-linear equations to figure out which form is optimal in the estimation of conditional expectation. As inspired by Shestopaloff [73], the four nonlinear equations adopted in this study include the quadratic polynomial, natural logarithmic (to the base of the Euler’s constant e), natural exponential and power functions, whose basic forms are shown in Equations (4)–(7), respectively.

$$y=a_2{x}^2+a_{1}x+b_1,$$

(4)

$$y=a_3{\mathit{log}}_e\left(x\right)+b_2=a_3\mathit{ln}\left(x\right)+b_2,$$

(5)

$$y={a_{4}e}^{a_{5}x},$$

(6)

$$y=a_6{x}^c,$$

(7)

where x and y are the series of the independent and dependent variables, respectively; $a_1$−$a_6$ are the coefficients; $b_1$ and $b_2$ represent the intercepts in polynomial and logarithmic functions, respectively; c denotes the order of the power function, as shown in Equation (7); and e is the Euler’s constant, the value of which is 2.718281. Furthermore, the coefficient of determination (COD), which is also known as R-squared (R²), was adopted in this study to compare the results from the use of different functions. As one of the most commonly used criteria, COD has the ability to examine how well the time series of one variable is reflected by another, and it can be expressed as [74]:

$$R^2=1-\frac{\sum _{i=1}^n{(y_i-x_i)}^2}{\sum _{i=1}^n{(y_i-\stackrel{-}{y})}^2},$$

(8)

where the subscription i denotes the index of the element in the sample dataset; n is the number of samples; $x_i$ and $y_i$ are the independent and dependent variables corresponding to the i-th epoch, respectively; and $\stackrel{-}{y}$ is the mean of all the dependent variables. Please note that in this study, all regression analyses were performed using the IBM SPSS software package (https://www.ibm.com/spss, accessed on 1 October 2022) [75]. Specifically, the common problem of autocorrelation in the regression analysis was tackled by using the Cochrane-Orcutt procedure embodied in the software [76].

3.3. Mean Value Analysis

Mean value analysis is used to simply calculate the mean value of any type of variable over a certain period. Although this operation is easy to conduct, what really matters is the selection of the period. In this study, by comparing the mean values over different periods, e.g., with precipitation, without precipitation and with precipitation of different intensities, the responses of different variables to precipitation can also be revealed to some extent. In addition, this practice can also be adopted to figure out some precursor information of precipitation if the calculation period were determined as several hours prior to the occurrences of precipitation events.

Overall, it must be noted that the three methods described above are generally their basic forms. In the following experiments, some innovative practices and methods developed based on these methods were also incorporated to make a more general analysis.

3.4. Principal Component Analysis

In this study, the PCA method [77,78] was also employed, whose main function is to conduct dimensional reduction, i.e., perform a change of basis on the whole dataset, by calculating the principal components (PCs). Then, the contribution of each variable to the target data, e.g., precipitation in this study, can be further analyzed and determined [79]. From the perspective of data analysis, the PCA method is the simplest among true eigenvector-based analytical methods, and the PCs represent the eigenvectors of the samples’ covariance matrix. Therefore, a matrix with the dimension of m × n needs to be constructed, where m and n are the numbers of the sample observations and variables, respectively. In this study, based on the 12-year sample observation data, m was set to 101,462, and n was 12. The constructed matrix denoted by X is:

$$X=\left[{\tilde{V}}_1,{\tilde{V}}_2,{\tilde{V}}_3,{\tilde{V}}_4,{\tilde{V}}_5,{\tilde{V}}_6,{\tilde{V}}_7,{\tilde{V}}_8,{\tilde{V}}_9,{\tilde{V}}_{10},{\tilde{V}}_{11},{\tilde{V}}_{12}\right],$$

(9)

where ${\tilde{V}}_{1–12}$ are the column vectors for the twelve variables. Each of the column vectors was normalized by subtracting the mean of the variable samples and then being divided by their respective standard deviation. The normalized matrix (denoted by $\widehat{X}$) becomes:

$$\widehat{X}=\left[\frac{{\tilde{V}}_1-{\stackrel{-}{V}}_1}{{\sigma }_1},\frac{{\tilde{V}}_2-{\stackrel{-}{V}}_2}{{\sigma }_2},\frac{{\tilde{V}}_3-{\stackrel{-}{V}}_3}{{\sigma }_3},\dots ,\frac{{\tilde{V}}_{11}-{\stackrel{-}{V}}_{11}}{{\sigma }_{11}},\frac{{\tilde{V}}_{12}-{\stackrel{-}{V}}_{12}}{{\sigma }_{12}}\right],$$

(10)

where ${\stackrel{-}{V}}_{1–12}$ and ${\sigma }_{1–12}$ are the mean and standard deviations of each of the twelve column vectors. Finally, from the normalized matrix $\widehat{X}$, the 12 × 12 covariance matrix of the samples (denoted by $Cov\left(\widehat{X}\right)$) was computed, as shown in the following equation.

$$Cov(\widehat{X})=\left(\begin{array}{cc}\begin{array}{cc}cov({\widehat{X}}_1,{\widehat{X}}_1)& cov({\widehat{X}}_1,{\widehat{X}}_2)\\ cov({\widehat{X}}_2,{\widehat{X}}_1)& cov({\widehat{X}}_2,{\widehat{X}}_2)\end{array}& \begin{array}{cc}\dots & cov({\widehat{X}}_1,{\widehat{X}}_{12})\\ \dots & cov({\widehat{X}}_2,{\widehat{X}}_{12})\end{array}\\ \begin{array}{cc}\dots & \dots \\ cov({\widehat{X}}_{12},{\widehat{X}}_1)& cov({\widehat{X}}_{12},{\widehat{X}}_2)\end{array}& \begin{array}{cc}\dots & \dots \\ \dots & cov({\widehat{X}}_{12},{\widehat{X}}_{12})\end{array}\end{array}\right),$$

(11)

where ${\widehat{X}}_{1–12}$ represent the twelve column vectors in the normalized matrix $\widehat{X}$. The twelve new axes defined by the orthogonal eigenvectors of $Cov\left(\widehat{X}\right)$ represent the twelve PCs, which are uncorrelated. The proportion of the variance contributed by each PC can be computed by dividing its corresponding eigenvalue to the sum of all eigenvalues. By analyzing the variances interpreted by each PC, some major PCs, i.e., those that contribute the most to the total variance, can be determined. Then, the variable loadings in those major PCs can also be analyzed to figure out the significance of each variable to the whole dataset. Please note that variable loading refers to the correlation coefficient between a PC and a variable, and the sum of the squared coefficients is equal to 1. The variable loadings for each PC can be found from the eigenvector matrix calculated from the obtained $Cov\left(\widehat{X}\right)$ [79,80]. The rows and columns of the eigenvector matrix correspond to variables and PCs, respectively. Finally, by reducing the dimension of the whole dataset to those major PCs, the potential of using the variables to discriminate precipitation events can be effectively revealed.

4. Cross-Relationships among the Twelve Variables

Prior to analyzing the responses of the selected twelve variables to precipitation events of different intensities, it is important to conduct preliminary analyses among the variables to uncover the relationships, if there are any, among them. Therefore, in this section, the cross-relationships among the twelve variables are carefully analyzed.

4.1. Cross-Correlation Analysis among the Twelve Variables

With regard to atmospheric time series data, especially over a rather longer-term period, the primary practice for investigating their internal relationships is to conduct a correlation analysis. Although this common practice has been performed in various previous studies [24,35], there are few studies that have tested a large number of variables [34]. This study firstly used the PCC as the main metric to carry out the cross-correlation analysis. Figure 1 depicts the PCC results among the twelve variables obtained at the HKSC-KP stations over the 12-year period 2008–2019.

In Figure 1, the lower left section of the plot shows the PCC values between each pair of the twelve variables; the negative correlation values are shown in italics. The PCC values are also displayed by using the darkness of the color on the upper right section of the plot. Roughly speaking, higher PCC values are mainly concentrated among the six typical variables of ZTD, PWV, T, WBT, DPT and P. The first reason is undeniably on account of their calculation mechanisms. For example, as stated in Section 2.2, PWV is directly computed from the ZTD estimate, which explains why the highest PCC value of 0.992 occurs between ZTD and PWV. It is noted that although previous studies have also confirmed their strong positive correlation and similar variation trends [63,81], our recent study also highlighted that if the two variables were used simultaneously, the performances of precipitation forecasts can be further improved [24]. Moreover, the high PCC value of 0.848 between DPT and T results from the fact that the former is derived from the latter and relative humidity. Similarly, although the WBT time series was measured from the KP station, it can also be calculated using T, DPT and P. Therefore, this effectively accounts for the fact that WBT has strong correlations with the three variables T, DPT and P, with PCC values of 0.903, 0.975 and –0.842, respectively. The second reason relates to the atmospheric conditions that these variables manifest. Since the variables of ZTD, PWV, DPT and WBT all have the ability to indicate the moisture content of the air, the PCC results between any two of them are all above 0.78. As T has a strong correlation with relative humidity [34], it also possesses high PCC values with the variables, e.g., DPT and PWV, representing atmospheric humidity.

Looking at the other six variables, it can be found that DOY and HOD both have the highest PCC results with T in comparison with the others. This is comprehensible as the temperature measurements in Hong Kong are generally higher in the summer season and the daytime. Moreover, the relative higher PCC values also corroborate the obvious temporal variation features contained in temperature time series. With respect to wind measurements, affected by monsoons, the W_d generally has certain directions in different seasons; e.g., south and north winds frequently occur in summer and winter, respectively [82,83,84]. Furthermore, since the Hong Kong region is surrounded by the South China Sea on all sides except the north, the low-level monsoonal streams often transport large amounts of water vapor to the sites [85,86]. This explains why W_d and W_s both have moderate correlations with PWV, ZTD, T, WBT, DPT and P. Lastly, the respective PCCs of 0.444 and 0.407 for cloud-ZTD and cloud-PWV can be attributed to the mechanism of retrieving GNSS-derived variables: the higher the cloud coverage rate value, the larger the atmospheric delays.

Since all the variables used in this study are time series data, it is necessary to take their rankings and distributions into account. Therefore, apart from the PCCs obtained above, the SCC values between each two of the twelve variables were also calculated, as shown in Figure 2. Please note, the negative correlation values are also shown in italics.

By comparing the results shown in Figure 1 and Figure 2, it can be easily concluded that all the correlations reflected by the metric of either PCC or SCC for any two types of variables are roughly at a similar level, which is also consistent with the findings of Dancey and Reidy [67]. Consequently, the findings in Figure 2 are generally the same as those stated above. However, there are three interesting phenomena that need to be mentioned. Firstly, the absolute values of SCC obtained between each two of the variables PWV, T, WBT and P are all above 0.7. According to the interpretation principles provided by Dancey and Reidy [67], these variables are strongly correlated. In addition, their respective SCCs are even larger compared with their PCC values. This indicates that by taking the variables’ rankings into consideration, their relationships become more prominent. Secondly, the correlations revealed from SCCs between GNSS atmospheric variables (ZTD and PWV), and time-varying parameters (DOY and HOD) are similar to those uncovered by using PCCs. Lastly, although the signs of SCC results obtained from SR-ZTD (from −0.036 to 0.012), SR-PWV (from −0.012 to 0.031) and cloud-T (from 0.022 to −0.091) have changed with respect to the PCC results, their values are all below 0.1, indicating that the three pairs of variables generally have little or almost no correlation. The signs of these SCC results only have the ability to reflect whether or not these variables have a same variation direction. Consequently, based on the above analyses from the metrics of PCC and SCC, the correlation relationships among the twelve variables are effectively revealed.

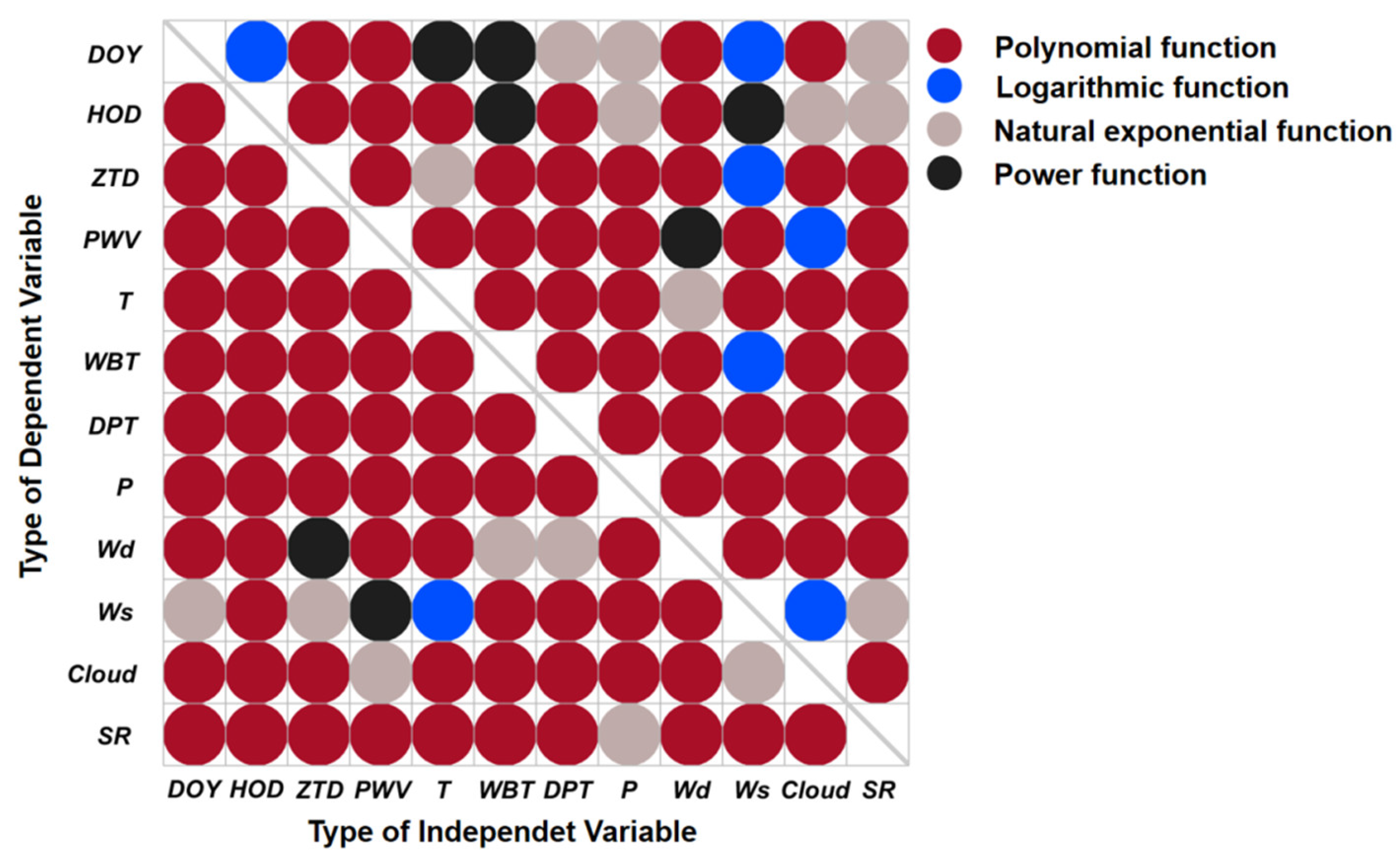
4.2. Regression Analysis among the Twelve Variables

Since the above correlation analysis mainly focused on the linear relationships, we also adopted the regression analysis to further investigate the nonlinear relationships between each pair of variables. It is noted that the focal point of this section is not on using one or a group of variables to predict another one; thus, in each experiment, the number of dependent and independent variables were both set to 1. In other words, the nonlinear regression analysis conducted in this section can also be recognized as a cross-regression analysis between each two of the twelve variables, thus figuring out which type of nonlinear functions can better reflect their relationships. As mentioned in Section 3.2, the four commonly used types of functions, including the quadratic polynomial, natural logarithmic, natural exponential and power functions, were tested. To establish a connection between the linear correlation and nonlinear regression analyses, the results obtained from linear fitting were also compared. By comparing the CODs resulting from different functions for each two sets of time series, Figure 3 shows the optimal functions for fitting their relationships. When conducting a regression analysis, dependent and independent variables should be determined beforehand. Therefore, each variable was designated as the independent and dependent variables separately, thus, to test all the possible situations.

It can be seen from this figure that the optimal results for most pairs of variables are from the use of the quadratic polynomial function. By changing the variables from being independent variables to being dependent ones, the optimal fitting function types for 26 (over 1/3) pairs of variables have changed (see the bottom left and upper right). For example, in terms of the data pair of T-ZTD, the natural exponential function is the optimal one for fitting the temporal variations of ZTD using the variable of T; while if their roles were exchanged, i.e., T and ZTD were designated as dependent and independent variables, respectively, the optimal form is the quadratic polynomial function. By comparing the detailed results, although these optimal function types vary greatly, the CODs obtained from the use of different functions are generally all comparable. Consequently, for applications that do not have extremely high demand on data accuracy, it is more efficient to simply adopt the linear function to fit their relationships; for the others, e.g., the prediction of a variable [36], it is better to use a function that has the potential to reflect their relationships in a more refined way.

5. Systematic Investigation on Responses of Twelve Variables to Precipitation

In this section, a systematic investigation on the responses of the selected twelve variables to precipitation events was conducted. Similar to Section 4, the methods of correlation and regression analyses were adopted. Furthermore, to investigate the performance of the variables prior to and during the occurrence of precipitation events, their mean values over different periods were also calculated and analyzed.

5.1. Comparing the Time Series of the Twelve Variables with Precipitation Record

5.1.1. Conventional Correlation Analysis

To conduct a more systematic correlation analysis, the precipitation record collected over the 12-year study period was further processed. As the original precipitation record simply contains the hourly precipitation amount, to highlight the occurrence of heavy precipitation and the intensities of precipitation, two sets of new precipitation records were reorganized in accordance with the hourly rainfall amounts. The first set is to use the value of “1” to indicate the occurrence of heavy precipitation, i.e., hourly precipitation amount is above 10 mm (see Table 2); while other epochs over the whole time series were marked as “0”. Since heavy precipitation is generally regarded as an extreme weather event that has caused considerable damages and casualties, the use of this new set of precipitation record is effective for this study to pay particular attention on this type of event. By using the definitions shown in Table 2, the other set of precipitation record is composed of the values of “0”, “1”, “2” and “3”, representing “no precipitation”, “slight precipitation”, “moderate precipitation” and “heavy precipitation”, respectively. This record is used to indicate the intensities of precipitation in each epoch. In terms of precipitation forecasts, the new record and the original one are especially designed for conducting qualitative detection and quantitative prediction, respectively. Therefore, in this study, the PCC results between each variable and each precipitation record were all calculated, as shown in

Table 3. Pearson and Spearman’s rank correlation coefficient results by comparing each of the twelve variables with precipitation records over the period 2008–2019.

Type	Precipitation	DOY	HOD	ZTD	PWV	T	WBT	DPT	P	Wd	Ws	Cloud	SR
PCC	Heavy precipitation	0.009	−0.007	0.107	0.107	0.038	0.056	0.066	−0.083	0.041	0.045	0.075	−0.046
	Precipitation Intensity	0.011	−0.024	0.264	0.256	0.054	0.114	0.151	−0.171	0.041	0.057	0.216	−0.121
	Precipitation amount	0.011	−0.012	0.151	0.150	0.048	0.074	0.092	−0.113	0.049	0.046	0.113	−0.067
SCC	Precipitation amount	0.008	−0.027	0.277	0.264	0.060	0.097	0.160	−0.161	0.020	0.017	0.292	−0.067

. Moreover, the SCC results obtained by comparing each variable with the hourly precipitation amount record were also listed in Table 3. The use of only the original record in the calculation of SCC results is mainly because only the precipitation amount record contains effective ranking information.

Firstly, by comparing the PCC results obtained for the three sets of precipitation records, it can be clearly seen that the absolute values of the results are all less than 0.3, indicating that these twelve variables do not have obvious correlation relationships with any of the records. After a close look at the values obtained for each record, apart from the variable of W_d, the highest PCC results (see the figures in bold type) for the other variables all exist in their comparisons with the record of precipitation intensity. This indicates the fact that if these data were used directly for precipitation forecasts (without the adoption of physically-based NWP models), it would be better to conduct qualitative detection rather than quantitative prediction. This finding also explains why previous studies [16,34,43], in which qualitative models were well-developed, achieved excellent detection performances.

Secondly, by comparing the results shown in the shaded rows in Table 3, it is obvious that most of the SCCs are significantly larger than their corresponding PCCs. This makes perfect sense because although the original record is hourly precipitation amount, based on the calculation mechanism of SCC, the information of precipitation intensity has also been taken into consideration by calculating the SCCs. Therefore, the results are quite similar to those PCC values obtained from the comparison with the precipitation intensity record. As a result, for the applications of precipitation forecasts, it is important to take the precipitation intensities fully into account to obtain better performances.

Lastly, by comparing the results obtained for each variable from an overall perspective, it is evident that the variables of ZTD, PWV and cloud have more evident and closer correlation relationships with precipitation, representing their great potential in the forecasting of rainfall events.

5.1.2. Correlational Analysis of PCC Results Obtained by Using Precipitation Record Moving Several Hours Forward

In the experiments conducted above, the data adopted for calculating PCCs and SCCs are all their original time series obtained over the study period 2008–2019. Each data pair corresponds to a fixed time epoch. To investigate some other interesting features contained in the time series data, the correlation analysis was further extended in this section. It is acknowledged that prior to the occurrence of precipitation events, especially heavy rainfall events, some precursory information is contained in the time series of atmospheric variables. For example, according to previous studies [14,43,49], during the evolution of most precipitation events, the ZTD and PWV time series tend to increase significantly till reaching a larger value, and then start to decrease considerably. Motivated by these phenomena, this study proposes to move the precipitation record several hours forward firstly, then calculate and analyze the PCC results obtained by comparing these new sets of precipitation records with each of the twelve variables, as shown in

Table 4. Comparison of Pearson correlation coefficient results of each of the twelve variables with precipitation record moving 0−12 h forward.

Shift (Hours)	DOY	HOD	ZTD	PWV	T	WBT	DPT	P	Wd	Ws	Cloud	SR
0	0.011	−0.012	0.151	0.150	0.048	0.074	0.092	−0.113	0.049	0.046	0.113	−0.067
1	0.011	−0.014	0.154	0.152	0.046	0.082	0.095	−0.114	0.040	0.047	0.108	−0.057
2	0.011	−0.015	0.157	0.154	0.043	0.086	0.096	−0.116	0.034	0.048	0.099	−0.049
3	0.011	−0.014	0.160	0.157	0.040	0.088	0.096	−0.117	0.030	0.048	0.093	−0.046
4	0.011	−0.015	0.163	0.160	0.036	0.088	0.096	−0.118	0.028	0.048	0.090	−0.045
5	0.011	−0.016	0.168	0.164	0.031	0.089	0.095	−0.119	0.026	0.049	0.087	−0.044
6	0.011	−0.012	0.172	0.168	0.026	0.089	0.095	−0.119	0.027	0.049	0.085	−0.042
7	0.011	−0.008	0.178	0.172	0.022	0.089	0.094	−0.119	0.030	0.050	0.084	−0.040
8	0.011	−0.005	0.181	0.176	0.038	0.089	0.094	−0.122	0.029	0.049	0.081	−0.040
9	0.011	−0.001	0.176	0.173	0.049	0.088	0.093	−0.126	0.029	0.049	0.080	−0.039
10	0.011	0.004	0.170	0.168	0.053	0.088	0.093	−0.127	0.030	0.049	0.079	−0.038
11	0.011	0.009	0.166	0.165	0.056	0.088	0.092	−0.128	0.031	0.048	0.079	−0.036
12	0.011	0.012	0.162	0.162	0.058	0.088	0.092	−0.128	0.031	0.047	0.078	−0.033

. Please note that the period for shifting the hourly precipitation record forward was determined as 12 h in this study, i.e., move the record forward from 0 to 12 h. This is because this period is defined by the World Meteorological Organization for the nowcasting and very short-range forecasting of meteorological events. In addition, precipitation, especially heavy precipitation, is regarded as an immediate meteorological event rather than a climatic phenomenon. Therefore, it is reasonable to use a 12 h period to uncover some precursory information of precipitation contained in different variables. The results obtained from this analysis can also reveal the potential lead times when using these variables to develop conventional threshold-based models for precipitation forecasts. It is noteworthy that the adoption of PCC rather than SCC in this experiment is because the main aim is to test their temporal variations instead of their rankings and distributions; the use of hourly precipitation amount rather than the other two sets of records (i.e., precipitation intensity and the occurrence of heavy precipitation) is due to the fact that the original record is the actual measured data, while the others are reprocessed records with values in the range 0–3.

In can be seen from Table 4 that a total of 13 sets of experiments were conducted by moving forward the hourly precipitation records from 0 to 12 h. The results shown in the first row, corresponding with “0 h”, were calculated by using their original time series, which are also shown in Table 3. Although the range of PCC values for these variables is different, they generally varied greatly with the change of moving hours. This could also reflect their instant variation features to some extent. The largest PCC values for each of the twelve variables are all marked in bold italic type. The detailed analysis regarding each of the twelve variables was conducted as follows:

• DOY. This variable is the only type in which its PCC results corresponding to all the scenarios stay the same. This is mainly on account of its data dimension. Even when the precipitation records were moved 12 h forward, it cannot be reflected in its PCC values with DOY, the values of which always stayed the same over a certain date. In addition, although the occurrence of precipitation had a close relationship with DOY as the most precipitation happened in the summer season, this cannot be fully revealed by only moving the record over a 12 h period.
• HOD and T. The largest PCC values for HOD and T appeared in the cases when the record moved 5 and 12 h forward, respectively. However, the meanings behind these values are unclear because the thirteen PCCs were unorderly distributed and their values are too small; thus, it is unreasonable to recognize their close correlation relationships with the precipitation amount record.
• ZTD and PWV. It is quite evident that their PCCs both started to increase till reaching their respective largest values (corresponding to “8 h”), then started to decrease with the steady increase of moving hours. This further corroborates the conclusion that with the use of ZTD and PWV to detect precipitation, the lead time is roughly 8 h in the context of the Hong Kong region [43,63].
• WBT, DPT and W_s. Similar to the results obtained above, the general lead times for WBT, DPT and W_s are in the ranges of 5–8 h, 2–4 h and 7 h, respectively.
• P. The larger the moving hours, the higher its correlation was with the precipitation record, and the inflection point for its PCC values did not exist over the 12 h period. This phenomenon can be explained by the formation process of precipitation, which often takes a longer time. From another perspective, it does not matter whether the PCC value of P would increase continuously, or an inflection point would occur over a longer period, as the period for the nowcasting and very short-range forecasting of precipitation is 12 h. Therefore, the lead time for taking this variable as an indicator to detect precipitation, especially heavy precipitation, is likely to be a lot longer than the others.
• Cloud, SR and W_d. The largest PCCs for these variables all corresponded to “0 h”, i.e., the occurrence of precipitation event, indicating the instantaneous responses of these variables to precipitation.

5.1.3. Regression Analysis

From the results obtained above, it can be observed that the linear relationships are not that evident, since most PCCs lie within the range defined for “slight correlation level”. Therefore, similar to Section 4.2, the regression method was also used to test which nonlinear function can better describe the relationships between each variable and precipitation record. In this part, the hourly precipitation record, as the target data, was determined as the dependent variable. Since the main aim here is to evaluate the nonlinear relationship, each variable was separately taken as the independent variable, i.e., only one independent variable was used at a time. According to the COD results of the twelve variables in comparison to the time series of the precipitation record, the optimal function for all twelve variables was found to be the quadratic polynomial function. By using the PCCs for each data pair as the reference (see Table 3), the CODs obtained from the use of the determined quadratic polynomial function are all larger than their respective linear fits, as shown in

Table 5. Coefficient of determination results obtained for each of the twelve variables compared with the precipitation record using the linear and quadratic polynomial functions over the period 2008–2019.

Type	DOY	HOD	ZTD	PWV	T	WBT	DPT	P	Wd	Ws	Cloud	SR
Linear fitting	0.0001	0.0001	0.023	0.023	0.002	0.005	0.008	0.012	0.002	0.002	0.013	0.004
Quadratic polynomial fitting	0.009	0.0004	0.037	0.035	0.003	0.006	0.01	0.014	0.003	0.011	0.027	0.005

.

It can be concluded that when using the variables to fit the hourly precipitation amount, the more appropriate way is to construct their respective quadratic polynomial function forms instead of using their original values. However, it can also be seen from Table 5 that all the results are less than 0.1, meaning that there is little possibility to accurately reflect the time series of precipitation amount using any one type of the twelve variables. Therefore, this also highlights a pressing need to adequately adopt a combination of these variables and better mine the information contained in them.

Apart from the fact that the results shown in Table 5 are all less than 0.04, those obtained using the linear and quadratic polynomial fittings also do not have a clear distinction. Moreover, the construction of the quadratic polynomial may cause some calculation efficiency issues, and the constructed fitting functions cannot reflect the atmospheric physics implications contained in the original values. Consequently, it is acceptable to use the original series of the variables when conducting the nowcasting and numerical prediction of precipitation events.

5.2. Analyzing the Mean Values of the Twelve Variables with Precipitation Record

5.2.1. Mean Value Analysis over the Whole Study Period

As described in Section 3.3, the aim of the mean value analysis is to calculate and analyze the mean values obtained for different situations over different periods. In this section, data collected over the whole 12-year study period 2008–2019 were firstly taken to calculate the mean values of the selected variables. It is noted that the two parameters of DOY and HOD were not included in this experiment; only the ten types of GNSS and weather variables were adopted. To test their performance under different scenarios, a total of six schemes, i.e., using data collected over six different periods, were designed. The periods determined for the first three schemes include the use of all the epochs, and epochs with and without precipitation. By analyzing the results from the three schemes, the diverse performances resulting from the ten variables in response to precipitation can be observed. The other three schemes were designed according to the intensities of precipitation events, i.e., using data collected at the epochs with slight, moderate and heavy precipitation to calculate their mean values. The three schemes can be viewed as the refinement of the above-mentioned scheme of using epochs with precipitation. By carefully analyzing the results from the three schemes, the responses of these variables to precipitation of different intensities can be captured. Based on these schemes,

Table 6. Mean values obtained under different precipitation circumstances over the period 2008–2019.

No.	Time Period	No. of Epochs	ZTD (mm)	PWV (mm)	T (°C)	WBT (°C)	DPT (°C)	P (hPa)	Wd (°)	Ws (m/s)	Cloud (%)	SR (MJ/m2)
Scheme 1	All the epochs	101,462	2568.95	42.68	23.90	20.49	18.71	1010.20	137.25	2.38	68.95	0.57
Scheme 2	Epochs with no precipitation	92,763	2562.19	41.46	23.84	20.31	18.40	1010.51	136.64	2.36	66.97	0.60
Scheme 3	Epochs with precipitation	8699	2641.04	55.70	24.60	22.41	21.95	1006.81	143.70	2.58	90.11	0.20
Scheme 4	Epochs with slight precipitation	6091	2632.17	53.87	24.06	21.89	21.35	1007.73	136.26	2.51	89.34	0.22
Scheme 5	Epochs with moderate precipitation	1866	2657.35	59.13	25.66	23.44	23.13	1004.99	154.83	2.64	91.26	0.16
Scheme 6	Epochs with heavy precipitation	722	2673.27	62.22	26.39	24.12	23.92	1003.80	177.42	3.07	93.67	0.09

lists the mean values calculated under different precipitation scenarios over the whole study period.

Apart from the mean values of the ten variables, the number of epochs used to calculate the mean values in each scheme are also displayed in Table 6. From the results shown in the first three schemes, some interesting phenomena can be found. Firstly, the huge difference contained in the numbers of epochs with and without precipitation (8699 vs. 92,763) further corroborates that precipitation, especially heavy precipitation, can be regarded as a type of rare event. Secondly, apart from P and SR, the mean values of the other eight variables calculated using data collected during the occurrence of precipitation are all larger than those obtained over the other periods. This is consistent with the finding obtained in Section 5.1.1. Thirdly, the results also confirm the finding that the closer the DPT value is to that of T, the higher the relative humidity and the moister the air. Lastly, according to the results and the statements in Section 2.1, southeastern wind is the most common prevailing wind in the study area, however, it tends to move southward when there is a precipitation event.

With regard to the last three schemes (see the shaded rows), which are divided from the third scheme according to the intensity of precipitation, a general phenomenon can be found: the higher the precipitation intensity, the larger the variable values (except the two variables of P and SR). By comparing Schemes 2 and 4, another issue contained in the variable of W_d can be found: the mean values determined for the two schemes are generally the same. This indicates that W_d is not quite sensitive to the occurrence of slight precipitation. In addition, the mean value of W_d in Scheme 6 even reaches the value of 177.42, representing that the heavy precipitation occuring in Hong Kong is more likely to be affected by southern winds.

To further extend the above analysis, as stated in Section 3.3, heavy precipitation was taken as the target event to test whether there is obvious precursory information contained in the ten variables. In addition to Scheme 6 listed in Table 6, another two sets of mean values calculated using data collected at the 6 h and 12 h periods prior to the onset of heavy precipitation were also adopted for comparison, as shown in

Table 7. Comparison of mean values obtained at the 6 h and 12 h periods prior to heavy precipitation over the period 2008–2019.

Time Period	No. of Epochs	ZTD (mm)	PWV (mm)	T (°C)	WBT (°C)	DPT (°C)	P (hPa)	Wd (°)	Ws (m/s)	Cloud (%)	SR (MJ/m2)
Epochs with heavy precipitation	722	2673.27	62.22	26.39	24.12	23.92	1003.80	177.42	3.07	93.67	0.09
6 h periods prior to heavy precipitation	3018	2674.72	62.44	26.34	24.70	24.20	1003.79	166.34	2.83	88.83	0.27
12 h periods prior to heavy precipitation	5387	2676.50	62.74	26.30	24.77	24.11	1003.79	164.41	2.74	86.55	0.40

.

An obvious finding from this table is the epochs used in the two new schemes are not 6 or 12 times of the number of epochs with heavy precipitation. This is because some hourly heavy precipitations happened continuously, e.g., an event lasts for several hours straight, thereby resulting in some overlaps contained in the 6 h and 12 h periods. In terms of the exact values, the performance of the ten variables can be classified into several categories.

• The first category includes ZTD, PWV and WBT. According to the results stated above, the mean values of the variables generally become larger with the increase of precipitation intensity. However, the mean values of the three variables obtained over the 12 h period is larger than the others. This possibly indicates their highest hourly values exist in the range of 6–12 h prior to heavy precipitation; in other words, there is an obvious inflection point contained in the time series about 6–12 h ahead of the onset of heavy precipitation. This finding corresponds to the results shown in Table 4; i.e., the possible lead times of the three variables are about 8 h.
• The second type only includes the variable of DPT. Its performance is similar to the first category, with the difference that, its largest mean value was obtained over the 6 h period, indicating that its inflection point occurs about 0–6 h before heavy precipitation. This confirms its potential lead time is about 2–4 h from Section 5.1.2 as well.
• The third category includes T, W_d, W_s and cloud. The performance of the variables simply conforms to the principle obtained from Table 6; i.e., in general, their values all increase continuously, and the largest values exist with the occurrence of heavy precipitation.
• The fourth category includes SR, with its general variation feature being similar to the variables in the third category. However, the variation direction of SR is diametrically opposed to that in the third category.
• The fifth category contains P, of which the mean values for the three schemes are almost in the same range. As already explained in Section 5.1.2, the use of a 12 h period is quite limited in evaluating the variation of site-level pressure.

Apart from the detailed analysis for each variable, it is noted that by comparing the differences between T and DPT, the smallest value (representing the maximum air humidity) exists in the range of 0–6 h ahead of heavy precipitation. Consequently, these findings on the response of the variables to heavy precipitation could also provide insights into heavy precipitation forecasts for future studies.

5.2.2. Mean Value Analysis over Different Seasons

The above analysis primarily focused on the overall performance of the considered variables and precipitation record. However, on account of the rapid-changing characteristics contained in GNSS and meteorological variables, their performance vary greatly in different periods, e.g., different seasons. Therefore, to test the seasonal response of the ten variables to precipitation, the 12-year period was divided into four parts, representing the four seasons of spring (from March to May), summer (from June to August), autumn (from September to November) and winter (from December to February). Same as the first three schemes shown in Table 6, the mean values of the ten variables under the three different precipitation scenarios for the four seasons are listed in

Table 8. Mean values obtained under different precipitation circumstances in the four seasons over the 12-year period 2008–2019.

Season	Time Period	No. of Epochs	ZTD (mm)	PWV (mm)	T (°C)	WBT (°C)	DPT (°C)	P (hPa)	Wd (°)	Ws (m/s)	Cloud (%)	SR (MJ/m2)
Spring	All the epochs	25,651	2575.21	43.55	23.38	20.46	19.11	1010.28	141.22	2.46	75.36	0.54
	Epochs with no precipitation	23,508	2571.04	42.83	23.44	20.42	18.98	1010.40	141.74	2.45	73.91	0.58
	Epochs with precipitation	2143	2620.99	51.40	22.72	20.89	20.52	1008.98	135.52	2.54	91.28	0.15
Summer	All the epochs	24,822	2643.12	57.93	29.04	26.00	24.96	1002.88	191.34	2.25	72.67	0.69
	Epochs with no precipitation	21,140	2636.81	56.88	29.24	26.11	24.96	1002.98	194.71	2.20	69.86	0.77
	Epochs with precipitation	3682	2679.38	63.94	27.86	25.40	24.99	1002.32	172.03	2.54	88.83	0.27
Autumn	All the epochs	25,455	2576.18	43.84	25.98	21.83	19.90	1010.51	114.45	2.49	62.98	0.60
	Epochs with no precipitation	23,659	2570.70	42.88	26.01	21.73	19.69	1010.70	113.94	2.46	60.96	0.63
	Epochs with precipitation	1796	2648.32	56.48	25.62	23.14	22.65	1008.04	121.24	2.93	89.63	0.18
Winter	All the epochs	25,534	2483.37	25.82	17.36	13.83	11.04	1016.90	103.41	2.31	64.84	0.45
	Epochs with no precipitation	24,456	2480.97	25.42	17.44	13.82	10.94	1016.95	103.53	2.31	68.60	0.47
	Epochs with precipitation	1078	2537.81	34.82	15.48	13.96	13.29	1015.79	100.64	2.23	92.97	0.10

.

First, by evaluating the column representing the number of epochs, it is obvious that the summer has the most precipitation, followed by spring and autumn, while the winter has the least. Secondly, from the mean value analysis using data over the whole period, the variation characteristics of the ten variables in response to precipitation have been revealed. However, some different phenomena about the variables of T, WBT, W_d and W_s are newly discovered from Table 8 (see those figures in bold type). According to the conclusion obtained before, the mean values of the variables T, WBT, W_d and W_s calculated using data collected at epochs with precipitation should be larger than those obtained corresponding to the epochs with no precipitation. However, the performance of T in the four seasons are totally opposite to the previous conclusion, i.e., the values of T tend to be smaller when there is a precipitation event irrespective of the season. The possible reason for this conflicting result is possibly due to the number of epochs included in the calculation. To be clear, compared with the number of epochs with no precipitation, the epochs with precipitation are only few; compared with the summer season, the other three seasons all have quite less precipitation. Therefore, these make the mean values of T shown in Table 6 convey an apparent conflicting result; this finding also highlights the role and effectiveness of analyzing their performance in different seasons. Similar phenomena can also be observed in the variables of WBT and W_s in the seasons of summer and winter, respectively. In terms of W_d, although its mean values in different seasons vary greatly, it is shown that this region is greatly affected by southeastern wind in the four seasons. Furthermore, as stated in Section 4.1, affected by the Asian summer monsoon, southern wind is the most common type in the summer season.

To explore the precursory information of precipitation contained in the variables over different periods,

Table 9. Comparison of mean values obtained at the 6 h and 12 h periods prior to heavy precipitation in the four seasons over the 12-year period 2008–2019.

Season	Time Period	No. of Epochs	ZTD (mm)	PWV (mm)	T (°C)	WBT (°C)	DPT (°C)	P (hPa)	Wd (°)	Ws (m/s)	Cloud (%)	SR (MJ/m2)
Spring	Epochs with heavy precipitation	152	2643.34	56.13	24.08	22.43	22.28	1006.32	183.82	2.41	95.49	0.06
	6 h periods prior to heavy precipitation	649	2644.35	56.17	23.91	22.98	22.53	1006.51	163.79	2.50	90.44	0.30
	12 h periods prior to heavy precipitation	1205	2649.97	57.14	24.04	23.01	22.47	1006.52	156.71	2.52	88.15	0.39
Summer	Epochs with heavy precipitation	411	2688.21	65.34	27.29	24.81	24.60	1002.25	187.15	2.94	92.99	0.09
	6 h periods prior to heavy precipitation	1720	2690.03	65.70	27.27	25.54	25.06	1002.01	175.97	2.67	88.37	0.25
	12 h periods prior to heavy precipitation	3040	2691.04	65.93	27.24	25.69	25.04	1001.91	175.61	2.60	86.41	0.41
Autumn	Epochs with heavy precipitation	152	2667.87	60.92	26.61	24.23	24.02	1004.96	145.07	4.12	93.51	0.11
	6 h periods prior to heavy precipitation	612	2670.44	61.23	26.72	24.60	23.96	1005.25	145.58	3.60	88.06	0.29
	12 h periods prior to heavy precipitation	1069	2671.61	61.39	26.68	24.66	23.82	1005.38	144.40	3.30	84.69	0.41
Winter	Epochs with heavy precipitation	7	2563.06	39.45	18.86	17.63	17.50	1014.81	170.00	2.40	98.29	0.08
	6 h periods prior to heavy precipitation	37	2566.45	40.54	19.21	17.43	17.16	1013.92	123.97	3.71	94.78	0.16
	12 h periods prior to heavy precipitation	73	2580.42	42.56	18.87	17.21	16.83	1013.99	117.81	3.70	93.07	0.18

lists the mean values calculated using data collected at the 6 h and 12 h periods prior to heavy precipitation, in the four seasons. The mean values obtained during the occurrences of heavy precipitation were also shown in Table 8 for comparison.

As shown in Table 9, many new findings can be obtained. Firstly, the statistics about the number of epochs with heavy precipitation further corroborates the results obtained from Table 8. In terms of heavy precipitation, the number of epochs in the summer season (411) is even larger than the total of those from the other three seasons (152, 152 and 7 for spring, autumn and winter, respectively). Secondly, it can be found that the performance of ZTD, PWV, cloud and SR in the four seasons are all consistent with their respective principles concluded from Table 7. It indicates that these four variables have roughly consistent responses to heavy precipitation throughout the whole year.

For the other types of variables, the figures in bold type show that their seasonal performance is different from the principles obtained before. For example, as stated in Section 5.1, there is an obvious inflection point contained in the series of WBT about 6–12 h before the onset of heavy precipitation. This is particularly true in spring, summer and autumn. However, the value of WBT is likely to continuously increase with the onset of heavy precipitation in winter, which is also the same case for reflecting the time series of DPT in autumn and winter seasons. With regard to T and P, their performance in the three seasons, except summer, deviates from their respective variation principles. For the W_d, its resultant responses to heavy precipitation in autumn is quite similar to the overall principle of DPT, i.e., a possible inflection point may lie in its time series in the range of 0–6 h prior to heavy precipitation. Lastly, it can also be seen from this table that the general rule obtained from the use of the whole dataset perfectly represents the performance of all the ten variables in summer season. This is largely due to the fact that heavy precipitation frequently happens in summer; thus, by using more data obtained in the summer in the calculation of mean values, the overall performances are considerably affected.

Therefore, based on the analyses, it can be concluded that it is quite difficult to find a general rule to adequately represent the responses of different variables to precipitation. Furthermore, it is also not very practical to establish only one unified model to achieve better forecasting of heavy precipitation throughout the whole year. In a sense, these findings also explain why our previous studies focus on developing models to detect heavy precipitation events only in the summer months [42].

6. Principal Component Analysis

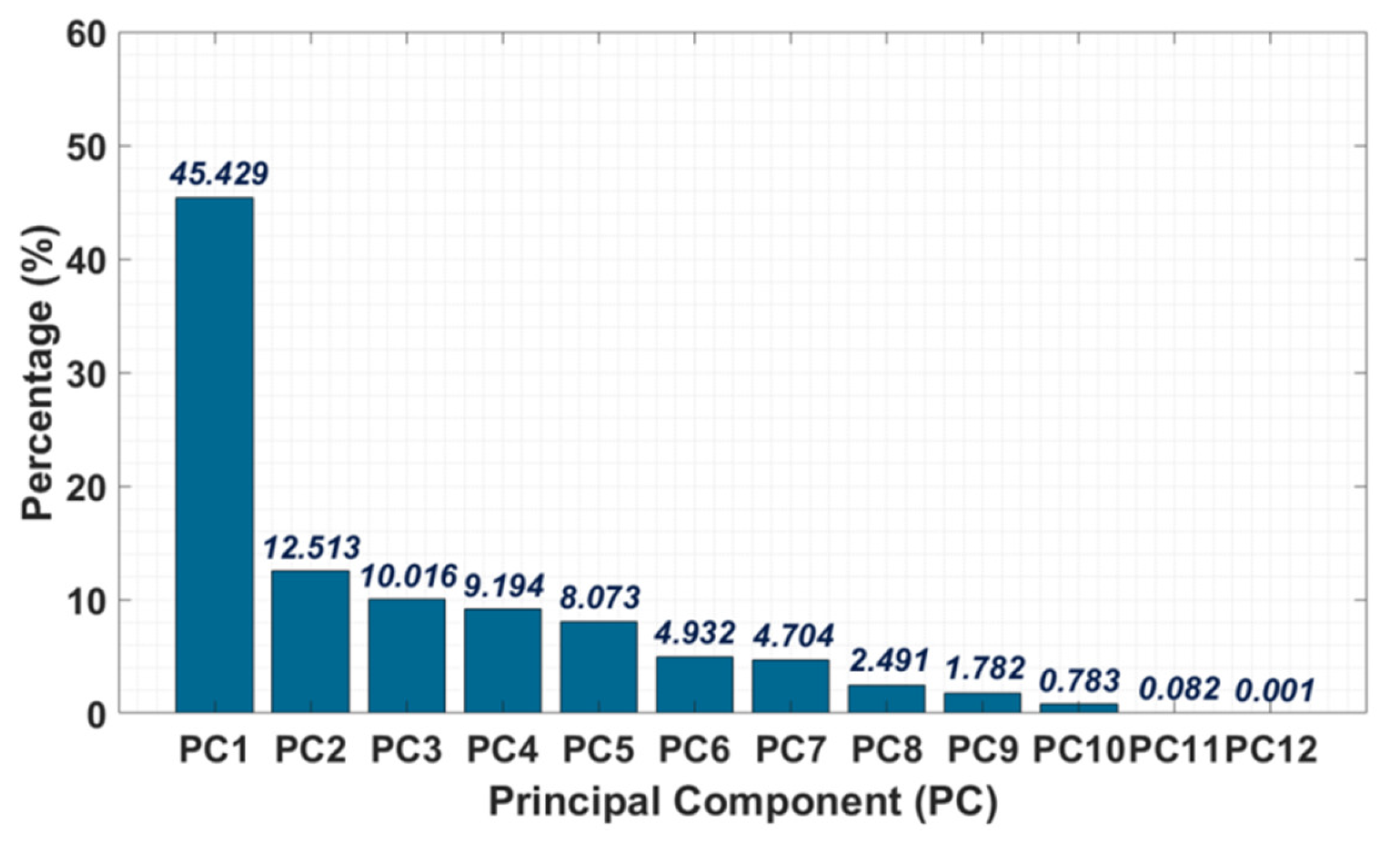
6.1. Variances Interpreted by Principal Components

The PCA method, which is often taken as a preparatory data processing step prior to the construction of any predictive models [24,77], was also adopted in this study to determine whether precipitation of different intensities can be effectively distinguished using the twelve variables. Firstly, by using the methods described in Section 3.4, i.e., Equations (9)–(11), Figure 4 shows the proportions of the total variance interpreted by each of the twelve PCs calculated in this study.

It can be seen from Figure 4 that the first PC, named PC1 in this study, accounts for 45.429% of the total variance, and the first five PCs together contributed 85.225% of the total variance. Since it is widely accepted that if the accumulated percentage of variance explained by the first few PCs reach the threshold of 85%, these PCs can be taken as the major ones for analyzing variable loadings [87,88,89]. Therefore, the first five PCs are taken as the major PCs in this study.

6.2. Analysis of Variable Loadings in Principal Components

As mentioned above, to determine the significance of each of the twelve variables to the whole dataset, the variable loadings in those major PCs should be analyzed. Hence, based on the five major PCs (PC1–5), loadings interpreted by each variable are listed in Figure 5.

The interpretation method for the variable loadings shown in Figure 5 is similar to that of PCC stated in Section 3. A positive loading value in a PC implies the variable is positively correlated with the PC, and vice versa. From the other aspect of data value, a larger loading value indicates that the variable has a stronger impact on the PC. Based on these principles, a loading threshold (denoted by “TH” shown in Figure 5) needs to be defined as a standard for deciding whether a variable can be regarded as a major factor for a PC. In this study, as suggested by [77], the loading threshold was simply determined based on the number of variables (n) using:

$$TH=\sqrt{1/n},$$

(12)

Since the value of n was set to 12, the loading threshold determined for this study is 0.289. The loading values that are above the threshold are also displayed in Figure 5. In the applications of PCA, each PC generally represents a unique phenomenon. It can be seen from Figure 5 that the six major variables of WBT, DPT, ZTD, PWV, T and P have greater impacts on the most critical component, i.e., PC1. Among the six variables, apart from P, all the others possess large positive values. This phenomenon is comprehensible for a precipitation case, especially a heavy precipitation event (as shown in Table 6), that WBT, DPT, ZTD, PWV and T values all increase prior to and during the occurrence of precipitation events, while P tends to drop. From another aspect, as stated in Section 4.1, the six variables are also those with high cross-correlativity. With regard to the second PC, only the values of SR and cloud were above the TH value. Their values with different signs not only confirm their opposite correlations, but also exactly reveal the phenomenon that they have opposite performances during the passing of precipitation events. Similarly, large loadings of HOD, W_s and SR are observed in PC3, which mainly reflects the diurnal variation of W_s and SR. The other major PCs (PC4–5) have the same two variables: DOY and HOD with stronger impacts. This might be useful in the interpretation of the temporal dependency of W_d, SR and precipitation events, e.g., most heavy precipitation events take place in the summer season according to statistics.

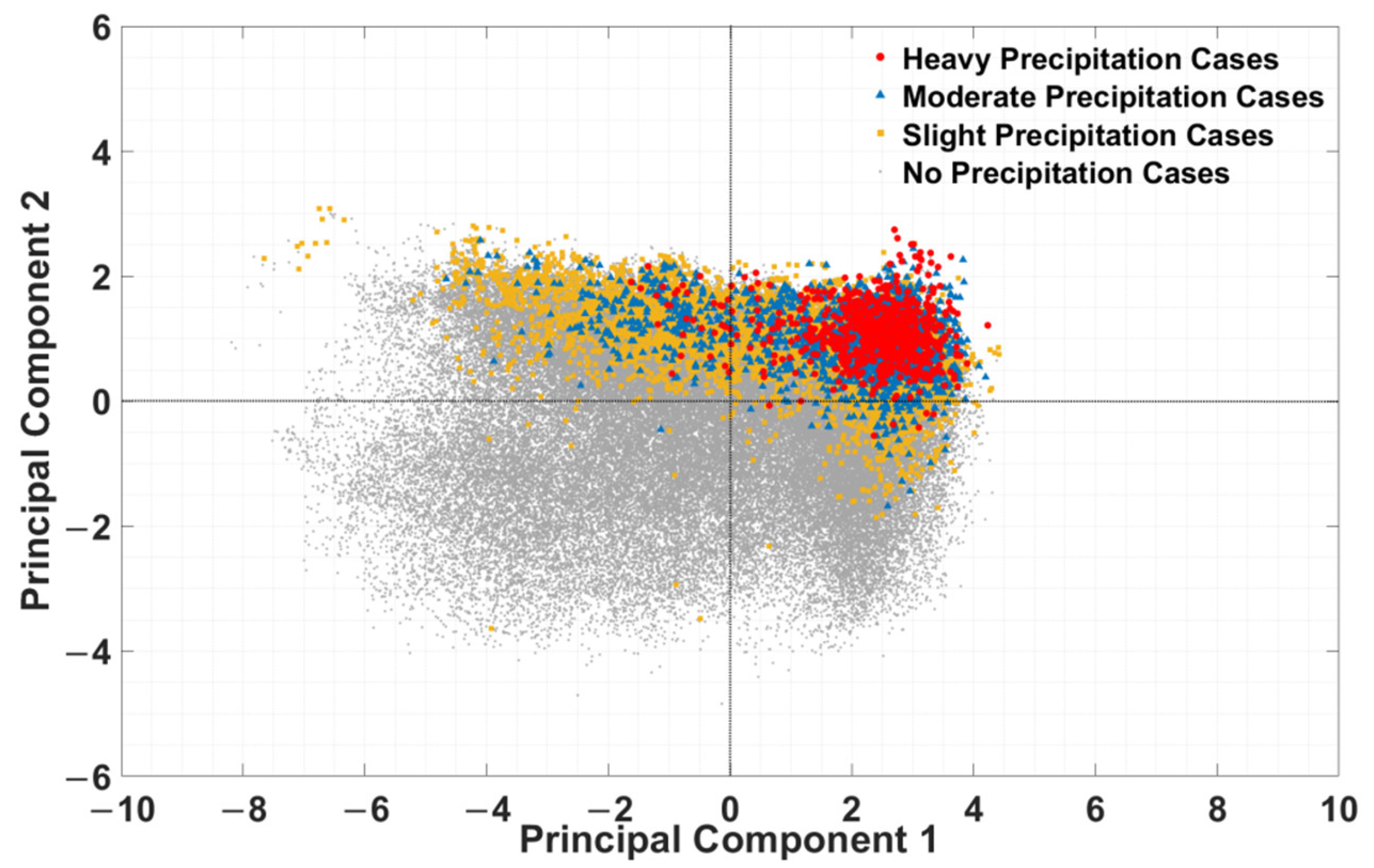
6.3. Potential of Using the Twelve Variables for Precipitation Discrimination

For an overall analysis, Figure 6 depicts the biplot representation of the twelve variables and the dimension of the whole dataset has been reduced to the two major PCs (PC1 and PC2), as shown in the two axes. The use of the first two major PCs is mainly on account of the fact that they account for 57.942% of the total variance, and so are recognized as the most important PCs. In addition, in accordance with the characteristics of the biplot representation, the results can only be displayed in the plane formed by the first two PCs [90]. The correlations between any two of the twelve variables can be found from the figure, e.g., WBT and P are negatively correlated and ZTD and PWV are positively correlated, which are the same as the analyses using PCC and SCC in Section 4.

With the distribution of these variables with respect to the first two PCs, the final step is to test the feasibility of using the twelve variables to discriminate precipitation events and their intensities. As conducted above, the original data matrix should be firstly reduced to a 2-dimensional (2D) matrix projected by the two major PCs similar to Figure 6. To be clear, the dimension reduction practice is conducted by multiplying the 101,462 × 12 normalized matrix $\widehat{X}$ by the first two columns of the eigenvector matrix of $Cov\left(\widehat{X}\right)$; i.e., PC1 and PC2. The obtained 101,462 × 2 matrix can be interpreted geometrically as the projection of the observations onto the first two PCs. Then, according to the actual precipitation record, all the samples over the whole 12-year study period can be classified into four categories, representing the heavy, moderate, slight and no precipitation cases. Figure 7 depicts the samples in the new 2D subspace for separating precipitation cases of different intensities.

Figure 7 indicates that the 2D subspace can effectively distinguish the four precipitation cases, especially the heavy precipitation cases. Compared with the distributions of the twelve variables shown in Figure 6, the distributions of the sample data representing heavy precipitation cases mainly concentrated in the upper-right corner, which is similar to the distribution trends of the three variables of PWV, ZTD and cloud. The finding emphasizes the fact that although the twelve variables could all contribute to the application of heavy precipitation classification, the three variables PWV, ZTD and cloud play more prominent roles, which corroborates the results analyzed above as well.

7. Summary and Discussion

In this study, the inter-relationships among twelve types of variables were comprehensively analyzed. Then, the responses of the twelve variables to precipitation were also systematically investigated. Finally, with the use of PCA method, this study tested whether these variables have the potential to effectively separate precipitation of different intensities. The variables adopted in this study include eight weather variables of T, P, WBT, DPT, SR, cloud, W_s and W_d, as well as two GNSS atmospheric products of ZTD and PWV and two statistical time-varying parameters of DOY and HOD. The time series of the variables and their corresponding hourly precipitation record over the 12-year study period 2008–2019 were collected at a pair of co-located GNSS/weather stations, i.e., the HKSC-KP stations, employed in the Hong Kong region.

At the first stage, a cross-correlation analysis was conducted to investigate the internal relationships among all the twelve variables. With the use of PCC, not only the correlations among these variables were clearly presented, but also their relationships were interpreted from the perspective of atmospheric physics. It was shown that the variables of ZTD, PWV, T, WBT, DPT and P have closer cross-correlativity. Motivated by the fact that all the variables used in this study are time series data, the metric of SCC was also adopted to further consider their rankings and distributions. By analyzing the signs of SCC results, the variation directions of these variables were revealed, e.g., P generally has opposite variation trends with nearly all the other variables. Since correlation analysis mainly evaluates the linear relationship, regression analysis was then employed to investigate their nonlinear relationships. By testing the nonlinear functions of polynomial, logarithmic, natural exponential and power functions, the optimal forms for fitting the relationship between each two sets of time series were determined.

At the second stage, we conducted a comprehensive investigation of the responses of the twelve variables to precipitation. The main conclusions are listed as follows:

• The conventional correlation analysis performed in this study not only took the original hourly precipitation amount record as the target data, two sets of new records indicating the occurrence of heavy precipitation and precipitation intensity were reorganized and involved in this analysis. From an overall perspective, the variables of ZTD, PWV and cloud have more evident correlations with precipitation. It was observed that the highest PCC values were all obtained from the comparisons with the record of precipitation intensity. Furthermore, the SCCs are generally all larger than their corresponding PCCs. These therefore indicate that it is important to take the precipitation intensity into account to obtain better performances. In addition, if the variables were used for precipitation forecasts without the use of NWP models, it would be better and more reasonable to conduct qualitative detection rather than quantitative prediction. Moreover, the variation directions of HOD, P and SR were proven to be different from that of precipitation amount.
• To investigate whether there is effective precursory information contained in the time series of the variables, this study extended the correlation analysis to test the PCCs obtained by using precipitation record moving several hours forward. The results can also provide valuable information about the lead times for precipitation forecasts. For example, it was found that the lead time of using ZTD and PWV to detect precipitation was approximately 8 h; similarly, the lead times for WBT, DPT and W_s are in the ranges of 5–8 h, 2–4 h and 7 h, respectively.
• By conducting the regression analysis, it was discovered that the optimal nonlinear function for fitting the relationship between each variable and precipitation record is the quadratic polynomial function.
• The mean value analysis was employed to capture the performances of variables in different precipitation scenarios, and to test their respective precursory information of heavy precipitation. By evaluating the data over the whole study period, it was found that, apart from the variables P and SR, the higher the precipitation intensity, the larger the variable values. From the analysis of the precursory information contained in each variable with respect to heavy precipitation, the inflection points in their series and their lead times for precipitation forecasts were obtained. With the use of GNSS products, the possible lead time for heavy precipitation detection is about 8 h.
• The seasonal responses of the variables to precipitation were analyzed. According to the statistics, summer has the most precipitation events, followed by spring, autumn and winter. By evaluating the performances of each variable in different seasons, it can be found that it is quite difficult to find a general rule to represent the responses of different variables to precipitation. Over different study periods in different study regions, a comprehensive analysis of variables should be conducted before developing any type of precipitation prediction model.

At the final stage, after reducing the original data matrix to a 2D subspace by using the PCA method, it was shown that precipitation, especially heavy precipitation cases, can be effectively distinguished using the whole dataset. Among all the variables, PWV, ZTD and cloud play more prominent roles in heavy precipitation classification. Overall, many findings from this study have the potential to help researchers in the profession to form a better and more systematic understanding of the intrinsic nature of the formation of precipitation and the effectiveness of using these variables to detect precipitation. Moreover, these findings could also provide useful clues for the development of models for precipitation forecasts. It is worth mentioning that some findings from this study are largely linked to the selected study region (location and climate conditions) and study period. Our future studies will be focusing on conducting these analyses in other regions using multiple variables (additional variables of air density, integrated liquid water and infrared brightness temperature will also be included) collected at more GNSS/weather stations over a longer-term period. In addition, our ongoing research will also effectively apply the findings from this study to develop more robust and reliable models for heavy precipitation predictions.