Next Article in Journal
The Influencing Mechanism of Urban Travel Carbon Emissions from the Perspective of Built Environment: The Case of Guangzhou, China
Next Article in Special Issue
Influences of the Mid-Level Vortex on the Formation of Tropical Cyclone Toraji (2013)
Previous Article in Journal
Impacts of Pollutant Emissions from Typical Petrochemical Enterprises on Air Quality in the North China Plain
Previous Article in Special Issue
Strategy for the Prediction of Typhoon Wind and Storm Surge Height Using the Parametric Typhoon Model: Case Study for Hinnamnor in 2022
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 14
Issue 3
10.3390/atmos14030546
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Seasonality of Relationship between Tropical Cyclone Frequency over the Southern Hemisphere and Tropical Climate Modes

by
Tomomichi Ogata
Japan Agency for Marine-Earth Science and Technology, Yokohama 236-0001, Japan
Atmosphere 2023, 14(3), 546; https://doi.org/10.3390/atmos14030546
Submission received: 17 January 2023 / Revised: 28 February 2023 / Accepted: 9 March 2023 / Published: 13 March 2023
(This article belongs to the Special Issue Typhoon/Hurricane Dynamics and Prediction)
Browse Figures
Versions Notes

Abstract

In this study, the author examined the tropical cyclone (TC) activity over the southern hemisphere (SH) and its relationship with tropical climate modes, such as the El Niño–Southern Oscillation (ENSO), during the austral summer (December–January–February; DJF) and fall (March–April–May; MAM). The correlation analysis between the TC activity and the global sea surface temperature (SST) suggested that an increased TC activity over the southwestern and southeastern Indian Ocean (SWIO and SEIO) was associated with a La Niña-like SST pattern, while an increased TC activity over the southwestern Pacific (SWP) was associated with an El Niño-like SST pattern. The atmospheric conditions accompanying the TC increase over the SWIO/SEIO indicated that a La Niña induces tropospheric cooling over the tropics with cyclonic circulation anomalies over the TC genesis region. Both the SST anomalies and the cyclonic circulation anomalies were significantly correlated with TC genesis parameters, suggesting that they contributed to TC genesis. To investigate the SST precursors, a lead-lag correlation analysis was performed. For the TC variations over the SEIO, an SST pattern that resembled the Pacific Meridional Mode (PMM) was statistically significant at a two-season lead. However, such a TC-ENSO relationship is seasonally dependent, with different patterns during DJF and MAM. These results suggest that the Matsuno-Gill response to ENSO is an important factor in TC activity but that this influence is seasonally modulated over the SH.

1. Introduction

Tropical cyclones (TCs) are important extreme weather events that have a socioeconomic impact on populated areas through strong winds and heavy precipitation. Over East Asia and North America, TCs commonly cause socioeconomic damages when they make landfall [1,2,3,4]. In 2013, for example, typhoon Haiyan made landfall in the Philippines as an extreme TC with wind speeds exceeding 80 m/s, and more than 7000 people were reported as either dead or missing. In 2019, typhoon Hagibis caused rainfall of over 1000 mm between 10 and 13 October in Japan, leading to the death of ~100 people and the loss of USD 5 billion by flooding. In the autumn of 2020, frequent TC activity caused considerable flooding over Vietnam, thus leaving approximately 200 people dead and resulting in economic losses totaling USD 1.5 billion. To mitigate such impacts, it is vital to improve the predictive skill of forecast models. This requires a deeper understanding of the regional features of TC activity [5,6].
TCs are not limited to the northern hemisphere (NH) but also occur in the southern hemisphere (SH). In 2016, Cyclone Winston was recorded as an extreme TC with wind speeds exceeding 80 m/s when it made landfall in Fiji. It caused the death of approximately 50 people and the loss of USD 1.4 billion. In 2022, Cyclone Batsirai, with a central pressure of 930 hPa and wind speeds of 70 m/s, approached Madagascar, causing the death of about 100 people and the loss of USD 190 million.
The tropical oceans show variability on interannual time scales that are associated with tropical climate modes, such as El Niño, the Indian Ocean Dipole (IOD) [7], and El Niño Modoki [8]. Previous studies have revealed that these climate modes influence both TC genesis and TC activity over the tropical Pacific on interannual times scales [9,10]. For example, during the canonical El Niño events, SSTs warm over the eastern equatorial Pacific (often measured using the Niño-3 index, which is defined as the area average of SST over the area 5° S–5° N, 90–150° W). This contributes to an east–west shift in the TC frequency (TCF), which depends on both TC genesis and subsequent development. The El Niño Modoki events, on the other hand, lead to a basin-wide increase in the TCF over the western north Pacific (WNP) in observation [10]. Furthermore, the contribution of the Pacific meridional mode (PMM) [11] has been investigated [12,13,14,15]. Using ensemble simulations [16,17], our previous studies have investigated the influence of SST on the potential predictability of TC activity and its seasonality.
Similar to the NH, TC activity over the SH and its relationship with tropical climate modes have been examined in previous studies [18,19]. These have shown that, during El Niño events, TC tracks tend to extend further eastward over the southwestern Pacific (SWP), while their activity decreases in the southeastern Indian Ocean (SEIO). The El Niño events also contribute to subsurface warming over the southwestern Indian Ocean (SWIO), which may lead to an increased TC activity over the SWIO [20]. In addition, recent studies have pointed out that the negative IOD is associated with an increased TC activity over the SEIO [21]. In the SWP, previous studies [22,23,24] have suggested that ENSO can contribute to the interannual variability of the TC activity over the SWP through the variability of the South Pacific Convergence Zone (SPCZ). Recent studies [25,26] have also revealed the impact of ENSO diversity on TC activity over the SWP. For example, El Niño Modoki (or CP El Niño) has the largest influence on TC formation over the SWP. In the SIO, previous studies have investigated the TC-ENSO relationship [27,28,29]. In their studies, an increase in TC frequency in the SEIO can be seen in the developing La Niña events.
As mentioned above, the air-sea variability by tropical climate modes is important for the TC variability through environmental change. In the atmospheric response to ENSO, the Walker circulation can affect the low convective activity over the western Pacific [29,30]. In addition, the Walker circulation in response to ENSO can also impact the tropical IO; one impact is on the IO basin-wide warming [31,32], and another is on the IOD [33,34]. For the IO basin-wide warming, SWIO thermocline deepening is important for maintaining the atmospheric response [35,36,37]. It should be noted that although the IOD is often triggered by an ENSO as an inter-basin interaction, the IOD is recognized as an independent mode [7,38].
Most previous studies have not examined the seasonality of these linkages. For example, most previous studies jointly analyzed the austral summer and fall (November-May). It is well known, however, that the ENSO and the IOD have strong seasonality. For example, an ENSO is triggered by the westerly wind burst (WWB) during March-April-May (MAM), grows from June-July-August (JJA) to September-October-November (SON) and matures in December-January-February (DJF). The IOD is typically triggered during MAM, grows during JJA, and matures during SON. This seasonal dependence of the tropical climate modes can be expected to modulate their impacts on TC activity. To this end, the present study investigates the differences in the interannual relationship between the austral summer (DJF) and fall (MAM).
In this study, to focus on how TC activity is related to tropical climate variability over the SH, the author examined the TC activity over the SH and its relationship with the global SST and circulation anomalies, both of which play an important role in TC genesis. To highlight the impacts of climate modes (El Niño, IOD, and El Niño Modoki) as precursors of TC activity, a lead-lag correlation analysis was also conducted.

2. Methods

In this study, the seasonal climatology of TCF was used, which is defined as the number of TC tracks (segment of the TC trajectory) that falls within a 5° × 5° bin during one season. This was computed from observations and made available by the IBTrACS project [39]. For comparison with the simulated climatological and year-to-year environmental fields, the NCEP/NCAR Reanalysis 1 dataset was used [40]. For ocean datasets, monthly Optimally Interpolated Sea Surface Temperature (OISST) analysis [41] was used. As a proxy for subsurface thermocline variability, sea surface height (SSH) from the NCEP Global Ocean Data Assimilation System (GODAS) was used [42]. The analysis period was from 1983–2020. In order to extract low-frequency variabilities such as linear trends and decadal variability, a 7-year high-pass filter was applied to focus on the interannual variability.
Figure 1 shows the seasonal climatology of TCF over the SH. DJF is the peak season (Figure 1b), and the TCF during MAM is smaller, but there is some activity over the SH (Figure 1c). The TCF during SON is very low (Figure 1a). In light of this seasonality, DJF and MAM are focused. In addition, there are three regional peaks around 60° E (western Indian Ocean), 110° E (eastern Indian Ocean), and 160° E (western Pacific). Accordingly, three areas are defined: SWIO (10–30° S, 40–70° E), SEIO (10–30° S, 90–120° E), and SWP (10–30° S, 150–180° E). The TCF is averaged over these areas and correlated with the resulting indices with oceanic and atmospheric variables.
As mentioned in the Introduction, several climate modes have been identified in the tropics, each with distinct influences on TCF variability. These modes are characterized using the Niño-3 index, the Dipole Mode Index (DMI), and the El Niño Modoki Index (EMI). The Niño-3 index is defined as the SST averaged over 5° S–5° N and 90°–150° W, whereas the DMI is defined as the SST difference of the western box (10° S–10° N, 50°–70° E) minus the eastern box (0–10° S, 90°–110° E). The EMI is defined as SSTA-0.5 × SSTB–0.5 × SSTC, where SSTA is the central equatorial Pacific (averaged over 10° S–10° N, 165° E–140° W), SSTB is the eastern equatorial Pacific (15° S–5° N, 70–110° W), and SSTC is the western equatorial Pacific (10° S–20° N, 125–145° E). These indices were derived from monthly SST anomalies from 1983–2020.

3. Observed Relationship between TC Frequency and Global Circulation

3.1. Comparison of Observed TCF and SST/SSH

Figure 2 shows the correlation map between anomalies of the TCF over the SWIO and the global SST (left panels) and SSH (right panels). The SSH variability in the tropics is considered to resemble the subsurface thermocline variability [43,44]. Actually, Figure 3 of Trenary and Han (2012) shows a good agreement between the SSH and 20 °C subsurface thermocline anomalies [44]. During DJF, there is a negative correlation over the equatorial Pacific, resembling a La Niña (Figure 2a). The SSH correlation pattern (Figure 2b) also shows negative (positive) values in the eastern (western) equatorial Pacific, consistent with La Niña conditions. During MAM, compared with the DJF case, the La Niña-like negative correlation over the equatorial Pacific associated with the SWIO TCF variability (Figure 2c) becomes more significant. Similar to the SST, the SSH correlation pattern (Figure 2d) also becomes more significant, negative (positive) in the eastern (western) equatorial Pacific as a feature of the La Niña. On the other hand, the contribution of the Indian Ocean SST and SSH is not significant. Previous studies have indicated that both the positive phase of the IOD and El Niño led to subsurface warming (and therefore thermocline deepening and positive SSH anomalies) in the SWIO. Therefore, the remote impacts from La Niña may counteract the local SWIO subsurface warming. This point will be discussed in Section 4.
Figure 3 shows the correlation maps between the TCF in the SEIO and the global SST (left panels) and SSH (right panels). During DJF, the correlation patterns indicate that an increased TCF in the SEIO is associated with La Niña-like conditions in the tropical Pacific. The patterns are similar to those in Figure 2 but more pronounced (Figure 3a,b). These patterns weaken during MAM. The results suggest that the TC activity in the SEIO is related to La Niña during both DJF and MAM, but there is a significant seasonality as the relationship between the TCF and ENSO is much clearer during DJF than MAM.
Figure 4 shows the correlation map between TCF anomalies in the SWP and SST (left panels) and SSH (right panels). During DJF, the most unique feature is the negative correlation over the western equatorial Pacific (west of the dateline; Figure 4a) and the negative SSH correlation (Figure 4b) in the western equatorial Pacific. The correlations are weak but statistically significant, and they indicate that an increased TCF in the SWP is associated with El Niño-like conditions. This is in contrast to the SWIO (Figure 2) and SEIO (Figure 3), where an increased TCF is associated with La Niña-like conditions. During MAM, the SSH correlation pattern becomes more pronounced (Figure 4d). It may resemble a feature of triggering an El Niño by warm Kelvin wave propagation. These results suggest that TC activity in the SWP shows significant seasonality; an increased SWP TCF is associated with cold SST anomalies in the western equatorial Pacific (positive SSH anomalies in the eastern equatorial Pacific) during DJF (MAM).

3.2. Comparison of Atmospheric Conditions

Large-scale atmospheric conditions are an important factor in TC activity. Previous studies have identified several atmospheric conditions that are key to TC genesis [45,46]. In this section, the relationship between the TCF and atmospheric circulation patterns is investigated. Figure 5 shows the correlation map between the TCF in the SWIO and z850 (left panels) and tropospheric thickness (z200-z850; right panels). During DJF, a significant negative correlation resembling the Matsuno-Gill pattern [47,48] can be seen in the Indian Ocean and western Pacific (Figure 5a), indicating a response to the increased diabatic heating over the Maritime Continent (MC) during La Niña. Another unique feature is the negative correlation with tropospheric thickness anomalies (Figure 5b) across the tropics. Such a negative tropospheric anomaly (tropospheric cooling) is expected to be more convectively unstable, which is favorable for the TC genesis. Compared to DJF, the negative correlation pattern in z850 (cyclonic Matsuno-Gill-like pattern) and tropospheric thickness (tropospheric cooling) becomes less significant during MAM (Figure 5c,d). These results suggest that the atmospheric response to ENSO shows significant seasonality; the atmospheric response is significant (less clear) during DJF as the ENSO mature phase (MAM as ENSO decay phase). As a result, the SWIO TCF variability is significantly related to a negative Matsuno-Gill-like anomaly in response to La Niña, but seasonal differences can be seen during DJF and MAM.
Figure 6 shows the correlation map between TCF in the SEIO and z850 (left panels) and tropospheric thickness (z200-z850; right panels). During DJF, a negative correlation pattern is significant and very clear in the Indian Ocean and western Pacific (Figure 6a), which is consistent with the Matsuno-Gill-like response to increased diabatic heating over the MC during La Niña. In addition, the negative correlation pattern of the tropospheric thickness (Figure 6b) in the tropics is also very pronounced. Such a negative correlation pattern of the tropospheric thickness (tropospheric cooling) is expected to be more convectively unstable, which is favorable for the TC genesis. Compared to DJF, the negative correlation pattern in z850 and tropospheric thickness (Figure 6c,d) becomes less significant during MAM. These results suggest that the SEIO TCF variability is significantly related to a negative Matsuno-Gill-like anomaly in response to La Niña during both DJF and MAM, but the signal is more pronounced during DJF than MAM.
Figure 7 shows the correlation map between TCF in the SWP and z850 (left panels) and tropospheric thickness (z200-z850; right panels). The features in the SWP TCF case in Figure 6 are very different from those in the SWIO (Figure 5) and SEIO (Figure 6) cases. During DJF, a positive correlation resembling an anticyclonic anomaly is significant in the northwestern Pacific (Figure 7a), which is consistent with the southward divergent wind anomalies over the western equatorial Pacific. A correlation map of the tropospheric thickness (Figure 7b), on the other hand, does not show any clear patterns in the tropics. The anticyclonic signal seen in Figure 7a may play an important role in the negative SST signal in the western equatorial Pacific (Figure 4a) through negative heat flux anomalies (defined as downward positive) caused by an increased wind speed. This point will be discussed in Section 4. During MAM, the circulation patterns change drastically, with a positive (negative) signal in z850 (tropospheric thickness) resembling a Matsuno-Gill-like response (anticyclonic z850 and tropospheric cooling; Figure 7c,d) over the tropical Indian Ocean. To the east of the Masuno-Gill pattern, divergent westerly winds are expected. Therefore, westerly anomalies over the equatorial Pacific may form a cyclonic vorticity anomaly, which is favorable for TC genesis. These results suggest that the atmospheric circulation patterns related to the SWP TCF variability are significantly different between DJF and MAM.
As mentioned before, previous studies have identified several atmospheric variables as the key parameters in TC genesis [45,46]. Table 1 shows the correlation coefficients between the TCF indices and four important parameters that are included in the TC genesis potential index (GPI; [46]): relative vorticity at 850 hPa (Vort850), relative humidity at 600 hPa (RH600), maximum potential intensity (MPI; [49]), and vertical wind shear between 200 and 850 hPa (Ushear). In general, correlations with relative vorticity (Vort850) are significant (except for the SWIO TCF variability in MAM), and, therefore, it seems to play an important role. In contrast, MPI is generally negatively correlated with TCF, and hence, it seems to act as a negative factor. The negative MPI contribution is due to the cold local SST anomalies. The MPI is generally larger over warmer SST [49], which seems consistent with the La Niña-induced Indian Ocean cooling (for the SWIO and SEIO cases) and western Pacific cooling during El Niño (for the SWP case). The contribution from the relative humidity (RH600) shows seasonality, with DJF being significant in contrast to MAM. The seasonal march of the intertropical convergence zone may contribute to this seasonality. In the case of the SWIO TCF during MAM, the contribution from the relative vorticity is very small, and only vertical wind shear (Ushear) contributes positively to TC genesis.
It should be noted that the SST-TCF relationship means that both the “active TCF causes SST cooling” and the “SST warming causes active TCF”. More specifically, the storm passage over the ocean cools down the SST in several days through vertical mixing, entrainment, and Ekman pumping [50,51,52,53]. Therefore, such a short-term air-sea interaction process may cause a cold SST over the active TCF area. Similarly, the vorticity-TCF relationship means that both the “active TCF causes cyclonic vorticity” and the “cyclonic vorticity causes active TCF”. Previous studies have shown that cyclonic vorticity and rainfall anomalies can be formed by individual TCs [16,54]. On the other hand, the NCEP dataset is too coarse, and therefore, previous studies reported that the TC contributions using the NCEP might be too small [16]. Conventionally, most studies did not consider the individual TC feedback to the mean field on the environmental change of TC genesis. In order to prove the impact of the short-term air-sea interaction on the SST-TCF relationship and of the individual TC contributions to the vorticity-TCF relationship, further studies using high-resolution air-sea datasets will be needed.
In addition, the Southern Annular Mode (SAM) is an important factor for the atmospheric variability in the SH [55,56,57]. Figure 8 shows the simultaneous correlation map of z850 (left panels) and z200 (right panels) anomalies to the observed TCF anomaly over the SWIO region (averaged over 10–30° S, 40–70° E). During DJF, a positive SAM structure can be seen in both z200 and z850 (Figure 8a,b). A positive SAM can be interpreted as a degree of decoupling between Antarctica and southern mid-latitude [56], which may contribute to thermodynamically favorable TC genesis conditions. On the other hand, there is no significant annular mode structure during MAM (Figure 8c,d). On the other hand, in the SEIO and SWP cases, there are no significant annular mode structures (figure not shown).

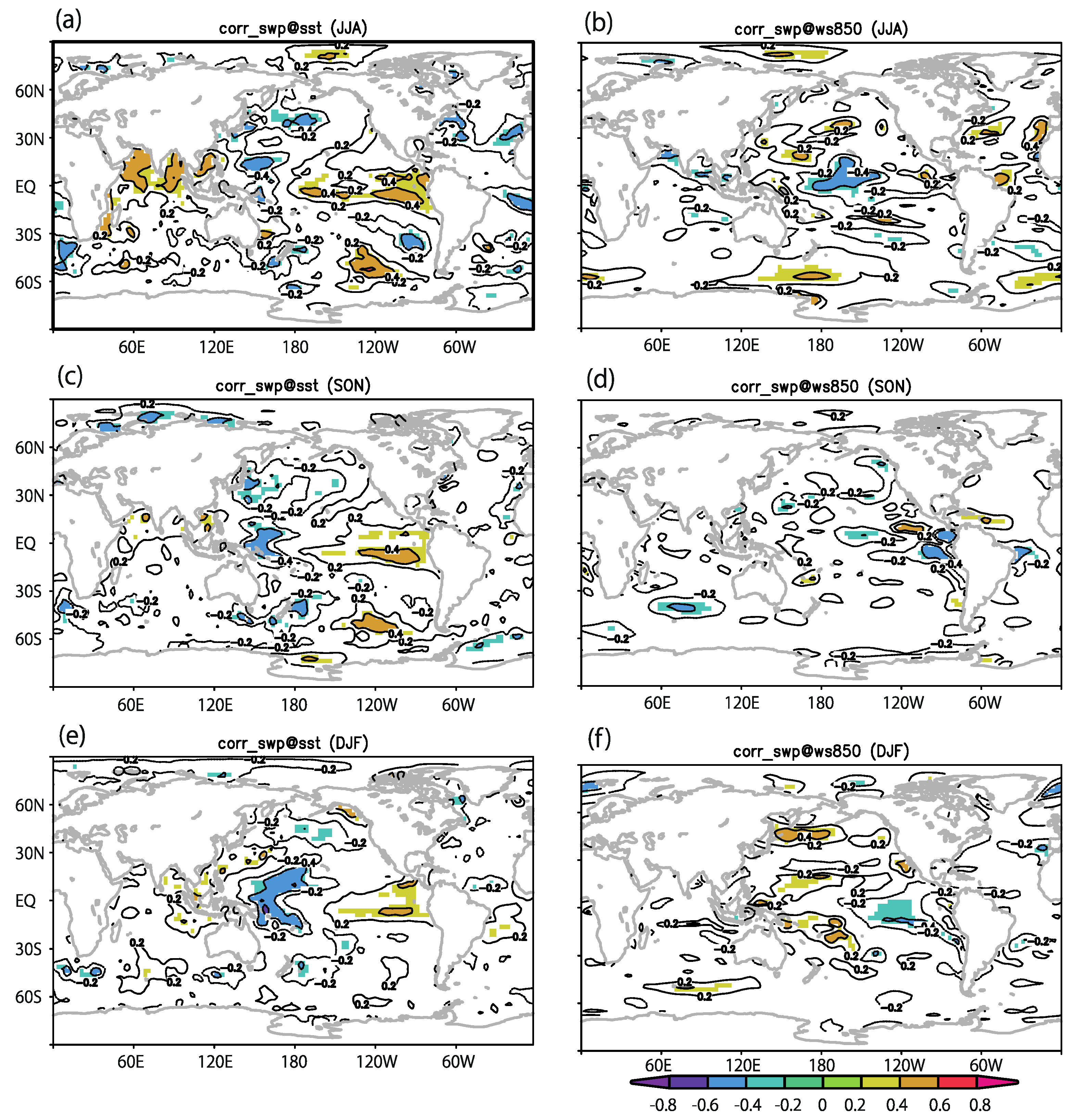
3.3. Possible Precursors of the SH-TCF Variability

In Section 3.1 and Section 3.2, the simultaneous relationships between the TC activity and the global fields were investigated. If signals can be traced back by several seasons, this may allow us to identify the precursors of the TC activity. This is addressed by performing lead-lag correlation analysis. Figure 9 shows the correlation map between the anomalous MAM TCF in the SWIO and the global SST (left panels) and SSH (right panels). At a two-season lead (SON), a negative SST signal appears west of California but is weak (Figure 9a). At a one-season lead (DJF), a warm SST signal appears over the northwestern Pacific (Figure 9c). No precursors are apparent in the lagged SSH correlations (Figure 9b,d).
Figure 10 shows the correlation map between the DJF TCF anomaly over the SEIO and SST (left panels) and SSH (right panels). In contrast to the SWIO case (Figure 9), clear and significant SST and SSH signals can be traced back to two seasons before (JJA), with a significant negative SST signal appearing over the northern tropical Pacific (Figure 10a). At a one-season lead (SON), this negative SST signal moves equatorward and forms a La Niña-like pattern (Figure 10c). Consistent with the development of La Niña, a negative SSH signal becomes pronounced over the equatorial Pacific. At a two-season lead (JJA), a significant negative SSH signal appears over the central equatorial Pacific (Figure 10b). At one season before (SON), this negative SSH signal moves eastward and forms a canonical La Niña-like pattern (Figure 10d). These results suggest that a La Niña is an important precursor for DJF TCF in the SEIO. A recent study has pointed out that there is possible feedback between the CP El Niño events and the PMM [58,59]. The SST precursors seen in Figure 10a,c are consistent with an ENSO event triggered by the PMM. It should also be noted that such SST anomalies over the central North Pacific may be traced back to the so-called seasonal footprint mechanism (SFM) and the PMM during the boreal winter through spring [60,61,62].
Figure 11 shows the correlation map between the anomalous DJF TCF in the SWP and SST (left panels) and SSH (right panels). Compared to the SEIO case (Figure 10), weaker but significant SST and SSH signals can be traced back to a two-season lead time (JJA), with a significantly positive SST signal appearing over the eastern equatorial Pacific that resembles a canonical El Niño (Figure 11a). It should be noted that a significant positive SST signal can be seen over the northern Indian Ocean, suggesting that the El Niño induced Indian Ocean warming. At one-season lead (SON), this positive SST signal still remains over the eastern equatorial Pacific (Figure 11c). Consistent with the El Niño-like SST pattern, there is a zonal SSH dipole in the equatorial Pacific. At a two-season lead (JJA), a significant positive (negative) SSH signal appears over the eastern (western) equatorial Pacific (Figure 11b). This feature persists at the one-season lead (SON; Figure 11d). These results suggest that an El Niño can be regarded as a climate precursor for the DJF TCF in the SWP.
As a summary, Table 2 shows the lead-lag correlation coefficients (R) between all three TCF indices and all three climate indices (Niño-3, EMI, and DMI). In the SWIO, there are no significant correlations. It should be noted that the DJF TCF features a higher correlation with the Niño-3 index (R = −0.31 at the one-season lead and R = −0.31 at the two-season lead) than the MAM TCF (R = −0.23 at the one-season lead and R = −0.17 at the two-season lead), which may be due to the seasonal dependence of the ENSO evolution (DJF is the mature phase while MAM is the decay phase). For the SEIO TCF during DJF, there are statistically significant correlations with the Niño−3 and EMI indices. At the two-season lead (JJA), the correlation with the EMI (R = −0.41) is higher than that with the Niño-3 (R = −0.26). This is consistent with the features seen in Figure 8. During MAM, the simultaneous correlations are not statistically significant, but the Niño-3 index is significantly correlated at the one-season lead (DJF, R = −0.37) and the two-season lead (SON, R = −0.4). This is also consistent with the seasonal dependence of the ENSO evolution. For the SWP TCF during DJF, the simultaneous correlations are not statistically significant, but the Niño-3 index is significantly correlated at the two-season lead (JJA; R = 0.37). This is consistent with the features seen in Figure 11. On the other hand, there is no significant precursor during MAM. These results suggest that the precursor signals depend on regions and seasons and that these relations are affected by the seasonality of large-scale variability patterns such as the ENSO.

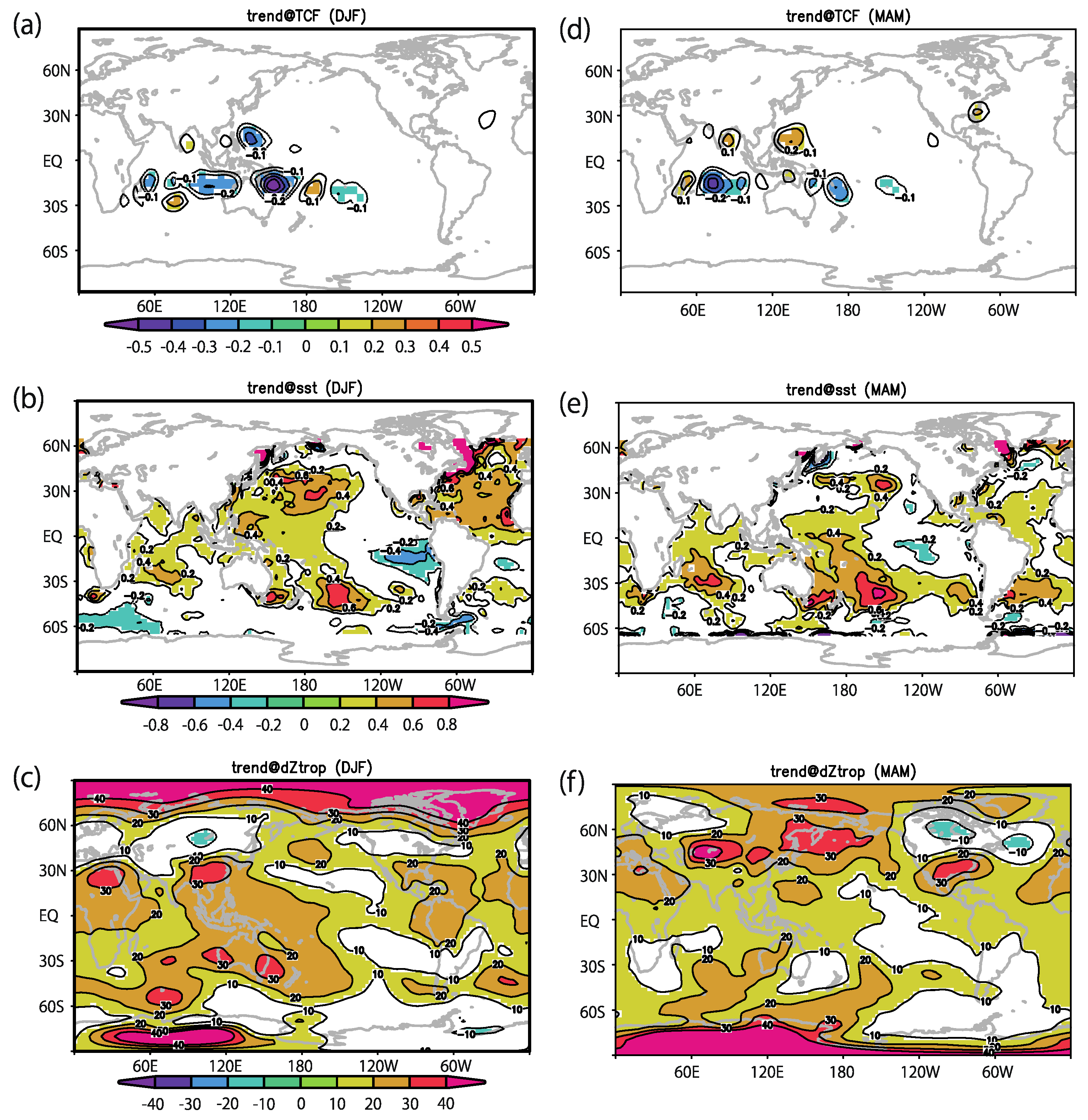
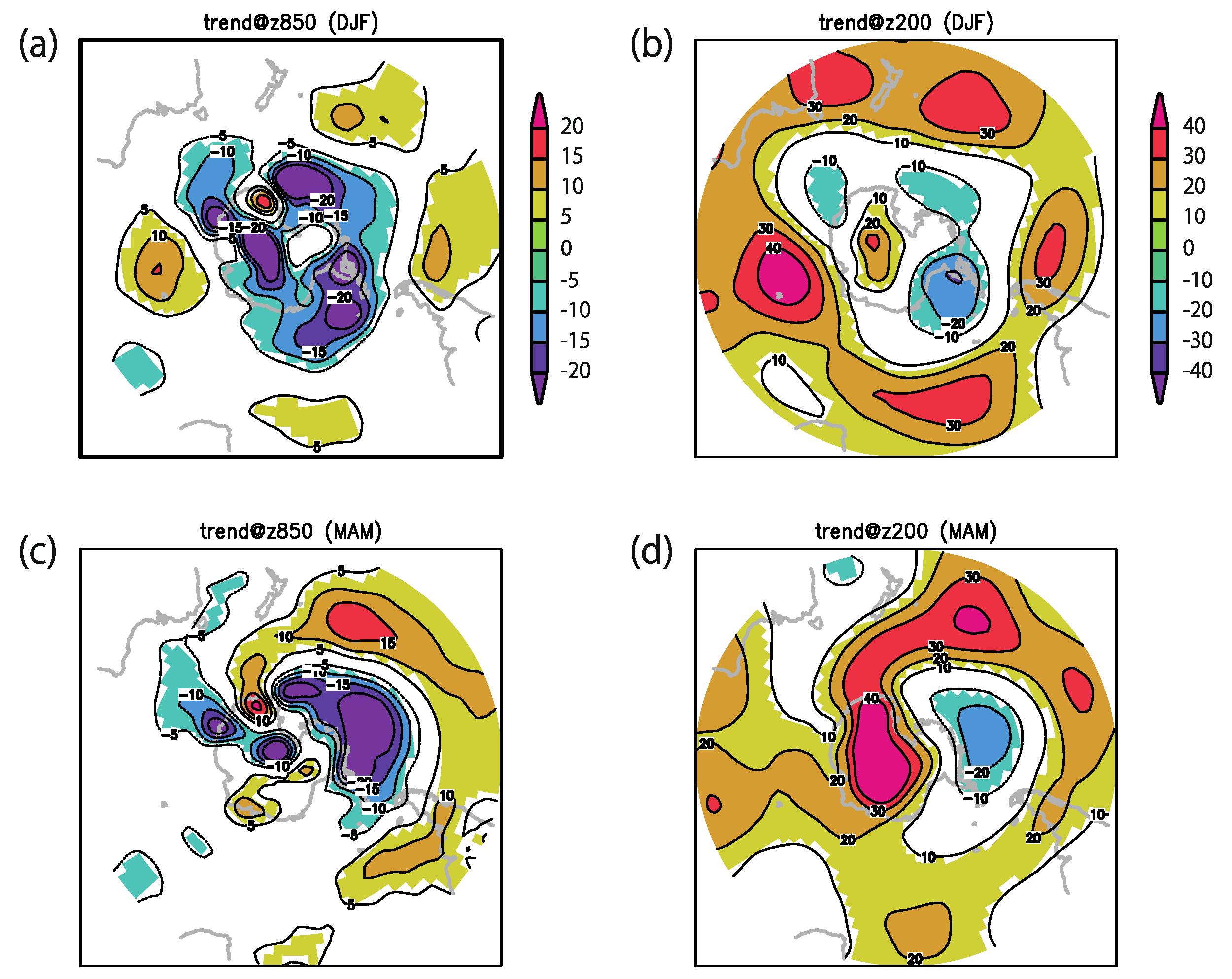
3.4. Long-Term Trend

In addition to interannual variability, the long-term trend over the SH was also investigated. Figure 12 shows the TCF, SST, and tropospheric thickness (z200-z850) difference of the seasonal mean between 1983–2001 and 2002–2020. The TCF pattern shows a generally decreasing trend over the SH (Figure 12a,d). The SST pattern (Figure 12b,e) shows a warming trend over the tropical IO and the western Pacific. The tropospheric thickness pattern (Figure 12c,f) shows a warming trend over the tropics. These results are consistent with previous studies of future climate projection under the global warming scenario; the SST warming and tropical circulation slow down by stabilization [63] as the TC activity decreases [64,65,66]. In addition, a positive SAM trend appears during DJF (Figure 13a,b). The positive SAM can be interpreted as a degree of decoupling between Antarctica and the southern mid-latitude [56]. In the long-term trend, the positive SAM may contribute to reduced TC activity through the change of TC seeding from mid-latitude. During MAM, a zonally asymmetric structure (planetary wavenumber 1) seems more apparent (Figure 13c,d).

4. Discussion

During the MAM TCF anomaly over the SWIO, the La Niña-like negative SST correlation over the equatorial Pacific associated with the SWIO TCF variability (Figure 2c) is significant. Similar to the SST, the SSH correlation pattern (Figure 2d) is also significant; a negative (positive) correlation in the eastern (western) equatorial Pacific is a feature of La Niña. On the other hand, the contribution of the Indian Ocean SST and subsurface thermocline (SSH) is not significant. According to previous studies, a positive IOD or El Niño causes subsurface warming (thermocline deepening, positive SSH anomaly) in the SWIO. Therefore, the remote impact of La Niña and the local impact of the SWIO subsurface warming may cancel each other out. In order to focus on the local impact of the SWIO subsurface warming, a partial correlation analysis was performed. Figure 14 shows a partial correlation map (Niño-3 index regressed out) between the TCF in the SWIO and the global SST (left panels) and SSH (right panels). During DJF, a significantly positive SST signal appears in the SWIO (Figure 14a). The SSH pattern (Figure 14b) also shows significantly positive values (associated with thermocline deepening) over the SWIO. These features are consistent with the results of previous studies [20]. During MAM, on the other hand, there are no statistically significant correlations (Figure 14c,d). In Figure 14d, a previous study dealing with dendrochronology had similar results in the high mountains of Costa Rica [67].
Finally, the SST formation mechanism seen in Figure 4a (correlation with the DJF TCF variability in the SWP) is investigated. In Figure 7a, there is an anticyclonic anomaly in the northwestern Pacific, which is expected to produce southward divergent wind anomalies over the western equatorial Pacific. This anticyclonic anomaly may play an important role in the negative SST signal in the western equatorial Pacific (Figure 4a) by inducing a negative heat flux anomaly due to the increased wind speed. Figure 15 shows lead-lag correlation maps between the DJF TCF in the SWP and global SST (left panels) and wind speed (right panels). During DJF, a wind speed increase can be seen over the cold SST signal west of the dateline (Figure 15e). This is consistent with the above hypothesis that an increased wind speed leads to SST cooling through the surface heat flux. It should be noted that the SST warming (cooling) and wind speed decrease (increase) can be seen in other cases. For example, the SST warming and wind speed decrease can be seen in the eastern equatorial Pacific during DJF (Figure 15f). This is probably due to the reduction of the trade winds during El Niño. Over the northern Indian Ocean, the SST warming, and wind speed decrease, can be seen during JJA (Figure 15b). This is consistent with the El Niño induced Indian Ocean warming.

5. Conclusions

In this study, the author examined the tropical cyclone (TC) activity over the southern hemisphere (SH) and its relationship with tropical variability patterns. Our focus was on the seasonality of interannual variability during the austral summer (December–January–February; DJF) and fall (March–April–May; MAM). According to the correlation analysis between TC activity and global sea surface temperature (SST), the TC activity over the southwestern and southeastern Indian Ocean (SWIO and SEIO) is significantly correlated with a La Niña SST pattern (Figure 2 and Figure 3). On the other hand, an increased TC activity over the southwestern Pacific (SWP) is associated with an El Niño-like SST pattern (Figure 4). The TC increase over the SWIO/SEIO, on the other hand, is associated with a La Niña-like SST pattern, which is accompanied by tropospheric cooling and cyclonic circulation anomalies over the TC genesis region (Figure 5 and Figure 6). The correlation analysis suggests that this cyclonic vorticity is favorable to TC genesis, while the cold SST anomalies are unfavorable. To investigate potential precursors, a lead-lag correlation analysis was performed. An increased TC activity over the SEIO was preceded by an SST pattern resembling the Pacific Meridional Mode (PMM) by two seasons (Figure 10). This TC-ENSO relationship is seasonally dependent, with different patterns during DJF and MAM.
Motivated by the observational analysis presented here, seasonal forecasts of the TC activity using a general circulation model (GCM) is in the planning. Over the northwestern Pacific, our previous study [16] demonstrated that the TCF variability is well-reproduced by an atmospheric GCM (AGCM) during JJA but not during SON. Previous studies concluded that this difference is due to internal atmospheric variability. However, a newly developed convection scheme [68,69] may improve the skill during SON [17]. AGCM experiments with a higher resolution (about 50 km in the horizontal) that use the new convection scheme will be required to investigate the potential sensitivity to the convective parameterization. As a possible driver of the monsoon circulation, the land-sea contrast plays an important role for the NH. In contrast, the contribution of continental heating is smaller in the SH because a wider area is covered by the ocean. Therefore, the impact of the new convective parameterization on the TCF may be more apparent in the SH.
Furthermore, recent studies have reported that air–sea coupling is important for improving the seasonal or longer timescale TCF forecasts in order to represent the entrainment of the subsurface water and its impact on the SST and extreme TC activity predictions [50,51,52,53], which is not considered in SST-prescribed AGCMs. Further investigation of this topic using a coupled GCM (CGCM) is in planning in the near future.
Finally, it should be noted that synoptic and intraseasonal variability, such as Equatorial Rossby (ER), Mixed Rossby Gravity (MRG) waves, and Madden Julian Oscillation (MJO), is important for forming TCs and modulating TC activity [70,71,72,73]. In addition, previous studies noted that TCs might cause anomalous equatorial westerly events such as the WWB, and they can trigger an ENSO [74,75]. From these results, intraseasonal atmospheric variability is also important for TC activity, and its multi-scale interaction with ENSO is expected.

Funding

This work is supported, in part, by the Japan Society for the Promotion of Science (JSPS) through a Grant-in-Aid for Scientific Research 22H00176.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Datasets used in this study is available through following links; IBTrACS (https://www.ncei.noaa.gov/products/international-best-track-archive, accessed on 16 January 2023), NCEP/NCAR reanalysis 1 (https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html, accessed on 16 January 2023), OISST (https://www.ncei.noaa.gov/products/optimum-interpolation-sst, accessed on 16 January 2023), and GODAS (https://psl.noaa.gov/data/gridded/data.godas.html, accessed on 16 January 2023).

Acknowledgments

The author would like to appreciate Yohei Yamada for providing the processed IBTrACS data, and Ingo Richter for providing helpful comments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Maldonado, T.; Alfaro, E.J.; Hidalgo, H.G. A review of the main drivers and variability of Central America’s Climate and seasonal forecast systems. Rev. De Biol. Trop. 2018, 66, S153–S175. [Google Scholar] [CrossRef]
  2. Quesada-Román, A.; Villalobos-Chacón, A. Flash flood impacts of Hurricane Otto and hydrometeorological risk mapping in Costa Rica. Geogr. Tidsskr. Dan. J. Geogr. 2020, 120, 142–155. [Google Scholar] [CrossRef]
  3. Hidalgo, H.G.; Alfaro, E.J.; HernÃandez-Castro, F.; Pérez-Briceño, P.M. Identification of Tropical Cyclones’ Critical Positions Associated with Extreme Precipitation Events in Central America. Atmosphere 2020, 11, 1123. [Google Scholar] [CrossRef]
  4. Hidalgo, H.G.; Alfaro, E.J.; Valverde, K.T. Probability of induced extreme precipitation events in Central America due to tropical cyclone positions in the surrounding oceans. Nat. Hazards 2022, 1–17. [Google Scholar] [CrossRef]
  5. Li, R.; Zhou, W. Revisiting the intraseasonal, interannual and interdecadal variability of tropical cyclones in the western North Pacific. Atmos. Ocean. Sci. Lett. 2018, 11, 198–208. [Google Scholar] [CrossRef]
  6. Roberts, M.J.; Vidale, P.L.; Senior, C.; Hewitt, H.T.; Bates, C.; Berthou, S.; Chang, P.; Christensen, H.M.; Danilov, S.; Demory, M.-E. The benefits of global high resolution for climate simulation: Process understanding and the enabling of stakeholder decisions at the regional scale. Bull. Am. Meteorol. Soc. 2018, 99, 2341–2359. [Google Scholar] [CrossRef]
  7. Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef]
  8. Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean. 2007, 112, C11007. [Google Scholar] [CrossRef]
  9. Chen, G.; Tam, C.-Y. Different impacts of two kinds of Pacific Ocean warming on tropical cyclone frequency over the western North Pacific. Geophys. Res. Lett. 2010, 37, L01803. [Google Scholar] [CrossRef]
  10. Kim, H.-M.; Webster, P.J.; Curry, J.A. Modulation of North Pacific tropical cyclone activity by three phases of ENSO. J. Clim. 2011, 24, 1839–1849. [Google Scholar] [CrossRef]
  11. Chiang, J.C.H.; Vimont, D.J. Analogous Pacific and Atlantic meridional modes of tropical atmosphere–ocean variability. J. Clim. 2004, 17, 4143–4158. [Google Scholar] [CrossRef]
  12. Zhang, W.; Vecchi, G.A.; Murakami, H.; Villarini, G.; Jia, L. The Pacific meridional mode and the occurrence of tropical cyclones in the western North Pacific. J. Clim. 2016, 29, 381–398. [Google Scholar] [CrossRef]
  13. Gao, S.; Zhu, L.; Zhang, W.; Chen, Z. Strong modulation of the Pacific meridional mode on the occurrence of intense tropical cyclones over the western North Pacific. J. Clim. 2018, 31, 7739–7749. [Google Scholar] [CrossRef]
  14. Qian, Y.; Murakami, H.; Nakano, M.; Hsu, P.-C.; Delworth, T.L.; Kapnick, S.B.; Ramaswamy, V.; Mochizuki, T.; Morioka, Y.; Doi, T. On the mechanisms of the active 2018 tropical cyclone season in the North Pacific. Geophys. Res. Lett. 2019, 46, 12293–12302. [Google Scholar] [CrossRef]
  15. Takaya, Y. Positive phase of Pacific meridional mode enhanced western North Pacific tropical cyclone activity in summer 2018. Sola 2019, 15A, 55–59. [Google Scholar] [CrossRef]
  16. Ogata, T.; Taguchi, B.; Yamamoto, A.; Nonaka, M. Potential Predictability of the Tropical Cyclone Frequency Over the Western North Pacific with 50-km AGCM Ensemble Experiments. J. Geophys. Res. Atmos. 2021, 126, e2020JD034206. [Google Scholar] [CrossRef]
  17. Ogata, T.; Baba, Y. Variability of tropical cyclone frequency over the western north Pacific in 2018–2020. Front. Clim. 2021, 3, 770785. [Google Scholar] [CrossRef]
  18. Camargo, S.J.; Emanuel, K.A.; Sobel, A.H. Use of a genesis potential index to diagnose ENSO effects on tropical cyclone genesis. J. Clim. 2007, 20, 4819–4834. [Google Scholar] [CrossRef]
  19. Kuleshov, Y.; Qi, L.; Fawcett, R.; Jones, D. On tropical cyclone activity in the Southern Hemisphere: Trends and the ENSO connection. Geophys. Res. Lett. 2008, 35, L14S08. [Google Scholar] [CrossRef]
  20. Xie, S.P.; Annamalai, H.; Schott, F.A.; McCreary, J.P. Structure and mechanisms of South Indian Ocean climate variability. J. Clim. 2002, 15, 864–878. [Google Scholar] [CrossRef]
  21. Liu, K.S.; Chan, J.C.L. Interannual variation of Southern Hemisphere tropical cyclone activity and seasonal forecast of tropical cyclone number in the Australian region. Int. J. Climatol. 2012, 32, 190–202. [Google Scholar] [CrossRef]
  22. Vincent, D.G. The South Pacific convergence zone (SPCZ): A review. Mon. Weather. Rev. 1994, 122, 1949–1970. [Google Scholar] [CrossRef]
  23. Vincent, E.M.; Lengaigne, M.; Menkes, E.M.; Jourdain, N.C.; Marchesiello, P.; Madec, G. Interannual variability of the South Pacific Convergence Zone and implications for tropical cyclone genesis. Clim. Dyn. 2011, 36, 1881–1896. [Google Scholar] [CrossRef]
  24. Dowdy, A.J.; Qi, L.; Jones, D.; Ramsay, H.; Fawcett, R.; Kuleshov, Y. Tropical cyclone climatology of the South Pacific Ocean and its relationship to El Niño–Southern Oscillation. J. Clim. 2012, 25, 6108–6122. [Google Scholar] [CrossRef]
  25. Chand, S.S.; McBride, J.L.; Tory, K.J.; Wheeler, M.C.; Walsh, K.J.E. Impact of different ENSO regimes on southwest Pacific tropical cyclones. J. Clim. 2013, 26, 600–608. [Google Scholar] [CrossRef]
  26. Magee, A.D.; Verdon-Kidd, D.C.; Diamond, H.J.; Kiem, A.S. Influence of ENSO, ENSO Modoki, and the IPO on tropical cyclogenesis: A spatial analysis of the southwest Pacific region. Int. J. Climatol. 2017, 37, 1118–1137. [Google Scholar] [CrossRef]
  27. Ho, C.-H.; Kim, J.-H.; Jeong, J.-H.; Kim, H.-S.; Chen, D. Variation of tropical cyclone activity in the South Indian Ocean: El Niño–southern oscillation and madden-Julian oscillation effects. J. Geophys. Res. Atmos. 2006, 111, D22101. [Google Scholar] [CrossRef]
  28. Dowdy, A.; Kuleshov, Y. An analysis of tropical cyclone occurrence in the Southern Hemisphere derived from a new satellite-era data set. Int. J. Remote Sens. 2012, 33, 7382–7397. [Google Scholar] [CrossRef]
  29. Bjerknes, J. Atmospheric teleconnections from the equatorial Pacific. Mon. Weather. Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
  30. Rasmusson, E.M.; Wallace, J.M. Meteorological aspects of the El Nino/southern oscillation. Science 1983, 222, 1195–1202. [Google Scholar] [CrossRef]
  31. Kawamura, R. A possible mechanism of the Asian summer monsoon-ENSO coupling. J. Meteorol. Soc. Jpn. Ser. II 1998, 76, 1009–1027. [Google Scholar] [CrossRef]
  32. Lau, K.M.; Wu, H.T. Principal modes of rainfall–SST variability of the Asian summer monsoon: A reassessment of the monsoon–ENSO relationship. J. Clim. 2001, 14, 2880–2895. [Google Scholar] [CrossRef]
  33. Ohba, M.; Ueda, H. Basin-wide warming in the equatorial Indian Ocean associated with El Niño. Sola 2005, 1, 89–92. [Google Scholar] [CrossRef]
  34. Tokinaga, H.; Tanimoto, Y. Seasonal transition of SST anomalies in the tropical Indian Ocean during El Niño and Indian Ocean dipole years. J. Meteorol. Soc. Jpn. Ser. II 2004, 82, 1007–1018. [Google Scholar] [CrossRef]
  35. Rao, S.A.; Behera, S.K. Subsurface influence on SST in the tropical Indian Ocean: Structure and interannual variability. Dyn. Atmos. Ocean. 2005, 39, 103–135. [Google Scholar] [CrossRef]
  36. Yokoi, T.; Tozuka, T.; Yamagata, T. Seasonal variation of the Seychelles Dome. J. Clim. 2008, 21, 3740–3754. [Google Scholar] [CrossRef]
  37. Xie, S.-P.; Hu, K.; Hanfer, J.; Tokinaga, H.; Du, Y.; Du, Y.; Huang, G.; Sample, T. Indian Ocean capacitor effect on Indo–western Pacific climate during the summer following El Niño. J. Clim. 2009, 22, 730–747. [Google Scholar] [CrossRef]
  38. Behera, S.K.; Luo, J.J.; Masson, S.; Rao, S.A.; Sakuma, H.; Yamagata, T. A CGCM study on the interaction between IOD and ENSO. J. Clim. 2006, 19, 1688–1705. [Google Scholar] [CrossRef]
  39. Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The international best track archive for climate stewardship (IBTrACS) unifying tropical cyclone data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
  40. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, R.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
  41. Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
  42. Behringer, D.; Xue, Y. Evaluation of the global ocean data assimilation system at NCEP: The Pacific Ocean. In Proceedings of the Proc. Eighth Symp. on Integrated Observing and Assimilation Systems for Atmosphere, Oceans, and Land Surface, Seattle, WA, USA, 12 January 2004. [Google Scholar]
  43. Fu, L.-L. Ocean circulation and variability from satellite altimetry. In International Geophysics; Academic Press: Cambridge, MA, USA, 2001; p. 141-XXVIII. [Google Scholar]
  44. Trenary, L.L.; Han, W. Intraseasonal-to-interannual variability of South Indian Ocean sea level and thermocline: Remote versus local forcing. J. Phys. Oceanogr. 2012, 42, 602–627. [Google Scholar] [CrossRef]
  45. Gray, W.M. Global view of the origin of tropical disturbances and storms. Mon. Weather. Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
  46. Emanuel, K.; Nolan, D.S. Tropical cyclone activity and the global climate system. In Proceedings of the 26th Conference on Hurricanes and Tropical Meteorology, Miami, FL, USA, 3–7 May 2004. [Google Scholar]
  47. Matsuno, T. Quasi-geostrophic motions in the equatorial area. J. Meteorol. Soc. Jpn. Ser. II 1966, 44, 25–43. [Google Scholar] [CrossRef]
  48. Gill, A.E. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980, 106, 447–462. [Google Scholar] [CrossRef]
  49. Emanuel, K.A. The maximum intensity of hurricanes. J. Atmos. Sci. 1988, 45, 1143–1155. [Google Scholar] [CrossRef]
  50. Vincent, E.M.; Lengaigne, M.; Madec, G.; Vialard, J.; Samson, G.; Jourdain, N.C.; Menkes, C.E.; Jullien, S. Processes setting the characteristics of sea surface cooling induced by tropical cyclones. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
  51. Ogata, T.; Mizuta, R.; Adachi, Y.; Murakami, H.; Ose, T. Effect of air-sea coupling on the frequency distribution of intense tropical cyclones over the northwestern Pacific. Geophys. Res. Lett. 2015, 42, 10415–10421. [Google Scholar] [CrossRef]
  52. Ogata, T.; Mizuta, R.; Adachi, Y.; Murakami, H.; Ose, T. Atmosphere-ocean coupling effect on intense tropical cyclone distribution and its future change with 60 km-AOGCM. Sci. Rep. 2016, 6, 29800. [Google Scholar] [CrossRef]
  53. Ma, Z.; Fei, J.; Huang, X.; Cheng, X. Modulating effects of mesoscale oceanic eddies on sea surface temperature response to tropical cyclones over the western North Pacific. J. Geophys. Res. Atmos. 2018, 123, 367–379. [Google Scholar] [CrossRef]
  54. Hsu, H.-H.; Hung, C.-H.; Lo, A.-K.; Wu, C.-C.; Hung, C.-W. Influence of tropical cyclones on the estimation of climate variability in the tropical western North Pacific. J. Clim. 2008, 21, 2960–2975. [Google Scholar] [CrossRef]
  55. Marshall, A.G.; Hemer, M.A.; Hendon, H.H.; McInnes, K.L. Southern annular mode impacts on global ocean surface waves. Ocean. Model. 2018, 129, 58–74. [Google Scholar] [CrossRef]
  56. Spensberger, C.; Reeder, M.J.; Spengler, T.; Patterson, M. The connection between the southern annular mode and a feature-based perspective on Southern Hemisphere midlatitude winter variability. J. Clim. 2020, 33, 115–129. [Google Scholar] [CrossRef]
  57. Lubis, S.W.; Hassanzadeh, P. The Intrinsic 150-day Periodicity of the Southern Hemisphere Extratropical Large-Scale Atmospheric Circulation. Authorea Prepr. 2022. [Google Scholar] [CrossRef]
  58. Stuecker, M.F. Revisiting the Pacific meridional mode. Sci. Rep. 2018, 8, 3216. [Google Scholar] [CrossRef]
  59. Richter, I.; Stuecker, M.F.; Takahashi, N.; Schneider, N. Disentangling the North Pacific Meridional Mode from tropical Pacific variability. NPJ Clim. Atmos. Sci. 2022, 5, 94. [Google Scholar] [CrossRef]
  60. Vimont, D.J.; Wallace, J.M.; Battisti, D.S. The seasonal footprinting mechanism in the Pacific: Implications for ENSO. J. Clim. 2003, 16, 2668–2675. [Google Scholar] [CrossRef]
  61. Chang, P.; Zhang, L.; Saravanan, R.; Vimont, D.J.; Chiang, J.C.H.; Ji, L.; Seidel, H.; Tippett, M.K. Pacific meridional mode and El Niño—Southern oscillation. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
  62. Ogata, T.; Doi, T.; Morioka, Y.; Behera, S. Mid-latitude source of the ENSO-spread in SINTEX-F ensemble predictions. Clim. Dyn. 2019, 52, 2613–2630. [Google Scholar] [CrossRef]
  63. Held, I.M.; Soden, B.J. Robust responses of the hydrological cycle to global warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
  64. Murakami, H.; Wang, Y.; Yoshimura, H.; Mizuta, R.; Sugi, M.; Shindo, E.; Adachi, Y.; Yukimoto, S.; Hosaka, M.; Kusunoki, S.; et al. Future changes in tropical cyclone activity projected by the new high-resolution MRI-AGCM. J. Clim. 2012, 25, 3237–3260. [Google Scholar] [CrossRef]
  65. Roberts, M.J.; Vidale, P.L.; Mizielinski, M.S.; Demory, M.-E.; Schiemann, R.; Strachan, J.; Hodges, K.; Bell, R.; Camp, J. Tropical cyclones in the UPSCALE ensemble of high-resolution global climate models. J. Clim. 2015, 28, 574–596. [Google Scholar] [CrossRef]
  66. Yamada, Y.; Kodama, C.; Satoh, M.; Sugi, M.; Roberts, M.J.; Mizuta, R.; Noda, A.T.; Nasuno, T.; Nakano, M.; Vidale, P.L. Evaluation of the contribution of tropical cyclone seeds to changes in tropical cyclone frequency due to global warming in high-resolution multi-model ensemble simulations. Prog. Earth Planet. Sci. 2021, 8, 1–17. [Google Scholar] [CrossRef]
  67. Quaseda-Roman, A.; Ballesteros-Canovas, J.A.; Guillet, S.; Madrigal-Gonzalez, J.; Stoffel, M. Neotropical Hypericum irazuense shrubs reveal recent ENSO variability in Costa Rican páramo. Dendrochronologia 2020, 61, 125704. [Google Scholar] [CrossRef]
  68. Baba, Y. Spectral cumulus parameterization based on cloud-resolving model. Clim. Dyn. 2019, 52, 309–334. [Google Scholar] [CrossRef]
  69. Baba, Y. Influence of a spectral cumulus parametrization on simulating global tropical cyclone activity in an AGCM. Q. J. R. Meteorol. Soc. 2021, 147, 1170–1188. [Google Scholar] [CrossRef]
  70. Frank, W.M.; Roundy, P.E. The role of tropical waves in tropical cyclogenesis. Mon. Weather. Rev. 2006, 134, 2397–2417. [Google Scholar] [CrossRef]
  71. Schreck, C.J.; Molinari, J.; Aiyyer, A. A global view of equatorial waves and tropical cyclogenesis. Mon. Weather. Rev. 2012, 140, 774–788. [Google Scholar] [CrossRef]
  72. Lubis, S.W.; Jacobi, C. The modulating influence of convectively coupled equatorial waves (CCEWs) on the variability of tropical precipitation. Int. J. Climatol. 2015, 35, 1465–1483. [Google Scholar] [CrossRef]
  73. Feng, X.; Yang, G.Y.; Hodges, K.I.; Methven, J. Equatorial waves as useful precursors to tropical cyclone occurrence and intensification. Nat. Commun. 2023, 14, 511. [Google Scholar] [CrossRef] [PubMed]
  74. Vecchi, G.A.; Harrison, D.E. Tropical Pacific sea surface temperature anomalies, El Niño, and equatorial westerly wind events. J. Clim. 2000, 13, 1814–1830. [Google Scholar] [CrossRef]
  75. Seiki, A.; Takayabu, Y.N. Westerly wind bursts and their relationship with intraseasonal variations and ENSO. Part I: Statistics. Mon. Weather. Rev. 2007, 135, 3325–3345. [Google Scholar] [CrossRef]
Atmosphere 14 00546 g001
Figure 1. Climatological TCF (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SH in (a) SON, (b) DJF, and (c) MAM. More than 0.3 are only shaded.
Figure 1. Climatological TCF (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SH in (a) SON, (b) DJF, and (c) MAM. More than 0.3 are only shaded.
Atmosphere 14 00546 g001
Atmosphere 14 00546 g002
Figure 2. Simultaneous correlation map of SST (left panels) and SSH (right panels) anomalies with the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) averaged over the SWIO region (averaged over 10–30° S, 40–70° E). Significant areas above the 90% confidence level are shaded. Correlation map of (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Figure 2. Simultaneous correlation map of SST (left panels) and SSH (right panels) anomalies with the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) averaged over the SWIO region (averaged over 10–30° S, 40–70° E). Significant areas above the 90% confidence level are shaded. Correlation map of (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Atmosphere 14 00546 g002
Atmosphere 14 00546 g003
Figure 3. Same as Figure 2 but for the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SEIO region (averaged over 10–30° S, 90–120° E). (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Figure 3. Same as Figure 2 but for the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SEIO region (averaged over 10–30° S, 90–120° E). (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Atmosphere 14 00546 g003
Atmosphere 14 00546 g004
Figure 4. Same as Figure 2 but for the TCF anomaly over the SWP region (averaged over 10–30° S, 150–180° E). (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Figure 4. Same as Figure 2 but for the TCF anomaly over the SWP region (averaged over 10–30° S, 150–180° E). (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Atmosphere 14 00546 g004
Atmosphere 14 00546 g005
Figure 5. Same as Figure 2 but for z850 (left panels) and tropospheric thickness (z200-z850; right panels) anomalies. (a) DJF z850, (b) DJF z200-z850, (c) MAM z850, (d) MAM z200-z850.
Figure 5. Same as Figure 2 but for z850 (left panels) and tropospheric thickness (z200-z850; right panels) anomalies. (a) DJF z850, (b) DJF z200-z850, (c) MAM z850, (d) MAM z200-z850.
Atmosphere 14 00546 g005
Atmosphere 14 00546 g006
Figure 6. Same as Figure 5 but for the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SEIO region (averaged over 10–30° S, 90–120° E). (a) DJF z850, (b) DJF z200-z850, (c) MAM z850, (d) MAM z200-z850.
Figure 6. Same as Figure 5 but for the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SEIO region (averaged over 10–30° S, 90–120° E). (a) DJF z850, (b) DJF z200-z850, (c) MAM z850, (d) MAM z200-z850.
Atmosphere 14 00546 g006
Atmosphere 14 00546 g007
Figure 7. Same as Figure 5 but for the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SWP region (averaged over 10–30° S, 150–180° E). (a) DJF z850, (b) DJF z200-z850, (c) MAM z850, (d) MAM z200-z850).
Figure 7. Same as Figure 5 but for the TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SWP region (averaged over 10–30° S, 150–180° E). (a) DJF z850, (b) DJF z200-z850, (c) MAM z850, (d) MAM z200-z850).
Atmosphere 14 00546 g007
Atmosphere 14 00546 g008
Figure 8. Simultaneous correlation map of z850 (left panels) and z200 (right panels) anomalies to observed TCF anomaly over the SWIO region (averaged over 10–30° S, 40–70° E). Significant areas above 90% are shaded. (a) DJF z850, (b) DJF z200, (c) MAM z850, (d) MAM z200.
Figure 8. Simultaneous correlation map of z850 (left panels) and z200 (right panels) anomalies to observed TCF anomaly over the SWIO region (averaged over 10–30° S, 40–70° E). Significant areas above 90% are shaded. (a) DJF z850, (b) DJF z200, (c) MAM z850, (d) MAM z200.
Atmosphere 14 00546 g008
Atmosphere 14 00546 g009
Figure 9. Lead-lag correlation map of SST (left panels) and SSH (right panels) anomalies to MAM observed TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SWIO region (averaged over 10–30° S, 40–70° E). Significant areas above 90% are shaded. (a) SON SST, (b) SON SSH, (c) DJF SST, (d) DJF SSH.
Figure 9. Lead-lag correlation map of SST (left panels) and SSH (right panels) anomalies to MAM observed TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SWIO region (averaged over 10–30° S, 40–70° E). Significant areas above 90% are shaded. (a) SON SST, (b) SON SSH, (c) DJF SST, (d) DJF SSH.
Atmosphere 14 00546 g009
Atmosphere 14 00546 g010
Figure 10. Same as Figure 9 but for the DJF observed TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SEIO region (averaged over 10–30° S, 90–120° E). (a) JJA SST, (b) JJA SSH, (c) SON SST, (d) SON SSH.
Figure 10. Same as Figure 9 but for the DJF observed TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SEIO region (averaged over 10–30° S, 90–120° E). (a) JJA SST, (b) JJA SSH, (c) SON SST, (d) SON SSH.
Atmosphere 14 00546 g010
Atmosphere 14 00546 g011
Figure 11. Same as Figure 9 but for the DJF observed TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SWP region (averaged over 10–30° S, 150–180° E). (a) JJA SST, (b) JJA SSH, (c) SON SST, (d) SON SSH.
Figure 11. Same as Figure 9 but for the DJF observed TCF anomaly (defined as occurrence in 5° × 5° bins, units are TCs per season) over the SWP region (averaged over 10–30° S, 150–180° E). (a) JJA SST, (b) JJA SSH, (c) SON SST, (d) SON SSH.
Atmosphere 14 00546 g011
Atmosphere 14 00546 g012
Figure 12. Difference in seasonal means between 1983–2001 and 2002–2020. (a) TCF, (b) SST, and (c) z200-z850 in DJF. (d–f) are same as (a–c) but during MAM.
Figure 12. Difference in seasonal means between 1983–2001 and 2002–2020. (a) TCF, (b) SST, and (c) z200-z850 in DJF. (d–f) are same as (a–c) but during MAM.
Atmosphere 14 00546 g012
Atmosphere 14 00546 g013
Figure 13. Difference in seasonal means between 1983–2001 and 2002–2020. (a) z850, and (b) z200 in DJF. (c,d) are same as (a,b) but during MAM.
Figure 13. Difference in seasonal means between 1983–2001 and 2002–2020. (a) z850, and (b) z200 in DJF. (c,d) are same as (a,b) but during MAM.
Atmosphere 14 00546 g013
Atmosphere 14 00546 g014
Figure 14. Same as Figure 2 but removed Niño-3 index for partial correlation map. (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Figure 14. Same as Figure 2 but removed Niño-3 index for partial correlation map. (a) DJF SST, (b) DJF SSH, (c) MAM SST, (d) MAM SSH.
Atmosphere 14 00546 g014
Atmosphere 14 00546 g015
Figure 15. Same as Figure 11 but for wind speed anomaly at 850 hPa (ws850; right panels). (a) JJA SST, (b) JJA ws850, (c) SON SST, (d) SON ws850, (e) DJF SST, (f) DJF ws850.
Figure 15. Same as Figure 11 but for wind speed anomaly at 850 hPa (ws850; right panels). (a) JJA SST, (b) JJA ws850, (c) SON SST, (d) SON ws850, (e) DJF SST, (f) DJF ws850.
Atmosphere 14 00546 g015
Table 1. Simultaneous correlation coefficients between TCF anomalies and each GPI-related indices. Vort850 and Ushear are sign-reversed so that positive values mean increased GPI. Bold indicates above 90% significance.
Table 1. Simultaneous correlation coefficients between TCF anomalies and each GPI-related indices. Vort850 and Ushear are sign-reversed so that positive values mean increased GPI. Bold indicates above 90% significance.
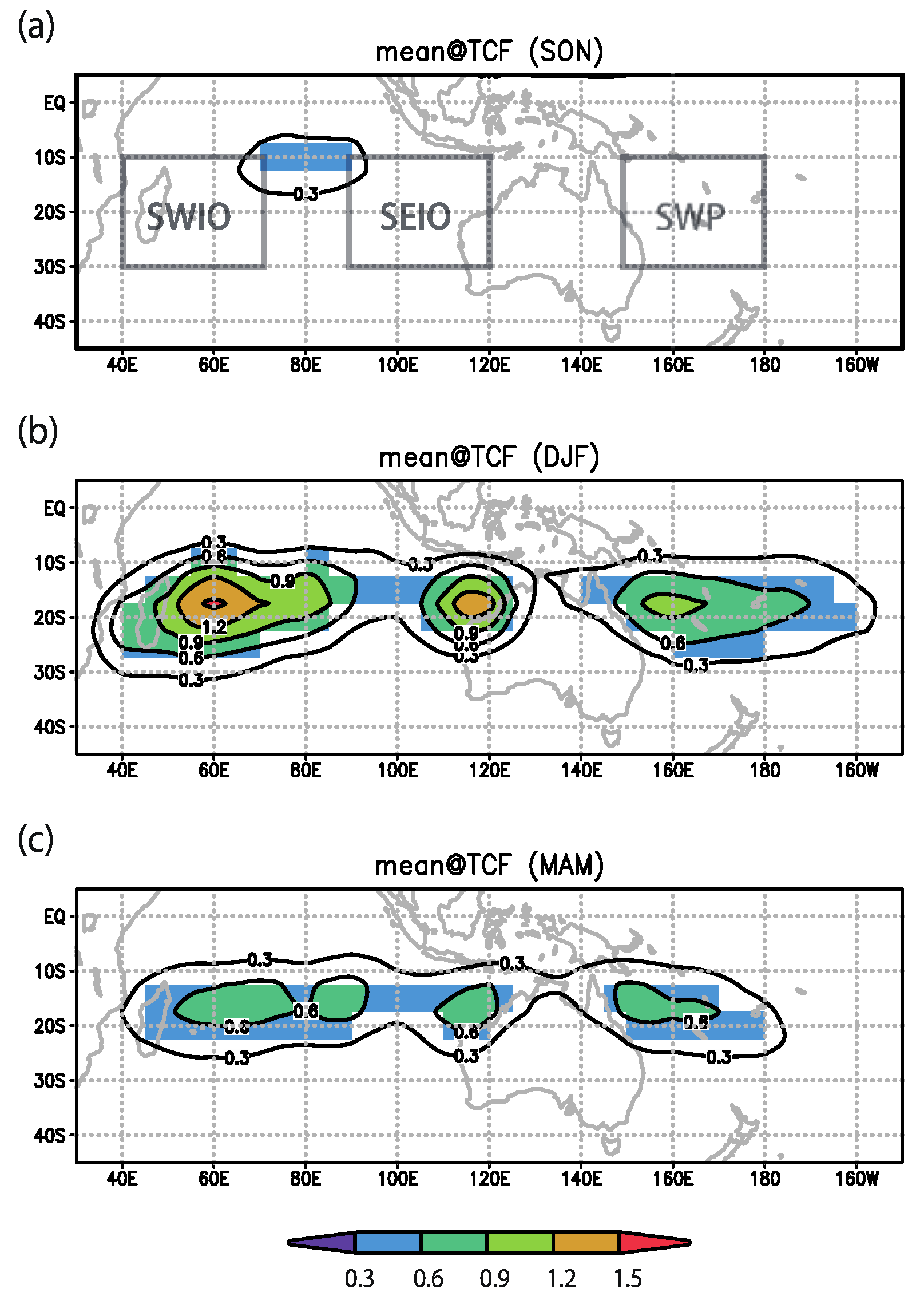
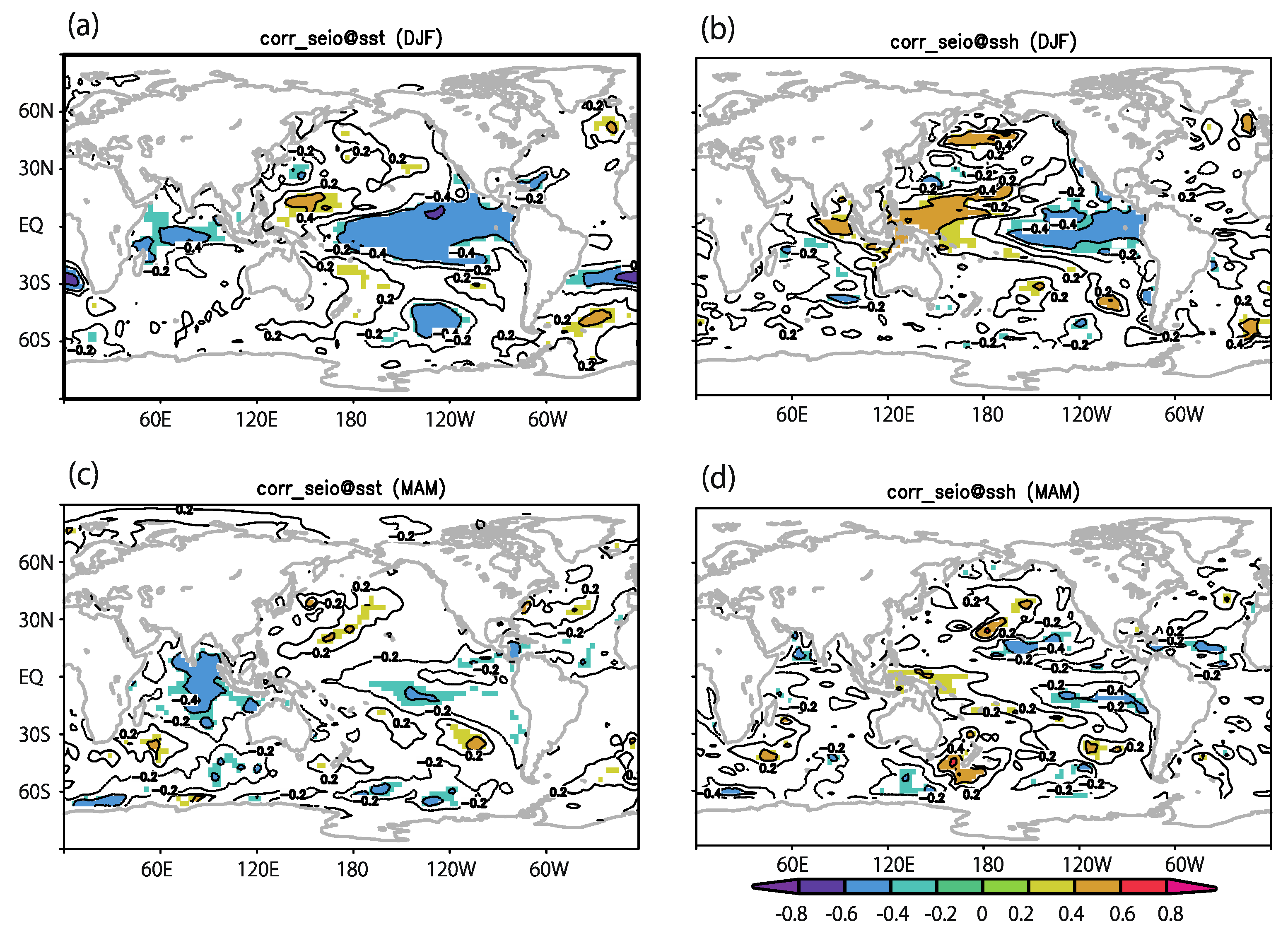
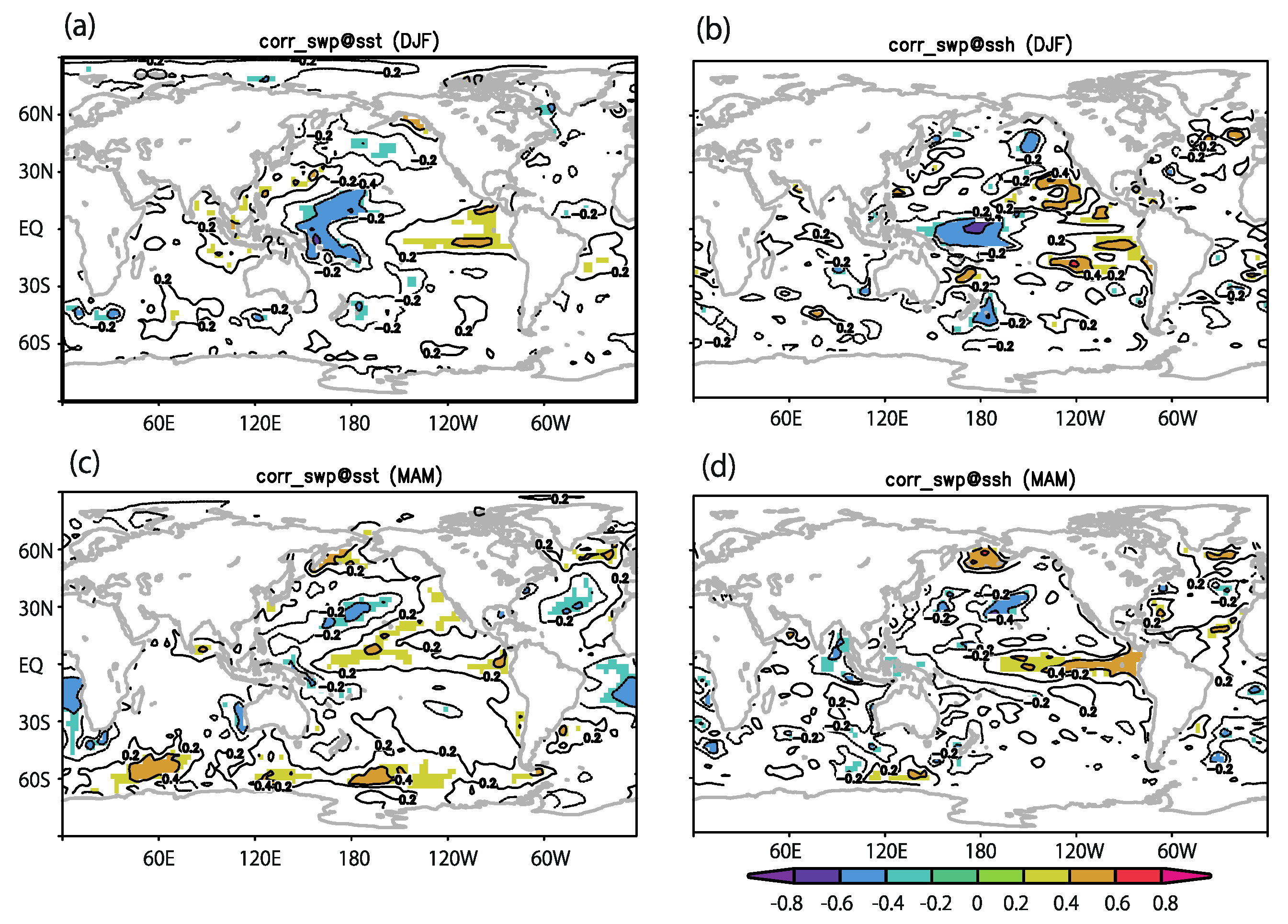
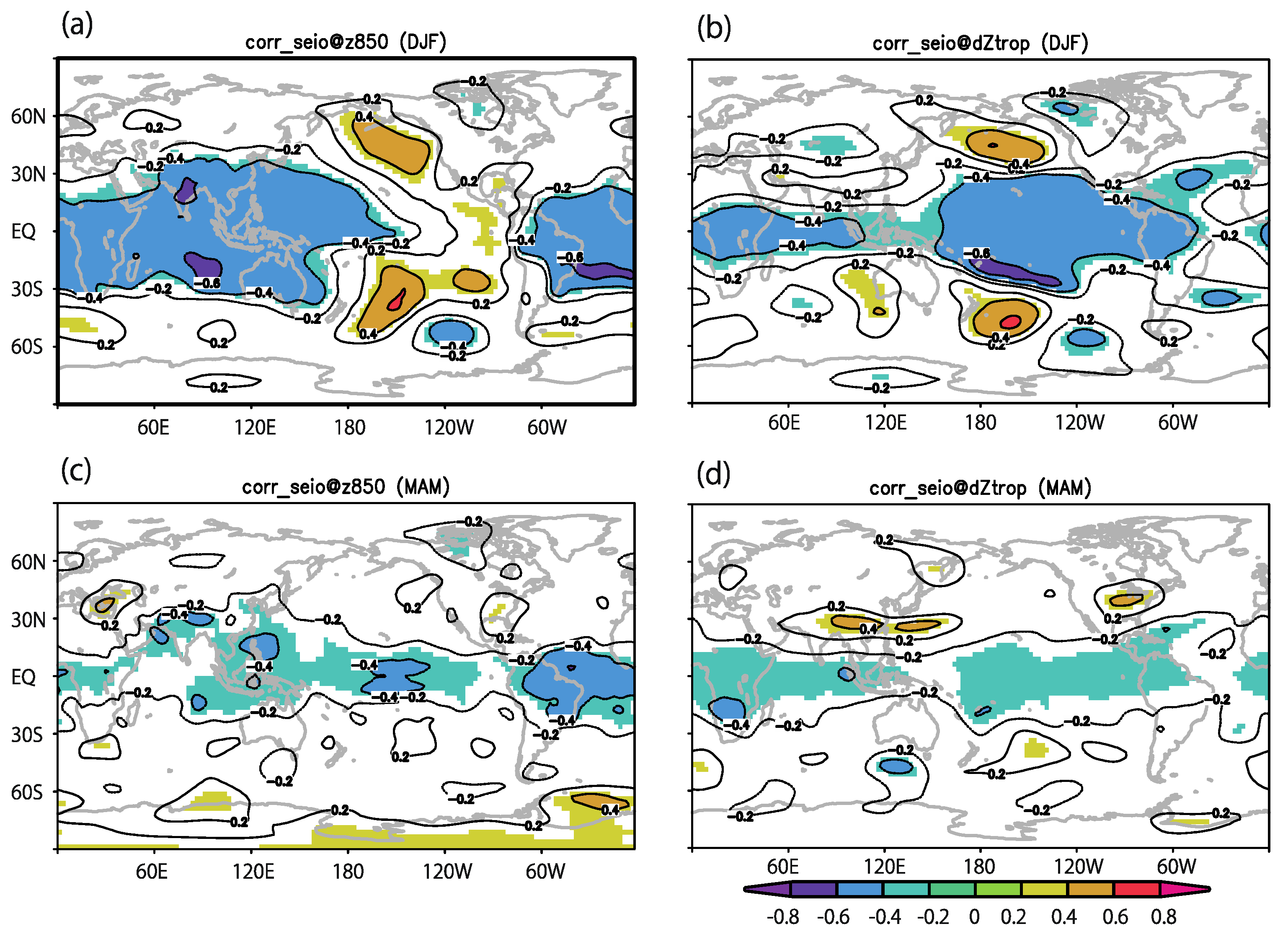
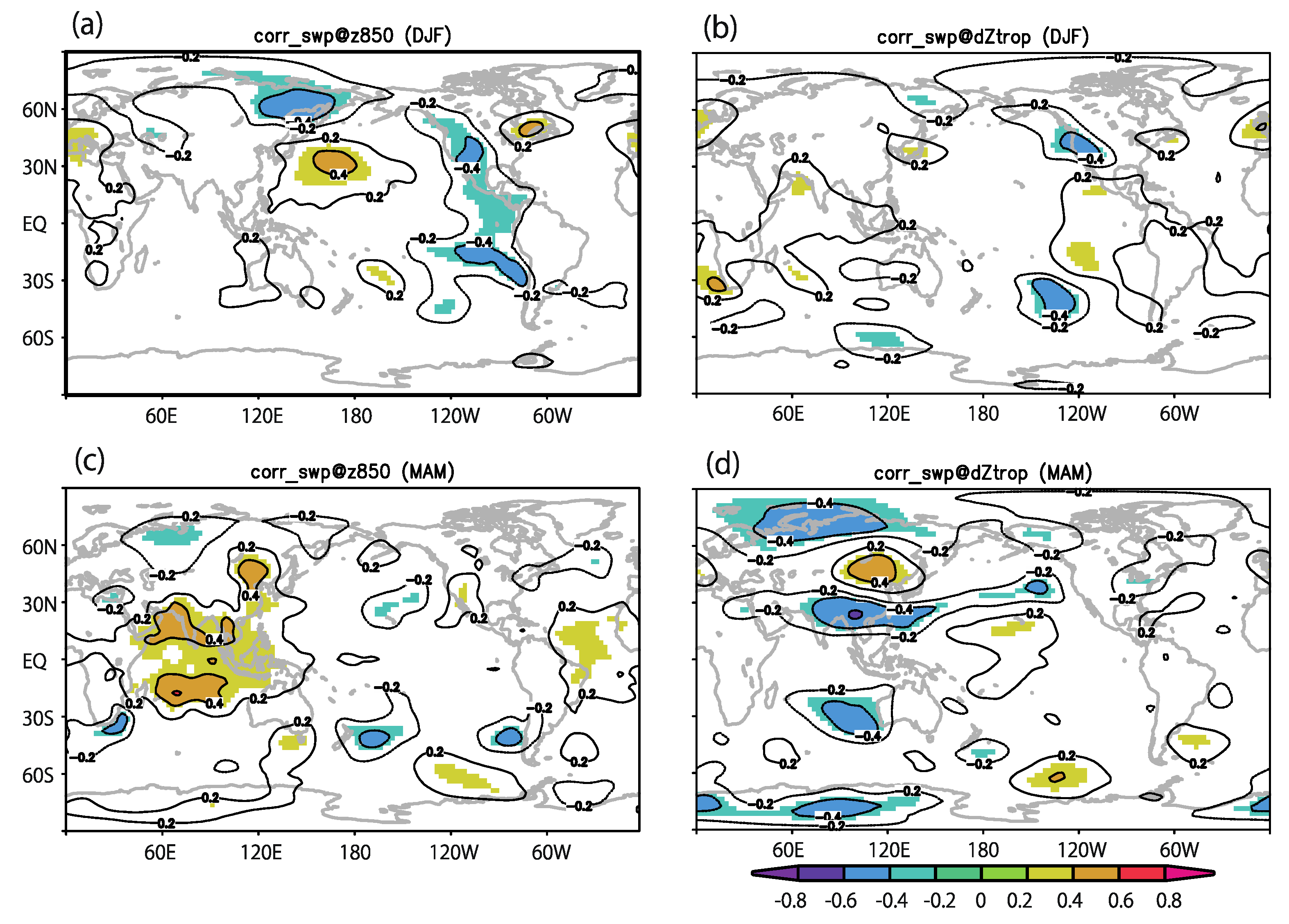
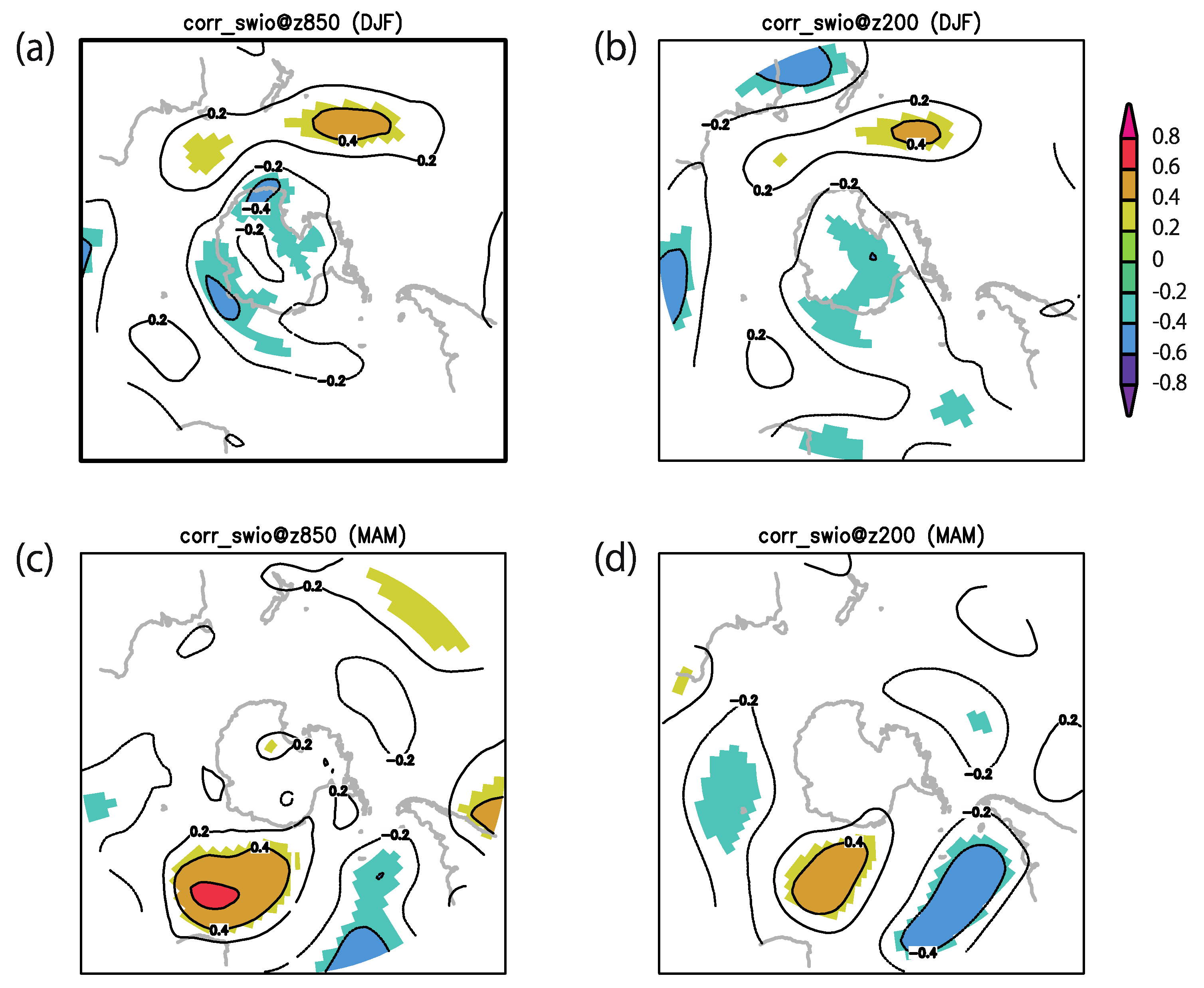
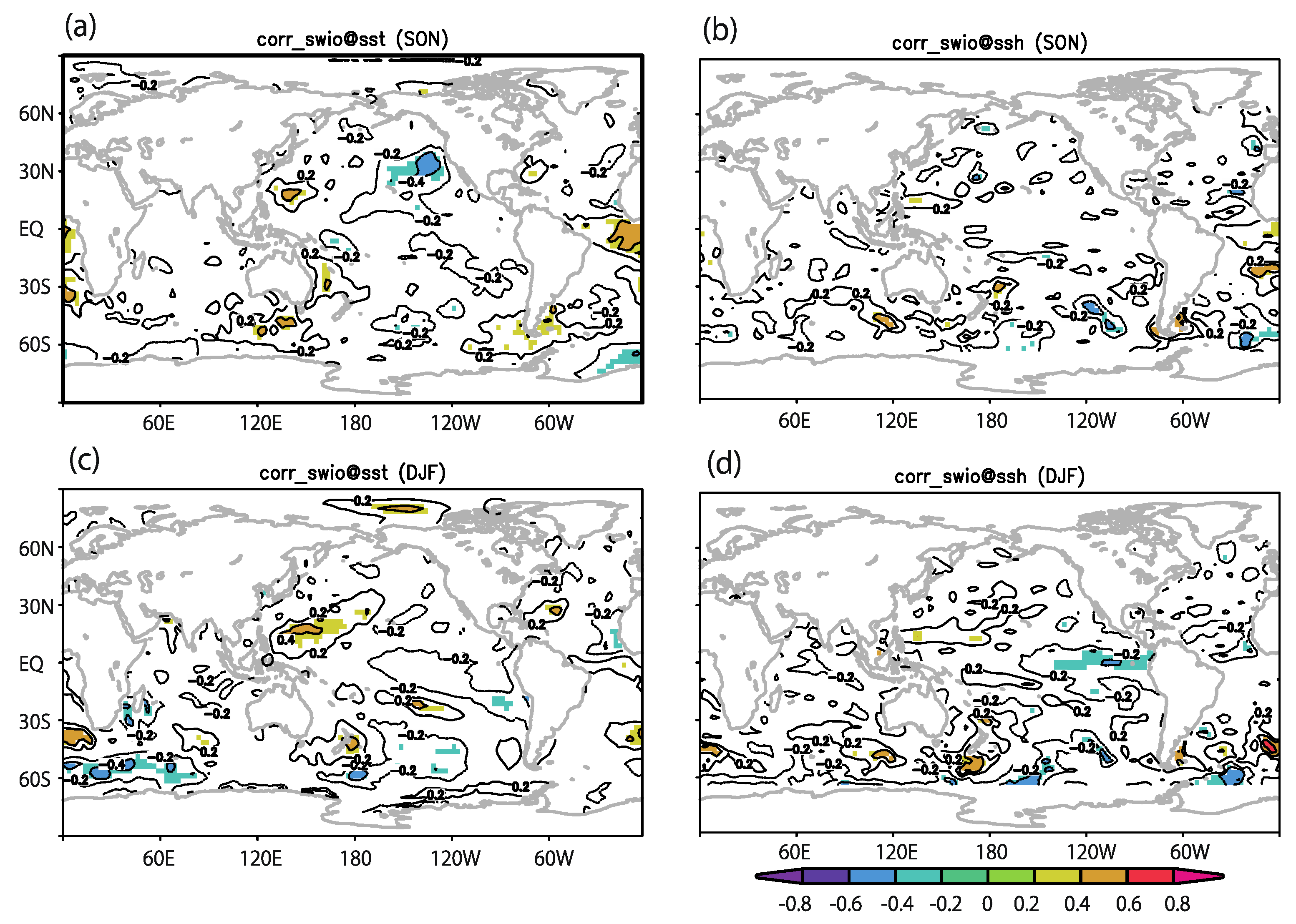
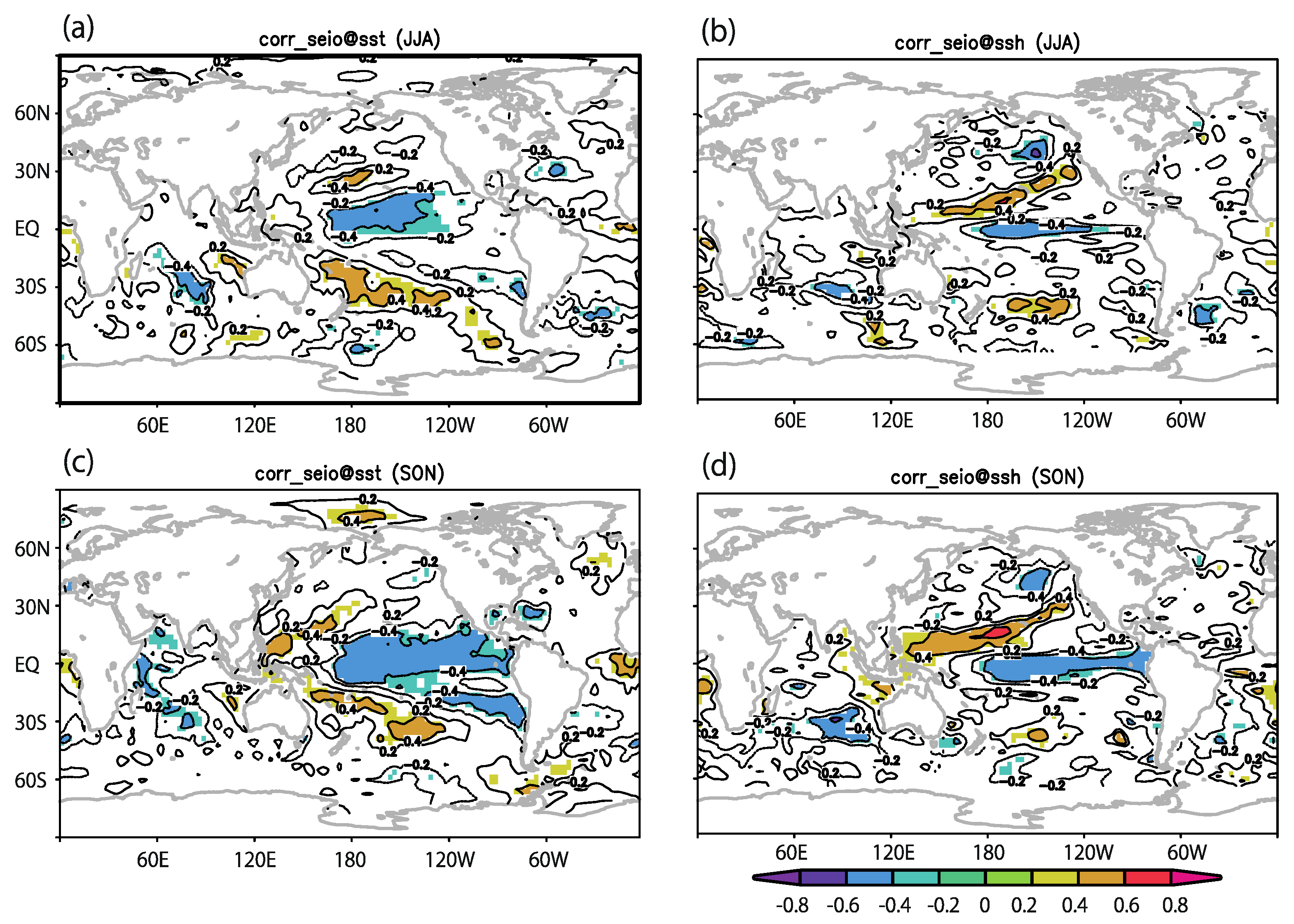
Vort850RH600MPIUshear
SWIO-DJF0.460.55−0.47−0.4
SEIO-DJF0.510.55−0.050.14
SWP-DJF0.30.07−0.37−0.04
SWIO-MAM0.006−0.019−0.410.35
SEIO-MAM0.380.05−0.380.26
SWP-MAM0.48−0.21−0.32−0.23
Table 2. Lead-lag correlation coefficients between TCF anomalies and each climate indices. Left/middle/right values indicate DJF/SON/JJA (MAM/DJF/SON) coefficients during DJF (MAM) TCF cases. Bold indicates above 90% significance.
Table 2. Lead-lag correlation coefficients between TCF anomalies and each climate indices. Left/middle/right values indicate DJF/SON/JJA (MAM/DJF/SON) coefficients during DJF (MAM) TCF cases. Bold indicates above 90% significance.
Niño-3EMIDMI
SWIO-DJF−0.36/−0.31/−0.31−0.04/−0.09/−0.130.03/0.11/0.12
SWIO-MAM−0.4/−0.23/−0.170.13/−0.14/−0.160.3/0.18/0.13
SEIO-DJF−0.55/−0.47/−0.26−0.35/−0.42/−0.41−0.18/−0.27/−0.05
SEIO-MAM−0.3/−0.37/−0.4−0.1/−0.18/−0.080.26/−0.17/−0.26
SWP-DJF0.28/0.33/0.37−0.24/−0.18/−0.1−0.2/0.08/0.1
SWP-MAM0.25/0.09/0.110.1/0.23/0.12−0.06/0.29/−0.16
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ogata, T. Seasonality of Relationship between Tropical Cyclone Frequency over the Southern Hemisphere and Tropical Climate Modes. Atmosphere 2023, 14, 546. https://doi.org/10.3390/atmos14030546

AMA Style

Ogata T. Seasonality of Relationship between Tropical Cyclone Frequency over the Southern Hemisphere and Tropical Climate Modes. Atmosphere. 2023; 14(3):546. https://doi.org/10.3390/atmos14030546

Chicago/Turabian Style

Ogata, Tomomichi. 2023. "Seasonality of Relationship between Tropical Cyclone Frequency over the Southern Hemisphere and Tropical Climate Modes" Atmosphere 14, no. 3: 546. https://doi.org/10.3390/atmos14030546

APA Style

Ogata, T. (2023). Seasonality of Relationship between Tropical Cyclone Frequency over the Southern Hemisphere and Tropical Climate Modes. Atmosphere, 14(3), 546. https://doi.org/10.3390/atmos14030546

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop