Forecasting Air Quality in Tripoli: An Evaluation of Deep Learning Models for Hourly PM2.5 Surface Mass Concentrations
Abstract
1. Introduction
1.1. Literature Review
1.2. The Aime of the Study
2. Methodology
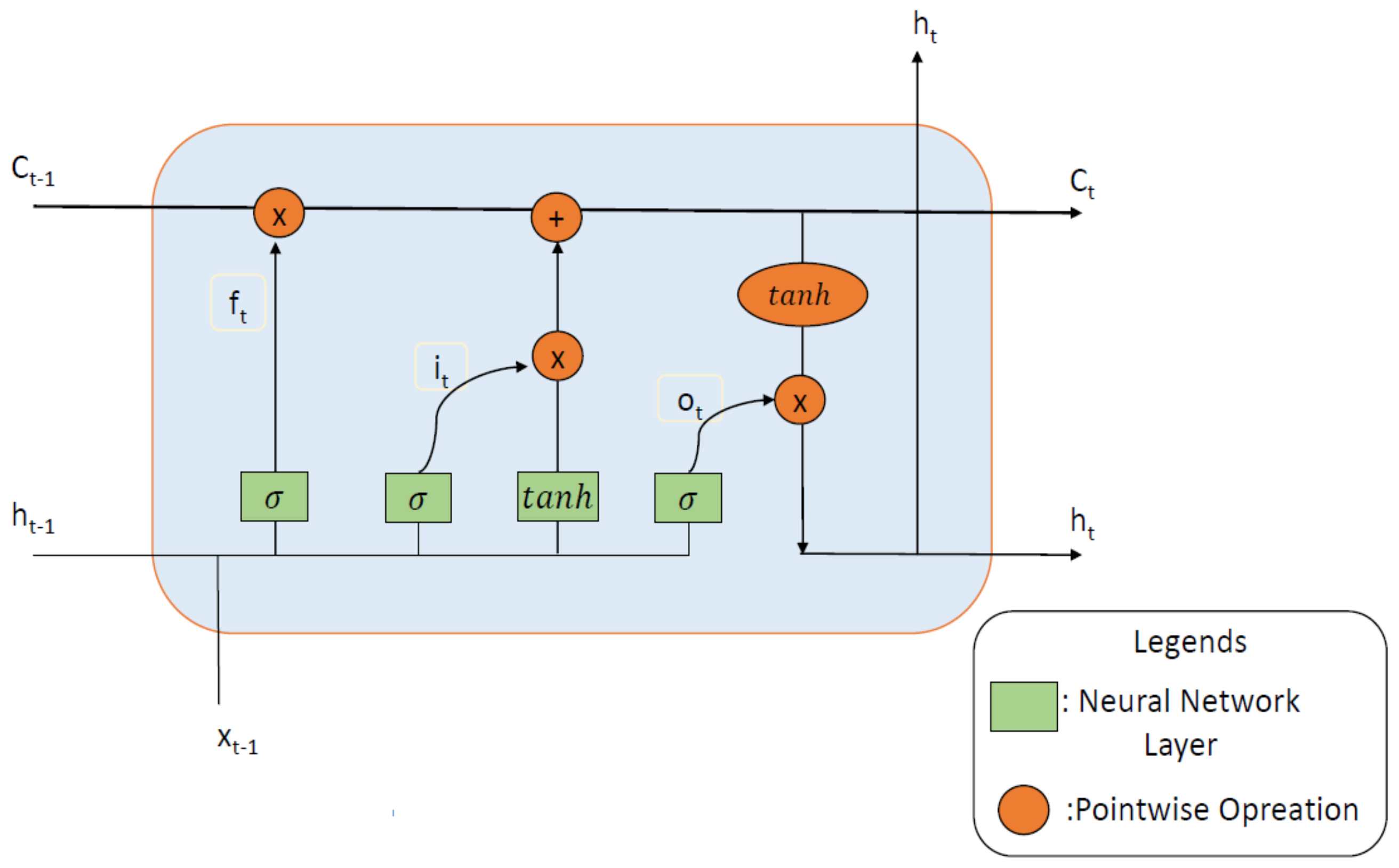
2.1. Long Short-Term Memory
2.2. Gated Recurrent Unit
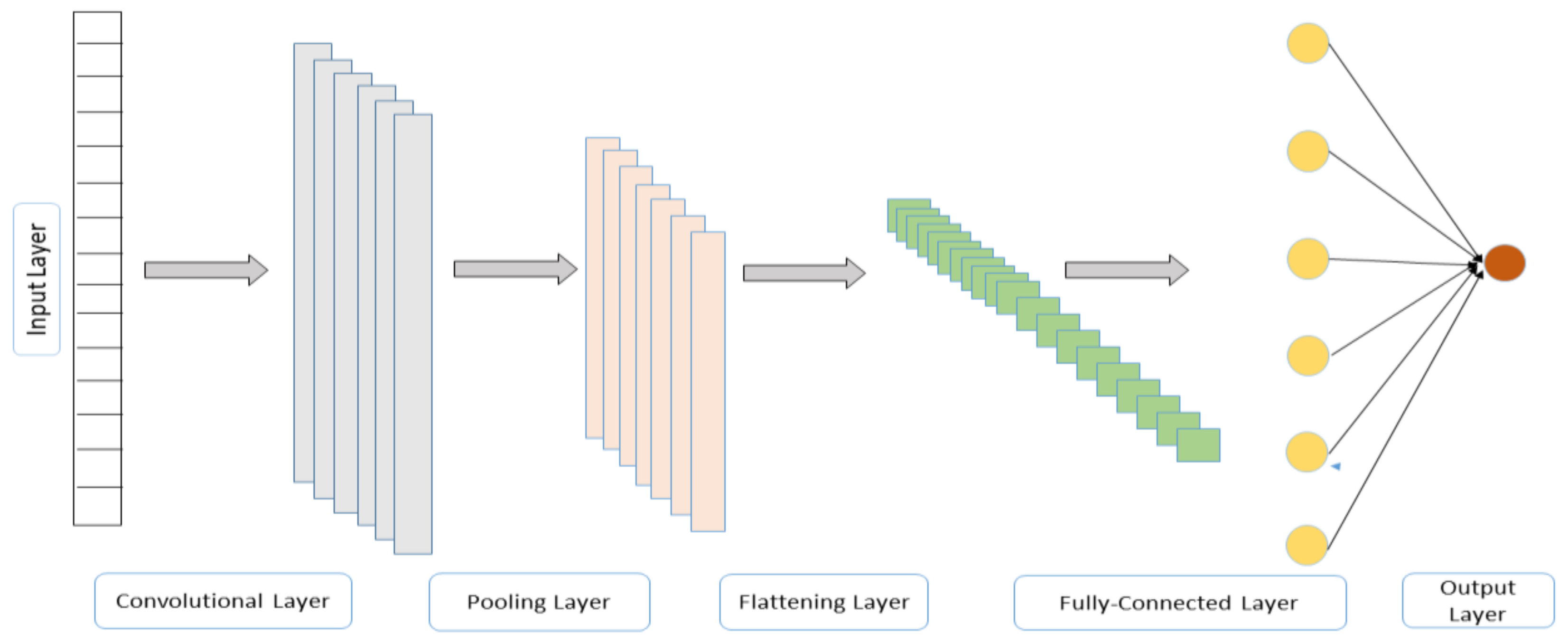
2.3. Convolutional Neural Networks
2.4. Performance Metrics
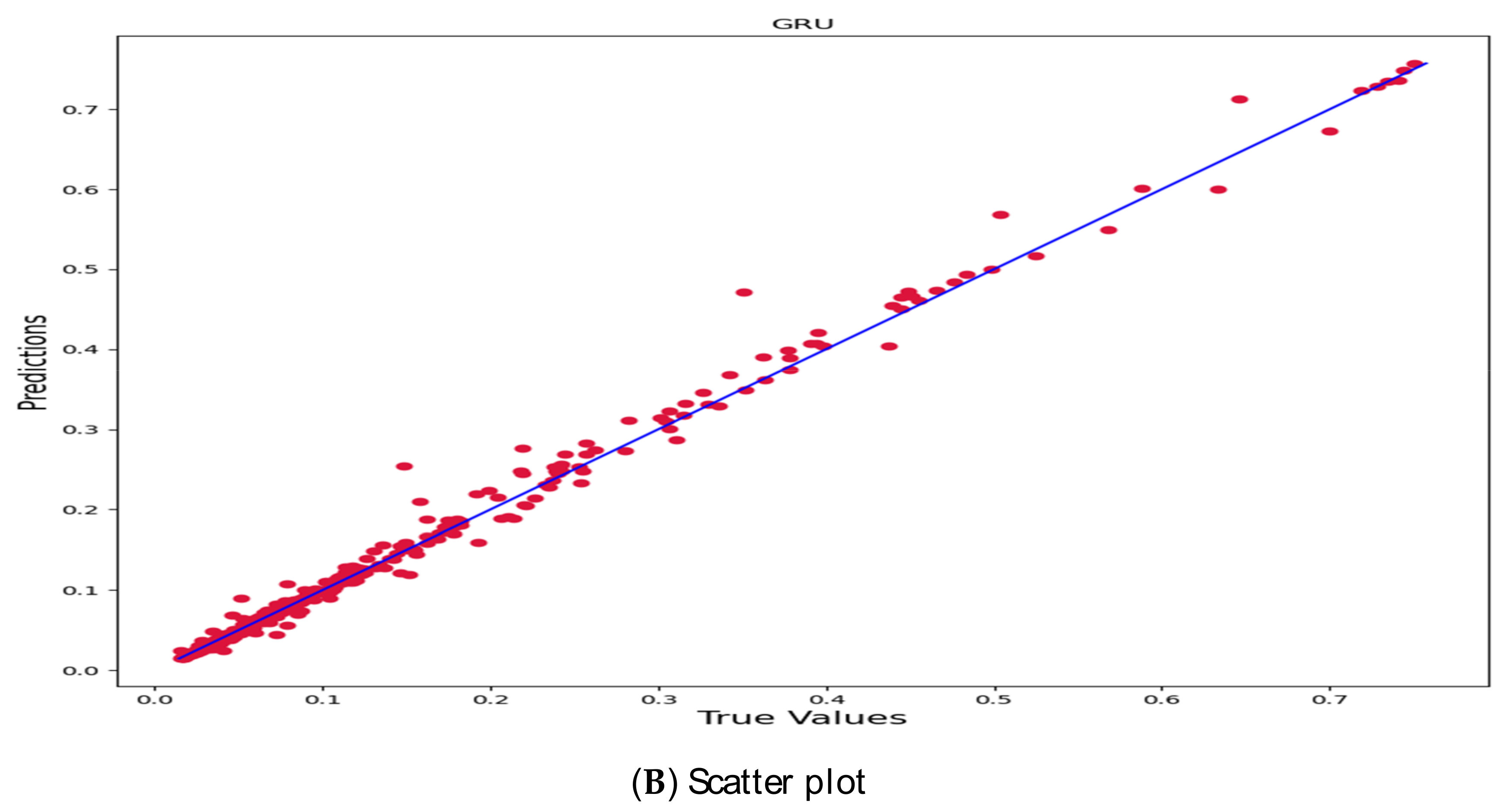
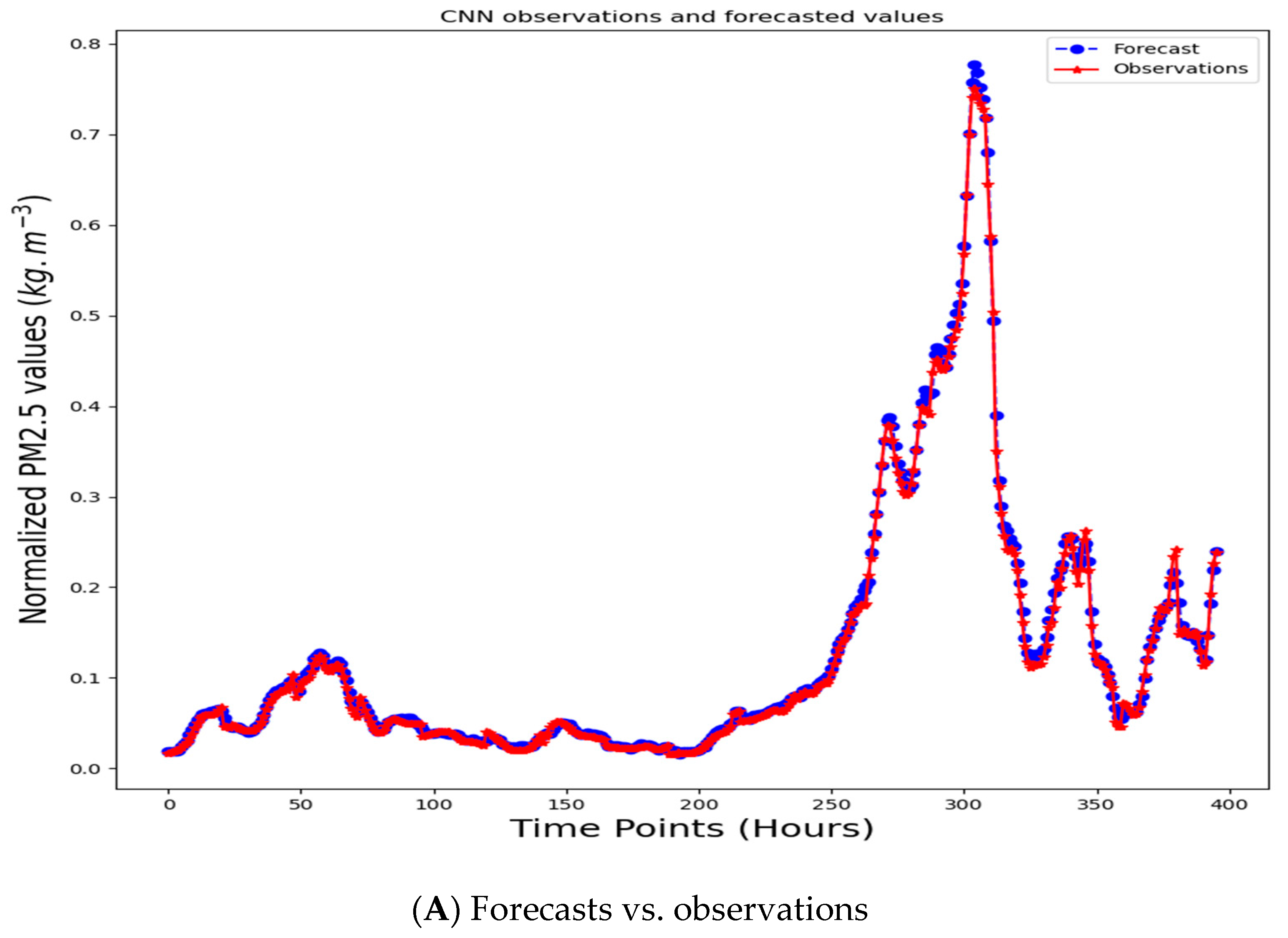
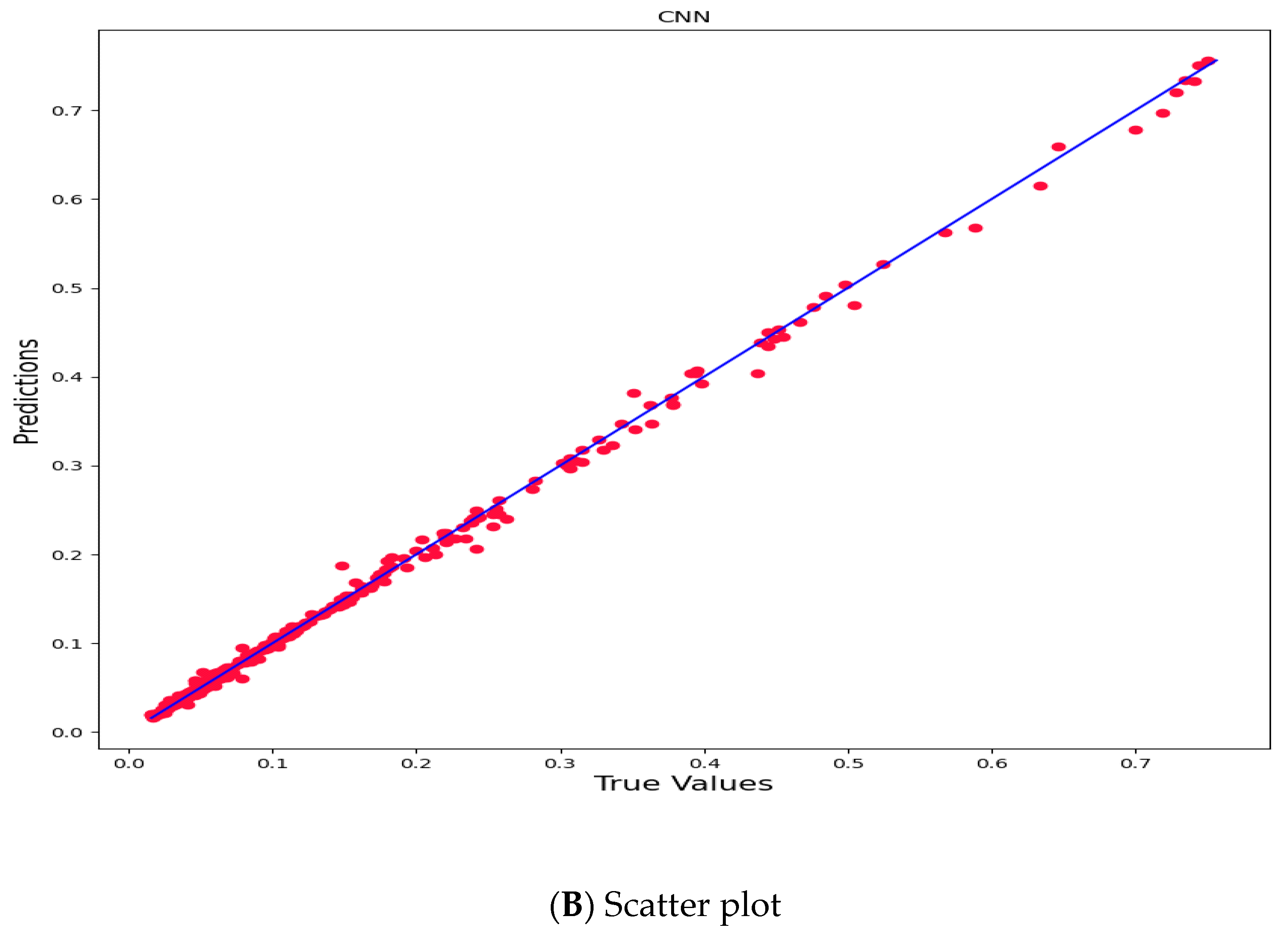
3. Empirical Evidence
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tiwary, A.; Williams, L. Air Pollution: Measurement, Modeling, and Mitigation, 4th ed.; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Airly. Available online: https://airly.org/en/what-are-the-natural-sources-of-air-pollution-and-how-do-they-affect-our-health/ (accessed on 16 January 2023).
- Striegel, M.F.; Guin, E.B.; Hallett, K.; Sandoval, D.; Swingle, R.; Knox, K.; Best, F.; Fornea, S. Air pollution, coatings, and cultural resources. Prog. Org. Coat. 2003, 48, 281–288. [Google Scholar] [CrossRef]
- Camfil. Available online: https://cleanair.camfil.us/2018/02/09/diseases-caused-by-air-pollution-risk-factors-and-control-methods/ (accessed on 15 January 2023).
- Jiang, X.Q.; Mei, X.D.; Feng, D. Air pollution and chronic airway diseases: What should people know and do? J. Thorac. Dis. 2016, 8, E31–E41. [Google Scholar] [CrossRef]
- Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar] [CrossRef]
- Herndon, J.M. Air pollution, not greenhouse gases: The principal cause of global warming. J. Geog. Environ. Earth Sci. Int. 2018, 17, 1–8. [Google Scholar] [CrossRef]
- Stephens, E.R. Temperature inversions and the trapping of air pollutants. Weatherwise 1965, 18, 172–175. [Google Scholar] [CrossRef]
- Hamad, T.A.; Agll, A.A.; Hamad, Y.M.; Sheffield, J.W. Solid waste as renewable source of energy: Current and future possibility in Libya. Case Stud. Therm. Eng. 2014, 4, 144–152. [Google Scholar] [CrossRef]
- AL-Salihi, A.M.; Mohammed, T.H. The effect of dust storms on some meteorological elements over Baghdad, Iraq: Study Cases. J. Appl. Phys. 2015, 7, 1–7. [Google Scholar]
- GMAO. Global Modeling and Assimilation Office (GMAO). MERRA-2 tavg1_2d_aer_Nx: 2d, 1-Hourly, Time-Averaged, Single-Level, Assimilation, Aerosol Diagnostics V5.12.4, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2015. Available online: https://giovanni.gsfc.nasa.gov/giovanni/ (accessed on 3 November 2022).
- WHO. World Health Organization, Report about AMBIEN (Outdoor) Air Quality and Health. Available online: https://www.who.int/media%20Centre/%20fact%20sheets/Fs%20313/en/ (accessed on 18 January 2023).
- WHO-World Health Organization, Household Air Pollution. Available online: http://www.who.int/news-room/fact-sheet/detail/household-air-pollution-and-heath (accessed on 19 January 2023).
- MANA. Available online: https://www.mana.md/indoor-air-vs-outdoor-air/ (accessed on 18 January 2023).
- Ramsundar, B.; Zadeh, R.B. TensorFlow for Deep Learning: From Linear Regression to Reinforcement Learning; O’Reilly Media: Sebastopol, CA, USA, 2018; pp. 3–52. [Google Scholar]
- Akdi, Y.; Okkaoğlu, Y.; Gölveren, E.; Yücel, M.E. Estimation and forecasting of PM10 air pollution in Ankara via time series and harmonic regressions. Int. J. Environ. Sci. Technol. 2020, 17, 3677–3690. [Google Scholar] [CrossRef]
- Okkaoğlu, Y.; Akdi, Y.; Ünlü, K.D. Daily PM10 periodicity and harmonic regression model: The case of London. Atmos. Environ. 2020, 238, 117755. [Google Scholar] [CrossRef]
- Cholianawati, N.; Cahyono, W.E.; Indrawati, A.; Indrajad. A Linear Regression Model for Predicting Daily PM2. 5 Using VIIRS-SNPP and MODIS-Aqua AOT. IOP Conf. Ser. Earth Environ. Sci. 2019, 303, 012039. [Google Scholar] [CrossRef]
- Gregório, J.; Gouveia-Caridade, C.; Caridade, P.J.S.B. Modeling PM2.5 and PM10 Using a Robust Simplified Linear Regression Machine Learning Algorithm. Atmosphere 2022, 13, 1334. [Google Scholar] [CrossRef]
- Ng, K.Y.; Awang, N. Multiple linear regression and regression with time series error models in forecasting PM10 concentrations in Peninsular Malaysia. Environ. Monit. Assess. 2018, 190, 63. [Google Scholar] [CrossRef]
- Akdi, Y.; Gölveren, E.; Ünlü, K.D.; Yücel, M.E. Modeling and forecasting of monthly PM2.5 emission of Paris by periodogram-based time series methodology. Environ. Monit. Assess. 2021, 193, 1–15. [Google Scholar] [CrossRef]
- Shams, S.R.; Jahani, A.; Kalantary, S.; Moeinaddini, M.; Khorasani, N. The evaluation on artificial neural networks (ANN) and multiple linear regressions (MLR) models for predicting SO2 concentration. Urban Clim. 2021, 37, 100837. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, X.; Xue, B.; Zhang, J.; Ren, W. Short period PM2.5 predictions based on multivariate linear regression model. PloS ONE 2018, 13, e0201011. [Google Scholar] [CrossRef]
- Kim, H.S.; Han, K.M.; Yu, J.; Kim, J.; Kim, K.; Kim, H. Development of a CNN+LSTM Hybrid Neural Network for Daily PM2.5 Prediction. Atmosphere 2022, 13, 2124. [Google Scholar] [CrossRef]
- Kumar, S.; Mishra, S.; Singh, S.K.A. machine learning-based model to estimate PM2. 5 concentration levels in Delhi’s atmosphere. Heliyon 2020, 6, e05618. [Google Scholar] [CrossRef]
- Xiao, F.; Yang, M.; Fan, H.; Fan, G.; Al-qaness, M.A.A. An improved deep learning model for predicting daily PM2.5 concentration. Sci. Rep. 2020, 10, 20988. [Google Scholar] [CrossRef]
- Suleiman, A.; Tight, M.R.; Quinn, A.D. Applying machine learning methods in managing urban concentrations of traffic-related particulate matter (PM10 and PM2. 5). Atmos. Pollut. Res. 2019, 10, 134–144. [Google Scholar] [CrossRef]
- Akbal, Y.; Ünlü, K.D. A deep learning approach to model daily particular matter of Ankara: Key features and forecasting. Int. J. Environ. Sci. Technol. 2022, 19, 5911–5927. [Google Scholar] [CrossRef]
- Ding, W.; Zhu, Y. Prediction of PM2.5 Concentration in Ningxia Hui Autonomous Region Based on PCA-Attention-LSTM. Atmosphere 2022, 13, 1444. [Google Scholar] [CrossRef]
- Aldegunde, J.A.Á.; Sánchez, A.F.; Saba, M.; Bolaños, E.Q.; Palenque, J.Ú. Analysis of PM2.5 and Meteorological Variables Using Enhanced Geospatial Techniques in Developing Countries: A Case Study of Cartagena de Indias City (Colombia). Atmosphere 2022, 13, 506. [Google Scholar] [CrossRef]
- Bralewska, K.; Rogula-Kozłowska, W.; Mucha, D.; Badyda, A.J.; Kostrzon, M.; Bralewski, A.; Biedugnis, S. Properties of Particulate Matter in the Air of the Wieliczka Salt Mine and Related Health Benefits for Tourists. Int. J. Environ. Res. Public Health 2022, 19, 826. [Google Scholar] [CrossRef]
- Yue, H.; Duan, L.; Lu, M.; Huang, H.; Zhang, X.; Liu, H. Modeling the Determinants of PM2.5 in China Considering the Localized Spatiotemporal Effects: A Multiscale Geographically Weighted Regression Method. Atmosphere 2022, 13, 627. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Tsai, M.-C. An Intelligent Time Series Model Based on Hybrid Methodology for Forecasting Concentrations of Significant Air Pollutants. Atmosphere 2022, 13, 1055. [Google Scholar] [CrossRef]
- Wen, W.; Shen, S.; Liu, L.; Ma, X.; Wei, Y.; Wang, J.; Xing, Y.; Su, W. Comparative Analysis of PM2.5 and O3 Source in Beijing Using a Chemical Transport Model. Remote Sens. 2021, 13, 3457. [Google Scholar] [CrossRef]
- Kim, H.-K.; Lee, S.; Bae, K.-H.; Jeon, K.; Lee, M.-I.; Song, C.-K. An Observing System Simulation Experiment Framework for Air Quality Forecasts in Northeast Asia: A Case Study Utilizing Virtual Geostationary Environment Monitoring Spectrometer and Surface Monitored Aerosol Data. Remote Sens. 2022, 14, 389. [Google Scholar] [CrossRef]
- Ünlü, K.D. A Data-Driven Model to Forecast Multi-Step Ahead Time Series of Turkish Daily Electricity Load. Electronics 2022, 11, 1524. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Akbal, Y.; Ünlü, K.D. A univariate time series methodology based on sequence-to-sequence learning for short to midterm wind power production. Renew. Energy 2022, 200, 832–844. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Özmen, A.; Weber, G.W. RMARS: Robustification of multivariate adaptive regression spline under polyhedral uncertainty. J. Comput. Appl. Math. 2014, 259, 914–924. [Google Scholar] [CrossRef]
- Liu, T.; You, S. Analysis and Forecast of Beijing’s Air Quality Index Based on ARIMA Model and Neural Network Model. Atmosphere 2022, 13, 512. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, T.; Zhao, H.; Wang, Z. Updated Prediction of Air Quality Based on Kalman-Attention-LSTM Network. Sustainability 2023, 15, 356. [Google Scholar] [CrossRef]
- Erden, C. Genetic algorithm-based hyperparameter optimization of deep learning models for PM2.5 time-series prediction. Int. J. Environ. Sci. Technol. 2023. [Google Scholar] [CrossRef]
- Birim, N.G.; Turhan, C.; Atalay, A.S.; Gokcen Akkurt, G. The Influence of Meteorological Parameters on PM10: A Statistical Analysis of an Urban and Rural Environment in Izmir/Türkiye. Atmosphere 2023, 14, 421. [Google Scholar] [CrossRef]
- Merenda, M.; Porcaro, C.; Iero, D. Edge Machine Learning for AI-Enabled IoT Devices: A Review. Sensors 2020, 20, 2533. [Google Scholar] [CrossRef]
- Loukatos, D.; Kondoyanni, M.; Alexopoulos, G.; Maraveas, C.; Arvanitis, K.G. On-Device Intelligence for Malfunction Detection of Water Pump Equipment in Agricultural Premises: Feasibility and Experimentation. Sensors 2023, 23, 839. [Google Scholar] [CrossRef]



| Number of Nodes | MAE | MSE | RMSE | R2 | MAPE |
|---|---|---|---|---|---|
| 10 | 0.0081 | 0.0002 | 0.0154 | 0.9885 | 0.0721 |
| 20 | 0.0081 | 0.0002 | 0.0146 | 0.9897 | 0.0746 |
| 30 | 0.0123 | 0.0003 | 0.0181 | 0.9843 | 0.1672 |
| 40 | 0.0157 | 0.0009 | 0.0307 | 0.9545 | 0.1253 |
| 50 | 0.0084 | 0.0003 | 0.0165 | 0.9868 | 0.0751 |
| 60 | 0.0119 | 0.0003 | 0.0167 | 0.9865 | 0.1741 |
| 70 | 0.0079 | 0.0002 | 0.0155 | 0.9884 | 0.0723 |
| 80 | 0.0091 | 0.0003 | 0.0168 | 0.9864 | 0.0877 |
| 90 | 0.0118 | 0.0004 | 0.0199 | 0.9807 | 0.1181 |
| 100 | 0.0094 | 0.0003 | 0.0184 | 0.9837 | 0.0887 |
| Number of Nodes | MAE | MSE | RMSE | R2 | MAPE |
|---|---|---|---|---|---|
| 10 | 0.0080 | 0.0024 | 0.0155 | 0.9885 | 0.0737 |
| 20 | 0.0069 | 0.0002 | 0.0135 | 0.9912 | 0.0602 |
| 30 | 0.0082 | 0.0002 | 0.0147 | 0.9897 | 0.0733 |
| 40 | 0.0064 | 0.0002 | 0.0134 | 0.9914 | 0.0613 |
| 50 | 0.0097 | 0.0002 | 0.0158 | 0.9880 | 0.1028 |
| 60 | 0.0085 | 0.0002 | 0.0142 | 0.9902 | 0.1177 |
| 70 | 0.0148 | 0.0004 | 0.0196 | 0.9816 | 0.2181 |
| 80 | 0.0111 | 0.0002 | 0.0154 | 0.9886 | 0.1559 |
| 90 | 0.0076 | 0.0002 | 0.0135 | 0.9912 | 0.0922 |
| 100 | 0.0066 | 0.0002 | 0.0136 | 0.9911 | 0.0621 |
| Number of Nodes | MAE | MSE | RMSE | R2 | MAPE |
|---|---|---|---|---|---|
| 10 | 0.0034 | 0.0001 | 0.0056 | 0.9985 | 0.0418 |
| 20 | 0.0116 | 0.0004 | 0.0189 | 0.9827 | 0.1321 |
| 30 | 0.0070 | 0.0001 | 0.0094 | 0.9958 | 0.0922 |
| 40 | 0.0043 | 0.0001 | 0.0068 | 0.9977 | 0.0528 |
| 50 | 0.0049 | 0.0001 | 0.0074 | 0.9974 | 0.0682 |
| 60 | 0.0069 | 0.0001 | 0.0115 | 0.9936 | 0.0661 |
| 70 | 0.0047 | 0.0001 | 0.0076 | 0.9972 | 0.0532 |
| 80 | 0.0045 | 0.0001 | 0.0068 | 0.9977 | 0.0556 |
| 90 | 0.0043 | 0.0001 | 0.0065 | 0.9980 | 0.0573 |
| 100 | 0.0036 | 0.0001 | 0.0063 | 0.9981 | 0.0404 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esager, M.W.M.; Ünlü, K.D. Forecasting Air Quality in Tripoli: An Evaluation of Deep Learning Models for Hourly PM2.5 Surface Mass Concentrations. Atmosphere 2023, 14, 478. https://doi.org/10.3390/atmos14030478
Esager MWM, Ünlü KD. Forecasting Air Quality in Tripoli: An Evaluation of Deep Learning Models for Hourly PM2.5 Surface Mass Concentrations. Atmosphere. 2023; 14(3):478. https://doi.org/10.3390/atmos14030478
Chicago/Turabian StyleEsager, Marwa Winis Misbah, and Kamil Demirberk Ünlü. 2023. "Forecasting Air Quality in Tripoli: An Evaluation of Deep Learning Models for Hourly PM2.5 Surface Mass Concentrations" Atmosphere 14, no. 3: 478. https://doi.org/10.3390/atmos14030478
APA StyleEsager, M. W. M., & Ünlü, K. D. (2023). Forecasting Air Quality in Tripoli: An Evaluation of Deep Learning Models for Hourly PM2.5 Surface Mass Concentrations. Atmosphere, 14(3), 478. https://doi.org/10.3390/atmos14030478








