Ensemble of Below-Cloud Scavenging Models for Assessing the Uncertainty Characteristics in Wet Raindrop Deposition Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Below-Cloud Scavenging Models
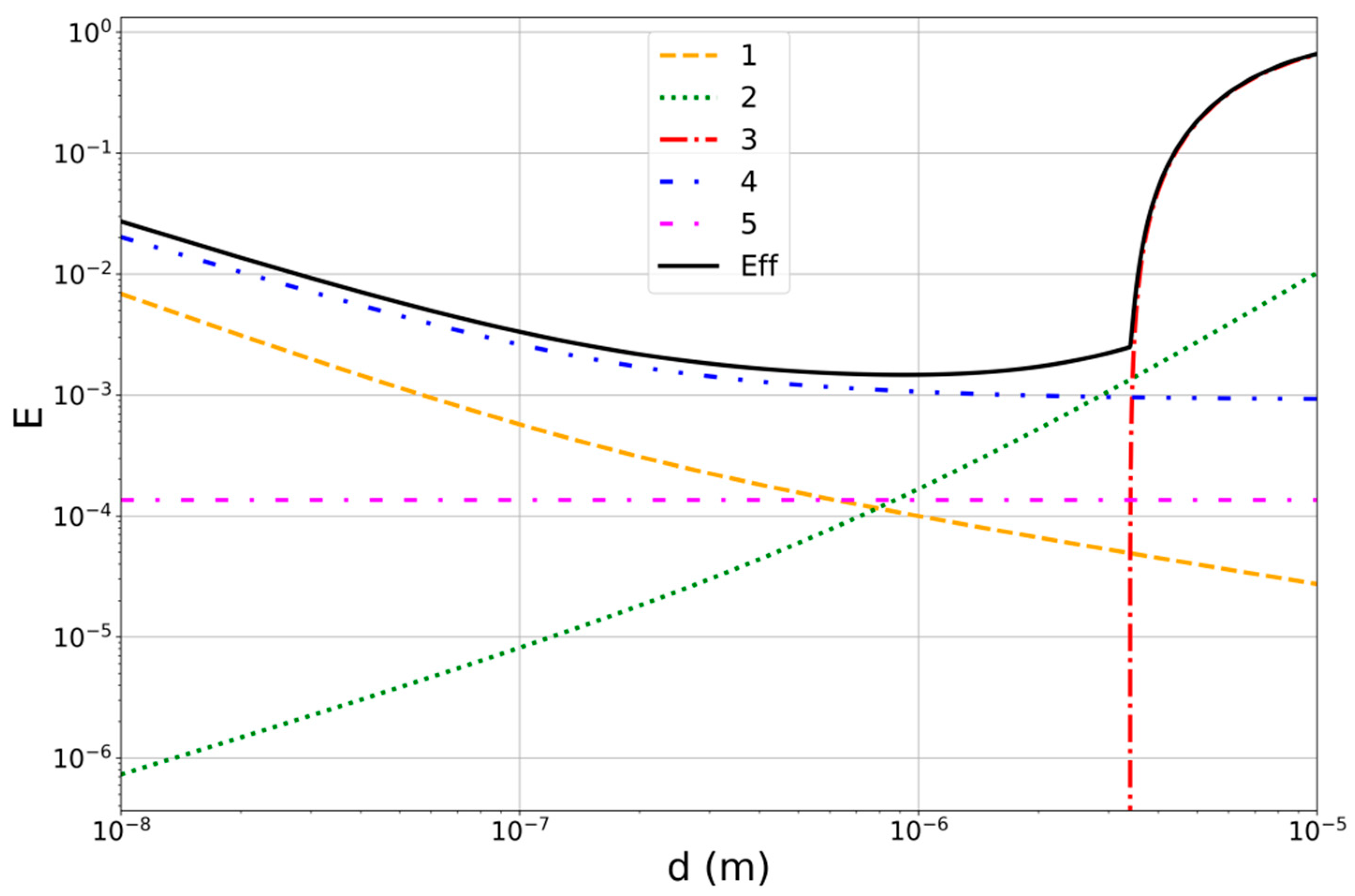
2.1.1. Collision Efficiency E
2.1.2. Terminal (Falling) Velocity V
2.1.3. Raindrop Size Distribution N(D)
2.1.4. Models for Comparison of Concentration Loss for the Integral Spectrum of Aerosol Particles
2.2. Statistics
2.3. Ensemble Verification
2.4. Experimental Data
3. Results and Discussion
3.1. Set of Below-Cloud Scavenging Models
3.2. Partitioning of the Study Area According to Diameter Ranges
3.3. Results of Calculations of Statistical Metrics
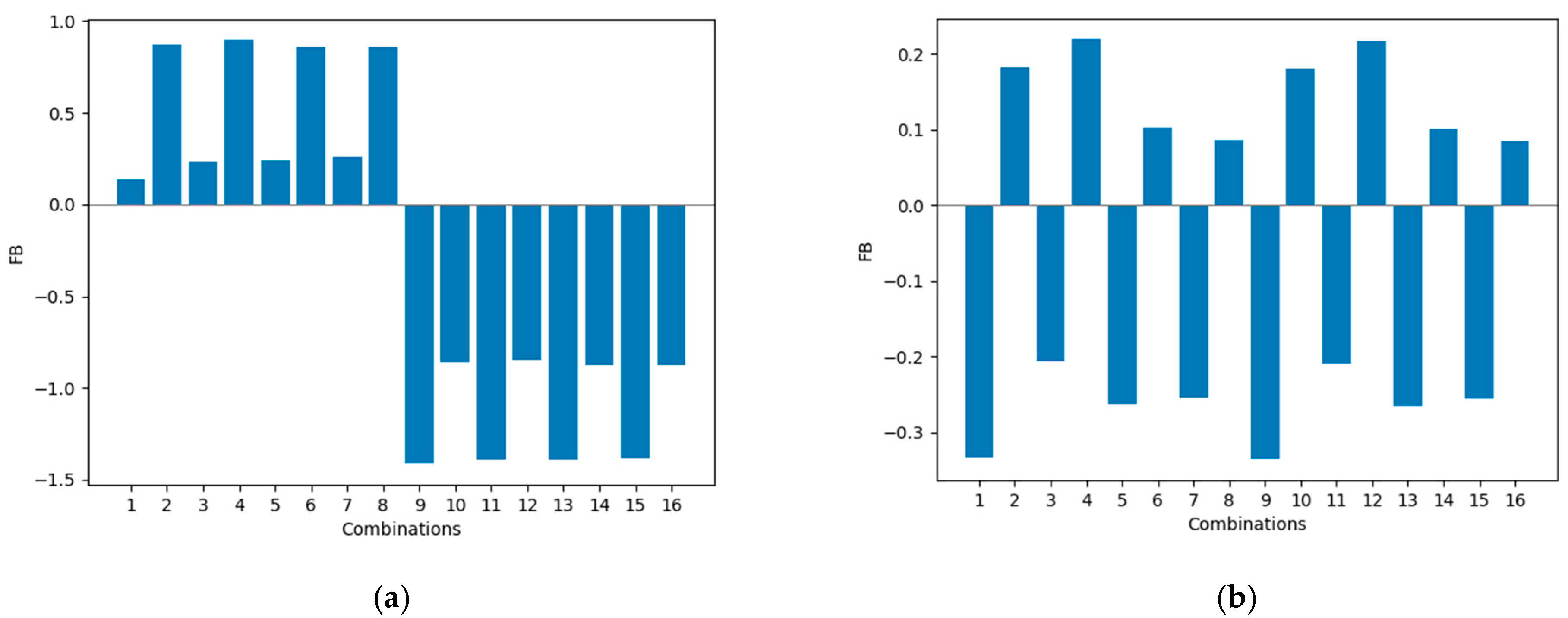
3.4. Construction of Rank Histograms
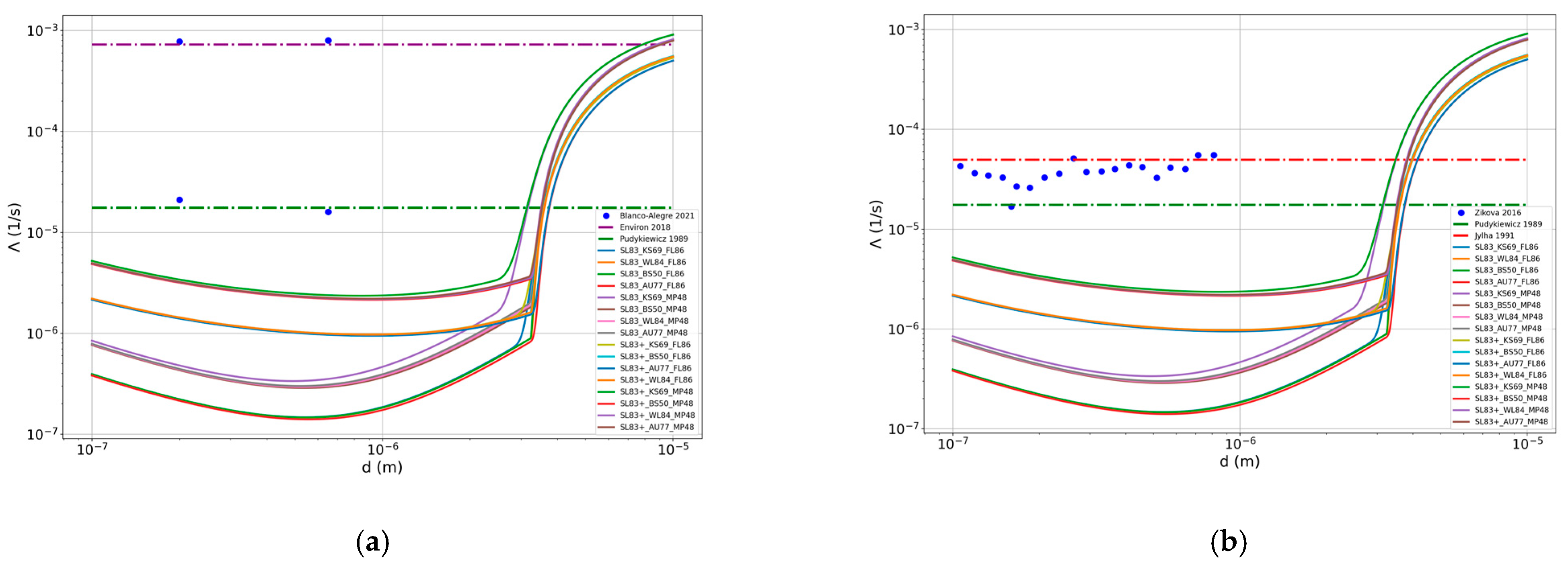
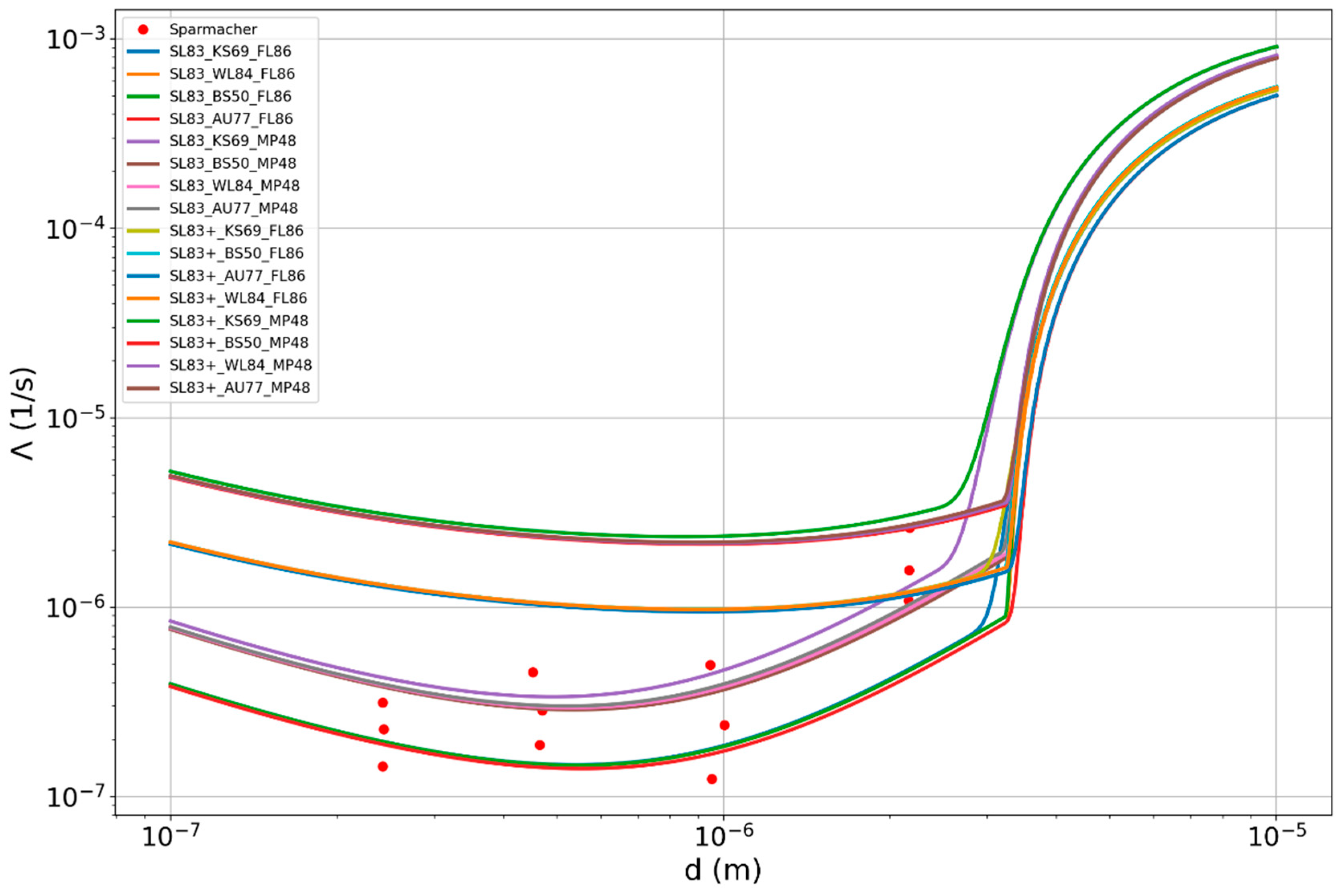
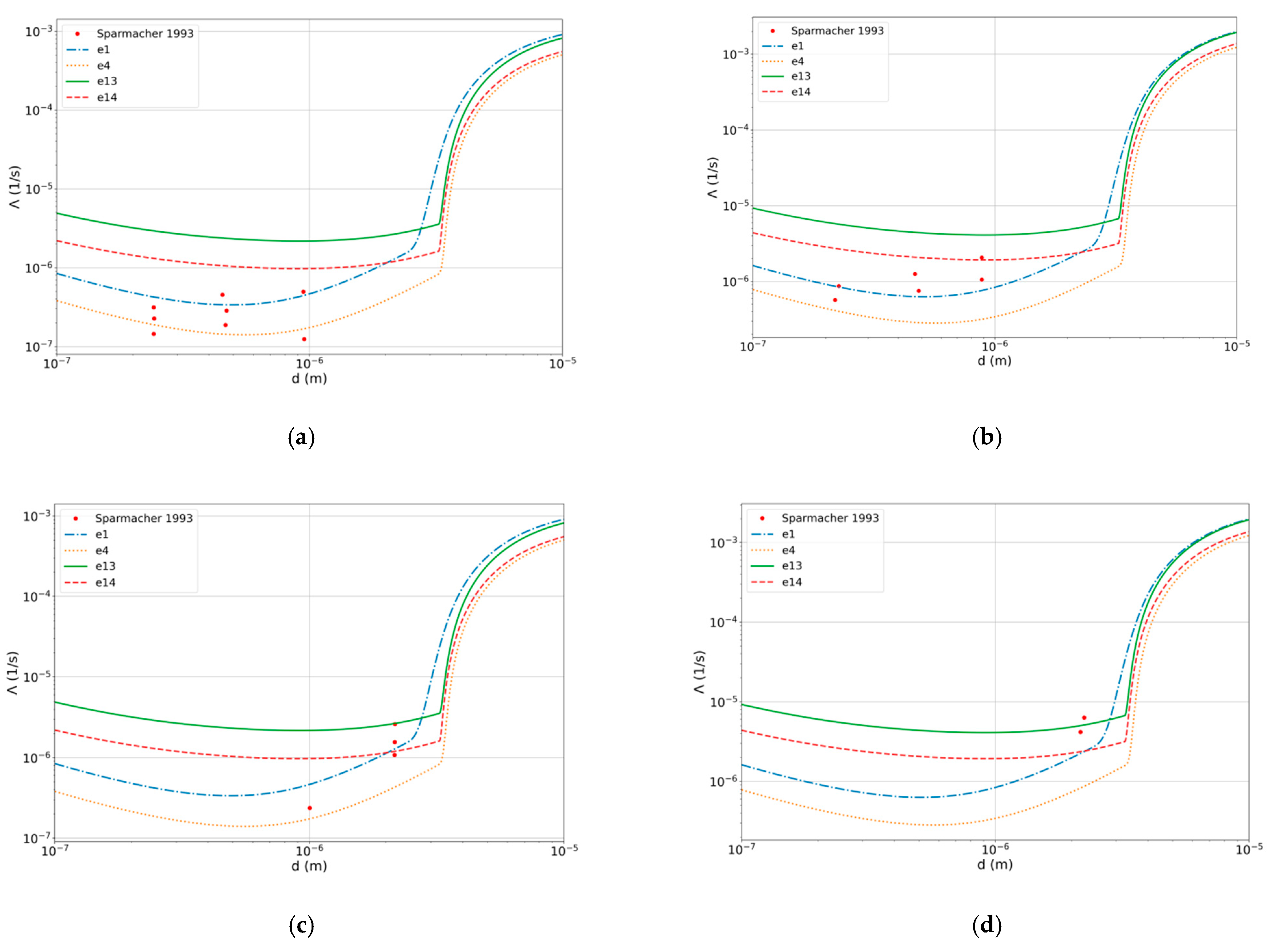
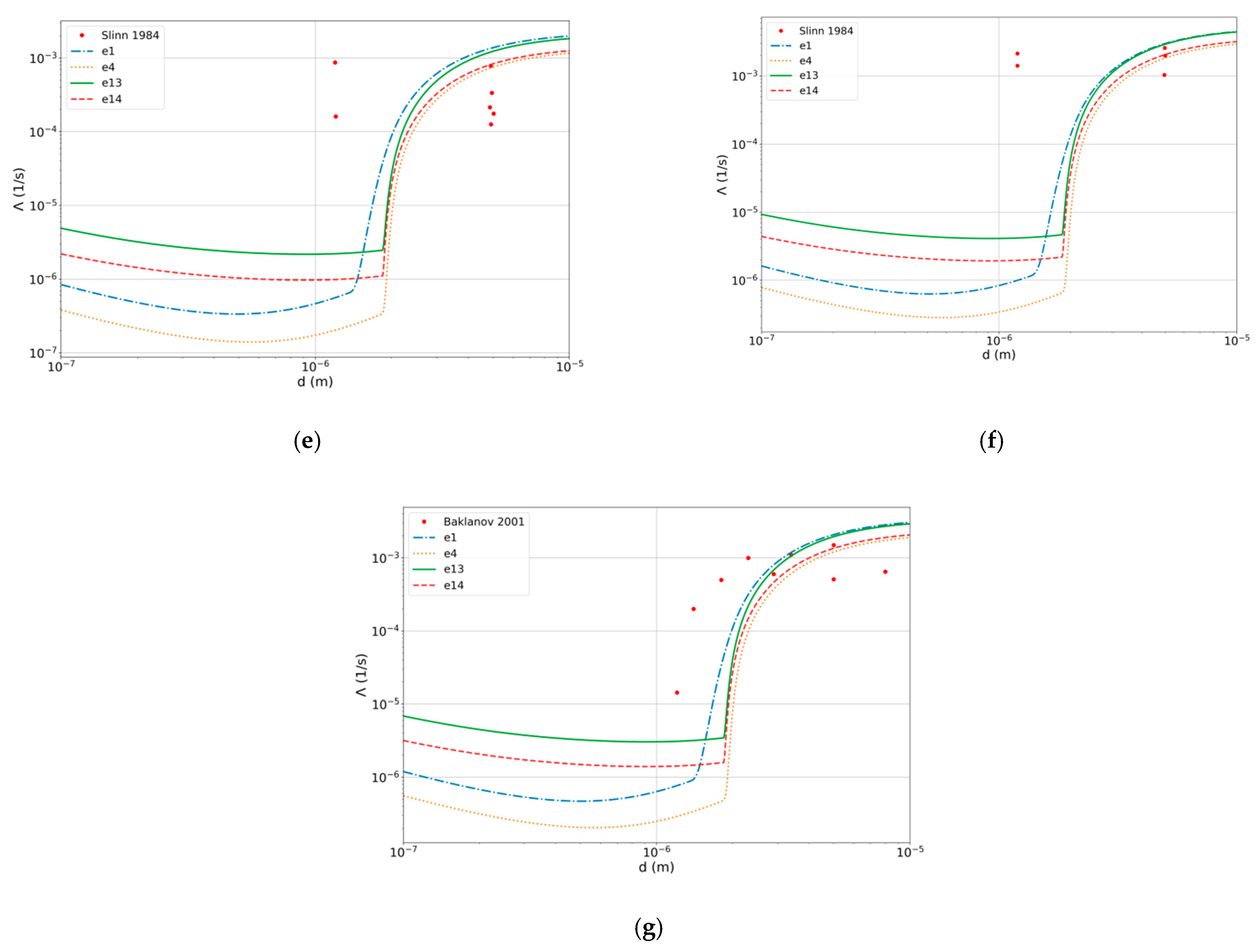
3.5. Comparison of the Results of Model Calculations for the Ensemble with Experimental Data
- Groups of diameters were selected in the experimental data, for which the scavenging value was within the error of the experimental data. This was used to separate the coarse areas from the fine areas;
- Model calculations of the below-cloud scavenging coefficient Λ were carried out for the average diameter of an aerosol particle corresponding to the experiment in the considered group of diameters;
- Then, using the obtained values, the average value and standard deviation was calculated;
- The fractions of the experimental values that fall into the ranges , and were analyzed.
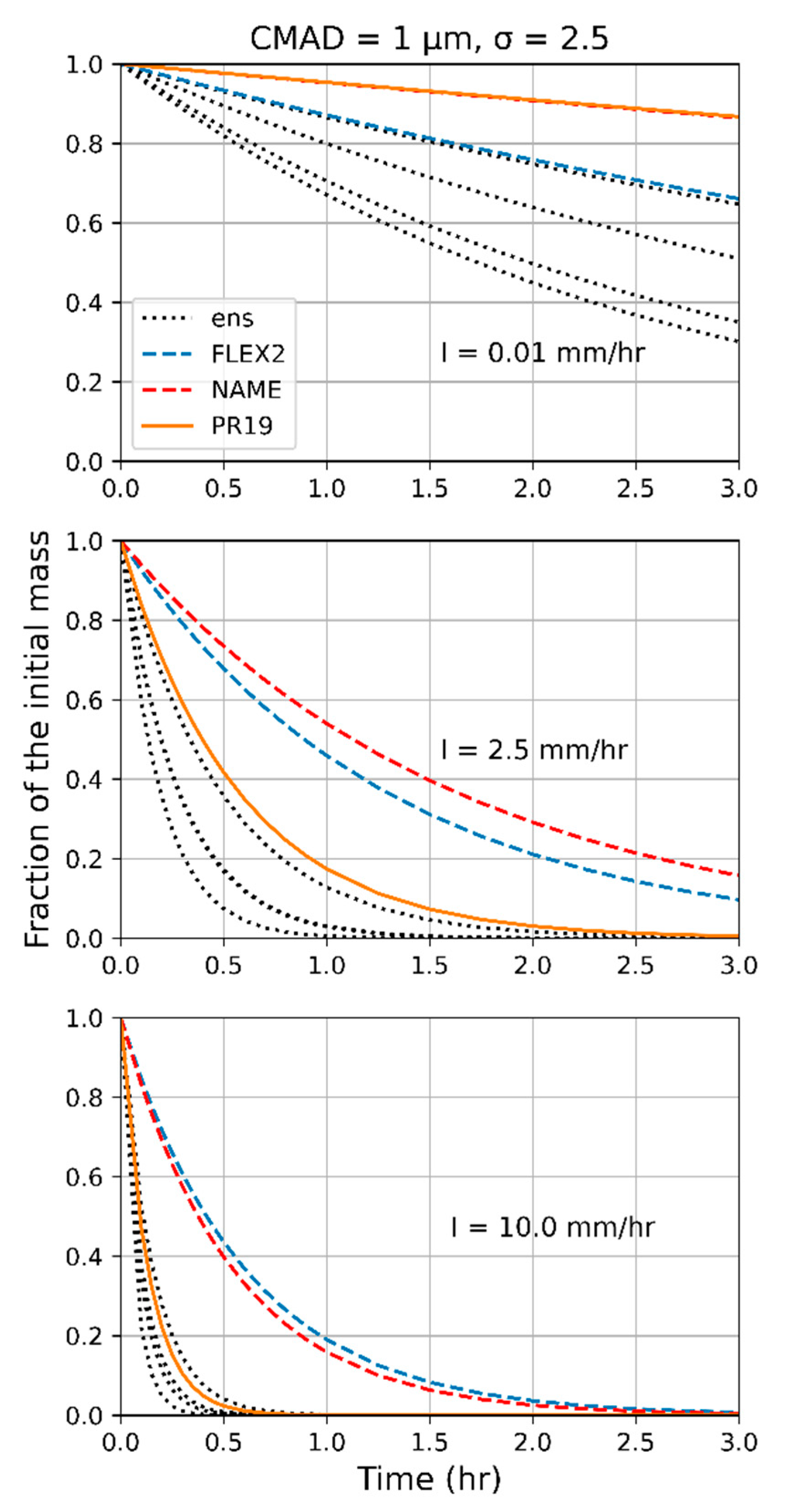
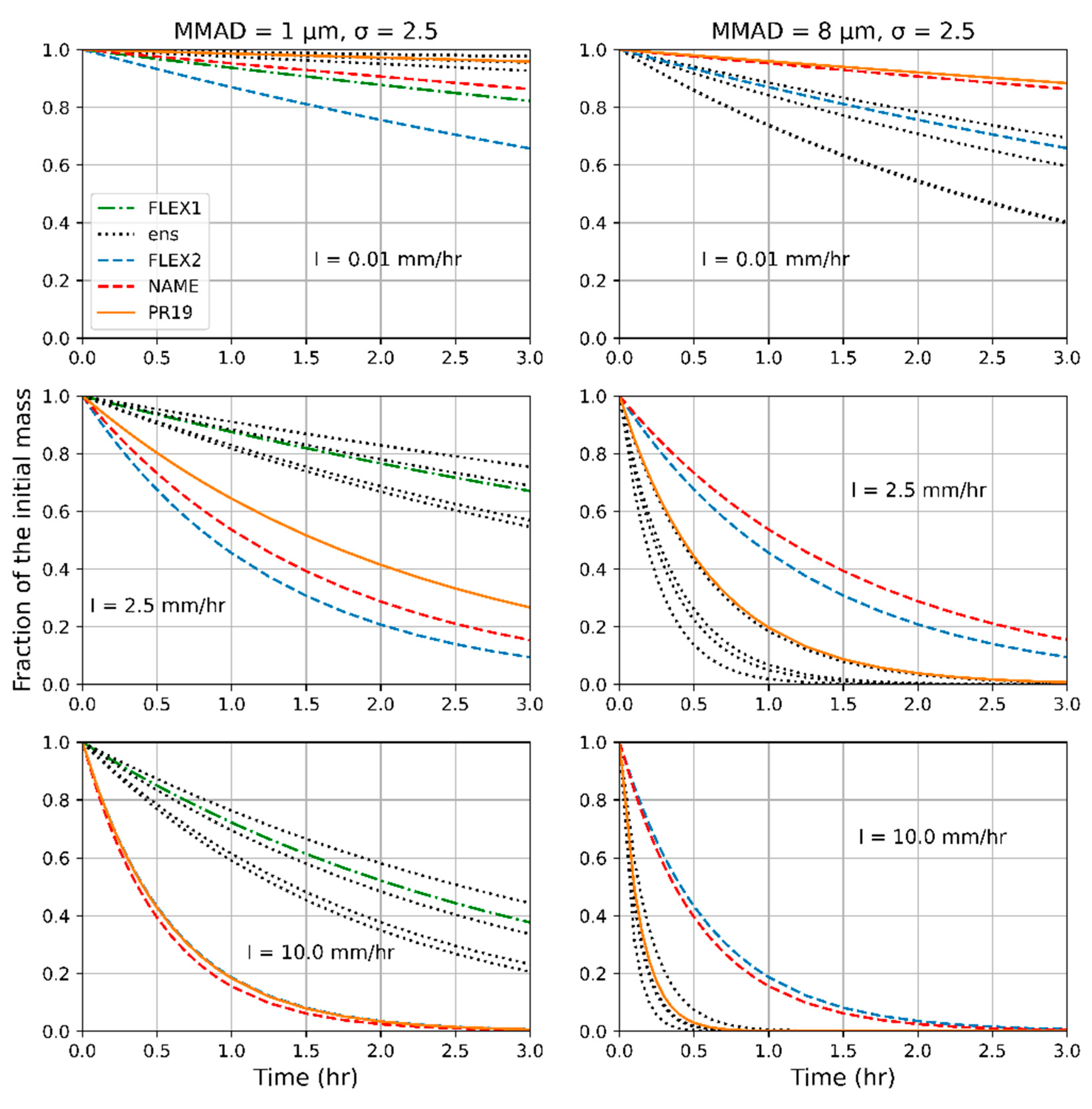
3.6. Calculation of Polydisperse Aerosol Scavenging from a Control Volume
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| µ, μw | Dynamic viscosity of air and water, kg/m·s |
| C(d) | Concentration of aerosol particles with diameter d, 1/m3 |
| Cc | Cunningham correction for aerosol particle glide |
| D | Diameter of a raindrop, m |
| d | Diameter of a particle, m |
| Ddiff | Diffusion coefficient of aerosol particles in air, m2/s |
| Ddiff water | Water vapor diffusion coefficient in the air, m2/s |
| E(D) | Aerosol particle collision efficiency |
| EBr | Efficiency of Brownian diffusion |
| Eine | Efficiency of inertial impaction |
| Eint | Efficiency of interception |
| Edph | Efficiency of diffusiophoresis |
| Eth | Efficiency of thermophoresis |
| H | Vertical size of the reference volume (from 102 to 103 m) |
| I | Rain intensity, mm/hour |
| ka, kp | Thermal conductivity of air, particles, W/m∙K |
| kb | Boltzmann constant, J/K |
| Mw, Ma | Molecular masses of water and air, a.m.u. |
| N(D) | Raindrop size distribution, m−4 |
| n(d) | Volume concentration of raindrops, m−3 |
| P | Normal atmospheric pressure, Pa |
| Pressure of water vapor at temperatures , Pa | |
| Pr | Prandtl number |
| r | Entanglement parameter |
| ReD | Reynolds number calculated for a raindrop with a diameter D |
| Sc | Schmidt number |
| Scw | Schmidt number for water vapor in air |
| St | Stokes number |
| St* | Critical Stokes number |
| t | Interaction time of precipitation and aerosol, s |
| Ta, Ts | Absolute air temperature and absolute temperature of the raindrop surface, K |
| V(D) | Raindrop terminal velocity, m/s |
| v(d) | Particle velocity, m/s |
| α | Partial density of raindrops (varies from 10−5 to 10−10 for raindrops with a size of 0.1–6 mm, respectively) |
| γ | Coefficient depending on the macroscopic parameters of the medium (~1.0) |
| η | Coefficients of inertial diffusion capture and capture due to entanglement |
| Λ | Below-cloud scavenging coefficient, 1/s |
| λa | Rean free path of air molecules, m |
| ν | Rinematic viscosity, m2/s |
| ρa, ρp | Rir density, particle density, kg/m3 |
| τ | Relaxation time of particles, s |
References
- International Atomic Energy Agency. Dispersion of Radioactive Material in Air and Water and Consideration of Population Distribution in Site Evaluation for Nuclear Power Plants; Safety Standards Series No. NS-G-3.2; International Atomic Energy Agency: Vienna, Austria, 2002. [Google Scholar]
- International Atomic Energy Agency. Operations Manual for IAEA Assessment and Prognosis During a Nuclear or Radiological Emergency; Emergency Preparedness and Response; IAEA: Vienna, Austria, 2020. [Google Scholar]
- Wang, Y.; Schmid, F.; Harou, A. Guidelines for Nowcasting Techniques; World Meteorological Organization: Geneva, Switzerland, 2017; ISBN 978-92-63-11198-2. [Google Scholar]
- Chen, X.; Wang, M.; Wang, S.; Chen, Y.; Wang, R.; Zhao, C.; Hu, X. Weather Radar Nowcasting for Extreme Precipitation Prediction Based on the Temporal and Spatial Generative Adversarial Network. Atmosphere 2022, 13, 1291. [Google Scholar] [CrossRef]
- Leadbetter, S.J.; Jones, A.R.; Hort, M.C. Assessing the value meteorological ensembles add to dispersion modelling using hypothetical releases. Atmos. Chem. Phys. 2022, 22, 577–596. [Google Scholar] [CrossRef]
- Bakin, R.I.; Gubenko, I.; Dolganov, K.; Ignatov, R.; Ilichev, E.; Kiselev, A.; Krasnoperov, S.; Konyaev, P.; Rubinshtein, K.; Tomashchik, D. Application of ensemble method to predict radiation doses from a radioactive release during hypothetical severe accidents at Russian NPP. J. Nucl. Sci. Technol. 2020, 58, 635–650. [Google Scholar] [CrossRef]
- Elahi, E.; Khalid, Z.; Tauni, M.Z.; Zhang, H.; Lirong, X. Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, Pakistan. Technovation 2022, 117, 102255. [Google Scholar] [CrossRef]
- Abid, M.; Scheffran, J.; Schneider, U.A.; Elahi, E. Farmer Perceptions of Climate Change, Observed Trends and Adaptation of Agriculture in Pakistan. Environ. Manag. 2019, 63, 110–123. [Google Scholar] [CrossRef] [PubMed]
- COST ES1006; Best Practice Guidelines. COST Action ES1006. University of Hamburg: Hamburg, Germany, 2015.
- Hegarty, J.; Draxler, R.R.; Stein, A.F.; Brioude, J.; Mountain, M.; Eluszkiewicz, J.; Nehrkorn, T.; Ngan, F.; Andrews, A. Evaluation of Lagrangian Particle Dispersion Models with Measurements from Controlled Tracer Releases. J. Appl. Meteorol. Climatol. 2013, 52, 2623–2637. [Google Scholar] [CrossRef]
- Olesen, H.R. User’s Guide to the Model Validation Kit; Research Notes from NERI no. 226; National Environmental Research Institute: Roskilde, Denmark, 2005; p. 72. Available online: http://research-notes.dmu.dk (accessed on 26 January 2023).
- Khan, T.R.; Perlinger, J.A. Evaluation of five dry particle deposition parameterizations for incorporation into atmospheric transport models. Geosci. Model Dev. 2017, 10, 3861–3888. [Google Scholar] [CrossRef]
- Saylor, R.D.; Baker, B.D.; Lee, P.; Tong, D.; Li, P.; Hicks, B.B. The particle dry deposition component of total deposition from air quality models: Right, wrong or uncertain? Tellus B Chem. Phys. Meteorol. 2019, 71, 1550324. [Google Scholar] [CrossRef]
- Wesely, M.L.; Hicks, B.B. A Review of The Current Status of Knowledge on Dry Deposition. Atmos. Environ. 2000, 34, 2261–2282. [Google Scholar] [CrossRef]
- Mun, C.; Cantrel, L.; Madic, C. A Literature Review on Ruthenium Behaviour in Nuclear Power Plant Severe Accidents. Nucl. Technol. 2007, 156, 332–346. [Google Scholar] [CrossRef]
- Paesler-Sauer, J. Comparative Calculations and Validation Studies with Atmospheric Dispersion Models; Kernforschungszentrum Karlsruhe: Karlsruhe, Germany, 1986. [Google Scholar]
- Sportisse, B. A review of parameterizations for modelling dry deposition and scavenging of radionuclides. Atmos. Environ. 2007, 41, 2683–2698. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Moran, M.D. Uncertainty assessment of current size-resolved parameterizations for below-cloud particle scavenging by rain. Atmos. Chem. Phys. 2010, 10, 5685–5705. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. The main regularities of turbulent mixing in the surface layer of the atmosphere. Proc. Geophys. Inst. Acad. Sci. USSR 1954, 151, 163–187. (In Russian) [Google Scholar]
- Piskunov, V.N. Parameterization of Aerosol Dry Deposition Velocities onto Smooth and Rough Surfaces. J. Aerosol Sci. 2009, 40, 664–679. [Google Scholar] [CrossRef]
- Fang, S.; Zhuang, S.; Goto, D.; Hu, X.; Sheng, L.; Huang, S. Coupled modeling of in- and below-cloud wet deposition for atmospheric 137Cs transport following the Fukushima Daiichi accident using WRF-Chem: A self-consistent evaluation of 25 scheme combinations. Environ. Int. 2022, 158, 106882. [Google Scholar] [CrossRef]
- Ulimoen, M.; Berge, E.; Klein, H.; Salbu, B.; Lind, O.C. Comparing model skills for deterministic versus ensemble dispersion modelling: The Fukushima Daiichi NPP accident as a case study. Sci. Total Environ. 2022, 806, 150128. [Google Scholar] [CrossRef]
- Leadbetter, S.J.; Andronopoulos, S.; Bedwell, P.; Chevalier-Jabet, K.; Geertsema, G.; Gering, F.; Hamburger, T.; Jones, A.; Klein, H.; Korsakissok, I.; et al. Ranking uncertainties in atmospheric dispersion modelling following the accidental release of radioactive material. Radioprotection 2020, 55, S51–S55. [Google Scholar] [CrossRef]
- Galmarinia, S.; Bianconi, R.; Klug, W.; Mikkelsen, T.; Addis, R.; Andronopoulos, S.; Astrup, P.; Baklanov, A.; Bartniki, J.; Bartzis, J.C.; et al. Ensemble dispersion forecasting—Part I: Concept, approach and indicators. Atmos. Environ. 2004, 38, 4607–4617. [Google Scholar] [CrossRef]
- Sorensen, J.H.; Amstrup, B.; Feddersen, H.; Bartnicki, J.; Klein, H.; Simonsen, M.; Lauritzen, B.; Cordt Hoe, S.; Israelson, C.; Lindgren, J. Fukushima Accident: UNcertainty of Atmospheric Dispersion Modelling (FAUNA); NKS Secretariat: Roskilde, Denmark, 2016; p. 43. ISBN 978-87-7893-421-5. [Google Scholar]
- Straume, A.G.; Koffi, E.N.; Nodop, K. Dispersion Modeling Using Ensemble Forecasts Compared to ETEX Measurements. J. Appl. Meteorol. 1998, 37, 1444–1456. [Google Scholar] [CrossRef]
- Perillat, R.; Korsakissok, I.; Mallet, V.; Mathieu, A.; Sekiyama, T.; Kajino, M.; Adachi, K.; Igarashi, Y.; Didier, D. Using meteorological ensembles for atmospheric dispersion modelling of the Fukushima nuclear accident. In Proceedings of the 18th International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Bologna, Italy, 9–12 October 2017. [Google Scholar]
- Kajino, M.; Sekiyama, T.T.; Mathieu, A.; Korsakissok, I.; Périllat, R.; Quélo, D.; Quérel, A.; Saunier, O.; Adachi, K.; Girard, S.; et al. Lessons learned from atmospheric modeling studies after the Fukushima nuclear accident: Ensemble simulations, data assimilation, elemental process modeling, and inverse modeling. Geochem. J. 2018, 52, 85–101. [Google Scholar] [CrossRef]
- Kajino, M.; Sekiyama, T.T.; Igarashi, Y.; Katata, G.; Sawada, M.; Adachi, K.; Zaizen, Y.; Tsuruta, H.; Nakajima, T. Deposition and dispersion of radio-cesium released due to the Fukushima nuclear accident: Sensitivity to meteorological models and physical modules. J. Geophys. Res. Atmos. 2019, 124, 1823–1845. [Google Scholar] [CrossRef]
- Yegnan, A.; Williamson, D.G.; Graettinger, A.J. Uncertainty analysis in air dispersion modeling. Environ. Model. Softw. 2002, 17, 639–649. [Google Scholar] [CrossRef]
- Mandal, S.; Madhipatla, K.K.; Guttikunda, S.; Kloog, I.; Prabhakaran, D.; Schwartz, J.D. GeoHealth Hub India Team, Ensemble averaging based assessment of spatiotemporal variations in ambient PM2.5 concentrations over Delhi, India, during 2010–2016. Atmos. Environ. 2020, 224, 117309. [Google Scholar] [CrossRef] [PubMed]
- Webster, H.; Thomson, D. The NAME wet deposition scheme Forecasting Research. Tech. Rep. 2014, 584, 41. [Google Scholar]
- Pisso, I.; Sollum, E.; Grythe, H.; Kristiansen, N.I.; Cassiani, M.; Eckhardt, S.; Arnold, D.; Morton, D.; Thompson, R.L.; Zwaaftink, C.D.G.; et al. The Lagrangian particle dispersion model FLEXPART version 10.4. Geosci. Model Dev. 2019, 12, 4955–4997. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 900–929. [Google Scholar]
- Slinn, W.G.N. Precipitation scavenging. In Atmospheric Sciences and Power Production—1979, Chap. 11; Division of Biomedical Environmental Research, U.S. Department of Energy: Washington, DC, USA, 1983. [Google Scholar]
- Andronache, C.; Grönholm, T.; Laakso, L.; Phillips, V.; Venäläinen, A. Scavenging of ultrafine particles by rainfall at a boreal site: Observations and model estimations. Atmos. Chem. Phys. 2006, 6, 4739–4754. [Google Scholar] [CrossRef]
- Pripachkin, D.A.; Budyka, A.K. Influence of the parameters of aerosol particles on their scavenging from the atmosphere by raindrops, Izvestiya RAN. Phys. Atmos. Ocean. 2020, 56, 203–209. (In Russian) [Google Scholar]
- Montgomery, R.B. Viscosity And Thermal Conductivity Of Air And Diffusivity Of Water Vapor In Air. J. Atmos. Sci. 1947, 4, 193–196. [Google Scholar] [CrossRef]
- Bae, S.Y.; Jung, C.H.; Kim, Y.P. Relative contributions of individual phoretic effect in the below-cloud scavenging process. J. Aerosol Sci. 2009, 40, 621–632. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrop with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Feingold, G.; Levin, Z. The lognormal fit to raindrop spectra from frontal convective clouds in Israel. J. Clim. Appl. Meteorol. 1986, 25, 1346–1363. [Google Scholar] [CrossRef]
- Laakso, L. Ultrafine particle scavenging coefficients calculated from 6 years field measurements. Atmos. Environ. 2003, 37, 3605–3613. [Google Scholar] [CrossRef]
- Anctil, F.; Ramos, M.H. Verification Metrics for Hydrological Ensemble Forecasts; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Sparmacher, H.; Fülber, K.; Bonka, H. Below-cloud scavenging of aerosol particles: Particle-bound radionuclides—Experimental. Atmos. Environ. 1993, 27A, 605–618. [Google Scholar] [CrossRef]
- Baklanov, B.; Sørensen, J.H. Parameterization of radionuclides deposition in atmospheric long-range transport modelling. Phys. Chem. Earth B 2001, 26, 787–799. [Google Scholar] [CrossRef]
- Blanco-Alegre, C.; Calvo, A.; Castro, A.; Oduber, F.; Alonso-Blanco, E.; Fraile, R. Scavenging of submicron aerosol particles in a suburban atmosphere: The raindrop size factor. Environ. Pollut. 2021, 285, 117371. [Google Scholar] [CrossRef]
- Zikova, N.; Zdimal, V. Precipitation scavenging of aerosol particles at a rural site in the Czech Republic. Tellus B Chem. Phys. Meteorol. 2016, 68, 27343. [Google Scholar] [CrossRef]
- Gonfiotti, B.; Paci, S. Stand-alone containment analysis of Phébus FPT tests with ASTEC and MELCOR codes: The FPT-2 test. Heliyon 2018, 4, e00553. [Google Scholar] [CrossRef]
- Met Office: National Meteorological Library and Archive. Fact Sheet No. 3—Water in the Atmosphere; Met Office: Devon, UK, 2007. [Google Scholar]
- Jylhä, K. Relationship between the Scavenging Coefficient for Pollutants in Precipitation and the Radar Reflectivity Factor. Part I: Derivation. J. Appl. Meteorol. 1999, 38, 1421–1434. [Google Scholar] [CrossRef]
- User’s Guide Comprehensive Air Quality Model with Extensions Version 7.10; Ramboll Environment and Health: Copenhagen, Denmark, 2020.
- Pudykiewicz, J. Simulation of the Chernobyl dispersion with a 3-D hemispheric tracer model. Tellus 1989, 41B, 391–412. [Google Scholar] [CrossRef]
- Jones, C.; Hill, A.; Hemmings, J.; Lemaitre, P.; Quérel, A.; Ryder, C.L.; Woodward, S. Below-cloud scavenging of aerosol by rain: A review of numerical modelling approaches and sensitivity simulations with mineral dust in the Met Office’s Unified Model. Atmos. Chem. Phys. 2022, 22, 11381–11407. [Google Scholar] [CrossRef]
- Ogorodnikov, B.I.; Budyka, A.K.; Pavlyuchenko, N.I. Observation of radioactive aerosol emissions from the sarcophagus at the chernobyl nuclear power plant. At. Energy 2004, 96, 202–213. [Google Scholar] [CrossRef]
- Dorrian, M.; Bailey, M. Particle size distributions of radioactive aerosols measured in workplaces. Radiat. Prot. Dosim. 1995, 60, 119–133. [Google Scholar] [CrossRef]
- Sugiyama, G.; Gowardhan, A.; Simpson, M.; Nasstrom, J. Deposition Velocity Methods for DOE Site Safety Analyses; Lawrence Livermore National Lab.: Livermore, CA, USA, 2014. [Google Scholar]
- Telly Bah, O.; Hebert, D.; Connan, O.; Solier, L.; Laguionie, P.; Bourlès, D.; Maro, D. Measurement and modelling of gaseous elemental iodine (I2) dry deposition velocity on grass in the environment. J. Environ. Radioact. 2020, 219, 106253. [Google Scholar] [CrossRef] [PubMed]




| Kessler 1969 | |
| Atlas 1977 | |
| Willis 1984 | |
| Best 1950 |
| N | Source | Precipitation Intensity, mm/h | Density of Aerosol Particles, g/cm3 | Coefficient Λ, 1/s |
|---|---|---|---|---|
| 1 | Sparmacher 0.1 ≤ dp ≤ 1.0 µm | 2.0–5.0 | 1.0 | (1.4–4.9) × 10−7 |
| 2 | 5.0–12.0 | (0.6–2.0) × 10−6 | ||
| 3 | Sparmacher 1.0 ≤ dp ≤ 10.0 µm | 2.0–5.0 | 1.0 | (0.2–2.6) × 10−6 |
| 4 | 5.0–12.0 | (4.2–6.2) × 10−6 | ||
| 5 | Slinn 1.0 ≤ dp ≤ 10.0 µm | 2.0–5.0 | 3.0 * | (1.6–8.6) × 10−4 |
| 6 | 5.0–12.0 | (1.0–2.1) × 10−3 | ||
| 7 | Baklanov 1.0 ≤ dp ≤ 10.0 µm | 5.0 | 3.0 * | (0.1–15.0) × 10−4 |
| 8 | Blanco-Alegre 0.1 ≤ dp ≤ 1.0 µm | 1.0–3.0 | 1.0 ** | (0.2–8.0) × 10−5 |
| 9 | Zikova 0.1 ≤ dp ≤ 1.0 µm | 2.0–5.0 *** | 1.0 ** | (1.7–5.5) × 10−5 |
| N | Collision Efficiency | Distribution of Raindrops | Terminal Raindrop Velocity | N | Collision Efficiency | Distribution of Raindrops | Terminal Raindrop Velocity |
|---|---|---|---|---|---|---|---|
| 1 | SL83 | MP48 | KS69 | 9 | SL83+ | MP48 | KS69 |
| 2 | SL83 | FL86 | KS69 | 10 | SL83+ | FL86 | KS69 |
| 3 | SL83 | MP48 | AU77 | 11 | SL83+ | MP48 | AU77 |
| 4 | SL83 | FL86 | AU77 | 12 | SL83+ | FL86 | AU77 |
| 5 | SL83 | MP48 | WL84 | 13 | SL83+ | MP48 | WL84 |
| 6 | SL83 | FL86 | WL84 | 14 | SL83+ | FL86 | WL84 |
| 7 | SL83 | MP48 | BS50 | 15 | SL83+ | MP48 | BS50 |
| 8 | SL83 | FL86 | BS50 | 16 | SL83+ | FL86 | BS50 |
| N | Collision Efficiency | Distribution of Raindrops | Terminal Raindrop Velocity | FB (Fine) | FB (Coarse) | Pearson (Fine) | Pearson (Coarse) | FAC5 (Fine) | FAC5 (Coarse) | FAC10 (Fine) | FAC10 (Coarse) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | SL83 | MP48 | KS69 | 0.14 | −0.33 | 0.68 | 0.50 | 1.00 | 0.63 | 1.00 | 0.70 |
| 2 | SL83 | FL86 | KS69 | 0.88 | 0.18 | 0.61 | 0.50 | 0.93 | 0.59 | 1.00 | 0.74 |
| 3 | SL83 | MP48 | AU77 | 0.23 | −0.21 | 0.64 | 0.51 | 1.00 | 0.59 | 1.00 | 0.74 |
| 4 | SL83 | FL86 | AU77 | 0.90 | 0.22 | 0.61 | 0.51 | 0.93 | 0.59 | 1.00 | 0.70 |
| 5 | SL83 | MP48 | WL84 | 0.24 | −0.26 | 0.65 | 0.51 | 1.00 | 0.63 | 1.00 | 0.74 |
| 6 | SL83 | FL86 | WL84 | 0.86 | 0.10 | 0.63 | 0.52 | 0.93 | 0.59 | 1.00 | 0.74 |
| 7 | SL83 | MP48 | BS50 | 0.26 | −0.25 | 0.64 | 0.52 | 1.00 | 0.63 | 1.00 | 0.74 |
| 8 | SL83 | FL86 | BS50 | 0.86 | 0.09 | 0.63 | 0.52 | 0.93 | 0.59 | 1.00 | 0.74 |
| 9 | SL83+ | MP48 | KS69 | −1.41 | −0.34 | 0.54 | 0.50 | 0.29 | 0.63 | 0.64 | 0.74 |
| 10 | SL83+ | FL86 | KS69 | −0.86 | 0.18 | 0.55 | 0.50 | 0.71 | 0.67 | 1.00 | 0.74 |
| 11 | SL83+ | MP48 | AU77 | −1.39 | −0.21 | 0.54 | 0.51 | 0.29 | 0.59 | 0.64 | 0.78 |
| 12 | SL83+ | FL86 | AU77 | −0.85 | 0.22 | 0.55 | 0.51 | 0.71 | 0.67 | 1.00 | 0.70 |
| 13 | SL83+ | MP48 | WL84 | −1.39 | −0.26 | 0.54 | 0.51 | 0.29 | 0.63 | 0.64 | 0.78 |
| 14 | SL83+ | FL86 | WL84 | −0.87 | 0.10 | 0.56 | 0.52 | 0.71 | 0.67 | 1.00 | 0.74 |
| 15 | SL83+ | MP48 | BS50 | −1.38 | −0.26 | 0.54 | 0.52 | 0.29 | 0.63 | 0.64 | 0.78 |
| 16 | SL83+ | FL86 | BS50 | −0.88 | 0.08 | 0.56 | 0.52 | 0.71 | 0.67 | 1.00 | 0.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiselev, A.; Osadchiy, A.; Shvedov, A.; Semenov, V. Ensemble of Below-Cloud Scavenging Models for Assessing the Uncertainty Characteristics in Wet Raindrop Deposition Modeling. Atmosphere 2023, 14, 398. https://doi.org/10.3390/atmos14020398
Kiselev A, Osadchiy A, Shvedov A, Semenov V. Ensemble of Below-Cloud Scavenging Models for Assessing the Uncertainty Characteristics in Wet Raindrop Deposition Modeling. Atmosphere. 2023; 14(2):398. https://doi.org/10.3390/atmos14020398
Chicago/Turabian StyleKiselev, Alexey, Alexander Osadchiy, Anton Shvedov, and Vladimir Semenov. 2023. "Ensemble of Below-Cloud Scavenging Models for Assessing the Uncertainty Characteristics in Wet Raindrop Deposition Modeling" Atmosphere 14, no. 2: 398. https://doi.org/10.3390/atmos14020398
APA StyleKiselev, A., Osadchiy, A., Shvedov, A., & Semenov, V. (2023). Ensemble of Below-Cloud Scavenging Models for Assessing the Uncertainty Characteristics in Wet Raindrop Deposition Modeling. Atmosphere, 14(2), 398. https://doi.org/10.3390/atmos14020398





